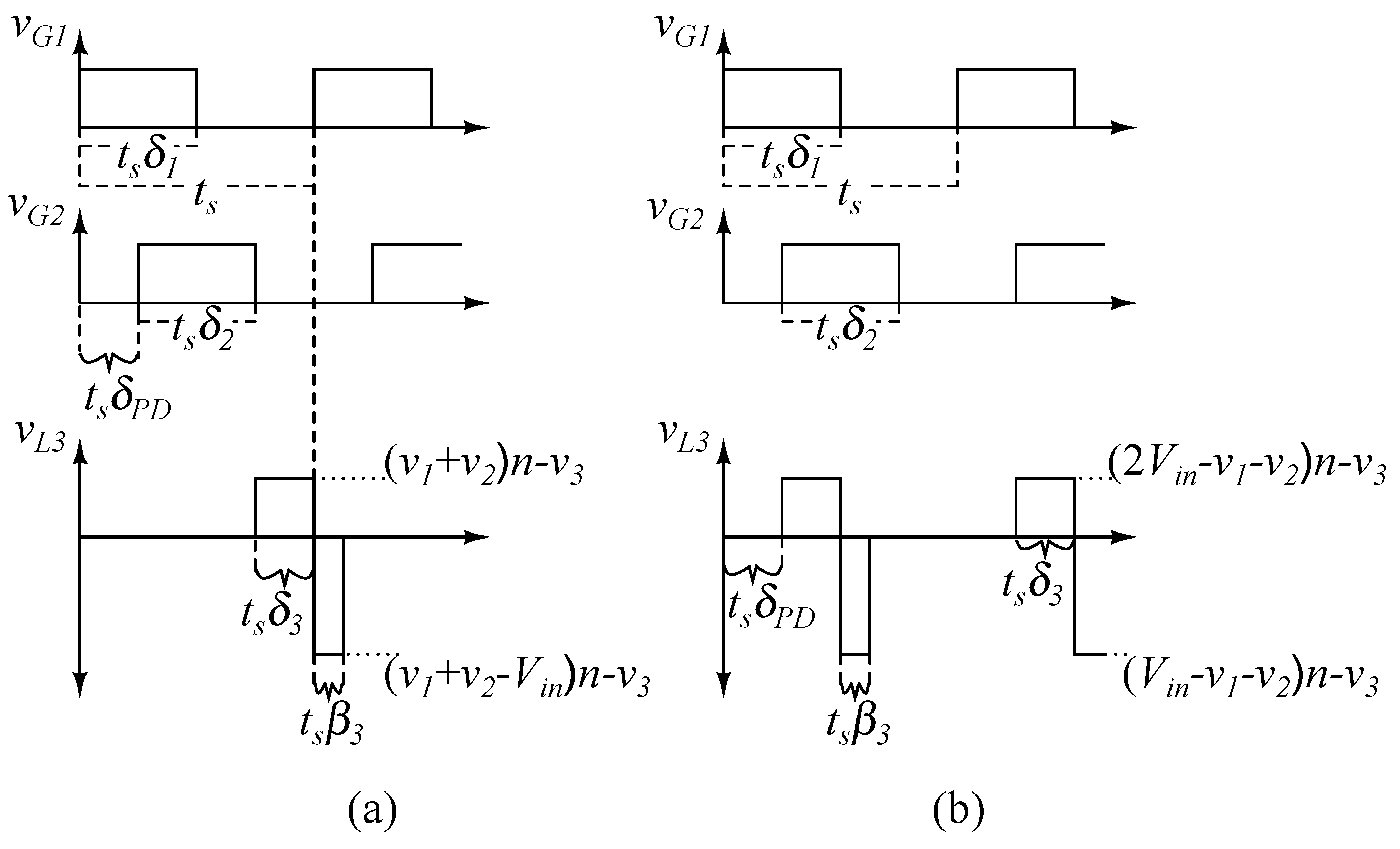Multiple-Output DC-DC Converters with a Reduced Number of Active and Passive Components

Abstract

Multiple-output converters have been widely used where individual outputs are required. Compared with conventional separate converters, the advantage of multiple outputs is to have a lower number of active and passive components. In this paper, first, a pulse-width-modulation (PWM)-pulse-frequency-modulation (PFM) method is used for two-output converters that have only one coil and one active switch. Secondly, three-output converter topologies are proposed where the third output is controlled by phase delay (PD). These converters need only two coils and two active switches to regulate three outputs. How to obtain PD at different switching frequencies is discussed next, and a PWM-PFM-PD controlled five-output buck converter is presented. The proposed solution uses only two active switches and two magnetic cores to adjust five-output voltages independently. A modeling and digital control method are proposed in order to regulate the five output voltages. A prototype circuit with independent 15 V/1.5 A, 12 V/1.5 A, 5 V/0.8 A, −5 V/0.6 A and 3.3 V/0.45 A outputs is assembled to validate the analysis, and it was proved that it regulates the output voltages at different loads.

1. Introduction

The size and cost of a multiple output converter can be less than that of separate converters. However, one of the main drawbacks of a multiple output converter is its cross regulation. One way to obtain multiple outputs is to have a single power converter such as a flyback or forward converter with multiple secondary windings. Usually, these converters regulate only the output that is defined as the master one; the other outputs depend on the load conditions [1]. If there are no conduction losses and no leakage inductance, closed-loop regulation of the master output will regulates all the outputs in continuous conduction mode (CCM) [1]. However, perfect cross-regulation in real life may not be easy to achieve. Therefore, post regulators are applied to adjust the additional outputs [2,3].

The single-switch pulse-width modulation (PWM)-pulse-frequency modulation (PFM) converter uses PFM in order to regulate the second output voltage [4,5]. This converter has two separate inductors. One of the output circuits operates in CCM, while the other operates in discontinuous conduction mode (DCM). Both outputs can be controlled independently by orthogonally modulating both the duty cycle and the switching frequency of the single active switch. The work described in [6] is based on such a PWM-PFM method, however, instead of DCM, the second output is controlled in zero-current-switching (ZCS) quasi-resonant (QR) mode. A further PWM-phase delay (PD) control method produces a regulated third output [7,8]. In this case, two active switches are required. The active switches are operated at the same switching frequency, which is a requirement for implementing PD, and the PD then makes it easy to adjust the third-output voltage. Some researchers have used the PWM-PFM and PWM-PD methods with isolated dc-dc converters [9,10,11,12]. However, extra active switches are required to implement these converters. The study reported in [13] outlines a PWM-PFM-PD control method, but the converter can adjust only three-output voltages.

Firstly, the PWM-PFM method for two-output converters that have only one coupled inductor and one active switch is described. Next, a three-output converter topology is proposed in which the third output is controlled by PD. Subsequently, PWM-PFM and PWM-PD methods are merged, and a PWM-PFM-PD method is proposed to control a five-output converter [14]. Finally, alternative PWM-PFM-PD controlled five-output converter topologies are proposed. The proposed solutions use only two active switches and two magnetic cores to adjust five-output voltages independently. Two active switches have five independent control parameters, i.e., duty cycle ${\displaystyle {\delta }_1}$ and switching frequency ${\displaystyle f_1}$ of the first gate signal, duty cycle ${\displaystyle {\delta }_2}$ and switching frequency ${\displaystyle f_2}$ of the second gate signal, and finally phase delay ${\displaystyle {\delta }_{PD}}$ between the first and the second gate signals. Two of the outputs are adjusted using PWM in CCM, while the other two use PFM in DCM, and the fifth load is regulated by PD. Using “burst mode” in one of the two switches enables the use of PD operation for signals that do not have the same frequency. This technique creates the opportunity to regulate five outputs with a significantly reduced number of active and passive components.

Section 2 presents PWM-PFM controlled two-output converters. Then, Section 3 describes PWM-PD controlled three-output converters and Section 4 shows PWM-PFM-PD controlled five-output converters. Each section has design criteria and experimental results of the converters. Also, Section 4 has a comparison between the proposed five-output converter and other multiple converters. Section 5 explains how to model the five-output converter and Section 6 presents a control method to regulate five output voltages and its experimental results. Conclusions are given in Section 7.

2. PWM-PFM Controlled Two-Output Converters

The PWM-PFM method for two-output dc-dc converters with one active switch is introduced in [4]. In the paper, one output is controlled by PWM and the other by PFM. One of the inductors is designed for CCM, and the other for DCM. While the duty cycle of the switch determines both output voltages, its switching frequency only adjusts the output voltage in DCM. Hence both output voltages can be regulated independently, subject to DCM constraints.

Another way to obtain auxiliary outputs without using additional active switches is to place multiple windings onto the inductor of a buck converter [15,16]. The primary of the coupled inductor is used for the first output, and the secondary voltage is rectified and filtered to create a second output. This second output depends on the turns ratio of the coupled inductor, n. The polarity of the coupled inductor determines whether energy is transferred to the secondary in flyback or forward mode.

The first output is regulated by the PWM of the active switch, while a zener diode or a linear regulator is often included on the secondary side to regulate the second output voltage [2,3]. These methods reduce the efficiency of the converter.

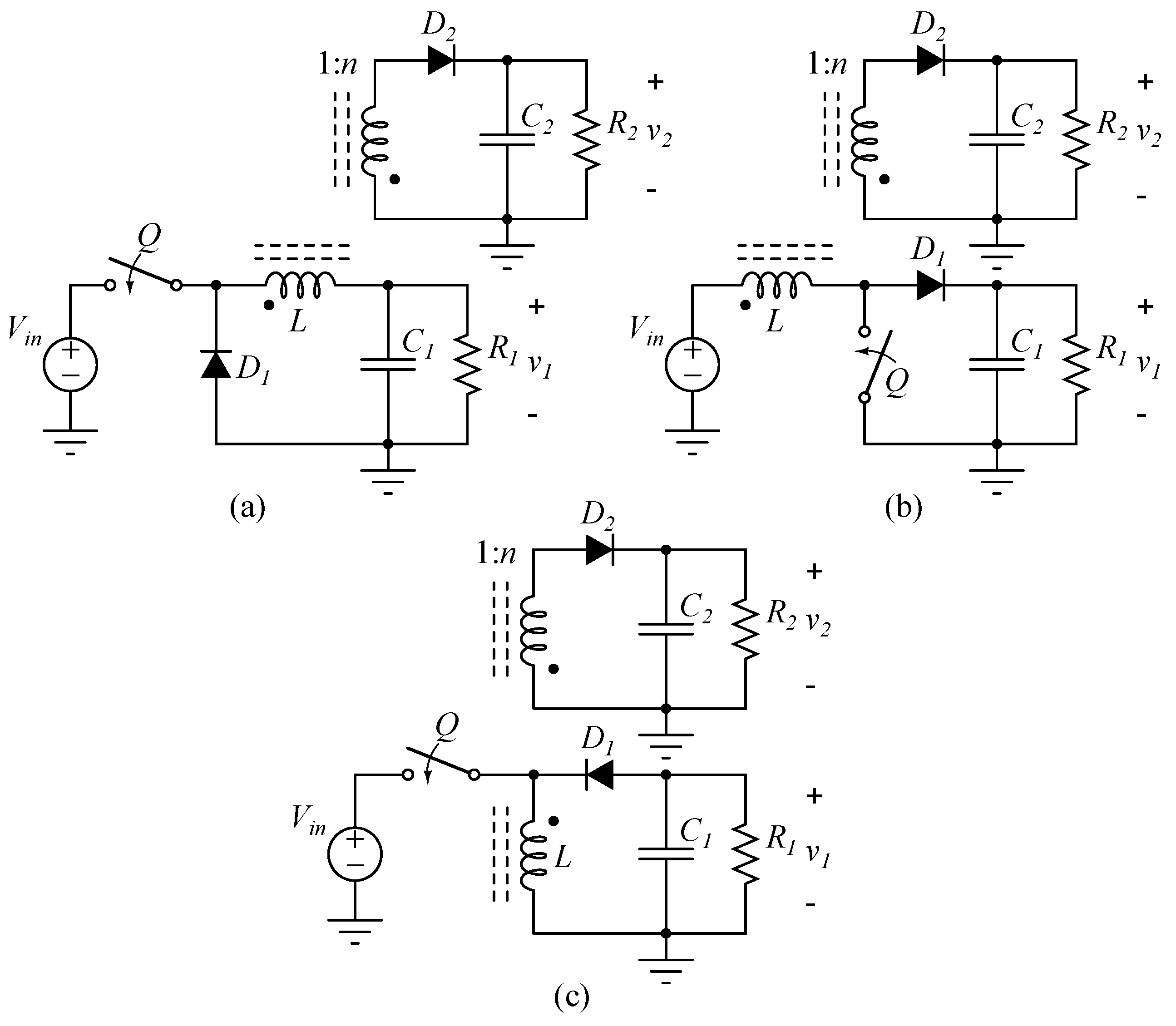
PFM can be used as a control parameter to regulate the second output when it is operated in DCM. The magnetizing inductance of the coupled inductor is used for the PWM output, and the leakage inductance is used for the PFM output. The two-output buck converters that are shown in Figure 1a are explained in this chapter. Note that the exact same approach is possible for other dc-dc converters, e.g., the boost and buck-boost converters that are depicted in Figure 1b,c.

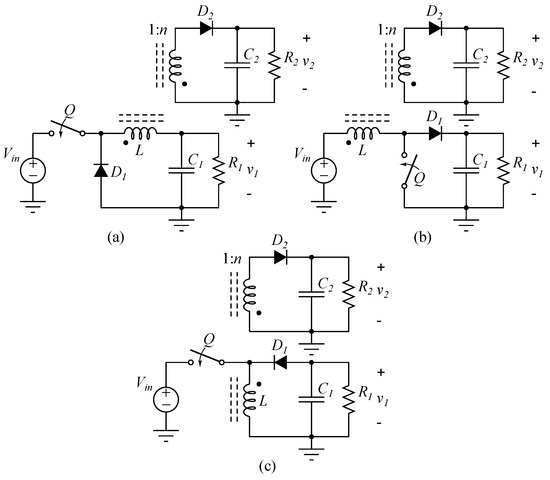
Figure 1. (a) A two-output buck converter. (b) A potential two-output boost converter; (c) A potential two-output buck-boost converter.

2.1. Two-Output Fly-Buck Converter

Using a fly-buck converter (Figure 1a) as a simple two-output converter is proposed in [17,18]. Only one of the outputs is controlled, causing severe cross-regulation issues for the second output. In order to remediate the cross-regulation problem, adding an active switch to the secondary of the coupled inductor was proposed in [19].

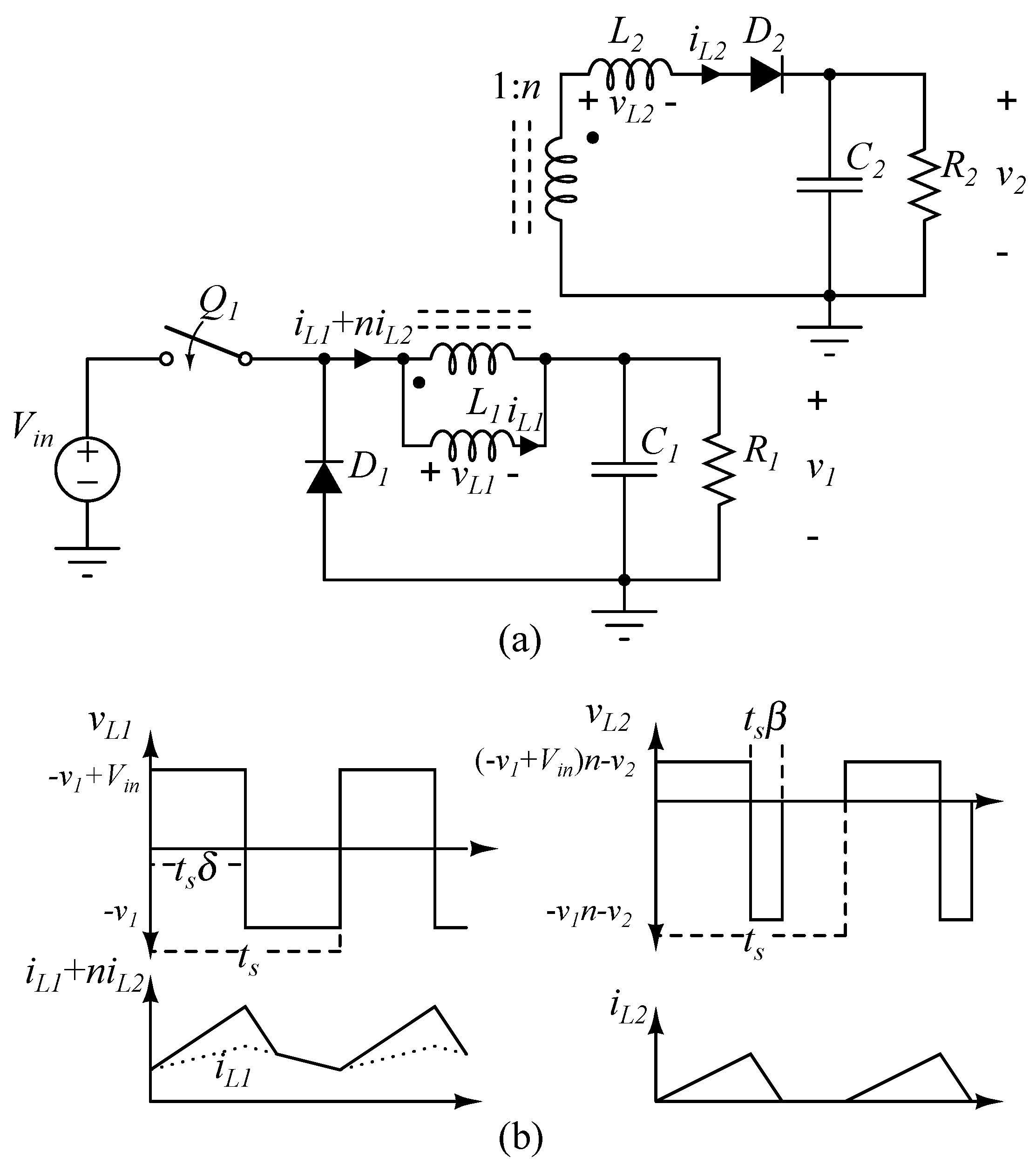
As an alternative to the conventional uncontrolled fly-buck converter, Figure 2a shows a two-output buck converter whose second output is obtained from a flyback type coupled inductor with magnetizing inductance L${}_1$ and substantial leakage inductance L${}_2$. The steady-state equation of the first output voltage v${}_1$ is the same as for the conventional buck converter. When the first switch Q${}_1$ is off, energy is transferred to the secondary switch. The steady-state equation of the second output voltage v${}_2$ is:

$$\begin{array}{cc}\hfill v_2& =n(V_1-V_{in}\frac{\beta }{1-\delta +\beta })\hfill \\ \hfill & =n{V}_{in}(1-\delta )(-0.5+\frac{(\delta -1)R_2{t}_s}{4L_2}+\hfill \\ \hfill & \frac{\sqrt{4L_2^2+4(1+\delta )L_2{R}_2{t}_s+{(\delta -1)}^2{R}_2^2{t}_s^2}}{4L_2}),\hfill \end{array}$$

(1)

where n is the turns ratio of the coupled inductor, V${}_{in}$ is the input voltage, $\delta$ is the duty cycle of the switch Q${}_1$, and $\beta$ is the normalized (t${}_s$) demagnetizing interval of the leakage inductor L${}_2$ (see Figure 2b). As shown in (1), the switching period t${}_s$ is a possible control parameter of V${}_2$. This explains why the switching frequency, f${}_s$ = 1/t${}_s$, can be used to restrain the cross-regulation problem without adding additional components. Figure 3 is constructed from (1) to show the regulation that is possible with the switching frequency.

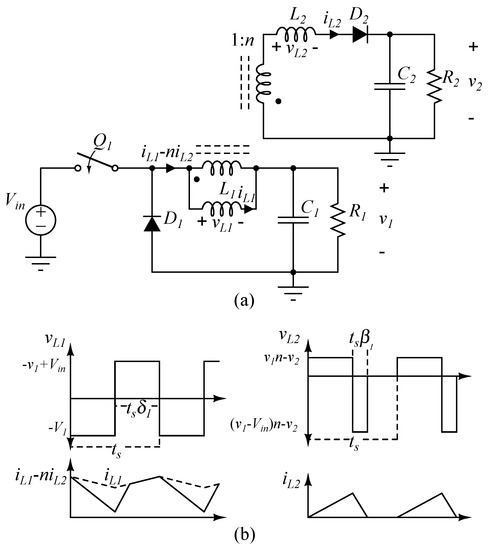
Figure 2. (a) A fly-buck type two-output buck converter; (b) Voltage and current waveforms of the magnetizing and leakage inductances of the coupled inductor v${}_{L1}$, i${}_{L1}$-ni${}_{L2}$, v${}_{L2}$ and i${}_{L2}$, respectively.

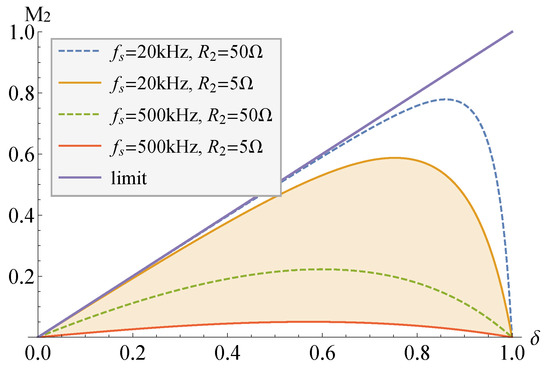
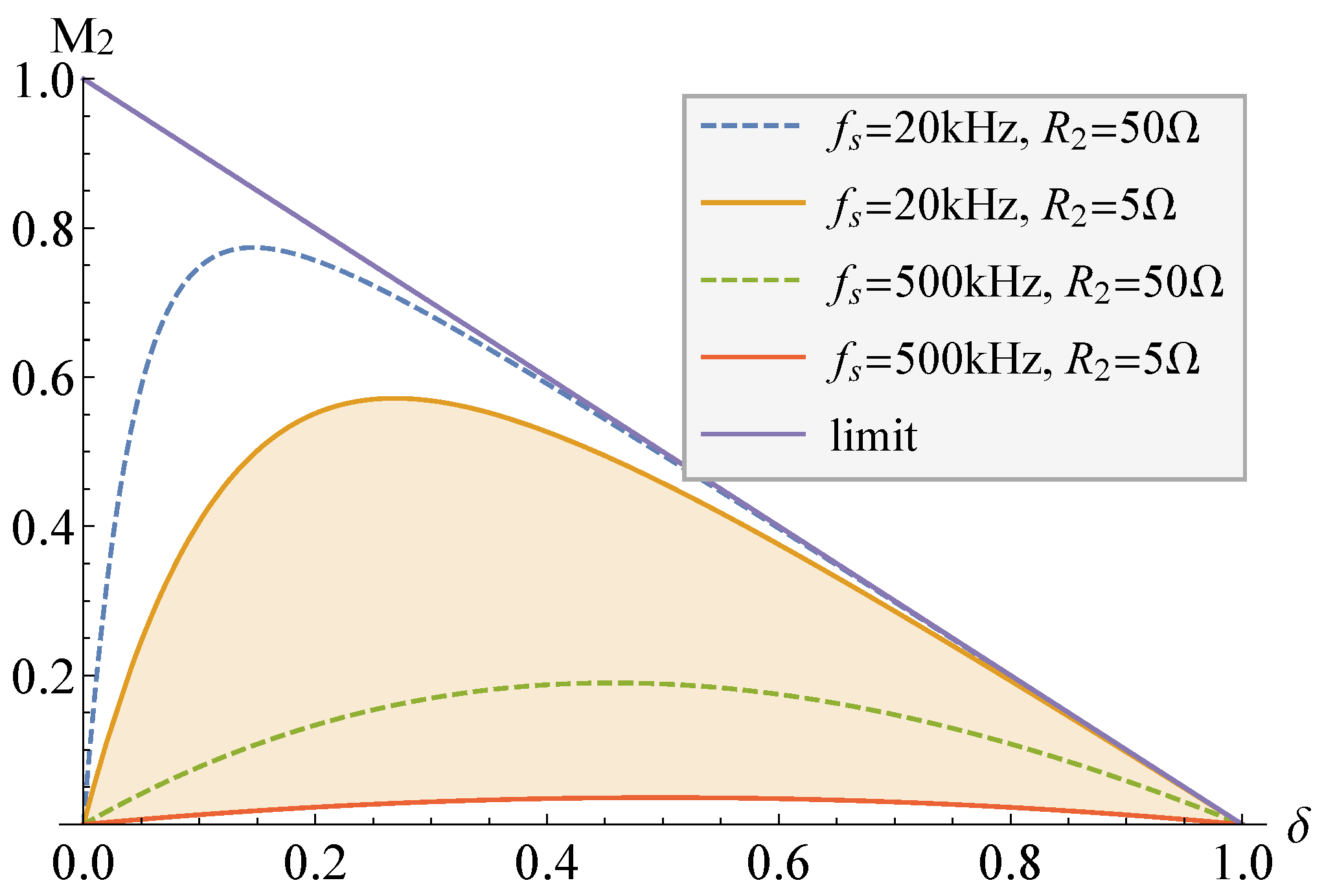
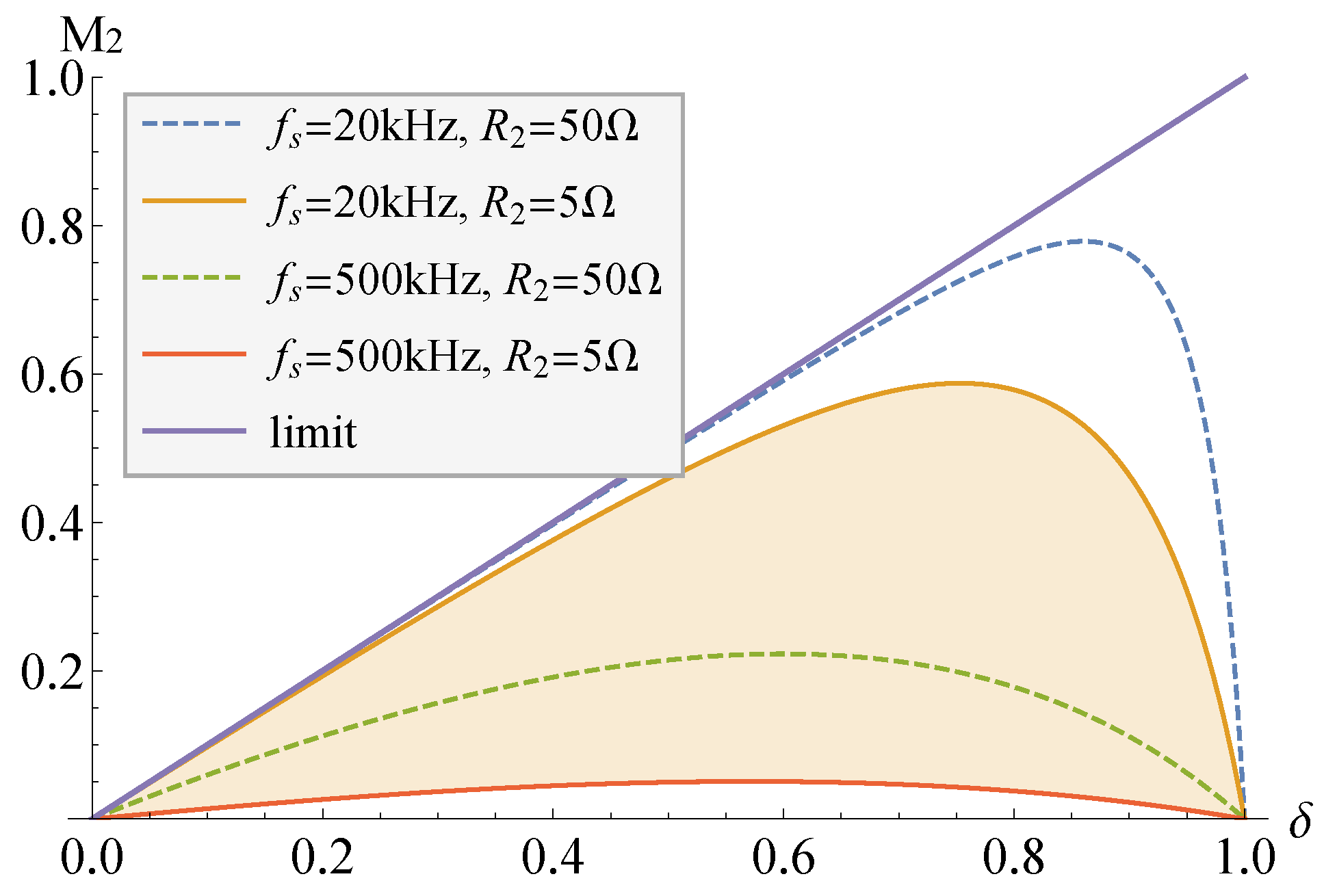
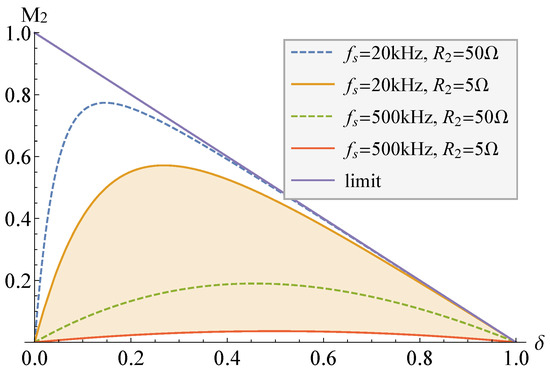
Figure 3. Conversion ratio of the second output, M${}_2$ = v${}_2$/V${}_{in}$, versus the duty cycle $\delta$ at different switching frequencies f${}_s$ combined with the second load R${}_2$ of the fly-buck converter when the turns ratio of the coupled inductor n is 1. For the other components, see Table 1. Results are obtained by using (1).

From Figure 3 it can be deduced that it is preferable to adjust the second output in the fly-buck mode when the duty cycle is higher than 50%. This is because more energy can be transferred during the switch-off period to support a wider range of load conditions.

2.1.1. Design Criteria

L${}_2$’s value depends on the turns ratio of the coupled inductor, n. However, n needs to be known to calculate L${}_2$. The minimum value of n is:

$$min\left(n\right)=\underset{\beta \to 0}{lim}\frac{v_2}{v_1},$$

(2)

and so n can be calculated from (1) by numerical iteration. If a higher L${}_2$ inductance is needed, it can be increased by additional inverse windings [20] or by changing the overlap ratio of the secondary winding [21].

Inductor L${}_2$ is needed to adjust the second output v${}_2$. L${}_2$’s inductance should be relatively small compared to the magnetizing inductance in order to correctly operate this second output in DCM. Moreover, L${}_2$ is also used to restrict the peak value of the inductor current i${}_{L2,pk}$. It follows that

$$i_{L2,pk}=(n{V}_1-V_2)(1-\delta )t_s/L_2.$$

(3)

For the fly-buck converter, the peak current of ni${}_{L2}$ should be lower than the minimum current of i${}_{L1}$ if a conventional buck converter is used:

$$n{i}_{L2,pk}<{\mathit{I}}_{\mathit{L}\mathit{1}}-\Delta {\mathit{i}}_{\mathit{L}\mathit{1}},$$

(4)

where Δi${}_{L1}$ is ripple of i${}_{L1}$, as i${}_{L1}$-ni${}_{L2}$ cannot be negative because of the diode D${}_1$. When this condition is false, i${}_{L1}$ decreases and the first output voltage drops. Instead of a diode, a MOSFET can be used to allow i${}_{L1}$-ni${}_{L2}$ to become negative.

2.1.2. Experimental Results

A fly-buck converter whose output voltages are 15 V/1.5 A and 5 V/0.8 A was built. The parameters of the prototype are shown in Table 1. The 15 V output was chosen as the reference output because the available power from the reference output is higher than that from the second output.

Table 1. Components of the fly-buck and forward-buck two-output prototypes.

Component	Value	Model
C${}_1$	2 × 22 $\mathsf{\mu }$F	TMK325B7226MM
C${}_2$	47 $\mathsf{\mu }$F	C1210C476M4PACTU
L${}_1$	150 $\mathsf{\mu }$H	produced in-house
	(turns ratio is 1/0.7)
L${}_2$	3.5 $\mathsf{\mu }$H
Q${}_1$		MTD3055VL
Gate Driver		LTC4440
D${}_1$, D${}_2$		CD214B-B230LF

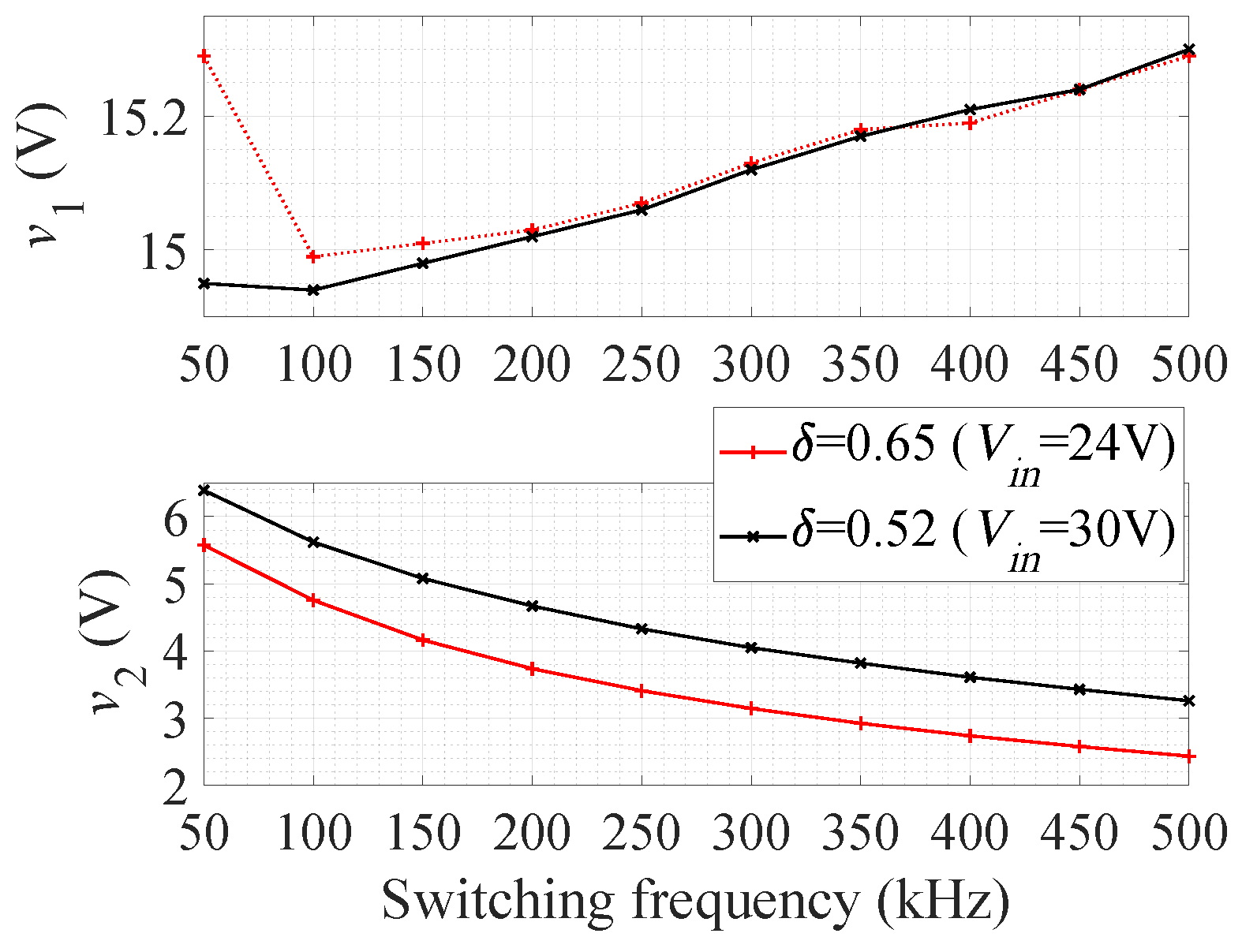
Figure 4 shows that v${}_2$ changes for different switching frequencies. The duty cycle $\delta$ is kept the same for both these plots. There is a small change in v${}_1$ when f${}_s$ changes because of cross-regulation. Figure 4 shows that the voltage range of the second output is slightly larger when $\delta$ is higher.

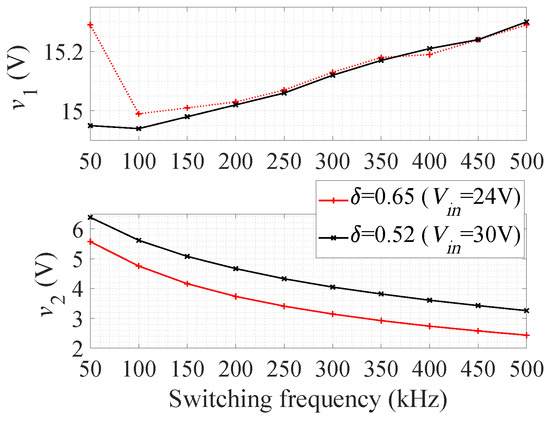
Figure 4. Experimentally measured output voltages of the proposed fly-buck two-output converter for different f${}_s$ (R${}_1$ = 10 $\Omega$ and R${}_2$ = 6.25 $\Omega$).

In Table 2, the control values and efficiencies of the circuit at different loads are given. When the first output current i${}_1$ is changed from 0.75 A to 1.5 A, $\delta$ must be increased from 58.7% to 64.5%. Note that $\delta$ is the control parameter of v${}_2$. Therefore, it is possible to increase f${}_s$ from 27 kHz to 84 kHz to keep v${}_1$ at 5 V. Even if f${}_s$ is not a control parameter of v${}_1$, $\delta$ is slightly changed from 64.5% to 64.2% when the second output current i${}_2$ is changed from 0.8 A to 0.2 A. The reason for this slight change is again due to cross-regulation issue. An appropriate PWM-PFM method can keep the output voltages the same at both operating points.

Table 2. Experimental results of the fly-buck converter (V${}_{in}$ = 24 V).

v${}_1$ (V)	v${}_2$ (V)	i${}_1$ (A)	i${}_2$ (A)	$\mathit{\delta }$ (%)	f${}_{\mathit{s}}$ (kHz)	$\mathit{\eta }$ (%)
15.02	5.02	0.75	0.81	58.7	27.0	91.4
15.02	5.02	1.00	0.81	61.1	66.0	92.5
15.02	5.02	1.25	0.80	63.2	79.0	93.1
15.00	5.03	1.50	0.81	64.5	84.0	93.5
15.01	5.01	1.50	0.60	65.3	117.0	93.8
15.02	5.01	0.75	0.60	60.7	97.0	93.2
15.02	5.03	1.50	0.40	64.3	184.0	94.4
15.01	5.00	0.75	0.40	63.8	183.0	94.0
15.02	5.00	1.50	0.20	64.2	420.0	94.3
15.00	5.01	0.75	0.20	63.5	410.0	94.3

As shown in Table 2, the minimum efficiency of the circuit is 91.4% when i${}_1$ is at the minimum operating point. The more i${}_1$ increases, the more the efficiency increases. The efficiency at the lower switching frequencies is generally lower than the efficiency at the higher switching frequencies. This is because the ripple of i${}_{L2}$ decreases when f${}_s$ increases. The conduction losses also decrease because of this reason.

2.2. Two-Output Forward-Buck Converter

Figure 5a shows a two-output forward-buck converter where the second output is obtained by introducing a forward-mode coupled inductor. The circuit is the same as for the fly-buck circuit, except that the polarity of the coupled inductor is reversed. When Q${}_1$ is switched on, energy stored in magnetizing inductor is transferred to the secondary. The conversion ratio of the first output voltage M${}_1$ is the same as for the conventional buck converter. The value for the second output voltage v${}_2$ can be calculated by the following equation:

$$\begin{array}{cc}\hfill v_2& =n(V_{in}\frac{\delta }{\delta +\beta }-V_1)\hfill \\ \hfill & =n\delta V_{in}(-0.5-\frac{\delta R_2{t}_s}{4L_2}+\hfill \\ \hfill & \frac{\sqrt{4L_2^2+R_2{t}_s(8L_2-4\delta L_2+{\delta }^2{R}_2{t}_s)}}{4L_2}).\hfill \end{array}$$

(5)

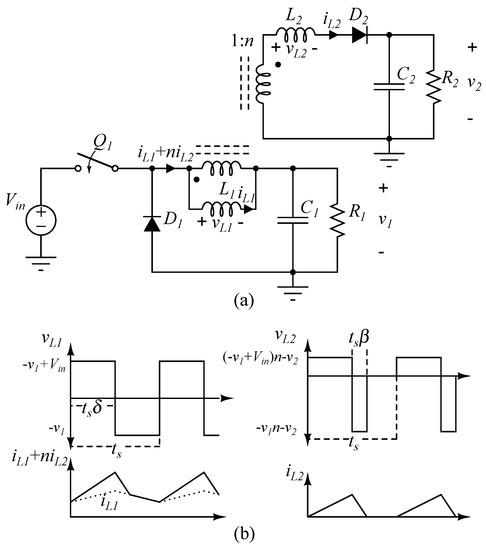
Figure 5. (a) Forward-buck type two-output buck converter; (b) Voltage and current waveforms of the magnetizing and leakage inductances of the coupled inductor v${}_{L1}$, i${}_{L1}$ + ni${}_{L2}$, v${}_{L2}$ and i${}_{L2}$, respectively.

As shown in Figure 6 and (5), the switching frequency t${}_s$ = 1/f${}_s$ can be used to adjust the second output voltage. Also, Figure 6 shows that the conversion ratio range increases when the duty cycle $\delta$ decreases. This is the opposite situation to that of the fly-buck converter (see Figure 3 and Figure 6). The polarity of the transformer can be selected, depending on $\delta$ as required by the application, to create the widest possible voltage range for the second output. In particular, if $\delta$ is less than 0.5, the forward-buck topology is selected, otherwise the fly-buck topology is more appropriate.

Figure 6. The conversion ratio of the second output of the forward-buck two-output converter, M${}_2$ = v${}_2$/V${}_{in}$, versus the duty cycle $\delta$ at different f${}_s$, and the second load R${}_2$. The turns ratio of the coupled inductor n is 1. For the other components, see Table 1. Results are obtained by using (5).

2.2.1. Design Criteria

The minimum value of the turns ratio n is:

$$min\left(n\right)=\underset{\beta \to 0}{lim}\frac{v_2}{V_{in}(1-\delta )}.$$

(6)

The initial n-value can be computed from (5) by using numerical procedures.

A leakage inductance L${}_2$ is needed to adjust the second output v${}_2$. The peak value of the inductor current i${}_{L2,pk}$ is required for the selection process:

$$i_{L2,pk}=(n(V_{in}-V_1)-V_2)\delta t_s/L_2.$$

(7)

For the forward-buck type, the average of the current i${}_{L2}$ must be lower than the minimum current of i${}_{L1}$:

$$ave\left({\mathit{ni}}_{\mathit{L}\left(\mathit{2}\right)}\right)<{\mathit{I}}_{\mathit{L}\mathit{1}}-\Delta {\mathit{i}}_{\mathit{L}\mathit{1}}.$$

(8)

This is because i${}_{L1}$ + ni${}_{L2}$ cannot be negative because of the diode D${}_1$. This is the same reasoning as applies to the fly-buck type.

2.2.2. Experimental Results

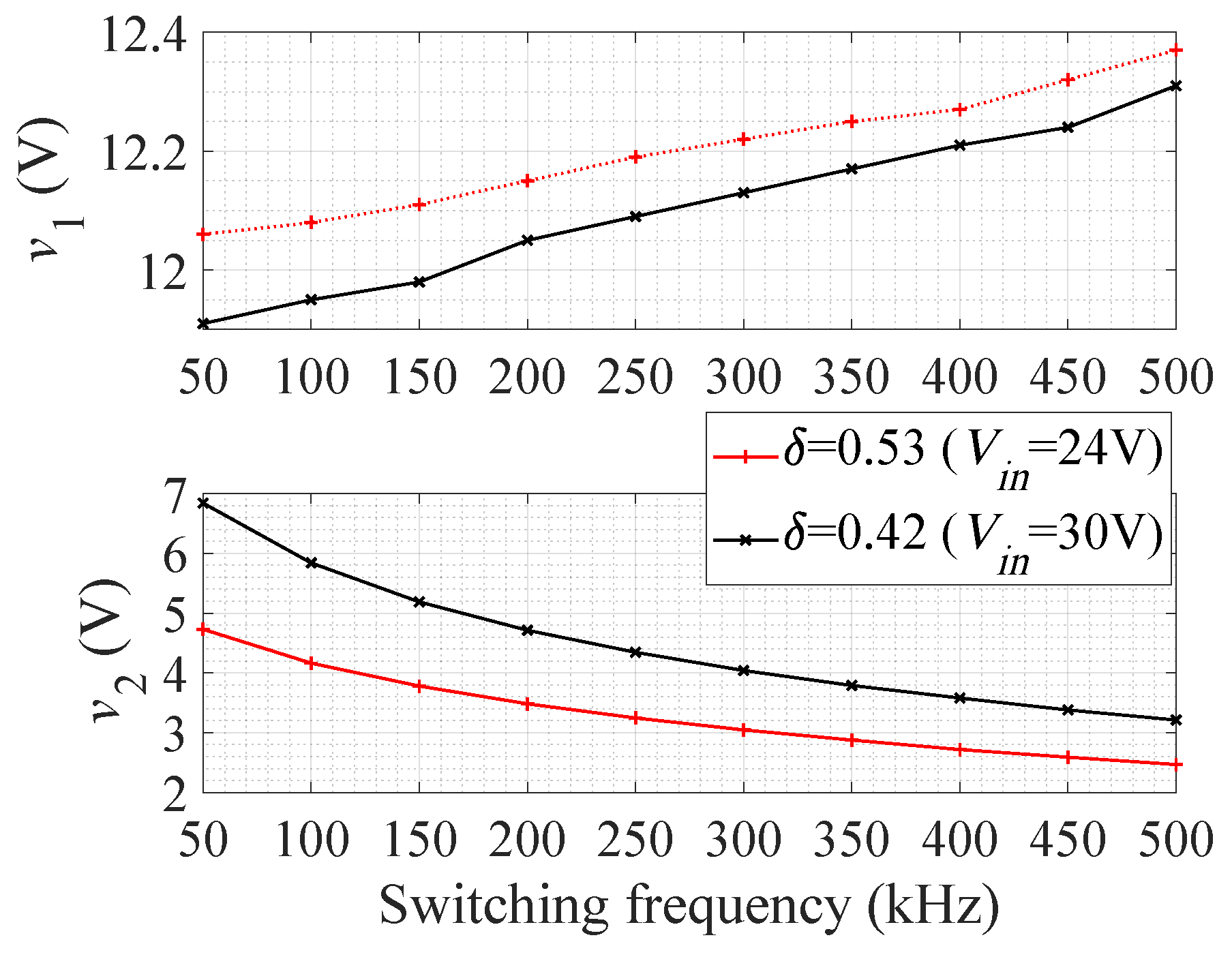
A forward-buck converter with outputs of 12 V/1.5 A and 5 V/0.6 A was designed and built. The parameters of the prototype, which were the same as for the fly-buck converter, are shown in Table 1. Figure 7 shows the experimental results of the change in v${}_2$ versus f${}_s$, same as for the fly-buck converter. The change in f${}_s$ from 50 kHz to 500 kHz causes (approximately) a 3.5 V drop in v${}_2$ when $\delta$ = 0.42. v${}_1$ changes only +0.4 V from 50 kHz to 500 kHz, because of cross-regulation issues. This is enough to control the two-outputs independently, as Table 3 shows. The control values and efficiency of the forward-buck converter under different load conditions are also shown in Table 3. The efficiency at lower switching frequencies is generally lower than that at higher switching frequencies, matching the behavior of the fly-buck converter.

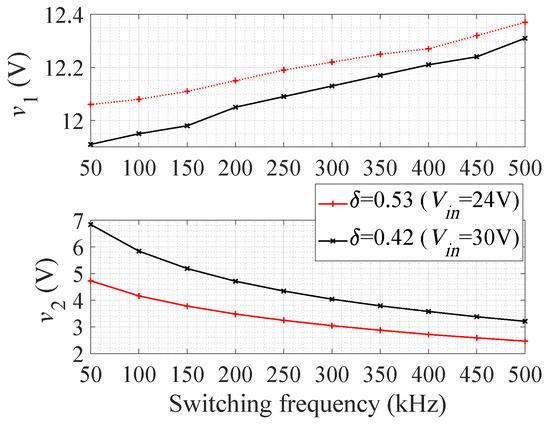
Figure 7. Experimentally measured output voltages of the proposed forward-buck two-output converter depending on f${}_s$ (R${}_1$ = 12 $\Omega$ and R${}_2$ = 8.3 $\Omega$).

Table 3. Experimental results of the forward-buck converter (V${}_{in}$ = 24 V).

v${}_1$ (V)	v${}_2$ (V)	i${}_1$ (A)	i${}_2$ (A)	$\mathit{\delta }$ (%)	f${}_{\mathit{s}}$ (kHz)	$\mathit{\eta }$ (%)
12.02	5.06	0.754	0.610	51.9	45.0	91.7
12.06	5.01	1.000	0.605	52.5	45.0	91.7
12.03	5.03	1.252	0.606	53.1	40.0	91.9
12.02	5.00	1.518	0.602	53.6	40.0	91.6
12.02	5.01	1.502	0.300	52.9	97.0	93.1
12.07	5.01	0.751	0.300	51.8	110.0	93.3
12.03	5.01	1.503	0.101	52.7	380.0	93.3
12.03	5.00	0.748	0.101	51.2	470.0	92.9

3. PWM-PD Controlled Three-Output Converters

The PWM-PD method for non-isolated three-output dc-dc converters with two active switches is presented in [7,8]. It requires two square wave voltages and builds a third square voltage from them. The first and the second output voltage are controlled by $\delta$${}_1$ and $\delta$${}_2$, respectively. The third output is adjusted by the duty cycle $\delta$${}_3$, which is equal to the total of $\delta$${}_{PD}$ and $\delta$${}_2$ in [7,8]. This is why a third switch is not needed to obtain a third output; however, additional diodes and an extra magnetic core must be added [7,8].

A PWM-PD controlled three-output converter which needs only two inductors is shown in Figure 8. In order to obtain the third adjustable output, additional windings are added to the inductors L${}_1$ and L${}_2$ of the buck converters. To use this method, the switching frequencies of the active switches should be the same. The polarity of the windings can be chosen in two ways, and boost or buck-boost converters may be used instead of buck converters. The secondaries of the coupled inductors are connected in series so that the combined leakage inductance of the coupled inductors, L${}_3$, can be used to adjust the third output. This third output is adjusted by the duty cycle $\delta$${}_3$, which is a function of the phase delay $\delta$${}_{PD}$ between the gate signals of Q${}_1$ and Q${}_2$.

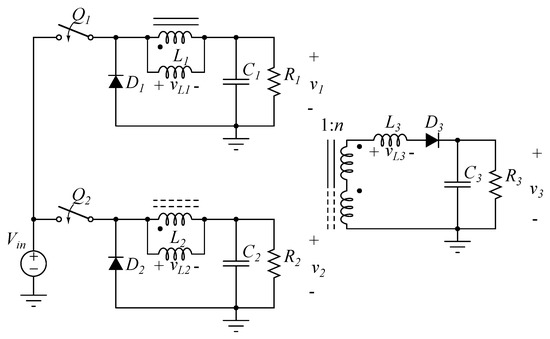
Figure 8. PWM-PD controlled three-output forward-type buck converter.

3.1. A PWM-PD Controlled Fly-Buck Type Three-Output Converter

The secondary windings of the coupled inductors of the two buck converters are connected in series. L${}_3$ is equal to the total leakage inductance of the first and second coupled inductors. The polarity of the secondaries is similar to that of a flyback converter. When the voltage across both magnetizing inductors is negative, the energy is transferred to the secondary. The duty cycle $\delta$${}_3$ of this third output square wave is

$${\delta }_3=(1-{\delta }_2-{\delta }_{PD}),$$

(9)

as shown in Figure 9a. The third output voltage v${}_3$ of the fly-buck type converter can thus be calculated as:

$$\begin{array}{cc}\hfill v_3=& (2L_{3}n(V_1+V_2-V_{in})-{\delta }_3^{2}n{R}_3{t}_s{V}_{in}+\hfill \\ \hfill & [n^2(8{\delta }_3^2{L}_3{R}_3{t}_s(V_1+V_2)V_{in}+\hfill \\ \hfill & {(-2L_3(V_1+V_2-V_{in})+{\delta }_3^2{R}_3{t}_s{V}_{in})}^2{\left)\right]}^{\frac{1}{2}})/4L_3.\hfill \end{array}$$

(10)

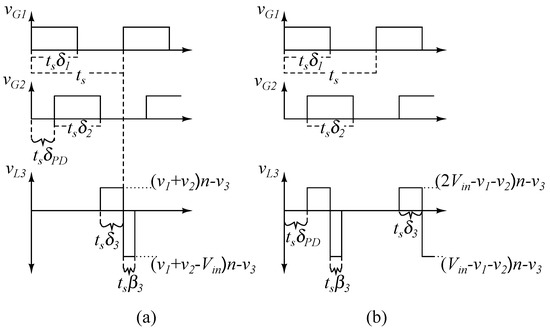
Figure 9. The gate voltage of the switches v${}_{G1}$ and v${}_{G2}$, and the voltage waveform of the tertiary inductor, v${}_{L3}$ of (a) a fly-buck type converter and (b) a forward-buck type three-output converter.

3.1.1. Design Criteria

The minimum value of n is:

$$min\left(n\right)=\underset{\beta \to 0}{lim}\frac{v_3}{v_1+v_2}.$$

(11)

The current passing through L${}_3$, i${}_{L3,pk}$, is formulated as:

$$i_{L3,pk}=(n(V_1+V_2)-V_3){\delta }_3{T}_s/L_3.$$

(12)

3.1.2. Experimental Results

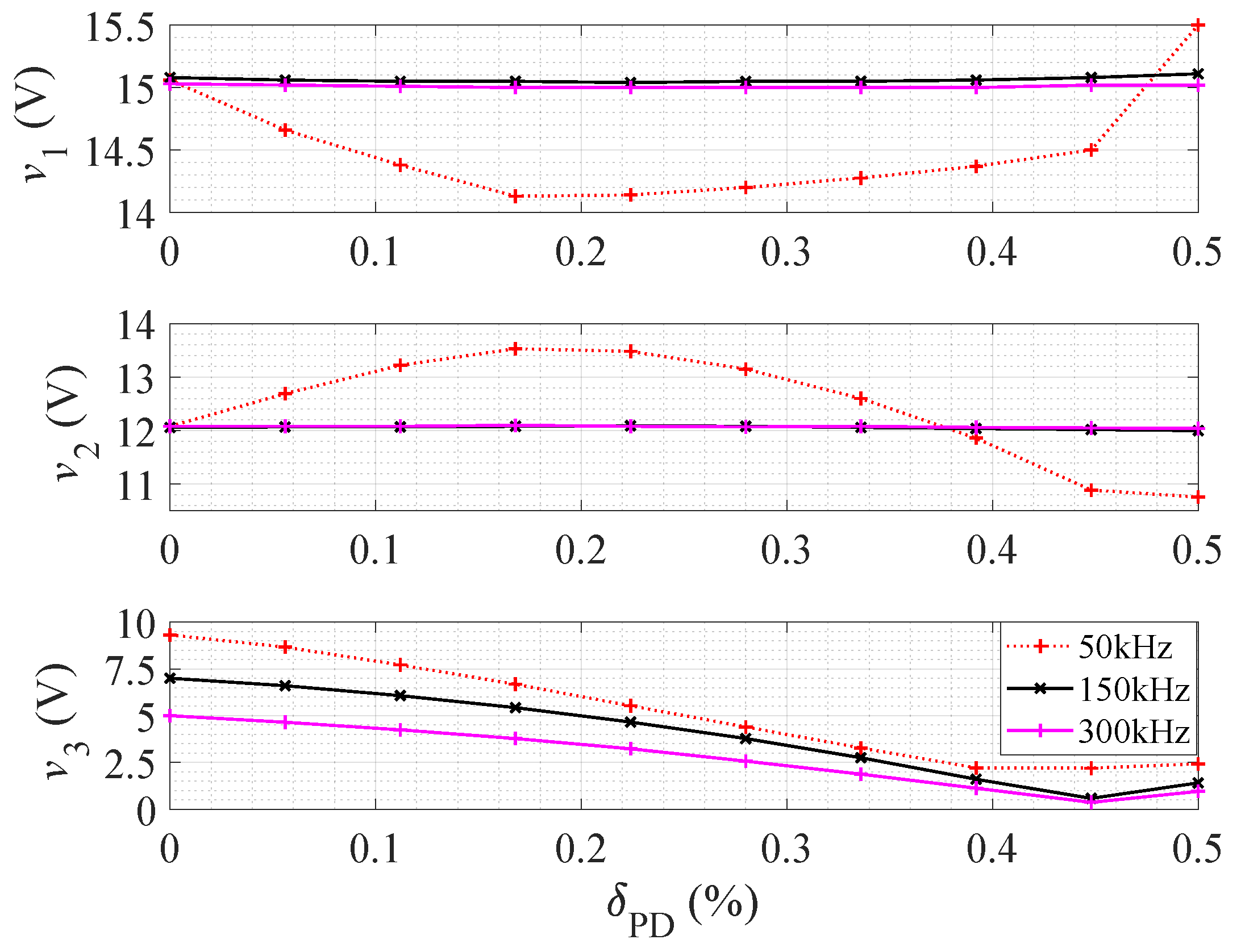
A fly-buck three-output converter was built to verify the preceding analysis. The parameters of the prototype were the same as for the two-output converters and are shown in Table 1. Figure 10 shows the experimental results for v${}_3$ and how they change as a function of the phase delay. The first output, 15 V/1.5 A, and the second, 12 V/1.5 A, are kept the same for different third-output voltages. The cross-regulation at 50 kHz is 2–3 V for v${}_1$ and v${}_2$ as shown in Figure 10. Note that the change in v${}_1$ and v${}_2$ is only 0.2 V at higher frequencies.

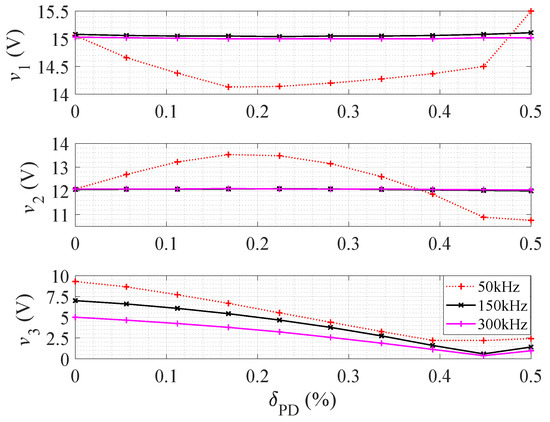
Figure 10. Experimentally measured output voltages of the proposed fly-buck three-output converter, depending on different phase delays ${\delta }_{PD}$ ($V_{in}$ = 24 V, $R_1$ = 10 $\Omega$, $R_2$ = 8 $\Omega$ and $R_3$ = 7.5 $\Omega$).

Table 4 shows the operating points, control parameters and efficiencies of the converter for different loads. When $\delta$${}_{PD}$ or $\delta$${}_3$ is chosen as the control parameter for the third output, the output voltages can be kept the same at different loads. For example, when only the third load is changed in the first four rows, then the related control parameter, the phase delay, is able to keep the third output constant, i.e., 3.3 V.

Table 4. Experimental results with a fly-buck type three-output converter (V${}_{in}$ = 24 V and f${}_s$ = 150 kHz).

v${}_1$ (V)	v${}_2$ (V)	v${}_3$ (V)	i${}_1$ (A)	i${}_2$ (A)	i${}_3$ (A)	${\mathit{\delta }}_1$ (%)	${\mathit{\delta }}_2$ (%)	${\mathit{\delta }}_{\mathit{PD}}$ (%)	$\mathit{\eta }$ (%)
15.00	12.02	3.32	1.498	1.498	0.442	65.4	52.7	20.5	94.4
15.00	12.01	3.30	1.498	1.497	0.309	65.4	52.7	24.3	94.7
15.01	12.01	3.30	1.498	1.496	0.152	65.4	52.7	28.6	95.1
15.01	12.00	3.30	1.499	1.496	0.074	65.4	52.7	30.7	95.1
15.04	12.03	3.31	0.753	0.750	0.077	64.2	51.6	31.2	95.3
15.02	12.03	3.30	0.252	0.252	0.078	63.0	50.6	31.9	92.6
15.25	12.12	3.30	0.256	0.253	0.300	55.5	33.6	7.7	91.9

The efficiency of the converter $\eta$ is 94.4% at the rated load, and it can be even higher for other loads, as shown in Table 4.

3.2. A PWM-PD Controlled Forward-Buck Type Three-Output Converter

The forward-buck type three-output converter is the same as a fly-buck type three-output converter, except for the polarity of the secondary windings. The polarity of the secondaries is similar to that of a forward converter. When the voltage across both magnetizing inductors is positive, energy is transferred to the secondary.

The $\delta$${}_3$ of the forward-buck circuit is:

$${\delta }_3=({\delta }_1-{\delta }_{PD}),$$

(13)

as shown in Figure 9b. The third-output voltage v${}_3$ can be calculated as:

$$\begin{array}{cc}\hfill & v_3=(-2L_{3}n(V_1+V_2-V_{in})-{\delta }_3^{2}n{R}_3{t}_s{V}_{in}+\hfill \\ \hfill & [n^2(-8{\delta }_3^2{L}_3{R}_3{t}_s(V_1+V_2-2V_{in})V_{in}\hfill \\ \hfill & +{(2L_3(V_1+V_2-V_{in})+{\delta }_3^2{R}_3{t}_s{V}_{in})}^2{\left)\right]}^{\frac{1}{2}})/4L_3\hfill \end{array}$$

(14)

3.2.1. Design Criteria

The minimum value of n is:

$$min\left(n\right)=\underset{\beta \to 0}{lim}\frac{v_3}{V_{in}-(v_1+v_2)}.$$

(15)

The current of L${}_3$, i${}_{L3,pk}$, is formulated as:

$$i_{L3,pk}=(n(2V_{in}-V_1-V_2)-V_3){\delta }_3{t}_s/L_3.$$

(16)

3.2.2. Experimental Results

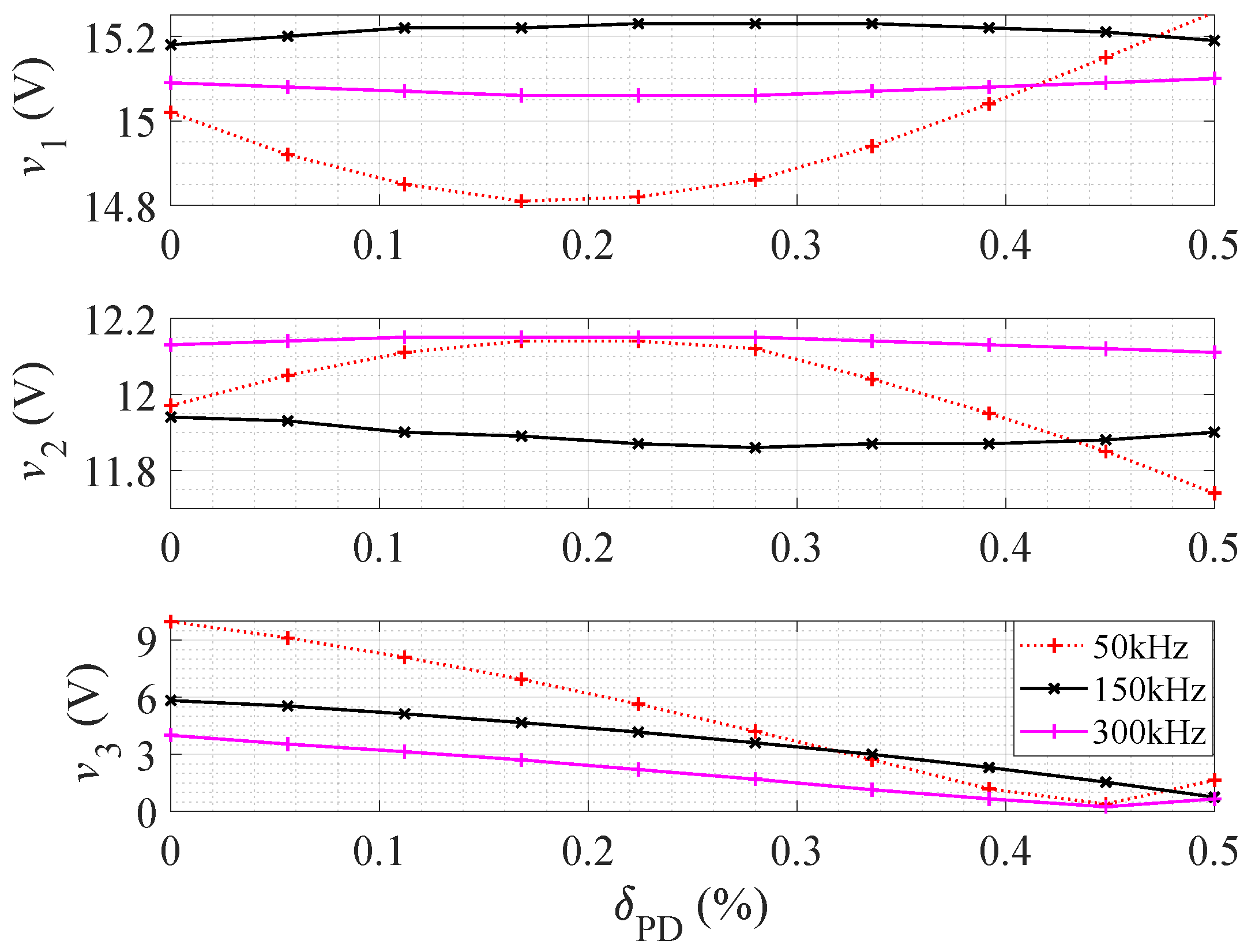
The same components used for the fly-buck type were used to build a forward-buck three-output converter. Figure 11 shows the experimental results of v${}_3$, as a function of $\delta$${}_{PD}$. Figure 11 shows that cross-regulation for the forward-buck converter at 50kHz is appreciably worse than at the other switching frequencies.

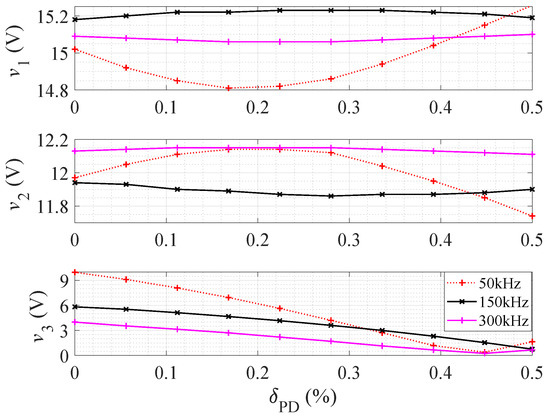
Figure 11. Experimentally measured output voltages of the proposed forward-buck three-output converter depending on different phase delays ${\delta }_{PD}$ ($V_{in}$ = 24 V, $R_1$ = 10 $\Omega$, $R_2$ = 8 $\Omega$ and $R_3$ = 7.5 $\Omega$).

Table 5 shows the operating points, control parameters, and efficiencies of the forward-buck type converter for different loads. It can be seen that $\delta$${}_{PD}$ or $\delta$${}_3$ is a valid control parameter of the third output. The efficiency of the converter $\eta$ is 94.4% at the rated load. The efficiency values of the converter are similar to those for the fly-buck type.

Table 5. Experimental results for a forward-buck type three-output converter (V${}_{in}$ = 24 V and f${}_s$ = 150 kHz).

v${}_1$ (V)	v${}_2$ (V)	v${}_3$ (V)	i${}_1$ (A)	i${}_2$ (A)	i${}_3$ (A)	${\mathit{\delta }}_1$ (%)	${\mathit{\delta }}_2$ (%)	${\mathit{\delta }}_{\mathit{PD}}$ (%)	$\mathit{\eta }$ (%)
14.99	12.07	3.30	1.512	1.500	0.456	65.5	53.0	14.4	94.4
14.99	12.07	3.31	1.511	1.500	0.303	65.5	53.0	23.1	94.7
14.99	12.05	3.31	1.512	1.500	0.150	65.5	53.0	32.2	94.9
15.02	12.02	3.31	1.516	1.491	0.075	65.5	53.0	47.5	94.9
15.00	12.10	3.30	0.751	0.751	0.075	64.1	52.0	38.9	95.1
15.02	12.04	3.30	0.252	0.250	0.307	63.0	50.7	23.1	90.7
15.02	12.06	3.30	0.251	0.250	0.075	63.0	50.8	38.0	92.1

As is evident from (10) and (14), $\delta$${}_3$ is the obvious control parameter for the third output. The maximum range of $\delta$${}_3$ is 50% when $\delta$${}_1$ and $\delta$${}_2$ are 50%.

4. PWM-PFM-PD Controlled Five-Output Converters

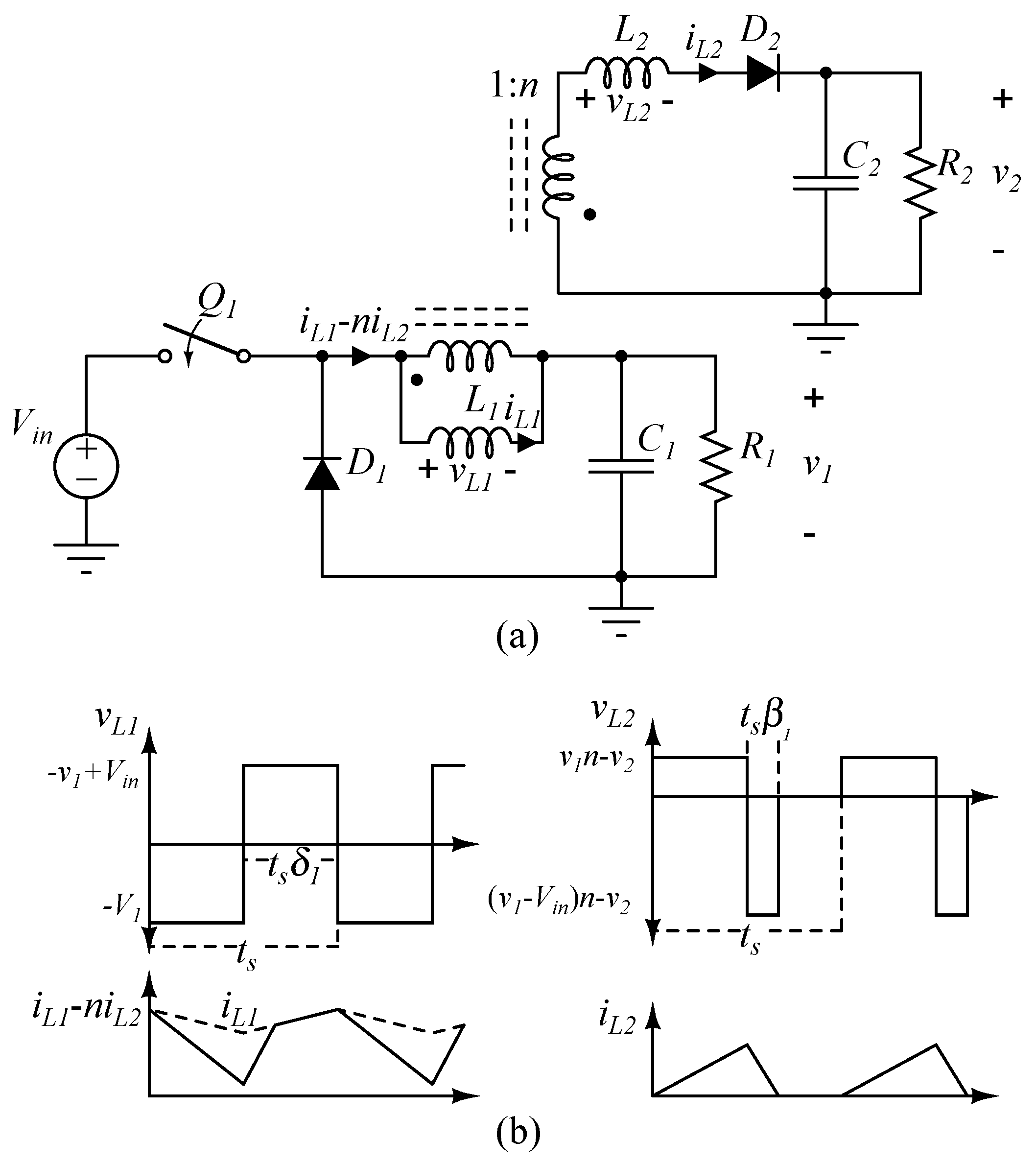
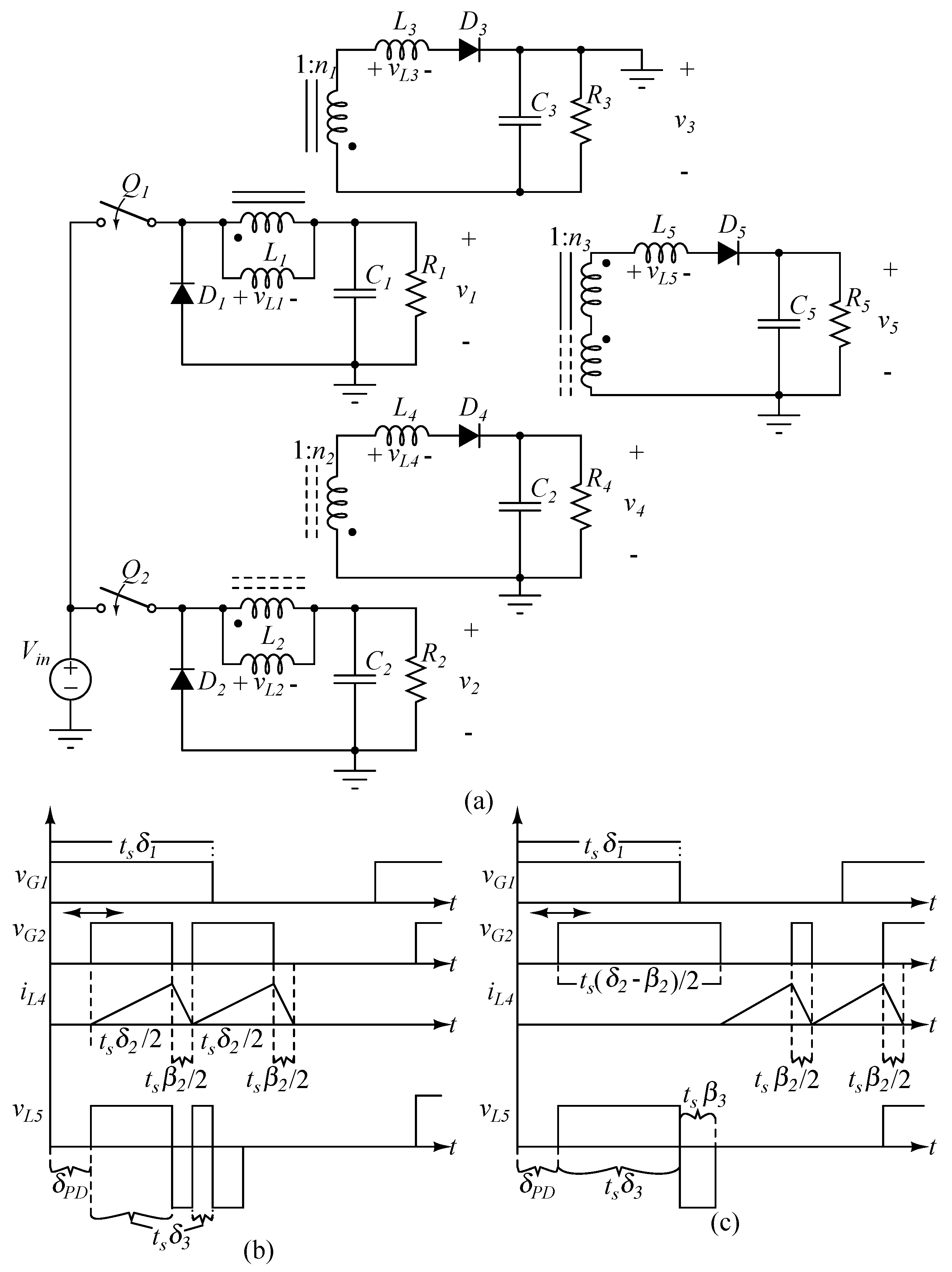
In this section, the PWM-PFM controlled two-output and the PWM-PD controlled three-output converters are merged to obtain five independently controlled outputs. The resulting PWM-PFM-PD controlled five-output converter, which has only two coils and two active switches, is shown in Figure 12a. In order to obtain the extra three adjustable outputs, two additional windings are added to the inductors of the buck converters and flyback diodes are then connected to the secondaries of these coupled inductors to construct the third and the fourth output. The leakage inductors L${}_3$ and L${}_4$ are designed to control the third and the fourth output voltage in DCM. Therefore, the total of the leakage inductance of the coupled inductors L${}_5$, which is obtained by connecting the tertiaries of the coupled inductors in series with diodes, can be used to adjust the fifth output by PD.

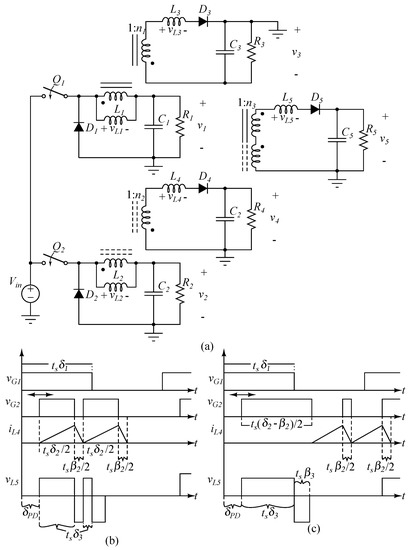
Figure 12. (a) PWM-PFM-PD controlled five-output converter. Waveforms of gate voltages, current through the fourth inductor ${\displaystyle i_{L4}}$ and the voltage across the fifth inductor ${\displaystyle v_{L5}}$ when the fifth output is connected in (b) a fly-buck type and (c) forward-buck type converter.

In order to use the PD method with non-equal frequency waveforms, it is proposed that the second switch operates in “burst” mode. The second switching frequency ${\displaystyle f_2}$ is synchronized to the first switching frequency, ${\displaystyle f_1}$ = 1/${\displaystyle t_s}$. It is then possible to insert a PD between the starting points of the signals as shown in Figure 12b,c. Frequency ${\displaystyle f_2}$ can be represented by:

$$f_2=k{f}_1.$$

(17)

The PWM signal is divided into segments depending on the required number of pulses, k. In burst mode, the turn-on time of the second signal is affected by the demagnetizing ratio of the fourth inductor $\beta$${}_2$ as can be seen in Figure 12b,c. When the inductor current drops to zero, the next segment is triggered. The inductor voltage waveform of the fifth output for the fly-buck type converter ${\displaystyle v_{L5}}$ is divided into k pulses as shown in Figure 12b. $\delta$${}_3$ in burst mode is:

$${\delta }_3=(1-{\delta }_2-{\delta }_{PD}-{\beta }_2(k-1)/k).$$

(18)

The range of $\delta$${}_3$ in burst mode is reduced by k and $\beta$${}_2$ for the fly-buck type’s fifth output. As shown in Figure 12c, instead of dividing the PWM signal into equal sub-pulses, there is a gap between the pulses in the case of a forward-buck type converter. This gap is needed for the demagnetizing duration of i${}_{L4}$ to operate the fourth output in DCM. In other words, the demagnetizing duration does not affect the range of $\delta$${}_3$, and (13) can be used for the forward-buck type converter in burst mode. The forward-buck type converter for the fifth output is preferable to the burst mode as it has a wider effective range and operates with less adverse effects.

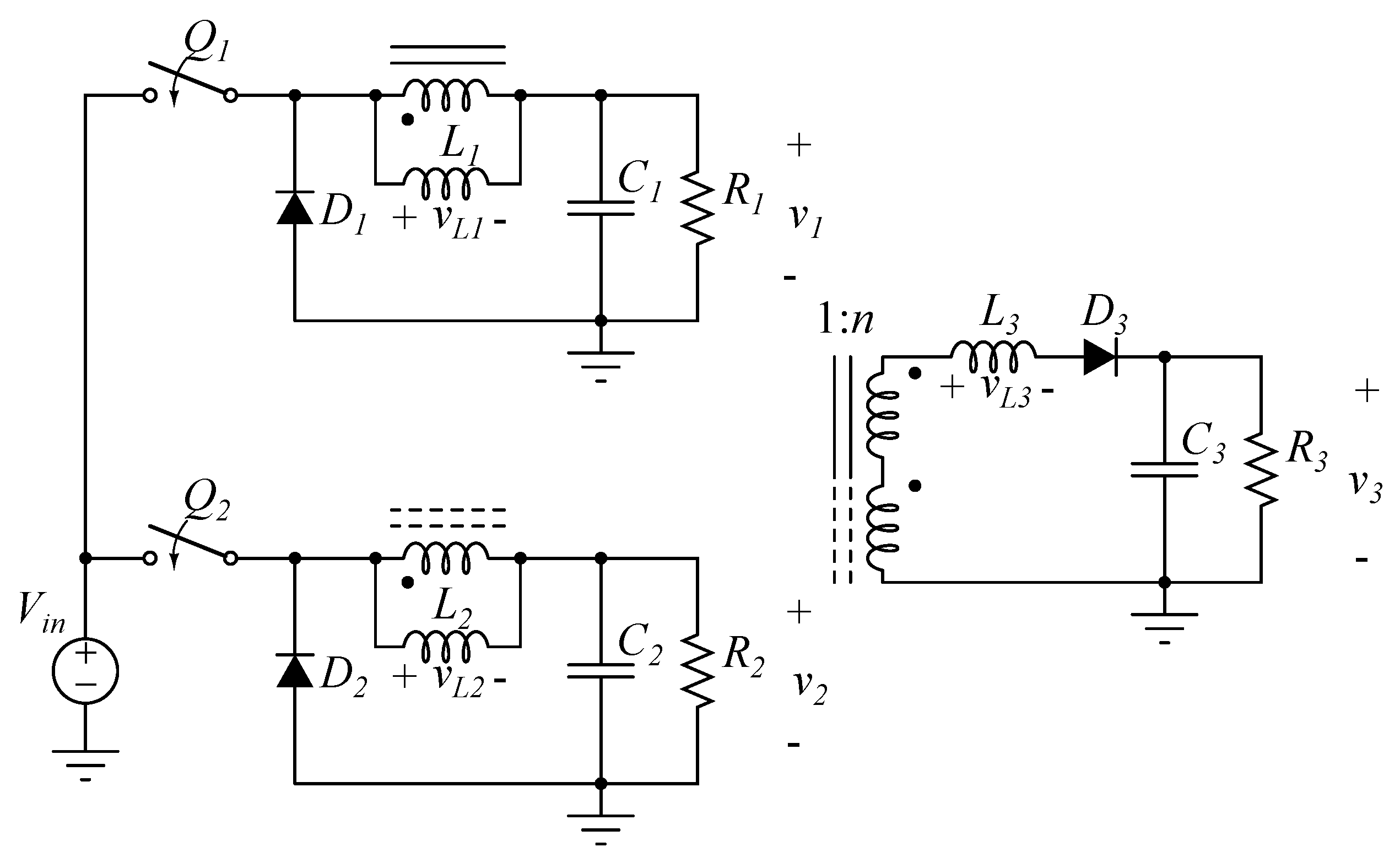
4.1. Topology Comparison

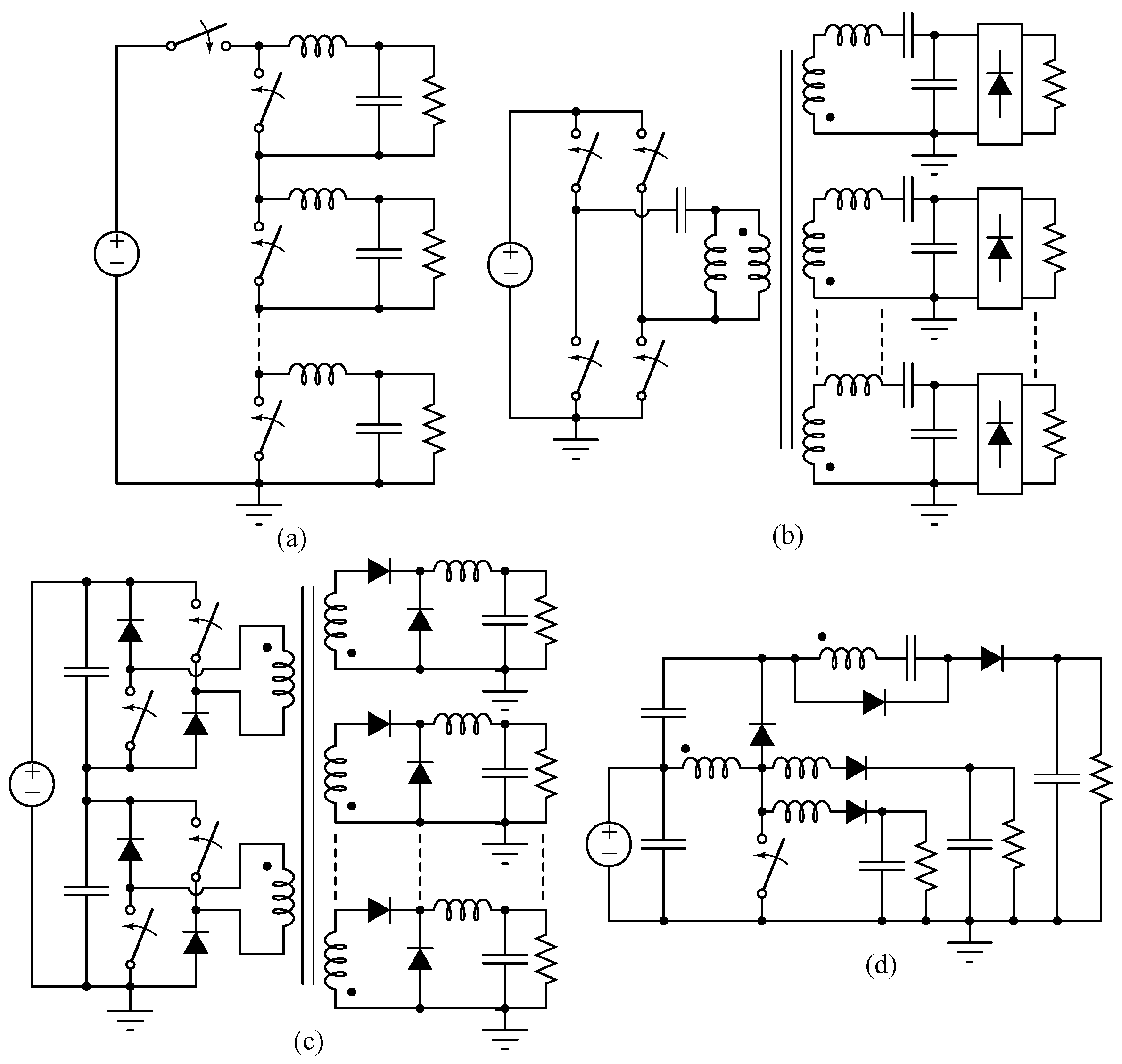
One method to reduce the size of a converter is to reduce the total number of components, e.g., by sharing common functionality as mentioned in the previous sections. Comparisons in this respect for the proposed five-output converter with similar research in [22,23,24,25] are summarized in Table 6. Figure 13 shows the reviewed multiple-output dc-dc converters, i.e., (a) the integrated multiple-output synchronous buck converter (IMOSBC) from [22]; (b) the multiple-output narrow-band resonant converter (MONBRC) from [23]; (c) the multiple-output two-transistor forward converter (MOTTFC) from [24] and (d) the single-input multiple-output dc-dc converter (SIMOC) from [25].

Table 6. Comparison of multiple-output converters.

References	IMOSBC [22]	MONBRC [23]	MOTTFC [24]	SIMOC [25]	Proposed
Switches	6	4	4	1	2
Diodes	0	20	12	5	5
Magnetic components	5	6	2	3	2
Capacitors	5	16	4	5	5
Outputs	5	5	4	3	5

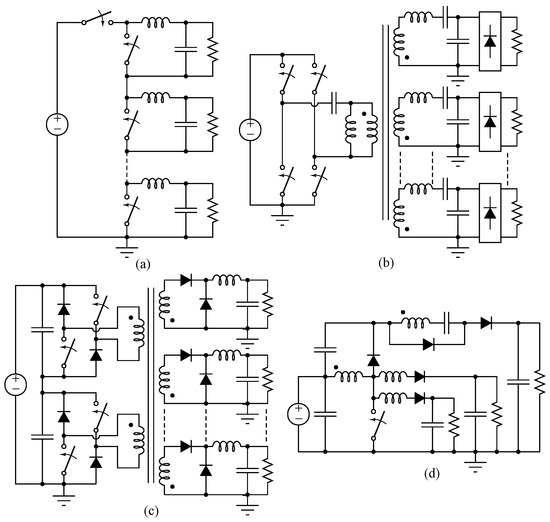
Figure 13. Multiple-output dc-dc converters from the literature: which are (a) an integrated multiple-output synchronous buck converter (IMOSBC) in [22]; (b) a multiple-output narrow-band resonant converter (MONBRC) in [23]; (c) a multiple-output two-transistor forward converter (MOTTFC) in [24] and (d) a single-input multiple-output dc-dc converter (SIMOC) in [25].

The IMOSBC uses fewer switches and diodes than those of its individual converters, but Figure 13a shows that it does not have less magnetic components. The MOTTFC from [24] and SIMOC from [25] are conceived to minimize cross-regulation, because the converters can not regulate all their outputs independently. Although the MONBRC regulates all outputs independently, it has more components than those of five individual converters, as shown in Figure 13b. As can be seen in Table 6, the proposed converter has the least number of components per output when compared to the others.

TMONBRC, MOTTFC and SIMOC are designed for high conversion ratios. However, the proposed topology can use forward converters instead of the buck converters for its first and second outputs, thereby also achieving high gain.

4.2. Design Criteria

The design rules for the PWM-PFM and PWM-PD converters can also be used for PWM-PFM-PD converters. As an example, the design of a five-output converter is shown in this subsection. The input voltage V${}_{in}$ is 24 V, and the outputs are 15 V/1.5 A, 12/1.5 A, −5 V/0.8 A, 5 V/0.6 A and 3.3 V/0.45 A, respectively.

The first and second outputs are operated in CCM. Therefore, the heaviest loads, 15 V/1.5 A, 12/1–1.5 A, are selected for these outputs. The topology can be selected to be buck, boost or buck-boost depending on the input voltage. Moreover, $\delta$${}_1$ and $\delta$${}_2$ should be close to 0.5, depending on the $\delta$${}_1$ and $\delta$${}_2$ values, in order to ensure a wide $\delta$${}_3$. In this chapter, the requirement is a buck converter; and so only the buck converter is analyzed.

The third and fourth outputs are operated in DCM, and a fly-buck or forward-buck type is selected according to the $\delta$${}_1$ and $\delta$${}_2$ values, because how the range of the fly-buck and forward-buck type converters changes depends on the $\delta$${}_1$ and $\delta$${}_2$ values.

Given these considerations, the 5 V and +5 V outputs are chosen for these outputs and the fly-buck topology is used because $\delta$${}_{1,2}$≥ 0.5. Accordingly, the turn ratios of the coupled inductors n${}_1$ and n${}_2$ are chosen to be 0.707.

The fifth output voltage is 3.3V. The forward-buck type in burst mode is selected to control this output by PD, as discussed before.

The design of this output is similar to that of the third and fourth output. The turns ratio of the coupled inductor’s n${}_3$ is calculated from (13), depending on the maximum and minimum load values. n${}_3$ is selected to have the same value, 0.707, as n${}_{1,2}$.

The parameters of the five-output converter prototype are the same as for the two-output converter, and can be found in Table 7.

Table 7. Components of the five-output converter prototypes.

Component	Value	Model
C${}_1$, C${}_2$	2 × 22 $\mathsf{\mu }$F	TMK325B7226MM
C${}_3$, C${}_4$, C${}_5$	47 $\mathsf{\mu }$F	C1210C476M4PACTU
L${}_1$, L${}_2$	150 $\mathsf{\mu }$H	produced in-house
	(turns ratios are 1/0.7/0.7)
L${}_3$, L${}_4$	3.5 $\mathsf{\mu }$H
L${}_5$	7.3 $\mathsf{\mu }$H
Q${}_1$, Q${}_2$		MTD3055VL
Gate Drivers		LTC4440
D${}_1$, D${}_2$, D${}_3$, D${}_4$, D${}_5$		CD214B-B230LF

4.3. Experimental Results with the Open-Loop Five-Output Prototype

After the design and the simulation were complete, a hardware prototype was built as shown in Figure 14, and tested in order to verify the analysis.

Figure 14. Five output converter prototype.

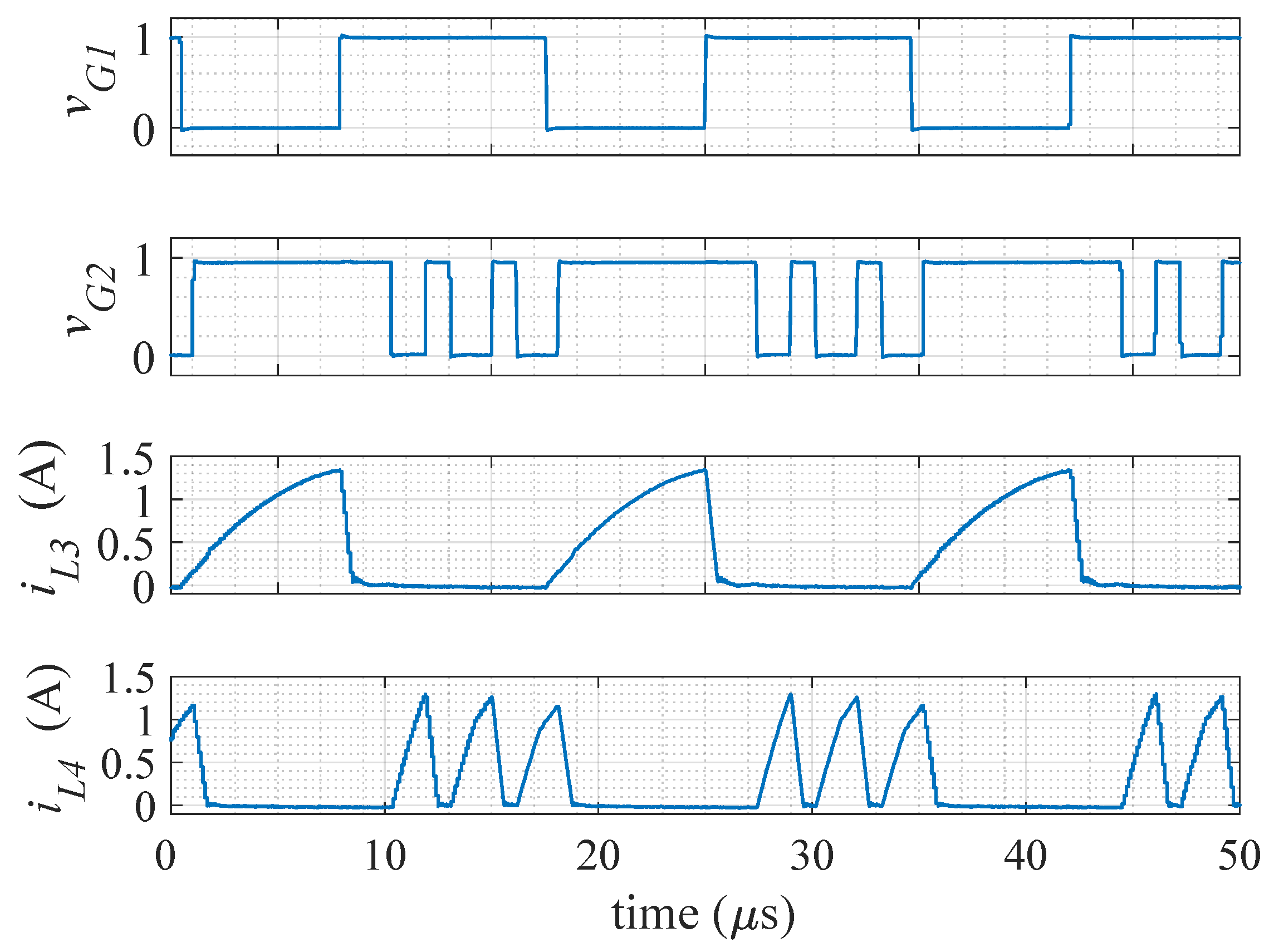
A two-channel waveform generator was used to generate all PWM signals. The second output of the waveform generator is a single signal, of which the duty cycle, phase delay, and number of pulses can be controlled independently, as shown in Figure 15.

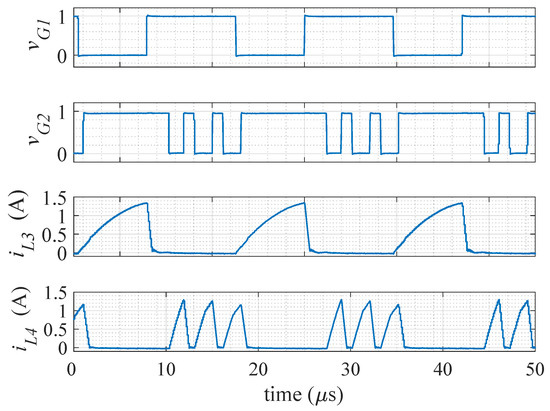
Figure 15. Experimental waveforms of the gate voltages ${\displaystyle v_{G1}}$ and ${\displaystyle v_{G2}}$, and current through the third and fourth leakage inductors when ${\delta }_1$ = 56.4%, ${\delta }_3$ = 57.3%, ${\delta }_2$ = 16%, f${}_1$ = 58.5 kHz and k = 3.

Table 8 and Table 9 show the operating points, control parameters and efficiencies of the five-output converter for a number of different loads. The efficiency varied between 92.5% and 93.5%.

Table 8. Experimental results for a five-output converter (V${}_{in}$ = 24 V).

	v${}_1$ (V)	v${}_2$ (V)	v${}_3$ (V)	v${}_4$ (V)	v${}_5$ (V)	i${}_1$ (A)	i${}_2$ (A)	i${}_3$ (A)	i${}_4$ (A)	i${}_5$ (A)
Case 1	15.17	12.11	−5.08	4.76	3.28	1.54	1.54	0.81	0.57	0.45
Case 2	15.09	11.99	−5.00	4.74	3.30	0.75	0.98	0.50	0.39	0.30
Case 3	15.04	12.13	−4.91	5.28	3.32	0.76	1.53	0.65	0.79	0.31
Case 4	15.15	12.10	−4.80	4.76	3.37	1.52	1.03	0.58	0.77	0.48
Case 5	15.12	12.13	−4.98	5.13	3.39	1.52	1.54	0.41	0.80	0.47
Case 6	15.00	11.96	−5.06	5.38	3.30	1.50	1.49	0.62	0.61	0.45
Case 7	15.16	12.10	−5.00	5.16	3.40	1.54	1.56	0.60	0.80	0.31

Table 9. The control parameters of a five-output converter at the operating points shown in Table 8.

	$\mathit{\eta }$ (%)	${\mathit{\delta }}_1$ (%)	${\mathit{\delta }}_2$ (%)	${\mathit{\delta }}_3$ (%)	f${}_1$ (kHz)	k
Case 1	92.9	67.28	54.70	11.84	85.5	3
Case 2	93.5	64.67	52.07	15.46	129.5	3
Case 3	92.5	59.40	53.78	7.04	66.3	2
Case 4	92.7	66.26	51.80	13.57	51.0	5
Case 5	93.0	65.91	54.53	9.91	69.7	5
Case 6	92.6	64.89	53.20	10.37	88.5	2
Case 7	92.9	66.84	55.10	3.12	65.2	3

5. Modeling

Models of dc-dc converters are required to design the controller. Therefore, many modeling researches for PWM converters, which are given either continuous or discrete-time modeling, have been made. However, the sequence of state variables to each other is important for discrete-time modeling. For instance, the demagnetizing time of ${\displaystyle i_{L3}}$, ${\displaystyle {\beta }_1{t}_s}$ can be higher than the total of the phase shift time and the demagnetizing time of ${\displaystyle i_{L4}}$, ${\displaystyle {\beta }_2{t}_s}$ at the five-output converter. Therefore, at least two models, with ${\beta }_1<{\beta }_2$ and ${\beta }_1>{\beta }_2$, are required for this condition when using discrete-time modeling. In addition, the sequence of the state variables is independent to each other with state-space averaging. Moreover, the work in [26] shows that asymptotic stability of the averaged system model implies asymptotic stability of the actual system. Therefore, the controllers can replicate the design of these models.

In this section, two PWM signals are used in order to describe the PWM-PFM-PD control scheme. Therefore, five-output voltages can be regulated independently. First, state-space average (SSA) model is used for the multiple output converter. The large-signal models are nonlinear, and the models are linearized around a desired operating point by Taylor-expansion. After obtaining large and small models of the five-output converter, the models are compared by simulation to verify them. Depending on the small signal model, the dominant poles of the system are placed in the desired points at close-loop. Then, to decrease the steady-state error of the system, error cancellation algorithm is proposed. In the end, the experimental results of the prototype are given to verify the analyses.

All components of the converter are considered ideal. There are ten state variables, ${\displaystyle i_{L1}}$, ${\displaystyle v_{C1}}$, ${\displaystyle i_{L2}}$, ${\displaystyle v_{C2}}$, ${\displaystyle i_{L3}}$, ${\displaystyle v_{C3}}$, ${\displaystyle i_{L4}}$, ${\displaystyle v_{C4}}$, ${\displaystyle i_{L5}}$ and ${\displaystyle v_{C5}}$, to model the converter. When burst mode is on (k > 1), the frequency of ${\displaystyle i_{L4}}$ is different than the main frequency, ${\displaystyle f_1}$. The state variables at the different switching frequencies for SSA is then explained. One of the advantages of SSA is that the state variables can be averaged independently from each other.

5.1. Averaging and Correcting

Suppose the dynamics of a state variable ${\displaystyle x_l}$ of a dc-dc converter can be described by a piecewise-linear state-space model as:

$$\dot{x_l}\left(t\right)={\mathrm{a}}_1{x}_l\left(t\right)\mathrm{for}t\in [0,q_1{t}_s)$$

(19)

$$\dot{x_l}\left(t\right)={\mathrm{a}}_2{x}_l\left(t\right)\mathrm{for}t\in [q_1{t}_s,(q_1+q_2)t_s)$$

(20)

$$\dot{x_l}\left(t\right)={\mathrm{a}}_{\mathrm{i}}{x}_l\left(t\right)\mathrm{for}t\in [(q_1+q_2+\cdots q_{i-1})t_s,(q_1+q_2+\cdots q_i)t_s)$$

(21)

where ${\displaystyle l}$ is the number of state variables, ${\displaystyle q_i}$ is the switching function, ${\displaystyle i}$ is the number of the switching stage (the sub-circuit), and ${\mathrm{a}}_{\mathrm{i}}$ are the state coefficients. Then state-space averaging (SSA) technique can be applied to a state variable that has multiple switching functions according to the following average model:

$$⟨\dot{x_l⟩}\left(t\right)=[q_1{\mathrm{a}}_1+q_2{\mathrm{a}}_2+\cdots q_i{\mathrm{a}}_{\mathrm{i}}]⟨x_l⟩\left(t\right).$$

(22)

Generalizing this procedure, it was taken into account that a state variable may depend on all other state variables. For instance, state variable ${\displaystyle i_{L1}}$ has two stages and each state equation is multiplied by the related switching interval in SSA. When these two stages are multiplied by the related switching interval ${\displaystyle {\delta }_1{t}_s}$ and ${\displaystyle (1-{\delta }_1)t_s}$, they become:

$$L_1⟨\dot{i_{L1}}⟩\left(t\right)=(⟨v_{in}⟩\left(t\right)-⟨v_{C1}⟩\left(t\right)){\delta }_1{t}_s+(-⟨v_{C1}⟩\left(t\right))(1-{\delta }_1)t_s,$$

(23)

And, after simplification:

$$⟨\dot{i_{L1}}⟩\left(t\right)=t_s\frac{({\delta }_1⟨v_{in}⟩\left(t\right)-⟨v_{C1}⟩\left(t\right))}{L_1}.$$

(24)

Now consider that all state variables (${\displaystyle i_{L1}}$, ${\displaystyle v_{C1}}$, ${\displaystyle i_{L2}}$, ${\displaystyle v_{C2}}$, ${\displaystyle i_{L3}}$, ${\displaystyle v_{C3}}$, ${\displaystyle i_{L4}}$, ${\displaystyle v_{C4}}$, ${\displaystyle i_{L5}}$, ${\displaystyle v_{C5}}$) and input(s) (${\displaystyle v_{in}}$) in Figure 12a are subjected to this averaging, then the differential equations that describe the multiple-output converter can be defined in vector notation as:

$$\dot{\mathit{x}}={\mathbf{A}}_{\mathbf{av}}\mathit{x},$$

(25)

in which the state vector x and coefficient matrix ${\mathbf{A}}_{\mathbf{av}}$ are:

$$\begin{array}{c}\hfill \mathit{x}=[⟨i_{L1}⟩,⟨v_{C1}⟩,⟨i_{L2}⟩,⟨v_{C2}⟩,⟨i_{L3}⟩,\\ \hfill ⟨v_{C3}⟩,⟨i_{L4}⟩,⟨v_{C4}⟩,& ⟨i_{L5}⟩,⟨v_{C5}⟩,⟨v_{in}⟩{]}^T,\hfill \end{array}$$

(26)

$${\mathbf{A}}_{\mathbf{av}}=\left[\begin{array}{ccccccccccc}0& -\frac{1}{L_1}& 0& 0& 0& 0& 0& 0& 0& 0& \frac{{\delta }_1}{L_1}\\ \frac{1}{C_1}& -\frac{1}{C_1{R}_1}& 0& 0& -\frac{n_1{h}_1}{C_1}& 0& 0& 0& \frac{n_3{h}_3}{C_1}& 0& 0\\ 0& 0& 0& -\frac{1}{L_2}& 0& 0& 0& 0& 0& 0& \frac{{\delta }_2}{L_2}\\ 0& 0& 0& -\frac{1}{C_2{R}_2}& 0& 0& -\frac{n_2{h}_2}{C_2}& 0& \frac{n_3{h}_3}{C_2}& 0& 0\\ 0& \frac{n_1{h}_1}{L_3}& 0& 0& 0& -\frac{h_1}{L_3}& 0& 0& 0& 0& -\frac{n_1{\beta }_1}{L_3}\\ 0& 0& 0& 0& \frac{h_1}{C_3}& -\frac{1}{C_3{R}_3}& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{n_2{h}_2}{L_4}& 0& 0& 0& \frac{-h_2}{L_4}& 0& 0& -\frac{n_2{\beta }_2}{L_4}\\ 0& 0& 0& 0& 0& 0& \frac{h_2}{C_4}& -\frac{1}{C_4{R}_4}& 0& 0& 0\\ 0& \frac{-n_3{h}_3}{L_5}& 0& \frac{-n_3{h}_3}{L_5}& 0& 0& 0& 0& 0& \frac{-h_3}{L_5}& \frac{n_3(2{\delta }_3+{\beta }_3)}{L_5}\\ 0& 0& 0& 0& 0& 0& 0& 0& \frac{h_3}{C_5}& -\frac{1}{C_5{R}_5}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right],$$

(27)

where

$$h_1=(1-{\delta }_1+{\beta }_1),$$

(28)

$$h_2=(1-{\delta }_2+{\beta }_2)\mathrm{and}$$

(29)

$$h_3=({\delta }_3+{\beta }_3).$$

(30)

PWM converters that are operated in CCM have two switching intervals: the active switch is either on (${\displaystyle q_1}$) or off (${\displaystyle q_2}$). In CCM, the average of the derivatives of the inductor current is the same as the product of the averages; and SSA is equal to explicit averaging of the circuit equations. Contrary to CCM, DCM operation involves an additional interval where the inductor currents and therefore its average is zero, and the average of this third interval is zero. In addition, in DCM the average of the product terms ${\displaystyle [q_1{\mathrm{a}}_1+q_2{\mathrm{a}}_2+q_3{\mathrm{a}}_3]i_L}$ is not the same as the averaged product of the individual waveforms. The studies described in [27,28] explain this situation and offer a correction matrix. The difference between the actual average and SSA charging currents is shown, based on [27] in Table 10. The matrix $\mathbf{M}$ corrects mismatch of the inductor currents in DCM as follows:

$$\mathbf{M}=\mathrm{diag}\left[\begin{array}{cccccccccc}1& 1& 1& 1& \frac{1}{(1-{\delta }_1+{\beta }_1)}& 1& \frac{1}{(1-{\delta }_2+{\beta }_2)}& 1& \frac{1}{({\delta }_3+{\beta }_3)}& 1\end{array}\right].$$

(31)

Table 10. Charging capacitors over the entire period using an inductor operating in DCM.

SSA Equivalent	Actual Equivalent
Charging Current	Charging Current
${\displaystyle i_{L3,pk}{(1-{\delta }_1+{\beta }_1)}^2/2}$	${\displaystyle i_{L3,pk}(1-{\delta }_1+{\beta }_1)/2}$
${\displaystyle i_{L4,pk}{(1-{\delta }_2+{\beta }_2)}^2/2}$	${\displaystyle i_{L4,pk}(1-{\delta }_2+{\beta }_2)/2}$
${\displaystyle i_{L5,pk}{({\delta }_3+{\beta }_3)}^2/2}$	${\displaystyle i_{L5,pk}({\delta }_3+{\beta }_3)/2}$

With this correction matrix, the modified SSA model in (25) becomes:

$$\dot{\mathit{x}}={\mathbf{A}}_{\mathbf{av}}\mathbf{M}\mathit{x}.$$

(32)

5.2. Full-Order Averaged Models

It is possible to calculate what the average of the inductor currents is from the peak value of the inductor currents without requiring the demagnetizing duration ratios ${\displaystyle {\beta }_1}$, ${\displaystyle {\beta }_2}$ and ${\displaystyle {\beta }_3}$. The peak current of the inductor currents is defined as:

$$i_{L3,pk}=\frac{(n_1{v}_1-v_3)(1-{\delta }_1)t_s}{L_3},$$

(33)

$$i_{L4,pk}=\frac{(n_2{v}_2-v_4)(1-{\delta }_2)(t_s/k)}{L_4}\mathrm{and}$$

(34)

$$i_{L5,pk}=\frac{(n_3(2v_{in}-v_1-v_2)-v_5){\delta }_3{t}_s}{L_5}.$$

(35)

The average of the inductor currents can then be written as:

$$\begin{array}{cc}\hfill ⟨i_{L3}⟩& =\frac{i_{L3,pk}(1-{\delta }_1+{\beta }_1)}{2}\hfill \\ & =\frac{(n_1{v}_1-v_3)(1-{\delta }_1)(1-{\delta }_1+{\beta }_1)t_s}{2L_3},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill ⟨i_{L4}⟩& =\frac{i_{L4,pk}(1-{\delta }_2+{\beta }_2)}{2}\hfill \\ & =\frac{(n_2{v}_2-v_4)(1-{\delta }_2)(1-{\delta }_2+{\beta }_2)(t_s/k)}{2L_4},\mathrm{and}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill ⟨i_{L5}⟩& =\frac{i_{L5,pk}({\delta }_3+{\beta }_3)}{2}\hfill \\ & =\frac{(n_3(2v_{in}-v_1-v_2)-v_5){\delta }_3({\delta }_3+{\beta }_3)t_s}{2L_5}.\hfill \end{array}$$

(38)

The demagnetizing duration ratios of the inductors operated in DCM can be found from the average value of the inductor currents, (36)–(38). Hence, the new demagnetizing constraints for the multiple output converter are:

$${\beta }_1=\frac{2L_3⟨i_{L3}⟩}{t_s(n_1{v}_1-v_3)(1-{\delta }_1)}-(1-{\delta }_1),$$

(39)

$${\beta }_2=\frac{2L_4⟨i_{L4}⟩}{(t_s/k)(n_2{v}_2-v_4)(1-{\delta }_2)}-(1-{\delta }_2)\mathrm{and}$$

(40)

$${\beta }_3=\frac{2L_5⟨i_{L5}⟩}{t_s(n_3(2v_{in}-v_1-v_2)-v_5){\delta }_3}-{\delta }_3.$$

(41)

Substituting these magnetizing durations, (39)–(41), into (32) gives the following full-order averaged model for the converter:

$$\dot{\mathit{x}}={\mathbf{A}}_{\mathbf{f}}(\mathit{x},\mathit{u})\mathit{x}$$

(42)

with

$${\mathbf{A}}_{\mathbf{f}}(\mathit{x},\mathit{u})=[\begin{array}{ccccccccccc}\begin{array}{c}0\end{array}& -\frac{1}{L_1}& 0& 0& 0& 0& 0& 0& 0& 0& \frac{{\delta }_1}{L_1}\\ \frac{1}{C_1}& -\frac{1}{C_1{R}_1}& 0& 0& -\frac{n_1}{C_1}& 0& 0& 0& \frac{n_3}{C_1}& 0& 0\\ 0& 0& 0& -\frac{1}{L_2}& 0& 0& 0& 0& 0& 0& \frac{{\delta }_2}{L_2}\\ 0& 0& \frac{1}{C_2}& -\frac{1}{C_2{R}_2}& 0& 0& -\frac{n_2}{C_2}& 0& \frac{n_3}{C_2}& 0& 0\\ 0& 0& 0& 0& a_1& 0& 0& 0& 0& 0& \frac{n_1(1-{\delta }_1)}{L_3}\\ 0& 0& 0& 0& \frac{1}{C_3}& -\frac{1}{C_3{R}_3}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& a_2& 0& 0& 0& \frac{n_2(1-{\delta }_2)}{L_4}\\ 0& 0& 0& 0& 0& 0& \frac{1}{C_4}& -\frac{1}{C_4{R}_4}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& a_3& 0& \frac{n_3{\delta }_3}{L_5}\\ 0& 0& 0& 0& 0& 0& 0& 0& \frac{1}{C_5}& -\frac{1}{C_5{R}_5}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}],$$

(43)

where

$$a_1=\frac{2}{t_s(1-{\delta }_1)}\left(1-\frac{n_1{v}_{in}}{(n_1{v}_{C1}-v_{C3})}\right),$$

(44)

$$a_2=\frac{2}{(t_s/k)(1-{\delta }_2)}\left(1-\frac{n_2{v}_{in}}{(n_2{v}_{C2}-v_{C4})}\right)\mathrm{and}$$

(45)

$$a_3=\frac{2}{t_s{\delta }_3}\left(1-\frac{n_3{v}_{in}}{(n_3(2v_{in}-v_{C1}-v_{C2})-v_{C5})}\right),$$

(46)

$$\begin{array}{c}\hfill \mathit{x}=[⟨i_{L1}⟩,⟨v_{C1}⟩,⟨i_{L2}⟩,⟨v_{C2}⟩,⟨i_{L3}⟩,\\ \hfill ⟨v_{C3}⟩,⟨i_{L4}⟩,⟨v_{C4}⟩,& ⟨i_{L5}⟩,⟨v_{C5}⟩,⟨v_{in}⟩{]}^T,\hfill \end{array}$$

(47)

$$\mathit{u}={[{\delta }_1,{\delta }_2,f_1,k,{\delta }_3]}^T.$$

(48)

The state matrix includes switching frequency information, as shown in (43)–(46). Therefore, the model is able to predict correctly even when the frequencies are different and the burst mode is active. In fact, the frequency information of ${\displaystyle i_{L4}}$ is defined as ${\displaystyle t_s/k}$ in (45), and, depending on the value of ${\displaystyle k}$, the state variable ${\displaystyle i_{L4}}$ changes correspondingly.

5.3. Linearization

The large-signal model is nonlinear since the state matrix ${\mathbf{A}}_{\mathbf{f}}$ in (43) changes for each operating point. The matrix can be rewritten in the following form:

$$\dot{\mathit{x}}=\mathbf{F}(\mathit{x},\mathit{u})\approx \mathbf{A}({\mathit{x}}^{*},{\mathit{u}}^{*})(\mathit{x}-{\mathit{x}}^{*})+\mathbf{B}({\mathit{x}}^{*},{\mathit{u}}^{*})(\mathit{u}-{\mathit{u}}^{*}),$$

(49)

where the state variable and the input vectors are:

$$\begin{array}{c}\hfill \mathit{x}=[⟨i_{L1}⟩,⟨v_{C1}⟩,⟨i_{L2}⟩,⟨v_{C2}⟩,⟨i_{L3}⟩,\\ \hfill ⟨v_{C3}⟩,⟨i_{L4}⟩,⟨v_{C4}⟩,& ⟨i_{L5}⟩,⟨v_{C5}⟩,⟨v_{in}⟩{]}^T,\hfill \end{array}$$

(50)

$$\mathit{u}={[{\delta }_1,{\delta }_2,f_1,k,{\delta }_3]}^T.$$

(51)

The function in (49) is linearized by taking the first-order Taylor approximation around the operating point ${\displaystyle [{\mathit{u}}^{*},{\mathit{x}}^{*}]}$, according to:

$$\frac{\partial (\mathit{x}-{\mathit{x}}^{*})}{dt}=\frac{\partial \mathrm{F}(\mathit{x},\mathit{u})}{\partial \mathit{x}}{|}_{{\mathit{x}}^{*},{\mathit{u}}^{*}}(\mathit{x}-{\mathit{x}}^{*})+\frac{\partial \mathrm{F}(\mathit{x},\mathit{u})}{\partial \mathit{u}}{|}_{{\mathit{x}}^{*},{\mathit{u}}^{*}}(\mathit{u}-{\mathit{u}}^{*}),$$

(52)

where ${\displaystyle \frac{\partial \mathbf{F}(\mathit{x},\mathit{u})}{\partial \mathit{x}}{|}_{{\mathit{x}}^{*},{\mathit{u}}^{*}}=\mathbf{A}({\mathit{x}}^{*},{\mathit{u}}^{*})}$ is the Jacobian matrix of ${\displaystyle \mathbf{F}(\mathit{x},\mathit{u})}$ with respect to the ${\displaystyle \mathit{x}}$ vector, and ${\displaystyle \frac{\partial \mathbf{F}(\mathit{x},\mathit{u})}{\partial \mathit{u}}{|}_{{\mathit{x}}^{*},{\mathit{u}}^{*}}=\mathbf{B}({\mathit{x}}^{*},{\mathit{u}}^{*})}$ is the Jacobian matrix of ${\displaystyle \mathbf{F}(\mathit{x},\mathit{u})}$ with respect to the ${\displaystyle \mathit{u}}$ vector.

5.4. Discretization

The obtained SSA models in (49) are continuous, and they need to be discretized to be applicable to digital control. The discrete model can be described as:

$$\mathit{x}[l+1]=\mathbf{\Phi }\left[l\right]\mathit{x}\left[l\right]+\mathbf{\Gamma }\mathit{u}\left[l\right],$$

(53)

$$\mathbf{y}\left[l\right]=\mathbf{C}\mathit{x}\left[l\right],$$

(54)

where

$$\mathbf{\Phi }=e^{\mathbf{A}{t}_s}$$

(55)

$$\mathbf{\Gamma }={\int }_0^{t_s}\left(e^{\mathbf{A}(t_s-\tau )}d\tau \right)\mathbf{B}={\mathbf{A}}^{-1}(\mathbf{\Phi }-\mathbf{I})\mathbf{B},$$

(56)

where $\mathbf{I}$ is the identity matrix, and ${\displaystyle t_s}$ is the sampling time of the discrete model. As ${\displaystyle t_s}$ is equal to the switching period of the converter, it is a variable.

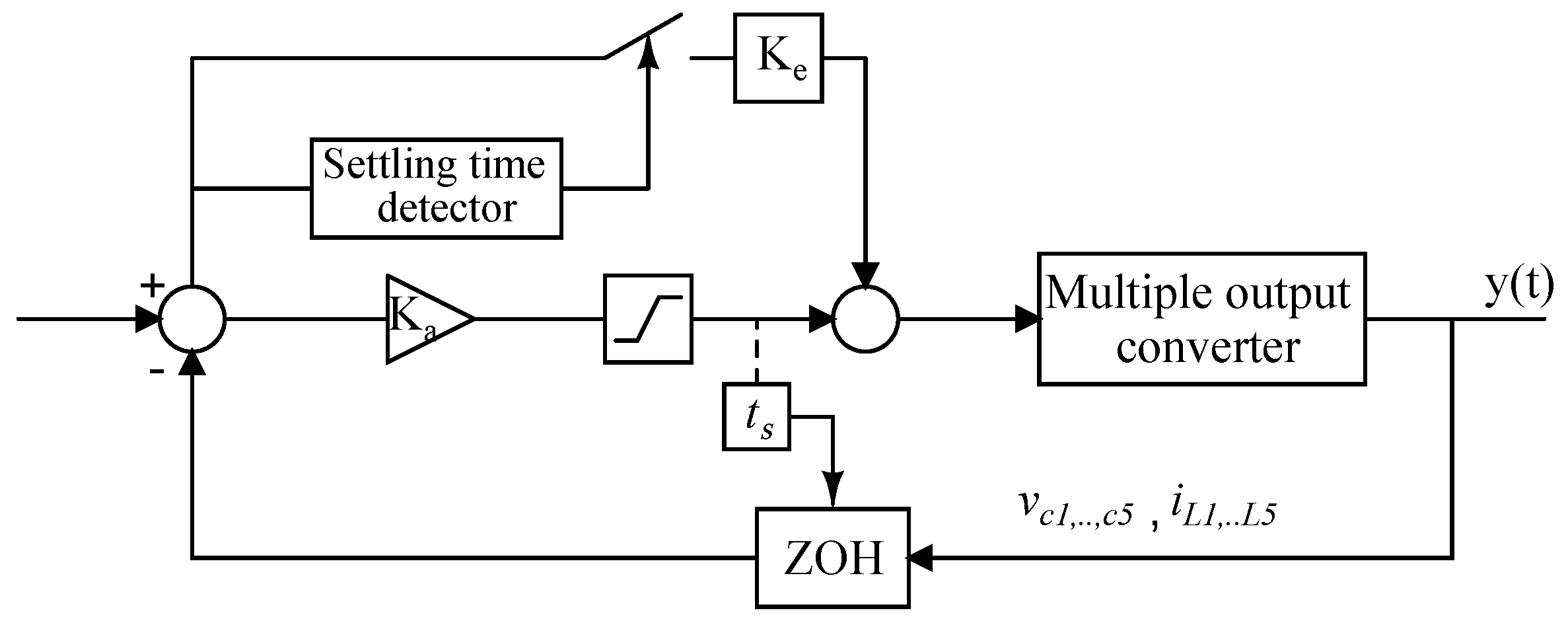
The analog-to-digital converter (ADC) of the system microcontroller is triggered by this variable switching period, as depicted in Figure 16. The microcontroller captures the inputs with a sample-hold circuit, and the data is kept constant until the next sample. The microcontroller also holds the outputs after the starting point of the PWM sequence.

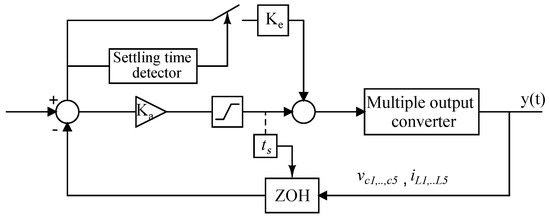
Figure 16. Closed-loop block diagram of a state-feedback controller with error cancelation function.

6. Digital Control of Multiple-Output Converters

In this section, the output voltage regulation of a multiple-output converter is studied.

PID (proportional-integral-derivative) controllers are still very popular in many control applications thanks to their simple structure and performance. Integral action, which indicates infinite loop gain at steady-state, guarantees zero steady-state tracking error, and zero steady-state effect of constant output disturbances. In general, the excessive integral gain yields closed-loop instability. As state variables of multiple input-multiple output (MIMO) affect each other, oscillation is caused more critical than for single input-single output (SISO) systems [29]. This is the reason why regulating a multiple-output converter is complicated: there are interdependencies between the different outputs. To solve this kind of regulation problem, digital control provides many options. Sophisticated algorithms and accurate calculation can be implemented in microcontrollers or even field programmable gate arrays (FPGAs).

6.1. Pole Placement by Digital State Feedback

According to [30], the poles of a closed-loop system can be placed in any desired location by manipulating the state feedback gains. These techniques can be applied to a system of any order.

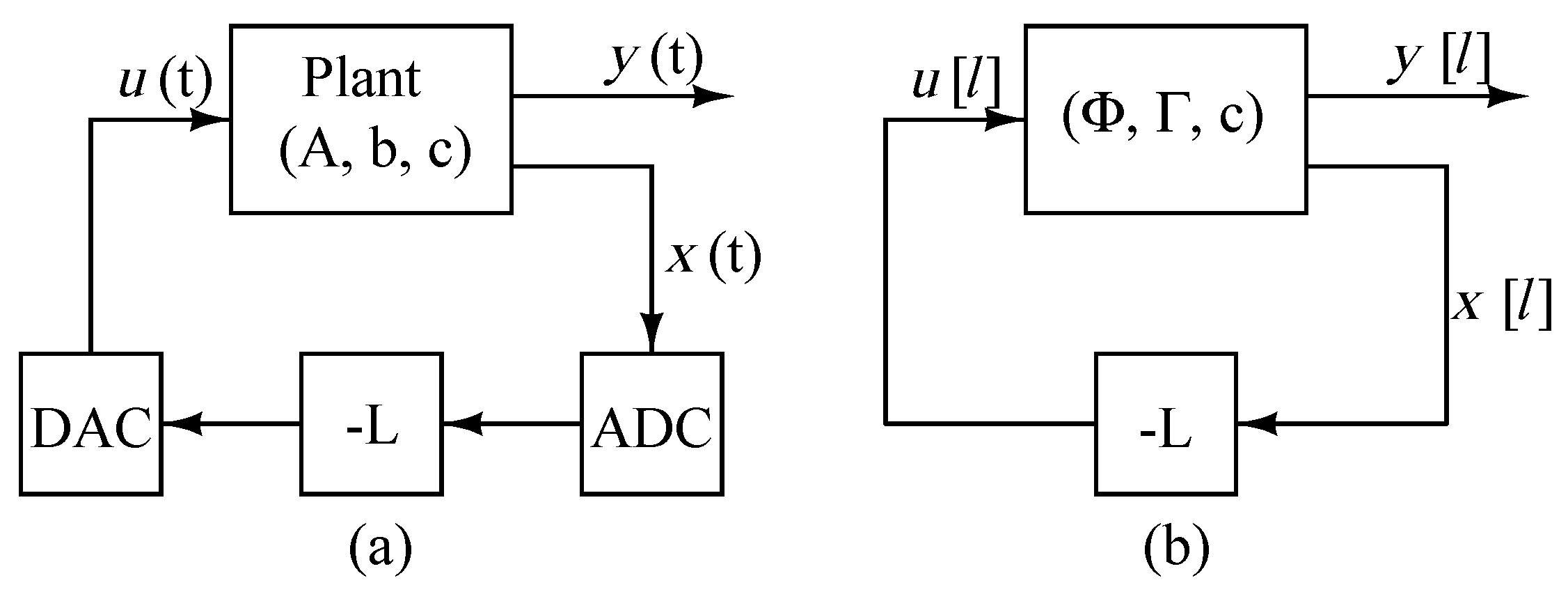
A multiple-output converter system controlled by a discrete-time control platform and having variable switching frequency is shown in Figure 16. A system which is regulated by a feedback vector -$\mathbf{L}$ is depicted in Figure 17a. All of the state variables ${\displaystyle \mathit{u}\left[t\right]}$ are sampled by ADCs, and these variables are weighted by the state-feedback gains to result in the plant input vector $\mathit{u}$[$\mathit{l}$]. Next, these variables are transformed back to the analog domain using digital-to-analog converters (DACs). The ZOH equivalent of the plant is shown in Figure 17b, and it is described with (53). The equation for the feedback gain is:

$$\mathit{u}\left[l\right]=-\mathbf{L}\mathit{x}\left[l\right].$$

(57)

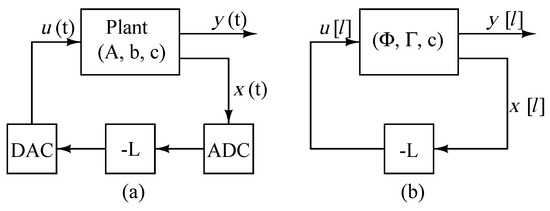
Figure 17. (a) A regulation system using digital state feedback; (b) A zero-order hold (ZOH) design model for digital state feedback.

Substituting (53) into (57) gives:

$$\mathit{x}[l+1]=\mathbf{\Phi }\left[l\right]\mathit{x}\left[l\right]+\mathbf{\Gamma }(-\mathbf{L}\mathit{x}[l\left]\right)=(\mathbf{\Phi }[l]-\mathbf{L}\mathbf{\Gamma }[l\left]\right)\mathit{x}\left[l\right].$$

(58)

The vector of feedback gains $\mathbf{L}$ is calculated from (58), and the eigenvalues of the closed system set to their the desired values. The Matlab function “place” is used to calculate $\mathbf{L}$ [31].

Choosing the Settling Interval

The speed of the controller is desired to be as fast as possible. The deadbeat control is one of the most popular control methods, as the steady-state error goes to zero in a finite number of switching periods [30]. This approach supplies a faster dynamic response than other control techniques.

If the poles of a continuous-time closed-loop system are moved far left in the s domain, the system response becomes faster. Using the fact that from the formula $z=e^{s{t}_s}$ it follows that s = −∞ maps to z = 0, the z-domain poles should be moved to the origin of the z plane in order to make the system as fast as possible. This method is called deadbeat control. According to the Cayley-Hamilton Theorem, “deadbeat" means that the eigenvalues of the $(\mathbf{\Phi }[l]-\mathbf{L}\mathbf{\Gamma }[l\left]\right)$ matrix are made zero when:

$${(\mathbf{\Phi }\left[l\right]-\mathbf{\Gamma }\left[l\right]\mathbf{L})}^d=0,$$

(59)

where d is the dimension of the system. Therefore,

$$\mathit{x}\left[l\right]={(\mathbf{\Phi }\left[l\right]-\mathbf{L}\mathbf{\Gamma }\left[l\right])}^d\mathit{x}\left[0\right]=0.$$

(60)

It follows from (60) that the regulator moves the poles to zero in order to settle ${\displaystyle d}$ time steps. In theory, the settling time of the regulator therefore becomes ${\displaystyle d{t}_s}$ seconds. If the feedback gain is made higher than described by (60), a damped oscillation is observed at half the sampling frequency [32]. Moreover, parameter mismatches of the model, model uncertainties, and noise from the measurement signals can cause a steady-state error and reduce the settling time. One of the disadvantages of deadbeat controllers is that measurements are needed to adjust the feedback gains, using trial and error [33]. The component values of the converters, such as inductance, capacitance, and resistance, will vary, e.g., because of temperature effects and aging.

This causes variation in $\mathbf{\Phi }\left[l\right]$ and $\mathbf{\Gamma }\left[l\right]$ and thus in the pole locations. Another drawback of the deadbeat technique is that, because the processor forces the control signal to match the state variables to the reference in ${\displaystyle d{t}_s}$ seconds, the control signal can saturate, and then the settling time becomes much longer than the expected ${\displaystyle d{t}_s}$ seconds.

As the settling time of buck converters operated at CCM (the 1st and 2nd outputs) is higher than those at DCM (the 3rd, 4th and 5th outputs), the maximum settling time can be analyzed depending on these CCM outputs.

A buck converter with an appropriate deadbeat controller was simulated in LTspice IV. The parameters of the buck converter are: inductor 150 $\mathsf{\mu }$H, capacitor 40 $\mathsf{\mu }$F, load 10 $\Omega$, switching frequency 150 kHz, feedback gains 0.9 (for current) and 1.05 (for voltage). The duty cycle ${\displaystyle V_{\delta 1}}$ settles in 2${\displaystyle t_s}$ when the input voltage ${\displaystyle V_{in}}$ is changed from 23 V to 24 V. The maximum duty cycle settles at 0.9, and the duty cycle saturates, when the change of input voltage is increased substantially, such as from 19 V to 24 V. The settling time becomes 7${\displaystyle t_s}$ instead of 2${\displaystyle t_s}$.

The settling time was chosen as 10${\displaystyle t_s}$ to make the results robust against component variations and saturation effects. $\mathbf{L}$ was chosen depending on the settling time, and Bessel polynomials were used for the controller prototype [30].

6.2. Error Cancelation

6.2.1. Settling Time Detector

In Section 6.1, the steady-state error problem is mentioned. In order to detect this steady-state error, the system under control first needs to settle. Accordingly, a settling time detector is used to detect whether the system is in the steady-state, as shown in Figure 16a.

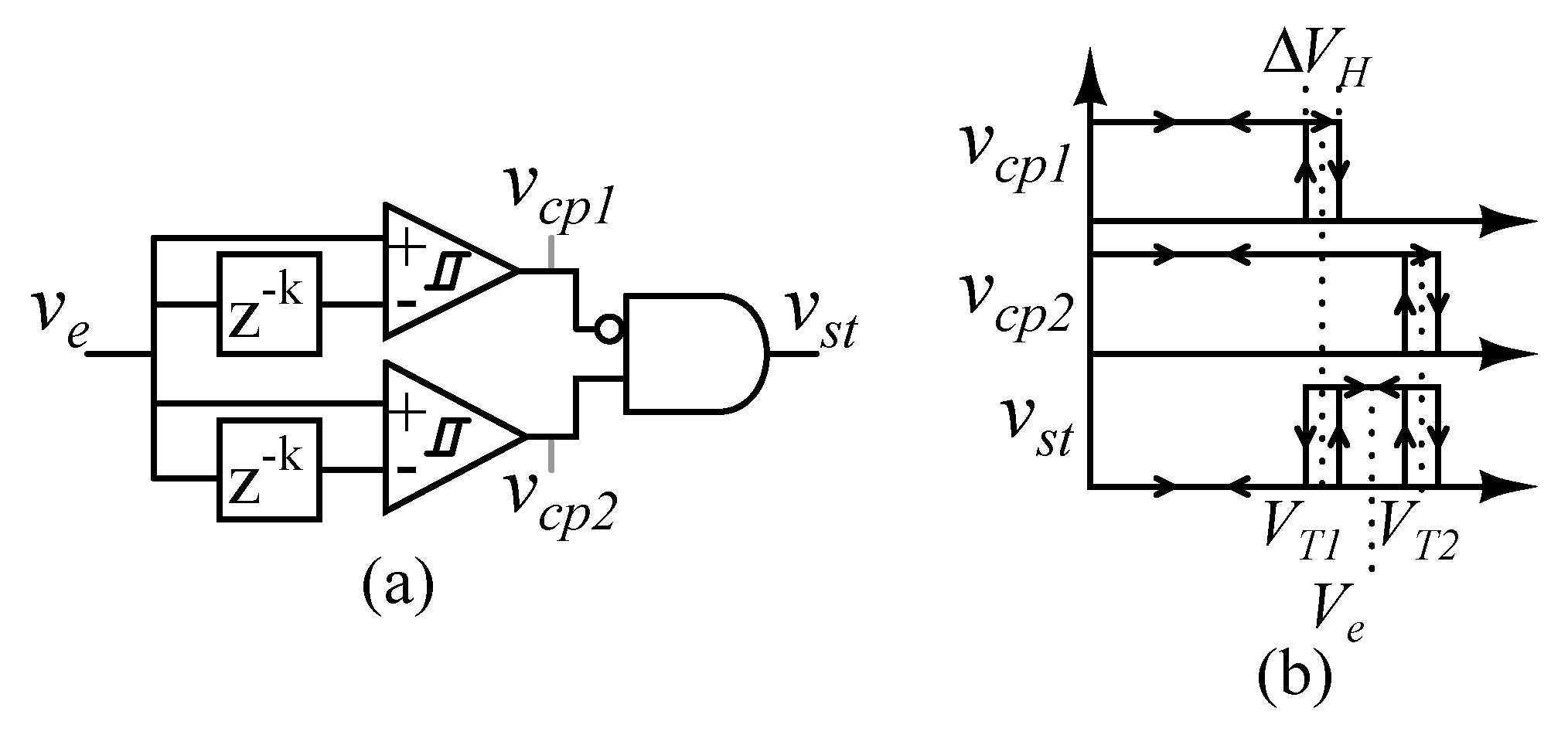
After the system reaches the steady-state, the change in the error is approximately zero. Following reference [34], an analog circuit is used to detect the settling time of a signal. To detect its change, a signal can be compared to a delayed copy of itself. The input signal and the delayed signal are therefore connected to two hysteresis comparators, as shown in Figure 18a.

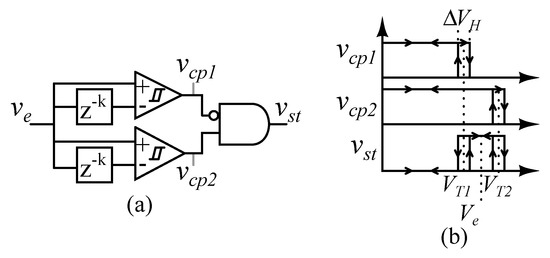
Figure 18. (a) The block diagram of the detection circuit; (b) Output signals of the comparators and “and” gate as function of the delayed input signal.

The delayed error signal can be smaller or greater than the error signal during the transient. Therefore, two hysteresis comparators are used to cover both cases, as shown in Figure 18b. The threshold voltages ${\displaystyle V_{T1}}$ and ${\displaystyle V_{T2}}$ are selected to be close to the expected error signal ${\displaystyle V_e}$, which is zero, as shown in Figure 18b. The comparators are designed with hysteresis to avoid oscillations at the comparator outputs [34].

6.2.2. Cancelation Algorithm

The system is modeled without considering the voltage drop of diodes, the losses caused by parasitic components or the uncertainties- and the nonlinear characteristics-of components. Therefore, the required control effort could be larger than the predicted one. In each period, errors are made in the control parameter calculations, and these ultimately cause a steady-state error. In order to compensate for this, an error cancelation scheme is introduced. This circuit becomes active when the controller error signal stops changing.

The required control parameters are calculated using the small-signal model. Because the calculation depends on ideal components, in practice cross-regulation issues cause offsets from the desired output values. This procedure is therefore repeated until such time that the output voltages are inside the requested tolerance band.

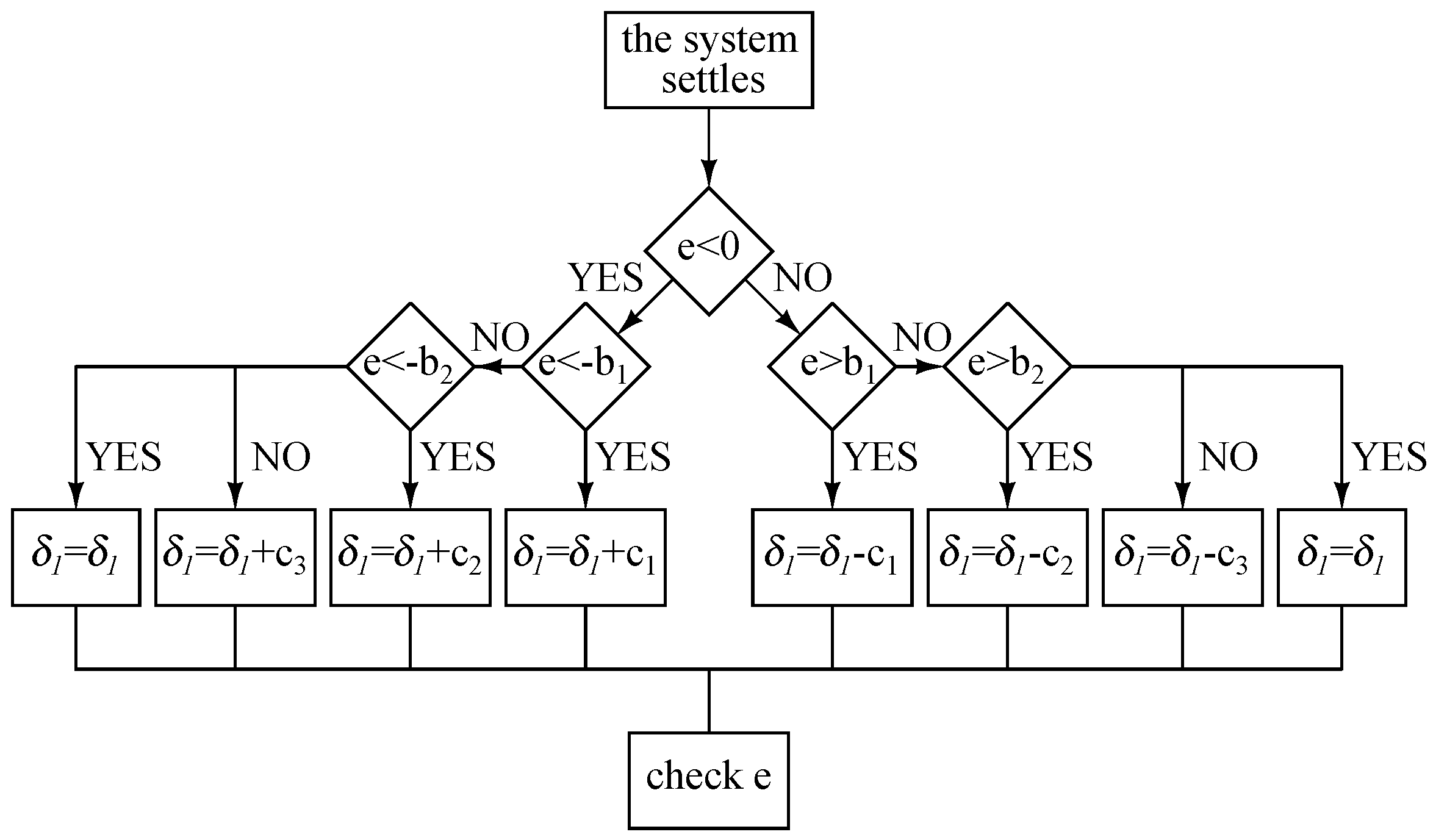
Figure 19 shows the steady-state error cancelation algorithm for the first output voltage ${\displaystyle v_1}$. As ${\displaystyle {\delta }_1}$ is the control parameter of ${\displaystyle v_1}$, ${\displaystyle {\delta }_1}$ is decreased or increased, depending on the amount of error. The same algorithm is issued for the other output voltages.

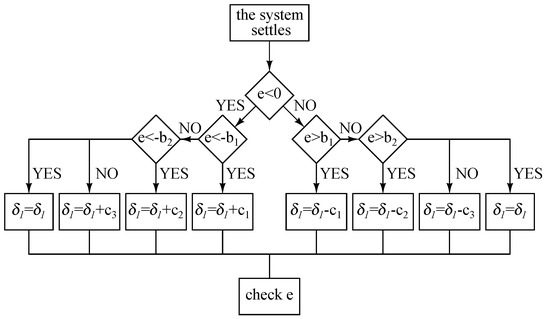
Figure 19. Steady-state error(e) cancelation algorithm for the ${\displaystyle {\delta }_1}$ control parameter.

6.3. Experimental Results with the Close-Loop Five-Output Prototype

As proof of concept, a five-output closed-loop converter was built. The schematic of the converter is depicted in Figure 12a. The same power circuit was used as in the previous chapter. A C2000 Delfino F28379D microcontroller functioned as a controller to measure the state variables and to generate all gate signals. A PWM module of the microcontroller was used for each pulse of the burst mode PWM signal. In total, five PWM modules were used and these five signals were connected to an OR gate. Measurements circuits were used between the microcontroller and the output voltages ${\displaystyle v_1,v_2,v_3,v_4}$ and ${\displaystyle v_5}$.

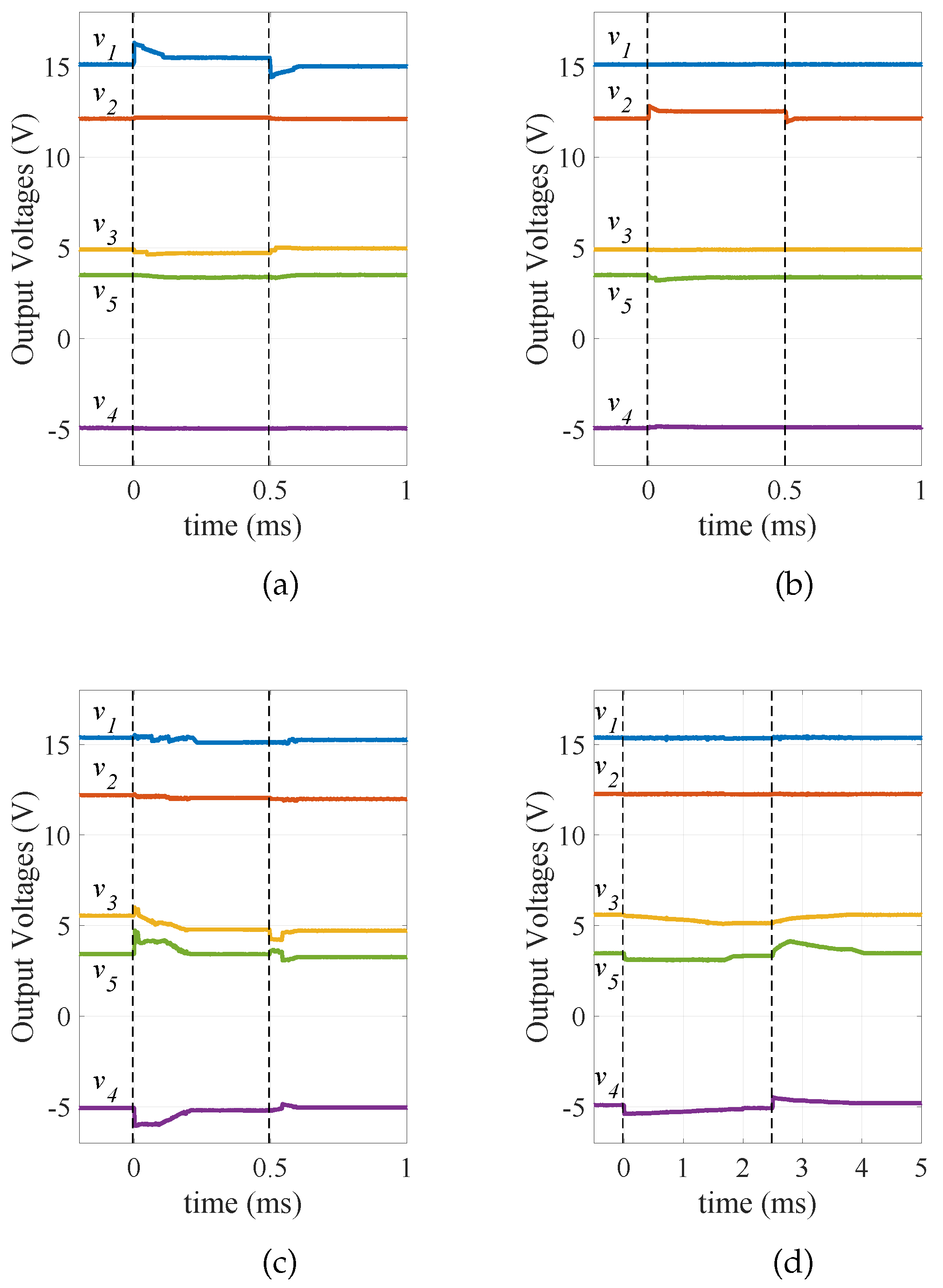
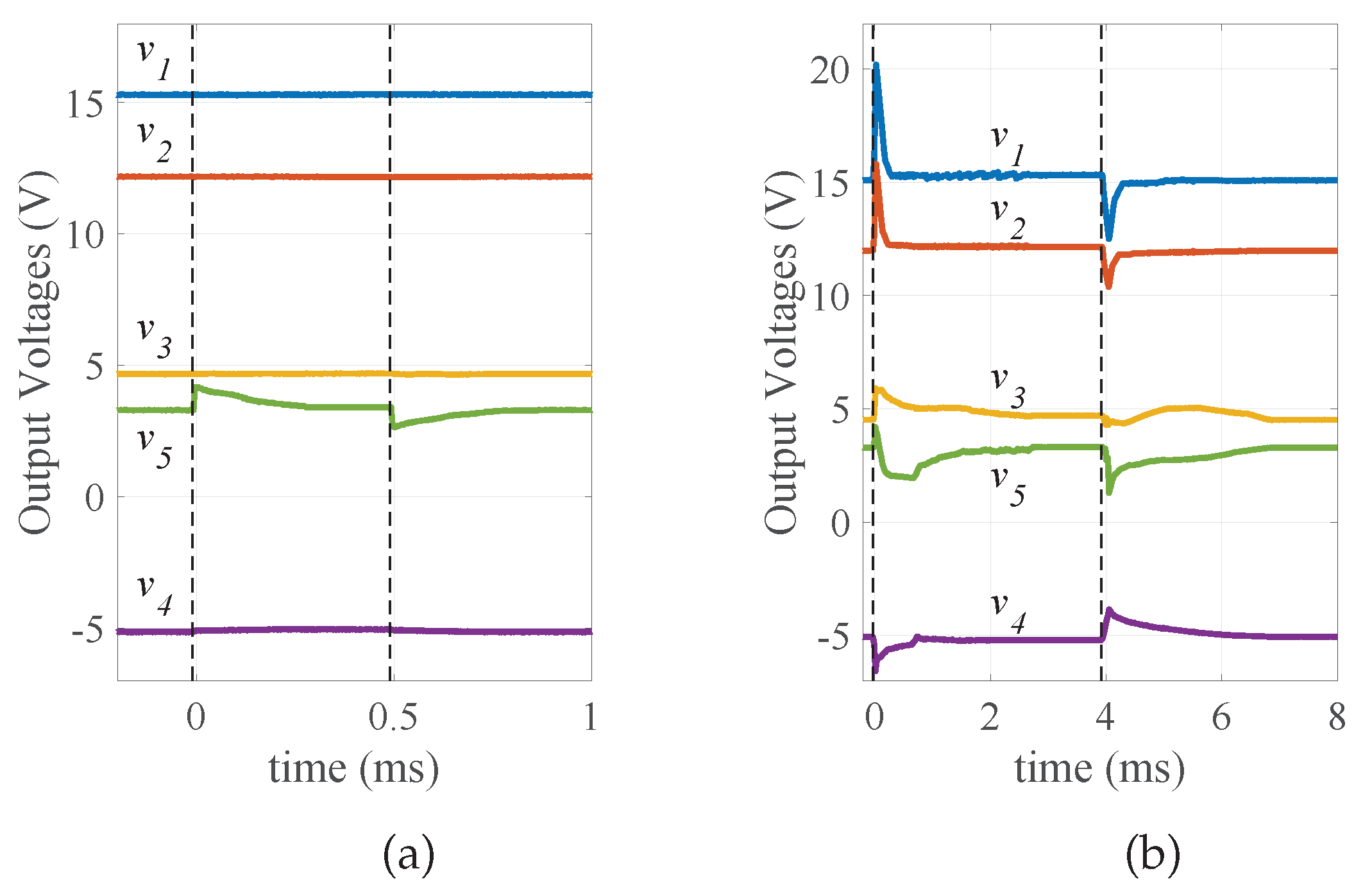
Experimental results for load and input voltage changes are shown in Figure 20 and Figure 21. Initially the five-output converter is in steady-state. Each output current is changed one at a time, keeping the the other output currents constant. Finally, the input voltage is changed.

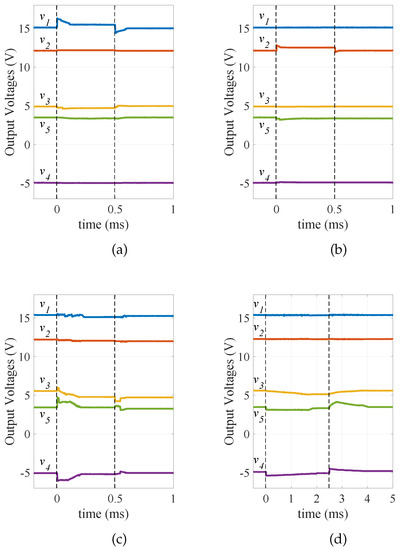
Figure 20. Experimental results from the closed-loop five-output prototype: Output voltage responses (a) when the first output current changes from 1.5 A to 0.75 A, and from 0.75 A to 1.5 A; (b) when the second output current changes from 1.5 A to 1 A, and from 1 A to 1.5 A; (c) when the third output current changes from 0.8 A to 0.5 A, and from 0.5 A to 0.8 A; (d) when the fourth output current changes from 0.6 A to 0.4 A, and from 0.4 A to 0.6 A.

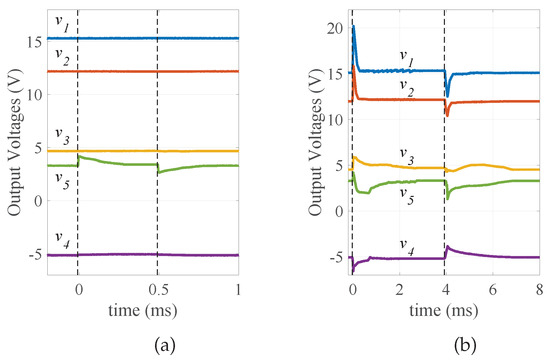
Figure 21. Experimental results from the closed-loop five-output prototype: Output voltage responses (a) when the fifth output current changes from 0.45 A to 0.3 A, and from 0.3 A to 0.45 A; (b) when the input voltage changes from 21 A to 30 V, and from 30 V to 21 V.

As shown in Figure 20a, at t = 0 s, the first output current ${\displaystyle i_1}$ is stepped down from 1.5 A to 0.75 A, and at t = 0.5 ms, ${\displaystyle i_1}$ is stepped up from 0.75 A to 1.5 A. The change at ${\displaystyle i_1}$ affects ${\displaystyle v_3}$, because ${\displaystyle {\delta }_1}$ is also a control parameter of ${\displaystyle v_3}$. The controller adjusts ${\displaystyle f_1}$ from 82.4 kHz to 66.3 kHz in order to keep ${\displaystyle v_3}$ at the desired voltage.

Likewise, at t = 0 s, the second output current ${\displaystyle i_2}$ is stepped down from 1.5 A to 1 A, and at t = 0.5 ms, ${\displaystyle i_2}$ is stepped back up to 1.5 A, as shown in Figure 20b. The controller reduces ${\displaystyle {\delta }_2}$ from 67.3% to 66.3% to keep ${\displaystyle v_2}$ at 12 V after the change at t = 0 s. Since ${\displaystyle {\delta }_2}$ is a control parameter of ${\displaystyle v_4}$, ${\displaystyle k}$ increases from 3 to 5.

Furthermore, at t = 0 s, the third-output current ${\displaystyle i_3}$ is stepped down from 0.8 A to 0.5 A, and at t = 0.5 ms, ${\displaystyle i_3}$ is stepped back to 0.8 A, as shown in Figure 20c. As the main control parameter of ${\displaystyle v_3}$ is ${\displaystyle f_1}$, the change of ${\displaystyle f_1}$ affects ${\displaystyle v_4}$ and ${\displaystyle v_5}$. This happens because they are operated in DCM and are synchronized to ${\displaystyle f_1}$. There is some hunting around of ${\displaystyle v_1}$ and ${\displaystyle v_2}$, because of cross-regulation issues. However, the system eventually finds the steady-state operating points.

Next, at t = 0 s, the fourth output current ${\displaystyle i_4}$ is stepped down from 0.6 A to 0.4 A, and at t = 2.5 ms, ${\displaystyle i_4}$ is stepped back to 0.6 A as shown in Figure 20d. ${\displaystyle k}$ is changed from 3 to 5 after the change at t = 0 s. This change affects other outputs, and accordingly ${\displaystyle f_1}$ decreases from 85.5 kHz to 69.7 kHz. This is why the settling time needed for the system to recover from this change is longer than for the previous changes.

The fifth output current ${\displaystyle i_5}$ is stepped down from 0.45 A to 0.33 A at t = 0 s, and ${\displaystyle i_6}$ is stepped back to 0.45 A as seen in Figure 21a at t = 0.5 ms. The phase delay ratio ${\displaystyle {\delta }_{PD}}$ is the only control parameter of ${\displaystyle v_5}$. Therefore, changes of only ${\displaystyle v_5}$ are observed, as shown Figure 21a, when ${\displaystyle {\delta }_{PD}}$ is increased from 33.5% to 42.0%.

Lastly, the input voltage is changed from 21 V to 30 V at t = 0 s, and from 30 V to 21 V at t = 4 ms. This change affects all the outputs, so regulation is apparent at every output in Figure 21b.

7. Conclusions

This paper introduces methods to obtain additional outputs without increasing the number of switches and coils. After proposing new multiple output converters, modeling and a digital controller for multiple output converters are presented.

First, multiple output dc-dc converters with reduced number of active and passive components are presented. Two PWM-PFM controlled two-output topologies, fly-buck and forward-buck, are shown. These two-output converters have only one switch and one coupled inductor to regulate two outputs independently. Then, two topologies controlled by PWM-PD are shown. These three-output converters need only two switches and two coupled inductors to regulate three-outputs independently. The two-output and three-output converters were implemented, and experimental results were obtained to validate the analysis and design procedure. The procedure to obtain PD at the different frequencies is discussed, and then a PWM-PFM-PD method is shown that exploits the full control potential of the two signals. Also, this signal pattern is applied to a five-output converter which has only two switches and two coupled inductors to control five-outputs. The design criteria for this five-output converter are presented, and the analysis is verified experimentally.

Next, a discrete converter model and corresponding control method are proposed for multiple output converters. First, the SSA technique is used to describe the multiple output converter. The application of SSA modeling to a multiple output converter, wherein state variables operate at different frequencies, is also explained.

To verify the regulation, a pole-placement feedback method is applied to the small signal model of the converter after this model is discretized by variable sampling time ZOH. A tuning method is presented to reduce the steady-state error of all the independently regulated outputs.

Finally, a prototype of the close loop system is presented. The controller is implemented with a F28379D microcontroller, and the measurement results of the five-output converter show that the analyses are valid.