Abstract
We discuss mathematical and physical arguments contrasting continuous and discrete, limitless discretization as arbitrary granularity. In this regard, we focus on Incomputable (lacking an algorithm that computes in finite time) Real Numbers (IRNs). We consider how, for measurements, the usual approach to dealing with IRNs is to approximate to avoid the need for more detailed, unrealistic surveys. In this regard, we contrast effective computation and emergent computation. Furthermore, we consider the alternative option of taking into account the properties of the decimal part of IRNs, such as the occurrence, distribution, combinations, quasi-periodicities, and other contextual properties, e.g., topological. For instance, in correspondence with chaotic behaviors, quasi-periodic solutions, quasi-systems, uniqueness, and singularities, non-computability represents and corresponds to theoretically incomplete properties of the processes of complexity, such as emergence and quantum-like properties. We elaborate upon cases of equivalences and symmetries, characterizing complexity and infiniteness as corresponding to the usage of multiple non-equivalent models that are constructively and theoretically incomplete due to the non-exhaustive nature of the multiplicity of complexity. Finally, we detail alternative computational approaches, such as hypercomputation, natural computing, quantum computing, and analog and hybrid computing. The reality of IRNs is considered to represent the theoretical incompleteness of complex phenomena taking place through collapse from equivalences and symmetries. A world of precise finite values, even if approximated, is assumed to have dynamics that are zippable in analytical formulae and to be computable and symbolically representable in the way it functions. A world of arbitrary precise infinite values with dynamics that are non-zippable in analytical formulae, non-computable, and, for instance, sub-symbolically representable, is assumed to be almost compatible with the coherence of emergence. The real world is assumed to be a continuous combination of the two—functioning and emergent—where the second dominates and is the norm, and the first is the locus of primarily epistemic extracts. Research on IRNs should focus on properties representing and corresponding to those that are detectable in real, even if extreme, phenomena, such as emergence and quantum phenomena.
1. Introduction
There is an intense discussion of the mathematical and philosophical literature on contrasting continuous and discrete in terms of limitless discretization and arbitrary granularity, using formalistic and constructivist views (see, for example, [,]). For instance, in [], Chaitin writes:
“Mathematicians, however, freely fantasize with infinite-precision real numbers. Nevertheless within pure math the notion of a real number is extremely problematic.”
Here, we consider this problem as being related to the contrast in the discrete–continuum in the infinitesimal (arbitrary small) and the infinite (arbitrary large) as well as the corresponding effective computation versus continuous–emergent computation.
In the first case, we deal with effective computation and its finite, complete attributes (computable numbers are the real numbers that can be computed by a Turing machine terminating in a finite amount of time and with arbitrary precision). In Scheme 1, we present a schematic overview of number types considered in number theory.

Scheme 1.
A schematic representation considered in number theory.
Irrational, decimal unlimited numbers are not computable in a finite amount of time. The continuum seems to be plagued by the problem of the theoretical and practical admissibility of the infinitesimally small. Symmetrically, there is the problem of the infinitely, arbitrarily large, which is more easily admissible but, nevertheless, equally incomputable, as it cannot be computed in a finite amount of time. Approximation and discretization have always been good approaches to dealing with the infinitely small without knowing the trend or the numerically, infinitely small behavior, whereas for the infinitely large, it is important to know the trend and growth hypotheses in order to produce approximations in temporal instances, e.g., in cosmology. It is unrealistic to effectively take both the infinitesimally small and large into account when they are considered effective measurements, whereas it is realistic when dealing with their properties and as representations of phenomena such as the theorical incompleteness of the dynamics of complex systems and the infiniteness of quantum phenomena. Discretization approaches and growth hypotheses, respectively, deal with the infinitesimal (arbitrary small) and the infinite (arbitrary large).
In the second case (emergent computation), we consider the situation where the computation cannot be completely analytically represented and acquired properties cannot be anticipated by considering the formal computation process. This is the case, for instance, for artificial neural networks (ANNs) and cellular automata (CA), as elaborated in Section 2. Examples of cases used in physics are spontaneous symmetry breaking (SSB) and the spontaneous acquisition of roles, such as ergodic (see Section 3.1). We also mention how this second case relates, for instance, to analytically irreducible paths of processes of emergence, and the infiniteness of continuity is a requirement for theoretical incompleteness (closely related to the uncertainty principles in physics, when phenomena are partially represented by multiple non-equivalent models; see Section 3) to represent the phenomenology of emergence, i.e., sequences of equivalences and their collapse under arbitrary weak forces, multiple coherences, and sequences of coherence loss and recovery. Determination of the freedom of emergence between any level of discrete precision and any specific model requires the use of multiple theoretical, inexhaustible, nonconverging modeling stages. The approach used is to induce acquisitions and variations of properties in combination with the usual prescriptive ones. Emergence is intended to be a continuous [], irregular, and unpredictable process involving the acquisition of sequences of properties from complex systems that are non-equivalent, non-deducible from one another, and locally coherent [,]. The generic process of emergence is intended to involve multiple selections, through fluctuations and weak forces, of multiple configurations while maintaining coherence. Selection through fluctuations and weak forces is at the root of the radical unpredictability of classic radical emergence and is characterized by singularities, e.g., order–disorder transitions, protein folding, and the formation and conservation of dissipative structures, whereas quantum radical emergence relates to phenomena such as superconductivity and superfluidity.
In the following text, when conceptually dealing with the discrete–continuum contrast and the corresponding effective computation–emergent computation, we refer tout court to Incomputable (unavailability of an algorithm that computes in finite time and with arbitrary precision) Real Numbers (IRNs) and their properties, including algebraical irrational, trigonometric (based on Euler’s formula), transcendent numbers, some points of convergence, and some special numbers, such as the Chaitin omega number. We mention that an algebraic number is any number x, real or complex, that satisfies an algebraic equation of the form anxn + an − 1xn−1 + …a1x + a0 = 0, where an are rational numbers that are not all null. Algebraic irrational numbers are irrational numbers that can be obtained as solutions to an algebraic equation. They include polynomials, fractions, and their powers with integer or fraction exponents, e.g., x3/5 + 7x = 0. Transcendent numbers are non-algebraic irrational numbers. Furthermore, Euler’s formula states that, for any real number x, we have
where e is the base of natural logarithms, i is the imaginary unit, and sine and cosine are trigonometric functions. Euler’s formula gives rise to the so-called Euler identity, which relates e, i, π, 1, and 0:
eix = cos x + i sinx
ei π + 1 = 0.
The geometric interpretation of the formula allows complex numbers to be viewed as points in the plane.
We consider several theoretical aspects and conclude that the theoretical incompleteness of IRNs corresponds and is required to represent the theoretical incompleteness of real physical phenomena, such as quantum phenomena and the phenomenology of emergence. This relates to issues of betweenness interfaces, such as between macro and micro, between open and closed, between levels of emergence, and transience between validity regimes (see Section 3). This is the reality of IRNs. In Table 1, we contrast IRNs and non-IRNs.

Table 1.
Cases of IRNs and non-IRNs.
A world of precise finite values, even if approximated, with dynamics that are zippable in analytical formulae and computable and symbolically representable, is supposed to function. A world of arbitrary precise infinite values with dynamics that are non-zippable in analytical formulae, non-computable, and, for instance, sub-symbolically representable, is supposed to have the possibility of emerging effectively.
The real world is supposed to be a continuous combination of the two.
2. Computational Processes and Emergent Computation
In some ways, the discrete–continuous and effective–emergent computation contrasts resemble axiomatic vs. non-axiomatic approaches in terms of what Feynman considered “Greek” versus “Babylonian” mathematics. The “Greek” approach to mathematics is characterized by the tendency to arrange theories on an axiomatic basis, whereas Feynman wrote:
“What I have called the Babylonian idea is to say, ‘I happen to know this, and I happen to know that, and maybe I know that; and I work everything out from there. Tomorrow I may forget that this is true, but remember that something else is true, so I can reconstruct it all again. I am never quite sure of where I am supposed to begin or where I am supposed to end. I just remember enough all the time so that as the memory fades and some of the pieces fall out I can put the thing back together again every day’”([], p. 45).
and
“In physics we need the Babylonian method, and not the Euclidian or Greek method”(Ibid., p. 47).
From a constructivist point of view, we differentiate between symbolic computational processes and their effective computability. In the second case, although the computation process is formally available, it may be not Turing-computable; for instance, it may occur in non-limited time. In such a case, we do not use results; rather, we use representations of computational processes, such as numbers with exponents and numerical fractions. We use and do not compute such computational representations.
Some irrational numbers that are algebraic, e.g., solutions to x2 − 2 = 0 as well as IRNs in general, correspond to, represent, and are the implicit generative computational processes that are only sometimes effectively computable. We process their generative mechanisms, rather than their approximated values.
Another case relates to the non-explicitness of the computing, for example, for emergent computation [].
In the case of explicit, complete representation, the program explicitly and completely represents and is the processing, whether it is effectively computable or not. When computable, knowledge of the program is equivalent to knowledge of the result.
We consider cases where the computation cannot be analytically represented and where acquired properties may not be anticipated by considering the computation process, requiring instead that computation be performed in full until the results and the properties are acquired. In Table 2, we contrast effective computability, incomputability, and emergent computation.

Table 2.
Effective computation, incomputability, and emergent computation.
An example of non-explicitness is sub-symbolic computing in ANN [,,,]. This involves multi-layered weighted nets according to which the computation is distributed. The computational processing is represented in a non-analytical way through levels and weighted connections whose weights can change contextually during the process [], as schematized in Figure 1.
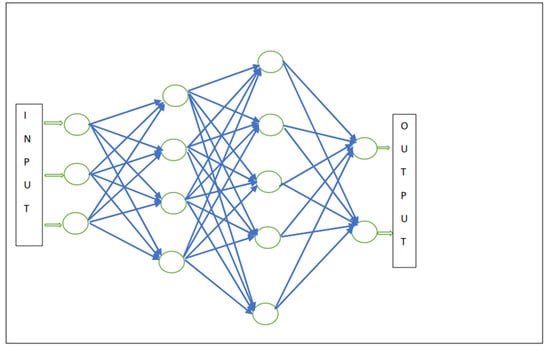
Figure 1.
A generic schema of an ANN.
A specific case is represented by recurrent neural networks (RNNs) [], which can use their internal states to process sequences of inputs. An example of an acquired property is machine learning.
For this reason, the processing is considered non-explicit and not analytically represented, and it is called sub-symbolic, even if the program performing the ANN/RNN is an explicit, computable algorithm. Systemically, this is easily understood as non-reductionism; namely, the biological neural networks are not the thought but the context from which it emerges.
If we consider the ANN instant by instant as the calculation is carried out, the process will be incomprehensible; thus, we must wait for the final result (in correspondence with the fact that knowledge of the instantaneous behavioral configurations of a flock does not allow us to determine the subsequently acquired properties of its global behavior).
The whole set of weights and levels used cannot be “zipped” or analytically represented as individual general formulae or functions, being, instead, a dynamic, contextual, ongoing process of computational emergence [].
We specify how the term ‘‘zipped’’ applies to the possibility of algorithmic compression according to Chaitin and Kolmogorov [,,].
This situation also applies to properties acquired by other computational processes, such as cellular automata (CA), which involve the acquisition of the emergence of localized patterns that can alternatively grow and contract. An example of an acquired property is the well-known Conway’s Game of Life.
3. Arbitrary Discretization
In the literature, the following statement can be found:
“Experimental physicists know how difficult accurate measurements are. No physical quantity has ever been measured with more than 15 or so digits of accuracy”[].
This also relates to the usage and modeling of the so-called “grey systems,” which are characterized by practical incompleteness in measurements when system information about the elements, the structure, the boundary, and the system’s behaviors is incomplete [,].
We consider that infinite aspects of IRNs do not represent a maniacal, unrealistic search for completeness and precision, but only some aspects to be considered non-computationally, and even computationally in case of deterministic chaos that is very sensitive to the initial conditions (see Equation (3)).
Approximability relates to effective functioning in terms of its unavoidable finiteness and context of finite granularity, whereas in their decimal parts, IRNs can correspond to and represent the theoretical incompleteness [,,] of intangible processes such as indefinite interchangeability, allowing ergodicity ([], pp. 302–305; [], pp. 107, 165) and dynamics of the multiplicity of emergence [], processes of decision-making from information and timings, Big Data [], and quantum phenomena. Multiple systems are established by considering the multiple roles of their interacting components and their interchangeability, such as in in ergodic behavior. Components of populations assume ergodic behaviors if they interact in such a way that when x% of the population is in a particular state at any moment in time, then each component of the population spends x% of time in that state. In real cases, we consider percentages that establish significant levels of ergodicity. Realistically, components assume the same roles at different times as well as assuming different roles simultaneously but with the same percentages. This is a matter of interchangeability of components that play the same role at different times. Ergodicity is a recurrence property of statistical systems. Equivalences and various multiple interactions are used to establish multiple roles.
The consideration of approximations and granularity substitutions in impossible analytical representations hides characterizing properties such as the dynamics of coherences, their loss and recovery, correlations, power laws, multiplicities, SSB-like and spontaneous acquisition of roles, and the incompleteness of properties that are irregularly and unevenly present [,], as graphically represented in Figure 2.
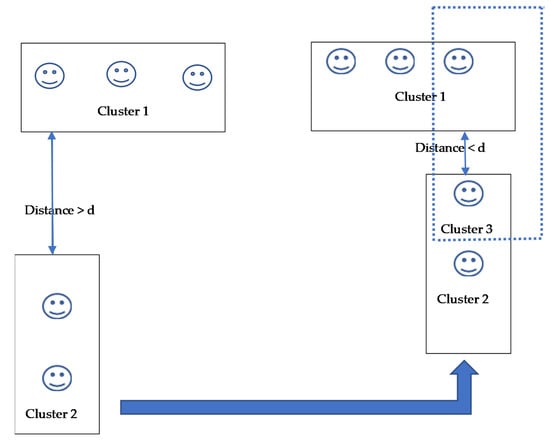
Figure 2.
The Cluster 3 is spontaneously established by movement of cluster 2.
Furthermore, as for any phenomenon, when considering constraints and limit values, their formal respect is just one aspect of the behavioral properties of a system, whereas the modalities with which the constraints are respected, e.g., assuming values that are close to the max and min, as well as random, can provide information that would be otherwise ignored.
The reality of IRNs lies in the representative modeling roles of some of their properties, such as their infiniteness, uniqueness, singularities, and non-computability, which represent and correspond to theoretical incomplete properties of processes such as emergence and quantum-like phenomena, whereas theoretical representation, partly differentiating from the classical representation, can be applied to model very complicated transient dynamics between phases occurring when classical and quantum aspects mix.
In the case of IRNs, their generative processes, e.g., exponential, can be symbolically processed; for example, they can be simplified and added to one another in the same way as imaginary numbers.
While the usual numerical strategy of using IRNs consists of simplifying them by using their approximated values from truncated computations, determining the granularity assuming the insignificance of lower levels, and assuming de facto a conceptual reverse reductionist approach that is microscopically limited, the use of other approaches may relate to the consideration of properties of decimal parts of IRNs, such as how they occur, e.g., level of randomicity; distribution, e.g., clusterizations; combinations of cases; quasi-periodicities, e.g., in correspondence with properties of chaotic behaviors and attractors in the phase space and in whirlpool-like phenomena, quasi-periodic solutions, and quasi-systems []; and other contextual properties, e.g., topological. Quasi-periodicity is intended to be related, for instance, to irregular periodicity, recurrences with a component of unpredictability, and increasing regularity over multiple periods. We focus on their properties and usage rather than on their computation in analogy, for instance, with imaginary numbers, e.g., the use of imaginary time in some approaches for special relativity and quantum mechanics.
Furthermore, the completeness of real numbers (for instance, Dedekind and Cauchy completeness) may be intended as a source and representation of theoretical incompleteness and indefiniteness, i.e., always having reachable non-equivalences, uniqueness and singularities, and non-computability.
Furthermore, the infiniteness of IRNs corresponds and allows us to represent arbitrary symmetries and levels of equivalence between sequences of values, with the equivalence being broken only when arbitrary infinitesimal differences are reached. Arbitrary infinitesimal differences between IRNs are considered to correspond to virtual selections between equivalences and symmetries at any level, for example, collapsing under arbitrary weak forces, e.g., in nuclear physics, and when there is an unlimited lower percentage of all forces involved at a given moment or virtual one, e.g., IRNs used as data, information, and in quantum systems with an infinite number of states.
The research on IRNs should then not be considered an abstract exercise of mathematicians but as research in a field considered to possess properties representing and corresponding to those detectable in real, even if extreme, phenomena, such as emergence and quantum phenomena.
3.1. Equivalences and Symmetries
However, the collapse of equivalences may also relate to the collapse of symmetries. There are invariable symmetries, such as those for fractals, which are approximated in nature.
We may consider systems that, due to their evolution or external influences, lose the symmetry of their evolutionary numerical paths and solutions, but not of their analytical descriptions.
A case of collapsing is represented by the phenomenon known as symmetry breaking, which occurs when a symmetry transformation leaves the form of the evolution equations invariant but changes the form of their solutions. Spontaneous symmetry breaking (SSB) occurs when a physical system in a symmetric state ends up in an asymmetric state. As an example, we may consider the theory of phase transitions (PT) using the spontaneous symmetry breaking (SSB) mechanism in quantum field theory (QFT) [,].
To represent a general, dynamic symmetry condition, let us consider an ideal condition, such as a symmetric upward dome with a trough circling the bottom—a metaphoric “Mexican Hat.” If we place a ball at the very peak of the dome, the system is symmetric with respect to rotation around its central axis. The ball is positioned in an unstable equilibrium. If an even infinitesimal energetic variation that is sufficient (role of the IRNs) to break the equilibrium occurs, the ball will roll down the gradient to some position in the circular valley at the bottom. The ball will come to rest at some fixed point on the perimeter. The “Mexican Hat” and the ball will retain their individual symmetry, but the system will not.
The ball may be material and thus sensible to infinitesimal energy, or it may be virtual, such as in the form of data values and information; however, its energetic aspects, represented by IRNs, collapse into decisions, information, and a quantum infinite number of states. The spontaneity of the SSB lies in the fact that after the rolling of the ball, the system is no longer symmetric.
The rolling down represents a process of radical emergence phenomena. In the event that one of the parameters is linked to the available energy changes, the system distributes itself in one of the possible ground states with consequent energy redistribution characterizing its macroscopic properties.
We mention how such spontaneous configurational changes are also related to cases where, in collective systems, e.g., interacting agents, the dynamics cause elements to simultaneously belong to multiple specific clusters (considering, for instance, classes of distances or patterns in multiple collective systems) having, for instance, unwanted ergodic roles ([], pp. 302–305) represented by IRNs (see Figure 2) and Table 3.

Table 3.
Equivalence and coherence.
The breaking of equivalences corresponds to the breaking of symmetries as particular equivalences. The infinitesimal digits of IRNs may lead to bifurcations, i.e., SSB, and the differentiation between crucial initial conditions in chaotic behaviors, triggering completely different behaviors. We remind the reader of the so-called Lorenz equations that model the occurrence of deterministic chaos, i.e., apparently random motion stemming from deterministic equations. The very sensitive dependence on initial conditions is the essence of deterministic chaos. In such a case, at any point in time, the difference between two behaviors with two different initial conditions increases exponentially over time, however small their difference is. The Lorenz equations are
where r, b, and σ are control parameters.
Furthermore, in physics, quantum systems with an infinite number of states are different non-unitarily equivalent representations of the same possible system, and accordingly, PT can structurally modify the system by means of the SSB. Phenomena on different scales are considered SSB processes, such as Cooper pairs (of electrons bound together at low temperatures in superconductivity phenomena), the Higgs mechanism, and multiple vacuum states in elementary particle physics phonons in a crystal.
3.2. Discretization, Multiple Modeling, and Non-Predictability
In classic systems, arbitrary discretization, i.e., the possibility of selecting any discretization that is arbitrarily small, is then a requirement and a necessary approach for effectively and approximatively dealing with non-analytically representable phenomena, e.g., emergence.
Furthermore, the use of partial modeling also conceptually corresponds to arbitrary discretization. Phenomena of multiple emergence are non-analytically representable and require simultaneous multiple representations and multiple non-equivalent models, as considered by the DYnamic uSAge of Models (DYSAM) ([], pp. 64–70), see Figure 3, including the well-known Bayesian method, statistical approaches based on “continuous exploration” of the events, the well-known uncertainty principles [], the complementarity principle, so-called ensemble learning using machine learning techniques [], and the so-called evolutionary game theory [,]. Non-equivalent models may be of any number; however, because of the theoretical incompleteness of complex phenomena, they cannot reach final convergence to complete models. This multiple, incomplete form of modeling shares properties with IRNs, such as incomputability and indefiniteness. Examples include chaotic and collective emergent behaviors.
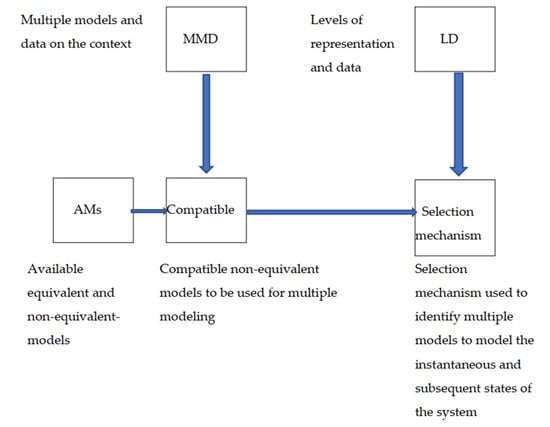
Figure 3.
The selection mechanism is the core of DYSAM. The selection is implemented as a strategy, for example, in ensemble learning and evolutionary game theory.
The usual approach consists of considering complex phenomena that are sufficiently approximated with single models in limited numbers. This allows the phenomenon to be tractable and approachable, even through approximations and simplifications, and for details that are deemed irrelevant to be neglected. The alternative strategy for dealing with complex systems is to have available approaches that can influence the system and submit suitable input to be then processed by the systems; that is, it involves combining prescriptions, imposing changes, and allowing the system to process configurational, balance-proposed, induced variations. It is a question of establishing hypothetical, continuous negotiations with the system in the context of confirmatory and try-and-try-again iterations.
Multiple modeling is an approach that was developed to propose changes to be processed by the system and not only to impose changes. This is a typical approach used in medicine and learning. It should be considered theoretically.
In this regard, we mention the two contrasting concepts of logically closed modeling and logical openness introduced in the literature ([], pp. 111–112; [], pp. 47–51; []) on which DYSAM is based.
The first case is intended to occur when there is conceptual availability of a complete, formal description of the relations between the state variables of the phenomenon of the system and of complete, analytically describable representations of the interactions between the phenomenon or system and its environment. Such availability allows all possible assumable states to be deduced. It may be intended to correspond to the concept of computability or the situation where a finite procedure is intended to exhaust the representation of a process.
The second case relating to logical openness is intended to be based on violation of the above points (see Table 4). Logical openness relates to the undefined, non-depleting number of degrees of freedom in a phenomenon or system, including the environment, which is, in principle, independent, and therefore makes the system incomplete. In addition to phenomenological multiplicity and incompleteness, logical openness relates to the constructivist nature of models—the inexhaustible multiplicity of the constructivist reality corresponding to the logical openness of both the world and of understanding.

Table 4.
Logical openness as a violation of logical closedness.
Furthermore, we may consider incompleteness as being related to non-predictability.
We may distinguish between at least two types of probability.
Certain probability is intended to represent computable probability, identifying significant possible extremes, e.g., maximum–minimum, of the phenomenological becoming of the process under study. The process can take place within such extremes, which can be computed, for instance, through the Bayes’ theorem. However, we neglect to consider the modalities with which the extremes are respected.
Uncertain probability is intended as non-computable and refers to the non-predictability of the processes under study, for example, contexts having, as a component, an environment with turbulence, processes of emergence, and autonomous processes that cannot be completely, explicitly, and uniquely defined. Uncertainty relates to probabilities that are inevitably calculated with reference to a context considered by the observer. This is a matter of contexts that cannot be assumed to be property-invariant and devoid of influencing properties []. The term “certain probability” should be intended as a simplification.
In this regard, we know that a string is algorithmically random when it is incompressible [,]. Empirical data sets should be intended to be algorithmically random strings of digits. With regard to non-zippability, empirical data exhibit maximal algorithmic complexity [,].
It is also worth mentioning the other well-known case of fuzzy systems whose elements have membership degrees [].
We end this section by stressing that:
- The infiniteness of IRNs corresponds to the theoretical incompleteness of several phenomena and processes mentioned above, such as the processes of emergence and the phenomena of continuous balance between equivalences and interchangeabilities, e.g., ergodic, and quantum.
- The non-computability of subsets of real numbers, such as irrational algebraic and transcendent, i.e., IRNs, corresponds to their non-zippability into complete analytical formulae or exhaustive single models and their combinations of complexity, such as processes of emergence, phenomena that continuously acquire, lose, and recover multiple coherences, e.g., collective behaviors.
3.3. Computability
At this point, it is also worth mentioning suitable possible approaches that are integrative or alternative to the classic numerical simulations and deal with non-Turing computability (see Table 5).

Table 5.
Turing computability.
It is well known that various versions of the Turing machine are all computationally equivalent []. It is also well known that Turing himself introduced a possible window for different levels [,,] of non-equivalent computability by introducing the concept of the oracle, an abstract machine that is supposed to be able to solve decision problems of any class of complexity as undecidable problems, e.g., the well-known halting problem. However, although the alternative hypercomputations considered below are supposed to be able to determine whether particular Turing machines will halt on particular inputs, they cannot determine whether or not machines equivalent to themselves will halt.
In this regard, hypercomputers [,,] have been introduced to perform hypercomputations intended to be super-Turing computations. This refers to models of computation that are non-equivalent to Turing computability, i.e., able to solve problems that Turing computations cannot [,,].
Examples of hypercomputation include:
- Nondeterministic computation when, from a given input and state, the abstract machine may jump to several different possible states;
- Probabilistic computation when considering the probability of a given initial state given by a stochastic vector and the probability of a particular state transition [] ([], pp. 341–347).
- Hypercomputation of the so-called Ω Chaitin constant or the halting probability, consisting of a real number expressing the probability that a randomly constructed program will halt depending on the program encoding used and its length [,,,]. The importance of the Chaitin constant lies in the fact that various problems in number theory are equivalent to solving the halting problem for special programs, such as searching for counterexamples and halting if one is found. For instance, this is the case for the so-called Goldbach conjecture, which states that every even integer number greater than 2 can be always expressed as the sum of two primes [].
Examples of hypercomputers include:
- Inductive Turing machines, which perform a list of defined instructions depending on the initial states and acquire a series of successive states by applying inductive reasoning and being dependent on environment phenomenology [].
- Quantum computers, which are based on the possibility of being in superposed states. Whereas a bit can only have two states, i.e., 0 or 1, a qubit state is a linear superposition of the basis states that is described by probability amplitudes. Multiple qubits can exhibit quantum entanglement. The Quantum Universal Turing Machine (QUTM) takes advantage of the superposition principle and the entanglement among qubits [,,,,,], raising the research issue of whether or not it is a Turing machine.
Other cases to be mentioned are as follows:
- Qualitative analysis, which involves determining and elaborating qualitative properties of a phenomenon in a way that allows the identification or exclusion of subsequently acquired properties, such as convergence, that deal with numerical sequences, analytic properties of a function without calculating it, and pattern and multiple dynamic coherence recognition. We believe this is a very promising field of research and one that can be used to introduce new, unimaginable approaches.
- Analog and hybrid computers use the continuously changing properties of physical phenomena, such as electrical, hydraulic, and mechanical properties, to model the problem being solved rather than computing it [,].
- Natural computing uses natural processing abstracted from natural phenomena [,].
A typical example of a field of application for such approaches is that of Big Data, where, for example, the properties of infraclusters can be considered [,].
In summary, we can make the following conclusions:
- The infiniteness of IRNs corresponds to the necessary but unpredictable collapse of any equivalence, reaching arbitrary points of difference at suitable levels of description, e.g., the quantum description level;
- The incomputability of IRNs corresponds to the non-zippability of complexity into a single analytical formula or exhaustive single model [].
4. Conclusions
In this paper, we elaborated the reality of real numbers. In particular, we focused on the reality of IRNs, whose reality is not denied by their incomputability, but rather, remains in their properties, representing physical aspects. We considered the properties of their decimal parts, such as those related to their occurrence, distribution, combinations, quasi-periodicities, and topological properties. The focus was on their properties and uses, rather than on their computation in analogy, for instance, with imaginary numbers. Furthermore, the incompleteness of IRNs is related to the theoretical incompleteness of their complexity. Moreover, the infiniteness of IRNs corresponds to any arbitrary symmetries and levels of equivalence where arbitrary infinitesimal differences are intended to correspond to selections, for example, due to collapsing under arbitrary weak forces, or even virtual, such as data, information, and quantum systems with an infinite number of states. We considered properties that do not relate to computability.
The reality of IRNs thus lies in representing the incompleteness of phenomena occurring, such as those collapsing from equivalences with any arbitrary dimensions, collapsing and occurring at any decimal digit, and those representing, for instance, infinitesimal but crucial weak forces and fluctuations.
Whereas in physical phenomena involving matter (even with particles of infinitesimal size), the nth decimal digit can reasonably be considered limited or in any case adequately approximable, this is not true for physical phenomena, such as those of a quantum nature, e.g., optical phenomena and those where the infinite number of states of quantum systems needs to be considered; temporal and cognitive; and those dealing with theoretical incompleteness and a latent order of complexity [,] requiring multiple types of modeling, such as logical openness and DYSAM.
We discussed suitable possible approaches that are integrative or alternative to classic numerical simulations and deal with non-Turing computability, such as hypercomputation, hypercomputers, quantum computing, and qualitative analysis.
The consideration of IRNs is not reduced to approximations, but the consideration of their properties in correspondence and validation of theoretical incompleteness is an alternative to discrete understanding, logically closed, and is always assumable as a particular case, whereas the reverse is not true.
The research on IRNs should be considered research in a field that is considered to have properties representing and corresponding to those detectable in real, even if non-classic, phenomena, such as emergence and quantum phenomena [].
The present research work is dedicated to the memory of Eliano Pessa to celebrate his valuable insights and expertise in the science of complexity.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Maietti, M.E.; Sambin, G. Toward a minimalist foundation for constructive mathematics. In From Sets and Types to Topology and Analysis. Towards Practicable Foundations for Constructive Mathematics; Crosilla, L., Schuster, P., Eds.; Clarendon Press: Oxford, UK, 2005; pp. 91–114. [Google Scholar]
- Kawai, T.; Sambin, G. The principle of point free continuity. Log. Methods Comput. Sci. 2019, 15, 22:1–22:25. [Google Scholar]
- Chaitin, G. How real are real numbers? Int. J. Bifurc. Chaos 2006, 16, 1841–1848. [Google Scholar] [CrossRef]
- Paperin, G.; Green, D.G.; Sadedin, S. Dual-phase evolution in complex adaptive systems. Interface 2011, 8, 609–629. [Google Scholar] [CrossRef]
- Batterman, R. Emergence, singularities, and symmetry breaking. Found. Phys. 2011, 41, 1031–1050. [Google Scholar] [CrossRef]
- Minati, G. Phenomenological structural dynamics of emergence: An overview of how emergence emerges. In The Systemic Turn in Human and Natural Sciences. A Rock in the Pond; Ulivi, L.U., Ed.; Springer: New York, NY, USA, 2019; pp. 1–39. [Google Scholar]
- Feynmann, R. The Character of Physical Law; The MIT Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Licata, I.; Minati, G. Emergence, Computation and the Freedom Degree Loss Information Principle in Complex Systems. Found. Sci. 2016, 21, 863–881. [Google Scholar] [CrossRef]
- Younger, A.S.; Redd, E.; Siegelmann, H. Development of Physical Super-Turing Analog Hardware. In Unconventional Computation and Natural Computation; Ibarra, O., Kari, L., Kopecki, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8553, pp. 379–392. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: New York, NY, USA, 2018. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bach, F. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Kelleher, J.D. Deep Learning; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Shields, M.W.; Casey, M.C. A theoretical framework for multiple neural network systems. Neurocomputing 2008, 71, 1462–1476. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. Recurrent Neural Networks for Short-Term Load Forecasting: An Overview and Comparative Analysis; Springer: New York, NY, USA, 2017. [Google Scholar]
- Faloutsos, C.; Megalooikonomoum, V. On data mining, compression, and Kolmogorov complexity. Data Min. Knowl. Discov. 2007, 15, 3–20. [Google Scholar] [CrossRef]
- Li, M.; Vitányi, P.M.B. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Chaitin, G.J. How Much Information Can There be in a Real Number? Int. J. Bifurc. Chaos 2007, 17, 1933–1935. [Google Scholar] [CrossRef]
- Javanmardi, E.; Liu, S.; Xie, N. Exploring the Philosophical Paradigm of Grey Systems Theory as a Postmodern Theory. Found. Sci. 2020, 25, 905–925. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Y. A brief introduction to grey systems theory. Grey Syst. Theory Appl. 2012, 2, 89–104. [Google Scholar] [CrossRef]
- Longo, G. Interfaces of Incompleteness. In Systemics of Incompleteness and Quasi-Systems; Minati, G., Abram, M.R., Pessa, E., Eds.; Springer: New York, NY, USA, 2019; pp. 3–55. [Google Scholar]
- Longo, G. Reflections on concrete incompleteness. Philos. Math. 2011, 19, 255–280. [Google Scholar] [CrossRef]
- Minati, G. Knowledge to Manage the Knowledge Society: The Concept of Theoretical Incompleteness. Systems 2016, 4, 26. [Google Scholar] [CrossRef]
- Minati, G.; Pessa, E. Collective Beings; Springer: New York, NY, USA, 2006. [Google Scholar]
- Minati, G.; Pessa, E. From Collective Beings to Quasi-Systems; Springer: New York, NY, USA, 2018. [Google Scholar]
- Minati, G.; Licata, I. Emergence as Mesoscopic Coherence. Systems 2013, 1, 50–65. [Google Scholar] [CrossRef]
- Minati, G. Big Data: From Forecasting to Mesoscopic Understanding. Meta-Profiling as Complex. Systems. Systems 2019, 7, 8. [Google Scholar] [CrossRef]
- Cruchtfield, J.P. The calculi of emergence: Computation, dynamics and induction. Physica D 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Pessa, E. Emergence, self-organization, and quantum theory. In Proceedings of the First Italian Conference on Systemics; Minati, G., Ed.; Apogeo Scientifica: Milano, Italy, 1998; pp. 59–79. [Google Scholar]
- Anderson, P.W. Can broken symmetry occur in driven systems? In Equilibrium and Nonequilibrium Statistical Mechanics; Nicolis, G., Dewel, G., Turner, P., Eds.; Wiley: New York, NY, USA, 1981; pp. 289–297. [Google Scholar]
- Anderson, P.W.; Stein, D.L. Broken symmetry, emergent properties, dissipative structures, life. Are they related? In Self Organizing Systems: The Emergence of Order; Yates, F.E., Ed.; Plenum Press: New York, NY, USA, 1985; pp. 445–457. [Google Scholar]
- Liu, B. Uncertainty Theory; Springer: Berlin, Germany, 2014. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Maynard-Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Minati, G.; Penna, M.P.; Pessa, E. Thermodynamic and Logical Openness in General Systems. Syst. Res. Behav. Sci. 1998, 15, 131–145. [Google Scholar] [CrossRef]
- De Finetti, B. Theory of Probability; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Calude, C.S. Information and Randomness; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- McAllister, J.W. Algorithmic randomness in empirical data. Stud. Hist. Philos. Sci. 2003, 34, 633–646. [Google Scholar] [CrossRef]
- Chaitin, G. Information, Randomness, and Incompleteness; Word Scientific: Singapore, 1990. [Google Scholar]
- Kolmogorov, A.N. Three Approaches to the Quantitative Definition of Information. Probl. Inf. Transm. 1965, 1, 3–11. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. (Eds.) Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A. Zadeh; World Scientific: Singapore, 1996. [Google Scholar]
- Wolfram, S. The principle of computational equivalence. In A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; pp. 5–6. [Google Scholar]
- Siegelmann, H.T. Computation beyond the Turing Limit. Science 1995, 268, 545–548. [Google Scholar] [CrossRef]
- Copeland, B.J.; Sylvan, R. Beyond the Universal Turing Machine. Australas. J. Philos. 1999, 77, 46–67. [Google Scholar] [CrossRef]
- Copeland, B.J.; Posy, C.J.; Shagrir, O. Computability: Turing, Gödel, Church, and Beyond; MIT: Cambridge, MA, USA, 2013. [Google Scholar]
- Siegelmann, H.T. Neural and super-Turing computing. Minds Mach. 2003, 13, 103–114. [Google Scholar] [CrossRef]
- Cabessa, J.; Villa, A.E.P. The super-Turing computational power of interactive evolving recurrent neural networks. In ICANN 2013; Mladenov, V., Koprinkova-Hristova, P., Palm, G., Villa, A.E.P., Appollini, B., Kasabov, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8131, pp. 58–65, Lecture Notes in Computer Science (LNCS). [Google Scholar]
- Hogarth, M.L. Non-Turing Computers and Non-Turing Computability. In Proceedings of the Philosophy of Science Association (PSA); Hull, D., Forbes, M., Burian, R.M., Eds.; Philosophy of Science Association: Chicago, IL, USA, 1994; Volume 1, pp. 126–138. [Google Scholar]
- Shagrir, O.; Pitowsky, I. Physical Hypercomputation and the Church–Turing Thesis. Minds Mach. 2003, 13, 87–101. [Google Scholar] [CrossRef]
- Cotogno, P. Hypercomputation and the Physical Church-Turing Thesis. Br. J. Philos. Sci. 2003, 54, 181–223. [Google Scholar] [CrossRef]
- Syropoulos, A. Hypercomputation: Computing Beyond the Church-Turing Barrier; Springer: New York, NY, USA, 2008. [Google Scholar]
- Inoue, K.; Ito, A.; Takanami, I. On 1-inkdot alternating Turing machines with small space. Theor. Comput. Sci. 1994, 127, 171–179. [Google Scholar] [CrossRef]
- Martin, J. Introduction to Languages and the Theory of Computation; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Chaitin, G.J. A theory of program size formally identical to information theory. J. Assoc. Comput. Mach. 1975, 22, 329–340. [Google Scholar] [CrossRef]
- Chaitin, G.J. Meta Math! The Quest for Omega; Pantheon Books: New York, NY, USA, 2005. [Google Scholar]
- Wang, Y. The Goldbach Conjecture; Word Scientific: Singapore, 2002. [Google Scholar]
- Burgin, M. Superrecursive Algorithms; Springer: New York, NY, USA, 2005. [Google Scholar]
- Calude, C.S.; Dinneen, M.J.; Svozil, K. Reflections on quantum computing. Complexity 2000, 6, 35–37. [Google Scholar] [CrossRef][Green Version]
- Deutsch, D. Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 400, 96–117. [Google Scholar]
- Deutsch, D. Quantum computational networks. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1989, 425, 73–90. [Google Scholar]
- Deutsch, D. The Beginning of Infinity: Explanations That Transform the World; Penguin: London, UK, 2012. [Google Scholar]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1992, 439, 553–558. [Google Scholar]
- Rosenblum, B.; Kuttner, F.; Penrose, R. Quantum Physics of Consciousness; Cosmology Science Publishers: Cambridge, MA, USA, 2011. [Google Scholar]
- Siegelmann, H.T. Neural Networks and Analog Computation: Beyond the Turing Limit; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Ulmann, B. Analog and hybrid computer programming. In De Gruyter Textbook; De Gruyter Oldenbourg: Oldenbourg, Germany, 2020. [Google Scholar]
- Mac Lennan, B.J. Natural computation and non-Turing models of computation. Theor. Comput. Sci. 2004, 317, 115–145. [Google Scholar] [CrossRef]
- Brabazon, A.; O’Neill, M.; McGarraghy, S. Natural Computing Algorithms; Springer: New York, NY, USA, 2015. [Google Scholar]
- Nural, M.; Cotterell, M.E.; Miller, J. Using semantics in predictive big data analytics. In Proceedings of the 2015 IEEE International Congress on Big Data, Big Data Congress, Santa Clara, CA, USA, 29 October–1 November 2015; pp. 254–261. [Google Scholar]
- Cooper, B. The incomputable reality. Nature 2012, 482, 465. [Google Scholar] [CrossRef] [PubMed]
- Blasone, M.; Jizba, P.; Vitiello, G. Quantum Field Theory and its Macroscopic Manifestations; Imperial College Press: London, UK, 2011. [Google Scholar]
- Giuliani, A.; Zbilut, J. The Latent Order of Complexity; NovaScience: New York, NY, USA, 2008. [Google Scholar]
- Zizzi, P.A. Emergence of Universe from a Quantum Network. In Physics of Emergence and Organization; Licata, I., Sakaji, A., Eds.; World Scientific: Singapore, 2008; pp. 313–325. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).