A Comparative Machine Learning Study Identifies Light Gradient Boosting Machine (LightGBM) as the Optimal Model for Unveiling the Environmental Drivers of Yellowfin Tuna (Thunnus albacares) Distribution Using SHapley Additive exPlanations (SHAP) Analysis
Simple Summary
Abstract
1. Introduction
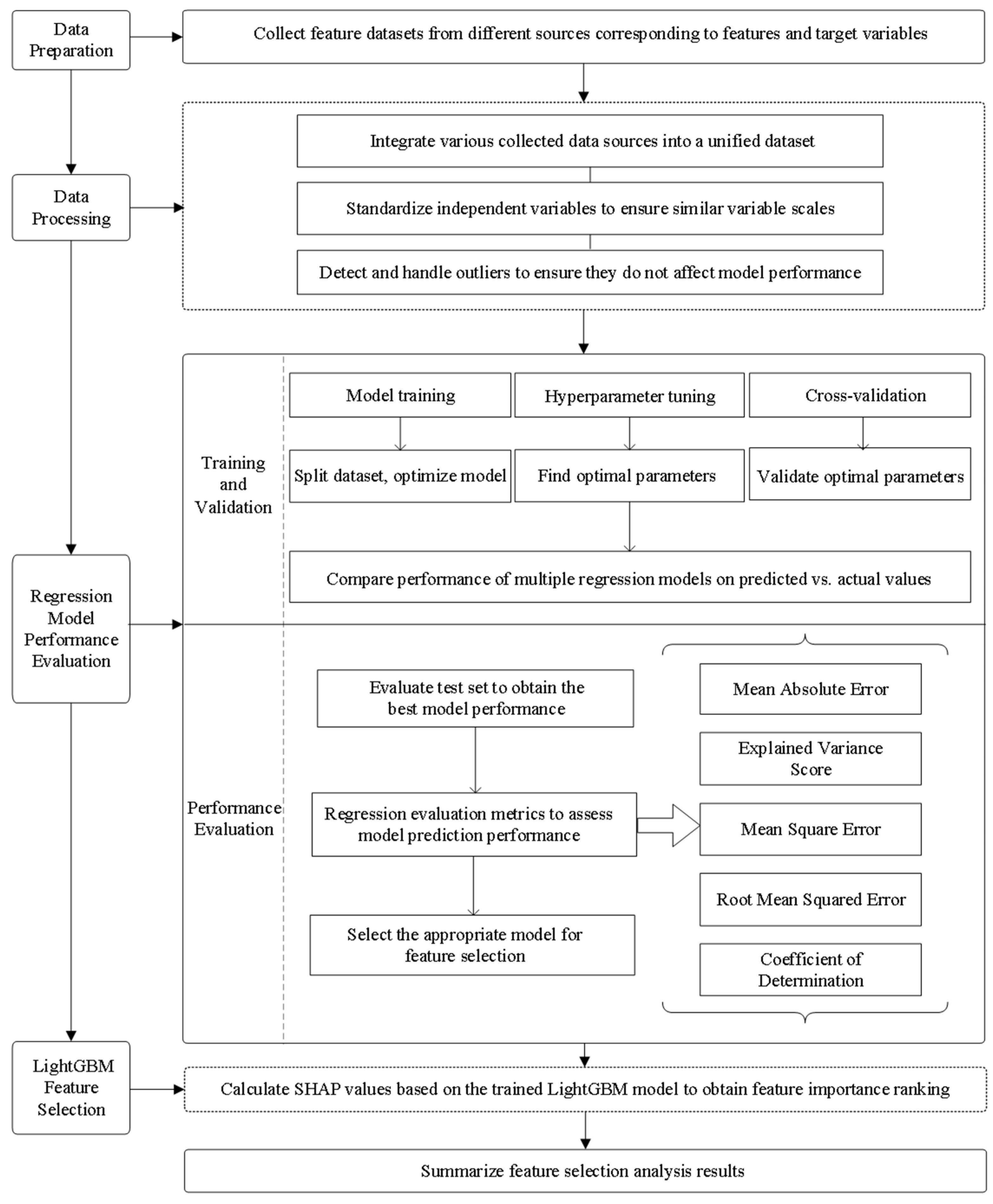
2. Materials and Methods
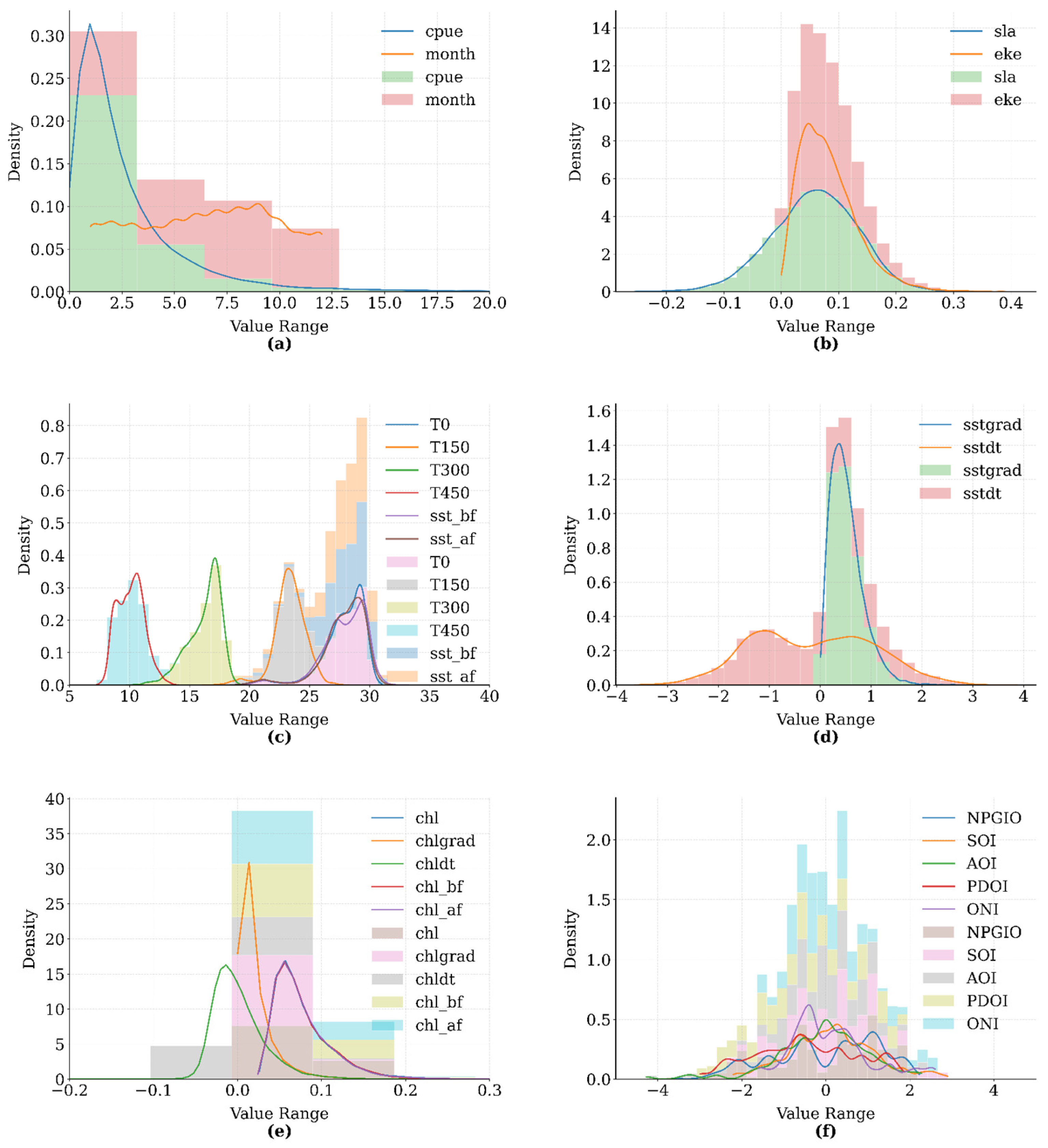
2.1. Data Processing
2.1.1. Marine Environmental Data
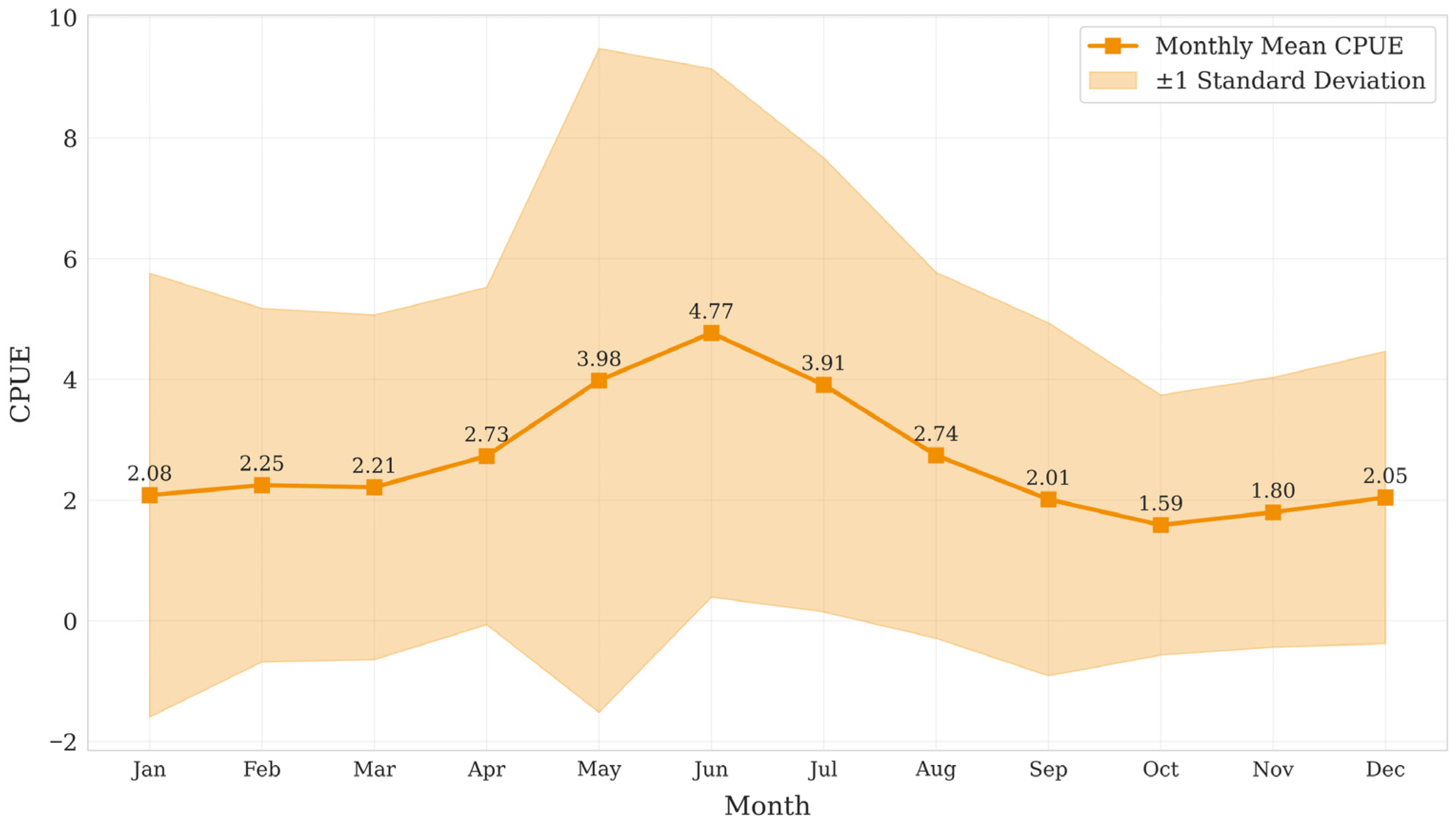
2.1.2. Fishery Resource Abundance
2.1.3. Data Preprocessing
2.2. Research Methods
2.2.1. Introduction to Regression Algorithms
2.2.2. Model Performance Rating
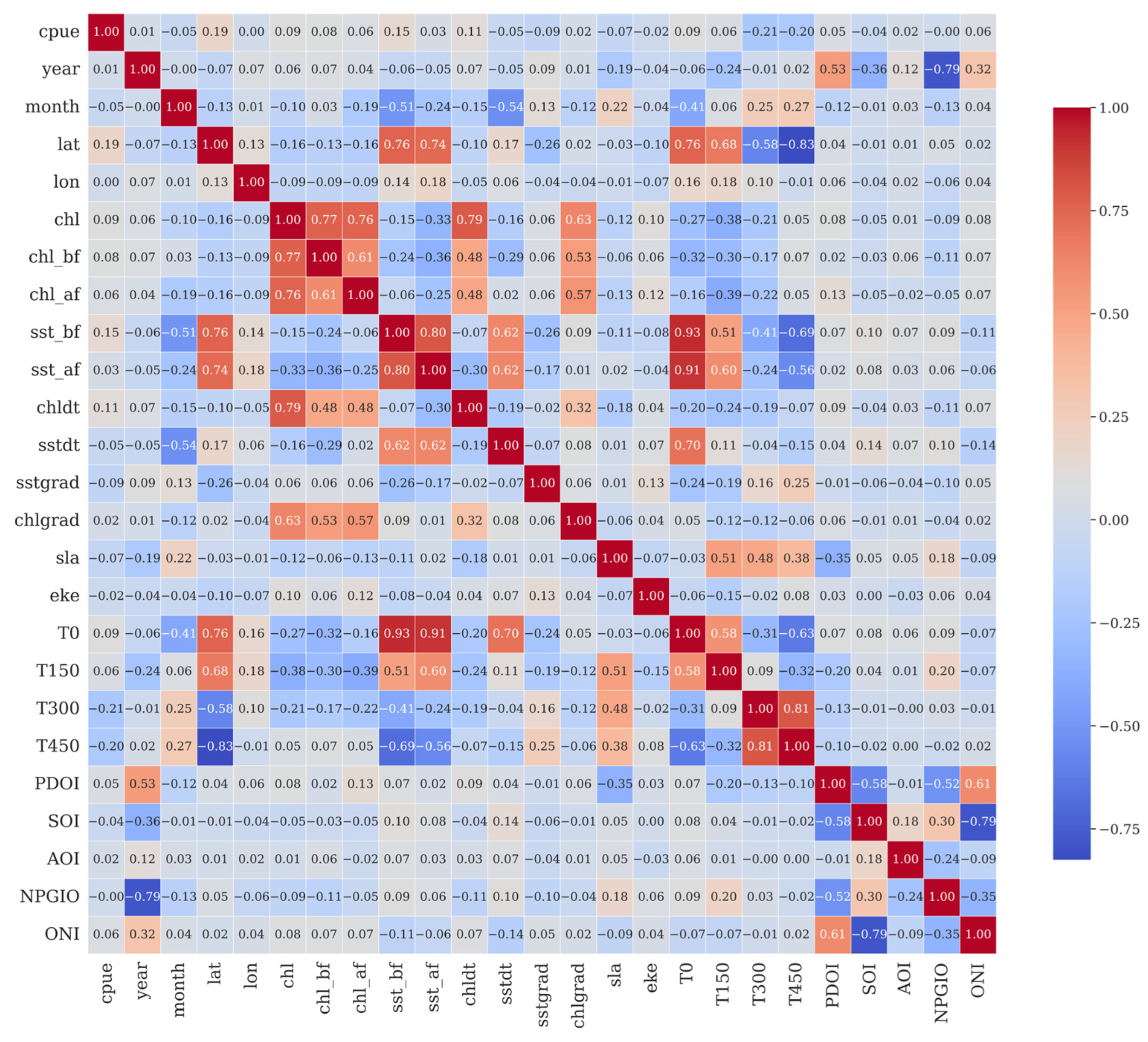
2.2.3. Variable Screening and Feature Selection
3. Environmental Drivers Identification
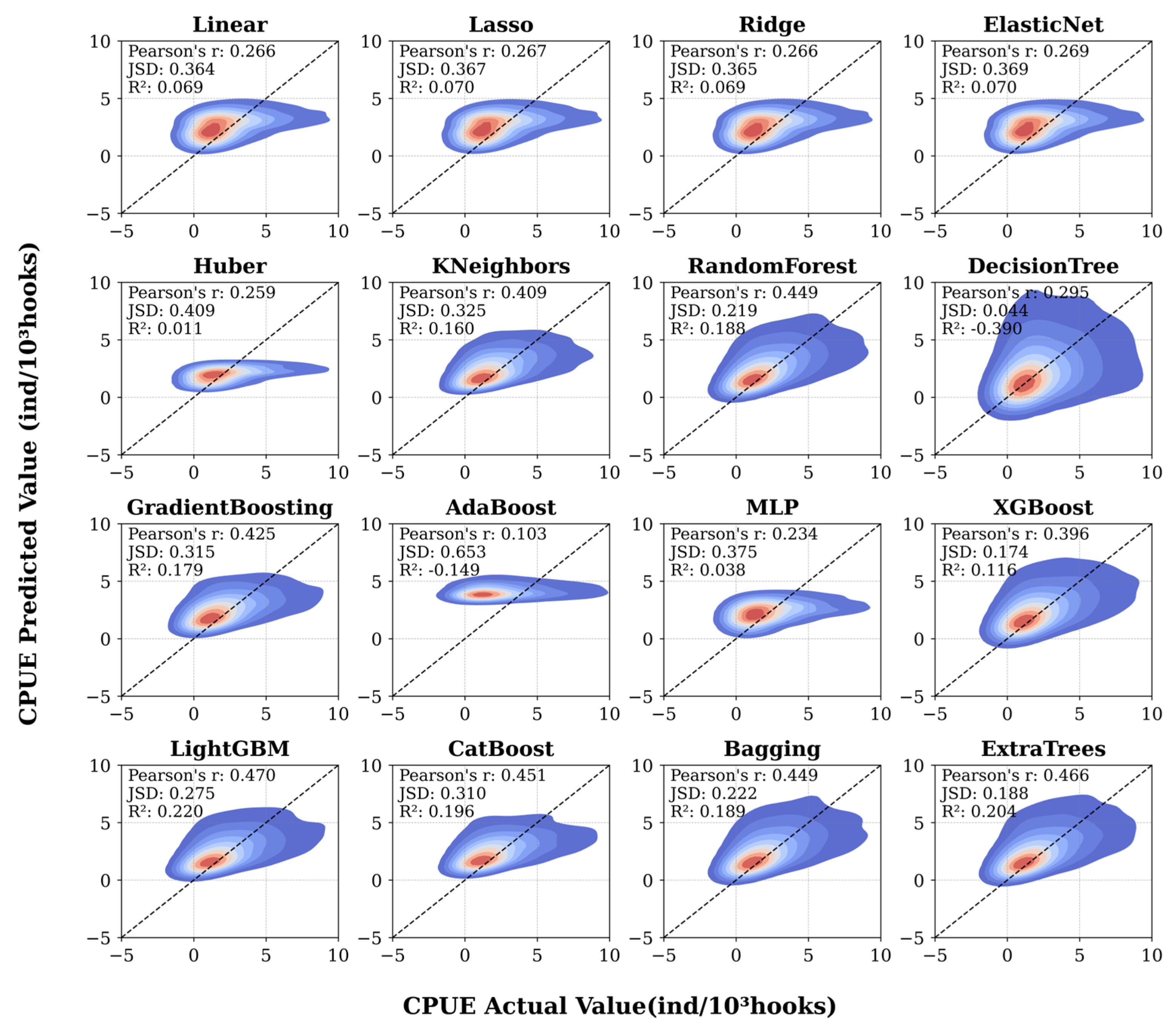
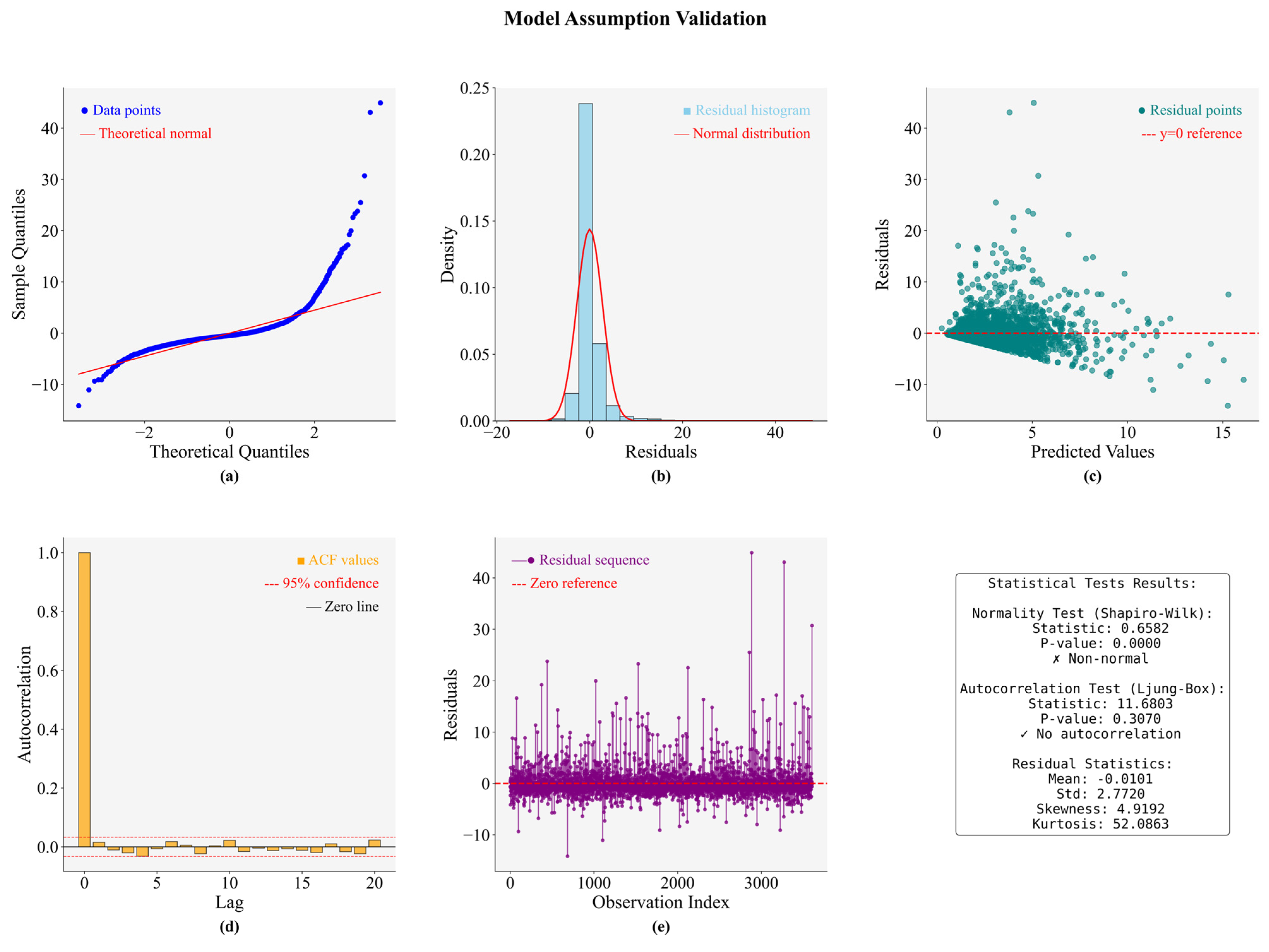
3.1. Comparison Between Actual and Predicted Values
3.2. Comparison of Regression Models’ Performance
3.3. Comprehensive Scores
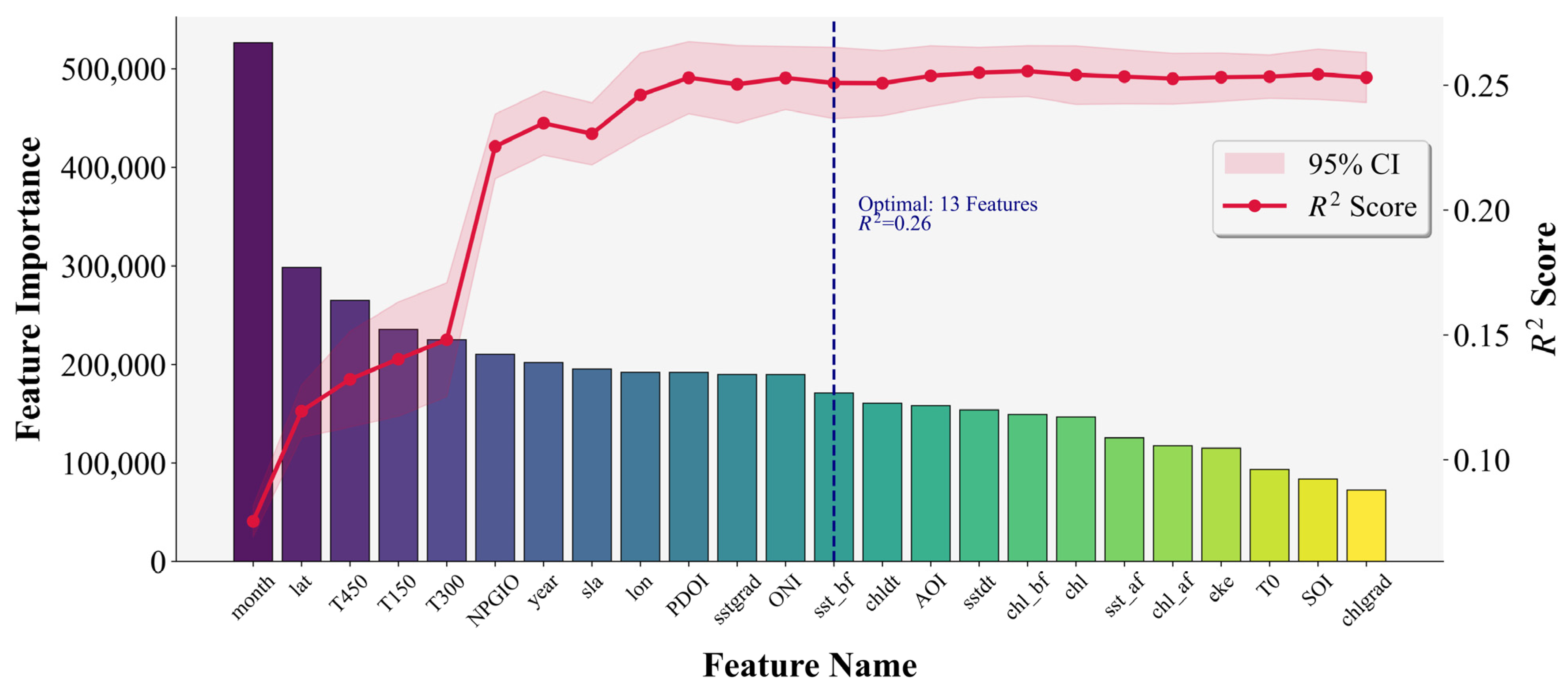
3.4. Feature Selection of LightGBM
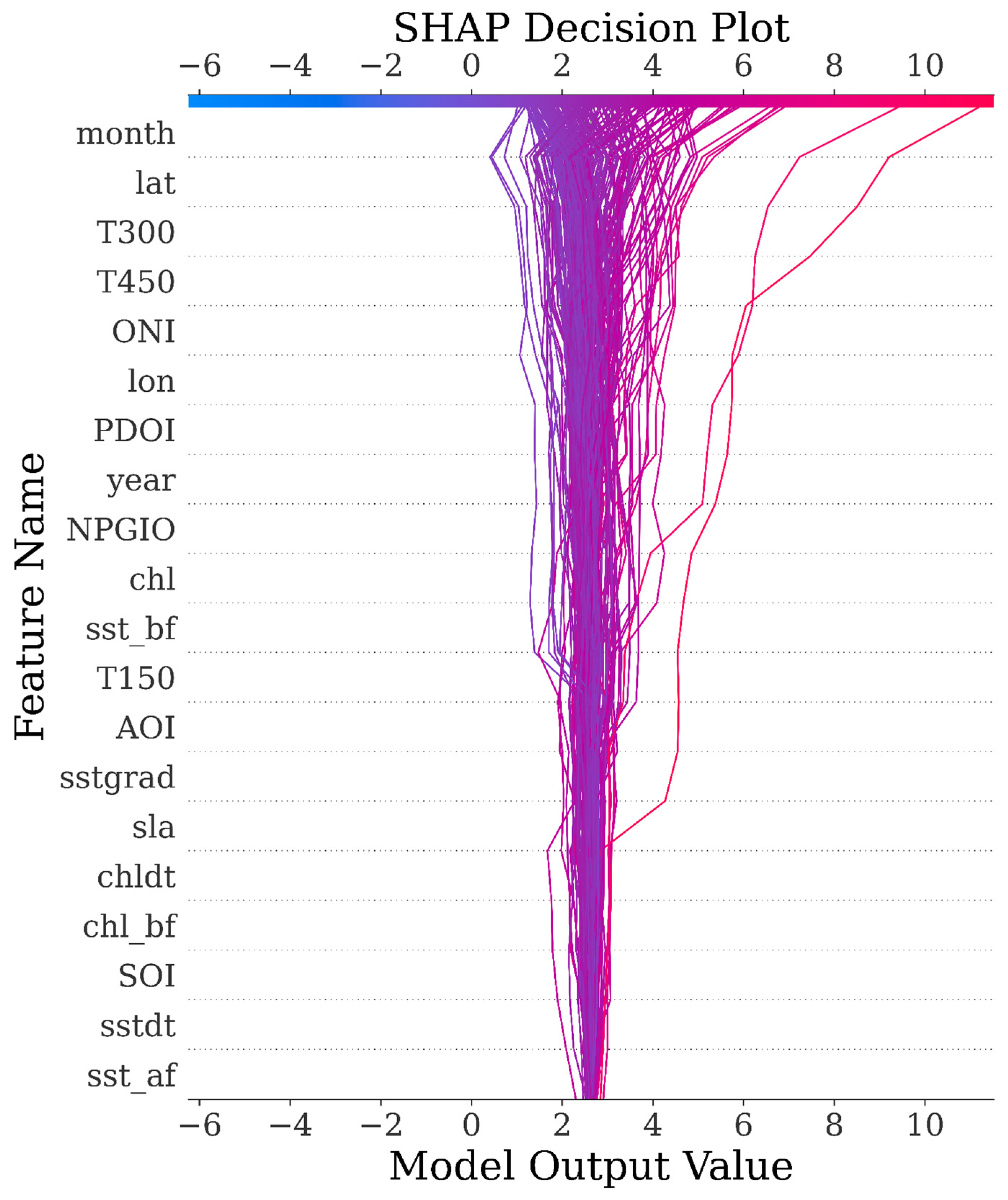
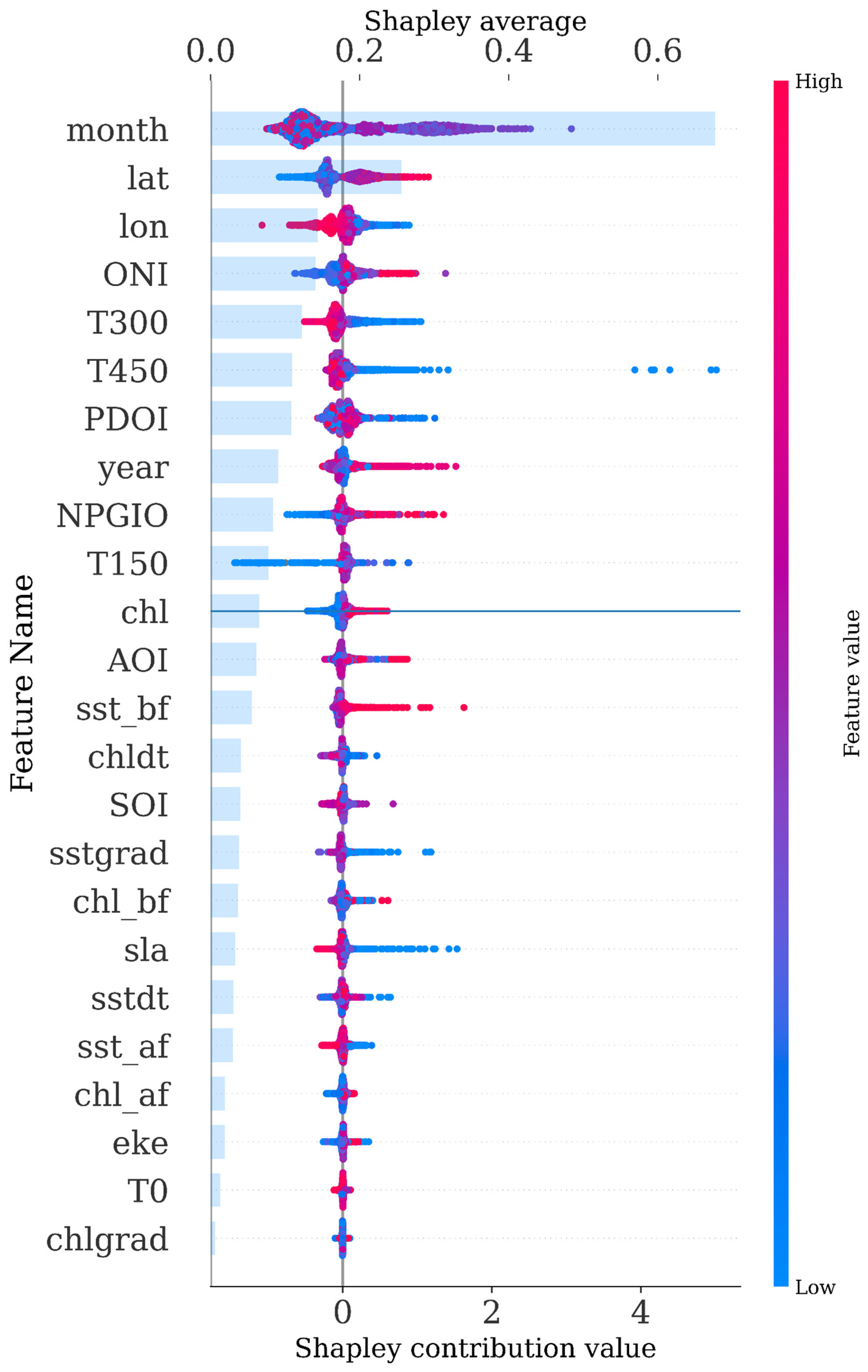
3.5. SHAP Analysis
4. Discussion
4.1. Comparative Analysis of Different Regression Models
4.2. Comparative Analysis of Feature Selection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Boyd, C.E.; McNevin, A.A.; Davis, R.P. The contribution of fisheries and aquaculture to the global protein supply. Food Secur. 2022, 14, 805–827. [Google Scholar] [CrossRef]
- Skirtun, M.; Pilling, G.M.; Reid, C.; Hampton, J.J.M.P. Trade-offs for the southern longline fishery in achieving a candidate South Pacific albacore target reference point. Mar. Policy 2019, 100, 66–75. [Google Scholar] [CrossRef]
- Lan, K.-W.; Evans, K.; Lee, M.-A. Effects of climate variability on the distribution and fishing conditions of yellowfin tuna (Thunnus albacares) in the western Indian Ocean. Clim. Change 2013, 119, 63–77. [Google Scholar] [CrossRef]
- Wang, W.; Fan, W.; Yu, L.; Wang, F.; Wu, Z.; Shi, J.; Cui, X.; Cheng, T.; Jin, W.; Wang, G. Analysis of multi-scale effects and spatial heterogeneity of environmental factors influencing purse seine tuna fishing activities in the Western and Central Pacific Ocean. Heliyon 2024, 10, e38099. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Gao, F.; Liu, Y. Impacts of changing scale on Getis-Ord Gi* hotspots of CPUE: A case study of the neon flying squid (Ommastrephes bartramii) in the northwest Pacific Ocean. Acta Oceanol. Sin. 2018, 37, 67–76. [Google Scholar] [CrossRef]
- Yaseen, Z.M. A new benchmark on machine learning methodologies for hydrological processes modelling: A comprehensive review for limitations and future research directions. Knowl. Based Eng. Sci. 2023, 4, 65–103. [Google Scholar] [CrossRef]
- Liu, W.; Li, R. Variable selection and feature screening. In Macroeconomic Forecasting in the Era of Big Data: Theory and Practice; Fuleky, P., Ed.; Springer: Cham, Switzerland, 2020; Volume 52, pp. 293–326. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, W.; Tang, F.; Shi, Y.; Fan, W. Prediction Model of Yellowfin Tuna Fishing Ground in the Central and Western Pacific Based on Machine Learning. Trans. Chin. Soc. Agric. Eng. 2022, 38, 330–338. [Google Scholar]
- Zagaglia, C.R.; Lorenzzetti, J.A.; Stech, J.L. Remote sensing data and longline catches of yellowfin tuna (Thunnus albacares) in the equatorial Atlantic. Remote Sens. Environ. 2004, 93, 267–281. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, W. Feature Selection for Explaining Yellowfin Tuna Catch per Unit Effort Using Least Absolute Shrinkage and Selection Operator Regression. Fishes 2024, 9, 204. [Google Scholar] [CrossRef]
- Braun, M.T.; Oswald, F.L. Exploratory regression analysis: A tool for selecting models and determining predictor importance. Behav. Res. Methods 2011, 43, 331–339. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Linear regression. In An Introduction to Statistical Learning: With Applications in Python; Springer: Cham, Switzerland, 2023; pp. 69–134. [Google Scholar]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J.A. LASSO regression. J. Br. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Sun, Q.; Zhou, W.-X.; Fan, J. Adaptive huber regression. J. Am. Stat. Assoc. 2020, 115, 254–265. [Google Scholar] [CrossRef]
- Sitienei, M.; Otieno, A.; Anapapa, A. An application of K-nearest-neighbor regression in maize yield prediction. Asian J. Probab. Stat. 2023, 24, 1–10. [Google Scholar] [CrossRef]
- Czajkowski, M.; Kretowski, M. The role of decision tree representation in regression problems–An evolutionary perspective. Appl. Soft Comput. 2016, 48, 458–475. [Google Scholar] [CrossRef]
- Dong, J.; Chen, Y.; Yao, B.; Zhang, X.; Zeng, N. A neural network boosting regression model based on XGBoost. Appl. Soft Comput. 2022, 125, 109067. [Google Scholar] [CrossRef]
- Truong, V.-H.; Tangaramvong, S.; Papazafeiropoulos, G. An efficient LightGBM-based differential evolution method for nonlinear inelastic truss optimization. Expert Syst. Appl. 2024, 237, 121530. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Ridwan, R.L.; Muhammed, M.M.; Abdulaziz, R.O.; Saheed, G.A. Comparison of the CatBoost classifier with other machine learning methods. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 738–748. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Solomatine, D.P. Experiments with AdaBoost. RT, an improved boosting scheme for regression. Neural Comput. 2006, 18, 1678–1710. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Maqbool, J.; Aggarwal, P.; Kaur, R.; Mittal, A.; Ganaie, I.A. Stock prediction by integrating sentiment scores of financial news and MLP-regressor: A machine learning approach. Procedia Comput. Sci. 2023, 218, 1067–1078. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. [Google Scholar] [CrossRef]
- Hoyos-Osorio, J.K.; Sanchez-Giraldo, L.G. The representation jensen-shannon divergence. arXiv 2023, arXiv:2305.16446. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Das, K.; Jiang, J.; Rao, J. Mean squared error of empirical predictor. Ann. Statist. 2004, 32, 818–840. [Google Scholar] [CrossRef]
- LaHuis, D.M.; Hartman, M.J.; Hakoyama, S.; Clark, P.C. Explained variance measures for multilevel models. Organ. Res. Methods 2014, 17, 433–451. [Google Scholar] [CrossRef]
- Di Bucchianico, A. Coefficient of determination (R2). In Encyclopedia of Statistics in Quality and Reliability; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Van den Broeck, G.; Lykov, A.; Schleich, M.; Suciu, D. On the tractability of SHAP explanations. J. Artif. Intell. Res. 2022, 74, 851–886. [Google Scholar] [CrossRef]
- Wen, X.; Xie, Y.; Wu, L.; Jiang, L. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Rani, S.J.; Ioannou, I.; Swetha, R.; Lakshmi, R.D.; Vassiliou, V. A novel automated approach for fish biomass estimation in turbid environments through deep learning, object detection, and regression. Ecol. Inform. 2024, 81, 102663. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Chen, X.; Zhu, J. Identifying optimal variables for machine-learning-based fish distribution modeling. Can. J. Fish. Aquat. Sci. 2024, 81, 687–698. [Google Scholar] [CrossRef]
- Hou, J.; Zhou, W.; Fan, W.; Zhang, H. Research on fishing grounds forecasting models of albacore tuna based on ensemble learning in South Pacific. South China Fish. Sci. 2020, 16, 42–50. [Google Scholar] [CrossRef]
- Salih, A.K.; Hussein, H.A.A. Lost circulation prediction using decision tree, random forest, and extra trees algorithms for an Iraqi oil field. Iraqi Geol. J. 2022, 55, 111–127. [Google Scholar] [CrossRef]
- Altelbany, S. Evaluation of ridge, elastic net and lasso regression methods in precedence of multicollinearity problem: A simulation study. J. Appl. Econ. Bus. Stud. 2021, 5, 131–142. [Google Scholar] [CrossRef]
- Lan, K.-W.; Lee, M.-A.; Lu, H.-J.; Shieh, W.-J.; Lin, W.-K.; Kao, S.-C. Ocean variations associated with fishing conditions for yellowfin tuna (Thunnus albacares) in the equatorial Atlantic Ocean. ICES J. Mar. Sci. 2011, 68, 1063–1071. [Google Scholar] [CrossRef]
- Matsubara, N.; Aoki, Y.; Aoki, A.; Kiyofuji, H. Lower thermal tolerance restricts vertical distributions for juvenile albacore tuna (Thunnus alalunga) in the northern limit of their habitats. Front. Mar. Sci. 2024, 11, 1353918. [Google Scholar] [CrossRef]
- Erauskin-Extramiana, M.; Arrizabalaga, H.; Hobday, A.J.; Cabré, A.; Ibaibarriaga, L.; Arregui, I.; Murua, H.; Chust, G. Large-scale distribution of tuna species in a warming ocean. Glob. Change Biol. 2019, 25, 2043–2060. [Google Scholar] [CrossRef]
- Nimit, K.; Masuluri, N.K.; Berger, A.M.; Bright, R.P.; Prakash, S.; TVS, U.; Rohit, P.; Ghosh, S.; Varghese, S.P. Oceanographic preferences of yellowfin tuna (Thunnus albacares) in warm stratified oceans: A remote sensing approach. Int. J. Remote Sens. 2020, 41, 5785–5805. [Google Scholar] [CrossRef]
- Cai, L.; Xu, L.; Tang, D.; Shao, W.; Liu, Y.; Zuo, J.; Ji, Q. The effects of ocean temperature gradients on bigeye tuna (Thunnus obesus) distribution in the equatorial eastern Pacific Ocean. Adv. Space Res. 2020, 65, 2749–2760. [Google Scholar] [CrossRef]
- Alvarez, I.; Rasmuson, L.K.; Gerard, T.; Laiz-Carrion, R.; Hidalgo, M.; Lamkin, J.T.; Malca, E.; Ferra, C.; Torres, A.P.; Alvarez-Berastegui, D. Influence of the seasonal thermocline on the vertical distribution of larval fish assemblages associated with Atlantic bluefin tuna spawning grounds. Oceans 2021, 2, 64–83. [Google Scholar] [CrossRef]
- Song, L.M.; Zhang, Y.; Xu, L.X.; Jiang, W.X.; Wang, J.Q. Environmental preferences of longlining for yellowfin tuna (Thunnus albacares) in the tropical high seas of the Indian Ocean. Fish. Oceanogr. 2008, 17, 239–253. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Lan, K.-W.; Evans, K.; Chang, Y.-J.; Chan, J.-W. Effects of decadal climate variability on spatiotemporal distribution of Indo-Pacific yellowfin tuna population. Sci. Rep. 2022, 12, 13715. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H.; Fan, W.; Jin, S. Impact of abnormal climatic events on the CPUE of yellowfin tuna fishing in the central and western Pacific. Sustainability 2022, 14, 1217. [Google Scholar] [CrossRef]
- Sebastian, P.; Stibor, H.; Berger, S.; Diehl, S. Effects of water temperature and mixed layer depth on zooplankton body size. Mar. Biol. 2012, 159, 2431–2440. [Google Scholar] [CrossRef]
- Wright, S.R.; Righton, D.; Naulaerts, J.; Schallert, R.J.; Griffiths, C.A.; Chapple, T.; Madigan, D.; Laptikhovsky, V.; Bendall, V.; Hobbs, R. Yellowfin tuna behavioural ecology and catchability in the South Atlantic: The right place at the right time (and depth). Front. Mar. Sci. 2021, 8, 664593. [Google Scholar] [CrossRef]

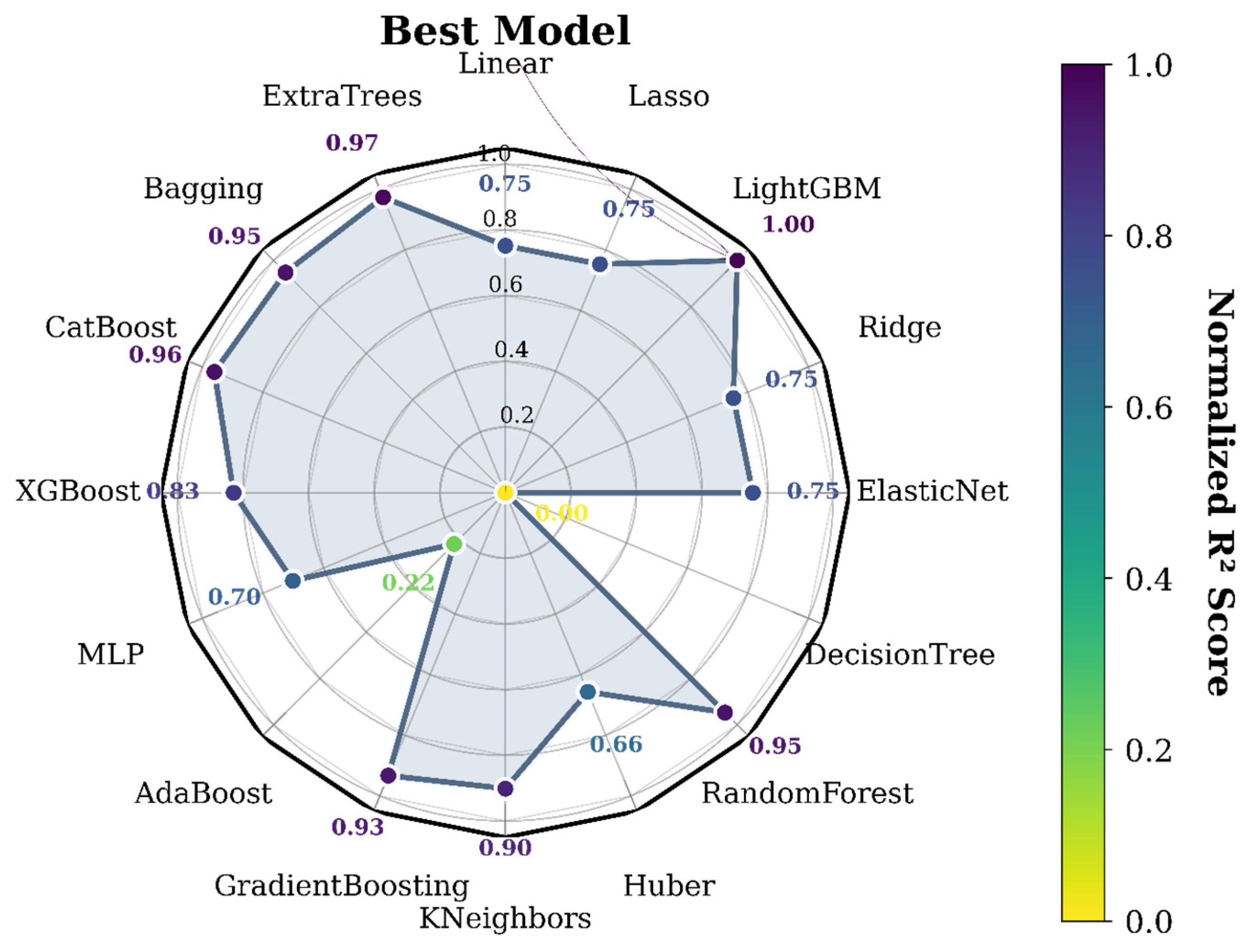
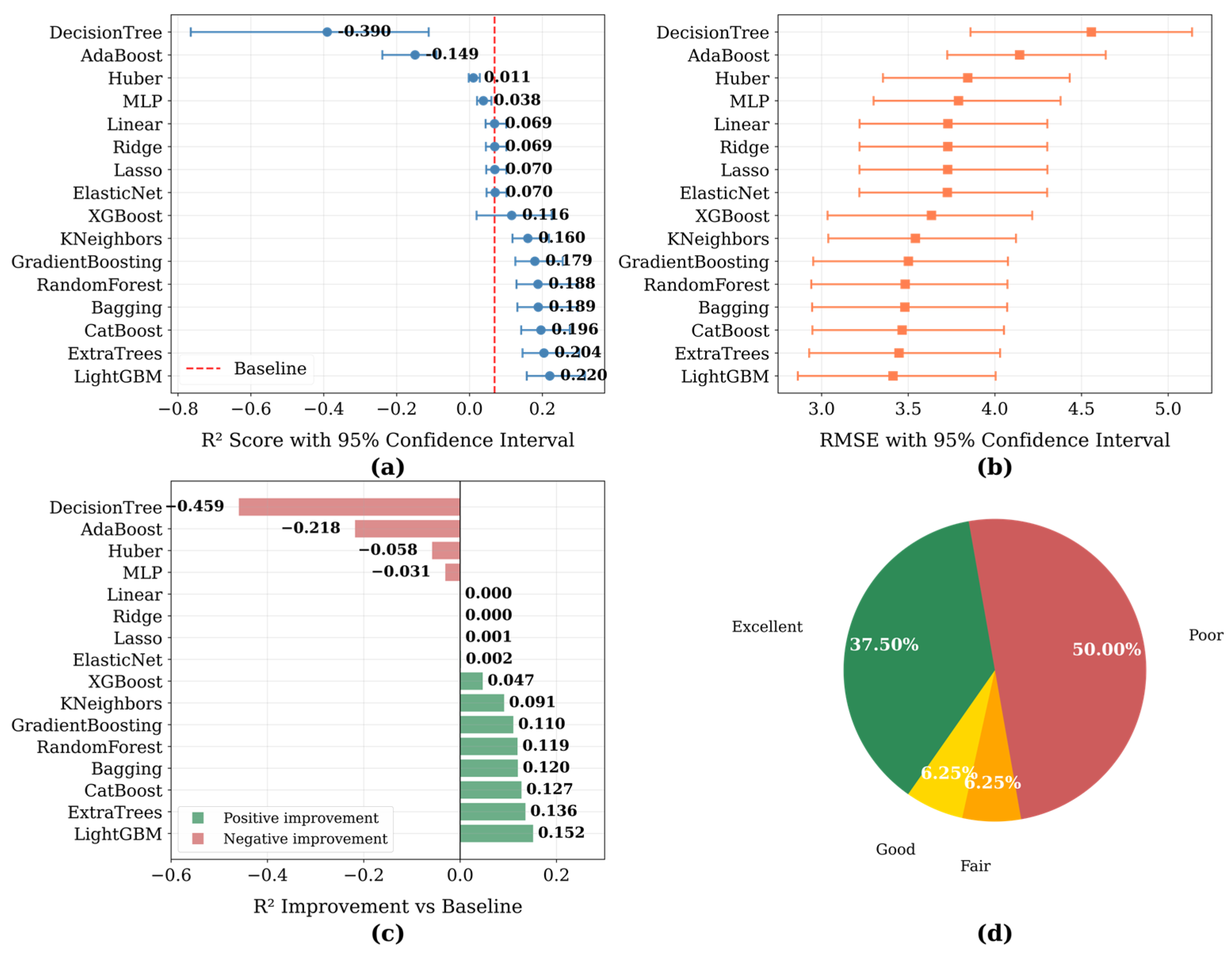
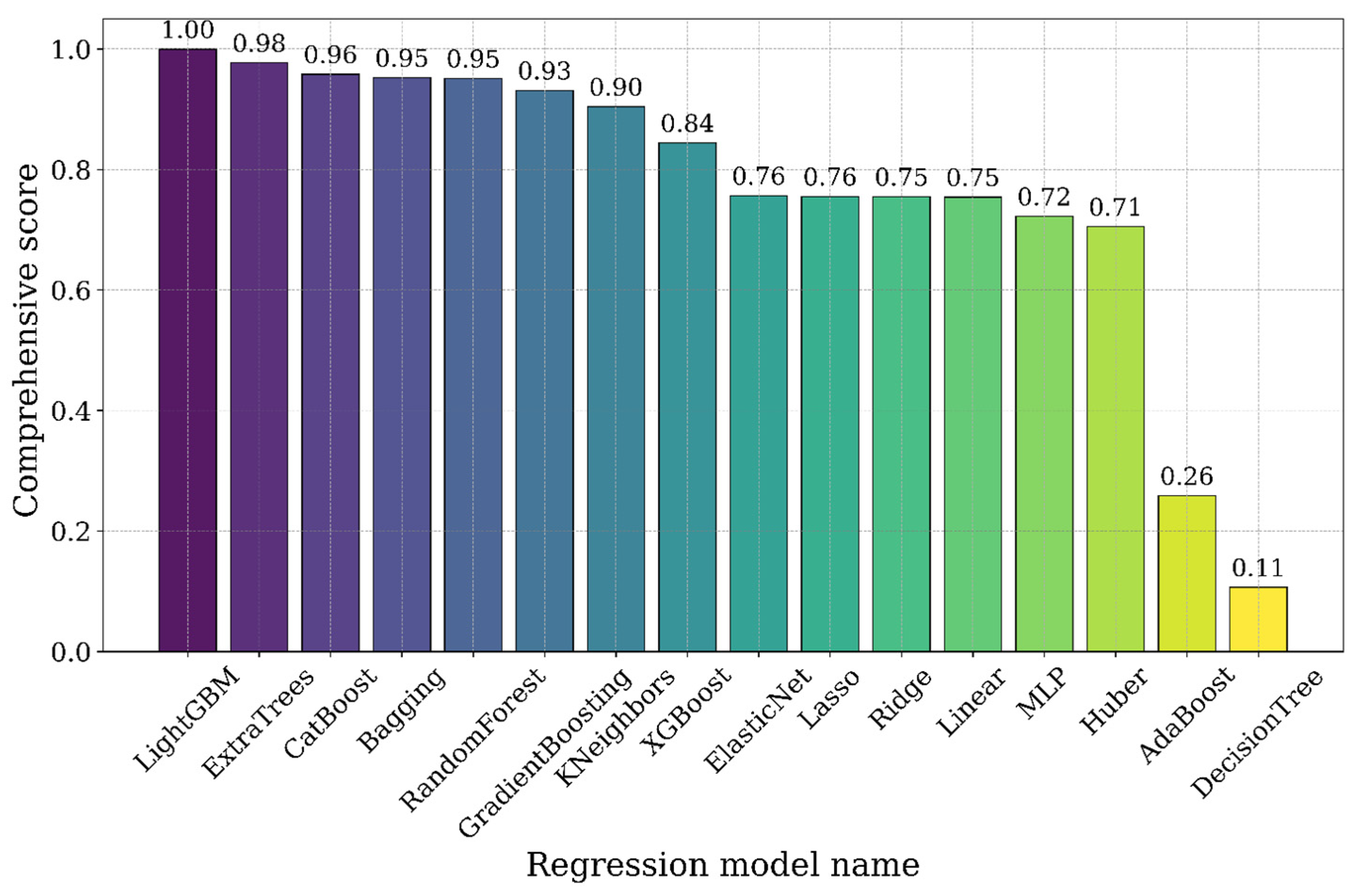
| Model\Score | MAE | MSE | RMSE | EVS | R2 |
|---|---|---|---|---|---|
| LightGBM | 1.611484 | 11.643110 | 3.412200 | 0.221116 | 0.220319 |
| ExtraTrees | 1.610001 | 11.887523 | 3.447829 | 0.204035 | 0.203952 |
| CatBoost | 1.677910 | 12.004651 | 3.464773 | 0.197216 | 0.196108 |
| RandomForest | 1.634359 | 12.091773 | 3.477323 | 0.190333 | 0.190274 |
| Bagging | 1.636302 | 12.130093 | 3.482828 | 0.187753 | 0.187708 |
| GradientBoosting | 1.706000 | 12.256261 | 3.500894 | 0.180118 | 0.179259 |
| KNeighbors | 1.709640 | 12.541822 | 3.541443 | 0.161668 | 0.160137 |
| XGBoost | 1.690276 | 13.205482 | 3.633935 | 0.116058 | 0.115695 |
| ElasticNet | 1.911213 | 13.881904 | 3.725843 | 0.072130 | 0.070398 |
| Lasso | 1.911046 | 13.894650 | 3.727553 | 0.071288 | 0.069545 |
| Ridge | 1.911232 | 13.899188 | 3.728161 | 0.071003 | 0.069241 |
| Linear | 1.911564 | 13.906065 | 3.729084 | 0.070548 | 0.068780 |
| MLP | 1.872767 | 14.365285 | 3.790156 | 0.054812 | 0.038029 |
| Huber | 1.802355 | 14.773407 | 3.843619 | 0.057400 | 0.010699 |
| AdaBoost | 3.057544 | 18.747417 | 4.329829 | −0.064498 | −0.255421 |
| DecisionTree | 2.131442 | 20.764380 | 4.556795 | −0.390487 | −0.390487 |
| Parameter Category | Parameter Name | Optimal Value | Description |
|---|---|---|---|
| Basic Parameters | learning_rate | 0.01 | Controls the learning step size; smaller values improve model stability. |
| n_estimators | 800 | Number of decision trees; a higher number may enhance model performance. | |
| max_depth | 10 | Maximum depth of each tree; limits complexity to reduce overfitting. | |
| Regularization | reg_alpha | 0.1 | L1 regularization coefficient; encourages sparsity in the model. |
| reg_lambda | 10 | L2 regularization coefficient; prevents excessively large weights. | |
| Feature and Sampling | colsample_bytree | 0.9 | Proportion of features sampled per tree (90%). |
| subsample | 0.9 | Proportion of samples used for training (90%), enhancing generalization. | |
| importance_type | gain | Feature importance evaluation method. | |
| Tree Structure | max_bin | 700 | Number of bins for continuous features; higher values improve precision. |
| num_leaves | 35 | Maximum number of leaves per tree; balances complexity and performance. | |
| min_child_samples | 20 | Minimum number of samples in a leaf to prevent overfitting. | |
| min_split_gain | 0.2 | Minimum gain required to make a split. | |
| Randomness Control | bagging_freq | 10 | Performs bagging every 10 iterations. |
| random_state | 42 | Global random seed to ensure reproducibility. | |
| bagging_seed | 42 | Random seed for the bagging process. | |
| Computational Efficiency | n_jobs | −1 | Uses all available CPU cores to accelerate training. |
| Evaluation Metric | Best Score | 0.255 | Best model performance on the validation set. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhou, W.; Zhang, C.; Tang, F. A Comparative Machine Learning Study Identifies Light Gradient Boosting Machine (LightGBM) as the Optimal Model for Unveiling the Environmental Drivers of Yellowfin Tuna (Thunnus albacares) Distribution Using SHapley Additive exPlanations (SHAP) Analysis. Biology 2025, 14, 1567. https://doi.org/10.3390/biology14111567
Yang L, Zhou W, Zhang C, Tang F. A Comparative Machine Learning Study Identifies Light Gradient Boosting Machine (LightGBM) as the Optimal Model for Unveiling the Environmental Drivers of Yellowfin Tuna (Thunnus albacares) Distribution Using SHapley Additive exPlanations (SHAP) Analysis. Biology. 2025; 14(11):1567. https://doi.org/10.3390/biology14111567
Chicago/Turabian StyleYang, Ling, Weifeng Zhou, Cong Zhang, and Fenghua Tang. 2025. "A Comparative Machine Learning Study Identifies Light Gradient Boosting Machine (LightGBM) as the Optimal Model for Unveiling the Environmental Drivers of Yellowfin Tuna (Thunnus albacares) Distribution Using SHapley Additive exPlanations (SHAP) Analysis" Biology 14, no. 11: 1567. https://doi.org/10.3390/biology14111567
APA StyleYang, L., Zhou, W., Zhang, C., & Tang, F. (2025). A Comparative Machine Learning Study Identifies Light Gradient Boosting Machine (LightGBM) as the Optimal Model for Unveiling the Environmental Drivers of Yellowfin Tuna (Thunnus albacares) Distribution Using SHapley Additive exPlanations (SHAP) Analysis. Biology, 14(11), 1567. https://doi.org/10.3390/biology14111567






