Abstract
A spectral filter utilizing dispersive prisms and an optical fiber collimator is presented as an attractive alternative to diffraction grating-based spectral filters. A simplified analytical expression for this prism-based spectral filter is derived. A spectral filter constructed using SF11 flint glass prisms demonstrates Gaussian spectral filter profiles with bandwidths of 8 nm and 4 nm, closely matching with theoretical predictions. Using these filters, we demonstrate two types of mode-locking regimes: a dissipative soliton (DS) pulse and a self-similar (SS) pulse. The dissipative soliton pulses deliver 3.3 nJ with dechirped pulse durations of 206 fs, while the self-similar pulses deliver 2.1 nJ with durations of 120 fs. The results demonstrate that the prism-based filters are well-suited for ultrafast mode-locked fiber lasers.
1. Introduction
Spectral filters play a crucial role in the operation of mode-locked fiber lasers. By adjusting the bandwidth (BW) of spectral filters in the fiber lasers, various types of mode-locking operations can be achieved, including dissipative soliton (DS) pulses and self-similar (SS) pulses [1,2]. Spectral filters can be implemented in various ways, such as bandpass filters [3], birefringent filters [4,5,6], and grating–collimator filters. In particular, the grating–collimator filter—featuring a lens–fiber configuration, commonly referred to as a collimator, to couple grating-diffracted light into a fiber—presents an appealing filter design for a mode-locked fiber laser since the filter utilizes a fiber [7,8,9].
Recently, Ryu et al. [10] derived an analytical expression for diffraction grating––collimator spectral filters, demonstrating that the spectral filtering effect arises due to deviations from the ideal fiber coupling—where ideal coupling occurs when grating-diffracted light at the center wavelength is optimally coupled into the fiber. According to the spectral filter BW equation, the BW decreases with increasing input beam diameter and grating density, as these factors reduce the coupling efficiency, thereby enhancing the spectral filtering effect.
Nevertheless, there are practical limitations to arbitrarily selecting beam diameter and grating density. In the previous study [10], a BW of ~4 nm at 1030 nm (Ytterbium (Yb)-doped fiber laser case) was achieved using a beam diameter of 1 mm with a 300 lines/mm grating. A higher grating density cannot be used, as it would result in a very narrow spectral BW inhibiting mode-locking. Although a 300 lines/mm grating can generate ~4 nm spectral BW for SS fiber lasers, achieving a larger BW is challenging since a lower density grating would lead to higher-order diffractions, thereby reducing the overall efficiency. Similarly, at 1550 nm (Erbium (Er)-doped fiber laser case), a BW of 4 nm was achieved using a beam diameter of 0.5 mm and a 600 lines/mm grating, while such a small beam size makes optical alignment more challenging [7].
These limitations indicate that combining an optical element with weaker diffractive effects with a larger input beam diameter is preferable. A promising alternative is the dispersive prism, which inherently exhibits a weaker spatial dispersion compared to a diffraction grating. Moreover, prisms are advantageous over diffraction gratings in building mode-locked fiber lasers for three key reasons: (1) unlike gratings, prisms do not produce higher-order diffractions or scatter light due to artifacts (e.g., groove defects), enabling high transmission over a broad wavelength range; (2) prisms are easier to maintain, while gratings are prone to degradation over time due to environmental factors such as humidity and dust; (3) the group-delay dispersion (GDD) of prism spectral filters is in the order of 10−6 of that of grating spectral filters, owing to their inherently weaker spatial dispersion. Therefore, the prism spectral filter has a minimal impact on the pulse propagation in the fiber cavity, making it a desirable choice.
In this manuscript, we demonstrate that prism-based spectral filters are promising alternatives to diffraction grating-based spectral filters. An analytical approach for prism-based spectral filters, derived using the ABCDEF matrix formalism, is presented. By utilizing multiple SF11 prisms, spectral filters with various BWs can be created. Furthermore, we experimentally demonstrate the operation of mode-locked fiber lasers by integrating these filters, achieves stable mode-locking in both DS and SS fiber lasers.
2. Analysis of Prism-Based Spectral Filters
The schematic of the prism–collimator spectral filter is shown in Figure 1, where denotes the separation distance between the prism and the lens, the focal length of the lens, and the Brewster angle. As the beam passes through the prism, an arbitrary wavelength experiences a different refractive index , resulting in beam refraction within the prism. After being refracted by the prism, each wavelength is focused onto a different point on the tip of a single-mode fiber (SMF), leading to both translational and angular offsets relative to , which induce the spectral filtering effect [10]. We refer to this lens–SMF configuration as the collimator throughout this paper.
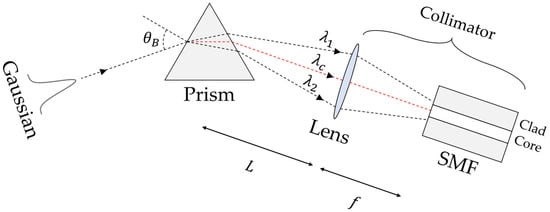
Figure 1.
Schematic of prism-based spectral filter. , the separation distance between the prism and the lens; , the focal length of the lens; , Brewster angle; SMF, single-mode fiber.
The ABCD matrix, also known as the ray transfer matrix, is commonly used to describe the effect of optical elements on the beam [11]. To account for both translational error and angular error , this formalism is extended to the ABCDEF matrix, as shown by Equation (1) [12]. Equation (2) lists the ABCDEF matrices corresponding to free space, lenses, and prisms.
The ABCDEF matrix allows us to compute the final position and angle of a beam, accounting for errors accumulated during propagation through the optical system. In this configuration, the prism introduces an angular error owing to refraction, which can be expressed as an offset relative to the ideal deviation angle.
We utilize the Brewster angle to minimize the loss. When the angles of incidence and emergence are equal, as shown in Figure 2, the deviation angle can be calculated using Equation (3), where denotes the refractive index of the prism and is the apex angle of the prism. SF11 flint glass was selected as the prism material in this study due to its relatively high refractive index among commercially available optical glasses.
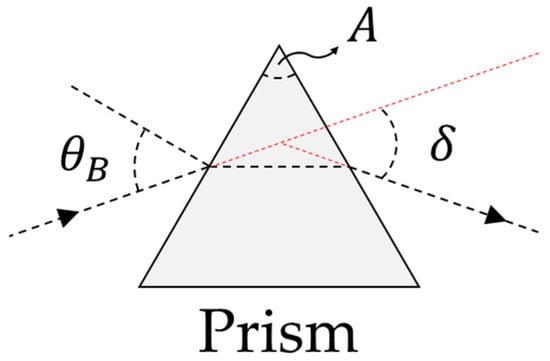
Figure 2.
Schematic of deviation angle. , deviation angle; , apex angle; , Brewster angle.
The angular error introduced by the prism can be approximated using a Taylor expansion around , as given by Equation (4), where is the derivative of with respect to . Since the second-order term contributes less than 1% of the first-order term within the considered spectral filter’s BW range (), higher-order terms can be neglected in this approximation.
By incorporating this angular error into the prism matrix and multiplying the matrices corresponding to the configuration shown in Figure 1, the final matrix at the tip of the fiber can be obtained using Equation (5) [10].
Assuming that a Gaussian input beam is focused onto the single-mode fiber (SMF) with the translational error and the angular error , the SMF coupling efficiency is given by Equation (6) [13], where denotes the input beam radius and the mode field radius of the SMF.
Here, , the total transmission of the prism-based spectral filter, indicates a Gaussian spectral filter shape. Accordingly, the full width at half maximum (FWHM), representing the BW, of the SF11 prism-based spectral filter (hereafter, the SF11 filter) is calculated using Equation (7) [10], where denotes the input beam diameter and the mode field diameter (MFD) of the SMF.
We investigated a typical case of a 1030 nm Yb-doped fiber laser design. It is assumed that an input beam with a diameter of propagates over a free-space distance , and is then focused by a lens with a focal length into an HI1060 fiber, whose mode field diameter is at . Figure 3a illustrates the BW of an SF11 filter as a function of the separation distance , calculated using Equation (6) with the assumed parameters. By utilizing two prisms in the filter, the spectral filter BW can be further reduced. Each curve in Figure 3 corresponds to a configuration involving either (a) one or (b) two SF11 prisms, hereafter referred to as the single- and dual-SF11 filters, respectively.
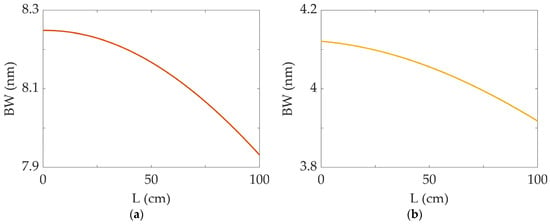
Figure 3.
Bandwidth (BW) vs. separation distance for (a) single- and (b) dual-SF11 prism spectral filters. The parameters are set to , , and , with .
The BW of the single-SF11 filter is approximately 8 nm and does not vary significantly with changes in . A narrower spectral filter is clearly achieved by introducing a second SF11 prism, placed after the first and aligned at the Brewster angle. Using the same calculation procedure as in the single-SF11 case, except that includes additional free-space and prism ABCDEF matrices, the dual-SF11 filter yields the BW of approximately 4 nm.
Figure 4 presents the experimental results for the (a) single- and (b) dual-SF11 filters, along with corresponding Gaussian fits. The transmission was calculated by comparing the spectra of a mode-locked pulse before and after propagation through the SF11 filters.
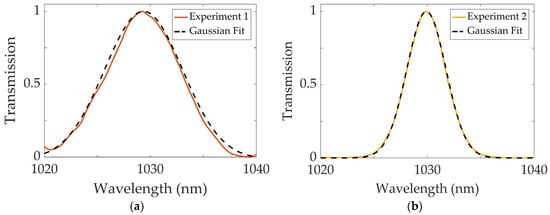
Figure 4.
Transmission spectra of the (a) single- and (b) dual-SF11 prism spectral filters with Gaussian fits.
From the transmission data, the FWHM (BW) of the single- and dual-SF11 filters are approximately 8.7 nm and 4.3 nm, respectively. Overall, the experimental spectral profiles exhibit good agreement with the Gaussian fits, consistent with the assumed Gaussian filtering effect. It is notable that multiple prisms can be incorporated into the spectral filter with minimal loss, provided that the polarization of the incident beam is properly aligned and the prisms are oriented at the Brewster angles.
3. Design of Mode-Locked Fiber Lasers
We confirmed that the single-SF11 filter can provide a BW of ~8 nm, while the dual-SF11 filter achieves a narrower BW of ~4 nm. Furthermore, the single- and dual-SF11 filters satisfy requirements for spectral filter BW ranges for DS (~8 nm) and SS (~4 nm) pulse operation, respectively [14].
Figure 5 shows the schematic of a DS fiber laser design (outlined in orange) and SS fiber laser design (outlined in yellow), incorporating the single- and dual-SF11 filters, respectively. In both designs, the total fiber cavity length is approximately 4 m, comprising 2.4 m of HI1060 fiber (SMF 1 and the WDM section), 0.6 m of Yb-doped fiber (Coractive, YB 401) pumped via the WDM with a 980 nm pump diode, and another 1 m of HI1060 fiber (SMF 2). Correspondingly, Figure 6 shows the experimental configuration of the SS fiber laser, with the beam path indicated by yellow arrows.
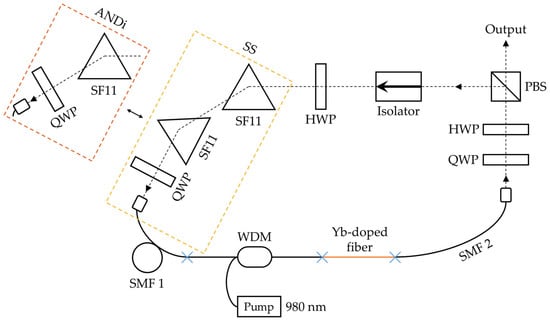
Figure 5.
Schematic of dissipative soliton (DS) and self-similar (SS) fiber lasers, with the spliced part indicated by the cross. QWP, quarter-wave plate; HWP, half-wave plate; PBS, polarizing beam splitter; SMF, single-mode fiber; WDM, wavelength-division multiplexer.

Figure 6.
The experimental configuration of the self-similar (SS) fiber laser.
In our configurations, the group-delay dispersion (GDD) introduced by the SF11 filters is on the order of −10−8 ps2, which is negligible compared to that of grating–collimator filters (on the order of −10−2 ps2) [10]. This minimal dispersion ensures that the overall GDD in our laser designs remains well within the normal dispersion regime.
In the operation of lasers, the SF11 filters function as a spectral filter (SF). A half-wave plate placed in front of the SF11 prism is used to align the polarization of the incident beam to the transverse magnetic (TM) field with respect to the prism. Additionally, quarter-wave plates, half-wave plates, and polarizers along the beam path act as a saturable absorber (SA) by manipulating the nonlinear polarization evolution (NPE).
4. Experimental Results
By adjusting waveplates in the lasers, stable mode-locked operations are achieved. Figure 7 shows (a) the output spectrum of the DS fiber laser, and (b) the corresponding interferometric auto-correlation (AC) signal measured after dechirping the pulses using a pair of transmission diffraction gratings.
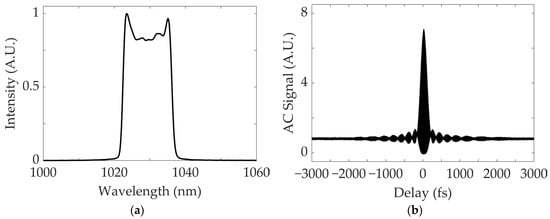
Figure 7.
Output of the dissipative soliton (DS) fiber laser: (a) spectrum, and (b) dechirped auto-correlation (AC) signal.
The DS fiber laser achieves a pulse energy of 3.3 nJ, corresponding to an average power of 160 mW at a repetition rate of 49 MHz, with a dechirped pulse duration of 206 fs. Based on the output spectrum, the steep edge and bat-ear-shaped profile clearly indicate that the laser is operating in a DS regime [2,15,16].
Figure 8 shows (a) the output spectrum of SS fiber laser, and (b) the corresponding AC signal.
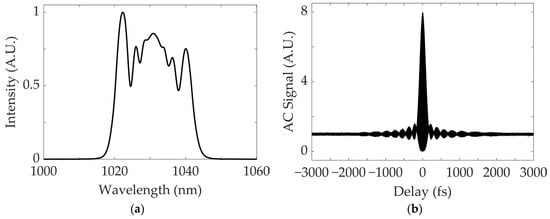
Figure 8.
Output of the self-similar (SS) fiber laser: (a) spectrum, and (b) dechirped auto-correlation (AC) signal.
By contrast, the SS fiber laser achieves a pulse energy of 2.1 nJ, corresponding to an average power of 100 mW at a repetition rate of 48 MHz, with a dechirped pulse duration of 120 fs. The smoother spectral edge and mode-locking with a narrower spectral filter, compared to the DS fiber laser, confirm that the output is characteristic of an SS fiber laser [2,14,17]. The longer grating pair separation distance was required to dechirp the pulse generated by the laser in the DS regime. This indicates that the pulse directly from the laser is longer in the DS regime compared to the SS regime. In both cases, self-starting mode-locking—which occurs simply by increasing the pump power—can be achieved by randomly rotating the intracavity wave plates. These experimental results clearly verify that prism-based filters can be effectively used in practical applications, such as mode-locked fiber lasers operating at various wavelengths [7,18,19].
5. Conclusions
In this study, we designed and experimentally demonstrated prism-based spectral filters by using SF11 prisms, for integration into mode-locked fiber lasers. By implementing single- and dual-SF11 filters, we achieved Gaussian-shaped spectral filter bandwidths of ~8 nm and ~4 nm, respectively. This filtering behavior is consistent with theoretical predictions. The prism filters were successfully implemented in both DS and SS fiber laser configurations.
In addition to their spectral filtering performance, prisms exhibit negligible anomalous GDD and offer practical advantages over diffraction gratings, such as higher transmission efficiency and improved environmental durability. These benefits highlight the potential of prism-based spectral filters as a compelling alternative to grating-based filters in ultrafast mode-locked fiber lasers.
Author Contributions
Conceptualization, A.C.; methodology, A.C.; software, A.C. and M.K.; validation, A.C.; formal analysis, A.C.; investigation, M.K and T.S.; data curation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, A.C.; visualization, M.K.; supervision, A.C.; project administration, A.C.; funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Research Foundation of Korea (NRF) funded by the Korea government (MSIT) [Grant No. RS-2022-NR069920] and the Global Learning & Academic research institution for Master’s · PhD students, and Postdocs (LAMP) Program of the National Research Foundation of Korea (NRF), grant-funded by the Ministry of Education [No. RS-2023-00301938], and IITP (Institute of Information & Communications Technology Planning & Evaluation)-ITRC (Information Technology Research Center), grant-funded by the Korea government (Ministry of Science and ICT) (IITP-2025-RS-2020-II201606).
Data Availability Statement
Data underlying the results presented in this paper are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Z.; Zhan, L.; Fang, X.; Luo, H. Spectral Filtering Effect on Mode-Locking Regimes Transition: Similariton-Dissipative Soliton Fiber Laser. J. Opt. Soc. Am. B 2017, 34, 2325–2333. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Chen, N.-K.; Xie, Y.; Zhang, X.; Tian, X.; Bai, C. Generation of Dissipative Solitons and Self-Similar Pulses by a Mode-Locked Fiber Laser Using a Bandwidth Tunable Mach-Zehnder Interferometer Filter. Results Phys. 2022, 42, 106035. [Google Scholar] [CrossRef]
- Regelskis, K.; Želudevičius, J.; Viskontas, K.; Račiukaitis, G. Ytterbium-Doped Fiber Ultrashort Pulse Generator Based on Self-Phase Modulation and Alternating Spectral Filtering. Opt. Lett. 2015, 40, 5255–5258. [Google Scholar] [CrossRef] [PubMed]
- Özgören, K.; Ilday, F.Ö. All-Fiber All-Normal Dispersion Laser with a Fiber-Based Lyot Filter. Opt. Lett. 2010, 35, 1296–1298. [Google Scholar] [CrossRef] [PubMed]
- Demırbas, U. Off-Surface Optic Axis Birefringent Filters for Smooth Tuning of Broadband Lasers. Appl. Opt. 2017, 56, 7815–7825. [Google Scholar] [CrossRef] [PubMed]
- Kobtsev, S. Birefringent Filters in Fiber Systems. J. Opt. Soc. Am. B 2025, 42, 489–494. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Z.; Lamb, E.S.; Wise, F. Self-Similar Erbium-Doped Fiber Laser with Large Normal Dispersion. Opt. Lett. 2014, 39, 1019–1021. [Google Scholar] [CrossRef] [PubMed]
- Nyushkov, B.; Kobtsev, S.; Antropov, A.; Kolker, D.; Pivtsov, V. Femtosecond 78-Nm Tunable Er:Fibre Laser Based on Drop-Shaped Resonator Topology. J. Light. Technol. 2019, 37, 1359–1363. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, H.; Chen, J.; Zhan, Q. Tunable Mode-Locked Fiber Laser to Generate Ultrashort Cylindrical Vector Beams. Laser Phys. Lett. 2021, 18, 035102. [Google Scholar] [CrossRef]
- Ryu, S.; Jeong, J.; Kang, M.; Son, T.; Chong, A. Spectral filtering effect of diffraction gratings with a lens coupling to optical fibers. arXiv 2025, arXiv:2503.17925. [Google Scholar] [CrossRef]
- Bélanger, P.A. Beam Propagation and the ABCD Ray Matrices. Opt. Lett. 1991, 16, 196–198. [Google Scholar] [CrossRef] [PubMed]
- Siegman, A.E. Complex paraxial wave optics. In Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Saruwatari, M.; Nawata, K. Semiconductor Laser to Single-Mode Fiber Coupler. Appl. Opt. 1979, 18, 1847–1856. [Google Scholar] [CrossRef] [PubMed]
- Renninger, W.H.; Chong, A.; Wise, F.W. Self-Similar Pulse Evolution in an All-Normal-Dispersion Laser. Phys. Rev. A 2010, 82, 021805. [Google Scholar] [CrossRef] [PubMed]
- Renninger, W.H.; Chong, A.; Wise, F.W. Dissipative Solitons in Normal-Dispersion Fiber Lasers. Phys. Rev. A 2008, 77, 023814. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative Solitons for Mode-Locked Lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Zhao, Z.; Jin, L.; Set, S.Y.; Yamashita, S. Broadband Similariton Generation in a Mode-Locked Yb-Doped Fiber Laser. Opt. Lett. 2022, 47, 2238–2241. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Li, Y.; Xu, Y.; Wang, F. Carbon Nanotube Mode-Locked Thulium Fiber Laser With 200 Nm Tuning Range. Sci. Rep. 2017, 7, 45109. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wang, Y.; Chen, H.; Luan, K.; Tao, M.; Si, J. Wavelength-Tunable Passively Mode-Locked Mid-Infrared Er3+-Doped ZBLAN Fiber Laser. Sci. Rep. 2017, 7, 14913. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).