Abstract
A popular water pipe system, used in many countries, is one formed by prestressed cylindrical concrete pipes (PCCP). This study used the results of an experimental investigation on ten (10) PCCP samples taken from an existing water pipeline. The objective was to investigate their bearing capacity under three-edge bending or internal hydraulic pressure loads to check the capability of specific retrofitting/strengthening schemes to upgrade this bearing capacity and thus enhance the operational period (Part A). In this part B study, the measured response of the PCCP pipes was made to validate a numerical approach aimed at numerically simulating the behavior of the original and retrofitted PCCP pipes under hydraulic internal pressure. From the obtained numerical results, it was seen that the assumed nonlinear mechanisms for the concrete volume and steel membrane were verified by comparing numerical predictions with measurements in terms of strain response of the steel membrane, damage patterns of the concrete volume, and the overall internal pressure versus radial expansion response. The numerical predictions of the bearing capacity contribution of the fully active prestress as well as the three specific jacketing schemes, including carbon fiber reinforced polymer (CFRP) or reinforced concrete (RC) jackets, were also verified from comparisons with the corresponding measured response.
1. Introduction
The examined prestressed concrete cylinder pipes are widely used worldwide in various water distribution systems. An existing major pipeline generated this research. It was the decision of the owner of this pipeline to apply specific retrofitting schemes after 70 years of operation. Part A [1] of the study detailed tested specimens representing the modulus of the pipe in situ, which was almost identical to the modulus that makes up the actual pipeline that is in operation. By comparing the bearing capacity of the retrofitted specimens with that of the one without any retrofit, the effectiveness of the retrofitting scheme could be evaluated in a comparative manner. The prototype specimens of the pipeline were subjected in the laboratory to: (a) hydraulic internal pressure and/or (b) three-edge vertical load bending. All important details describing the applied loading, the resulting displacement and strain response, and the structural damage observed during this experimental sequence are included in Part A and, due to space limitations, are not duplicated here. The objective of this part of the study (Part B) was to apply commercially available software in an effort to numerically simulate the measured behavior of the tested specimens. This was done using the exact dimensions, technical details, mechanical properties of the various materials and laboratory conditions in applying the load and measuring the response of the tested specimens. Therefore, the numerical simulation is also a step towards proving the validity of such a numerical approach to realistically approximate the observed behavior. Among the tested specimens, one represented the prototype pipeline whereas three specimens represented three different retrofitting schemes; two of these retrofitting schemes employed carbon reinforcing fiber polymer (CFRP) jackets (either internally or externally for the pipe) and the third retrofitting scheme employed an external reinforced concrete (RC) jacket [1]. Because such pipelines have been in operation for many decades, it is of interest to be able to examine their current safe performance as well as to investigate the effectiveness of specific retrofitting schemes to ensure their desired performance in the future. Several researchers have conducted experimental testing supplemented with numerical simulations. Zarghamee et al. [2,3] carried out nonlinear simulations of prestressed concrete pipes subjected to water pressure and dead loads. The numerical simulation used composite shell elements combined with a constitutive law which included compressive crushing, tensile softening, and cracking. External radial pressure was used to simulate the prestress. The prestress loss was simulated by removing this external pressure either from the entire model or from a certain length of the pipe. For a PCCP with a diameter of 6300 mm, it was shown that the principal mode of failure was the failure of wires rather than the compressive crushing of the concrete. For relatively small diameter pipes (equal to 1850 mm), the dominant mode of failure was the rupture of the internal steel membrane. The performance of PCCP under combined internal and external loads was studied numerically by Hajali et al. [4]. They focused on the effect of broken wires and the performance of the joint regions. Five-layer composite elements were utilized in this numerical simulation, representing the inner concrete, the steel membrane, the outer concrete, the prestressing wires and the external coating, assuming perfect bonds between these layers. Nonlinear concrete material laws were assumed for each layer based on the tensile strength and compressive strength for either the concrete or steel. The full interaction between the pipe modulus was assumed at their joint regions. A sensitivity analysis was performed to study the effect of the number and respective location of broken prestressing wires. The effect of prestress loss was also investigated by Gomez et al. [5] using a 3D model to predict the response of the pipe with different numbers of broken wires under dead load and internal water pressure. The concentration of failed wires in one section was found to be the most unfavorable scenario. The effectiveness of retrofitting by applying FRP sheets depended on the percentage of failed wires.
Feng et al. [6] numerically simulated the performance of PCCP using an equivalent homogenized material instead of the detailed cross section with the steel membrane and prestressing wires. They numerically simulated 16 PCCP modulus assuming that at their joints a friction coefficient was equal to 0.7. This numerical simulation also included the soil volume employing solid elements and assuming a soil—pipe friction coefficient equal to 0.2. They observed that a differential settlement above 35 cm leads to pipe failure. Gong et al. [7] numerically studied the behavior of PCCPs with an external reinforced concrete cover, assuming suitable material models for concrete and steel, while including the interface failure between the various layers. Pre-tensioning of the pipe was applied using an equivalent temperature variation. Towards evaluating the effectiveness of specific jacketing schemes, they numerically simulated the performance of PCCP segments tested under three-edge bearing external or axial loads. Zhai et al. [8] investigated the application of prestressed FRP jackets as a retrofitting technique. They adopted the concrete damage plasticity constitutive law for the concrete core and elastic-plastic material laws for either the steel cylinder or the prestressed wires in their numerical simulations. The steel cylinder and the wires were embedded in the concrete core, whereas the FRP sheets were assigned with a linear—brittle law; the prestressing was applied as a temperature decrease in these numerical simulations. Three models were examined; one with the PCCP without repair, the second with the PCCP repaired but without the FRP jacket prestressed and the third with the FRP jacket prestressed. Further numerical analyses [9,10] investigated the effect of different percentages and locations of prestress loss. The contribution of the strengthening coating was shown to increase with an increase in the number of broken wires.
Hu et al. [11] investigated the application of CFRP layers on the internal surface of PCCPs as a repair and retrofitting technique. They studied the performance of the examined PCCPs under internal hydraulic pressure through testing and numerical simulations. The concrete parts were simulated by 3D finite elements adopting a concrete damage plasticity (CDP) constitutive law, whereas the prestressing wires and the steel cylinder were simulated by truss elements and shell elements, respectively. CFRP layers were also numerically simulated by shell elements being attached to the inner concrete surface with cohesive elements. They used a sequential deactivation of the prestressing wires. In this sequence, it was found that the progressive failure of the PCCP begins with the cracking of the outer concrete surface, the cracking of the inner concrete core, the yield of the steel cylinder, and finally the CFRP failure. Dong et al. [12] developed a numerical simulation for a PCCP module based on the provisions of AWWA C304 [13]. They employed 3D solid finite elements for the concrete core (CDP), shell elements for the steel cylinder and truss elements for the prestressed wires. The prestress was transferred from the prestressing wires to the concrete through linear spring elements, whereas the prestressing wires themselves were simulated with nonlinear spring elements. They also utilized an equivalent temperature variation toward applying the prestress force. Xiong et al. [14] performed a numerical simulation of prestressed pipes proposing a new methodology with the name “wire-wrapping model”. This method attempts to simulate the manufacturing process of a PCCP. They compared the predicted stress state of the prestressing with that resulting from either the equivalent external radial pressure method or the standard analytical method AWWA C304 (2007) [13].
The validation process to be presented here follows a step-by-step numerical simulation approach. Chapter 2 includes a summary description of the tested samples and the loading conditions and how they were numerically simulated. The full description is given by Manos et al. [1]. Chapter 3 includes a comparison of the measured response and the corresponding numerical predictions for each specimen tested. Initially, the original pipe specimens without and with prestressed wires (spec. 10 and spec. 7, [1]) subjected to hydraulic internal pressure are numerically simulated. The numerical simulation was then extended to include the retrofitted specimens with three different retrofitting schemes (spec. 5, spec. 3 and spec. 1, [1]). The validity of each numerical simulation is based on comparing the overall measured and numerically predicted response of the internal hydraulic pressure amplitude versus the corresponding radial expansion for each of the five specimens. In chapter 4 the same numerical methodology is followed in an effort to numerically simulate the measured response of specimens that were tested having been inflicted with prestressing defects. This numerical simulation was first tried for the two specimens with prestressing defects tested in the laboratory, the original pipe (spec. 7, [1]) and the pipe strengthened with an internal CFRP jacket (spec. 5, [1]). This simulation effort that includes a prestressing defect was next extended for the other two retrofitting schemes, one having an external CFRP jacket (spec. 3, [1]), and the second with an RC jacket (spec 1, [1]). These two subsequent numerical simulations did not have any experimental results to be compared with. Chapter 5 states the basic conclusions of this study.
2. Description of the Numerical Simulation Used
2.1. Description of the Numerical Methodology Used
The various details of water pipe systems built with this particular technology and the various problems they present were described in the companion paper (Part A [1]) and will not be repeated here. The aim is to validate a numerical simulation methodology utilizing all the experimental results presented in the companion paper (Part A [1]), which includes the original pipe, the retrofitted pipe with three different schemes, and all these being inflicted with prestressing defects. Towards this end, use is made of the options included in commercial software to numerically simulate the following: (a) The presence of prestressing wires capable of introducing the desired initial prestress level and responding to a given nonlinear constitutive law, based on laboratory measurements, during the subsequently applied loads. (b) The nonlinear behavior of the volume of concrete both in compression but, more importantly, in tension, based also on laboratory tests. (c) The nonlinear behavior, also based on testing, of the steel, which forms the internal steel membrane that is part of the pipe. (d) The mechanical characteristic of the materials, also defined by testing, that were used for the internal and external jackets. A basic assumption followed in this numerical process, apart from the above nonlinear material characteristics, was the fact that all these various materials that formed the original and retrofitted pipes were working together without the possibility of slip at their common interfaces. This assumption is considered to be realistic because of the closed cylindrical shape of the prestressing wires, the steel membrane, the CFRP jackets, and the reinforcement of the RC jacket. Construction details were adopted that ensured that this assumption is realistic. Numerical models were formed by placing all these various materials at their exact location and exact geometry, which was accurately defined during the experimental campaign.
A typical cross section is shown in Figure 1 including the CFRP jacket at the internal face of the pipe. Alternatively, the CFRP or RC jacket was placed on the outside face of the pipe. The first numerical model was initially formed from the internal face (without the CFRP jacket) up and including the steel membrane (corresponding to specimen 10). The second numerical model, excluding any jacketing, was formed from the internal to the external face of the pipe, including the prestressing wires, but excluding the protective mortar being of no structural significance (corresponding to specimen 7). The 3rd, 4th, and 5th numerical models are an extension of the 2nd numerical model with the inclusion of the studied retrofitting schemes; e.g., the internal CFRP jacket, the external CFRP jacket, and the RC jacket. In all cases, the concrete volume was tied to the steel membrane. Cross sections of each numerical model discussed here are depicted in Figure 2 together with a 3D representation (Figure 3) of the numerical models with RC jacket and external CFRP jacket. In these figures, the concrete core is depicted in gray, the steel cylinder in red, the prestressing wires in blue, the CFRP jacket in green and the reinforcing bars of the RC jacket in yellow. Following an initial mesh sensitivity analysis, the mesh size was common for all solid elements, shell elements, and truss elements with a basic dimension approximately equal to 20 mm in all directions. Due to the radial symmetry of the structure and the applied loading, the numerical simulation could have been performed for only a portion of the tested specimens. However, it was decided to numerically simulate the exact geometry of the pipe specimens as they were tested in the laboratory [1].
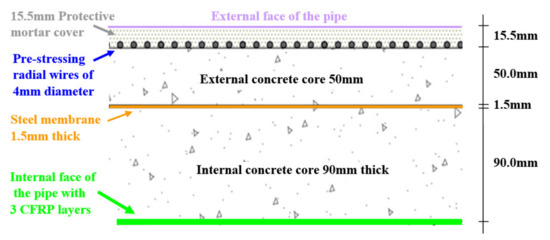
Figure 1.
Typical cross-section of the tested pipe specimens.
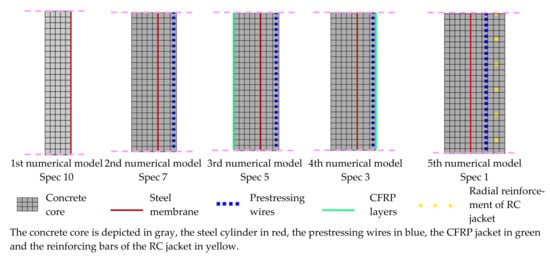
Figure 2.
Typical cross-sections of developed numerical models.

Figure 3.
3D view of the model (a) with the RC jacket (b) with the external CFRP jacket.
A series of 3D numerical simulations were next performed using: solid elements for the concrete volume (either for the original cylinder or the RC jacket), shell elements for the steel membrane and the CFRP jackets (internally or externally), and truss elements for the prestressing wires and reinforcing rebars of the RC jacket. Each of these elements were provided with nonlinear constitutive laws, which followed the measured behavior (see part A [1], Figure 3, Figure 4, Figure 5 and Figure 6 for the steel membrane, for the prestressing wires for the pipe-concrete and for the CFRP layers, respectively). The concrete samples were used to measure compressive behavior (Figure 4a). The adopted tensile behavior is the one depicted in Figure 4b, with the direct tensile strength being approximately equal to 37% of the measured flexural tensile strength, found from testing [1]. Such a tensile concrete behavior is also employed by other researchers [11,12,13]. As can be seen in Figure 4b, in this constitutive law, the initial linear branch is followed by a horizontal plateau when the tensile stress reaches the tensile strength value for a relatively small range of axial strain values before the descending branch. This is included in order to avoid numerical instabilities at this stage of the nonlinear solution process.
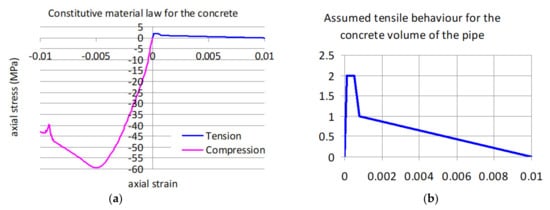
Figure 4.
(a) The adopted constitutive law for the concrete (b) The magnified tensile behavior.
2.2. Particulars of the Loading Process
A step-by-step nonlinear analysis was utilized first by applying the prestress force. The prestress level specified by the AWWA specifications for this pipeline was equal to 1370 MPa. The nonlinear numerical analysis followed the following subsequent distinct loading conditions:
1. First, the prestressing force was applied as an initial loading condition, defining the desired prestress level for each of the fifty-two (52) prestressing wires within the 1 m length of the tested samples, numerically simulated as truss elements. The actual prestress level of each specimen was not exactly known during testing. A prestress level equal to 1300 MPa was adopted for all specimens as an initial prestress level. Due to the deformability of the concrete volume at the end of the first loading condition, the resulting balanced prestress level for the numerical model was equal to 1270 MPa, also approximating in this way the loss of prestress due to creep.
2. The hydraulic internal pressure was applied at the second loading condition, starting from the state of deformation, stress, and strain domain at the end of the first loading condition. This pressure, was uniformly distributed in an axisymmetric way all around the internal face of the numerical model. The hydraulic internal pressure was applied in successive numerous steps of the nonlinear analysis process of continuously increasing amplitude, thus simulating exactly the hydraulic internal pressure which was gradually applied during testing (see part A, [1]).
3. The adopted boundary conditions prevented the pipe from moving as a rigid body. This was done by constraining the horizontal displacement in a direction parallel to the axis of the cylinder for all the nodes located at the cross section of the vertical plane of symmetry for the pipe as well as the vertical displacement, the horizontal displacement normal to the axis of the cylinder, and the rotation around the same axis at the central point of the whole structure. The boundaries of the two cross sections at the end of the vertical pipe as well as all the cylindrical surfaces of the internal and external pipe were left free from any displacement constraints. This is again in line with the relevant boundary conditions of the tested specimens, a fact that was ensured following specific fixtures of the loading experimental arrangement [1].
3. Obtained Numerical Results
The numerical results obtained are first presented by plotting the variation of the applied internal hydraulic pressure versus the variation of the resulting radial expansion, as was also done in Part A [1]. Next, the stress and strain response of the various parts that form the pipe, e.g., concrete volume, steel membrane, prestressing wires, and the various added jackets is depicted for specific levels of internal pressure in order to describe and discuss important response mechanisms of these various parts. This is done for all the numerically simulated specimens tested in the laboratory, which are listed in Table 1. As can be seen in this table, the numerical simulation included two specimens, namely specimen 7 and specimen 5, which after the completion of a first sequence of tests, having all the prestressing wires active, an additional testing sequence was followed whereby a number of prestressing wires became inactive, as is described in part A [1]. This is done to study the influence of prestressing defects. The current numerical investigation was extended to include such a simulation of the prestressing defects for specimens with external strengthening, either CFRP or RC jackets, although such defective specimens were not tested in the laboratory. The relevant results are presented in Section 4.

Table 1.
Numerical models and the corresponding tested specimens.
3.1. Numerical Simulation of the Pipe with the Prestressed Wires Removed
In Figure 5a the numerically predicted radial expansion versus internal pressure response is compared with the one measured during testing. In Figure 5b, the numerically predicted zones of plastic strain with relatively large values are shown when the internal pressure amplitude is equal to 2.45 bar, indicating in this way the initiation of concrete cracking. This was also identified from the measured response (see a change of slope of the plotted curves in Figure 5a) but at somewhat higher internal pressure value (approximately 3.0 bar). At this pressure level, the predicted radial displacement response exhibits a horizontal plateau of 0.8 mm, which is not present in the measured response. This could be attributed to the constitutive law adopted for the concrete volume, which also has a plateau for the tensile strength value (ft) prior to the descending branch (Figure 4b). When the internal pressure is increased further than 2.5 bar and up to 5.7 bar the numerically predicted response develops a larger radial expansion than the corresponding measured values, possibly due to the mentioned plateau. The maximum pressure reached during the numerical simulation (6.1 bar) is also higher than the one reached during testing (5.2 bar). In Figure 6a,b the numerically predicted radial axial stresses response of the steel membrane is shown for internal pressure amplitudes equal to 4.0 bar and 5.7 bar, respectively. For internal pressure equal to 4.0 bar the steel membrane is predicted to reach yield at four narrow zones indicated with red colour whereas for internal pressure equal 5.7 bar the whole steel membrane is beyond yield. This agrees with the predicted and observed radial expansion versus internal pressure variation response shown in Figure 5a, which indicates a nonlinear behavior similar to the constitutive material law adopted for the steel membrane based on laboratory testing (see Figure 3, Part A, [1]).
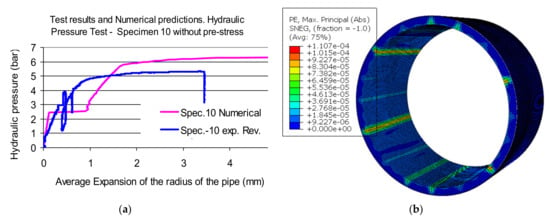
Figure 5.
(a) Internal hydraulic pressure versus radial expansion response. Measured and numerically predicted (b) The numerical simulation of the zones with concentrated large concrete plastic strains.
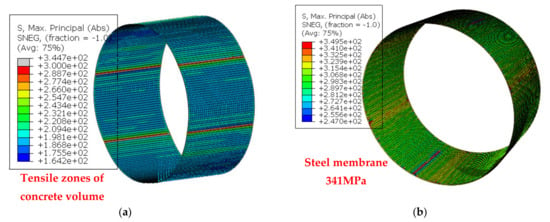
Figure 6.
The numerically predicted radial axial tensile stress distribution for the steel membrane. (a) For internal pressure amplitude equal to 4.0 bar. (b) For internal pressure amplitude equal to 5.7 bar.
For pressure values higher than the concrete cracking pressure the nullification of the concrete volume contribution to resisting the internal pressure occurs, thus having only the steel membrane to resist the internal pressure. From Figure 5a it can be seen that the widespread yield of the steel membrane occurred for 5.0 bar internal pressure during testing whereas this was predicted to occur for 5.9 bar. Figure 7a depicts the numerically predicted zones with relatively large plastic strain values for the concrete volume. The damaged concrete during testing of this specimen as seen from the interior of the pipe after the end of the internal hydraulic pressure test is also shown in Figure 7b. As can be seen, the actual concrete cracking is more widely spread than the large plastic strain zones predicted by the numerically simulation. This discrepancy could also be attributed to the adopted constitutive law for the tensile behavior of the concrete volume, as previously underlined.

Figure 7.
(a) The numerical simulation of the zones with concentrated large concrete plastic strains. (b) The damaged internal concrete after the end of the hydraulic pressure test for specimen 10.
In order to check the effect of the adopted tensile behavior of the concrete an alternative constitutive law was tried, which is depicted in Figure 8a against the initially assumed tensile behavior for the concrete. This alternative constitutive concrete law (law-2) assumes a concrete tensile strength value larger than before (2.4 MPa against 2.0 MPa) with a horizontal plateau and a descending branch similar to the initial constitutive law (law-1, Figure 8a). This change is arbitrary because the tensile strength was derived indirectly from test data of the concrete flexural tensile strength (Part A, [1]).
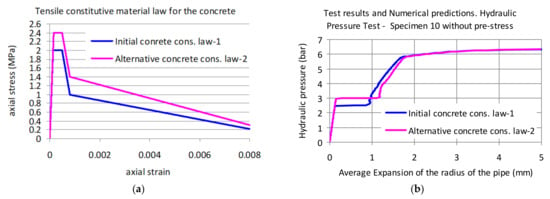
Figure 8.
(a) Initial and alternative constitutive law assumed for the tensile behavior of the concrete. (b) Internal hydraulic pressure versus radial expansion response resulting from the initial and the alternative concrete constitutive laws.
The resulting radial displacement versus internal hydraulic pressure response obtained numerically for specimen “spec. 10”, assuming this alternative constitutive law for the tensile behavior of the concrete volume is compared in Figure 8b with the corresponding response assuming the initial concrete constitutive law (law-1). As can be seen, the change of the tensile strength value resulted mainly in changing the horizontal plateau of the response curve to an increased internal pressure value whereas the response for higher pressure values than this remained almost the same. Based on this, subsequent numerical simulations were performed with the initial concrete constitutive law that assumes a rather conservative tensile strength value for the concrete volume. This numerical approach for simulating the observed response of spec. 10 can be considered as acceptable, despite the mentioned discrepancies, as it represents in a reasonable way the nonlinear behavior of both the concrete volume and the steel membrane. Therefore, the same numerical simulation approach is subsequently employed for all the remaining specimens (spec. 7, spec. 5, spec. 3, and spec. 1) that follow.
3.2. Numerical Simulation of the Pipe with All the Prestressing Wires Fully Active
As described, the numerical analysis commenced by first applying to all the prestressing wires a prestress force corresponding to a radial axial stress equal to 1300 MPa. This resulted in radial axial stress distribution for the concrete volume and the steel membrane, are shown in Figure 9a,b, respectively. Figure 10a shows the corresponding radial axial stress distribution for the prestressing wires equal to 1271 MPa. The concrete develops compressive stress values equal to 3.19 MPa and 2.70 near the internal and the external pipe surface, respectively. The predicted compressive stress value of the steel membrane is equal to 40 MPa.
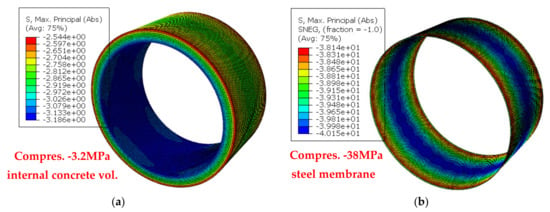
Figure 9.
The numerically predicted radial axial stress distribution after applying the prestress force. (a) For the concrete volume. (b) For the steel membrane.
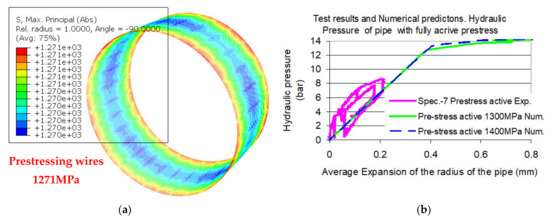
Figure 10.
Measured and numerically predicted for specimen 7: (a) the resulting radial axial stress distribution at the prestressing wires after applying the prestress force. For the concrete volume; and (b) internal hydraulic pressure versus radial expansion response.
As already discussed, the actual level of prestress for the tested specimens is not known. To study the effect of a prestress level variation an additional numerical analysis was performed for this specimen by introducing a small increase to the prestress level thus applying a prestress level equal to 1400 MPa, instead of 1300 MPa. This corresponds to a balance prestress level equal to 1370 MPa at the end of this loading condition. The resulting variation of the internal hydraulic pressure versus the radial expansion is also plotted in Figure 10b. As can be seen, the resulting differences are relatively small. Therefore, all subsequent numerical simulations were performed and the corresponding results were derived for prestress level equal to 1300 MPa.
The radial axial stress response for the steel membrane and the prestressing wires is shown in Figure 11a,b, respectively, when the internal pressure reaches 14.6 bar. For this pressure, the steel membrane and the prestressing wires are stressed beyond yield, which agrees with the previously stated comments. For this internal pressure amplitude, the plastic strains of the concrete volume have already developed, as shown in Figure 11c-mid which shows that the predicted concrete damage zones coincide with the steel membrane yield zones, whereas on the contrary the prestressing wires exhibit relatively low values than at the neighboring regions.
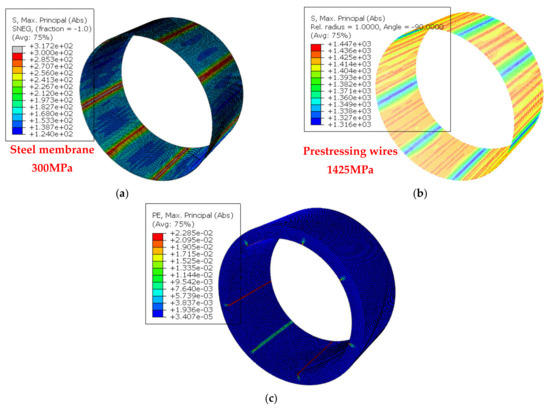
Figure 11.
The predicted radial axial stress and plastic strain distribution for internal hydraulic pressure of 14.6 bar: (a) at the steel membrane; (b) at the prestressing wires; and (c) plastic strains for the concrete volume.
3.3. The Pipe with an Internal FRP Jacket and the Prestressing Wires Fully Active
The same procedure was followed in this model, which was formed by adding in the previous numerical simulation an internal layer of shell finite elements corresponding to the internal CFRP jacket of specimen-5 [1]. The assumed prestressing level was equal to 1300 MPa and the initial constitutive law was used for the tensile behavior of the concrete. Figure 12b depicts the comparison between measured and numerically predicted internal pressure versus radial expansion response. The numerical simulation was extended to pressure levels higher than the pressure levels applied during testing. Moreover, the numerical simulation did not attempt load-unload cycles. The predicted radial displacement versus internal pressure response compares in a reasonable way with the corresponding measured response up to the pressure level of 8.25 bar. Beyond this pressure level no measurements are available.
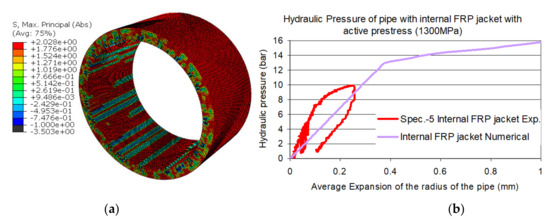
Figure 12.
Measured and numerically predicted for specimen 5: (a) the predicted radial axial stress distribution of the concrete volume for internal hydraulic pressure equal to 14.4 bar; and (b) internal hydraulic pressure versus radial expansion response.
Figure 12a shows the radial axial stress distribution of the concrete volume for internal pressure amplitude equal to 14.4 bar, which is a pressure value higher than the value that the predicted pressure-radial expansion response exhibits a significant change of slope. As can be seen, the concrete volume has widespread zones indicating almost zero values. For the same internal pressure amplitude Figure 13a–c depicts the predicted stress response for the steel membrane, for the prestressing wires, and for the CFRP jacket, respectively. As can be seen, the steel membrane is well below yield, and the CFRP is well below their axial tensile strength. Only the prestressing wires are close to their yield.
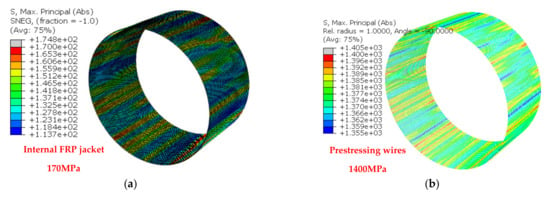
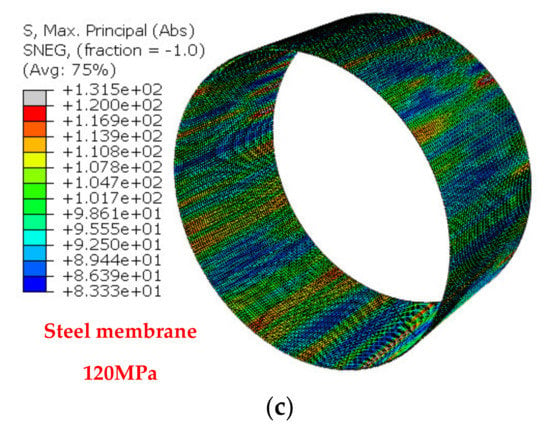
Figure 13.
Internal hydraulic pressure of 14.4 bar: (a) steel membrane below yield stress; (b) near the yield stress of the prestressing wires; and (c) the steel membrane below yield (120 MPa).
The same predicted stress response is depicted in Figure 14a–c for internal pressure amplitude equal to 18.5 bar. This time both the steel membrane and the prestressing wires are beyond yield. However, the CFRP jacket is still below its tensile strength. From all these predictions it can be concluded that the internal CFRP jacket can be quite successful in increasing the hydraulic internal pressure capacity for this pipe. Moreover, the level of 10 bar maximum internal pressure amplitude reached during testing for this specimen is below the pressure amplitude that would have resulted in the yield of the steel membrane or the prestressing wires, provided that the actual prestress level was not considerably smaller than what was assumed in the analysis. Again, the predicted radial displacement versus internal pressure response compares in a reasonable way with the corresponding measured response up to the pressure level of 10.0 bar. Beyond this pressure level no measurements are available.
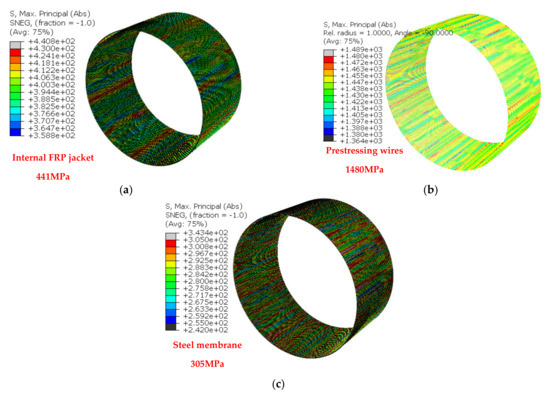
Figure 14.
Internal hydraulic pressure of 18.5 bar: (a) steel membrane below yield stress; (b) near the yield stress of the prestressing wires; and (c) the steel membrane below yield (120 MPa).
3.4. Numerical Simulation of the Pipe with an External FRP Jacket and the Prestressing Wires Fully Active
The same procedure described before was repeated by adding in the numerical simulation of an external layer of shell finite elements corresponding to the external FRP jacket of specimen 3. The assumed prestressing level was equal to 1300 MPa and the initial constitutive law was used for the tensile behavior of the concrete. Figure 15b depicts the comparison between measured and numerically predicted internal pressure versus radial expansion response whereas Figure 15a shows the radial axial stress distribution of the concrete volume for internal pressure amplitude equal to 14.4 bar. This is a pressure value higher than the value that the pressure-radial expansion response exhibits a significant change of slope. As can be seen, the concrete volume has widespread zones indicating almost zero values. For the same internal pressure amplitude Figure 16a–c depicts the predicted stress response for the steel membrane, for the prestressing wires and for the CFRP jacket, respectively. As can be seen, the steel membrane is well below yield and the CFRP is well below their axial tensile strength. Only the prestressing wires are close to their yield. The same stress response is depicted in Figure 17a–c for internal pressure amplitude equal to 15.0 bar.
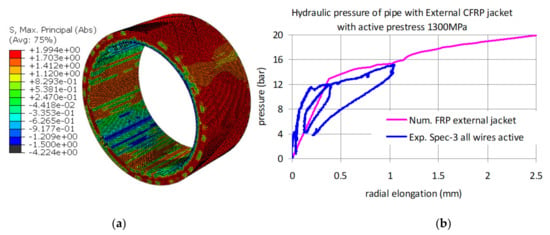
Figure 15.
Measured and numerically predicted for specimen 3: (a) the predicted radial axial stress distribution of the concrete volume for internal hydraulic pressure equal to 14.6 bar; and (b) internal hydraulic pressure versus radial expansion response.
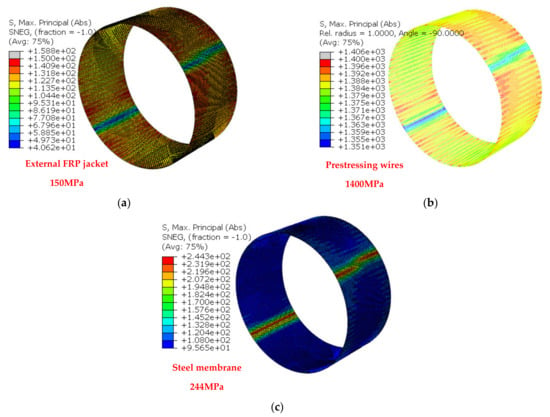
Figure 16.
Internal hydraulic pressure of 14.6 bar: (a) steel membrane below yield stress; (b) near the yield stress of the prestressing wires and (c) the steel membrane below yield (120 MPa).
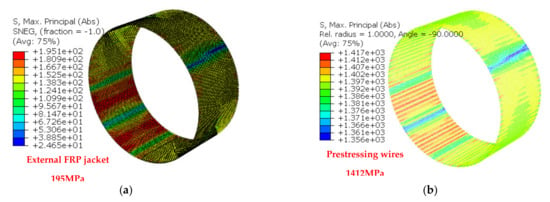
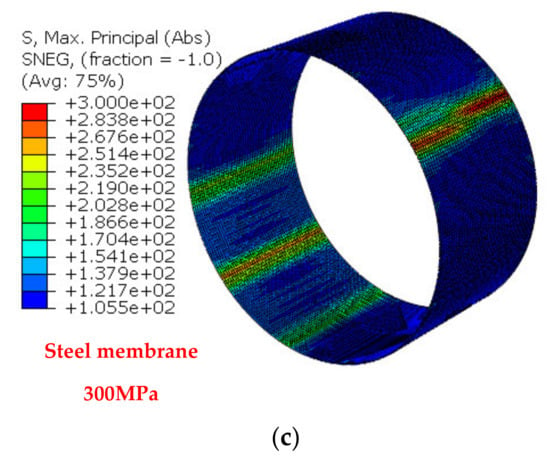
Figure 17.
Internal hydraulic pressure of 15.0 bar: (a) steel membrane below yield stress; (b) near the yield stress of the prestressing wires; and (c) the steel membrane below yield (120 MPa).
This time both the steel membrane and the prestressing wires are beyond yield. However, the CFRP jacket is still below its tensile strength. From all these predictions it can be concluded that the external CFRP jacket can be quite successful in increasing the hydraulic internal pressure capacity for this pipe. Moreover, the level of 15.2 bar maximum internal pressure amplitude reached during the 2nd loading cycle of testing for this specimen is at the pressure amplitude level that would result in the yield of the steel membrane or the prestressing wires, as predicted by this numerical simulation. As can be seen in Figure 15b the predicted radial displacement versus internal hydraulic pressure response compares reasonably well with the corresponding observed response. This time, the obtained agreement includes nonlinear mechanisms for the concrete volume, for the steel membrane and for the prestressing wires.
3.5. Numerical Simulation of the Pipe with an External Reinforced Concrete (RC) Jacket and the Prestressing Wires Fully Active
This time, the numerical simulation includes external layers of solid finite elements together with line truss elements corresponding to the external RC jacket of specimen 1. The line elements simulated the radial reinforcement of this jacket with mechanical properties specified for the actual jacket. The yield stress of this steel reinforcement was equal to 481.9 MPa measured during the experimental campaign (Part A [1]). The same constitutive law for the concrete tensile behavior was also assumed (Figure 4).
Figure 18a depicts the numerical simulation of the pipe with the external RC jacket, whereas Figure 18b shows the plastic strain of the concrete volume when the internal pressure reaches the maximum value of 24 bar, demonstrating the simulation that developed at this pressure level. Figure 18c shows the comparison of the measured and the predicted response in terms of the variation of the internal pressure versus the radial expansion. For an internal pressure value equal to 14.5 bar the steel membrane and the prestressing wires are below yield, as shown in Figure 19a,b, respectively. On the contrary, when the internal pressure reaches its maximum value equal to 24 bar all the parts, e.g., the steel membrane, the prestressing wires and the reinforcement of the RC jacket, are beyond yield, as shown in Figure 20a,b. Again, the predicted radial displacement versus internal pressure response compares reasonably well with the corresponding measured response up to the pressure level of 22.5 bar, which is a maximum pressure level reached both during testing as well as in the numerical simulation. This time the obtained agreement between predicted and observed response incudes nonlinear mechanisms for the concrete volume, for the steel membrane and for the prestressing wires as well as for the external RC jacket. For specimen 7 and specimen 5, pressure limitations were introduced during testing because of safety reasons as well as because the same specimens were planned to be utilized again by introducing prestress defects as to be presented in Section 4 and discussed in Part A [1].
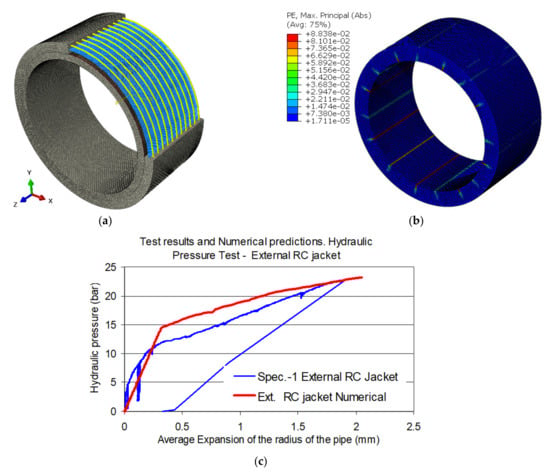
Figure 18.
Measured and numerically predicted for specimen 1: (a) pipe with external RC jacket; (b) top right predicted plastic strain distribution of the concrete volume for internal hydraulic pressure equal to 14.6 bar; and (c) internal hydraulic pressure versus radial expansion response.
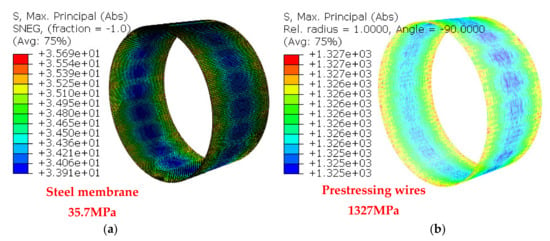
Figure 19.
Internal pressure 14.5 bar: (a). steel membrane; and (b) prestressing wires.
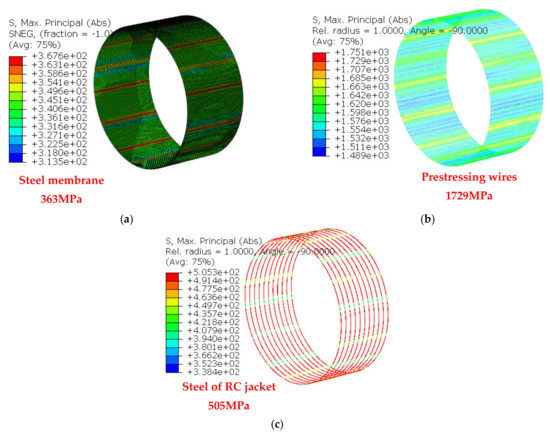
Figure 20.
Internal pressure 24 bar: (a) steel membrane; (b) prestressing wires; and (c) steel of RC jacket.
The numerical predictions of the internal pressure versus the radial expansion response for all studied specimens is shown in Figure 21. As can be seen, in contrast to the response of the original pipe with no jacket, the presence of all the jacketing schemes restrains the development of radial expansion to relatively low levels even for high internal pressure values. As was discussed, the presence of jacketing does not allow the yielding of either the steel membrane and/or the prestressing wires to develop but for internal pressure values considerably higher than without the presence of such jacketing. In all cases, such yielding is predicted to develop for internal pressure values well above 14 bar. This pressure level is 60% higher than the maximum operating internal pressure specified for such pipes. This represents a satisfactory safety precaution on condition that the prestressing wires are fully active, as was assumed up to now in this numerical investigation. For the extreme case of the prestressing wires becoming totally inactive the opposite effect becomes evident. Both the test results and the numerical predictions show that in this case an internal pressure amplitude beyond 4 bar leads to an unsatisfactory performance (Figure 5 and Figure 6). The possibility of the prestressing becoming partially ineffective was studied during the experimental investigation presented in part A (Section 5). An effort to numerically investigate such a prestress defect is presented and discussed next in Section 4.
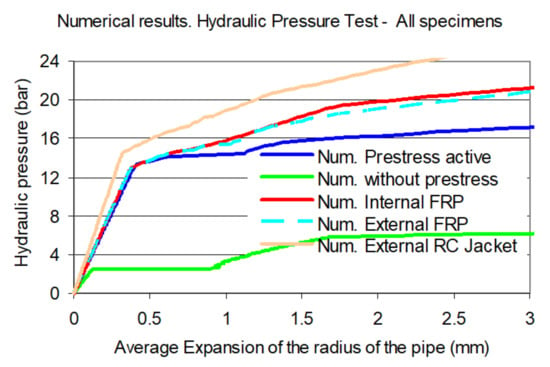
Figure 21.
Numerical predictions of the internal versus radial expansion response for all specimens.
4. Numerical Simulation of the Prestress Defect
The process of simulating prestress defects for water pipes under hydraulic internal pressure in the laboratory was performed for two specimens after they were subjected to internal hydraulic pressure tests with all the wires being fully active. In this case, selected prestressing wires were partially neutralized by cutting them at their Eastern cross section. This cross-section was selected arbitrarily, representing a typical cross-section of the pipe specimen (Part A, [1]). The same numerical methodology that was presented in the previous section was repeated here. The employed numerically simulations included distinct regions either with or without prestressing wires corresponding to the relevant regions of the tested specimens. A S. Shatnawi et al. [15] also used numerical simulations of multi stepped type of the corroded regions in order to capture many polynomial curves of the corroded regions. Whereas during testing the partial neutralization of the prestress was applied in a stepwise manner, cutting sequentially 4, 8 and finally 20 prestressing wires the subsequent numerical simulation to be presented here is performed by removing completely 20 prestressing wires as was done at the final step during testing. Moreover, this represented the initial numerical formation of the pipe that was subjected to the first loading condition of applying the same prestress level of 1300 MPa at each of the remaining 32 prestressing wires. Therefore, any stress redistribution which could result from the wire cutting process during the experimental sequence was not numerically simulated. As described in Section 2, the wire cutting process was tried for two specimens during the experimental sequence, namely specimen 7 without any jacketing, and specimen 5 having an internal CFRP jacket. Instead, the numerical simulation was tried for all four specimens, that is not only specimen 7 and specimen 5 but also specimen 3 (external CFRP jacket) and specimen 1 (external RC jacket) whereby such wire cutting process was not possible during the experimental sequence (see Table 1). Therefore, this numerical investigation of simulated prestress defect was studied for the original as well as for all three applied jacketing schemes. In what follows, the obtained numerical response in terms of internal pressure versus radial expansion response is first compared with the corresponding experimental results for the tested specimen 7 and specimen 5 (see Table 1). Then, the obtained numerical results for all specimens without and with the simulated prestress defect are also compared and discussed.
Comparison of the Observed and Numerically Predicted Prestress Defect
In Figure 22 the obtained measured response for the pipe (specimen 7) without any jacket being initially loaded to 8.5 bar internal pressure in a number of loading cycles with all prestressing wires fully active and then subsequently cutting up to 20 wires applying each time an additional internal pressure loading-unloading cycle. As can be seen, the simulated prestress defect by wire cutting results in an increase of radial expansion for relatively lower internal pressure amplitudes for each subsequent loading cycles, being accompanied by permanent radial expansion.
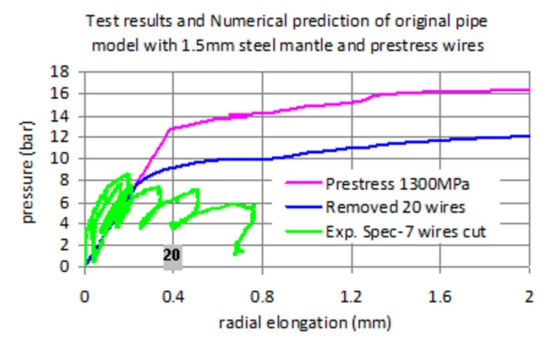
Figure 22.
Measured and numerically predicted including the effect of the numerically simulated defect for specimen 7. The initiation of the loading cycle whereby 20 wires were cut is indicated by the gray square.
In the same Figure, the corresponding numerical response predictions are also plotted. First with all prestressing wires fully active then for 20 wires removed and the remaining 32 wires fully active. The fully active wires in both cases are initially stressed with 1300 MPa. As can be seen, the prestress defect numerically simulated in this way results, as expected, in a considerable decrease of the internal pressure amplitude for the same amplitude of radial expansion, demonstrating a reasonable agreement with the corresponding measured response. The same is done for the pipe (specimen 5) with an internal CFRP jacket and plotted in Figure 23. As can be seen, the prestress defect numerically simulated in this way results again in a considerable decrease of the internal pressure amplitude for the same amplitude of radial expansion, demonstrating a somewhat reasonable similarity with the corresponding measured response. It must be underlined that during testing the pre-stressing wires were cut between each loading-unloading cycle in sequentially increasing numbers of 4, 8 and 20 wires, whereas the numerical simulation approximated in the way described only the case with 20 wires cut.
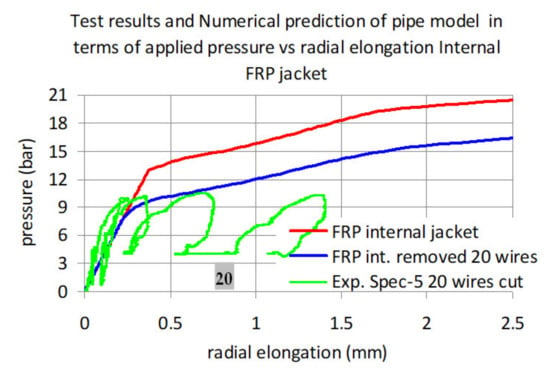
Figure 23.
Measured and numerically predicted including the result of the numerically simulated defect for specimen 5 (internal CFRP jacket). The initiation of the loading cycle whereby 20 wires were cut is indicated by the gray square.
From the preceded comparison, it can be concluded that the used numerical methodology results in a reasonable approximation of the prestress defect. Therefore, based on this the same methodology is tried for the specimen with an external CFRP jacket and the specimen with an external RC jacket which were not tested with cut wires.
In Figure 24 the results for the pipe (specimen 3) with an external CFRP jacket are plotted. It must be noted that the tested pipe specimen remained with all wires fully active for all loading cycles without any of these wires being removed. The measured response for all loading cycles up to internal amplitude of just above 15 bar compares well with the corresponding predictions. At the same time, the numerical predicted response for the case of the 20 removed prestressing wires results again in a considerable decrease of the internal pressure amplitude for the same amplitude of radial expansion.
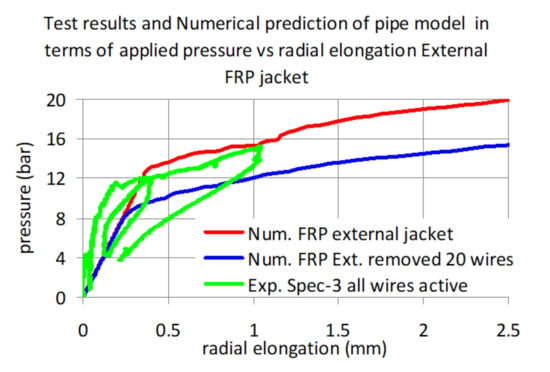
Figure 24.
Measured and numerically predicted response for external FRP jacket (specimen 3).
Similarly, in Figure 25 the results for the pipe (specimen 1) with an external RC jacket are plotted. It must be noted that the tested pipe specimen remained with all wires fully active for all loading cycles without any of these wires being removed. The measured response for all loading cycles up to internal amplitude of just above 24 bar compares well with the corresponding predictions. At the same time, the numerical predicted response for the case of the 20 removed prestressing wires results again in a considerable decrease of the internal pressure amplitude for the same amplitude of radial expansion.
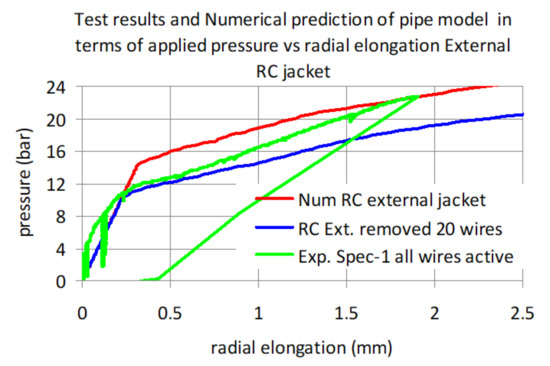
Figure 25.
Measured and numerically predicted response for external RC jacket (specimen 1).
The summary of all the numerical predictions of the original and the jacketed pipes having 20 prestressing wires removed is depicted in Figure 26. In the same Figure the corresponding numerical response of the pipe with all the prestressing wires removed is also shown. It can be seen in the case of a prestressing defect all jacketing schemes provide an increased by containing the radial expansion for hydraulic internal pressure amplitudes larger than 10 bar. This observation is conditional to the accuracy of the performed numerical simulation, which was validated only for specimens representing either the original pipe or the pipe with an internal CFRP jacket. As can be seen from the numerical simulations having test results to compare with, the numerical predictions were rather non-conservative for either the specimen of the original pipe (specimen 7) or for the specimen with an internal CFRP jacket (specimen 5).
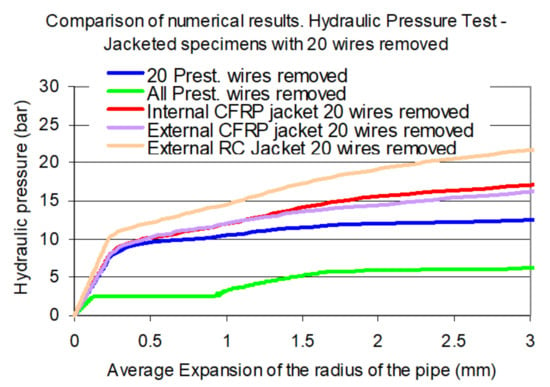
Figure 26.
Numerically predicted response for all the original and the jacketed specimens having 20 prestressing wires removed.
5. Validity of the Obtained Numerical Results—Conclusions
As was underlined in Section 2, Section 3 and Section 4, all the assumptions used in this numerical investigation were based on the measured geometry, actual structural detailing, and mechanical properties of the constituent materials derived from testing. Moreover, in the way the numerical results were presented the development of the specific nonlinear mechanisms included in the numerical simulation were identified and discussed in detail. More specifically:
(a) For all the tested specimens, reasonable agreement could be seen between measured and predicted radial displacement versus internal pressure response for the pressure levels that were employed during testing;
(b) For the retrofitting schemes of external jacketing, either CFRP or RC, as well as for the original pipe the acceptance of the numerical predictions is based on the fact that the important nonlinear mechanisms of the various parts were numerically replicated in the numerical simulations. For internal hydraulic pressure levels, the predicted response agrees with the observed response either in terms of the variation of the radial displacement versus internal hydraulic pressure or the variation of the strains of the steel membrane when available (Part A, [1]). These nonlinear mechanisms are: (1) Cracking of the concrete volume; (2) Yielding and plastification of the steel membrane beyond yield; (3) Yielding and reaching the tensile strength of the prestressing wires; and (4) Cracking of the concrete and yielding of the steel reinforcement of the RC jacket. In the numerical simulations, the predicted behavior of the CFRP jackets remains linear elastic in all cases. This was also confirmed by the observed performance.
(c) This numerical methodology was also based on: (1) Full contact between all the various layers (concrete, steel membrane, prestressing wires and jackets made either of RC or CFRP); and (2) Prohibiting the slip or debonding of the CFRP jackets at the end cross sections by specific construction detailing.
From all the above and despite the noted limitations the following conclusions can be reached:
1. The assumed nonlinear mechanisms of the concrete volume and steel membrane were verified by comparing numerical predictions with measurements in terms of strain response of the steel membrane, when available, damage patterns of the concrete volume and the overall internal pressure versus radial expansion response;
2. The numerical predictions of the contribution in the bearing capacity of the fully active prestress as well as the three specific jacketing schemes were also verified from comparisons with the corresponding measured pressure versus radial expansion response;
3. From these comparisons it can be concluded that the used numerical simulation methodology results in acceptable predictions of the internal pressure–radial expansion response for such pipes in their original construction;
4. Similarly, from these comparisons it can be concluded that the used numerical simulation methodology also results in acceptable predictions of the internal pressure versus radial expansion response for such pipes when retrofitted with the studied jacketing schemes employing either CFRP or RC concrete jackets;
5. The numerical predictions for the cases having 20 prestressing wires removed have a rather limited validation based on comparisons with only two specimens. Moreover, these comparisons indicate that the numerical predictions in this case should be considered as rather non-conservative and need further research;
6. From all the above, it can be concluded that the employed numerical simulation methodology can be a valid tool for predicting the bearing capacity of this type of water pipes, either in their original form or retrofitted with the specific studied schemes provided that the employed assumptions are realistic. Apart from the material properties a very important assumption is the level of the existing prestressing. The way prestressing defects are recorded in-situ is of great importance. The level of confidence of such numerical predictions is directly linked with the validity of all these important assumptions;
7. The used numerical methodology can be employed in examining the effectiveness of retrofitting schemes similar to the ones studied here. While there are tools to assess the cost-effectiveness and to optimize the strengthening scheme [16,17], this study was limited in presenting the fundamentals of the structural performance of the studied retrofitting schemes and did not extend to examine issues of durability and construction costs that can influence a selection process for such retrofitting;
8. All used retrofitting schemes resulted in at least 25% increase in the maximum bearing capacity for specimens without cut wires, based on the results of all numerical simulations combined with the measured response. For the tested specimens with 20 prestressing wires cut this maximum bearing capacity increase is of the order of 30%. However, as stated in conclusion No. 5, this is in need of further research;
9. Finally, it must be underlined that the current study did not examine any performance acceptance criteria that could be based on the possibility of initiation and spreading of leakage under the considered hydraulic internal pressure levels. Obviously, the amplitude of the radial expansion can be used for this purpose. However, this study did not simulate the effect of the hydraulic internal pressure in amplifying the concrete cracking after its initial formation.
Author Contributions
Conceptualization, G.M.; methodology, K.K., L.M., G.M. and V.S.; investigation, K.K., L.M., G.M. and V.S.; data curation, K.K., L.M. and G.M.; writing—original draft preparation K.K., L.M., G.M. and V.S.; writing—review and editing, G.M.; visualization, K.K., L.M. and V.S.; supervision, G.M.; project administration, K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The excellent assistance of all personnel of the Laboratory of Strength of Materials and Structuresof Aristotle University, especially V. Kourtidis and T. Koukouftopoulos, is also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Manos, G.; Katakalos, K.; Soulis, V.; Melidis, L.; Bardakis, V. Experimental Investigation of the Structural Performance of Existing and RC or CFRP Jacket-Strengthened Prestressed Cylindrical Concrete Pipes (PCCP)—Part A. Fibers 2022, 10, 71. [Google Scholar] [CrossRef]
- Zarghamee, M.S.; Eggers, D.W.; Ojdrovic, R.P. Finite element modeling of failure of PCCP with broken wires subjected to combined loads. In Beneath Our Feet: Challengers and Solutions, Proceedings of the ASCE Pipeline Division Specialty Conference, Cleveland, OH, USA, 4–7 August 2002; ASCE: Reston, VA, USA, 2002; Volume 66, pp. 1–17. [Google Scholar] [CrossRef]
- Zarghamee, M.S.; Erbay, O.; Eggers, D.W.; Kendall, D.R. Ultimate Strength Prediction of Steel Liners Using Nonlinear Finite Element Analysis, Proceedings of the Pipelines 2006, Chicago, IL, USA, 30 July–2 August 2006; ASCE: Reston, VA, USA, 2006; pp. 1–9. [Google Scholar] [CrossRef]
- Hajali, M.; Alavinasab, A.; Shdid, C.A. Structural performance of buried prestressed concrete cylinder pipes with harnessed joints interaction using numerical modeling. Tunn. Undergr. Space Technol. 2016, 51, 11–19. [Google Scholar] [CrossRef]
- Gomez, R.; Muñoz, D.; Vera, R.; Escobar, J.A. Structural Model for Stress Evaluation of Prestressed Concrete Pipes of The Cutzamala System, Proceedings of Pipeline Division Specialty Congress; ASCE: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Feng, X.; Li, H.; Chen, B.; Zhao, L.; Zhou, J. Numerical investigations into the failure mode of buried prestressed concrete cylinder pipes under differential settlement. Eng. Fail. Anal. 2020, 111, 104492. [Google Scholar] [CrossRef]
- Gong, Q.; Zhu, H.; Yan, Z.; Huang, B.; Zhang, Y.; Dong, Z. Fracture and Delamination Assessment of Prestressed Composite Concrete for Use with Pipe Jacking Method. Math. Probl. Eng. 2015, 2015, 579869. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Guo, C.; Ni, P.; Wu, H.; Wang, F. Full-scale experiment and numerical simulation of prestressed concrete cylinder pipe with broken wires strengthened by prestressed CFRP. Tunn. Undergr. Space Technol. 2021, 115, 104021. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Fu, B.; Wang, F.; Hu, B. Mechanical response of externally bonded CFRP on repair of PCCPs with broken wires under internal water pressure. Constr. Build. Mater. 2020, 239, 117878. [Google Scholar] [CrossRef]
- Hu, B.; Fang, H.; Wang, F.; Zhai, K. Full-scale test and numerical simulation study on load-carrying capacity of prestressed concrete cylinder pipe (PCCP) with broken wires under internal water pressure. Eng. Fail. Anal. 2019, 104, 513–530. [Google Scholar] [CrossRef]
- Hu, H.; Dou, T.; Niu, F.; Zhang, H.; Su, W. Experimental and numerical study on CFRP-lined prestressed concrete cylinder pipe under internal pressure. Eng. Struct. 2019, 190, 480–492. [Google Scholar] [CrossRef]
- Dong, X.; Dou, T.; Cheng, B.; Zhao, L. Failure analysis of a prestressed concrete cylinder pipe under clustered broken wires by FEM. Structures 2021, 33, 3284–3297. [Google Scholar] [CrossRef]
- AWWA C304-14(R19); Design of Prestressed Concrete Cylinder Pipe, Revision of AN-SI/AWWA C304-07. American Water Works Association: Denver, CO, USA, 2019; ISBN 978-1-62576-372-3. [CrossRef]
- Xiong, H.; Li, P.; Li, Q. FE model for simulating wire-wrapping during prestressing of an embedded prestressed concrete cylinder pipe. Simul. Model. Pract. Theory 2010, 18, 624–636. [Google Scholar] [CrossRef]
- Shatnawi, A.S.; Al-Sadder, S.Z.; Abdel-Jaber, M.S.; Beale, R. Symmetrical and Anti-Symmetrical Buckling of Long Corroded Cylindrical Shell Subjected to External Pressure. Jordan J. Civ. Eng. 2010, 4, 106–118. [Google Scholar]
- Sojobi, A.O.; Liew, K.M. Flexural behaviour and efficiency of CFRP-laminate reinforced recycled concrete beams: Optimization using linear weighted sum method. Compos. Struct. 2021, 260, 113259. [Google Scholar] [CrossRef]
- Sojobi, A.O.; Xuan, D.; Li, L.; Liu, S.; Poon, C.S. Optimization of gas-solid carbonation conditions of recycled aggregates using a linear weighted sum method. Dev. Built Environ. 2021, 7, 100053. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).