The Thickness Dependence of the Superconducting Properties of MgB₂ Spherical Shells Deposited on 1 mm Diameter Si₃N₄ Spheres

Abstract

Superconducting spherical shells have important application value or potential in various fields, such as inertial navigation, gravity measurement, and nuclear fusion. Depending on the needs of the applications, the thickness of the superconducting shell may vary from micrometers to nanometers. We report an investigation into the superconducting properties of ${\mathrm{MgB}}_2$ spherical shells deposited on 1 mm diameter Si₃N₄ spheres, with the shell thickness varying from approximately 200 nm to 720 nm. The upper critical field $H_{c2}$, the lower critical field $H_{c1}$, and the superconducting critical current density $J_c$ were determined from electrical resistance, initial magnetization, and magnetization hysteresis loop measurements, respectively. As the shell thickness decreased, it was observed that $H_{c2}$ was enhanced, $H_{c1}$ declined, and $J_c$ rose. This systematic evolution of the superconducting properties is suggested to have arisen from a reduction in the grain size with a decrease in the shell thickness, as shown by surface morphology images of the shells. A reduction in the grain size leads to increased grain boundaries and scattering strength, which decrease the electron diffusivities, thereby enhancing $H_{c2}$ and suppressing $H_{c1}$ as the shell thickness diminishes. The proliferation of grain boundaries would also provide more effective flux pinning in the shell, giving rise to an improvement in $J_c$. Our study demonstrated a close correlation between the microstructure, specifically, the grain size, and the superconducting properties in ${\mathrm{MgB}}_2$ spherical shells and the effectiveness of tuning them by varying the thickness of the shell. Moreover, it also revealed that the superconducting properties of the fabricated spherical shells, particularly their evolutions with the shell thickness, were critically influenced by the multiband superconductivity of ${\mathrm{MgB}}_2$. These findings would provide a helpful reference for fabricating ${\mathrm{MgB}}_2$ superconducting shells with desired thicknesses and properties, enabling them to better meet the requirements of applications in various fields.

1. Introduction

Among superconducting materials, magnesium diboride (${\mathrm{MgB}}_2$) possesses unique properties that make it important for both basic scientific research and practical technological applications. With a simple crystal structure and composed of inexpensive light elements, ${\mathrm{MgB}}_2$ has a superconducting transition temperature of $T_c\sim 39\mathrm{K}$, which is the highest among intermetallic compounds [1]. In contrast to high-$T_c$ cuprate superconductors, the grain boundaries in ${\mathrm{MgB}}_2$ do not show a weak-link effect [2]. These characteristics make ${\mathrm{MgB}}_2$ very appealing in developing various superconducting machines and electronic devices functioning at elevated temperatures of ∼20 K, including superconducting magnets, generators, detectors, etc. [3,4,5,6]. Moreover, ${\mathrm{MgB}}_2$ shows unique multiband superconductivity, which distinguishes it from most other superconductors [7]. Two sets of bands, namely the $\sigma$ and $\pi$ bands, cross the Fermi level in ${\mathrm{MgB}}_2$, resulting in two distinct groups of superconducting energy gaps, the $\sigma$ and $\pi$ gaps [8,9]. Research on multiband superconductivity has garnered significant attention, as it not only exhibits properties markedly different from those of single-band superconductors but also holds the promise of unveiling novel physics that is inaccessible in its single-band counterparts [10,11,12,13,14].

Core/shell structures, typically realized by coating inner core materials with outer shells, constitute an important class of architectures, particularly at the nanoscale. These structures have drawn widespread interest due to their diverse applications in various fields, including catalysis, optics, biomedicine, energy, and information technology [15]. For example, core/shell spherical ${\mathrm{Ge/Fe}}_3{\mathrm{O}}_4$ nanocrystals have demonstrated high-performance resistive switching and memory effects, showing potential in neuromorphic devices [16], and core/shell ${\mathrm{Al/TiO}}_2$ nanoparticles have been found to be excellent photocatalysts in the visible light regime [17]. As a specific type of core/shell structure, superconducting spherical shells, coating specific inner spherical substrates or designed with a hollow core, have long been a subject of study because of their unique combination of a three-dimensional structure and curved spherical geometry. Theory suggests that, compared to planar superconducting films, the extension to the third dimension, together with the constraints imposed by curvilinear geometry, may introduce new effects on the superconductivity of superconducting spherical shells, particularly on their vortex matter properties [18,19]. For instance, novel vortex patterns such as giant and ringlike vortices and their coexistence with the Meissner state have been predicted for mesoscopic superconducting spherical shells in applied magnetic fields, which are awaiting experimental confirmation [20,21]. From a practical application perspective, superconducting spherical shells made from low-$T_c$ superconductors have been successfully utilized in the development of sensitive superconducting gravimeters and gyroscopes, leveraging their stable magnetic levitation properties and/or the magnetic moments associated with their rotating states [22,23,24,25]. By using ${\mathrm{MgB}}_2$ in place of currently used low-$T_c$ materials (typically Nb), the operating temperature of such instruments could be substantially increased, which would therefore facilitate their employment in a wider range of applications. Recently, in laser-driven inertial confinement fusion (ICF) [26], the magnetic levitation of the fusion target, that is, a realization of the non-contact support of the target, has also been proposed to enhance the implosion performance and fusion yield by coating the spherical target with a thin superconducting shell [27,28]. In this case, the operating temperature required is ∼20 K, which exceeds the capabilities of traditional low-$T_c$ materials, and the superconducting shell should be composed of elements with low atomic numbers, which renders high-$T_c$ cuprate superconductors not suitable, thereby leaving ${\mathrm{MgB}}_2$ as the most promising candidate [27,28].

In the above practical or potential applications of superconducting spherical shells, the thickness of the superconducting shell may vary from micrometers to nanometers, depending on the needs of the applications. For instance, in superconducting gyroscopes, the superconducting spherical shell utilized usually has a thickness on the micrometer scale. In the well-known Gravity Probe B experiment, each of the four gyroscopes had a coated Nb superconducting spherical shell with a thickness of 1.25 μm [24]. In comparison, for the proposed ICF application, it has been estimated that a potentially suitable thickness of the ${\mathrm{MgB}}_2$ superconducting spherical shell could be around 100–200 nm [27,29]. Therefore, in the process of promoting the application of ${\mathrm{MgB}}_2$ in these diverse fields, it is desirable to fabricate and study ${\mathrm{MgB}}_2$ superconducting spherical shells with varying thicknesses. In this paper, we present an investigation into the superconducting properties of ${\mathrm{MgB}}_2$ spherical shells with a shell thickness ranging from $200\mathrm{nm}$ to $720\mathrm{nm}$. These ${\mathrm{MgB}}_2$ spherical shells have been fabricated very recently on $1\mathrm{mm}$ diameter Si₃N₄ spheres using a hybrid physical–chemical vapor deposition (HPCVD) method. Through electrical transport and magnetization measurements, the superconducting critical fields, both the upper critical field $H_{c2}$ and the lower critical field $H_{c1}$, and the superconducting critical current density $J_c$ were determined and their thickness dependencies were examined. The contrasting behavior of $H_{c2}$ and $H_{c1}$ with a variation in the thickness was observed and discussed within the framework of the multiband superconductivity of ${\mathrm{MgB}}_2$. Furthermore, with the aid of surface morphology images, a correlation between the superconducting properties and microstructure of the spherical shells was revealed.

2. Experimental Details

The ${\mathrm{MgB}}_2$ spherical shells studied in this work were fabricated using the HPCVD method, as documented in detail recently [30,31]. They were deposited onto spherical polycrystalline silicon nitride (Si₃N₄) substrates with a diameter of $d=1$ mm. The thicknesses of the shells, which varied from approximately $200\mathrm{nm}$ to $720\mathrm{nm}$, were adjusted by varying the deposition time in increments from $12\min$ to $32\min$ during the deposition process. The actual thicknesses of the shells were measured via cross-sectional scanning electron microscopy (SEM) analysis [31]. The superconducting transition temperatures $T_c$ of the shells were characterized as ∼38–39 K through both a resistance–temperature $R\left(T\right)$ measurement with zero external magnetic fields and a diamagnetic moment–temperature $m\left(T\right)$ measurement under the condition of zero-field cooling (ZFC) [31].

In the present study, to further explore the superconducting properties of the shells, the $R\left(T\right)$ curves of the shells were measured under various magnetic fields, ${\mu }_{0}H$, up to $9\mathrm{T}$ using a physical property measurement system (Quantum Design). The $R\left(T\right)$ measurement was performed using the traditional four-probe method (Supplementary Material, Section S1). The electrodes were made using $20$ μm diameter gold wires bonded to the shell with silver paste (DuPont 4922N), which were cured in air at room temperature, yielding low contact resistances of a few ohms. The temperature sweep rate was maintained at $2\mathrm{K}/\min$ during the measurement. From the $R\left(T\right)$ curves, the upper critical fields $H_{c2}\left(T\right)$ and the irreversibility fields $H_{irr}\left(T\right)$ of the shells were determined. The isothermal initial magnetization was measured at different temperatures under ZFC in a magnetic property measurement system (Quantum Design), with the diamagnetic moment m recorded as a function of H up to $500\mathrm{Oe}$ at a sweep rate of $1.6\mathrm{Oe}/\mathrm{s}$. The lower critical fields $H_{c1}\left(T\right)$ were extracted from the resulting $m\left(H\right)$ curves. Isothermal magnetization hysteresis loops were also measured in a field range of $\pm 40$ kOe with a sweep rate of $200\mathrm{Oe}/\mathrm{s}$. From these $m\left(H\right)$ hysteresis loops, the superconducting critical current density $J_c(T,H)$ was determined as a function of both T and H. To compare the results for resistance and magnetization, the surface morphologies of the shells were imaged by SEM (FEI Nova NanoSEM 430), similarly to our previous reports [30,31]. To check the compositions of the shells, X-ray photoelectron spectroscopy (XPS) was also conducted using a PHI VersaProbe 4 with a monochromatic Al K$\alpha$ source.

3. Results and Discussion

3.1. Surface Morphology

Figure 1 presents SEM images of the ${\mathrm{MgB}}_2$ spherical shells with varying thicknesses: (a) 200 nm, (b) 320 nm, and (c) 550 nm. These images demonstrate that all shells were composed of thin, hexagonally shaped grains that were randomly aligned and closely packed, showing the polycrystalline structure of the shells [31]. The hexagonal shape of the grain is typical of ${\mathrm{MgB}}_2$ crystallite. As previously noted [30], such a surface morphology of the shells is similar to that of ${\mathrm{MgB}}_2$ films deposited through HPCVD on various other polycrystalline or amorphous substrates, such as B-buffered Si [32], SiC fibers [33], and Nb substrates [34]. This appears to indicate that the non-epitaxial growth of ${\mathrm{MgB}}_2$ films via HPCVD exhibits a relatively low dependence on the substrate material, or in other words, it follows similar growth modes or mechanisms across different substrate materials.

Figure 1. SEM images of the surface morphology of the ${\mathrm{MgB}}_2$ spherical shells. The thicknesses of the shells were (a) 200 nm, (b) 320 nm, and (c) 550 nm.

While the shells shared a similar polycrystalline structure, it can be observed from Figure 1a–c that the size of the ${\mathrm{MgB}}_2$ grains comprising the shells increased noticeably as the thickness of the shell increased [31]. To better perceive the evolution of the ${\mathrm{MgB}}_2$ grain size with the shell thickness, the lateral sizes and thicknesses of the ${\mathrm{MgB}}_2$ grains in each image in Figure 1 were evaluated (Supplementary Material, Section S2). Within each image, a large number of discernible ${\mathrm{MgB}}_2$ grains were measured in terms of their lateral sizes and thicknesses. For each measurement term, a total of 150–200 counts were taken for each shell, from which the statistical average values and the standard deviations were calculated to provide an estimation of the grain size variation and distribution. The results are depicted in Figure 2, which shows that both the average lateral size and thickness of the ${\mathrm{MgB}}_2$ grains increased approximately linearly with the increase in the shell thickness. This reveals a clear correlation between the ${\mathrm{MgB}}_2$ grain size and the shell thickness. As the shell thickness increased from 200 nm to 550 nm, the grain’s lateral side length increased by ∼120% (from about 150 nm to 330 nm), which was comparable to the ∼80% increase in the grain thickness (from about 50 nm to 90 nm). This indicates that the ${\mathrm{MgB}}_2$ grains roughly kept pace with each other in terms of growth in both the in-plane and out-of-plane directions. Figure 2 also shows that the distribution of the size of the ${\mathrm{MgB}}_2$ grains became larger in thicker shells, particularly in the 550 nm shell, suggesting that the ${\mathrm{MgB}}_2$ grain size is more uniform in thinner shells. In thicker ${\mathrm{MgB}}_2$ spherical shells prepared over longer deposition times, there could be spatial confinement effects for the growth of some of the ${\mathrm{MgB}}_2$ grains and the appearance of new grains due to secondary nucleation events during the deposition, thus promoting a broader grain size distribution compared to thinner shells, where the growth environments for the grains should be more homogeneous.

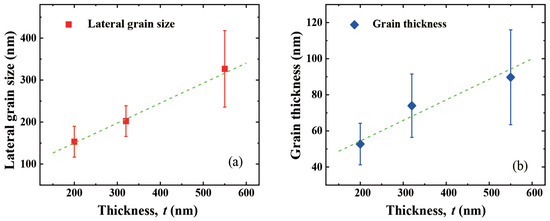
Figure 2. Shell thickness dependence of the ${\mathrm{MgB}}_2$ grain size: (a) the grain’s lateral side length and (b) grain thickness. The dashed lines are linear fits to the data, serving as a guide to the eye.

In addition to investigating the surface morphology, the compositions of the spherical shells were also investigated through XPS measurements in the Mg 1s and B 1s regions (Supplementary Material, Section S3). In both regions, the spectra were observed to match those from prior studies on ${\mathrm{MgB}}_2$ bulks and films, and remained similar across all shells, indicating that the compositions of the shells were typical of ${\mathrm{MgB}}_2$ samples and showed no apparent variations as the thickness varied from 200 nm to 720 nm.

3.2. Upper Critical Field H_c2(T) and Irreversibility Field H_irr(T)

To determine the upper critical field $H_{c2}$, the resistance R(T) under different magnetic fields up to 9 T was measured, as displayed in Figure 3a–c for shells with thicknesses of (a) 200 nm, (b) 320 nm, and (c) 720 nm. This showed that, as the magnetic field increased, for all shells the superconducting transition shifted progressively to lower temperatures, reflecting the suppression of superconductivity by magnetic fields. By applying the criterion of 99%$R_n$, where $R_n$ represents the normal-state resistance immediately above the superconducting transition, we extracted the $H_{c2}$(T) from the R(T) curves, as shown in Figure 3d–f. For all shells, the $H_{c2}$(T) exhibited a positive curvature in the vicinity of the $T_c$, a characteristic feature of ${\mathrm{MgB}}_2$ arising from its unique two-band superconductivity [35]. Accordingly, to describe the $H_{c2}$(T), we used the following equation, which was derived incorporating the two-band effect of ${\mathrm{MgB}}_2$ [36]:

$$a_0[\ln x+\mathit{U}\left({\mathit{D}}_{\sigma }y\right)][\ln x+\mathit{U}\left({\mathit{D}}_{\pi }y\right)]+a_1[\ln x+\mathit{U}\left({\mathit{D}}_{\sigma }y\right)]+a_2[\ln x+\mathit{U}\left({\mathit{D}}_{\pi }y\right)]=0,$$

(1)

where $x=T/T_c$, $y=\hslash {\mu }_0{H}_{c2}/\left(2{\Phi }_0{k}_{B}T\right)$, with ℏ being the reduced Planck’s constant, ${\Phi }_0$ the magnetic flux quantum, and $k_B$ the Boltamann’s constant, and $U\left(p\right)=\Psi (1/2+p)-\Psi (1/2)$, with $\Psi$ being the di-gamma function, $a_0=2w/{\lambda }_0$, $a_1=1+{\lambda }_{-}/{\lambda }_0$, $a_2$ = $1-{\lambda }_{-}/{\lambda }_0$, and $D_{\sigma }$ ($D_{\pi }$) being the diffusivity of the $\sigma$($\pi$) band. Here, w = ${\lambda }_{\sigma \sigma }$$\lambda$${}_{\pi \pi }-$${\lambda }_{\sigma \pi }$${\lambda }_{\pi \sigma }$, ${\lambda }_{-}$ = $\lambda$${}_{\sigma \sigma }-$${\lambda }_{\pi \pi }$, and ${\lambda }_0$ = (${\lambda }_{-}^2$ + 4${\lambda }_{\sigma \pi }$${\lambda }_{\pi \sigma }$)^1/2, with ${\lambda }_{\sigma \sigma }$≃ 0.96, ${\lambda }_{\pi \pi }$≃ 0.29, ${\lambda }_{\sigma \pi }$≃ 0.23, and ${\lambda }_{\pi \sigma }$≃ 0.17 being the electron–phonon coupling constant matrix elements in ${\mathrm{MgB}}_2$ given by first-principles calculations [7]. As shown by the solid lines in both the main panel and inset of Figure 3d–f, the $H_{c2}$(T) of the shells can be well accounted for by Equation (1).

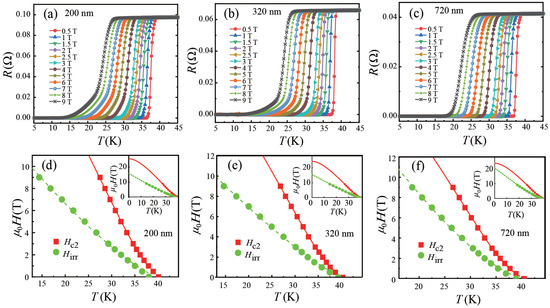
Figure 3. (a–c): Superconducting transitions of the ${\mathrm{MgB}}_2$ spherical shells under various magnetic fields. The thicknesses of the shells were (a) 200 nm, (b) 320 nm, and (c) 720 nm. (d–f): The upper critical field $H_{c2}$(T) and the irreversibility field $H_{irr}$(T) (symbols) determined from (a–c). The solid lines are fits to $H_{c2}$(T) by Equation (1), while the dashed lines are fits to $H_{irr}$(T) by an empirical power law relation, $H_{irr}$(T) = $H_{irr}\left(0\right)(1-T/T_c{)}^n$, as described in the main text. The insets in (d–f) show the same as their respective main panels, displaying the fits down to a temperature of zero.

Two parameters were yielded from the above description of $H_{c2}\left(T\right)$, that is, the electron diffusivities $D_{\sigma }$ and $D_{\pi }$. Figure 4a plots $D_{\sigma }$ and $D_{\pi }$ against the thickness of the shell. It shows that both $D_{\sigma }$ and $D_{\pi }$ decreased as the shell thickness decreased. Compared with $D_{\sigma }$, which was in the order of $1{\mathrm{cm}}^2{\mathrm{s}}^{-1}$, $D_{\pi }$ was considerably higher, showing values of ∼25–$40 {\mathrm{cm}}^2{\mathrm{s}}^{-1}$. This $\pi$ band being much cleaner than the $\sigma$ band is consistent with the high $T_c$ of the shells. As previous studies have suggested [37], in ${\mathrm{MgB}}_2$ films with a high $T_c$ close to the bulk value of $39\mathrm{K}$, the $\pi$ band looks somewhat cleaner than the $\sigma$ band, while in ${\mathrm{MgB}}_2$ films with a relatively lower $T_c$, the cleanness of the $\pi$ and $\sigma$ bands becomes comparable, with the $\pi$ band becoming even dirtier than the $\sigma$ band for a significantly decreased $T_c$. As the shell became thinner, the reduction in both $D_{\sigma }$ and $D_{\pi }$ shown in Figure 4a indicates that the disorder or impurity scattering in the shell became higher. According to theory [36], this would imply an enhancement in the $H_{c2}$ in thinner shells. Indeed, Figure 4b shows that both the experimental $H_{c2}$ at $30\mathrm{K}$ and the $H_{c2}\left(0\right)$ at $0\mathrm{K}$ as derived from the above two-band analysis went up when the shell thickness was decreased. Considering the surface morphologies of the shells illustrated in Figure 1 and described earlier, it is natural to connect the rise in the disorder level or scattering strength with the reduction in the grain size occurring as the thickness of the shell decreased. With the ${\mathrm{MgB}}_2$ grains becoming smaller, the electron scattering within the shell was increased due to the emergence of more grain boundaries, which then led to an elevation of the $H_{c2}$ value in thinner shells. We noticed that a correlation between the decrease in the grain size and the enhancement in $H_{c2}$ was also observed in carbon-doped epitaxial ${\mathrm{MgB}}_2$ films when tuning the carbon concentration [38]. Within the two-band framework, it is noteworthy from Figure 4a,b that as the shell thickness reduced from $720\mathrm{nm}$ to $200\mathrm{nm}$, the enhancement in $H_{c2}\left(0\right)$ (∼8.5%) was comparable to the decrease in $D_{\sigma }$ (∼8.7%), although the decrease in $D_{\pi }$ was considerably larger (∼38.8%), which suggests a closer relationship between the $H_{c2}\left(0\right)$ and $D_{\sigma }$ of the shell. This aligns well with theory that, in a two-band superconductor, the value of $H_{c2}\left(0\right)$ is determined by the band with the smaller diffusivity [36].

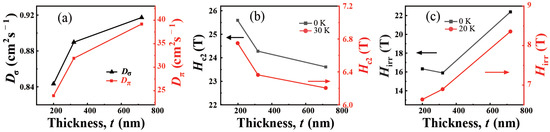
Figure 4. Thickness dependence of (a) the diffusivities $D_{\sigma }$ and $D_{\pi }$, (b) the upper critical field $H_{c2}$ at 0 K and 30 K, and (c) the irreversibility field $H_{irr}$ at 0 K and 20 K.

In Figure 3d–f, the irreversibility field $H_{irr}$(T) of the shells is also shown, identified as the points where the resistance becomes 1%$R_n$. To describe its temperature dependence and make a rough estimation of $H_{irr}$(0) at a temperature of zero, we fitted the data to the empirical power law relation $H_{irr}$(T) = $H_{irr}$(0)($1-T/{T_c)}^n$, which has been widely adopted in the literature to describe $H_{irr}$(T) [39]. The fits are shown as dashed lines in both the main panels and insets in Figure 3d–f, which reproduce the data well. The values of n were 1.3, 1.2, and 1.4 for the thicknesses of 200 nm, 320 nm, and 720 nm, respectively. These values are close to each other, indicating a similar temperature dependence of $H_{irr}$(T) for all shells. The obtained $H_{irr}$(0) is displayed in Figure 4c, plotted together with the $H_{irr}$ at 20 K as determined directly from the R(T) curves. We can see both $H_{irr}$(0) and $H_{irr}$(20 K) essentially decreased as the shell thickness decreased, except for the $H_{irr}$(0) at 200 nm, whose value was slightly larger than that at 320 nm. This general behavior of $H_{irr}$ in terms of the shell thickness seems not to have been expected from the results for the surface morphology (Figure 1), as one might speculate that with a decrease in the shell thickness, the proliferation of grain boundaries because of the decrease in the grain size would enhance flux pinning in the shell and give rise to an increase in the $H_{irr}$ value. Indeed, in the aforementioned study of carbon-doped ${\mathrm{MgB}}_2$ films, the $H_{irr}$ was observed to increase concurrently with $H_{c2}$ as the grain size decreased, owing to an increase in the carbon concentration [38]. The origin of the contrasting behavior of $H_{irr}$ observed in our work needs to be further investigated. Unlike the carbon-doped films, which exhibited a c-axis orientation, our fabricated spherical shells were polycrystalline, with randomly oriented grains. Another difference lies in that in the present work, the decrease in the grain size was realized by decreasing the shell thickness, not by increasing the doping level of carbon in films of the same thickness. These discrepancies may have rendered the properties of flux pinning or depinning with relatively high fields in our shells different from in the case of carbon-doped films. In particular, from Figure 4b,c, we can observe that as the shell thickness decreased, the field region between $H_{irr}$(0) and $H_{c2}$(0) widened. A separation between $H_{irr}$(0) and $H_{c2}$(0) has been reported for ${\mathrm{MgB}}_2$ films and discussed in the context of novel vortex motion driven by quantum fluctuations [40,41]. According to this scenario, there might be an intriguing possibility that as the shell thickness decreases, the vortex liquid regime of the shell expands due to a stronger vortex quantum fluctuation effect, which lowers the $H_{irr}$(0).

3.3. Lower Critical Field H_c1(T)

To determine the lower critical field $H_{c1}$(T), measurements of the initial magnetization were conducted under the ZFC condition at different fixed temperatures, as illustrated in Figure 5 for shells with thicknesses ranging from 200 nm to 720 nm. These showed that the diamagnetic moment m evolved similarly for all shells as a function of both the applied field H and the temperature T. For each shell, m initially decreased linearly with the increase in H, as indicated by a dashed line labeled as the Meissner line, a manifestation of the shell in the Meissner state. The slope of the Meissner line, namely the susceptibility $\chi$ = 4$\pi$M/H (in CGS units), was observed to be close to $-1$, suggesting all the shells exhibited the ideal diamagnetism in the Meissner state. Here, 4$\pi$M (in CGS units), as shown by the right axis in each panel of Figure 5, is the magnetization in terms of the applied field H determined after correction for the demagnetization effect. Specifically, $4\pi M\simeq 4\pi M_{exp}(1-N)$, where $M_{exp}=m/V$ is the measured magnetization, with $V=\pi d^3/6$ being the volume of the sphere enclosed by the circular supercurrent in the ${\mathrm{MgB}}_2$ shell, and $N=1/3$ is the demagnetization factor for spheres [30].

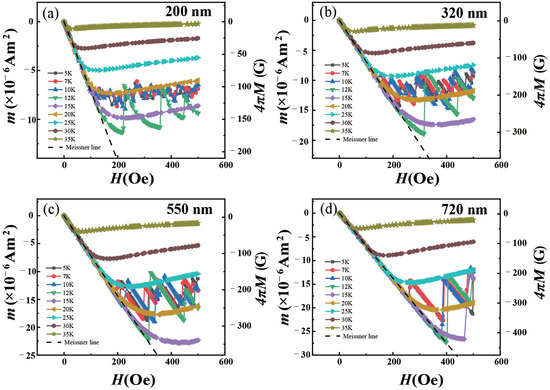
Figure 5. Isothermal initial magnetization of ${\mathrm{MgB}}_2$ spherical shells as a function of H under the condition of zero-field cooling. The thicknesses of the shells were (a) 200 nm, (b) 320 nm, (c) 550 nm, and (d) 720 nm. In each panel, the right axis represents the magnetization 4$\pi$M (in CGS units) determined from m (left axis) after correction for the demagnetization effect, and the dashed line is the Meissner line showing the linear dependence of m on H in the Meissner state.

At higher magnetic fields, it was observed that the moment m departed from the Meissner line, indicating the penetration of vortices as the shells transitioned into a mixed state. The field at which m initiates this departure is designated as $H_{c1}$(T), which is depicted in Figure 6a for all shells. Figure 5 shows that at temperatures below about 12 K, m exhibited strong oscillations with respect to H once it departed from the Meissner line, in contrast with the behavior observed at relatively higher temperatures, where m evolved continuously with H, as generally expected. This indicates the occurrence of flux jumps at low temperatures, a phenomenon that has been frequently observed in various forms of ${\mathrm{MgB}}_2$ samples, including ${\mathrm{MgB}}_2$ bulks [42,43], planar thin films [44,45], and thicker spherical shells [30]. In this instance, the $H_{c1}$ determined was actually the first flux jump field, denoted as $H_{fj}$ in some of the literature. The values of $H_{c1}$ are represented by open symbols in Figure 6a.

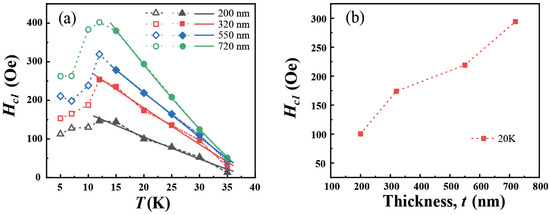
Figure 6. (a) The lower critical field $H_{c1}$(T) (symbols) of the ${\mathrm{MgB}}_2$ spherical shells determined from the initial magnetization as shown in Figure 5. Open symbols show the values at low temperatures with the presence of flux jumps in the m(H) curves. Solid lines are fits to the data at higher temperatures (solid symbols) by using the empirical relation $H_{c1}$(T) = $H_{c1}$(0)($1-T$/T_c )ⁿ, as described in the main text. (b) Thickness dependence of $H_{c1}$ at 20 K.

For temperatures above 12 K without the influence from flux jumps, Figure 6a shows that the $H_{c1}$(T) (solid symbols) displayed a nearly linear temperature dependence for all shells, and as the shell thickness decreased, the $H_{c1}$(T) decreased significantly. For this temperature range, we used the empirical relation $H_{c1}$(T) = $H_{c1}$(0)($1-T/{T_c)}^n$ to describe the $H_{c1}$(T), as shown by solid lines in Figure 6a. The exponent n yielded from this description exhibited values of 1.1, 1.0, 1.0, and 1.2 for thicknesses of 200 nm, 320 nm, 550 nm, and 720 nm, respectively, confirming the nearly linear relationship between $H_{c1}$(T) and the temperature for all shells. The parameter $H_{c1}$(0) had values of 228 Oe, 376 Oe, 458 Oe, and 672 Oe for thicknesses of 200 nm, 320 nm, 550 nm, and 720 nm, respectively, showing a clear reduction upon the decrease in the shell thickness. Figure 6b plots the measured $H_{c1}$ at 20 K as a function of the shell thickness. Like the derived $H_{c1}$(0), the $H_{c1}$ at 20 K also dropped significantly as the shell thickness decreased, showing a decrease of $\sim 66\%$ from 294 Oe at 720 nm to 100 Oe at 200 nm.

We observed that this evolution of $H_{c1}$(T) in terms of the shell thickness aligned with the variation in electron diffusivities obtained from the analysis of $H_{c2}$(T). As the shell thickness decreased, both electron diffusivities, $D_{\sigma }$ and $D_{\pi }$, diminished, as illustrated in Figure 4a and previously discussed. According to theory, this decrease in the diffusivities would lead to an increase in the magnetic penetration depth $\lambda$. Since $H_{c1}$ is inversely proportional to $\lambda$, a larger penetration depth would consequently result in a lower $H_{c1}$ in thinner shells, in agreement with the experimental results. Furthermore, it is noteworthy that, according to the two-band theory [36], contrary to $H_{c2}$(0), the $\lambda$, and hence $H_{c1}$, is determined by the cleaner band with the higher diffusivity. This implies that, for currently fabricated ${\mathrm{MgB}}_2$ shells, the $\pi$ band governs the $H_{c1}$ value as $D_{\pi }$ is considerably higher than $D_{\sigma }$. This accounts for the observed trend that as the thickness decreased from 720 nm to 200 nm, the reduction in $H_{c1}$ (∼66%) was much more closely correlated with the decrease in $D_{\pi }$ (∼38.8%) than with the decrease in $D_{\sigma }$ (∼8.7%). Therefore, both the results obtained in this work—the relatively mild enhancement in $H_{c2}$(0) and the more significant decrease in $H_{c1}$ as the thickness decreased—can be consistently explained by invoking the two-band superconductivity of ${\mathrm{MgB}}_2$.

3.4. Superconducting Critical Current Density J_c(T,H)

We further evaluated the superconducting critical current density $J_c(T,H)$ of the ${\mathrm{MgB}}_2$ spherical shells by measuring the isothermal magnetization hysteresis loops, as shown in Figure 7a–c for shells with a thickness of (a) 320 nm, (b) 550 nm, and (c) 720 nm. The m(H) loops were shown to be similar among the shells. Based on the Bean critical-state model [46,47], the $J_c$ of a superconducting spherical shell is given by

$$J_c={\displaystyle \frac{2\Delta \mathit{m}}{\pi g\left(s_0\right){(\mathit{r}+\mathit{t})}^4}},$$

(2)

where $\Delta$m is the width of the m(H) hysteresis loop, r is the radius of the underlying sphere, t is the thickness of the superconducting shell, $s_0=1/(1+t/r)$, and $g\left(s_0\right)$ is a numerical factor that can be closely approximated by $g\left(s_0\right)\doteq -1.15455+7.64165s_0-6.4871s_0^2$ for $0.98\le s_0\le 1$ [30]. For the three shells shown in Figure 7a–c, we obtained results of $r\simeq 500$ μm, $t\simeq 0.32$ μm, $0.55$ μm, and $0.72$ μm, respectively. With these parameters, the $J_c$ wa determined using Equation (2) for the three shells, as depicted in Figure 7d–f. This showed that the variation in $J_c$ with respect to both the magnetic field H and temperature T was similar for all three shells, as can be expected from the similar m(H) loops displayed in Figure 7a–c. For each shell, the $J_c$ decreased as the fields increased, and this decrease became more pronounced as the temperature rose.

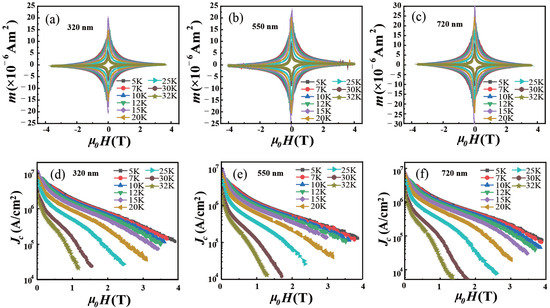
Figure 7. (a–c) Isothermal magnetization hysteresis loops of ${\mathrm{MgB}}_2$ spherical shells with varying thicknesses of (a) 320 nm, (b) 550 nm, and (c) 720 nm. (d–f) The superconducting critical current density $J_c$ determined from (a–c) as a function of the applied magnetic field.

To better perceive the variation in $J_c(T,H)$ and its dependence on the thickness, we plotted the $J_c$ values for typical magnetic fields and temperatures as a function of either the temperature or thickness, as shown in Figure 8. In the figure, the $J_c$ values in the $200\mathrm{nm}$ thick shell, as recently reported [31], are also included. Figure 8a shows the $J_c$ values for three different magnetic fields, namely $0\mathrm{T}$, $1\mathrm{T}$, and $2\mathrm{T}$, as a function of the temperature. At zero applied fields (i.e., in self-field conditions), the maximum $J_c$ occurred at a temperature of $15\mathrm{K}$ for all shells, showing values of $0.74-1.2\times {10}^7 {\mathrm{A/cm}}^2$. These values are comparable to those of high-quality epitaxial ${\mathrm{MgB}}_2$ thin films [48], suggesting a high supercurrent-carrying capability of the shells. As the temperature increased from $15\mathrm{K}$, the $J_c$ decreased, but it still maintained a value of around $2\times {10}^6{\mathrm{A}/\mathrm{cm}}^2$ at $32\mathrm{K}$, indicating the persistence of a high $J_c$ at elevated temperatures. As the temperature decreased from $15\mathrm{K}$, the $J_c$ also became lower. This reduction in $J_c$ in the low-temperature region, as circled in Figure 8a, arose from the occurrence of flux jumps below $15\mathrm{K}$, as demonstrated in Figure 5 and mentioned earlier. As previously observed [30,42,44], flux jumps, also known as vortex avalanches, diminish the central peak of the m(H) loop in the low-field region (by up to ∼0.2–0.3 T in this study), leading to a suppression of $J_c$ near zero fields. Figure 8a shows that, for higher fields of $1\mathrm{T}$ and $2\mathrm{T}$ in the absence of flux jumps, the $J_c$ exhibited its traditional behavior of monotonically decreasing with an increasing temperature. At $5\mathrm{K}$, the $J_c$ was $1.2-2.1\times {10}^6 {\mathrm{A/cm}}^2$ at $1\mathrm{T}$ and $5.1-8.3\times {10}^5 {\mathrm{A/cm}}^2$ at $2\mathrm{T}$, which are similar results to those reported for carbon-doped or oxygen ion-irradiated ${\mathrm{MgB}}_2$ films at nearly the same temperatures [38,49].

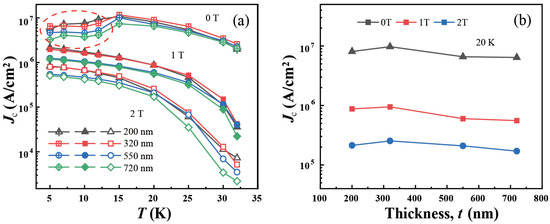
Figure 8. (a) Temperature dependence of the $J_c$ under magnetic fields of 0 T, 1 T, and 2 T for ${\mathrm{MgB}}_2$ spherical shells with thicknesses varying from 200 nm to 720 nm. Dashed circle indicates the temperature region where flux jumps are present in $m\left(H\right)$ curves, as shown in Figure 5. (b) The $J_c$ at 20 K as a function of the shell thickness under magnetic fields of 0 T, 1 T, and 2 T.

Figure 8b depicts the evolution of the $J_c$ at $20\mathrm{K}$ as a function of the thickness under three different magnetic fields. For all fields, it shows that the $J_c$ increased roughly linearly as the thickness decreased from $720\mathrm{nm}$ to $320\mathrm{nm}$, exhibiting an enhancement of approximately $50\%$ within this thickness range. In view of the thickness evolution of the shell’s surface morphology, we may attribute this enhancement in $J_c$ to the reduction in the ${\mathrm{MgB}}_2$ grain size. The decrease in the grain size potentially resulted in enhanced flux pinning in thinner shells, facilitated by the proliferation of grain boundaries, which then gave rise to a higher $J_c$. One may notice that this attribution does not seem to align well with our earlier discussion on $H_{irr}$. We propose that this may possibly hint at a potential difference in the flux pinning behavior of the shells between relatively low fields (pertinent to the discussion of $J_c$) and high fields (pertinent to the discussion of $H_{irr}$). Further investigations are required to clarify this issue. As the shell thickness decreased further to $200\mathrm{nm}$, Figure 8a shows that the $J_c$ did not continue the trend observed in thicker shells of increasing; instead, it declined slightly for all three fields. As indicated by the decline in $J_c$ with zero applied fields as well, this could be ascribed to a slight degradation in the grain connectivity in the $200\mathrm{nm}$ thick shell. When the shell thickness diminishes to a certain point, the grain connectivity may not be as robust as in thicker shells, due to the concurrent reduction in both the grain size and shell thickness. This could counteract the effect of flux pinning from the proliferation of grain boundaries, leading to a decline in $J_c$. Nonetheless, Figure 8a shows that the $J_c$ in the $200\mathrm{nm}$ thick shell was still higher than that in shells with thicknesses of $550\mathrm{nm}$ or $720\mathrm{nm}$, which is attractive for potential superconducting magnetic levitation applications, such as in ICF.

4. Conclusions

In summary, we investigated the superconducting properties as well as the surface morphologies and compositions of ${\mathrm{MgB}}_2$ spherical shells deposited on $1\mathrm{mm}$ diameter Si₃N₄ spheres as the shell thickness varied from $200\mathrm{nm}$ to $720\mathrm{nm}$. While the compositions of the shells seemed not to show apparent variation with the shell thickness, SEM images revealed a clear correlation between the shell thickness and the size of the ${\mathrm{MgB}}_2$ grains comprising the shell, as both the lateral size and thickness of the lamellar grains decreased approximately linearly with the decrease in the shell thickness. Through electrical transport and magnetization measurements, characteristic superconducting fields, including the upper critical field $H_{c2}$, the lower critical field $H_{c1}$, and the irreversibility field $H_{irr}$, were determined and their thickness dependencies were examined. From a two-band model analysis of the $H_{c2}\left(T\right)$, both the electron diffusivities $D_{\sigma }$ and $D_{\pi }$ were extracted. This showed that $D_{\pi }$ was considerably higher than $D_{\sigma }$ for each shell, and while both $D_{\sigma }$ and $D_{\pi }$ decreased as the shell thickness decreased, indicating an increasing scattering strength in thinner shells, the decrease in $D_{\sigma }$ was significantly weaker than that in $D_{\pi }$. This disparity in the two bands was found to underline the somewhat contrasting behavior of $H_{c2}\left(0\right)$ and $H_{c1}\left(0\right)$ as a function of the thickness; that is, as the shell thickness decreased, the observed mild enhancement in $H_{c2}\left(0\right)$ corresponded to the smaller decrease in $D_{\sigma }$, while the more significant decline in $H_{c1}\left(0\right)$ originated from the stronger suppression of $D_{\pi }$. From the magnetization hysteresis loops, the superconducting critical current density $J_c(T,H)$ was also determined. It exhibited an increase as the thickness decreased, except for in the thinnest shell of $200\mathrm{nm}$, where a slight decline in $J_c(T,0)$ indicated that the connectivity of the ${\mathrm{MgB}}_2$ grains may not have been as robust as in thicker shells.

When linking the superconducting properties to the surface morphologies of the shells, a clear picture emerges: as the shell thickness diminishes, the ${\mathrm{MgB}}_2$ grains shrink in size, leading to a proliferation of grain boundaries. This proliferation, accompanied by an increase in the scattering strength, results in a decrease in electron diffusivities. Consequently, $H_{c2}$ is enhanced, while $H_{c1}$ is suppressed. Furthermore, the increased number of grain boundaries provides more effective flux pinning, which improves the $J_c(T,H)$, as long as the connectivity between the grains remains intact and does not degrade. We observed that the dependence of $H_{irr}$ on the shell thickness, which essentially means it decreases as the shell thickness decreases, does not seem to align well with this picture. Whether this indicates a reversal in the flux pinning properties at relatively high fields requires further investigation. Overall, the present study demonstrated a close correlation between the microstructure, specifically, the grain size, and the superconducting properties in ${\mathrm{MgB}}_2$ spherical shells and the effectiveness of tuning them by varying the thickness of the shell. In particular, it suggests that the superconducting critical fields of the shells might be individually tuned by selectively engineering the intra-band scattering within either the $\sigma$ or $\pi$ band, owing to the unique two-band superconductivity of ${\mathrm{MgB}}_2$. These results can be helpful in guiding the fabrication of ${\mathrm{MgB}}_2$ superconducting shells with enhanced properties, thereby better fulfilling the requirements of applications in various appealing fields.