The Thickness Dependence of the Superconducting Properties of MgB2 Spherical Shells Deposited on 1 mm Diameter Si3N4 Spheres
Abstract
1. Introduction
2. Experimental Details
3. Results and Discussion
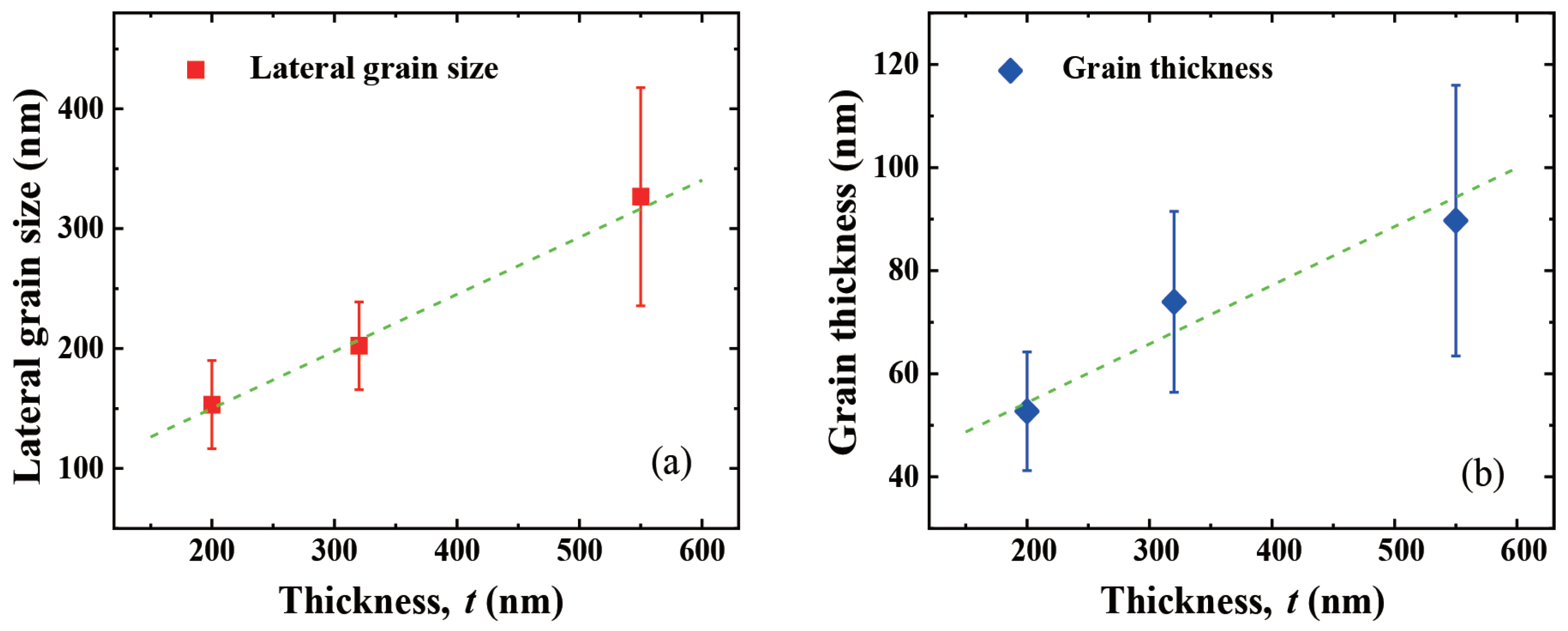
3.1. Surface Morphology
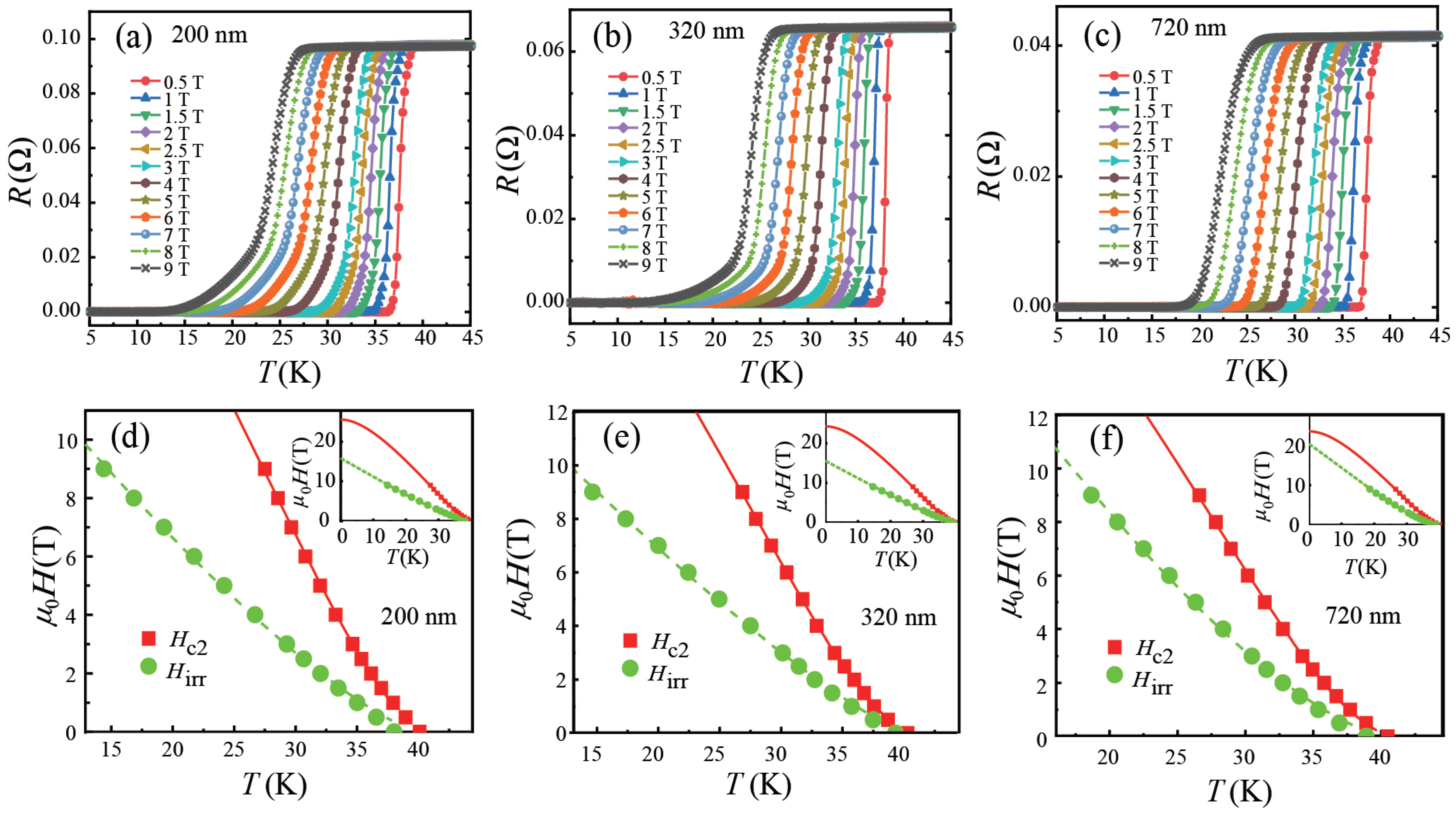
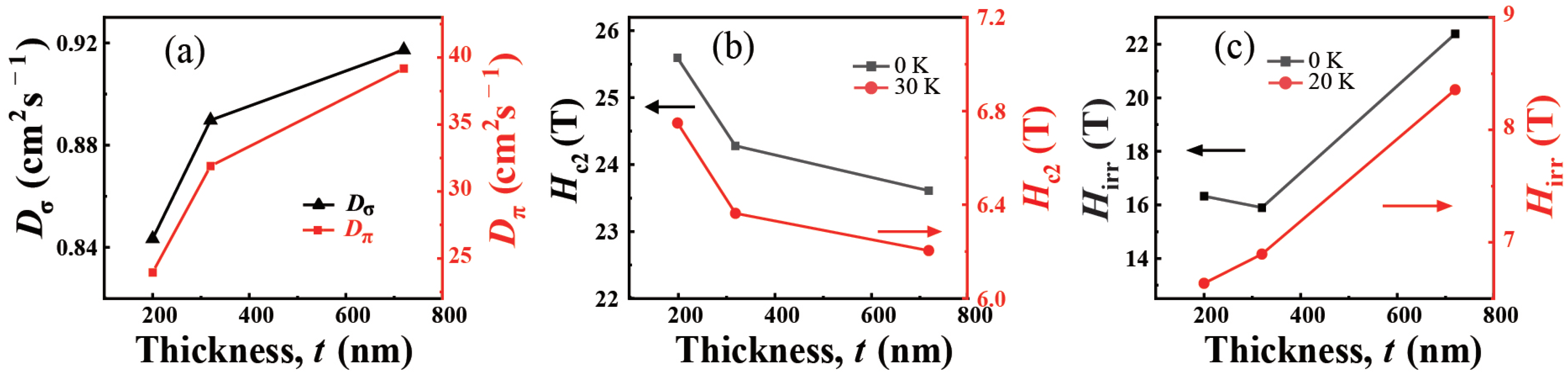
3.2. Upper Critical Field Hc2(T) and Irreversibility Field Hirr(T)
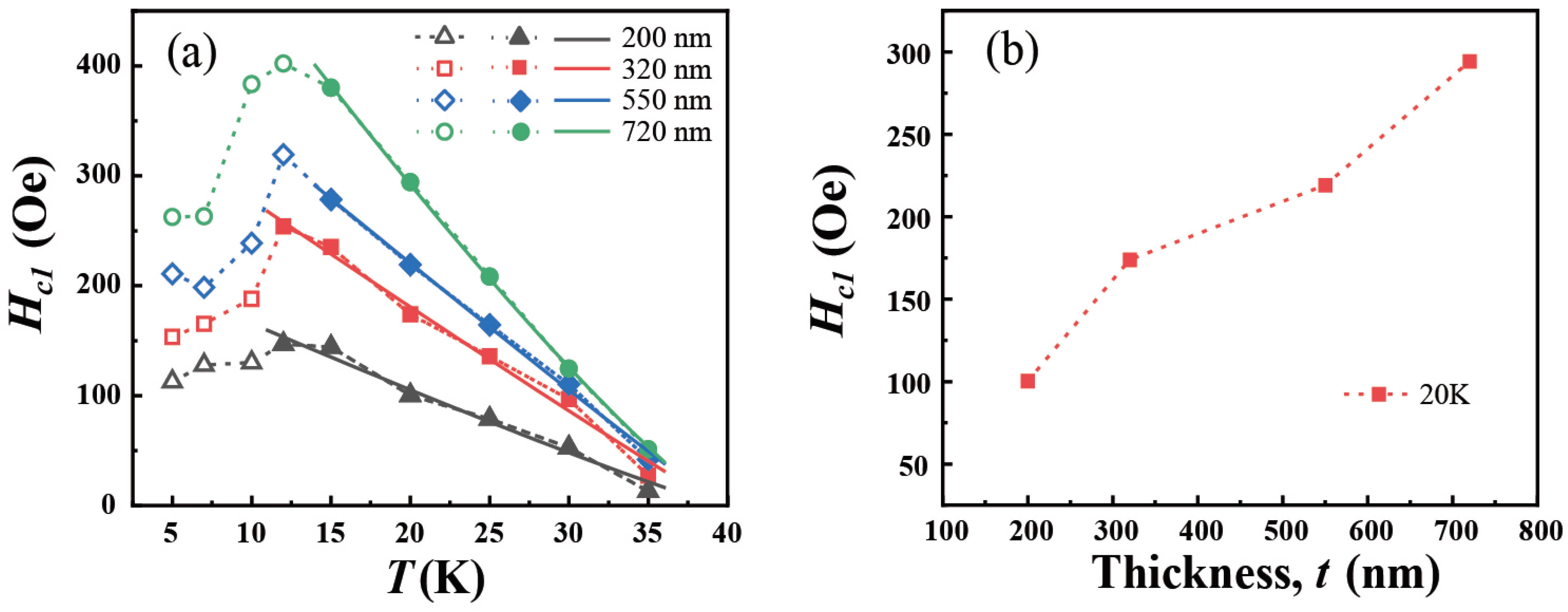
3.3. Lower Critical Field Hc1(T)
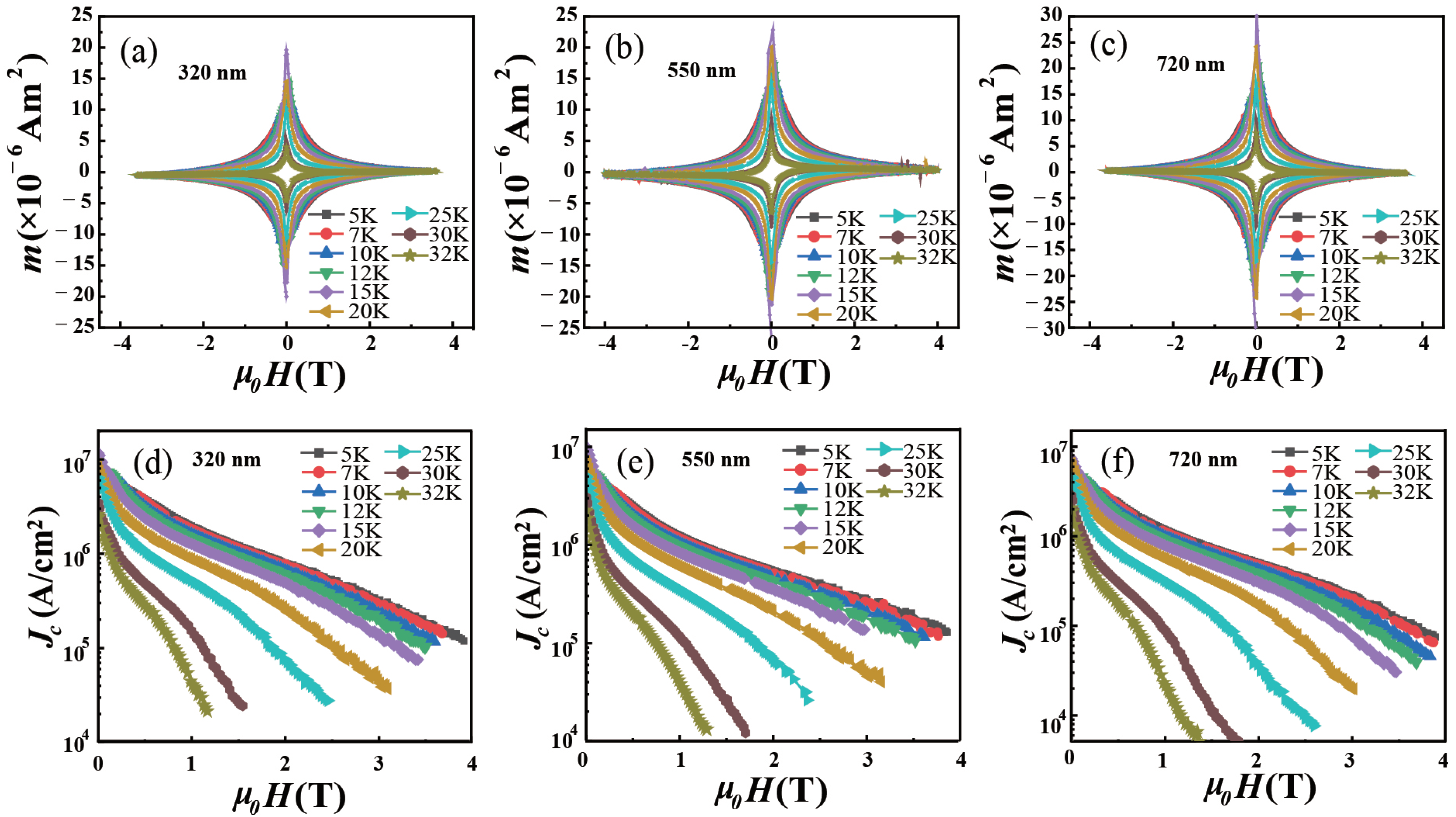
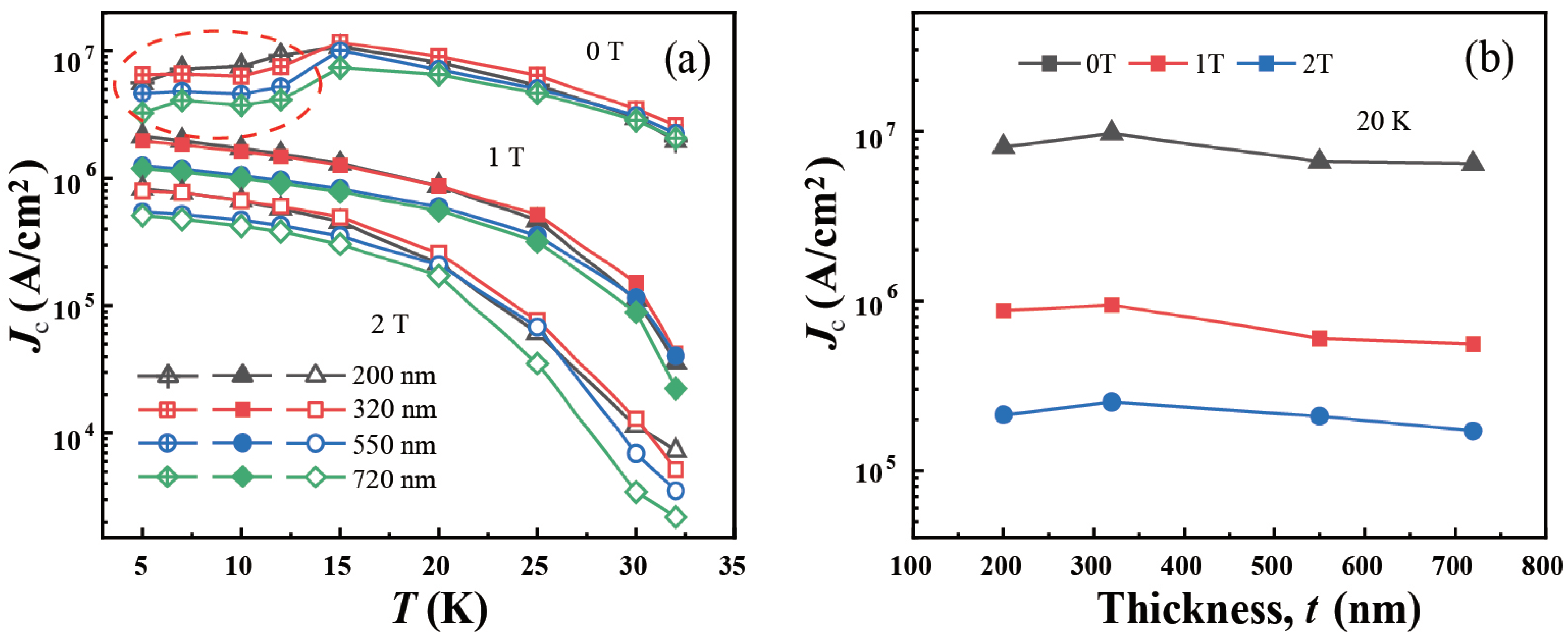
3.4. Superconducting Critical Current Density Jc(T,H)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Larbalestier, D.C.; Cooley, L.D.; Rikel, M.O.; Polyanskii, A.A.; Jiang, J.; Patnaik, S.; Cai, X.Y.; Feldmann, D.M.; Gurevich, A.; Squitieri, A.A.; et al. Strongly linked current flow in polycrystalline forms of the superconductor MgB2. Nature 2001, 410, 186–189. [Google Scholar] [CrossRef]
- Yao, C.; Ma, Y. Superconducting materials: Challenges and opportunities for large-scale applications. iScience 2021, 24, 102541. [Google Scholar] [CrossRef]
- Brinkman, A.; Rowell, J. MgB2 tunnel junctions and SQUIDs. Phys. C 2007, 456, 188–195. [Google Scholar] [CrossRef]
- Yang, C.; Niu, R.R.; Guo, Z.S.; Cai, X.W.; Chu, H.M.; Yang, K.; Wang, Y.; Feng, Q.R.; Gan, Z.Z. Lumped element kinetic inductance detectors based on two-gap MgB2 thin films. Appl. Phys. Lett. 2018, 112, 022601. [Google Scholar] [CrossRef]
- Thimont, Y.; Xing, Y.; Bernstein, P.; Miryala, M.; Noudem, J. Joining Superconducting MgB2 Parts by Spark Plasma Sintering: A New Technique with High Potential for Manufacturing Future Superconducting Devices. Coatings 2022, 12, 1151. [Google Scholar] [CrossRef]
- Xi, X.X. Two-band superconductor magnesium diboride. Rep. Prog. Phys. 2008, 71, 116501. [Google Scholar] [CrossRef]
- Kortus, J.; Mazin, I.; Belashchenko, K.; Antropov, V.; Boyer, L. Superconductivity of metallic Boron in MgB2. Phys. Rev. Lett. 2001, 86, 4656–4659. [Google Scholar] [CrossRef]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Louie, S.G. The origin of the anomalous superconducting properties of MgB2. Nature 2002, 418, 758–760. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Y.; Zhuang, C.; Shi, J.; Yao, Y.; Massidda, S.; Monni, M.; Jia, Y.; Xi, X.; Li, Q.; et al. Fully Band-Resolved Scattering Rate in MgB2 Revealed by the Nonlinear Hall Effect and Magnetoresistance Measurements. Phys. Rev. Lett. 2008, 101, 067001. [Google Scholar] [CrossRef]
- Gutierrez, J.; Raes, B.; Silhanek, A.V.; Li, L.J.; Zhigadlo, N.D.; Karpinski, J.; Tempere, J.; Moshchalkov, V.V. Scanning Hall probe microscopy of unconventional vortex patterns in the two-gap MgB2 superconductor. Phys. Rev. B 2012, 85, 094511. [Google Scholar] [CrossRef]
- Milošević, M.V.; Perali, A. Emergent phenomena in multicomponent superconductivity: An introduction to the focus issue. Supercond. Sci. Technol. 2015, 28, 060201. [Google Scholar] [CrossRef]
- Babaev, E.; Carlström, J.; Silaev, M.; Speight, J. Type-1.5 superconductivity in multicomponent systems. Phys. C 2017, 533, 20–35. [Google Scholar] [CrossRef]
- Kovalev, S.; Dong, T.; Shi, L.Y.; Reinhoffer, C.; Xu, T.Q.; Wang, H.Z.; Wang, Y.; Gan, Z.Z.; Germanskiy, S.; Deinert, J.C.; et al. Band-selective third-harmonic generation in superconducting MgB2: Possible evidence for the Higgs amplitude mode in the dirty limit. Phys. Rev. B 2021, 104, L140505. [Google Scholar] [CrossRef]
- El-Toni, A.M.; Habila, M.A.; Labis, J.P.; ALOthman, Z.A.; Alhoshan, M.; Elzatahry, A.A.; Zhang, F. Design, synthesis and applications of core–shell, hollow core, and nanorattle multifunctional nanostructures. Nanoscale 2016, 8, 2510–2531. [Google Scholar] [CrossRef]
- Ishibe, T.; Maeda, Y.; Terada, T.; Naruse, N.; Mera, Y.; Kobayashi, E.; Nakamura, Y. Resistive switching memory performance in oxide hetero-nanocrystals with well-controlled interfaces. Sci. Technol. Adv. Mater. 2020, 21, 195–204. [Google Scholar] [CrossRef]
- Bayles, A.; Tian, S.; Zhou, J.; Yuan, L.; Yuan, Y.; Jacobson, C.R.; Farr, C.; Zhang, M.; Swearer, D.F.; Solti, D.; et al. Al@TiO2 Core–Shell Nanoparticles for Plasmonic Photocatalysis. ACS Nano 2022, 16, 5839–5850. [Google Scholar] [CrossRef]
- Yeo, J.; Moore, M.A. Noninteger flux quanta for a spherical superconductor. Phys. Rev. B 1998, 57, 10785–10789. [Google Scholar] [CrossRef]
- Du, Q.; Ju, L. Numerical simulations of the quantized vortices on a thin superconducting hollow sphere. J. Comput. Phys. 2004, 201, 511–530. [Google Scholar] [CrossRef]
- Gladilin, V.N.; Tempere, J.; Silvera, I.F.; Devreese, J.T.; Moshchalkov, V.V. Vortices on a superconducting nanoshell: Phase diagram and dynamics. Phys. Rev. B 2008, 77, 024512. [Google Scholar] [CrossRef]
- Makarov, D.; Volkov, O.M.; Kákay, A.; Pylypovskyi, O.V.; Budinská, B.; Dobrovolskiy, O.V. New Dimension in Magnetism and Superconductivity: 3D and Curvilinear Nanoarchitectures. Adv. Mater. 2022, 34, 2101758. [Google Scholar] [CrossRef]
- Goodkind, J.M. The superconducting gravimeter. Rev. Sci. Instrum. 1999, 70, 4131–4152. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Buchman, S.; Lipa, J.A.; Keiser, G.M.; Muhlfelder, B.; Turneaure, J.P. The Gravity Probe B gyroscope. Class. Quantum Grav. 2015, 32, 224004. [Google Scholar] [CrossRef]
- Huang, X.; Hu, X.; Cui, C.; Wang, H.; Niu, F.; Zhang, Y.; Wang, L.; Wang, Q.; Hao, X.; Liu, M.; et al. Design and Construction of a Superconducting Gravimeter Prototype. IEEE Trans. Instrum. Meas. 2022, 71, 9502410. [Google Scholar] [CrossRef]
- Tollefson, J. US nuclear-fusion lab enters new era: Achieving ’ignition’ over and over. Nature 2024, 625, 11. [Google Scholar] [CrossRef]
- Li, X.; Xiao, T.; Chen, F.; Zhang, Y.; Li, X.; Wu, W. A novel superconducting magnetic levitation method to support the laser fusion capsule by using permanent magnets. Matter Radiat. Extremes 2018, 3, 104–109. [Google Scholar] [CrossRef]
- Smalyuk, V.A.; Robey, H.F.; Alday, C.L.; Amendt, P.; Aracne-Ruddle, C.; Bigelow, J.R.; Bunn, T.; Casey, D.T.; Chen, K.C.; Clark, D.S.; et al. Review of hydro-instability experiments with alternate capsule supports in indirect-drive implosions on the National Ignition Facility. Phys. Plasmas 2018, 25, 072705. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Li, Z.; Zeng, Y.; Zhong, M.; Wang, Y. Spherical Superconducting MgB2 Thin Film. J. Supercond. Nov. Magn. 2022, 35, 3537–3542. [Google Scholar] [CrossRef]
- Xu, T.Q.; Sun, R.N.; Zhao, J.X.; Wang, Y.; Wang, F.R.; Gan, Z.Z. Properties of superconducting MgB2 spherical shells deposited on 2mm and 1mm diameter Si3N4 spheres. Supercond. Sci. Technol. 2023, 36, 095006. [Google Scholar] [CrossRef]
- Sun, R.N.; Xu, T.Q.; Wang, Y.; Wang, F.R.; Gan, Z.Z. Fabrication and characterization of MgB2 spherical shells with reduced thickness on 1 mm diameter Si3N4 spheres. Chin. Phys. B, 2025; submitted. [Google Scholar]
- Withanage, W.K.; Penmatsa, S.V.; Acharya, N.; Melbourne, T.; Cunnane, D.; Karasik, B.S.; Xi, X.X. Growth of magnesium diboride thin films on boron buffered Si and silicon-on-insulator substrates by hybrid physical chemical vapor deposition. Supercond. Sci. Technol. 2018, 31, 075009. [Google Scholar] [CrossRef]
- Ferrando, V.; Orgiani, P.; Pogrebnyakov, A.V.; Chen, J.; Li, Q.; Redwing, J.M.; Xi, X.X.; Giencke, J.E.; Eom, C.B.; Feng, Q.R.; et al. High upper critical field and irreversibility field in MgB2 coated-conductor fibers. Appl. Phys. Lett. 2005, 87, 252509. [Google Scholar] [CrossRef]
- Tan, T.; Wolak, M.A.; Xi, X.X.; Tajima, T.; Civale, L. Magnesium diboride coated bulk niobium: A new approach to higher acceleration gradient. Sci. Rep. 2016, 6, 35879. [Google Scholar] [CrossRef]
- Eisterer, M. Magnetic properties and critical currents of MgB2. Supercond. Sci. Technol. 2007, 20, R47. [Google Scholar] [CrossRef]
- Gurevich, A. Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors. Phys. Rev. B 2003, 67, 184515. [Google Scholar] [CrossRef]
- Iavarone, M.; Di Capua, R.; Koshelev, A.E.; Kwok, W.K.; Chiarella, F.; Vaglio, R.; Kang, W.N.; Choi, E.M.; Kim, H.J.; Lee, S.I.; et al. Effect of disorder in MgB2 thin films. Phys. Rev. B 2005, 71, 214502. [Google Scholar] [CrossRef]
- Zhuang, C.G.; Meng, S.; Yang, H.; Jia, Y.; Wen, H.H.; Xi, X.X.; Feng, Q.R.; Gan, Z.Z. Significant improvements of the high-field properties of carbon-doped MgB2 films by hot-filament-assisted hybrid physical-chemical vapor deposition using methane as the doping source. Supercond. Sci. Technol. 2008, 21, 082002. [Google Scholar] [CrossRef]
- Xie, W.; Liu, Y.H.; Wen, H.H. Generalized phenomenological model for the magnetic field penetration and magnetization hysteresis loops of a type-II superconductor. Phys. Rev. B 2022, 105, 014505. [Google Scholar] [CrossRef]
- Wen, H.H.; Li, S.L.; Zhao, Z.W.; Jin, H.; Ni, Y.M.; Kang, W.N.; Kim, H.J.; Choi, E.M.; Lee, S.I. Magnetic relaxation and critical current density of MgB2 thin films. Phys. Rev. B 2001, 64, 134505. [Google Scholar] [CrossRef]
- Yang, H.; Jia, Y.; Shan, L.; Zhang, Y.; Wen, H.H.; Zhuang, C.; Liu, Z.; Li, Q.; Cui, Y.; Xi, X. I − V characteristics of the vortex state in MgB2 thin films. Phys. Rev. B 2007, 76, 134513. [Google Scholar] [CrossRef]
- Jin, S.; Jin, H.; Bower, C.; van Dover, R.B. High critical currents in iron-clad superconducting MgB2 wires. Nature 2001, 411, 563–565. [Google Scholar] [CrossRef] [PubMed]
- Chabanenko, V.; Puźniak, R.; Nabiałek, A.; Vasiliev, S.; Rusakov, V.; Huanqian, L.; Szymczak, R.; Szymczak, H.; Jun, J.; Karpiński, J.; et al. Flux Jumps and H-T Diagram of Instability for MgB2. J. Low Temp. Phys. 2003, 130, 175–191. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Li, S.L.; Ni, Y.M.; Yang, H.P.; Liu, Z.Y.; Wen, H.H.; Kang, W.N.; Kim, H.J.; Choi, E.M.; Lee, S.I. Suppression of superconducting critical current density by small flux jumps in MgB2 thin films. Phys. Rev. B 2002, 65, 064512. [Google Scholar] [CrossRef]
- Johansen, T.H.; Baziljevich, M.; Shantsev, D.V.; Goa, P.E.; Galperin, W.N.; Kang, W.N.; Kim, H.J.; Choi, E.M.; Kim, M.S.; Lee, S.I. Dendritic magnetic instability in superconducting MgB2 films. Europhys. Lett. 2002, 59, 599. [Google Scholar] [CrossRef]
- Bhagwat, K.; Chaddah, P. Hysteretic loss in hard superconductor samples with non-zero demagnetization factor. Phys. C 1990, 166, 1–8. [Google Scholar] [CrossRef]
- Farinon, S.; Iannone, G.; Fabbricatore, P.; Gambardella, U. 2D and 3D numerical modeling of experimental magnetization cycles in disks and spheres. Supercond. Sci. Technol. 2014, 27, 104005. [Google Scholar] [CrossRef]
- Xi, X.X. MgB2 thin films. Supercond. Sci. Technol. 2009, 22, 043001. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, C.G.; Li, J.; Wu, Z.W.; Li, S.; Chu, H.F.; Feng, Q.R.; Zheng, D.N. Enhancement of critical current density and flux pinning in oxygen ion-irradiated MgB2 thin films. Supercond. Sci. Technol. 2009, 22, 045020. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Xu, T.; Wang, Y.; Wang, F.; Gan, Z. The Thickness Dependence of the Superconducting Properties of MgB2 Spherical Shells Deposited on 1 mm Diameter Si3N4 Spheres. Coatings 2025, 15, 377. https://doi.org/10.3390/coatings15040377
Sun R, Xu T, Wang Y, Wang F, Gan Z. The Thickness Dependence of the Superconducting Properties of MgB2 Spherical Shells Deposited on 1 mm Diameter Si3N4 Spheres. Coatings. 2025; 15(4):377. https://doi.org/10.3390/coatings15040377
Chicago/Turabian StyleSun, Ruining, Tiequan Xu, Yue Wang, Furen Wang, and Zizhao Gan. 2025. "The Thickness Dependence of the Superconducting Properties of MgB2 Spherical Shells Deposited on 1 mm Diameter Si3N4 Spheres" Coatings 15, no. 4: 377. https://doi.org/10.3390/coatings15040377
APA StyleSun, R., Xu, T., Wang, Y., Wang, F., & Gan, Z. (2025). The Thickness Dependence of the Superconducting Properties of MgB2 Spherical Shells Deposited on 1 mm Diameter Si3N4 Spheres. Coatings, 15(4), 377. https://doi.org/10.3390/coatings15040377




