Thermal Analysis and Optimization of Nano Coated Radiator Tubes Using Computational Fluid Dynamics and Taguchi Method

Abstract

Automotive heat removal levels are of high importance for maximizing fuel consumption. Current radiator designs are constrained by air-side impedance, and a large front field must meet the cooling requirements. The enormous demand for powerful engines in smaller hood areas has caused a lack of heat dissipation in the vehicle radiators. As a prediction, exceptional radiators are modest enough to understand coolness and demonstrate great sensitivity to cooling capacity. The working parameters of the nano-coated tubes are studied using Computational Fluid Dynamics (CFD) and Taguchi methods in this article. The CFD and Taguchi methods are used for the design of experiments to analyse the impact of nano-coated radiator parameters and the parameters having a significant impact on the efficiency of the radiator. The CFD and Taguchi methodology studies show that all of the above-mentioned parameters contribute equally to the rate of heat transfer, effectiveness, and overall heat transfer coefficient of the nanocoated radiator tubes. Experimental findings are examined to assess the adequacy of the proposed method. In this study, the coolant fluid was transmitted at three different mass flow rates, at three different coating thicknesses, and coated on the top surface of the radiator tubes. Thermal analysis is performed for three temperatures as heat input conditioning for CFD. The most important parameter for nanocoated radiator tubes is the orthogonal array, followed by the Signal-to-Noise Ratio (SNRA) and the variance analysis (ANOVA). A proper orthogonal array is then selected and tests are carried out. The findings of ANOVA showed 95% confidence and were confirmed in the most significant parameters. The optimal values of the parameters are obtained with the help of the graphs.

1. Introduction

Surface engineering involves the development of a wide range of technologies for component surface characteristics and adaptation. Surface modifications may be used to reduce friction, increase surface wear, increase resistance to corrosion, increase heat transfer, and alter the physical or mechanical properties of the component [1]. Surface additives may also be paired with surface coating methods, such as laser coating, physical vapor deposition (PVD), chemical vapor deposition (CVD), a thermal spraying method, sol-gel, coating and galvanizing. This blend improves the benefits of surface coating and surface modification to meet individual safety and needs. The automotive radiator is a key component of the engine cooling system. The problem of inadequate dissipation rates in automotive radiators has been caused by the demand for more powerful vehicles in smaller hoods. Moreover, a large number of heaters should be redesigned to become lighter while still having sufficient cooling capabilities [2].

Engine oils and lubricants decompose at temperatures above the optimum range and induce expansion in moving parts. Engines are assembled to fit tightly, which leads to dangerous metal contact due to the marginal expansion of the parts [3]. Likewise, an overcooled engine can be exposed to high thermal stress and a loss of material strength (i.e., below optimal temperature). This is because the temperature is monitored using a thermostat in most radiator cooling systems [4]. This thermostat will remain closed until the temperature of the coolant reaches a certain point, under which the coolant is maintained within the engine [5,6].

Today’s engine requires higher efficiency with less space available to allow for the flow of coolant. This requires a better knowledge of the complex refractive fluid stream characteristics and heat quality of the heat sink [7].

Normally, the heat transfer from surfaces can be increased by increasing the coefficient of heat transfer between the surface and its surroundings, by enhancing the surface area of heat transfer, or by both. There are many approaches to improve the characteristics of heat transfer, which can primarily be separated into active and passive techniques [8].

Active techniques are more convenient to use and design components. As the system needs some external power input, it will induce the desired change inflow and increase the rate of heat transfer. It requires limited use due to the need for external control in many functional applications. Increased heat transfer by this process can be accomplished by mechanical use, surface vibration, fluid vibration, electrostatic forces, compression, suction, and jet impingement.

Passive methods typically use surface or geometric modifications to the flow channel by adding extensions or unessential contrivances to promote higher coefficients of heat transfer by disturbing or modifying the subsistent flow attitudes, such as treated surfaces, rough surfaces, elongated surfaces, displacement enhancement contrivances, swirl flow contrivances, coiled tubing, and surface tension contrivances. Passive techniques are more important in these contexts, since active techniques are more complex from a design viewpoint [9,10].

Material coatings are often used for tribological applications to reduce friction, fouling, and wear. Although the make-up of the nano-coating was classified as proprietary in nature in this report, an analysis of the related literature is provided to include contextual details for their intent, intended usage and implementation. Nano-coatings may be broadly described as any substance having at least one component occurring on the nanometer scale where the main component is called the matrix and the fillers are scattered throughout [11].

The evaluated nano-coating technology may also be a solution to increase the effectiveness of thermal exchangers and thus the overall engine performance. Through using a material layer that helps to increase the heat transfer rate or decrease the friction between the fluid flow and the corresponding cooler walls on the current base, the performance of the engine can be improved while decreasing fuel consumption. The use of material coatings on heat exchanger surfaces will reduce some of the implications, resulting in higher heat transfer levels. From a macroscopic perspective, it has been shown that, generally, the engine output is improved considerably when fuel consumption is decreased after cooler operations.

2. Taguchi Method

The experimental design using the Taguchi orthogonal array will full-fill the requirements of problem-solving and product optimization projects economically [12]. By introducing Taguchi methodologies, the time, effort, and money for experimental work can be minimized by researchers, engineers, and scientists. The design of experiments (DOE) defines the relationship between the variable’s input and output. The DOE with Taguchi orthogonal array needs good preparation, intelligent experiment structure, and specialist result interpretation. The Taguchi method became the traditional DOE method [13,14]. It was designed by Dr. Genechi Taguchi (1940 by the Japanese engineer) and came to be known as one of the best plays for scientists and engineers [15].

The DOE’s principal goal is for the input and output parameters to be further and more practical. A large number of experiments are needed for more and more accurate knowledge. However, modern experimental theory indicates that this is not always valid [16]. The full number of experiments is an enormous mistake in terms of cost. It is easier to collect more and more practical data when playing with less [17]. Taguchi’s approach is one of the best examples. Taguchi developed a technique called orthogonal selection to review all process parameters with minimum equilibrium tests only [18]. The primary purpose of the DOE is to analyze the parameter (entry) that affects the performance more effectively. The approach to enhance product quality is well known, strong, and unique [19].

Taguchi is computational techniques for optimizing design, using the traditional “Orthogonal Arrays” to construct an experiment matrix to achieve minimum experimental numbers for the greatest number of data. In Taguchi techniques, the number of parameters can be measured at a time with probably fewer experiments than others. Moreover, the technique contains all the knowledge needed to optimize the problem. The main advantage of Taguchi techniques is not only the smallest number of experiments possible, but the best quantity of each parameter with each parameter divided into the problem [20]. Qualitative features and design criteria for the product/process, experimental design and behavior, results evaluation for optimal specifications, and confirmatory tests to be carried out under optimal conditions are all key steps of the Taguchi process shown in Figure 1.

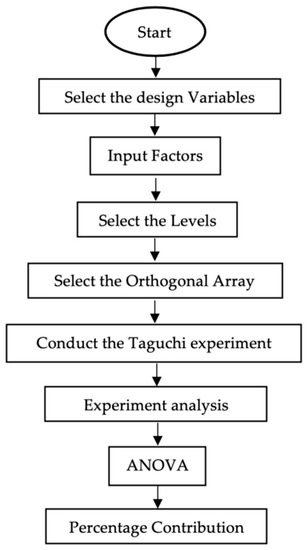
Figure 1. Flow chart–Process of Taguchi Analysis.

The better and less all the values observed are calculated by the equation in the Taguchi method. The findings in this analysis include the mean, minimum and average output values, effectiveness and overall coefficient of heat transfer. Parameters for control (Design factors) and their levels are listed in Table 1 and Three level considerations orthogonal array for L9 are listed in Table 2.

Table 1. Parameters for control (Design factors) and their Levels.

Control Parameters	Level_One	Level_Two	Level_Three
Heat input (K)	323	343	363
Mass flow rate (L/min)	0.15	0.30	0.45
Coating thickness (µm)	50	80	100

Table 2. Three level considerations Orthogonal Array for L9.

Condition	Level_One	Level_Two	Level_Three
One	One	One	One
Two	One	Two	Two
Three	One	Three	Three
Four	Two	One	Two
Five	Two	Two	Three
Six	Two	Three	One
Seven	Three	One	Three
Eight	Three	Two	One
Nine	Three	Three	Two

3. Analysis of Variance (ANOVA)

The following experimental results were evaluated with variance analyses.

$$\mathrm{Variance} (V) = \frac{\mathrm{Sum} \mathrm{of} \mathrm{Squares}}{\mathrm{Degrees} \mathrm{of} \mathrm{Freedom}} = \frac{S_{\mathrm{T}}}{f}$$

(1)

S_T = nσ² − nm²

(2)

S_m = σ² − nm²

(3)

S_e = S_T − S_m = (n − 1)σ²

(4)

Also, as previously mentioned, variance (V) is V = $\frac{S}{f}$. Therefore,

V_T = S_T/f_T = σ² + m² (Total Variance)

(5)

V_m = S_m/f_m = σ² + nm² (Mean Variance)

(6)

V_e = (S_T − S_m)/f_e = σ² (Error Variance)

(7)

The sound-to-noise ratio analysis (S/N ratio) has been designed for quality measurement.

4. Result Conversion to S/N Ratios

A collection of measurements, the SNRA, is converted into one single number in two steps. Next, measurement is made of the mean square deviation (MSD) of the package. Third, by definition, the SNRA determined from the MSD,

S/N = −10log₁₀ (MSD)

(8)

MSD = (Y₁² + Y₂² + …Y_N²)/N

(9)

$$\mathrm{Correction} \mathrm{factor} (\mathrm{C}.\mathrm{F}) = \frac{\left(\mathrm{Sum} \mathrm{of} \mathrm{SNRA}\right){ }^2}{N}$$

(10)

$$\mathrm{Sum} \mathrm{of} \mathrm{Squares} = \frac{\left\{\left(\mathrm{sum} \mathrm{of} \mathrm{SNRA} 1\mathrm{st} \mathrm{level}\right) + \left(\mathrm{sum} \mathrm{of} \mathrm{SNRA} 2\mathrm{nd} \mathrm{level}\right) + \left(\mathrm{sum} \mathrm{of} \mathrm{SNRA} 3\mathrm{rd} \mathrm{level}\right) – \mathrm{C}.\mathrm{F}\right\}}{2}$$

(11)

$$\mathrm{Percentage} \mathrm{of} \mathrm{Contribution} = \frac{\mathrm{Sum} \mathrm{of} \mathrm{Squares} \mathrm{of} \mathrm{a} \mathrm{Parameters}}{\mathrm{Total} \mathrm{Sum} \mathrm{of} \mathrm{Squares}}$$

(12)

where Y_i is the characteristic for output or performance and N is the total number of experiments.

5. Experimental Setup

The experimental diagram and setup are shown in Figure 2 and Figure 3. Table 3, displays the design of the radiator and engine set-up of the nano-coated tube radiator. A radiator is one kind of heat exchanger. The intention is to transfer heat from the coolant to the fan’s air.

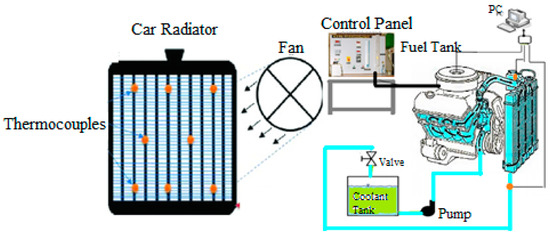
Figure 2. Experimental schematic diagram and Thermocouple Position in Radiator.

Figure 3. Experiment-Radiator Thermal analysis.

Table 3. Engine and Radiator Specification.

Engine Specification		Radiator Specification
Type	Water Cooled Sohc Engine	Radiator’s Type	Compact Heat Exchanger-Circular Tube with Continuous Fin
Fuel Used	Petrol	Radiator’s Volume	P × L × T = 500 × 30 × 550 mm3
Max. Power (bhp@rpm)	37bhp @5000 rpm	Tube Diameter	10 mm
Engine Displacement	796 CC	Tube Length	330 mm
Max. Torque	59 nm @2500 rpm	Number of Row	2
No. of Cylinders	4	Number of tubes per Row	8
No. of valves	2 valves/cylinder	Pit Length	11 mm
Valve Train	Sohc	Material	Coper coated Aluminium tubes
Fuel train	Mpfi	Fin Material	Aluminium
Pressure Ratio	8.8:1	Fin thickness	0.1 mm

Instead of formability and costs, most modern cars use aluminium radiators. Copper coated aluminium tubes are used in place of aluminium pipes, and thin aluminium fins are used to make these radiators. The coolant passes through several tubes in parallel from the entrance to the outlet. The fins led the heat through the heat sink, from the tube to the air [21,22].

Copper has a higher thermal conductivity than aluminum to dissipate more heat at a higher rate, thereby increasing the engine power to the next level, and measuring the efficiency of the radiator [23]. Experimental procedures have been replicated for different water mass flow rates and different radiator tube thicknesses have been reported, as well as observations.

6. CFD Model Analysis

In solid work, the three-dimensional model of the radiator was generated and exported to an IGS file as a single layer. The original designs have been modeled as one region, and characteristics not involved in internal flow have been eliminated. ANSYS CFD software was used in meshing and CFD analysis.

7. Geometry

A cuboid, supplied with porous media, was the heart of the radiator. The center of the calculation has dimensions of 500 × 500 × 30 mm³. There is an entrance pipe in the header over the radiator and there was an outlet pipe below the header that guided the water flow. The air regions were represented by the two cuboids in front of and behind the radiator [17,24]. The inlet and outlet for both fluids and interfaces between the various bodies was created before the meshing and selection of the physical model [25]. A new area was established to define different borders.

8. Mesh

The core section of the geometric model was given a finer mesh (Figure 4) than the other geometry regions to reduce the time of the CPU and load on the computer. The basic dimensions for the core section were 0.64 m. The base size was set at 2.56 m for the air region.

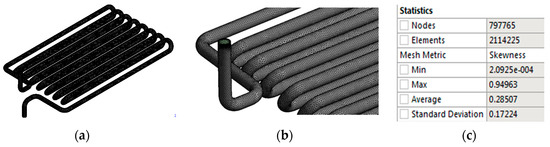
Figure 4. (a) Mesh Created; (b) Zoomed View; (c) Geometry Statistics.

9. Physical Models

The physical model for the radiator was chosen to determine the type of flow.

Different models have been developed as two fluids have been studied.

• Two Layer All and Wall Treatment
• Realizable K-Epsilon
• Two Layer Reynolds-Mean

Navier-Stokes Separate Fluid Temperature Air physical model:

Gas Water physical model: Two-dimensional Gradient Steady Stream One Layer Two Layer All and Wall Treated Towers.

10. Boundary Conditions

Coolant Inlet	Mass Flow Rate
Coolant Outlet	Pressure Outlet
Air Inlet	Velocity Inlet
Air Outlet	Velocity Outlet

11. Thermal Simulation

It is required to analyze the thermal performance of a tube composed by aluminium and a coat of copper. The dimensions of the tube are presented in Figure 5, and the physical properties of the materials considered are shown in Table 4. Water enters to the tube at a temperature of 323, 343, and 363 K and with a mass flow rate of 0.15, 0.30, and 0.45 L/min, whilst the tube is exposed to air at 25 °C with a convective heat transfer coefficient of 450 W m⁻² K⁻¹. Three different thicknesses will be simulated for the copper coating, $t$, namely 50, 80, and 100 µm.

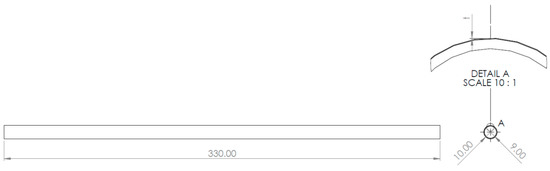
Figure 5. Principal tube dimensions.

Table 4. Material properties.

Material	Thermal Conductivity (W m−1 K−1)	Density (kg/m3)	Specific Heat (J kg−1 K−1)	Viscosity (kg m−1 s−1)
Aluminium	190	2719	871	-
Copper	401	3210	385	-
Water	0.6	998.2	4182	0.001003

The CFD analysis methodology is shown in Figure 6. According to the dimensions presented in Figure 5, the geometry was made using ANSYS Design Modeler, and the resulting 3D model and cut section view is presented in Figure 7.

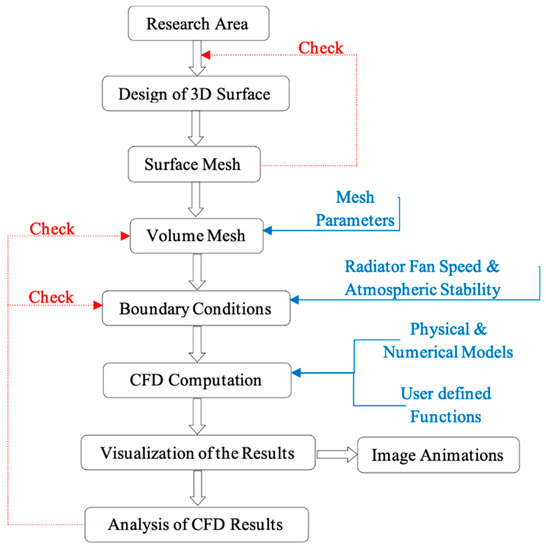
Figure 6. Methodology.

Figure 7. (a) Aluminium Radiator (Before coating) and (b) Copper Coated Cut Section View.

12. Optimization of Temperature

Based on the nine cases obtained in the orthogonal array in Table 2, the simulation was carried out in CFD for three levels of temperature as heat input, three levels of the mass flow rate of coolant fluid transmitted, and three different levels of coating thickness, as shown in Figure 8a–c.

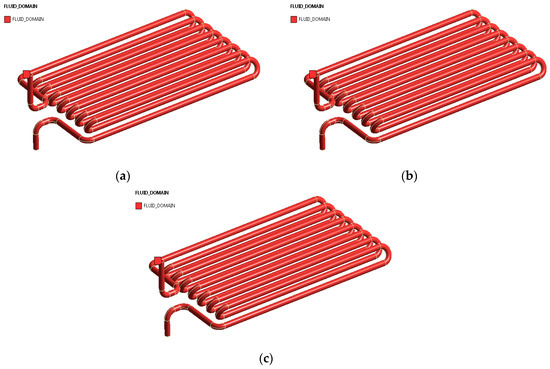
Figure 8. (a) 50 µm, (b) 80 µm, (c) 100 µm copper coating on Aluminium Radiator tubes.

To proceed with the Fluent setup, it was necessary to know the flow regime of the fluid. For this purpose, the Reynolds Number, R_e, was calculated as follows:

$$R_{\mathrm{e}}=\frac{4·\dot{m}}{\mathsf{\pi }·\mathsf{\mu }·D}$$

where $\dot{m}$ is the mass flow rate of water, $\mathsf{\mu }$ is the viscosity of water, and $D$ is the inner pipe diameter. Substituting the known values:

$$R_{\mathrm{e}}=\frac{4\times 0.05}{\mathsf{\pi }\times 0.001003\times 9\times {10}^{-3}}=7052.40$$

Since the Reynolds number is higher than 4000, the fluid flow can be considered as turbulent. Consequently, the Fluent setup was initialized, and the energy equation was activated. The selected viscous model was k-ε realizable, with enhanced wall treatment and thermal effects activated [26,27]. The working fluid was as specified as water, and the solids were aluminum and copper. Moreover, the boundary conditions were specified. The “Inlet” named selection received a boundary condition of “mass-flow-inlet”, with a magnitude of 0.15, 0.30, and 0.45 L/min along positive z-direction and a temperature of 323, 343, and 363 K. The “Outlet” named selection was specified as a “pressure-outlet” with 0 Pa gauge. The “Symmetry” named selection received the condition of “symmetry” and the “Convection” named selection received a “wall” condition subjected to convection, with a free stream temperature of 298 K and a convective heat transfer coefficient of 450 W m⁻² K⁻¹.

Furthermore, the solution scheme SIMPLEC was activated, and it was considered a spatial discretization of second order upwind for the energy, pressure, and momentum equations. The residuals convergence limits were specified as 1 × 10⁻⁶, and consequently, a hybrid initialization was carried out [28,29]. The simulation was executed for a maximum of 3000 iterations, and convergence was reached after approximately 1200 iterations for all the cases.

Figure 9 shows the SEM images of the samples coated surface. In Figure 10, The Y-axis shows counts and the X-axis shows the X-ray energy. The location of the summit helps to identify the elements and the maximum height helps to assess the concentration of each element. Table 5 shows the test results of the EDX of the coated surface.

Figure 9. SEM image of coating material (Characterization facility. SRMIST, Chennai). (a) 50 µm; (b) 80 µm; (c) 100 µm.

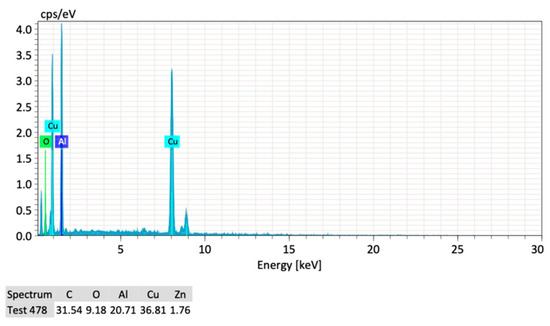
Figure 10. Typical EDX spectrum.

Table 5. EDX Test Results.

Element	At. No.	Mass [%]	Mass Norm [%]	Atom [%]	Abs. Error [%] (1 Sigma)	Rel. Error [%] (1 Sigma)
Cu	29	41.27	36.81	12.67	1.07	2.59
C	6	35.36	31.54	57.42	6.51	18.40
Al	13	23.22	20.71	16.78	1.22	5.25
O	8	10.29	9.18	12.55	2.16	21.02
Zn	30	1.97	1.76	0.59	0.10	5.04
		112.11	100.00	100.00

13. Data Analysis

Within this research, the key effects of the heat pipe activity parameters are calculated, the variance analysis (ANOVA) performed, and optimum conditions based on the Taguchi method defined. As seen in Figure 8a–c, key effects are used for the heat pipe analyzing to analyze the impacts of each element. The experiment of the L9 is capable of computing the efficiency of the heat pipe (ANOVA-significant factor) using the observations effectiveness, rate of heat transfer, and overall heat transfer co-efficient of Table 6. CFD Analysis readings for 323 K are listed in Table 7, ANOVA responses and means results are given respectively in Table 8 and Table 9. CFD Analysis readings for 343 K are listed in Table 10, ANOVA responses and means results are given respectively in Table 11 and Table 12. CFD Analysis readings for 363 K are listed in Table 13, ANOVA responses and means results are given respectively in Table 14 and Table 15 in terms of effectiveness, rate of heat transfer, and overall coefficient of heat transfer and each of the values are observed.

Table 6. Experimental Design for L₉ Orthogonal Array.

No. of Test	Heat Input (K)	Mass Flow Rate (L/min)	Coating Thickness (µm)	Rate of Heat Transfer (kW)	SNRA	Effectiveness	SNRA	Overall Heat Transfer Coefficient (W m−2 K−1)	SNRA
1	323	0.15	50	3.14	9.94	15.60	23.86	270.45	48.64
2	323	0.30	80	5.02	14.01	24.96	27.94	459.29	53.24
3	323	0.45	100	6.27	15.95	31.19	29.88	598.52	55.54
4	343	0.15	80	11.70	21.36	29.11	29.28	1284.52	62.17
5	343	0.30	100	14.63	23.30	36.39	31.21	1687.8	64.54
6	343	0.45	50	7.32	17.29	18.20	25.20	746.82	57.46
7	363	0.15	100	22.99	27.23	38.13	31.62	2816.56	68.99
8	363	0.30	50	11.50	21.21	19.06	25.60	1238.11	61.85
9	363	0.45	80	18.39	25.29	30.50	29.68	2135.89	66.59

Table 7. CFD Analysis Reading for 323 K.

Coating Thickness	Mass Flow Rate	Heat Input (K)	Heat Output (Without Coating) (K)	Heat Output (With Coating) (K)
50	0.15	323	314.5623	311.6682
80		323		311.2169
100		323		310.4896
50	0.30	323	315.9843	312.1283
80		323		311.8257
100		323		311.2673
50	0.45	323	317.2348	312.2314
80		323		311.9846
100		323		311.4213

Table 8. Response Table for SNRA.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	13.30	19.51	16.15
2	20.65	19.51	20.22
3	24.58	19.51	22.16
Delta	11.28	0.00	6.01
Rank	1	3	2

Table 9. Table of responses for means.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	4.810	12.610	7.320
2	11.217	10.383	11.703
3	17.627	10.660	14.630
Delta	12.817	2.227	7.310
Rank	1	3	2

Table 10. CFD Analysis Reading for 343 K.

Coating Thickness	Mass Flow Rate	Heat Input (K)	Heat Output (Without Coating) (K)	Heat Output (With Coating) (K)
50	0.15	343	328.2653	324.1464
80		343		323.6230
100		343		321.7859
50	0.30	343	330.8934	325.1792
80		343		324.6932
100		343		323.9572
50	0.45	343	332.3284	325.8741
80		343		324.7642
100		343		323.1260

Table 11. Response Table for SNRA.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	27.23	28.26	24.89
2	28.57	28.26	28.97
3	28.97	28.26	30.91
Delta	1.74	0.00	6.02
Rank	1	3	2

Table 12. Table of responses for means.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	23.92	27.61	17.62
2	27.90	26.80	28.19
3	29.23	26.63	35.24
Delta	5.31	0.98	17.62
Rank	1	3	2

Table 13. CFD Analysis Reading for 363 K.

Coating Thickness	Mass Flow Rate	Heat Input (K)	Heat Output (Without Coating) (K)	Heat Output (With Coating) (K)
50	0.15	363	341.1494	339.1287
80		363		336.8967
100		363		333.9843
50	0.30	363	344.8634	340.1275
80		363		337.1278
100		363		334.9483
50	0.45	363	347.9631	341.4793
80		363		338.4752
100		363		336.6382

Table 14. Response Table for SNRA.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	52.48	59.94	55.99
2	61.40	59.88	60.67
3	65.81	59.87	63.03
Delta	13.34	0.07	7.04
Rank	1	3	2

Table 15. Table of responses for means.

Level	Heat Input	Mass Flow Rate	Coating Thickness
1	442.80	1457.20	751.8
2	1239.7	1128.4	1239.2
3	2063.5	1160.4	1701.00
Delta	1620.80	328.80	949.20
Rank	1	3	2

14. Results & Discussion

14.1. Case 1: (Heat Input = 323 K)

Based on the nine orthogonal cases of Table 2, simulation in CFD for the provided heat input 323 K and three different thicknesses for the coating and three various flow rates of fluid were performed in CFD.

The effect of the coating of each element at various conditions is seen in Figure 11, Figure 12, Figure 13 and Figure 14 They prove that, with all three parameters, the efficiency of nano-coated tubes improves the characteristics of heat transfer. In Table 7, it can be observed that 100 μm of maximum coating thickness yield is higher and a minimum mass flow rate of 0.15 L/min is fine. So, the difference between the heat output without coating and with coating is 4.073 K.

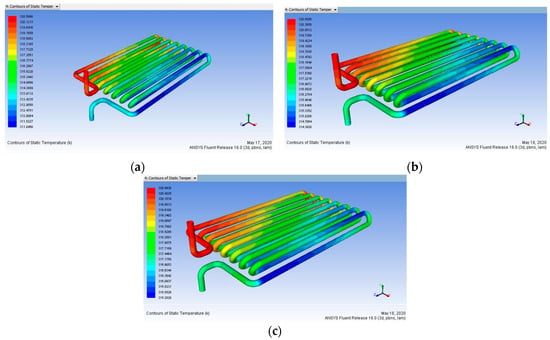
Figure 11. Heat input 323 K vs. mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (Before Coating).

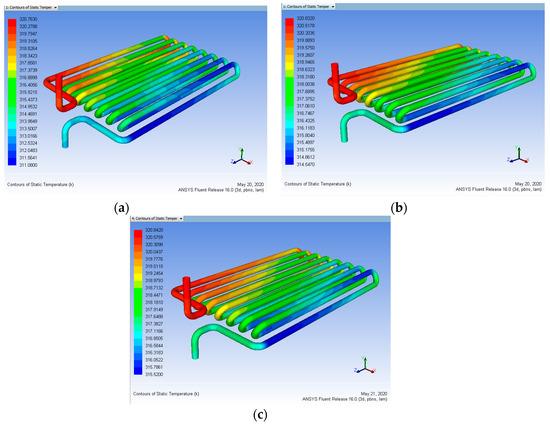
Figure 12. Heat input 323 K vs. Coating Thickness 50 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

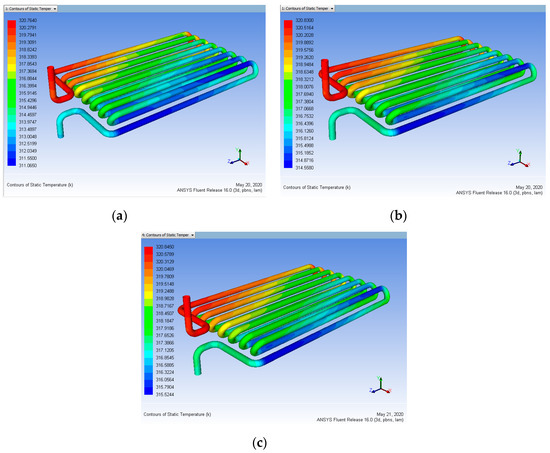
Figure 13. Heat input 323 K vs. Coating Thickness 80 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

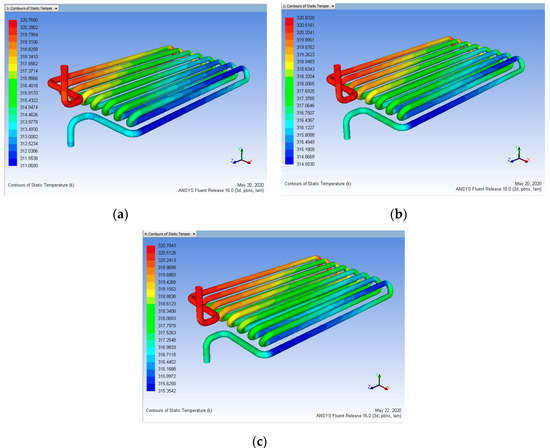
Figure 14. Heat input 323 K vs. Coating Thickness 100 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

The result of the main effects plot for means and SN ratios from each element to specific level conditions is seen in Figure 15. This indicates that for all three parameters, heat input, mass flow rate, and thickness of the coating. We observed that the overall coefficient of heat transfer and effectiveness of the nano-coated tubes is obviously increasing. The overall heat transfer and effectiveness are higher for 100 µm thickness and increases the overall heat transfer and effectiveness while the mass flow rate is 0.15 L/min.

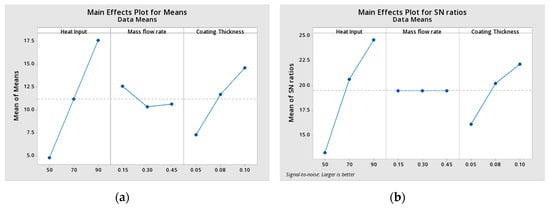
Figure 15. Taguchi Analysis for Rate of heat transfer Versus Heat Input, Mass Flow Rate and Coating Thickness. (a) Main Effects Plot for Means; (b) Main Effects Plot for SN ratios.

14.2. Case 2: (Heat Input = 343 K)

Based on the nine orthogonal cases of Table 2, simulation in CFD for the provided heat input 343 K and three different thicknesses for the coating and three various flow rates of fluid were performed in CFD.

The effect of the coating of each element at various conditions is seen in Figure 16, Figure 17, Figure 18 and Figure 19. They prove that, with all three parameters, the efficiency of nano-coated tubes improves the characteristics of heat transfer. In Table 10, we observe that 100 μm of maximum coating thickness yield is higher and a minimum mass flow rate of 0.15 L/min is fine. So, the difference between the heat output without coating and with coating is 6.478 K.

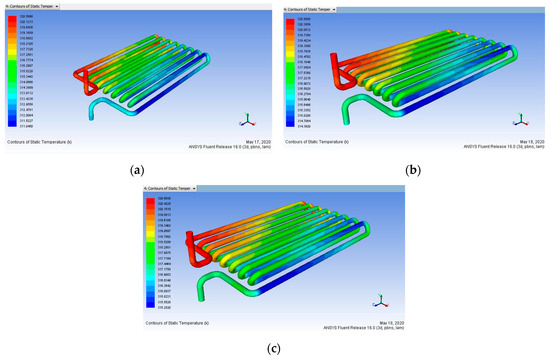
Figure 16. Heat input 343 K vs. mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (Before Coating).

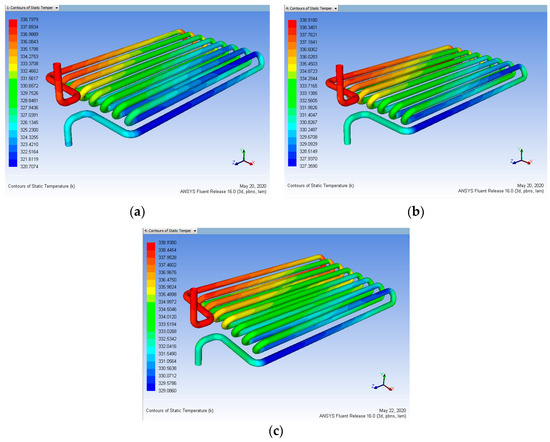
Figure 17. Heat input 343 K vs. Coating Thickness 50 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

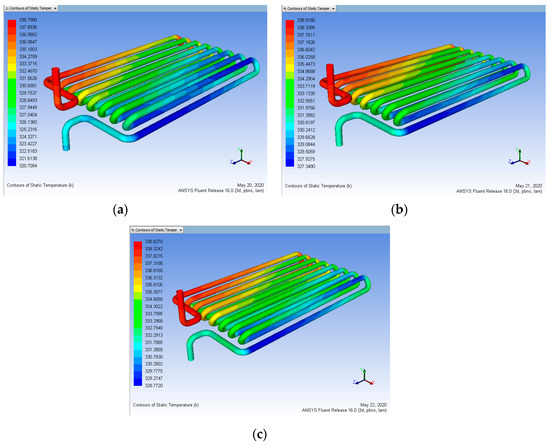
Figure 18. Heat input 343 K vs. Coating Thickness 80 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

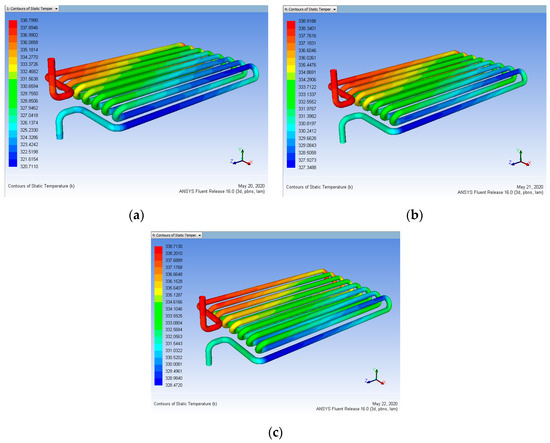
Figure 19. Heat input 343 K vs. Coating Thickness 100 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

The result of the main effects plot for means and SN ratios from each element to specific level conditions is seen in Figure 20. This indicates that, for all three parameters, namely heat input, mass flow rate, and thickness of the coating, we observed that the overall coefficient of heat transfer and effectiveness of the nano-coated tubes is obviously increasing. The overall heat transfer and effectiveness are higher for 100 µm thickness and increases the overall heat transfer and effectiveness while the mass flow rate is 0.15 L/min.

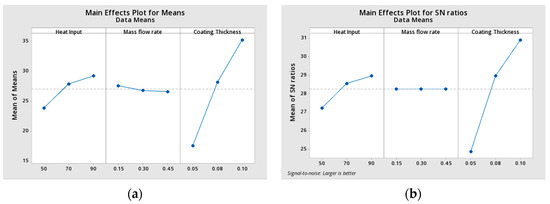
Figure 20. Taguchi Analysis for Effectiveness Versus Heat Input, Mass Flow Rate and Coating Thickness. (a) Main Effects Plot for Means; (b) Main Effects Plot for SN ratios.

14.3. Case 3: (Heat Input = 363 K)

Based on the nine orthogonal cases of Table 2, simulation in CFD for the provided heat input 363 K and three different thicknesses for the coating and three various flow rates of fluid were performed in CFD.

The effect of the coating of each element at various conditions is seen in Figure 21, Figure 22, Figure 23 and Figure 24. This proves that, with all three parameters, the efficiency of nano-coated tubes improves the characteristics of heat transfer. From Table 13, we observed that 100 μm of maximum coating thickness yield is higher and a minimum mass flow rate of 0.15 L/min is fine. So, the difference between the heat output without coating and with coating is 7.1651 K.

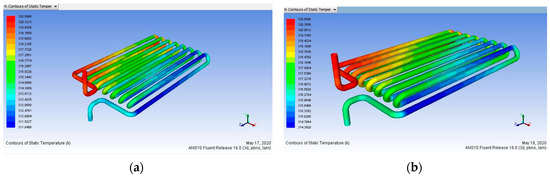
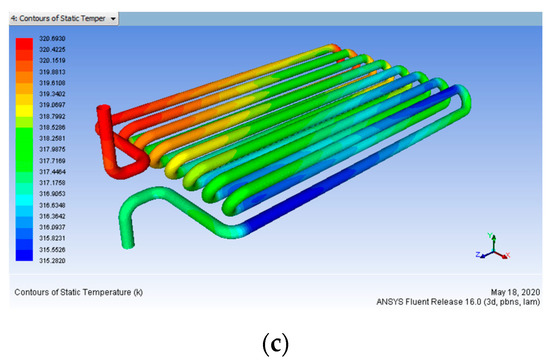
Figure 21. Heat input 363 K vs. mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (Before Coating).

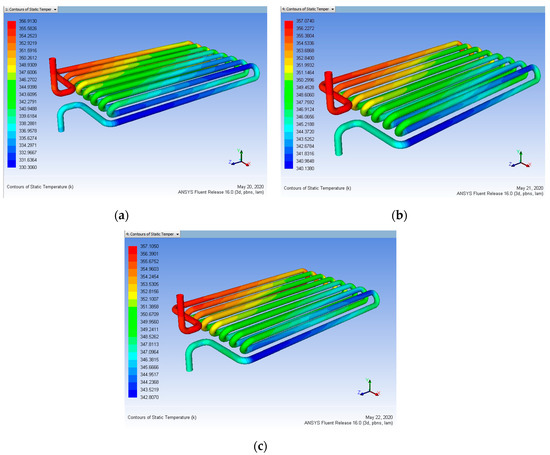
Figure 22. Heat input 363 K vs. Coating Thickness 50 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

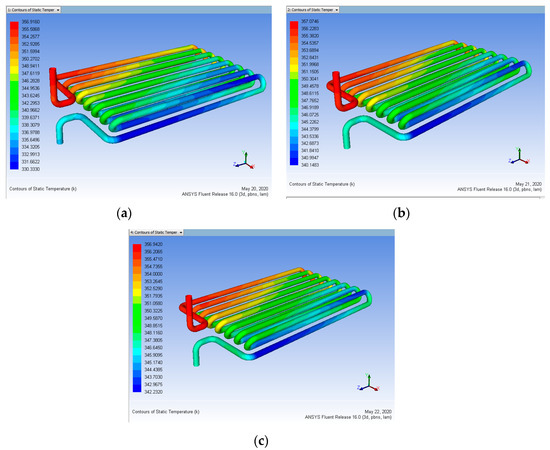
Figure 23. Heat input 363 K vs. Coating Thickness 80 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

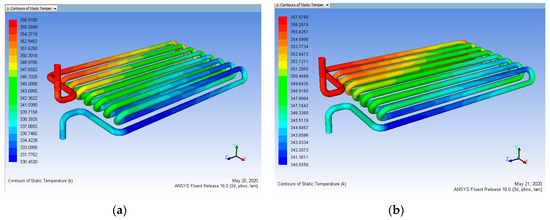
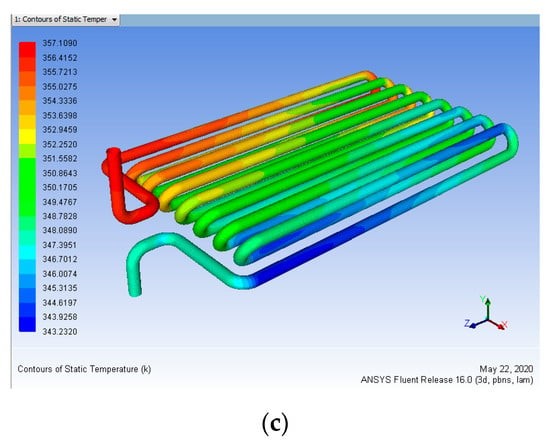
Figure 24. Heat input 363 K vs. Coating Thickness 100 µm for mass flow rate (a) 0.15, (b) 0.30, (c) 0.45 L/min (After Coating).

The result of the main effects plot for means and SN ratios from each element to specific level conditions is seen in Figure 25. This indicates that for all three parameters, heat input, mass flow rate, and thickness of the coating. We observed that the overall coefficient of heat transfer and effectiveness of the nano-coated tubes is obviously increasing. The overall heat transfer and effectiveness are higher for 100 µm thickness and increases the overall heat transfer while the mass flow rate is 0.15 L/min.

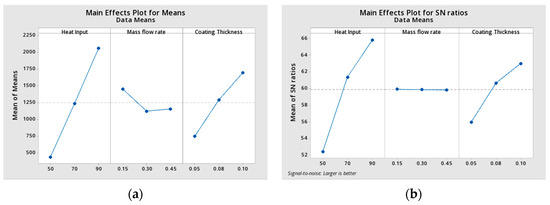
Figure 25. Taguchi Analysis for Overall heat transfer Versus Heat Input, Mass Flow Rate and Coating Thickness. (a) Main Effects Plot for Means; (b) Main Effects Plot for SN ratios.

15. Prediction of Optimum Results

Using the Taguchi methodology to determine ideal working parameters for nano-coated pipes, the measurements are carried out and the results are shown in Table 16.

Table 16. Measurements Results.

Heat Input	Mass Flow Rate	Coating Thickness	PSNRA	PMEANS
323	0.15	50	48.6098	154.40
323	0.30	80	53.2362	367.06
323	0.45	100	55.5790	806.80
343	0.15	80	62.2123	1492.80
343	0.30	100	64.5145	1571.75
343	0.45	50	57.4588	654.59
363	0.15	100	68.9889	2724.33
363	0.30	50	61.8926	1446.39
363	0.45	80	66.5596	2019.84

16. Conclusions

The findings for the monitoring of the nano-coated pipe efficiency after the tests are described as follows.

• The A1 B3 C2 of Taguchi analysis is found to be the optimum operating parameter level for temperature.
• 100 µm nano-coated pipes have higher heat transfer coefficients at all rates.
• For maximum temperature as heat input, 0.15 litre/min mass flow rate of coolant fluid conducted more heat.
• Optimal solutions using the Taguchi method provide better results for nano-coated pipes operations and the number of experiments required to find its efficiency metrics.
• Findings from experiments show that heat input, mass flow rate, and coating thickness play a significant role in the nano-coated pipe operations.

The design parameters of the Taguchi method and the CFD analysis are found to provide a simple, systematic, and efficient methodology for optimizing process parameters. The findings of ANOVA showed 95% confidence and were confirmed in the most significant parameters. The heat transfer efficiency of the radiator increases primarily due to the copper nano-coating on the aluminum core of the radiator. Through coating the copper particles on the aluminum tubes, the heat transfer properties of copper are accomplished by the heater core. Therefore, we can minimize the front portion of the vehicle by using a copper-coated aluminium tube radiator instead of a traditional aluminium radiator to cool the engine that produces high power to achieve maximum performance. The inner layer of aluminum has the same traditional properties and the outer layer of copper coating is free from rust and has less weight than the true copper alloy radiator.