Surface Plasmon Resonance Sensors Using Optical Vortices
Abstract
1. Introduction
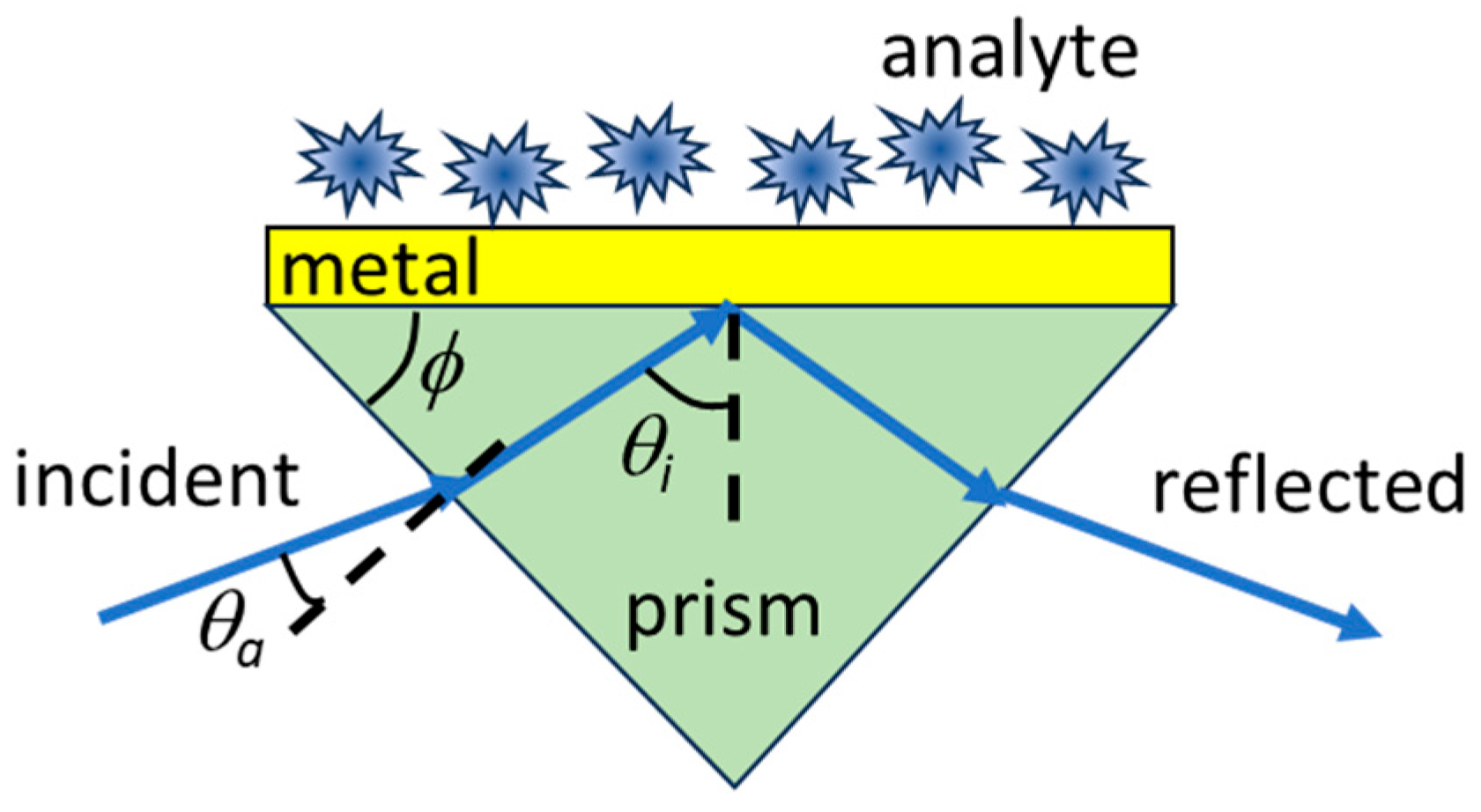
2. Methods: Reflectance of Optical Vortices from a Plane Surface
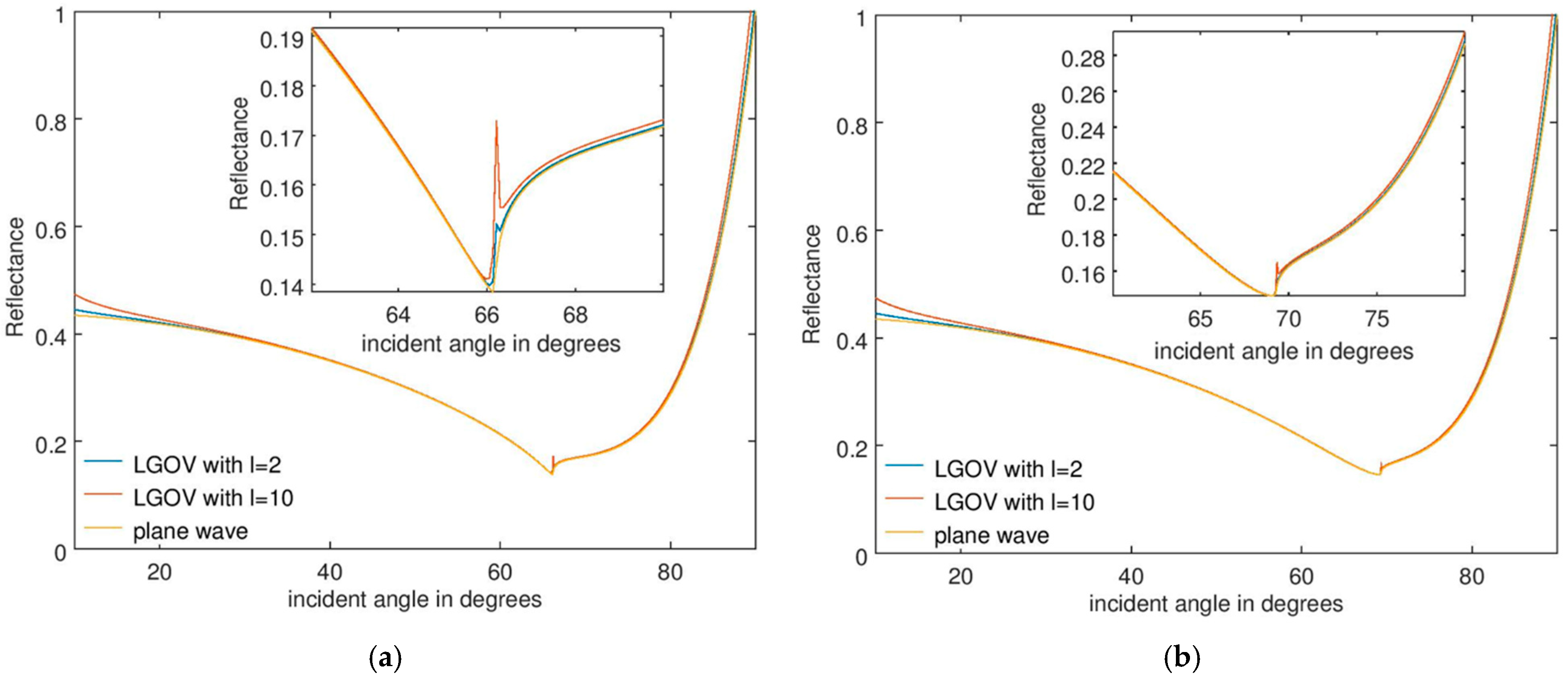
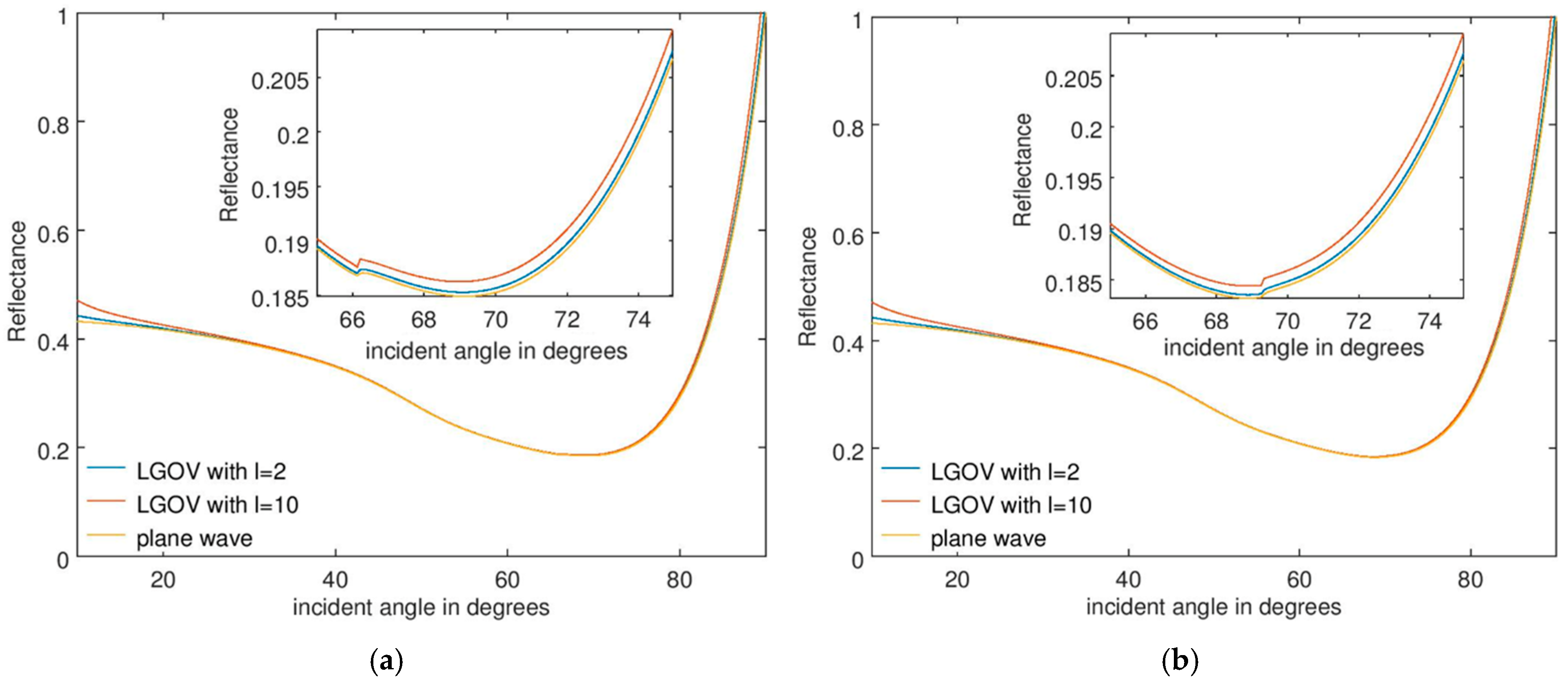
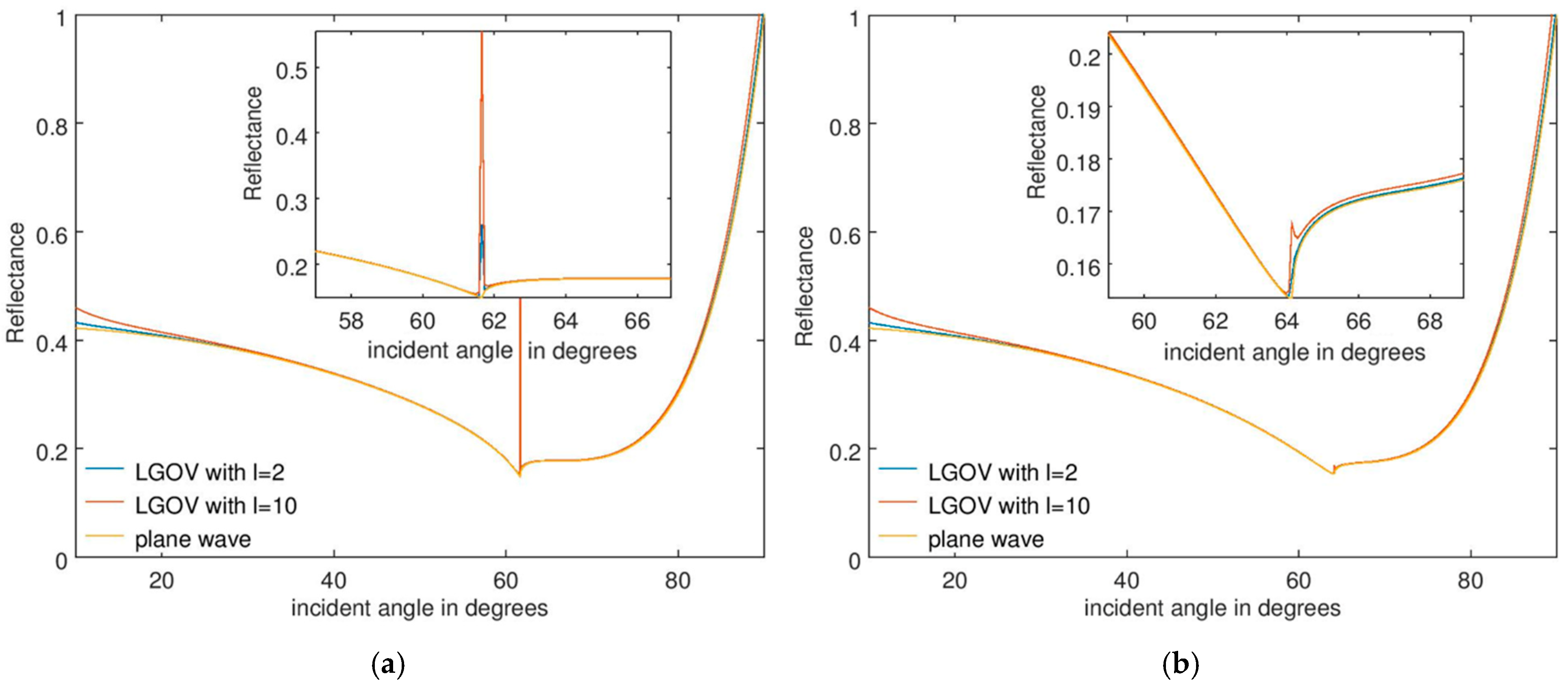
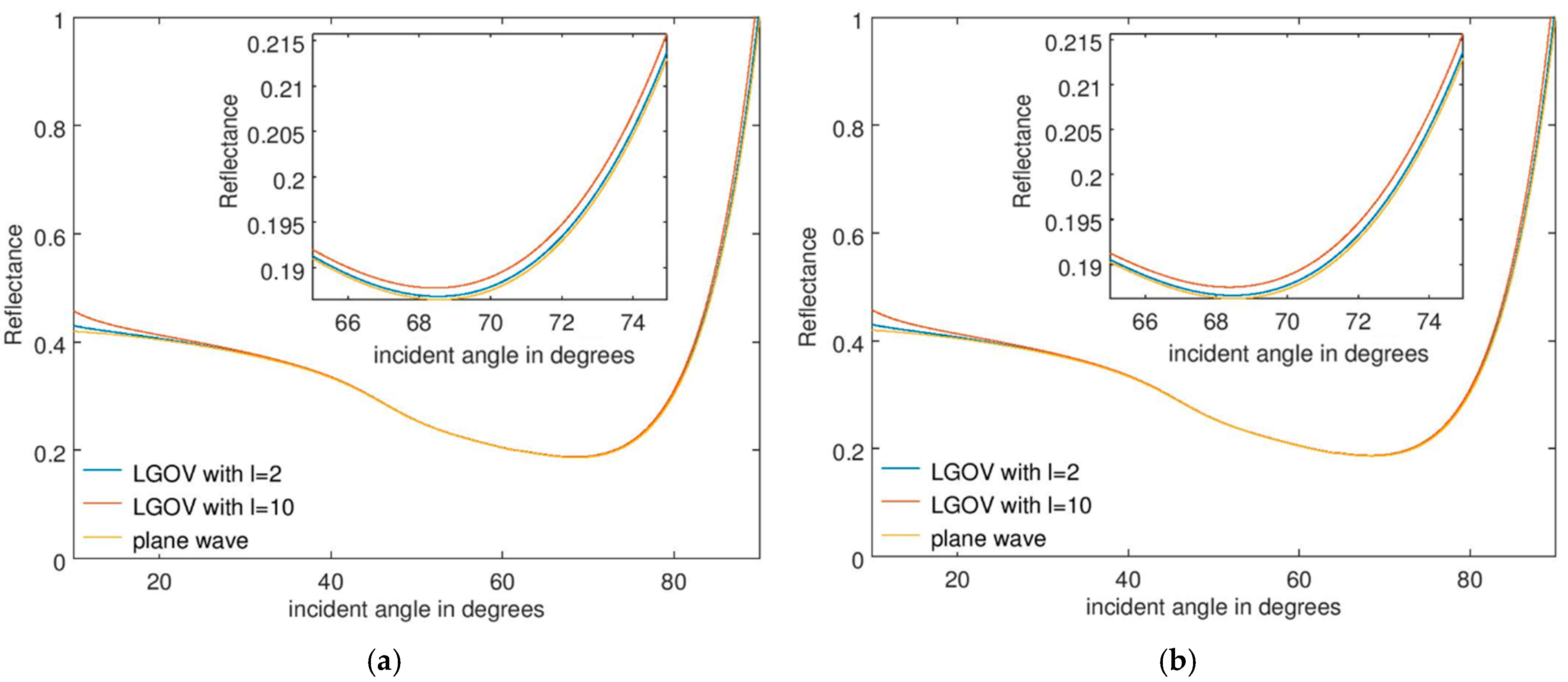
3. Results: Optical Vortices as Sources of SPR Sensors
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Bozhevolnyi, S.I. Plasmonic: Nanoguides and Circuits; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Tong, J.; Suo, F.; Ma, J.; Tobing, L.Y.M.; Qian, L.; Zhang, D.H. Surface plasmon enhanced infrared photodetection. Opto-Electron. Adv. 2019, 2, 180026. [Google Scholar] [CrossRef]
- Szunerits, S.; Boukherroub, R. Introduction to Plasmonics: Advances and Applications; Pan Stanford: New York, NY, USA, 2015. [Google Scholar]
- Panoiu, N.C.; Sha, W.E.I.; Lei, D.Y.; Li, G.-C. Nonlinear optics in plasmonic nanostructures. J. Opt. 2018, 20, 083001. [Google Scholar] [CrossRef]
- Ooi, K.J.A.; Chu, H.S.; Bai, P.; Ang, L.K. Electro-optical graphene plasmonic logic gates. Opt. Lett. 2014, 39, 1629–1632. [Google Scholar] [CrossRef]
- Vlădescu, E.; Dragoman, D. Reconfigurable plasmonic logic gates. Plasmonics 2018, 13, 2189–2195. [Google Scholar] [CrossRef]
- Dragoman, D.; Vlădescu, E. Ring-shaped plasmonic logic gates. Plasmonics 2019, 14, 71–78. [Google Scholar] [CrossRef]
- Denizli, A. Plasmonic Sensors and Their Applications; Wiley-VCH: Weinheim, Germany, 2021. [Google Scholar]
- Cho, S.H.; Choi, S.; Suh, J.M.; Jang, H.W. Advancements in surface plasmon resonance sensors for real-time detection of chemical analytes: Sensing materials and applications. J. Mater. Chem. C 2025, 13, 6484. [Google Scholar] [CrossRef]
- Gbur, G.J. Singular Optics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light: Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum; IoP Publishing: Bristol, UK, 2003. [Google Scholar]
- Zhao, N.; Li, X.; Li, G.; Kahn, J.M. Capacity limits of spatially multiplexed free-space communication. Nat. Photon. 2015, 9, 822–826. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Z.; Han, Y.; Hui, Y. Channel capacity of orbital-angular-momentum-based wireless communication systems with partially coherent elegant Laguerre–Gaussian beams in oceanic turbulence. J. Opt. Soc. Am. A 2019, 36, 471–477. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Karahroudi, M.K.; Moosavi, S.A.; Mobashery, A.; Parmoon, B.; Saghafifar, H. Performance evaluation of perfect optical vortices transmission in an underwater optical communication system. Appl. Opt. 2018, 57, 9148–9154. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.-M.; Zhu, L.; Wang, A.-D.; Chen, S.; Klitis, C.; Du, C.; Mo, Q.; Sorel, M.; Yu, S.-Y.; et al. Direct fiber vector eigenmode multiplexing transmission seeded by integrated optical vortex emitters. Light Sci. Appl. 2018, 7, 17148. [Google Scholar] [CrossRef]
- Harwit, M. Photon orbital angular momentum in astrophysics. Astrophys. J. 2003, 597, 1266–1270. [Google Scholar] [CrossRef]
- Torres, J.P.; Torner, L. Twisted Photons; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Popiołek-Masajada, A.; Masajada, J.; Kurzynowski, P. Analytical model of the optical vortex scanning microscope with a simple phase object. Photonics 2017, 4, 38. [Google Scholar] [CrossRef]
- Popiołek-Masajada, A.; Masajada, J.; Lamperska, W. Phase recovery with the optical vortex microscope. Meas. Sci. Technol. 2019, 30, 105202. [Google Scholar] [CrossRef]
- Cui, Z.; Hui, Y.; Ma, W.; Zhao, W.; Han, Y. Dynamical characteristics of Laguerre-Gaussian vortex beams upon reflection and refraction. J. Opt. Soc. Am. B 2020, 37, 3730–3740. [Google Scholar] [CrossRef]
- Prajapati, C.; Viswanathan, N.K. Observation of diffractive-correction and spin-orbit interaction induced effects around the Brewster angle. J. Opt. 2019, 21, 084002. [Google Scholar] [CrossRef]
- Gahagan, K.T.; Swartzlander, G.A., Jr. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914. [Google Scholar] [CrossRef]
- Simpson, N.B.; Allen, L.; Padgett, M.J. Optical tweezers and optical spanners with Laguerre-Gaussian modes. J. Mod. Opt. 1996, 43, 2485–2491. [Google Scholar] [CrossRef]
- Shen, Z.; Su, L.; Yuan, X.-C.; Shen, Y.-C. Trapping and rotating of a metallic particle trimer with optical vortex. Appl. Phys. Lett. 2016, 109, 241901. [Google Scholar] [CrossRef]
- Liaw, J.-W.; Chien, C.-W.; Liu, K.-C.; Ku, Y.-C.; Kuo, M.-K. 3D optical vortex trapping of plasmonic nanostructure. Sci. Rep. 2018, 8, 12673. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ren, Y.-X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Puiu, M.; Bala, C. SPR and SPR imaging: Recent trends in developing nanodevices for detection and real-time monitoring of biomolecular events. Sensors 2016, 16, 870. [Google Scholar] [CrossRef]
- Löfås, S.; McWhirter, A. The Art of Immobilization for SPR sensors. In Surface Plasmon Resonance Based Sensors; Homola, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 117–151. [Google Scholar]
- Georgiadis, R.; Peterlinz, K.P.; Peterson, A.W. Quantitative measurements and modeling of kinetics in nucleic acid monolayer films using SPR spectroscopy. J. Am. Chem. Soc. 2000, 122, 3166–3173. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Qiu, X.; Zhang, Z.; Xie, L.; Qiu, J.; Gao, F.; Du, J. Incident-polarization-sensitive and large in-plane photonic-spin-splitting at the Brewster angle. Opt. Lett. 2015, 40, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Kotlyar, V.V.; Kovalev, A.A.; Skidanov, R.V.; Moiseev, O.Y.; Soifer, V.A. Diffraction of a finite-radius plane wave and a Gaussian beam by a helical axicon and a spiral phase plate. J. Opt. Soc. Am. A 2007, 24, 1955–1964. [Google Scholar] [CrossRef]
- Tomlinson, W.J.; Gordon, J.P.; Smith, P.W.; Kaplan, A.E. Reflection of a Gaussian beam at a nonlinear interface. Appl. Opt. 1982, 21, 2041–2051. [Google Scholar] [CrossRef]
- New, G. Introduction to Nonlinear Optics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ritboon, A. The effect of astigmatism induced by refraction on the orbital angular momentum of light. J. Opt. 2020, 22, 075201. [Google Scholar] [CrossRef]
- Refractive Index Database. Available online: https://refractiveindex.info/ (accessed on 2 June 2025).
- Ou, J.; Jiang, Y.; Zhang, J.; He, Y. Reflection of Laguerre–Gaussian beams carrying orbital angular momentum: A full Taylor expanded solution. J. Opt. Soc. Am. A 2013, 30, 2561–2571. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulzan, G.A.; Dragoman, D. Surface Plasmon Resonance Sensors Using Optical Vortices. Nanomaterials 2025, 15, 877. https://doi.org/10.3390/nano15120877
Bulzan GA, Dragoman D. Surface Plasmon Resonance Sensors Using Optical Vortices. Nanomaterials. 2025; 15(12):877. https://doi.org/10.3390/nano15120877
Chicago/Turabian StyleBulzan, George A., and Daniela Dragoman. 2025. "Surface Plasmon Resonance Sensors Using Optical Vortices" Nanomaterials 15, no. 12: 877. https://doi.org/10.3390/nano15120877
APA StyleBulzan, G. A., & Dragoman, D. (2025). Surface Plasmon Resonance Sensors Using Optical Vortices. Nanomaterials, 15(12), 877. https://doi.org/10.3390/nano15120877







