Tunable Electronic Bandgaps and Optical and Magnetic Properties in Antiferromagnetic MPS3/GaN (M = Mn, Fe, and Ni) Heterobilayers
Abstract
1. Introduction
2. Computational Information
3. Results and Discussion
3.1. Structural Properties and Stability
3.2. Charge Analysis
3.3. Electronic Properties
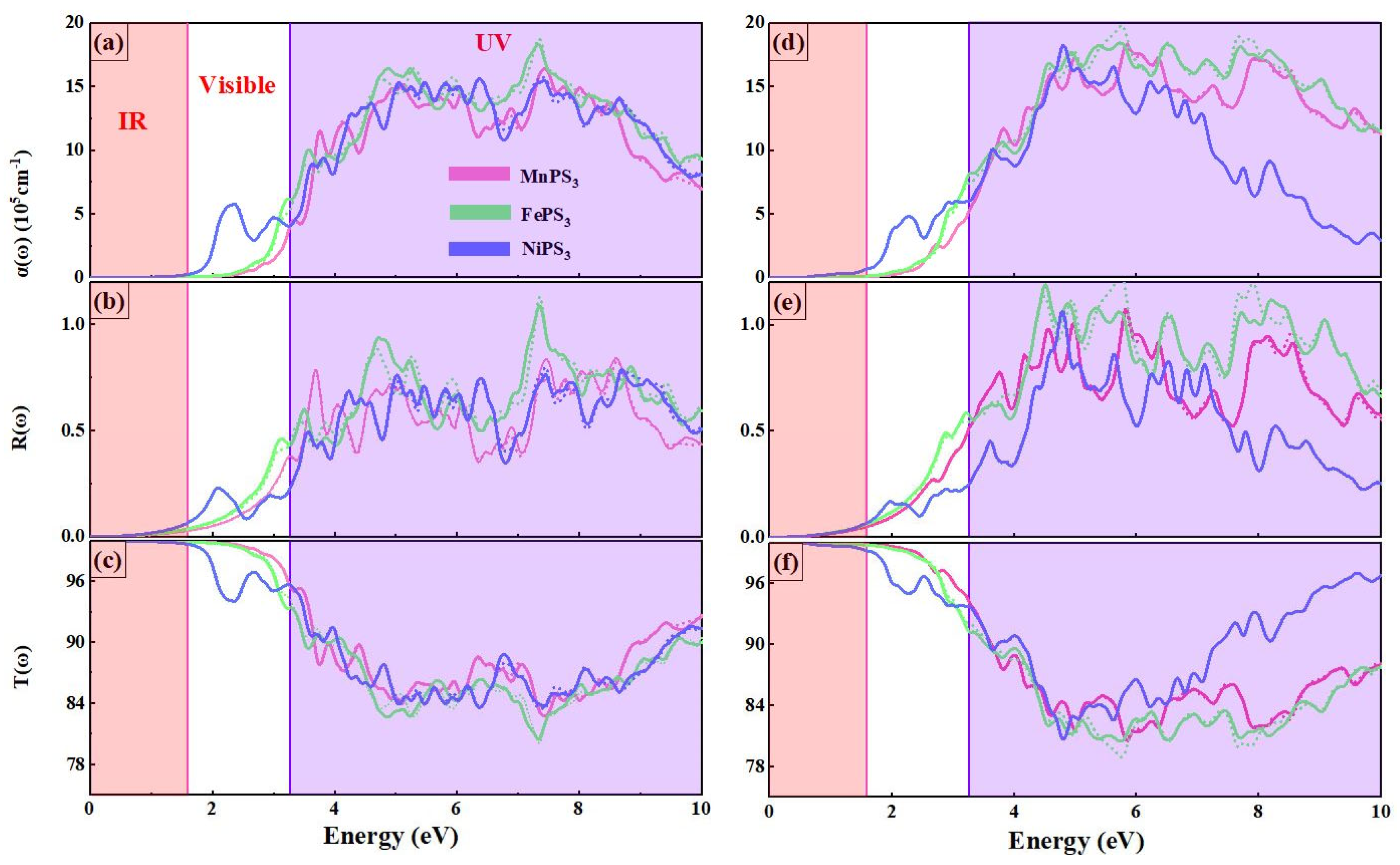
3.4. Optical Properties
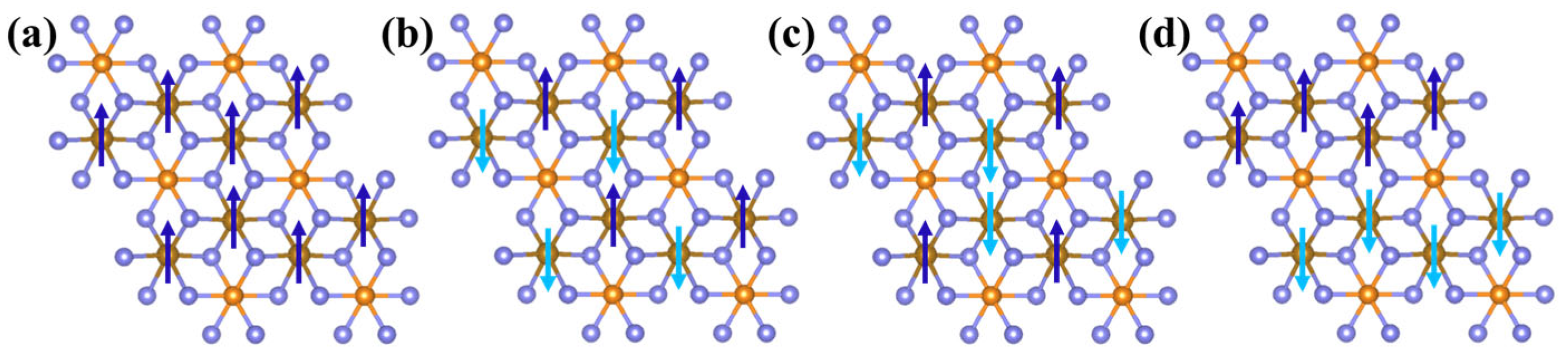
3.5. Magnetic Properties
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Ha, C.; Chung, Y.J. Thin films as practical quantum materials: A status quo and beyond. APL Mater. 2024, 12, 120901. [Google Scholar] [CrossRef]
- Boschker, H.; Mannhart, J. Quantum-Matter Heterostructures. Annu. Rev. Condens. Matter Phys. 2017, 8, 145–164. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals Heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of Intrinsic Ferromagnetism in Two-Dimensional van der Waals Crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Burch, K.S.; Mandrus, D.; Park, J.G. Magnetism in Two-Dimensional van der Waals Materials. Nature 2018, 563, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, P.; Tabrizian, R.; Feng, P.X.; Wu, Y. 2D Magnetic heterostructures: Spintronics and quantum future. NPJ Spintron. 2024, 2, 6. [Google Scholar] [CrossRef]
- Samarth, N. Magnetism in flatland. Nature 2017, 546, 216–217. [Google Scholar] [CrossRef]
- Ohno, H.; Chiba, D.; Matsukura, F.; Omiya, T.; Abe, E.; Dietl, T.; Ohno, Y.; Ohtani, K. Electric-field control of ferromagnetism. Nature 2000, 408, 944–946. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Kawakami, R.K.; Gmitra, M.; Fabian, J. Graphene spintronics. Nat. Nanotechnol. 2014, 9, 794–807. [Google Scholar] [CrossRef] [PubMed]
- Brec, R. Review on structural and chemical properties of transition metal phosphorous trisulfides MPS3. Solid State Ion. 1986, 22, 3–30. [Google Scholar] [CrossRef]
- Rule, K.C.; McIntyre, G.J.; Kennedy, S.J.; Hicks, T.J. Single-crystal and powder neutron diffraction experiments on FePS3: Search for the magnetic structure. Phys. Rev. B—Condens. Matter Mater. Phys. 2007, 76, 134402. [Google Scholar] [CrossRef]
- Susner, M.A.; Chyasnavichyus, M.; McGuire, M.A.; Ganesh, P.; Maksymovych, P. Metal Thio- and Selenophosphates as Multifunctional van der Waals Layered Materials. Adv. Mater. 2017, 29, 1602852. [Google Scholar] [CrossRef] [PubMed]
- Rahman, S.; Torres, J.F.; Khan, A.R.; Lu, Y. Recent Developments in van der Waals Antiferromagnetic 2D Materials: Synthesis, Characterization, and Device Implementation. ACS Nano 2021, 15, 17175–17213. [Google Scholar] [CrossRef]
- Joy, P.A.; Vasudevan, S. Magnetism in the layered transition-metal thiophosphates MPS3 (M = Mn, Fe, and Ni). Phys. Rev. B 1992, 46, 5425–5433. [Google Scholar] [CrossRef]
- Kim, H.-S.; Haule, K.; Vanderbilt, D. Mott Metal-Insulator Transitions in Pressurized Layered Trichalcogenides. Phys. Rev. Lett. 2019, 123, 236401. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kim, T.Y.; Sandilands, L.J.; Sinn, S.; Lee, M.-C.; Son, J.; Lee, S.; Choi, K.-Y.; Kim, W.; Park, B.-G.; et al. Charge-Spin Correlation in van der Waals Antiferromagnet NiPS3. Phys. Rev. Lett. 2018, 120, 136402. [Google Scholar] [CrossRef]
- Li, Y.; Wu, X.; Gu, Y.; Le, C.; Qin, S.; Thomale, R.; Hu, J. Topological superconductivity in Ni-based transition metal trichalcogenides. Phys. Rev. B 2019, 100, 214513. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Castro Neto, A.H. 2D materials and van der Waals heterostructure. Science 2016, 353, aac9439. [Google Scholar] [CrossRef]
- Meftakhutdinov, R.M.; Sibatov, R.T.; Kochaev, A.I.; Evseev, D.A. First-principles study of graphenylene/MoX2 (X = S, Te, and Se) van der Waals heterostructures. Phys. Chem. Chem. Phys. 2021, 23, 14315–14324. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.Q.; Wu, Q.; Ang, L.K.; Ang, Y.S. Tunable electronic properties and band alignments of MoSi2N4/GaN and MoSi2N4/ZnO van der Waals heterostructures. Appl. Phys. Lett. 2022, 120, 103101. [Google Scholar] [CrossRef]
- Peng, B.; Xu, L.; Zeng, J.; Qi, X.; Yang, Y.; Ma, Z.; Huang, X.; Wang, L.-L.; Shuai, C. Layer-dependent photocatalysts of GaN/SiC-based multilayer van der Waals heterojunctions for hydrogen evolution. Catal. Sci. Technol. 2021, 11, 3059–3069. [Google Scholar] [CrossRef]
- Rehman, G.; Khan, S.A.; Amin, B.; Ahmad, I.; Gan, L.-Y.; Maqbool, M. Intriguing electronic structures and optical properties of two-dimensional van der Waals heterostructures of Zr2CT2 (T = O, F) with MoSe2 and WSe2. J. Mater. Chem. C 2018, 6, 2830–2839. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, W. Tunable Band Alignments in 2D Ferroelectric α-In2Se3 Based Van der Waals Heterostructures. ACS Appl. Electron. Mater. 2021, 3, 5114–5123. [Google Scholar] [CrossRef]
- Yuan, H.; Su, J.; Zhang, S.; Di, J.; Lin, Z.; Zhang, J.; Zhang, J.; Chang, J.; Hao, Y. Interfacial transport modulation by intrinsic potential difference of janus TMDs based on CsPbI3/J-TMDs heterojunctions. Iscience 2022, 25, 103872. [Google Scholar] [CrossRef]
- Zhang, M.; Si, R.; Wu, X.; Dong, Y.; Fu, K.; Xu, X.; Zhang, J.; Li, L.; Guo, Y. Two-dimensional Hf2CO2/GaN van der Waals heterostructure for overall water splitting: A density functional theory study. J. Mater. Sci. Mater. 2021, 32, 19368–19379. [Google Scholar] [CrossRef]
- Zhou, B.; Gong, S.J.; Jiang, K.; Xu, L.; Zhu, L.; Shang, L.; Li, Y.; Hu, Z.; Chu, J. Ferroelectric and dipole control of band alignment in the two dimensional InTe/In2Se3 heterostructure. J. Phys. Condens. Matter. 2020, 32, 055703. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, K.; Shang, L.; Zhang, J.; Li, Y.; Zhu, L.; Gong, S.-J.; Hu, Z.; Chu, J. Enhanced carrier separation in ferroelectric In2Se3/MoS2 van der Waals heterostructures. J. Mater. Chem. C 2020, 8, 11160–11167. [Google Scholar]
- Zhu, J.; Ning, J.; Wang, D.; Zhang, J.; Guo, L.; Hao, Y. Tunable band offset in black Phosphorus/ReS2 van der Waals heterostructure with robust direct band and inherent anisotropy. Superlattices Microstruct. 2019, 129, 274–281. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Setyawan, W.; Gaume, R.M.; Lam, S.; Feigelson, R.S.; Curtarolo, S. High-throughput combinatorial database of electronic band structures for inorganic scintillator materials. ACS Comb. Sci. 2011, 13, 382–390. [Google Scholar] [CrossRef]
- Wu, R.; Freeman, A.J. Spin–orbit induced magnetic phenomena in bulk metals and their surfaces and interfaces. J. Magn. Magn. Mater. 1999, 200, 498–514. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, L.; Liang, Y.; Xie, R.; Hna, L.; Lan, S.; Lu, A.; Huang, Y.; Xing, H.; Chen, X. Room Temperature Ferromagnetic Properties of Ga14N16-nGd2Cn Monolayers: A First Principle Study. Crystals 2023, 13, 531. [Google Scholar] [CrossRef]
- Attia, A.A.; Jappor, H.R. Tunable electronic and optical properties of new two-dimensional GaN/Bas van der Waals heterostructures with the potential for photovoltaic applications. Chem. Phys. Lett. 2019, 728, 124–131. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, F.; Yuan, B.; Xiao, S.; Kuang, A.; Zhong, M.; Dang, S.; Long, X.; Zhang, W. Strain-Tunable Visible-Light-Responsive Photocatalytic Properties of Two-Dimensional CdS/g-C3N4: A Hybrid Density Functional Study. Nanomaterials 2019, 9, 244. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, R.; Wang, D.-s.; Freeman, A.J. Torque method for the theoretical determination of magnetocrystalline anisotropy. Phys. Rev. B 1996, 54, 61. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.M.; Movlarooy, T.; Kompany, A. First-principles study of the optical properties of PbTiO3. Eur. Phys. J. B-Condens. Matter Complex Syst. 2005, 46, 463–469. [Google Scholar] [CrossRef]
- Milman, V.; Warren, M.C. Elastic properties of TiB2 and MgB2. J. Phys. Condens. Matter 2001, 13, 5585. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
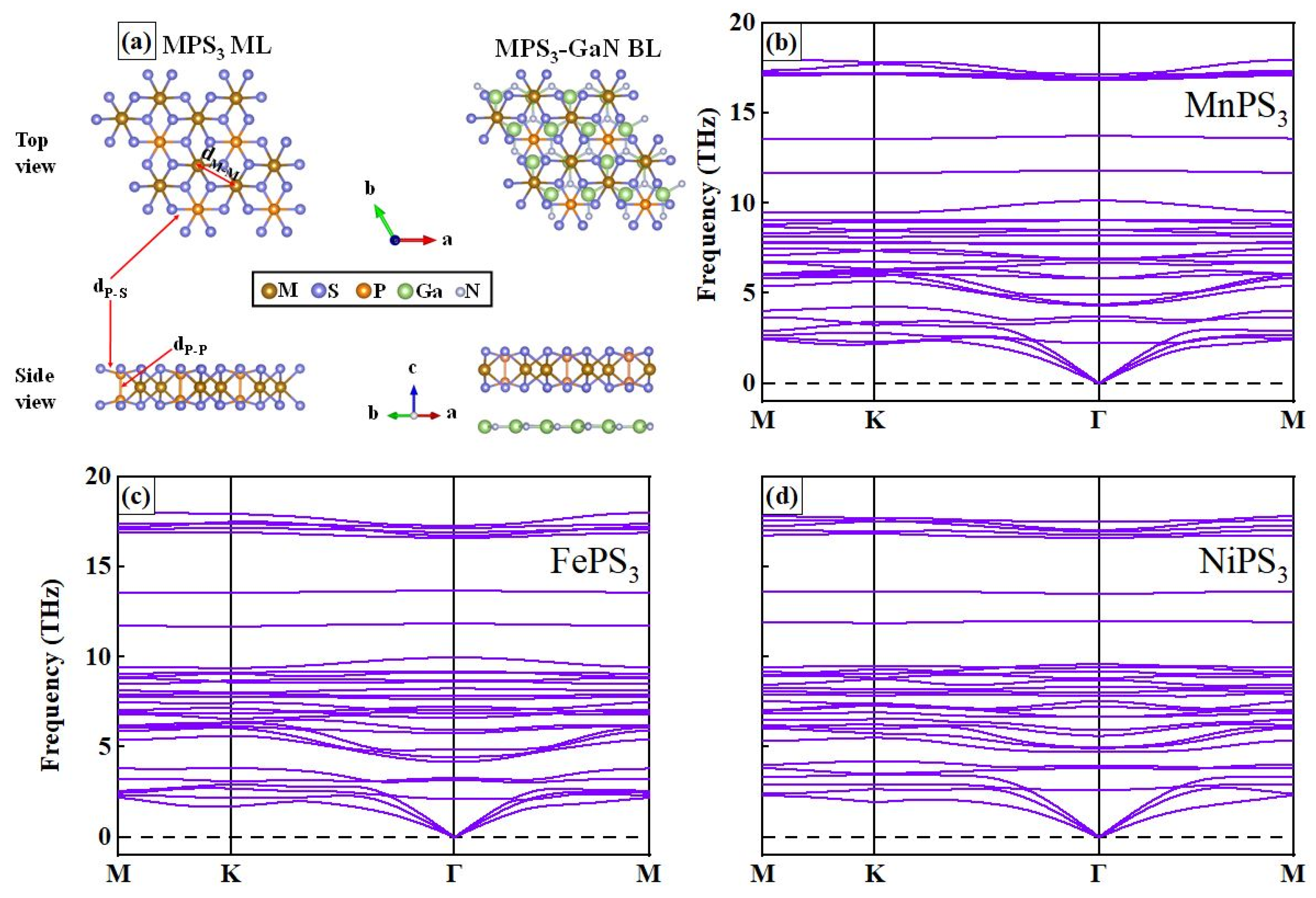
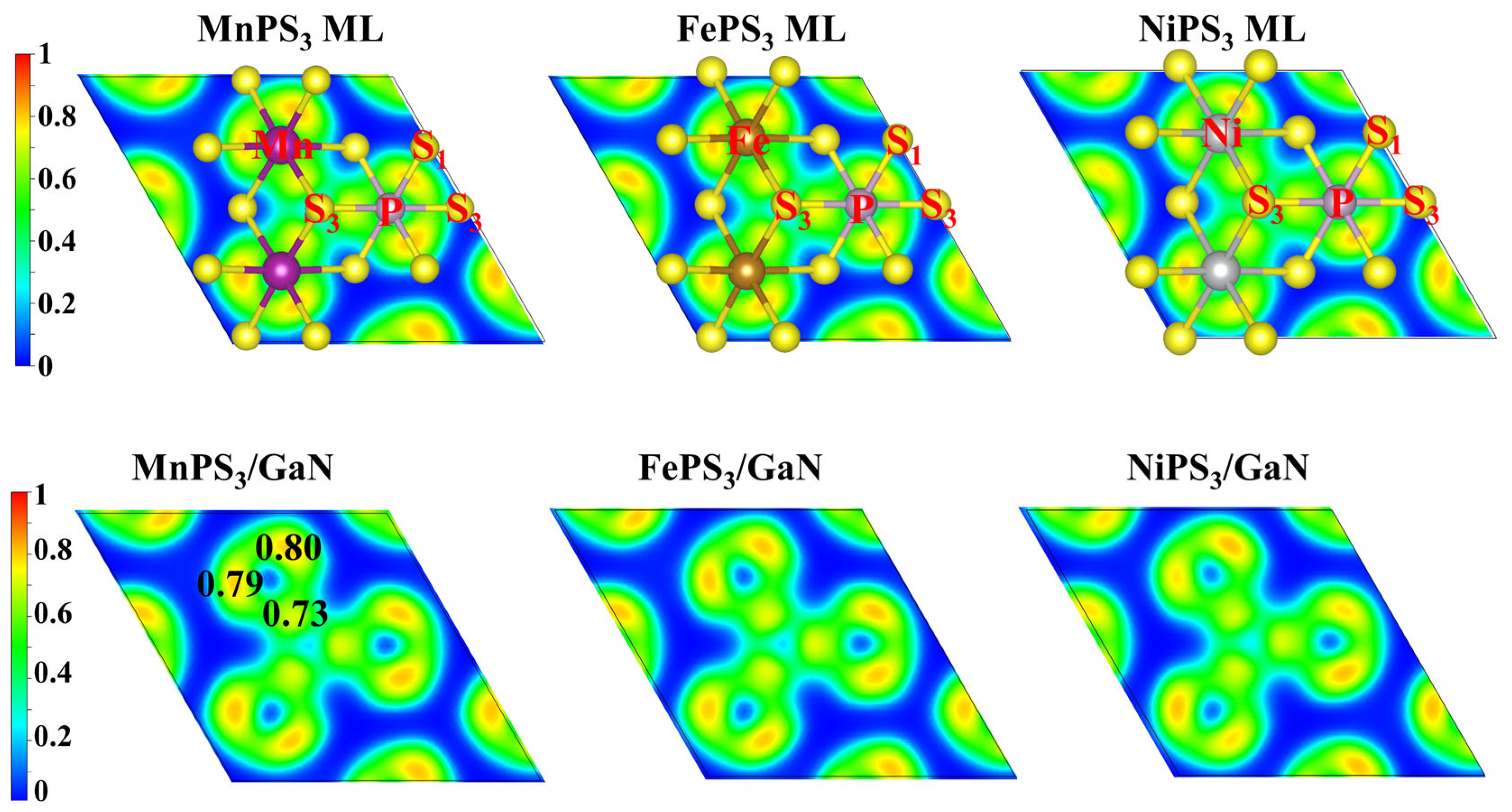
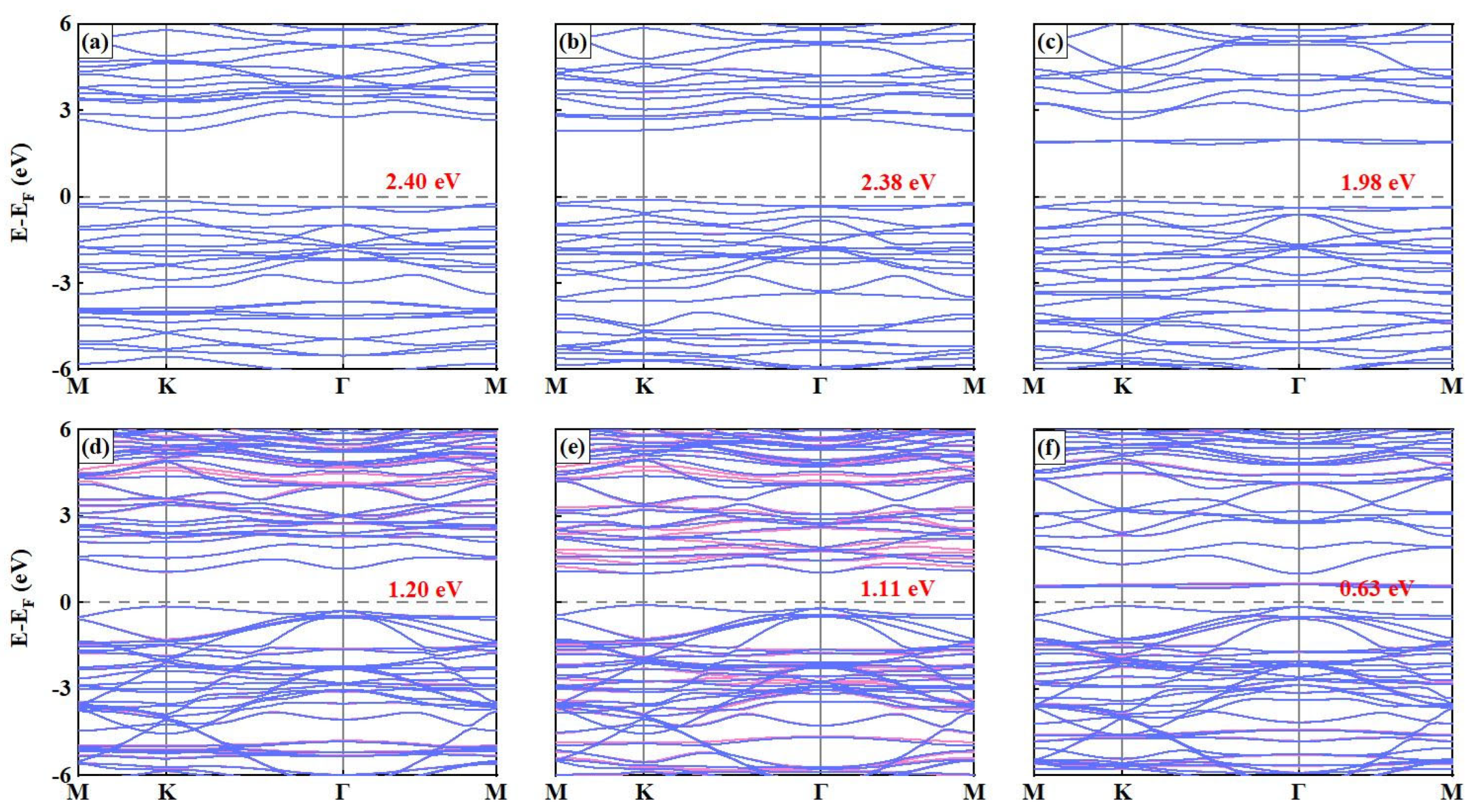
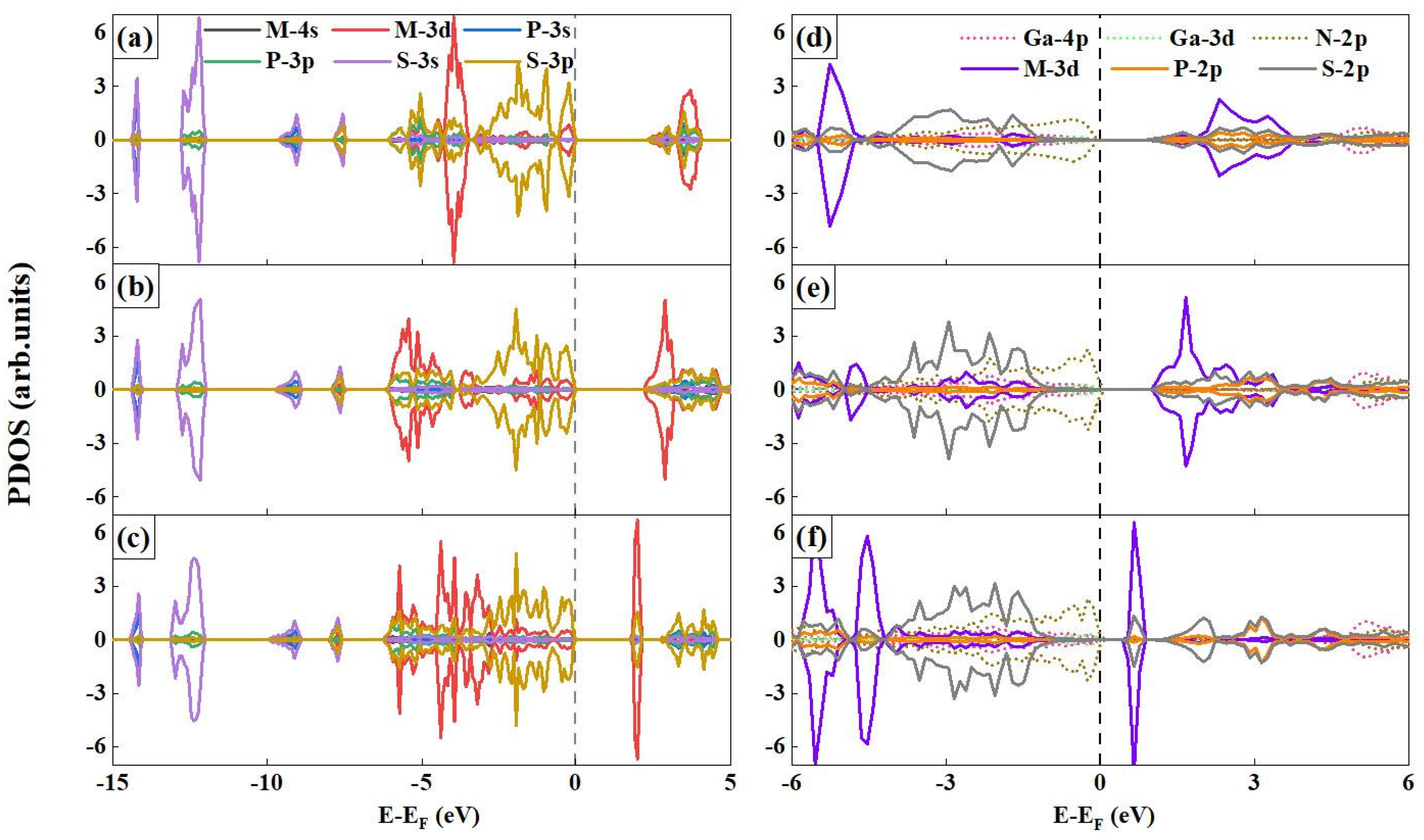
| Lattice Parameters (Å) | Bond Length (Å) | CT (|e|) | △E (meV) | E b(eV) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | dM-M | dP-S | dP-P | M | P | S | |||
| MPS3 MLs | ||||||||||
| MnPS3 | 6.13 | 6.13 | 3.54 | 2.04 | 2.21 | −1.191 | −0.979 | 0.723 | −59.57 | − |
| FePS3 | 6.00 | 6.03 | 3.42 | 2.05 | 2.20 | −1.065 | −0.970 | 0.678 | −52.51 | − |
| NiPS3 | 5.89 | 5.89 | 3.39 | 2.04 | 2.18 | −0.775 | 0.975 | 0.583 | −55.21 | − |
| vdWH BLs | ||||||||||
| MnPS3 | 6.31 | 6.31 | 3.65 | 2.05 | 2.19 | −1.226 | −0.952 | 0.731 | −44.81 | −0.566 |
| FePS3 | 6.27 | 6.27 | 3.59 | 2.06 | 2.18 | −1.085 | −0.927 | 0.676 | −17.44 | −0.571 |
| NiPS3 | 6.24 | 6.23 | 3.60 | 2.07 | 2.16 | −0.825 | −0.895 | 0.580 | −25.91 | −0.591 |
| MPS3 MLs | vdWHs | |||||
|---|---|---|---|---|---|---|
| M | Mn | Fe | Ni | Mn | Fe | Ni |
| △E-N (meV) | −279.73 | −165.96 | −238.98 | −152.81 | −68.56 | −162.27 |
| △E-S (meV) | −158.15 | −40.30 | 59.49 | −26.84 | −34.16 | 41.95 |
| △E-Z (meV) | −166.25 | −191.88 | −281.39 | −102.59 | −90.39 | −178.82 |
| MM () | 4.541 | 3.659 | 1.489 | 4.586 | 3.677 | 1.564 |
| MM-d () | 4.479 | 3.611 | 1.487 | 4.524 | 3.627 | 1.558 |
| MAE (meV) | −0.33 | 10.14 | −1.33 | −0.34 | −3.59 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Han, L.; Zhang, L.; Zhang, K.; Jiang, M.; Wang, J.; Lan, S.; Lv, X.; Zhang, Y.; Lu, A.; et al. Tunable Electronic Bandgaps and Optical and Magnetic Properties in Antiferromagnetic MPS3/GaN (M = Mn, Fe, and Ni) Heterobilayers. Nanomaterials 2025, 15, 832. https://doi.org/10.3390/nano15110832
Tian S, Han L, Zhang L, Zhang K, Jiang M, Wang J, Lan S, Lv X, Zhang Y, Lu A, et al. Tunable Electronic Bandgaps and Optical and Magnetic Properties in Antiferromagnetic MPS3/GaN (M = Mn, Fe, and Ni) Heterobilayers. Nanomaterials. 2025; 15(11):832. https://doi.org/10.3390/nano15110832
Chicago/Turabian StyleTian, Shijian, Li Han, Libo Zhang, Kaixuan Zhang, Mengjie Jiang, Jie Wang, Shiqi Lan, Xuyang Lv, Yichong Zhang, Aijiang Lu, and et al. 2025. "Tunable Electronic Bandgaps and Optical and Magnetic Properties in Antiferromagnetic MPS3/GaN (M = Mn, Fe, and Ni) Heterobilayers" Nanomaterials 15, no. 11: 832. https://doi.org/10.3390/nano15110832
APA StyleTian, S., Han, L., Zhang, L., Zhang, K., Jiang, M., Wang, J., Lan, S., Lv, X., Zhang, Y., Lu, A., Huang, Y., Xing, H., & Chen, X. (2025). Tunable Electronic Bandgaps and Optical and Magnetic Properties in Antiferromagnetic MPS3/GaN (M = Mn, Fe, and Ni) Heterobilayers. Nanomaterials, 15(11), 832. https://doi.org/10.3390/nano15110832






