Experimental Analysis of Hyperparameters for Deep Learning-Based Churn Prediction in the Banking Sector

Abstract

Until recently, traditional machine learning techniques (TMLTs) such as multilayer perceptrons (MLPs) and support vector machines (SVMs) have been used successfully for churn prediction, but with significant efforts expended on the configuration of the training parameters. The selection of the right training parameters for supervised learning is almost always experimentally determined in an ad hoc manner. Deep neural networks (DNNs) have shown significant predictive strength over TMLTs when used for churn predictions. However, the more complex architecture of DNNs and their capacity to process huge amounts of non-linear input data demand more time and effort to configure the training hyperparameters for DNNs during churn modeling. This makes the process more challenging for inexperienced machine learning practitioners and researchers. So far, limited research has been done to establish the effects of different hyperparameters on the performance of DNNs during churn prediction. There is a lack of empirically derived heuristic knowledge to guide the selection of hyperparameters when DNNs are used for churn modeling. This paper presents an experimental analysis of the effects of different hyperparameters when DNNs are used for churn prediction in the banking sector. The results from three experiments revealed that the deep neural network (DNN) model performed better than the MLP when a rectifier function was used for activation in the hidden layers and a sigmoid function was used in the output layer. The performance of the DNN was better when the batch size was smaller than the size of the test set data, while the RemsProp training algorithm had better accuracy when compared with the stochastic gradient descent (SGD), Adam, AdaGrad, Adadelta, and AdaMax algorithms. The study provides heuristic knowledge that could guide researchers and practitioners in machine learning-based churn prediction from the tabular data for customer relationship management in the banking sector when DNNs are used.

1. Introduction

Competitive customer-dependent organizations, such as those in the banking industry, are some of the most affected sectors by the free market economy, which allow service providers to compete against one another for the attention of customers [1]. Given that customers are the most valuable assets that have a direct impact on the revenue of the banking industry, customer churn is a source of major concern for service organizations [2]. It is therefore an important basic requirement that banks have good knowledge of customers’ data, find factors that increase customer churn and take the necessary actions to reduce it [2,3]. The advancement of technology in the last few decades has made it possible for banks and many other service organizations to collect and store data about their customers and classify them into either the churner or non-churner categories. Data by themselves do not have much value if they are not studied to reveal the information contained in them. To find valuable information from data, a process called data mining is applied [4]. Machine learning, a subset of data mining, allows organizations to study customers’ behaviors, including churn [5]. According to [6] and [7], churn describes a state where a customer unsubscribes or leaves an organization for its competitor, thereby leading to a loss in revenue and profit. Researchers and customer-dependent organizations have identified the need to study patterns and trends in data and draw conclusions from them, predicting whether or not a customer is a potential churner [8]. This vital knowledge enables banks to stay relevant and retain customers by adopting loyalty programs that increase customer satisfaction [9].

Given the importance of customers and the higher costs of attracting new customers compared with retaining existing ones, banks and other customer-dependent industries must be able to automate the process of predicting the behaviors of their customers using customers’ data in their database. Customer churn poses a serious concern for banks because it causes revenue loss for the industry. For this reason, banks would love to identify customers with the highest likelihoods to unsubscribe from their services. Churn prediction enables the use of customers’ transaction profiles to determine the likelihood of a customer abandoning a service.

Lately, deep neural networks (DNNs) have been used for churn prediction, but the process of selecting the training hyperparameters for churn modeling requires more time and effort, which could make the process more challenging for practitioners and researchers [10]. Few researchers have focused on determining the effects that different hyperparameters have on the performance of DNNs during churn prediction. Thus, there is an insufficient empirical basis for understanding the influences of different hyperparameters on the performance of DNNs when they are used for churn prediction. Due to this gap, empirically derived heuristic knowledge that can guide the selection of hyperparameters when DNNs are used for churn modeling is still lacking.

This study presents an experimental analysis of the impact of different hyperparameters when a feedforward deep neural network (DNN) is used for the prediction of customer churn in banks from tabular data. This study focuses on training the DNN with supervised learning techniques to test its accuracy before tuning its hyperparameters by experimenting with multiple classifier parameters.

The study seeks to answer the following research question: How do different parameters affect the performance of a deep neural network churn model for the banking sector? The objectives of the study are to determine the effects that various configurations of the monotonic activation function have on the training of a deep neural network (DNN) churn model for the banking sector (RO1); to determine the effect of different batch sizes in the training of a DNN churn model in the banking sector (RO2); and to evaluate the performance of different training algorithms with varied training parameters during churn modeling with a DNN (RO3).

Previous studies on the topic of churn prediction and churn modeling in the banking sector have not paid attention to the impact that the tuning of specific hyperparameters could have on the performance of deep neural networks when they are used for this application. The most recent systematic literature review papers on the topics of deep learning methods in banking and churn prediction in banking attest to this [11,12]. Therefore, relative to previous studies in terms of contributions, our work provides a basis for understanding the effect of different non-periodic and monotonic activation functions used for churn modeling in banking with a DNN. It also provides a basis for understanding the effects of different batch sizes on the performance of a DNN when used for churn modeling in banking. Lastly, it would enable the derivation of empirically based heuristics that can guide the selection of hyperparameters when DNNs are used for churn modeling in banking.

The remainder of the paper is structured as follows. Section 2 provides an overview of related works on churn prediction in the banking industry that are based on the use of traditional machine learning and deep learning methods. Section 3 describes the methodology adopted by the study. Section 4 presents the results from the experiments and discusses the results. The paper concludes in Section 5 with a brief note and an outlook of future research directions.

2. Background and Related Work

This section presents background on churn management in the banking sector and an overview of related works on traditional machine learning methods and deep learning methods for churn management in the banking sector.

2.1. Churn Management in the Banking Sector

Customer churn in the banking domain describes a lost customer who unsubscribes from a bank service and subscribes to another bank. Customer churn happens for several reasons. For instance, the authors in [7] noted that if an account with a bank was created for a specific purpose, the customer was likely to close it after achieving said purpose. Customer churn also happens if a customer is dissatisfied with a bank’s service or is relocating or moving to another location. Banks and other financial institutions keep a regular check on their customers’ transactions to detect common warning signs in a customer’s behavior before churn happens. Such behaviors, according to [13], include a reduction in the volume of transactions and dormancy of accounts. Churn management has become part of customer relationship management (CRM) because of the serious challenge of customer churn in the banking sector [7]. Churn management emphasizes the need for banks to take steps to prevent or minimize customer churn through several customer retention programs [14]. This also helps to establish long-term relationships with customers and maximize the value of their customer base [15].

Banks are affected by valuable customers who leave their services and take their investment or capital to competitors [16]. By keeping regular checks on customers’ transaction statuses, banks generate a huge amount of data, which makes it difficult for them to compute and obtain meaningful knowledge from it using traditional statistical methods [17,18]. This necessitated the development of powerful algorithms that use machine learning techniques to discover hidden patterns and predict behaviors and the likelihood of a customer unsubscribing from an organization’s services [4]. A host of studies have noted that it is more expensive to acquire new customers than spend to retain existing ones [7,16]. According to [19], it is 16 times more expensive to transform a new customer to a profitable customer than to retain a valuable one. Again, reducing the churn rate by 5% potentially increases profitability by 25–85%. Therefore, predicting the possibility of a valuable customer churning and taking steps to prevent its occurrence is cheaper than investing in brand new marketing campaigns to acquire new customers [20].

Data mining methods such as machine learning techniques are now being used to predict customer churn in competitive organizations and to discover hidden patterns that were previously too complex and time-consuming to uncover at first sight [4,9]. When machine learning algorithms are trained with valid data about customers’ transactions, useful knowledge in the data is discovered, and challenges in the bank are resolved by finding some regular patterns, causality, and correlation with business information. The likelihood of a customer unsubscribing from an organization’s service can also be predicted. This is important as it helps the bank’s management determine those customers who are at risk of leaving and analyzing whether they are worth retaining. As has been proven by several studies, machine learning churn models are vital for implementing CRM techniques in banks and many other industries to enhance customer retention rates [8,15,21].

2.2. Traditional Machine Learning Methods for Churn Management in the Banking Sector

According to Sabbeh [22], machine learning techniques were used to overcome customer churn challenges in the banking sector. The authors in [23] described a churn prediction model in the banking sector using Classification and Regression Trees (CART) and C5.0, and the results showed that the prediction success rate of the churn class by CART was higher than that of C 5.0. The work of [13] developed a multilayer perceptron (MLP)-based predictive model to predict customer churn in a financial institution. A dataset containing 50,000 data instances extracted from the database of one of the leading financial institutions in Nigeria was used for the study. The implementation, done in Python, was compared with another model in NeuroSolutions Infinity software. The results showed that the MLP implemented in Python had comparable performance with that obtained from the NeuroSolutions Infinity software.

In [24], unsupervised learning via an Artificial Neural Network (ANN) was used to detect changes in the patterns of behavior of customers of an international bank based on credit card transactions. The purpose of this was supporting customer relationship management and strategy. The results showed improvement in several aspects, such as customer service efficiency, customer retention, customer satisfaction, and customer revival. It also enabled the discovery of new customers. A self-organizing map (SOM) ANN with sigmoid activation functions was used to achieve this. In [4], an ANN was used to solve a complex bank churning problem that was difficult to solve with traditional statistical techniques. It was used within the Alyuda NeuroIntelligence software package to predict customers who were at risk of unsubscribing and analyzing whether those customers were worth retaining. The results of the experiment showed that customers who used more bank products were more loyal. The study, therefore, recommended that banks should focus on those customers who used less than three bank products and offer them products according to their needs. Using advanced data analytics methods on the transaction and operation data of an Iranian bank, a customer churn prediction model for several retail customers was described in [25]. The results of the experiments revealed that restaurants, fast food retailers, and technical services had the highest churn rates in the bank. This was followed by sports centers and households. The results also showed that counseling centers, kindergartens, and governmental organizations were the least risky corporate customers of the bank. Lastly, it was revealed that in retail customers, clients aged 30–40 years had the largest churn in the bank’s services. In another study [26], an enhanced deep feedforward neural network (EDFNN) to forecast customer churn in the banking domain was proposed. The study’s dataset was collected from the University of California, Irvine (UCI) Machine Learning Repository, which had 10,000 customers’ data with fourteen (14) attributes. Data cleaning and preprocessing were performed with optimized one-hot encoding and Tukey outliers’ algorithms. When compared with the results of the logistic regression, decision tree, and Gaussian naïve Bayes algorithms, the EDFNN model showed better performance in terms of accuracy. In [27], a combination of the support vector machine (SVM) and adaptive boosting (AdaBoost) methods was used with a dataset from a bank to detect the customers with a high possibility of leaving the bank. The results showed that the proposed method achieved high classification accuracy. The predictive strengths of machine learning methods were also demonstrated in the work of Li and Wang [28] when the problem of predicting customer churn in commercial banks was solved using logistic regression as a supervised learning method and an SVM for learning from label proportions. The training data was provided in groups, but only the proportion of each class in each group was known. Dalmia et al. [29] also did a study to compare the predictive strengths of various classifiers to solve the bank customer churn prediction challenge.

In [30], a dynamic churn prediction framework that enabled lead-time specific prediction of when customers were likely to churn was presented. The framework allowed training data from customer records to be generated and then used to determine when a customer was likely to churn within multiple time horizons by using standard classifiers. A case study of private banking customers of a European bank was used. The results showed that the framework performed better than survival analysis in terms of predictive accuracy for all lead times with much less variability. It also provided a ranking of customers in terms of the probability of churn during specific time horizons, which could enable the bank to devise appropriate retention efforts for each time. It was also revealed that the predictive accuracy of churn models could be improved by using multiple training observations per customer from different time periods (MPTD) instead of the traditional approach, which is based on the most recent observation for each customer. The authors in [31] proposed a dynamic approach to churn prediction by mining customer behavior patterns based on longitudinal data. Dynamic churn modeling for a US bank was done using a 3 year transaction dataset consisting of 32,000 records. A dynamic approach to optimizing the model specifications by time series predictors, multiple time periods, and rare event detection was used to optimize model specifications to enable dynamic and accurate churn prediction. It was found that using training data extracted over 6 months yielded a better understanding of customer behavioral patterns compared with using data over 4 months. It was also found that the use of a shorter prediction window of 2 months could help to avoid rapid accuracy decay.

In [32], a hybrid method was used to extract the rules from an SVM to facilitate effective customer relationship management. The extracted rules were used to provide notifications to the bank’s management on the likelihood of churn by the bank’s credit card customers. The hybrid approach involved a three-step process of SVM recursive feature elimination to reduce the feature set, extraction of an SVM model and support vectors from the reduced dataset, and extraction of the rules from the SVM model by using a naïve Bayes tree (NBTree). The results showed that the method extracted rules with smaller lengths, which improved the comprehensibility of the system. In addition, [33] utilized the lasso regression algorithm to optimize a radial basis function (RBF) neural network to predict bank customer churn. The experiment’s results showed that the lasso–RBF neural network outperformed logistic regression (Log-R), RBF, and boosting in terms of accuracy of classification. Thus, the Lasso–RBF neural network improved the capacity for decision-making on churn management in the banking sector. In [34], the application of an MLP ANN and an SVM was used to predict three possibilities of bank clients which were active, non-active, and churning. The main goal was to determine the likelihood of a customer departing from the bank’s services. The results showed that the MLP ANN had an average accuracy of 99.3% while the SVM’s accuracy was 99.6%, which revealed that the proposed model could accurately guide decision-making on churning by bank experts.

2.3. Deep Learning Methods for Churn Management in the Banking Sector

Deep learning, because of its good features and representation of input data, has exploded in the public consciousness, mainly for predictive and analytical tools in different application domains, including churn prediction, pattern recognition, targeted advertisements, and image processing [35,36]. Convolutional neural networks (CNNs) and recurrent neural networks (RNNs) are some of the most successful and widely used methods in the deep learning community [27]. Deep learning has been applied to churn prediction by many researchers. For instance, in [37], a DNN was proposed to predict bank customer churn. Using the accuracy, precision, recall, and F1 (which is the harmonic mean of the precision and recall) scores as the performance metrics, the DNN performed better than the logistic regression, decision tree, and random forest methods, which were used as baseline models. In [38], customer churn prediction models using real-life data from a European financial services provider was developed. A comparison of the results from CNNs against the current best practices for analyzing textual data showed that the CNNs outperformed the current best practices for text mining. In [39], the superiority of deep learning methods in classification problems was shown through the use of a deep ensemble classifier. The method integrated the predictive capabilities of individual classifiers in a meta-level model by stacking multiple predictions through the use of CNNs. When evaluated with an application to customer retention in a Canadian retail financial institution, the deep ensemble classifier produced outstanding performance, even with largely unbalanced customer data. The superiority of deep learning methods over traditional classification methods for predicting bank customer churn was shown in [40]. The results from the experiments showed that time-sequenced data used in a recurrent neural network-based long short-term memory (LSTM) model outperformed the baseline models when precision and recall were used as the metrics. In [41], deep learning and traditional machine learning models were developed for predicting heterogeneous patterns, such as risks and trader behaviors. The results confirmed a better feature learning capability of deep learning over traditional machine learning and rule-based benchmarks. Using the customer life value (CLV) variable, RNNs to identify churners based on CLV time series regression were proposed in [42]. The results showed that the RNNs had better performance when compared with that of the random forest technique. In [12], a deep learning model was developed to solve the classification problem of banking churn prediction. Using customers’ data, the results showed that the deep learning model predicted bank customer churn with 84% accuracy. In an experiment to establish the predictive strengths of various classifiers for churn prediction, the authors of [43] used recency, frequency, and monetary (RFM) value data from a financial services provider. The results of the experiment revealed that the RFM variables, in combination with LSTM neural networks, had a larger top-decile lift and expected maximum profit metrics than conventional logistic regression models with commonly used demographic variables. The results also showed that using the fitted probabilities from the LSTM neural networks as a feature increased the performance of the logistic regression model by 25% when compared with a model with only static features.

From the reviewed papers, we identified the robustness and popularity of traditional machine learning and deep learning approaches in dealing with customer churn predictions in the banking sector. Researchers have approached this from different directions, including prediction and classification methods [11], the type of business, variables affecting the churning or loyalty of the customer, dynamic churn, and the type of churning [44].

Even though the applicability of DNNs for churn modeling has been established, to the best of our knowledge, none of the previous studies have focused on what could be learned from the selection and tuning of different hyperparameters when DNNs are used for churn prediction in the banking sector. Our evaluation of the relevant review papers that are focused on deep learning methods in banking and churn prediction in banking, as presented in [11,12], confirms this position. Thus, empirically derived heuristic knowledge that can guide the selection of hyperparameters when DNNs are used for churn modeling in the banking sector is still lacking, which is the issue that is addressed in this paper.

3. Methodology

The data collection and experiments that were conducted in the study are described in this section.

3.1. Data Collection and Description of Dataset

It is common knowledge that banks do not reveal their customers’ transaction or profile information because of its sensitive nature. Consequently, the study’s dataset was downloaded from Kaggle.com (https://www.kaggle.com/barelydedicated/bank-customer-churn-modeling) on 5 July 2019. Kaggle is a data science and machine learning community where students, professionals, researchers, and enthusiasts compete and share machine learning techniques as well as datasets. The dataset represented a collection of information from a fictitious bank. Table 1 shows a description of the 14 parameters (13 independent variables and 1 dependent variable) of the dataset. In Table 2, we show a sample of the dataset, where the geography data field was customized to cities and locations in South Africa (see Table 2).

Table 1. Descriptions of the dataset parameters.

	Parameters	Description
	Independent Variables
1	RowNumber	Row number of the customer in the csv file. There were 10,000 customers in total.
2	CustomerId	Unique identification of each customer from the bank’s records
3	Surname	Surname of the customer
4	CreditScore	A score the bank assigns to each customer based on the customer’s personal credit history to measure the customer’s creditworthiness. The higher the credit score, the more creditworthy the customer is.
5	Geography	The location where the customer lives
6	Gender	Customer’s gender (male or female)
7	Age	Customer’s age
8	Tenure	How long the customer has been with the bank in years
9	Balance	Present monetary value of a customer’s account
10	NumOfProducts	Products the customer is currently using from the bank (e.g., Internet banking, loans, and currency or savings accounts, among others)
11	HasCrCard	Binary indication of whether a customer possesses a credit card or not
12	IsActiveMember	Indicator of whether a customer has used any of the bank’s products in the last 6 months
13	EstimatedSalary	Estimated customer salary
	Dependent Variable
14	Exited	This depends on a variable that indicates if the customer has left the bank after 6 months (1 for yes and 0 for no)

Table 2. The study’s sample dataset.

Row Number	1	2	3	4	5
CustomerId	15634602	15647311	15619304	15701354	15737888
Surname	Hargrave	Hill	Onio	Boni	Mitchell
CreditScore	619	608	502	699	850
Geography	Cape Town	Durban	Cape Town	Cape Town	Durban
Gender	Female	Female	Female	Female	Female
Age	42	41	42	39	43
Tenure	2	1	8	1	2
Balance	0	83,807.9	159,661	0	125,511
NumOfProducts	1	1	3	2	1
HasCrCard	1	0	1	0	1
IsActiveMember	1	1	0	0	1
EstimatedSalary	101,349	112,553	113,932	93,826.6	79,084.1
Exited	1	0	1	0	0

3.2. Methods

First, data pre-processing was performed, because the variables needed to be encoded and scaled equally in a process called feature scaling. Missing values were replaced with the mean (average) of the column where they were located. The experiments were performed on both the DNN and MLP churn models by changing the activation functions that were used in the hidden layers and the output layer. The batch sizes were the number of rows to be propagated to the network at once. It is through the training algorithm that the model learned, and different algorithms were comparatively assessed by changing the optimizer values. Samples of training data consisting of the independent variables (13 parameters) and the dependent variable (which was either 1 or 0 (1 to leave the bank or 0 to stay in the bank) in each instance were fed into the machine learning models of the DNN and the MLP models for each time. To help preserve the statistical properties of the original dataset and ensure that the unbalanced dataset had a good balance between the size and representation of the training and test sets [45], the data collected was divided into a training set (80%) and a test set (20%). The choice of an 80:20 dataset split ratio was firstly influenced by the fact that the number of data instances was considered to be sufficiently large. Secondly, with the large data instances, there would be no significant difference in using an 80:20 data split compared to a 90:10 or 70:30 data split for a computationally intensive operation using a DNN for churn modeling. Generally, having less training data led to greater variance in the parameter estimates, while less testing data led to greater variance in the static performance. The goal was to ensure that the data being split into training and test sets led to a variance that was not too high, which could be achieved by an 80:20 ratio data split for 10,000 data instances. From the thirteen (13) independent variables, ten (10) of them (CreditScore, Geography, Gender, Age, Tenure, Balance, NumOfProducts, HasCrCard, IsActiveMember, and EstimatedSalary), which were considered to have the most impact on the churn model, were chosen to compose the input layer.

Geography and gender were the two categorical variables which were encoded into numbers to enable the network to process them. It is noteworthy that, when encoded to numbers, these categorical variables had equal relational order (i.e., Cape Town is not more important than Durban, or male is not more important than female) for the network. The cities were encoded into numbers 0, 1, and 2, and the genders were assigned values such as 0 and 1 randomly. Feature scaling (data normalization) was performed to prevent some column values dominating other column values (credit score, for instance, being dominated by balance because of the disparity between these values). All the values in the dataset were rescaled in the range from −1 to 1 using standardization and feature scaling.

The rescaled values (see Table 3) were then used as input into the deep neural network (DNN) model. The ten (10) normalized values were inserted into the input layer, and the last column (Exited) was used to train the model, classifying them as churner or non-churner. The confusion matrix was set to a threshold of 0.5. If the classification was greater than the threshold, the customer was classified as a churner; otherwise, the customer was classified as a non-churner.

Table 3. Normalized data.

0	1	2	3	4	5	6	7	8	9	10
1.74309	−0.569844	0.169582	−1.09169	−0.464608	0.006661	−1.21572	0.809503	0.642595	−1.032227	1.106643
−0.573694	1.75487	−2.30456	0.916013	0.301026	−1.37744	−0.0063119	−0.92159	0.642595	0.968738	−0.748664
−0.573694	−0.569844	−1.1912	−1.09169	−0.943129	−1.03142	0.579935	−0.921591	0.642595	−1.03227	1.48533
1.74309	−0.569844	0.035566	0.916013	0.109617	0.006661	0.473128	−0.921591	0.642595	−1.03227	1.27653
1.74309	−0.569844	2.05611	−1.09169	1.73659	1.04474	0.810193	0.809503	0.642595	0.968738	0.558378

By taking from the best practices in backpropagation training, as advocated by LeCun et al. [46], the six-step procedure that we followed to train the DNN model was as follows:

• Initialize the weights close to 0 (but not 0)
• Input one observation at a time (one feature in one input node);
• Use forward propagation to determine how important each neuron is by the weights to get y;
• Compare the results to the actuals result and measure the margin of error;
• Backpropagate the error to the artificial neural network to adjust the weights;
• Repeat Steps 1–5 for each observation.

3.3. Experiment Design and Validation

The experimental set-up for the study was performed using a DNN. The input layer was made of 10 nodes, each one of them connected to every node of the first hidden layer. There were six fully connected nodes on each hidden layer, and all the nodes on the second hidden layer were connected to the single output layer, which produced the binary output. Thus, the DNN had a 10-6-6-1 neural architecture. The input layer received the pre-processed data, which were already rescaled in the form of batches and sent to the hidden layers. The batch size was the hyperparameter that set the number of samples that were propagated to the network at each epoch. Each node on the hidden layers had an activation function, which was responsible for introducing nonlinearity to the output layer. This was of crucial value because most datasets available in real life are nonlinear. These functions set the output to be within a pre-specified interval or threshold. The output layer had the output function, which mapped the inputs coming from the last hidden layer into a specific class of churner or non-churner.

Three experiments were performed in an attempt to address the three research objectives (RO1, RO2, RO3) that were specified for the study.

Experiment 1: Activation Function (Objective 1)

The first experiment involved trying different activation function configurations for the DNN and comparing how it performed against an MLP during the training and testing phases. This was to address the first objective of the study, which was to determine the effects that various configurations of monotonic activation functions had on the training of a DDN churn model in the banking sector.

A brief description of the main three nonlinear monotonic functions is as follows:

The sigmoid takes a value and squashes it to between 0 and 1. It is a very useful function because it provides probabilities, which is good for classification problems whose output is a binary outcome [45]. The sigmoid function fits well for churn prediction because the model can set a threshold to be churner = x ≥ 0.5 and non-churner = x ≤ 0.5. The sigmoid (see Figure 1) is denoted by

σ(x) = 1/(1 + exp(−x))

(1)

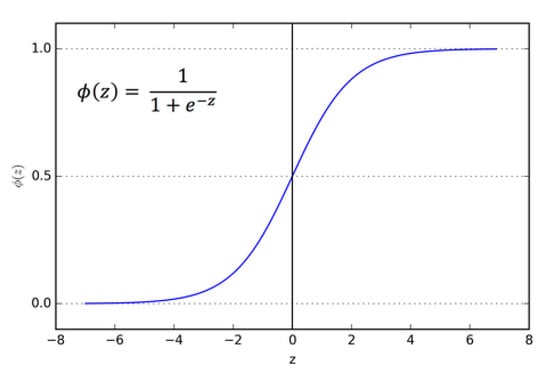
Figure 1. Sigmoid graph. Source: https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6 (accessed on 15 October2019).

The rectified linear unit (see Figure 2) takes a real value and thresholds it to 0, replacing negative values with zero as well. This was useful for the activation function because during training, the values coming from the input were sometimes negative, and the model was oftentimes configured to work with scaled real or positive numbers [4]. This is denoted as

f(x) = max(0, x)

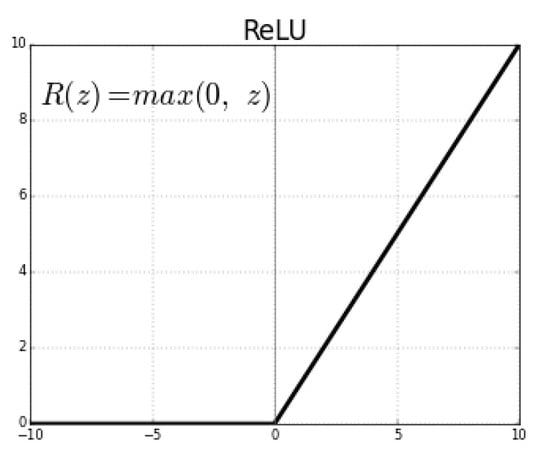
Figure 2. Rectifier function. Source: https://medium.com/@kanchansarkar/relu-not-a-differentiable-function-why-used-in-gradient-based-optimization-7fef3a4cecec (accessed on 15 October 2019).

A hyperbolic tangent (tanh) takes a real number and squashes it to a range between −1 and 1 (see Figure 3). This was a useful function for the hidden layer because the negative values would not be scaled like in the rectifier functions (to zero), and the input was mapped as strongly negative [4]. This is denoted as

tanh(x) = 2σ(2x) − 1

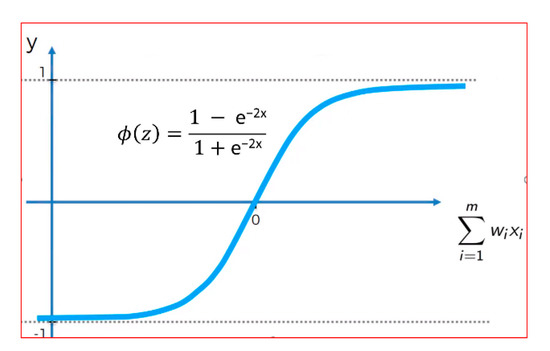
Figure 3. Tanh function. Source: https://medium.com/datadriveninvestor/neural-networks-activation-functions-e371202b56ff (accessed on 15 October 2019).

The combination of the activation functions used in the hidden layers and the output layers of the DNN and the MLP is shown in Table 4.

Table 4. Activation functions used in the deep neural networks (DNNs).

Hidden Layer	sigmoid	tanh	sigmoid	tanh	rectifier	rectifier	rectifier	tanh	sigmoid
Output Layer	sigmoid	tanh	tanh	sigmoid	sigmoid	tanh	rectifier	rectifier	rectifier

Experiment 2: Batch Sizes (Objective 2)

In the second experiment, batch sizes (number of rows) set the number of samples that were propagated through the network at each epoch during the training phase (see Table 5). The batch size values were incremented gradually to see how the DNN model performed against the MLP. This experiment aligned with the second objective of the study, which was to determine the effect of different batch sizes in the training of a DNN in the banking sector. The goal was to examine the effect of larger data sizes on the computation of the DNN and the MLP.

Table 5. Batch size.

Batch size	3	7	10	12	15	20	25	30	35
	40	50	70	90	110	140	180	230

Experiment 3: Training Algorithms (Objective 3)

The third experiment aligned with the third research objective, which was to evaluate the overall performance of the DNN model by trying three different training algorithms. During the training phase, the dataset was split into 10 folds, with the model training on the ninth fold and testing on the tenth fold (K-fold cross-validation). The k-fold cross-validation process enabled the model to be trained much more precisely because, instead of only testing on the test set, the model trained and tested at the same time, causing the error backpropagation to adjust the weights optimally. The algorithms that were used were stochastic gradient descent (SGD), an adaptive gradient algorithm (AdaGrad), and its variants such as Adadelta, root mean square propagation (RMSProp), Adam, and AdaMax.

SGD is a simple but efficient method for fitting linear algorithms and regressors under convex loss functions, such as a (linear) SVM and logistic regression. SGD performed a parameter update for each training example [47]. The authors in [48] described adaptive moment estimation (Adam) as an algorithm for first-order, gradient-based optimization of stochastic objective functions, based on the adaptive estimates of lower-order moments. Adam computes adaptive learning rates for each parameter and keeps an exponentially decaying average of past gradients. The adaptive gradient algorithm (AdaGrad) [49] is an algorithm that helps decay the learning rate very aggressively as the denominator grows. In other words, it is a gradient-based optimization algorithm that adapts the learning rate to the parameters, performing smaller updates (low learning rates) for parameters associated with frequently occurring features and larger updates (high learning rates) for parameters associated with infrequent features. It is for this reason that AdaGrad performs well even with sparse data. Adadelta [50] is an extension of AdaGrad that seeks to reduce its aggressive, monotonically decreasing learning rate. Instead of accumulating all past squared gradients, Adadelta restricts the window of accumulated past gradients to some fixed size. Root mean square propagation (RMSProp) is an extension of AdaGrad that deals with its radically diminishing learning rates. It is identical to Adadelta, except that Adadelta uses the RMSProp of parameter updates in the numerator update rule. AdaMax is a variant of Adam based on the infinity norm. The SGD, AdaGrad, Adadelta, Adam, Adamax, and RMSProp methods were used variously with the DNN and MLP.

4. Results and Discussion

According to the stated objectives of the study, we now present the results obtained from the three experiments, along with a discussion of their implications.

4.1. Experimental Results

For RO1, the first experiment tried different configurations of activation functions in the hidden layer and output layer and examined their effects on the model’s performance. The performance of the model, as shown in Table 6, varied depending on the selected function parameters for the MLP and DNN. The results show the effects of various configurations of the activation function on the performance of the DNN and MLP in terms of accuracy of churn prediction for the banking sector.

Table 6. Activation and output function results.

Activation Functions		Accuracy (%)
Hidden Layer	Output Layer	Multilayer Perceptron	Deep Neural Network
sigmoid	sigmoid	83.85	79.75
tanh	tanh	79.8	79.8
sigmoid	tanh	79.75	83.5
tanh	sigmoid	81.25	85.45
rectifier	sigmoid	83.45	86.9
rectifier	tanh	82	84.9
rectifier	rectifier	79.75	84.75
tanh	rectifier	79	80
sigmoid	rectifier	79.95	82.95

For RO2, the results of the second experiment, which was performed to determine the effect of the batch size on the training of a deep neural network churn model in the banking sector compared with an MLP, are presented in Table 7.

Table 7. Batch sizes.

	Accuracy (%)
Batch Size	Multilayer Perceptron	Deep Neural Network
3	84.3	85.2
7	84.25	85.75
10	84.05	84.9
12	84	84.15
15	83.91	84.2
20	83.95	84.3
25	83.88	84.1
30	83.85	84.1
35	83.8	84.35
40	83.1	84.2
50	82.9	84.25
70	82.2	84.45
90	80.3	83.8
110	80.04	84.25
140	79.9	85.15
180	79.7	83.8
230	79.75	83.15

For RO3, the results of the third experiment, which was performed to evaluate the performance of different training algorithms with varied training parameters, are presented in Table 8.

Table 8. Training algorithms.

	Accuracy (%)
Training Algorithm	MLP	DNN
SGD	79.75	83.1
AdaGrad	79.65	83.75
Adadelta	84.2	85.65
AdaMax	83.5	84.05
Adam	83.25	84.5
RMSProp	84.5	86.45

4.2. Discussion

We found in the first experiment that the MLP performed best (with 83.85% accuracy) when it was configured as a pure MLP, with a sigmoid on the hidden layer and a sigmoid on the output layer. However, it performed worst (with 79% accuracy) when it was configured with a tanh function on the activation function and a rectifier on the output layer (Table 6). However, the DNN had a better performance (86.9%) when configured with a rectifier in the hidden layers and a sigmoid on the output layer. The DNN model outperformed the MLP because it had more hidden layers so that values were propagated to various neurons and not only in a single layer. This allowed better segmentation of the data because the neurons were much more trained [47]. This means that the first objective of the study (to determine the effect that various configurations of the activation function have on the training of a deep neural network churn model in the banking sector) was achieved by using rectifiers as the activation function for the hidden layers, since this allowed the model to classify even negative values [4]. This also means that regardless of the input, the model did not miss values because they were outside of its range of analysis. We found that, generally, the DNN performed better when the rectifier (rectified linear unit, or ReLU) was used in the hidden layers.

From the second experiment, it was found that the batch size slightly affected the performance of the DNN, especially when the batch size was small (Table 7). In the range of 3–40 batch sizes, the performance of both the DNN and MLP was stable. The DNN had an average of 84.52, while the MLP had an average of 84.0. The performance of the DNN started to degrade as larger batches were fed into the DNN, but the performance of the MLP degraded progressively as the batch size exceeded 35. This was because, according to [50], the closer the batch size to the test set number (close to 2000), the faster the performance tends to drop because of the limited time to process each row individually. Although the performance dropped as bigger batch sizes were fed into the DNN model, it still performed better than the MLP. This was because the DNN was a larger neural network architecture with more capacity to handle large data. Depending on the number of epochs, the models did not learn, but rather just propagated the values.

As shown in the results from the third experiment in Table 8, the MLP performed best (84.5%) when RMSProp was selected as the training algorithm, but it had the worst performance (79.65%) when AdaGrad was selected as the training algorithm. The DNN also performed best (86.45%) when RMSProp was the selected training algorithm, but it had the worst performance (83.1%) when SGD was selected as the training algorithm.

Using the same dataset to train and test the MLP and DNN models, we were able to determine each customer’s likelihood of churning or not churning (either 1 or 0). From the 10,000 customers in the study dataset, it was found that 20% were churners while the remaining 80% were not churners, as can be seen in the graphical illustration (Figure 4).

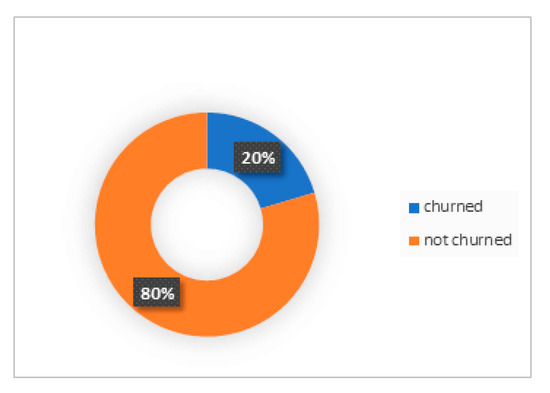
Figure 4. Churner and non-churner relationship from the original dataset.

As was mentioned earlier, the 10 most significant independent variables were used in the input layer to provide the numerical values needed to train and test the models. The test accuracy of the model was calculated from the confusion matrix. The true negatives and true positives (see Table 9) were the values that the model predicted correctly (churners predicted and vice versa with non-churners). The accuracy of the model is shown in Figure 5.

Table 9. Confusion matrix.

	Negative (0)	Positive (1)
Negative (0)	1514	81
Positive (1)	201	204

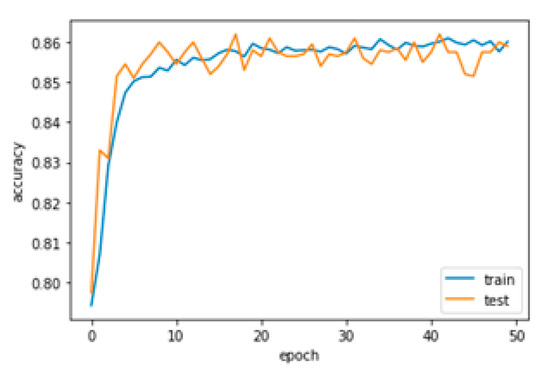
Figure 5. Accuracy of the deep neural network.

The model’s loss (error margin), which was the value that the model predicted incorrectly, was calculated using the same confusion matrix, but it considered only the false values (see Figure 6).

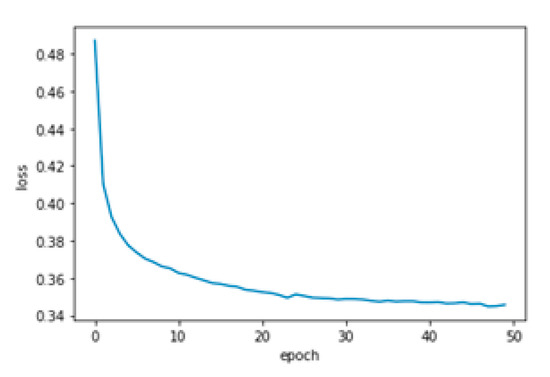
Figure 6. Loss margin result of one experiment.

5. Conclusions and Future Work

In this study, we explored the effects of different configurations of hyperparameters when a DNN was used for churn prediction in the banking sector compared to when an MLP was used. Three experiments were performed to determine (1) the effects of various combinations of monotonic activation functions when used in the hidden layers and the output layer, (2) the effect of the use of different batch sizes on the performance of a DNN during the training and testing phases in churn prediction in the banking sector, and (3) the performance of different training algorithms with varied training algorithms during churn prediction.

The results from the first experiment showed that with different configurations of monotonic activation functions in the hidden layers and the output layer, the DNN churn model performed better than the MLP churn model for the banking sector when it was configured with a rectifier function in the hidden layers and a sigmoid on the output layer. From the second experiment, it was found that the batch size had a significant influence on the performance of the DNN in the sense that the performance dropped as the batch size got closer to the test set data. The results from the last experiment showed that the MLP performed best when Adam was selected as the training algorithm because its architecture did not make it favorable to be trained with RMSProp, which was specially designed to train DNN models. The difference in performance between the DNNs and the MLP for churn modeling can make a huge difference for banks in terms of the accuracy of churn detection and increasing customer loyalty.

This study makes both theoretical and practical contributions. First, previous studies that focused on the impact of hyperparameter tuning on the performance of deep neural networks when they were used for churn prediction in the banking sector are rare. The most recent systematic literature review papers on the topics of deep learning methods in banking and churn prediction in banking attest to this fact [11,12]. Thus, this study makes a theoretical contribution because it provides a basis for understanding the effect that changes to specific hyperparameters and their various combinations could have on the training of deep neural network models when they are used for churn prediction in the banking industry. Specifically, it provides an understanding of the effects of different activation functions when used for churn modeling using a DNN, which is unlike previous studies. It also revealed the impact of different batch sizes on the performance of a DNN when used for churn modeling.

Second, in terms of practical contribution, this study provides a basis for the derivation of useful heuristic knowledge that could guide novice or upcoming machine learning researchers and practitioners during the process of churn modeling when DNNs are used for churn prediction, particularly as it relates to the banking sector. This form of heuristic knowledge will improve the efficiency of hyperparameter tuning during the training of DNNs for churn modeling, instead of the use of ad hoc methods or trial and error approaches which is currently prevalent [10]. This will enhance the efficiency of customer relationship management and customer retention in the banking sector.

5.1. Research Limitations

Despite the promising results presented in Section 4, the study had some limitations. The first limitation of the study was that the study dataset was only a fictitious dataset from a public data repository site, which may have been collected from only one bank within a short time period. In this case, the dataset may not apply to other banks, so generalizing the results to other banks should be done with extreme caution. In the future, more longitudinal studies are needed to test the reproducibility of the experiments, with more data samples collected over a long time from different banks for the generalization of the findings to the banking industry in general. Related to the first study limitation was that the study dataset was unbalanced in distribution (churners = 2000, non-churners = 8000). Although the stratified cross-validation method was used to ensure a representation of each category, this could have affected the prediction accuracy of the machine learning classifiers. It is, however, worthy of note that within the context of these limitations, the study achieved its three objectives stated in Section 1.

5.2. Future Work

We intend to extend the study by carrying out different architectures of DNNs for churn modeling, especially for the use of deep learning to predict not only churn, but loyalty as well. This architecture would output three categories of loyalty (very loyal, loyal, or not loyal), and the churn output would be a high, medium, or low chance of churning. Another possible area of extension of this study in the future would be to design a deep learning hybrid architecture that would not rely on human configurations, but autonomously determine the best parameters to use to train, test, and improve its performance. The third possible extension in the future is to design a model that first segments customers into valuable, moderately valuable, and not valuable. The model would only run on the valuable and moderately valuable customers, discarding the not valuable customers. Another aspect of interest is to experiment with different category of activation functions and not just focus on monotonic activation functions. We shall assess the effect of sinusoidal activation functions like sine and spline functions. We will also consider the effects of several variants of the ReLU on the performance of a DNN for church modeling. Experimentation on the effects of sinusoidal activation functions on deep neural architecture is still an active area of research where more investigation is required [50].