Abstract
In the finance market, the Black–Scholes equation is used to model the price change of the underlying fractal transmission system. Moreover, the fractional differential equations recently are accepted by researchers that fractional differential equations are a powerful tool in studying fractal geometry and fractal dynamics. Fractional differential equations are used in modeling the various important situations or phenomena in the real world such as fluid flow, acoustics, electromagnetic, electrochemistry and material science. There is an important question in finance: “Can the fractional differential equation be applied in the financial market?”. The answer is “Yes”. Due to the self-similar property of the fractional derivative, it can reply to the long-range dependence better than the integer-order derivative. Thus, these advantages are beneficial to manage the fractal structure in the financial market. In this article, the classical Black–Scholes equation with two assets for the European call option is modified by replacing the order of ordinary derivative with the fractional derivative order in the Caputo type Katugampola fractional derivative sense. The analytic solution of time-fractional Black–Scholes European call option pricing equation with two assets is derived by using the generalized Laplace homotopy perturbation method. The used method is the combination of the homotopy perturbation method and generalized Laplace transform. The analytic solution of the time-fractional Black–Scholes equation is carried out in the form of a Mittag–Leffler function. Finally, the effects of the fractional-order in the Caputo type Katugampola fractional derivative to change of a European call option price are shown.
1. Introduction
In 1973, Black and Scholes [1] constructed the mathematical model for pricing an options contract, known as the Black-Scholes model. In particular, the Black-Scholes model estimates the variation over time of financial instruments. The Black-Scholes equation with two assets of a European call option is defined by:
with the terminal condition:
and boundary conditions:
and
where
- u is the call option depending on the underlying asset prices at time
- are the asset price variables,
- are the volatility function of underlying assets,
- are coefficients so that all risky asset price are at the same level,
- is the volatility of and
- r is the risk-free interest rate,
- T is the expiration date,
- K is strike price of the underlying asset.
During the past 10–20 years, fractional calculus is extensively used for real-life problems in a variety of fields like chemistry, biology, physics, earth science and engineering [2,3,4,5,6,7,8,9,10]. Most of the fractional derivatives are represented in the integral form. Two fractional derivatives, which are the most popular, are Riemann-Liouville derivative [11] and Caputo derivative [12]. Katugampola [13,14] defined a generalized fractional derivative including Riemann-Liouville and Hadamard fractional integrals and derivatives. The Katugampola fractional derivative in Caputo type is defined by Almeida et al. [15] and Jarad et al. [16] that some researchers call this fractional derivative type the Caputo generalized fractional derivative.
The Black-Scholes equation with integer-order derivatives has been developed and studied by many researchers in [17,18,19,20]. Those studies show that the financial market has fractal characters both at home and abroad which is not enough to reflect the reality of the financial market. Recently, fractional differential equations are proved and accepted that fractional differential equations are a powerful tool in studying fractal geometry and fractal dynamics. The concept of the fractional derivative model helps to understand the data structure for the real-life matters deeper than the integer-order derivative model. This is the reason why researchers attempted to develop the integer-order Black-Scholes equation into the fractional-order Black-Scholes equation.
There are many analytical methods, used to find solutions of fractional Black-Scholes equations such as homotopy analysis method, homotopy perturbation method [21], modified homotopy perturbation method [22], Adomain decomposition method [23], analysis of decomposition method [24], finite difference method [25,26,27], variational iteration method with coupling of the Sumudu transform [28], Laplace homotopy perturbation method [29,30,31,32], and -Laplace homotopy perturbation method [33,34].
In 2017, K. Trachoo, W. Sawangtong and P. Sawangtong [32] studied the two dimensional Black-Scholes equation with the integer-order derivative. They used the Laplace homotopy perturbation method to solve the such equation. The analytic solution of this equation is carried out in the form of the special function, which is Mellin-Ross function.
In 2018, P. Sawangtong, K. Trachoo, W. Sawangtong and B. Wiwattanapataphee [31] solved the Black-Scholes equation with two assets in the Liouville-Caputo fractional derivative sense. By the Laplace transform homotopy perturbation method, the analytic solution obtained is in the form of the Generalized Mittag-Leffler function. Moreover, their presented results ensure that the fractional Black-Scholes model is more practical than the integer-order model.
As in previous descriptions, the characteristic of the finance market is fractal geometry and fractal dynamics, and the fractional differential equation is the powerful tool in studying such characteristics. Moreover, the self-similar property of fractional derivative makes can reply to the long-range dependence better than the integer-order derivative. The motivation of this work comes from the two above papers [31,32] and the advantages of fractional calculus. This article studies the fractional-order Black-Scholes equation with two assets described in the sense of the Katugampola Fractional Derivative in Caputo type. We obtain here the analytic solution of the time-fractional Black-Scholes equation with two assets by the technique of the generalized Laplace homotopy perturbation method. Such the method is the combination between homotopy perturbation method and generalized Laplace transform proposed by Jarad and Abdeljawad [35]. Furthermore, the Katugampola fractional derivative in Caputo type can be transformed to both the Caputo derivative and Caputo-Hadamard derivative [36]. In the particular case, analytic solutions of the time-fractional Black-Scholes equation with two assets in the sense of both Caputo derivative and Caputo-Hadamard derivative are shown. We moreover investigate that the fractional-order of the Caputo type Katugampola fractional derivative has an effect on the price of a European call option.
The paper is organized as follows. We introduce the definitions of fractional derivatives, the generalized Laplace transform and the generalized Mittag-Leffler function in Section 2. We recall the constructive partial differential equation associate with the Black-Scholes models in Section 3. In Section 4, the time fractional Black-Scholes equation with two assets of the European call option is determined and carried out by the generalized Laplace homotopy perturbation method. The analytic solutions of fractional Black-Scholes equations and numerical results are presented in Section 5 and Section 6, respectively. Finally, conclusions and a discussion of current work is given in Section 7.
2. Preliminaries
In this section, we give definitions of fractional derivatives and the generalized Laplace transform. Furthermore, some properties of generalized Laplace transform and two-parameters Mittag-Leffler function used throughout this work are shown.
Let and be any real number with and be a Gamma function.
Definition 1
([37]). The Riemann-Liouville fractional integral of f with order α has the following form:
Definition 2
([37]). The Riemann-Liouville fractional derivative of f with order α has the following form:
Definition 3
([37]). The Caputo fractional derivative of f with order α has the following form:
Definition 4
([38,39,40]). The Caputo-Hadamard fractional derivative of f with order α has the following form:
where the differential operator δ is defined by .
Definition 5
([37]). The Katugampola fractional derivative in Caputo type of f with order α has the following form:
where the differential operator γ is given by .
Note that if then the fractional derivative as Equation (4) becomes the Caputo fractional derivative with order . On the other hand, if approaches then the fractional derivative as Equation (4) results to the Caputo-Hadamard fractional derivative with order .
Next, we present the definition of the generalized Laplace transform.
Definition 6
([35]). Let be real valued functions such that is continuous and on . If the generalized Laplace transform of f exists, then
where s is the generalized Laplace transform parameter.
Obverse that if we set and in Equation (5), then the generalized Laplace transform becomes the classical Laplace transform but if we set and then the generalized Laplace transform reduces to the Laplace transform studied by Fall et al. [33].
Throughout this work, we call the generalized Laplace transform with and by -Laplace transform. Then, -Laplace transform is defined by:
We next give some properties of -Laplace transform.
Lemma 1
([37]).
- 1.
- 2.
Definition 7
([41,42]). The two-parameters Mittag-Leffler function is defined as follows:
where and
We give some properties of the two-parameters Mittag-Leffler function.
Lemma 2
([43]). The asymptotic expansion of with and is:
3. Constructive Equations
In this section, we let:
and
For more details of transformation, readers can be found in [31,44]. Finally, the Black–Scholes partial differential equation with two assets of the European call option Equation (1) can be transformed in the following form:
In this work, we consider the Black–Scholes equation in Equation (8) in the general form by replacing the integer-order time derivative with the time-fractional derivative. The time-fractional Black–Scholes equation is studied based on the Katugampola fractional derivative in Caputo type with given by:
with the initial condition:
and the boundary conditions:
where and .
4. The Generalized Laplace Homotopy Perturbation Method
In this section, we present the basic idea of the generalized Laplace homotopy perturbation method with and for the time-fractional differential equations.
Firstly, we consider the following problem:
with the initial condition:
where R and N are the linear and nonlinear operators and f and h are determined functions.
Step 1. By taking the generalized Laplace transform with respect to time variable t in Equation (12), we obtain:
Step 2. By using the generalized Laplace transform of Katugampola fractional derivative in Caputo type, we have:
Step 3. By taking the inverse generalized Laplace transform on the both sides in Equation (14), we get:
where
Step 4. By applying the homotopy perturbation technique [45,46], the homotopy function is defined by the homotopy equation:
where denote homotopy parameter and is an arbitrary initial approximation satisfying both the initial and boundary conditions of the problem [47].
Note that we can see that when in Equation (15), the homotopy function is the solution of the problem Equation (12). We assume that:
and the nonlinear term can be applied as:
The He’s polynomials can be calculated by using the following formula:
Step 6. By comparing the coefficient of like power of p on both sides of Equation (18), the sequence is carried out:
5. Analytic Solutions for the Time-Fractional Black–Scholes Equation
In this section, we solve the time-fractional Black–Scholes equation Equation (9) subjecting to the initial condition Equation (10) and the boundary conditions Equation (11) by the generalized Laplace homotopy perturbation method.
Note that since the nonlinear term is zero, the He’s polynomials for all .
From the recurrence relation Equation (19), we choose the function by:
We next find the function by using Equation (19). Then,
Therefore,
By Equation (19), we obtain that:
Hence,
It follows from Equation (19) that:
Then,
Like the same manner, we can conclude that by Equation (19),
for . Therefore, by Equation (15), the homotopy perturbation which corresponds to problem Equations (12) and (13) is in the form:
By Equation (20), we obtain the analytic solution of problem Equations (9)–(11) defined by:
or
where is the two-parameters Mittag–Leffler function defined by Equation (6).
Hence, the analytic solution of the time fractional Black-Scholes equations in the sense of Caputo type Katugampola fractional derivative Equations (9)–(11) is given by Equation (21).
It follows from [36] that as , the time-fractional Black–Scholes equation with two assets for the European call option based on Caputo type Katugampola fractional derivative becomes the time-fractional Black–Scholes equation with two assets for the European call option based on Caputo fractional derivative:
with the initial condition:
and the boundary conditions:
where and are constants.
By (21), the analytic solution of the time-fractional Black–Scholes equation with two assets for the European call option in Caputo fractional derivative sense is defined:
which differs from the solution studied in [31]. The reason is why we obtain another solution because choosing the initial function in recurrence relation (19) is different. In the particular case, if we let and then the time-fractional Black–Scholes equation reduces to the classical Black–Scholes equation with two assets as Equation (8). It follows from the property of Mittag–Leffler function with two parpmeters, that is , that the analytic solution of the classical Black–Scholes equation with two assets for the European call option is given by:
which differs from the solution obtained by [32] because choosing the initial function in recurrence relation (19) is different.
We next consider the case when approaches to
More precisely, as approaches to the time-fractional Black-Scholes equation with two assets for the European call option based on Caputo type Katugampola fractional derivative Equations (9)–(11) becomes the time-fractional Black-Scholes equation with two assets for the European call option in sense of the Caputo-Hadamard fractional derivative.
Consider the terms for .
By using the property in Lemma 2 as Equation (7) we have that for each ,
It follows from Equation (21) that the analytic solution of the time-fractional Black–Scholes equation in the Caputo–Hadamard fractional derivative is in the form:
We see that for all This means that is unbounded for any which contradicts to the initial condition: This implies that the time-fractional Black–Scholes equation with two assets in Caputo–Hadamard sense has no solution.
6. Numerical Results
In this section, we illustrate the analytic solution of the time-fractional Black–Scholes equation with two assets for European call option based on Caputo type Katugampola fractional derivative by using Python programming. The financial parameters are given in Table 1.

Table 1.
Parameters of the numerical solutions.
The classical values of the options defined by (22) are simulated in Figure 1. In Figure 2, Figure 3 and Figure 4, we have depicted the values of the options in Equation (21) for and , and , and and respectively. We note that the analytic solution of the time-fractional Black-Scholes equation described in the sense of Caputo type Katugampola fractional derivative and the analytic solution of the classical Black-Scholes equation with both of the two assets are in good agreement. The European call option prices for different values of and are shown in Table 2.
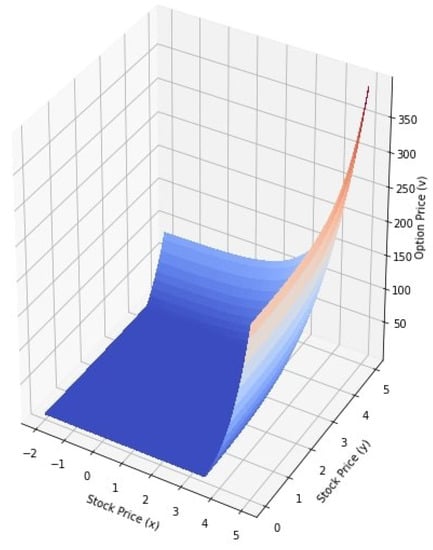
Figure 1.
Values of the options for
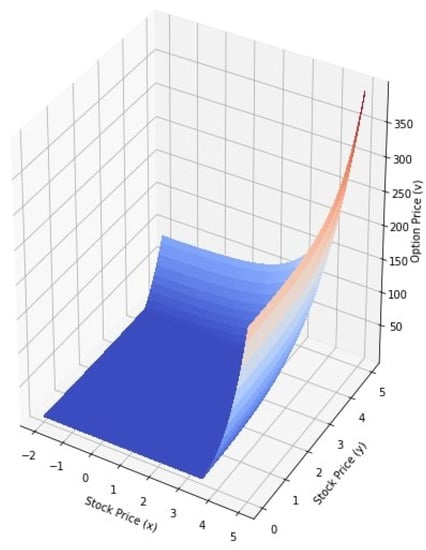
Figure 2.
Values of the options for and
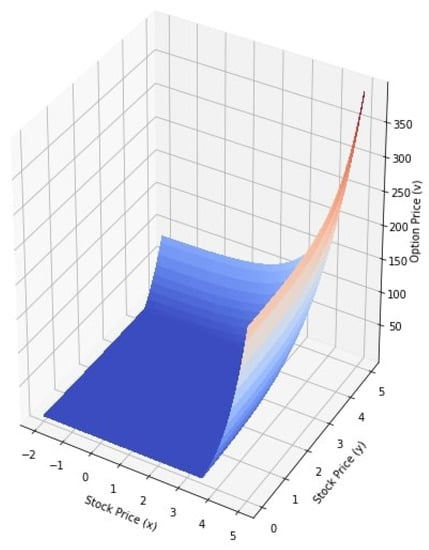
Figure 3.
Values of the options for and
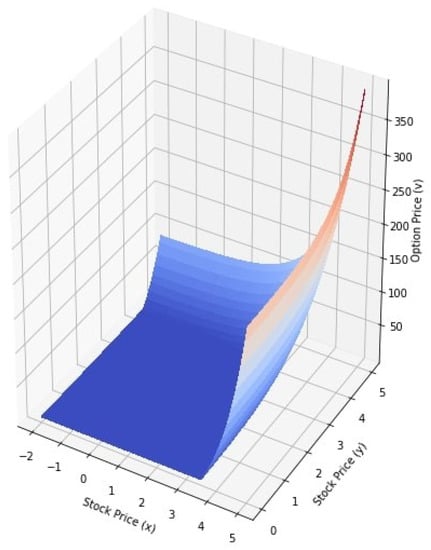
Figure 4.
Values of the options for and

Table 2.
Values of European call option.
We see that in Figure 5 and Figure 6, the values of x and y in the case are greater than the values of x and y in the case This means that the order of the Caputo type Katugampola fractional derivative has an acceleration effect in the diffusion process when On the other hand, in Figure 7 and Figure 8, the values of x and y in the case are less than the values of x and y in the case This implies that the order of the Caputo type Katugampola fractional derivative has a retardation effect in the diffusion process when .
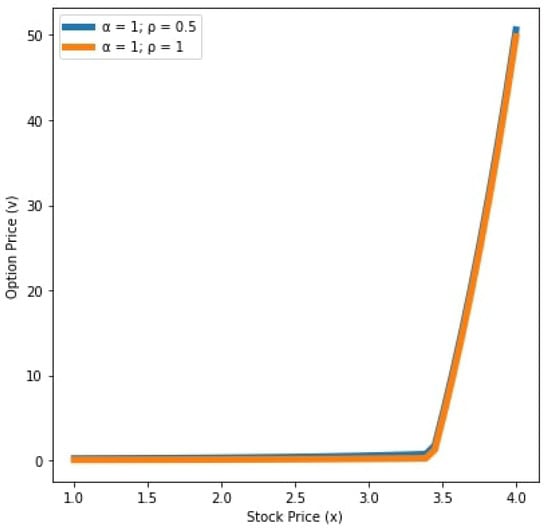
Figure 5.
Values of the options for and years with .
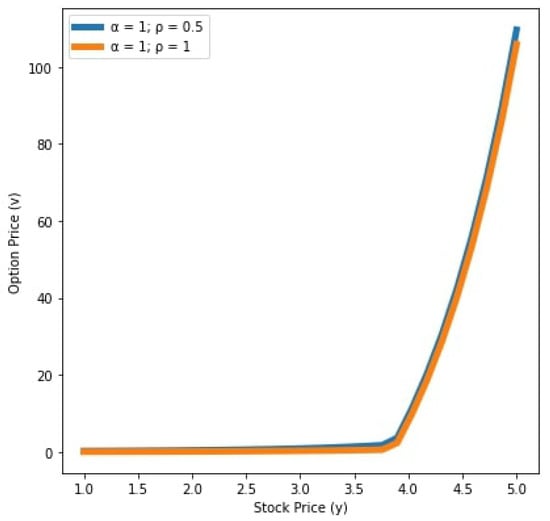
Figure 6.
Values of the options for and years with .
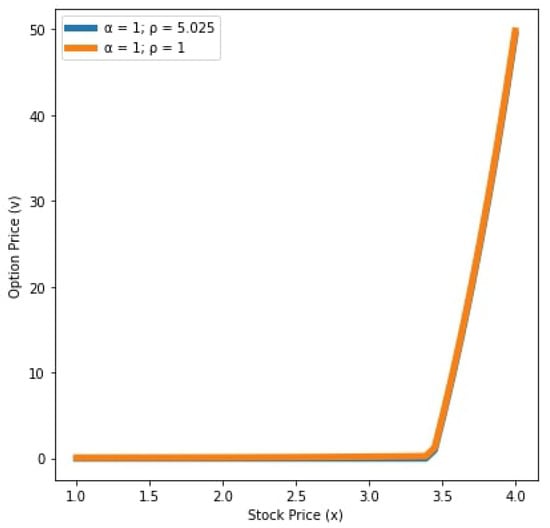
Figure 7.
Values of the options for and years with .
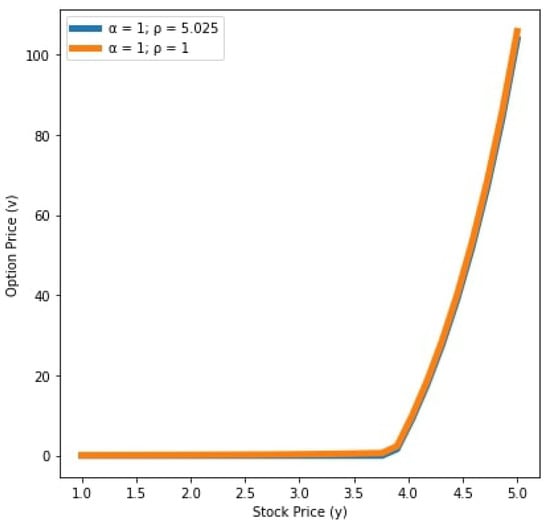
Figure 8.
Values of the options for and years with .
From the Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, we see that the payoff of the European option increases as decreases. Moreover, we observe that the European option price is overpriced when .
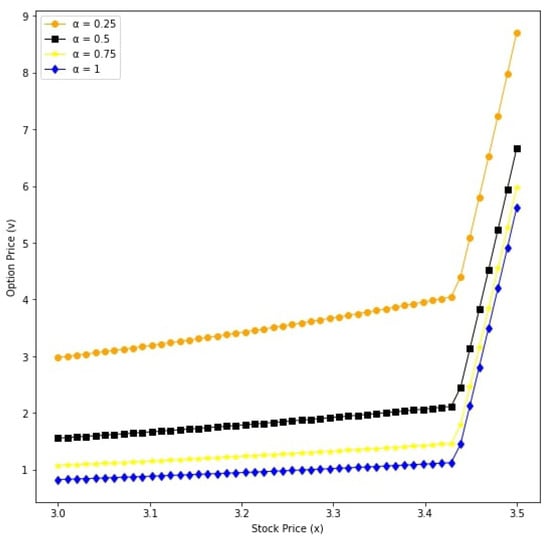
Figure 9.
Option prices with respect to underlying asset x for different values: v for and .
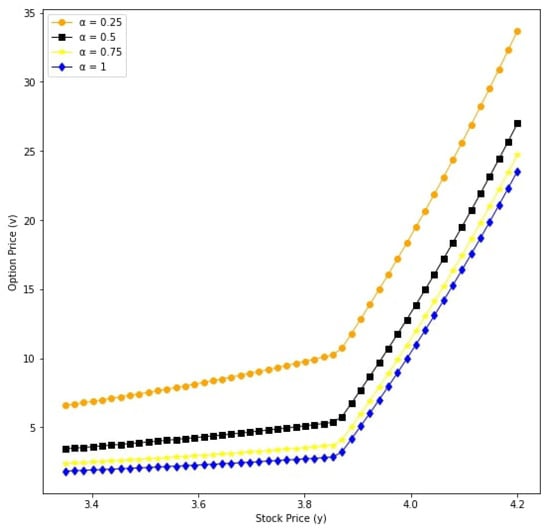
Figure 10.
Option prices with respect to underlying asset y for different values: v for and .
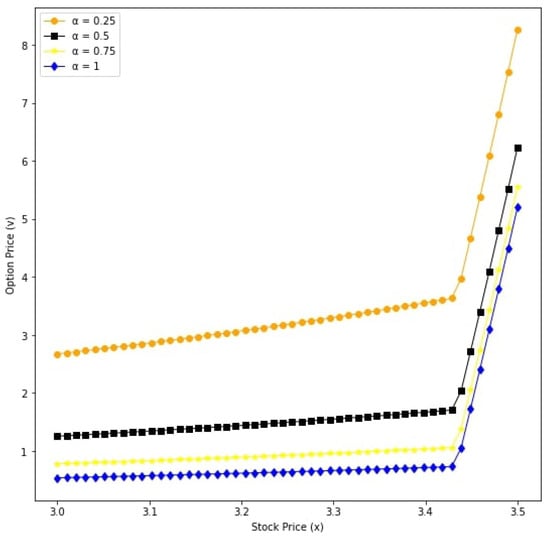
Figure 11.
Option prices with respect to underlying asset x for different values: v for and .
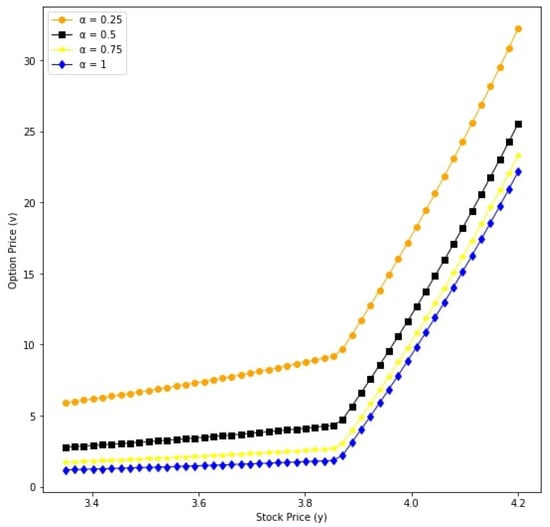
Figure 12.
Option prices with respect to underlying asset y for different values: v for and .
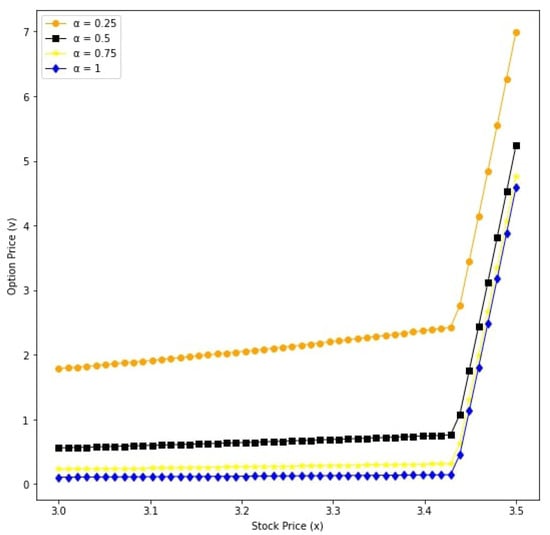
Figure 13.
Option prices with respect to underlying asset x for different values: v for and .
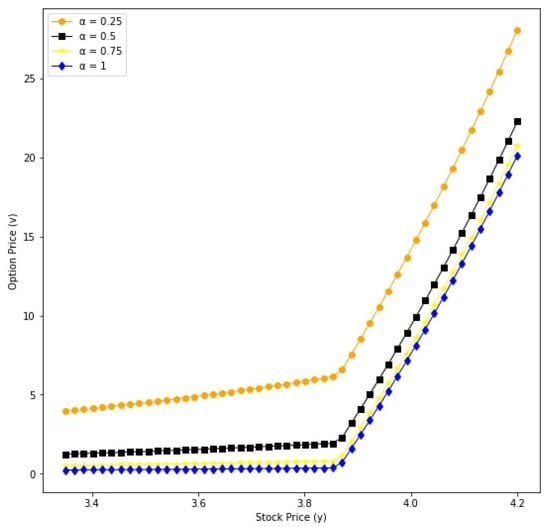
Figure 14.
Option prices with respect to underlying asset y for different values: v for and .
7. Conclusions
In this paper, we have discussed the analytic solution of the time-fractional Black–Scholes equation with two assets in sense of the Katugampola fractional derivative in Caputo type. The method, used here to provide analytical solutions, is called the generalized Laplace homotopy perturbation method. The idea of the generalized Laplace homotopy perturbation method comes from combining the technique of both the homotopy perturbation method and generalized Laplace transform. The result in Equation (21) shows that the analytic solution of the time-fractional Black–Scholes equations in the sense of Caputo type Katugampola fractional derivative can be carried out in the form of the two-parameters Mittag–Leffler function. Since the Katugampola fractional derivative in Caputo type generalizes both Caputo and Caputo–Hadamard derivatives, in the case of the time-fractional Black–Scholes equations in the Caputo derivative sense, the analytic solution is also obtained. Unfortunately, in the case of the time-fractional Black–Scholes equations in the Caputo-Hadamard derivative sense, there is no solution. Moreover, we can observe that the orders and of the Katugampola fractional derivative in Caputo type have an effect on the price of the European option. Moreover, the European option price is overpriced when .
Author Contributions
Conceptualization, P.S.; methodology, P.S. and S.T.; validation, P.S. and S.T.; formal analysis, S.T., W.S. and P.S.; writing—original draft preparation, S.T.; writing—review and editing, W.S. and P.S.; supervision, P.S.; project administration, P.S.; funding acquisition, P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Mongkut’s University of Technology North Bangkok, 133 contract no. KMUTNB-FF-65-58 and this research was partially supported by the Centre of Excellence in 134 Mathematics, PERDO, Commission on Higher Education, Ministry of Education, Thailand.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The information used to support the findings of this study are available in the article, in the links there provided or from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Hristov, T. A transient flow of a non-newtonian fluid modelled by a mixed time-space derivative: An improved integral-balance approach. In Mathematical Methods in Engineering; Springer: Cham, Switzerland, 2019; pp. 153–174. [Google Scholar]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 9, 1461–1477. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Rekhviashvili, S.; Pskhu, A.; Agarwal, P.; Jain, S. Application of the fractional oscillator model to describe damped vibrations. Turk. J. Phys. 2019, 3, 236–242. [Google Scholar] [CrossRef]
- Sene, N. Stokes’s first problem for heated flat plate with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Sofuoglu, Y.; Ozalp, N. Fractional order bilingualism model without conversion from dominant unilingual group to bilingual group. Differ. Equ. Dyn. Syst. 2017, 25, 1–9. [Google Scholar] [CrossRef]
- Tarasova, V.V.; Vasily, V.E. Elasticity for economic processes with memory: Fractional differential calculus approach. Fract. Diff. Calc. 2016, 6, 219–232. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K.; Agarwal, P. New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations. Adv. Differ. Equ. 2015, 18, 1–19. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Application of Fractional Differential Equations. In North Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Katugampola, U.N. New approach to a generalized factional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar]
- Katugampola, U.N. A new approach to generalized factional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional differential equations with dependence on the Caputo-Katugampola derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–413. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal structure in the capital markets. Financ. Anal. J 1989, 45, 32–37. [Google Scholar] [CrossRef]
- Li, H.Q.; Ma, C.Q. An empirical study of long-term memory of return and volatility in Chinese stock market. J. Financ. Econ. 2005, 31, 29–37. [Google Scholar]
- Huang, T.F.; Li, B.Y.; Xiong, J.X. Test on the chaotic characteristic of Chinese futures market. Syst. Eng. 2012, 30, 43–53. [Google Scholar]
- Kumar, S.; Kumar, D.; Singh, J. Numerical computation of fractional Black–Scholes equation arising in financial market. Egypt. J. Basic Appl. Sci. 2014, 1, 177–183. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, 13, 12. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2014, 6, 102–109. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional version of the Black–Scholes model: Approach via expansion in series. J. Nonlinear Sci. 2014, 17, 105–110. [Google Scholar]
- Huang, J.; Cen, Z.; Zhao, J. An adaptive moving mesh method for a time-fractional Black–Scholes equation. Adv. Differ. Equ. 2019, 2019, 516. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black–Scholes equation. J. Comput. Appl. Math. 2017, 17, 1699–1715. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. In Abstract and Applied Analysis; Hindawi: London, UK, 2013. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional Black-Scholes model with new Lagrange multipliers. Comput. Meth. Differ. Equ. 2014, 2, 1–10. [Google Scholar]
- Kumar, S.; Yildirim, A.; Khan, Y.; Jafari, H.; Sayevand, K.; Wei, L. Analytical solution of fractional Black-Scholes European option pricing equation by using Laplace transform. Fract. Calc. Appl. Anal. 2012, 2, 1–9. [Google Scholar]
- Prathumwan, D.; Trachoo, K. On the solution of two-dimensional fractional Black–Scholes equation for European put option. Adv. Differ. Equ. 2020, 2020, 146. [Google Scholar] [CrossRef]
- Sawangtong, P.; Trachoo, K.; Sawangtong, W.; Wiwattanapataphee, B. The Analytical Solution for the Black-Scholes Equation with Two Assets in the Liouville-Caputo Fractional Derivative Sense. Mathematics 2018, 6, 129. [Google Scholar] [CrossRef]
- Trachoo, K.; Sawangtong, W.; Sawangtong, P. Laplace transform homotopy perturbation method for the two dimensional Black Scholes model with European call option. Math. Comput. Appl. 2017, 22, 23. [Google Scholar] [CrossRef]
- Fall, A.N.; Ndiaye, S.N.; Ndolane, S. Black–Scholes option pricing equations described by the Caputo generalized fractional derivative. Chaos Solitons Fractals 2019, 125, 108–118. [Google Scholar] [CrossRef]
- Ampun, S.; Sawangtong, P. The approximate analytic solution of the time-fractional Black-Scholes equation with a European option based on the Katugampola fractional derivative. Mathematics 2021, 9, 214. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Disc. Cont. Dyn. Syst. S 2019, 13. [Google Scholar] [CrossRef]
- Oliveira, D.S.; de Oliveira, E.C. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2019, 10, 81–91. [Google Scholar] [CrossRef]
- Fahd, J.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Res. Nonlinear Anal. 2018, 2, 88–98. [Google Scholar]
- Fahd, J.; Abdeljawad, T.; Baleanu, D. Caputo-type modification of the Hadamard fractional derivatives. Adv. Differ. Equ. 2012, 142, 1–8. [Google Scholar]
- Aljoudi, S.; Ahmad, B.; Nieto, J.J.; Alsaedi, A. A coupled system of Hadamard type sequential fractional differential equations with coupled strip conditions. Chaos Solitons Fractal 2016, 91, 39–46. [Google Scholar] [CrossRef]
- Etemad, S.; Rezapour, S.; Sakar, F.M. On a fractional Caputo–Hadamard problem with boundary value conditions via different orders of the Hadamard fractional operators. Adv. Differ. Equ. 2020, 272, 1–20. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transforms Spec. Funct. 2004, 14, 31–49. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Simon, T. Mittag-Leffler functions and complete monotonicity. Integral Transform. Spec. Funct. 2015, 26, 36–50. [Google Scholar] [CrossRef]
- Contreras, M.; Llanquihuén, A.; Villena, M. On the Solution of the Multi-Assets Black–Scholes Model: Correlation, Eigenvalues and Geometry. J. Math. Financ. 2016, 71, 1772–1783. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. J. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- Baholian, E.; Azizi, A.; Saeidian, J. Some notes on using the homotopy perturbation method for solving time-dependent differential equations. Math. Comput. Model. 2009, 50, 213–224. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).