Abstract
Tank vehicles are widely used for the road transportation of dangerous goods and especially flammable liquid fuels. Existing gross weight limitations, in such transportations, render the self-weight of the tank structure a crucial parameter of the design. For the design and the construction of metallic tank vehicles carrying dangerous goods, the European Standard EN13094:2015 is applied. This Standard poses a minimum thickness for the shell thickness for the tank construction according to the mechanical properties of the construction material. In the present paper, primarily, the proposed design was investigated and a weight minimization of such a tank vehicle with respect to its structural integrity was performed. As test case, a tank vehicle with a box-shaped cross-section and low gross weight was considered. For the evaluation of the structural integrity of the tank construction, the mechanical analysis software ANSYS ® 2019R1 was used. The boundary values and the suitable computation for structural integrity were applied, as they are defined in the corresponding Standards. The thickness of the construction material was decreased to a minimum, lower than that posed by the standards, indicating that the limit posed by them was by no means boundary in terms of structural integrity.
1. Introduction
Tank vehicles are complex mechanical systems consisting of a heavy vehicle and a tank. These tanks can have a cyclical, elliptical, or box-shaped cross-section. Furthermore, their section can be rectangular, wedge-shaped, or cone-shaped and they can be compartmented or not. Moreover, they can be considered as systems where fluid and structure interaction occur [1]. A special type of tank vehicles is this used for the road transportation of liquid and granular dangerous materials. Flammable liquids are a subcategory of dangerous goods transported using tank vehicles. Due to their complexity and their cost of production, these tank vehicles, are, mainly, studied computationally in different level of detail.
Macroscopically, they can be investigated for their dynamic behavior with mathematical models of concentrated mass including [2,3,4,5,6,7] or neglecting [8,9] the sloshing effect of the liquid. Furthermore, their dynamic behavior can be optimized [10,11,12]. Their mechanical response to loads applied by the transported liquid substance can be studied with the use of the finite element method in a mesoscopic level, retrieving the developed stress on the tank structure [13,14,15,16,17] and, microscopically, looking into the behavior of the weldments of tank construction. Moreover, the fatigue [18] of the tank construction and its weldments [19] due to the repetitive loading of the transport can be investigated with the use of the finite element method. Numerical investigation of axle load sharing [20,21] has also been performed. Additionally, in the literature, a few real-life tank vehicle failures have been recorded and analyzed [22,23] and methods for the health monitoring of such tank vehicles have been documented [24].
The safety regulations for tank vehicles carrying dangerous goods are outlined by the “European Agreement Concerning the International Carriage of Dangerous Goods by Road” (ADR): Part 6 – Requirements for the construction and testing of packagings, intermediate bulk containers” [25]. The typical requirements for design, construction, testing, inspection, retesting, qualification and maintenance of such tanks are thoroughly described in the aforementioned text. Tanks, in general, can be divided into categories according to their construction material and their maximum working pressure. If the tank is metallic and its working pressure is not exceeding 0.5 bar, its design and construction is described in the European Standard EN 13094:2015 [26].
According to both the aforementioned Standards, a value for the minimum shell thickness for the tanks with respect to their construction material is provided, along with conditions to further reduce this thickness. An overall minimum thickness value is also provided per material [25,26]. Four different methods for the verification of the design of such a tank are reported in Annex A of the EN13094:2015, namely the (1) dynamic testing, (2) finite element stress analysis, (3) reference design, and (4) calculation method, or a combination of them. In order to perform the dynamic test and use the reference design, the tank needs to be constructed, while the finite stress analysis and the calculation method can be performed right after the preliminary design of the tank, prior to its construction, leaving space for the construction of an optimized design [15]. For the proposed finite element stress analysis and the calculation method, the shell thickness provided by the Standards is considered and the stress values on the shell, the ends, the partitions, and the support of the tank are monitored and compared to the design stress as it is defined in EN13094:2015. Along with these stresses, also the stresses developed on the weldment areas can be monitored and compared to the weldment strength, as it is defined in the EN13094:2015 through the weldment efficiency factor.
In the present paper, the safety factor implied by the Standard was calculated for different shell thicknesses for two typical construction materials. Furthermore, an attempt to investigate a tank design with material thickness below the reduced thickness value was made. In more details, the use of mild steel and a typical aluminum alloy for a tank for the road transportation of liquid fuels was investigated using the minimum shell thickness posed by EN13094:2015. Moreover, the shell thickness for both construction materials of this tank was reduced to the minimum posed by the same Standard and its structural integrity was monitored. Finally, the shell thickness was further reduced to the limits posed by the tensile strength of each material. The simulated tank vehicle consists of three compartments, and has a box-shaped cross-section and a rectangular section. The structural integrity of the tank vehicle was evaluated using the finite element (FE) method through the Computer Aided Engineering (CAE) software ANSYS ® 2019R1. The loading conditions of the FE models were defined according to the EN13094:2015 Standard and the structural integrity of the tank was computed with respect to the tensile strength of each construction material.
2. Materials and Methods
The geometrical model of the tank, built in SolidWorks® Computer Aided Design (CAD) software, consists of the shell walls, the front and rear end, two partitions, and three top openings, simulating the manholes. On the bottom area of the tank shell there are two supports with two mounting plates each. In Figure 1 the geometrical model of the tank is presented along with the detail of one of its supports with the attached plates. The supports consist of two bodies, a sheet metal mounted on the shell walls of the tank and a box-shaped support body.
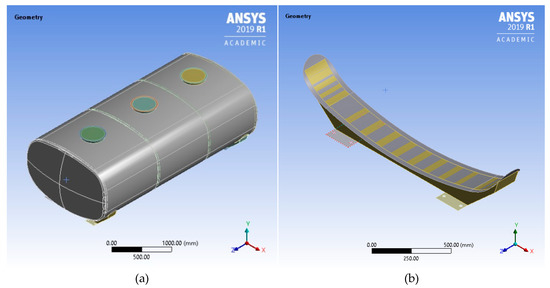
Figure 1.
(a) The 3D CAD model of the tank and (b) detail of the mounting on the vehicle.
The overall dimensions of the tank are presented in Table 1.

Table 1.
Overall tank dimensions in m.
The different components of the tank are considered to be in a fully bonded contact simulating weldment. Thus, the shell walls of the first compartment are in contact with the front end, the shell walls of the second compartment are in contact with the first partition, and the shell walls of the third compartment are in contact with the second partition and the rear end. Finally, each shell wall is in contact with the corresponding top opening.
The tank is mounted on the vehicle with the two supports, each one having two mounting plates bolted with four bolts each on corresponding plates welded on the frame of the vehicle. The sheet metal of each support is in contact with the shell walls of the corresponding compartment and support body. Finally, two mounting plates area in contact with each support body. The relative placement of the tank with its supports to the axles of the heavy vehicle is presented in Figure 2.
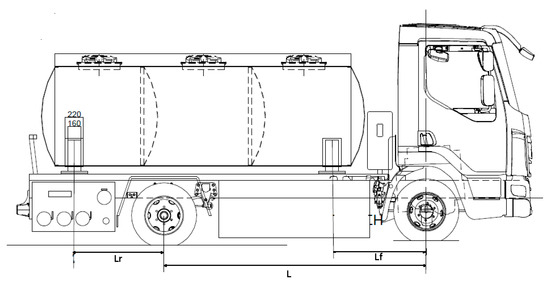
Figure 2.
Tank mounting on the heavy vehicle.
The distance (L) between the two axles is equal to 3.15 m, while the distance of the front support to the front axle (Lf) is 1.13 m and the distance of the rear support to the rear axle (Lr) is 1.08 m. The capacity of the tank is 7100 L, with the first compartment having a capacity of 2500 L and the second and the third one of 2300 L.
2.1. Minimum and Reduced Shell Thickness with Respect to Construction Material
According to EN13094:2015, and specifically paragraph 6.9.1, the minimum shell thickness depends on the construction material and the cross-sectional diameter of the tank. If the cross-section of the tank is not circular, then an equivalent diameter shall be calculated on the basis of the cross-sectional area [26]. The equivalent diameter of this tank is equal to 1.6 m, thus, the minimum thickness of its shell, according to the Standard, if mild steel is considered as construction material, is 5 mm. If a different material is used, its minimum shell thickness is calculated using Equation (1).
where is the minimum shell thickness of mild steel, is the minimum tensile strength, and is the minimum percentage elongation after fracture of the material used. For a typical aluminum alloy, EN 5182 H111, according to the Standard 14268:2008 [27], its minimum tensile strength equals 280 MPa and its minimum elongation equals 26%, resulting in minimum shell thickness of 6.2 mm.
Further reduction of the shell thickness can be performed with the use of paragraph 6.9.2.3, since the maximum tank compartment capacity is less than 3500 L, to 3 mm if mild steel is used and 4.2 mm if aluminum alloy is used as construction material. The shell thicknesses posed by EN13094:2015 are summarized in Table 2.

Table 2.
Shell thickness according EN13094:2015.
2.2. Finite Element Models
Two surface FE models were built simulating the tank with different construction material. The physical and mechanical properties of both construction materials are summarized in Table 3.

Table 3.
Physical and mechanical properties of aluminum alloy and mild steel.
The design stress was calculated with respect to the yield stress and the ultimate tensile strength of each material using Equation (2).
For the calculation of the weldment strength and the weldment design strength, the weld efficiency factor of 0.8 was used as a factor to the yield stress and the design stress, respectively, for each material [26].
The mesh in both FE models was identical and it is presented in Figure 3. The mesh consisted of SHELL181 surface FE and CONTA174 and TARGE170 surface contact FE. The criterion for meshing was uniformity and, after a convergence study, the maximum edge length of 50 mm was selected. SHELL181 is a FE suitable to model thin to moderately thick shell structures, such as pressure vessels and tanks [28,29]. SHELL181 consists of 4-nodes with six degrees of freedom at each node, three translational and three rotational ones, and it employs a five-point integration rule. The CONTA and TARGE elements were used to simulate the weldments between the parts of the tank, i.e., the shells to the ends, the shells to the partition, the shells to the supports, and the supports to the mounting plates. Both FE models consisted of 13,915 FE and 14,474 nodes. The average element quality of the mesh was 0.93. The metric of the element quality, for shell elements, is based on the ratio of the area of the elements to the sum of the square of the edge lengths and the value of 1.00 denotes a perfect square or an equilateral triangle.

Figure 3.
Finite element model of the tank.
For the FE analysis, the Sparse Direct solver was used, since it is suitable for structural linear analysis and, after a comparison with the iterative Preconditioned Conjugate Gradient solver, required less computational time.
In both FE models the material thickness for the supports was 6 mm and for the mounting plates was 20 mm.
2.3. Loading Conditions
In order to investigate the influence of the construction material and the shell thickness on the structural integrity of the tank, the loading conditions (LC) described in the Standard EN13094:2015 were implemented in each FE model. According to this Standard [26], the shell walls, the shell ends, the partitions, and their attachments shall be designed to withstand the stresses developed due to the (1) dynamic, (2) pressure, and (3) partial vacuum conditions. According to these conditions, the seven following LC were implemented.
As far as the dynamic conditions were concerned, four different LC simulating braking (LC1), cornering (LC2), and rollover (LC3 and LC4) were considered as follows:
- Acceleration of 2 g acting on the maximum design mass in the direction of the travel (Z axis).
- Acceleration of 1 g acting on the maximum design mass at right angles of the travel (X axis).
- Acceleration of 1 g acting on the maximum design mass vertically, upwards (Y axis).
- Acceleration of 2 g acting on the maximum design mass vertically downwards (- Y axis).
The abovementioned loads were applied along with the pressure of the breathing devices (Pts) consisting of LC1 to LC4. These LCs were applied once considering the payload of each compartment separately and once considering the total payload of the tank. In both cases the maximum design mass was considered, taking into account the full capacity of the tank/compartment and, as transported substance, water with density equal to 1.00 .
The pressure conditions simulated the pressure test of the full tank (LC5) and the pressure test per compartment (LC6). For LC5 the applied load was the maximum value of:
- The pressure created by a column of water equal to twice the depth of the tank multiplied by the density of the relative density of the denser substance.
- The pressure created by a column of water equal to twice the depth of the tank.
- 1.3 times the working pressure.
The load for LC6 was considered as the test pressure which equaled to 1.3 × (Pts + Pta) where Pts is the pressure of the breathing devices, which was equal to 0.012 MPa, while Pta is the pressure corresponding to the maximum design mass, which was also equal to 0.012 MPa for this tank. LC6 was applied considering the payload of each compartment separately.
Finally, in LC7, which simulated the vacuum condition, a pressure of 3 kPa below atmospheric pressure, was applied as load.
In all the aforementioned LCs the self-weight of the tank was taken into consideration using standard Earth gravity of 9.8 m/s2 acting on Y axis with downwards direction and the lower surface of each mounting plate was considered fully constrained, simulating the bolted connection of the tank to the frame of the heavy vehicle.
In Table 4 the type of load for each LC, its maximum value, and the area of its application are presented.

Table 4.
Maximum loading.
The pressure and the hydrostatic pressure loads simulated the added mass of the transported substance.
3. Results
In this section the results of the FE analysis for all the LC are presented, in terms of maximum values and contours of equivalent von Mises stress (SEQV), in order to identify the most dangerous LC and the areas of the tank construction that are more susceptible to damage. Furthermore, the highest stress developed on the areas of weldments is presented. Finally, the reaction forces on the mounting plates are monitored for the most dangerous LC, since they have an impact on the bolted connection of the tank construction to the frame of the heavy vehicle. The results of the LC considering the total payload (LC1–LC5 and LC7) are presented separately from those considering the payload of each compartment (LC1–LC4 and LC6). Firstly, the results are presented for the minimum material thickness, then for the reduced one, and, finally, the results for the weight minimization process are presented.
3.1. Minimum Thickness of Construction Material
In Figure 4 the maximum values of SEQV are presented for the minimum thickness (6.2 mm for aluminum alloy and 5.0 mm for mild steel) for (a) the LCs that considered the total payload of the tank and (b) the LCs that considered the payload per compartment.
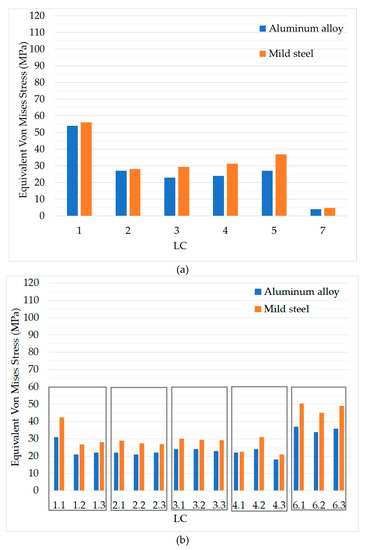
Figure 4.
Maximum values of equivalent von Mises stress (SEQV) for both construction materials for (a) LC1–LC5 and LC7 and (b) LC1–LC4 and LC6.
For the first type of LCs (total payload) the most dangerous LC was LC1, while for the second type of LCs (payload per compartment) LC6 was the most dangerous one. Still considering the design stress for both materials (Table 3), the overall maximum value of SEQV (55 MPa for LC1 and mild steel and 54 MPa for LC1 and aluminum alloy) was lower, regardless construction material.
The SEQV contours did not depend on the material. For this reason, in Figure 5 the SEQV contours for LC1–5 and LC7 considering the total payload of the tank are presented for the FE using aluminum alloy as construction material.
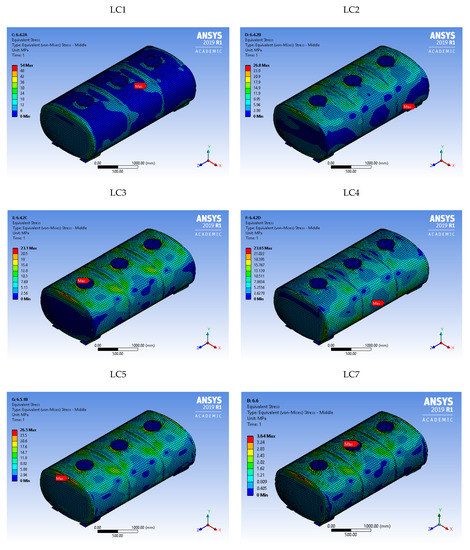
Figure 5.
SEQV contours for LC1–5 and LC7.
In Figure 6 the SEQV contours for LC6 are presented per compartment for aluminum alloy used as construction material.
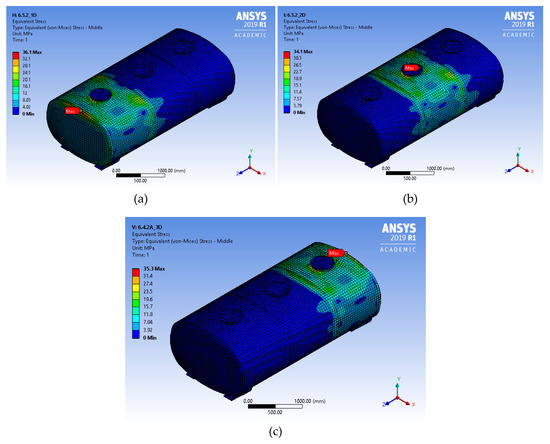
Figure 6.
SEQV contours for LC6 per compartment (a) 1 (b) 2 and (c) 3.
The SEQV contours, as well as the areas of the maximum value of SEQV, flagged in each figure, were the same, regardless of construction material, but their maximum value changed. The areas of the overall maximum values of SEQV per LC are listed in Table 5.

Table 5.
Areas of highest SEQV values per LC.
Detailed SEQV plots for the highest stressed component are provided for LC1–5 and LC7 in Figure 7 for the FE model using aluminum alloy as construction material. The area with the red color is the area of highest SEQV value.

Figure 7.
Detailed SEQV contours of the highest stressed components for LC1–5 and LC7.
The SEQV contours of components with the highest SEQV value for LC6 for each compartment are presented in Figure 8.
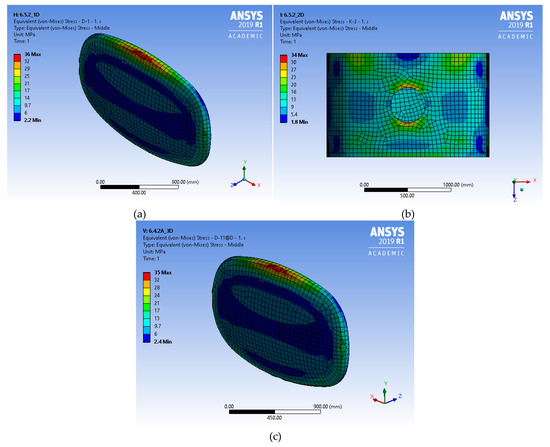
Figure 8.
Detailed SEQV contours for LC6 per compartment (a) 1, (b) 2, and (c) 3.
The stress developed on the weldments was also monitored in both FE models for all LCs for both construction materials. The weldments that had the highest frictional stress values were those of the shell walls to the ends or the partitions. In Table 6 the maximum frictional stress values for these weldments are presented for all LCs for both construction materials.

Table 6.
Contact stresses on weldments between the shell and the ends/partitions for both construction materials.
Regarding the weldments the most dangerous LC was LC6 for the first compartment with maximum value of frictional stress 37 MPa. Although the maximum values of frictional stress depended on the construction material, the frictional stress contours of frictional stress did not. In Figure 9 the frictional stress contours are provided for the weldments of the ends/partitions to the shell walls for the LCs that considered the total payload.
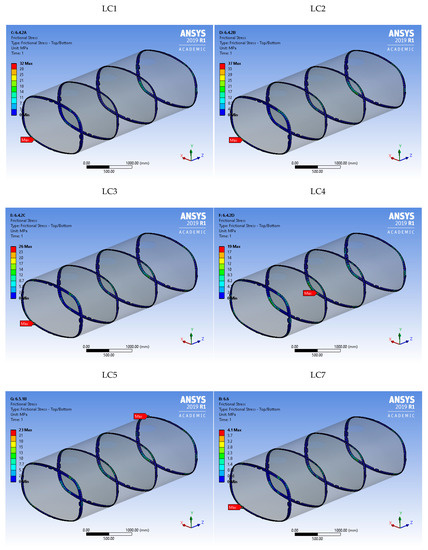
Figure 9.
Detailed frictional stress contours of the highest stressed weldments for LC1–5 and LC7.
In Figure 10 the frictional stress contours are presented for the same weldments for LC6, per compartment.
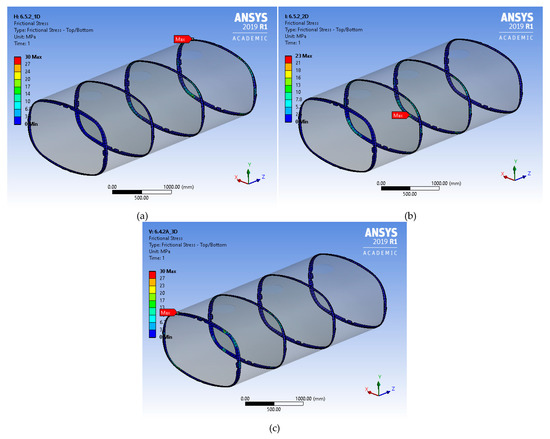
Figure 10.
Detailed frictional stress contours for LC6 per compartment (a) 1, (b) 2, and (c) 3.
In Figure 11 the values of the reaction forces per plate and force direction, according to the global coordinate system for both FE models, are presented for two LCs. Plates 1 and 2 are welded on the front support while plates 3 and 4 are welded on the rear support.
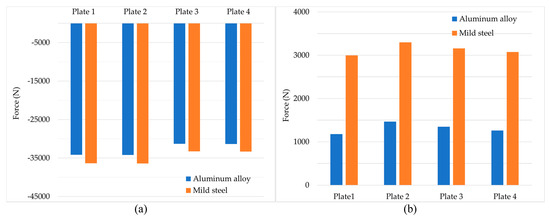
Figure 11.
Reaction force (a) on Z-axis for LC1 and (b) on Y-axis for LC5.
The reaction forces represent the forces acting on the bolted connection of the tank construction to the frame of the vehicle. Since the bolted connections are susceptible to failure due to shear stress, LC1, which simulated the braking of the tank vehicle having its total payload and led to the highest values of reaction forces on Z-axis, was selected. Additionally, the reaction forces on Y-axis in LC5 that simulates the pressure test of the tank vehicle are presented. During this LC the reaction forces were developed due to the self-weight of the tank construction.
In Figure 11 it is shown that the construction material influenced the values of the reaction forces on the mounting plates of the tank with mild steel resulting in higher values of reaction forces in both LCs. This phenomenon was more pronounced in LC5 where the tare weight of the tank was considered. Moreover, it is obvious that in LC1 the reaction forces on Z-axis had slightly higher values on the front support. However, when the reaction forces on Y-axis for LC 5 were considered it was shown that both supports were equally loaded. The almost equal distribution of the reaction forces to the two supports of the tank support the choice for the placement of the supports along the tank and with respect to the axles of the heavy vehicle.
The values of the reaction forces are decisive for the diameter and the category of the bolts that should be used to mount the tank on the frame of the heavy vehicle. Using the von Mises’ criterion that accounts for both the normal and the shear stress developed on the cross-section of the bolts due to the reaction forces, the bolts should withstand the loads. A safety coefficient in the area of 1.5 should also be considered.
3.2. Reduced Shell Thickness
In Figure 12 the maximum values of SEQV are presented for the reduced shell thickness (4.2 mm for aluminum alloy and 3.0 mm for mild steel) for (a) the LCs that considered the total payload of the tank and (b) the LCs that considered the payload per compartment.
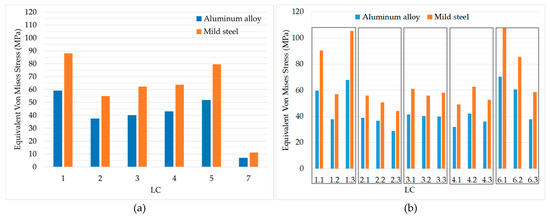
Figure 12.
Maximum values of SEQV for both construction materials for (a) LC1–LC5 and LC7 and (b) LC1–LC4 and LC6.
LC1 had the maximum value of SEQV considering the LCs with total payload. Considering the LCs per compartment, LC6 for the first compartment and LC1 for the third compartment provided the higher values of SEQV. Moreover, all maximum stress values were increased for both materials with the decrease of the shell thickness but the SEQV contours remained the same as when using minimum shell thickness.
Using the reduced material thickness it was still obvious (Figure 12) that mild steel provided higher values of SEQV, reaching 70 MPa for the third compartment in LC6 when using aluminum alloy and 110 MPa for the same LC when mild steel was used as construction material.
In Table 7 the maximum contact stress values are presented for all LCs.

Table 7.
Contact stresses on weldments between the shell and the ends/partitions for both construction materials.
The values of the maximum frictional stress increased with the reduction of the shell thickness.
In Figure 13 the values of the reaction forces per plate and force direction, according to the global coordinate system for both FE models, are presented for LC1 and LC5.
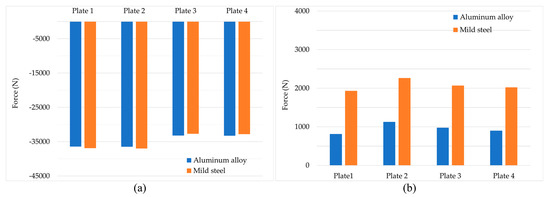
Figure 13.
Reaction force (a) on Z-axis for LC1 and (b) on Y-axis for LC5.
The values of the reaction forces for LC1 remained the same as when using material of minimum thickness, however they were reduced in LC5, since they depended on the self-weight of the tank.
3.3. Weight Minimization
For the minimization of the weight of the tank construction, the thickness of both construction materials was reduced from 4.0 mm up to 2.0 mm with a step of 0.5 mm for the shell, the ends, and the partitions, and the maximum SEQV was monitored for all LCs for both aluminum alloy and mild steel used as construction material. Reduction of the shell material thickness reflected to the tare weight of the tank construction and consequently to the weight of the liquid fuel that can be transported when gross mass limitations were taken under consideration.
In Table 8 the resulting tare weight of the tank construction for all cases is presented.

Table 8.
Tare weight of the tank construction for mild steel and aluminum alloy.
In order to evaluate the effect of the weight minimization to the tank construction the most dangerous LCs were selected. Consequently, the maximum values of SEQV for LC1 and LC5 were considered for the LCs that considered the total payload of the tank and LC6 for the loads that took into account the payload of each compartment separately.
In Figure 14, the ratio of the maximum value of SEQV to yield stress, for each design point and both materials, is presented for LC1 and LC5 that considered total payload.
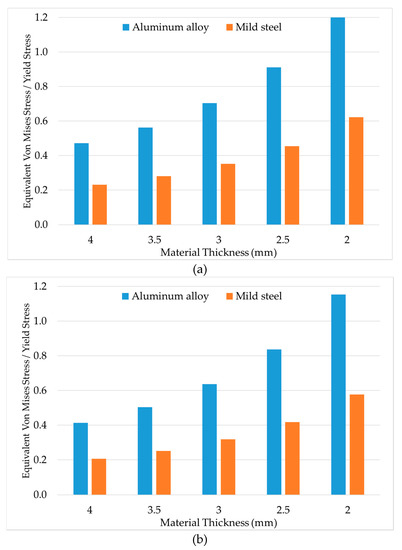
Figure 14.
Maximum value of SEQV for (a) LC1 and (b) LC5 with aluminum alloy and mild steel used as construction material.
In Figure 15 the maximum value of SEQV, per compartment for all design points and both materials, is presented for LC6.
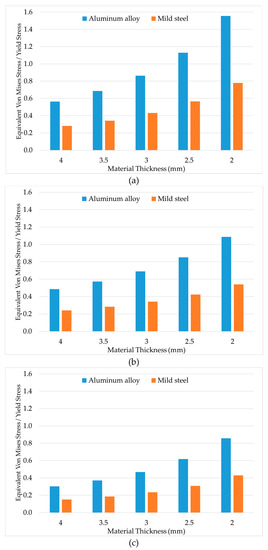
Figure 15.
Maximum value of SEQV for LC6 with aluminum alloy and mild steel used as construction material for the (a) first, (b) second, and (c) third compartments.
It can be noted (Figure 14 and Figure 15) that when using aluminum alloy with thickness of 2.5 mm as construction material the maximum SEQV value was higher than the yield stress in LC6.2. On the other hand, when using mild steel with thickness of 2.0 mm there was no yield in any loading case.
In Figure 16, the ratio of the highest stress value on the weldments to the weldment strength (Table 3) is provided, for the most dangerous loading case, which was LC6 for the second compartment. The weldment strength was not reached for any thickness or material.
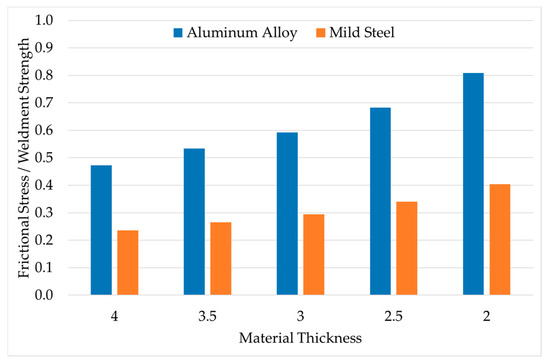
Figure 16.
Contact stresses on weldments between the shell and the ends/partitions when aluminum alloy is used as construction material.
4. Discussion
According to the aforementioned Standards, for the construction of a tank for the transportation of liquid fuels the minimum thickness of the material used for the shell, the ends, and the partitions has to be 5.0 mm, if the material is mild steel and 6.2 if the used material is aluminum alloy. Because of the cross-sectional geometry of the tank and the compartment capacity, further reduction of the shell thickness can be performed and for aluminum alloy the thickness can be 4.2 mm while for mild steel 3.0 mm. The tare weight of the tank (including its support and the mounting plates) was calculated for all four cases (Table 9).

Table 9.
Tare weight of the tank construction for mild steel and aluminum alloy for minimum and reduced shell thickness.
The maximum gross weight of such a tank vehicle is 12,000 kg and the tare weight of the heavy vehicle alone can be estimated to 5500 kg, leaving for the tank construction the maximum weight of 6500 kg. The tank has also accessories, i.e., openings and closures, that weight, approximately, 350 kg, meaning that the gross weight of the tank is 6150 kg.
For the minimum shell thickness, in the case of aluminum alloy, the tare weight of the tank consisted of almost 8% of the tank gross weight, while this percentage increased to 21% if mild steel was used as construction material. The weight of the supports and the mounting plates was equal to 58.6 kg and 173.0 kg if aluminum alloy and mild steel was used as construction material, respectively, consisting of approximately 11% for aluminum alloy and 14% for mild steel of the self-weight of the tank. Moreover, for the reduced shell thickness, the tare weight of the tank became 6% of its gross weight if aluminum alloy was used and 14% if mild steel was used. The weight of the supports and the mounting plates rose to 16% and 21%, respectively, of the tare weight of the tank.
The tank self-weight influenced the payload of tank. If UN1202 (Diesel Fuel) [25] is considered as the carried substance, with density of 0.85 , then the degree of filling for each tank could be calculated (Table 10).

Table 10.
Payload and degree of filling of the tank for minimum and reduced thickness for both construction materials considering UN1202 as transported material.
It is worth mentioning that the tank can be filled with the carried substance up to, approximately, 94% (maximum filling degree).
In Figure 4 and Figure 12 the maximum SEQV values per loading case for minimum and reduced shell thickness, for both construction materials, were presented. Using the ratio of overall maximum SEQV value per construction material to the design stress, the material usage (MU) and the implied safety factor (Sfd) for each tank construction can be provided (Table 11).

Table 11.
Material usage and safety factor per shell thickness for both construction materials.
It is obvious that the implied safety factor with respect to the design stress by the Standard was lower for aluminum alloy compared to mild steel. Two more safety factors could be calculated: The safety factor to yield (Sfy) and to failure (Sfu), using yield stress and ultimate strength, respectively (Table 12).

Table 12.
Safety factor with respect to yield stress and ultimate strength per shell thickness for both construction materials for reduced thickness.
Regarding weldments, the Sf for the minimum shell thickness was 2.7 for aluminum alloy and 3.81 for mild steel, while for reduced thickness the Sf reduced to 1.7 and 2.4, respectively.
In Figure 14, Figure 15 and Figure 16 it is obvious that for the aluminum alloy the shell thickness could not be reduced further than 3.0 mm without risking the structural integrity of the tank, while the shell thickness for mild steel could be reduced up to 2.0 mm. In Figure 17 the Sfy, for all loading conditions, is presented for a tank constructed with aluminum alloy of 3.0 mm thickness and mild steel of 2.0 mm thickness.
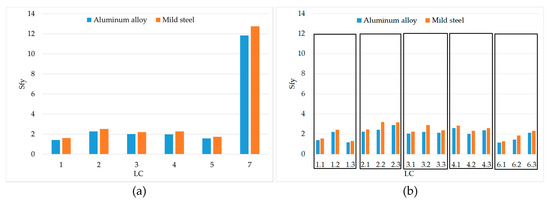
Figure 17.
Safety factor with respect to yield stress for all LCs considering full tank using (a) aluminum alloy (3.0 mm) and (b) mild steel (2.0 mm) as construction material.
The minimum value of the Sfy for aluminum alloy was 1.2 while for mild steel it was 1.3. The Sfy of the weldments of these shell thicknesses were 1.7 for aluminum alloy and 2.5 for mild steel.
5. Conclusions
In the present paper, FE analysis was performed on a two-axle tank vehicle with a box-shaped cross-section, three compartments, and total capacity equal to 7100 L. In the FE analysis two different construction materials, aluminum alloy and mild steel, and different shell thicknesses were considered. Their mechanical behavior in the LCs posed by the EN13094:2015 Standard was investigated. As it was expected, the use of aluminum alloy as construction material resulted in a lighter construction with lower values of SEQV. The LC with the highest value of SEQV was LC1 when the total payload was considered and LC6 when the payload per compartment was considered. At this point, it is important to note that for LC1–4 water was considered as the transported substance and the degree of filling was set equal to 100%, leading to overestimation of the developed stress on the construction of about 20%. As far as the weldments were concerned, the ones with higher stress values were those of the shell walls to the ends/partitions and the most dangerous LC was LC6. The values of the reaction forces on the mounting plates were slightly influenced by the construction material, but almost equally distributed between the front and the rear support.
For both the minimum and the reduced thickness it was proven that the Standard implied a different safety factor, Sf, which was higher for mild steel. Reducing the shell material thickness, the difference between the safety factors reduced and for aluminum alloy a safety factor of 1.4, while for mild steel of 1.6 was implied. This safety factor can be correlated to the ability of the tank construction to withstand the implication to a road accident. Actually, it implies that the structural integrity of the tank is not endangered for loads higher that the ones used in the performed FE analysis by this factor. Two more safety factors have been introduced, Sfy, indicating that in the case of a road accident, the tank construction will not yield and, Sfu, that it will not break causing leakage of the transported flammable liquid. Subsequently, further reduction of the shell thickness was performed in both FE models reducing it below the reduced shell thickness posed by the Standards and the same LCs were investigated. The minimum shell thickness, to avoid yield, was 3.0 mm for aluminum alloy and 2.0 mm. The applied loads that would lead to yield of the construction material were almost 15% higher than the applied loads in the FE model for aluminum alloy and 30% for mild steel. The safety factor with respect to the design stress (Sf) was of the same magnitude (1.3) for shell thickness of 4.0 mm for aluminum alloy and 2.5 mm for mild steel.
Using the FE method, it was shown that the construction material is crucial to the performance of the tank construction. A tank constructed with aluminum alloy can exploit more efficiently its capacity, maximizing its payload, which is translated to more efficient road transport while a tank constructed with mild steel is more resistant to the applied loads. Furthermore, the safety factor implied by the Standard, is higher for mild steel.
Through the performed weight minimization, it was shown that the thickness of both construction materials could be decreased to a minimum, lower than that posed by the EN13094:2015 Standard, without risking the structural integrity of the construction in the typical loading conditions. On the other hand, tanks constructed with aluminum alloy with 3.0 mm thickness or with mild steel with 2.0 mm thickness would be more susceptible in the case of an accident, when probably the construction material will yield, incapacitating the tank. Concluding, it is important to note that the self-weight of the tank is very crucial since weight restrictions, according to national laws, refer to the gross weight of the tank and its minimization.
Author Contributions
D.K. and C.V. have contributed equally to the work for conceptualization, writing, data curation, analysis, investigation, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This research was co-financed by the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call RESEARCH – CREATE – INNOVATE (T1EDK-03459).


Conflicts of Interest
The authors declare no conflict of interest.
References
- Shimanovsky, A.O. Recent Research of Dynamics and Strength of Tank Vehicles. Mech. Mach. Mech. Mater. 2016, 36, 59–70. [Google Scholar]
- Mantriota, G. Directional stability of articulated tank vehicles: A simplified model. Heavy Veh. Syst. 2003, 10, 144–165. [Google Scholar] [CrossRef]
- Ranganathan, R.; Rakheja, S.; Sankar, S. Influence of liquid load shift on the dynamic response of articulated tank vehicles. Veh. Syst. Dyn. 1990, 19, 177–200. [Google Scholar] [CrossRef]
- Ranganathan, R.; Yang, Y.S. Impact of liquid load shift on the braking characteristics of partially filled tank vehicles. Veh. Syst. Dyn. 1996, 26, 223–240. [Google Scholar] [CrossRef]
- Rakheja, S.; Sankar, S.; Ranganathan, R. Roll plane analysis of articulated tank vehicles during steady turning. Veh. Syst. Dyn. 1988, 17, 81–104. [Google Scholar] [CrossRef]
- Sankar, S.; Ranganathan, R.; Rakheja, S. Impact of dynamic fluid slosh loads on the directional response of tank vehicles. Veh. Syst. Dyn. 1992, 21, 385–404. [Google Scholar] [CrossRef]
- Zheng, X.; Li, X.; Ren, Y. Equivalent mechanical model for lateral liquid sloshing in partially filled tank vehicles. Math. Probl. Eng. 2012, 1–22. [Google Scholar]
- Peňáz, J.; Voltr, O. Dynamic Analysis of behavior of three-axle semi-trailer road tank going on special waved roadway. Period. Polytech. Transp. Eng. 2013, 41, 139–142. [Google Scholar] [CrossRef]
- Papadogiannis, A.; Michaelides, P.; Michalos, G.; Chondros, T. Road Tanker Design and Dynamic Response Simulation. Int. Rev. Mech. Eng. 2017, 11. [Google Scholar] [CrossRef]
- Koulocheris, D.; Dertimanis, V.; Spentzas, C. On the estimation of optimum structural parameters for a triaxial fixed-tank vehicle. In Proceedings of the 21st International Automotive Conference” Science & Motor Vehicles 07”, Belgrade, Serbia, 24–25 April 2007. [Google Scholar]
- Koulocheris, D.V.; Dertimanis, V.K. Calculation of a Fixed–Tank Vehicle Optimum Dynamic Performance. Procedia Soc. Behav. Sci. 2012, 48, 2230–2240. [Google Scholar] [CrossRef][Green Version]
- Koulocheris, D.V.; Dertimanis, V.K.; Spentzas, K.N. Analysis and optimization of a fixed-tank vehicle. Forsch. Im Ing. 2006, 70, 171–178. [Google Scholar] [CrossRef]
- Shimanovsky, A.O.; Kuznyatsova, M.G.; Pleskachevskii, Y.M. The strength analysis of the partitions in road tank reservoirs. Procedia Eng. 2012, 48, 607–612. [Google Scholar] [CrossRef]
- Koulocheris, D.V.; Vossou, C.G. Alternative Design for a Semi-Trailer Tank Vehicle. Vehicle Vozila I 2018, 51–69. [Google Scholar] [CrossRef]
- Vossou, C.; Koulocheris, D. A Novel Tank Vehicle Design Approach. In Proceedings of the IC-EPSMSO2019, Athens, Greece, 3–6 July 2019. [Google Scholar]
- Koulocheris, D.; Vossou, C. Finite Element Stress Analysis Vs Calculation Method For The Construction Of A Metallic Tank Used For Dangerous Goods Transportation. In Proceedings of the 2017 JUMV Automotive Conference, Belgrade, Serbia, 19–20 April 2017. [Google Scholar]
- Koulocheris, I.D.V.; Vossou, I.C.G. Computational assessment of a cylindrical tank vehicle structural integrity. In Proceedings of the 11th HSTAM International Congress on Mechanics, Athens, Greece, 27–30 May 2016. [Google Scholar]
- Savaidis, G.; Malikoutsakis, M.; Savaidis, A. Finite element simulation of road tanks for ADR and fatigue assessments. Int. J. Struct. Integr. 2013, 4, 383–395. [Google Scholar] [CrossRef]
- Sykaras, K.; Malikoutsakis, M.; Loulas, M.; Mihailidis, A. Parametric design and Finite Element Analysis of metallic tanks transporting dangerous goods. In Proceedings of the MATEC Web of Conferences, Thessaloniki, Greece, 7 August 2018; Volume 188, p. 04003. [Google Scholar] [CrossRef]
- Papadogiannis, A.S.; Farmakopoulos, A.G.; Chondros, T.G. Road tankers axles load share design. Int. J. Heavy Veh. Syst. 2010, 17, 256–275. [Google Scholar] [CrossRef]
- Papadogiannis, A.; Chondros, T. Road Tanker Design for Axle Load-Share and Lateral Stability. Proc. High. Educ. Inst. Machine 2013, 5, 49–59. [Google Scholar]
- Weltschev, M.; Schwarzer, S.; Otremba, F. Comparison of the operating life of tank containers, tank vehicles and rail tank cars for the carriage of dangerous goods in practice, analysis of causes of damage. Chem. Eng. 2013, 31, 559–564. [Google Scholar]
- Chondros, T.G.; Chondrou, D.T.; Papadigiannis, A.S.; Chondrou, I.T.; Fainekos, E.; Panteliou, S.D. Design Verification and Testing of Road Tankers Transporting Dangerous Goods. Извecmuя выcwux cyчeбhыx зaвeдehuй. Mawuhocmpoehue 2019, 2, 707. [Google Scholar] [CrossRef]
- Savaidis, G.; Malikoutsakis, M.; Jagenbrein, A.; Savaidis, A.; Soare, M.; Predoi, M.V.; Soare, A.; Diba, I.C. Structural Integrity and Health Monitoring of Road and Railway Tanks based on Acoustic Emission. Sdhm: Struct. Durab. Health Monit. 2013, 9, 129–154. [Google Scholar]
- ADR. European Agreement Concerning the International Carriage of Dangerous Goods by Road (ADR); Economic Commission for Europe: Geneva, Switzerland; Committee on Inland Transport: Geneva, Switzerland; United Nations: New York, NY, USA, 2017. [Google Scholar]
- EN13094. Tanks for the Transport of DANGEROUS Goods-Metallic Tanks with a Working Pressure not Exceeding 0.5 Bar Design and Construction; British Standards Institution (BSI): London, UK, 2015. [Google Scholar]
- EN 14286. Aluminium and Aluminium ALLOYS Weldable Rolled Products for Tanks for the Storage and Transportation of Dangerous Goods; European Committee for Standardization: Brussels, Belgium, 2008. [Google Scholar]
- ANSYS 2019 R1; ANSYS Inc.: Canonsburg, PA, USA, 2019.
- Das, S.; Sundaresan, M.K.; Hameed, A.S. FEA of Cylindrical Pressure Vessels with different radius of Openings. Int. J. Res. Appl. Sci. Eng. 2015, 3, 406–411. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).