Thermal Rectification in One-Dimensional Atomic Chains with Mass Asymmetry and Nonlinear Interactions

Abstract

Understanding and controlling thermal rectification is pivotal for designing phononic devices that guide heat flow in a preferential direction. This study investigates one-dimensional atomic chains with binary mass asymmetry and nonlinear interatomic potentials, focusing on how energy propagates under thermal and wave excitation. Two potential models—the β-FPU and Morse potentials—were employed to examine the role of nonlinearity and bond softness in energy transport. Simulations reveal strong directional energy transport governed by the interplay of mass distribution, nonlinearity, and excitation type. In FPU chains, pronounced rectification occurs: under “cold-heavy” conditions, energy in the left segment increases from ~1% to over 63%, while reverse (“hot-heavy”) cases show less than 4% net transfer. For wave-driven excitation, the rectification coefficient reaches ~0.58 at 100:1. In contrast, Morse-based systems exhibit weaker rectification (∆E < 1%) and structural instabilities at high asymmetry due to bond breaking. A comprehensive summary and heatmap visualization highlight how system parameters govern rectification efficiency. These findings provide mechanistic insights into nonreciprocal energy transport in nonlinear lattices and offer design principles for nanoscale thermal management strategies based on controlled asymmetry and potential engineering.

1. Introduction

Controlling thermal energy at the nanoscale is a fundamental challenge in modern materials science [1,2,3], with significant implications for technologies such as nanoscale electronics, thermal computing, and thermoelectric energy conversion [4,5,6]. Unlike electrons, phonons—the primary carriers of heat in non-metallic solids—lack intrinsic directionality, making rectification of thermal energy a nontrivial task [7,8,9]. To address this, considerable attention has been directed toward the development of thermal diodes, devices that allow heat to flow preferentially in one direction [10,11,12]. Inspired by their electronic counterparts, such devices promise breakthroughs in thermal management and logic operations based solely on phonon dynamics [13,14].

Among the various strategies for achieving thermal rectification, the use of asymmetric low-dimensional systems has emerged as a particularly robust and conceptually elegant approach [15,16,17]. One-dimensional atomic chains, in particular, provide a versatile theoretical playground for investigating fundamental aspects of phonon transport [18,19]. Structural asymmetries—such as graded mass distributions, compositional interfaces, or geometrical mismatches—can break the spatial symmetry of phonon transmission, especially when combined with nonlinear interactions [20,21]. These systems capture essential features of real materials like carbon nanotubes, polymeric chains, and quasi-1D nanowires, where thermal rectification has been observed experimentally and in simulations [9,22].

A key ingredient in enabling rectification is nonlinearity in the interatomic potential, which introduces phonon–phonon interactions and mode coupling effects that are absent in purely harmonic models [5,23]. The Fermi–Pasta–Ulam (FPU) potential, with its quartic anharmonic term, has long been used to model such nonlinear effects and is known to support solitonic transport, wave trapping, and mode mixing. In contrast, the Morse potential introduces a fundamentally different type of nonlinearity, one that models bond dissociation and exhibits energy-dependent stiffness. While both are nonlinear, they affect phonon propagation in qualitatively different ways, particularly in the presence of structural asymmetry [12,24,25,26].

Recent computational work has demonstrated that rectification can be strongly affected not only by the mass ratio between regions, but also by the type of excitation (thermal or mechanical), the direction of energy input, and the temperature configuration (i.e., whether the heavy atoms are hot or cold) [17,18,19,27,28]. However, a systematic comparison between qualitatively different classes of nonlinear potentials—such as symmetric anharmonic and asymmetric, bond-softening models—under identical structural and excitation conditions remains scarce in the literature [21,29].

While experiments offer valuable insights, analytical approaches have fundamentally advanced the theoretical understanding of thermal rectification in one-dimensional atomic chains. Thus, perturbative analytical frameworks form the cornerstone of thermal rectification theory. Defaveri and Anteneodo developed comprehensive analytical frameworks for minimal thermal diode systems using perturbation theory [30], yielding expressions J = J₀ + εJ₁ + O(ε²) that explicitly demonstrate thermal rectification requires both asymmetry and nonlinearity. The perturbation theory for systems with varying thermal conductivity was developed in [31], providing analytical formulas revealing linear relationships between rectification ratio and temperature difference while establishing physical connections among rectification, system length, and thermal conductivity.

Self-consistent phonon theories bridge harmonic and anharmonic systems through sophisticated renormalization approaches. Pioneering quantum self-consistent phonon theory (QSCPT) for thermal transport through anharmonic systems was developed in [32], renormalizing anharmonic Hamiltonians to effective harmonic ones using temperature-dependent trial parameters. Integration of QSCPT with NEGF produces “modified Caroli formulas” enabling analytical treatment of strongly anharmonic systems while achieving thermal rectification ratios approaching 98%.

Nonequilibrium thermal rectification at junction interfaces represents recent breakthroughs in analytical thermal diode theory. Work [33] reports the comprehensive analytical theory for thermal rectification at harmonic chain junctions, deriving exact expressions for diode coefficients and demonstrating that rectification depends critically on energy distribution among wave numbers. Authors in [34] showed that introducing ballistic spacers and longer-range (next-nearest-neighbor) couplings can significantly enhance or tune the rectification effect—demonstrating that more complex structural designs, such as the inclusion of ballistic spacers or longer-range (next-nearest-neighbor) couplings, can significantly enhance or tune the rectification effect, offering richer possibilities for thermal control beyond simple left–right asymmetry.

Advanced analytical approaches continue emerging for complex phenomena. Approaches for achieving perfect diode limits were addressed in [35], while [36] reports sufficient conditions for thermal rectification in graded materials. These analytical approaches collectively demonstrate universal features: (1) requirement of both asymmetry and nonlinearity, (2) scaling of conductivity with interfacial coupling strength, (3) dependence on temperature differences, and (4) the role of various asymmetry types in determining preferential heat flow directions.

Overall, this review shows that although many analytical approaches exist, each has important limitations due to simplifying assumptions. Key factors such as asymmetry, nonlinearity, interfacial effects, and temperature dependence cannot be fully captured by analytical models alone, nor are they easily accessible to experimental investigation. Thus, molecular dynamics is the most suitable method for a detailed and realistic analysis of these factors, as it directly simulates atomic interactions without restrictive assumptions. Motivated by this, we apply molecular dynamics to investigate thermal rectification in one-dimensional chains with mass asymmetry and nonlinear interactions, providing critical validation of theoretical predictions. In this paper, by rectification we mean the asymmetry of the interaction of individual phonon waves with the interface, and not the more complex problem of rectifying the heat flow in the thermal equilibrium regime [33]. Our study goes further by systematically comparing the β-FPU and Morse potentials under identical conditions and dual excitation protocols—revealing how the specific nature of nonlinearity, combined with extreme mass asymmetry, governs both rectification efficiency and structural stability. This comparative perspective offers new insights into the design principles for asymmetric energy transport in low-dimensional systems.

2. Materials and Methods

2.1. System Description

The system studied consists of a one-dimensional atomic chain comprising 1000 atoms, evenly split into two segments of 500 atoms each. Structural asymmetry was introduced by assigning different atomic masses to the two halves of the chain, creating a well-defined interface at the midpoint. Three mass ratios were explored to assess the influence of asymmetry: 10:1, 50:1, and 100:1 (m10, m50 and m100), with the heavier atoms always located on the right-hand side of the chain. This configuration allows for a clean analysis of directional transport phenomena, particularly under thermal gradients or dynamic wave excitation.

The chain was simulated with free-end boundary conditions, allowing both ends to move without external constraints. All simulations were carried out using dimensionless units, with no reference to specific physical scales, in order to isolate general features of rectification and energy flow. Figure 1 shows the scheme of the system.

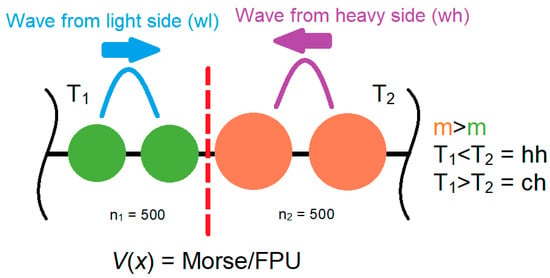
Figure 1. Schematic of the simulated 1D mass-graded chain under thermal and wave excitation.

Figure 1 illustrates the one-dimensional mass-graded chain used in simulations, with atoms on the left (lighter mass) and right (heavier mass) distinguished by size and color to reflect the mass asymmetry. The interatomic interactions are modeled using one of the potentials, depending on the simulation setup. Arrows depict localized wave pulses launched from light or heavy ends, while labels “T₁” and “T₂” refer to the temperature gradients across the simulation. This schematic provides a unified view of the system geometry and simulation protocols employed in this study.

2.2. Interatomic Potentials

Interactions between neighboring atoms were modeled using either the β-FPU potential [37] or the Morse potential [26], applied homogeneously along the entire chain without spatial variation or discontinuity. In the FPU case, the force was derived from the potential.

$$V_{FPU}\left(x\right)={\displaystyle \frac{1}{2}}{x}^2+0.1x^4,$$

(1)

where x represents the relative displacement from the equilibrium bond length. This form includes both harmonic and quartic anharmonic terms, making it suitable for exploring nonlinear energy transport and phonon–phonon interactions.

In the Morse case, the interaction potential was given by

$$V_{Morse}\left(x\right)={30(1-e^{-x/3})}^2,$$

(2)

which introduces a soft, bond-breaking nonlinearity with exponential dependence on bond stretching. Here, x again denotes deviation from equilibrium separation. Both potentials were applied to nearest-neighbor atom pairs only, with no long-range or angular interactions included.

2.3. Simulation Protocol

Simulations were performed using classical molecular dynamics with integration via the Velocity-Verlet algorithm [38]. A constant time step of 0.2 was used throughout, and all simulations were carried out for 250,000 steps. No attempt was made to relate simulation time to real physical timescales; instead, results were interpreted in relative terms within a dimensionless framework.

Two types of initial excitation were considered. In temperature-driven simulations, Langevin thermostats were applied to the first and last few atoms of the chain to maintain fixed temperatures at both ends establishing a sustained thermal gradient across the chain. To initialize the system under this gradient, atoms in each half were assigned initial velocities drawn from a Maxwell–Boltzmann distribution corresponding to their respective target temperatures [39]. The remainder of the system evolved under microcanonical (NVE) ensemble conditions, ensuring energy conservation in the bulk while allowing steady-state heat flow from hot to cold. Two thermal configurations were implemented: in the “hot-heavy” (“hh”) case, the high-mass segment was coupled to the hot thermostat; in the “cold-heavy” (“ch”) case, the light-mass segment was heated. Temperature gradients were established using three cold-to-hot temperature ratios: 10, 50, and 100 (T10, T50 and T100). For each configuration, eight independent simulations were conducted with randomized initial velocities to ensure statistical consistency.

In wave-driven simulations, no thermostats were used. The system was initialized with zero kinetic energy, and directional energy input was introduced as a localized half-sine wave pulse applied to approximately 150–170 atoms at one end of the chain. The wave represented an initial kinetic excitation and was introduced either from the light-mass side or from the heavy-mass side. The entire dynamics then proceeded under strict NVE conditions, allowing undisturbed propagation and interface interaction. No ensemble averaging was performed, and the focus was on assessing the system’s directional response to a single controlled excitation. Energy distribution was monitored at two characteristic moments: the first interaction with the mass interface, and the long-time behavior observed at the end of the 250,000-step simulation.

2.4. Energy Analysis

The energy of each half of the chain was evaluated as a combination of kinetic and potential contributions. Potential energy was computed using the same interaction model (FPU or Morse) used to evolve the system. For each snapshot in time, total energy was normalized by the system’s initial energy to allow for relative comparisons across configurations. In temperature-driven simulations, the primary observable was the difference between the initial and final energy content in each half of the chain, revealing how heat redistributed across the mass interface. In wave-driven simulations, the analysis focused on the fraction of the initial wave energy transmitted through the interface versus the amount reflected or localized.

3. Results and Discussion

3.1. Energy Redistribution in Temperature-Driven Systems

We begin by analyzing the behavior of energy redistribution in systems initialized with a temperature gradient. In these simulations, the initial energy was partitioned asymmetrically between the two halves of the chain by assigning velocities according to the Maxwell–Boltzmann distribution at two target temperatures. The evolution of total energy in each half of the system was tracked over 250,000 simulation steps, and representative results are presented in Figure 2, which shows the energy dynamics in the FPU model with T100 temperature gradient and m100 mass ratio. In Figure 2, the color intensity reflects the total energy density in each half of the chain over time, with warmer tones indicating higher energy. The left column corresponds to forward excitation (“ch”), where the light segment is initially hot, and the right column to reverse excitation (“hh”), with the heavy segment heated. In the “ch” configuration, energy rapidly flows from the light-hot segment into the heavy-cold region and gradually stabilizes at an uneven distribution. This behavior arises due to the momentum mismatch at the mass interface: light atoms with high initial kinetic energy are more effective in transmitting energy into the slower, heavier atoms, allowing significant transfer.

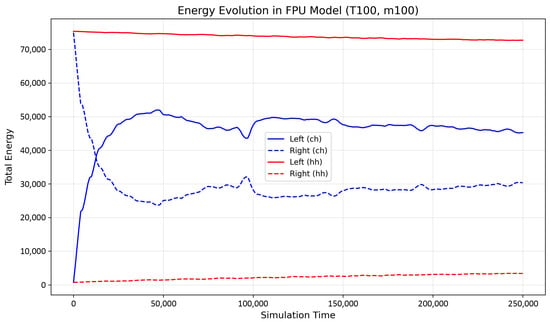
Figure 2. Time evolution of total energy in the left and right halves of the chain for the FPU model (T100, m100). Solid lines correspond to the left segment; dashed lines correspond to the right segment. Blue color denotes the “ch” configuration, and red color denotes the “hh” configuration.

In contrast, in the “hh” case, the energy remains strongly localized within the heavy segment throughout the simulation. The initial kinetic energy of heavy atoms produces vibrational motion that is poorly matched with the dynamics of the adjacent light atoms. As a result, most of the energy is reflected at the interface, preventing efficient transmission into the light segment. This direction-dependent energy flow is a clear manifestation of thermal rectification induced by mass asymmetry and nonlinear interactions.

To better illustrate the directional nature of energy redistribution under thermal gradients, Figure 3 presents the initial and final energy values in the left half of the chain for each simulated temperature difference (T10, T50, and T100). Each subplot corresponds to a distinct thermal gradient and includes results for different mass asymmetries (m10, m50, m100). Bars with hatching represent the system’s energy distribution at the beginning of the simulation, while solid bars show the final state after thermal relaxation. This visual format clearly highlights the net energy flow depending on the excitation direction and mass configuration.

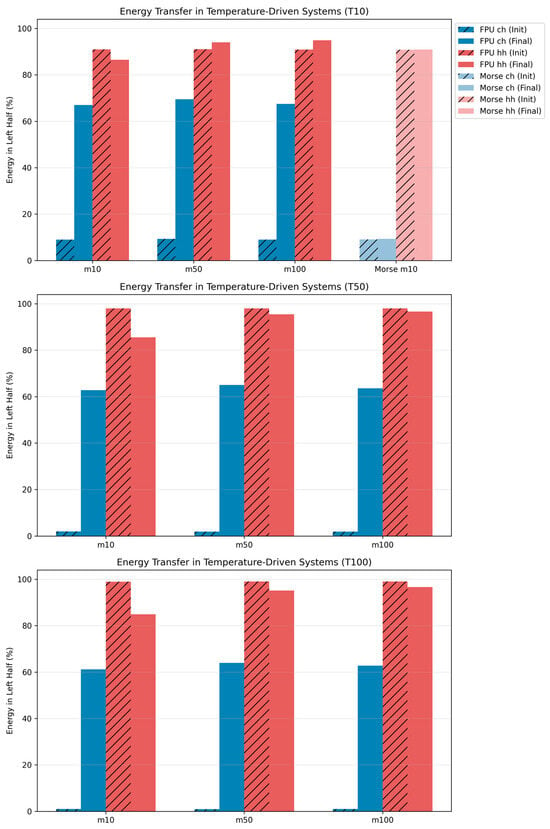
Figure 3. Initial and final energy in the left half of the chain for temperature-driven simulations using FPU and Morse potentials at all three considered temperature gradients. Each subplot corresponds to a specific temperature difference and presents results for each different mass ratios. Bars with hatching represent initial conditions, while solid bars show the outcome after thermal relaxation. Blue and red colors correspond to “ch” and “hh” configurations, respectively. The Morse potential is only included for T10 and m10, as higher gradients caused bond breaking and led to non-physical states in the light-mass region.

The comparison of initial and final energy distributions provides direct insight into the directionality and magnitude of heat transfer under controlled thermal gradients. By analyzing how energy redistributes depending on whether the heavy or light segment is initially heated, we can quantify the degree of thermal rectification—a key metric for phononic functionality. This approach allows us to distinguish between symmetric conduction (equal energy transfer in both directions) and asymmetric behavior driven by mass mismatch and anharmonicity. The significant increase in left-segment energy (e.g., from ~9% to ~67%) when the light side is hot confirms efficient forward energy flow, whereas minimal changes in the reverse case reveal strong suppression of backflow. Thus, Figure 3 serves as a fundamental demonstration of nonreciprocal transport, validating the core principle of thermal rectification in mass-asymmetric nonlinear lattices.

In “ch” configurations, where the light segment is initially hot and the heavy region is cold, energy consistently flows from the light to the heavy part of the chain. This transfer becomes particularly pronounced at high mass ratios in the FPU model—for instance, in the T10 case with m100, the energy on the left increases from ~1% to over 60%. This demonstrates a strong rectification effect, as energy accumulates in the heavier segment when excited from the light side.

Conversely, in “hh” setups, the majority of the energy remains confined within the initially excited heavy region. Only a small fraction is transferred to the light segment, reflecting the inertial mismatch at the mass interface: while light atoms efficiently transfer momentum to heavy atoms, the reverse process is suppressed due to the sluggish dynamics of the heavy segment.

For the Morse potential, data is presented only for the lowest thermal gradient T10 and m10. At higher temperature differences (T50 and T100), the light segment undergoes bond breaking due to excessive thermal excitation, leading to structural decoherence and loss of phonon transport assumptions. These configurations were excluded from analysis, as they represent a transition to a gas-like disordered state rather than a coherent solid, and therefore fall outside the scope of the current study.

3.2. Wave-Induced Directional Transport and Rectification

To further elucidate the dynamical behavior of energy propagation under wave excitation, Figure 4 presents the time evolution of the total energy in both halves of the system for four representative configurations. The upper row corresponds to simulations employing the FPU potential, while the lower row shows results for the Morse potential. In each row, the left subplot represents wave excitation from the light side, and the right—from the heavy side.

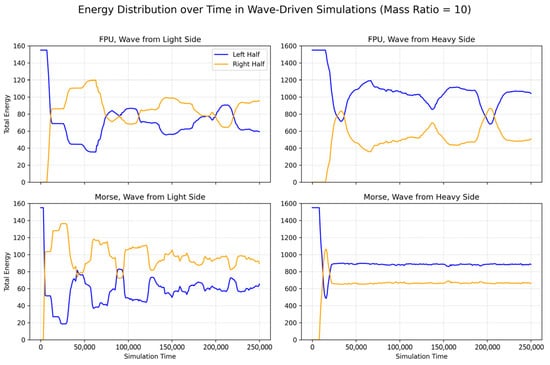
Figure 4. Time evolution of total energy in the left (blue) and right (orange) halves of the chain for wave-driven simulations at m10. Each subplot corresponds to a distinct case: wave excitation from the light or heavy side under either FPU or Morse interatomic potentials.

A key feature emerging across all cases is a clear asymmetry in energy transmission, strongly dependent on the direction of wave propagation. When the wave is launched from the light side, the energy transfer to the heavy half is severely limited, leading to a pronounced imbalance in energy distribution. In contrast, excitation from the heavy side results in a more efficient transmission across the interface.

This directional sensitivity underlies the wave-induced thermal rectification effect, which is notably more pronounced at large mass asymmetries. Additionally, while both potentials show qualitatively similar trends, the Morse case exhibits a more gradual onset of rectification at low mass ratios, consistent with its softer, bond-dissociative potential profile.

Finally, it is important to note that in all cases the interatomic potentials are applied symmetrically along the chain; the observed rectification arises solely due to the mass gradient. The vertical axis limits were independently optimized for each subplot to improve the clarity of the plotted curves, as the magnitude of the injected wave energy differs significantly depending on the direction of excitation.

The observed directional asymmetry in wave-induced energy transfer aligns qualitatively with theoretical predictions for impedance-mismatched systems [33], where low transmission occurs from light to heavy regions due to poor phonon mode overlap. Similar dynamics have been reported in simulations of graded carbon nanotubes and polymer junctions [9,22], supporting the generality of our findings across different physical platforms.

To evaluate the nonreciprocal nature of energy transfer associated with localized excitations, we define the wave rectification coefficient R_wave, which characterizes the asymmetry of energy transmission across the interface upon the first wave-interface interaction. The values T_forward and T_reverse, representing the percentage of energy transmitted to the opposite side of the interface when the wave originates from the light or heavy region respectively, were extracted from simulations at different mass ratios and potential types. The rectification coefficient is defined as:

$$R_{wave}={\displaystyle \frac{T_{forward}-T_{reverse}}{\mathrm{m}\mathrm{a}\mathrm{x}(T_{forward}, { T}_{reverse})}}$$

(3)

As shown in Figure 5, increasing the mass ratio leads to a monotonic rise in rectification for systems governed by the β-FPU potential. At low asymmetry (m = 10), energy transfer is nearly symmetric, resulting in minimal rectification. However, as the mass contrast increases (m = 50 and m = 100), waves launched from the heavy side experience strong reflection at the interface due to impedance mismatch—a phenomenon arising from the reduced ability of high-mass atoms to efficiently excite lighter ones. This results in highly asymmetric transmission and a corresponding increase in R_wave, reaching up to ~0.58 at 100:1. The trend confirms that extreme mass gradients can effectively break phonon reciprocity in systems with symmetric anharmonicity.

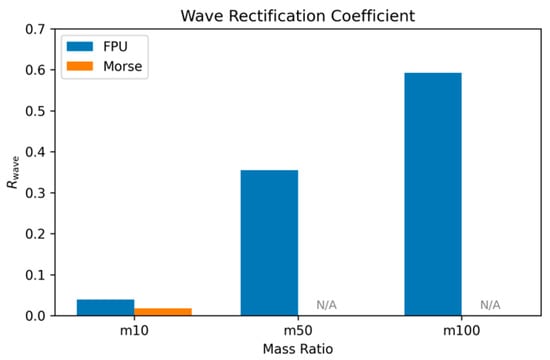
Figure 5. Wave rectification coefficient R_wave as a function of mass ratio for FPU and Morse potentials. The values are computed from the fraction of energy transmitted across the interface during the first wave-interface interaction. Gray markers indicate unavailable data due to unphysical chain breaking in Morse systems with high mass asymmetry.

In contrast, for chains modeled with the Morse potential, reliable rectification coefficients could only be determined at the lowest mass ratio (m = 10). At higher asymmetries, launching a wave from the light side induces large-amplitude vibrations in the already softer heavy segment, leading to excessive bond stretching and eventual chain fracture. Consequently, transmission cannot be meaningfully evaluated, and these points are omitted (gray markers). This stark difference underscores a critical insight: while both potentials are nonlinear, their impact on rectification and structural stability diverges significantly. The Morse potential, despite enabling bond-breaking realism, compromises coherent wave propagation under strong asymmetry—a key limitation for applications requiring robust directional control.

The observed chain fragmentation in the Morse potential arises from its intrinsic capacity for bond dissociation. Unlike the β-FPU potential, which confines atomic motion within a symmetric anharmonic well, the Morse potential features an asymmetric profile with a finite depth and a well-defined separation limit. Under high mass asymmetry and strong excitation—particularly when the wave is launched from the light side—energy accumulates in the heavy segment, driving interatomic distances beyond the dissociation threshold. This leads to irreversible bond rupture and loss of structural integrity. While the Morse potential captures realistic phenomena such as thermal expansion and softening, its application in highly asymmetric systems is limited by dynamical instability under intense energy input.

Thus, Figure 5 not only quantifies rectification efficiency across system parameters but also reveals a fundamental trade-off between nonlinearity type, structural integrity, and thermal diode functionality. It demonstrates that achieving high rectification requires not only structural asymmetry but also careful selection of interatomic interactions to balance nonlinearity and stability.

To further illustrate the wave-induced dynamics underlying rectification, Figure 6 presents a series of snapshots from the FPU simulation at mass ratio 100, where the wave is initiated from the light side. This case corresponds to the highest rectification coefficient observed in our study and serves as a representative example of strongly asymmetric energy transmission.

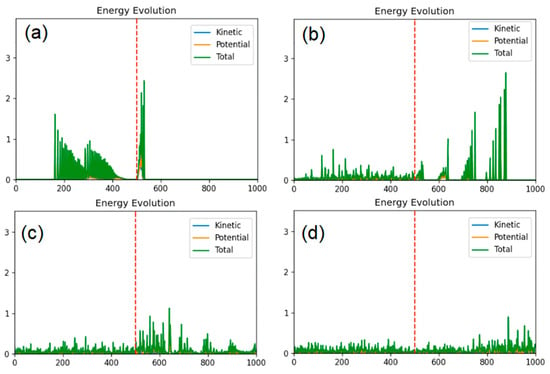
Figure 6. Time-lapse snapshots (a–d) from the wave-driven simulation using the FPU potential at m100, with excitation launched from the light side. The frames correspond to simulation steps: (a) 10,000; (b) 50,000; (c) 150,000; (d) 250,000. The sequence illustrates the progressive evolution of energy-carrying wave packets as they reflect between boundaries and interact with the mass interface.

In Figure 6a, the incident wave has undergone a single reflection from the heavy-light interface and begins returning toward the left boundary. The wavefront remains well-defined, and minimal energy has penetrated into the heavy side. In Figure 6b, following multiple reflections, four distinct wave packets of decreasing amplitude can be identified on the heavy side, while the wave on the light side becomes more dispersed and disordered, reflecting the gradual loss of coherence due to repeated interface interactions. Figure 6c captures a more advanced stage where many reflections have occurred. The system exhibits a highly mixed state, in which clear wave packet boundaries are no longer visible in the static image. However, visual inspection confirms the continued presence of propagating excitations. By Figure 6d, the wave amplitudes have noticeably decreased on both sides, and the system is approaching a quasi-stationary regime. Although local fluctuations persist, the overall energy landscape shows signs of progressive equilibration. These visualizations reinforce the asymmetric nature of wave transmission and energy dispersion across the mass-graded interface, in agreement with the rectification trends observed in earlier figures.

3.3. Summary of All Simulated Configurations

To provide a complete overview of all studied cases, Table 1 consolidates the results of energy redistribution for every simulated configuration. Each row specifies the interatomic potential, the type and parameters of excitation (temperature-driven or wave-driven), the directionality of the configuration (cold-heavy or hot-heavy for temperature excitation; wave from light (“wl”) or heavy (“wh”) side for wave excitation), the mass ratio, and the corresponding energy content in the left half of the chain at the beginning and end of the simulation. The last column reports the net change in energy, ∆E, serving as a concise indicator of rectification strength and directionality.

Table 1. Summary of all simulated configurations. ∆E represents the change in energy content in the left half of the chain during simulation. Positive ∆E indicates net energy accumulation in the left segment, while negative ∆E reflects energy depletion.

Potential	Excitation	Configuration	Mass Ratio	Eleft Init. (%)	Eleft Final (%)	∆E (%)
FPU	Temperature (T10)	ch	m10	9.02	67.0	+57.98
FPU	Temperature (T10)	ch	m50	9.35	69.5	+60.15
FPU	Temperature (T10)	ch	m100	9.03	67.5	+58.47
FPU	Temperature (T10)	hh	m10	90.93	86.5	−4.43
FPU	Temperature (T10)	hh	m50	91.06	94	+2.94
FPU	Temperature (T10)	hh	m100	90.9	94.85	+3.95
Morse	Temperature (T10)	ch	m10	9.11	9.44	+0.33
Morse	Temperature (T10)	ch	m50	8.97	9.17	+0.20
Morse	Temperature (T10)	ch	m100	9.12	9.31	+0.19
Morse	Temperature (T10)	hh	m10	90.7	85.2	−5.50
Morse	Temperature (T10)	hh	m50	90.74	93.4	+2.66
Morse	Temperature (T10)	hh	m100	91.06	94.1	+3.04
FPU	Temperature (T50)	ch	m10	2	62.75	+60.75
FPU	Temperature (T50)	ch	m50	1.9	65	+63.10
FPU	Temperature (T50)	ch	m100	1.94	63.6	+61.66
FPU	Temperature (T50)	hh	m10	98	85.5	−12.50
FPU	Temperature (T50)	hh	m50	97.97	95.4	−2.57
FPU	Temperature (T50)	hh	m100	98	96.6	−1.40
FPU	Temperature (T100)	ch	m10	1	61.2	+60.20
FPU	Temperature (T100)	ch	m50	0.98	64	+63.02
FPU	Temperature (T100)	ch	m100	1	62.8	+61.80
FPU	Temperature (T100)	hh	m10	98.98	84.9	−14.08
FPU	Temperature (T100)	hh	m50	99.03	95.15	−3.88
FPU	Temperature (T100)	hh	m100	99.03	96.6	−2.43
FPU	Wave	wl	m10	100	46.3	−53.70
FPU	Wave	wl	m50	100	41.7	−58.30
FPU	Wave	wl	m100	100	41.3	−58.70
FPU	Wave	wh	m10	100	65.2	−34.80
FPU	Wave	wh	m50	100	80.75	−19.25
FPU	Wave	wh	m100	100	84.9	−15.10
Morse	Wave	wl	m10	100	37.6	−62.4
Morse	Wave	wl	m50	100	35.3	−64.70
Morse	Wave	wl	m100	100	31.7	−68.30
Morse	Wave	wh	m10	100	57.1	−42.90

Table 1 provides a complete inventory of simulation outcomes, enabling direct comparison across potentials, excitation types, and system configurations. Notably, large positive ΔE values (up to +63.1%) occur consistently in FPU chains under “ch” thermal excitation, confirming strong rectification favoring energy accumulation in the heavy segment. In contrast, negative ΔE values in “hh” setups indicate energy retention in the initially excited region, underscoring the asymmetry of transport. For wave-driven cases, the difference in ΔE between “wl” and “wh” excitations exceeds 40 percentage points at high mass ratios, further validating directional control. Meanwhile, Morse potential results show negligible ΔE (<1%) across most configurations, reinforcing its limited effectiveness in generating rectification within this framework. Overall, Table 1 establishes a systematic dataset that supports the central conclusion: rectification strength is governed jointly by mass asymmetry, potential type, and excitation protocol. Our study goes further by systematically comparing the β-FPU and Morse potentials under identical conditions and dual excitation protocols—revealing how the specific nature of nonlinearity, combined with extreme mass asymmetry, governs both rectification efficiency and structural stability. This comparative perspective offers new insights into the design principles for asymmetric energy transport in low-dimensional systems.

To highlight the broader rectification trends and make the directional asymmetries visually intuitive, Figure 7 presents a heatmap of ∆E as a function of configuration type and mass ratio.

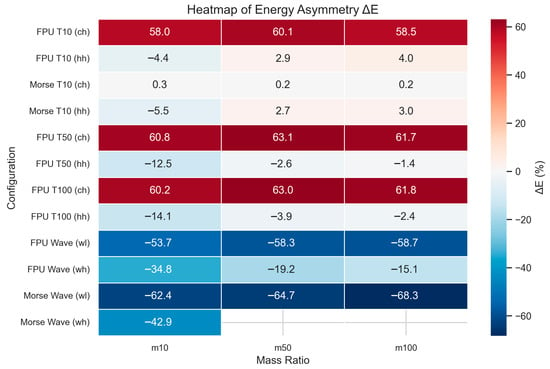
Figure 7. Heatmap of energy asymmetry (∆E) across all simulated configurations. Rows group results by interatomic potential and excitation type, while columns correspond to increasing mass ratio. Colors represent the net change in energy in the left half of the chain (∆E), with warm (positive) and cool (negative) values indicating energy accumulation or depletion, respectively.

Figure 7 provides a compact visual summary of rectification behavior across all studied systems. The vertical axis groups simulation results by potential model and excitation type (temperature gradient or wave input), while the horizontal axis corresponds to the mass ratio. Within each block, color intensity represents the magnitude and sign of ∆E—with warm tones (reds) denoting energy accumulation in the left segment (positive ∆E) and cool tones (blues) indicating depletion (negative ∆E).

This format immediately reveals that the strongest rectification occurs in the FPU model under wave excitation and in “ch” temperature configurations at high mass ratios. In these cases, the contrast between forward and reverse excitation becomes especially pronounced, producing asymmetric energy redistribution that aligns with theoretical expectations of impedance mismatch and nonlinear scattering at the mass interface. In contrast, Morse systems show weaker or inconsistent asymmetry, particularly under strong gradients or large mass differences, where structural instability emerges.

Notably, the heatmap also enables direct comparison between different driving mechanisms. Temperature-driven simulations exhibit systematic rectification that grows with mass ratio, while wave-driven systems display a more threshold-like response—with significant asymmetry only emerging beyond a certain mass contrast. This suggests that the mechanism of energy input—distributed (thermal) versus localized (wave)—plays a critical role in determining the onset and magnitude of rectification. Overall, Figure 7 reinforces the conclusion that thermal rectification is a multiscale and nonlinear phenomenon, rooted in the combined effects of mass asymmetry, interaction potential, and excitation modality.

The molecular dynamics results presented here provide systematic validation of key analytical predictions for thermal rectification in one-dimensional atomic chains. The observed strong rectification in FPU chains with mass asymmetry (∆E up to ~63% for “ch” configurations) confirms the fundamental requirement of both structural asymmetry and nonlinearity established by perturbation theory [29,30]. The scaling of rectification with mass ratio (m10 -> m50 -> m100) and the temperature dependence observed across T10, T50, and T100 conditions support analytical predictions, though saturation effects at high temperature differences suggest limitations of first-order perturbative approaches. The dramatic directional asymmetries in wave packet transmission scenarios (“wl” vs. “wh” configurations showing ∆E differences of ~40–45%) align closely with the junction interface theory developed in [32], which predicts strong rectification when energy spectra of connected chains have minimal overlap.

Nonlinearity of interparticle couplings can lead to the excitation of localized vibrational modes called discrete breathers [40,41], and they affect heat propagation by being strong scatterers of phonon waves. The appearance of discrete breathers can be expected under conditions far from equilibrium, for example, in metals when high-density electric current flows [42,43].

However, the comparison also reveals important deviations from idealized analytical models, particularly the substantially weaker rectification observed in Morse potential chains (∆E < 1% in many cases) compared to FPU systems, despite similar mass asymmetries. This demonstrates that the choice of interatomic potential critically determines rectification efficiency in ways not fully captured by simplified analytical treatments. The results thus validate the universal features identified analytically—requirement of asymmetry and nonlinearity, scaling with coupling strength, temperature dependence, and structural effects [34,35]—while highlighting that systematic in silico experiments are essential for understanding how these mechanisms manifest in realistic systems with complex potential energy surfaces and strong nonlinear effects beyond the scope of current analytical approximations.

It is important to note that neither the FPU nor the Morse potential can be considered universally “correct”—each serves a distinct modeling purpose. The β-FPU potential captures strong symmetric anharmonicity while preserving structural stability, making it ideal for studying coherent phonon transport and rectification. In contrast, the Morse potential includes bond-softening and dissociation effects, offering greater physical realism under extreme thermal or mechanical excitation. However, this realism comes at the cost of dynamical instability in highly asymmetric systems, as seen in our simulations where chain fracture occurs under high gradients. Thus, the choice of potential depends on the application: stability-focused designs favor FPU-like interactions, whereas failure-aware systems require Morse-like behavior. Our work does not advocate one over the other but highlights their context-dependent validity—a key insight for future modeling efforts.

4. Conclusions

This study elucidates the mechanisms underlying thermal rectification in one-dimensional atomic chains with binary mass asymmetry and nonlinear interatomic interactions. Through systematic molecular dynamics simulations, we demonstrate that strong directional energy transport arises from the interplay between structural asymmetry and anharmonicity, with the nature of the potential playing a decisive role. In systems governed by the β-FPU potential, pronounced rectification is observed under both thermal gradients and localized wave excitations, particularly at high mass ratios. Efficient energy transfer occurs from the light to the heavy segment, while reverse propagation is strongly suppressed due to impedance mismatch and nonlinear scattering at the interface.

In contrast, chains modeled with the Morse potential exhibit significantly weaker rectification and are prone to bond-breaking instabilities under large temperature differences or strong wave pulses, especially at high mass asymmetry. These limitations highlight the sensitivity of coherent phonon transport to the form of nonlinearity beyond simple anharmonic corrections.

Furthermore, the magnitude and onset of rectification depend critically on the excitation protocol: temperature-driven setups show gradual enhancement with increasing mass ratio, whereas wave-driven systems display a threshold-like response, becoming highly asymmetric only beyond a certain level of asymmetry. This distinction underscores the importance of excitation modality in probing and controlling nonreciprocal energy flow.

Overall, our results provide detailed mechanistic insights into how mass distribution, type of nonlinearity, and external driving conditions govern thermal rectification in low-dimensional systems. These findings contribute to the fundamental understanding of phonon-mediated heat control and may inform future strategies for engineering asymmetric thermal response in nanoscale materials and metamaterials.