Abstract
This manuscript focuses on the process of measuring the angular positions of radio sources using radio engineering systems. This study aims to improve the accuracy of measuring the angular positions of sources that radiate functionally determined signals and to expand the range of the unambiguous operation angles for multi-antenna radio direction finders. To achieve this goal, the following tasks were addressed: (1) defining the models of signals, noise, and their statistical characteristics, (2) developing the theoretical foundations of statistical optimization methods for measuring the angular positions of radio sources in multi-antenna radio direction finders, (3) optimizing the structures of radio direction finders with different configurations, (4) analyzing the accuracy and range of the unambiguous measurement angles in the developed methods, and (5) conducting experimental measurements to confirm the main results. The methods used are based on the statistical theory of optimization for remote sensing and radar systems. For the specified type of signals, given by functionally deterministic models, a likelihood function was constructed, and its maxima were determined for different multi-antenna direction finder configurations. The results of statistical synthesis were verified through simulation modeling and experiments. The primary approach to improving measurement accuracy and expanding the range of unambiguous angles involves combining antennas with different spatial characteristics and optimally integrating classical radio direction-finding methods. The following results were obtained: (1) theoretical studies and simulation modeling confirmed the existence of a contradiction between high resolution and the width of the range of the unambiguous measurements in two-antenna radio direction finders, (2) an improved signal processing method was developed for a four-antenna radio direction finder with a pair of high-gain and a pair of low-gain antennas, and (3) to achieve maximum direction-finding accuracy within the unambiguous measurement range, a new signal processing method was synthesized for a six-element radio receiver, combining processing in two amplitude direction finders and one phase direction finder. This work provides a foundation for further theoretical studies, highlights the specifics of combining engineering measurements in direction-finding systems, and offers examples of rapid verification of new methods through computer modeling and experimental measurements.
1. Introduction
Radio direction finders are crucial components in nearly all modern radio systems and complexes for detection [1], ranging [2], monitoring [3], navigation [4], and control [5]. Typically, the performance characteristics of these systems are determined by their radio direction finders. Key attributes include the operating frequency range, bearing accuracy, overall dimensions, and the range of angles for unambiguous measurements [6]. Particularly high demands are placed on these characteristics, especially when direction finders are installed on UAVs [7,8]. Modern trends in the expanding application of unmanned aerial vehicles, uncrewed marine vessels, and land vehicles necessitate enhancements in onboard systems for determining the angular positions of radio emission sources [9,10,11]. The primary challenge in direction finder operation lies in balancing a high bearing accuracy with a broad range of unambiguous measurement angles.
Several fundamental principles underpin direction finding, based on the measurement of parameters and statistical characteristics of received signals. The main types of direction finders include amplitude, phase, and correlation methods [12].
Amplitude direction finders [13] implement measurements through methods such as rotating a single high-gain antenna, switching between multiple high-gain antennas, electronically switching low-gain antennas in a circular array to simulate the rotation of a narrow beam, and utilizing a pair of Adcock antennas for measurements. Recent advancements have improved the accuracy of amplitude direction finding; however, these developments often overlook restrictions related to the overall size of the direction finder carrier.
Phase direction finders [14] operate on principles such as direct phase difference measurement between receivers with antennas spaced less than half a wavelength apart, interferometric phase difference measurement across multiple spatially dispersed receivers, and phase measurement of received signals with phase modulation induced by the Doppler effect through circular antenna rotation. Despite significant advancements in accuracy, digital signal processing, and size reduction, phase measurements in radio systems remain constrained to narrow value ranges or ambiguous measurements that require secondary processing, an issue still unresolved in the current literature.
Correlation direction finders [15] combine the advantages of amplitude and phase direction finders by determining the direction of radio emission sources through statistical processing of complex signal amplitudes. These systems, when equipped with a sufficiently large antenna array, can separate signals and interference in combined channels and isolate signals from coherent interference backgrounds. They utilize algorithms such as MUSIC, multilevel maximum likelihood estimation (MLE), and super-resolution direction finding (SR-DF). While these systems offer enhanced performance, they require significant prior information and are complex and costly to implement due to the necessity of coherent amplitude processing.
Given the analysis of current scientific research and the aforementioned challenges, there is a critical need to statistically synthesize and analyze methods for accurately and unambiguously determining the angular positions of radiation sources emitting functionally determined signals in multi-antenna direction finders. Addressing this need is expected to provide theoretical optimizations in signal processing that will benefit future research and offer practical recommendations for developing and conducting experimental studies on direction finders capable of high accuracy and wide-angle unambiguous measurements.
While recent advancements in direction-finding systems, such as those based on amplitude, phase, and correlation methods, have made significant progress, each has inherent limitations. For instance, amplitude direction finders face size constraints, phase direction finders suffer from ambiguity in phase measurements, and correlation methods are complex and costly to implement. In contrast, the proposed system must not only resolve the contradiction between the high bearing accuracy and wide angles of unambiguous measurements but also achieve a balance between system size and performance, making it more suitable for compact platforms such as UAVs. This represents a significant improvement over the state-of-the-art solutions described in the literature.
To achieve the objectives of the study, the following tasks needed to be addressed and completed: (1) establishing models for signals, noise, and their statistical characteristics received by the direction finder; (2) developing theoretical frameworks for statistically optimizing methods to measure the angular positions of radio sources in multi-antenna direction finders; (3) resolving specific optimization challenges related to radio direction finder structures with varying configurations; (4) evaluating the accuracy and range of the angles for unambiguous measurements using the developed methods; and (5) conducting experimental measurements to validate the primary results.
2. Materials and Methods
2.1. Observation Equation and Its Statistical Characteristics
We assume that the signals received by the direction finder can be generally described by the following functionally deterministic model:
where is the phase shift of the signal in each receiving channel relative to the phase center of the antenna array, is the difference in distances the electromagnetic waves travel from the source to each antenna, is the delta function determining the spatial position of the point source of radio emission in the direction , is the gain of the i-th receiving channel, is the directional diagram of the i-th antenna oriented by its maximum in the direction , is the complex envelope of the signal emitted by the source, is the harmonic oscillation in complex form with carrier frequency , is the time, are angle coordinates, is the electromagnetic wave propagation velocity, and .
In Figure 1, is the surface on which the boundary conditions are phenomenologically stated in the form of the scattering coefficient . The area is the area of observation and primary (before processing) description in a coherent form of the field, taking into account its amplitude and phase dependences. Within the region , there is a physical rectangular region of registration of scattered signals, which in the general case may have an arbitrary shape. The surface will be considered as flat or spherical surface. The coordinates of include a coherent image that takes into account, in its amplitude-phase structure, the influence of various inhomogeneities, such as inhomogeneities of chemical composition, inhomogeneities of the refractive index gradient, and irregularities of the real surface. The region emitting the probing signal may be outside the region or be aligned with the origin of the region . The only limitation is the wide emission angle of the probing signal, in particular the case of omnidirectional radiation. The geometry underlying model (1) is illustrated in Figure 1.
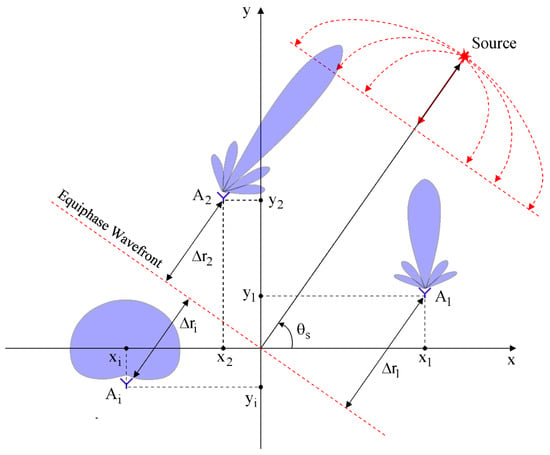
Figure 1.
General geometry of radio source angular position measurement in a multi-antenna direction finder.
Based on the model of useful signals (1), the input paths differ only in gain . We will assume that the internal noise in the receiving paths is white Gaussian noise, which is uncorrelated in different channels and has the same power spectral density . The correlation function of the internal noise is given by
where is the delta function.
The combination of signals and noise to be optimally processed in the direction finder will be referred to as observation equations. The general form of observation equations in multi-antenna direction finders is as follows:
where is the operator of the real part of the complex signal,
2.2. Elements of the Statistical Theory of Radio System Optimization
To solve optimization problems of synthesis signal processing algorithms in multichannel direction finders, we will use the statistical theory of optimization of radio engineering systems of remote sensing and radar [16,17,18]. According to this theory, the method of maximum likelihood function is recommended for use. The essence of this method lies in finding the parameter that maximizes the likelihood functional , which is the conditional probability density functional of a random process when value of the parameter is fixed. Instead of maximizing the likelihood functional directly, its logarithm is maximized as the logarithm function is monotonic and does not change the maximum point . To obtain the optimal parameter, estimates that it is necessary to solve the system of equations
where denotes the derivative operator evaluated at the true value of the parameter .
One of the critical steps in solving an optimization problem is determining Reference [16] outlines a methodology for constructing likelihood functionals applicable to a broad spectrum of radar and remote sensing issues. In this study, we will employ a likelihood functional of the following form:
where is the coefficient independent on and is the observation time. The parameter is a constant value.
Substituting (8) into (7), we obtain the system of likelihood equations
or in the other form
The left side of (10) outlines the essential optimal operations for processing the received oscillations in each channel. This should be compared with the right side, which represents the direction-finding characteristic of the multichannel direction finder, illustrating how the meter responds to changes in the angular position of the radiation source.
Initially, the analytical form of the direction-finding characteristic is determined based on the given parameters of the source’s signals, considering the spatial characteristics of the antennas, their geometry, observation time, and input path parameters. This theoretical characteristic must then be practically verified through experiments, with measurement results incorporated into the implemented device.
Discrepancies from theory arise due to various factors affecting each receiver element, deviations from nominal parameters, flicker noise, varying coherence indices of microwave elements, and more. By specifying useful signals in the observation equation and using expression (10), solutions to partial optimization problems in algorithm synthesis for different types of direction finders can be obtained.
3. Results
To develop a direction-finding method that balances high angular accuracy with a wide range of unambiguous measurements, it is advisable to first optimize the structure of a two-channel amplitude direction finder and identify its limitations. To address these drawbacks of obtained structure, a four-antenna amplitude direction finder is proposed. Considering the superior accuracy of phase direction finders, it is crucial to create an algorithm for integrating measurements from both amplitude and phase direction finders. These specific challenges will be addressed subsequently.
3.1. Two-Antenna Amplitude Direction Finder
Let us assume the signals from the radiation source are received by two identical antennas separated by an angular distance in their radiation patterns, The direction where equal signal values are observed in both receiving channels is called the equal-signal direction and is denoted by . A typical geometry for measuring angle in a two-antenna direction finder is shown in Figure 2. When determining the orientation angle of the antenna pattern’s maximum in (1), it is noted that , .
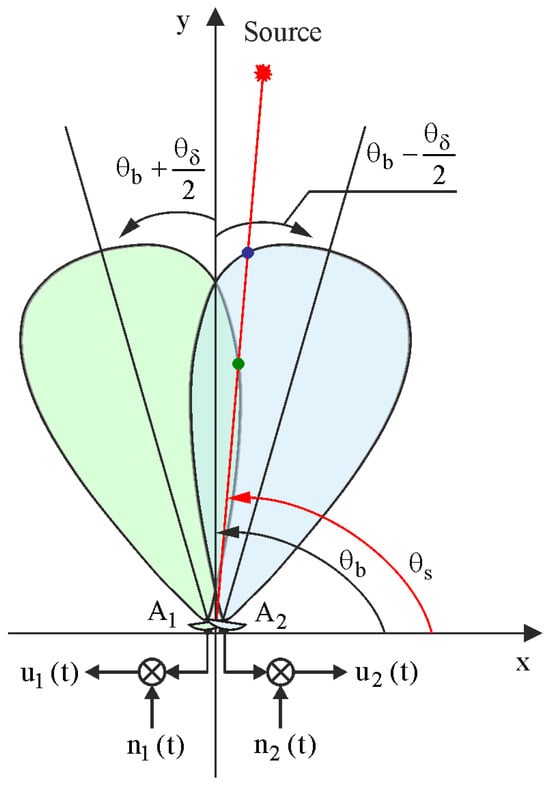
Figure 2.
Geometry of measurements in a two-antenna direction finder.
The models of useful signals under the specified measurement conditions in the two-antenna direction finder are as follows:
In the models given in Equations (11) and (12), the phase shift information is omitted because the processing is assumed to be incoherent within each channel.
In two-antenna direction finders, the equal-signal direction is typically chosen along the linear sections of the first and second diagrams, and all measurements are also performed along these linear segments. For instance, consider the radiation patterns of the two antennas represented as two real Gaussian functions in a Cartesian coordinate system (see Figure 3). Within these linear sections, the patterns and can be expanded into a Taylor series around the direction and represented by linear approximation
where
are slopes of the normalized directional patterns of the first and second antennas. For identical and symmetric diagrams with respect to the , we have . In the following, we will use only with different signs.
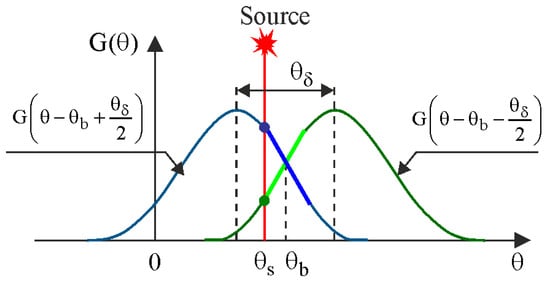
Figure 3.
Radiation patterns of two-antenna direction finder in Cartesian coordinate system.
Considering Equations (13) and (14), the observation equations will be expressed as follows:
Substituting (11), (12), (15), and (16) into (10), we obtain the inequality
Introducing the transmission coefficient of the optimal filter , we obtain in the left part of inequality (17) the optimal output effect of the direction finder
The right part of (17) is the bearing characteristic, which takes the form of a linear function after substituting (11) and (12)
where .
For the simplification introduced in this particular problem regarding the calculations within the linear section of the directional diagrams, it is possible to derive the measurement algorithm by substituting (19) and (18) into (17)
The main mathematical operations for signal processing in a two-antenna amplitude radio direction finder are matched filtering and the subtraction of the filtering results in different channels. The coefficient must be measured practically in advance to implement algorithm (19).
The range of unambiguous measurements in the resulting algorithm is determined by the size of the linear section, and the accuracy is proportional to the slope . As the slope increases, we achieve higher bearing accuracy, but the range of angles for unambiguous measurement of the radio source position narrows. Based on these results, the contradiction between the accuracy and range of unambiguous measurements appears.
3.2. Four-Antenna Amplitude Direction Finder
To overcome the contradiction between the accuracy and unambiguity of measurements over a wide range of angles, it is proposed to use two pairs of antennas. The first pair of antennas features wide radiation patterns, while the second pair has narrow radiation patterns. By doing so, the advantages of both types of direction finders can be combined to complete the measurements.
The geometry of measurements using a four-antenna direction finder is illustrated in Figure 4. The observation equation for this geometry is as follows:
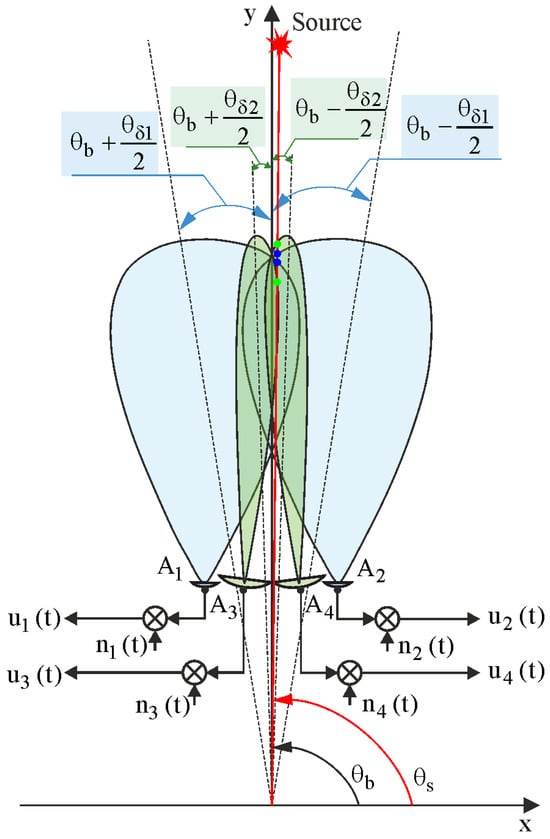
Figure 4.
Geometry of measurements in a four-antenna direction finder.
By substituting the observation Equation (20) and its constituent useful signals into (9), we obtain the likelihood equation
where is the energy of the signal emitted by the source,
is the bearing characteristic of a four-antenna radar system measuring the angular position of the radio emission sources.
The resulting algorithm is quite complex from both a technical standpoint and in terms of practical implementation, but the fundamental mathematical operations are clear. Unlike the direction-finding characteristic in the dual-antenna direction finder (18), which is a linear function, our calculations address a more general problem of analyzing direction finder performance. Firstly, the resulting formula of describes any type of radiation pattern, which may vary between antenna pairs. Secondly, we did not restrict measurements to the linear section of the direction finder’s operation; instead, we derived general multipliers for the rate of change in functions in each channel. This approach enables us to analyze the full range of viewing angles for the antennas and to select the widest angle range with unambiguous measurements.
The left part of Equation (21) represents a standard weighted addition of the measurement results and does not explicitly reveal the known algorithmic operations. However, the weight coefficients will vary in sign near equal-signal directions, leading to familiar algorithms for subtracting measurement results across different channels.
A more detailed analysis of the derived expressions, particularly in the context of functional descriptions of directional patterns, will be provided later in the simulation modeling of direction-finding characteristics.
The obtained algorithms merge the benefits of two-antenna direction finders with both narrow and wide patterns, overcoming the contradiction between the accuracy and angular range of the unambiguous measurements. Furthermore, there is interest in developing an algorithm that provides high bearing accuracy without signal loss across a wide range of angles.
3.3. Six-Antenna Amplitude-Phase Direction Finder
To achieve the highest accuracy in angle measurement, it is proposed to add two channels for measuring the phase difference in signals in the structure of the four-antenna direction finder. In this configuration the antenna measurements of the phase direction finder can be non-directional, but it is necessary to account the phase shift relative to the phase center in the received signals. The measurement geometry is illustrated in Figure 5. Noise in each channel is also considered as Gaussian white random processes, uncorrelated in time and between channels
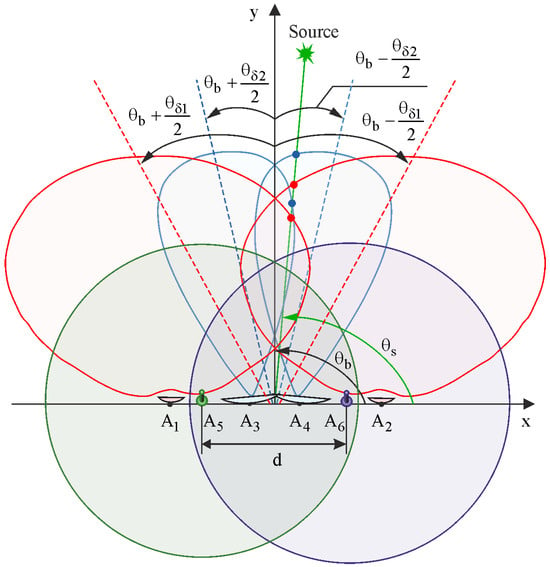
Figure 5.
Measurement geometry in a six-antenna direction finder.
Useful signals have the following models
where is the distance between the antennas of the phase direction finder located on the same line along the axis.
By substituting the observation equations, which consist of an additive mixture of useful signals and delta-correlated noise, into inequality (10), we obtain
As it mentioned before, the left side of Equation (26) shows the optimal operations to be performed on the received signals in each receive channel of the direction finder. The first four equations repeat the operations performed in a four-antenna direction finder. The fifth and sixth terms provide an estimate of the angular position of the radio source with the precision of phase measurements. The basic operations are as follows: (1) equations and must be passed through a filter which parameters are matched to the complex envelope and frequency of the transmitter signal; (2) the result of detection at low frequency is normalized by multiplying with coefficients ; (3) the normalized amplitudes must be processed in a quadrature detector, which is configured to measure the phase shift arising from the deviation of the radiation source from the equal-signal zone. The processing results are then converted into angles using the bearing curve calculated on the right side of Equation (26).
For given parameters of antenna placement and orientation in the direction finder, the right side of Equation (26) is a function of the angle . It is analytically impossible to evaluate or analyze the obtained expressions without specifying the forms of the directional diagrams. Therefore, it is advisable to perform simulation modeling of bearing characteristics and calculate the marginal errors of measurement.
4. Theoretical Analysis
To confirm the efficiency of the algorithms we will analyze the right-hand sides of the likelihood Equations (17), (22) and (26), which represent the bearing characteristics of various types of multi-antenna direction finders. The derived Equation (19) represents only the linear part of such characteristics and does not depend on the type of directional diagrams or their orientation in space. To visually compare all the obtained methods, the bearing characteristic of the two-antenna direction finder will be derived from the analysis of the bearing characteristic of the four-antenna direction finder. Simulation modeling will be conducted using the following expressions:
- (1)
- two-antenna amplitude direction finder
- (2)
- four-antenna amplitude direction finder
- (3)
- six-antenna amplitude-phase direction finder
All variables in the above expressions, except for , will be constants. As functions describing the directional patterns we will consider the following:
- (1)
- Gaussian function
- (2)
- Sinc function
The unit-normalized bearing curves of radio sources using function (30) with parameters , , , , , , , , , , are shown in Figure 6a.
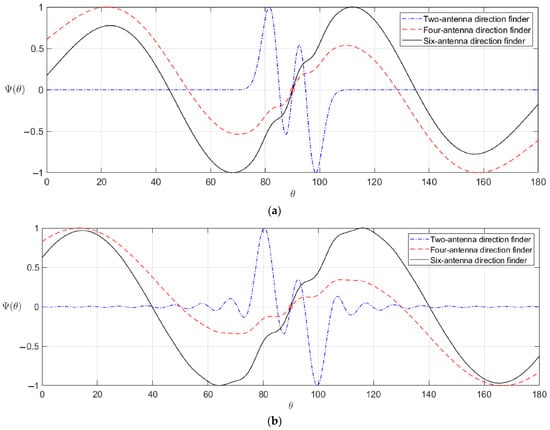
Figure 6.
The unit-normalized bearing curves: (a) directional patterns in the form of Gaussian functions, (b) directional patterns in the form of Sinc function.
The bearing characteristics for the given parameters when using antennas with the diagrams from Equation (31) are shown in Figure 6b.
Analyzing the obtained graphs, it follows that in the two-antenna direction finder, there is indeed a contradiction between the range of angles of unambiguous measurements, corresponding to the linear section of the direction-finding characteristic, and the receiver’s response to angle changes (accuracy).
In the four-antenna direction finder, this contradiction was overcome. The graphs indicate that the direction-finding characteristic has increased the range of unambiguous measurements by four times, but it has two sections with different slopes. The central part of the bearing characteristic has a steeper slope, allowing for high-accuracy problem-solving within the linear section of narrow antennas. Outside this section, the slope is smaller, but there is no observation failure or measurement ambiguity.
The operation of the six-antenna direction finder is better illustrated by its inclusion in an automatic tracking system for angular coordinates. Such a system begins to function after “catching” the angular position of the radio source. At the initial stage, the target is already within the operating range of the direction finder. For example, if the angular position of the target is 110°, the direction finder output will produce a positive voltage value, which will activate the antenna rotation mechanism to align the angles and With each new measurement, the voltage will decrease until the angles are equal and the output voltage becomes 0. The solid black curve in Figure 6, from the angle value of 110° to 90°, shows the sections with different slopes. The highest slope on the equal-signal circle will provide the highest measurement accuracy, while other sections will have lower accuracy. At the same time, from 110° to 90°, we have a descending curve without multiple maxima, in contrast to the bearing curve of the dual-antenna direction finder. This indicates that with each new measurement cycle, the automatic tracking-guidance system for angular coordinates will converge to the true direction . The advantage of the six-antenna over the four-antenna system is particularly evident at the final stage of tracking. The dual-antenna system has the highest slope but within a very narrow angular range. It can be concluded that the six-antenna direction finder offers a balanced compromise between accuracy and the range of unambiguous measurements, thereby overcoming the existing contradiction.
It is also useful to verify the obtained results by analyzing the expressions for the marginal errors of radio direction finder measurements. In the statistical theory of optimizing radio-technical systems [16,17,18], the limiting variance of the parameter estimation error is derived from the Cramer–Rao inequality
where is the sign of statistical averaging and is the operator of the secondary derivative.
The general analytical expression for the marginal estimation error of all direction finders is as follows:
The marginal variances of the angular position estimation errors (33) for the cases considered in this paper are as follows:
- (1)
- two-antenna amplitude direction finder
- (2)
- four-antenna amplitude direction finder
- (3)
- six-antenna amplitude-phase direction finder
It is useful to model the obtained expressions using the same parameters as those for the bearing characteristics shown in Figure 6. The results of such modeling are presented in Figure 7. The figures illustrate the root mean square (RMS) errors in estimating the angular position of the radio source in degrees as a function of the observation angle for the two types of directional patterns, (30) and (31). The chosen angles from 70° to 110° correspond to the widest range of unambiguous measurements in the six-antenna direction finder.
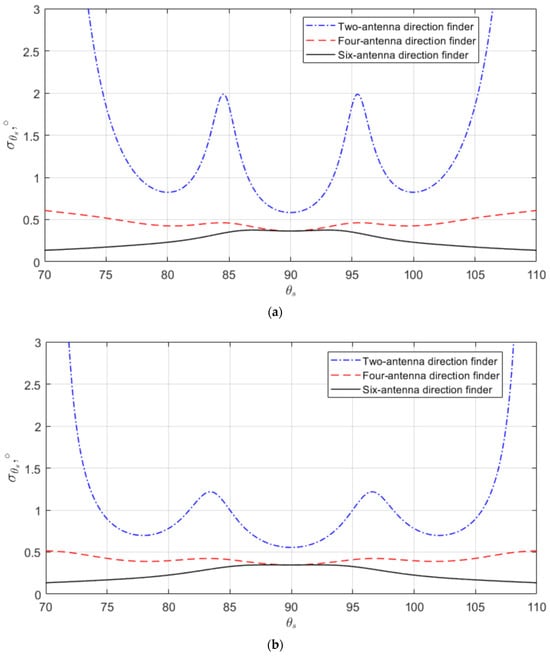
Figure 7.
RMS errors in estimating the angular position of the radio source: (a) directional patterns in the form of Gaussian functions, (b) directional patterns in the form of Sinc function.
5. Experiment
Simulation modeling was conducted under idealized conditions, with a directional pattern free of side lobes and a receiving path devoid of internal noise. Consequently, before interpreting the results, it is advisable to perform experimental validation of the proposed signal processing algorithm within the direction-finding system. To achieve this, the system depicted in Figure 8 was developed, based on the method (22). This system comprises four receiving antennas with RF paths calibrated to the frequency range of 2.4–2.48 GHz, a microprocessor-based data acquisition unit, and an automatic rotary device.

Figure 8.
An experimental prototype of a four-antenna direction-finding system includes a wide-beam antenna (1), a narrow-beam antenna (2), a processor with an ADC (3), and an antenna rotation mechanism (4).
Collinear antenna arrays were selected due to their straightforward implementation and tuning, lack of need for complex calculations, and easily adjustable pattern width by varying the number of sections in the antenna. The geometric relationships of the antenna elements relative to the wavelength used in the calculations are shown in Figure 9. In the antennas used during the experiment, L = 54 mm and d = 22 mm. The connection point for the 50-ohm impedance cable on the center loop was determined experimentally. The antenna with a wide radiation pattern consists of four receiving elements, while the one with a narrow radiation pattern consists of eight.
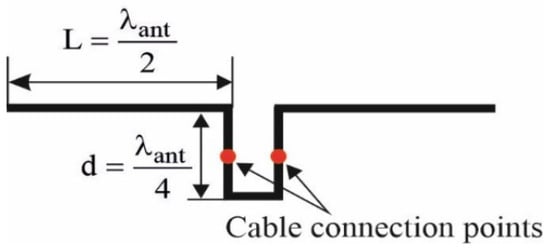
Figure 9.
Geometric dimensions of collinear antenna array elements.
The outputs of the antennas are connected to RF paths, one of which is depicted in Figure 10. This path includes a low-noise amplifier based on the MGA-86563 chip and an AD8361 power detector. The measured gain of the path is 19.5 dB, with parameter variations between different implementations not exceeding 0.3 dB.

Figure 10.
The input stage of the direction finder includes a low-frequency amplifier (1) based on the MGA-86563 chip and a power detector (2) using the AD8361 chip.
As the test radio source, a 1W video transmitter with a 2.4 GHz directional patch antenna was used, as illustrated in Figure 11.

Figure 11.
Test radio signal source.
In the experiment, the transmitter and direction finder were positioned 20 m apart, as shown in Figure 12.

Figure 12.
Conducting experiments with the transmitter (1) and the direction finder (2).
Initially, the directional patterns of the receiving antennas were measured and their alignment was fine-tuned. Figure 13 illustrates the shape and angular alignment of the direction finder’s antenna patterns after adjustment. For ease of comparison, the amplitudes were normalized.
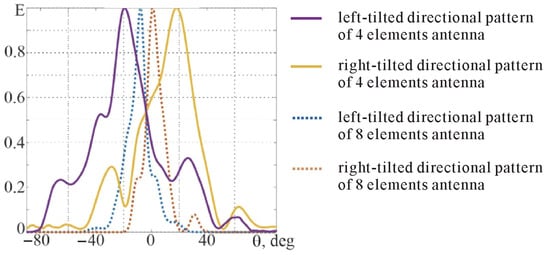
Figure 13.
Measured directional patterns of direction finder antennas.
From the obtained graphs, it was determined that the pattern width of the eight-element antennas is 17°, while that of the four-element antennas is 37°. The patterns of all antennas intersect at the 0.5 level at an angle of −3°. The offset of the intersection point from zero is not critical and will only result in a shift of the bearing characteristic zero. Figure 13 also shows that the radiation patterns of the various antennas are not symmetrical and have side lobes at the 0.5 level. This is due to manufacturing inaccuracies and mismatched coordination of individual antenna elements. However, for initial tests, such deviations are acceptable.
Next, the normalized bearing characteristics were plotted separately for antenna pairs with wide and narrow lobes. The resulting plots are presented in Figure 14. For antennas with wide lobes, the zone of unambiguous measurement is 36°, while for those with narrow lobes, it is 8°. Antennas with four elements offer a slope of the observational characteristic at 0.05 units per degree, whereas antennas with eight elements provide a slope of 0.25 units per degree.
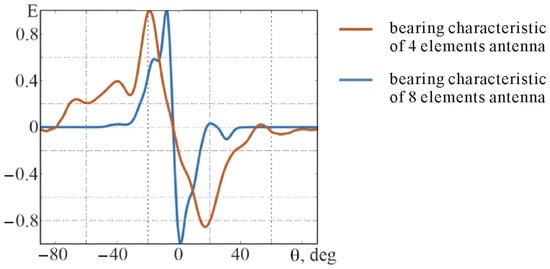
Figure 14.
Bearing characteristics of antennas with 4 elements and 8 elements.
The range of angles with unambiguous measurements is 9, 18, and 33° when respectively. Within the equal-signal zone, the slope of the bearing characteristic is 0.17 units per degree for the 9-degree range, 0.14 units per degree for the 18-degree range, and 0.10 units per degree for the 33-degree range.
The developed algorithm (22) was then applied to the system. The characteristics of the four-antenna direction finder were constructed under conditions of additional measurement amplification in channels with wide directional patterns. The gain coefficients were determined experimentally. The resulting plots are displayed in Figure 15.
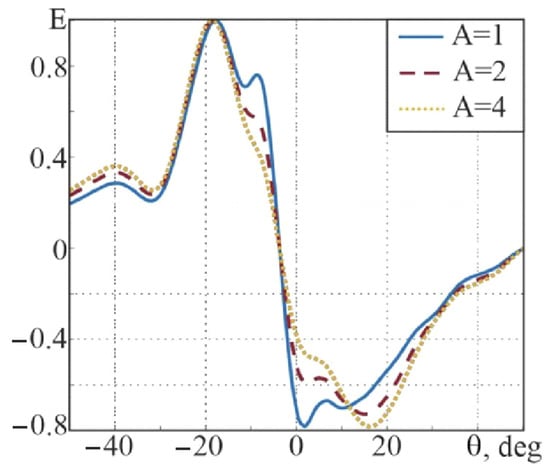
Figure 15.
Bearing characteristics of the system using the synthesized algorithm with varying signal amplification factors in the receiving channels with wide patterns.
The experiment using a four-antenna direction finder demonstrated the advantages of the developed methods. To create a six-antenna direction finder, improvements in the phase measurement layout are necessary. Working with phase measurements requires more precise design and implementation of new input paths. This task will be elaborated upon in future publications, where practical results and recommendations for six-antenna radio systems will be provided. In this paper, we conducted experiments that confirmed the fundamental principles of the proposed theory.
6. Discussion
The theoretical analysis of the simulated bearing curves in Figure 6 shows a contradiction in a two-antenna direction finder between the range of unambiguous measurement angles and the receiver’s response to angle changes (accuracy). This issue is resolved in a four-antenna system, where the range of unambiguous measurements quadruples, although with varying slopes in the characteristic curve. The six-antenna direction finder strikes a balance between accuracy and measurement range, effectively overcoming the previously mentioned contradiction.
Simulated RMS errors in estimating the angular position of the radio source in Figure 7 reveals that in the two-antenna direction finder the highest accuracy is found in the linear segments of the direction-finding characteristics. The four-antenna direction finder also exhibits fluctuations in marginal errors; however, due to the increased number of independent measurements, these fluctuations are minor, and overall, the marginal errors are lower compared to the two-antenna system. The six-antenna direction finder demonstrates the highest accuracy. However, due to the component involving a rapidly varying function , the accuracy drops significantly outside the equal-signal direction. At a specific point the marginal errors of the six-antenna direction finder match those of the four-antenna direction finder because .
The experiment validated the modeling results. Applying algorithm (22) in a four-antenna direction finder enables the achievement of a broad sector for unambiguous angle measurements and enhances the slope of the discriminative characteristic, provided that measurements from wide-beam antennas are adjusted with an additional proportionality factor greater than one. However, practical implementation of multiple antennas can be complicated by potential asymmetry and elevated side lobes in antenna patterns. For instance, Figure 15 shows an additional extremum in the discriminative characteristic at an angle of 7°, which is not present at the symmetric angle relative to the equal-signal zone (−13°). Addressing such issues in practice requires meticulous calibration of the direction-finding system, use of highly stable platforms, and precise positioning of the equipment.
7. Conclusions
Using the statistical theory of signal processing optimization in radio systems, the problem of synthesizing signal processing methods in direction finders with various combinations of receivers and antennas has been posed and solved. The analysis of the derived algorithms confirmed the assumption of an existing contradiction in dual-antenna amplitude direction finders between the accuracy of angular position measurements and the range of angles for unambiguous measurements. The obtained algorithms demonstrated the potential to overcome this contradiction by employing an additional pair of antennas in one case and incorporating phase measurements in another. Overall, the results suggest new opportunities for researchers to apply the mathematical theory of radio system optimization to enhance direction finders. The improvements in accuracy and widening of the range for unambiguous measurements were analytically verified through the Cramer–Rao inequality, simulation modeling, and experimental studies. The range of unambiguous measurements was increased by 3.6 times without decreasing accuracy.
Author Contributions
Conceptualization, S.Z.; methodology, E.T.; conducting the experiment, Y.V., S.S. and O.G.; validation, D.V. and V.K.; data curation, D.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work was funded by the National Research Foundation of Ukraine, supported by the University of Cambridge (Great Britain), and the state registration numbers of the projects is 0124U003671.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Demmel, F. Practical Aspects of Design and Application of Direction-Finding Systems. In Classical and Modern Direction-of-Arrival Estimation; Academic Press: Cambridge, MA, USA, 2009; pp. 53–92. [Google Scholar] [CrossRef]
- Gao, H.; Chen, M.; Du, Y.; Jakobsson, A. Monostatic MIMO Radar Direction Finding in Impulse Noise. Digit. Signal Process. 2021, 117, 103198. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y. Monostatic Multi-Source Direction Finding Based on I/Q Radio Frequency Data. AEU—Int. J. Electron. Commun. 2018, 97, 137–148. [Google Scholar] [CrossRef]
- Martian, A.; Paleacu, C.; Marcu, I.M.; Vladeanu, C. Direction-Finding for Unmanned Aerial Vehicles Using Radio Frequency Methods. Measurement 2024, 235, 114883. [Google Scholar] [CrossRef]
- Kozhabayeva, I.; Yerzhan, A.; Boykachev, P.; Manbetova, Z.; Imankul, M.; Yauheni, B.; Solonar, A.; Dunayev, P. Drone Direction Estimation: Phase Method with Two-Channel Direction Finder. Int. J. Electr. Comput. Eng. 2024, 14, 2779–2789. [Google Scholar] [CrossRef]
- Pau, G.; Arena, F.; Gebremariam, Y.E.; You, I. Bluetooth 5.1: An Analysis of Direction Finding Capability for High-Precision Location Services. Sensors 2021, 21, 3589. [Google Scholar] [CrossRef] [PubMed]
- Rutkowski, A.; Kawalec, A. Some of Problems of Direction Finding of Ground-Based Radars Using Monopulse Location System Installed on Unmanned Aerial Vehicle. Sensors 2020, 20, 5186. [Google Scholar] [CrossRef] [PubMed]
- Cook, H.A.; Kahn, M.T.E.; Balyan, V. Radio Direction-Finding Techniques for an Unmanned Aerial Vehicle. In Micro-Electronics and Telecommunication Engineering; Lecture Notes in Networks and Systems; Sharma, D.K., Balas, V.E., Son, L.H., Sharma, R., Cengiz, K., Eds.; Springer: Singapore, 2020; Volume 106. [Google Scholar] [CrossRef]
- Wibisono, A.; Piran, M.J.; Song, H.-K.; Lee, B.M. A Survey on Unmanned Underwater Vehicles: Challenges, Enabling Technologies, and Future Research Directions. Sensors 2023, 23, 7321. [Google Scholar] [CrossRef] [PubMed]
- Bae, I.; Hong, J. Survey on the Developments of Unmanned Marine Vehicles: Intelligence and Cooperation. Sensors 2023, 23, 4643. [Google Scholar] [CrossRef] [PubMed]
- Kandrot, S.; Hayes, S.; Holloway, P. Applications of Uncrewed Aerial Vehicles (UAV) Technology to Support Integrated Coastal Zone Management and the UN Sustainable Development Goals at the Coast. Estuaries Coasts 2022, 45, 1230–1249. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-X.; Liu, Q.-F.; Hong, R.-J.; Pan, P.-P.; Deng, Z.-M. A Novel Monopulse Angle Estimation Method for Wideband LFM Radars. Sensors 2016, 16, 817. [Google Scholar] [CrossRef] [PubMed]
- Yan, E.; Zhang, L.; Dong, M.; Lin, Z.; Xie, L.; Tian, Z.; Sun, X.; Cao, Y. Improving Accuracy of an Amplitude Comparison-Based Direction-Finding System by Neural Network Optimization. IEEE Access 2020, 8, 169688–169700. [Google Scholar] [CrossRef]
- Bakhvalov, V.; Zhyrov, G.; Khrashchevsky, R.; Romanenko, E.; Druzhynin, V. Phase Direction Finding Radio Engineering System. In Proceedings of the 2021 IEEE 6th International Conference on Actual Problems of Unmanned Aerial Vehicles Development (APUAVD), Kyiv, Ukraine, 21–23 September 2021; IEEE: New York, NY, USA, 2021; pp. 200–203. [Google Scholar] [CrossRef]
- Polikarovskykh, O.; Hula, I. Implementing the Search Algorithm of the Correlation Interferometer Direction Finder through the GNU Radio Software Platform. Secur. Infocommunication Syst. Internet Things 2023, 1, 02006. [Google Scholar] [CrossRef]
- Volosyuk, V.K.; Kravchenko, V.F. Statistical Theory of Radio Engineering Systems for Remote Sensing and Radar; Fizmatlit: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Volosyuk, V.; Zhyla, S. Statistical Theory of Optimal Stochastic Signals Processing in Multichannel Aerospace Imaging Radar Systems. Computation 2022, 10, 224. [Google Scholar] [CrossRef]
- Volosyuk, V.; Zhyla, S. Statistical Theory of Optimal Functionally Deterministic Signals Processing in Multichannel Aerospace Imaging Radar Systems. Computation 2022, 10, 213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).