Synthesis of Self-Checking Circuits for Train Route Traffic Control at Intermediate Stations with Control of Calculations Based on Weight-Based Sum Codes
Abstract
1. Introduction
2. Research Objective
3. General Research Approaches and Methodology
4. Requirements for the Operating Logic of Railway Trackside Equipment
 is the red signal indication;
is the red signal indication;  is the yellow signal indication;
is the yellow signal indication;  is the green signal indication;
is the green signal indication;  is the “Two yellow, upper flashing” signal indication;
is the “Two yellow, upper flashing” signal indication;  is the “Two yellow” signal indication.
is the “Two yellow” signal indication.- Route type (train or shunting);
- Departure point (the signal from which the route starts);
- Destination point (the signal to which or beyond which the route is constructed).
- The first section in the train route is released when the approach section is released, this section is occupied, the next section is occupied, and this section is released and remains free for at least 6 s;
- The first section in shunting routes is released when this section is occupied, the next one is occupied, and this section is released and remains free for at least 6 s;
- Any section that is not the first one is released when this section is occupied, the next one is occupied, and this section is released and remains free for at least 6 s;
- If the approach section was not released during the train route, then the route will be released after the train arrives at the route destination point.
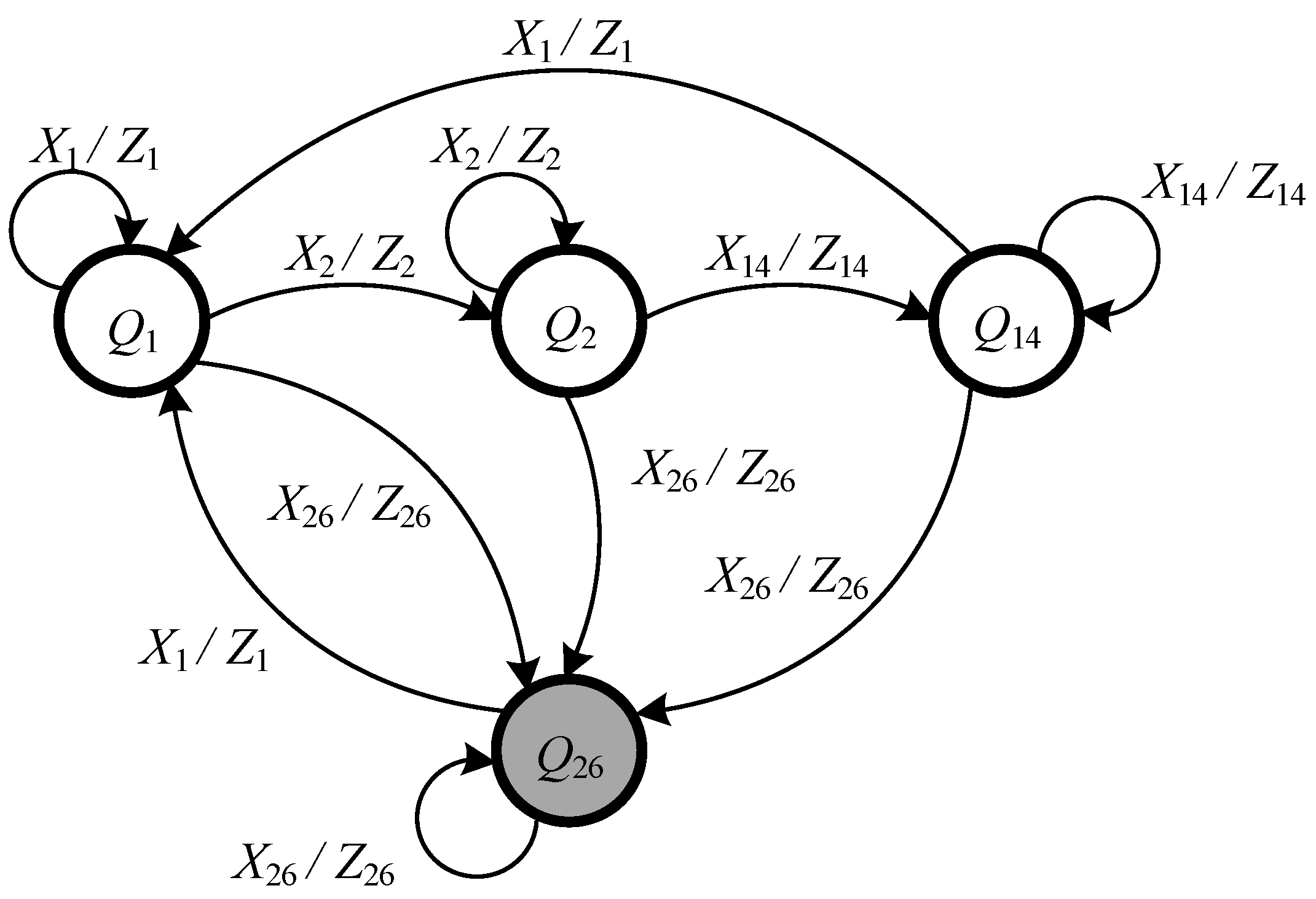
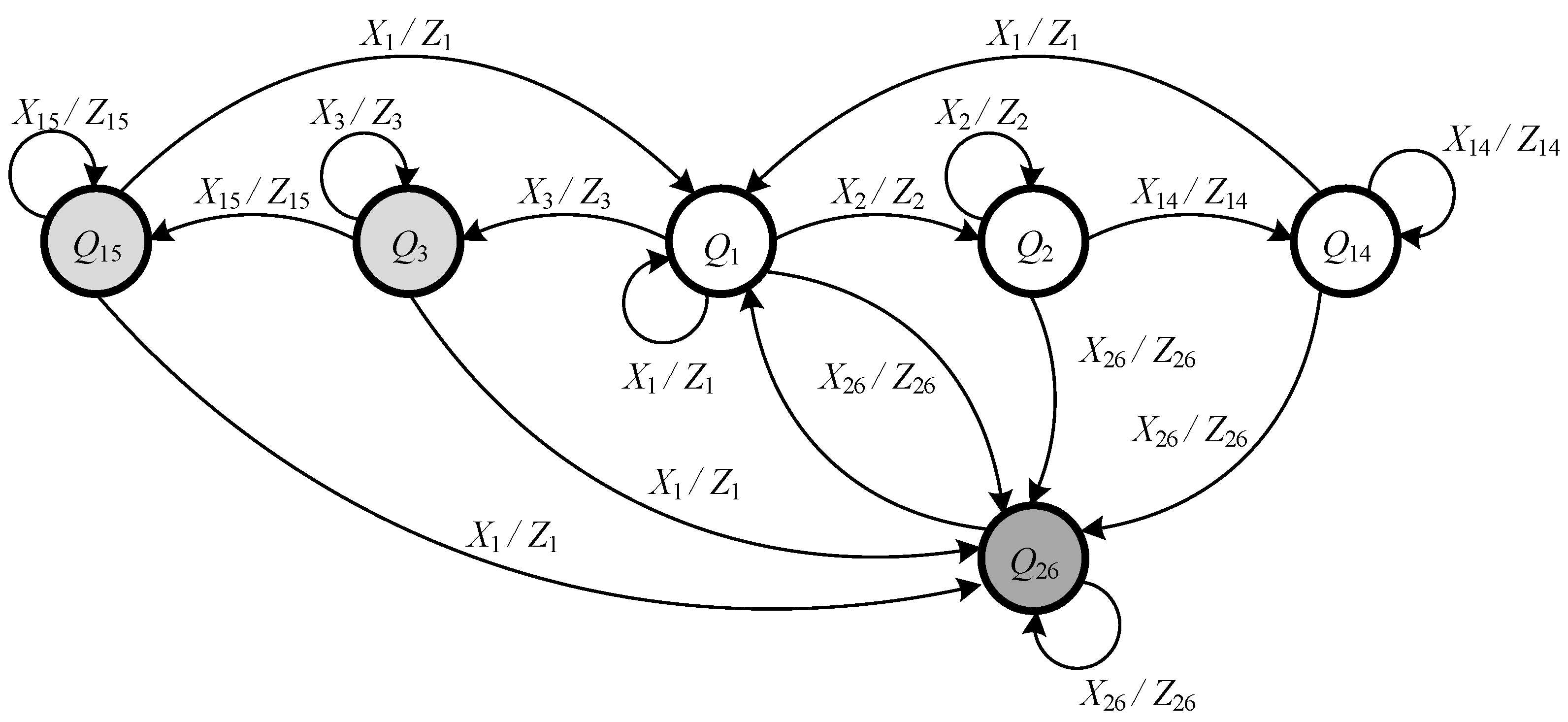
5. Principles of Forming the Transition Graph for an FSM
- x1 is the route type (0—not specified; 1—train; 2—shunting);
- x2 is the route departure point (0—not specified; 1—E; 2—O1; 3—O2; 4—O3; 5—S2);
- x3 is the route destination point (0—not specified; 1—O; 2—O1; 3—O2; 4—O3; 5—S2);
- x4 is the track and switch point section occupancy along the route (0—occupied; 1—free);
- x5 is switch point position 2 (0—plus position; 1—minus position; 2—no control);
- x6 is switch point position 4 (0—plus position, 1—minus position, 2—no control);
- x7 is the track and switch point sections locking (0—released; 1—locked);
- x8 is switch point locking 2 (0—released; 1—locked);
- x9 is switch point locking 4 (0—released; 1—locked);
- z1 is switch point state 2;
- z2 is switch point state 4;
- z3 is railway signal state E (0—forbidding indication; 1—permissive indication; 2—no indication);
- z4 is railway signal state O1 (0—forbidding indication; 1—permissive indication; 2—no indication);
- z5 is railway signal state O2 (0—forbidding indication; 1—permissive indication; 2—no indication);
- z6 is railway signal state O3 (0—forbidding indication; 1—permissive indication; 2—no indication);
- z7—is railway signal state S2 (0—forbidding indication; 1—permissive indication; 2—no indication);
- For an intermediate station, a switch points and signals interdependencies table is acquired from technical documentation [19].
- For each individual route, a graph is created that includes the following states:
- Initial state (in this case, there are no routes at the station);
- Route preparation state (one state for each route);
- Route locking state (one state for each route);
- Protective state;
- A state of the system in which one or more of the control devices go into a pre-failure state.
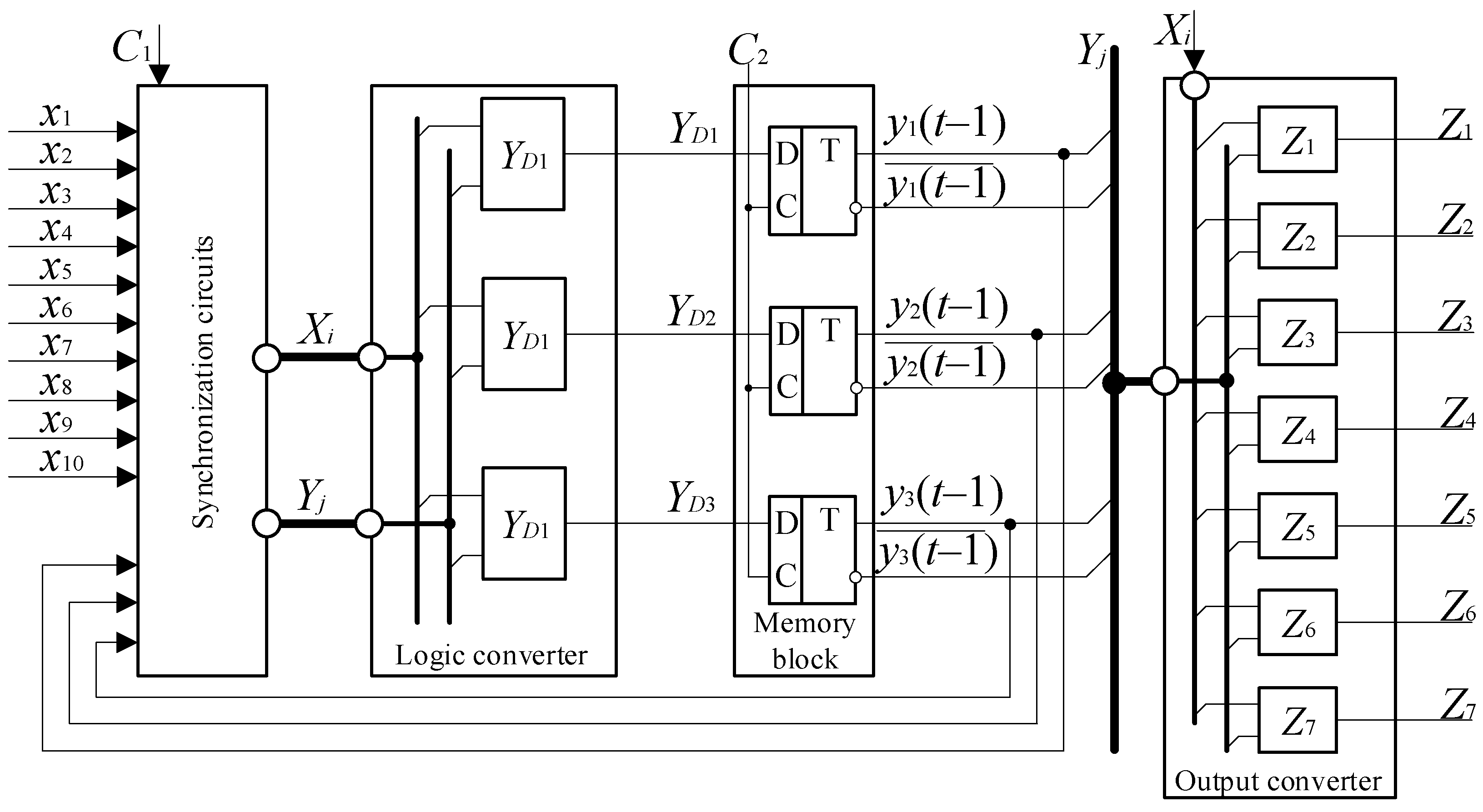
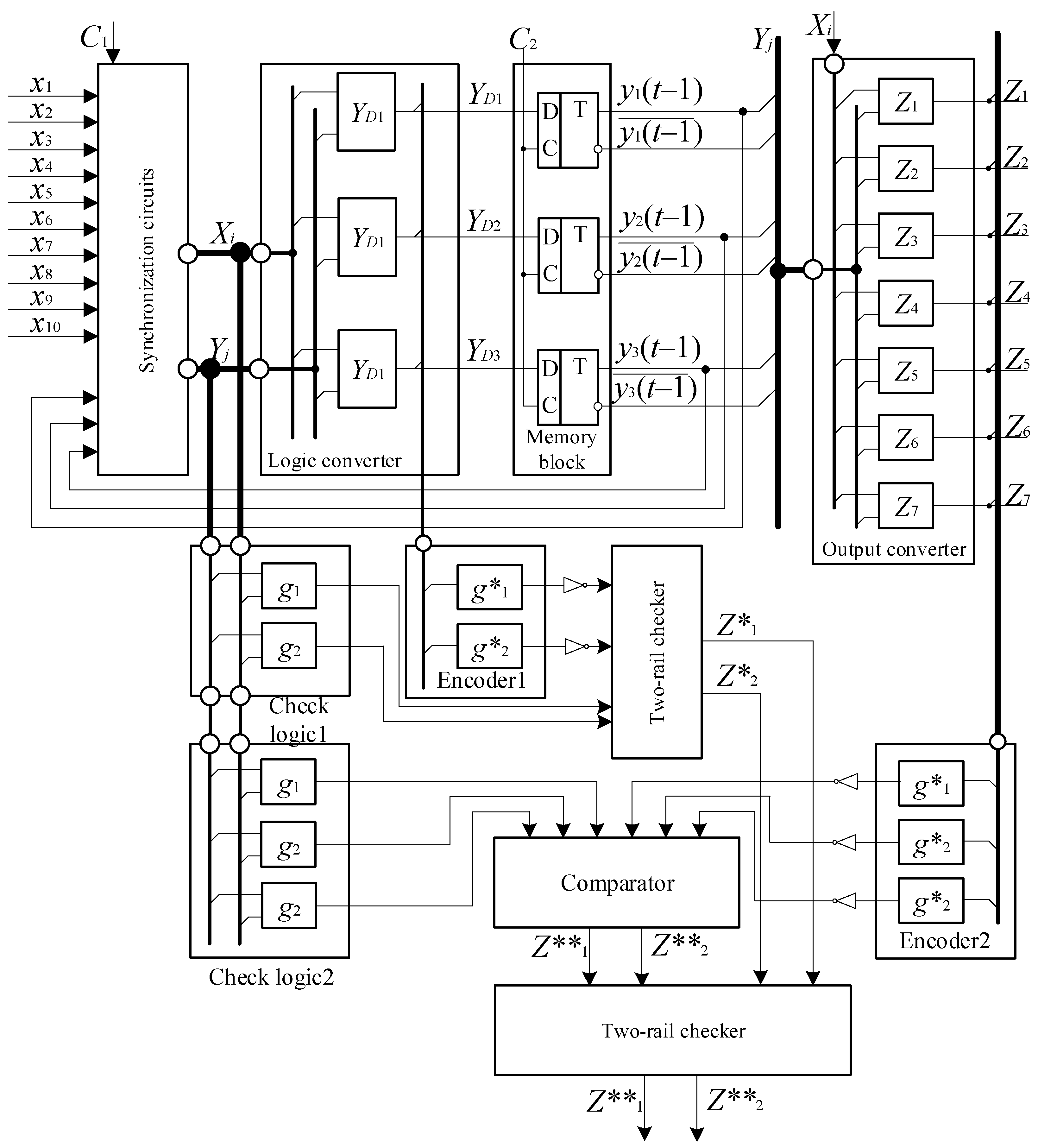
6. FPGA-Based FSM Synthesis
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Theeg, G.; Vlasenko, S. Railway Signalling & Interlocking, 3rd ed.; PMC Media House GmbH: Leverkusen, Germany, 2020; p. 552. [Google Scholar]
- Efanov, D.; Lykov, A.; Osadchy, G. Testing of Relay-Contact Circuits of Railway Signalling and Interlocking. In Proceedings of the 15th IEEE East-West Design & Test Symposium (EWDTS’2017), Novi Sad, Serbia, 29 September–2 October 2017; pp. 242–248. [Google Scholar] [CrossRef]
- Bădău, F. Railway Interlockings—A Review of the Current State of Railway Safety Technology in Europe. Promet Traffic Transp. 2022, 34, 443–454. [Google Scholar] [CrossRef]
- Dobiáš, R.; Kubátová, H. FPGA Based Design of Railway’s Interlocking Equipment. In Proceedings of the EUROMICRO Symposium on Digital System Design, Rennes, France, 31 August–3 September 2004; pp. 467–473. [Google Scholar] [CrossRef]
- Dobias, R.; Konarski, J.; Kubatova, H. Dependability Evaluation of Real Railway Interlocking Device. In Proceedings of the 2008 11th EUROMICRO Conference on Digital System Design Architectures, Methods and Tools, Parma, Italy, 3–5 September 2008; pp. 228–233. [Google Scholar] [CrossRef]
- Efanov, D.V.; Pashukov, A.V.; Khóroshev, V.V. FPGA Self-Diagnosing and Testable Control Devices for Railway Switch Point. In Proceedings of the 2023 Seminar on Networks, Circuits and Systems (NCS), St. Petersburg, Russia, 29–30 November 2023; pp. 54–59. [Google Scholar] [CrossRef]
- Heidmann, L. Smart Point Machines: Paving the Way for Predictive Maintenance. Signal Draht 2018, 110, 70–75. [Google Scholar]
- Eriş, O.; Mutlu, İ. Design of Signal Control Structures Using Formal Methods for Railway Interlocking Systems. In Proceedings of the 11th International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2010. [Google Scholar] [CrossRef]
- Karolak, J.; Daszczuk, W.B.; Grabski, W.; Kochan, A. Temporal Verification of Relay-Based Railway Traffic Control Systems Using the Integrated Model of Distributed Systems. Energies 2022, 15, 9041. [Google Scholar] [CrossRef]
- Sapozhnikov, V., VI. Synthesis of Train Traffic Control Systems at Railway Stations with the Exception of Dangerous Failures; Publishing house Nauka: Moscow, Russia, 2021; p. 229. (In Russian) [Google Scholar]
- Mirabadi, A.; Yazdi, M.B. Automatic generation and verification of railway interlocking control tables using FSM and NuSMV. Transp. Probl. 2009, 4, 103–110. [Google Scholar]
- Wang, J.; Zhang, X.; Shi, P.; Cao, B.; Wang, B. A DNA Finite-State Machine Based on the Programmable Allosteric Strategy of DNAzyme. Int. J. Mol. Sci. 2023, 24, 3588. [Google Scholar] [CrossRef] [PubMed]
- Potekhin, A.I. Logical Foundations of Group Traffic Control of Trains. Autom. Remote Control. 2020, 81, 883–896. [Google Scholar] [CrossRef]
- Gavzov, D.V.; Sapozhnikov, V.V.; Sapozhnikov, V., VI. Methods for Providing Safety in Discrete Systems. Autom. Remote Control. 1994, 55, 1085–1122. [Google Scholar]
- Bestemyanov, P.F. Methods of Providing Hardware Safety for Microprocessor Train Control Systems. Russ. Electr. Eng. 2020, 91, 531–536. [Google Scholar] [CrossRef]
- Ma, W.-G.; Hei, X.-H. An Approach for Design and Formal Verification of Safety-Critical Software. In Proceedings of the International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010. [Google Scholar] [CrossRef]
- Dincel, E.; Eris, O.; Kurtulan, S. Automata-Based Railway Signaling and Interlocking System Design [Testing Ourselves]. IEEE Antennas Propag. Mag. 2013, 55, 308–319. [Google Scholar] [CrossRef]
- Sapozhnikov, V., VI; Kononov, V.A. Electrical Interlocking Systems; Route: Moscow, Russia, 2002; p. 168. (In Russian) [Google Scholar]
- Gordon, M.A.; Vasilenko, P.A.; Sedykh, D.V. Synthesis of Full Functional Check Programs for Train Traffic Management Systems on a Railway Station. In Journal of Physics: Conference Series. 13. Series. “Computer-Aided Technologies in Applied Mathematics”; IOP Publishing: Bristol, UK, 2020; p. 012013. [Google Scholar] [CrossRef]
- Efanov, D.V.; Khoroshev, V.V.; Osadchy, G.V. Conceptual Foundations of the Synthesis of Safe Train Traffic Control Systems. World Transp. Transp. 2022, 20, 168–175. [Google Scholar] [CrossRef]
- Efanov, D.V.; Khóroshev, V.V.; Osadchy, G.V. Principles of Safety Signalling and Traffic Control Systems Synthesis on Railways. In Proceedings of the 9th International Conference on Industrial Engineering, Applications and Manufacturing (ICIE), Sochi, Russia, 15–19 May 2022; pp. 634–638. [Google Scholar] [CrossRef]
- Harris, D.M.; Harris, S.L. Digital Design and Computer Architecture; Morgan Kaufmann: San Francisco, CA, USA, 2012; p. 569. [Google Scholar]
- Salauyou, V. Synthesis of High-Speed Finite State Machines in FPGAs by State Splitting. In Proceedings of the 15th IFIP International Conference on Computer Information Systems and Industrial Management (CISIM), Vilnius, Lithuania, 14–16 September 2016; pp. 741–751. [Google Scholar] [CrossRef]
- Efanov, D.V.; Pashukov, A.V. Weight-Based Sum Codes with Arbitrary Modulus. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 25–28 January 2022; pp. 133–138. [Google Scholar] [CrossRef]
- Agibalov, G.P.; Evtushenko, N.V. Decomposition of Finite Automata; Tomsk University Press: Tomsk, Russia, 1985; p. 127. (In Russian) [Google Scholar]


| Route | Route Number | Route Name | Traffic Light | Railway Switch Points | |||
|---|---|---|---|---|---|---|---|
| 2 | 4 | 1 | 3 | ||||
| Even yard neck section | 1 | Reception to T1 | E | + | + | ||
| 2 | Reception to T2 | E | − | ||||
| 3 | Reception to T3 | E | + | − | |||
| 4 | Dispatch from T1 | O2 | + | + | |||
| 5 | Dispatch from T2 | O1 | − | ||||
| 6 | Dispatch from T3 | O3 | + | − | |||
| Odd yard neck section | 7 | Reception to T1 | O | + | + | ||
| 8 | Reception to T2 | O | + | − | |||
| 9 | Reception to T3 | O | − | ||||
| 10 | Dispatch from T1 | E1 | + | + | |||
| 11 | Dispatch from T2 | E2 | + | − | |||
| 12 | Dispatch from T3 | E3 | − | ||||
| Route | Route Number | Route Name | Route-Defining Railway Switch Point Electric Mechanism | ||
|---|---|---|---|---|---|
| Even yard neck section | From signal | S2 | 13 | To T1 | +2 +4 |
| S2 | 14 | To T2 | −2 | ||
| S2 | 15 | To T3 | +2 −4 | ||
| O1 | 16 | Beyond the signal S2 | +2 +4 | ||
| O3 | 17 | Beyond the signal S2 | −2 | ||
| O2 | 18 | Beyond the signal S2 | +2 −4 | ||
| Odd yard neck section | From signal | S1 | 19 | To T1 | +1 +3 |
| S1 | 20 | To T2 | +1 −3 | ||
| S1 | 21 | To T3 | −1 | ||
| E1 | 22 | Beyond the signal S1 | +1 +3 | ||
| E2 | 23 | Beyond the signal S1 | +1 −3 | ||
| E3 | 24 | Beyond the signal S1 | −1 | ||
| Route Name | Movement Direction Is Up | |||
|---|---|---|---|---|
| Railway Signal Indications | ||||
| E | E1 | E2 | E3 | |
| Reception to T1 |  |  | ||
| Reception to T2 |  |  | ||
| Reception to T3 |  |  | ||
| Pass through T1 |  |  ; ; | ||
| Pass through T2 | 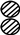 |  ; ; | ||
| Pass through T3 | 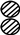 |  ; ; | ||
| Dispatch from T1 |  ; ; | |||
| Dispatch from T2 |  ; ; | |||
| Dispatch from T3 |  ; ; | |||
| Route Name | Movement Direction is Down | |||
| Railway Signal Indications | ||||
| O | O1 | O2 | O3 | |
| Reception to T1 |  |  | ||
| Reception to T2 | 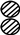 |  | ||
| Reception to T3 | 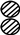 |  | ||
| Pass through T1 |  |  ; ; | ||
| Pass through T2 | 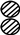 |  ; ; | ||
| Pass through T3 | 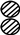 |  ; ; | ||
| Dispatch from T1 |  ; ; | |||
| Dispatch from T2 |  ; ; | |||
| Dispatch from T3 |  ; ; | |||
| State | Input Parameter Vectors <x1 x2 … x9> | Notation for the Parameter Vectors Set | Output Vector <z1 z2 … z7> | Notation for the Output Vectors Set |
|---|---|---|---|---|
| Q1—The route is released | 0 0 0 ~ ~ ~ 0 0 0 | X1 | ~ ~ 0 | Z1 |
| Route track preparation | ||||
| Q2—Reception from E to T1 | 1 1 2 1 0 0 0 0 0 | X2 | 1 1 0 0 0 0 0 | Z2 |
| Q3—Reception from E to T2 | 1 1 3 1 1 ~ 0 0 0 | X3 | 2 ~ 0 0 0 0 0 | Z3 |
| Q4—Reception from E to T3 | 1 1 4 1 0 1 0 0 0 | X4 | 1 2 0 0 0 0 0 | Z4 |
| Q5—Dispatch from T1 beyond E | 1 2 1 1 0 0 0 0 0 | X5 | 1 1 0 0 0 0 0 | Z5 |
| Q6—Dispatch from T2 beyond E | 1 3 1 1 1 ~ 0 0 0 | X6 | 2 ~ 0 0 0 0 0 | Z6 |
| Q7—Dispatch from T3 beyond E | 1 4 1 1 0 0 0 0 0 | X7 | 1 2 0 0 0 0 0 | Z7 |
| Q8—From S2 to T1 | 2 5 2 1 0 0 0 0 0 | X8 | 1 1 0 0 0 0 0 | Z8 |
| Q9—From S2 to T2 | 2 5 3 1 1 ~ 0 0 0 | X9 | 2 ~ 0 0 0 0 0 | Z9 |
| Q10—From S2 to T3 | 2 5 4 1 0 1 0 0 0 | X10 | 1 2 0 0 0 0 0 | Z10 |
| Q11—From T1 beyond signal S2 | 2 2 5 1 0 0 0 0 0 | X11 | 1 1 0 0 0 0 0 | Z11 |
| Q12—From T2 beyond signal S2 | 2 3 5 1 1 ~ 0 0 0 | X12 | 2 ~ 0 0 0 0 0 | Z12 |
| Q13—From T3 beyond signal S2 | 2 4 5 1 0 1 0 0 0 | X13 | 1 2 0 0 0 0 0 | Z13 |
| Route locking | ||||
| Q14—Reception from E to T1 | 1 1 2 1 0 0 1 1 1 | X14 | 5 5 1 0 0 0 0 | Z14 |
| Q15—Reception from E to T2 | 1 1 3 1 1 ~ 1 1 1 | X15 | 6 ~ 1 0 0 0 0 | Z15 |
| Q16—Reception from E to T3 | 1 1 4 1 0 1 1 1 1 | X16 | 5 6 1 0 0 0 0 | Z16 |
| Q17—Dispatch from T1 beyond E | 1 2 1 1 0 0 1 1 1 | X17 | 5 5 0 1 0 0 0 | Z17 |
| Q18—Dispatch from T2 beyond E | 1 3 1 1 1 ~ 1 1 1 | X18 | 6 ~ 0 0 1 0 0 | Z18 |
| Q19—Dispatch from T3 beyond E | 1 4 1 1 0 0 1 1 1 | X19 | 5 6 0 0 0 1 0 | Z19 |
| Q20—From S2 to T1 | 2 5 2 1 0 0 1 1 1 | X20 | 5 5 0 0 0 0 1 | Z20 |
| Q21—From S2 to T2 | 2 5 3 1 1 ~ 1 1 1 | X21 | 6 ~ 0 0 0 0 1 | Z21 |
| Q22—From S2 to T3 | 2 5 4 1 0 1 1 1 1 | X22 | 5 6 0 0 0 0 1 | Z22 |
| Q23—From T1 beyond signal S2 | 2 2 5 1 0 0 1 1 1 | X23 | 5 5 0 1 0 0 0 | Z23 |
| Q24—From T2 beyond signal S2 | 2 3 5 1 1 ~ 1 1 1 | X24 | 6 ~ 0 0 1 0 0 | Z24 |
| Q25—From T3 beyond signal S2 | 2 4 5 1 0 1 1 1 1 | X25 | 5 6 0 0 0 1 0 | Z25 |
| Q26—Protective state | X26 | ~ ~ 0 0 0 0 0 | Z26 | |
| State | Input Parameter Vectors | Notation for the Parameter Vectors Set | Output Vector Values | Notation for the Parameter Vectors Set |
|---|---|---|---|---|
| Q1—The route is released | 00 000 000 ~ ~~ ~~ 0 0 0 | X1 | 001 001 0 0 0 0 0 | Z1 |
| Route track preparation | ||||
| Q2—Reception from E to T1 | 01 001 010 1 00 00 0 0 0 | X2 | 001 001 0 0 0 0 0 | Z2 |
| Q4—Reception from E to T2 | 01 001 100 1 00 00 0 0 0 | X4 | 001 010 0 0 0 0 0 | Z’3 |
| Route locking | ||||
| Q14—Reception from E to T1 | 01 001 010 1 00 00 1 1 1 | X14 | 101 101 1 0 0 0 0 | Z14 |
| Q16—Reception from E to T2 | 01 001 100 1 01 00 1 1 1 | X16 | 101 110 1 0 0 0 0 | Z15 |
| Q26—Protective state | X26 | 000 000 0 0 0 0 0 | Z26 | |
| Q | x1x2x3x4x5x6x7x8x9x10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0000 000 000 | 0000 001 000 | 0000 010 000 | 0000 011 000 | 0000 100 000 | 0000 101 000 | 0000 110 000 | 0000 111 000 | 1101 101 000 | 1110 100 111 | 1101 100 111 | 1110 101 111 | A* | |
| 1 (Q1) | (1), Z1 | (1), Z1 | (1), Z1 | (1), Z1 | (1), Z1 | (1), Z1 | (1), Z1 | (1), Z1 | 2, Z2 | 3,Z4 | 6, Z26 | 6, Z26 | 6, Z26 |
| 2 (Q2) | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | (2), Z2 | 6, Z26 | 4,Z14 | 6, Z26 | 6, Z26 |
| 3 (Q4) | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | 6, Z26 | (3),Z4 | 6, Z26 | 5, Z16 | 6, Z26 |
| 4 (Q14) | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 6, Z26 | 6, Z26 | (4), Z14 | 6, Z26 | 6, Z26 |
| 5 (Q16) | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 6, Z26 | 6, Z26 | 6, Z26 | (5), Z16 | 6, Z26 |
| 6 (Q26) | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | 1, Z1 | (6), Z26 | (6), Z26 | (6), Z26 | (6), Z26 | (6), Z26 |
| Q | Encoded State |
|---|---|
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 000 |
| Q | x1x2x3x4x5x6x7x8x9x10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0000 000 000 | 0000 001 000 | 0000 010 000 | 0000 011 000 | 0000 100 000 | 0000 101 000 | 0000 110 000 | 0000 111 000 | 1101 101 000 | 1110 100 111 | 1101 100 111 | 1110 101 111 | A* | |
| 001 | (001) | (001) | (001) | (001) | (001) | (001) | (001) | (001) | 010 | 011 | 000 | 000 | 000 |
| 010 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | (010) | 000 | 100 | 000 | 000 |
| 011 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | (011) | 000 | 101 | 000 |
| 100 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 000 | 000 | (100) | 000 | 000 |
| 101 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 000 | 000 | 000 | (101) | 000 |
| 000 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | (000) | (000) | (000) | (000) | (000) |
| y(t ‒ 1) | y(t) | |
|---|---|---|
| 0 | 1 | |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| Decimal Number of a Binary Vector | x1x2x3x4x5x6x7x8x9x10 y1y2y3 | YD1 | YD2 | YD3 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | z10 | z11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0000000000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0000000000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0000000000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0000000000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0000000000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0000000000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 64 | 0000001000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 65 | 0000001000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 66 | 0000001000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 67 | 0000001000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 68 | 0000001000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 69 | 0000001000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 128 | 0000010000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 129 | 0000010000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 130 | 0000010000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 131 | 0000010000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 132 | 0000010000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 133 | 0000010000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 192 | 0000011000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 193 | 0000011000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 194 | 0000011000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 195 | 0000011000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 196 | 0000011000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 197 | 0000011000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 256 | 0000100000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 257 | 0000100000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 258 | 0000100000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 259 | 0000100000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 260 | 0000100000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 261 | 0000100000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 320 | 0000101000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 321 | 0000101000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 322 | 0000101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 323 | 0000101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 324 | 0000101000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 325 | 0000101000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 384 | 0000110000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 385 | 0000110000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 386 | 0000110000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 387 | 0000110000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 388 | 0000110000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 389 | 0000110000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 448 | 0000111000 000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 449 | 0000111000 001 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 450 | 0000111000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 451 | 0000111000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 452 | 0000111000 100 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 453 | 0000111000 101 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6968 | 1101100111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6969 | 1101100111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6970 | 1101100111 010 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 6971 | 1101100111 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6972 | 1101100111 100 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 6973 | 1101100111 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6976 | 1101101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6977 | 1101101000 001 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6978 | 1101101000 010 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6979 | 1101101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6980 | 1101101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6981 | 1101101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7488 | 1110101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7489 | 1110101000 001 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7490 | 1110101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7491 | 1110101000 011 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7492 | 1110101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7493 | 1110101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7544 | 1110101111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7545 | 1110101111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7546 | 1110101111 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7547 | 1110101111 011 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7548 | 1110101111 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7549 | 1110101111 101 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| - | A ** | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Family | Cyclone V |
|---|---|
| Device | 5CEBA2F17A7 |
| Logic utilization (in ALMs) | 14 |
| Total registers | 16 |
| Total pins | 17 |
| Decimal Number of a Binary Vector | x1x2x3x4x5x6x7x8x9x10y1y2y3 | YD1 | YD2 | YD3 | r | r (mod4) | g1 | g2 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0000000000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 1 | 0000000000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 2 | 0000000000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0000000000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0000000000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 5 | 0000000000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 64 | 0000001000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 65 | 0000001000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 66 | 0000001000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 67 | 0000001000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 68 | 0000001000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 69 | 0000001000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 128 | 0000010000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 129 | 0000010000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 130 | 0000010000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 131 | 0000010000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 132 | 0000010000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 133 | 0000010000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 192 | 0000011000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 193 | 0000011000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 194 | 0000011000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 195 | 0000011000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 196 | 0000011000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 197 | 0000011000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 256 | 0000100000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 257 | 0000100000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 258 | 0000100000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 259 | 0000100000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 260 | 0000100000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 261 | 0000100000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 320 | 0000101000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 321 | 0000101000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 322 | 0000101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 323 | 0000101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 324 | 0000101000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 325 | 0000101000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 384 | 0000110000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 385 | 0000110000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 386 | 0000110000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 387 | 0000110000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 388 | 0000110000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 389 | 0000110000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 448 | 0000111000 000 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 449 | 0000111000 001 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 450 | 0000111000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 451 | 0000111000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 452 | 0000111000 100 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 453 | 0000111000 101 | 0 | 0 | 1 | 3 | 3 | 1 | 1 |
| 6968 | 1101100111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6969 | 1101100111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6970 | 1101100111 010 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 6971 | 1101100111 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6972 | 1101100111 100 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 6973 | 1101100111 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6976 | 1101101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6977 | 1101101000 001 | 0 | 1 | 0 | 2 | 2 | 1 | 0 |
| 6978 | 1101101000 010 | 0 | 1 | 0 | 2 | 2 | 1 | 0 |
| 6979 | 1101101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6980 | 1101101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6981 | 1101101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7488 | 1110101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7489 | 1110101000 001 | 0 | 1 | 1 | 5 | 1 | 0 | 1 |
| 7490 | 1110101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7491 | 1110101000 011 | 0 | 1 | 1 | 5 | 1 | 0 | 1 |
| 7492 | 1110101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7493 | 1110101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7544 | 1110101111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7545 | 1110101111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7546 | 1110101111 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7547 | 1110101111 011 | 1 | 0 | 1 | 4 | 0 | 0 | 0 |
| 7548 | 1110101111 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7549 | 1110101111 101 | 1 | 0 | 1 | 4 | 0 | 0 | 0 |
| - | A** | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| YD1 YD2 YD3. | g*1 | g*2 |
|---|---|---|
| 0 0 0 | 0 | 0 |
| 0 0 1 | 1 | 1 |
| 0 1 0 | 1 | 0 |
| 0 1 1 | 0 | 1 |
| 1 0 0 | 0 | 1 |
| 1 0 1 | 0 | 0 |
| 1 1 0 | ~ | ~ |
| 1 1 1 | ~ | ~ |
| Decimal Number of a Binary Vector | x1x2x3x4x5x6x7x8x9x10y1y2y3 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | r | r (mod8) | g1 | g2 | g3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0000000000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0000000000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0000000000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0000000000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0000000000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0000000000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 64 | 0000001000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 65 | 0000001000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 66 | 0000001000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 67 | 0000001000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 68 | 0000001000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 69 | 0000001000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 128 | 0000010000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 129 | 0000010000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 130 | 0000010000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 131 | 0000010000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 132 | 0000010000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 133 | 0000010000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 192 | 0000011000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 193 | 0000011000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 194 | 0000011000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 195 | 0000011000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 196 | 0000011000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 197 | 0000011000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 256 | 0000100000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 257 | 0000100000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 258 | 0000100000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 259 | 0000100000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 260 | 0000100000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 261 | 0000100000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 320 | 0000101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 321 | 0000101000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 322 | 0000101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 323 | 0000101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 324 | 0000101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 325 | 0000101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 384 | 0000110000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 385 | 0000110000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 386 | 0000110000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 387 | 0000110000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 388 | 0000110000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 389 | 0000110000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 448 | 0000111000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 449 | 0000111000 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 450 | 0000111000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 451 | 0000111000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 452 | 0000111000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 453 | 0000111000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6968 | 1101100111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6969 | 1101100111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6970 | 1101100111 010 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 21 | 5 | 1 | 0 | 1 |
| 6971 | 1101100111 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6972 | 1101100111 100 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 21 | 5 | 1 | 0 | 1 |
| 6973 | 1101100111 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6976 | 1101101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6977 | 1101101000 001 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 9 | 1 | 0 | 0 | 1 |
| 6978 | 1101101000 010 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 9 | 1 | 0 | 0 | 1 |
| 6979 | 1101101000 011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6980 | 1101101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6981 | 1101101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7488 | 1110101000 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7489 | 1110101000 001 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 8 | 0 | 0 | 0 | 0 |
| 7490 | 1110101000 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7491 | 1110101000 011 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 8 | 0 | 0 | 0 | 0 |
| 7492 | 1110101000 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7493 | 1110101000 101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7544 | 1110101111 000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7545 | 1110101111 001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7546 | 1110101111 010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7547 | 1110101111 011 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 20 | 4 | 1 | 0 | 0 |
| 7548 | 1110101111 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7549 | 1110101111 101 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 20 | 4 | 1 | 0 | 0 |
| - | A ** | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| z1z2z3 z4 z5 z6 z7 | g*1 | g*2 | g*3 |
|---|---|---|---|
| 0 0 0 0 0 0 0 | 0 | 0 | 0 |
| 0 0 1 0 0 1 0 | 0 | 0 | 1 |
| 0 0 1 0 1 0 0 | 0 | 0 | 0 |
| 1 0 1 1 0 1 1 | 1 | 0 | 1 |
| 1 0 1 1 1 0 1 | 1 | 0 | 0 |
| A *** | ~ | ~ | ~ |
| Family | Cyclone V |
|---|---|
| Device | 5CEBA2F17A7 |
| Logic utilization (in ALMs) | 10 |
| Total registers | 0 |
| Total pins | 22 |
| Family | Cyclone V |
|---|---|
| Device | 5CEBA2F17A7 |
| Logic utilization (in ALMs) | 9 |
| Total registers | 0 |
| Total pins | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efanov, D.V.; Pashukov, A.V.; Mikhailiuta, E.M.; Khóroshev, V.V.; Abdullaev, R.B.; Plotnikov, D.G.; Banite, A.V.; Leksashov, A.V.; Khomutov, D.N.; Baratov, D.K.; et al. Synthesis of Self-Checking Circuits for Train Route Traffic Control at Intermediate Stations with Control of Calculations Based on Weight-Based Sum Codes. Computation 2024, 12, 171. https://doi.org/10.3390/computation12090171
Efanov DV, Pashukov AV, Mikhailiuta EM, Khóroshev VV, Abdullaev RB, Plotnikov DG, Banite AV, Leksashov AV, Khomutov DN, Baratov DK, et al. Synthesis of Self-Checking Circuits for Train Route Traffic Control at Intermediate Stations with Control of Calculations Based on Weight-Based Sum Codes. Computation. 2024; 12(9):171. https://doi.org/10.3390/computation12090171
Chicago/Turabian StyleEfanov, Dmitry V., Artyom V. Pashukov, Evgenii M. Mikhailiuta, Valery V. Khóroshev, Ruslan B. Abdullaev, Dmitry G. Plotnikov, Aushra V. Banite, Alexander V. Leksashov, Dmitry N. Khomutov, Dilshod Kh. Baratov, and et al. 2024. "Synthesis of Self-Checking Circuits for Train Route Traffic Control at Intermediate Stations with Control of Calculations Based on Weight-Based Sum Codes" Computation 12, no. 9: 171. https://doi.org/10.3390/computation12090171
APA StyleEfanov, D. V., Pashukov, A. V., Mikhailiuta, E. M., Khóroshev, V. V., Abdullaev, R. B., Plotnikov, D. G., Banite, A. V., Leksashov, A. V., Khomutov, D. N., Baratov, D. K., & Ruziev, D. K. (2024). Synthesis of Self-Checking Circuits for Train Route Traffic Control at Intermediate Stations with Control of Calculations Based on Weight-Based Sum Codes. Computation, 12(9), 171. https://doi.org/10.3390/computation12090171








