Analogue Computation Converter for Nonhomogeneous Second-Order Linear Ordinary Differential Equation
Abstract
1. Introduction
2. Mathematical Model
- –
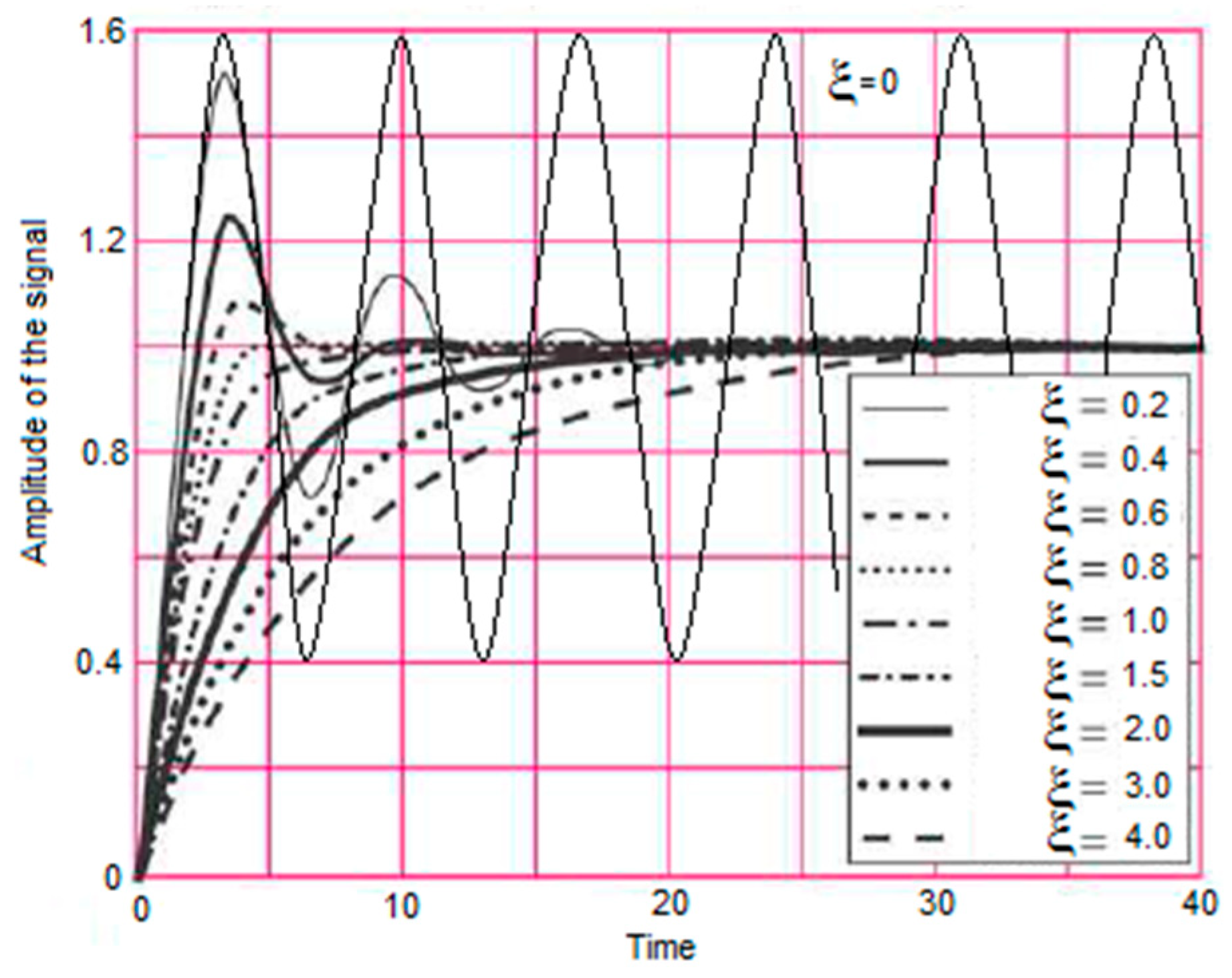
- If > 1 y(t) has the roots (8) (real and distinct roots), and y(t) has an underdamped response;
- –
- If = 1 x(t) has the roots (real equal roots), and y(t) has a critical underdamped response;
- –
- If < 1 x(t) has the roots (complex conjugate roots), and y(t) has a critical overdamped response with damped oscillation.
- –
- If = 0, x(t) has the roots (imaginary conjugate roots), and the response will be oscillation (without damped oscillation). In a real oscillator, the first root is useful for making oscillations: . This variant is the basis of the realization of the analogue computation converter.
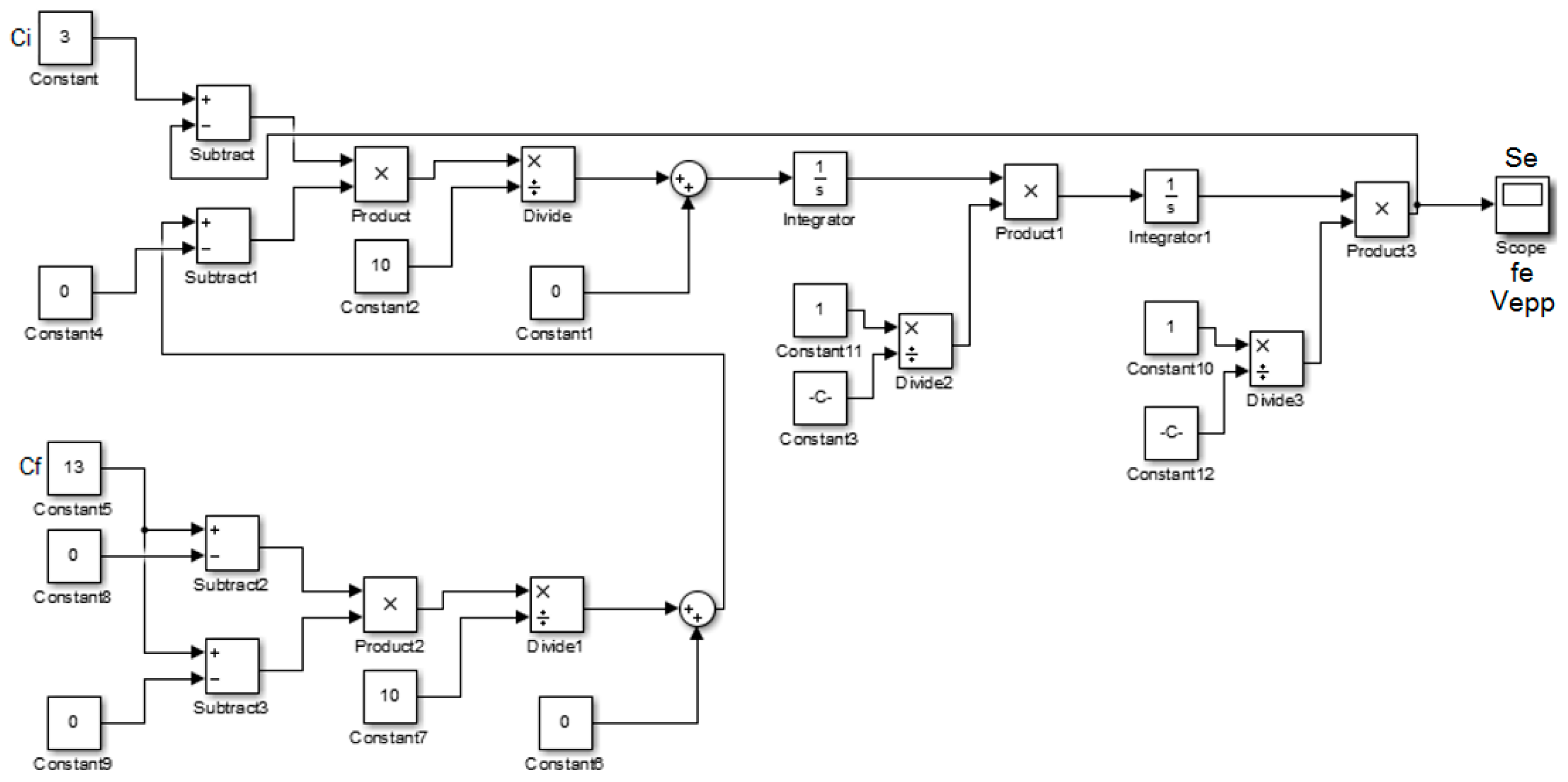
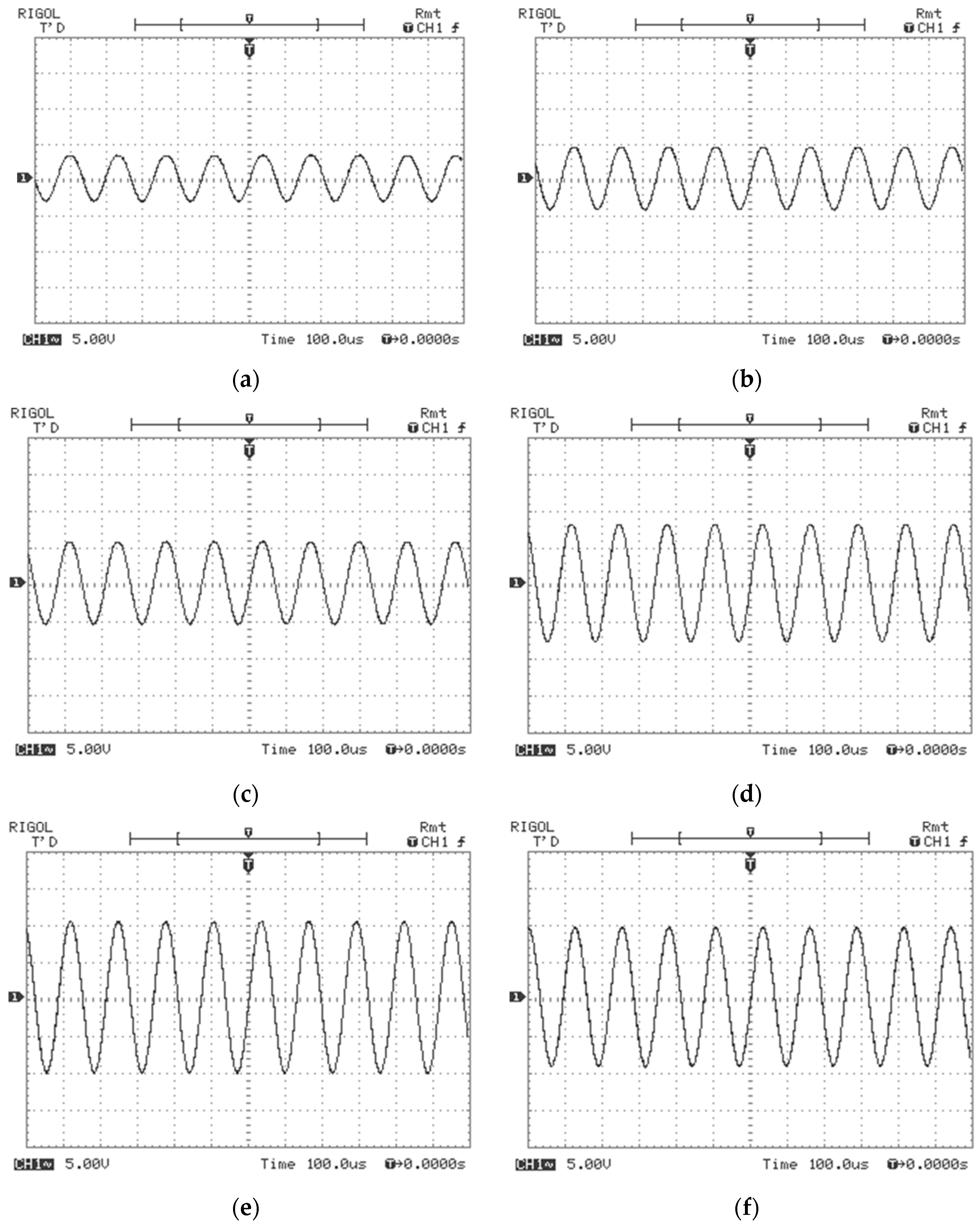
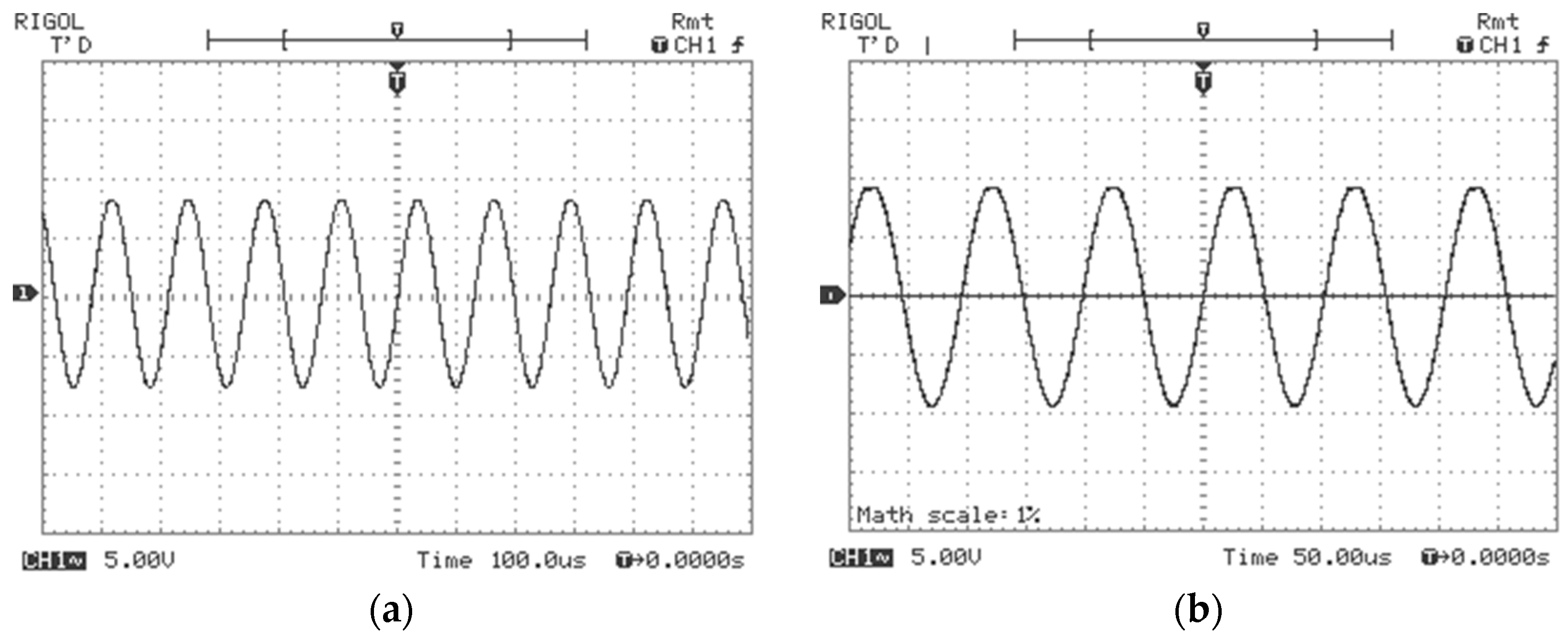
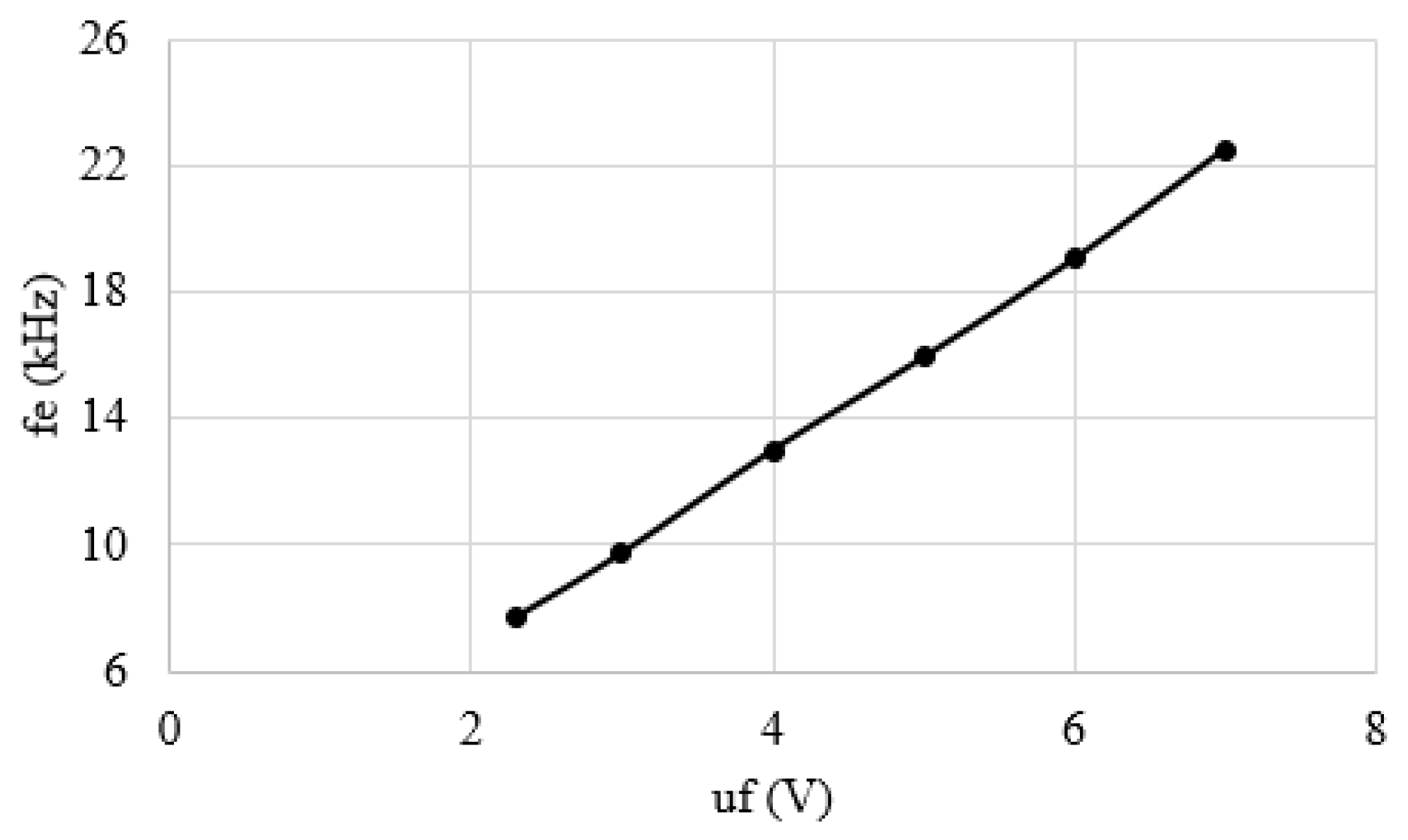
3. Simulations of an Analogue Computation Converter with Variable Frequency and Amplitude
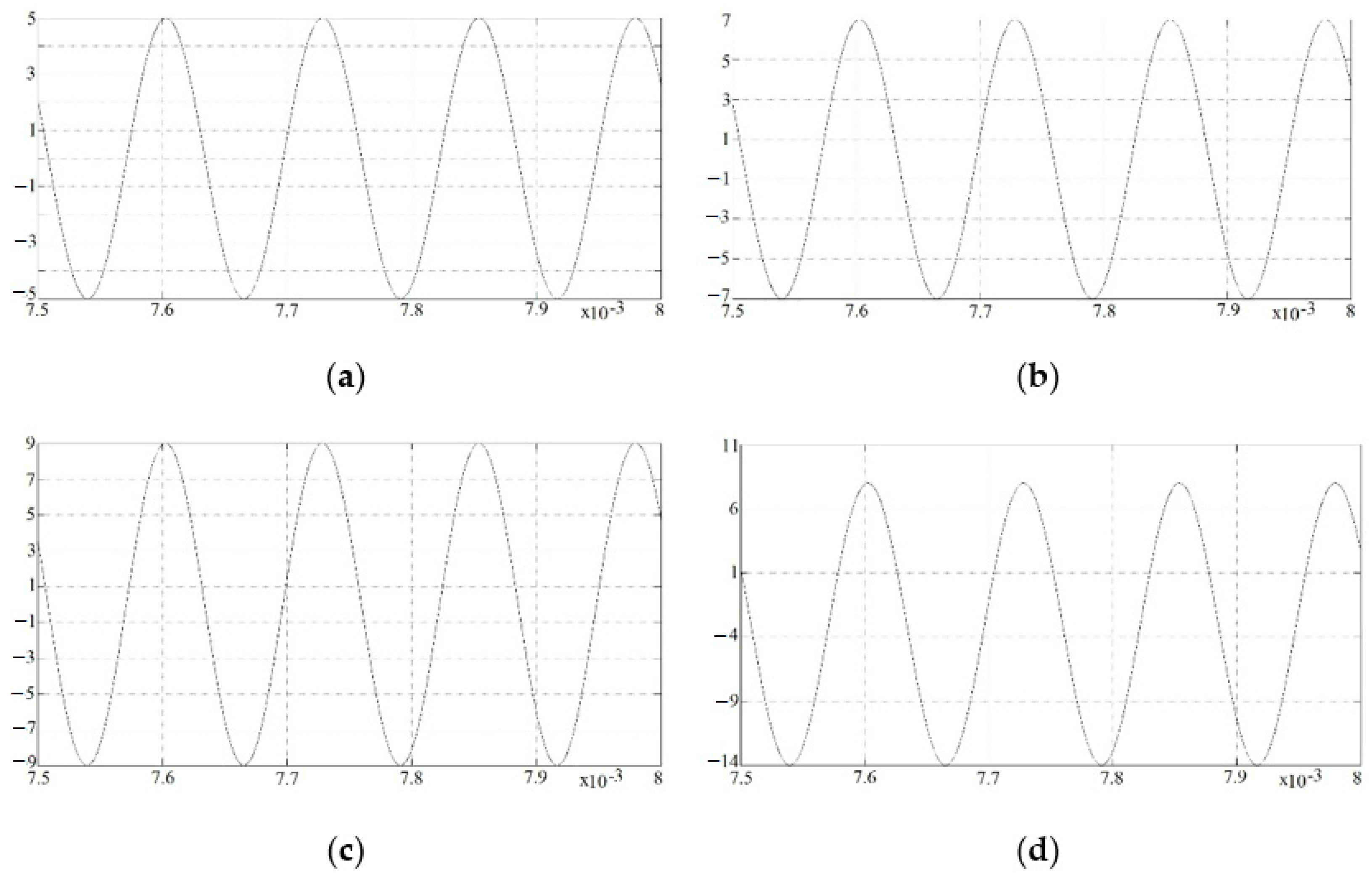
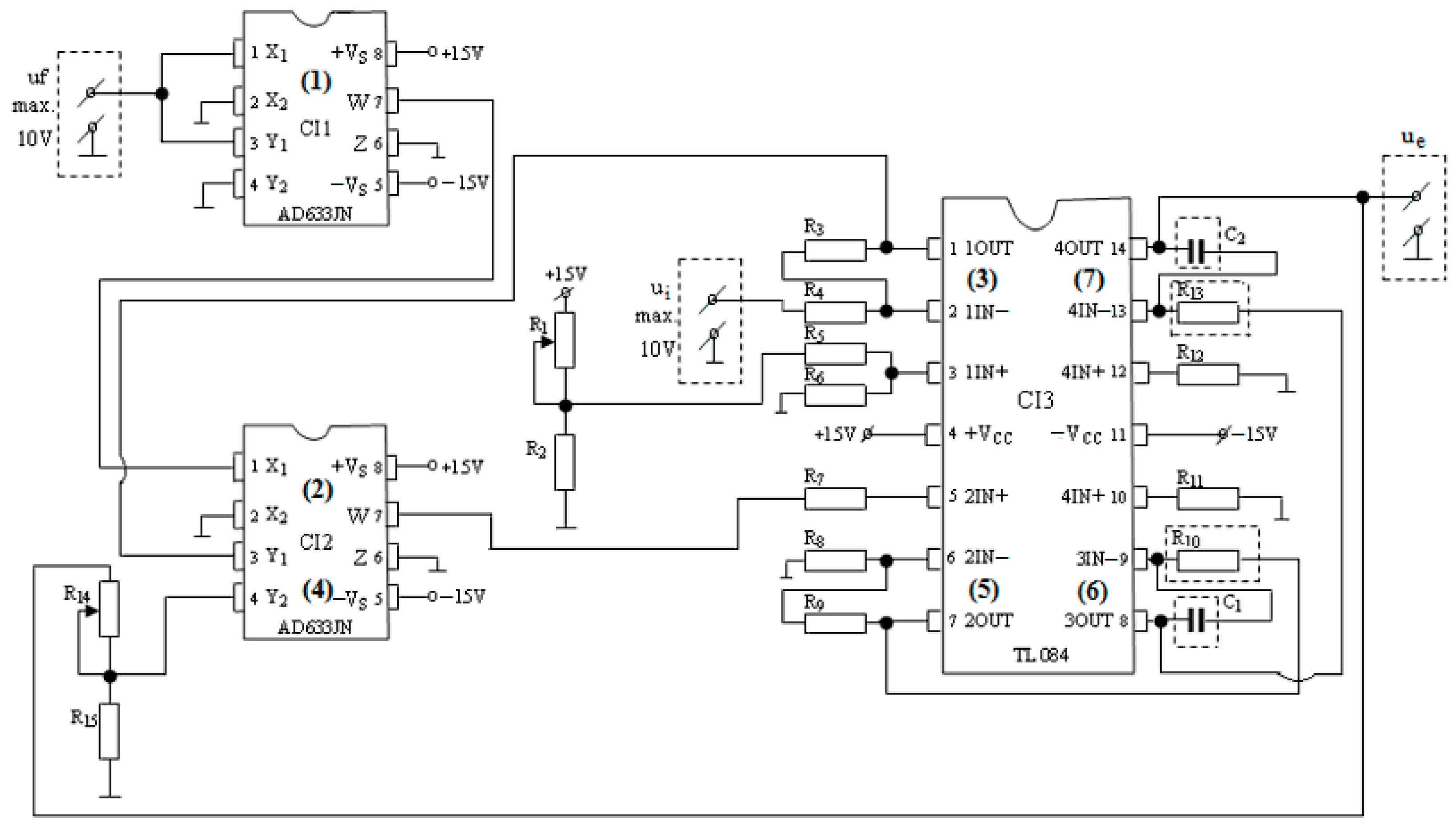
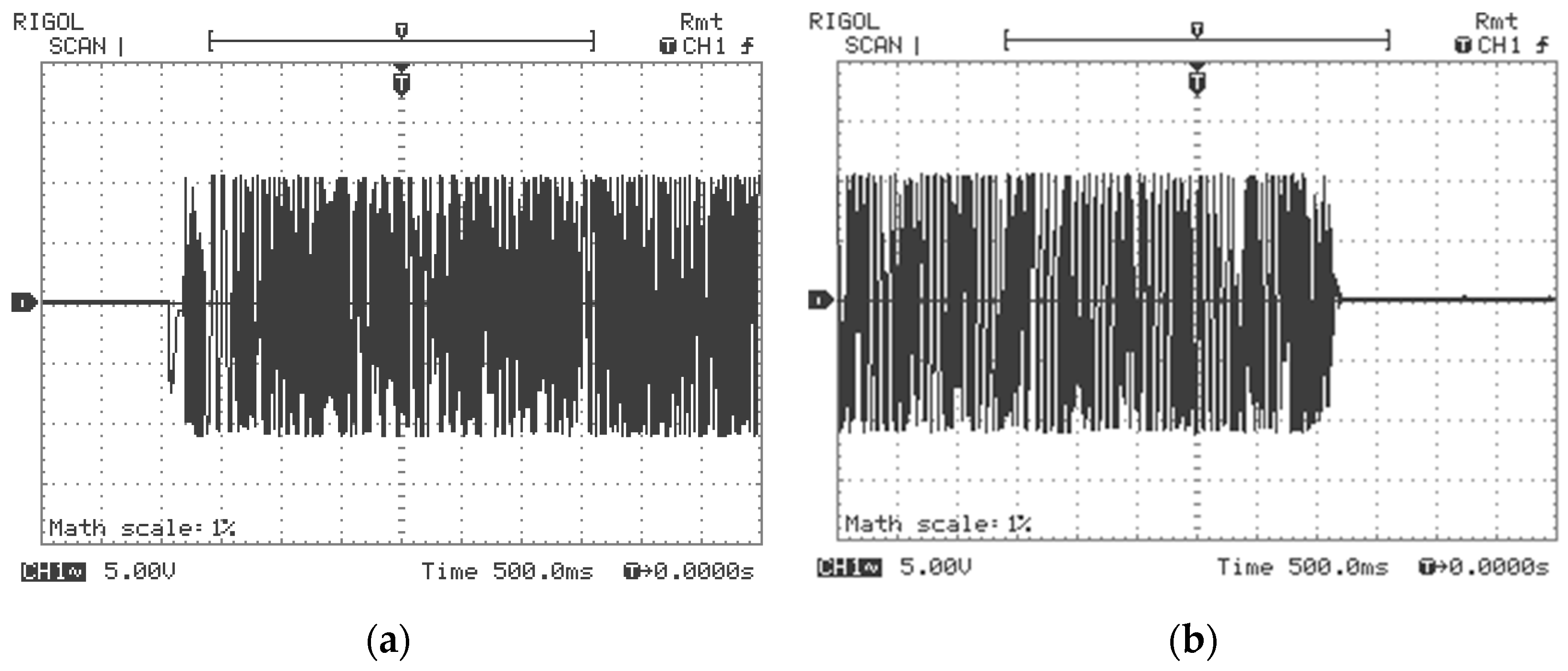
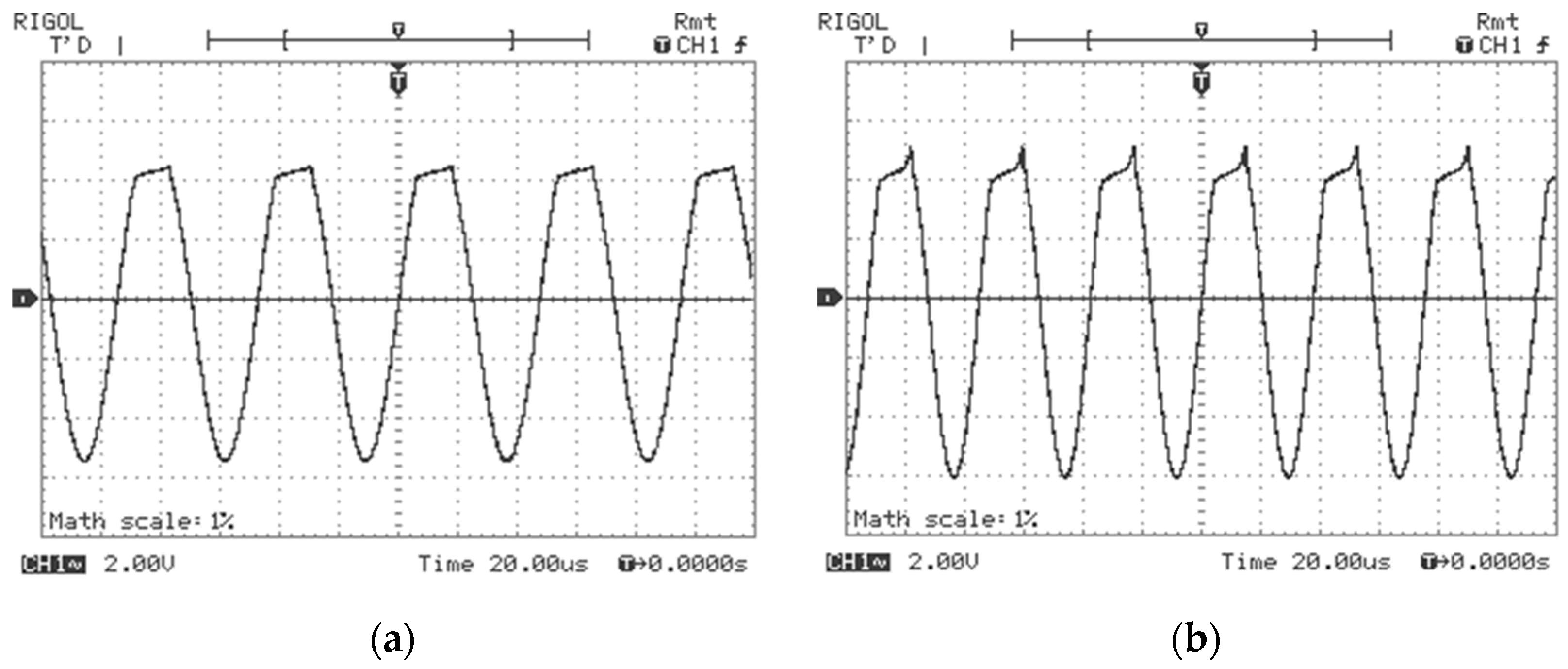
4. Experiments with Discussions
5. Applications of the Analogue Computation Converter Used with Sensors
5.1. Remote Transmission of a Measured Quantity via Electrical Wires
5.2. Temperature Measured with Thermistors
5.3. Temperature Measured with Resistance Temperature Detector
5.4. Temperature Measured with Thermocouples
6. Conclusions
- –
- An analogue computer was developed using the nonhomogeneous second-order linear ordinary differential equation to adjust the frequency and amplitude of the sinusoidal signal at the output using two DC voltages;
- –
- The output signal for ui and uf is sinusoidal and stable over time over a variety of DC voltages (non-damped operation mode);
- –
- The analogue converter has a straightforward design with two DC voltage inputs and one (sinusoidal voltage) output;
- –
- The response time is relatively short because the sinusoidal converter is only realised with analogue components;
- –
- The output signal has a frequency in the kHz range, and the operating range might be in the tens of kHz range;
- –
- The uf input of the sinusoidal converter can be used on analogue sensors that have a DC voltage at the output to convert the voltage into a sinusoidal signal.
- –
- The precise determination of the R-C component limit values for the I1 and I2 integrated circuits, for which the sinusoidal signal at the oscillator’s output has a linear dependence (amplitude and frequency) on the DC voltages at the input;
- –
- Connecting resistive (for linear, angular displacements, and so on) and capacitive transducers (liquid-level gauges, pressure metres, accelerometers, precision positioners, and so on) to integration circuits to convert the signals into a sinusoidal output signal proportional to the input size of the sensors;
- –
- Studies on signals with noise at the input of the converter to study the influence on the output of the converter.
7. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abuelma’atti, M.T.; Al-Ali, A.K.; Buhalim, S.S.; Ahmed, S.T. Digitally Programmable Partially Active-R Sinusoidal Oscillators. Act. Passiv. Electron. Compon. 1994, 17, 83–89. [Google Scholar] [CrossRef]
- Adragna, C.; Gritti, G.; Raciti, A.; Rizzo, S.A.; Susinni, G. Analysis of the Input Current Distortion and Guidelines for Designing High Power Factor Quasi-Resonant Flyback LED Drivers. Energies 2020, 13, 2989. [Google Scholar] [CrossRef]
- Baek, S.; Choi, D.; Bu, H.; Cho, Y. Analysis and Design of a Sine Wave Filter for GaN-Based Low-Voltage Variable Frequency Drives. Electronics 2020, 9, 345. [Google Scholar] [CrossRef]
- Groner, S. Low Distortion Oscillator Design. Master’s Thesis, Zurich University of the Arts, Zurich, Switzerland, 2010; pp. 1–88. [Google Scholar]
- Mechergui, H.; Haddouk, A. Amplitude control in sinusoidal oscillator. In Proceeding of the International Conference MS’07, Kolkata, India, 3–5 December 2007; pp. 1–7. [Google Scholar]
- Hong, B.; Hajimiri, A. A Phasor-Based Analysis of Sinusoidal Injection Locking in LC and Ring Oscillators. IEEE Trans. Circuits Syst. I 2019, 66, 355–368. [Google Scholar] [CrossRef]
- Linares-Barranco, B.; Rodriguez-Vázquez, A.; Sánchez-Sinencio, E.; Huertas, J.L. CMOS OTA-C High-Frequency Sinusoidal Oscillators. IEEE J. Solid State Circuits 1991, 26, 160–165. [Google Scholar] [CrossRef]
- Osa, J.I.; Carlosena, A. MOSFET-C Sinusoidal Oscillator with Variable Frequency and Amplitude. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems (ISCAS), Geneva, Switzerland, 28–31 May 2000; pp. 1–6. [Google Scholar]
- Jaikla, W.; Adhan, S.; Suwanjan, P.; Kumngern, M. Current/Voltage Controlled Quadrature Sinusoidal Oscillators for Phase Sensitive Detection Using Commercially Available IC. Sensors 2020, 20, 1319. [Google Scholar] [CrossRef]
- Lepkowski, J. Designing Operational Amplifier Oscillator Circuits for Sensor Applications; AN 866 DS00866A; Microchip Tehnology Inc.: Chandler, AZ, USA, 2003; pp. 1–16. [Google Scholar]
- Hybrid Oscillator and Demodulator LDT Modules; Solartron Metrology: Bognor Regis, UK, 2021.
- Oscilloscope Fundamentals; Tektronix: Singapore, 2022.
- Williams, J. Instrumentation Applications for a Monolithic Oscillator. A Clock for All Reasons; Application Note 93; Linear Technology Corporation: Milpitas, CA, USA, 2003; pp. 1–20. [Google Scholar]
- Oukaira, A.; Mellal, I.; Ettahri, O.; Tabaa, M.; Lakhssassi, A. Simulation amd FPGA Implementation of a Ring Oscillator Sensor for Complex System Design, Special Issue on Advancement in Engineering Technology. Adv. Sci. Technol. Eng. Syst. J. 2018, 3, 317–321. [Google Scholar] [CrossRef]
- Oscillator Design Guide for STM8AF/AL/S, STM32 MCUs and MPUs; AN 2867 Application Note; STMicroelectronics: Geneva, Switzerland, 2020.
- Serra, F.M.; Fernándezm, L.M.; Montoya, O.D.; Gil-González, W.; Hernández, J.C. Nonlinear Voltage Control for Three-Phase DC-AC Converters in Hybrid Systems: An Application of the PI-PBC Method. Electronics 2020, 9, 847. [Google Scholar] [CrossRef]
- Sagbas, M.; Ayten, U.E.; Herencsar, N.; Minaei, S. Current and Voltage Mode Multiphase Sinusoidal Oscillators Using CBTAs. RadioEngineering 2013, 22, 24–33. [Google Scholar]
- Cheng, J.; Chen, D.; Chen, G. Modeling and Compensation for Dead-Time Effect in High Power IGBT/IGCT Converters with SHE-PWM Modulation. Energies 2020, 13, 4348. [Google Scholar] [CrossRef]
- Fiore, J.M. Operational Amplifiers & Linear Integrated Circuits: Theory and Application; Creative Commons: Mountain View, CA, USA, 2020; pp. 1–589. [Google Scholar]
- Gasulla, M.; Li, X.; Meijer, G.C.M. The Noise Performance of a High-Speed Capacitive-Sensor Interface Based on a Relaxation Oscillator and a Fast Counter. IEEE Trans. Instrum. Meas. 2005, 54, 1934–1940. [Google Scholar] [CrossRef]
- Mancini, R.; Palmer, R. Sine-Wave Oscillator; Application Report SLOA060; Texas Instruments: Dallas, TX, USA, 2001; pp. 1–21. [Google Scholar]
- Pandiev, I.M.; Todorov, T.G.; Yakimov, P.I.; Doychev, D.D. A Practical Approach to Design and Analysis Sinusoidal Oscillators. Annu. J. Electron. 2009, 92–95. [Google Scholar]
- Stave, N.J. Analysis of BJT Colpitts Oscillators—Empirical and Mathematical Methods for Predicting Behavior. Master’s Thesis, Marquette University, Milwaukee, WI, USA, 2009; pp. 1–151. [Google Scholar]
- Rivera, M.; Rojas, S.; Restrepo, C.; Muñoz, J.; Baier, C.; Wheeler, P. Control Techniques for a Single-Phase Matrix Converter. Energies 2020, 13, 6337. [Google Scholar] [CrossRef]
- Chang, E.C. High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications. Micromachines 2020, 11, 585. [Google Scholar] [CrossRef]
- Vasan, B.K. Waveform Generation in Phase Shift Oscillators Using Harmonic Programming Techniques. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2013; pp. 1–151. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Horng, J.W.; Vrba, K.; Dostal, T. Simple Oscillator with Enlarged Tunability Range Based on ECCII and VGA Utilizing Commercially Available Analog Multiplier. Meas. Sci. Rev. 2016, 16, 35–41. [Google Scholar] [CrossRef]
- Lahiri, A. New Canonic Active RC Sinusoidal Oscillator Circuits Using Second-Generation Current Conveyors with Application as a Wide-Frequency Digitally Controlled Sinusoid Generator. Act. Passiv. Electron. Compon. 2011, 2011, 274394. [Google Scholar] [CrossRef]
- Mittal, N.; Charan, P.; Majeed, F. A Novel Tunable High Frequency Sinusoidal Oscillator Based on the Second Generation Current Controlled Conveyor. Int. J. Sci. Res. Publ. 2013, 3, 2250–3153. [Google Scholar]
- Khandi, M.R. Modeling and Estimation of Phase Noise in Oscillators with Colored Noise Sources. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2013. Technical Report No. R019. pp. 1–90. [Google Scholar]
- Razavi, B. A Study of Phase Noise in CMOS Oscillators. IEEE J. Solid State Circuits 1996, 31, 331–343. [Google Scholar] [CrossRef]
- Yan, J. A Low Total Harmonic Distortion Sinusoidal Oscillator Based on Digital Harmonic Cancellation Technique. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2012; pp. 1–129. [Google Scholar]
- Yamaguchi, T.; Ueno, A. Capacitive-Coupling Impedance Spectroscopy Using a Non-Sinusoidal Oscillator and Discrete-Time Fourier Transform: An Introductory Study. Sensors 2020, 20, 6392. [Google Scholar] [CrossRef]
- Odame, K.M.; Hasler, P. Theory and Design of OTA-C Oscillators with Native Amplitude Limiting. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 40–50. [Google Scholar] [CrossRef]
- Kolářová, E.; Brančík, L. Application of Stochastic Differential Equations in Second-Order Electrical Circuits Analysis. Przegląd Elektrotechniczny 2012, 88, 103–107. [Google Scholar]
- Maoil´eidigh, D.Ó.; Hudspeth, A.J. Sinusoidal-Signal Detection by Active, Noisy Oscillators on The Brink of Self-Oscillation. Phys. D Nonlinear Phenom. 2018, 378–379, 33–45. [Google Scholar] [CrossRef]
- Priandana, E.R.; Noguchi, T. Pure Sinusoidal Output Single-Phase Current-Source Inverter with Minimized Switching Losses and Reduced Output Filter Size. Electronics 2019, 8, 1556. [Google Scholar] [CrossRef]
- Sullivan, D.B.; Allan, D.W.; Howe, D.A.; Walls, W.L. Characterization of Clocks and Oscillators; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1990; pp. 1–364. [Google Scholar]
- Tindel, S. Second Order Linear Equations. Differential Equations; Purdue University: West Lafayette, IN, USA, 2019; pp. 1–115. [Google Scholar]
- Jang, J. Transient Analysis, Chapter 5, Electrical Engineering; Chung-Ang University: Seoul, Republic of Korea, 2018; pp. 1–22. [Google Scholar]
- Korn, G.A.; Korn, T.M. Electronic Analog and Hybrid Computers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Potter, D. Measuring Temperature with Thermistor—A Tutorial. National Instruments, Application Note 065, 340904B-01, November 1996, 8 p. Available online: https://users.wpi.edu/~sullivan/ME3901/Laboratories/03-Temperature_Labs/Thermistor_an065.pdf (accessed on 16 June 2024).
- Resistance Temperature Detectors (RTDs); Thermo Sensor Corporation: Garland, TX, USA, 2013.
- Park, R.M. Thermocouple Fundamentals; Marlin Manufacturing Corporation: Cleveland, OH, USA, 2015. [Google Scholar]

















| Types of Undamped Sinusoidal Oscillators | Characteristics | Advantages | Disadvantages |
|---|---|---|---|
| Tuned Circuit Oscillators | These oscillators use a tuned circuit consisting of inductors and capacitors and are used to generate high-frequency (radio frequency) signals. Such oscillators are Hartley, Colpitts, and Clapp oscillators, etc. |
|
|
| RC Oscillators | These oscillators use resistors and capacitors and are used to generate low- or audio-frequency signals. Thus, they are also known as audio-frequency oscillators. Such oscillators are Phase-shift and Wein-bridge oscillators. |
|
|
| Crystal Oscillators | These oscillators use quartz crystals to generate highly stabilized output signal with frequencies up to 10 MHz. The Piezo oscillator is an example of a crystal oscillator. |
|
|
| Negative-resistance Oscillator | These oscillators use the negative-resistance characteristic of the devices such as tunnel devices. A tuned diode oscillator is an example of a negative-resistance oscillator. |
|
|
| Analogue computation converter | Using analogue electronic circuits with two DC inputs and one output (sinusoidal voltage with controlled frequency and amplitude). It is an analogue computer that solves a nonhomogeneous second-order linear ordinary differential equation. |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, G.N.; Diniș, C.M. Analogue Computation Converter for Nonhomogeneous Second-Order Linear Ordinary Differential Equation. Computation 2024, 12, 169. https://doi.org/10.3390/computation12080169
Popa GN, Diniș CM. Analogue Computation Converter for Nonhomogeneous Second-Order Linear Ordinary Differential Equation. Computation. 2024; 12(8):169. https://doi.org/10.3390/computation12080169
Chicago/Turabian StylePopa, Gabriel Nicolae, and Corina Maria Diniș. 2024. "Analogue Computation Converter for Nonhomogeneous Second-Order Linear Ordinary Differential Equation" Computation 12, no. 8: 169. https://doi.org/10.3390/computation12080169
APA StylePopa, G. N., & Diniș, C. M. (2024). Analogue Computation Converter for Nonhomogeneous Second-Order Linear Ordinary Differential Equation. Computation, 12(8), 169. https://doi.org/10.3390/computation12080169





