Abstract
Multiple sequence alignment (MSA) stands as a critical tool for understanding the evolutionary and functional relationships among biological sequences. Obtaining an exact solution for MSA, termed exact-MSA, is a significant challenge due to the combinatorial nature of the problem. Using the dynamic programming technique to solve MSA is recognized as a highly computationally complex algorithm. To cope with the computational demands of MSA, parallel computing offers the potential for significant speedup in MSA. In this study, we investigated the utilization of parallelization to solve the exact-MSA using three proposed novel approaches. In these approaches, we used multi-threading techniques to improve the performance of the dynamic programming algorithms in solving the exact-MSA. We developed and employed three parallel approaches, named diagonal traversing, blocking, and slicing, to improve MSA performance. The proposed method accelerated the exact-MSA algorithm by around 4×. The suggested approaches could be basic approaches to be combined with many existing techniques. These proposed approaches could serve as foundational elements, offering potential integration with existing techniques for comprehensive MSA enhancement.
1. Introduction
Sequence alignment (SA) refers to the process of arranging and comparing biological sequences, such as DNA, RNA, and proteins, with the ability to reveal meaningful information about the similarities and differences among them. SA is one of the fundamental steps in most genomic analyses [1]. The classification of sequence alignment techniques encompasses two fundamental distinctions: global versus local alignment and pairwise versus multiple alignment. Global alignment algorithms, such as the Needleman–Wunsch algorithm, align sequences from the beginning to the end [2]. By contrast, the local sequence alignment is used to compare specific regions and to find contiguous regions of high similarity, such as that performed by the the Smith–Waterman algorithm [3]. The main two types of sequence alignment are also performed in two ways: the pairwise sequence alignment (PSA) [4] and the multiple sequence alignment (MSA) [5]. PSA involves the comparison of two sequences to identify regions of similarity and dissimilarity, while MSA extends the comparison to more than two sequences, identifying conserved regions and variations across a set of sequences.
The dynamic programming technique [6] provides an efficient computational approach for optimizing alignment scores by breaking down complex problems into smaller overlapping subproblems [7]. Common dynamic programming algorithms for pairwise sequence alignment include the Needleman–Wunsch algorithm, employed for global alignment, and the Smith–Waterman algorithm, utilized for local alignment. Dynamic programming extends its utility to multiple sequence alignment algorithms, such as the progressive and iterative methods [8,9]. Aligning N sequences using dynamic programming is an NP-Hard problem [10] that stems from the complexity of considering all possible combinations and alignments among the N sequences. To address complexity challenges in MSA, heuristic methods [11] and approximation algorithms [12] are employed in practice for the MSA of a large number of sequences. In addition to these algorithms, applying parallel computing techniques offers a promising avenue to mitigate the computational demands associated with MSA [13].
The primary objective of this study is to explore the dynamic programming technique for solving exact-MSA problems, employing various parallel computing approaches. Initially, we introduced an exact solution for multiple sequence alignments using the dynamic programming technique employing the Needleman–Wunch algorithm. Subsequently, we improved the proposed implementation using the multithreading technique and experimentally validated its efficiency. Our development encompassed three approaches leveraging multithreading technology to accelerate the exact-MSA.
In the initial parallel approach, we implemented the diagonal traversing that is described in Section 3.3.1. However, this approach did not provide an enhancement over the sequential dynamic programming method. Then, we introduced the second parallel approach employing the blocking method as shown in Section 3.3.2. The second approach distinctly enhances the performance over the sequential method for pairwise sequence alignment. In the third parallel approach, the slicing concept explained in Section 3.3.3, we used this method to enhance the execution time, and the approach was tested using 3, 4, and 5 sequences with different sizes. In the third parallel approach, employing the slicing concept as elucidated in Section 3.3.3, the slicing approach improved execution time. The effectiveness of the proposed approaches was tested using 3, 4, and 5 sequences with varying sizes.
The rest of this paper is structured as follows: Section 2 discusses the related works, exploring the existing literature. Then, Section 3 outlines the proposed methodology presenting the three developed approaches. Section 4 shows the enhancements achieved through each approach, contrasting them with the sequential implementation of MSA. Finally, Section 5 offers concluding remarks, summarizing the findings of this work, and outlines potential future directions.
2. Related Work
In this section, we explore various methods developed to address the sequence alignment problem. Initially, we delve into the techniques applied in pairwise sequence alignment (PSA), as detailed in Section 2.1. Following that, we highlight the main techniques utilized in multiple sequence alignments (MSAs), as presented in Section 2.2. Additionally, we provide insights into the methods employed to accelerate sequence alignment problems through various parallel computing techniques.
2.1. Pairwise Sequence Alignment (PSA)
Pairwise sequence alignment (PSA) is considered an important tool for aligning biological sequences such as DNA and protein sequences [14]. Haque et al. [15] presented a comprehensive overview of both local and global pairwise sequence alignment algorithms. They also included an identification of the techniques utilized in these algorithms and discussed their respective advantages and limitations. In [16], Edgar et al. distinguished between the main three methods used to align sequences: sequence–sequence methods (like BLAST), profile–sequence methods (like PSI-BLAST), and profile–profile methods (like CLUSTALW). The survey in [17] reviewed the wide range of aligning algorithms and tools developed to assess the quality of the aligned sequences. In [18], bacterial DNA sequences were aligned using pairwise alignment and dynamic programming. Table 1 shows an overview of the most well-known approaches utilized for PSA.

Table 1.
Pairwise sequence alignment techniques.
Several studies have aimed to accelerate the performance and the accuracy of the tools used in sequence alignment by using several parallelization techniques [27]. For example, Fakirah et al. [28] utilized a diagonal traversing approach to enhance the Needleman–Wunsch algorithm by utilizing the iterations used to fill the scoring matrix. Balhaf et al. [29] enhanced the Levenshtein edit distance algorithm’s performance by using the diagonal traversing approach, and the performance was enhanced using both CPU and GPU. Jararweh et al. [30] accelerated the Levenshtein and Damerau algorithms by using parallel implementation on a GPU. Jararweh et al. showed that using unified memory resulted in the best performance. Shehab et al. [31] enhanced the performance of multiple pairwise alignments in protein sequences by utilizing a hybrid CPU-GPU implementation. In [26], Puig et al. utilized a GPU (graphics processing unit) to compute exact gap-affine alignments based on the wavefront alignment (WFA) algorithm. They showed that the proposed tool is up to 29× faster than other GPU implementations.
2.2. Multiple Sequence Alignment
Numerous studies have employed various techniques to address the challenge of multiple sequence alignments (MSAs) [9]. One widely adopted technique is progressive alignment [32]. The progressive alignment method initially starts with pairwise alignments and progressively builds an MSA alignment through a series of pairwise alignments, producing accurate results for moderately sized sequence sets [33]. In addition to the progressive methods, iterative approaches have also played a crucial role in improving the accuracy of MSA [34]. Iterative methods generally refine alignments applying successive cycles of alignment improvement. Iterative refinement involves realigning sequences based on the initial solution and gradually converging toward a more accurate alignment. Iterative techniques often outperform progressive methods in terms of alignment accuracy, especially in cases where sequences are more distant [35]. Lupyan et al. proposed a hybrid algorithm that combined the progressive and iterative algorithms for MSA. The hybrid approach provided a significant advancement compared to earlier methods involving a notable decrease in computational cost.
In addition to progressive and iterative methods, several studies focus on the utilization of metaheuristics techniques for performing MSA [11]. Ali et al. [36] reviewed the landscape of metaheuristics in bioinformatics highlighting various metaheuristic approaches, including tabu search [37], simulated annealing [38], and particle swarm optimization [39], showcasing their applications in computational biology problems and MSA. Hatzou et al. [9] provided valuable insights centered on the heuristic-based progress of MSA methods. Similarly, Chowdhury et al. [40] offered an overview of MSA methods with a focus on the multi-objective approach. In contrast, Vega et al. [41] provided a comparative analysis of different formulations of multi-objective metaheuristics for MSA. In Table 2, we present some well-known tools for MSA and we show the general techniques used for each.

Table 2.
Multiple sequence alignment tools with techniques.
Limited studies have been directed towards seeking exact solutions for multiple sequence alignment due to the time complexity associated with obtaining the optimal results. Mojbak et al. [51] proposed an exact-MSA approach using forward dynamic programming. Also, in the comprehensive exploration of exact solutions, Hosseininasab et al. [52] proposed a framework employing a dynamic programming approach to construct a multivalued decision diagram, representing all PSAs. The synchronization of PSAs with the proposed decision diagram effectively incorporates modeling the MSA problem within polynomial space complexity. Moreover, Domínguez [53] delves into statistical and biological concepts employed in the MSAProbs-MPI tool to complete the alignments where high-performance computing techniques are employed for alignment acceleration. Additionally, Ju et al. [54] introduced an end-to-end deep neural network and called it CopulaNe, designed to directly estimate residue co-evolution from MSA, representing a cutting-edge approach in the finding of exact solutions for MSA.
In addition to the previously mentioned approaches, several parallelization strategies have been employed to tackle the challenges associated with MSA [55]. Some of these strategies focus on the parallelization of dynamic programming algorithms, such as in [56]. Other strategies aim to parallelize the progressive alignment [57]. Several studies focus on the parallelization of heuristic algorithms, such as [58]. Recently, many studies utilized GPU acceleration for MSA [59]. The optimization of parallel MSA is characterized by continuous innovation in algorithmic design and adaptation to emerging hardware architectures [55]. In our study, we employ various parallel computing approaches to enhance the basic dynamic programming approach for MSA, as shown in the next Section 3.
3. Methodology
In this section, we first describe the dataset used and the experimental setup as shown in Section 3.1. Then, in Section 3.2, we explain the dynamic programming technique used to solve the pairwise sequence alignment problem and how it is extended to solve the MSA problem. Following this, we delve into explaining three proposed approaches that utilized the multithreading technology to accelerate the implementation of MSA as shown in Section 3.3.
3.1. Dataset and Experimental Setup
The aligned sequences are taken from a real database (http://lab.malab.cn/soft/halign/) that was used in several studies, such as [60,61,62,63,64]. The website allows the viewers to download the dataset that was used in testing many tools.
In this research, we used the dataset called the 16s rRNA dataset that contains the RNA sequences of the small units of the ribosomes (prokaryotic ribosome). We used the 16s rRNA dataset to test the proposed work. The sequences in this dataset are of several lengths between 1300 and 2000 characters. We used the following sequence length for the experiments we performed in our studies. The final length employed in each experiment is constrained by the computational complexity of the runtime for the approaches used.
- 1024, 2048, 4096, and 8192 characters for 2-sequence alignment.
- 128, 256, 512, and 1024 characters for 3-sequence alignment.
- 64, 128, 256, and 512 characters for 4-sequence alignment.
- 64, 128, and 256 characters for 5-sequence alignment.
The objective of this work is to measure the improvements gained by using different parallel implementations of the Needleman–Wunsch (NW) algorithm extended for the MSA problem. The performance of each implementation is measured by the total time needed to compute the correct alignment of the input sequences. The improvement gain of any parallel implementation is computed by dividing the sequential implementation’s time over its time, as shown in Equation (1). Ten different tests are conducted for each sequence length using ten different sequences and their average is reported.
3.2. Sequential Implementation
In this sub-section, we discuss the algorithm used to solve the pairwise sequence alignment problem and how we extended it to solve the MSA problem.
3.2.1. Sequential Pairwise Sequence Alignment
The main goal of pairwise sequence alignment is to identify regions of similarity that might indicate functional, structural, and/or evolutionary relationships between two pairs of biological sequences. Pairwise sequence alignment is divided mainly into two main types of problems: global alignment and local alignment. Many approaches have been used as dynamic programming algorithms to compute a global alignment of two sequences such as the Needleman–Wunsch algorithm [2]. The NW algorithm utilizes a dynamic programming algorithm to find the global alignment between a pair of sequences. It works as follows. Consider that we are aligning two sequences, A and B, each of length N characters. A two-dimensional array of size (N + 1) × (N + 1) is created. The value of each cell in this array is computed based on three other values in the array, as shown in Figure 1. Specifically, the optimal value at cell , denoted by , is computed using the following Equation (2):
where is equal to the match value when or the mismatch value when , is the penalty for inserting a gap into the alignment (i.e., aligning a character from one sequence with a gap in the other), and .
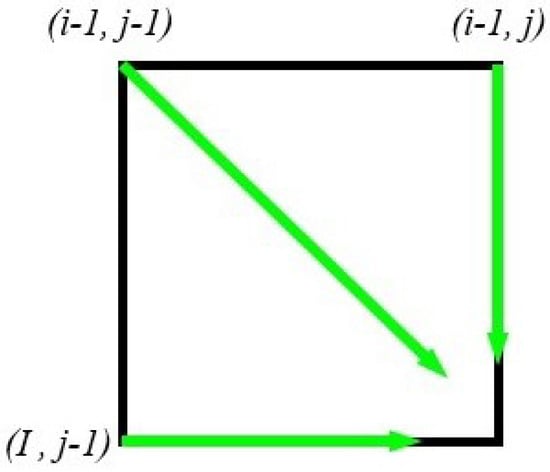
Figure 1.
Values used to compute cell in the 2D array created for 2-sequence alignment.
Finally, in the constructed matrix, each path from cell to cell (N, N) represents an alignment, where the objective is to select the path with the maximum score.
Algorithm 1 discusses the sequential implementation of sequence alignment problem. The algorithm takes two unaligned sequences of length N. Then, it constructs a matrix of size (N + 1) × (N + 1). The first row and column of this matrix are filled according to lines 1–6 in the algorithm below. Then, the rest of the matrix is filled according to lines 7–14. As we mentioned before, there are three possible solutions for the 2D problem calculated at each iteration (lines 9–11), and the maximum value will be stored (line 12). We repeat the process until the matrix is filled. Using this matrix and a back-tracking method we finally get two aligned sequences as output.
| Algorithm 1 Sequential implementation of two sequences |
Input: Two unaligned sequences Output: Two aligned sequences 1. for i = 0 to length(A) 2. F(I,0) ← gap * i 3. End for 4. for j = 0 to length(B) 5. F(0,j) ← gap * j 6. End for 7. for i = 1 to length(A) 8. for j = 1 to length(B) 9. S1 ← F(i−1,j−1) + S(Ai,Bj) 10. S2 ← F(i−1,j) + gap 11. S3 ← F(I,j−1) + gap 12. F(I,j) ← max(s1, s2, s2) 13. End for 14. End for |
3.2.2. Sequential Multiple Sequence Alignment
For three sequences, seven possible solutions come from seven different locations. These solutions are shown in Figure 2.
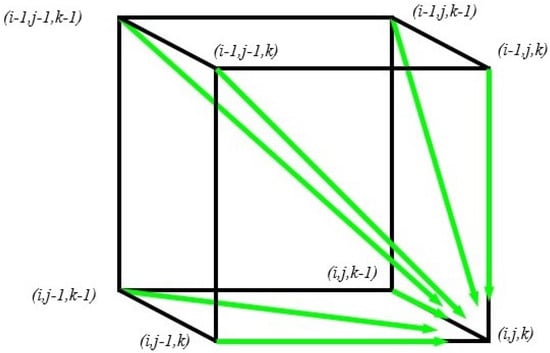
Figure 2.
Possible solutions for three sequences.
The NW dynamic programming used to align three sequences works using the following Equation (3):
where F0,0,0 = 0 S(Ai, Bj, Ck) is an entry in a 3D scoring matrix that gives a scoring depending on the similarity of the characters.
Algorithm 2 discusses the sequential implementation of 3D problem representation. The algorithm takes three unaligned sequences of length N. Then, it constructs a matrix of size (N + 1) × (N + 1) × (N + 1). The first three rows of this matrix will be filled according to lines 1–9 in Algorithm 2. Then, the rest of the matrix is filled according to lines 10–23. As we mentioned before, there are seven possible solutions for the 3D problem calculated at each iteration (lines 13–19), and the maximum value will be stored (line 20). The process is repeated until the matrix is filled. Using this matrix and a back-tracking method, we finally get three aligned sequences as output. Since all sequences are of the same length, the created matrix would be a cube and there are three surfaces shared between every two sequences. Those surfaces are filled using Algorithm 1 and solved as a 2D problem. The extension for 4- and 5-sequence alignment algorithms and implementations are available upon request. Figure 3 illustrates the general concept behind the employed framework showing a representation of aligning 3 sequences in 3D. As shown in Figure 3, the proposed framework initiates with Step 1, involving the input of N unaligned sequences; in this example, it is three sequences, along with a scoring matrix and gap value. Subsequently, in Step 2, we undertake the task of populating indices ranging from (1, 0, 0) to (N, 0, 0), (0, 1, 0) to (0, N, 0), and (0, 0, 1) to (0, 0, N). Moving forward to Step 3, the goal is to fill the surfaces of the optimal matrix, with each surface being shared between two sequences and resolved as a 2D problem utilizing Algorithm 1. Progressing to Step 4, the focus shifts to completing the remaining indices of the optimal matrix, spanning from index (1, 1, 1) to index (N, N, N), employing Algorithm 2. Subsequently, Step 5 shows the process of finding alignments through a reverse engineering technique. Starting from index (N, N, N), we trace back the alignment to index (0, 0, 0). Finally, in Step 6, the output of the framework is realized, producing three aligned sequences.
| Algorithm 2 Sequential Implementation of Three Sequences |
Input: Three unaligned sequences Output: Three aligned sequences 1. for i = 0 to length(A) 2. F(i,0,0) ← gap * i 3. End for 4. for j = 0 to length(B) 5. F(0,j,0) ← gap * j 6. End for 7. for k = 0 to length(C) 8. F(0,0,k) ← gap * k 9. End for 10. For i = 1 to length(A) 11. for j = 1 to length(B) 12. for k = 1 to length(C) 13. S1 ← F(i−1,j−1,k−1) + S(Ai,Bj,Ck) 14. S2 ← F(i−1,j−1,k) + S(Ai,Bj,−) 15. S3 ← F(i−1,j,k−1) + S(Ai,−,Ck) 16. S4 ← F(i,j−1,k−1) + S(−,Bj,Ck) 17. S5 ← F(i−1,j,k) + S(Ai,−,−) 18. S6 ← F(i,j−1,k) + S(−,Bj,−) 19. S7 ← F(i,j,k−1) + S(−,−,Ck) 20. F(i,j,k) ← max(s1, s2, s2,…,s7) 21. End for 22. End for 23. End for |
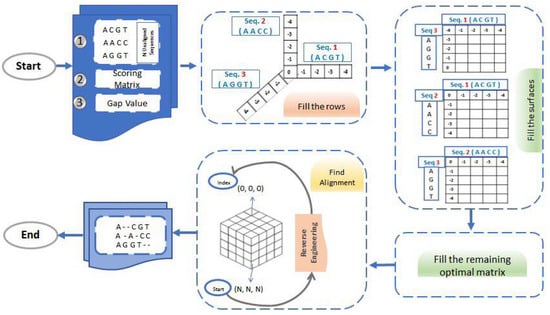
Figure 3.
The Dynamic programming for MSA.
3.3. Parallel Implementation
In the Needleman–Wunsch algorithm, the value of a cell is calculated based on three value cells (left, upper, and left), as shown in Figure 4. Hence, filling the matrix is performed with data dependency between cells. There are two ways to fill the matrix: sequential or diagonal traversing methods. In the sequential traversing approach, as in [65], the algorithm starts from the cell with index (1, 1), (1, 2) and continues until it reaches cell (1, N), as shown in Figure 5a. Then, it moves to the next row using the same approach, while the diagonal traversing method works by filling cells diagonally simultaneously. Figure 5 shows the difference between sequential traversing (a) and diagonal traversing (b).
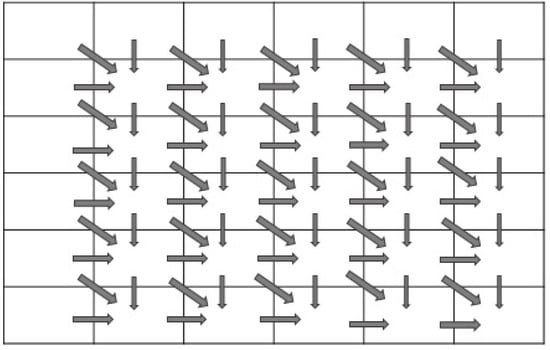
Figure 4.
Data dependency between cells.
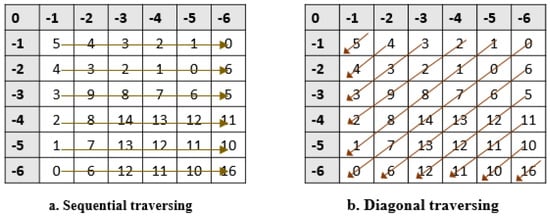
Figure 5.
Traversing methods used to fill scoring matrix.
Figure 5 shows a visual representation of the ways used to fill the matrix: the sequential traversing approach, as shown in Figure 5a, and the diagonal traversing method inspired by the methodology proposed in [65], as shown in Figure 5b. The Sequential traversing initiates from the top-left corner (cell index (1, 1)), sequentially progressing through each cell in the first row (1, 2) to (1, N) and then systematically advancing to subsequent rows. This method provides a clear, step-by-step progression, as illustrated in (Figure 5a). In contrast, the diagonal traversing approach, as depicted in (Figure 5b), demonstrates a simultaneous filling of cells along the diagonals. Starting from the top-left corner, cells are computed diagonally, resulting in a distinctive traversal pattern. This diagonal strategy showcases a more intricate filling pattern, potentially impacting computational complexity and algorithmic efficiency. The alternative diagonal traversing approach is more effective than the sequential traversing approach since it takes fewer iterations to fill the scoring matrix. In this work, we proposed three parallel approaches to accelerate the MSA. In this section, we presented these approaches in detail, as shown in the following section.
3.3.1. First Parallel Approach: Diagonal Traversing
In this work, the parallel implementation was performed using a multithreading technique. The multithreading method is used to reduce the time taken by the sequential implementation. We explored the following two methods to accelerate MSA: In the first method, we tried to increase the number of threads used to fill the optimal matrix. So, as we diagonally traverse the optimal matrix, every cell is sent to a separate thread to calculate its value. For example, assuming we are aligning two sequences of a length of 1000 characters, an array of threads is created per each sequence. This array contains a million threads. Each thread is used to calculate a value of the 1000 × 1000 optimal matrix. The execution time of the parallel code in this way compared to the sequential time is too high. The sequential time takes 282 milliseconds, while the parallel code takes 97,661 milliseconds. Also, it took too many threads for longer sequences and is not practical. We also tried to execute this methodology using a fixed number of threads without violating the device resources, but the parallel execution time was not reduced as we hoped. When we used a fixed number of threads equal to 4, the execution time was 297,025 milliseconds. When we used 8 threads, the execution time was 594,750 milliseconds, while when we used 500 threads, the execution time was 376 milliseconds. These results are listed in the Results Section 4.
In the second method, we tried to use a dynamic array of threads, where the number of threads used to fill the optimal matrix is equal to the number of diagonals in the same optimal matrix. Assuming we are aligning a matrix of 1000 × 1000 elements, a matrix of 1000 X2-1 will be created. So, as we diagonally traverse the optimal matrix, every group of cells is included (the cells on the same diagonal will be sent to a thread to calculate its values). The execution time of the parallel code in this way takes 210 milliseconds compared to the sequential time of 282 milliseconds, which is a reduced amount 25% lower than the sequential execution time.
3.3.2. Second Parallel Approach: Using Blocks
As shown before, diagonal traversing can be used to fill the matrix effectively. Let us assume that we are filling a matrix of size N × N. Then, the sequential traversing needs N × N iterations to fill the matrix, while the diagonal traversing needs iterations. This method is already extended from our work in [66]. The main idea of the block method is that when a matrix is filled diagonally, there is a part of it that is called a block which is treated as a single cell. The short-read accelerator uses a different block strategy. It computes the alignment score around a specific space (it does not fill the whole matrix). The blocks’ sizes were used as suitable with the length of the sequence and took the values of K = 1, 2, 4, 8, 16, and 32. Using blocks with diagonal traversing gives a result with outstanding improvement, as shown in the Results Section 4.
3.3.3. Third Parallel Approach: Slicing
To solve the three-sequence problem, we work in three different ways to solve this problem: Firstly, we assume that the created array represents three sequences from a cube, and this array is processed as shown in Figure 6. We take a slice of the cube and treat it as a 2D array. Then, we process this 2D array in a zig-zag fashion. The zig-zag fashion is shown in Figure 6 and marked in dark arrows. We re-try the process until we complete the whole matrix. Note that every cell in this matrix represents a block (a group of cells).
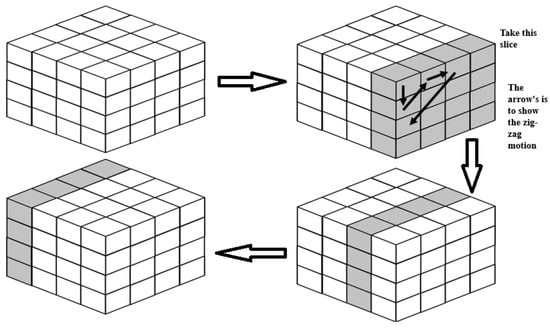
Figure 6.
The proposed approach 1 to solve 3D problem.
In the second way, we assume that the created array represents three sequences from a cube, and this array is processed as shown in Figure 7. We treat the cube matrix as a 2D array, with nothing different from processing a 2D matrix.
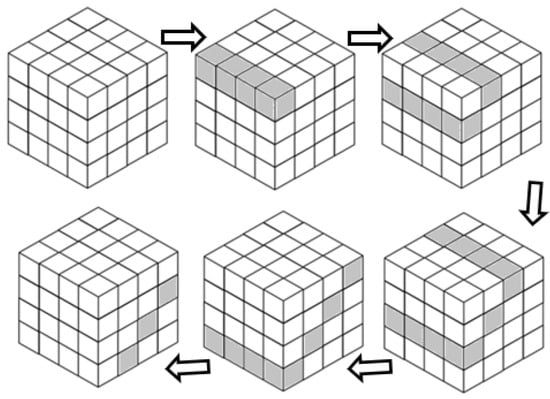
Figure 7.
The proposed approach 2 to solve 3D problem.
In the third way, a 3D matrix is a matrix of 2D matrices. So, when we want to describe a 3D matrix, we usually describe it as a book, and each page in that book represents a 2D matrix. Our third way depends on this description. This method is like the first method but with one difference. In the first method, we took a slice of a cube (a group of papers and processed them in a zig-zag fashion) and processed it as a 2D matrix. Here, we just took a paper every time and processed it as a 2D matrix in a zig-zag fashion. We noticed that in the first two methods, we reached an improvement of around 2×. However, in this improvement, we obtain 4× as much using the third method; the results are discussed in the Results Section 4. The same process is applied to solve 4- and 5-sequence alignments in the same manner; algorithms and implementations are available upon request.
4. Results
In this section, we reported the results we obtained from applying the different approaches explained above in Section 3. First, we show the result obtained from the sequential algorithms for PSA in Section 4.1.1 and for MSA in Section 4.1.2. Then, we present the results obtained from different parallel approaches developed in this work.
4.1. Sequential Implementation Results
4.1.1. Sequential Pairwise Sequence Alignment Results
The results of the sequential implementation, shown Section 3.2.1, are listed in Table 3. When we aligned two sequences of length 1024, the average execution time was 282.3 milliseconds. Meanwhile, aligning two sequences of lengths 2048, 4096, and 8192 takes an average execution time of 758.3, 2909.5, and 11,473.5 milliseconds, respectively. These times are calculated by running the code on ten different sequences and the execution time of every experiment, and then the average is reported.

Table 3.
Execution time for pairwise sequence alignment for different problem sizes using sequential approach.
4.1.2. Sequential Multiple Sequence Alignment
The results of the sequential implementation, shown Section 3.2.2, are listed in Table 4. When we sequentially align three sequences of length 128, the average execution time was 760.9 milliseconds. Meanwhile, aligning three sequences of lengths 256, 512, and 1024 takes an average execution time of 5817.7, 45,980.6, and 270,720.8 milliseconds, respectively. These times are calculated by running the code on ten different sequences and obtaining the execution time of every experiment, and then the average is reported. Here, we presented the results for the three-sequence alignments. From these results, it is experimentally shown that the execution time is increased when the number of sequences is increasing. The largest length of sequence that can be handled with the hardware used to align five sequences using the sequential approach is 256, which takes 435,095 milliseconds.

Table 4.
Execution time for three-sequence problem using the sequential approach.
4.2. Parallel Implementation Results
In this subsection, we reported the results obtained from applying different parallel techniques developed in this work. In Section 4.2.1, we presented the results obtained from applying the parallel diagonal traversing approach explained in Section 3.3.1. Then, in Section 4.2.2, we presented the results from applying the idea of the parallel approach that deploys the blocking concept explained in Section 3.3.2. In the final part of this section in Section 4.2.3, we display the results acquired from applying the parallel approach to the slicing idea used and explained in Section 3.3.3.
4.2.1. First Parallel Approach (Diagonal Traversing) Results
The results obtained from using the parallel approach that applied the diagonal traversal method explained in Section 3.3.1 are shown in Table 5.

Table 5.
The execution time for the first parallel approach using different numbers of threads, in milliseconds.
Table 5 presents the outcomes derived from employing the parallel approach, utilizing the diagonal traversal method elaborated in Section 3.3.1. The experiments were conducted with varying numbers of threads (Thread = 4, Thread = 8, Thread = 500, and Thread = ) to assess the performance of the parallel implementation in terms of execution time. The results, as displayed in the table, show that this parallel approach does not yield a noticeable enhancement over the sequential approach, even with increasing the number of threads. For example, the execution time when the Thread = 4 is less than the execution time when the Thread = 8. Table 5 demonstrates that despite utilizing parallelism and the incorporation of the diagonal traversal strategy, there is no significant improvement in performance compared to the sequential implementation. This unexpected observation prompts us to explore alternative parallelization approaches. The results also show that the extremely high thread counts might not always result in enhancing performance due to factors like overhead and resource contention.
4.2.2. Second Parallel Approach (Using Blocks) Results
In the second approach in the proposed methodology, we optimized the diagonal traversing technique elucidated in Section 3.3.2 by using the block concept. Rather than traversing individual cells within each diagonal, this approach involves traversing clusters of cells called ’blocks’. This innovative strategy aims to enhance parallel traversing efficiency. To evaluate the efficacy of this proposed parallel approach, firstly, we conducted experiments using a sequence of length 1024 characters and employing various block sizes (K = 4, 8, and 16). The results of these experiments are presented in Table 6. Table 6 shows a notable trend that an increase in block size correlates with a decrease in the required execution time. For example, the execution time when the block size is (k = 16) is lower than when the block size is (k = 4). This result suggests that larger blocks contribute to improved computational efficiency. The experiments are repeated using several sequence lengths and block size = 8 and the results are reported in Table 7. As noted from these results, the average execution time for this parallel approach is 48.6 compared to 282.3 milliseconds for sequential implementation required to align two sequences of length 1024. The improvement is calculated for the different sequence lengths, and the experiments show a significant improvement in execution time, about 4.9 times faster.

Table 6.
The execution time for the parallel approach using different block sizes, in milliseconds.

Table 7.
Comparison between sequential and parallel implementations for two-sequence alignment for different sequence lengths.
4.2.3. Third Parallel Approach (Slicing) Results
In the third approach in the proposed methodology, we deployed the slicing method explained in Section 3.3.3 to optimize the parallel traversing technique. To evaluate the efficacy of this approach, we conducted experiments using sequences of lengths 128, 256, 512, and 1024. Table 8 presents the average execution times (in milliseconds) from ten different runs for aligning three sequences using the slicing approach with different block sizes (BK = 1, BK = 16, and BK = 32) across varying sequence lengths. From the table, it is noticeable that as the sequence length increases, there is an increase in execution times across all approaches. This is expected as the increase in computational complexity is associated with longer sequences. Comparing the sequential approach with the parallel approach using a small block size such as (Bk = 1), there is a slight reduction in execution time for the applied parallel approach, while substantially more significant improvements are observed when the block sizes are increased, as shown with BK = 16 and BK = 32. There is a clear effect of increasing block size (BK) in reducing the execution time, and this demonstrates the importance of tuning the block size to the characteristics of the alignment problem.

Table 8.
The average execution time of ten runs for aligning three sequences for different sequence lengths and using the slicing approach with block sizes (BK) = 1, 16, and 32.
This approach is evaluated by aligning three sequences, four sequences, and five sequences with various sequence lengths of 128, 256, 512, and 1024, and with block sizes (BK) = 1, 2, 4, 8, 16, and 32. The best obtained results for each sequence length are reported in Table 9 for aligning three sequences, in Table 10 for aligning four sequences, and in Table 11 for aligning five sequences. Table 9 presents the average execution times for aligning three sequences with varying lengths using the proposed slicing approach. As noted from the results, as the sequence length increases, both the sequential and parallel execution times increase, which is expected due to the growing computational complexity. The ‘improvement’ column demonstrates that the parallel approach consistently outperforms the sequential approach across all sequence lengths, showcasing an average improvement factor exceeding 4×.

Table 9.
The average execution time of ten runs for the alignments of three sequences for different sequence lengths using the slicing approach.

Table 10.
The average execution time for four sequences of different lengths using the slicing approach.

Table 11.
The average execution time for five sequences of different lengths using the slicing approach.
Table 10 shows the results of four sequence alignments, providing insights into the performance of the proposed slicing approach for different sequence lengths. Similar to the three-sequence alignment, the parallel approach outperforms the sequential approach, demonstrating substantial improvements in execution time. The ‘improvement’ values reflect notable speedup where the improvement factor exceeds 3×. The chosen block sizes (8, 16, and 32) contribute to the overall effectiveness of the proposed approach, while there is no noted relation in this case between the block size and the approach execution time. Table 11 shows the further investigation of five sequences. The results obtained from this experiment emphasize the efficacy of parallelization, showcasing significant improvement factors across different sequence lengths with around 4×. In summary, the obtained results from Table 9, Table 10 and Table 11 collectively highlight the consistent success of the slicing parallelization approach in improving alignment execution times. The findings also underscore the importance of choosing appropriate block sizes experimentally for optimal parallelization benefits across the numbers and lengths of sequences.
The experimental work conducted in this research investigated the efficiency of three proposed parallelization strategies utilized for sequence alignment and MSA problems. The results obtained and presented in this section (as shown before) consistently demonstrated the superiority of the utilized parallel approaches over the applied sequential approach. The slicing approach achieves up to a 4.8× reduction in execution time when implemented with an optimal block size. The experiments underscored the significance of block size selection in the utilized parallel strategy, where mostly the larger block sizes contributed significantly to enhanced parallel efficiency.
5. Conclusions and Future Work
The dynamic programming (DP) algorithm is widely used to solve both local and global alignment problems. The most obvious drawback of DP algorithms is high execution time and slow performance, especially when applied to solve multiple sequence alignment problems. In this study, we focused on enhancing the efficiency of solving exact multiple sequence alignment exact-MSA problems through three proposed parallelization approaches. The experimental findings consistently highlight the superiority of parallel approaches compared to the sequential method. For example, the slicing parallel approach exhibits a remarkable 4.8× reduction in execution time when implemented with an optimal block size. The experiments emphasized the crucial role of block size selection in the chosen utilized parallel strategy. On average, the parallel implementation was 4× faster than the sequential implementations for several sequences of lengths. The proposed approaches could be merged with many existing techniques to enhance the performance and accuracy of current MSA tools. In the future, we will investigate the possibility of extending this framework to solve more than sequences or even aligning any given N sequences. Also, we will explore the possibility of utilizing the MSA framework using graphics processing unit (GPU) technologies. We also intend to increase the lengths of the sequences used to solve 3D, 4D, and 5D problems and test the approaches with diverse datasets. Another aim is to work on the proposed implementation to optimize the approach to obtain better results.
Author Contributions
Conceptualization, Q.B.B. and M.A.-A.; Methodology, R.A.A.-H., Q.B.B. and M.A.-A.; Investigation, Q.B.B. and M.A.-A.; Writing—original draft, Q.B.B.; Writing—review & editing, Q.B.B.; Supervision, Q.B.B. and M.A.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The code developed and data used in this work is available upon request from the authors.
Acknowledgments
We thank Ajman University for supporting the final published version of the article.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Diab, S.; Nassereldine, A.; Alser, M.; Gómez Luna, J.; Mutlu, O.; El Hajj, I. A framework for high-throughput sequence alignment using real processing-in-memory systems. Bioinformatics 2023, 39, btad155. [Google Scholar] [CrossRef]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Agrawal, A.; Huang, X. Pairwise statistical significance of local sequence alignment using sequence-specific and position-specific substitution matrices. IEEE/ACM Trans. Comput. Biol. Bioinform. 2009, 8, 194–205. [Google Scholar] [CrossRef] [PubMed]
- Edgar, R.C.; Batzoglou, S. Multiple sequence alignment. Curr. Opin. Struct. Biol. 2006, 16, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 2015; Volume 2050. [Google Scholar]
- Chao, J.; Tang, F.; Xu, L. Developments in algorithms for sequence alignment: A review. Biomolecules 2022, 12, 546. [Google Scholar] [CrossRef] [PubMed]
- Saeed, F.; Khokhar, A. An Overview of Multiple Sequence Alignment Systems. arXiv 2009, arXiv:0901.2747. [Google Scholar]
- Chatzou, M.; Magis, C.; Chang, J.M.; Kemena, C.; Bussotti, G.; Erb, I.; Notredame, C. Multiple sequence alignment modeling: Methods and applications. Briefings Bioinform. 2016, 17, 1009–1023. [Google Scholar] [CrossRef]
- Zemali, E.a.; Boukra, A. A new hybrid bio-inspired approach to resolve the multiple sequence alignment problem. In Proceedings of the 2016 International Conference on Control, Decision and Information Technologies (CoDIT), Saint Julian’s, Malta, 6–8 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 108–113. [Google Scholar]
- Amorim, A.R.; Zafalon, G.F.D.; de Godoi Contessoto, A.; Valêncio, C.R.; Sato, L.M. Metaheuristics for multiple sequence alignment: A systematic review. Comput. Biol. Chem. 2021, 94, 107563. [Google Scholar] [CrossRef]
- Bafna, V.; Lawler, E.L.; Pevzner, P.A. Approximation algorithms for multiple sequence alignment. Theor. Comput. Sci. 1997, 182, 233–244. [Google Scholar] [CrossRef][Green Version]
- Nowicki, M.; Bzhalava, D.; BaŁa, P. Massively parallel implementation of sequence alignment with basic local alignment search tool using parallel computing in java library. J. Comput. Biol. 2018, 25, 871–881. [Google Scholar] [CrossRef]
- Chiaromonte, F.; Yap, V.B.; Miller, W. Scoring pairwise genomic sequence alignments. In Biocomputing 2002; World Scientific: Singapore, 2001; pp. 115–126. [Google Scholar]
- Haque, W.; Aravind, A.; Reddy, B. Pairwise sequence alignment algorithms: A survey. In Proceedings of the 2009 Conference on Information Science, Technology and Applications, Sliema, Malta, 11–16 October 2009; pp. 96–103. [Google Scholar]
- Edgar, R.C.; Sjölander, K. A comparison of scoring functions for protein sequence profile alignment. Bioinformatics 2004, 20, 1301–1308. [Google Scholar] [CrossRef]
- Li, H.; Homer, N. A survey of sequence alignment algorithms for next-generation sequencing. Briefings Bioinform. 2010, 11, 473–483. [Google Scholar] [CrossRef]
- Abbasi, M.; Paquete, L.; Liefooghe, A.; Pinheiro, M.; Matias, P. Improvements on bicriteria pairwise sequence alignment: Algorithms and applications. Bioinformatics 2013, 29, 996–1003. [Google Scholar] [CrossRef]
- Gotoh, O. An improved algorithm for matching biological sequences. J. Mol. Biol. 1982, 162, 705–708. [Google Scholar] [CrossRef]
- Pearson, W.R. Rapid and sensitive sequence comparison with FASTP and FASTA. Methods Enzym. 1990, 183, 63–98. [Google Scholar]
- Altschul, S.F.; Gish, W.; Miller, W.; Myers, E.W.; Lipman, D.J. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef] [PubMed]
- Rice, P.; Longden, I.; Bleasby, A. EMBOSS: The European molecular biology open software suite. Trends Genet. 2000, 16, 276–277. [Google Scholar] [CrossRef] [PubMed]
- Daily, J. Parasail: SIMD C library for global, semi-global, and local pairwise sequence alignments. BMC Bioinform. 2016, 17, 81. [Google Scholar] [CrossRef] [PubMed]
- Li, H. Minimap2: Pairwise alignment for nucleotide sequences. Bioinformatics 2018, 34, 3094–3100. [Google Scholar] [CrossRef] [PubMed]
- Issa, M.; Hassanien, A.E.; Oliva, D.; Helmi, A.; Ziedan, I.; Alzohairy, A. ASCA-PSO: Adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment. Expert Syst. Appl. 2018, 99, 56–70. [Google Scholar] [CrossRef]
- Aguado-Puig, Q.; Marco-Sola, S.; Moure, J.C.; Matzoros, C.; Castells-Rufas, D.; Espinosa, A.; Moreto, M. WFA-GPU: Gap-affine pairwise alignment using GPUs. bioRxiv 2022. [Google Scholar] [CrossRef]
- Kaur, K.; Chakraborty, S.; Gupta, M.K. Accelerating Smith-Waterman Algorithm for Faster Sequence Alignment using Graphical Processing Unit. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2161, p. 012028. [Google Scholar]
- Fakirah, M.; Shehab, M.A.; Jararweh, Y.; Al-Ayyoub, M. Accelerating needleman-wunsch global alignment algorithm with gpus. In Proceedings of the 2015 IEEE/ACS 12th International Conference of Computer Systems and Applications (AICCSA), Marrakech, Morocco, 17–20 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Balhaf, K.; Shehab, M.A.; Wala’a, T.; Al-Ayyoub, M.; Al-Saleh, M.; Jararweh, Y. Using gpus to speed-up levenshtein edit distance computation. In Proceedings of the 2016 7th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 5–7 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 80–84. [Google Scholar]
- Jararweh, Y.; Al-Ayyoub, M.; Fakirah, M.; Alawneh, L.; Gupta, B.B. Improving the performance of the needleman-wunsch algorithm using parallelization and vectorization techniques. Multimed. Tools Appl. 2019, 78, 3961–3977. [Google Scholar] [CrossRef]
- Shehab, M.A.; Ghadawi, A.A.; Alawneh, L.; Al-Ayyoub, M.; Jararweh, Y. A hybrid CPU-GPU implementation to accelerate multiple pairwise protein sequence alignment. In Proceedings of the 2017 8th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 4–6 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 12–17. [Google Scholar]
- Sievers, F.; Higgins, D.G. Clustal Omega, accurate alignment of very large numbers of sequences. Mult. Seq. Alignment Methods 2014, 1079, 105–116. [Google Scholar]
- Boyce, K.; Sievers, F.; Higgins, D.G. Instability in progressive multiple sequence alignment algorithms. Algorithms Mol. Biol. 2015, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wallace, I.M.; Higgins, D.G. Evaluation of iterative alignment algorithms for multiple alignment. Bioinformatics 2005, 21, 1408–1414. [Google Scholar] [CrossRef]
- Notredame, C. Recent evolutions of multiple sequence alignment algorithms. PLoS Comput. Biol. 2007, 3, e123. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.F.; Hassanien, A.E. A survey of metaheuristics methods for bioinformatics applications. In Applications of Intelligent Optimization in Biology and Medicine: Current Trends and Open Problems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 23–46. [Google Scholar]
- Riaz, T.; Wang, Y.; Li, K.B. Multiple sequence alignment using tabu search. In Proceedings of the Second Conference on Asia-Pacific Bioinformatics, Dunedin, New Zealand, 18–22 January 2004; Volume 29, pp. 223–232. [Google Scholar]
- Kim, J.; Pramanik, S.; Chung, M.J. Multiple sequence alignment using simulated annealing. Bioinformatics 1994, 10, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Chen, Y. A method for multiple sequence alignment based on particle swarm optimization. In Proceedings of the Emerging Intelligent Computing Technology and Applications. With Aspects of Artificial Intelligence: 5th International Conference on Intelligent Computing, ICIC 2009, Ulsan, Republic of Korea, 16–19 September 2009; Proceedings 5. Springer: Berlin/Heidelberg, Germany, 2009; pp. 965–973. [Google Scholar]
- Chowdhury, B.; Garai, G. A review on multiple sequence alignment from the perspective of genetic algorithm. Genomics 2017, 109, 419–431. [Google Scholar] [CrossRef]
- Zambrano-Vega, C.; Nebro, A.J.; García-Nieto, J.; Aldana-Montes, J.F. Comparing multi-objective metaheuristics for solving a three-objective formulation of multiple sequence alignment. Prog. Artif. Intell. 2017, 6, 195–210. [Google Scholar] [CrossRef]
- Smirnov, V. Recursive MAGUS: Scalable and accurate multiple sequence alignment. PLoS Comput. Biol. 2021, 17, e1008950. [Google Scholar] [CrossRef]
- Steenwyk, J.L.; Buida III, T.J.; Li, Y.; Shen, X.X.; Rokas, A. ClipKIT: A multiple sequence alignment trimming software for accurate phylogenomic inference. PLoS Biol. 2020, 18, e3001007. [Google Scholar] [CrossRef] [PubMed]
- Lassmann, T.; Sonnhammer, E.L. Kalign—An accurate and fast multiple sequence alignment algorithm. BMC Bioinform. 2005, 6, 298. [Google Scholar] [CrossRef] [PubMed]
- Do, C.B.; Mahabhashyam, M.S.; Brudno, M.; Batzoglou, S. ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome Res. 2005, 15, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Edgar, R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004, 32, 1792–1797. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Misawa, K.; Kuma, K.i.; Miyata, T. MAFFT: A novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002, 30, 3059–3066. [Google Scholar] [CrossRef] [PubMed]
- Notredame, C.; Higgins, D.G.; Heringa, J. T-Coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 2000, 302, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Morgenstern, B. DIALIGN 2: Improvement of the segment-to-segment approach to multiple sequence alignment. Bioinformatics 1999, 15, 211–218. [Google Scholar] [CrossRef]
- Thompson, J.D.; Higgins, D.G.; Gibson, T.J. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994, 22, 4673–4680. [Google Scholar] [CrossRef]
- Mojbak, J.; Pedersen, C. Exact Multiple Sequence Alignment Using Forward Dynamic Programming; Bioinformatics Research Center: Singapore, 2010. [Google Scholar]
- Hosseininasab, A.; van Hoeve, W.J. Exact multiple sequence alignment by synchronized decision diagrams. INFORMS J. Comput. 2021, 33, 721–738. [Google Scholar] [CrossRef]
- González-Domínguez, J. Fast and Accurate Multiple Sequence Alignment with MSAProbs-MPI. In Multiple Sequence Alignment; Springer: Berlin/Heidelberg, Germany, 2021; pp. 39–47. [Google Scholar]
- Ju, F.; Zhu, J.; Shao, B.; Kong, L.; Liu, T.Y.; Zheng, W.M.; Bu, D. CopulaNet: Learning residue co-evolution directly from multiple sequence alignment for protein structure prediction. Nat. Commun. 2021, 12, 2535. [Google Scholar] [CrossRef] [PubMed]
- Almanza-Ruiz, S.H.; Chavoya, A.; Duran-Limon, H.A. Parallel protein multiple sequence alignment approaches: A systematic literature review. J. Supercomput. 2023, 79, 1201–1234. [Google Scholar] [CrossRef]
- Helal, M.; El-Gindy, H.; Mullin, L.; Gaeta, B. Parallelizing optimal multiple sequence alignment by dynamic programming. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing with Applications, Sydney, NSW, Australia, 10–12 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 669–674. [Google Scholar]
- Hung, C.L.; Lin, Y.S.; Lin, C.Y.; Chung, Y.C.; Chung, Y.F. CUDA ClustalW: An efficient parallel algorithm for progressive multiple sequence alignment on Multi-GPUs. Comput. Biol. Chem. 2015, 58, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, M.; Toya, T.; Hoshida, M.; Nitta, K.; Ogiwara, A.; Kanehisa, M. Multiple sequence alignment by parallel simulated annealing. Bioinformatics 1993, 9, 267–273. [Google Scholar] [CrossRef] [PubMed]
- Blazewicz, J.; Frohmberg, W.; Kierzynka, M.; Wojciechowski, P. G-MSA—A GPU-based, fast and accurate algorithm for multiple sequence alignment. J. Parallel Distrib. Comput. 2013, 73, 32–41. [Google Scholar] [CrossRef]
- Zou, Q.; Hu, Q.; Guo, M.; Wang, G. HAlign: Fast multiple similar DNA/RNA sequence alignment based on the centre star strategy. Bioinformatics 2015, 31, 2475–2481. [Google Scholar] [CrossRef]
- Wan, S.; Zou, Q. HAlign-II: Efficient ultra-large multiple sequence alignment and phylogenetic tree reconstruction with distributed and parallel computing. Algorithms Mol. Biol. 2017, 12, 25. [Google Scholar] [CrossRef]
- Zou, Q.; Wan, S.; Zeng, X.; Ma, Z.S. Reconstructing evolutionary trees in parallel for massive sequences. BMC Syst. Biol. 2017, 11, 100. [Google Scholar] [CrossRef]
- Su, W.; Liao, X.; Lu, Y.; Zou, Q.; Peng, S. Multiple sequence alignment based on a suffix tree and center-star strategy: A linear method for multiple nucleotide sequence alignment on spark parallel framework. J. Comput. Biol. 2017, 24, 1230–1242. [Google Scholar] [CrossRef]
- Chen, X.; Wang, C.; Tang, S.; Yu, C.; Zou, Q. CMSA: A heterogeneous CPU/GPU computing system for multiple similar RNA/DNA sequence alignment. BMC Bioinform. 2017, 18, 315. [Google Scholar] [CrossRef]
- Siriwardena, T.; Ranasinghe, D. Accelerating global sequence alignment using CUDA compatible multi-core GPU. In Proceedings of the 2010 Fifth International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 17–19 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 201–206. [Google Scholar]
- Al-Hussien, R.A.; Baker, Q.B.; Al-Ayyoub, M. Fast exact sequence alignment using parallel computing. In Proceedings of the 2018 9th International Conference on Information and Communication Systems (ICICS), Security Lille, France, 29–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 187–191. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).