Abstract
A novel approach was developed that combined LP-based row generation with optimization-based sorting to tackle computational challenges posed by budget allocation problems with combinatorial constraints. The proposed approach dynamically generated constraints using row generation and prioritized them using optimization-based sorting to ensure a high-quality solution. Computational experiments and case studies revealed that as the problem size increased, the proposed approach outperformed simplex solutions in terms of solution search time. Specifically, for a problem with 50 projects (N = 50) and 2,251,799,813,685,250 constraints, the proposed approach found a solution in just 1.4 s, while LP failed due to the problem size. The proposed approach demonstrated enhanced computational efficiency and solution quality compared to traditional LP methods.
1. Introduction
Budget allocation problems, commonly referred to as capital budgeting problems, often involve many constraints [1]. These constraints typically consist of 2N investment patterns, which further increase to 2 ✕ (2N − 1) patterns when considering upper and lower bounds. Consequently, efficiently and effectively solving these problems becomes increasingly challenging, particularly when considering the total number of projects represented by N. Traditional optimization techniques may struggle to handle the combinatorial explosion of constraints, often resulting in time-consuming computations and no guarantee of optimal solutions within a reasonable timeframe [2]. However, recent advancements in linear programming-based row generation and optimization-based sorting methods offer promising solutions to address these challenges.
Linear programming (LP) provides a powerful framework for modeling and solving optimization problems with linear constraints. By formulating the budget allocation problem as an LP model, decision makers can systematically allocate resources to various activities while considering multiple objectives and constraints [3,4,5]. However, when faced with many combinatorial constraints, the traditional LP formulation may become computationally intractable.
An innovative approach combines linear programming-based row generation to overcome this challenge. Row generation involves iteratively generating new constraints (rows) added to the problem formulation, effectively expanding the solution space and refining the solution quality [6]. By iteratively adding constraints that are most relevant to the current solution, the row generation process enables efficient exploration of the combinatorial constraint space.
Furthermore, optimization-based sorting methods enhance the row-generation process by incorporating sorting algorithms tailored to the specific constraints and objectives of the budget allocation problem. This algorithm employs intelligent search strategies to efficiently discover the optimal solutions. With a focus on practical applications, the optimization-based sorting method has demonstrated the ability to generate optimal solutions within a reasonable timeframe [7,8].
The combination of linear programming-based row generation and optimization-based sorting methods offers a powerful approach to solving budget allocation problems with a combinatorial number of constraints. This integrated methodology allows decision makers to handle large-scale optimization problems, allocate resources efficiently, and identify optimal budget allocation strategies.
This study aims to explore and analyze the proposed method by investigating theoretical foundations, outlining the advantages and challenges of related techniques, and discussing practical implementation. Randomly generated structural problems are examined to illustrate the efficiency and potential of this approach in complex budget allocation scenarios. Extensive computational experiments and case studies demonstrate that our approach outperforms simplex solutions in solution search time as the problem size increases.
By leveraging the capabilities of linear programming-based row generation and optimization-based sorting, decision makers can make informed budget allocation decisions, optimize resource utilization, and achieve superior financial outcomes. The proposed methodology holds immense promise for organizations facing complex budget allocation challenges, enabling them to navigate the intricate landscape of constraints and make strategic resource allocation decisions. Further elaboration on our proposed approach can be found in Section 3, Section 4, Section 5, Section 6 and Section 7. Section 3 introduces problem structures and notations. Section 4 applies row generation to solve the budget allocation model. Section 5 demonstrates the application of sorting methods in the row-generation process. Section 6 proves the optimal solutions derived from sorting methods. Finally, Section 7 showcases the model’s application in solving budget allocation problems.
2. Literature Review
Budget allocation problems with combinatorial constraints are complex optimization models originating from the study by Weingartner [9], which has found applications in various fields such as resource allocation and project planning. Linear programming (LP) is a widely used technique to solve such problems efficiently. However, when dealing with a large number of constraints, the computational complexity of LP becomes time-consuming to solve. This literature review explores the application of the row-generation techniques to enhance the efficiency of solving budget allocation problems with combinatorial constraints using sorting methods.
Row generation, a sub-technique within Benders decomposition, is a powerful approach initially proposed by Unger [10,11], which offers an application for solving large-scale LP problems in budget allocation. It focuses on generating a subset of constraints, known as “rows”, dynamically during the optimization process. Hummeltenberg [12], Zak [13], Muter et al. [14], Muter and Sezer [15] and Witthayapraphakorn et al. [16] consistently highlight the advantages of employing a row generation algorithm that incorporates a warm-start strategy and an approximation scheme, surpassing the performance of linear programming, particularly in scenarios involving a substantial number of constraints. These compelling findings affirm the efficacy of row-generation technique as an effective approach for addressing linear programming problems characterized by a comprehensive set of constraints. According to the literature reviews over the past decade, a limited number of studies have investigated the application of row-generating techniques in the context of budget allocation problems; however, notable research by Fard et al. [17] has contributed to this area. Their study presents a model employing the bender decomposition method for budgeting purposes within international humanitarian organizations and provides analytical insights into the optimal solution. Additional scholarly studies employ the row generation method to allocate various types of resources, such as energy [18] and location [19,20]. Although the row generation method accelerates solution discovery in large linear problems, its efficacy may diminish with an abundance of constraints, leading to slower solution times. Consequently, researchers are exploring additional methods, such as sorting techniques [21], to enhance the effectiveness of row generation in addressing very large-scale problems. However, there is no observed research integrating heuristics into row generation to address problem solving in large-scale linear programming problems, existing heuristics for solving LP problems with combinatorial constraints prioritize finding the best solution without guaranteeing optimization [22].
The possibility of utilizing effective heuristic methods to generate initial starting points in combinatorial optimization motivates the exploration of applying sorting techniques, specifically in budget allocation problems known for their exceptional efficiency in identifying feasible solutions [21]. Sorting is a technique that aims to prioritize constraints based on their potential impact on the solution quality. This approach involves assigning weights or scores to constraints and ordering them in a way that maximizes the likelihood of finding a feasible solution quickly. Sorting has been successfully employed in various allocation problems. For example, Song and Mu [23] propose a heuristic algorithm based on assignment to solve the sequence sorting problem of large-scale automated storage requests in multiple input/output (multi-I/O) depots. The proposed algorithm considers equivalent merging and minimum cost merging methods of subloops to eliminate subloops that emerged in the sorting process. Their proposed algorithm offers a solution to optimize the sequence of storage requests in multi-I/O depots, which can improve efficiency and cost-effectiveness in practice. Weiner et al. [24] provide valuable insights into the utilization of sorting in subproblems optimization and highlight its potential for solving large-scale mixed-integer programs (MIPs). Specifically, their research demonstrates the effective utilization of machine learning (ML) for ranking constraint relaxations of MIPs. Their proposed method outperforms existing heuristic and ML-based methods in terms of solution quality and computational time. The authors suggest that their approach has the potential to be applied to other optimization problems beyond MIPs.
The feasibility of using row generation methods (i.e., Benders decomposition) is hindered by the complexity of combinatorial constraints and the limited time availability for solution generation. Consequently, the utilization of sorting techniques is motivated by the intricate nature of combinatorial constraints while also taking into account the potential implementation of row-generation methods within the available computational time and the problem size to be solved. The current literature on budget allocation problems lacks evidence supporting the effectiveness of combining heuristics and LP approaches (i.e., integer programming, Benders decomposition, and row generation) in achieving optimal solutions. Moreover, studies in related fields, like location allocation and network allocation, provide insights into the comparative speed of solution discovery using mixed methods. Fischetti et al. [25] demonstrate the practical effectiveness and straightforward implementation of their proposed approach, which applies Benders decomposition to solve the facility allocation master problem with non-separable subproblems. By employing a simple sorting application on Benders cut, their study showcases the successful application of generalized Benders cuts for convex problems. Furthermore, numerous studies have explored alternative heuristics beyond sorting to identify optimal solutions in combination with the Benders decomposition method. For example, Maher [26] reveals how large neighborhood search heuristics can enhance Benders decomposition algorithms and improve mixed-integer programming solvers. Costa and Gendron [27], Maheo et al. [28], and Oliveira et al. [29] employ heuristic techniques, such as branch-and-cut, local search, Pareto-optimal cuts, and multiple cuts, to generate additional cuts when solving the master problem through Benders decomposition. Their respective studies focus on fixed-charge network design [27], bin allocation for waste management [28], and multiple allocation hub network design [29].
The review provides a comprehensive overview of the evolution in budget allocation or capital budgeting research, transitioning from traditional linear programming and row generation to the utilization of diverse heuristic approaches, specifically focusing on the utilization of sorting algorithms. Our main contribution to this study is represented in the implementation of linear programming-based row generation using optimization-based sorting methods for budget allocation problems. The study compares the efficiency of solution-finding, measured in terms of time, by employing linear programming, the row generation method, and a hybrid approach combining row generation and sorting. Through computational experiments and case studies, we have demonstrated the advantages of this combined approach and proved whether employing sorting methods will yield equivalent results with binary programming or integer programming techniques, particularly when compared to the conventional row generation method and linear programming.
3. Problem Structures and Notations
The problem structure of budget allocation involves determining how available budget resources should be allocated among different projects within an organization or government entity, considering factors such as maximizing profits and constraint-based resource limitations. When making investment decisions for each project, there are two options: invest or not invest. This results in a total of 2N possible patterns, considering all projects N. Furthermore, when considering budget allocation within the investment boundaries as lower and upper bounds, there are a total of 2 ✕ (2N − 1) combinatorial constraints to be considered. Efficiently solving large problems involves employing the principle of row generations while considering maximum and minimum total investments for project groups. Furthermore, utilizing the sorting method to rank constraints enhances problem-solving efficiency through row generation.
The proposed approach for budget allocation, following the structure described by Sangkhasuk et al. [30], can be stated as:
- The objective is to maximize the overall benefits obtained from allocating budget resources among the different projects.
- Each project receives a budget allocation proportional to its potential benefits, with allocations not exceeding 1.
- The total budget allocation across all projects is limited to a maximum of 1.
- Combinatorial constraints consist of 2 ✕ (2N − 1) constraints, where N represents the number of projects.
- Each investment pattern has a lower and upper boundary of each constraint that is proportional to the amount of investment. For instance, if there are five projects, an investment pattern must allocate between 0.1 and 0.8 of the investment, resulting in N − 1 boundary values.
The notations in order to formulate the above model are as follows:
Z—Objective function, which aims to maximize investment benefits.
cj—Benefits obtained from investment project j based on the allocated funds.
xj—Decision variable, which is the proportion of investment in project j.
aij—Allocated investment pattern i in project j (j = 1, 2, …, N) among 2 to N − 1 projects, denoted by aij = 1 or 0.
N—Total number of projects.
Uk—Upper bound constraint set on the proportion of investment in k projects.
Lk—Lower bound constraint set on the proportion of investment in k projects.
uk—Proportional investment for a total number of allocated investment projects used to create the upper bound constraint of investment in Equation (2), where uk < uk+1 and 0 < uk < 1.
lk—Proportional investment for a total number of allocated investment projects used to create the lower bound constraint of investment in Equation (3), where lk < uk and lk < lk+1 and 0 < lk < 1.
Lowj—Lower bound of xj
Upj—Upper bound of xj
The mathematical model (1)–(5) is used for budget allocation problems as follows:
subject to
where the values of and are related to the total number of allocated investment projects k.
The objective function (1) is formulated to optimize investment profits. The upper () bound (2) and lower () bound (3) serve to establish boundaries for the investment pattern. In this particular context, binary sequences are employed to conveniently represent investment patterns, with 1 indicating funding and 0 denoting a lack of funding (e.g., 1 1 0 0 0 or 1 0 1 0 0 for five projects). Constraint (4) ensures cumulative investment proportions for funded projects do not exceed 1, maintaining the total investment within available budgets. Additionally, constraint (5) imposes a restriction on the investment proportion, confining it within the range of 0 to 1. Table 1 presents the values of variables and in constraints (2) and (3), respectively, which are dependent on the total number of allocated investment projects.

Table 1.
Relationship between Uk and Lk with the total number of allocated investment projects.
4. Row Generation Applied to Solving Budget Allocation Model
The utilization of the row generation method in the context of the budget allocation problem encompasses three distinctive sub-models, which consist of:
- Mathematical model for relaxed budget allocation;
- Row generation applied to the upper bound model;
- Row generation applied to the lower bound model.
4.1. Sub-Model 1: Mathematical Model for Relaxed Budget Allocation
Introduce relaxations to account for flexibility in the budget allocation process. Relaxations allow for partial allocations or fractional allocations of the budget. Instead of using binary variables, we may allow fractional values for decision variables. This enables allocating a portion of the budget to multiple alternatives, allowing for more fine-grained resource allocation. The mathematical model for relaxed investment allocation incorporates the objective function (1) and constraints (4) and (5), with constraints (2) and (3) substituted by constraints (6) and (7), respectively,
where the and represent the upper and lower bounds of investment in project j for round r of solution finding, the initial solution is obtained by utilizing the objective function (1), and constraints (4) and (5) during the first round (r = 0). Subsequently, constraints (6) and (7) are incrementally added in each subsequent round until the most feasible and optimal solution is achieved at round R, where .
4.2. Sub-Model 2: Row Generation Applied to the Upper Bound Constraint
By iteratively generating new constraints, row generation refines the mathematical model and progressively narrows down the feasible solution space. The lower bound is gradually improved by finding better feasible solutions at each iteration, while the upper bound is tightened by adding new constraints to the model. This process continues until the optimal solution is obtained or until the termination criterion is satisfied. Specifically, in the case of row generation for the upper bound model, the mathematical model can be expressed as follows:
subject to
where is the target value, in an unconventional form, represents the objective of finding an investment pattern that violates the upper limit constraint under k investment projects, is the decision variable for investing in project j in case of allocating k investment projects that violates the highest upper limit constraint, is a constant obtained from finding the value of in the mathematical model for capital budgeting under relaxed conditions in the previous round r − 1, and k is the sum of the number of investment projects, with a value ranging from 1 to N − 1.
The model described in (8)–(11) is utilized to generate constraints (6) in round r. The objective function (8) aims to identify an investment pattern that surpasses the upper limit constraint the most among k investment projects. Constraint (9) outlines the requirement for investing in k investment projects. Constraint (10) determines the decision of investing or not in project j, given the allocation of k investment projects. Constraint (11) ensures that all potential solutions are iterated for N − 1 rounds using the objective function (8) under constraints (9) and (10). The value of that yields the highest positive value of is then then transferred to in constraint (6).
4.3. Sub-Model 3: Row Generation Applied to the Lower Bound Constraint
During row generation for the lower bound constraint, the feasible solution space undergoes further refinement, integrating stricter constraints and narrowing down the range of potential solutions. This iterative process facilitates the exploration of various allocations and enhances resource optimization, taking into account the lower bound. The model for this process is as follows:
subject to
where is the target value with the objective of violating the lowest upper bound investment format under k investment projects, is the decision variable for investing in project j in the case where there is investment in project k, which violates the lower bound constraint the most, and k is the total number of investment projects with a value ranging from 1 to N − 1.
The model represented in (12) to (15) is utilized for generating the constraints (7) in round r. The objective function (12) is designed to identify the investment pattern in project k that maximally violates the lower bound constraint. Constraint (13) establishes the investment constraint for project k. Constraint (14) determines the investment status of project j when project k is being investment. Constraint (15) sets the condition for exploring all possible solutions in N − 1 rounds by the objective function (12) under constraints (12) to (14). Subsequently, it assigns the value of that yields the lowest negative value of to in in constraint (7).
The working process of row generation applied to solving the budget allocation model, using three sub-models, can be summarized concisely based on the steps outlined in Figure 1. The specific details of each step are as follows:
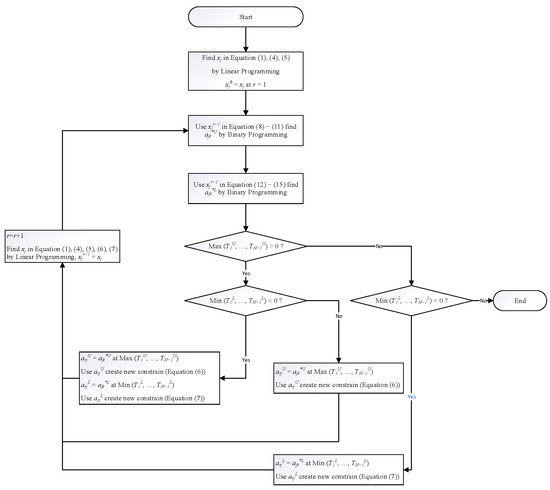
Figure 1.
Row generation in budget allocation model with three sub-models.
- Step 1: Find the value of in round r = 1 using linear programming with Equations (1), (4) and (5), then set = ;
- Step 2: Use and Equations (8) to (11) to find the value of using binary programming;
- Step 3: Use and Equations (12) to (15) to find the value of using binary programming;
- Step 4: Check the values of Max(, ,…,) and Min(, ,…,), and separate into four conditions:Max(, ,…,) > 0 and Min(, ,…,) < 0, proceed to Step 5;Max(, ,…,) > 0 and Min(, ,…,) ≥ 0, proceed to Step 6;Max(, ,…,) ≤ 0 and Min(, ,…,) < 0, proceed to Step 7;Max(, ,…,) ≤ 0 and Min(, ,…,) ≥ 0, proceed to Step 9;
- Step 5: Set = , where is the set of answers for Max(, ,…,), then use to create Equation (6). Set = , where is the set of answers for Min(, ,…,), then use to create Equation (7). Proceed to Step 8;
- Step 6: Set = , where is the set of answers for Max(, ,…,), then use to create Equation (6). Proceed to Step 8;
- Step 7: Set = , where is the set of answers for Min(, ,…,), then use to create Equation (7). Proceed to Step 8;
- Step 8: Adjust the value of r = r + 1, find the value of in round r using Linear Programming with Equations (1), (4), (5), (6) and (7), then set = . Return to Step 2;
- Step 9: stops the search for solutions, with being the final solution set that provides the best result. The entire process of the nine steps can be summarized as shown in Figure 1.
5. Application of Sorting Method in Row Generation Process
The row generation process in the budget allocation model incorporates a sorting method that utilizes descending order sorting for determining from Equations (8) to (11), and ascending order for determining from Equations (12) to (15). This sorting method is utilized as an alternative to binary programming in order to derive the solutions for and variables during steps 2 and 3 of the row generation process outlined in Section 4. The sorting technique proposed by Witthayapraphakorn et al. [16] is adopted, although its effectiveness in yielding the maximum value of for all values of k and the absence of lower boundary conditions is yet to be formally proven. Consequently, this section focuses on explaining the procedure for obtaining the solution for . The proof demonstrating that the sorting method attains the maximum value of for all values of k is presented in Section 6. The proof employs a case-by-case approach similar to that used for , but modified to demonstrate the attainment of the minimum value instead of the maximum value. The steps for the sorting method, aiming to minimize the value of , are presented concisely in Figure 2. The following are the detailed explanations for each step:
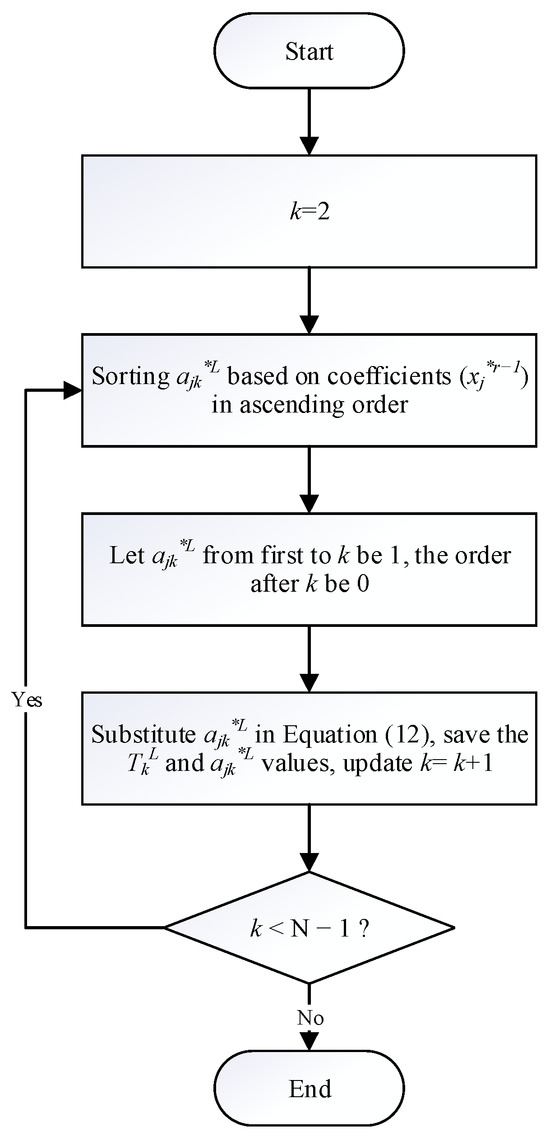
Figure 2.
Applying the sorting method to find in row generation.
- Step 1: Set k = 2;
- Step 2: Sort in ascending order using the value of ;
- Step 3: Set to 1 for the first k elements and 0 for the remaining elements;
- Step 4: Compute using Equation (12) with the updated values of , and record the value of and . update k = k + 1;
- Step 5: Check if k < N − 1. If true, go to Step 2; otherwise, go to Step 6;
- Step 6: End the process and return the values of and for use in the Row Generation process.
For determining the value of , a comparable methodology to that presented in Figure 2 will be employed, with the exception that step 2 will involve sorting in descending order, and step 4 will entail determining the value of using Equation (8). A comprehensive overview of the entire procedure is depicted in Figure 3.
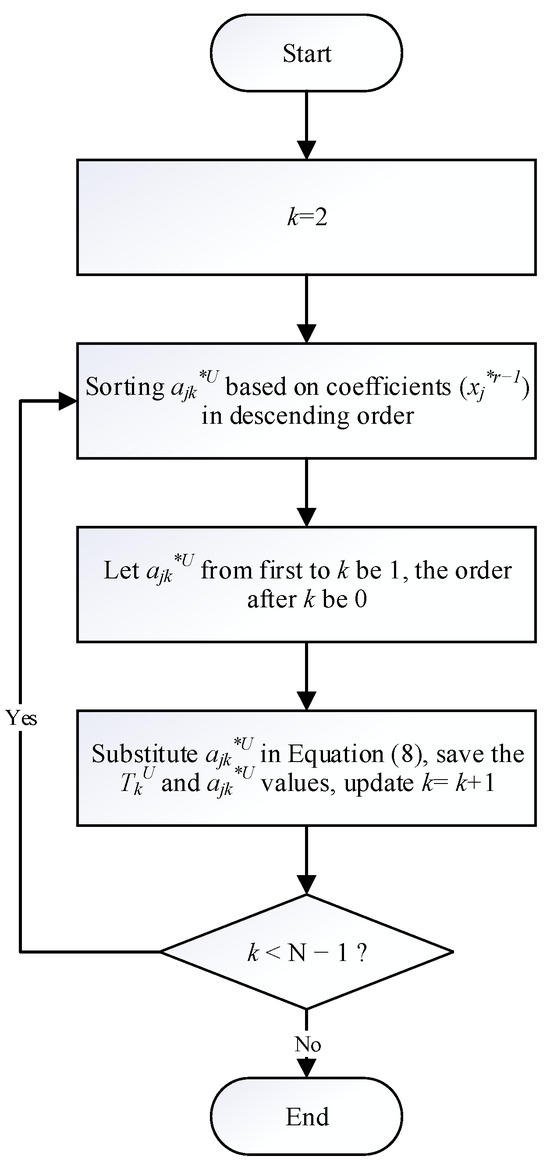
Figure 3.
Applying the sorting method to find in row generation.
In the sorting method outlined in Figure 2 and Figure 3, when applied to row generation (as explained in Section 4, it serves as an alternative to binary programming in determining the values of and in steps 2 and 3. The resulting flow chart is similar to Figure 1, but Figure 4 highlights notable differences with two distinct colored text boxes.
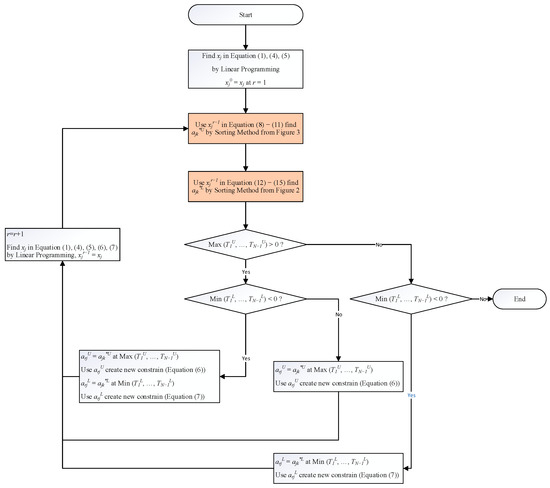
Figure 4.
Row generation sorting for determining upper and lower bounds in the capital budgeting model.
6. Proving Optimal Solutions Derived from Sorting Methods
In this section, our objective is to provide proof of optimality for the sorting method presented in Figure 3, specifically in determining the optimal value of for any feasible solution . We aim to demonstrate that the value obtained from the sorting method is greater than or equal to the value of obtained from .
Let represent an arbitrary feasible solution. Without loss of generality, we assume that the coefficients are sorted in descending order as b(j), following the prescribed sorting method.
For any k = 2,…, N − 1, in accordance with the sorting method, we assign = 1 to the k largest coefficients in b, denoted by b(j), while setting = 0 for the remaining coefficients. Let S denote the set of indices corresponding to the k largest coefficients in b, defined as S = {j: b(j) belongs to the k largest coefficients in b}. Consequently, we have = 1 for j ∈ S, and = 0 for j ∉ S.
Subsequently, we proceed to calculate the value of for the solution obtained through the sorting method:
The rationale behind the final step is based on the fact that is assigned a value of 1 for j ∈ S, where S represents the indices corresponding to the k largest coefficients in b. This implies that the elements within S are indeed the k largest coefficients in b.
Moving forward, let us now proceed to compute for the arbitrary solution :
= ∑(), for j ∈ S (because = 1 for j ∈ S) + ∑(), for j ∉ S (because = 0 for j ∉ S).
Since is sorted in descending order as b(j), we have b(j) ≥ for all j. Therefore:
By combining the aforementioned inequalities, we obtain the following expression:
It has been demonstrated that the value of obtained from the sorting method solution is greater than or equal to the value derived from any alternative feasible solution . Consequently, the sorting method yields an optimal solution.
In order to establish the validity of the sorting method presented in Figure 2, we can employ a similar proof approach as previously used, wherein we demonstrate the minimization of the obtained value and subsequently apply the sorting method in ascending order.
7. Computational Studies
This section applies the proposed approach to exemplify a budget allocation problem and compares the solving time among three methods: linear programming, row generation, and the proposed model (row generation using an optimization-based sorting method: ROS).
7.1. Experimental Model
The experiments are conducted using Matlab Version R2022b with Computer Spec Processor IntelI CoreI i7-7700 3.60 GHz, RAM 32.0 GB solving by linprog function for linear programming and intlinprog for binary programming.
To formulate the problem, random values cj, uk, and lk will be generated in accordance with the assumptions specified in Equations (1) to (5). Initially, there will be a substantial gap between the values of uk and lk for an equivalent number of projects to preclude the occurrence of infeasible solutions; the Matlab code for configuring the problem can be accessed from the following link: http://surl.li/ngrgi (accessed on 20 November 2023). The experiments are conducted in two parts:
- Comparison of processing time for all three methods with project sizes ranging from 5 to 20 projects, with one additional project added for each iteration;
- Comparison of processing time for row generation and ROS methods for larger problem sizes, with project sizes ranging from 5 to 50 projects, with an additional five projects added for each iteration.
To gather data on processing time, the initial 10 examples were recorded, and any outliers were eliminated through the utilization of box plots. Subsequently, further data were acquired until no outliers remained, and the average processing time was computed. The process is visually presented in Figure 5.
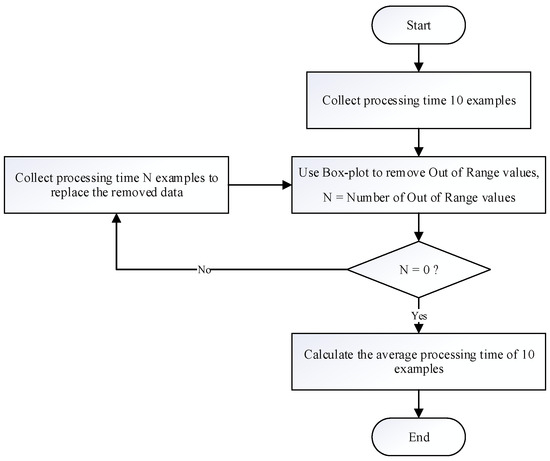
Figure 5.
Processing time data collection and outlier elimination process.
7.2. Experimental Results
The experimental findings involved a comparative assessment of processing time across three different methods within the context of a linear problem structure, categorized by problem sizes. These sizes were divided into two ranges: (1) spanning from 5 to 20 projects and (2) spanning from 5 to 50 projects. Table 2 presents the outcomes of the processing time comparison for problem sizes ranging from 5 to 20 projects, visually represented in Figure 6 and Figure 7. Additionally, Figure 8 illustrates the comparison for problem sizes ranging from 5 to 50 projects.

Table 2.
Average processing time in seconds.
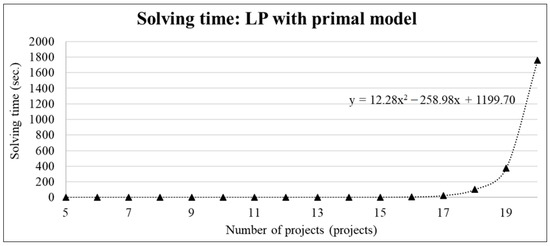
Figure 6.
Solving time of LP with primal model for 5–20 projects.
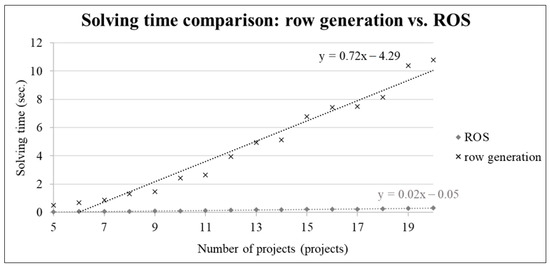
Figure 7.
Solving time comparison between row generation and ROS method for 5–20 projects.
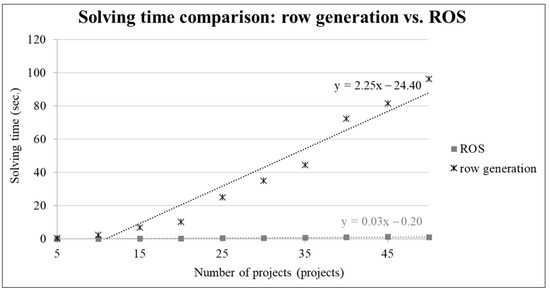
Figure 8.
Solving time comparison between row generation and ROS method for 5–50 projects.
Table 2 demonstrates the superiority of the linear programming primal model over alternative methods in speed for problem sizes from 5 to 9 projects. For larger sizes (11 projects or more), the ROS method outperforms the linear programming model. Furthermore, a comparison with the row generation method consistently shows that the ROS method provides faster performance, attributed to the efficiency of sorting algorithms in identifying optimal solutions from sortable values. Figure 6 and Figure 7 visually illustrate the processing time and problem size relationships, indicating an exponential increase for the primal model in linear programming with problem size, while both row generation and ROS methods exhibit linear correlations, particularly noticeable for smaller problem sizes (N < 17 for row generation or N < 9 for ROS, as indicated in Table 2).
The advantage of employing the primal model in linear programming is evident for smaller problem sizes due to its smaller matrix structure and the need for only a single computation cycle, unlike the row generation method requiring multiple rounds (R rounds) and more time. However, for larger sizes, such as 20 projects, the primal model’s matrix dimensions can become impractically large, making it less time-efficient. In contrast, the row generation and ROS methods, despite requiring multiple rounds, often prove faster due to their more compact problem matrices. The ROS method, in particular, exhibits a less steep slope in processing time compared to the row generation method. Figure 8 confirms the consistent linear relationship between processing time and problem size for both row generation and ROS methods at 50 projects, with the ROS method displaying a less pronounced slope. Additional experiments were performed to clarify the relationship between processing time and problem size for these methods. Furthermore, a comparative analysis of solutions derived from linear programming with the primal model and the ROS method underscores the markedly smaller matrix size produced by the row generation approach, detailed in Section 8.
The row generation and ROS methods developed in this study rely on a unique structure defined by Equations (1) to (5). Their applicability is limited to problems strictly adhering to these assumptions, rendering them ineffective for deviations from the specified structure. This specificity extends to the experimental design, requiring even randomly generated examples to align with predetermined assumptions. In contrast, the linear programming approach remains adaptable to solution-finding within the scope of a linear model, regardless of structural changes in the problem.
8. Comparative Analysis: Solving Solutions Utilizing the Primal Model and ROS Method
This section illustrates a comparative example between solutions obtained through linear programming with the primal model and the ROS method. The focus is on assessing solution equivalence and exploring the extent of matrix size differences between the two approaches. The hypothetical scenario involves a company with eight projects, each having a distinct return on investment, as detailed in Table 3. Specific investment conditions, including upper and lower limits as a percentage of the total investment, are outlined in Table 4. Additionally, individual project investment constraints are specified as a percentage of the total investment in Table 5. With a total investment budget of USD 4,000,000, the objective is to determine the optimal investment pattern maximizing profit under the given conditions.

Table 3.
Individual project earnings in dollars.

Table 4.
Investment limit based on the number of projects.

Table 5.
Individual project investment limit.
8.1. Demonstration of Problem Solving with the Primal Model
The given problem statement transforms into the primal model with the following mathematical representation:
subject to
Solving the matrix size of for the primal model using linear programming and applying the results to the investment scenario yields an USD 86.2 million return (Z = 21.55), representing the solution to this example problem as detailed in Table 6.

Table 6.
Results obtained through the application of the primal model-solving approach.
8.2. Demonstration of Problem Solving with the ROS Method
Applying the ROS method for problem solving involves structuring the example problem into a mathematical model with Equations (1), (4) and (5), as follows:
subject to
The established mathematical model reveals a smaller initial problem size with a matrix dimension of , which is significantly smaller than the primal model. This smaller size leads to faster computation when solving with linear programming, as demonstrated in Table 7. Substituting obtained solutions into facilitates the calculation of and . By arranging in descending order (, , , , , , , ), the solution pattern for maximizing the value of (2 ≤ k ≤ N − 1) is presented in Table 8. Choosing the pattern from with the highest value, we convert it into Equation (6) and incorporate it into the initial model. Before proceeding, it’s crucial to identify the solution pattern for minimizing . Arranging values in ascending order yields the sequence , , , , , , , , with the resulting pattern displayed in Table 9.

Table 7.
Results of .

Table 8.
Results of and .

Table 9.
Results of and .
Based on Table 9 solutions, we apply solution pattern from , featuring the lowest value. Integrating this value into Equation (7) and incorporating it into the initial model, we derive Equations (6) and (7) during the solution process for and . These equations are added to the original model, resulting in the articulated updated model. Following the revised mathematical model, the solution is derived using the process outlined in Figure 4 until completion, with summarized results and matrix sizes in each round r presented in Table 10. The updated model is as follows:
subject to

Table 10.
The results and the size of the matrix in each round r.
Table 10 illustrates the completion of nine rounds, with incremental conditions added in each round for solution derivation. In the final round, the problem structure had a matrix size of , significantly smaller than the primal model’s . Despite the smaller size, the outcome, with Z = 21.55, yields an identical profit of USD 86.2 million as obtained using the primal model. These results demonstrate that employing the ROS method leads to a more compact problem structure, facilitating faster solution processing in each round r. However, for scenarios with fewer investment projects, the cumulative rounds in the ROS method may result in longer processing times than the primal model. Conversely, in scenarios with a larger number of projects, the primal model’s significantly larger matrix size makes the ROS method comparatively faster due to its smaller matrix size in each round, as evident from the experiments shown in Section 7.2.
9. Conclusions
The budget allocation problem addressed in this study is a matrix-structured problem that becomes increasingly complex as the number of projects (N) increases. The traditional linear programming approach faces significant challenges due to the exponential growth of constraints, making it computationally expensive and impractical for larger problem sizes. To overcome this issue, the study proposes a novel solution using the principles of row generation and sorting methods. The row generation technique incrementally adds constraints to the problem, eliminating the need to include all constraints upfront. This approach reduces complexity and improves computational efficiency. Additionally, the binary programming method traditionally used to create constraints is replaced with the sorting method, which proves to be faster and less complex for generating subproblems.
The experimental results demonstrate that the row-generation hybrid sorting method significantly decreases computation time compared to linear programming. For instance, when N = 20 with 2,097,150 constraints, the linear programming method takes an average computation time of 1757.13 s, while the row generation hybrid sorting method only requires 0.30 s. Even when the problem size increases to N = 50 with 2,251,799,813,685,250 constraints, the row generation hybrid sorting method is completed in just 1.4 s, while linear programming fails to find a solution due to problem scales.
Comparisons among the three methods, including linear programming with the primal model, row generation, and the ROS method, reveal valuable insights. Linear programming excels for smaller problem sizes but becomes inefficient for larger ones. The ROS method consistently demonstrates faster processing times compared to both linear programming and the row generation method. This efficiency can be attributed to the inherent advantages of sorting algorithms in finding optimal solutions among sorted values. The relationship between processing time and problem size is visualized in Figure 5 and Figure 6, indicating that linear programming exhibits a polynomial regression, while the row generation and ROS methods exhibit linear regressions. The ROS method shows a lower slope than the row generation method, signifying superior efficiency in scaling with increasing problem sizes.
In summary, the results underscore the considerable time consumption associated with linear programming for larger problem sizes. Conversely, the row generation hybrid sorting method and the ROS method maintain a linear relationship with problem size, providing more efficient solutions. These insights offer a comparative understanding of method performance concerning problem size and processing time, offering guidance for addressing similar matrix-structured problems, such as the capital budgeting problem studied in this research. Utilizing the row generation and ROS methods introduced here requires exclusive applicability to problems adhering to mathematical structures outlined by Equations (1) to (5). Adapting these methods to analogous structures with different conditions or variables mandates a thorough study of the modified structure for appropriate adjustments. However, it is crucial to emphasize that, even with a comprehensive investigation of the problem’s structure, there is no guarantee of consistently successful adaptations of the row generation and ROS methods.
10. Further Research
Given Equations (3) and (4), the careful assignment of values to Uk and Lk is crucial to avoid infeasible solutions. To address the potential for infeasibility, a two-stage LP (stochastic linear programming) approach can be employed, which helps mitigate the risk of constraint infeasibility. This involves introducing two types of variables into Equations (3) and (4): corrective action variables and opportunity cost variables. However, it is important to note that incorporating these variables may significantly increase the model’s complexity, resulting in a substantial growth in the number of variables to for each variable type, thereby leading to an LP model with an exceedingly large number of constraints and variables. This aspect opens avenues for future research and investigation.
Author Contributions
Conceptualization, A.W., S.J. and P.C.; methodology, A.W. and P.C.; software, A.W.; validation, A.W., S.J. and P.C.; formal analysis, A.W. and P.C.; investigation, A.W. and S.J.; resources, A.W.; data curation, A.W. and S.J.; writing—original draft preparation, A.W. and S.J.; writing—review and editing, A.W., S.J. and P.C.; visualization, A.W. and S.J.; supervision, P.C.; project administration, A.W. and S.J.; funding acquisition, A.W. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to express our sincere appreciations to all constructive comments and recommendations from anonymous reviewers leading to the improved final version of this manuscript. This study was supported by the Faculty of Engineering, University of Phayao, Thailand, and the Faculty of Engineering at Kamphaeng Saen, Kasetsart University, Thailand.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, C.; Lahrichi, N.; Matta, A. Optimal budget allocation policy for tabu search in stochastic simulation optimization. Comput. Oper. Res. 2023, 150, 106046. [Google Scholar] [CrossRef]
- Yannakakis, M. Expressing combinatorial optimization problems by linear programs. J. Comput. Syst. Sci. 1991, 43, 441–466. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Miller, M.H. Application of linear programming to financial budgeting and the costing of funds. J. Bus. 1959, 32, 20–46. [Google Scholar] [CrossRef]
- Norris, W.T. Application of linear programming to financial budgeting and the costing of funds. Eng. Econ. 1960, 5, 55–56. [Google Scholar]
- Candler, W.; Boehlje, M. Use of linear programming in capital budgeting with multiple goals. Am. J. Agric. Econ. 1971, 53, 325–330. [Google Scholar] [CrossRef]
- Benders, J.F. Partitioning procedures for solving mixed-variables programming problems. Numer. Math. 1962, 4, 238–252. [Google Scholar] [CrossRef]
- Kalra, M.; Tyagi, S.; Kumar, V.; Kaur, M.; Mashwani, W.K.; Shah, H.; Shah, K. A comprehensive review on scatter search: Techniques, applications, and challenges. Math. Probl. Eng. 2021, 2021, 5588486. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: London, UK, 2009; pp. 5–15. [Google Scholar]
- Weingartner, H.M. Mathematical Programming and the Analysis of Capital Budgeting Problems, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1963; pp. 139–157. [Google Scholar]
- Unger, V.E. Capital budgeting and mixed zero-one integer programming. AIIE Trans. 1970, 2, 28–36. [Google Scholar] [CrossRef]
- Unger, V.E. Duality results for discrete capital budgeting models. Eng. Econ. 1974, 19, 237–251. [Google Scholar] [CrossRef]
- Hummeltenberg, W. Capital budgeting with benders decomposition. Eur. J. Oper. Res. 1985, 21, 318–329. [Google Scholar] [CrossRef]
- Zak, E.J. Row and column generation technique for a multistage cutting stock problem. Comput. Oper. Res. 2002, 29, 1143–1156. [Google Scholar] [CrossRef]
- Muter, I.; Birbil, S.I.; Bülbül, K. Benders decomposition and column-and-row generation for solving large-scale linear programs with column-dependent-rows. Eur. J. Oper. Res. 2018, 264, 29–45. [Google Scholar] [CrossRef]
- Muter, I.; Sezer, Z. Algorithms for the one-dimensional two-stage cutting stock problem. Eur. J. Oper. Res. 2018, 271, 20–32. [Google Scholar] [CrossRef]
- Witthayapraphakorn, A.; Thavorn, E.; Tippayasak, R.; Charnsethikul, P. Row generation technique to solve the problems of capital budgeting allocation under combinatorial constraints. TJOR 2018, 6, 10–21. [Google Scholar]
- Fard, M.K.; Ljubić, I.; Papier, F. Budgeting in international humanitarian organizations. Manuf. Serv. Oper. Manag. 2021, 24, 1261–1885. [Google Scholar]
- Qorbani, M.; Amraee, T. Long term transmission expansion planning to improve power system resilience against cascading outages. Electr. Power Syst. Res. 2022, 192, 106972. [Google Scholar] [CrossRef]
- Han, J.; Zhang, J.; Zeng, B.; Mao, M. Optimizing dynamic facility location-allocation for agricultural machinery maintenance using Benders decomposition. Omega 2021, 105, 102498. [Google Scholar] [CrossRef]
- Karamyar, F.; Sadeghi, J.; Yazdi, M.M. A Benders decomposition for the location-allocation and scheduling model in a healthcare system regarding robust optimization. Neural. Comput. Appl. 2018, 29, 873–886. [Google Scholar] [CrossRef]
- Shabaz, M.; Kumar, A. SA sorting: A novel sorting technique for large-scale data, Discrete. J. Comput. Netw. Commun. 2019, 2019, 3027578. [Google Scholar] [CrossRef]
- Wang, H.; Alidaee, B. A new hybrid-heuristic for large-scale combinatorial optimization: A case of quadratic assignment problem. Comput. Ind. Eng. 2023, 179, 109220. [Google Scholar] [CrossRef]
- Song, Y.B.; Mu, H.B. Large-scale storage/retrieval requests sorting algorithm for multi-I/O depots automated storage/retrieval systems. Discret. Dyn. Nat. Soc. 2021, 2021, 6646180. [Google Scholar] [CrossRef]
- Weiner, J.; Ernst, A.T.; Li, X.; Sun, Y. Ranking constraint relaxations for mixed integer programs using a machine learning approach. EURO J. Comput. Optim. 2023, 11, 100061. [Google Scholar] [CrossRef]
- Fischetti, M.; Ljubić, I.; Sinnl, M. Benders decomposition without separability: A computational study for capacitated facility location problems. Eur. J. Oper. Res. 2016, 253, 557–569. [Google Scholar] [CrossRef]
- Maher, S.J. Enhancing large neighbourhood search heuristics for Benders’ decomposition. J. Heuristics 2021, 27, 615–648. [Google Scholar] [CrossRef]
- Costa, A.M.; Gendron, B. Accelerating Benders decomposition with heuristic master problem solutions. Pesqui. Operacional. 2012, 32, 3–20. [Google Scholar] [CrossRef]
- Mahéo, A.; Rossit, D.G.; Kilby, P. A Benders decomposition approach for an integrated bin allocation and vehicle routing problem in municipal waste management. Eur. J. Oper. Res. 2021, 1408, 3–18. [Google Scholar]
- Oliveira, F.A.; de Sá, E.M.; de Souza, S.R. Benders decomposition applied to profit maximizing hub location problem with incomplete hub network. Comput. Oper. Res. 2022, 142, 105715. [Google Scholar] [CrossRef]
- Sangkhasuk, R.; Vivithkeyoonvong, T.; Phuangchampee, B.; Anurak, S.; Leartsiriphesaj, S.; Charnsethikul, P. Capital budgeting problem with combinatorial allocation constraints by column generation method. TJOR 2020, 8, 37–48. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).