Wind Farm Cable Connection Layout Optimization Using a Genetic Algorithm and Integer Linear Programming
Abstract
:1. Introduction
2. Electrical Power Grid Modeling
3. Methodology
3.1. Genetic Algorithms
| Algorithm 1: Genetic Algorithm |
 |
3.2. Integer Linear Programming
4. Substation Selection and Cable Layout
4.1. Substation Assignment Algorithm
4.2. Cable Connection Layout Model
5. Results and Discussion of the Case Studies
5.1. Alto da Coutada Wind Farm
5.2. WF-S3 Wind Farm
5.3. WF-S4 Wind Farm
5.4. Alto Minho Wind Farm
5.5. Genetic Algorithm versus Clustering Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMST | Capacitated Minimum Spanning Tree |
| GA | genetic algorithm |
| ILP | integer linear programming |
| MILP | mixed-integer linear programming |
| WF | wind farm |
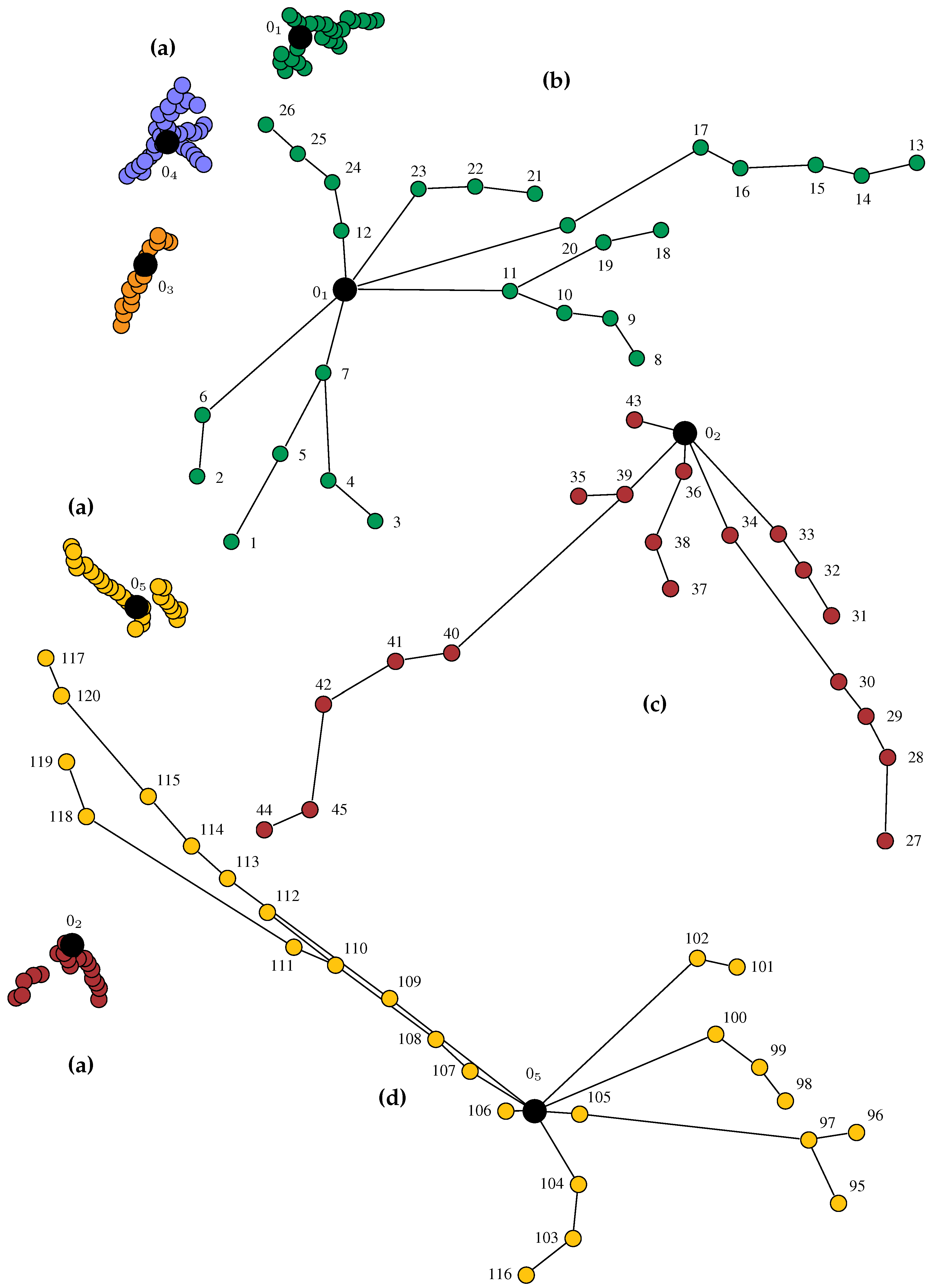
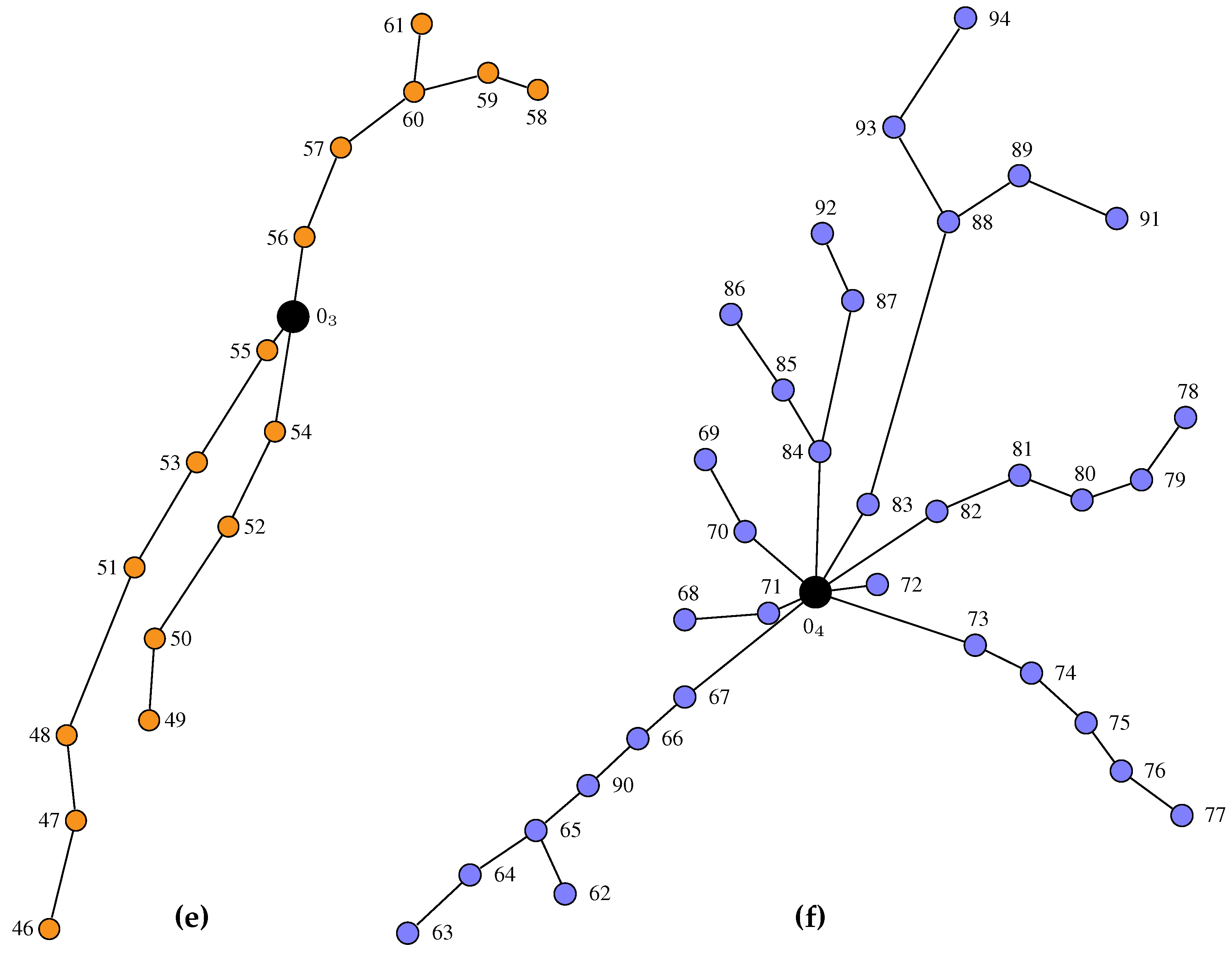
Appendix A. Wind Farm Coordinates
| No. | Latitude | Longitude | No. | Latitude | Longitude | No. | Latitude | Longitude |
|---|---|---|---|---|---|---|---|---|
| 1000.0 | 1000.0 | 24 | 187.5 | 2225.0 | 50 | 3800.0 | 1000.0 | |
| 1687.5 | 3187.5 | 25 | 1375.0 | 2225.0 | 51 | 3000.0 | 1812.0 | |
| 2875.0 | 1625.0 | 26 | 1800.0 | 2225.0 | 52 | 3375.0 | 1812.0 | |
| 1 | 187.5 | 187.5 | 27 | 1800.0 | 2600.0 | 53 | 3375.0 | 2225.0 |
| 2 | 187.5 | 600.0 | 28 | 1375.0 | 3000.0 | 54 | 3375.0 | 2600.0 |
| 3 | 600.0 | 600.0 | 29 | 1000.0 | 3000.0 | 55 | 3800.0 | 2600.0 |
| 4 | 600.0 | 187.5 | 30 | 600.0 | 3000.0 | 56 | 3800.0 | 187.5 |
| 5 | 1000.0 | 187.5 | 31 | 187.5 | 3000.0 | 57 | 3800.0 | 1410.0 |
| 6 | 1000.0 | 600.0 | 32 | 187.5 | 3410.0 | 58 | 3800.0 | 3000.0 |
| 7 | 1375.0 | 1000.0 | 33 | 1375.0 | 3410.0 | 59 | 3375.0 | 3000.0 |
| 8 | 1375.0 | 600.0 | 34 | 1000.0 | 3410.0 | 60 | 3000.0 | 2225.0 |
| 9 | 1800.0 | 600.0 | 35 | 1375.0 | 3812.0 | 61 | 3000.0 | 2600.0 |
| 10 | 1800.0 | 187.5 | 36 | 1000.0 | 3812.0 | 62 | 3000.0 | 1410.0 |
| 11 | 2600.0 | 187.5 | 37 | 600.0 | 3812.0 | 63 | 3000.0 | 1000.0 |
| 12 | 2187.5 | 600.0 | 38 | 1800.0 | 3410.0 | 64 | 3000.0 | 600.0 |
| 13 | 2187.5 | 1000.0 | 39 | 1800.0 | 3812.0 | 65 | 3375.0 | 600.0 |
| 14 | 1800.0 | 1000.0 | 40 | 2187.5 | 3812.0 | 66 | 3375.0 | 187.5 |
| 15 | 1800.0 | 1410.0 | 41 | 2187.5 | 3410.0 | 67 | 2600.0 | 2225.0 |
| 16 | 1800.0 | 1812.0 | 42 | 2187.5 | 3000.0 | 68 | 2187.5 | 2225.0 |
| 17 | 1375.0 | 1812.0 | 43 | 2187.5 | 2600.0 | 69 | 2187.5 | 1812.0 |
| 18 | 1000.0 | 2225.0 | 44 | 2600.0 | 3000.0 | 70 | 2600.0 | 1410.0 |
| 19 | 600.0 | 1410.0 | 45 | 3000.0 | 3000.0 | 71 | 2187.5 | 1410.0 |
| 20 | 187.5 | 1000.0 | 46 | 3000.0 | 3410.0 | 72 | 2600.0 | 1000.0 |
| 21 | 600.0 | 1812.0 | 47 | 3000.0 | 3812.0 | 73 | 2600.0 | 600.0 |
| 22 | 187.5 | 1410.0 | 48 | 3375.0 | 3410.0 | 74 | 2600.0 | 1812.0 |
| 23 | 187.5 | 1812.0 | 49 | 3800.0 | 3812.0 |
| No. | Latitude | Longitude | No. | Latitude | Longitude | No. | Latitude | Longitude |
|---|---|---|---|---|---|---|---|---|
| 5985 | 0 | 25 | 10,080 | 1260 | 53 | 8820 | 3780 | |
| 5985 | 5670 | 26 | 0 | 1890 | 54 | 9450 | 3780 | |
| 0 | 2835 | 27 | 630 | 1890 | 55 | 630 | 4410 | |
| 11,970 | 2835 | 28 | 1260 | 1890 | 56 | 2520 | 4410 | |
| 1 | 0 | 05 | 29 | 1890 | 1890 | 57 | 3150 | 4410 |
| 2 | 1890 | 0 0 | 30 | 2520 | 1890 | 58 | 3780 | 4410 |
| 3 | 3150 | 0 0 | 31 | 3150 | 1890 | 59 | 4410 | 4410 |
| 4 | 4410 | 0 5 | 32 | 3780 | 1890 | 60 | 5040 | 4410 |
| 5 | 5670 | 0 5 | 33 | 4410 | 1890 | 61 | 5670 | 4410 |
| 6 | 6930 | 0 0 | 34 | 8190 | 1890 | 62 | 8190 | 4410 |
| 7 | 8190 | 0 | 35 | 8820 | 1890 | 63 | 10,080 | 4410 |
| 8 | 9450 | 0 0 | 36 | 9450 | 1890 | 64 | 11,340 | 4410 |
| 9 | 10,080 | 0 0 | 37 | 10,080 | 1890 | 65 | 0 | 5040 |
| 10 | 11,340 | 0 5 | 38 | 2520 | 2520 | 66 | 630 | 5040 |
| 11 | 1890 | 630 5 | 39 | 3150 | 2520 | 67 | 1260 | 5040 |
| 12 | 2520 | 630 0 | 40 | 5670 | 2520 | 68 | 5040 | 5040 |
| 13 | 3150 | 630 | 41 | 11,340 | 2520 | 69 | 5670 | 5040 |
| 14 | 5040 | 630 | 42 | 1260 | 3150 | 70 | 6930 | 5040 |
| 15 | 6930 | 630 | 43 | 1890 | 3150 | 71 | 7560 | 5040 |
| 16 | 8190 | 630 | 44 | 5040 | 3150 | 72 | 8820 | 5040 |
| 17 | 9450 | 630 | 45 | 7560 | 3150 | 73 | 9450 | 5040 |
| 18 | 10,080 | 630 | 46 | 8190 | 3150 | 74 | 10,710 | 5040 |
| 19 | 10,710 | 630 | 47 | 10,080 | 3150 | 75 | 0 | 5670 |
| 20 | 11,970 | 630 | 48 | 10,710 | 3150 | 76 | 1260 | 5670 |
| 21 | 0 | 1260 | 49 | 1260 | 3780 | 77 | 4410 | 5670 |
| 22 | 3150 | 1260 | 50 | 3780 | 3780 | 78 | 10,080 | 5670 |
| 23 | 6930 | 1260 | 51 | 5040 | 3780 | 79 | 11,340 | 5670 |
| 24 | 7560 | 1260 | 52 | 6300 | 3780 |
| No. | Latitude | Longitude | No. | Latitude | Longitude | No. | Latitude | Longitude |
|---|---|---|---|---|---|---|---|---|
| 42.06812000 | −8.20812000 | 38 | 41.9795820 | −8.55953200 | 80 | 42.0275590 | −8.24460800 | |
| 41.98118500 | −8.55398750 | 39 | 41.9781410 | −8.55709100 | 81 | 42.0252110 | −8.24368200 | |
| 42.00911250 | −8.29478600 | 40 | 41.9693360 | −8.56515400 | 82 | 42.0220860 | −8.24504800 | |
| 42.01750000 | −8.24810000 | 41 | 41.9664830 | −8.56558400 | 83 | 42.0194900 | −8.24478800 | |
| 42.00574800 | −8.42527700 | 42 | 41.9628160 | −8.56775600 | 84 | 42.0176670 | −8.24278100 | |
| 1 | 42.06234500 | −8.22093000 | 43 | 41.9786220 | −8.55331000 | 85 | 42.0162820 | −8.24046600 |
| 2 | 42.06061100 | −8.21760300 | 44 | 41.9598050 | −8.57412400 | 86 | 42.0143180 | −8.23761500 |
| 3 | 42.06966000 | −8.21988600 | 45 | 41.9621250 | −8.57310700 | 87 | 42.0189080 | −8.23708900 |
| 4 | 42.06727800 | −8.21781200 | 46 | 41.9999080 | −8.31788900 | 88 | 42.0225180 | −8.23411100 |
| 5 | 42.06482800 | −8.21646400 | 47 | 42.0009200 | −8.31379700 | 89 | 42.0251990 | −8.23237600 |
| 6 | 42.06087800 | −8.21449400 | 48 | 42.0005580 | −8.31057700 | 90 | 42.0089230 | −8.25538300 |
| 7 | 42.06702400 | −8.21233900 | 49 | 42.0036710 | −8.31001200 | 91 | 42.0288660 | −8.23399900 |
| 8 | 42.08295100 | −8.21161000 | 50 | 42.0038960 | −8.30693100 | 92 | 42.0177650 | −8.23455500 |
| 9 | 42.08160400 | −8.20957200 | 51 | 42.0031320 | −8.30424600 | 93 | 42.0204670 | −8.23054900 |
| 10 | 42.07927000 | −8.20931100 | 52 | 42.0066620 | −8.30269800 | 94 | 42.0231690 | −8.22642100 |
| 11 | 42.07651500 | −8.20818400 | 53 | 42.0054850 | −8.30027200 | 95 | 42.0211900 | −8.42995600 |
| 12 | 42.06792900 | −8.20512400 | 54 | 42.0084240 | −8.29911700 | 96 | 42.0221080 | −8.42636000 |
| 13 | 42.09718500 | −8.20167500 | 55 | 42.0081260 | −8.29605300 | 97 | 42.0196790 | −8.42674400 |
| 14 | 42.09437000 | −8.20232700 | 56 | 42.0095310 | −8.29178600 | 98 | 42.0184890 | −8.42476200 |
| 15 | 42.09203400 | −8.20177600 | 57 | 42.0109160 | −8.28841400 | 99 | 42.0171740 | −8.42304700 |
| 16 | 42.08821600 | −8.20194500 | 58 | 42.0183410 | −8.28622900 | 100 | 42.0149590 | −8.42136400 |
| 17 | 42.08619100 | −8.20089400 | 59 | 42.0164640 | −8.28558600 | 101 | 42.0160320 | −8.41794900 |
| 18 | 42.08417600 | −8.20509100 | 60 | 42.0136670 | −8.28629400 | 102 | 42.0140210 | −8.41750800 |
| 19 | 42.08125300 | −8.20571900 | 61 | 42.0139670 | −8.28374200 | 103 | 42.0077070 | −8.43174300 |
| 20 | 42.07943700 | −8.20484700 | 62 | 42.0080580 | −8.25947500 | 104 | 42.0079810 | −8.42899900 |
| 21 | 42.07777800 | −8.20324800 | 63 | 42.0021230 | −8.26095700 | 105 | 42.0080450 | −8.42543600 |
| 22 | 42.07474000 | −8.20288700 | 64 | 42.0044680 | −8.25875600 | 106 | 42.0042880 | −8.42527700 |
| 23 | 42.07185900 | −8.20300800 | 65 | 42.0069610 | −8.25708500 | 107 | 42.0024680 | −8.42325200 |
| 24 | 42.06747100 | −8.20266400 | 66 | 42.0108030 | −8.25362200 | 108 | 42.0007390 | −8.42163800 |
| 25 | 42.06572200 | −8.20121100 | 67 | 42.0125670 | −8.25204400 | 109 | 41.9983780 | −8.41955800 |
| 26 | 42.06410900 | −8.19974500 | 68 | 42.0125660 | −8.24913300 | 110 | 41.9956310 | −8.41785700 |
| 27 | 41.99135700 | −8.57469800 | 69 | 42.0133550 | −8.24308600 | 111 | 41.9935100 | −8.41694600 |
| 28 | 41.99148500 | −8.57044800 | 70 | 42.0148410 | −8.24581000 | 112 | 41.9921770 | −8.41517200 |
| 29 | 41.99038800 | −8.56836700 | 71 | 42.0157250 | −8.24887900 | 113 | 41.9901420 | −8.41345200 |
| 30 | 41.98899400 | −8.56661400 | 72 | 42.0198430 | −8.24780400 | 114 | 41.9883050 | −8.41180300 |
| 31 | 41.98863900 | −8.56326000 | 73 | 42.0235240 | −8.25009200 | 115 | 41.9861220 | −8.40928800 |
| 32 | 41.98721600 | −8.56094000 | 74 | 42.0256560 | −8.25114200 | 116 | 42.0053200 | −8.43361200 |
| 33 | 41.98593000 | −8.55911400 | 75 | 42.0277040 | −8.25301400 | 117 | 41.9809160 | −8.40226200 |
| 34 | 41.98348100 | −8.55917900 | 76 | 42.0290400 | −8.25483500 | 118 | 41.9829660 | −8.41030700 |
| 35 | 41.97579100 | −8.55719200 | 77 | 42.0313290 | −8.25651100 | 119 | 41.9819610 | −8.40752800 |
| 36 | 41.98112700 | −8.55592400 | 78 | 42.0314560 | −8.24149400 | 120 | 41.9817090 | −8.40417400 |
| 37 | 41.98044700 | −8.56189100 | 79 | 42.0298050 | −8.24384500 |
References
- Kabouris, J.; Kanellos, F.D. Impacts of Large-Scale Wind Penetration on Designing and Operation of Electric Power Systems. IEEE Trans. Sustain. Energy 2010, 1, 107–114. [Google Scholar] [CrossRef]
- British Petroleum. BP Statical Review of World Energy 2019; Technical Report; British Petroleum: London, UK, 2019. [Google Scholar]
- Cerveira, A.; Baptista, J.; Solteiro Pires, E.J. Wind farm distribution network optimization. Integr.-Comput.-Aided Eng. 2016, 23, 69–79. [Google Scholar] [CrossRef]
- Cerveira, A.; de Sousa, A.; Solteiro Pires, E.J.; Baptista, J. Optimal Cable Design of Wind Farms: The Infrastructure and Losses Cost Minimization Case. IEEE Trans. Power Syst. 2016, 31, 4319–4329. [Google Scholar] [CrossRef]
- Wędzik, A.; Siewierski, T.; Szypowski, M. A new method for simultaneous optimizing of wind farm’s network layout and cable cross-sections by MILP optimization. Appl. Energy 2016, 182, 525–538. [Google Scholar] [CrossRef]
- Hertz, A.; Marcotte, O.; Mdimagh, A.; Carreau, M.; Welt, F. Optimizing the Design of a Wind Farm Collection Network. INFOR Inf. Syst. Oper. Res. 2012, 50, 95–104. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. On the Impact of using Mixed Integer Programming Techniques on Real-world Offshore Wind Parks. In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems, Porto, Portugal, 23–25 February 2017; pp. 108–118. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. Mixed Integer Linear Programming for new trends in wind farm cable routing. Electron. Notes Discret. Math. 2018, 64, 115–124. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Han, R.; Wang, T. Minimizing Energy Loss by Coupling Optimization of Connection Topology and Cable Cross-Section in Offshore Wind Farm. Appl. Sci. 2019, 9, 3722. [Google Scholar] [CrossRef]
- Žarković, S.D.; Shayesteh, E.; Hilber, P. Onshore wind farm—Reliability centered cable routing. Electr. Power Syst. Res. 2021, 196, 107201. [Google Scholar] [CrossRef]
- Cerveira, A.; Baptista, J.; Pires, E.J.S. Optimization design in wind farm distribution network. In Proceedings of the International Joint Conference SOCO’13-CISIS’13-ICEUTE’13, Salamanca, Spain, 11–13 September 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 109–119. [Google Scholar]
- Chen, Z.; Zhao, M.; Blaabjerg, F. Optimisation of electrical system for offshore wind farms via genetic algorithm. IET Renew. Power Gener. 2009, 3, 205–216. [Google Scholar] [CrossRef]
- Baptista, J.; Solteiro Pires, E.J.; Cerveira, A. Wind Farm Distribution Network Optimization Based in a Hierarchical GA. In Proceedings of the ISAP2013—Seventeenth International Conference on Intelligent System Applications to Power Systems, Tokyo, Japan, 1–4 July 2013; p. 6. [Google Scholar]
- Chen, Y.; Li, H.; Jin, K.; Song, Q. Wind farm layout optimization using genetic algorithm with different hub height wind turbines. Energy Convers. Manag. 2013, 70, 56–65. [Google Scholar] [CrossRef]
- Veeramachaneni, K.; Wagner, M.; O’Reilly, U.M.; Neumann, F. Optimizing energy output and layout costs for large wind farms using particle swarm optimization. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation (CEC), Brisbane, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Hou, P.; Hu, W.; Chen, Z. Optimisation for offshore wind farm cable connection layout using adaptive particle swarm optimisation minimum spanning tree method. IET Renew. Power Gener. 2016, 10, 694–702. [Google Scholar] [CrossRef]
- Qi, Y.; Hou, P.; Yang, L.; Yang, G. Simultaneous Optimisation of Cable Connection Schemes and Capacity for Offshore Wind Farms via a Modified Bat Algorithm. Appl. Sci. 2019, 9, 265. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. Optimizing wind farm cable routing considering power losses. Eur. J. Oper. Res. 2018, 270, 917–930. [Google Scholar] [CrossRef]
- Cerveira, A.; Pires, E.J.S.; Baptista, J. Wind farm cable connection layout optimization with several substations. Energies 2021, 14, 3615. [Google Scholar] [CrossRef]
- Srikakulapu, R.; U, V. Optimized design of collector topology for offshore wind farm based on ant colony optimization with multiple travelling salesman problem. J. Mod. Power Syst. Clean Energy 2018, 6, 1181–1192. [Google Scholar] [CrossRef]
- Zuo, T.; Zhang, Y.; Meng, K.; Tong, Z.; Dong, Z.Y.; Fu, Y. Collector System Topology Design for Offshore Wind Farm’s Repowering and Expansion. IEEE Trans. Sustain. Energy 2021, 12, 847–859. [Google Scholar] [CrossRef]
- Dutta, S.; Overbye, T.J. A clustering based wind farm collector system cable layout design. In Proceedings of the 2011 IEEE Power and Energy Conference at Illinois, Champaign, IL, USA, 25–26 February 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y. Collection line optimisation in wind farms using improved ant colony optimisation. Wind Eng. 2021, 45, 589–600. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Wang, T.; Han, R. An optimization method based on random fork tree coding for the electrical networks of offshore wind farms. Renew. Energy 2020, 147, 1340–1351. [Google Scholar] [CrossRef]
- Pillai, A.; Chick, J.; Johanning, L.; Khorasanchi, M.; de Laleu, V. Offshore wind farm electrical cable layout optimization. Eng. Optim. 2015, 47, 1689–1708. [Google Scholar] [CrossRef]
- Chen, T.; Chen, M.; Hwang, K.; Kotas, P.; Chebli, E.A. Distribution system power flow analysis-a rigid approach. IEEE Trans. Power Deliv. 1991, 6, 1146–1152. [Google Scholar] [CrossRef]
- Das, D.; Nagi, H.S.; Kothari, D.P. Novel method for solving radial distribution networks. IEE Proc.—Gener. Transm. Distrib. 1994, 141, 291–298. [Google Scholar] [CrossRef]
- Moon, Y.-H.; Choi, B.K.; Cho, B.-H.; Kim, S.-H.; Ha, B.-N.; Lee, J.-H. Fast and reliable distribution system load flow algorithm based on the Y/sub BUS/ formulation. In Proceedings of the 1999 IEEE Power Engineering Society Summer Meeting. Conference Proceedings (Cat. No.99CH36364), Edmonton, AL, Canada, 18–22 July 1999; Volume 1, pp. 238–242. [Google Scholar]
- Gómez Expósito, A.; Romero Ramos, E. Reliable load flow technique for radial distribution networks. IEEE Trans. Power Syst. 1999, 14, 1063–1069. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F.F. Optimal sizing of capacitors placed on a radial distribution system. IEEE Trans. Power Deliv. 1989, 4, 735–743. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Holland, J.H. An Adaptation in Natural and Artificial Systems: An Introduction Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Pires, E.S.; Machado, J.T. A trajectory planner for manipulators using genetic algorithms. In Proceedings of the 1999 IEEE International Symposium on Assembly and Task Planning (ISATP’99) (Cat. No. 99TH8470), Porto, Portugal, 21–24 July 1999; pp. 163–168. [Google Scholar]
- Lu, F.; Bi, H.; Huang, M.; Duan, S. Simulated annealing genetic algorithm based schedule risk management of IT outsourcing project. Math. Probl. Eng. 2017, 2017, 6916575. [Google Scholar] [CrossRef]
- Leitao, S.; Pires, E.S.; de Moura Oliveira, P. Road tunnels lighting using genetic algorithms. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009; pp. 1–6. [Google Scholar]
- Wolsey, L. Integer Programming; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison–Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Gouveia, L. A 2n Constraint Formulation for the Capacitated Minimal Spanning Tree Problem. Oper. Res. 1995, 43, 130–141. [Google Scholar] [CrossRef]
- Nemhauser, G.; Wolsey, L. Integer and Combinatorial Optimization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Pricope, R.; Neagu, B. Optimal Reconfiguration of a Wind Farm Power Distribution Network. Bul. Inst. Politeh. Iasi 2015, LXI (LXV), 91–101. [Google Scholar]

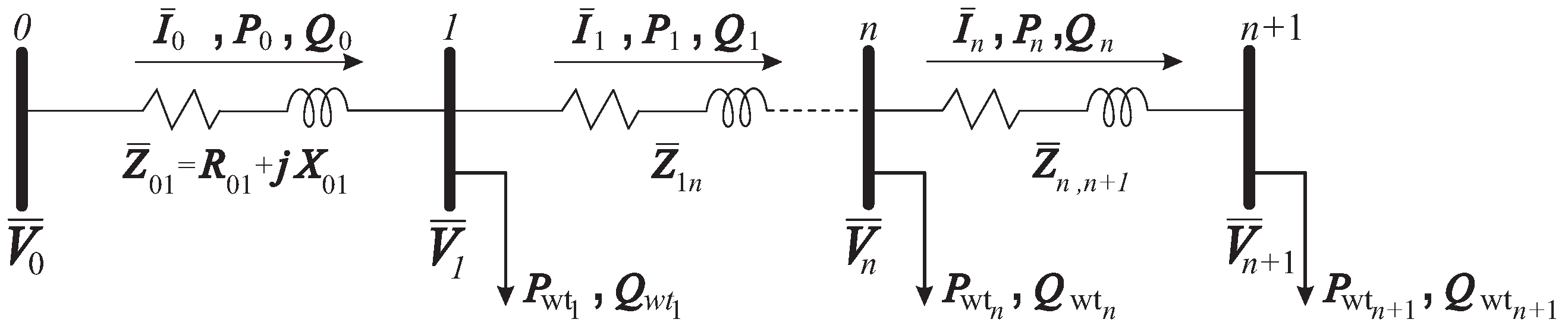






| Type k | Section (mm2) | Inductance L (mH/km) | Electrical Resistance R (Ω/km) | Max. Current Iz (A) | Price (EUR/m) |
|---|---|---|---|---|---|
| 1 | 50 | 0.62 | 0.6410 | 169 | 6.80 |
| 2 | 70 | 0.59 | 0.4430 | 207 | 7.12 |
| 3 | 95 | 0.57 | 0.3200 | 247 | 7.98 |
| 4 | 120 | 0.55 | 0.2530 | 281 | 8.70 |
| 5 | 150 | 0.54 | 0.2060 | 313 | 12.77 |
| 6 | 185 | 0.53 | 0.1640 | 354 | 13.23 |
| 7 | 240 | 0.50 | 0.1250 | 408 | 14.89 |
| 8 | 300 | 0.49 | 0.1000 | 458 | 17.50 |
| 9 | 400 | 0.47 | 0.0778 | 519 | 21.09 |
| 10 | 500 | 0.46 | 0.0605 | 585 | 23.77 |
| Parameter | Value |
|---|---|
| Chromosome length, l | Number of turbines |
| Selection | Tournament of two |
| Crossover probability, | |
| Mutation probability, | |
| Population | 100 |
| Generations | 500 |
| Wind Field | k | Links | #Links | Cost (EUR) |
|---|---|---|---|---|
| 0 | 3 | (, 3), (, 4), (2, 1), (10, 11), (14, 15) | 5 | = 1,239,980.2 |
| 4 | (0, 2), (9, 10), (13, 14) | 3 | = 690,802.4 | |
| = 15 | 7 | (8, 9), (12, 13) | 2 | = 298,316.2 |
| 8 | (5, 8), (7, 12) | 2 | = 250,861.6 | |
| 10 | (, 5), (, 6), (6, 7) | 3 | ||
| 0 | 3 | (17, 16), (21, 19), (22, 23), (25, 26), (29, 30), (32, 31), (35, 34), (45, 44), (50, 48), (50, 49) | 10 | = 3,555,950.5 |
| 4 | (18, 17), (21, 22), (24, 25), (28, 29), (33, 32), (46, 45) | 6 | = 1,944,381.7 | |
| = 35 | 7 | (, 50), (20, 18), (27, 28), (35, 33), (41, 24), (47, 46) | 6 | = 852,218.4 |
| 8 | (, 47), (36, 21), (37, 20), (40, 41), (43, 27) | 5 | = 759,350.4 | |
| 10 | (, 35), (, 37), (, 38), (, 39), (, 42), (38, 36), (39, 40), (42, 43) | 8 | ||
| 4,795,930.7 |
| Wind Field | k | Links | #Links | Cost (EUR) |
|---|---|---|---|---|
| 0 | 3 | (, 17), (, 20), (3, 1), (3, 2), (3, 4), (6, 5), (7, 14), (8, 9), (8, 10), (19, 21), (19, 22), (23, 24) | 12 | = 658,709.8 |
| 4 | (, 6), (, 7), (19, 23) | 3 | = 463,373.1 | |
| 7 | (0, 8) | 1 | = 126,267.6 | |
| 8 | (0, 3) | 1 | = 69,069.1 | |
| 10 | (0, 19) | 1 | ||
| 0 | 3 | (25, 18), (27, 26), (30, 31), (33, 35), (34, 32), (36, 37), (38, 39), (38, 40), (42, 43), (44, 45), (46, 47), (48, 49) | 12 | = 1,036,720.6 |
| 4 | (, 25), (, 27), (29, 30), (33, 34), (33, 36), (42, 44), (46, 48) | 7 | = 663,759.7 | |
| 7 | (0, 38), (28, 29) | 2 | = 234,065.8 | |
| 8 | (00, 28), (, 42), (41, 46) | 3 | = 138,895.2 | |
| 10 | (0, 33), (0, 41) | 2 | ||
| 0 | 3 | (13, 12), (51, 52), (54, 59), (55, 58), (57, 50), (60, 61), (63, 64), (65, 56), (65, 66), (67, 68), (69, 16), (71, 15), (73, 11) | 13 | = 1,142,690.6 |
| 4 | (0, 57), (0, 67), (53, 55), (60, 54), (62, 63), (70, 13), (70, 71), (72, 73), (74, 69) | 9 | = 741,715.7 | |
| 7 | (0, 72), (0, 74), (51, 53), (62, 65) | 4 | = 261,035.2 | |
| 8 | (, 60) | 1 | = 139,939.7 | |
| 10 | (0, 51), (0, 62), (0, 70) | 3 | ||
| f = 2,838,121.1 |
| Wind Field | k | Links | #Links | Cost (EUR) |
|---|---|---|---|---|
| 0 | 3 | (4, 3), (7, 16), (13, 22), (14, 33), (15, 24), (33, 32) | 6 | = 1,217,848.1 |
| 4 | (4, 13), (15, 25), (24, 34) | 3 | = 771,301.4 | |
| = 15 | 7 | (, 14), (6, 7) | 2 | = 289,847.9 |
| 8 | (5, 8), (7, 12) | 2 | = 156,698.7 | |
| 10 | (, 6), (, 15), (5, 4) | 3 | ||
| 0 | 3 | (, 77), (44, 40), (45, 46), (51, 44), (59, 50), (59, 58), (70, 71) | 7 | = 1,760,766.6 |
| 4 | (52, 45), (58, 57), (60, 51), (68, 59) | 4 | = 1,089,737.5 | |
| = 20 | 7 | (69, 60) | 1 | = 392,414.2 |
| 8 | (69, 60), (71, 62) | 2 | = 278,614.9 | |
| 10 | (, 52), (, 68), (, 69), (, 70) | 4 | ||
| 0 | 3 | (, 65), (11, 2), (11, 12), (29, 30), (30, 31), (43, 38) | 6 | = 2,080,631.6 |
| 4 | (21, 1), (28, 29), (42, 43) | 3 | = 1,297,036.9 | |
| = 23 | 7 | (, 26), (, 55), (26, 21), (27, 11), (38, 39) | 5 | = 501,304.0 |
| 8 | (, 27), (, 28), (, 42), (, 49) | 4 | = 282,290.6 | |
| 0 | 3 | (9, 8), (18, 17), (20, 10), (36, 35), (48, 47), (48, 63) | 6 | = 2,099,821.7 |
| 4 | (, 20), (19, 9), (37, 25), (41, 37), (54, 53) | 5 | = 1,297,584.1 | |
| = 21 | 7 | (37, 36), (47, 54) | 2 | = 466,272.4 |
| 8 | (, 41), (, 64) | 2 | = 335,965.2 | |
| 10 | (, 19), (, 48), (19, 18) | 3 | ||
| 7,159,067.8 |
| Wind Field | k | Links | #Links | Cost (EUR) |
|---|---|---|---|---|
| 0 | 3 | (4, 3), (5, 1), (6, 2), (9, 8), (15, 14), (17, 13), (19, 18), (22, 21), (25, 26) | 9 | = 1,255,170.4 |
| = 26 | 4 | (0, 6), (7, 4), (7, 5), (10, 9), (16, 15), (20, 17), (20, 19), (23, 22), (24, 25) | 9 | = 715,716.4 |
| 7 | (0, 16), (0, 23), (11, 10), (12, 24) | 4 | = 296,430.9 | |
| 8 | (0, 11), (0, 12) | 2 | = 243,023.2 | |
| 10 | (0, 7), (0, 20) | 2 | ||
| 0 | 3 | (0, 43), (28, 27), (32, 31), (38, 37), (39, 35), (45, 44) | 6 | = 873,066.6 |
| 4 | (29, 28), (33, 32), (36, 38), (42, 45) | 4 | = 503,792.0 | |
| = 19 | 7 | (0, 33), (0, 36), (30, 29), (41, 42) | 4 | =201,297.4 |
| 8 | (34, 30), (40, 41) | 2 | = 167,977.2 | |
| 10 | (0, 34), (0, 39), (39, 40) | 3 | ||
| 0 | 3 | (47, 46), (50, 49), (59, 58), (60, 61) | 4 | = 595,478.1 |
| 4 | (48, 47), (52, 50), (60, 59) | 3 | ||
| = 16 | 7 | (51, 48), (54, 52) | 2 | = 346,205.8 |
| 8 | (0, 54), (53, 51), (57, 60) | 3 | = 139,633.1 | |
| 10 | (0, 55), (0, 56), (55, 53), (56, 57) | 4 | = 109,639.2 | |
| 0 | 3 | (0, 72), (64, 63), (65, 62), (70, 69), (71, 68), (76, 77), (79, 78), (85, 86), (87, 92), (89, 91), (93, 94) | 11 | = 1,304,863.9 |
| =38 | 4 | (0, 70), (0, 71), (65, 64), (75, 76), (80, 79), (84, 85), (84, 87), (88, 89), (88, 93), (74, 75), (81, 80), (73, 74), (82, 81), (90, 65) | 14 | = 758,211.4 |
| 7 | (74, 75), (81, 80) | 2 | = 305,002.4 | |
| 8 | (73, 74), (82, 81), (90, 65) | 3 | = 241,650.1 | |
| 10 | (0, 67), (0, 73), (0, 82), (0, 83), (0, 84),(66, 90), (67, 66), (83, 88) | 8 | ||
| 0 | 3 | (0, 106), (97, 95), (97, 96), (99, 98), (102, 101), (103, 116), (110, 112), (118, 119), (120, 117) | 9 | = 1,411,230.2 |
| 4 | (0, 102), (100, 99), (104, 103), (111, 118), (115, 120) | 5 | = 807,677.4 | |
| = 26 | 7 | (0, 100), (0, 104), (105, 97), (110, 111), (114, 115) | 5 | = 336,226.6 |
| 8 | (0, 105), (113, 114) | 2 | = 267,326.1 | |
| 10 | (0, 107), (0, 109), (107, 108), (108, 110), (109, 113) | 5 | ||
| 5,439,809.2 |
| Alto da Coutada | WF-S3 | WF-S4 | Alto Minho | |
|---|---|---|---|---|
| GA (costs) | 4,795,930.7 | 2,838,121.1 | 7,159,067.9 | 5,439,809.2 |
| Minimum | 29 | 091 | 135 | 185 |
| Maximum | 56 | 137 | 326 | 466 |
| Median | 39 | 096 | 171 | 265 |
| Mean | 40.7 | 103.2 | 195.8 | 303.6 |
| Standard deviation | 13.5 | 019.1 | 076.7 | 124.4 |
| Clustering (costs) | 4,800,839.0 | 2,839,945.3 | 7,170,952.2 | 5,439,809.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pires, E.J.S.; Cerveira, A.; Baptista, J. Wind Farm Cable Connection Layout Optimization Using a Genetic Algorithm and Integer Linear Programming. Computation 2023, 11, 241. https://doi.org/10.3390/computation11120241
Pires EJS, Cerveira A, Baptista J. Wind Farm Cable Connection Layout Optimization Using a Genetic Algorithm and Integer Linear Programming. Computation. 2023; 11(12):241. https://doi.org/10.3390/computation11120241
Chicago/Turabian StylePires, Eduardo J. Solteiro, Adelaide Cerveira, and José Baptista. 2023. "Wind Farm Cable Connection Layout Optimization Using a Genetic Algorithm and Integer Linear Programming" Computation 11, no. 12: 241. https://doi.org/10.3390/computation11120241
APA StylePires, E. J. S., Cerveira, A., & Baptista, J. (2023). Wind Farm Cable Connection Layout Optimization Using a Genetic Algorithm and Integer Linear Programming. Computation, 11(12), 241. https://doi.org/10.3390/computation11120241








