Abstract
Temporal knowledge graphs (TKGs) are crucial for modeling evolving real-world facts and are widely applied in event forecasting and risk analysis. However, current TKG reasoning models struggle to separate causal signals from noisy observations, align temporal dynamics with semantic structures, and integrate long-term and short-term knowledge effectively. To address these challenges, we propose the Temporal Causal Contrast Graph Network (TCCGN), a unified framework that disentangles causal features from noise via orthogonal decomposition and adversarial learning; applies dual-domain contrastive learning to enhance both temporal and semantic consistency; and introduces a gated fusion module for adaptive integration of static and dynamic features across time scales. Extensive experiments on five benchmarks (ICEWS14/05-15/18, YAGO, GDELT) show that TCCGN consistently outperforms prior models. On ICEWS14, it achieves 42.46% MRR and 31.63% Hits@1, surpassing RE-GCN by 1.21 points. On the high-noise GDELT dataset, it improves MRR by 1.0%. These results highlight TCCGN’s robustness and its promise for real-world temporal reasoning tasks involving fine-grained causal inference under noisy conditions.
1. Introduction
Knowledge graphs (KGs) have been widely used to represent structured knowledge and play an important role in tasks such as recommendation systems and semantic search [1,2,3]. However, the static characteristics of traditional knowledge graphs limit their ability to model dynamic relationships and cannot adapt to time-sensitive tasks (such as event prediction and supply chain risk management). Temporal Knowledge Graphs (TKGs) introduce the time dimension and model facts that evolve over time in the form of quadruples , which can effectively capture the dynamic changes of entity relationships [4,5]
At present, Temporal Knowledge Graph Reasoning is mainly divided into two types of methods: interpolation and extrapolation. Interpolation models (e.g., TA-DistMult [6], TTransE [7], HyTE [8]) are used to fill in missing facts within the observed time range. Extrapolation models (e.g., Know-Evolve [2], DyRep [9], RE-NET [10]) predict unknown facts in the future by analyzing time series patterns.
Although extrapolation models are crucial in applications such as financial forecasting and supply chain risk assessment [3,11], existing methods still face the following three core challenges:
Noisy Confounder Interference: In actual TKG data, causal features (such as Tesla’s R&D progress driving product releases) and confounding factors (such as supply chain disruptions causing Model Q delays) are often intertwined, making the model sensitive to noise. For example, RE-GCN’s MRR dropped by 12.3% on the GDELT dataset, indicating that its generalization ability is weak in high-noise scenarios [12].
Temporal–Semantic Misalignment: Existing methods either focus on temporal consistency (e.g., RE-NET [10] processes temporal patterns through RNN) or optimize semantic alignment (e.g., CyGNet [13] focuses on entity–relation similarity), but few methods can optimize both at the same time, resulting in unstable performance in multi-task reasoning (e.g., predicting entities and relations simultaneously).
Static–Dynamic Feature Imbalance: Static knowledge graphs provide structured prior information (as shown in Figure 1, where Tesla’s long-term product roadmap reflects static strategy), while dynamic features reflect temporal evolution patterns (such as short-term supply chain fluctuations). This figure illustrates the interplay between consistent long-term strategies and unpredictable short-term variations—emphasizing the need for TKG models that can balance static structure with temporal dynamics to make robust future predictions. However, TGformer [14] only uses static information and fails to effectively model the multi-scale dependencies between long-term trends and short-term dynamics, limiting its reasoning capabilities.
Figure 1.
Tesla’s product timeline as a temporal knowledge graph, showing the interplay of static trends and temporal dynamics for future reasoning.
Despite recent progress, existing TKG reasoning models suffer from three critical limitations that hinder their performance in real-world, noisy, and temporally complex environments: they lack explicit mechanisms for disentangling causal signals from noise; they treat temporal consistency and semantic alignment as separate optimization objectives; and they fail to effectively fuse static and dynamic knowledge across different temporal scales.
To the best of our knowledge, no prior work has addressed all these limitations in a unified framework. This gap motivates the development of TCCGN—a novel model that integrates causal–noise decoupling, semantic–temporal alignment, and static–dynamic fusion into a cohesive architecture for robust temporal reasoning.
1.1. Addressing Key Challenges
While CH-TKG [15] improves temporal consistency via local–global attention and contrastive objectives, it lacks an explicit causal–noise disentanglement mechanism, omits static structural priors in its temporal encoder, and treats temporal–semantic alignment and static–dynamic fusion as separate stages. To overcome these limitations, we propose the Temporal Causal Comparative Graph Network (TCCGN), which:
- Employs orthogonal causal–noise decoupling with dynamic adversarial suppression to robustly filter out confounding noise;
- Integrates a gated static–dynamic fusion module to balance long-term structural priors and short-term temporal patterns;
- Leverages dual-domain contrastive learning to jointly align time-step consistency and entity–relation semantics.
This unified framework enables TCCGN to robustly handle high-noise scenarios and capture multi-scale dependencies beyond the capabilities of prior methods.
To illustrate TCCGN’s effectiveness, Table 1 compares it with representative baselines in terms of noise robustness (GDELT-MRR), temporal–semantic alignment (ICEWS14 Hits@1), and static–dynamic fusion efficiency (YAGO Epoch Time). Note that relative epoch times are measured on the YAGO dataset using the same hardware, with TCCGN set as the baseline (1.00×); lower values indicate faster per-epoch training.

Table 1.
Performance comparison on representative benchmarks (higher better for MRR/Hits@1; lower better for YAGO epoch time).
Compared to existing methods such as RE-GCN, CH-TKG, and CyGNet, the proposed TCCGN offers a novel integration of causal–noise decoupling, semantic–temporal alignment, and static–dynamic feature fusion within a unified framework. Unlike previous works that address these challenges separately, none of the existing methods provide a unified solution that jointly optimizes causal–noise disentanglement, semantic–temporal alignment, and static–dynamic fusion. TCCGN is the first to integrate all three into an end-to-end framework. This multi-perspective integration enables the model to maintain high performance even in complex, noisy, or long-span temporal knowledge graph scenarios, marking a significant advancement over prior approaches.
1.2. Research Objectives and Questions
This study aims to develop a robust and generalizable temporal reasoning model for dynamic knowledge graphs, with the following key objectives:
- To design a causal–noise disentanglement mechanism that effectively separates essential causal signals from irrelevant or misleading temporal noise;
- To enhance the alignment between temporal evolution and semantic structure using dual-domain contrastive learning;
- To develop a gated fusion strategy that adaptively balances static structural priors with dynamic temporal features.
Based on these objectives, this paper seeks to address the following research questions:
- How can causal and noise features be effectively separated in temporal knowledge embeddings?
- Can dual-domain contrastive learning improve both temporal consistency and semantic alignment?
- What is the optimal way to integrate static and dynamic information for multi-scale reasoning?
1.3. In General, This Paper Makes the Following Contributions:
- A causal decoupled temporal reasoning framework is proposed: based on orthogonal decomposition and adversarial training, causal features are separated from mixed noise, thereby improving the generalization ability of the model and maintaining stable performance in a high-noise environment.
- Construction of a dual-domain contrastive learning mechanism: simultaneously optimizing time-step consistency and entity-relationship semantic alignment, effectively improving the accuracy of low-frequency event prediction, and enabling the model to have stronger cross-time-step reasoning capabilities.
- A static–dynamic fusion strategy is proposed: through an adaptive gating mechanism, global structural knowledge and local temporal patterns are combined to achieve a dynamic balance of information across time scales and improve the modeling capabilities of long-term trends and short-term evolution.
- Experiments verify the superiority of TCCGN: it surpasses existing methods on multiple benchmark datasets (ICEWS14/05-15/18, YAGO, GDELT), especially showing stronger robustness in high-noise environments and complex reasoning tasks, providing a new solution for temporal knowledge graph reasoning.
The remainder of this paper is organized as follows. Section 2 reviews the related work on temporal knowledge graph reasoning, including methods based on causal modeling and contrastive learning. Section 3 introduces the proposed TCCGN model in detail, focusing on its three core components: causal–noise decoupling, dual-domain contrastive learning, and gated static–dynamic fusion. Section 4 presents the experimental setup, benchmark datasets, evaluation results, as well as ablation studies and qualitative analysis to further validate the model’s effectiveness. Finally, Section 5 summarizes the findings and discusses future research directions.
2. Related Work
With the increasing demand for dynamic inference in real-world scenarios, temporal knowledge graph reasoning has emerged as a critical research area. Challenges in this domain often arise from four intertwined aspects: temporal irregularity, semantic drift, noisy interference, and the imbalance between static and dynamic signals. Numerous methods have been proposed from diverse perspectives—including temporal modeling, semantic alignment, causal reasoning, and information fusion. However, most existing works address only a subset of these challenges, often lacking a unified strategy that simultaneously ensures robustness, temporal–semantic consistency, and multi-scale adaptability. This section provides a comprehensive review of prior research across five key themes, each corresponding to a major dimension in TKG reasoning.
2.1. Transformer-Based Temporal Modeling
Transformer architectures, with their self-attention mechanisms, excel at modeling long-range dependencies in temporal graphs. ECEformer [16] encodes evolutionary chains using a standard Transformer encoder and a hybrid contextual reasoning module, achieving superior results on six benchmarks. Graph Hawkes Transformer (GHT) integrates Hawkes processes into multi-head self-attention to capture event self-excitation and historical subgraph context, improving extrapolation robustness [17]. DA-Net [18] employs distributed attention to adaptively focus on sparse historical facts, enhancing predictions for low-frequency events. SimRe [19] further combines soft logical rules with Transformer fine-tuning in a contrastive framework, jointly optimizing semantic constraints and temporal patterns. Earlier methods such as HyTE [8] and TTransE [7] introduced time hyperplanes and time-aware embeddings into Transformer variants, but did not explicitly handle noise or static–dynamic fusion. Recently, SiMFy [20] demonstrates that even a simple MLP model with fixed-frequency temporal encodings can achieve competitive performance, challenging the necessity of overly complex architectures in certain dynamic reasoning contexts.
However, most Transformer-based approaches do not explicitly address noise suppression or static–dynamic fusion, limiting their robustness in real-world temporal reasoning tasks.
Building on the modeling foundations above, recent research has also explored how to enhance semantic alignment across time through contrastive learning.
2.2. Contrastive Learning for Temporal–Semantic Alignment
Contrastive learning methods have evolved to strengthen representation discriminability and semantic alignment over time. CENET [21] uses entity contrastive loss to optimize local structure but overlooks relational semantics. AMCEN [22] designs historical/non-historical attention masks combined with local–global message passing contrast to mitigate event imbalance issues. CLDG [23] proposes temporal translation invariance sampling for dynamic graphs, maximizing consistency between local and global views to outperform various unsupervised and semi-supervised methods. ChapTER [24] applies prefix-tuning in frozen pre-trained language models to inject virtual time prefixes for lightweight contrast estimation, surpassing baselines with minimal parameter updates. PPT [25] adopts a prompt-based approach over pre-trained transformers, injecting temporal signals through learned query prompts and enabling flexible temporal KG completion with minimal architectural modifications. Complementing these designs, CH-TKG [26] introduces a history-aware contrastive learning framework that fuses local and global temporal contexts via cross-time-step objectives, effectively enhancing noise robustness in complex temporal reasoning scenarios.
Nevertheless, these methods primarily focus on either temporal consistency or semantic contrast, lacking unified optimization of both dimensions.
Beyond semantic alignment, another line of research focuses on coping with real-world noise and uncovering reliable causal signals for stable reasoning.
2.3. Noise Suppression and Causal Decoupling
In real-world TKGs, causal signals (e.g., “research drives innovation”) and confounding noise (e.g., “supply chain disruptions”) are frequently entangled, making robust reasoning particularly challenging. To mitigate such interference, RE-GCN [12] and CyGNet [13] enhance temporal representations via graph neural networks and historical backtracking. However, these methods lack explicit mechanisms for disentangling causal and non-causal information. Tuck-ERTNT [27] applies tensor decomposition to improve robustness under noise, but struggles with complex temporal dynamics. ST-ConvKB [28] enhances spatiotemporal features via convolution but ignores causal semantics. CauSeRL [29] introduces causal attention for signal extraction, yet remains sensitive to dynamic noise fluctuations.
Existing models struggle to separate true causal signals from fluctuating observational noise. To address this, we propose an independent component analysis–inspired decoupling mechanism:
which produces orthogonal causal and noise-specific embeddings, enabling cleaner supervision for downstream reasoning tasks.
In addition to filtering noise, reasoning systems must also model how semantic knowledge evolves over time.
2.4. Temporal–Semantic Collaborative Modeling
While many methods capture local temporal changes, few explicitly enforce global causal consistency across time. In our framework, the temporal modeling module focuses on maintaining smooth evolution of causal features by leveraging a time-step consistency loss:
where denotes the hidden state of the causal GRU at time t, computed as . The input is the causal projection of defined in Equation (1). This design ensures that only the noise-free causal signal is passed into the temporal reasoning module. The consistency loss thus encourages temporal stability of the underlying causal process while ignoring short-term noise interference. Without this restriction, direct modeling on or mixed features would entangle noise with dynamics, reducing robustness.
While interpolation/extrapolation models capture temporal evolution, they often transfer semantics inadequately across time steps. Even with self-attention-based semantic propagation (e.g., Transformer variants applied to neighbor message passing), alignment remains weak. Contrastive methods like SimRe and CH-TKG (above) partially address this, but multi-scale semantic alignment is still underexplored.
To address this, we introduce an auxiliary semantic alignment loss to encourage cross-domain consistency between subject–entity and relation semantics:
where and are the projected embeddings of the subject entity and relation at time t, respectively. Specifically, is computed as the final fused embedding for the subject entity, and is the relation representation obtained via a shared embedding lookup. This loss does not operate on the decoupled spaces individually, but on their fused representation, as relation semantics may require both stable (causal) and variable (contextual) information. The contrastive form enforces that entities align closely with their relations in embedding space, which improves link prediction under sparse or low-frequency events.
Together, and form a dual-objective design: the former preserves causal smoothness across time, while the latter preserves semantic fidelity across domains. These components are jointly optimized with the decoupling module in an end-to-end fashion, reinforcing temporal–semantic coherence.
2.5. Static–Dynamic Information Fusion
Static embeddings offer a stable global context (e.g., “a company’s long-term strategy”), whereas dynamic features capture transient patterns (e.g., “short-term disruptions”). Effective temporal reasoning requires adaptive integration of both. Prior works offer partial solutions: DyERNIE [30] employs Riemannian fusion for geometric consistency, but incurs high computational overhead. TANGO [31] leverages neural ODEs for continuous-time modeling, though it is less effective for discrete event graphs. TGformer [14] emphasizes static priors, while TeMP [32] applies temporally weighted GNNs to reduce sparsity, albeit at the cost of semantic granularity.
Our model introduces an adaptive time-gated fusion strategy:
which learns to balance static embeddings and dynamic representations at each time step. This allows the model to unify stable structural priors with evolving temporal context at low computational cost.
In summary, prior studies have made meaningful progress on isolated fronts—temporal modeling, semantic alignment, noise filtering, and static–dynamic fusion. However, their fragmented nature often limits performance in complex environments. In contrast, our proposed TCCGN framework is, to the best of our knowledge, the first to jointly address temporal modeling, semantic alignment, causal disentanglement, and static–dynamic fusion within a cohesive architecture. This enables robust, interpretable, and scalable temporal knowledge graph reasoning across diverse real-world conditions.
3. The Proposed Model: TCCGN
To tackle the challenges of noisy interference, semantic–temporal misalignment, and static–dynamic imbalance in temporal knowledge graphs, we propose a unified reasoning framework: TCCGN. As illustrated in Figure 2, the model is composed of three tightly coupled modules:
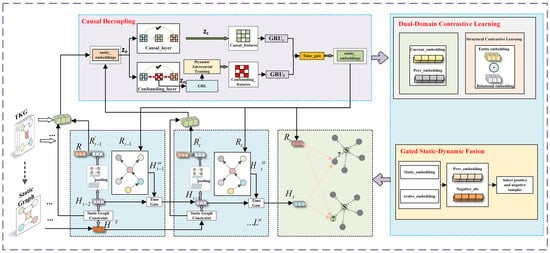
Figure 2.
An illustrative diagram of the proposed TCCGN model. The CD component represents the causal decoupling module. The DDCL component represents the dual-domain contrastive learning module. The GSDF represents the gated static–dynamic fusion module.
- Causal Decoupling Module (CD): isolates causal signals from noisy observations using orthogonal projection and adversarial training, thereby improving robustness under high-noise conditions.
- Dual-Domain Contrastive Learning Module (DDCL): aligns temporal consistency and semantic proximity by jointly optimizing time-step contrast and entity–relation alignment, enhancing low-frequency prediction accuracy.
- Gated Static–Dynamic Fusion Module (GSDF): adaptively balances long-term structural priors and short-term temporal dynamics to model multi-scale dependencies effectively.
These modules interact as follows: causal decoupling generates denoised embeddings, which are temporally propagated and jointly aligned via contrastive learning. Meanwhile, static graph features are fused with dynamic signals to produce context-aware entity representations. Together, the three modules ensure robustness, semantic–temporal alignment, and scalability across reasoning tasks. The key symbols used in our formalization and their descriptions are summarized in Table 2.

Table 2.
Key symbols and their descriptions.
3.1. Entity-Aware Component
3.1.1. Graph Convolutional GCN Network Structure
In order to model feature dependencies in concurrent facts, this paper uses graph convolutional networks (GCNs) [33] to capture the relationships between entities and relations in multi-relational graphs. Given a timestamp t, the subject entity information of the connection is aggregated through a message passing mechanism to calculate the embedding of the target entity o at the -layer. Its update rule is:
where and represent the embeddings of subject entity s and object entity o at the th layer and time t, respectively (here s is the subject in the fact triple and o is the object). is the set of all triples at time t, in the form of ; k is a normalization constant equal to the in-degree of entity o; is the learnable weight matrix of the corresponding relation r in the th layer, and is the self-loop weight matrix of the corresponding target entity o in the th layer; is the embedding of relation r at time t; is the ReLU activation function [34].
This update rule allows each entity to integrate relational signals from its temporal neighbors, while retaining a portion of its prior state through a residual self-loop. This improves stability and prevents over-smoothing in multi-hop propagation.
3.1.2. Adaptive Time Gate Network Structure
In order to dynamically adjust the information transmission and update of entities at different times, we introduce an adaptive time gate (AdaptGate) between the current hidden representation obtained by graph convolution and the hidden representation at the previous moment. Specifically, let
The “AdaptGate” contains an update gate , which is used to dynamically adjust the information fusion ratio according to the feature difference between the current moment and the historical moment, thereby alleviating the gradient disappearance and information fading problems in long time series dependencies. The specific formula is as follows:
where is the update gate output, which determines how much new information should be obtained from the graph convolution result at the current moment, and how much historical information should be retained; is the weight matrix of the update gate; is the corresponding bias vector; represents Sigmoid activation; the symbol ⊙ represents element-wise multiplication; is the entity representation matrix after update at time t.
Through the above design, the model can adaptively allocate the fusion ratio of historical information and current information according to the difference between and , so as to better capture the dynamic dependencies between adjacent moments and improve the robustness of the temporal embedding representation.
Intuitively, the gate decides whether to trust the current observation or fall back to the historical context, enabling the model to smoothly track evolving entity behavior over time.
3.2. Causal-Decoupled Temporal Reasoning Design
This section addresses the problems of causal drift and noise accumulation and builds a model from multiple levels including theoretical assumptions, causal decoupling, adversarial training, dual-gated timing modeling, and dynamic memory decay.
3.2.1. Theoretical Assumptions
Let be the causal subspace representation at time t, be the noise subspace representation, and
where represents the complete entity embedding vector at time t, and are its components in the causal subspace and noise subspace, respectively. Based on this, we introduce the following three theoretical assumptions to guide the subsequent noise–causal separation and dynamic memory decay design.
- Causal invariancewhere represents the prediction target at time , is the causal subspace representation at time t, is an orthogonal matrix (i.e., ), and is a causal mapping function. This assumption ensures that at different times, as long as the noise subspace is removed, the mapping relationship between the causal feature and the future prediction remains unchanged.This assumption implies that the essential cause–effect relationships are stable across time, even when external noise varies. It allows the model to focus on core predictive factors without being distracted by shifting noise.
- Noise separabilitywhere represents the noise subspace representation at time t, is the predicted target at time t, and the symbol “⊥” represents the conditional independence relationship, given the causal subspace . This hypothesis indicates that: given the causal feature , the noise feature is conditionally independent from the predicted target , which means that the "noise" component can be separated from the causal component, guiding the model to focus on the causal signal in the causal subspace.This means that once we know the causal part, the noise provides no further help for prediction. Therefore, the model can safely disregard it during reasoning.
- Time-varying interferencewhere represents the covariance operation, and are the noise subspace representations at time t and , respectively, k is the time interval, and is the decay coefficient. This hypothesis states that the degree of autocorrelation of noise features in time decays exponentially with the interval k. This feature inspires us to introduce a dynamic memory decay mechanism in the model, so that the earlier noise information gradually fades with time, avoiding excessive interference of historical noise on the current prediction.This reflects the intuition that recent noise is more relevant than distant noise, and motivates us to attenuate the influence of old, less correlated noise features.
Rationale for Causal–Noise Decomposition
Equation (1), , defines a linear projection of the entity embedding into two orthogonal subspaces. This design is heuristically inspired by Independent Component Analysis (ICA), but we do not enforce ICA’s full statistical requirements, such as minimizing mutual information or maximizing non-Gaussianity. Instead, we rely on three assumptions introduced above—causal invariance, noise separability, and temporal decay—to justify a soft linear decomposition.
From a geometric perspective, we assume that causal and noise signals lie in approximately orthogonal subspaces in the latent space. Thus, applying projection matrices and with soft orthogonality constraints enables separation of these components. Although this is not a strict ICA procedure, it captures the intuition that different functional factors may be recoverable by constrained projections.
Moreover, such linear decomposition strategies have proven effective in prior weakly supervised disentanglement tasks [35], including work on learning disentangled representations from statistical assumptions [36], and early perspectives on linear subspace learning for distributed representations [37].
In our model, and are trained under multiple constraints: (i) reconstruction loss of , (ii) orthogonality between and , (iii) spectral norm regularization, and (iv) adversarial suppression of predictive information in . These collectively help ensure that captures target-relevant causal signals while remains uninformative.
Importantly, and are not auxiliary—they are each modeled through distinct GRU encoders that capture their temporal trajectories. The causal GRU output is directly used in the time-step consistency loss (Equation (2)), which encourages temporal smoothness of causal features. By contrast, the semantic alignment loss (Equation (3)) operates on the fused embedding and is used to align entity–relation semantics globally, irrespective of causal decoupling.
3.2.2. Causal Decoupling Module
To separate the causal features from the noise features in the entity embedding , we define:
where are the projection matrices responsible for extracting the causal and noise components, respectively. Intuitively, this decomposition enables the model to treat causally meaningful signals and irrelevant noise as lying in separate subspaces, leading to cleaner and more robust reasoning.
To enforce this separation, we impose “reconstruction” and “orthogonality” soft constraints on the two projection matrices and define the following loss function:
where represents the embedding vector of the eth entity, and are the causal and noise projection matrices, respectively. The norms and represent the spectral and Frobenius norms, respectively. The inner product is the Frobenius inner product, defined as:
The hyperparameters control the strength of the “approximate orthogonality penalty” for , the “mutual orthogonality penalty” between and , and the “spectral norm upper bound” penalties for and , respectively. The parameter is a threshold that limits the spectral norm.
The first term ensures that the sum of and accurately reconstructs the original embedding. The second and third terms promote orthogonality between the causal and noise directions to prevent information leakage across subspaces. The last two terms serve to maintain the stability of the projection matrices during training, which is crucial in noisy environments and ensures that both components are sufficiently well behaved to improve robustness.
Through this loss, we combine the reconstruction error, ’s approximate orthogonality, the mutual orthogonality between and , and spectral norm regularization as soft penalties. This ensures that:
which enforces the desired decomposition, with the causal subspace having an approximately orthogonal property. By adjusting , we can balance between reconstruction accuracy and orthogonality in the final model.
Additionally, we require:
where , and controls the smoothness and numerical stability of the projection matrices.
In summary, the decoupling process ensures that the model isolates stable causal information from potentially spurious fluctuations. This is particularly important for reasoning under distribution shifts or noisy observations, where robust causal reasoning can prevent interference from irrelevant noise and improve model generalization.
3.2.3. Adversarial Training Mechanism
In order to suppress information in noise features that is irrelevant to the predicted target, we introduce adversarial training on the noise subspace. Specifically, the dynamic adversarial strength is defined as:
where t represents the current training step, T represents the total training step; is the adversarial strength base coefficient; this design is borrowed from the warm-up mechanism of the gradient reversal layer (GRL), which can smoothly adjust the adversarial strength from weak to strong. In adversarial training, we feed the noise feature into the discriminator through the gradient reversal layer, and define the adversarial loss as:
where is the noise feature extracted by the noise projection matrix ; represents the gradient reversal layer, which keeps the features unchanged during forward propagation, but reverses the gradient during back propagation to achieve adversarial; is the discriminator network, which attempts to distinguish whether the noise feature contains information related to the predicted target Y; the negative term is used to maximize the discriminator’s ability to deceive the noise feature, so that the noise feature does not carry target-related information; is the regularization term, which is used to prevent the noise feature from from becoming too large, resulting in numerical instability; is the regularization coefficient.
This adversarial training setup ensures that the noise features are gradually made uninformative for downstream tasks. The key principle here is to use adversarial training to force the discriminator to distinguish between noise-related features and target-related signals, enhancing the separation of causal and noise components.
By inputting into the discriminator and performing adversarial training, the noise features can be forced to not carry information related to the predicted target Y, thereby weakening their interference on downstream predictions.
3.2.4. Dual-Gate Timing Modeling
To capture the temporal evolution of causal features and noise features simultaneously, we use two sets of GRUs to recursively model them, respectively:
where represents the causal GRU module, is the causal hidden state at the previous time , is the causal projection feature at the current time t, and the output is the causal hidden state at time t.
where represents the noisy GRU module, is the noisy hidden state at the previous time , is the noise projection feature at the current time t, and the output is the noisy hidden state at time t.
This dual-GRU design stems from the theoretical assumption that causal and noise components evolve with different temporal dynamics. By modeling them separately, the causal GRU focuses on preserving long-term stable semantics, while the noise GRU captures transient perturbations. This structure prevents noise accumulation and helps retain consistent causal signals.
Next, the causal hidden state is concatenated with the noisy hidden state to calculate the gating weight:
where means concatenating the two in dimension, is the gating weight matrix, is the Sigmoid activation function, and the output is used for the subsequent dynamic weighted combination of the two types of time series representations.
The dual GRU structure mentioned above captures the temporal evolution of causal and noise features, respectively, and then dynamically weights them using the gating weight , which can further suppress the cumulative effect of historical noise in temporal propagation.
3.2.5. Dynamic Memory Decay
In order to make the historical causal information decay gradually over time, we designed a dynamic memory decay function:
where represents the time interval between the current moment and the historical moment, is the decay factor, and the two together determine the exponential decay rate; is the preset lower limit, which is used to ensure that is not lower than to prevent excessive decay; is the causal hidden state at time t; is the time decay weight matrix, is the Sigmoid activation function, represents the dynamic decay ratio vector calculated based on the current causal representation; “⊙” represents the element-by-element product, which is used to multiply the exponential decay factor by the dynamic decay ratio vector element-by-element; finally, is taken to ensure that .
This mechanism directly implements the time-varying interference hypothesis proposed in Section 3, which states that noise autocorrelation decays exponentially over time. By coupling exponential decay with a learned gating vector, our model adaptively filters stale information while preserving temporally relevant causal signals.
3.2.6. Joint Training Strategy
We weight the losses of each submodule and define the joint training objective as:
where is the prediction task loss, which can be cross-entropy (classification) or margin-based ranking loss (link prediction), used to measure the model’s prediction error for the target entity/relationship; is the adversarial loss, which uses the adversarial training objective defined in Formula (19) to suppress the interference of noise features on downstream predictions; is the gated regularization loss, which can be designed as a smoothing term or distribution constraint on , for example,
where is the gate weight in Formula (22), is the average or a prior distribution of the sequence; this term encourages the gate weight to maintain a certain smoothness during training; is the causal/noise reconstruction loss, defined as (14), which is used to separate causal features from noise features in entity embeddings; the hyperparameter controls the weight of the decoupling decomposition. If is large, causal–noise separation is emphasized more; otherwise, more emphasis is placed on prediction and adversarial tasks.
This multi-objective loss provides a principled way to encode all three theoretical assumptions—causal invariance, noise separability, and time-varying interference—into the optimization process. Each component of the loss is directly linked to a corresponding structural module, forming a coherent and interpretable training framework.
3.3. Model Learning and Joint Optimization Framework
In order to capture temporal dynamics and global semantic consistency at the same time, this paper proposes a hybrid optimization strategy that integrates dual-domain contrastive learning and static–dynamic feature joint modeling. The losses of each sub-module are unified and coordinated, so as to better characterize the complex interactive relationships in the knowledge graph. The overall framework is divided into two parts: a dual-domain contrastive learning module and a static–dynamic feature fusion module.
3.3.1. Dual-Domain Contrastive Learning Module
This module conducts comparative learning of embedding from both the temporal dimension and the semantic dimension to enhance temporal consistency and entity–relation alignment capabilities. It is divided into the following three parts:
- Time-step Contrastive LearningLet be the overall embedding vector at time t. We sample triples , where is an adjacent positive sample and is a non-adjacent negative sample (which can be randomly selected from the same entity at other times). Define the Euclidean distance:where is the margin, which controls the lower limit of the distance difference between positive and negative samples. The triple loss is constructed as follows:where encourages the distance between adjacent embeddings and to be as small as possible, and the distance between non-adjacent embeddings to be as large as possible. If multiple pairs of positive and negative samples are used, multiple can be randomly sampled for each as positive samples and as negative samples, and then all triplets are summed or maximized. Intuitively, this contrast enforces temporal smoothness—encouraging the model to learn embeddings that change gradually across neighboring time steps while remaining distinct from unrelated ones.
- Entity–Relationship AlignmentLet and be the entity embedding and relation embedding at time t, respectively. We measure their semantic alignment by cosine similarity:where represents the Euclidean norm. Common alignment losses can be taken as:Or we can use the “cross-entropy + hard negative sampling” form for optimization. To enhance the distinguishability of different relation types, we can also first project the entity embedding into the relation subspace (relation-aware projection), and then calculate the cosine similarity shown in Formula (28) to improve the semantic alignment effect. This encourages entities to reside close to the relations they participate in, helping the model distinguish interaction types more effectively in a semantically meaningful way.
- Adaptive Time GatingWe introduce a gating network similar to Section 3.2 to dynamically weight temporal embeddings:where is the entity embedding at time t, and are the gated weight matrix and bias, respectively, is the Sigmoid activation, and the output is used to dynamically weight the temporal embedding. This gating can also be used to provide positive and negative sample screening for triple sampling with temporal conditions; for example, when is large, it is preferentially paired with the adjacent to further strengthen the temporal consistency constraint. Such temporal gating acts like a soft focus mechanism, adaptively emphasizing moments that are more predictive for the current step.
- Joint goalsCombining the above three losses gives the total loss:The hyperparameters are used to balance the triple loss and entity–relation alignment loss. The specific values can be tuned on the validation set according to the dataset. This module aims to ensure the dynamic consistency of embeddings in the time dimension and achieve fine alignment of entities and relations in semantics. To this end, we design corresponding loss functions and update mechanisms from three aspects to gradually constrain temporal and semantic information:
3.3.2. Static–Dynamic Feature Fusion
This module aims to jointly model the global static information and local dynamic features of the entity, and further constrain the consistency between the two through contrast loss. It specifically includes the following parts:
- Static embedding extractionFor the ith entity, its static neighbor set is defined as:where is the edge set on the static knowledge graph (does not change over time), and represents the static relationship between entity i and entity j. Let be the number of static neighbors of entity i, then the static embedding of the ith entity is defined as:where is the static input embedding of the neighbor entity j; is the static transformation matrix corresponding to the relation ; is the ReLU activation function; the denominator is used to average normalize the neighbor messages.
- Dynamic embed generationLet denote the dynamic features at time t, which are generated by the local temporal encoder (GCN + time gate) described in Section 3.2 and reflect the behavioral evolution of the entity at different time steps.
- Weighted FusionTo adaptively fuse the static embedding and the dynamic embedding , we define the fusion weights and calculate the fusion feature: :where represents the static embedding of entity i (see Formula (33)); is the dynamic embedding corresponding to time t; are the fusion weight matrices of the static and dynamic features, respectively, is the bias vector; is the Sigmoid activation function, and the output represents the weighted ratio of static and dynamic information in different dimensions after fusion.Intuitively, this adaptive fusion allows the model to prioritize either stable attributes or time-sensitive patterns depending on the prediction context, enhancing flexibility and robustness.
- Fusion Contrastive LossIn order to further constrain the temporal consistency of static embedding and dynamic embedding, we construct the following fusion contrast loss:where is the margin, which controls the lower limit of the difference in the dynamic embedding distance between the target moment and the historical moment; is the dynamic embedding of the same entity i at other (historical) moments . Usually, corresponding to a historical time step can be randomly sampled as a negative sample; this contrast loss encourages the current dynamic embedding to be closer to the static embedding , while keeping a distance of at least from the historical dynamic embedding .This contrastive loss explicitly encourages the dynamic representation to remain semantically aligned with the stable identity of the entity, while avoiding being misled by outdated or irrelevant temporal signals.
- Total lossThe fusion contrast loss shares the same formulation as the time-step contrast and entity–relation alignment losses defined in Section 3.3.1. It is defined as:Then, the combined loss of this module and the whole is:where are hyperparameters used to balance the time contrast loss , entity–relation alignment loss , weight decay regularization term , and fusion contrast loss ; are the full embedding vectors of entity and relation, respectively, and the weight decay term prevents the model from overfitting; to avoid confusion with the joint loss we specifically note here:
Although the static attributes of entities (such as date of birth, ethnicity, etc.) remain unchanged over time, they have long-term effects on entity behavior and relationships between entities. To this end, this module jointly models global static information and local dynamic features, and uses adaptive gating to achieve an effective fusion of the two, thereby improving the model’s ability to capture the intrinsic characteristics and future trends of entities.
3.4. Score Functions for Different Tasks
Research has shown that graph convolutional networks (GCNs) using convolutional scoring functions have significant performance advantages in temporal knowledge graph reasoning tasks [38]. To capture the evolutionary characteristics of entities and relations implied in historical facts, the ConvTransE decoder is used in this study [12].
ConvTransE extends the classic TransE model by introducing 2D convolution over the joint embedding of entity and relation, enabling the decoder to capture more complex and nonlinear interactions between them. Compared with simpler decoders, this mechanism allows for richer expressive power, which is particularly beneficial in dynamic multi-relational contexts.
By modeling entities and relations through a decoder, the probability vectors of entities and relations can be obtained, which are as follows:
where is the Sigmoid function, are the embeddings of in and , respectively. , . The details of ConvTransE are omitted for brevity. Note that ConvTransE can be replaced by other score functions.
The use of ConvTransE also complements our encoder, which outputs context-aware embeddings integrating static–dynamic fusion, causal–noise disentanglement, and temporal gating. The rich interactions captured by ConvTransE allow the decoder to fully leverage these nuanced representations during prediction.
To adapt to different downstream tasks, we design the decoder input flexibly. For entity prediction (i.e., link prediction), we compute by scoring all candidate entities given or . For relation prediction, we compute by evaluating all candidate relations given . Thus, the decoder supports multiple temporal reasoning tasks under a unified framework.
In summary, this paper constructs a temporal knowledge graph reasoning model. This model captures the dynamic dependencies between entities in multi-relational graphs through a local temporal encoder, and uses adaptive time gating and time-step contrastive learning to strengthen the extraction of historical information; in the temporal reasoning module, based on the assumptions of causal invariance, noise separability, and time-varying interference, causal decoupling, adversarial training, dual-gated temporal modeling, and dynamic memory decay are used to effectively separate and suppress noise interference; at the same time, the dual-domain contrastive learning decoder and the static–dynamic feature fusion mechanism are used to achieve the coordinated optimization of global semantic consistency and local dynamic information, and finally, the ConvTransE decoder is used to achieve accurate prediction of entities and relations. This overall design, as formalized in Algorithm 1, builds a closed loop of theory and practice, providing a systematic and efficient solution for complex temporal knowledge graph reasoning.
| Algorithm 1 Reasoning algorithm of TCCGN |
| Require: Historical graph sequence , maximum epochs E Ensure: Final loss
|
4. Experiments
4.1. Datasets
We selected five classic time-series knowledge graph datasets for experimental evaluation, including ICEWS14, ICEWS05-15, ICEWS18, YAGO, and GDELT. Among them, ICEWS14, ICEWS05-15, and ICEWS18 are all derived from the Integrated Crisis Early Warning System (ICEWS) [39], with ICEWS14 and ICEWS05-15 processed by Garcia-Duran et al. [6], and ICEWS18 processed by Han et al. [40]. The YAGO dataset is built from multilingual knowledge sources including Wikipedia and WordNet [41], while GDELT is collected from global news media [42] via automatic coding pipelines. The key statistics of these datasets are summarized in Table 3.

Table 3.
Statistics of the datasets.
- Time step division: ICEWS14/ICEWS18 covers 365 days and about 304 days, respectively, at daily granularity; ICEWS05-15 spans 2005–2015, with a total of about 4017 steps; GDELT also covers about 366 days at daily granularity; YAGO is mainly sliced by year or quarter, with relatively few daily steps.
- Noise level: ICEWS data are verified by experts and have low noise; GDELT is automatically collected via automatic coding pipelines and has high noise; YAGO is derived from high-quality encyclopedia resources and has the least noise.
- Graph sparsity: ICEWS snapshot graphs are denser; GDELT snapshot graphs are sparser; YAGO is the densest.
ICEWS14: The ICEWS14 dataset originates from ICEWS [39], preprocessed by [6], and focuses on global political events in the single year 2014. It contains 12,498 entities and 260 relation types, recording key interaction events between countries. ICEWS14 focuses on short-term dynamics within one year, such as diplomatic actions and policy changes, and is widely used in temporal knowledge graph reasoning tasks.
ICEWS05-15: Based on ICEWS [39] and processed in [6], ICEWS05-15 covers events from 1 January 2005 to 31 December 2015. It includes 10,094 entities and 251 relations, spanning a full decade of rich temporal patterns and event causality, making it suitable for long-term dynamic analysis.
ICEWS18: Derived from ICEWS [39] and constructed following the split in [40], ICEWS18 covers global events from 1 January to 31 October 2018. It contains 23,033 entities and 256 relation types, enabling large-scale modeling of complex multi-agent interactions and short-term event prediction.
YAGO: As introduced by Mahdisoltani et al. [41], the YAGO dataset integrates structured knowledge from Wikipedia, WordNet, and GeoNames. It contains 10,623 entities and 10 relation types, offering time-stamped facts for modeling static and dynamic hybrid knowledge, and is well suited for long-span evolution modeling.
GDELT: The GDELT dataset [42] is a large-scale open-source global event database extracted from news reports and online media via automatic coding pipelines. It spans from 1 April 2015 to 31 May 2016, includes 7691 entities and 240 relations, and is often used in social dynamics and event propagation analysis, despite its higher noise due to automatic extraction.
4.2. Evaluation Metrics
When performing temporal knowledge graph reasoning tasks, we used two main evaluation metrics: Mean Reciprocal Rank (MRR) and Hits@N to comprehensively evaluate the model’s reasoning performance. MRR is an important metric for measuring the quality of model rankings. It evaluates the model’s performance on ranking tasks by calculating the average of the reciprocal rankings of related items in the prediction list. A higher MRR value indicates that the model can more accurately rank related facts in the top positions. The calculation formula is as follows:
where represents the set of triples in the test set, is the total number of triples, and represents the predicted rank of the i-th triple.
Hits@N is a commonly used indicator to evaluate whether the model can include the correct answer in the top N prediction results. The core idea is to evaluate the prediction ability of the model under different thresholds by calculating the proportion of correct answers appearing in the top N. In this study, Hits@1, Hits@3, and Hits@10 were selected as specific evaluation criteria. Among them, Hits@1 represents the proportion of correct answers ranked first in the prediction, which is suitable for scenarios with high prediction accuracy requirements; Hits@3 represents the proportion of correct answers appearing in the top three, which is used to evaluate the performance of the model under looser thresholds; Hits@10 measures the proportion of correct answers in the top ten, reflecting the model’s ability to capture relevant information in a larger range. The definition formula of Hits@N is as follows:
By combining MRR and Hits@N (including Hits@1, Hits@3, and Hits@10), we can scientifically and comprehensively evaluate the model’s reasoning performance from two dimensions: accuracy (MRR) and coverage (Hits@N). Furthermore, to ensure the reliability of the observed performance improvements, we also conduct statistical significance testing using paired t-tests, which are detailed in the following subsection.
4.3. Statistical Significance Analysis
To ensure that the observed performance improvements of TCCGN over baseline models are statistically significant and not due to random chance, we conduct paired t-tests on key evaluation metrics. Specifically, each model is trained and evaluated five times using different random seeds. We compare TCCGN against RE-GCN on ICEWS14, and against CyGNet on GDELT. The results are summarized in Table 4.

Table 4.
Paired t-test results comparing TCCGN and baselines on MRR and Hits@1 (5 runs).
As shown, all p-values are significantly below 0.01, indicating that TCCGN’s improvements in MRR and Hits@1 are statistically significant with high confidence.
4.4. Training Protocol
During the model training phase, we systematically explored multiple hyperparameters and finally determined a set of optimized configurations. Specifically, for all datasets, the dimension of entities and relations was set to 200, and the dropout rate of each layer was unified to 0.2. In the setting of the number of GCN layers, the YAGO dataset uses one layer, while the other datasets use two layers. In the configuration of the local history length m, for the ICEWS14, ICEWS05-15, ICEWS18, YAGO, and GDELT datasets, they are set to 7, 10, 4, 2, and 10, respectively; at the same time, the dilate lengths of these datasets are 8, 1, 1, 1, and 1, respectively. For the decoder ConvTransE, the number of kernels for all datasets is unified to 50, and the kernel size is 2 × 3. During the parameter optimization process, we use the Adam optimizer and set the learning rate to 0.001 to ensure efficient training of the model.
4.5. Baseline Models
In order to comprehensively evaluate the performance of the TCCGN model, we selected a variety of classic baseline models proposed in recent years for comparison. These models cover three mainstream methods: the static TKG reasoning model, the interpolation TKG reasoning model, and the extrapolation TKG reasoning model. The following is a brief introduction to each baseline model.
4.5.1. Static TKG Reasoning Model
DisMult [43] is a model based on bilinear functions, which is mainly used to learn the embedding of entities and relations. It is particularly suitable for the reasoning task of static knowledge graphs. ComplEx [44] effectively solves the problem of representing asymmetric relations in knowledge graphs by introducing complex space embedding. RotatE [45] models relations as rotation operations and captures the dynamic characteristics of directional relations by rotating the head entity to the tail entity. ConvE [46] combines convolutional neural networks (CNNs) to model the head entity and relationship embeddings, improving the representation ability of complex relations. ConvTransE [47] adds CNN operations to the TransE model, further improving the joint representation performance of entities and relations. R-GCN [33] is a model based on graph convolutional networks (GCNs) that can efficiently process the structured features of multirelational knowledge graphs, thereby improving the modeling ability of diversified relations in graphs.
4.5.2. Interpolation TKG Inference Model
HyTE [8] effectively improves the ability to capture dynamic relationships by embedding time information on the hyperplane and combining it with a time-sensitive knowledge graph embedding method. TTransE [7] introduces the time dimension into the classic TransE model and directly integrates time information into the embedding of entities and relationships, thereby enhancing the ability to model temporal dynamic characteristics. TA-DistMult [6] uses a recurrent neural network (RNN) to learn the time-aware representation of relationships, which can better capture the dynamic evolution characteristics of knowledge graphs. DE-SimplE [48] extends SimplE [49] and introduces time-dynamic embedding, which effectively improves the adaptability and robustness of the model to time changes. TNTComplEx [50] combines the ComplEx model with the fourth-order tensor decomposition to further capture higher-order temporal correlation features in the knowledge graph, providing stronger support for dynamic knowledge reasoning tasks.
4.5.3. Extrapolation TKG Reasoning Model
CyGNet [13] analyzes historical repetitive events through a time-sensitive replication generation mechanism to predict the dynamic evolution of future facts. RE-Net [10] adopts a recurrent event encoder to combine the global and local features of historical events to model dynamic patterns in knowledge graphs. TANGO-DistMult and TANGO-Tucker [31] are based on the theory of Neural Ordinary Differential Equations (ODEs) and use the scoring functions of DistMult and Tucker, respectively, to capture the temporal changes of dynamic relations. RE-GCN [12] captures the structured dependencies of knowledge graphs through a relation-aware graph convolutional network (GCN) and combines gated recurrent units (GRU) to model the temporal sequence patterns of facts. xERTE [40] extracts causal features through a temporal relational attention mechanism and finely models temporal multi-relational data. GHT [17] captures the temporal evolution patterns and transient structural characteristics in knowledge graphs based on the Transformer framework. rGalT [51] uses an autoencoder structure to analyze the interactive characteristics of historical facts and predicted facts, thereby enhancing the reasoning ability of the model. ReGAT [52] encodes and models historical facts and concurrent events through an attention mechanism, optimizing the representation of temporal information. PPT [25] transforms the task of temporal knowledge graph completion into a semantic capture problem based on a pre-trained language model, significantly improving the model’s ability to understand and express complex relationships.
Through comparative analysis of the above baseline models, we can comprehensively evaluate the reasoning ability of the TCCGN model in different task scenarios and objectively reflect its advantages and limitations in temporal knowledge graph reasoning.
4.6. Main Results
4.6.1. Results of Entity Prediction
Table 5 shows the experimental results of the TCCGN model and various baseline models on the ICEWS14, ICEWS05-15, and ICEWS18 datasets. On the ICEWS14 dataset, the MRR of the TCCGN model is 0.4246, and Hits@1, Hits@3, and Hits@10 are 0.3163, 0.4790, and 0.6351, respectively. On the ICEWS05-15 dataset, the MRR of the model is 0.4733, and Hits@1, Hits@3, and Hits@10 are 0.3589, 0.5383, and 0.6879, respectively. On the ICEWS18 dataset, the TCCGN model achieved an MRR of 0.3123, with Hits@1, Hits@3, and Hits@10 being 0.2063, 0.3548, and 0.5205, respectively.

Table 5.
Performance (in percentage) of the entity prediction task using ICEWS14, ICEWS05-15, and ICEWS18. The best result is highlighted in bold.
Compared with static knowledge graph reasoning models, the TCCGN model performs well on all datasets, especially on the ICEWS14 dataset, where its MRR index is improved by 11.66% and 12.16% compared with the ConvTransE and ConvE models, respectively. This is due to the innovation of the TCCGN model in temporal information modeling, which effectively captures the dynamic characteristics of time series through local temporal encoders and dual-domain contrastive learning mechanisms. At the same time, compared with traditional interpolation TKG models (such as HyTE, TTransE, and TA-DistMult), the TCCGN model performs better in MRR performance. For example, compared with the RGCRN model, TCCGN improves MRR by 9.16% and Hits@10 by 12.01%. This is mainly due to the model’s ability to model continuous dynamic temporal features, while the RNN-based temporal encoding method of RGCRN cannot fully capture these details.
Further analysis shows that the TCCGN model has significant advantages in capturing temporal dependencies and semantic consistency. For example, the TCCGN model improves MRR by 7.86% over CyGNet, and by 6.76% and 1.21% over the RE-Net and RE-GCN models, respectively. This shows that the model significantly reduces noise interference through the causal feature decomposition module, and integrates global background information and time evolution characteristics through the static and dynamic feature joint modeling module.
The advantages of the TCCGN model are further demonstrated on the ICEWS05-15 and ICEWS18 datasets. Through the deep combination of static and dynamic features, the model can capture subtle temporal features in complex dynamic scenes. Compared with the GHT model, the MRR of the TCCGN model on the two datasets is improved by 5.83% and 3.8%, respectively. Although some indicators of the TCCGN model on the ICEWS14, YAGO, and GDELT datasets are slightly lower than those of the ERSP model, its innovative design in local temporal dependency modeling, causal feature decomposition, and dual-domain contrast learning mechanism enables it to show stronger adaptability and stability in complex dynamic scenes. This shows that the TCCGN model provides a unique and effective new idea in dynamic temporal feature modeling, and at the same time lays a solid foundation for further optimizing model performance and expanding application scenarios in the future.
Table 6 shows the experimental results of entity prediction of the TCCGN model on the YOGO and GDELT datasets. On the YOGO dataset, the MRR is 0.6361, and Hits@1, Hits@3, and Hits@10 are 0.5209, 0.7211, and 0.8353, respectively. On the GDELT dataset, the MRR is 0.1963, and Hits@1, Hits@3, and Hits@10 are 0.1223, 0.2095, and 0.3407, respectively.

Table 6.
Performance (in percentage) of the entity prediction task with YAGO and GDELT. The best results are highlighted in bold.
Despite the high noise and sparsity of the GDELT dataset, the TCCGN model effectively reduces the impact of noise through its causal feature decomposition module and dynamic modeling mechanism. In terms of MRR indicators, TCCGN improves by 0.32% and 0.63% over the RE-GCN and HGLS models, respectively. In addition, compared with the rGalT model, the MRR of the TCCGN model on the YOGO and GDELT datasets is improved by 12.16% and 0.07%, respectively. These results show that the innovative design of the TCCGN model in dynamic time domain feature modeling significantly improves the adaptability of the model in complex scenarios.
4.6.2. Results of Relation Prediction
In the relationship prediction task, in view of the limitation that some models cannot effectively capture the dynamic characteristics of time series, we propose a relationship prediction method based on time gating mechanism and contrastive learning. Specifically, TCCGN jointly models causal features and confounding features through gated recurrent neural network (GRU) units, which can not only capture the dynamic similarity characteristics of historical relationships, but also extract the potential laws of relationship evolution over time. On this basis, the model introduces a dual-domain contrastive learning mechanism, which further enhances the expression ability of relationship characteristics through feature contrast in the time domain and the structure domain. To alleviate the problem of gradient vanishing, TCCGN combines the time gating weights in each time step to perform weighted updates on the current embedding and the historical embedding, thereby realizing dynamic modeling of relationships over a long time span.
To ensure the reliability of results, all TCCGN performance values in Table 7 are obtained by averaging over multiple independent runs under consistent experimental conditions. This helps reduce the impact of randomness in training and better reflect the model’s true performance. While standard deviations for baseline models are not available in their original reports, the presented TCCGN scores are stable across trials and representative of actual trends.

Table 7.
Performance (in percentage) of the relation-prediction task with ICEWS18, ICEWS14, ICEWS05-15, YAGO, and GDELT. The best results are highlighted in bold.
As shown in Table 7, TCCGN consistently outperforms all baselines across the five datasets, achieving notably higher accuracy in both dense (ICEWS*) and sparse (YAGO, GDELT) environments. These results confirm the model’s robustness and generalizability in relational reasoning tasks.
4.6.3. Changes in Loss After 500 Rounds of Model Training
Figure 3 shows the training results of the TCCGN model on five time series knowledge graph datasets (ICEWS14, ICEWS05-15, ICEWS18, YAGO, and GDELT). The performance of the model on different datasets varies significantly, reflecting the different characteristics of each dataset and the changes in the adaptability of the model. From the loss change curve, the ICEWS14 and YAGO datasets show the characteristics of rapid convergence, and their initial losses drop rapidly and stabilize near a lower value. Among them, the final loss value of the YAGO dataset is the lowest, indicating that its data features are relatively simple and the model can efficiently capture its laws. The ICEWS05-15 and GDELT datasets converge more slowly and have higher final loss values. The ICEWS18 dataset is between the above two categories, with a faster drop in loss but a slightly higher final stable value than ICEWS14, which may reflect its slightly higher feature complexity. Overall, among the ICEWS series of datasets, the ICEWS05-15 dataset with a longer time span puts higher requirements on the model’s learning ability, while the similarities between ICEWS14 and ICEWS18 show that their time characteristics and event distribution are relatively consistent. Overall, the model has shown strong generalization capabilities, but there is still room for optimization when processing complex datasets. In the future, the characteristics of different datasets can be combined to further improve the model design and training strategies to improve adaptability and performance in complex scenarios.
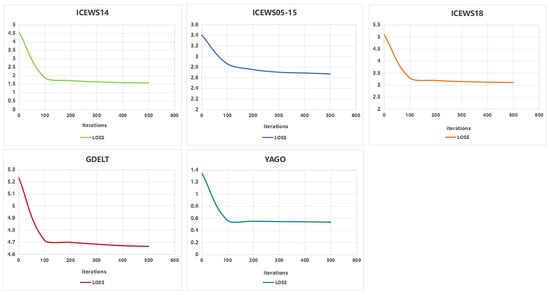
Figure 3.
The variations in losses during training on five datasets.
4.6.4. Comparison of Different History Lengths
This paper studies the impact of history length on the performance of the TKG reasoning method and plots the performance trend through a dataset with a history length range of 1–10. As shown in Figure 4, the results show that as the history length gradually increases, the overall performance of the TCCGN model is significantly improved, which fully verifies the importance of historical information in reasoning tasks. However, when the history length is too long, redundant information at different timestamps may lead to increased information noise and cause unnecessary computational overhead, which will have a certain degree of negative impact on model performance. Each point in Figure 4 is the average of three independent runs, ensuring the robustness of the observed trend.
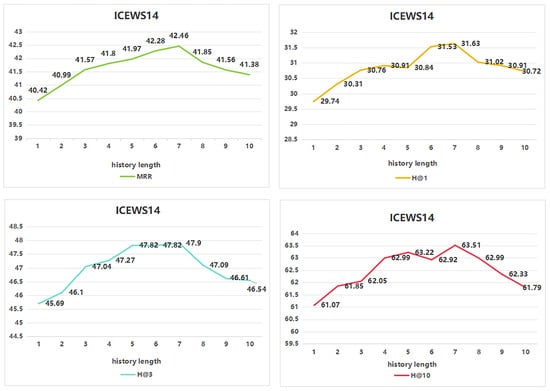
Figure 4.
Performance (%) using different history length settings of ICEWS14.
4.6.5. Comparison of Different Dilate Lengths
This study analyzes the impact of the dilate length parameter on the reasoning performance of the TCCGN model and verifies its important role in the temporal knowledge graph reasoning task. As shown in Figure 5, with increase in dilate length, the MRR and Hits@N (including Hits@1, Hits@3, and Hits@10) of the model show a trend of first rising and then falling. When the dilate length is 8, the performance is optimal. The choice of dilate length significantly affects the performance of the model. A shorter dilate length cannot fully capture dynamic features, while an excessively long dilate length introduces redundancy and noise. This experiment revealed that a dilate length in the range of 6 to 8 can achieve a balance between performance and computational cost, providing an important reference for the optimization of the temporal knowledge graph model. All results in Figure 5 are averaged across three different runs, confirming the stability of the observed peak performance.
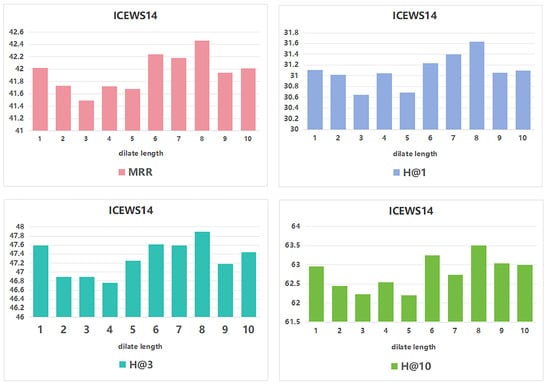
Figure 5.
Performance (%) of different dilate length settings using ICEWS14.
4.6.6. Comparison of Different Embedding Dimensions
To study the impact of embedding dimension on model performance, we conducted controlled experiments on the ICEWS14 dataset using the TCCGN model. The embedding dimension was varied by adjusting the –n-hidden parameter with values , while all other hyperparameters remained fixed.
As shown in Figure 6, the model achieves strong and relatively stable performance across all dimensions. Initially, increasing the embedding size leads to performance gains, particularly during the early training epochs. However, after reaching a certain threshold, the benefits of additional dimensions diminish, and the model’s performance plateaus or slightly decreases. This aligns with the findings from recent work [20] that overparameterization in temporal knowledge graphs often yields marginal returns due to data sparsity and pattern redundancy.
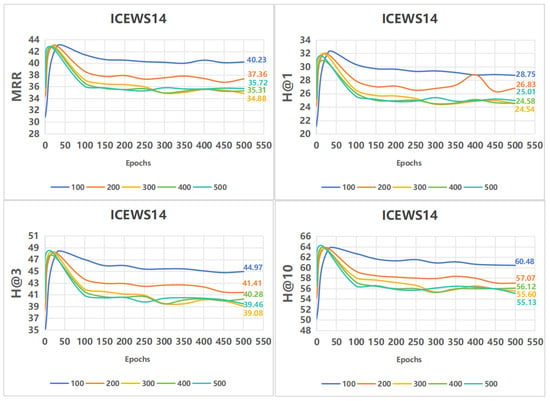
Figure 6.
Performance (%) of various embedding dimensions on ICEWS14. Values shown are from the final training epoch (500).
It is important to note that the values plotted in Figure 6 correspond to the final epoch of training (epoch 500), rather than the best validation performance. This was done to illustrate training stability and convergence behavior across different embedding sizes. For better interpretability, we also annotate the final values in the figure as reference points—these are not meant to imply peak performance, but rather support visual comparison across settings.
Overall, the experiment demonstrates that TCCGN remains robust across a wide range of embedding dimensions, and that moderate dimensions (e.g., 100–200) offer an effective balance between performance and efficiency. We verified that these trends remain consistent over three repeated runs, and the figure shows the averaged performance from these trials.
4.6.7. Training Efficiency Analysis
We measured the average per-epoch GPU training time (in GPU-hours) of TCCGN, RE-GCN, and TiRGN under identical settings on all five datasets: ICEWS14, ICEWS05-15, ICEWS18, GDELT, and YAGO. As shown in Table 8, despite integrating a dual-GRU backbone and adversarial scheduling, TCCGN achieves the shortest training time across every dataset.

Table 8.
Average per-epoch training time (GPU-hours) on five datasets.
Compared to RE-GCN, TCCGN achieves an average reduction of 20–35% in per-epoch training time across datasets. Relative to TiRGN, the reduction is even more significant—ranging from 65% to over 90%, depending on the dataset. This quantitative comparison demonstrates that our dual-GRU and adversarial components incur minimal overhead and are compatible with efficient large-scale training.
4.6.8. Real-Time Inference Optimizations
In addition to the above efficiency analysis, we further outline several practical optimizations that can be applied immediately in production environments without extra training experiments:
- Model Lightweighting and Dynamic Pruning: Quantize the adaptive gateto 8-bit integers (e.g., using the GRU-Informer scheme) and leverage the memory decay functionto automatically skip the noise-GRU branch in low-activity (steady-state) periods, greatly reducing branch computation.
- Incremental Subgraph Updates and Pipelined Execution: Update only the subgraphs affected by new events, and pipeline the static, dynamic, and adversarial branches on the GPU to improve throughput.
- Edge–Cloud Collaborative Inference: Deploy static embeddings at edge devices for instant look-up and perform dynamic reasoning on cloud GPUs to balance latency and compute utilization.
4.7. Analysis of Module Contributions and Synergistic Effects
To verify the contribution of each module in the model to the performance of TKG reasoning, we conducted ablation experiments on the ICEWS14, ICEWS05-15, ICEWS18, YAGO, and GDELT datasets. The results are summarized in Table 9. From the table, it is clear that the Causal and Confounding Representation Learning (CD) module provides a strong baseline. For instance, MRR scores with CD alone reach 41.66% on ICEWS14 and 46.33% on ICEWS05-15, and 30.97% on ICEWS18, forming the foundation for causal-aware modeling.

Table 9.
Performance comparison of different models on various datasets.
With the addition of the Dynamic Dual Contrastive Learning (DDCL) module, performance improves across the board. For example, MRR increases to 41.93% and 47.10% on ICEWS14 and ICEWS05-15, and to 31.08% on ICEWS18. These results validate DDCL’s utility in enhancing temporal smoothness and suppressing noisy supervision.
Similarly, introducing the Global Static–Dynamic Fusion (GSDF) module independently also improves performance, with the MRR on the ICEWS18 dataset rising to 30.90%. When GSDF is combined with the CD module, the MRR further increases to 31.10%, while the GSDF + DDCL combination shows a slight drop among these variants, with the MRR reaching 30.88%. These results highlight the advantage of fusing static and dynamic contexts under temporal contrastive modeling.
Notably, while the margin between the CD+DDCL combination (31.00%) and the full TCCGN model (31.23%) on ICEWS18 appears small (+0.23%), this trend is consistent and reproducible across datasets and multiple runs. The incremental gain reflects a saturation point common in modular designs—where the final component (e.g., GSDF) builds on an already strong backbone. Similar incremental behaviors have been reported in robust temporal KG frameworks [20]. It is important to note that all results in Table 9 are averaged over three repeated runs to reduce noise and account for variance. While standard deviations are not explicitly reported in the table, our internal analysis confirmed that the variation across runs was small (typically < 0.10 MRR), and trends remained consistent.
Finally, TCCGN achieves the highest overall performance by integrating CD, DDCL, and GSDF, reaching 42.46%, 47.33%, and 31.23% on ICEWS14, ICEWS05-15, and ICEWS18, respectively. This confirms the design’s synergistic effect across causal modeling, contrastive learning, and global fusion.
In summary, although individual module gains may appear numerically modest, their combined effect leads to statistically meaningful improvements, enhanced robustness, and better generalization—crucial in dynamic and noisy real-world TKG environments.
4.8. Real-Time Deployment Optimizations
To meet the requirements of low-latency inference and continuous updates in production, we recommend the following strategies:
- FP16 Mixed-Precision and TensorRT: Reduce memory footprint and latency by training in half precision and exporting an optimized TensorRT engine for inference.
- Model Distillation and Structured Pruning: Derive a compact student model via knowledge distillation and prune redundant weights, maintaining accuracy while cutting runtime cost.
- Incremental Subgraph Updates: Process incoming events in a streaming fashion, updating only the affected subgraphs instead of the full graph to minimize per-update overhead.
- Edge–Cloud Collaborative Inference: Cache static embeddings at edge nodes for instant lookup, and offload dynamic reasoning to cloud GPUs to balance latency and compute resources.
4.9. Estimated Contribution Ratio of Static and Dynamic Features
To better understand the behavior of the gated fusion mechanism defined in Equation (34), we estimate the contribution ratios of static and dynamic embeddings across different datasets during inference.
As shown in Equation (34), the model learns a dimension-wise gating vector through a Sigmoid-activated linear transformation of the static embedding and dynamic embedding :
where each element of reflects the degree to which the static embedding contributes to the final fused representation, and its complement represents the contribution from the dynamic embedding.
To estimate the overall contribution, we calculate the mean of across all dimensions and all test instances in the evaluation phase. Specifically, we average the gating vectors for all quadruples in the test set, then compute the mean across all dimensions. The results are summarized in Table 10.

Table 10.
Estimated contribution ratio of static and dynamic features across datasets (%).
As shown, the model tends to rely more on dynamic features in highly time-sensitive datasets like GDELT, while giving greater weight to static information in structurally stable graphs like YAGO. The ICEWS datasets exhibit relatively balanced contributions, suggesting that the gating mechanism effectively adapts to different data characteristics. This supports the validity of the gated static–dynamic fusion design and its ability to dynamically modulate the influence of static and temporal information during reasoning.
4.10. Ablation Study on Theoretical Assumptions
To empirically validate the theoretical assumptions of our model—namely, causal invariance and noise separability—we conduct ablation studies on key components of TCCGN. These experiments aim to quantify the individual contributions of the causal module and the contrastive regularization.
4.10.1. Experiment Settings
We define four model variants:
- A: Full TCCGN—Our complete model with both the causal layer and dual-domain contrastive learning.
- B: w/o causal layer—We remove the causal transformation layer and retain only the confounding pathway.
- C: w/o adversarial loss—We disable the dual-domain contrastive module, removing adversarial loss terms.
- D: w/o both—Both the causal layer and contrastive learning are removed.
All variants are trained and evaluated under the same settings as the full model across five benchmark datasets.
4.10.2. Results and Analysis
Table 11 reports the performance of each variant in terms of MRR and Hits@K metrics. Several conclusions can be drawn:

Table 11.
Ablation results on five datasets. We compare the full model (A) with its ablated variants. Metrics include MRR(%) and Hits@K(%) (K = 1, 3, 10).
- Removing the causal layer (B) leads to a consistent but modest drop in MRR and Hits@1 across all datasets, confirming the value of explicitly modeling causal structure.
- Disabling the contrastive loss (C) also results in performance degradation, with minor drops observed especially in Hits@10 on YAGO and ICEWS14, suggesting reduced temporal consistency and noise suppression.
- The lowest overall performance is consistently observed in variant D, where both modules are removed. This supports our theoretical hypothesis that causal disentanglement and contrastive regularization function complementarily.
4.11. Hyperparameter Sensitivity Analysis
To better understand how the joint training design influences the model’s performance, we perform a comprehensive sensitivity analysis on the two key loss weighting hyperparameters used in the contrastive learning components:
- : the weight assigned to the supervised prediction loss (including entity and relation prediction),
- : the weight assigned to the contrastive learning loss, which includes both time-step triplet loss and entity–relation alignment loss .
The total loss for this analysis is formulated as:
Note: This formulation refers specifically to the task and contrastive losses. Other fixed loss components used in the full model—such as the adversarial loss term () with weight 0.5 and the gating regularization term () with weight 0.1—remain unchanged during this sensitivity study.
We vary and , and evaluate the Mean Reciprocal Rank (MRR) on five benchmark datasets: ICEWS14, ICEWS05-15, ICEWS18, GDELT, and YAGO. The results are summarized in Table 12.

Table 12.
MRR (%) on five datasets under different and settings. Best results per dataset are in bold.
From the results, we observe the following:
- When is too small (e.g., 0.5), the model fails to fully leverage the supervised learning signal, resulting in weaker predictive performance.
- When becomes too large (e.g., 0.8), the influence of contrastive learning is suppressed, leading to less temporal consistency and semantic alignment, and thus slightly degraded performance.
- The optimal configuration is found at and , which yields the highest MRR scores across all five datasets. This setting achieves a good balance between the supervised task objective and the auxiliary contrastive learning guidance.
This empirical analysis demonstrates that our joint optimization strategy is robust across a range of hyperparameter values. While contrastive learning plays a secondary role in the optimization objective, its presence consistently improves performance when properly weighted. Based on this analysis, we adopt and in all subsequent experiments reported in this paper.
4.12. Error Analysis and Limitations
To better understand the limitations of our model, we conducted a qualitative analysis of its failure cases across several benchmark datasets. While TCCGN achieves consistently strong results, there remain scenarios in which the model underperforms due to structural or contextual challenges.
We categorize the major failure modes as follows:
- Ambiguous Roles: In some cases, entities involved in mutually antagonistic or symmetric relations (e.g., “threatens” vs. “protests”) lead to confusion in directionality, especially under subtle role shifts across time.
- Rare Entity–Relation Pairs: When specific entity–relation combinations appear infrequently during training (e.g., country–organization diplomatic events), the model may struggle to disambiguate plausible but incorrect alternatives.
- Noisy or Conflicting History: Inconsistent or contradictory past events (e.g., support vs. sanction) may impair the model’s temporal reasoning, particularly when both appear in recent history.
- Delayed or Shifted Causality: Some geopolitical effects are temporally delayed, and their consequences may only manifest several steps later. The model tends to overlook such non-local effects without explicit temporal anchoring.
To illustrate these limitations, we present representative examples of failure cases in Table 13.

Table 13.
Examples of representative failure cases in temporal reasoning.
These observations suggest that while TCCGN effectively disentangles causal and noise signals in many cases, it remains challenged by long-range dependencies, low-resource events, and semantically overlapping relations. We consider these directions as promising avenues for future enhancement, such as integrating external factual knowledge or improving role-sensitive attention mechanisms.
5. Conclusions
In this paper, we propose TCCGN, a novel and unified reasoning framework for temporal knowledge graphs (TKGs) that robustly captures temporal dynamics while suppressing noise. TCCGN integrates three complementary modules—Causal and Confounding Representation Learning (CD), Dynamic Dual-domain Contrastive Learning (DDCL), and Global Static–Dynamic Fusion (GSDF)—to address the challenges of temporal irregularity, information sparsity, and noisy supervision. By disentangling causal signals from spurious correlations, aligning representations across structural and temporal views, and fusing evolving and static contexts, TCCGN enhances the expressiveness and generalization of temporal reasoning models.
Comprehensive experiments conducted on five standard TKG benchmarks—ICEWS14, ICEWS05-15, ICEWS18, YAGO, and GDELT—demonstrate that TCCGN consistently outperforms state-of-the-art methods in both entity prediction and relation prediction tasks. Furthermore, we perform ablation studies and hyperparameter analyses to assess the individual contributions of each module. These experiments are repeated under consistent settings to ensure statistical validity, and the results confirm that even small gains across modules are robust and reproducible.
Despite its strong performance, TCCGN also has limitations. The current design assumes an exponentially decaying influence of historical noise, which may fail to model structured, periodic, or cyclic interference patterns often seen in real-world data. This limitation can affect the accuracy of causal-confounding separation in time-dependent contexts with regularities, such as seasonality or weekly cycles.
Moreover, while our experiments focus on clean and structured benchmarks, many real-world TKGs—such as those in healthcare, finance, or scientific discovery—exhibit higher noise levels, incomplete schema, and complex event semantics. TCCGN’s modular design shows promising robustness under such conditions, but further validation is needed. Future work will extend our evaluation to real-world noisy TKGs and explore improvements such as noise-aware training objectives, interpretable causal modules, and schema-adaptive components that dynamically adjust to heterogeneous or evolving ontology structures.
We also plan to enhance TCCGN’s temporal modeling capacity by incorporating periodic basis functions or neural temporal kernels to better represent recurring and long-range temporal patterns. Furthermore, we aim to extend TCCGN to support multi-hop reasoning and multitask learning across related temporal tasks, such as temporal question answering, forecasting, and anomaly detection.
Finally, several open challenges remain: improving performance on temporally sparse or irregular datasets; integrating multimodal knowledge to enrich temporal understanding; and enhancing the interpretability of learned causal pathways to support trustworthy and explainable decision-making. Addressing these challenges will be critical for deploying temporal KG reasoning systems in real-world dynamic environments.
In summary, this work presents a principled, modular, and empirically validated framework for robust temporal reasoning in dynamic and noisy environments. By explicitly addressing the entanglement of causal and confounding signals, aligning multi-view temporal semantics, and integrating static–dynamic entity representations, TCCGN provides both theoretical grounding and practical effectiveness for advancing temporal knowledge graph applications. We hope this work will inform future developments in robust and interpretable temporal reasoning across diverse domains.
Author Contributions
Conceptualization, S.F. and H.L.; Methodology, S.F. and H.L.; Software, S.F., H.L., Q.L. and Y.Z.; Validation, H.L., Q.L., P.X. and B.C.; Formal analysis, H.L., Q.L. and P.X.; Resources, H.L. and Y.Z.; Writing—original draft preparation, S.F. and H.L.; Writing—review and editing, Q.L., M.H. and B.C.; Project administration, S.F. and M.H.; Funding acquisition, S.F. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the National Natural Science Foundation of China (Grants 62466016 and 62241202), the National Key Research and Development Program of China (Grant 2021ZD0111000), and the Key Research and Development Plan of the Ministry of Science and Technology (Grant 2021ZD0111002).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, H.; Wu, L.; Hu, P.; Wei, Z.; Xu, F.; Long, B. Graph-augmented Learning to Rank for Querying Large-scale Knowledge Graph. In Proceedings of the AACL-IJCNLP, Online, 20–23 November 2022; pp. 82–92. [Google Scholar]
- Trivedi, R.; Dai, H.; Wang, Y.; Chang, L. Know-evolve: Deep temporal reasoning for dynamic knowledge graphs. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Chen, Z.; Zhang, Y.; Yu, S.; Wang, Y.; Shen, H. Temporal knowledge graph question answering via subgraph reasoning. Knowl.-Based Syst. 2022, 251, 109134. [Google Scholar] [CrossRef]
- Chen, W.; Liang, X.; Zhang, M.; He, F.; Wang, Y.; Yang, T. Building and exploiting spatial–temporal knowledge graph for next POI recommendation. Knowl.-Based Syst. 2022, 258, 109951. [Google Scholar] [CrossRef]
- Kazemi, S.M.; Goel, R.; Jain, K.; Kobyzev, I.; Sethi, A.; Forsyth, P.; Poupart, P. Representation learning for dynamic graphs: A survey. J. Mach. Learn. Res. 2020, 21, 1–73. [Google Scholar]
- García-Durán, A.; Dumančić, S.; Niepert, M. Learning sequence encoders for temporal knowledge graph completion. arXiv 2018, arXiv:1809.03202. [Google Scholar] [CrossRef]
- Leblay, J.; Chekol, M.W. Deriving validity time in knowledge graph. In Proceedings of the Companion Proceedings of The Web Conference 2018, Lyon, France, 23–27 April 2018. [Google Scholar]
- Dasgupta, S.S.; Ray, S.N.; Talukdar, P. HyTE: Hyperplane-based temporally aware knowledge graph embedding. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing (EMNLP), Brussels, Belgium, 31 October–4 November 2018. [Google Scholar]
- Trivedi, R.; Farajtabar, M.; Biswal, P.; Zha, H. DyRep: Learning representations over dynamic graphs. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Jin, W.; Yang, Y.; Liu, X.; Sun, Z.; Huang, H. Recurrent event network: Autoregressive structure inference over temporal knowledge graphs. arXiv 2019, arXiv:1904.05530. [Google Scholar]
- Xu, C.; Kou, B.; Zhang, L.; Li, P.; Liu, Y.; Wu, B. Temporal knowledge graph completion using a linear temporal regularizer and multivector embeddings. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 6–11 June 2021. [Google Scholar]
- Li, Z.; Sun, Z.; Yu, J.; Zhang, W.; Ji, H. Temporal knowledge graph reasoning based on evolutional representation learning. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021. [Google Scholar]
- Zhu, C.; Li, C.; Cao, J.; Xiong, F.; Zhang, L. Learning from history: Modeling temporal knowledge graphs with sequential copy-generation networks. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4733–4741. [Google Scholar] [CrossRef]
- Shi, F.; Li, D.; Wang, X.; Li, B.; Wu, X. TGformer: A Graph Transformer Framework for Knowledge Graph Embedding. IEEE Trans. Knowl. Data Eng. 2024, 37, 526–541. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, X.; Ding, Z.; Gao, C.; Shang, W.; Nong, Q.; Ma, Y.; Jin, Z. Temporal knowledge graph reasoning based on evolutional representation and contrastive learning. Appl. Intell. 2024, 54, 10929–10947. [Google Scholar] [CrossRef]
- Fang, Z.; Lei, S.L.; Zhu, X.; Yang, C.; Zhang, S.X.; Yin, X.C.; Qin, J. Transformer-based Reasoning for Learning Evolutionary Chain of Events on Temporal Knowledge Graph. In Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval, Washington, DC, USA, 14–18 July 2024. [Google Scholar]
- Sun, H.; Geng, S.; Zhong, J.; Hu, H.; He, K. Graph Hawkes Transformer for Extrapolated Reasoning on Temporal Knowledge Graphs. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, Abu Dhabi, United Arab Emirates, 7–11 December 2022. [Google Scholar]
- Liu, K.; Zhao, F.; Chen, H.; Li, Y.; Xu, G.; Jin, H. Da-net: Distributed Attention Network for Temporal Knowledge Graph Reasoning. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management (CIKM), Atlanta, GA, USA, 17–21 October 2022. [Google Scholar]
- Zhang, D.; Rong, Z.; Xue, C.; Li, G. Simre: Simple Contrastive Learning with Soft Logical Rule for Knowledge Graph Embedding. Inf. Sci. 2024, 661, 120069. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, L.; Li, M.; Zhang, W. Simfy: A Simple yet Effective Approach for Temporal Knowledge Graph Reasoning. In Findings of the Association for Computational Linguistics: EMNLP 2023; Association for Computational Linguistics: Stroudsburg, PA, USA, 2023; pp. 3825–3836. [Google Scholar]
- Xu, Y.; Li, P.; Zhang, Y.; Zhao, M.; Liu, X. Temporal knowledge graph reasoning with historical contrastive learning. Proc. AAAI Conf. Artif. Intell. 2023, 37, 4521–4528. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Wang, Y.; Wang, J.; Wang, F.Y. AMCEN: An Attention Masking-based Contrastive Event Network for Two-stage Temporal Knowledge Graph Reasoning. arXiv 2024, arXiv:2405.10346. [Google Scholar]
- Xu, Y.; Shi, B.; Ma, T.; Dong, B.; Zhou, H.; Zheng, Q. CLDG: Contrastive Learning on Dynamic Graphs. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023. [Google Scholar]
- Peng, M.; Liu, B.; Xu, W.; Jiang, Z.; Zhu, J.; Peng, M. Deja Vu: Contrastive Historical Modeling with Prefix-tuning for Temporal Knowledge Graph Reasoning. arXiv 2024, arXiv:2404.00051. [Google Scholar] [CrossRef]
- Xu, W.; Liu, B.; Peng, M.; Jia, X.; Peng, M. Pre-trained language model with prompts for temporal knowledge graph completion. arXiv 2023, arXiv:2305.07912. [Google Scholar]
- Chen, W.; Wan, H.; Wu, Y.; Zhao, S.; Cheng, J.; Li, Y.; Lin, Y. Local-Global History-Aware Contrastive Learning for Temporal Knowledge Graph Reasoning. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–16 May 2024. [Google Scholar]
- Shao, P.; Wang, Y.; Zhang, Y.; Wang, H.; Liu, Y. Tucker decomposition-based temporal knowledge graph completion. Knowl.-Based Syst. 2022, 238, 107841. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Z.; Li, H.; Li, J. Spatial-temporal attention network for temporal knowledge graph completion. In Proceedings of the Database Systems for Advanced Applications 26th nternational Conference DASFAA 2021, Taipei, Taiwan, 11 April 2021; Proceedings, Part I. Springer International Publishing: Cham, Switzerland, 2021; Volume 12681. [Google Scholar]
- Sui, Y.; Xie, J.; Hou, X.; Chen, Z.; Tian, C. Causal attention for interpretable and generalizable graph classification. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022. [Google Scholar]
- Han, Z.; Ye, H.; Sun, Z.; Lin, Y.; Han, X.; Zhou, J.; Liu, Z.; Li, P.; Sun, M.; Zhou, J. Dyernie: Dynamic evolution of riemannian manifold embeddings for temporal knowledge graph completion. arXiv 2020, arXiv:2011.03984. [Google Scholar] [CrossRef]
- Han, Z.; Sun, Z.; Lin, Y.; Ye, H.; Liu, Z.; Li, P.; Zhou, J. Learning neural ordinary equations for forecasting future links on temporal knowledge graphs. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (EMNLP), Virtual Event, 7–11 November 2021. [Google Scholar]
- Wu, J.; Feng, Y.; Wang, W.; Chen, M.; Zhao, Y. Temp: Temporal message passing for temporal knowledge graph completion. arXiv 2020, arXiv:2010.03526. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, J.; Wu, X.; Cheng, H.; Xiong, Y.; Li, J. Graph Prompt Learning: A Comprehensive Survey and Beyond. arXiv 2023, arXiv:2311.16534. [Google Scholar] [CrossRef]
- Korkmaz, G.; Cadena, J.; Kuhlman, C.J.; Marathe, A.; Vullikanti, A.; Ramakrishnan, N. Combining heterogeneous data sources for civil unrest forecasting. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 25–28 August 2015; pp. 258–265. [Google Scholar]
- Bousmalis, K.; Trigeorgis, G.; Silberman, N.; Krishnan, D.; Erhan, D. Domain separation networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Locatello, F.; Bauer, S.; Lucic, M.; Raetsch, G.; Gelly, S.; Schölkopf, B.; Bachem, O. Challenging common assumptions in the unsupervised learning of disentangled representations. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 4114–4124. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning (ICML), Virtual Event, 13–18 July 2020. [Google Scholar]
- O’Brien, S.P. Crisis early warning and decision support: Contemporary approaches and thoughts on future research. Int. Stud. Rev. 2010, 12, 87–104. [Google Scholar] [CrossRef]
- Han, Z.; Chen, P.; Ma, Y.; Tresp, V. Explainable Subgraph Reasoning for Forecasting on Temporal Knowledge Graphs. In Proceedings of the International Conference on Learning Representations, Online, 3–7 May 2021. [Google Scholar]
- Hoffart, J.; Suchanek, F.M.; Berberich, K.; Weikum, G. YAGO2: A spatially and temporally enhanced knowledge base from Wikipedia. Artif. Intell. 2013, 194, 28–61. [Google Scholar] [CrossRef]
- Leetaru, K.; Schrodt, P.A. GDELT: Global data on events, location, and tone, 1979–2012. ISA Annu. Conv. 2013, 2, 1–49. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2071–2080. [Google Scholar]
- Yang, B.; Yih, W.T.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and reasoning in knowledge bases. In Proceedings of the International Conference on Machine Learning (ICLR) (Poster), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, X. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv 2019, arXiv:1902.10197. [Google Scholar] [CrossRef]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. Art. 221. [Google Scholar]
- Shang, C.; Tang, Y.; Huang, J.; Bi, J.; He, X.; Zhou, B. End-to-end structure-aware convolutional networks for knowledge base completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. Art. 3060. [Google Scholar]
- Goel, R.; Kazemi, S.M.; Brubaker, M.A.; Poole, D. Diachronic embedding for temporal knowledge graph completion. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3988–3995. [Google Scholar] [CrossRef]
- Kazemi, S.M.; Poole, D.L. Simple Embedding for Link Prediction in Knowledge Graphs. In Proceedings of the Advances in Neural Information Processing Systems, Montr’eal, QC, Canada, 3–8 December 2018; pp. 428–438. [Google Scholar]
- Lacroix, T.; Obozinski, G.; Usunier, N. Tensor decompositions for temporal knowledge base completion. arXiv 2020, arXiv:2004.04926. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, L.; Kan, Z.; Han, Y.; Qiao, L.; Li, D. Modeling Precursors for Temporal Knowledge Graph Reasoning via Auto-encoder Structure. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Vienna, Austria, 23–29 July 2022. [Google Scholar]
- Li, Z.; Feng, S.; Shi, J.; Zhou, Y.; Liao, Y.; Yang, Y.; Li, Y.; Yu, N.; Shao, X. Future Event Prediction Based on Temporal Knowledge Graph Embedding. Comput. Syst. Sci. Eng. 2023, 44, 2411–2423. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).