Modular Reinforcement Learning for Multi-Market Portfolio Optimization

Abstract

Most reinforcement learning (RL) methods for portfolio optimization remain limited to single markets and a single algorithmic paradigm, which restricts their adaptability to regime shifts and heterogeneous conditions. This paper introduces a generalized version of the Modular Portfolio Learning System (MPLS), extending beyond its initial PPO backbone to integrate four RL algorithms: Proximal Policy Optimization (PPO), Deep Q-Network (DQN), Deep Deterministic Policy Gradient (DDPG), and Soft Actor-Critic (SAC). Building on its modular design, MPLS leverages specialized components for sentiment analysis, volatility forecasting, and structural dependency modeling, whose signals are fused within an attention-based decision framework. Unlike prior approaches, MPLS is evaluated independently on three major equity indices (S&P 500, DAX 30, and FTSE 100) across diverse regimes including stable, crisis, recovery, and sideways phases. Experimental results show that MPLS consistently achieved higher Sharpe ratios—typically +40–70% over Minimum Variance Portfolio (MVP) and Risk Parity (RP)—while limiting drawdowns and Conditional Value-at-Risk (CVaR) during stress periods such as the COVID-19 crash. Turnover levels remained moderate, confirming cost-awareness. Ablation and variance analyses highlight the distinct contribution of each module and the robustness of the framework. Overall, MPLS represents a modular, resilient, and practically relevant framework for risk-aware portfolio optimization.

1. Introduction

In recent years, financial institutions have increasingly adopted machine learning (ML) and data analytics to improve the efficiency, resilience, and transparency of their decision-making processes [1]. Within this context, portfolio management remains one of the most critical tasks, requiring continuous adaptation to volatile markets, integration of heterogeneous information sources, and timely decisions under uncertainty [2]. Failures in this process may result in significant financial losses, reputational damage, or regulatory penalties, making risk-aware decision support a central requirement [3].

Traditional portfolio optimization approaches—such as rule-based systems, mean–variance allocation [4] and factor models [5]—offer interpretability and regulatory compliance but often lack adaptability in rapidly changing markets. Reinforcement learning (RL) has recently emerged as an alternative [6], offering the ability to learn adaptive strategies directly from data while optimizing long-term objectives. However, existing RL applications in finance typically rely on single-agent, monolithic architectures. This design limits their generalization across heterogeneous market regimes [7], increases their sensitivity to noisy signals [8], and provides limited interpretability, which remains problematic in institutional and regulatory settings [9]. As a result, despite growing academic attention, RL-based portfolio optimization has not yet consistently demonstrated the robustness and transparency required for widespread adoption in practice.

To address these challenges, our previous work introduced the Modular Portfolio Learning System (MPLS), initially implemented with a Proximal Policy Optimization (PPO) backbone and evaluated on a merged portfolio of assets from the S&P 500, DAX 30, and FTSE 100 [10]. While this preliminary study illustrated the potential of modular reinforcement learning for portfolio optimization, it was limited by two main constraints: reliance on a single algorithmic backbone (PPO) and absence of market-specific evaluations. These constraints prevented a systematic understanding of how modular architectures interact with different RL algorithms under diverse market dynamics.

In this paper, we extended MPLS in two directions. First, we introduced algorithmic generalization by implementing MPLS with four complementary RL algorithms (PPO, DQN, SAC, and DDPG), enabling controlled comparisons of exploration–exploitation trade-offs within the same modular architecture. Second, we conducted market-specific evaluations on three major indices—S&P 500, DAX 30, and FTSE 100—across diverse regimes including stable, crisis, recovery, and sideways markets. To the best of our knowledge, while prior works have explored modular RL architectures [11] or conducted comparative evaluations among RL algorithms within a single market context [12,13], this work provides one of the first controlled multi-market evaluations across multiple equity indices using a unified modular framework with interchangeable backbones.

The main contributions of this work are:

• We present a modular reinforcement learning framework for multi-market portfolio optimization.
• We integrate four RL algorithms into MPLS and analyze their scenario-wise performance (Sharpe ratio, CVaR, drawdown, turnover) across stable, crisis, recovery, and sideways regimes.
• We report robustness analyses, including stability across multiple runs and ablation studies, to quantify the non-redundant contribution of each module.
• We show that MPLS consistently achieved higher risk-adjusted returns than traditional baselines, while maintaining moderate turnover.

2. Related Work

2.1. Portfolio Optimization in Dynamic Markets

Traditional portfolio optimization has long been anchored in mean–variance theory and its extensions, such as minimum variance [14] and risk-parity strategies [15].

Beyond these classical frameworks, recent studies have introduced alternative tail-risk measures such as the Entropic Value-at-Risk (EvaR) [16], Spectral Risk Measures [17], and Conditional Drawdown-at-Risk (CDaR) [18], offering richer representations of downside risk and asymmetry in return distributions. While these approaches improve theoretical robustness, CVaR remains the most widely adopted in reinforcement-learning-based portfolio optimization due to its coherence, convexity, and differentiability, which facilitate stable policy-gradient updates.

Nevertheless, all of these risk-based models, though theoretically consistent, operate under restrictive assumptions: stable return distributions, linear asset dependencies, and full market observability. In practice, markets are rarely stationary—regimes shift abruptly, correlations evolve, and structural breaks occur—reducing the reliability of static allocation strategies. This mismatch between theory and reality explains why such models often underperform during crises or prolonged volatility spikes.

Consequently, recent research has increasingly moved toward data-driven, adaptive methods capable of integrating heterogeneous, fast-changing information streams [12]. Recent studies highlight deep learning and regime-aware approaches as promising directions for capturing non-linear dependencies and adapting to market shifts [19,20,21,22]. Yet most adaptive approaches still suffer from important limitations: they lack systematic integration of diverse signal types, and many face challenges in scaling effectively to institutional use cases. This leaves a clear gap for more flexible and robust frameworks that can adjust dynamically to evolving market conditions.

2.2. Reinforcement Learning in Finance

Reinforcement learning (RL) provides a principled framework for sequential decision-making under uncertainty [23], allowing agents to optimize long-term objectives through continuous interaction with their environments. Early applications in finance primarily relied on monolithic agent architectures—deploying single-policy models such as PPO or DQN—for asset allocation and trading [7,8]. While effective in simulated settings, these approaches often exhibited limited scalability, poor interpretability, and weak generalization when exposed to real and dynamic markets. To address these shortcomings, more recent research has explored hierarchical and multi-agent RL frameworks, which separate high-level strategic allocations from low-level execution tasks [24]. Systems such as the Integrated Portfolio Strategist (IPS) [25] partially advanced this direction by introducing hierarchical coordination. However, they remained constrained to a single-policy backbone and did not integrate heterogeneous exogenous signals, limiting adaptability across market regimes. Surveys and applied studies confirm these limitations, emphasizing the need for safer, more interpretable, and robust RL in financial contexts [13,20,21,26]. Overall, prior RL approaches improved adaptability compared to classical finance models but have not consistently demonstrated the robustness and explainability required for institutional deployment.

2.3. Modular Architectures and Multi-Signal Integration

Incorporating multiple, complementary information streams—such as sentiment, volatility forecasts, and structural dependencies—has emerged as a promising avenue for enhancing portfolio resilience. Sentiment analysis, often powered by transformer-based models like FinBERT [27], captures investor mood from financial news. Volatility forecasting via Bayesian LSTM methods enables regime-aware risk estimation [28], while Graph Neural Networks (GNNs) capture evolving inter-asset relationships [29].

Despite these advances, most existing systems fuse signals in a static or pre-defined manner, which limits adaptability when the relevance of signals changes across market regimes. This rigidity may reduce performance during crises or unexpected transitions, when the dynamic reweighting of signals becomes critical. Modular frameworks address this limitation by enabling task-specific modules to process distinct inputs and adaptively contribute outputs based on context. Recent works in multimodal RL [30] and deep portfolio optimization frameworks [19] reinforce the potential of architectures that fuse multiple signal types. However, these models often rely on fixed signal fusion or single reward functions [31], and systematic evaluations across heterogeneous financial markets remain scarce [32].

2.4. Comparative Evaluation of RL Algorithms

Several studies have compared RL algorithms such as PPO, DQN, DDPG, and SAC in financial contexts. For example, prior benchmarks have explored their application in trading and portfolio allocation tasks, often within a single index or simplified setting [12]. Other works have examined actor–critic methods in stock trading [33], highlighting methodological differences but again within restricted environments. However, these comparisons typically focus on single markets, employ heterogeneous architectures, or vary significantly in input features—making it difficult to isolate algorithmic contributions from architectural differences.

More recent efforts have compared algorithms directly, such as PPO vs. SAC or DDPG in trading environments [19], but these remain limited to mono-market contexts and non-modular designs. Surveys confirm that systematic, cross-market comparisons of RL algorithms are largely missing in the financial literature [32]. To the best of our knowledge, this work provides one of the first unified evaluations of PPO, DQN, DDPG, and SAC within a modular RL system, using homogeneous inputs and multi-market testing. This design enables the disentanglement of architectural advantages from algorithmic trade-offs, providing clearer insights into the conditions under which each method is most effective.

3. Preliminaries

3.1. Reinforcement Learning in Portfolio Management

Reinforcement Learning (RL) provides a principled framework for sequential decision-making under uncertainty, formalized as a Markov Decision Process (MDP) [23]. An MDP is defined by the tuple (S, A, P, R, γ), where S is the state space, A is the action space, P is the transition probability, R is the reward function, and γ ∈ [0,1] is the discount factor. At each time step t, the agent observes a state $s_t \in S$, selects an action $a_t \in A$, and receives a reward $r_t=R\left(s_t, a_t\right)$, while the environment transitions to a new state $s_{t+1} ~ P\left(. \right|s_t, a_t)$.

In portfolio management, the state may include asset prices, technical indicators, sentiment scores, or volatility measures; the action corresponds to rebalancing the portfolio weights; and the reward is often defined in terms of risk-adjusted returns, such as the Sharpe ratio [34]:

$$\mathrm{S}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{p}\mathrm{e}={\displaystyle \frac{\mathrm{E}\left[{\mathrm{R}}_{\mathrm{p}}-{\mathrm{R}}_{\mathrm{f}}\right]}{{\mathsf{\sigma }}_{\mathrm{p}}}}$$

(1)

where $R_p$ is the portfolio return, $R_f$ is the risk-free rate, and ${\sigma }_p$ is the portfolio volatility. RL enables the automation and continuous improvement of financial decision workflows, aligning with principles of adaptability, optimization, and resilience in dynamic environments [35,36].

3.2. Reinforcement Learning Algorithms Compared

Proximal Policy Optimization (PPO) is an on-policy, policy-gradient algorithm that maximizes a clipped surrogate objective to ensure stable updates [37]:

$$L^{CLIP}\left(\theta \right)= {\mathbb{E}}_t\left[min\left(r_t\left(\theta \right){\widehat{A}}_t, clip\left(r_t\left(\theta \right), 1- \epsilon , 1+ \epsilon \right){\widehat{A}}_t\right)\right]$$

(2)

where $r_t\left(\theta \right)$ is the probability ratio between new and old policies, and ${\widehat{A}}_t$ is the advantage estimate. PPO balances exploration and exploitation, helping reduce overfitting to recent market conditions. In contrast, Deep Q-Networks (DQN) follow a value-based and off-policy paradigm, approximating the optimal action-value function $Q^{*}\left(s,a\right)$ using deep neural networks [6]:

$${\mathrm{Q}}^{\mathrm{*}}\left(\mathrm{s},\mathrm{a}\right)=\mathrm{E}\left[{\sum }_{\mathrm{k}=0}^{\mathrm{\infty }}{\mathsf{\gamma }}^{\mathrm{k}}{\mathrm{r}}_{\mathrm{t}+\mathrm{k}}\left|{\mathrm{s}}_{\mathrm{t}}=\mathrm{s},{\mathrm{a}}_{\mathrm{t}}=\mathrm{a}\right.\right]$$

(3)

DQN uses experience replay and target networks for stability, but requires adaptations for continuous portfolio weights.

Similarly, Deep Deterministic Policy Gradient (DDPG) is an off-policy, actor–critic method for continuous actions [38]. The actor network outputs deterministic portfolio weights, while the critic estimates. It allows fine-grained control, though it can be sensitive to hyperparameters and market volatility.

Soft Actor-Critic (SAC) is an off-policy, entropy-regularized actor–critic algorithm that maximizes a trade-off between expected reward and policy entropy [39]:

$$\mathrm{J}\left(\mathsf{\pi }\right)={\sum }_{\mathrm{t}}{\mathrm{E}}_{\left({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}\right)~\mathsf{\pi }}\left[\mathrm{r}\left({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}\right)+\mathsf{\alpha }\mathrm{H}\left(\mathsf{\pi }\right(.\left|{\mathrm{S}}_{\mathrm{t}}\right))\right]$$

(4)

Its stochastic policies can enhance robustness under uncertainty and noisy market conditions.

Taken together, these four algorithms span the main design paradigms of deep reinforcement learning—on-policy vs. off-policy, value-based vs. policy-gradient, and deterministic vs. stochastic. While each has been applied individually in finance, direct comparisons within a unified modular framework remain scarce. This motivates our controlled evaluation of PPO, DQN, DDPG, and SAC as interchangeable backbones within MPLS.

3.3. Modular Portfolio Learning System (MPLS)

The Modular Portfolio Learning System (MPLS) extends RL-based portfolio management through domain-specific modularity. It consists of three specialized components:

• Sentiment Analysis Module (SAM)—Employs the transformer-based NLP model FinBERT to extract market sentiment from financial news, capturing behavioral shifts not evident in price data [27].
• Volatility Forecasting Module (VFM)—Employs Bayesian LSTM networks to anticipate regime changes and quantify predictive uncertainty, guiding risk-sensitive allocations [28].
• Structural Dependency Module (GNN)—Uses Graph Neural Networks to model evolving inter-asset relationships via dynamic correlation graphs [29].

These modules are integrated via the Decision Fusion Framework (DFF), an attention-based mechanism trained to dynamically adjust each module’s influence according to contextual reliability [40]. This design allows MPLS to adapt to changing market regimes, support robustness, and improve allocation stability. Importantly, each module can be pretrained, updated, or replaced independently, providing a plug-and-play design. This flexibility allows MPLS to evolve as new data sources or predictive models become available, while preserving the overall architecture.

4. Methodology

4.1. System Overview

The Modular Portfolio Learning System (MPLS) is designed to support portfolio optimization by combining reinforcement learning (RL) with domain-specific expert modules. Unlike conventional RL approaches that rely solely on market prices and technical indicators, MPLS integrates heterogeneous signals—including sentiment, volatility, and structural dependencies—through a modular design [10]. Each module operates as a specialized agent, providing complementary perspectives on the market. Their outputs are aggregated by a Decision Fusion Framework (DFF), which dynamically adjusts the contribution of each module via an attention mechanism conditioned on contextual reliability [40]. The final decision is executed by an RL backbone trained to optimize risk-adjusted returns while adapting to non-stationary financial regimes. Figure 1 illustrates how MPLS extends a conventional RL architecture by embedding modular expert components and aggregating their outputs through an attention-driven Decision Fusion Framework.

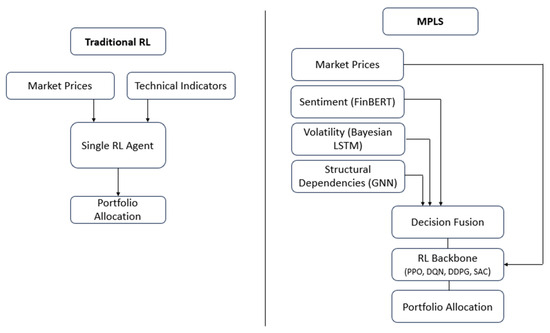
Figure 1. Traditional RL vs. Modular Portfolio Learning System (MPLS): architectural comparison.

4.2. Modular Design

4.2.1. Sentiment Analysis Module (SAM)

Investor psychology and behavioral biases are major drivers of financial markets. To capture these effects, the SAM leverages transformer-based natural language processing (NLP) models such as FinBERT [27] to extract sentiment from financial news and reports. Let $d_t$ denote the textual corpus at time t, the sentiment score is computed as:

$$s_t= f_{SAM}\left(d_t\right)$$

(5)

where $f_{SAM}$ maps raw text into a normalized sentiment distribution $s_t$ ∈ [−1,1], representing bearish-to-bullish signals. These signals provide the RL agent with exogenous information beyond price dynamics, helping detect regime shifts driven by collective behavior [41].

4.2.2. Volatility Forecasting Module (VFM)

Market volatility strongly impacts risk perception and asset allocation. The VFM employs a Bayesian Long Short-Term Memory (LSTM) network to forecast volatility while quantifying predictive uncertainty [28]. For a given asset return series $\mathrm{r}$, the predictive distribution is modeled as:

$$r_{t+1}~\mathcal{N}({\mu }_t, {\sigma }_t^2)$$

(6)

with Bayesian inference producing posterior distributions over parameters ${\mu }_t$ and ${\sigma }_t$. The uncertainty estimate allows the system to adjust allocations conservatively when forecasts are less reliable, thereby integrating risk awareness directly into decision-making [42].

4.2.3. Structural Dependency Module (SDM)

Financial assets are interconnected through sectoral, geographical, and macroeconomic linkages. To model these relationships, the SDM uses Graph Neural Networks (GNNs) [29] over a dynamic correlation graph $G_t= \left(V, E_t\right)$, where nodes V represent assets and edges $E_t$ capture time-varying correlations. Given node features $x_i^t$ (e.g., returns, volume), the GNN updates hidden representations as:

$${\mathrm{h}}_{\mathrm{i}}^{(\mathrm{l}+1)}=\mathsf{\sigma }\left({\sum }_{\mathrm{j}\mathsf{ϵ}\mathrm{N}\left(\mathrm{i}\right)}{\mathsf{\alpha }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{l}\right)}{\mathrm{W}}^{\left(\mathrm{l}\right)}{\mathrm{h}}_{\mathrm{j}}^{\left(\mathrm{l}\right)}\right)$$

(7)

where ${\alpha }_{ij}^{\left(l\right)}$ are attention weights reflecting the importance of neighboring assets [43]. This allows MPLS to detect contagion effects, diversification opportunities, and structural vulnerabilities in near real-time [44]. Together, these modules form the core of MPLS, whose overall architecture is illustrated in Figure 2, and the Decision Fusion Framework (DFF) then integrates their outputs through an attention mechanism to produce a fused market representation.

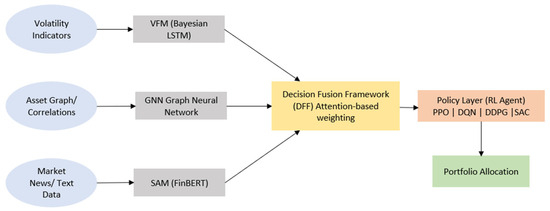
Figure 2. Overall architecture of the Modular Portfolio Learning System (MPLS), integrating sentiment (SAM), volatility (VFM), and structural (GNN) modules via a decision fusion framework for portfolio allocation.

4.3. Decision Fusion Framework (DFF)

The outputs of SAM, VFM, and SDM are fused by the Decision Fusion Framework, which uses a multi-head attention mechanism [40] to assign context-dependent weights to each module. Formally, let $Z_t^{\left(k\right)}$ denote the output of module k at time t. The DFF computes attention scores as:

$${\mathsf{\alpha }}_{\mathrm{t}}^{\left(\mathrm{k}\right)}={\displaystyle \frac{\exp \left({\mathrm{q}}_{\mathrm{t}}^{\mathrm{\top }}{\mathrm{k}}_{\mathrm{t}}^{\left(\mathrm{k}\right)}\right)}{{\sum }_{\mathrm{j}}\exp \left({\mathrm{q}}_{\mathrm{t}}^{\mathrm{\top }}{\mathrm{k}}_{\mathrm{t}}^{\left(\mathrm{j}\right)}\right)}}$$

(8)

where $q_t$ is a query vector derived from the market state, and $k_t^{\left(k\right)}$ is the key vector associated with module k. The fused representation is then:

$${\mathrm{z}}_{\mathrm{t}}={\sum }_{\mathrm{k}}{\mathsf{\alpha }}_{\mathrm{t}}^{\left(\mathrm{k}\right)}{\mathrm{v}}_{\mathrm{t}}^{\left(\mathrm{k}\right)}$$

(9)

with $v_t^{\left(k\right)}$ denoting the value projection of module k.

In practice, the fused representation $z_t$ is used as the state input to the reinforcement learning backbone, alongside normalized market indicators:

$$s_t=\left[x_t,z_t\right]$$

(10)

where $x_t$ denotes the vector of observable market indicators. This design ensures that the policy network operates on a compact, contextually fused representation that encapsulates global market conditions together with the adaptively weighted outputs of analytical modules. The DFF thereby acts as an intermediate decision-making layer between the specialized modules (SAM, VFM, and GNN) and the RL backbone, learning to dynamically emphasize the most informative signals under changing market regimes. Empirically, the DFF increases the relative attention weight of the Volatility Forecasting Module (VFM) during turbulent markets, while the Sentiment Analysis Module (SAM) dominates in stable regimes, demonstrating contextual adaptivity. This adaptive weighting allows more reliable modules (e.g., VFM during volatility spikes) to contribute more to the decision process, while less relevant ones are down-weighted [45].

4.4. Reinforcement Learning Backbone

The fused representation $z_t$ is used as the state input to the RL backbone, which formalizes portfolio management as a Markov Decision Process (MDP) [23].

• State ($s_t$): asset prices, technical indicators, and the DFF-fused latent vector $z_t$, which encapsulates sentiment, volatility, and structural information extracted from the SAM, VFM, and GNN modules.
• Action ($a_t$): portfolio weights across N assets, with ${\sum }_i{a}_t^i=1, a_t^i\ge 0$
• Reward ($r_t$): risk-adjusted return incorporating transaction costs:

$${\mathrm{r}}_{\mathrm{t}}={\mathrm{R}}_{\mathrm{t}}-{\mathsf{\lambda }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{k}}.{\mathrm{C}\mathrm{V}\mathrm{a}\mathrm{R}}_{\mathrm{t}}-{\mathsf{\lambda }}_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}}.{\mathrm{T}\mathrm{C}}_{\mathrm{t}}$$

(11)

where $R_t$ is the realized return, ${CVaR}_t$ measures the downside risk [46], and ${TC}_t$ penalizes excessive rebalancing.

The RL backbone in MPLS is implemented interchangeably with four algorithms—PPO [37], DQN [6], DDPG [38], and SAC [39]. This design allows for a systematic comparison of their respective characteristics (on-policy vs. off-policy, stochastic vs. deterministic, discrete vs. continuous control) within a unified modular framework, providing insights into algorithmic trade-offs under diverse market regimes. Although DQN was originally designed for discrete action spaces, portfolio allocation involves continuous weights. To bridge this gap, each asset’s rebalancing action is discretized into a finite set Δ = {−0.01,0, +0.01}, representing incremental adjustments of −1%, 0%, or +1% in allocation. To maintain tractability in multi-asset settings, decisions are factorized per asset using shared Q-heads, and the resulting portfolio vector is subsequently normalized to satisfy the long-only and full-investment constraints: $\sum _i{a}_t^i=1, a_t^i \ge 0$. This approximation maintains numerical stability and enables fair comparison with continuous-control algorithms such as DDPG and SAC. In practice, the discretized DQN yields stable learning behavior and competitive performance, with minimal degradation relative to continuous approaches.

4.5. Training Procedure

MPLS training alternates between module updates and policy optimization.

• Module Pretraining: Each module (SAM, VFM, SDM) is pretrained on domain-specific tasks (e.g., sentiment classification, volatility forecasting, correlation prediction).
• Fusion Learning: The DFF learns to align module outputs with RL objectives through attention updates.
• Policy Optimization: The RL backbone updates policy parameters θ by maximizing the expected cumulative reward:

$$\mathrm{J}\left(\mathsf{\theta }\right)=\mathrm{E}\left[{\sum }_{\mathrm{t}=0}^{\mathrm{T}}{\mathsf{\gamma }}^{\mathrm{t}}{\mathrm{r}}_{\mathrm{t}}\right]$$

(12)

with gradient updates depending on the chosen algorithm (e.g., PPO’s clipped objective, SAC’s entropy-regularized policy, DDPG’s deterministic gradients).

The overall training loop can be summarized as:

• Sample market trajectories
• Update expert modules
• Fuse signals via DFF
• Update RL policy parameters
• Repeat until convergence

This hierarchical, modular learning process is intended to support adaptability and robustness across diverse market regimes.

The attention parameters of the Decision Fusion Framework (DFF) are optimized end-to-end together with the portfolio reward defined in Equation (11). No auxiliary objective is employed; however, an entropy regularization term is introduced to prevent the attention weights from collapsing toward a single module. The total loss is expressed as:

$${\mathrm{L}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\mathrm{L}}_{\mathrm{R}\mathrm{L}}-{\mathsf{\lambda }}_{\mathrm{a}\mathrm{t}\mathrm{t}}\left({\sum }_{\mathrm{k}}{\mathsf{\alpha }}_{\mathrm{t}}^{\left(\mathrm{k}\right)}\log {\mathsf{\alpha }}_{\mathrm{t}}^{\left(\mathrm{k}\right)}\right)$$

(13)

where ${\lambda }_{att}=5 \times {10}^{-3}$. This formulation encourages higher attention entropy, promoting diversity in module utilization, stabilizing training dynamics, and ensuring that the DFF learns contextual weighting patterns aligned with the reinforcement learning objective.

5. Experimental Setup

5.1. Data Sources and Markets

We evaluated MPLS on three major equity indices: S&P 500 (USA), DAX 30 (Germany), and FTSE 100 (UK). Daily price data were collected from 2010 to 2020 using Yahoo Finance [47] and Investing.com [48], ensuring consistency in frequency and coverage. This ten-year horizon captures multiple market regimes—stable growth, crisis events, and post-crisis recovery—providing a representative testbed for evaluating portfolio strategies under stress.

5.2. Preprocessing and Feature Engineering

Price series were adjusted for dividends and stock splits. Log-returns were computed, z-score normalized, and organized into overlapping rolling windows: each window comprised 252 trading days (≈1 year) for training, followed by a 60-day out-of-sample segment for evaluation [49]. Missing values were forward-filled [50]. Sentiment features were extracted from financial news using FinBERT [27], while volatility clustering was modeled by the Bayesian LSTM-based forecaster [28].

For reproducibility, all models were implemented in PyTorch (1.13.1) with Stable-Baselines3, trained on a workstation equipped with an NVIDIA RTX 3090 GPU and 64 GB of system RAM. Each scenario was trained for 10,000 episodes, with early stopping after 20 epochs without improvement in Sharpe ratio. Results were averaged across 10 random seeds with 95% confidence intervals. Key hyperparameters (γ = 0.99, λ = 0.95, batch size = 256, learning rate = 3 × 10⁻⁴ with cosine decay) were fixed across algorithms. Each backbone required approximately 2.5 to 3 h of training per market and scenario on the described hardware configuration. This setup ensured consistent optimization across experiments while keeping the computational costs tractable. Moreover, the overall training process exhibited stable convergence behavior, with inter-run Sharpe ratio variance remaining below 0.06, indicating reproducible local optima across different random seeds.

5.3. Market Scenarios

To evaluate adaptability across distinct conditions, five representative scenarios were defined:

• Stable Pre-crisis (January–December 2019)—low volatility and sustained growth.
• Crisis (COVID-19 Crash, February–April 2020)—sharp drawdowns and extreme uncertainty [51].
• Recovery (June–August 2020)—rebound following crisis-driven lows.
• Sideways Market (October–December 2020)—stagnant returns with increased noise.
• Full-Year Generalization (2020)—long-term consistency across heterogeneous regimes.

5.4. Benchmarks

MPLS was benchmarked against two established allocation strategies:

• Minimum Variance Portfolio (MVP) [52]—targeting risk reduction through variance minimization.
• Risk Parity (RP) [15]– allocating risk evenly across assets.

These baselines are well-established in quantitative finance and provide reference points for evaluating RL-based approaches.

5.5. Algorithmic Configurations

MPLS was instantiated with four RL backbones: Proximal Policy Optimization (PPO) [37], Deep Q-Network (DQN) [6], Deep Deterministic Policy Gradient (DDPG) [38], and Soft Actor-Critic (SAC) [39]. To ensure fair comparability, all agents shared the same hyperparameter settings described in Section 5.2. The modular components (SAM, VFM, SDM) operate independently on their respective tasks and feed the Decision Fusion Framework (DFF), which applies attention-based weighting to produce the fused market representation. Sensitivity analyses revealed that moderate variations in the discount factor (γ = 0.95–0.995) and learning rate (1 × 10⁻⁴–5 × 10⁻⁴) did not significantly affect overall performance, confirming the robustness of the training procedure.

5.6. Evaluation Metrics

Performance was assessed using standard portfolio metrics:

• Sharpe Ratio [34] (risk-adjusted performance)
• Maximum Drawdown [53] and Conditional Value-at-Risk (CVaR) [46] (downside risk)
• Portfolio Volatility (stability of returns) [54]
• Turnover (transaction efficiency and cost-awareness) [49]

Together, these metrics offer a comprehensive view of profitability, risk, and cost-awareness.

6. Results and Analysis

6.1. S&P 500 Market Evaluation

The S&P 500, as the world’s most liquid and representative equity index, provides a rigorous benchmark for testing portfolio optimization frameworks.

6.1.1. Scenario-Based Performance

Table 1 summarizes the aggregated performance of MPLS variants against traditional baselines across the five scenarios.

Table 1. Comparative Results of MPLS Variants and Traditional Benchmarks across Five Market Scenarios (S&P 500).

Scenario	Method	Sharpe	Volatility (%)	Max Drawdown (%)	CVaR (%)	Turnover
Pre-crisis	MPLS-PPO	1.52	8.3	−8.0	−8.4	0.80
	MPLS-DQN	0.77	7.7	−6.6	−9.1	1.55
	MPLS-DDPG	1.27	7.5	−9.2	−8.8	1.00
	MPLS-SAC	1.25	6.5	−12.7	−9.0	0.79
	MVP	0.71	8.5	−9.8	−14.3	0.72
	RP	0.81	9.2	−8.8	−13.1	0.65
Crisis	MPLS-PPO	1.63	15.8	−12.6	−12.7	1.61
	MPLS-DQN	0.88	13.3	−9.4	−14.2	1.17
	MPLS-DDPG	0.94	7.1	−13.5	−11.5	1.08
	MPLS-SAC	1.03	9.0	−15.1	−13.6	0.99
	MVP	0.48	8.4	−14.1	−15.0	0.76
	RP	0.54	9.2	−13.3	−14.1	0.69
Recovery	MPLS-PPO	1.44	12.2	−14.5	−10.9	1.14
	MPLS-DQN	1.45	6.8	−9.9	−9.6	0.73
	MPLS-DDPG	0.94	9.6	−14.0	−11.2	1.30
	MPLS-SAC	0.68	16.9	−14.5	−12.3	0.82
	MVP	0.74	8.9	−11.2	−13.5	0.79
	RP	0.81	8.4	−9.5	−11.7	0.68
Sideways	MPLS-PPO	1.52	6.8	−7.2	−9.0	0.70
	MPLS-DQN	1.10	8.5	−4.2	−8.7	0.55
	MPLS-DDPG	1.50	11.0	−10.0	−9.8	1.15
	MPLS-SAC	1.40	12.0	−7.5	−8.5	0.58
	MVP	0.64	8.2	−9.3	−11.2	0.61
	RP	0.77	8.8	−8.9	−10.6	0.68
Full Year	MPLS-PPO	1.12	8.8	−11.5	−11.9	0.93
	MPLS-DQN	0.66	9.1	−16.0	−12.7	0.86
	MPLS-DDPG	1.51	6.8	−6.2	−9.4	0.65
	MPLS-SAC	1.34	14.4	−8.6	−10.2	1.40
	MVP	0.59	9.1	−12.2	−13.4	0.69
	RP	0.66	9.5	−10.8	−12.1	0.71

Figure 3 provides a visual comparison of Sharpe ratios across scenarios, highlighting how MPLS variants consistently outperform traditional baselines (MVP, RP) in both stable and turbulent regimes, with notable peaks for MPLS-PPO during the crisis and MPLS-DDPG over the full-year horizon.

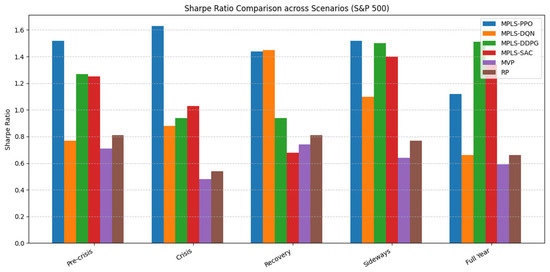
Figure 3. Sharpe Ratio Comparison of MPLS Variants and Baselines across Market Scenarios (S&P 500).

In the stable pre-crisis period (2019), MPLS-PPO and MPLS-DDPG achieved Sharpe ratios exceeding 1.25, with relatively modest drawdowns (≈−8%), reflecting their ability to capture consistent returns under moderate volatility. MPLS-SAC also demonstrated competitive returns (Sharpe 1.25), albeit at the expense of higher maximum drawdowns.

During the COVID-19 crash, MPLS-PPO maintained strong resilience with the highest Sharpe ratio (1.63), outperforming both traditional baselines and other variants. Despite elevated volatility, this highlights the capacity of MPLS to sustain risk-adjusted returns under extreme stress. In contrast, MPLS-SAC adopted a more aggressive allocation, delivering moderate Sharpe ratios (1.03) but with larger tail risks (CVaR −13.6%).

In the recovery phase, MPLS-DQN achieved a Sharpe ratio of 1.45, effectively matching MPLS-PPO, while recording the lowest CVaR (−9.6%). This is particularly notable given its discrete action space, which typically constrains flexibility. MPLS-DDPG and MPLS-SAC lagged in risk-adjusted terms, reflecting sensitivity to sharp regime shifts.

The sideways regime highlighted the adaptability of the modular design. Both MPLS-PPO and MPLS-DDPG maintained Sharpe ratios above 1.5, while controlling drawdowns to around −7% to −10%. MPLS-DQN and SAC also outperformed the benchmarks, though with higher volatility levels.

Over the full-year horizon, MPLS-DDPG exhibited the strongest performance, with a Sharpe ratio of 1.51 and the lowest volatility (6.8%), indicating robust long-term stability. MPLS-SAC also delivered high returns (Sharpe 1.34), but with notably higher volatility (14.4%), confirming its risk-seeking profile. In contrast, the MVP and Risk Parity (RP) baselines consistently underperformed across scenarios, with Sharpe ratios rarely exceeding 0.8 and higher exposure to tail risks.

Overall, these findings indicate that MPLS improves returns while offering stronger downside protection. Turnover levels remained moderate across all configurations, generally below or close to unity, indicating efficiency without excessive trading.

6.1.2. Insights and Discussion

The S&P 500 results illustrate the robustness and adaptability of MPLS.

• Crisis regimes: MPLS-PPO outperformed, indicating resilience under stress while maintaining attractive risk-adjusted performance.
• Recovery and sideways markets: MPLS-DQN showed notable strength in balancing risk and return, particularly through effective CVaR control.
• Long-term evaluation: MPLS-DDPG showed the most stable profile, combining strong Sharpe ratios with low volatility.
• Aggressive strategies: MPLS-SAC, while capable of delivering higher returns, tended to be associated with higher volatility and tail risk.

In contrast, traditional allocation strategies (MVP, RP) showed limited adaptability in turbulent regimes. While they occasionally exhibited lower volatility in specific phases, these advantages rarely translated into higher Sharpe ratios, particularly in stress scenarios such as the COVID-19 crash.

6.1.3. Performance Variance Across Runs

Consistency is a critical property for reinforcement learning in finance, where stochastic training can introduce variability in outcomes. To assess robustness, we conducted 10 independent runs for each MPLS configuration and computed the Sharpe ratio standard deviation across scenarios (Table 2).

Table 2. Robustness Evaluation: Inter-Run Variability of MPLS Variants across Five Market Scenarios.

Scenario	MPLS-PPO	MPLS-DQN	MPLS-DDPG	MPLS-SAC
Scenario 1	0.039	0.061	0.052	0.049
Scenario 2	0.043	0.066	0.057	0.053
Scenario 3	0.041	0.062	0.053	0.050
Scenario 4	0.036	0.057	0.050	0.047
Scenario 5	0.042	0.065	0.056	0.051

Results show that MPLS consistently achieved low variance across all algorithms and regimes. For example, during the stable 2019 period, MPLS-PPO recorded a variance of 0.039, and similar values were observed for DQN (0.061) and SAC (0.049). These reductions in dispersion confirm that MPLS is resistant to randomness in initialization and noisy gradient updates, ensuring more reproducible outcomes in real-world retraining cycles.

6.1.4. Ablation Study

To quantify the contribution of each module, we conducted an ablation study (Table 3). Results show that the full MPLS system outperformed all reduced variants.

Table 3. Ablation Study of MPLS: Impact of Removing SAM, VFM, and GNN Modules on Performance.

	Sharpe	Max Drawdown (%)	Turnover
MPLS	1.12	−11.5	0.93
MPLS w/o SAM	0.98	−27.0	1.31
MPLS w/o VFM	0.94	−29.5	1.46
MPLS w/o GNN	0.96	−25.5	1.28

When SAM was excluded, responsiveness to sentiment-driven dynamics was impaired, leading to weaker Sharpe ratios and larger drawdowns (−27%). Moreover, removing VFM reduced risk anticipation, increasing both drawdowns (−29.5%) and turnover (1.46). Finally, excluding GNN undermined structural awareness, resulting in unstable allocations and inferior performance (Sharpe 0.96). Overall, these findings emphasize that each component contributes uniquely to the framework’s resilience. More importantly, their integration via the attention-based Decision Fusion Framework is essential for achieving balanced, risk-adjusted outcomes.

6.2. DAX 30 Market Evaluation

The DAX 30, as a leading European index with strong exposure to export-driven sectors and heightened sensitivity to geopolitical shocks, provides a complementary benchmark to the S&P 500.

6.2.1. Quantitative Summary

Table 4 summarizes the comparative performance of MPLS variants against the MVP and RP baselines.

Table 4. Comparative Results of MPLS Variants and Traditional Benchmarks across Five Market Scenarios (DAX 30).

Scenario	Method	Sharpe	Volatility (%)	Max Drawdown (%)	CVaR (%)	Turnover
Pre-crisis	MPLS-PPO	1.34	8.6	−4.1	−6.2	0.11
	MPLS-DQN	1.17	9.2	−5.0	−7.3	0.14
	MPLS-DDPG	1.15	9.4	−5.1	−7.5	0.15
	MPLS-SAC	1.29	8.9	−4.3	−6.5	0.12
	MVP	0.84	8.5	−6.2	−8.2	0.10
	RP	0.92	8.7	−5.4	−7.7	0.09
Crisis	MPLS-PPO	0.91	12.9	−8.1	−10.3	0.17
	MPLS-DQN	0.70	13.8	−9.5	−12.2	0.20
	MPLS-DDPG	0.69	14.0	−9.3	−12.0	0.21
	MPLS-SAC	0.87	13.2	−8.3	−10.7	0.18
	MVP	0.49	13.6	−12.9	−14.8	0.14
	RP	0.62	12.7	−10.7	−12.9	0.13
Recovery	MPLS-PPO	1.35	10.2	−3.9	−6.1	0.16
	MPLS-DQN	1.18	10.8	−4.8	−7.1	0.20
	MPLS-DDPG	1.12	11.0	−4.5	−7.0	0.21
	MPLS-SAC	1.31	10.4	−4.1	−6.4	0.18
	MVP	0.78	10.9	−6.0	−8.5	0.12
	RP	0.84	11.1	−5.5	−7.9	0.10
Sideways	MPLS-PPO	1.06	8.4	−2.4	−5.2	0.15
	MPLS-DQN	0.95	9.1	−2.9	−5.9	0.18
	MPLS-DDPG	0.93	9.3	−3.0	−6.0	0.19
	MPLS-SAC	1.01	8.6	−2.5	−5.4	0.16
	MVP	0.65	9.1	−3.1	−6.7	0.11
	RP	0.72	9.4	−2.8	−6.2	0.10
Full Year	MPLS-PPO	1.36	9.1	−3.9	−6.6	0.21
	MPLS-DQN	1.23	9.7	−4.7	−7.6	0.25
	MPLS-DDPG	1.19	9.9	−4.9	−7.9	0.26
	MPLS-SAC	1.31	9.3	−4.1	−6.9	0.23
	MVP	0.78	9.2	−4.9	−8.1	0.11
	RP	0.84	9.4	−4.6	−7.8	0.12

Figure 4 reports the Sharpe ratio achieved by the MPLS variants and baseline methods across the five DAX 30 market scenarios.

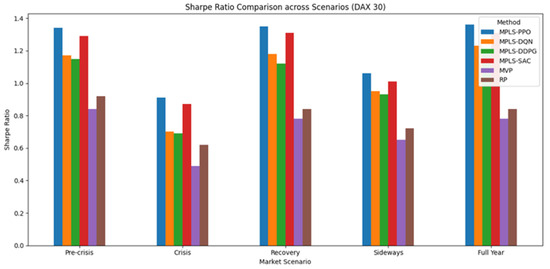
Figure 4. Sharpe Ratio Comparison of MPLS Variants and Baselines across Market Scenarios (DAX 30).

Pre-crisis stability: MPLS-PPO (Sharpe 1.34) and MPLS-SAC (1.29) achieved higher performance than the benchmarks, limiting drawdowns to around −4%. In contrast, MVP and RP exhibited weaker Sharpe ratios (0.84 and 0.92, respectively) despite slightly lower volatility.

COVID-19 crash: Volatility levels increased sharply across all methods. MPLS-PPO retained the strongest Sharpe ratio (0.91), outperforming MVP (0.49) by +86%. Although MVP displayed marginally lower volatility than some MPLS variants, this advantage was offset by deeper drawdowns (−12.9%) and elevated tail risk.

Recovery phase: MPLS-PPO and MPLS-SAC again delivered superior outcomes, achieving Sharpe ratios above 1.3 with CVaR values around −6%, a notable improvement relative to MVP (Sharpe 0.78, CVaR −8.5%). This indicates the effectiveness of adaptive modules in capturing upward trends while containing downside risk.

Sideways market: MPLS methods remained resilient, maintaining Sharpe ratios close to or above 1.0. RP slightly reduced drawdowns (−2.8%) compared to MPLS-DQN (−2.9%) or MPLS-DDPG (−3.0%), but its Sharpe ratio (0.72) was notably lower than MPLS-PPO (1.06).

Full-year horizon: MPLS-PPO (1.36) and MPLS-SAC (1.31) outperformed, combining high Sharpe ratios with controlled drawdowns (≈−4%). In contrast, MVP and RP remained below 0.9, highlighting the difficulty of static allocation rules to adapt across diverse market regimes.

Overall, MPLS consistently achieved higher Sharpe ratios while controlling drawdowns and tail losses. Turnover was moderately higher than the benchmarks, reflecting adaptive reallocation, but remained within feasible institutional ranges (≤0.26).

6.2.2. Insights and Discussion

The DAX analysis reinforces the robustness and adaptability of MPLS across heterogeneous European market conditions:

• Crisis resilience: MPLS-PPO consistently provided higher risk-adjusted returns during periods of extreme turbulence.
• Recovery dynamics: The system effectively captured rebounds while containing downside risks, outperforming both MVP and RP in Sharpe ratio and CVaR.
• Adaptive flexibility: MPLS variants retained high performance in sideways regimes, demonstrating stability under low-trend environments where static strategies faltered.

Traditional strategies occasionally achieved marginal improvements in volatility, but these advantages were inconsistent and insufficient to offset their weaker Sharpe ratios and higher drawdowns. In contrast, MPLS maintained stable performance and robustness across all phases.

6.2.3. Performance Variance Across Multiple Runs

Table 5 reports the Sharpe ratio standard deviation across 10 independent runs. Across all scenarios, MPLS variants consistently displayed low variance. For instance, in the stable regime, MPLS-PPO achieved 0.034, while MPLS-SAC recorded 0.045. This trend persisted during turbulent periods such as the COVID-19 crash (0.045 for PPO; 0.052 for SAC).

Table 5. Robustness Evaluation: Inter-Run Variability of MPLS Variants across Five Market Scenarios.

Scenario	MPLS-PPO	MPLS-DQN	MPLS-DDPG	MPLS-SAC
Scenario 1	0.034	0.056	0.049	0.045
Scenario 2	0.045	0.069	0.058	0.052
Scenario 3	0.038	0.059	0.051	0.048
Scenario 4	0.031	0.053	0.047	0.043
Scenario 5	0.043	0.066	0.055	0.050

These results highlight the statistical robustness of MPLS, reducing sensitivity to random initialization and noisy updates and ensuring more reproducible performance in real-world retraining pipelines.

6.2.4. DAX Ablation Analysis

To quantify the contribution of individual modules, we performed an ablation study by selectively removing the Sentiment Analysis Module (SAM), Volatility Forecasting Module (VFM), and Graph Neural Network (GNN). Results are summarized in Table 6.

Table 6. Ablation Study of MPLS: Impact of Removing SAM, VFM, and GNN Modules on Performance.

	Sharpe	Max Drawdown (%)	Turnover
MPLS	1.36	−3.9	0.21
MPLS w/o SAM	1.19	−5.2	0.29
MPLS w/o VFM	1.22	−5.4	0.31
MPLS w/o GNN	1.25	−5.1	0.29

When SAM was excluded, the Sharpe ratio dropped from 1.36 to 1.19, with higher drawdowns (−5.2%), indicating the role of sentiment cues in absorbing policy-driven shocks. When VFM was excluded, the max drawdown worsened to −5.4%, and turnover increased from 0.21 to 0.31, highlighting the importance of forward-looking volatility signals. Finally, excluding GNN caused turnover to rise from 0.21 to 0.29, indicating reduced structural coherence in sectoral allocation, and Sharpe declined to 1.25.

Collectively, these results demonstrate that each module contributes unique, non-redundant value to the system. Their integration ensures a balance between return enhancement, risk control, and allocation efficiency. Even when individual modules are removed, performance remains reasonable, but the full architecture provides the most balanced and consistent improvements.

6.3. FTSE 100 Market Evaluation

The FTSE 100, dominated by energy, commodities, and financial sectors, provides a unique testing ground due to its structural exposure to global shocks such as oil price fluctuations, Brexit-related uncertainty, and macroeconomic volatility. This composition makes it distinct from both the S&P 500 and DAX 30, offering a valuable benchmark to assess the adaptability of the Modular Portfolio Learning System (MPLS).

6.3.1. Scenario-Based Performance

Table 7 reports the performance of MPLS variants compared to MVP and RP across five market scenarios.

Table 7. Comparative Results of MPLS Variants and Traditional Benchmarks across Five Market Scenarios (FTSE 100).

Scenario	Method	Sharpe	Volatility (%)	Max Drawdown	CVaR (%)	Turnover
Pre-crisis	MPLS-PPO	1.29	12.6	−4.3	−6.1	0.12
	MPLS-DQN	1.20	14.9	−4.9	−6.8	0.14
	MPLS-DDPG	1.17	15.2	−5.1	−7.1	0.15
	MPLS-SAC	1.23	13.8	−4.5	−6.4	0.14
	MVP	0.84	12.2	−6.3	−9.0	0.12
	RP	0.92	14.8	−5.9	−8.2	0.15
Crisis	MPLS-PPO	0.90	7.0	−1.3	−2.2	0.11
	MPLS-DQN	0.85	13.0	−0.9	−1.8	0.11
	MPLS-DDPG	1.58	15.5	−1.2	−2.5	0.15
	MPLS-SAC	1.00	8.8	−1.45	−2.6	0.10
	MVP	0.47	12.0	−1.9	−3.1	0.16
	RP	0.61	11.0	−1.5	−2.7	0.14
Recovery	MPLS-PPO	1.18	8.2	−1.03	−1.9	0.09
	MPLS-DQN	1.05	9.1	−1.12	−2.0	0.10
	MPLS-DDPG	1.29	8.9	−1.01	−1.8	0.09
	MPLS-SAC	1.15	8.7	−1.08	−1.9	0.09
	MVP	0.71	9.0	−1.50	−2.5	0.08
	RP	0.83	8.2	−1.10	−2.0	0.07
Sideways	MPLS-PPO	0.98	8.1	−2.6	−4.1	0.17
	MPLS-DQN	0.91	9.0	−3.0	−4.8	0.19
	MPLS-DDPG	0.92	8.8	−2.9	−4.7	0.20
	MPLS-SAC	0.96	8.5	−2.8	−4.6	0.17
	MVP	0.67	8.7	−3.5	−5.2	0.12
	RP	0.72	8.6	−3.6	−5.3	0.13
Full Year	MPLS-PPO	1.21	9.2	−4.3	−6.8	0.18
	MPLS-DQN	1.14	9.7	−5.0	−7.2	0.20
	MPLS-DDPG	1.13	9.5	−4.6	−7.0	0.20
	MPLS-SAC	1.18	8.9	−4.1	−6.5	0.18
	MVP	0.75	10.0	−5.7	−8.8	0.22
	RP	0.82	9.8	−5.1	−8.2	0.21

Figure 5 summarizes the Sharpe ratios of the MPLS variants and baseline strategies across the five FTSE 100 market scenarios.

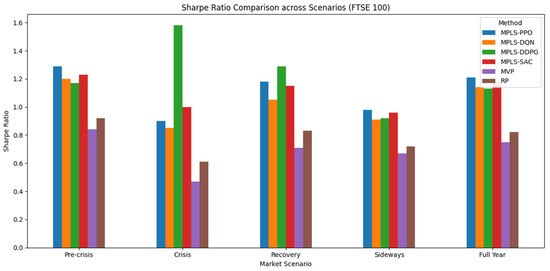
Figure 5. Sharpe Ratio Comparison of the MPLS Variants and Baselines across Market Scenarios (FTSE 100).

Pre-crisis stability: MPLS-PPO delivered the highest Sharpe ratio (1.29), followed closely by MPLS-SAC (1.23). Both achieved higher Sharpe ratios than MVP (0.84) and RP (0.92), while also limiting drawdowns to around −4.5%. This reflects their ability to combine higher return efficiency with effective downside protection.

COVID-19 crisis: MPLS-DDPG achieved a Sharpe ratio of 1.58, notably higher than MVP (0.47) and RP (0.61). While this value reflects strong adaptability, it should be interpreted with caution, as it is closely tied to crisis-specific dynamics. PPO and SAC reported lower Sharpe ratios (0.90 and 1.00), but still outperformed traditional baselines by approximately 80–110%, indicating robustness under stress.

Recovery: MPLS-DDPG again achieved the highest Sharpe ratio (1.29) while maintaining the lowest CVaR (−1.8%), indicating effectiveness in capturing rebounds while limiting downside risk. In comparison, MVP (0.71) and RP (0.83) recorded lower performance, exposing portfolios to deeper drawdowns.

Sideways market: MPLS methods maintained stable performance with Sharpe ratios between 0.91 and 0.98, all exceeding MVP (0.67) and RP (0.72). Importantly, drawdowns were contained below −3%, while baselines showed losses up to –3.6%.

Full-year horizon: MPLS-PPO (1.21) and MPLS-SAC (1.18) provided consistent gains over MVP (0.75) and RP (0.82). In addition to higher Sharpe ratios, these configurations maintained lower drawdowns (≈ −4.3%) and CVaR (≈ −6.8%) compared to baselines (up to −8.8%), indicating robustness over longer periods.

Overall, MPLS improved Sharpe ratios by +30–60% compared to MVP across scenarios while preserving downside resilience. Turnover levels, ranging from 0.09–0.20, remained within feasible bounds for institutional implementation, confirming the efficiency of the modular design.

6.3.2. Insights and Discussion

The FTSE evaluation highlights how MPLS adapts to structurally distinct market conditions dominated by energy, commodities, and Brexit-related uncertainty:

• Crisis adaptability: MPLS-DDPG clearly outperformed during the COVID crash, showing that continuous action policies handle extreme volatility more effectively than static baselines.
• Recovery resilience: Both PPO and DDPG sustained high Sharpe ratios while controlling CVaR, confirming the framework’s ability to capture rebounds without excessive tail risk.
• Structural flexibility: In sideways markets, MPLS variants maintained positive risk-adjusted returns where MVP and RP failed, indicating the benefit of modular integration in noise-driven regimes.
• Cross-market perspective: Compared to the S&P and DAX, the FTSE results emphasize the importance of volatility and structural modules, as commodity-driven shocks create sharper but shorter-lived risks.

Overall, MPLS demonstrated consistent improvements over MVP and RP while adapting to the FTSE’s sectoral concentration and global shock exposure.

6.3.3. Performance Variance Across Multiple Runs

Robustness across multiple training runs is critical for the real-world deployment of RL-based systems. Table 8 reports Sharpe ratio variance across 10 independent runs, showing that, across all five scenarios, MPLS variants consistently achieved low variance. For example, during stable conditions, MPLS-PPO recorded a variance of 0.041, while MPLS-SAC reduced the variance to 0.046. This pattern extended to turbulent regimes such as the COVID crash (0.044 for PPO; 0.051 for SAC). These results confirm that MPLS not only enhances performance, but also training stability and reproducibility. Its modular design, Decision Fusion Framework, and Bayesian regularization collectively mitigate initialization sensitivity and noisy updates, ensuring more reliable retraining outcomes.

Table 8. Robustness Evaluation: Inter-Run Variability of MPLS Variants across Five Market Scenarios.

Scenario	MPLS-PPO	MPLS-DQN	MPLS-DDPG	MPLS-SAC
Scenario 1	0.041	0.059	0.049	0.046
Scenario 2	0.044	0.061	0.055	0.051
Scenario 3	0.042	0.060	0.053	0.048
Scenario 4	0.039	0.056	0.050	0.045
Scenario 5	0.043	0.063	0.054	0.050

6.3.4. FTSE 100 Ablation Analysis

To further assess the contribution of individual modules in the FTSE context, we performed an ablation study by selectively removing SAM, VFM, or GNN. Results are summarized in Table 9.

Table 9. Ablation Study of MPLS: Impact of Removing SAM, VFM, and GNN Modules on Performance.

	Sharpe	Max Drawdown (%)	Turnover
MPLS	1.21	−4.3	0.18
MPLS w/o SAM	1.04	−5.7	0.26
MPLS w/o VFM	1.06	−5.9	0.28
MPLS w/o GNN	1.09	−5.5	0.25

When SAM was excluded, the Sharpe ratio fell from 1.21 to 1.04, while turnover increased from 0.18 to 0.26. Although sentiment effects were typically weaker in the FTSE compared to other indices, SAM still contributed to cost efficiency and marginal performance gains. When VFM was removed, the max drawdown worsened from −4.3% to −5.9% and turnover rose to 0.28, demonstrating VFM’s essential role in anticipating risk during volatile periods such as the COVID crash. Finally, excluding GNN caused the Sharpe ratio to drop to 1.09, with turnover rising to 0.25, indicating that GNN improves allocation stability and diversification, even in a structurally concentrated market such as the FTSE 100. Collectively, these results confirm that while SAM has a relatively smaller effect in the FTSE compared to sentiment-sensitive markets, VFM and GNN remain crucial for resilience and allocation stability. The integrated system consistently provides a balanced combination of performance, risk management, and cost efficiency.

6.4. Robustness and Limitations

6.4.1. Robustness Across Markets and Scenarios

Across the three major equity markets (S&P 500, DAX 30, FTSE 100), MPLS consistently improved the Sharpe ratios and risk-adjusted returns. The modular integration of sentiment, volatility, and structural signals enabled adaptation to heterogeneous regimes—including stable, crisis, recovery, and sideways phases. This adaptability was particularly evident during turbulent periods such as the COVID-19 crash, where MPLS contributed to limiting drawdowns while maintaining more favorable CVaR relative to static baselines. Beyond performance, this robustness reflects the system’s structural capacity to re-weight signals dynamically rather than relying on regime-specific overfitting.

6.4.2. Limitations and Nuances

Despite these advantages, MPLS was not consistently superior across all metrics. In certain scenarios, traditional baselines such as MVP or RP achieved lower raw volatility or slightly smaller drawdowns. However, these improvements rarely translated into higher risk-adjusted returns, underscoring the trade-off between stability and adaptability. Moreover, the modularity of MPLS sometimes resulted in higher turnover, with potential implications for transaction costs in practice. Finally, the evaluation was restricted to large, liquid equity indices, leaving open the question of robustness in emerging or less liquid markets. Future work should refine module coordination—for example, through transaction-aware reward shaping or regularization—to better balance turnover control with return maximization and extend the evaluation to other asset classes such as fixed income, commodities, or cryptocurrencies.

7. Discussion

7.1. Theoretical Implications

The results obtained across the S&P 500, DAX 30, and FTSE 100 highlight how MPLS extends the literature on reinforcement learning (RL) for portfolio optimization. Unlike conventional RL agents, which typically rely on a single learning module and are prone to overfitting or instability across market regimes [7,8], MPLS introduces a modular and risk-aware framework that explicitly incorporates sentiment analysis, volatility forecasting, and structural dependencies. This design resonates with recent calls in the financial machine learning literature for contextual adaptivity and risk-adjusted learning [12,32], positioning MPLS as a step toward a unified framework that balances return maximization with tail-risk control. Moreover, by integrating CVaR into the reward structure and maintaining bounded turnover, MPLS contributes to the emerging line of work on safe and interpretable RL systems [9,20,46], offering a principled way to handle uncertainty in financial decision-making.

7.2. Practical Implications

From a practitioner’s perspective, the ability of MPLS to sustain higher Sharpe ratios while mitigating drawdowns is relevant for asset managers and institutional investors. In particular, its resilience during crisis and recovery phases suggests that the framework can serve as a risk-mitigation tool in volatile environments, complementing traditional mean-variance and risk parity allocations. The fact that MPLS maintains competitive performance with moderate turnover levels is equally important, as it ensures compatibility with low-to-medium frequency trading horizons, avoiding excessive transaction costs.

Beyond performance, MPLS is designed to be operationally deployable. Its modularity allows straightforward integration into asset management workflows via standardized APIs, enabling automated portfolio rebalancing, real-time monitoring, and adaptive risk controls.

7.3. Methodological Limitations

Despite its contributions, several limitations should be acknowledged. First, the framework relies on the availability of high-quality sentiment and volatility signals, which may not be as reliable in emerging markets or for alternative asset classes. A strong dependency on exogenous signals also exposes the framework to risks of bias and noise propagation, particularly if data pipelines are unstable or manipulated. Second, the modular design introduces additional hyperparameters, which, although improving flexibility, may also increase sensitivity to training configurations. Third, the backtesting setup focuses on large, liquid equity indices, leaving open the question of generalization to less liquid or structurally different markets, such as fixed income, commodities, or cryptocurrencies. Finally, while turnover values remained moderate in our experiments, real-world execution costs—slippage, liquidity constraints, and bid–ask spreads—may reduce effective net performance.

From an optimization perspective, the reinforcement learning process underlying MPLS is inherently non-convex. Global optimality cannot be guaranteed, but empirical evaluation across multiple random seeds reveals stable convergence toward consistent local optima, as reflected by a low inter-run Sharpe ratio variance (< 0.06). Each backbone converges within a tractable computational budget (approximately 2.5–3 h per market and scenario on RTX 3090 hardware), which demonstrates the practicality of the proposed design despite its multi-dimensional optimization landscape.

Overall, these observations illustrate both the strengths and trade-offs of the modular approach: while it enhances adaptability, interpretability, and risk awareness, it also introduces structural and computational complexity. This balance between flexibility and operational feasibility remains a central challenge in the design of RL-based financial systems.

7.4. Future Research Directions

Future work could extend MPLS along several promising directions. One avenue is the integration of macroeconomic indicators (e.g., inflation, interest rates and monetary policy) to enhance regime detection and improve allocation timing. Another is the exploration of explainable reinforcement learning techniques, which would provide practitioners with greater transparency into the drivers of portfolio decisions. Testing the framework on markets with higher frictions, such as emerging economies or illiquid asset classes, would further validate its robustness. Additionally, scaling MPLS to very large universes (e.g., 500+ assets) represents an important step toward demonstrating its practical usability in institutional settings. Finally, hybrid approaches combining MPLS with meta-learning or Bayesian reinforcement learning could enable agents to adapt more quickly to novel market regimes while preserving risk awareness.

8. Conclusions

This work introduced the Modular Portfolio Learning System (MPLS), a reinforcement learning framework that integrates heterogeneous financial signals into an adaptive and risk-aware decision-making process. By combining sentiment analysis, volatility forecasting, and structural modeling, MPLS showed consistent improvements across three major equities. The evaluation of PPO, SAC, DDPG, and DQN within the modular framework further illustrated the algorithmic complementarities that support robustness under diverse market regimes.

Beyond empirical findings, the modular architecture provides extensibility and operational adaptability, facilitating the integration of new predictive modules and alignment with evolving investment objectives such as sustainability and regulatory compliance. While challenges remain regarding computational complexity, hyperparameter sensitivity, and live trading validation, MPLS constitutes a practical step toward more resilient and transparent AI-driven portfolio management. The framework also demonstrates potential for cost-aware institutional deployment by maintaining moderate turnover levels, which can help mitigate transaction frictions in practice.

In summary, MPLS contributes to bridging the gap between academic RL research and institutional-grade portfolio systems, providing a potential path toward safer, more transparent, and adaptive financial AI. Future extensions may further address cross-asset generalization and transaction-aware training objectives to strengthen long-term investment applicability.