A Comparative Study of Quantum Haar Wavelet and Quantum Fourier Transforms for Quantum Image Transmission
Abstract
1. Introduction
- Extension of the QHWT into the domain of quantum image transmission as an encoding method, marking its first application beyond image representation and compression.
- Systematic comparative analysis of QFT- and QHWT-based transmission frameworks under identical experimental conditions.
- Evaluation of performance at the image level using PSNR, SSIM, and UQI, rather than relying solely on quantum state fidelity.
- Provision of practical insights for the design of noise-resilient quantum communication systems tailored to image data.
2. Related Works
3. Methodology
3.1. Input Image
3.2. Source Encoder and Decoder
3.3. Channel Encoder and Decoder
3.4. Quantum State Encoder
3.4.1. Representing Classical Bits as Qubits
3.4.2. Multi-Qubit State Construction
3.5. Quantum Fourier Transform (QFT)
3.5.1. General Definition
3.5.2. Matrix Form of QFT
3.5.3. Example: Two-Qubit Transformation
3.6. Inverse Quantum Fourier Transform (IQFT)
3.6.1. Mathematical Formulation of Decoding in the Noiseless Case
3.6.2. Mathematical Formulation of Decoding in the Presence of Noise
3.7. Quantum Haar Wavelet Transform (QHWT)
3.7.1. General Definition
3.7.2. Recursive Structure of Quantum Haar Matrices
3.7.3. Example: Two-Qubit Transformation
3.8. Inverse Quantum Haar Wavelet Transform (IQHWT)
3.8.1. Mathematical Formulation of Decoding in the Noiseless Case
3.8.2. Mathematical Formulation of Decoding in the Presence of Noise
3.9. Quantum Channel
3.9.1. Bit-Flip Noise
3.9.2. Phase-Flip Noise
3.9.3. Depolarizing Noise
3.9.4. Amplitude Damping
3.9.5. Phase Damping
3.9.6. Composite Channel Model
3.9.7. Noise Parameterization via SNR
3.10. Quantum State Decoder
4. Results and Discussion
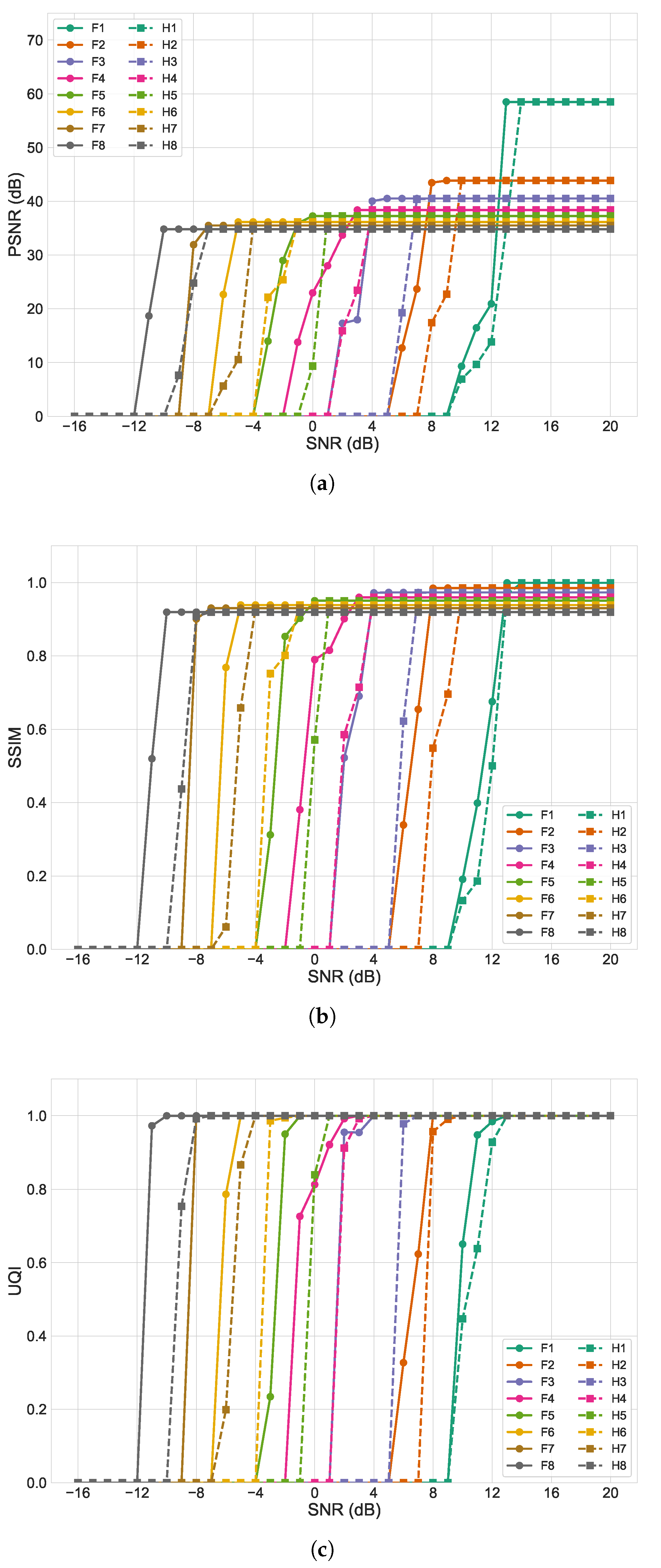
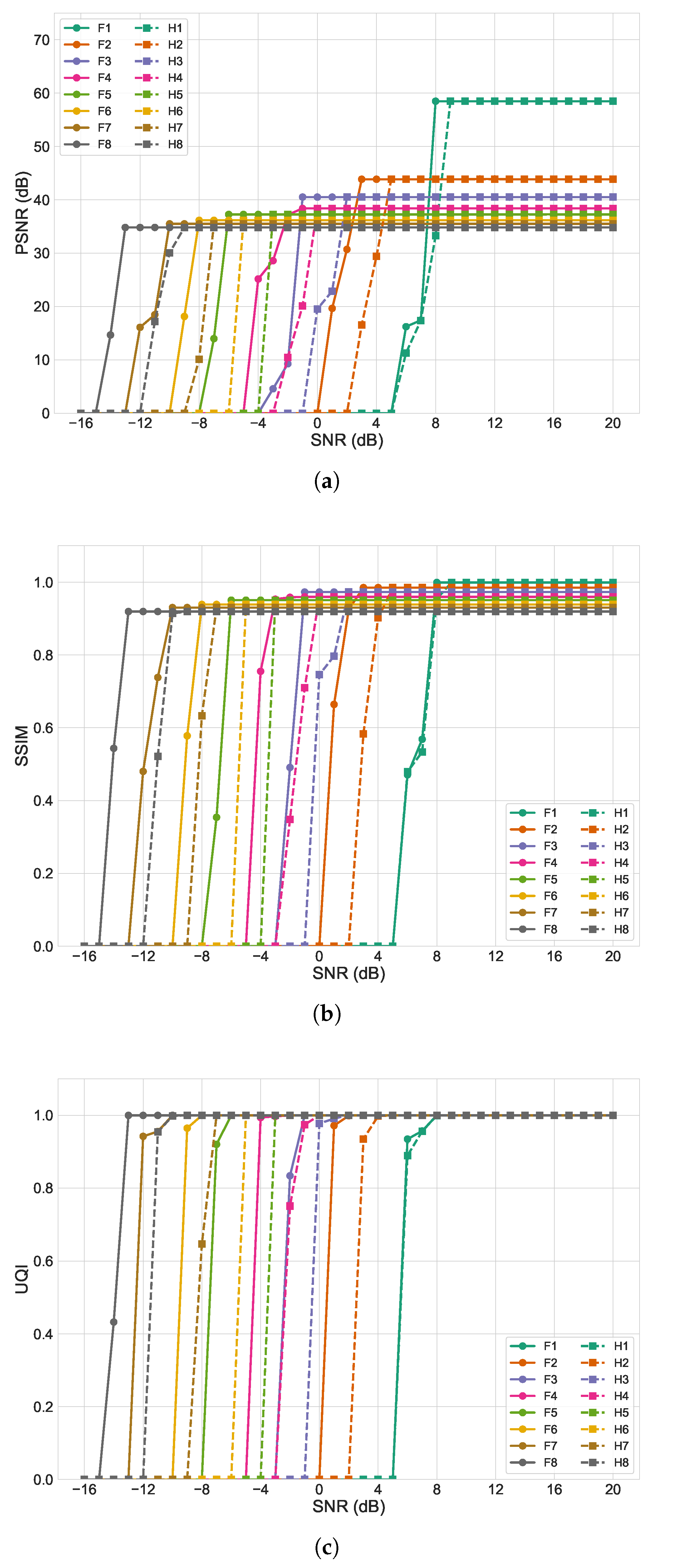
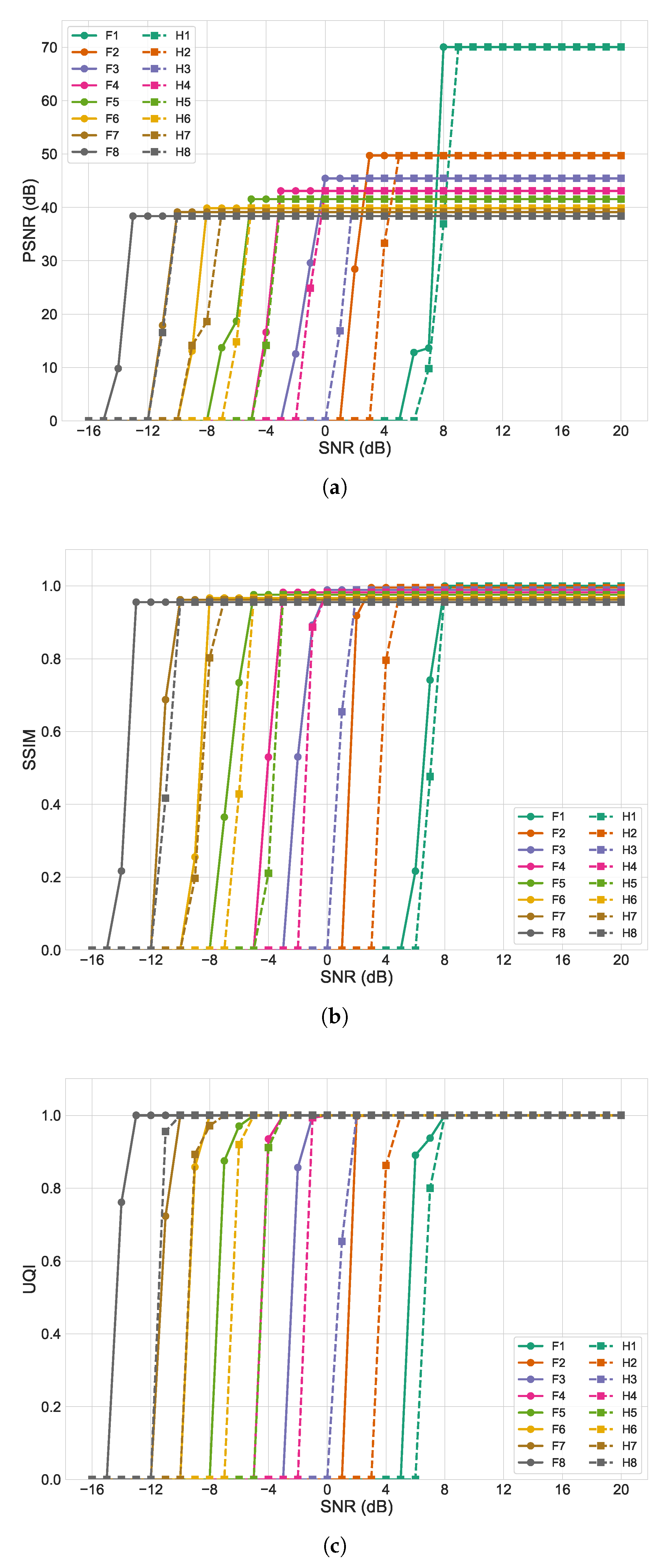
4.1. JPEG Image Transmission Under Uncoded Scenario
4.2. JPEG Image Transmission Under Channel-Coded Scenario
4.3. HEIF Image Transmission Under Uncoded Scenario
4.4. HEIF Image Transmission Under Channel-Coded Scenario
4.5. Sample of Decoded Images
4.6. Comparative Advantages of QFT in Noisy Quantum Image Transmission
4.7. Complexity and Hardware Realizability
4.8. Scalability
4.9. Simulation-Based Evaluation: Strengths and Applications
5. Conclusions and Future Work
5.1. Conclusions
5.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HEIF | High-Efficiency Image Format |
| JPEG | Joint Photographic Experts Group |
| LDPC | Low-Density Parity-Check |
| MIMO | Multi-Input Multi-Output |
| NISQ | Noisy Intermediate Scale Quantum |
| PSNR | Peak Signal-to-Noise Ratio |
| QEC | Quantum Error Correction |
| QFT | Quantum Fourier Transform |
| QHWT | Quantum Haar Wavelet Transform |
| QKD | Quantum Key Distribution |
| QP | Quantization Parameters |
| SNR | Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index Measure |
| UQI | Universal Quality Index |
References
- Wallace, G. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Hannuksela, M.M.; Lainema, J.; Malamal Vadakital, V.K. The High Efficiency Image File Format Standard [Standards in a Nutshell]. IEEE Signal Process. Mag. 2015, 32, 150–156. [Google Scholar] [CrossRef]
- Hasan, S.R.; Chowdhury, M.Z.; Sayem, M.; Jang, Y.M. Quantum Communication Systems: Vision, Protocols, Applications, and Challenges. IEEE Access 2023, 11, 15855–15877. [Google Scholar] [CrossRef]
- Sridhar, G.T.; P, A.; Tabassum, N. A Review on Quantum Communication and Computing. In Proceedings of the 2023 2nd International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 4–6 May 2023; pp. 1592–1596. [Google Scholar] [CrossRef]
- Leong, W.Y.; Leong, Y.Z.; Leong, W.S. Quantum Consumer Technology: Advancements in Coherence, Error Correction, and Scalability. In Proceedings of the 2024 International Conference on Consumer Electronics—Taiwan (ICCE-Taiwan), Taichung, Taiwan, 9–11 July 2024; pp. 79–80. [Google Scholar] [CrossRef]
- Zou, N. Quantum Entanglement and Its Application in Quantum Communication. J. Phys. Conf. Ser. 2021, 1827, 012120. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Ganearachchi, Y.; Fernando, T.; Fernando, A. Quantum communications for image transmission over error-prone channels. Electron. Lett. 2024, 60, e13300. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Kushantha, N.; Fernando, T.; Fernando, A. A Robust Multi-Qubit Quantum Communication System for Image Transmission over Error Prone Channels. IEEE Trans. Consum. Electron. 2025, 1. [Google Scholar] [CrossRef]
- Deb, S.; Pan, W. Quantum Image Compression: Fundamentals, Algorithms, and Advances. Computers 2024, 13, 185. [Google Scholar] [CrossRef]
- Fijany, A.; Williams, C.P. Quantum Wavelet Transforms: Fast Algorithms and Complete Circuits. In Quantum Computing and Quantum Communications, Proceedings of the First NASA International Conference, QCQC ’98, Palm Springs, CA, USA, 17–20 February 1998, Selected Papers; Lecture Notes in Computer Science; Williams, C.P., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1509, pp. 10–33. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Is there a relationship between peak-signal-to-noise ratio and structural similarity index measure? IET Image Process. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Caleffi, M.; Simonov, K.; Cacciapuoti, A.S. Beyond Shannon Limits: Quantum Communications Through Quantum Paths. IEEE J. Sel. Areas Commun. 2023, 41, 2707–2724. [Google Scholar] [CrossRef]
- Noirie, L. From Existing Quantum Key Distribution Systems Towards Future Quantum Networks. In Proceedings of the 2024 13th International Conference on Communications, Circuits and Systems (ICCCAS), Xiamen, China, 10–12 May 2024; pp. 339–344. [Google Scholar] [CrossRef]
- Peelam, M.S.; Sai, S.; Chamola, V. Explorative Implementation of Quantum Key Distribution Algorithms for Secure Consumer Electronics Networks. IEEE Trans. Consum. Electron. 2024, 70, 5576–5584. [Google Scholar] [CrossRef]
- Brazaola-Vicario, A.; Ruiz, A.; Lage, O.; Jacob, E.; Astorga, J. Quantum key distribution: A survey on current vulnerability trends and potential implementation risks. Opt. Contin. 2024, 3, 1438–1460. [Google Scholar] [CrossRef]
- Yan, X.Y.; Zhou, N.R.; Gong, L.H.; Wang, Y.Q.; Wen, X.J. High-dimensional quantum key distribution based on qudits transmission with quantum Fourier transform. Quantum Inf. Process. 2019, 18, 271. [Google Scholar] [CrossRef]
- Huang, D.; Chen, Z. Quantum Key Distribution Based on Multi-qubit Hadamard Matrices. In Proceedings of the 2008 The Fourth International Conference on Information Assurance and Security, Naples, Italy, 8–10 September 2008; pp. 333–337. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Ul Ain, N.; Waqar, M.; Bilal, A.; Kim, A.; Ali, H.; Ullah Tariq, U.; Shahroz Nadeem, M. A Novel Approach Based on Quantum Key Distribution Using BB84 and E91 Protocol for Resilient Encryption and Eavesdropper Detection. IEEE Access 2025, 13, 32819–32833. [Google Scholar] [CrossRef]
- Zulfa, M.F.; Anwar, K. Development of Quantum Key Distribution (QKD) with E91 Protocol for Future Secure Quantum Networks. J. Phys. Conf. Ser. 2025, 2980, 012038. [Google Scholar] [CrossRef]
- Langenfeld, S.; Welte, S.; Hartung, L.; Daiss, S.; Thomas, P.; Morin, O.; Distante, E.; Rempe, G. Quantum Teleportation between Remote Qubit Memories with Only a Single Photon as a Resource. Phys. Rev. Lett. 2021, 126, 130502. [Google Scholar] [CrossRef]
- Fu, Y.; Li, D.; Hua, X.; Jiang, Y.; Zhu, Y.; Zhou, J.; Yang, X.; Tan, Y. A Scheme for Quantum Teleportation and Remote Quantum State Preparation of IoT Multiple Devices. Sensors 2023, 23, 8475. [Google Scholar] [CrossRef]
- Harraz, S.; Cong, S.; Nieto, J.J. Protected Quantum Teleportation Through Noisy Channel by Weak Measurement and Environment-Assisted Measurement. IEEE Commun. Lett. 2022, 26, 528–531. [Google Scholar] [CrossRef]
- Mastriani, M. Multi-qubit teleportation and multi-bit superdense coding via cascade splitting. Opt. Quantum Electron. 2023, 55, 1026. [Google Scholar] [CrossRef]
- Li, C.L.; Yin, H.L.; Chen, Z.B. Asynchronous Quantum Repeater using Multiple Quantum Memory. Rep. Prog. Phys. 2024, 87, 127901. [Google Scholar] [CrossRef] [PubMed]
- Janani, T.; Brindha, M. A secure medical image transmission scheme aided by quantum representation. J. Inf. Secur. Appl. 2021, 59, 102832. [Google Scholar] [CrossRef]
- Johnson, S.; Rarity, J.; Padgett, M. Transmission of quantum-secured images. Sci. Rep. 2024, 14, 11579. [Google Scholar] [CrossRef] [PubMed]
- Hariprasad, Y.; Iyengar, S.; Chaudhary, N.K. Securing the Future: Advanced Encryption for Quantum-Safe Video Transmission. IEEE Trans. Consum. Electron. 2025, 71, 140–153. [Google Scholar] [CrossRef]
- Mallick, B.; Parida, P.; Nayak, C.; Khalifa, T.; Kumar Panda, M.; Ali, N.; Uttam Patil, G.; Prasad, B. Multi-Channel Multi-Protocol Quantum Key Distribution System for Secure Image Transmission in Healthcare. IEEE Access 2025, 13, 62476–62505. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Pollwaththage, N.; Ganearachchi, Y.; Fernando, T.; Fernando, A. Quantum Communication for Video Transmission Over Error-Prone Channels. IEEE Trans. Consum. Electron. 2025, 71, 1148–1155. [Google Scholar] [CrossRef]
- Thakur, V.S.; Kumar, A.; Das, J.; Dev, K.; Magarini, M. Quantum Error Correction Codes in Consumer Technology: Modeling and Analysis. IEEE Trans. Consum. Electron. 2024, 70, 7102–7111. [Google Scholar] [CrossRef]
- Roffe, J. Quantum error correction: An introductory guide. Contemp. Phys. 2019, 60, 226–245. [Google Scholar] [CrossRef]
- Thakur, V.S.; Kumar, A.; Dev, K. Quantum Error Correction in Green Communications: Towards Sustainable Quantum Networks. IEEE Trans. Green Commun. Netw. 2025, 1. [Google Scholar] [CrossRef]
- Chatterjee, A.; Phalak, K.; Ghosh, S. Quantum Error Correction for Dummies. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 17–22 September 2023; Volume 1, pp. 70–81. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Fernando, T.; Ganearachchi, Y.; Samarathunga, P.; Fernando, A. Quantum Communication-Based Image Transmission with Transmit and Receive Diversity in MIMO Communication Systems. IEEE Trans. Consum. Electron. 2025, 71, 2500–2507. [Google Scholar] [CrossRef]
- Zhou, S.S.; Loke, T.; Izaac, J.A.; Wang, J.B. Quantum Fourier transform in computational basis. Quantum Inf. Process. 2017, 16, 82. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Fernando, T.; Fernando, A. High-Fidelity Image Transmission in Quantum Communication with Frequency Domain Multi-Qubit Techniques. Algorithms 2025, 18, 501. [Google Scholar] [CrossRef]
- Mu, X.; Wang, H.; Bao, R.; Wang, S.; Ma, H. An improved quantum watermarking using quantum Haar wavelet transform and Qsobel edge detection. Quantum Inf. Process. 2023, 22, 223. [Google Scholar] [CrossRef]
- Mukhamedieva, D.T.; Sobirov, R.A.; Turg’unova, N.; Samijonov, B.N. Quantum Fourier Transform in Image Processing. In Information Technologies and Intelligent Decision Making Systems, Proceedings of the Third International Scientific and Practical Conference, ITIDMS 2023, Moscow, Russia, 12–14 December 2023, Revised Selected Papers; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2024; pp. 143–151. [Google Scholar] [CrossRef]
- Camps, D.; Van Beeumen, R.; Yang, C. Quantum Fourier transform revisited. Numer. Linear Algebra Appl. 2021, 28, e2331. [Google Scholar] [CrossRef]
- Mahmud, N.; El-Araby, E. Dimension Reduction Using Quantum Wavelet Transform on a High-Performance Reconfigurable Computer. Int. J. Reconfigurable Comput. 2019, 2019, 1949121. [Google Scholar] [CrossRef]
- Devarapalli, S.H.R.; Jadhav, H.; Dontabhaktuni, J. Image compression using quantum wavelet transforms. In Quantum Computing, Communication, and Simulation V, Proceedings of the QUANTUM WEST, San Francisco, CA, USA, 25–31 January 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13391, p. 1339117. [Google Scholar] [CrossRef]
- Lin, T.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision–ECCV 2014, Proceedings of the 13th European Conference, Zurich, Switzerland, 6–12 September 2014, Proceedings, Part V; Lecture Notes in Computer Science; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; Volume 8693, pp. 740–755. [Google Scholar] [CrossRef]
- Pathak, P.; Bhatia, R. Performance Analysis of Polar codes for Next Generation 5G Technology. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Arikan, E. Systematic Polar Coding. IEEE Commun. Lett. 2011, 15, 860–862. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check codes. IRE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Berrou, C.; Pyndiah, R.; Adde, P.; Douillard, C.; Le Bidan, R. An overview of turbo codes and their applications. In Proceedings of the European Conference on Wireless Technology, 2005, Paris, France, 3–4 October 2005; pp. 1–9. [Google Scholar] [CrossRef]
- Berman, A.; Shany, Y.; Tamo, I. Explicit Subcodes of Reed-Solomon Codes That Efficiently Achieve List Decoding Capacity. IEEE Trans. Inf. Theory 2025, 71, 5898–5911. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Chakraborty, M.; Mukherjee, A.; Nag, A.; Chandra, S. Hybrid Quantum Noise Model to Compute Gaussian Quantum Channel Capacity. IEEE Access 2024, 12, 14671–14689. [Google Scholar] [CrossRef]




| Reference | System | Advantages | Limitations |
|---|---|---|---|
| [9] | Quantum image compression | Efficient encoding and decoding and high data reduction | Limited to compression, hardware dependency and scalability challenges in practice |
| [38] | Multi-qubit frequency-domain transmission | Enhanced scalability and noise resilience | Increased system complexity |
| [39] | QHWT + Qsobel quantum watermarking | Ensures high invisibility and robustness with reversible embedding | Lack of evaluation under noisy transmission, scalability, and hardware feasibility |
| [40] | QFT-based quantum image compression | Provides efficient frequency-domain data reduction | Limited to compression with scalability and hardware constraints |
| [41] | QFT-based quantum image compression | Provides efficient frequency-domain data reduction | Limited to compression |
| [42] | QWT for dimensionality reduction | Enables efficient handling and reconstruction of high-resolution data | Lacks evaluation under noisy transmission |
| [43] | QHWT-based quantum image compression | Provides higher PSNR, faster runtime, and better detail preservation | lacks evaluation under noisy transmission, limited by hardware immaturity, encoding dependency, and narrow benchmarking scope |
| Aspect | QFT | QHWT |
|---|---|---|
| Primary Gates | Hadamard, Controlled-Phase | Hadamard, SWAP |
| Gate Complexity | (exact), (approx.) | |
| Circuit Depth | Linear, deeper due to sequential rotations | Linear, shallower, supports parallelism |
| Connectivity | Long-range/global | Local/nearest-neighbor |
| Ancilla Requirement | None | May be needed for multilevel decomposition |
| Hardware Suitability | Trapped-ion, photonic, high-connectivity superconducting | Grid-based superconducting or solid-state processors |
| Experimental Maturity | High | Limited/early-stage demonstrations |
| Near-Term Realizability | Feasible with approximate circuits | Feasible for small-scale implementations |
| Medium-Term Realizability | Scalable with error mitigation and compiler support | Scalable with improved hardware and multilevel designs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayasinghe, U.; Fernando, T.; Fernando, A. A Comparative Study of Quantum Haar Wavelet and Quantum Fourier Transforms for Quantum Image Transmission. Information 2025, 16, 962. https://doi.org/10.3390/info16110962
Jayasinghe U, Fernando T, Fernando A. A Comparative Study of Quantum Haar Wavelet and Quantum Fourier Transforms for Quantum Image Transmission. Information. 2025; 16(11):962. https://doi.org/10.3390/info16110962
Chicago/Turabian StyleJayasinghe, Udara, Thanuj Fernando, and Anil Fernando. 2025. "A Comparative Study of Quantum Haar Wavelet and Quantum Fourier Transforms for Quantum Image Transmission" Information 16, no. 11: 962. https://doi.org/10.3390/info16110962
APA StyleJayasinghe, U., Fernando, T., & Fernando, A. (2025). A Comparative Study of Quantum Haar Wavelet and Quantum Fourier Transforms for Quantum Image Transmission. Information, 16(11), 962. https://doi.org/10.3390/info16110962







