Abstract
This paper presents a series of dynamic simulations for a ship towed by kite. To ensure time efficient computations, seakeeping analysis with forward speed correction factors is carried out in the frequency domain and then transformed in the time domain by convolution. The seakeeping modeling is coupled with a zero-mass kite modeling assuming linear dependence of aerodynamic characteristics with respect to turning rate. Decoupled (segregated) and coupled (monolithic) approaches are assessed and compared in different environmental conditions. Results show that in regular beam waves, strong interactions between the kite and the ship motions are captured by the monolithic approach. Around the wave frequency, especially for the lower one tested (0.4 rad/s), a kite lock-in phenomenon is revealed. It is concluded that the mean kite towing force can be increased whereas the ship roll amplitude can even be decreased compared to a non-kite assisted ship propulsion configuration.
1. Introduction
This work is part of the beyond the sea® research program launched by Yves Parlier and managed in partnership with French Ministry of Defence with the support of French Environment and Energy Management Agency (ADEME). The project attempts to develop a tethered kite system as an auxiliary device for the propulsion of merchant ships. The existing knowledge on ships towed by kite has demonstrated great prospects for this technology in terms of CO2 emissions and fuel savings. However, studies on the limitations of this concept to guarantee the safety and the integrity of the ship are very limited.
Considering the mean kite towing force, Leloup et al. [1] and Naaijen et al. [2] solved the horizontal balance equations of a ship towed by kite to determine the fuel savings. Ran et al. [3] studied the contribution of a kite to the mean ship thrust, drift angle and rudder angle. All these previous studies neglected the interactions between the kite and the ship. The kite force is imposed as a predefined external force to the ship. The motions of such a system are highly dynamic since a kite experiences a periodic dynamic flight. In Bigi et al. [4], the influence of the kite attachment point on the deck is investigated on a fishing vessel equipped with a kite. This study is limited to horizontal ship motions. A maneuvering modeling is implemented with a monolithic coupling approach between the ship and the kite. The water is supposed to be calm and Bigi et al. [4] did not take into account the effect of the radiated waves on the ship motions. Thus, the influence of the kite excitation frequency on the added mass and damping of the ship is neglected. Since the hydrodynamic added mass and damping may depend strongly on the frequency of the motion [5,6,7,8], this assumption is questionable.
A ship sailing in waves is commonly studied through seakeeping codes based on the potential flow theory under the assumption of linear response of the ship to a given perturbation on a mean path. These studies are usually carried out in the frequency domain [9,10]. However, since the kite and the ship may be strongly coupled, their interactions cannot be directly computed through a spectral description of the kite excitation. Such computations are therefore limited to weak coupling. To perform a strong coupling between the kite and the ship, a time domain formulation is required. The aim of this paper is to assess the importance of taking into account the coupling between the kite and the ship motions by a time domain method.
As highlighted by Skejic [11], fast time-domain methods able to compute the 6 dof combining horizontal and vertical motions of a ship are based on the concept of linear convolution [12,13,14]. Such methods are first introduced by Cummins [15] in 1962. Böttcher [12] developed unified theories that couple the linear manoeuvring and seakeeping. In specific, he extended the method to simulate large amplitude motions taking into account nonlinear effects with Froude–Krilov effort and nonlinear roll damping for instance. To enable a fast computation of the linear convolution product, the use of state-space systems is introduced [13,16,17]. The identification of the state-space systems is detailed in [18] for the zero forward speed case. In this paper, this method is extended to the forward speed case.
Kite modeling is formulated under the zero mass assumption. Behrel et al. [19] presents experimental results comparing zero mass and point mass modeling. Differences are about few percent. Actually, both modelings give the same results when their coefficients identification is consistent. If taking into account the mass can be important for control issue, this is clearly not the case for performance assessment. Studies on kite performance assessment as ship propulsion device are based on zero-mass assumption (e.g., Wellicome and Wilkinson [20], Naaijen et al. [2], Dadd et al. [21] and Leloup et al. [1]). In addition, a linear evolution of the kite aerodynamics with the radius of trajectory curvature is proposed in this paper.
Section 2 presents the considered modeling of a ship towed by kite. Section 3 presents the results. First, the kite characteristics identification is detailed, then Section 3.2 defines the case study on the surface vessel combatant DTMB 5512. Section 3.3 and Section 3.4 investigate respectively through a calm water case and a regular beam wave case, the coupling between ship and kite. A general discussion on the methods and results is provided in Section 4 before to conclude.
2. Ship Towed by Kite Modeling
2.1. Reference Frame and Parametrization
The Earth fixed frame , the ship fixed frame and the hydrodynamic frame are sketched in Figure 1. The earth fixed frame is centered on with pointing downward. The ship fixed frame is composed of pointing forward in the ship symmetry plane, pointing downward and completing the direct orthogonal basis. is normal to free surface when the ship is at the equilibrium. The origin of denoted by is in the ship symmetry plane at a longitudinal distance from the aft perpendicular and at a vertical distance from the baseline. For a point P, the expression of its coordinates in a frame is or . The vectors of a frame are , and and the origin is denoted . The generalized position vector of the ship denoted by is the assembly of the position of and the ship Euler’s angles with respect to the frame. The generalized ship velocity at expressed in with respect to the frame is denoted by , where the first three components are the linear velocities and the last three components are the turning rates. The transformation of a vector expressed in the frame denoted by can be expressed in the frame with , where is the direct cosine matrix expressed as:
where, and denote respectively the cosine and the sinus functions. The turning rates and the time derivatives of the ship Euler’s angles satisfy the following relationship:
where,
The hydrodynamic frame is used by the seakeeping theory. It can be considered as Galilean since moves at the constant mean ship forward speed on a straight path with respect to the earth fixed frame. The generalized position vector of the ship expressed in the frame is denoted by , where the first three components are the distance between and a point H fixed to the ship. The three last components are the Euler’s angle of the ship with respect to the frame. It is assumed that H is in the symmetry plane of the ship and with respect to the frame.
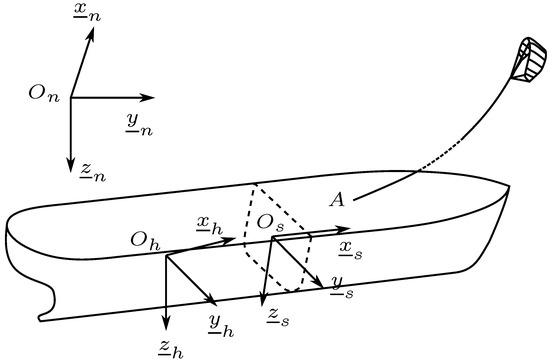
Figure 1.
Earth fixed reference frame; hydrodynamic reference frame; ship fixed reference frame.
Figure 2 illustrates the notations used for the kite modeling. The relative wind coordinates system moves at the tether attachment point velocity with respect to the Earth fixed frame. The relative wind velocity defined in Equation (4) is the difference between the true wind velocity and the velocity of the tether attachment point.
and is defined as: . In order to define a direct orthogonal coordinates system, is defined as follows: . It should be noticed that the relative wind frame depends on the considered altitude due to the wind gradient. Consequently, the relative wind frame is defined with respect to a given point P and is thus denoted . For instance, the relative wind frame drawn in Figure 2 is . At the kite location, the relative wind frame is obtained from:
The apparent kite wind velocity is denoted by and can be expressed as follows:
where denotes the kite velocity with respect to the frame; the kite reference frame centered on K is defined as follows: , and ; the kite velocity is directed by . The kite elevation angle is given by:
The kite azimuth angle is defined as follows:
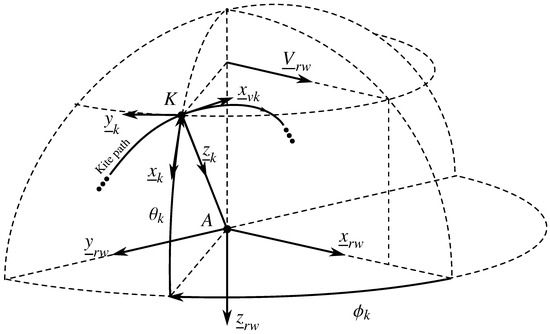
Figure 2.
Kite reference frames.
2.2. Ship Modeling
As introduced in Section 1, a time domain formulation is a priori mandatory to represent the complete interaction between kite and ship motions. For the ship motion’s modeling part, we implemented the very classical and efficient method described by Fossen [22]. Appendix A gives details on the state space technique used. Appendix A.1 describes the equations of motion for a ship in a seaway. Appendix A.2 shows how hydrodynamics are computed using strip method theory and how is carried out the computation of linear convolution terms. Appendix A.3 provides details on the calculation of wave forces.
2.2.1. Ship Motions
The equations describing the motion of the system can be transformed into a system of first order differential equations as in Equation (9). This system is obtained with the transformation of the generalized ship velocity vector from the frame to the frame and Equations (A9) and (A12).
Equation (9) represents 12 scalar equations for the ship and 75 scalars equations for the state-space systems. Assuming, for instance, that the order of each state space system is 5 and taking into account the ship symmetry. Thus, with the present modeling, the ship is described by 87 scalar equations depending on the state space modeling orders. This system of differential equations is numerically integrated with the 4th order Runge–Kutta scheme with a fixed time step.
2.2.2. Ship Modeling Validation
The present ship modeling was compared to Experimental Fluid Dynamic (EFD) data and to the STF strip theory results on the David Taylor Model Basin (DTMB) 5512. The model tested is a 1:46.6 scale model. The hull form and its characteristics are respectively plotted in Figure 3 and summarized in Table 1. The experimental data are provided by the University of Iowa [23] and are presented in Irvine et al. [24]. The EFD data concern the heave and pitch motions in regular head waves, with and without forward speed.
Figure 3.
DTMB 5512 hull sections at the scale of 1:46.6.

Table 1.
DTMB 5512 hull and full scale characteristics.
The computed ship motions were performed at zero forward speed and at a Froude number of 0.28, which corresponds to m.s−1 and with frequency head waves from 1 rad.s−1 to 7.5 rad.s−1. was defined at the ship center of gravity, hence and . Figure 4 and Figure 5 plot the heave and pitch transfer function obtained with the experimental data, with the STF strip theory and with the present modeling. The experimental data are obtained for different wave steepness . The amplitude of the transfer function for heave motion (a) is directly the ratio of the heave amplitude motion to the wave amplitude. The amplitude of the transfer function for the pitch motion (c) is given by the ratio of the motion amplitude (in radians) to the wave amplitude multiplied by the wave number k. The phase angle of the present modeling is obtained by cross correlation between the free surface elevation and the ship motion time series.
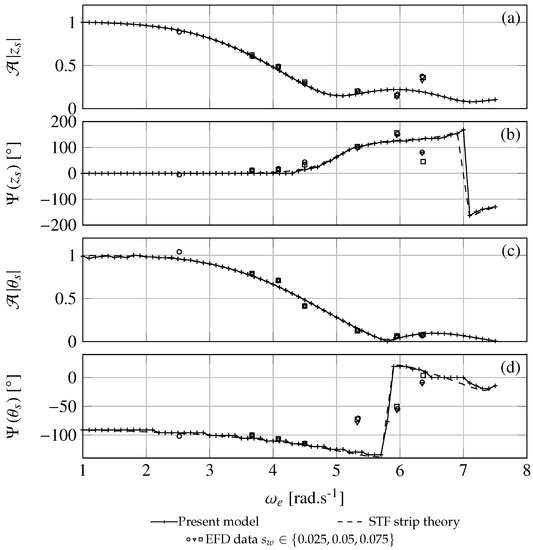
Figure 4.
Heave and pitch transfer function at function of the frequency of encounter . Amplitudes are plotted for heave (a) and pitch (c). Phases are plotted for heave (b) and pitch (d). The results are obtained with the frequency domain and time domain approaches, experimental data for different wave steepness and with the STF strip theory.
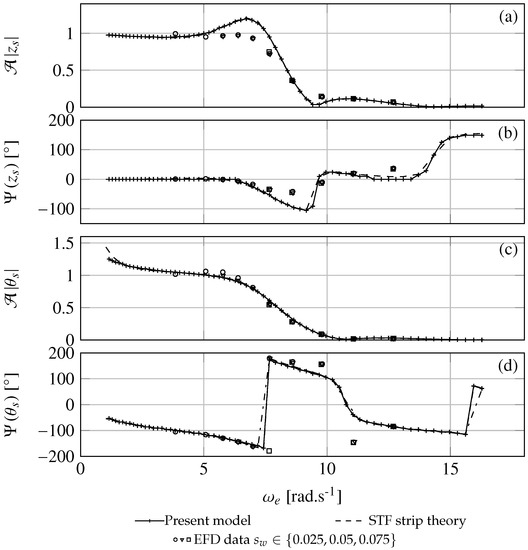
Figure 5.
Heave and pitch transfer function at m.s−1 according to the frequency of encounter . Amplitudes are plotted for heave (a) and pitch (c). Phases are plotted for heave (b) and pitch (d). The results are obtained with the frequency domain and time domain approaches, experimental data for different wave steepness and with the STF strip theory.
Concerning the amplitude, an overall good agreement is found with (Figure 5) and without (Figure 4) forward speed between the EFD data, the STF strip theory, the time domain and the frequency domain modeling. For the considered waves, the influence of the wave steepness on the EFD data is not significant. As shown in Figure 4 and Figure 5, the STF strip theory and the time domain approach match with a very good accuracy for the amplitude. Very small differences can be observed in terms of phase angle, but these differences are probably caused by the post-processing method (Figure 4 and Figure 5). The very small differences with the STF strip theory are due to the approximations performed with the identification method of the transfer functions . As a conclusion for the heave and pitch motions, the transformation of the equation of motion into the ship reference frame and the state-space modeling identification method are consistent and accurate enough.
The roll motion is much more difficult to predict with a linear modeling. Full-scale results are presented in Figure 6. Results by Ikeda et al. [25] are considered as a reference. In the present method, the extra roll damping was set to kg.m.s−1 in order to obtain the same roll amplitude at the natural frequency. As shown in Figure 6, for frequencies greater than 1 rad.s−1, the roll motion amplitude is well predicted despite a slight difference in phase. Nevertheless predictions appear to be less accurate for the lower frequencies, except for the natural roll frequency, rad.s−1, where, by identification, both modelings match.
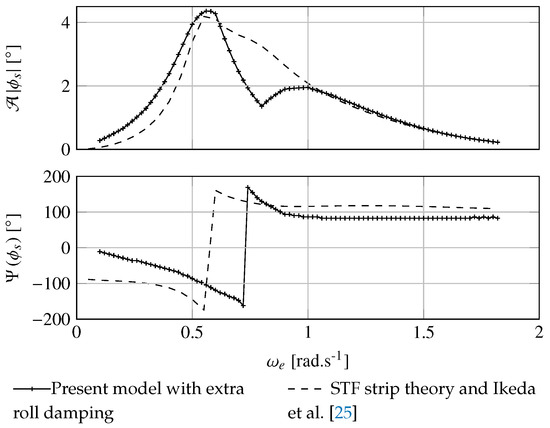
Figure 6.
Roll response amplitude operator and phase at m.s−1 as function of the frequency of encounter with DTMB 5512 at full scale. The results are obtained with the present model and the STF strip theory with the roll damping modeled with the method proposed by Ikeda et al. [25].
2.3. Kite Modeling
2.3.1. Short Literature Survey
Kites are mostly studied as a power generation system since 1980 [26]. Comparing the weight of the kite on the one hand and the traction provided on the other, Loyd considers that it is relevant to neglect the mass of the kite. Thus, he developed the so-called zero-mass modeling. Taking the skysails system, the most advanced industrial example, gives us a good illustration of the relevance of this assumption. Paulig et al. [27] computes a pulling force to mass ratio of 50daN/kg in the case of a 320 m2 kite with 360 m tether. Wellicome extended the zero-mass modeling defining a figure-8 trajectory for the dynamic mode [20,28]. Argatov et al. [29] proposed more recently a simpler trajectory definition. In addition, Argatov definition allows a much faster calculation and its formulation avoids discontinuities in kite acceleration. The size of the trajectory can easily be modified thanks only to azimuth and elevation amplitude parameters. In 2006, Naaijen et al. [2] computes the fuel savings on a full range of true wind angles for the British Bombardier, a 50000 DWT tanker. In 2011, Dadd et al. [21] improved the calculations with more realistic trajectories using the Wellicome formalism. In 2014, Leloup et al. [1,30] proposed a fully analytical solution for the zero-mass modeling that allows faster and more reliable computations avoiding optimization process failures. Leloup takes into account adequately the wind gradient effect and takes advantage of the Argatov trajectory definition for even faster computations.
2.3.2. Zero-Mass Kite Model
According to the zero-mass kite modeling, the masses of the tether and the kite are neglected and the tether is assumed to be straight and of constant length . Consequently, the kite velocity with respect to the frame is normal to and for any configuration the tether tension is opposed to the aerodynamic kite force. Assuming that the kite flies with a constant lift to drag ratio and that the apparent wind velocity is in its symmetry plane, Leloup et al. [1] expressed the kite velocity according to a given kite velocity direction in Equation (10):
The kite velocity is a real number if the following condition is satisfied:
Then, the tether tension is given by the following formula:
The generalized tether force vector acting on the ship at with respect to frame is expressed as follows:
In order to represent the wind friction with the sea, the true wind velocity is function of the altitude according to the wind gradient law recommended by the ITTC [31].
2.3.3. Kite Control According to a Trajectory
The kite velocity direction is controlled in order to follow a trajectory denoted by (Figure 7). The kite velocity direction is defined by the target point expressed as follows:
where is the curvilinear abscissa of the closest point of the trajectory from the current kite position K. Hence, the kite velocity direction is defined as follows:
The point is determined according to the following equation:
where is the tangent vector to the trajectory at curvilinear abscissa . Equation (17) is solved numerically with a Newton–Raphson algorithm.
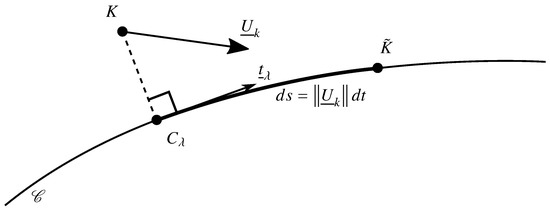
Figure 7.
Schema describing the target point to control the kite velocity direction .
2.3.4. Theoretical Lemniscate Trajectory
To perform a dynamic flight, the considered theoretical trajectory is the eight shaped Lissajous curve as used by Argatov et al. [29] and Leloup [32]. This type of trajectory has the advantage to avoid twists of the tether system. The Lissajous trajectories are defined in terms of elevation and azimuth :
where, . and are the elevation and the azimuth of the center of the trajectory denoted by . The trajectory is defined with respect to , the relative wind frame with respect to the wind measurement altitude. On a sphere of radius , a point C of the trajectory is defined in terms of elevation and azimuth with respect to frame as follows:
As shown in Figure 8, the lemniscate trajectories can be rotated by an angle around . Any point of the trajectory must satisfy Equation (11) insuring the realness of the kite velocity. The benefit to defining the trajectory with respect to the relative wind frame is that the realness of the kite velocity along the trajectory does not depend on the ship motions. Nevertheless, the ship motions may modify significantly the shape of the trajectory with respect to the Earth fixed frame . Vertical motions are especially known to cause unwanted overloads and flight instabilities [27]. Consequently, two trajectory definitions are investigated further in the paper. The first definition takes into account all components of the tether attachment point velocity. The second definition takes only the horizontal components of the tether attachment point velocity with respect to the earth fixed frame to compute the relative wind frame. This modified relative wind frame of trajectory definition is denoted by and is defined from:
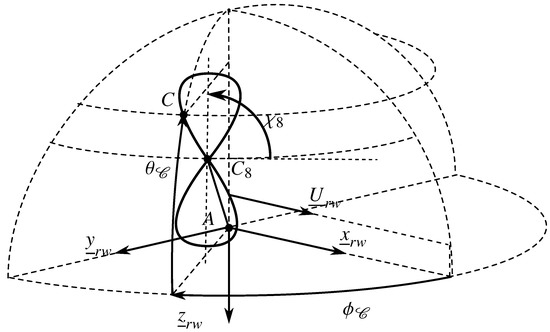
Figure 8.
Lissajous trajectory parametrization.
2.4. Two Coupling Methods
The tether tension induces motions to the ship. The expression of generalized kite force acting on the ship is expressed as follows:
In addition, according to the zero-mass kite modeling (cf. Section 2.3.2 and Equation (5)), the ship motions can modify the kite flight and the tether tension through the relative wind speed at the kite altitude with respect to the tether attachment point A:
Two coupling approaches are investigated in this paper: a monolithic and a segregated approaches. The monolithic approach takes into account all the coupling terms between the kite and the ship modeling. Here, the considered segregated approach assumes a predefined kite force and then solves the ship equations of motion separately.
2.4.1. A Monolithic Approach
The monolithic equations of motion of a ship towed by kite are obtained with Equations (9) and (10) as follows:
Equation (23) adds 3 scalar equations for the kite. With the monolithic approach, the fully coupled system between the ship motions and the kite motions is solved. This monolithic system of differential equations is numerically integrated with the 4th order Runge–Kutta scheme with fixed time step.
2.4.2. A Segregated Approach
By contrast to the monolithic approach, the segregated approach considers only the mean tether attachment point velocity on the ship. The ship motions are computed applying the time series of the kite towing force as an external forces. Thus, the ship equation of motion can be expressed as follows:
where denotes the external forces such as rudder, propeller and windage forces excluding the kite forces applied as a time series . This segregated approach could be very practical to study the motions of a ship towed by kite. Even if here, this approach is performed into the time domain, the segregated approach can be performed into the frequency domain applying the kite excitation spectrum directly in Equation (A1).
3. Results
3.1. Validation and Comments on the Kite Aerodynamic Characteristics
On the basis of the experimental data obtained by Behrel et al. [19,33], the zero-mass modeling is compared to the experimental data. The zero mass kite modeling is dependent of two parameters, the kite lift coefficient and the glide angle . These coefficients must be adapted in order to fit the data. The onshore full scale trials [19,33] were performed with a classical kite Cabrinha® Switchblade2016 of 5 m2 designed for kite-surfing. The tether length was 80 m long. During the run, the kite performed eight shaped trajectory controlled by an autopilot based on the algorithm proposed in [34,35]. The experimental kite position is determined with a 3D load cell assuming that the tethers are straight. The evolution of the wind velocity with the altitude was identified thanks to a SOnic Detection And Ranging (SODAR). The experimental results presented here correspond to a phase averaging post-processing of a 5-minute kite flight run. For the presented case, the wind velocity was interpolated from the SODAR data with the following linear function:
The wind gradient function in Equation (25) is used for the following presented simulation results.
The zero-mass modeling presented in [1] assumes a constant glide angle and a constant lift coefficient. The kite velocity depends only on its direction and position in the wind window and on the glide angle . Consequently, the present zero-mass modeling results are obtained with a glide angle enabling that the simulated kite trajectory has the same period than the experimental data, which is 5.86 s. The kite towing force is dependent of the kite lift coefficient. Hence, the kite lift coefficient is adjusted in order to obtain the same mean towing force. The kite trajectory used for the simulation is the same than the kite trajectory of the experimental measurements. The position of the kite is integrated with the 4th order Runge–Kutta scheme with a time step of 0.1 s.
Figure 9 shows the evolution of the magnitude of the kite velocity (a) and the evolution of the magnitude of the tether tension at A on the average trajectory (b). The experimental velocity is obtained by finite differentiation, which induces some noise in the signal sampled at 50 Hz. This noise in terms of speed and tension for the simulated results is still present since the simulation uses the average kite trajectory of the experimental data. However, this noise is barely visible since the sampling frequency of the simulation is only 10 Hz. The kite glide angle and the lift coefficient used for the zero-mass modeling are respectively 12.45° and 0.855. The main difference between the experimental data and the results concerns the tether tension and the kite velocity amplitude. The simulated amplitude is slightly underestimated for the velocity and is particularly underestimated for the tension. The tether tension given by Equation (12) is a quadratic function of the apparent wind velocity. Therefore, for a relative kite velocity error, the relative tension error is twice. In order to perform an eight trajectory, the back tethers are steered. The difference between the back tethers lengths leads to important modifications of the kite flying shape. Hence, it can be expected a modification of the kite lift coefficient and of the glide angle leading to the significant differences observed between the zero-mass modeling with constant aerodynamic characteristics and the measurements. Leloup [36] and Duport [37] demonstrated the variation of the aerodynamic characteristics with respect to the turning rate. Even without considering tip vortices, the yaw rate induces an evolution of the local inflow velocity along the kite span. According to Equation (10), the kite velocity is independent of its area. Consequently, for a given radius of curvature of the trajectory, the evolution of the local inflow along the span and the effect of the flying shape deformation are more consequent with larger kites. Here it is assumed that the evolution of the kite glide angle and lift coefficient are proportional to the ratio of a characteristic length of the kite with the radius of curvature of the trajectory. For a given aspect ratio, the characteristic length of the kite can be . Denoting the trajectory radius of curvature , the glide angle and the lift coefficient could written as follows:
where, and are two coefficients. Equation (26) can be rewritten in terms of heading rate according to the relationship between the radius of curvature of the trajectory and the kite velocity. Furthermore, according to Equation (10), the kite velocity is proportional to the relative wind speed, thus the correction proposed can be rewritten as functions of the time derivative of the heading and the relative wind speed as follows:
The determination of the coefficient , , and can be evaluated by comparison with the experimental data. First, and are identified in order to obtain respectively the same maximum and minimum speed than the experiments. Then, and are identified in order to obtain respectively the same maximum and minimum tether tension than the experiments. According to this method, the following coefficient values are identified:
These values are consistent with the ones by Behrel et al. [19], who did the identification with a quite different and more straightforward method. The results in terms of kite velocity and tether tension are plotted in Figure 9. With the modification of the glide angle and the lift coefficient, the noise in the kite velocity and the tether tension time series is more significant. Indeed, the computation of the kite yaw rate requires two finite differentiations of the kite position. As expected with the identification method of , , and , the amplitude of the kite velocity and the amplitude of the tether tension are respected.
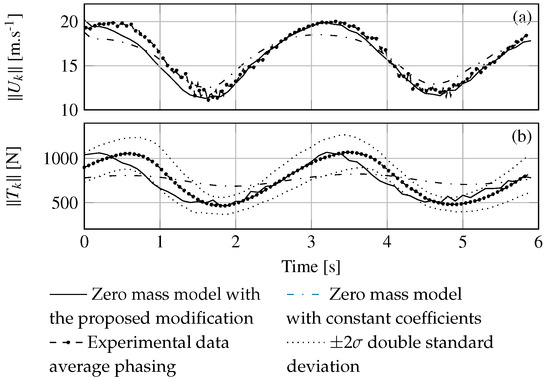
Figure 9.
Evolution of the kite velocity (a) and of the tether tension at A, along the average trajectory (b); comparison between the zero mass model with constant aerodynamics and the model with a linear modification of the kite aerodynamic characteristics using phase averaging of experimental data from Behrel et al. [33].
An overall good agreement is found in terms of velocity but a slight phase difference is observable between the simulation results and the experimental data. The linear modifications of the glide angle and of the lift coefficient with the kite yaw rate lead to a better agreement with the experimental results than the zero mass modeling. However, these modifications should be confirmed with more experimental cases. Since at the first order the ship motions are proportional to the amplitude of the excitation forces, these modifications enhancing the prediction of the kite excitation force amplitude are crucial.
Moreover, the minimum allowable radius of curvature of the trajectory can be estimated according to Equation (26). Indeed, during a kite flight must be positive. This means that the trajectory radius of curvature must satisfy the following condition:
As a numerical application, the minimum trajectory radius of curvature of the 5 m2 Cabrinha® Switchblade is m, Which is a little less than twice the projected wingspan. Given that the lift coefficient must have a strictly positive value in order to fly, we are here outside the validity domain of the proposed modeling. However, the order of magnitude is confirmed by Fagiano who evaluated the minimum turning radius at 2.5 times the wingspan [38,39]. The coefficients , , and are dimensionless quantities. Consequently, the presented modifications in Equations (27) and (28) are retained as formulated for the rest of the paper.
3.2. Study Case
In order to simplify the analysis, only vertical ship motions (heave, roll and pitch) of the DTMB 5512 at full scale were considered here. The analysis was focused on the roll motion. Thus, in the scope to observe significant roll motion, a true wind angle was chosen. A true wind speed of reference 10 m.s−1 corresponding to the high range of a fresh breeze from the Beaufort scale was considered. The ship speed was set to 7.5 m.s−1 since it corresponds to a common sailing speed condition of the world merchant ship fleet. A kite with an area of 500 m2 and with the aerodynamic characteristics determined in Equation (28) was used. The tether attachment point was in the center plane, 7.9 m above the water line and 25 m in front of the center of gravity.
The kite flight trajectory corresponded to a Lissajous trajectory as defined in Section 2.3.4. The amplitudes of the trajectory were arbitrarily set to and . According to the formulation of the lift coefficient in Equation (26), the tether length condition to obtain a positive lift coefficient was m. The kite excitation was studied by varying the tether length. Tether length between 360 m and 1000 m were investigated. The center of the trajectory and the angle of the trajectory around the axis were determined optimizing of the longitudinal kite towing force with the same code used by Leloup et al. [1]. In this configuration, the kite provided about 16% of the propulsive power, provided the data from [40].
Figure 10a–c show respectively the evolution of the , and with the tether length. A calm water case and three regular beam wave cases are considered. A regular beam wave of 2.5 m high consistent with a fresh breeze. Three wave frequencies were investigated rad.s−1. The 0.56 rad.s−1 wave frequency corresponded to the natural roll ship frequency. For all following results, the simulation time was 1640 s with a time step of 0.3 s.
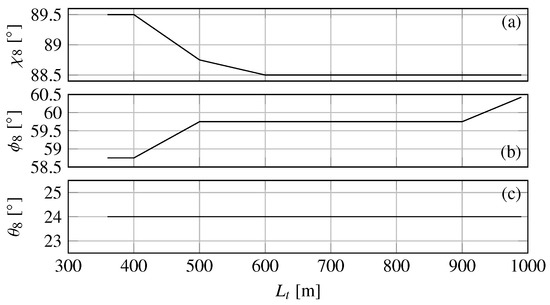
Figure 10.
Kite flight trajectory parameter versus tether length. (a) Trajectory angle ; (b) Azimuth of the center of the trajectory; (c) elevation of the center of the trajectory.
3.3. Calm Water Case
3.3.1. Kite Excitation Spectrum
Figure 11a,b show respectively the time series and the spectrum of the kite roll excitation moment obtained with the segregated approach for a tether length m. Only the varying part of the kite excitation is taken into account to compute the kite excitation spectrum. With the segregated approach, the kite flight is not modified by the ship motions. It can be noticed in Figure 11 that the roll excitation moment is mainly composed of several harmonics. For convenience, the harmonics are denoted where i is a natural number. Only the first, the second and the fourth harmonics are significant. The whole spectrum is not represented but the other harmonics that occur at higher frequencies are not significant. The second and the fourth harmonics are the most powerful. The second harmonic should appear to be the most critical for the ship motions due to its proximity with the natural roll ship frequency.
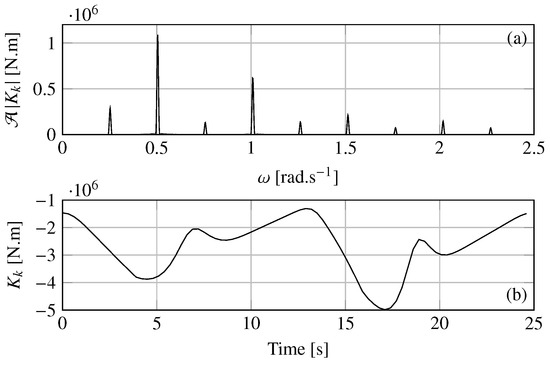
Figure 11.
With a tether length m; (a) spectrum of the kite excitation moment around the longitudinal ship axis ; (b) time history of the kite excitation moment around the longitudinal ship axis over the last loop.
3.3.2. Comparison of the Segregated Approach with the Monolithic Approach
Figure 12 shows the evolution of the roll amplitude, first kite excitation harmonic frequency and amplitude kite moment with respect to the tether length. Three methods are compared: the segregated approach in dashed-dotted line and the two monolithic approaches with the kite trajectories defined in and in respectively in solid and dashed lines.
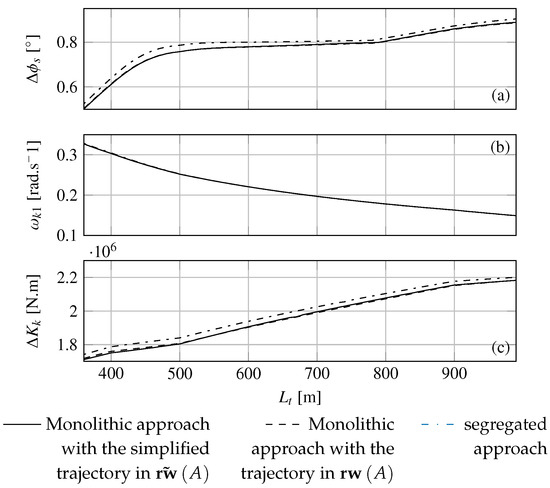
Figure 12.
(a) Amplitude of the ship roll motion, (b) first kite harmonic frequency and (c) amplitude of the kite moment of excitation for different tether lengths from 360 m to 990 m by step length of 10 m in calm water.
As expected, the first kite excitation harmonic decreases with the tether length since the angular amplitude of the Lissajous trajectories is remained constant. No major difference can be noticed between the three approaches in terms of harmonics frequencies. The roll amplitude and the amplitude of the kite roll moment predicted by the segregated are higher than those predicted by the two monolithic approaches. The two trajectory definitions in and give almost the same results both in terms of roll amplitude and kite roll moment amplitude. For all approaches presented, the roll amplitude evolution is similar. The kite moment amplitude increase quasi linearly with the tether length. Four ruptures (mainly three) can be observed in the evolution of the kite moment amplitude. These ruptures corresponds to the evolution of the trajectory parameters with the tether length as shown in Figure 10. Due to the wind gradient, the longer the tether is, the larger the kite roll moment is. This increase in kite roll moment explains the continuous increase in roll amplitude. However, two important increases can be noticed between m and m and from m, which are not explained by the kite roll moment. In fact, these two increases are due to the proximity between the two most powerful kite roll excitation harmonics and the vessel natural roll frequency. Indeed, for m the second harmonic frequency is almost equal to the natural roll frequency of the ship. From m, the fourth harmonic frequency approaches the natural roll ship frequency. In case of a slower true wind speed, the increase of the kite roll moment with the tether length would be less significant. Thus, it could be observed a maximum of roll amplitude for tether length corresponding to a match between a kite harmonic frequency and the natural roll frequency of the ship. According to these results in calm water, the segregated approach is slightly conservative with respect to both monolithic approaches.
3.4. Regular Beam Wave Case
To investigate a case closer to a real ocean environment, the influence of regular beam waves is studied. The wave considered is a 2.5 m high at the frequencies of 0.4 rad.s−1, 0.56 rad.s−1 and 0.8 rad.s−1. As for the calm water case, the frequency domain of kite excitation is scanned with different tether lengths from m to m with a tether length step of 10 m.
3.4.1. Ship Vertical Motion Influence on Kite Trajectory
This section focuses on the influence of ship vertical motion on kite flight trajectory. Paulig et al. [27] underlined the major disturbances caused by this motion in terms of flight control and overload. Although this is in line with the rare feedback from experiences at sea, this has never been simulated before, all published studies being carried out so far in cases of calm water. Figure 13 shows the trajectory defined neglecting the ship vertical motion in solid line and the trajectory defined in the actual relative wind frame in dashed line. The latter has considerably reduced turning radius. It is not in line with the relationship on the minimum kite flight radius highlighted by Fagiano nor with the experiments by Behrel presented in Section 3.1. Such a sharp trajectory could not be achieved in the real world. As a consequence, in the rest of the paper, all the trajectories will be defined in and will be called.
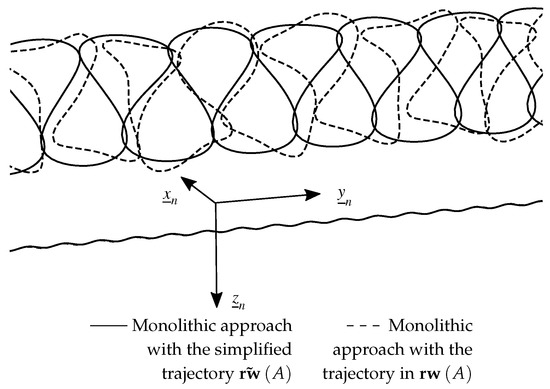
Figure 13.
Kite and ship path with respect to for m with a wave of 2.5 m high at the frequency rad.s−1.
3.4.2. Interactions with Regular Beam Waves
Figure 14, Figure 15 and Figure 16 show respectively for three wave frequencies, the roll amplitude of the ship, the first kite harmonic frequency and roll moment. For each wave cases, the monolithic approach is compared to the segregated approach. The dashed-dotted line corresponds to the roll amplitude of the ship due to the wave excitation without kite. For all wave cases, the roll amplitude and the amplitude of the kite roll moment increase globally with the tether length as for the calm water case. In contrary to the calm water case, the amplitude of the kite roll moment obtained with the monolithic approach is globally larger than the one obtained with the segregated approach. However, it should be noticed some drops in the evolutions of the roll amplitude and amplitude of the kite roll moment. For instance, in Figure 15a, for the tether length m, a significant drop of the roll amplitude can be noticed in the segregated case. This phenomenon of interaction between the kite and the ship can explained the fact that the monolithic approach predicts a smaller roll amplitude despite a larger kite roll moment amplitude compared to the segregated approach. Indeed, the secondary kite harmonic at the wave frequency has a relative phase with the ship motion. As an example, for the case plotted in Figure 17, the difference in phase angle between the ship motion and the kite excitation at rad.s−1 is 60.7°. For the case with the frequency wave rad.s−1, the interaction between the kite and the ship is less significant since the wave frequency is far from the most powerful kite harmonic frequencies. Moreover, in contrary to the calm water case, the segregated approach is not necessarily conservative with respect to the monolithic approach as shown by Figure 16a.
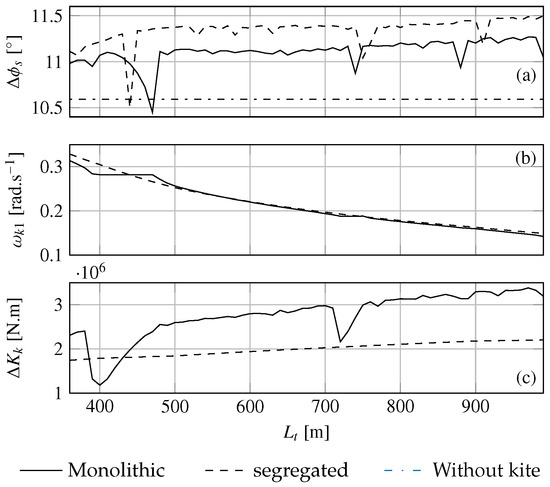
Figure 14.
(a) Amplitude of the ship roll motion, (b) first kite harmonic frequency and (c) amplitude of the kite moment of excitation for different tether lengths from 360 m to 990 m by step length of 10 m with a beam regular wave of 2.5 m high at a frequency of rad.s−1.
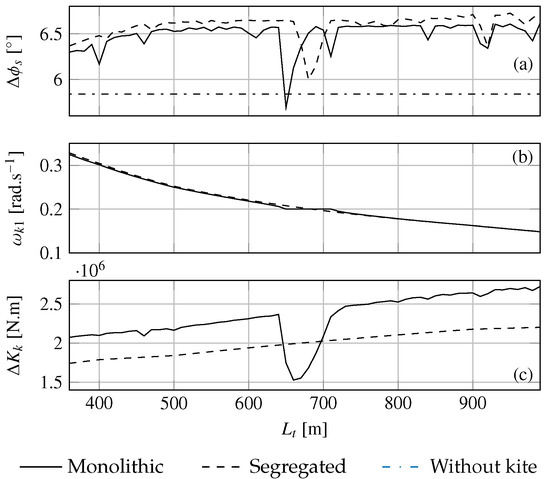
Figure 15.
(a) Amplitude of the ship roll motion, (b) first kite harmonic frequency and (c) amplitude of the kite moment of excitation for different tether lengths from 360 m to 990 m by step length of 10 m with a beam regular wave of 2.5 m high at a frequency of rad.s−1.
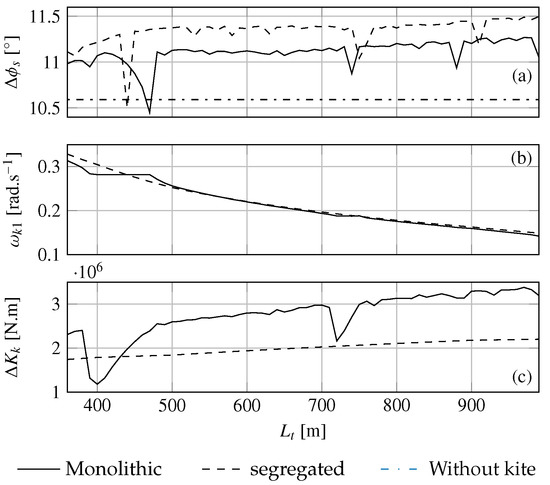
Figure 16.
(a) Amplitude of the ship roll motion, (b) first kite harmonic frequency and (c) amplitude of the kite moment of excitation for different tether lengths from 360 m to 990 m by step length of 10 m with a beam regular wave of 2.5 m high at a frequency of rad.s−1.
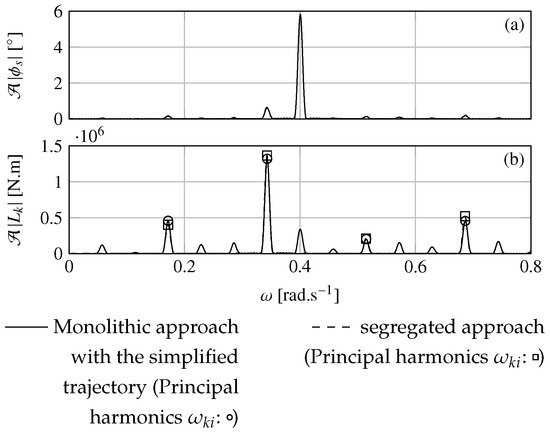
Figure 17.
With a tether length m at the wave frequency rad.s−1; (a) Spectrum of the roll motion of the ship; (b) Spectrum of the kite excitation moment around the longitudinal ship axis.
Concerning the evolution of the first harmonic frequency, differences can be noted between the two approaches. Indeed, for certain ranges of tether length, the harmonic frequency obtained with the monolithic approach remains constant. For instance, on Figure 15b, the first harmonic frequency remains constant to half the wave frequency for tether lengths within the range m. A sharp evolution of the roll amplitude concerns both approaches. In the monolithic case, this phenomenon does not occur only when a harmonic frequency of the kite corresponds to the wave frequency. With a wave frequency of 0.4 rad.s−1 and a tether length m, a drop of the ship roll amplitude can be noticed. Figure 17 shows that no principal kite harmonic frequency corresponds to the wave frequency. However, due to coupling between kite and ship motions, secondary harmonics appear. The secondary harmonic frequencies are denoted . This phenomenon occurs when the frequency gap between the closest principal harmonic frequency and the wave frequency is a submultiple of the first kite harmonic frequency. For the case presented in Figure 17, . Furthermore, it should be noted that these drops in roll amplitude are due to the interactions between the kite and the ship. With the monolithic approach, these drops are independent from initial conditions. The most important drops in roll amplitude occur when or . The importance of the phenomenon occurring at decreases with the increasing value of the integer n. Moreover, the importance of the phenomenon decreases when the interaction with the wave concerns high harmonic orders.
3.4.3. Kite Lock-in Phenomenon
As shown in the previous section, an important interaction phenomenon between the kite and the ship occured. We observed the appearance of plateaus which were all the more pronounced as they were located near the first harmonics of the moment of excitation produced by the kite. It can be observed in Figure 14a and Figure 15a respectively at m and m, that the drop in roll amplitude predicted by the monolithic approach is important enough to lead to smaller roll amplitude than the case without kite. A particular attention is paid to the case where the wave frequency rad.s−1 and m, because the interaction between the kite and the ship is win-win. Indeed, for this case the mean kite towing force predicted by the monolithic approach is 8.0% more important than the mean kite towing force predicted with the segregated approach. In addition, the ship roll amplitude is 1.4% weaker than without kite.
Figure 18 shows the spectrum of the roll motion (a) and the spectrum of the kite excitation (b). It can be noticed that the second harmonic of the kite roll moment is attracted towards the wave frequency. Since the kite harmonic frequency is increased towards the wave frequency, the kite performed the whole trajectory faster. The time to perform the trajectory is decreased by 5.7%. This leads to a higher apparent wind speed and therefore to a higher average kite towing force. Moreover, the difference in phase angle between the roll motion and the kite roll moment is 18.2°, leading to a reduction of the roll amplitude. This attraction towards the wave frequency can be noticed also on the secondary harmonic corresponding to the case . However, the effects are less significant. This phenomenon is similar to the lock-in phenomenon happening with the vortex-induced vibrations [41,42]. Henceforth, this phenomenon is called the kite lock-in.
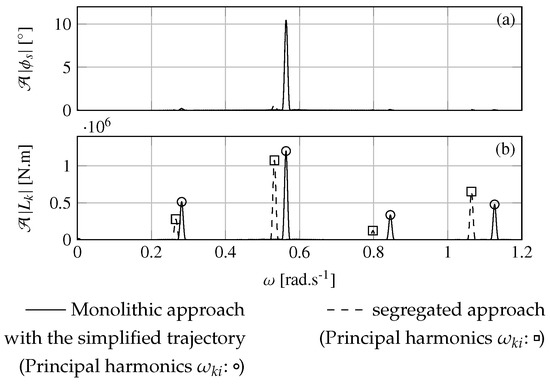
Figure 18.
With a tether length m at the wave frequency rad.s−1; (a) Spectrum of the roll motion of the ship; (b) Spectrum of the kite excitation moment around the longitudinal ship axis .
4. Discussion
A method coupling a time domain seakeeping and a zero-mass kite modeling was developed to investigate the dynamic motion of ship towed by kite. The zero-mass kite modeling neglects the inertial forces, its deformation and the dynamic behavior of the tether. The ship modeling was based on the linear seakeeping STF strip theory [9]. A monolithic approach coupling the kite and the ship modeling was compared to a segregated approach, which neglected the coupling terms. Both methods allowed fast computation. Implemented in Python, the monolithic approach computed faster than the real-time. The computation of the considered cases were five time faster than the real time on a processor Intel(R) Xeon(R) CPU E3-1220 v3 with a CPU frequency of 3.10 GHz.
The ship modeling provides satisfactory results in terms of heave and pitch motions. Since the roll motion is highly nonlinear, the linear prediction of the roll motion is less accurate. However, a similar evolution of the predicted roll motion was noticed between the proposed roll motion modeling and the modeling by Ikeda et al. [25] used as reference here. Consequently, a good confidence in the kite influence on the roll motion could be attributed in terms of evolution. Nevertheless, the value of the results in terms of roll motion should be considered with caution. Moreover, the ship motions were restricted to heave, pitch and roll motions and existing couplings, such as roll and sway coupling, were neglected.
A linear dependency of the kite aerodynamic characteristics was proposed to correct the kite velocity amplitude and the tether tension amplitude in order to get a better agreement between the experiments and the proposed kite modeling. The identification of the kite modeling was carried out with experimental data on a single run of 5 minutes. A more extensive validation should investigate the influence of the true wind speed and the influence of the trajectory position and orientation. Moreover, the determination of the kite aerodynamic coefficients was entirely based on experimental data. It could be interesting to be able to estimate by simulation the kite aerodynamic characteristics for a deeper understanding.
In case of a dynamic flight, the high tensions developed lead to small tether sags, justifying the assumption that the lines are straight and inelastic. However, the tether acts as an interface between the kite and the ship. The dynamic tether effect may have a significant influence on the interaction between the kite and the ship. In particular, additional theoretical research should be carried out to study the effect of the tether on the kite lock-in phenomenon.
Moreover, in order to validate the modeling approach proposed in this paper, several strategies could be implemented. Full scale experiments on a 6-meter long dedicated experimental boat towed by kite were carried out by Behrel et al. [33,43]. However, measurement of the environment is challenging at full scale. With towing tank tests, similarity issues are also difficult to solve, as Martin et al. [44] emphasize this in the case of offshore floating wind turbines. In order to get around the problem of similitude and to take benefit from the towing tank test conditions, the kite could be modeled with a hardware in the loop method such as proposed by Giberti and Ferrari [45] for classical sailing yacht.
5. Conclusions and Future Work
A dynamic modeling of a ship towed by a kite was developed by combining two modelings. One for the ship and the other for the kite. Each modeling was validated independently. Two coupling approaches between the kite and the ship were compared: a segregated approach where the kite force was applied as a predefined time series and a monolithic approach where all the coupling terms were taken into account.
The computation of the linear convolution term for the ship motion modeling was performed with a state-space approach in order to provide time efficient computations. The identification of the state-space modeling was revisited in order to fit the forward speed case requirements. Kite modeling was modified using linear correction terms for aerodynamic characteristics. These modifications improved significantly the predicted amplitude of kite velocity and tether tension.
In the calm water case, the coupling between the ship and the kite decreases the kite forces and consequently, the segregated approach was conservative compared to the monolithic one. Different tether lengths were tested with a constant angular trajectory size leading to an evolution of the kite excitation frequencies. For the considered case, the effect of the wind gradient led to a continuous increase in roll amplitude according to the tether length and excitation frequency. The vicinity between the kite harmonics and the ship natural roll frequency led to further local significant increases.
In case of regular beam waves, the interaction between the kite and the ship was more significant. The definition of the kite trajectory into the relative wind frame taking into account the vertical ship velocity led to unrealistic trajectories with very short radius of curvature. This problem was avoided by neglecting the vertical component of the vessel motion when defining the kite’s trajectory. Moreover, a kite lock-in phenomenon to the frequency of the waves was highlighted, which can be win-win. Indeed, for some configurations, the mean kite towing force was increased while the ship roll amplitude remained smaller than the case without kite.
Author Contributions
Conceptualization, K.R. and N.B.; methodology, K.R., J.-B.L.; Software, N.B.; formal analysis, J.-B.L.; Validation, J.-B.L., K.R. and N.B.; Writing—original draft preparation, N.B.; Writing—review and editing, K.R.; Supervision, K.R., J.-B.L.; Project administration, Y.P.; Funding acquisition, Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the French Environment and Energy Management Agency. GRANT NUMBER: 1482C0090.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; In the writing of the manuscript, or in the decision to publish the results.
Nomenclature
| dof | Degree(s) of freedom |
| EFD | Experimental Fluid Dynamic |
| Representations | |
| Earth fixed reference frame (inertial) | |
| Ship fixed frame | |
| Hydrodynamic reference frame | |
| Relative wind frame | |
| Kite reference frame | |
| Representations | |
| Vertical position of with respect to ship the baseline [m] | |
| Longitudinal position of with respect to the oft perpendicular of the ship [m] | |
| Variables | |
| Generalized velocity vector of the ship at with respect to the frame expressed in the frame [m.s−1, rad.s−1] | |
| Generalized position vector of the ship with respect to the frame expressed in the frame[m, rad] | |
| Generalized position vector of the ship with respect to the frame expressed in the frame[m, rad] | |
| Mean ship forward speed [m.s−1] | |
| Parameters | |
| K | Kite position () |
| A | Tether attachment point |
| Origin of the Ship reference frame | |
| Origin of the hydrodynamic reference | |
| Origin of the Earth reference frame | |
| Origin of the kite reference frame | |
| Relative wind velocity [m.s−1] | |
| True wind velocity [m.s−1] | |
| Reference wind speed at 10m altitude [m.s−1] | |
| Kite attachment point velocity [m.s−1] | |
| Apparent wind velocity to the kite [m.s−1] | |
| Kite velocity with respect to the frame [m.s−1] | |
| Parameters | |
| Angular frequency of the motion [rad.s−1] | |
| Angular frequency of the wave [rad.s−1] | |
| Angular frequency of encounter [rad.s−1] | |
| Angular frequency of encounter [rad.s−1] | |
| Angular frequency of the ith principal kite roll moment harmonic [rad.s −1] | |
| Angular frequency of the ith secondary kite roll moment harmonic [rad.s −1] | |
| k | Wave number [m−1] |
| Tether length [m] | |
| Tether tension [N] | |
| Glide angle of the kite [rad] | |
| Kite lift coefficient | |
| Kite surface area [m2] | |
| Measurement altitude of the wind [m] | |
| SODAR | Sonic Detection And Ranging |
| FFT | Fast Fourier Transform |
| g | Gravitational constant (9.81) [m.s−2] |
| Wave spectrum | |
| Wave direction with respect to the frame [rad] | |
| Parameters | |
| Impulse response function of the retardation matrix | |
| Laplace transform of the retardation matrix | |
| Kite trajectory | |
| Transformation matrix of the time derivatives of the Euler’s angle with respect to to the turning rates in | |
| Generalized added mass matrix with respect to for a given frequency of motion and at infinite frequency; with respect to | |
| Generalized damping matrix with respect to for a given frequency of motion and at infinite frequency; with respect to | |
| Generalized restoring matrix with respect to ; with respect to | |
| Azimuth of the centre of the kite trajectory [rad] | |
| Elevation of the centre of the trajectory [rad] | |
| Rotation angle of the trajectory around the axis defined by its centre and the tether attachment point A | |
| Heeling angle of the ship [rad] | |
| Phase angle of the Froude-Krilov force with respect to the free surface elevation [rad] | |
| True wind velocity at altitude of measurement [m.s−1] | |
| Trajectory radius of curvature [m] | |
| Amplitude of the kite roll moment [N.m] | |
| Amplitude of the ship heeling angle [rad] | |
| Amplitude of the Fourier transform | |
| Phase of the Fourier transform |
Appendix A. Ship Modeling
Appendix A.1. Time Domain Equations of Motion
This section is an overview of the work of Fossen [22]. The starting point of the mathematical modeling is the linearized frequency domain equation of motion, Equation (A1), used by the STF strip theory [9]:
where, , , and denote respectively the generalized mass matrix, added mass matrix, damping matrix and the restoring matrix with respect to the frame. is an extra generalized damping matrix accounting only for the roll motion as proposed in [9]. denotes the sum of the generalized external forces (forces and moments) applied to the ship expressed in the frame. is the mean value of . It should be noticed that Equation (A1) holds only for a given frequency, , with small amplitude sinusoidal motions. Since, and are frequency dependent. This assumption leads to the relationship:
In addition, the direct cosine matrix between the frame and the frame can be simplified considering small angles:
Defining , can be expressed from:
where,
and,
The detailed of this transformation is presented in [22]. Using Equation (A4), the equation of motion in Equation (A1) can be expressed in terms of as:
where,
Equation (A7) can be solved directly for a single frequency excitation. Nevertheless, since a kite and a ship may have strongly coupled motions, it is preferable to transform Equation (A7) into the time domain using the impulse response function as proposed by Cummins [15,17,46]. The steady state corresponds to and . Due to the special structure of , it can be noticed that . Consequently, the ship equation of motion for arbitrary motions and using the parametrization in is:
where, and . is defined as follows:
where denotes the impulse response of the retardation matrix. Strictly speaking, the integral boundaries of the convolution term should be and . However, assuming that for , the left boundary can be replaced by zero. In addition, assuming that the ship is a causal system, the right boundary can be truncated to t. , the Laplace transform of the retardation matrix, can be identified with Equation (A1) assuming unit sinusoidal motions in Equation (A9).
where .
Appendix A.2. Hydrodynamic Data and Linear Convolution Term
Each convolution component can be approximated by state space systems in Equation (A12), as introduced by Kristiansen and Egeland in [16].
where, represents the state-space modeling corresponding to a transfer function denoted by fitting , for . At zero forward speed, the properties of the retardation functions as described in [18] impose the form of the transfer function as follows:
In order to get finite results, according to the Riemann–Lebesgue Lemma, the transfer functions must be stable [47]. The denominator should respect the Routh–Hurwitz criterion [48,49]. With forward speed, the retardation function may not tend towards zero at zero frequency. Indeed can be different from [5]. Consequently, on the contrary to the zero speed case, the limit towards zero of can be non zero. This condition is not satisfied with the form given in Equation (A13). Thus, in case of forward speed, should have the form:
where the coefficient and should respect the following condition:
The data are obtained with the added mass and damping obtained according to the STF strip theory [9]. The 3D added mass and damping are expressed in terms of sectional added mass and damping. For instance, the STF strip theory expressed and in terms of sectional added mass and damping as follows:
where is the longitudinal position of the aft perpendicular section. The sectional added mass and damping are obtained with the Shipmo seakeeping software developed by the Marin® assuming an infinite depth. The frequency range of the data depends on the ship size, but for a commercial ship, the low frequency limit is generally about 0.1 rad.s−1 and the high frequency limit does not generally exceed 3 rad.s−1. To improve the quality of the identification method an extrapolation of the hydrodynamic data toward the asymptotic value is necessary. As shown by Newman [5], assuming a potential flow, at zero and infinite frequency, the sectional damping is zero. Hence, each sectional damping are then extrapolated at high frequency with the function in Equation (A17), proposed by Greenhow [50]:
where and are two constants chosen in order to provide continuity and differentiability. At zero frequency, the sectional damping is linearly extrapolated to zero. The sectional added mass are linearly extrapolated. At high frequency, the sectional added mass remains almost constant, consequently, a constant extrapolation is performed. The identification of can be identified either into the frequency domain or into the time domain, see [18]. Here, a time domain identification method is used to initialize the frequency domain identification method. The time domain identification is performed with the singular value decomposition method proposed by Kung [51]. This step is performed with a modified Matlab® function “imp2ss” to control the order. This method is efficient but the identified transfer function has the following form:
Consequently, to comply with the form imposed with Equation (A14), is set to zero, is set to and is set to . This first estimate of the transfer function is used as initial solution of the frequency domain identification method. The frequency identification step is performed with the “oe” function of the Matlab® system identification toolbox. This function use local optimization under constraints algorithm based on gradient methods. The structure of the transfer function, as proposed in Equation (A14), can be imposed to the frequency domain optimization algorithm. These two steps are repeated for several transfer function orders, for instance from 2 to 10. Then, the best transfer function order is selected according to a criterion based on the normalized quadratic error from:
Appendix A.3. Wave Forces
The Froude-Krilov and diffraction forces are obtained with the STF 2D strip theory [9]. Assuming an infinite depth, the dispersion relationship is , where k is the wave-number and g the gravity. Thus the frequency of encounter denoted by can be approximated by the following relationship:
where and denote respectively the wave angular frequency in rad.s−1 and the angle of the waves with respect to the ship heading. is given by , where denotes the wave angle with respect to . With , each component of the Froude–Krilov and diffraction forces generated by a single unit wave can be expressed by the following expression:
where is the amplitude of the ith component of and is a random phase.
For any wave spectrum , the Froude–Krilov and diffraction forces can be expressed as follows:
where is a random phase equidistributed between 0 and to obtain a Gaussian wave spectrum.
References
- Leloup, R.; Roncin, K.; Behrel, M.; Bles, G.; Leroux, J.B.; Jochum, C.; Parlier, Y. A continuous and analytical modeling for kites as auxiliary propulsion devoted to merchant ships, including fuel saving estimation. Renew. Energy 2016, 86, 483–496. [Google Scholar] [CrossRef]
- Naaijen, P.; Koster, V.; Dallinga, R. On the power savings by an auxiliary kite propulsion system. Int. Shipbuild. Prog. 2006, 53, 255–279. [Google Scholar]
- Ran, H.; Janson, C.E.; Allenström, B. Auxiliary kite propulsion contribution to ship thrust. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; pp. 1–9. [Google Scholar]
- Bigi, N.; Behrel, M.; Roncin, K.; Leroux, J.B.; Nême, A.; Jochum, C.; Parlier, Y. Course Keeping of Ship Towed by Kite. In Proceedings of the 15th Journees de l’Hydrodynamique, Brest, France, 22–24 November 2016; pp. 1–14. [Google Scholar]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Molin, B. Hydrodynamique des Structures Offshore; Editions Technip: Paris, France, 2002. [Google Scholar]
- Faltinsen, O.M. Hydrodynamics of High-Speed Marine Vehicles; Cambridge University Press: Cambridge, UK, 2005; pp. 1–476. Available online: http://xxx.lanl.gov/abs/arXiv:1011.1669v3 (accessed on 5 June 2020).
- Bertram, V. Practical Ship Hydrodynamics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Salvesen, N.; Tuck, E.; Faltinsen, O. Ship motions and sea loads. Trans. SNAME 1970, 78, 250–287. [Google Scholar]
- Lee, C.H. WAMIT Theory Manual; Massachusetts Institute of Technology, Department of Ocean Engineering: Cambridge, MA, USA, 1995. [Google Scholar]
- Skejic, R. Ships Maneuvering Simulations in a Seaway—How close are we to reality? In Proceedings of the International Workshop on Next Generation Nautical Traffic Models, Delft, The Netherlands, 6 November 2013; pp. 91–101. [Google Scholar]
- Böttcher, H. Simulation of Ship Motions in a Seaway; Technical Report; Institut für Schiffbau der Universität Hamburg: Hamburg, Germany, 1989. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. An implementation of the Method of Auxiliary State Variables for solving seakeeping problems. Int. Shipbuild. Prog. 2005, 52, 357–384. [Google Scholar]
- Sutulo, S.; Soares, C. A generalized strip theory for curvilinear motion in waves. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Estoril, Portugal, 15–20 June 2008; Volume 6, pp. 359–368. [Google Scholar] [CrossRef]
- Cummins, W. The Impulse Response Function and Ship Motions; Technical Report; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Kristiansen, E.; Hjulstad, A.; Egeland, O. State-space representation of radiation forces in time-domain vessel models. Ocean Eng. 2005, 32, 2195–2216. [Google Scholar] [CrossRef]
- Fossen, T.I.; Smogeli, Ø.N. Nonlinear time-domain strip theory formulation for low-speed manoeuvring and station-keeping. Model. Identif. Control 2004, 25, 201–221. [Google Scholar] [CrossRef]
- Pérez, T.; Fossen, T.I. Time-vs. frequency-domain Identification of parametric radiation force models for marine structures at zero speed. Model. Identif. Control 2008, 29, 1–19. [Google Scholar] [CrossRef]
- Behrel, M.; Roncin, K.; Leroux, J.B.; Montel, F.; Hascoet, R.; Neme, A.; Jochum, C.; Parlier, Y. Application of phase averaging method for measuring kites performance: Onshore results. J. Sail. Technol. 2018. [Google Scholar]
- Wellicome, J.F.J.F.; Wilkinson, S. Ship Propulsive Kites: An Initial Study; Technical Report; Department of Ship Science, University of Southampton: Southampton, UK, 1984. [Google Scholar]
- Dadd, G.M.; Hudson, D.A.; Shenoi, R.A. Determination of kite forces using three-dimensional flight trajectories for ship propulsion. Renew. Energy 2011, 36, 2667–2678. [Google Scholar] [CrossRef]
- Fossen, T. A Nonlinear Unified State-Space Model for Ship Maneuvering and Control in a Seaway. Int. J. Bifurc. Chaos 2005, 15, 2717–2746. [Google Scholar] [CrossRef]
- The University of Iowa. EFD Data, The University of Iowa, Iowa City, USA. 2013. Available online: https://www.iihr.uiowa.edu/shiphydro/efd-data/ (accessed on 30 June 2020).
- Irvine, M.; Longo, J.; Stern, F. Pitch and Heave Tests and Uncertainty Assessment for a Surface Combatant in Regular Head Waves. J. Ship Res. 2008, 52, 146–163. [Google Scholar]
- Ikeda, Y.; Himeno, Y.; Tanaka, N. A Prediction Method for Ship Roll Damping; Technical Report; Department of Naval Architecture, University of Osaka Prefecture: Osaka, Japan, 1978. [Google Scholar]
- Loyd, M.L. Crosswind kite power (for large-scale wind power production). J. Energy 1980, 4, 106–111. [Google Scholar] [CrossRef]
- Paulig, X.; Bungart, M.; Specht, B. Conceptual Design of Textile Kites Considering Overall System Performance. In Airborne Wind Energy; Springer: Berlin/Heidelberg, Germany, 2013; pp. 547–562. [Google Scholar]
- Wellicome, J. Some comments on the relative merits of various wind propulsion devices. J. Wind Eng. Ind. Aerodyn. 1985, 20, 111–142. [Google Scholar] [CrossRef]
- Argatov, I.; Rautakorpi, P.; Silvennoinen, R. Estimation of the mechanical energy output of the kite wind generator. Renew. Energy 2009, 34, 1525–1532. [Google Scholar] [CrossRef]
- Leloup, R.; Roncin, K.; Bles, G.; Leroux, J.B.; Jochum, C.; Parlier, Y. Kite and classical rig sailing performance comparison on a one design keel boat. Ocean Eng. 2014, 90, 39–48. [Google Scholar] [CrossRef]
- Group, I.Q.S. ITTC Symbols and Terminology List Version 2014. Technical Report. In Proceedings of the International Towing Tank Conference, Copenhagen, Denmark, 31 August–5 September 2014. [Google Scholar]
- Leloup, R. Modelling Approach and Numerical Tool Developments for Kite Performance Assessment and Mechanical Design; Application to Vessels Auxiliary Propulsion. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2014. [Google Scholar]
- Behrel, M.; Roncin, K.; Leroux, J.B.; Neme, A.; Jochum, C.; Parlier, Y. Experimental set up for measuring onshore and onboard performances of leading edge inflatable kites—Presentation of onshore results. In Proceedings of the 4th Innov’Sail Conference, Lorient, France, 28–30 June 2017. [Google Scholar]
- Fagiano, L.; Zgraggen, A.U.; Khammash, M.; Morari, M. Automatic control of tethered wings for airborne wind energy: Design and experimental results. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 992–997. [Google Scholar]
- Fagiano, L.; Zgraggen, A.U.; Morari, M. On Modeling, Filtering and Automatic Control of Flexible Tethered Wings for Airborne Wind Energy. In Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 167–180. [Google Scholar]
- Leloup, R.; Roncin, K.; Blès, G.; Leroux, J.B.; Jochum, C.; Parlier, Y. Estimation of the effect of rotation on the drag angle by using the lifting line method. In Proceedings of the 13th Journees de L’Hydrodynamique, Chatou, France, 21–23 November 2012. [Google Scholar]
- Duport, C.; Leroux, J.B.; Roncin, K.; Jochum, C.; Parlier, Y. Comparison of 3D non-linear lifting line method calculations with 3D RANSE simulations and application to the prediction of the global loading on a cornering kite. In Proceedings of the 15th Journees de L’Hydrodynamique, Brest, France, 22–24 November 2015. [Google Scholar]
- Fagiano, L. Control of Tethered Airfoils for High–Altitude Wind Energy Generation. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2009. [Google Scholar]
- Fagiano, L.; Milanese, M.; Piga, D. Optimization of airborne wind energy generators. Int. J. Robust Nonlinear Control 2012, 22, 2055–2083. [Google Scholar] [CrossRef]
- Longo, J.; Stern, F. Resistance, sinkage and trim, wave profile, and nominal wake tests and uncertainty assessment for DTMB model 5512. In Proceedings of the 25th American Towing Tank Conference, Iowa City, IA, USA, 1998; Available online: https://pdfs.semanticscholar.org/3799/7310985bd531109d91e38c08e6508353f4c9.pdf (accessed on 30 June 2020).
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Behrel, M.; Roncin, K.; Iachkine, P.; Hascoet, R.; Leroux, J.B.; Montel, F.; Parlier, Y. Boat towed by kite: Methodolgy for sea trials. In Proceedings of the 16th Journées de l’Hydrodynamique, Marseille, France, 27–29 November 2018. [Google Scholar]
- Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for Wind/Wave Basin Testing of Floating Offshore Wind Turbines. J. Offshore Mech. Arct. Eng. 2014, 136, 021902. [Google Scholar] [CrossRef]
- Giberti, H.; Ferrari, D. A novel hardware-in-the-loop device for floating offshore wind turbines and sailing boats. Mech. Mach. Theory 2015, 85, 82–105. [Google Scholar] [CrossRef]
- Ogilvie, F.T. Recent Progress Towards the Understanding and Prediction of Ship. In Proceedings of the 6th Symposium on Naval Hydrodynamics, Bergen, Norway, 10–12 September 1964; pp. 3–79. [Google Scholar]
- Riemann, B. Ueber die Darstellbarkeit Einer Function Durch eine Trigonometrische Reihe; Dieterichschen Buchhandlung: Göttingen, Germany, 1867. [Google Scholar]
- Routh, E.J. A Treatise on the Stability of a Given State of Motion: Particularly Steady Motion; Macmillan and Company: London, UK, 1877. [Google Scholar]
- Hurwitz, A. Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt. Math. Ann. 1895, 46, 273–284. [Google Scholar] [CrossRef]
- Greenhow, M. High- and low-frequency asymptotic consequences of the Kramers-Kronig relations. J. Eng. Math. 1986, 20, 293–306. [Google Scholar] [CrossRef]
- Kung, S.Y. A New Identification and Model Reduction Algorithm via Singular Value Decompositions. In Proceedings of the 12th Asilomar Conference on Circuits, Systems and Computers, Pacific Grove, CA, USA, 6–8 November 1978; pp. 705–714. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).