Abstract
Understanding of the reflection characteristics of coastal seawalls is crucial for design. Wave reflection can cause difficulties in small vessel manoeuvring at harbour entrances; this can cause damage to the toe of coastal structures by scouring. Previous studies have examined the reflection characteristics of coastal seawalls under random wind-generated waves without considering the effects of wave bimodality created by the presence of swell waves. This present study focuses on the influence of random wave bimodality on the reflective characteristics of coastal seawalls. 823 experimental tests were conducted to examine the reflection performance of impermeable sloping seawalls under bimodal waves. Reflection coefficients were computed from each test. The analysis of the results suggests that both unimodal and bimodal waves give similar reflection characteristics. However, the reflection coefficient in bimodal sea states seems to be more prolonged than in the unimodal sea states. It was found that the reflection coefficients of coastal seawalls are strongly influenced by the seawall slope, the wave steepness, the relative water depth, and the surf similarity parameters. A new empirical reflection equation to describe the influence of wave bimodality on the reflection characteristics of coastal seawalls has been formulated based on this study.
1. Introduction
Waves incident on coastal seawalls will be partially reflected unless they are fully absorbed by the structure. The reflected wave component will interact with the incoming wave, creating interference. This can lead to wave amplification, wave breaking, and standing waves according to Lykke Anderson [1]. In the case of vertical walls, standing waves can be pronounced (Zanuttigh and van der Meer [2]). Standing waves lead to an amplification of wave-induced velocities, which can lead to exacerbated scouring of sediments near the toe of the structure, and eventually to its failure and collapse. At locations exposed to local storm waves and open oceans, long-period swell waves can be present, leading to bimodal wave conditions. Existing literature provides little guidance on reflection characteristics in this situation, which Hawkes et al. [3] consider as constituting the worst-case scenario in terms of wave conditions. Recent studies by Thompson et al. and Poliodoro et al. [4,5] provide evidence that bimodal wave conditions constitute worse conditions than pure wind–wave conditions of similar total energy content. There remains a gap in our understanding of seawall performance under bimodal wave conditions. This paper presents the results of laboratory experiments of bimodal waves impinging an impermeable seawall.
In real life, there are impermeable, permeable, and rough structures. Consequently, in Zanuttigh and van der Meer [2], two approaches to laboratory modelling of wave reflections of coastal seawalls have been noted. The first is to use impermeable structures and then to apply an empirical roughness factor to adjust for permeability and roughness. Alternatively, permeable/rough structures can be directly applied in the laboratory. There are advantages and disadvantages to both. In the first case, the simulation is based on a ‘perfect’ situation not usually encountered in real life, but then the results are adjusted through an empirical factor. In the second case, a dynamic similarity is assumed; that is, the form of turbulence and energy dissipation will remain the same at the smaller laboratory scales as it does at full scale. Earlier studies, including those of Miche, Ursell, and Battjes [6,7,8], provide insights into the reflection of impermeable sloping seawalls. Miche [6] developed formulations for the reflection coefficients of monochromatic waves on a plane beach, and hypothesised that the reflection coefficient of the monochromatic wave can be directly related to the critical steepness of the wave. The constant of proportionality was defined in the form of a Miche number M. Based on physical experiments conducted by Ursell [7] and Battjes [8], it was noted that Miche’s hypothesis significantly overestimated the exhibited by both regular and irregular waves. Thus, Miche’s hypothesis was reformulated [8] for breaking and non-breaking waves. It was based on the wave breaker parameter in conformance with an earlier study conducted by Iribarren [9]. Further studies on the reflection characteristics of smooth impermeable slopes were later presented by Seelig [10]. The study reveals the adequacy of [8] in predicting the reflection of plane slopes, but still deemed overprediction for greater than 2.3. In this way, further prediction standards were provided by Seelig & Ahrens [11]. From the aforementioned studies, wave height H, the structure slope , and the wave period T were respectively identified as the three fundamental factors that influence the reflection coefficients of smooth slopes.
Further studies are devoted to investigate the effects of porosity and surface roughness on the reflection performance of coastal seawalls. Both the transmission and the energy dissipation properties of the propagating waves can be significantly varied and their effects can be inspected. Davidson et al. [12] fully reviewed these studies. Coastal structures were described in terms of their surface roughness and permeability by Gunbak [13], DeBok and Sollitt [14], and Seelig [10]. Equations describing the reflection characteristics of these structures can be found in Seelig & Ahrens [11]. In these new equations, additional parameters were identified which influence the reflection characteristics of sloping seawalls. These parameters include the water depth h at the toe of the structure and the diameter of the rock components D. The reduction factor of was determined based on the combination of these parameters. Full details of the implementation are described in the Shore Protection Manual [15]. Numata [16] presented the reflection and transmission performances of artificial blocks in a dimensionless form by comparing the ratio of breakwater width to the diameter of the armour. In order to achieve the formulations, the rock diameters were varied from previous studies.Davidson et al. [12] pointed out the two-fold effects of increasing rock diameters, as presented by Numata [16]. More energy dissipation was created by the increase in rock diameter, and a higher dissipation rate based on the void in the rock samples was introduced.
Alternatively, Gimenez-Curto [17] presented the exponential form of the reflection characteristics of the flow behaviours around the rough and fully permeable structures. Well-defined interaction curves obtained from wave heights and periods of regular waves were applied to obtain probabilistic standards, which serve as the input for predicting flow patterns of equivalent irregular wave actions. The exponential probability model proposed by Losada and Gimenez-Curto was validated using experimental datasets [18]. Postma [19] applied 300 wave tests to investigate the rock slopes under irregular wave attack, which showed a greater dependence of the reflection coefficient on the breaker index . Effects of various parameters such as toe water depth, the structure’s angle of slope, and the rocks’ notional permeabilities were bench-marked against previous formulations of reflection coefficients. Postma [19] compared the results with those of Allsop and Channell [20] to derive a comparable empirical relationship with Battjes [8]. However, a weaker correlation was obtained in the relationship between with spectral characteristics and depth at the structure’s toe. In order to improve the fitness of the datasets, van der Meer [21] applied multiple regression analysis on the combination of the newly captured laboratory results with previously acquired datasets from Postma [19]. More refined relationships between and were obtained by applying a multiple regression analysis combining the influences of the characteristics of waves (in terms of heights and periods) and the structures (slope and permeability).
Full-scale models were then developed to test the adequacy of the previously developed formulations at predicting the reflection characteristics of coastal structures. Oumeraci and Partensky [22] and Muttray [23] performed large-scale tests with accropods and tetrapods, but at a different scale to Allsop and Hettiarachi [24]. The effects of scales were significant in these studies, because the larger-scale models presented by Oumeraci and Paternsky [22] gave a larger estimate of reflection (up to 25%) than those of smaller-scale tests. However, lesser percentages (less than 10%) were observed in other large-scale models by DeBok [14] and DeBok Shimada et al [25]. A modified version of the study by Seelig and Ahrens [11] was presented by Allsop and Hettiarachi [24]. Here, values of wave steepness from 0.043 to 0.042 were investigated, which correspond to ideal wind–sea states. Lower wave steepness, which corresponds to swell-driven sea conditions under bimodal wave conditions, has not been considered. Newer coefficient values for predicting reflection performances of random waves were derived. A more recent study was presented by Neelamani and Sandhya [26]. Predictive equations were proposed based on a series of experimental tests derived from wave reflection measurements of several wave heights and wave periods. Different seawall types, including plane, dentated, and serrated, and one water depth were used in all measurements obtained. Wang et al. [27] and Zanuttigh and Andersen [28,29] presented studies of wave reflection under directional wave spreading and wave obliquity. Higher values of reflection coefficients were obtained for short-crested waves than for long-crested ones. However, wave reflection was observed to decrease with increasing obliquity with over-dependence of on the incident angle. In the case of [27], over-dependence of reflection on the angle of incidence was presented. More recent studies applied different porosity components to investigate under regular waves (Koraim and Rageh [30]) and irregular waves for submerged structures (Young and Testik [31], Koraim et al. [32]). Combinations of regular and irregular wave cases were recently applied to investigate the properties of partly or fully perforated caisson seawalls by Lee and Shin [33] and Esmaeili et al. [34]).
Here, we investigate values of wave steepness from 0.043 to 0.042, which corresponds to ideal wind–sea states. Lower wave steepness would correspond to swell-driven sea conditions under bimodal wave conditions. As observed in some previous studies, including Thompson et al. [4], Poliodoro et al. [5], and Orimoloye et al. [35], bimodality in sea waves generally increases the wavelength of the wave train. It would, in turn, reduce the wave steepness, and could usually alter the breaker-parameter indices. These occurrences have not yet been fully investigated for bimodal sea cases. In this study, the physical model tests were performed on three different seawalls to examine reflection performances under bimodal wave scenarios. Only the non-breaking wave cases were considered, and the experiments reported in this paper did not include any impulsive breaking waves, where waves breaking onto a vertical wall cause impulsive impacts in which the entrapped air is compressed and then decompressed, as noted by Allsop et al. [36]. Our experiments did not include such cases. As such, the vertical walls are set as the limit of the increasing slope. Unimodal and bimodal cases were compared with previous formulations. A new prediction formula which considers reflection coefficients under wave bimodality is proposed. The paper is divided into five sections; the following section (Section 2) briefly explains the formulation of the analytical energy-conserved bimodal spectrum. Section 3 details the numerical modelling of the discretised waves, Section 4 presents and discusses the results, and the conclusions are presented in Section 5.
2. Reflection Characteristics of Smooth Impermeable Slopes
Battjes [8] identified the surf similarity parameter as a critical parameter affecting the reflection characteristics of sloping impermeable slopes with slope angle under incident monochromatic waves. It can be expressed mathematically as:
In this equation, H and T represent the significant wave height and the wave period of the monochromatic wave, respectively. Values of correspond to breaking waves, while for , non-breaking waves occur. The equation showing a simplified relationship between the reflection coefficient and the breaker parameter of breaking monochromatic waves has also been described in the same study (Battjes [8]), and is:
This expression is only valid for breaking monochromatic waves , as illustrated by Figure 1. In Seelig and Ahrens [11], a modified version of Equation (2) has been presented. The modified relationship between the reflection coefficient and the breaker parameter is presented in Equation (3):
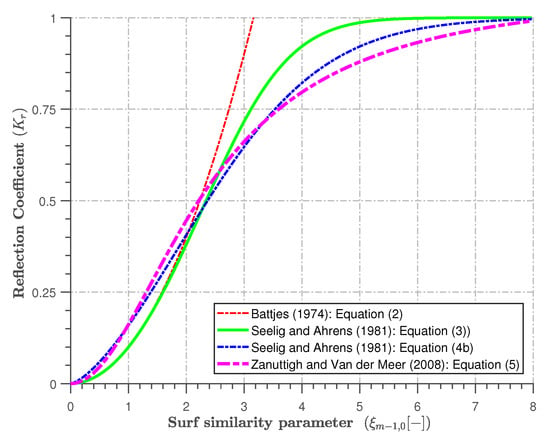
Figure 1.
An illustration of the prediction of the reflection characteristics of smooth impermeable slopes.
It is worth noting that Equation (2) is an approximation close to Equation (3) for small values of the surf similarity parameter. For larger values of the parameter, Equation (3) tends asymptotically to 1. The mathematical expression from Seelig and Ahrens [11] is valid for both breaking and non-breaking monochromatic waves.
More accurate expressions were also proposed, based on several experimental studies that were performed to describe the reflection behaviours of other sea defences, including revetments, beaches, and breakwater. These expressions consider both the peak periods of irregular waves and the spectrally determined breaker parameter . These are described in Equations (4a) and (4b) below:
Equation (4b) is valid for 1.0 ≤≤ 6.2 and sloping seawalls with 1.5 ≤ cot ≤ 2.5, respectively.
Zanuttigh and van der Meer [2] proposed a revised version of Equation (4b) from over 4000 reflection coefficient experimental test results. This can be generally expressed as:
This equation extends the range of applicability to structure slopes with 1.5 ≤ cot ≤ 4.0 and 1.0 ≤≤ 4.1 with a dimensionless crest freeboard of 0.58 ≤≤ 4.5.
3. Material and Methods
3.1. Design of Model Tests
The Coastal Laboratory wave tank at Swansea University consists of an Armfield wave tank 30 m in length, 0.8 m in width, and 1.2 m in depth. Waves are generated with an HR Wallingford computer-controlled piston paddle which has the capability of reproducing user-defined spectra of different types; this includes a second-order wave correction due to Schäffer [37], and is also equipped with an active wave absorption system to minimise the wave reflection from the wave board. Each test was performed in this wave tank by applying an energy-conserved bimodal spectrum (Figure 2).
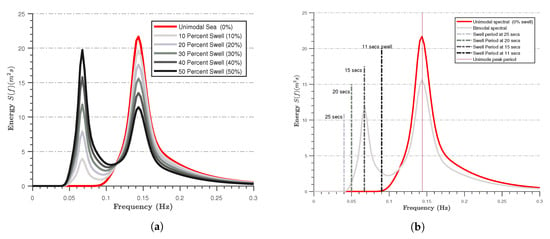
Figure 2.
(a) An example of the bimodal spectra. (b) Shifting patterns of swell peak periods from 11–25 s [35].
We refer to a sea state that has a fixed amount of energy but varying proportions of swell and wind–sea as ’energy-conserved’ bimodal waves. The extremes of these conditions are ’pure wind–sea’ at one end and ’pure swell’ at the other, with both cases resulting in a unimodal spectrum. For each test, sequences of 1000 random waves were generated.
Figure 3 shows the experimental set-up of an impermeable sloping seawall constructed of aluminium. The construction had a fixed 1:20 beach with a separate section that allowed seawalls of different slopes to be inserted. Three different slope angles (Cot = 1.5, 3, 0) were investigated at three different water levels. The details of the wave conditions and hydraulic parameters tested in this study are given in Table 1. A total of 823 bimodal wave conditions were tested to examine the influence of slope, swell peak periods, and swell percentages on the reflection performances of the impermeable seawall. An array of four wave gauges was positioned around the centre (with constant water depth) to capture both incident and reflected wave elevations effectively. As observed in Allsop and Hettiarachi [24], a wide range of frequencies can be obtained at central areas with constant water depth. The gauges were placed at central positions to meet the minimum requirements specified in Zelt and Skjelbreia [38]. The distances were computed using wavelengths computed from the dispersion relationships represented by individual wave conditions as X1 = 0, X12 = L/10, X13 = L/4, and X14 = L/3, as shown in the detailed experimental set up. The full details of the experiment can be found in Orimoloye et al. [39].
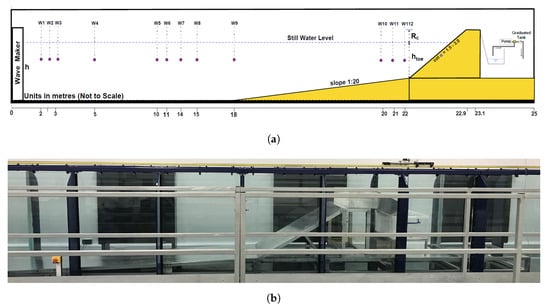
Figure 3.
(a) Layout of a schematic cross-section of the wave gauges applied for reflection analysis. (b) Photograph of the constructed model.

Table 1.
Bimodal wave conditions with the peak period of wind waves () and peak periods of swell waves tested in the present study.
3.2. Reflection Analysis
The reflection analysis of the acquired signals was performed using the HR-Daq data acquisition and processing software that was incorporated into the wavemaker control system. This package separates reflected waves from the total signals using the method of Zelt and Skjelbreia [38]. This method is an extension of the three-wave-gauge least-squares solution of reflection analysis first introduced by Mansard and Funke [40]. The wave signals were analysed using Fast Fourier Transform (FFT) into frequency components in the frequency domain. Some portions of wave elevation at earlier and later parts of each simulation were ignored to allow for consistency of the wave elevations. The maximum lengths of the discarded portions were 60 s at the beginning and 120 s at the end. Bandpass filtering was applied to isolate the frequency band of ≤≤.
The reflection analyses of Mansard and Funke and Zelt and Skjelbreia [38,40] apply strictly to linear waves. For the breaking wave cases, the non-linearity of the reflection performances cannot be accurately estimated by this method. The accuracy of the Zelt and Skjelbreia method was determined using the flume without any structure. The free reflection characteristics of the open flume were used to calibrate the performance of the method of [38]. It was observed that the accuracy of the method was up to 90 percent. These adjustments were applied to all wave cases studied.
3.3. Estimation of Reflection Parameters
Some of the reflection parameters required for this study were estimated. These include the linear wave length, wave steepness, and the dimensionless Iribarren number. The relationships obtained from these parameters are of special relevance to this study. The linear wave length applied here was calculated using the Newton–Raphson iteration technique on the dispersion relationship (e.g., Reeve [41]):
In Equation (6), h is the offshore water depth, and represents the spectral wave period. In addition, the wave steepness can be defined in terms of the dimensionless ratio of the spectral wave height and the wave length obtained from Equation (7):
Similarly, the surf similarity parameter can be estimated from Equation (8):
The other relevant parameters are the non-dimensional wave height and non-dimensional water depth . Table 1 presents the wave conditions tested in this study: for each of the test numbers, there are four different swell peak periods across three different sloping seawalls.
4. Results and Discussions
To derive a functional improvement of the reflection coefficient of impermeable walls under bimodal sea conditions, in this section, the effects of various secondary factors influencing will be considered. These factors include the wall slope, water depth, wave steepness, and crest freeboard.
4.1. Influence of Wall Slope on Reflection Characteristics
The reflection characteristics of a coastal seawall can be determined by the steepness of the wall’s slope. The combined plots of the relationship between the reflection coefficient and the breaker index parameters are presented in Figure 4. Figure 4a–c presents the comparison between the results of a unimodal sea state and the reflection results due to bimodal sea states. In general, for unimodal and bimodal sea conditions, varies between 0.4 and 1.038. As expected, lower values of are observed with a gentle slope of 1:3, while higher of are clearly observed for the case of the vertical seawall. These results are consistent with the findings of Seelig and Ahrens [11] and Allsop and Hettiarachi [24]. shows great dependencies on the structure’s slope. It was observed during the experiments that overtopping increases with the gentleness of the slope, which in turn reduces the reflective properties of the seawall. This observation is consistent with previous studies [36,42]. The range of for a vertical wall depends largely on the degree of wave overtopping, and it increases as the crest freeboard increases. For sloped seawalls, the is directly proportional to of the incident waves. In bimodal seas, a higher bound of is created, which corresponds to the swells of long periods exhibited by the bimodal seas.
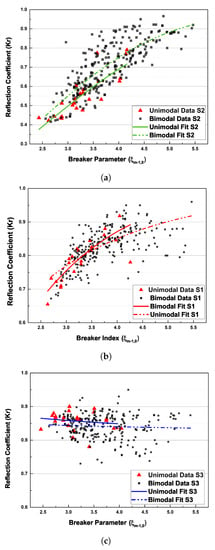
Figure 4.
Comparison of the reflection coefficient and breaker parameters between unimodal and bimodal seas across three slopes for: (a) cot , (b) cot , and (c) cot .
Figure 5 shows a combined plot of the best-fit curves of against for both unimodal (solid lines) and bimodal (dotted lines) seas across different slopes. It was obtained by applying the non-linear fit algorithm to all of the datasets from the unimodal and bimodal seas. Unimodal sea states exhibited similar trends to those of the bimodal sea conditions under the same test conditions. However, the relationship between and is more extensive in the bimodal sea states than in the unimodal sea conditions. The long periods in the bimodal seas are responsible for this occurrence. As the wave period increases, there is a further reduction in wave steepness, while the values of increase. It follows that values of are inversely proportional to the wave steepness, as reported in previous studies [11].
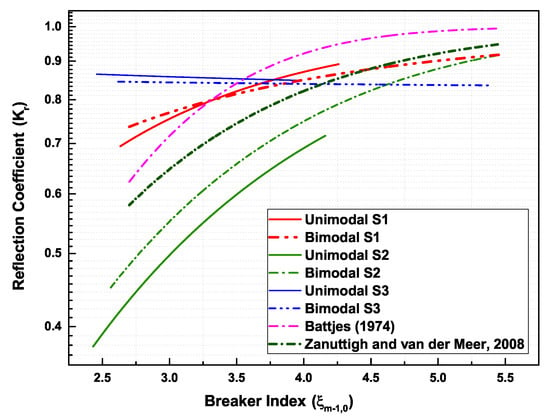
Figure 5.
Variations of the reflection coefficient with breaker index across three different slopes.
The least amount of reflection was observed for the gentle slope (cot = 3.0), which is in accordance with the observations of van Gent [43] and Neelamani and Sandya [26], and is a result of the wave energy dissipation.
Further examination of these results shows that the relationships between and for unimodal states obtained in this study are within the bounds of previous studies by Battjes [8] and Zanuttigh and van der Meer [2]. However, a better fit is obtained from the modified formulation derived by Zanuttigh and van der Meer [2]. The fitted coefficients of [2] do not accurately fit for the relationship between and in bimodal seas.
4.2. Influence of Water Depth Variations
In this section, the influence of water depth, , on the reflection coefficient, , was investigated across three slopes (i.e., cot , cot , and cot ). Figure 6 presents these results for all of the datasets acquired during this study. Generally, for the steep- (cot ) and the mild-sloping (cot ) seawalls, it was found that the value of decreases with increasing relative depth . This behaviour is consistent with the findings of previous studies Neelamani and Sandya [26] and Nassar and Negm [44,45]. These observations are peculiar to plunging-wave-breaking phenomena. For the vertical seawall, the reflection coefficient is almost independent of water depth. This is expected because of the reflection of waves by vertical walls irrespective of the depth limiting values. Standing waves are formed during these tests, and more energy is reflected than with sloping walls. These observations are similar for both the unimodal and bimodal sea states.
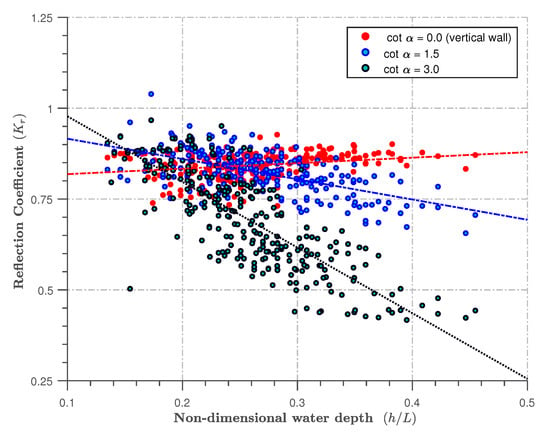
Figure 6.
Variations of the reflection coefficient with non-dimensional water depth across the three different slopes investigated.
4.3. Influence of Wave Steepness
Many sloping and vertical impermeable seawalls are built solely to dissipate wave energies that are directly incident on them. Reflected waves are produced whenever the waves are incident on the plain seawalls. In sloping seawalls, it has been suggested in Goda [46] that values of the reflection coefficient are inversely proportional to the incident wave steepness . The suggestion is true for the observations recorded in this study, as shown in Figure 7. A completely similar correlation with the influence of water depth observed in the previous section is formed. However, the vertical seawall totally deviated from this theory in both cases.
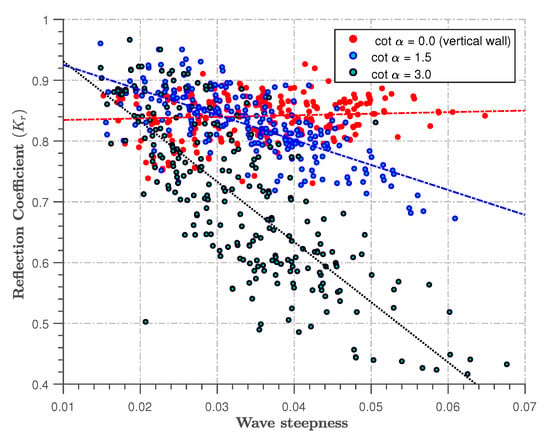
Figure 7.
Relationships between wave steepness and the reflection coefficient across the three different slopes investigated.
The performance of the vertical seawall, as shown in Figure 7 and Figure 8, suggests that vertical seawalls would provide a more valuable protection to cities, harbours, or ports, as previously prescribed in previous studies, for example.
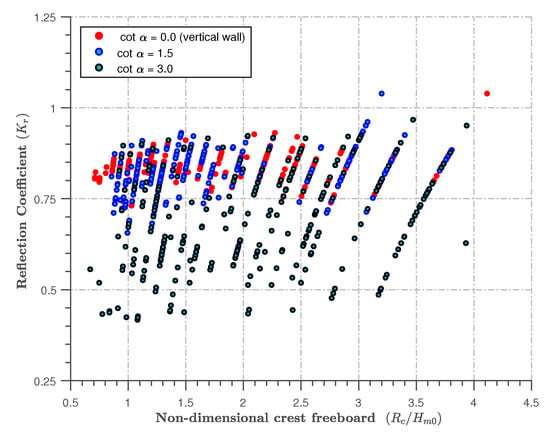
Figure 8.
Influence of dimensionless crest freeboard with the reflection coefficient across the three different slopes investigated.
4.4. Effects of the Crest Freeboard
The accurate selection of the size of the crest freeboard is an essential requirement for designing coastal seawalls against wave overtopping and to serve as a flood barrier. The reliable prediction of the reflection characteristics of a coastal seawall suitable for the selected is also key. In Figure 8, is presented in terms of only across three seawall slopes. It can be seen that is directly proportional to the values of . As the crest freeboard increases, the value of also gradually increases. This implies that, as crest freeboard is reduced, there is more wave overtopping and there is a greater tendency for the reduction of reflection altogether.
5. Reflection Coefficients of Steep Slopes Under Bimodal Waves
In order to establish an improved formulation for the reflection coefficient for bimodal sea conditions, a more detailed analysis of the results was performed. Figure 9 presents a more detailed relationship obtained by performing a non-linear regression analysis of the results between and across each slope for the bimodal cases.
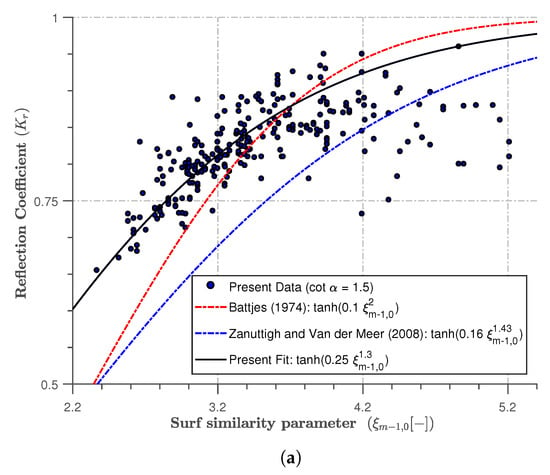
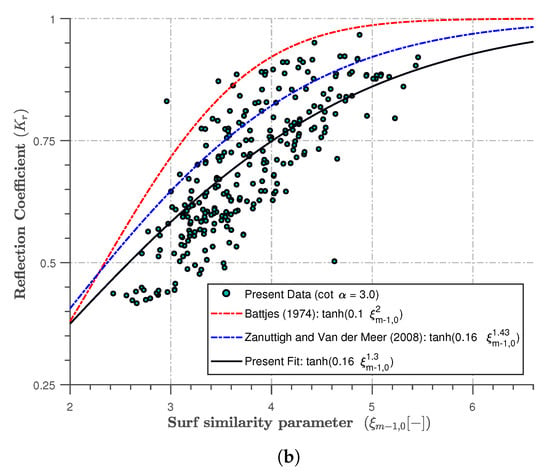
Figure 9.
A representation of the non-linear multi-regression fit between and for the sloping seawall with: (a) cot = 1.5; (b) cot = 3.0.
Based on the multiple regression analysis of the observed datasets, a predictive equation that considers the effects of reflection due to bimodal waves is proposed. The equation contains two corresponding calibration coefficients applied in defining the of different impermeable slopes. It can only be applied for sloping seawalls under bimodal sea conditions.
The coefficients are slightly modified from those of Zanuttigh and van der Meer [2]. For simplicity, a more general form of Equation (5) can be written in terms of the coefficients a and b presented in Equation (9):
As a general rule of conditions for bimodal seas, the values of a and b can be simplified:
To assess the suitability and conformance of the new formulation, a correlation assessment of the new equation with that of Zanuttigh and van der Meer [2] was made. Figure 10 shows a verification obtained in the present study, represented by Equations (5), (10) and (11) from Zanuttigh and van der Meer [2]. The observed and the predicted are fully described in this figure for the two slopes ((a) cot = 1.5; (b) cot = 3.0).
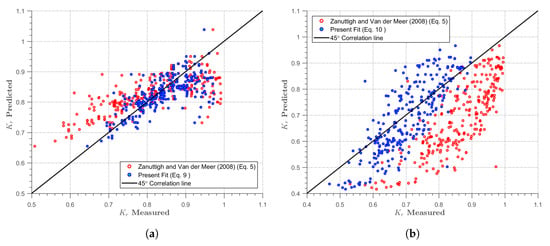
Figure 10.
Comparison between the measured and the predicted of the wave reflection coefficient (a) cot = 1.5; and (b) cot = 3.0.
As shown in these figures, observed data points are well distributed on either side within a 45° correlation line. It can be deduced from the slight convergence of the agreement between the observed and predicted values that Equations (10) and (11) work better in defining the reflection characteristics of sloping seawalls under the influence of bimodal waves than Equation (5). The prediction of a prolonged breaker index imposed by longer periods in swell waves is more accurately made with Equations (10) and (11) than with Equation (5). This under-predicts under the bimodal cases, especially with increasing gentle slopes. The present formulation, (Equations (10) and (11)) will be applicable at locations exposed to local storm waves and open oceans under bimodal wave conditions. Figure 11 expresses the appropriateness of the equation in predicting in bimodal seas, as represented in the residual plots described by the new formulations for both the steep slope (cot = 1.5) and gentle slope (cot = 3.0).
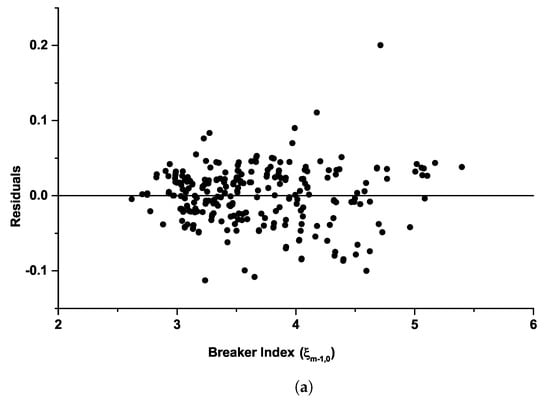
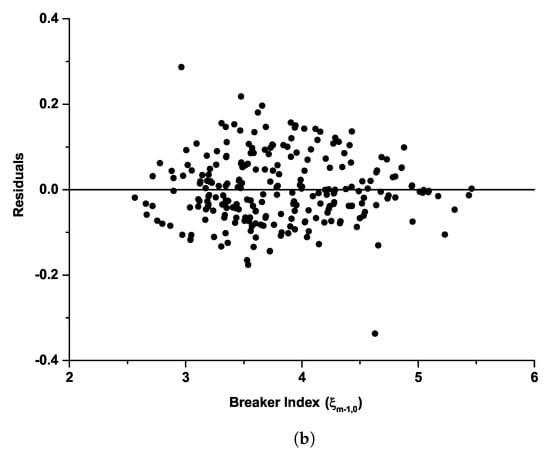
Figure 11.
Comparison between the measured and the predicted of the wave reflection coefficient (a) cot = 1.5; and (b) cot = 3.0.
6. Conclusions
This study examined the reflection performance of a smooth sloping impermeable aluminium seawall in bimodal sea states. Three different sloping seawalls were investigated at three different water levels to conduct 823 successful storm tests. An array of four wave gauges positioned around the centre (with constant water depth) was applied to effectively capture both incident and reflected wave elevations. The Fast Fourier Transform (FFT) was applied to decompose the analysed wave signals from the four wave gauges into frequency components in the frequency domain. The analysed reflection response of the studied coastal seawall is highly dependent on the seawall slope and wave bimodality. The resultant reflection coefficient also increases with swell peak periods and swell percentages. The results of the reflection tests presented and analysed in this paper yield an improved empirical formula for determining reflection under bimodal sea conditions. New expressions for the reflection coefficient that take into account swell-driven seas with wave bimodality have been proposed.
Author Contributions
S.O. conceived and wrote the paper draft. S.O. performed the experimental work and simulations. H.K. and D.E.R. contributed to the analysis and discussion of the results and also revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Petroleum Technology Trust Fund (PTDF), Nigeria (Grants No. OSS/PHD/842/16).
Acknowledgments
The author would like to acknowledge Jose Horrillo-Caraballo and Thomas van Veelen for their great assistance while conducting the experimental tests. The author also acknowledges Thomas Lykke Andersen and Peter Frigaard for the generous workshop on the generation and analysis of waves in physical models. It also valuable to mention the useful technical advice of N.W.H. Allsop on generating swell-driven bimodal waves and on how to determine the reflection coefficients of the waves during one of his visits to the Swansea University Coastal Engineering Flume.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| The structure slope | |
| Breaker index or surf similarity parameter | |
| Breaker Index with based on | |
| Breaker Index with based on | |
| Peak period | |
| FFT | Fast Fourier Transform |
| g | Acceleration due to gravity |
| h | Water depth |
| H | Wave height |
| Significant wave height | |
| IFFT | Inverse Fast Fourier Transform |
| H | Significant wave height |
| Jonswap | Joint North Sea Wave Project |
| Reflection coefficient | |
| The linear wave length | |
| Crest freeboard | |
| SSER | Sea-swell energy ratio |
| The spectra wave period | |
| Peak periods of swell wave at 11 s | |
| Peak periods of swell wave at 15 s | |
| Peak periods of swell wave at 20 s | |
| Peak periods of swell wave at 25 s | |
| Peak period of wind wave | |
| UK | United Kingdom |
| Wave steepness derived from | |
| Reflection coefficient |
References
- Andersen, T.L.; Frigaard, P.; Burcharth, H.F. Lecture Notes for the Course in Water Wave Mechanics; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2014. [Google Scholar]
- Zanuttigh, B.; van Der Meer, J.W. Wave reflection from coastal structures in design conditions. Coast. Eng. 2008, 55, 771–779. [Google Scholar] [CrossRef]
- Hawkes, P.J.; Coates, T.; Jones, R.J. Impacts of Bimodal Seas on Beaches, Hydraulic Research Wallingford. Hydraul. Res. Wallingford 1998, 265, 80. [Google Scholar]
- Thompson, A.D.; Reeve, D.E.; Karunarathna, H. Modelling extreme wave overtopping at Aberystwyth Promenade. Water 2017, 9, 663. [Google Scholar] [CrossRef]
- Polidoro, A.; Pullen, T.; Eade, J. Gravel beach profile response allowing for bimodal sea states. Proc. Inst. Civ. Eng. Marit. Eng. 2018, 171, 145–146. [Google Scholar] [CrossRef]
- Miche, M. Le pouvoir reflêchissant des ouvrages maritimes exposés à l’action de la houl. Annales de Ponts et Chaussées 1951, 121, 285–319. [Google Scholar]
- Ursell, J.; Dean, R.G.; Yu, Y. Forced small amplitude water waves: a comparison of theory and experiment. J. Fluid Mech. 1960, 7, 33–52. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf similarity. In Proceedings of the 14th International Conference on Coastal Engineering, ASCE, Copenhagen, Denmark, 24–28 June 1974; pp. 460–480. [Google Scholar]
- Iribarren, C.; Nogales, C. Protection des Ports. In Proceedings of the XVIIth International Naval Congress, Lisbon, Portugal, 1 January 1949; Volume 4, pp. 31–80. [Google Scholar]
- Seelig, W.N. Two-Dimensional Tests of Wave Transmission and Reflection Characteristics of Laboratory Breakwaters; Technical Report; Coastal Engineering Research Centre: Fort Belvoir, VA, USA, 1980. [Google Scholar]
- Seelig, W.N.; Ahrens, J.P. Estimation of Wave Reflection and Energy Dissipation Coefficients for Beaches, Revetments, and Breakwaters; Technical Paper No. 81-1; US Army Corps of Engineers: Washington, DC, USA, 1981; pp. 1–41. [Google Scholar]
- Davidson, M.; Bird, P.; Bullock, G.; Huntley, D. A new non-dimensional number for the analysis of wave reflection from rubble mound breakwaters. Coast. Eng. 1996, 28, 93–120. [Google Scholar] [CrossRef]
- Gunbak, A. The Stability of Rubble Mound Breakwaters in Relation to Wave Breaking and Run-Down Characteristics and to the Tan; Div. Port and Ocean Eng., The Norwegian Institute of Technology: Trondheim, Norway, 1976. [Google Scholar]
- DeBok, D.H. A Large Scale Model Study of Placed Stone Breakwaters. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 1977. [Google Scholar]
- Manual, S.P. Department of the Army; US Army Corps of Engineers: Washington, DC, USA, 1984. [Google Scholar]
- Numata, A. Laboratory formulation for transmission and reflection at permeable breakwaters of artificial blocks. Coast. Eng. Jpn. 1976, 19, 47–58. [Google Scholar] [CrossRef]
- Gimenez-Curto, L. Behaviour of Rubble Mound Breakwaters Under Wave Action. Ph.D. Thesis, University of Santander, Cantabria, Spain, 1979. [Google Scholar]
- Losada, M.A.; Gimenez-Curto, L.A. An approximation to the failure probability of maritime structures under a sea state. Coast. Eng. 1981, 5, 147–157. [Google Scholar] [CrossRef]
- Postma, G. Wave Reflection From Rock Slopes under Random Wave Attack. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 1989. [Google Scholar]
- Allsop, N.; Channell, A. Wave Reflections in Harbours: The Reflection Performance of Wave Screens; Report OD; HR Wallingford: Wallingford, UK, 1988; Volume 102. [Google Scholar]
- Van der Meer, J.W. Conceptual design of rubble mound breakwaters. In Advances In Coastal And Ocean Engineering: (Volume 1); World Scientific: Singapore, 1995; pp. 221–315. [Google Scholar]
- Oumeraci, H.; Partenscky, H. Wave-induced pore pressure in rubble mound breakwaters. In Coastal Engineering; ASCE: Delft, The Netherlands, 1991; pp. 1334–1347. [Google Scholar]
- Muttray, M.; Oumeraci, H.; Zimmermann, C.; Partenscky, H. Wave energy dissipation on and in rubble mound structures. In Coastal Engineering; ASCE: Venice, Italy, 1993; pp. 1434–1447. [Google Scholar]
- Allsop, N.; Hettiarachchi, S. Reflections from Coastal Structures. Proceedings of the 21st International Conference on Coastal Engineering, Torremolinos, Spain, 20–25 June 1988; Edge, B.L., Ed.; American Society of Civil Engineers: New York, NY, USA, 1988; pp. 782–794. [Google Scholar]
- Shimada, A.; Fujimoto, T.; Saito, S.; Sakakiyama, T.; Hirakuchi, H. Scale effects on stability and wave reflection regarding armor units. In Coastal Engineering; ASCE: New York, NY, USA, 1987; pp. 2238–2252. [Google Scholar]
- Neelamani, S.; Sandhya, N. Wave reflection, run-up, run-down and pressures on plane, dentated and serrated seawalls. Coast. Eng. J. 2004, 46, 141–169. [Google Scholar] [CrossRef]
- Wang, B.; van der Meer, J.W.; Otta, A.K.; Chadwick, A.J.; Horrillo-Caraballo, J. Reflection of obliquely incident waves at low-crested structures. In Coastal Dynamics 2005: State of the Practice; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–12. [Google Scholar]
- Zanuttigh, B.; Andersen, T.L. Wave reflection in 3D conditions. Coast. Eng. 2010, 57, 531–538. [Google Scholar] [CrossRef]
- Li, Y.; Dong, G.; Liu, H.; Sun, D. The reflection of oblique incident waves by breakwaters with double-layered perforated wall. Coast. Eng. 2003, 50, 47–60. [Google Scholar] [CrossRef]
- Koraim, A.; Rageh, O. Hydrodynamic performance of vertical porous structures under regular waves. China Ocean. Eng. 2013, 27, 451–468. [Google Scholar] [CrossRef]
- Young, D.M.; Testik, F.Y. Wave reflection by submerged vertical and semicircular breakwaters. Ocean. Eng. 2011, 38, 1269–1276. [Google Scholar] [CrossRef]
- Koraim, A.S.; Heikal, E.M.; Zaid, A.A. Hydrodynamic characteristics of porous seawall protected by submerged breakwater. Applied Ocean Research 2014, 46, 1–14. [Google Scholar] [CrossRef]
- Lee, J.I.; Shin, S. Experimental study on the wave reflection of partially perforated wall caissons with single and double chambers. Ocean. Eng. 2014, 91, 1–10. [Google Scholar] [CrossRef]
- Esmaeili, M.; Rahbani, M.; Khaniki, A.K. Experimental investigating on the reflected waves from the caisson-type vertical porous seawalls. Acta Oceanol. Sin. 2019, 38, 117–123. [Google Scholar] [CrossRef]
- Orimoloye, S.; Karunarathna, H.; Reeve, D.E. Effects of Swell on Wave Height Distribution of Energy-Conserved Bimodal Seas. J. Mar. Sci. Eng. 2019, 7, 79. [Google Scholar] [CrossRef]
- Allsop, N.; Bruce, T.; Pearson, J.; Besley, P. Wave overtopping at vertical and steep seawalls. Mar. Eng. 2005, 158, 103–114. [Google Scholar] [CrossRef]
- Schäffer, H.A. Second-order wavemaker theory for irregular waves. Ocean. Eng. 1996, 23, 47–88. [Google Scholar] [CrossRef]
- Zelt, J.; Skjelbreia, J.E. Estimating incident and reflected wave fields using an arbitrary number of wave gauges. In Proceedings of the 23rd ICCE, Venice, Italy, 4–9 October 1992; pp. 777–788. [Google Scholar]
- Orimoloye, S.; Horrillo-Caraballo, J.; Karunarathna, H.; Reeve, D.E. Modelling wave overtopping of steep impermeable structures under bimodal sea conditions. In Proceedings of the Coastal Structures, Hannover, Germany, 30 September–2 October 2019. [Google Scholar]
- Mansard, E.P.; Funke, E. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Coastal Engineering Conference, Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- Reeve, D.; Chadwick, A.; Fleming, C. Coastal Engineering: Processes, Theory and Design Practice; Spon: London, UK, 2015; 518p. [Google Scholar]
- Owen, M. Design of Seawalls Allowing for Wave Overtopping; HR Report number Ex 924; Hydraulic Station: Wallingford, UK, 1988. [Google Scholar]
- Van Gent, M.R. The modelling of wave action on and in coastal structures. Coast. Eng. 1994, 22, 311–339. [Google Scholar] [CrossRef]
- Nassar, K.; Negm, A. Determination of optimum wave reflection of seawalls via experimental modeling. In Scour and Erosion: Proceedings of the 8th International Conference on Scour and Erosion, Oxford, UK, 12–15 September 2016; CRC Press: Boca Raton, FL, USA, 2016; p. 255. [Google Scholar]
- Negm, A.; Nassar, K. Determination of Wave Reflection Formulae for Vertical and Sloped Seawalls Via Experimental Modelling. Procedia Eng. 2016, 154, 919–927. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2010; p. 708. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).