Identifying the Frequency Dependent Interactions between Ocean Waves and the Continental Margin on Seismic Noise Recordings
Abstract
1. Introduction
2. Materials and Methods
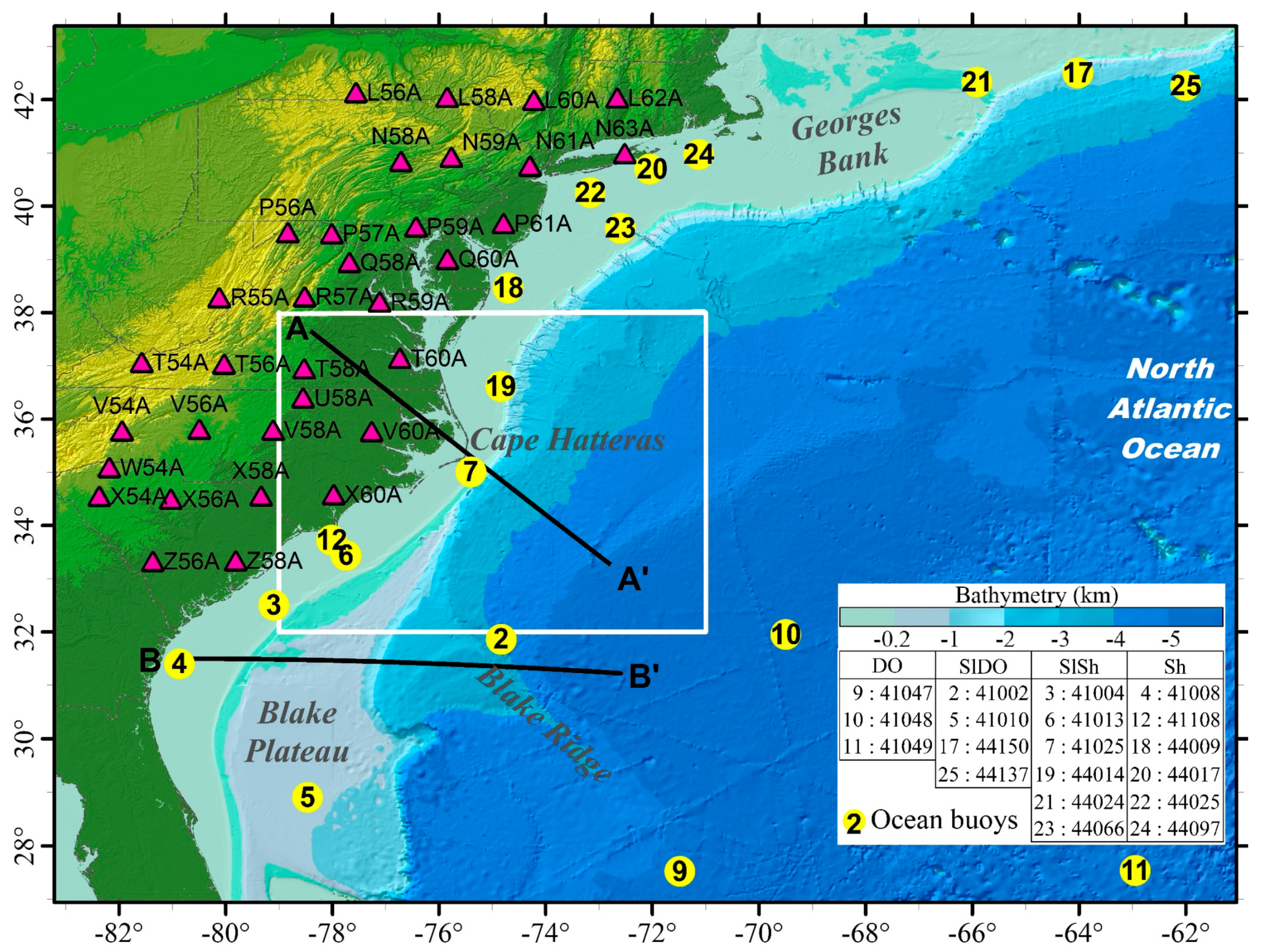
2.1. Ambient Noise Data
- (1)
- (2)
- Apply fast Fourier transform with a 10% cosine taper on the filtered segments in three directions to calculate spectra (, , and ) and then smooth them using Konno–Ohmachi method with a bandwidth coefficient of 40 [51].
- (3)
- (4)
- Plot the PSDs of all segments at each station in time-frequency domain .
- (5)
- Apply band-pass filter using the frequency bands, F = 0.1–0.2 Hz (DF1), 0.2–0.3 Hz (DF2), and 0.3–0.4 Hz (DF3) to each 1-h segment to produce filtered amplitude-time series , , and .
- (6)
- Rotate the two horizontal components by an angle φ into radial (R) and transverse (T) components [54] in each segment:in which φ is defined as the back-azimuth angle between the north and the radial direction from the recording station toward the source.
- (7)
- Calculate the root mean square of and in each segment and their ratio .
- (8)
- Repeat steps 6 and 7 to calculate at every 1° increment of angle φ in 1°–360°.
- (9)
- Calculate average values of for all segments at a station and determine the azimuth for the maximum value of these averages. The angle is taken as the primary vibration direction by method.
- (10)
- Further parse the filtered 1 h segments in step 6 into ten 120 s windows and determine , , , where i = 1, 2, and 3 (separating DF1, DF2, and DF3 contents) and j = 1, 2, …, 30 (number of windows). For each window, build the three-component covariance matrix M:
- (11)
- Calculate the three eigenvalues and associated eigenvectors of the covariance matrix by solving:and define the maximum eigenvalue , and associated eigenvectors .
- (12)
- Find the back azimuth angle corresponding to the major axis of the polarized ellipse:
2.2. Ocean Data
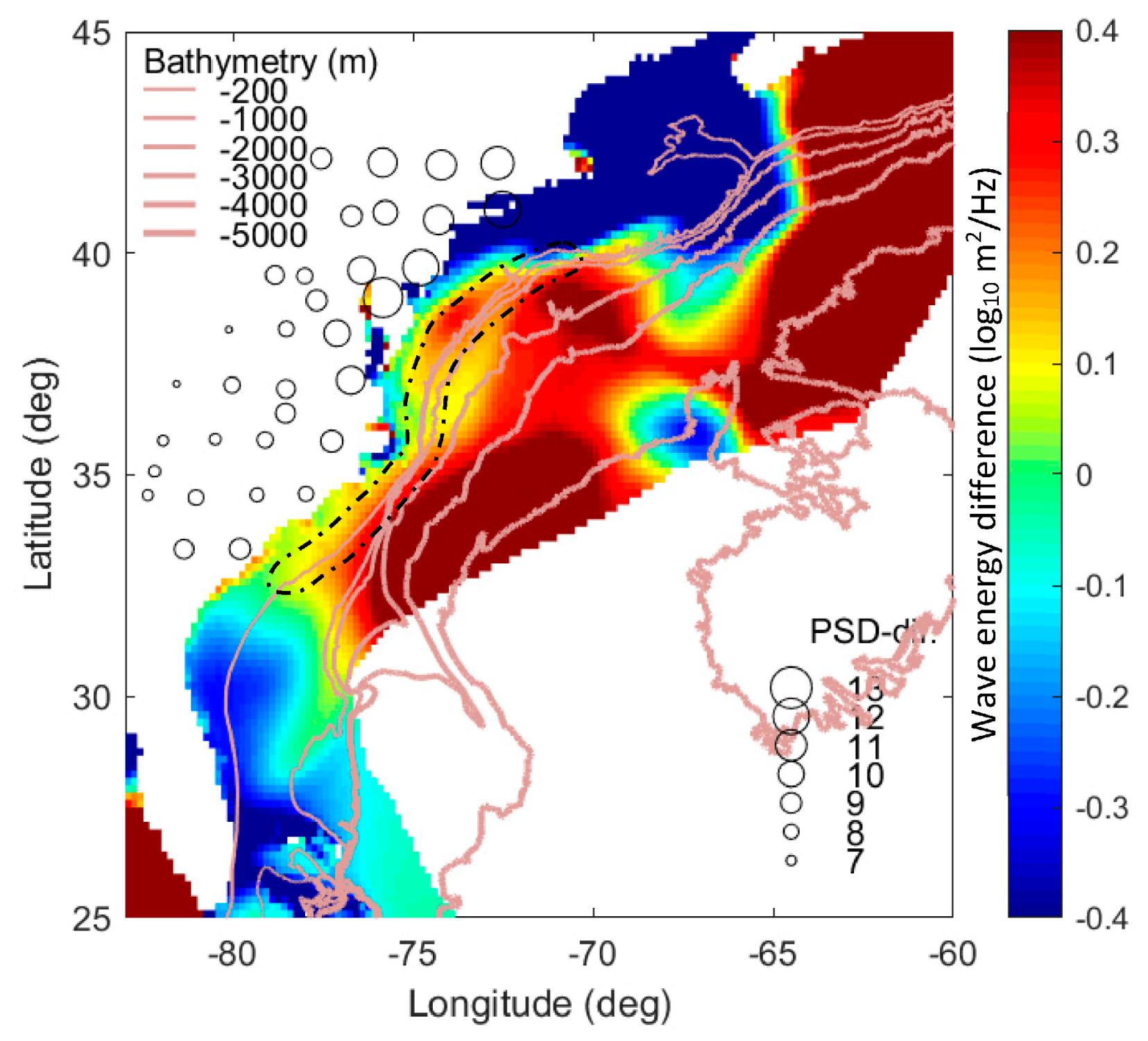
2.3. Source Regions of DF Microseisms
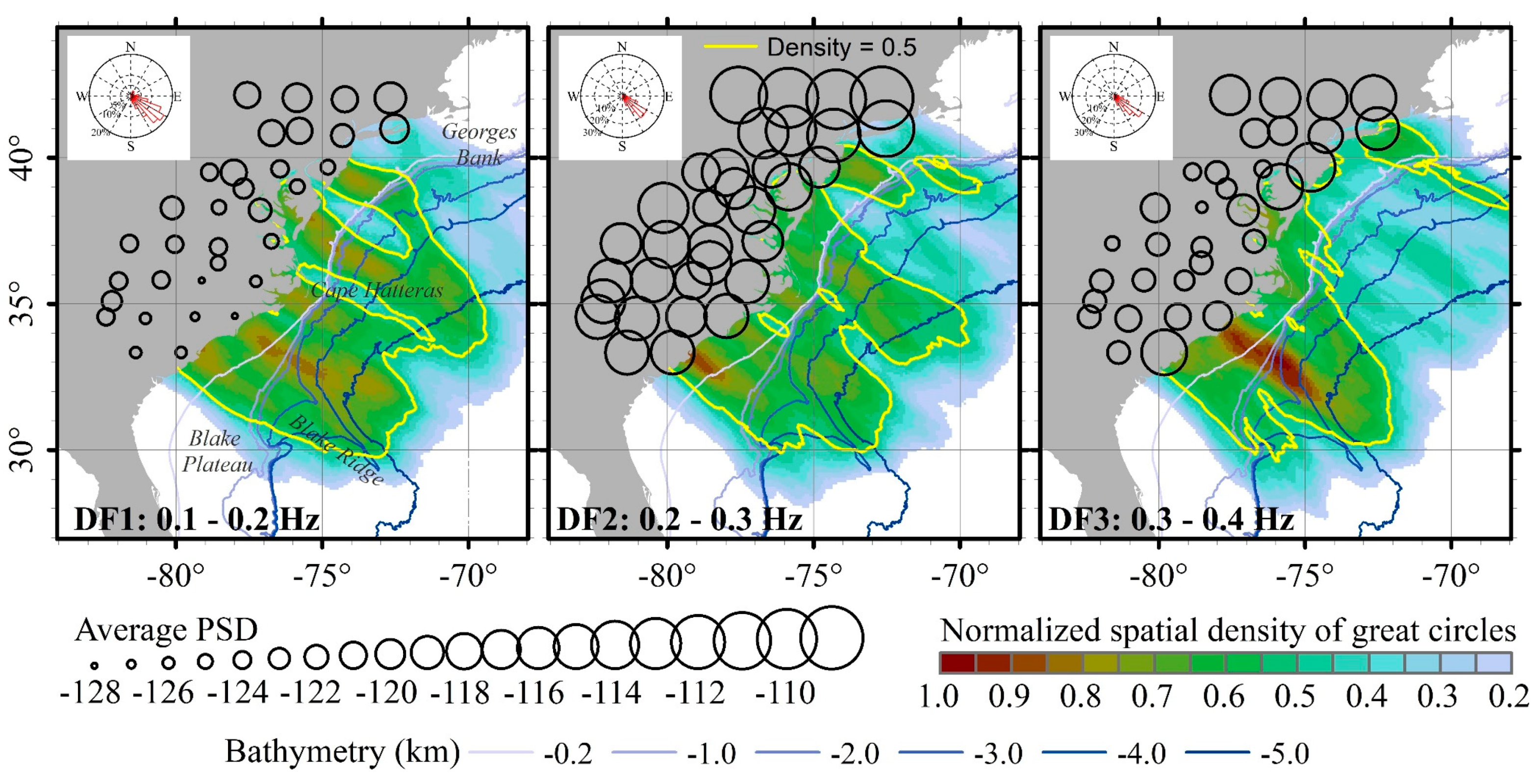
2.3.1. Spatial Density of Primary Vibration Directions
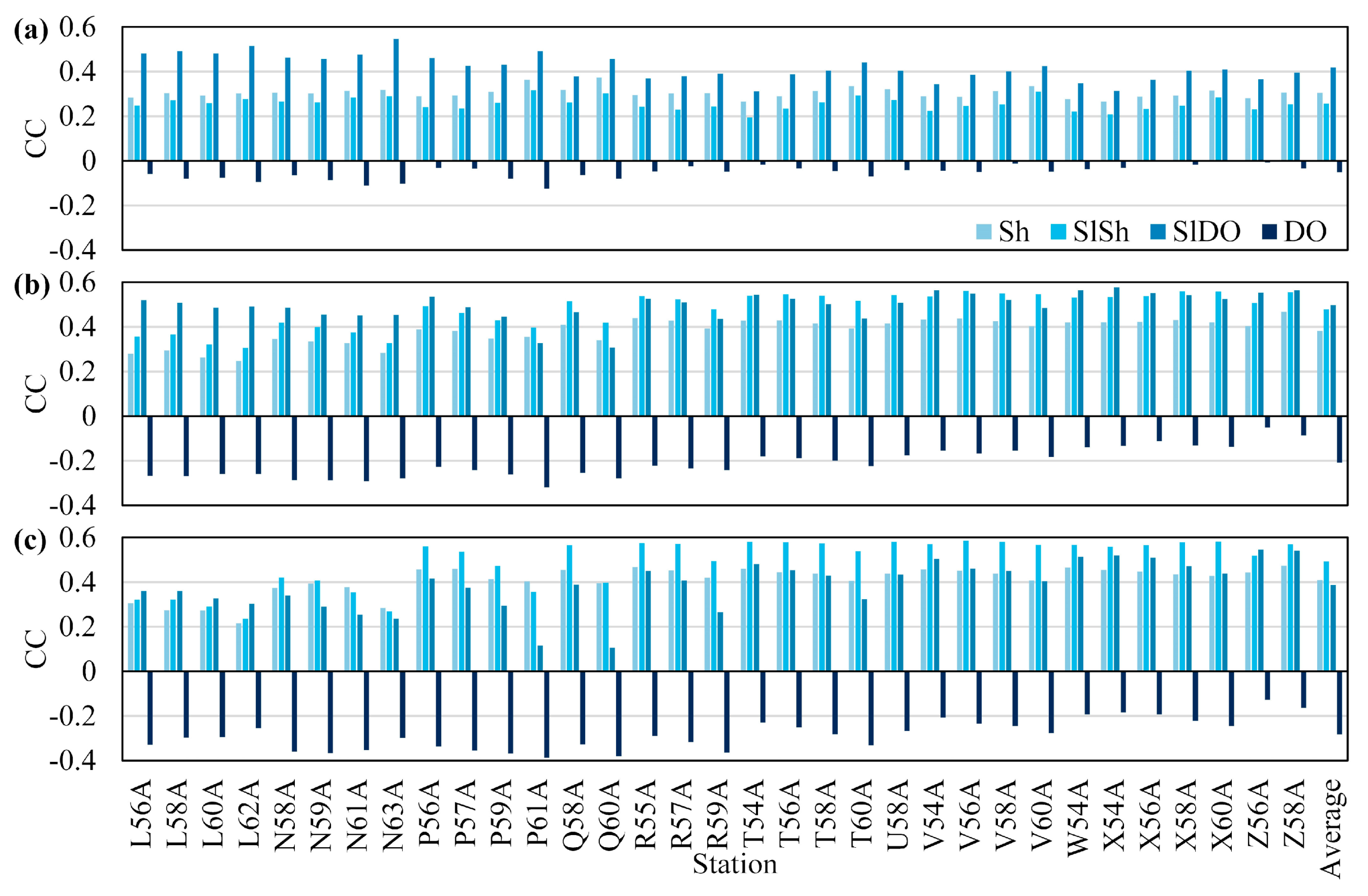
2.3.2. Correlation Analyses
3. Results
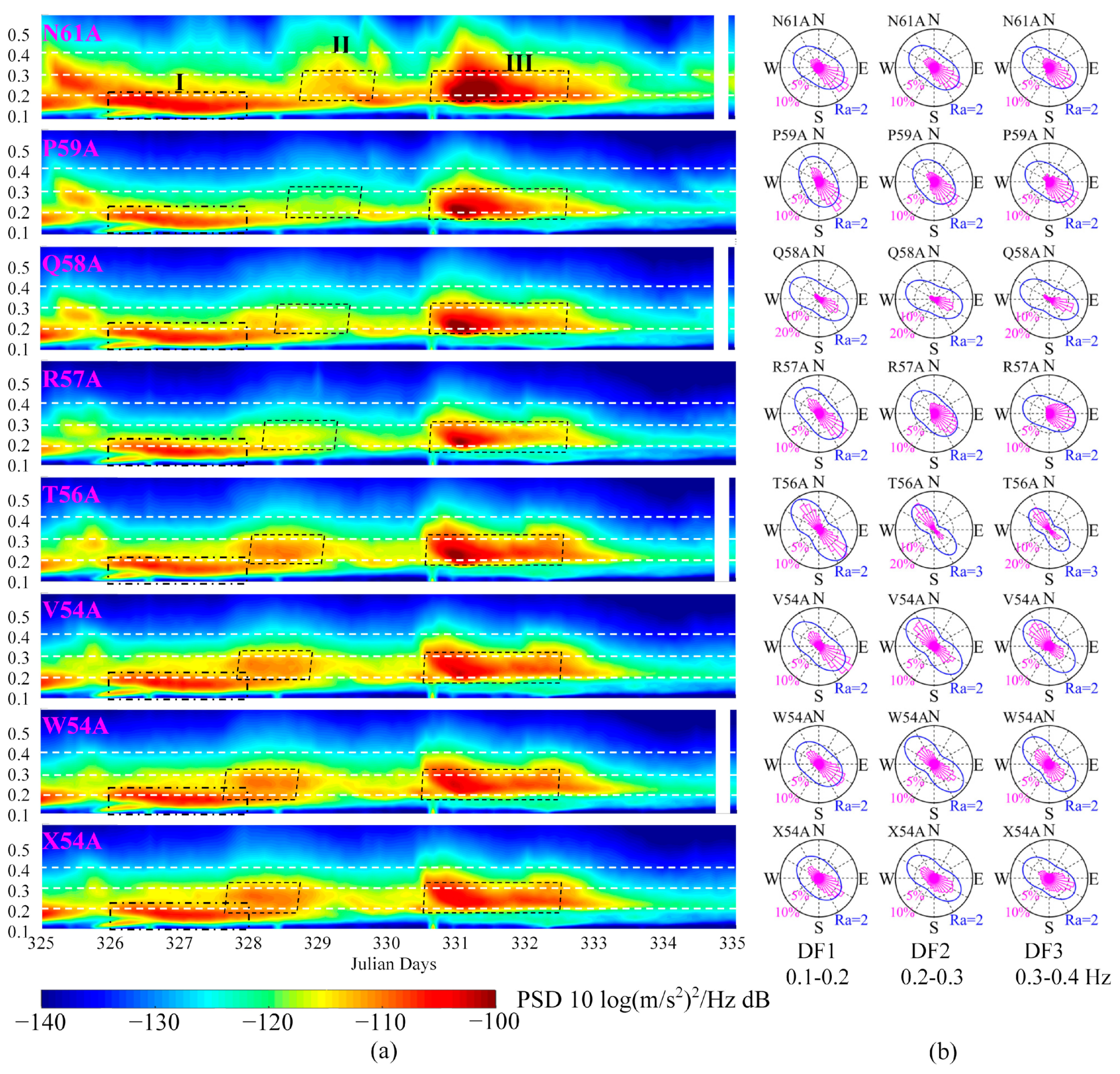
3.1. Power Spectral Density (PSD)
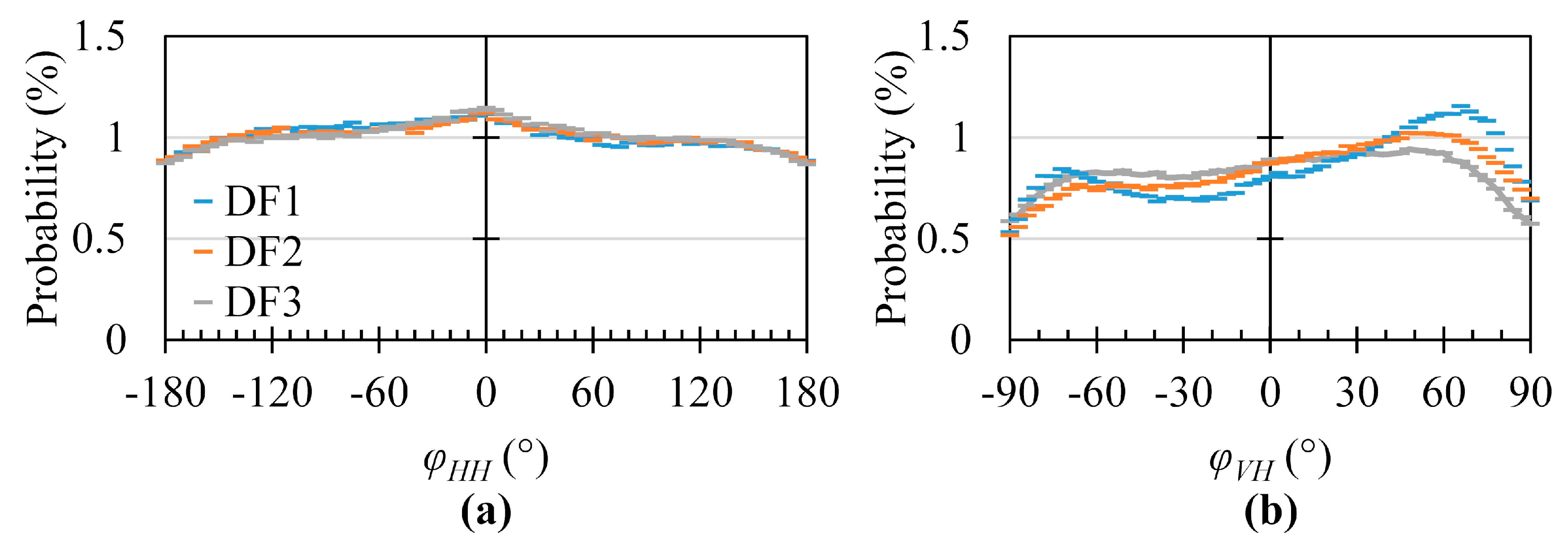
3.2. Primary Vibration Directions at DF Peaks
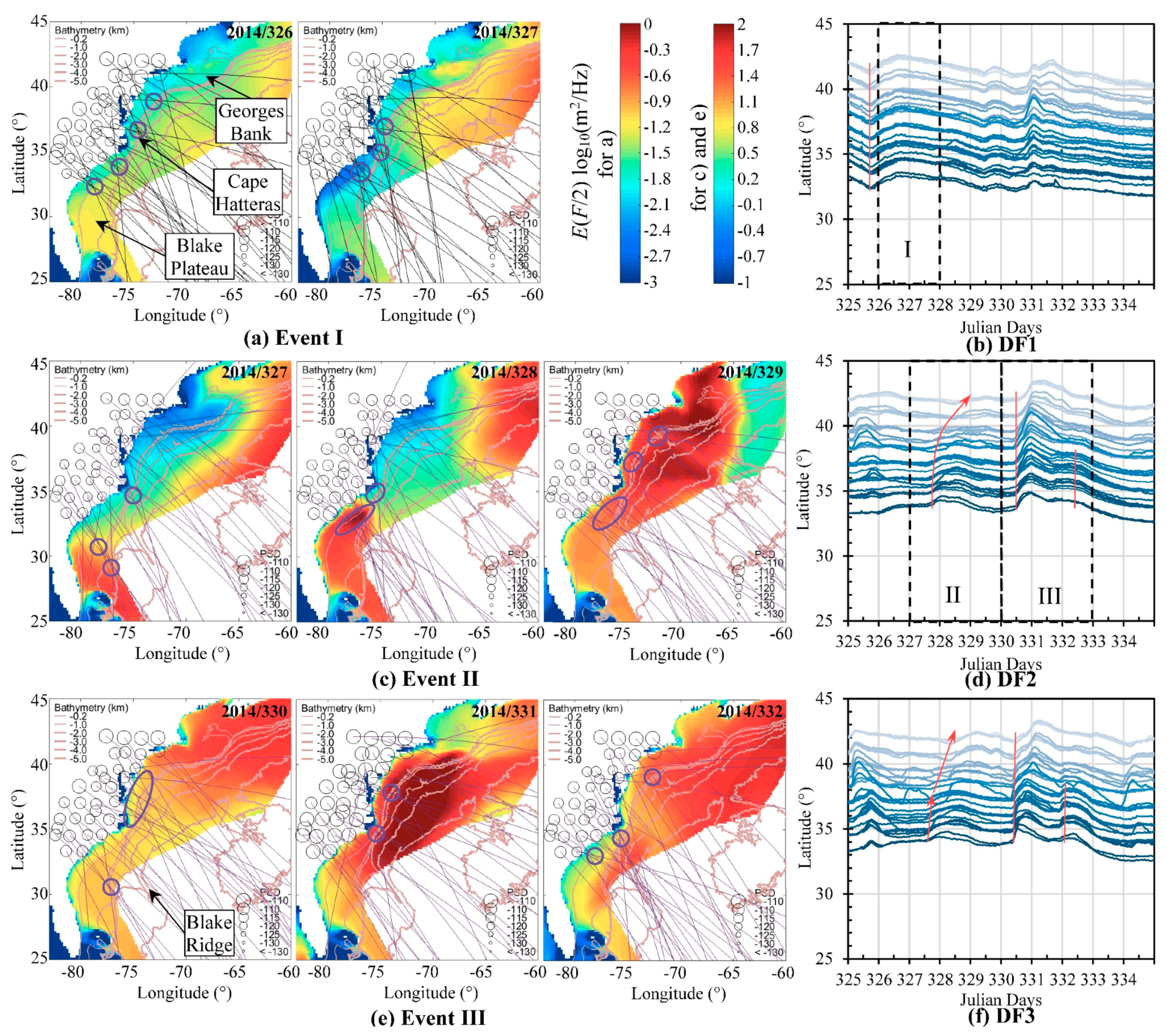
3.3. Excitation of the Three Relatively Strong DF Microseism Events
3.3.1. Event I
3.3.2. Event II
3.3.3. Event III
3.4. Correlation between DF Microseisms and Ocean Wave Parameters
4. Discussion
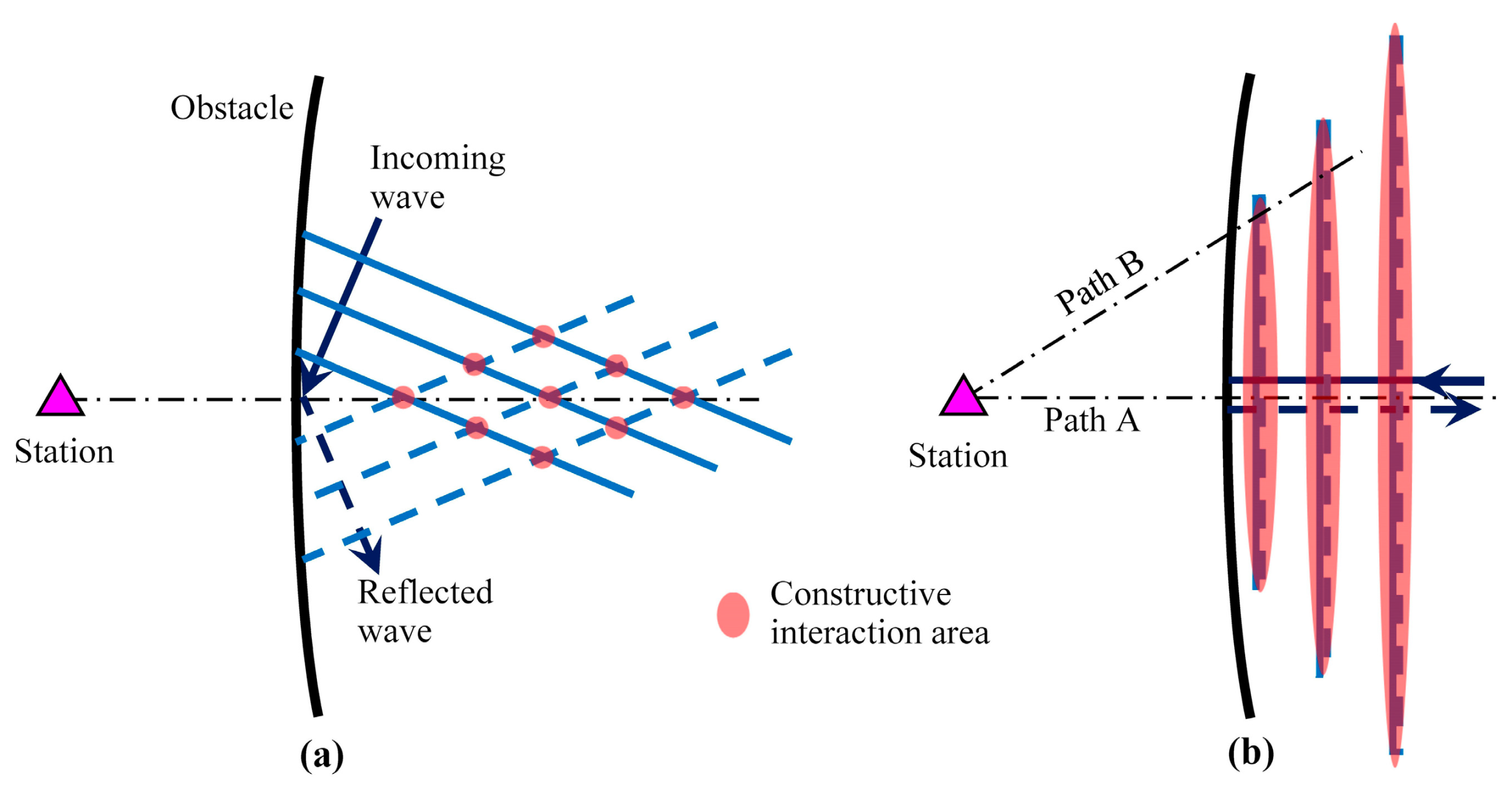
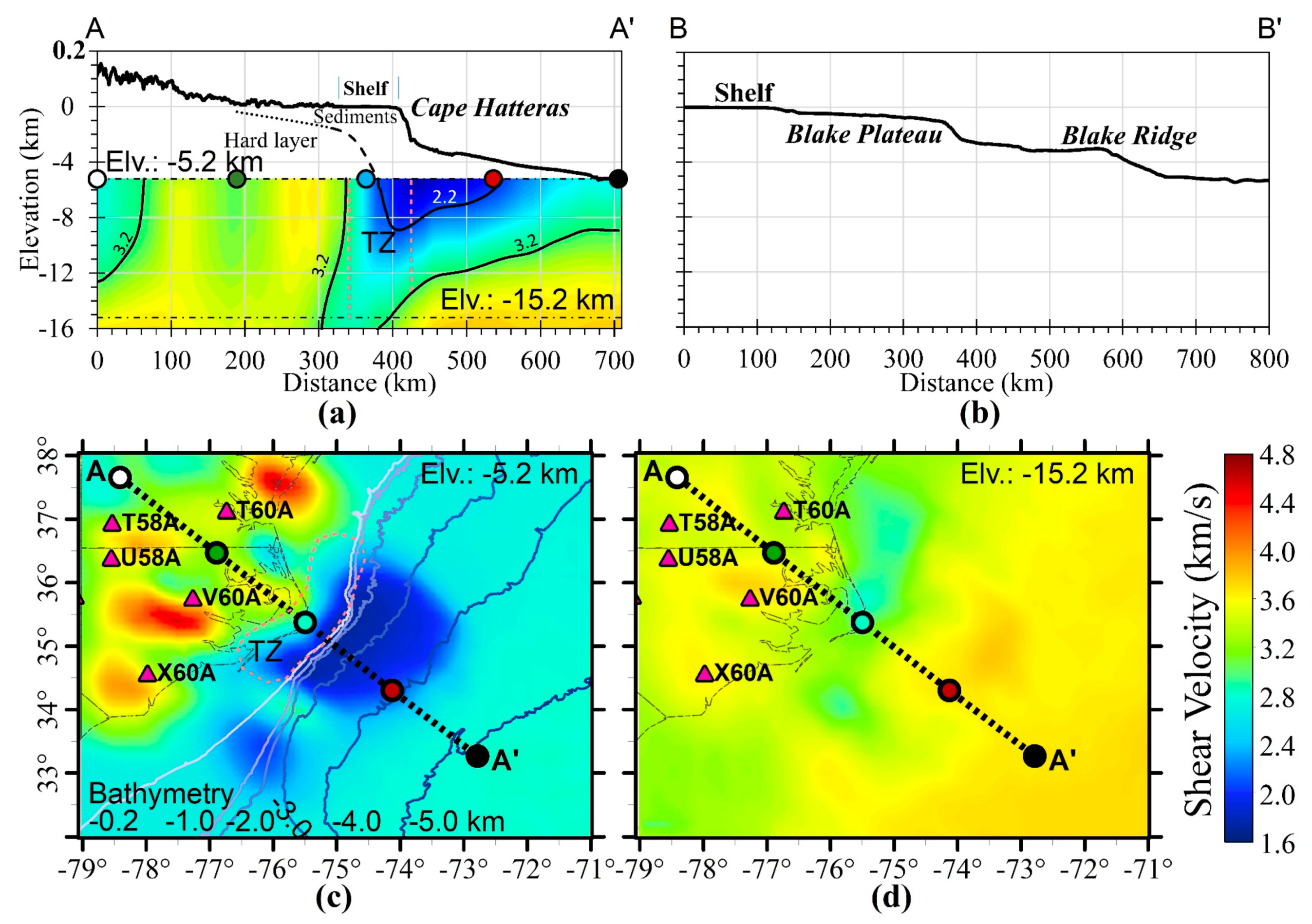
4.1. Hypothesis on the Significance of Continental Slope for the Origination of DF Microseisms
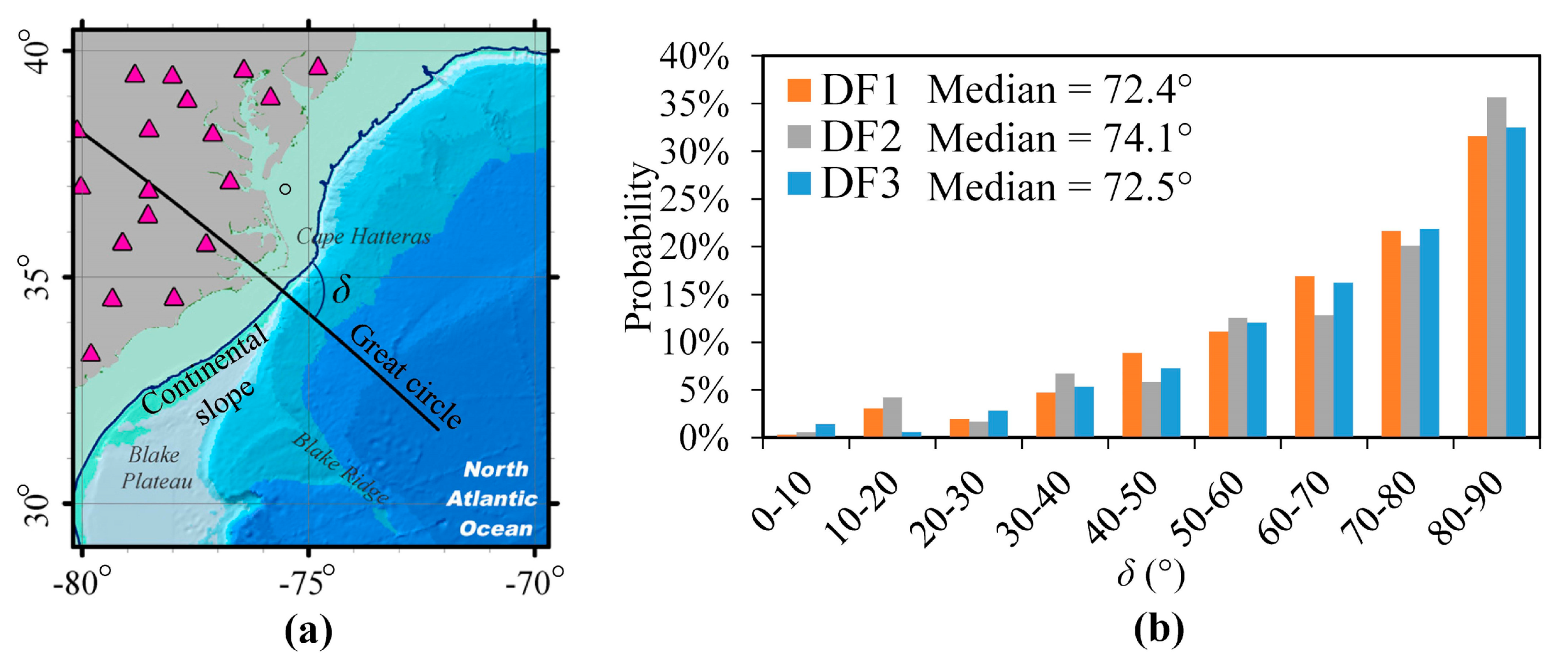
4.2. Types of Continental Margin
4.3. Rayleigh Wave Refraction
4.3.1. Refraction at the Water–Solid Earth Interface
4.3.2. Refraction within the Solid Earth
4.4. Rayleigh Wave Refraction
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. QR of RTRI 1989, 30, 25–33. [Google Scholar]
- Bodin, P.; Horton, S. Broadband microtremor observation of basin resonance in the Mississippi embayment, Central US. Geophys. Res. Lett. 1999, 26, 903–906. [Google Scholar] [CrossRef]
- Bodin, P.; Smith, K.; Horton, S.; Hwang, H. Microtremor observations of deep sediment resonance in metropolitan Memphis, Tennessee. Eng. Geol. 2001, 62, 159–168. [Google Scholar] [CrossRef]
- Bard, P.-Y.; SESAME-team. Guideline for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations-Measurements, Processing and Interpretations; SESAME European Research Project EVG1-CT-2000-00026, D23.12. 2005. Available online: http://sesame-fp5.obs.ujf-grenoble.fr/index.htm (accessed on 19 February 2020).
- Guo, Z.; Aydin, A.; Kuszmaul, J. Microtremor recording in northern Mississippi. Eng. Geol. 2014, 179, 146–157. [Google Scholar] [CrossRef]
- Lobkis, O.I.; Weaver, R.L. On the emergence of the Green’s function in the correlations of a diffuse field. J. Acoust. Soc. Am. 2001, 110, 3011–3017. [Google Scholar] [CrossRef]
- Snieder, R. Extracting the Green’s function from the correlation of coda waves: A derivation based on stationary phase. Phys. Rev. E 2001, 69, 046610. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Campillo, M. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett. 2004, 31, L07614. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. High resolution surface wave tomography from ambient seismic noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef]
- Sabra, K.G.; Gerstoft, P.; Roux, P.; Kuperman, W.A.; Fehler, M.C. Extracting time-domain Green’s function estimates from ambient seismic noise. Geophys. Res. Lett. 2005, 32, L03310. [Google Scholar] [CrossRef]
- Sabra, K.G.; Gerstoft, P.; Roux, P.; Kuperman, W.A.; Fehler, M.C. Surface wave tomography from microseisms in Southern California. Geophys. Res. Lett. 2005, 32, L14311. [Google Scholar] [CrossRef]
- Yang, Y.; Ritzwoller, M. Characteristics of ambient seismic noise as a source for surface wave tomography. Geochem. Geophys. Geosyst. 2008, 9, Q02008. [Google Scholar] [CrossRef]
- Yang, Y.; Ritzwoller, M.; Levshin, A.; Shapiro, N. Ambient noise Rayleigh wave tomography across Europe. Geophys. J. Int. 2007, 168, 259–274. [Google Scholar] [CrossRef]
- Stephenson, W.J.; Hartzell, S.; Frankel, A.D.; Asten, M.; Carver, D.L.; Kim, W.Y. Site characterization for urban seismic hazards in lower Manhattan, New York City, from microtremor array analysis. Geophys. Res. Lett. 2009, 36, L03301. [Google Scholar] [CrossRef]
- Lynner, C.; Porritt, R.W. Crustal structure across the eastern North American margin from ambient noise tomography. Geophys. Res. Lett. 2017, 44, 6651–6657. [Google Scholar] [CrossRef]
- Guo, Z.; Aydin, A. A modified HVSR method to evaluate site effect in Northern Mississippi considering ocean wave climate. Eng. Geol. 2016, 200, 104–113. [Google Scholar] [CrossRef]
- Stehly, L.; Campillo, M.; Shapiro, N.M. A study of the seismic noise from its long-range correlation properties. J. Geophys. Res. 2006, 111, B10306. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Ritzwoller, M.H.; Bensen, G.D. Source location of the 26 sec microseism from cross-correlation of ambient seismic noise. Geophys. Res. Lett. 2006, 33, L18310. [Google Scholar] [CrossRef]
- Tsai, V.C. On establishing the accuracy of noise tomography travel-time measurements in a realistic medium. Geophys. J. Int. 2009, 178, 1555–1564. [Google Scholar] [CrossRef]
- Zeng, X.; Ni, S. A persistent localized microseismic source near the Kyushu Island, Japan. Geophys. Res. Lett. 2010, 37, L24307. [Google Scholar] [CrossRef]
- Ermert, L.; Villaseñor, A.; Fichtner, A. Cross-correlation imaging of ambient noise sources. Geophys. J. Int. 2016, 204, 347–364. [Google Scholar] [CrossRef]
- Guo, Z.; Xue, M.; Aydin, A.; Ma, Z. Exploring source regions of single- and double-frequency microseisms recorded in eastern North American margin (ENAM) by cross-correlation. Geophys. J. Int. 2020, 220, 1352–1367. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. A theory for the generation of microseisms. Philos. Trans. R. Soc. Lond. 1950, 243, 1–35. [Google Scholar]
- Hasselmann, K. A statistical analysis of the generation of microseisms. Rev. Geophys. Space Phys. 1963, 1, 177–210. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Duennebier, F.K.; Stephen, R.A. Mid-ocean microseisms. Geochem. Geophys. Geosyst. 2005, 6, Q04009. [Google Scholar] [CrossRef]
- Essen, H.-H.; Krüger, F.; Dahm, T.; Grevemeyer, I. On the generation of secondary microseisms observed in northern and central Europe. J. Geophys. Res. 2003, 108, 2506. [Google Scholar] [CrossRef]
- Obrebski, M.J.; Ardhuin, F.; Stutzmann, E.; Schimmel, M. How moderate sea states can generate loud seismic noise in the deep ocean. Geophys. Res. Lett. 2012, 39, L11601. [Google Scholar] [CrossRef]
- Rhie, J.; Romanowicz, B. A study of the relation between ocean storms and the Earth’s hum. Geochem. Geophys. Geosyst. 2006, 7, Q10004. [Google Scholar] [CrossRef]
- Schimmel, M.; Stutzmann, E.; Ardhuin, F.; Gallart, J. Polarized Earth’s ambient microseismic noise. Geochem. Geophys. Geosyst. 2011, 12, Q07014. [Google Scholar] [CrossRef]
- Stephen, R.A.; Spiess, F.N.; Collins, J.A.; Hildebrand, J.A.; Orcutt, J.A.; Peal, K.R.; Vernon, F.L.; Wooding, F.B. Ocean seismic network pilot experiment. Geochem. Geophys. Geosyst. 2003, 4, 1092. [Google Scholar] [CrossRef]
- Webb, S.C. Broadband seismology and noise under the ocean. Rev. Geophys. 1998, 36, 105–142. [Google Scholar]
- Traer, J.; Gerstoft, P.; Bromirski, P.D.; Shearer, P.M. Microseisms and hum from ocean surface gravity waves. J. Geophys. Res. 2012, 117, B11307. [Google Scholar] [CrossRef]
- Nishida, K.; Takagi, R. Teleseismic S wave microseism. Science 2016, 353, 919–921. [Google Scholar] [CrossRef] [PubMed]
- Gerstoft, P.; Bromirski, P. “Weather bomb” induced seismic signals. Science 2016, 353, 869–870. [Google Scholar] [CrossRef] [PubMed]
- Elgar, S.; Herbers, T.H.C.; Guza, R.T. Reflection of ocean surface gravity waves from a natural beach. J. Phys. Oceanogr. 1994, 24, 1503–1511. [Google Scholar] [CrossRef]
- Ardhuin, F.; Stutzmann, E.; Schimmel, M.; Mangeney, A. Ocean wave sources of seismic noise. J. Geophys. Res. 2011, 116, C09004. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Duennebier, F.K. The near-coastal microseism spectrum: Spatial and temporal wave climate relationships. J. Geophys. Res. 2002, 107, B8. [Google Scholar] [CrossRef]
- Ardhuin, F.; Roland, A. Coastal wave reflection, directional spread, and seismoacoustic noise sources. J. Geophys. Res. 2012, 117, C00J20. [Google Scholar] [CrossRef]
- Gualtieri, L.; Stutzmann, E.; Capdeville, F.; Farra, V.; Mangeney, A.; Morelli, A. On the shaping factors of the secondary microseismic wavefield. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Sutton, G.; Barstow, N. Ocean bottom microseisms from a distant supertyphoon. Geophys. Res. Lett. 1996, 23, 499–502. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Flick, R.E.; Graham, N. Ocean wave height determined from inland seismometer data: Implications for investigating wave climate change in the NE Pacific. J. Geophys. Res. 1999, 104, 20753–20766. [Google Scholar] [CrossRef]
- Dorman, L.M.; Schreiner, A.E.; Bibee, L.D.; Hildebrand, J.A. Deep-Water Seafloor Array Observations of Seismo-Acoustic Noise in the Eastern Pacific and Comparisons with Wind and Swell, in Natural Physical Source of Underwater Sound; Kerman, B., Ed.; Springer: New York, NY, USA, 1993; pp. 165–174. [Google Scholar]
- Ebeling, C.W. Chapter One–inferring ocean storm characteristics from ambient seismic noise: A historical perspective. Adv. Geophys. 2012, 53, 1–33. [Google Scholar]
- Guo, Z.; Aydin, A. Double-frequency microseisms in ambient noise recorded in Mississippi. Bull. Seismol. Soc. Am. 2015, 105, 1691–1710. [Google Scholar] [CrossRef]
- Park, J.; Verono III, F.L.; Lindberg, C.R. Frequency dependent polarization analysis of high-frequency seismograms. J. Geophys. Res. 1987, 92, 12664–12674. [Google Scholar] [CrossRef]
- Cessaro, R.K. Sources of primary and secondary microseisms. Bull. Seismol. Soc. Am. 1994, 84, 142–148. [Google Scholar]
- Friedrich, A.; Krüger, F.; Klinge, K. Ocean-generated microseismic noise located with the Gräfenberg array. J. Seismol. 1998, 2, 47–64. [Google Scholar] [CrossRef]
- Nishida, K.; Kawakatsu, H.; Fukao, Y.; Obara, K. Background Love and Rayleigh waves simultaneously generated at the Pacific Ocean floors. Geophys. Res. Lett. 2008, 35, L16307. [Google Scholar] [CrossRef]
- Paskevich, V. Srtm30plus-na_pctshade.tif—SRTM30PLUS color-encoded shaded relief image of North America (approximately 1km)—GeoTIFF image: Open-File Report 2005-1001, U.S. Geological Survey, Coastal and Marine Geology Program; Woods Hole Science Center: Woods Hole, MA, USA, 2005; 30p. [Google Scholar]
- Bard, P.-Y. Microtremor measurements: A tool for site effect estimation? In Proceedings of the 2nd International Symposium on the Effects of Surface Geology on Seismic Motion, Yokohama, Japan, 1–3 December 1998; pp. 1251–1279. [Google Scholar]
- Konno, K.; Ohmachi, T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Seismol. Soc. Am. 1998, 88, 28–241. [Google Scholar]
- McNamara, D.E.; Buland, R.P. Ambient noise levels in the continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Havskov, J.; Ottemoller, L. Routine Data Processing in Earthquake Seismology; Springer: New York, NY, USA, 2010; 347p. [Google Scholar]
- Koper, K.D.; Burlacu, R. The fine structure of double-frequency microseisms recorded by seismometers in North America. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Babcock, J.M.; Kirkendall, B.A.; Orcutt, J.A. Relationship between ocean bottom noise and the environment. Bull. Seismol. Soc. Am. 1994, 84, 1991–2007. [Google Scholar]
- Kibblewhite, A.C.; Ewans, K.C. Wave-wave interactions, microseism, and infrasonic ambient noise in the ocean. J. Acoust. Soc. Am. 1985, 78, 981–994. [Google Scholar] [CrossRef]
- Schreiner, A.E.; Dorman, L.M. Coherence lengths of seafloor noise: Effect of ocean bottom structure. J. Acoust. Soc. Am. 1990, 88, 1503–1514. [Google Scholar] [CrossRef]
- Lee, W.S.; Sheen, D.H.; Yun, S.; Seo, K.W. The origin of double-frequency microseism and its seasonal variability at King Sejong Station, Antarctica. Bull. Seismol. Soc. Am. 2011, 106, 1446–1451. [Google Scholar] [CrossRef]
- Koper, K.D.; Hawley, V.L. Frequency dependent polarization analysis of ambient seismic noise recorded at a broadband seismometer in the central United States. Earthq. Sci. 2010, 23, 439–447. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Stephen, R.A.; Gerstoft, P. Are deep-ocean-generated surface-wave microseisms observed on land? J. Geophys. Res. 2013, 118, 3610–3629. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Huang, Y.; Aydin, A.; Xue, M. Identifying the Frequency Dependent Interactions between Ocean Waves and the Continental Margin on Seismic Noise Recordings. J. Mar. Sci. Eng. 2020, 8, 134. https://doi.org/10.3390/jmse8020134
Guo Z, Huang Y, Aydin A, Xue M. Identifying the Frequency Dependent Interactions between Ocean Waves and the Continental Margin on Seismic Noise Recordings. Journal of Marine Science and Engineering. 2020; 8(2):134. https://doi.org/10.3390/jmse8020134
Chicago/Turabian StyleGuo, Zhen, Yu Huang, Adnan Aydin, and Mei Xue. 2020. "Identifying the Frequency Dependent Interactions between Ocean Waves and the Continental Margin on Seismic Noise Recordings" Journal of Marine Science and Engineering 8, no. 2: 134. https://doi.org/10.3390/jmse8020134
APA StyleGuo, Z., Huang, Y., Aydin, A., & Xue, M. (2020). Identifying the Frequency Dependent Interactions between Ocean Waves and the Continental Margin on Seismic Noise Recordings. Journal of Marine Science and Engineering, 8(2), 134. https://doi.org/10.3390/jmse8020134





