Abstract
The wave energy sector is experiencing lively years of conceptual innovation and technological advances. Among the great variety of candidates, only a few are going to be able to reach maturity and, eventually, industrial feasibility and competitiveness. The essential requisite for success is the continuous innovation in response to the incremental experience gained during the design and prototyping stages. In particular, the ability to generate detailed mathematical models, representative of every phenomenon involved in the system, is crucial for informing the design and control stages, allowing to maximize productivity while minimizing costs, and inspiring technological breakthrough and innovation. This papers considers the case of the ISWEC (Inertial Sea Wave Energy Converter), where a technological leap is tightly linked with the modelling of aerodynamic losses around its spinning flywheel, the core of the energy conversion chain. Two mathematical models of increasing complexity are considered, one semi-empiric and one based on computational fluid dynamics, which are successfully validated against experimental data. Such models are used to quantify the benefits of a technological innovation consisting of enclosing the flywheel in a sealed container, allowing pressure regulation to reduce aerodynamic friction. Compared to the free configuration, power losses with the enclosed configuration are about half already at atmospheric pressure, and about one third at half the atmospheric pressure.
1. Introduction
The constantly rising demand and offer of clean energy experienced worldwide in recent years is increasing the level of competitiveness in the renewable energy market, inducing higher pressure on developers to achieve economic viability as soon as possible. Numerous and variegated technologies exist, most of which are past the proof-of-concept stage and have confirmed their potentiality after prototype testing. However, substantial technological leaps are needed to reduce the cost of energy enough to justify commercialization and further development to industrial scale. Such a progression in the maturity of a technology requires a deeper and more detailed understanding of each small phenomenon within the involved, along with representative mathematical models, in order to maximize the efficiency of power conversion and significantly reduce expenditures. In fact, accurate models are essential for the effectiveness of control strategies [1], prediction of motion [2] and loads [3], hence for a parsimonious design of components.
Although a vast variety of concepts exist, the most recurrent technologies in the wave energy field are point absorbers [4,5], oscillating water column (OWC) [6,7], and flaps [8]. However, recent years have witnessed the increasing popularity of enclosed pitching bodies with the conversion system not in contact with the water [9,10,11,12], with the main benefit being the absence of moving parts in water and survivability resilience. This paper focuses on the Inertial Sea Wave Energy Converter (ISWEC) [13], which is based on a spinning flywheel inside a closed hull: thanks to the gyroscopic effect, the pitching motion of the floater is converted into roll oscillations, and ultimately converted into electrical power by means of an electrical power take-off (PTO). Note that spinning flywheels are also employed in renewable energy plants and in industrial systems as either mechanical energy storage or to smooth the generated power output [14]. Among the main competitive advantages of employing a gyroscopic system for power production, as in the ISWEC, are the high reliability, ease of accessibility and maintenance in loco, and propensity to implement active control strategies [15,16,17]. However, a necessary condition for energy conversion is to keep the flywheel in constant rotation, inherently representing an item of power loss and decreasing the overall efficiency [18]. Therefore, in order to maximize the power extraction and to reduce the levelized cost of energy (LCOE), it is crucial to numerically and experimentally quantify such losses, and to produce mathematical models which can finally lead to strategic design actions.
The flywheel rotational speed () is daily tuned according to the forecasted sea state [19], while it is kept constant during operation. Therefore, in normal working conditions, no acceleration is required and the provided torque is used just to balance the following three sources of dissipations: bearing losses , seals losses , and the windage losses due to fluid (air) drag . This papers shows that drag losses are both the largest source of dissipation and the most challenging phenomenon to predict and quantify. However, an accurate model is needed for evaluating the sensitivity of such losses to control parameters (especially ) in order to allow the controller to maximize the efficiency of the overall power conversion. Furthermore, a reliable mathematical model is essential for assessing the effectiveness of eventual design countermeasures to limit aerodynamic losses.
This paper considers two configurations, one with a flywheel spinning in an open environment at atmospheric pressure (hereafter referred to as free configuration) and one with a flywheel rotating within a pressure-regulated sealed container (hereafter referred to as in housing configuration). The benefit of the in housing configuration is the possibility to reduce the pressure of the fluid field where the flywheel is rotating, hence decrease friction and aerodynamic losses. Such an advantage is paid with additional power consumption to maintain the depression in the container, and increased mass of the supporting structure (hence costs of material and loads). This paper purports to define a mathematical model that can assist the quantitative study of the cost/efficiency trade-off, in order to define if there is a depression threshold that makes the in housing configuration overall more beneficial than the simpler free configuration. However, the aerodynamic models proposed in this paper can be applied to other applications where flywheels are employed, either for energy generation, storage, or smoothing.
Two numerical models are considered: one simple semi-empiric model, based on the superposition of two semi-analytical solutions of the Navier–Stokes equations (NSE) for a simplified representative model of the system, and one based on the full resolution of the NSE through CFD (Computational Fluid Dynamics) simulation. Such models are compared and then validated against experimental data.
The reminder of the paper is organized as follows: Section 2 describes in detail the geometry of the system and the two configurations considered; Section 3 presents the semi-empiric model and Section 4 shows its results applied to the ISWEC case study; Section 5 discusses setup and results of the CFD simulations; Section 6 describes the dedicated setup of the experimental test rig; Section 7 compares all models and Section 8 presents some final discussion and conclusions.
2. Geometry
In this work, two different geometric configurations are studied, as shown in Figure 1. In the first configuration, the flywheel is contained inside a cylindrical case with two hemispherical caps, thus leaving a narrow gap of fluid between the two walls. The housing is completely sealed from the outside, so it is possible to adjust the inner pressure through a vacuum pump. In the second configuration, the flywheel rotates in almost ideal free air conditions, at atmospheric pressure. By giving up the ability to reduce the pressure of the fluid field around the flywheel, the free configuration achieves a simpler and cheaper setup, minimizing the weight, loads, and costs of the supporting structure.
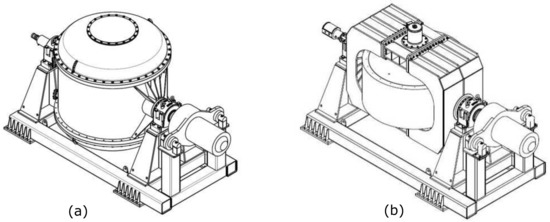
Figure 1.
Gyroscope units. (a): In housing configuration. (b): Free configuration.
Both configurations install the same flywheel, composed of a cylinder of radius m and height m. In the real system, the flywheel is mounted on a shaft of radius m, supported by two radial bearings and two thrust bearings (axial). An electric motor drives the flywheel, controlling its speed and providing the power needed to overcome the losses. The housing of the first configuration is a cylinder of inner radius m, with two hemispherical caps. The fluid is constrained in the axial direction by two wheels, which support the bearings and connect the flywheel structure to the housing. The distance between the flywheel and the supporting wheels determines the axial gap of fluid: m. The maximum speed of the gyro is 800 rpm, corresponding to a circumferential stress of MPa. Given the high speeds and loads on the bearings, both a lubrication and cooling system are needed to extract the power dissipated due to friction. This entails the need of an oil circuit and the insertion of oil seals between the flywheel shaft and the bearings, preventing leakages.
Three different sources of friction losses are present: the bearings friction, the seals friction and the aerodynamic friction due to the rotation at high speed. Since the bearing friction and seals friction are provided by the manufacturers, the analysis carried out in the present work is focused on the aerodynamic friction torque, which is the most challenging to determine during the design stage. The study is divided in two phases: in a first part, the use of simplified models for the calculation of the aerodynamic torque is proposed. The equations are based on an analytical formulation of the problem, with the addition of empirical coefficients identified through experimental campaigns. However, in order to apply the analytical solutions, the geometry is simplified as an ideal cylinder with the same dimensions of the flywheel, but without shaft.
The in housing model consists of two coaxial cylinders with radius respectively (flywheel) and (housing), as shown in Figure 2. The idealization consists of neglecting the semispherical caps and the supporting wheels’ spokes. The flywheel spins around its rotation axis with angular speed .

Figure 2.
In housing configuration simplified model scheme.
The aerodynamic torque (friction torque applied by the fluid on the flywheel surface) is a function of the fluid field motion inside the gap between the flywheel and the housing. The motion field inside the annulus depends on: the fluid properties, the geometrical properties of the system, the angular speed , and the absolute pressure of the annulus (). In the present application, the flywheel and the housing oscillate due to the gyroscopic effect activated by the pitch motion of the hull in response to the incoming wave, so the oscillation period is of the same order of magnitude of the wave period. Therefore, although and its precession axis () are dynamically coupled during operation, can be neglected, since it is at least one order of magnitude smaller than . Such an approximation leads to a considerable simplification of the analytical analysis. In Appendix A, the problem of negligibility of the inertial effects induced by the incoming wave is discussed.
In the free configuration, the geometry consists of a simple cylinder with the same dimensions of the flywheel. In this numerical study, the effect of the supporting structure will not be considered.
3. Semi-Empiric Model
In this section, both configurations (in housing and free air) are considered for the evaluating the contribution of the aerodynamic torque to power losses. A semi-analytical solution of the Navier–Stokes equations is obtained for a simplified model of the system. After presenting the theoretical background in Section 3.1, two loss components are identified for the in housing configuration, discussed in Section 3.2 and Section 3.3, and other two for the free configuration, discussed in Section 3.4 and Section 3.5.
3.1. Theoretical Background
The flow of a viscous fluid confined in a gap between two coaxial rotating cylinders is one of the classical fluid dynamics problems, historically studied to analyze turbulence [20]. If the cylinders have steady rotational speeds and if the flow is laminar, exact solutions of the governing equations can be obtained [21]. Assuming the flow steady and fully developed along the -axis, a convenient representation of the Navier–Stokes equations (NSE) for such an axisymmetric problem is obtained using cylindrical coordinates , with the z-axis along the axis of the cylinders [20]:
where v is the fluid velocity vector, p is the fluid pressure and is the fluid density. Since the problem is axisymmetric, the boundary conditions are derived as:
Equations from (1) to (3) have two limit solutions in the case of still outer cylinder [22]. If , the fluid flows between moving parallel planes, which is the so-called two-dimensional Couette flow; if , the cylinder is effectively isolated and insensitive to the outer cylinder. However, the analytical formulation assumes two cylinders of infinite length, while, in the real case, the effect of the terminations is likely to not be negligible. Moreover, in real working conditions, the flow is seldom laminar, so experimental corrections are necessary to improve the fitting of the analytical solutions to empirical observations, hence defining semi-empiric models.
To obtain a solution of the simplified problem requires a further linear assumption of superposition of effects, namely considering the following two contributions to the aerodynamic friction torque:
- Axial contribution: closed-form analytic solution of the NSE for the flow field within the radial gap between two cylinders (Taylor–Couette flow);
- Transversal contribution: closed-form analytic solution of the NSE for the motion field of a fluid on a rotating disk.
3.2. Axial Contribution—In Housing
Different flow patterns and states have been observed and characterized, depending on the angular velocity, radii of the cylinders, temperature and pressure gradients, and surface conditions [23]. The phenomenon results in a typical shear flow driven by the viscous drag force. At low angular velocities of the inner cylinder, the regime is laminar and the flow is steady and azimuthal, realizing a Couette type of flow. When the inner cylinder reaches a critical speed, the flow becomes unstable, causing transport in the azimuthal momentum. This phenomenon is known as Taylor instability (or Taylor vortex), described and experimentally confirmed in [24]. The Taylor vortices completely fill the annulus between the two cylinders; they are axisymmetric and rotate in alternating opposite directions. Increasing the velocity, the vortices length scale decreases until the coherence length of the structure becomes smaller than the gap width. At this point, turbulence starts to develop in the bulk. As the turbulence increases, the instability become more complex, until no patterns or flow structures are recognizable any more.
Therefore, in order to quantify drag effects on the cylinder, it is necessary to pinpoint the type of flow regime, usually by means of the Taylor number, which is defined as:
where is the kinematic viscosity and is the radial gap. The Taylor number is a dimensionless number representing the ratio of centrifugal forces to viscous forces. The instability of the flow starts above the critical value of , whereas it is fully turbulent at [21]. All the application cases studied in this paper are characterized by a turbulent flow regime in the gap. Under such conditions, neither the linear theory proposed by Taylor [24], nor the nonlinear theory developed by Stuart [25] are valid, so it becomes necessary to implement semi-empiric formulas tuned on experimental results.
Bilgen and Boulos, respectively in [26,27], developed a relationship that expresses the moment coefficient for an annulus with the rotating inner cylinder and no axial pressure gradient. The moment coefficient is defined as [21]:
where M is the torque and is the fluid density modeled as an ideal gas. Table 1 shows that can be expressed as a function of the dimensionless ratio and the Couette Reynolds number, defined as:

Table 1.
Moment coefficient on the cylinder for the In housing configuration.
The equations in Table 1 have been validated with several experimental results, with a maximum mean deviation of [26].
3.3. Transversal Contribution—In Housing
The transversal contribution considers the friction due to the fluid on the top and bottom disks of the cylinder. The solution of NSE in the proximity of a rotating planar disk with a wet side can be used to estimate the transversal component of the power loss. The end disk is adjacent to another stationary disk, creating a tight cavity known as a rotor–stator cavity or wheel-space [27]. This problem is of particular interest in a wide range of applications, for example disk drives, rotary machines and flywheels. Because of the viscosity and the no-slip condition on the wall, the fluid is entrained from the core, transported by the disk, and pushed away in the radial direction by the centrifugal force. Therefore, the disk works as a centrifugal pump. Furthermore, if the gap is larger than the boundary-layer thickness, on both the rotating disk and the housing a boundary layer will form; consequently, in the core, the fluid will rotate at an angular velocity about half of the rotor velocity. These phenomena can be described with the Batchelor model [27].
According to Schlichting [21], the resulting friction torque contribution, for a disk wetted on one side, is a function of the square of the angular velocity, and it is possible to write the friction torque M as a function of the dimensionless torque coefficient :
where the dimensionless torque is . Table 2 shows three different possible motion regimes, based on the dimensionless number in (8), and confirmed by experimental data by Daily and Nece [28]:

Table 2.
Moment coefficient on the disk for the In housing configuration.
3.4. Axial Contribution—Free
Without the housing, the flywheel can be studied as a simple cylinder rotating around its axis and immersed in a fluid. The fluid around the cylinder will experience centrifugal forces due to the no-slip wall condition. Therefore, the flow regime will be influenced by both friction drag and centrifugal forces. The dimensionless torque coefficient is defined as in Equation (5), according to Schlichting [21]. For a free cylinder, transition arises when the Reynolds number is in between 40 and 60 [27]. Since the considered working points of the flywheel are all above , flow regimes are from moderately to highly turbulent.
However, unlike for the annulus considered in Section 3.2, no instability is to be expected because there is no constriction on the fluid motion and the velocity gradient is slower. For turbulent flow, the friction torque can be calculated using the empirical correlation found by Theodorsen and Regier [29] on the basis of experimental results:
Equation (9) is solved iteratively, and converge is found in five iterations [27].
3.5. Transversal Contribution—Free
The transversal (radial) flow is caused by the centrifugal forces, generated by the shear between the fluid and the disk. As in the cavity case, the fluid is entrained axially into the boundary layer causing the free-disk pumping effect [27]. Two flow regimes need to be distinguished as a function of the Reynolds number . The dimensionless torque for one wetted side is defined as in Table 3 [21].

Table 3.
Moment coefficient on the disk for the Free configuration.
4. Case Study: Semi-Empiric Model
The set of equations provided in Section 3 is applied to the case of the flywheel presented in Section 2. For both configurations, the axial and transversal contributions to the aerodynamic torque are calculated in a variety of working conditions, investigating different combinations of flywheel speed and fluid pressure. Table 4 summarizes the consequent Reynolds numbers under study. It is possible to observe that the flow regimes vary from laminar to turbulent, therefore all the different formulations presented in Section 3 are used to calculate the total friction torque.

Table 4.
Extreme values of the Reynolds number for the different configurations.
4.1. In Housing
In this subsection, the resulting inrque for the In housing configuration are presented. Figure 3 and Figure 4 show that both contributions to the aerodynamic torque are proportional to the pressure, with increasing slope with rotation velocity. Moreover, for each working point, the total transversal contribution (of both disks) is about of the total friction torque, confirming the expectations that it is not negligible, as discussed in Section 3.3.

Figure 3.
Axial component of the fluid friction torque as a function of the pressure at different rotational velocities.

Figure 4.
Transversal component on each disk of the fluid friction torque as a function of the pressure at different rotational velocities.
Considering the full operative range for both pressure and velocity, the maximum torque, shown in Figure 5, is about 200 times the minimum value, highlighting once more how crucial it is to model such losses, already in the preliminary design stage.
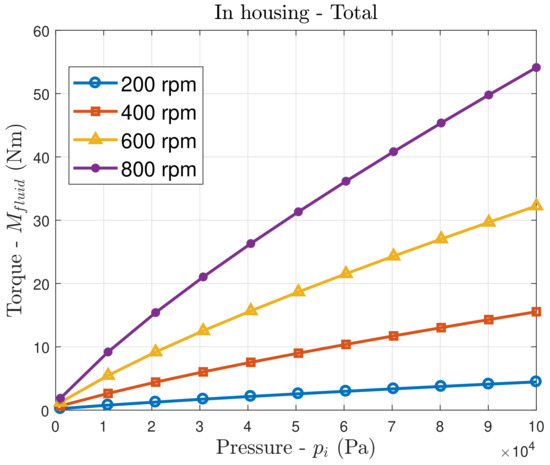
Figure 5.
Total fluid friction torque as a function of the pressure at different rotational velocities.
For the particular configuration considered in this work, where the radii ratio is and the gap between the two cylinders is classified as small [30], the torque at atmospheric pressure ( kPa) is about 20 times greater than the torque at vacuum conditions ( kPa), for the lowest rotational speed (200 rpm), and about 30 times greater, for the maximum rotational speed (800 rpm). On the other hand, Figure 6 shows that the total torque at a given pressure is about linearly proportional to the flywheel velocity, with a ratio between the lowest and the highest torques () equal to 12.
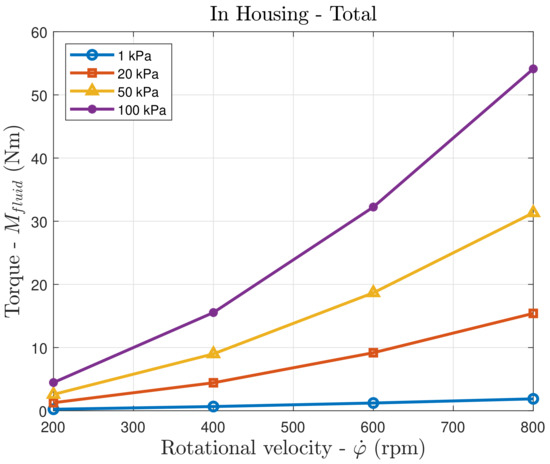
Figure 6.
Total fluid friction torque as a function of the rotational velocity at different pressure values.
4.2. Free
For the free configuration, no pressure regulation is available and the fluid is at atmospheric pressure. The total torque, along with its axial and transversal breakdowns, is shown in Figure 7. As in the in housing configurations, the impact of the top and bottom disks is not negligible, accounting for about of the total friction torque (slightly higher than the in housing configuration).

Figure 7.
Total fluid friction torque as a function of the rotational velocity without housing.
5. CFD Model
Results presented in Section 4 provide great insight on the relative importance of each torque component, on their sensitivity to design () and control () parameters, and ultimately provide a quantitative comparison between different configurations. However, such results are based on a simplified model, presented in Section 3, so it is necessary to generate a higher-fidelity model, as CFD, for benchmarking and accuracy evaluation.
Benchmarking with experimental data are, ideally, a further necessary step for a full validation of the model. However, as the dimension of the prototype increases, experimental tests become excessively expensive and eventually unfeasible. Conversely, no intrinsic limitation is present in a fully-nonlinear numerical model. Therefore, it is essential to define a reliable CFD model to support detailed analysis and design. The CFD model is first calibrated on the basis of the outputs of the simplified numerical model, and then validated against experimental data. The finite-volume multi-physics commercial software Star-CCM+ [31] is used, which discretizes and solves numerically the NSE.
In the past few decades, several numerical techniques and modelling approaches have been developed for simulating turbulent flows, including Direct Numerical Simulation (DNS), Large Eddy Simulation (LES) and Reynolds-Averaged Navier–Stokes (RANS). DNS is the most accurate approach, since the NSE are numerically solved without the aid of any simplifying turbulence model, resulting in an extremely high computational cost. In LES, the computational burden is reduced by ignoring the smallest length scales of turbulence, while considering only large eddies. However, the objective of the present work is to estimate the friction torque on the flywheel wall, while there is no interest in the detailed representation of creation and evolution of vortexes structures in the fluid bulk. Thus, the RANS model is the most suitable, since it provides the overall torque with good accuracy at the lowest computational time.
5.1. RANS Turbulence Model
Since the flywheel works at constant rotational speed, it is possible to assume that the flow is fully developed and steady. The RANS model is based on the decomposition of the NSE into a mean value and a fluctuating component, providing accurate estimations of average properties, such as forces on a body [32]. However, in order to provide a closure to the governing equations, a turbulence model must be adopted. In this work, the Realizable K-Epsilon two layer () model is chosen, since it provides a good compromise between robustness, computational cost, and accuracy [31]. The realizable two-layer model provides a new transport equation for the turbulent dissipation rate , expressing such a critical coefficient of the model as function of the mean flow and turbulences properties, rather than constant. This lets the model satisfy certain mathematical constraints on the normal stress, consistently with the physics of turbulence (which is referred to as “realizability”).
5.2. Numerical Grid
The same geometry used in the semi-empiric model is considered, plus the inclusion of the flywheel shaft. Taking advantage of the axisymmetry of the problem, the computational cost is decreased by reducing the simulated domain to a 10-degree slice of the whole geometry. A tridimensional hexahedral mesh is used by means of a trimmed cell mesher, which guarantees a minimal cell skewness. For an appropriate representation of the wall shear stress and, consequently, of the friction torque, the grid prismatic cell layer should be monitored: Table 5 shows the main properties of the grid. Both of the configurations have the same mesh refinement at walls, but a different number of cells in the core. The free configuration counts more cells because the computational domain is larger than the in housing one. The surface averaged value of y+ on the walls is around 1 for 200 rpm cases and 5 for 800 rpm cases. The computational grid is the same for all the rotational velocities because the realizable two layer k-epsilon approach is based on a hybrid modelling of the turbulent boundary layer. This strategy switches the wall boundary condition between a Law of the Wall model for local high Reynolds flow regime and, if the mesh is fine enough at the boundary, the solution of the viscous sublayer for local low Reynolds flow regime. Figure 8 shows an example of the computed fluid velocity field for the in housing configuration, with of 1 kPa.

Table 5.
Numerical grid properties.

Figure 8.
Fluid velocity field for the in housing configuration, with of 1 kPa and of 200 rpm and 800 rpm, on the left and right of the figure, respectively.
The convergence of the numerical simulation is verified by means of two criteria. The first (strong) criterion is based on the decrease of residuals’ values, normalized by the initial guess. The second (weak) criterion is based on the convergence of integral coefficients. For instance, simulations are stopped when the maximum residual (among continuity, pressure, turbulent quantities) is lower than if such a condition is not achieved and the maximum residual is greater than and lower than . Moreover, the simulation is stopped if the torque coefficient around the rotation axis is stable with 0.1% bounded fluctuations.
5.3. CFD Tests Map and Results
In order to perform a comprehensive and representative analysis, a total of 12 CFD simulations are considered, studying six different working points for both configurations. For sake of computational time, only the extreme values of flywheel angular velocity range are simulated (200 rpm and 800 rpm), whereas three pressure levels are considered: 1000, 50,500, and 100,000 Pa. CFD simulation results are reported and compared with the semi-empiric models, for both configurations in Figure 9. Only bars at atmospheric pressure are presented for the free configuration, since no pressure regulation is available. For cases with the same , the same scale for the torque-axis has been used in order to facilitate the visual comparison of the differences between configurations. Overall, CFD and the semi-empiric models are in good agreement for both configurations and at both rotational speeds. As expected, the higher the rotational speed, the higher the aerodynamic torque. Likewise, the torque (and losses) also increases with the pressure. It is interesting to remark that, even when both configurations are at the same (atmospheric) pressure, the torque for the in housing configuration is about half the torque in the free configuration. This is due to the different flow regime conditions, as discussed in Section 3. In order to better highlight the improvements brought by enclosing the flywheel, Table 6 shows the ratio between the aerodynamic torque in the free configuration and the in housing configuration, for different rotational speeds and depressions in the sealed container.
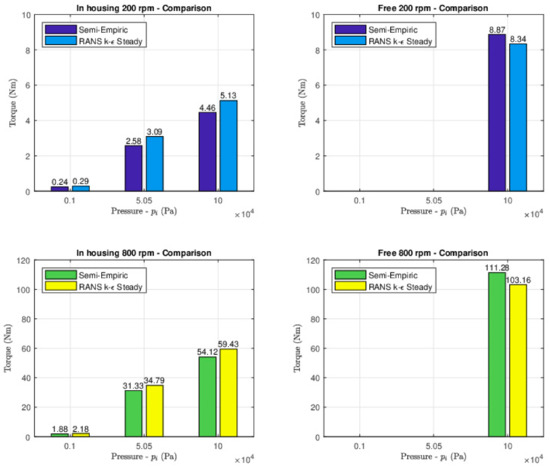
Figure 9.
Total fluid friction torque for the In housing configuration: Semi-empiric vs. CFD.

Table 6.
Ratio of the aerodynamic torque in the free configuration and the in housing configuration, for different rotational speeds and depressions in the sealed container. Absolute values are shown in Figure 9.
6. Experimental Test Rig
The test rigs for the experimental campaign are the gyroscopic units installed on the ISWEC device. Therefore, experiments are run on the full real system, avoiding approximations due to prototype simplification and scaling effects. Figure 10 shows a functional scheme of the test rig, while the characteristics of the main components are reported in Table 7. The gyroscope units are composed of a flywheel connected to the support frame by a couple of roller bearings. The supporting structure is able to rotate with respect to an axis orthogonal to the flywheel rotation axis. The flywheel is driven by a permanent magnet AC (alternating current) synchronous motor, directly mounted on its shaft. It is worth remarking that, in the case of In housing configuration, the flywheel support frame coincides with the vacuum chamber. The flywheel is regulated through a closed control loop: the feedback velocity, given by a rotary encoder, is used to adjust the output drive voltage and, therefore, the flywheel speed. A more detailed explanation of the control loop is provided in Section 6.1.

Figure 10.
Layout of the test rig with the main components.

Table 7.
Test rig main properties.
6.1. Test Rig Operation Mode
During operation, the driver powers the motor to reach the desired flywheel speed, set according to the current seas state. The electrical power take-off (PTO) exploits the resulting precession motion of the flywheel, converting mechanical power into electrical power. In this work, only the spinning motion of the flywheel is of interest. Therefore, both gyroscope units are tested outside of the floater and with the PTO axis mechanically locked. Different velocities are tested in order to obtain the characterize of power losses.
Figure 11 represents the working scheme of the flywheel motor during the experimental session. A torque control loop and a velocity control loop are in cascade, internally closed in the control unit [33]. The velocity set is the only input of the control unit, while the velocity feedback is acquired by an encoder. A first velocity loop is closed with a PID (proportional integral derivative) control law, returning a set value of torque () as output. Then, is compared with the measured mechanical torque () to calculate the torque variation () necessary to balance the load and obtain a constant velocity. In detail, a coordinate converter and a transformation block, embedded in the motor driver, compute the torque-generating current () from the acquired phase currents. An observer model, whose inputs are phase voltages and currents from the motor three phases, estimates the torque to factor. The mechanical torque is obtained dividing by the torque to factor. Once the torque variation is computed, an internal driver conversion calculates the actual phase currents and phase voltages values to give input to the motor.
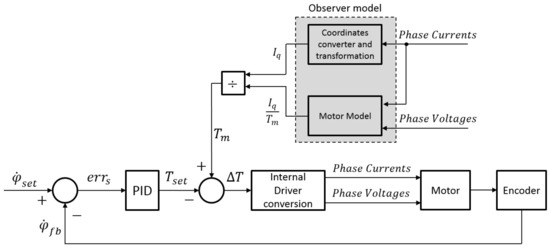
Figure 11.
Block scheme of the control logic for the tests at constant rotational velocity.
6.2. Data Acquisition
The acting torque on the flywheel () and are acquired by a SCADA system that reads data directly from the motor driver bus interface (Siemens motor module [33]), as schematically shown in Figure 10. This acquisition system is composed of a National Instruments Compact RIO (cRIO) 9081 with a Profibus interface used to communicate with the motor driver. The cRIO CPU is also in charge to provide the speed reference signal to the motor drive in order to maintain the constant speed.
The flywheel system has been tested at different rotational velocities in its working range. All tests are run with the spinning axis in vertical position to avoid any load on the radial bearings and simplify the analysis. Once the acceleration transient is finished, experimental data are recorded for a time period of 2 min at a sampling frequency of 100 Hz. The measured values are then post-processed to calculate the regime power value requested to balance the power losses. A mechanical power curve is thus obtained as a function of the flywheel velocity, as shown in Figure 12 for the example of free configuration.

Figure 12.
Experimental mechanical power at the flywheel motor shaft. Free configuration.
The experimental data can be fitted by a third degree polynomial curve, function of the flywheel velocity:
where and are the fitting polynomial coefficients, shown in Figure 12. The total mechanical power provided by the flywheel motor balances the sum of the aerodynamic losses and the mechanical losses, namely due to bearings (see Section 6.4) and seal (see Section 6.3). Therefore, the aerodynamic losses are obtained as the difference between the power provided by the motor and the mechanical losses.
6.3. Seals Friction
Two radial VITON shaft seals are also mounted on the flywheel shaft and contribute to the power losses. It is possible to calculate this amount of power from the relation:
where is the specific friction force supplied by the constructor [34]. Note that the power loss due to the seals is proportional to .
6.4. Bearings Friction
A reliable estimation of the bearing losses is provided by the constructor [35]. The friction torque due to the bearings is computed as:
where is a constant friction coefficient (provided by the constructor), is the bearing bore diameter, and E is the equivalent dynamic bearing load.
The flywheel shaft is supported by two radial bearings, in charge of the radial loads, and two thrust bearings, in charge of the axial loads. According to the schematics presented in Figure 13, it is possible to compute E: the flywheel, along with its supporting shaft and two couples of bearings, is presented at three different precession angles (), namely, from left to right of Figure 13, at 0, 45 and 90 degrees. Once the top and bottom bearings distance from the flywheel ( and , respectively) are assigned, the radial and axial loads can be calculated for any generic angular position of the flywheel axis:
where m and J are the mass and moment of inertia of the flywheel, respectively. Note that the power dissipated by the bearings is , and is proportional to the loads in (13). It follows that:

Figure 13.
Loading scheme of the bearings for different precession angles, equal to 0, 45 and 90 degrees, from left to right.
- (a)
- If there is no gyroscopic effect (), E and are insensitive to . Consequently, the power needed to overcome the bearings friction is proportional to ;
- (b)
- If the gyroscope is activated by the pitch motion of the device, and the power losses become proportional to .
Note that the experimental test rig falls under condition (a), so, likewise for the bearing power loss, the loss due to bearings is linearly proportional to . The aerodynamic contribution can be extracted from the total mechanical power by subtraction of the—linear—contribution of bearings and seals.
7. Experimental and Numerical Models Results Comparison
Finally, this section compares the numerical results to experimental measurements. Considering the free configuration first, Figure 14 shows the comparison between the semi-empiric model and experimental data on top, and the consequent percentage relative error on the bottom. Consistent with the discussion in Section 6, aerodynamic losses show a nonlinear dependence on the flywheel speed. The semi-empiric model is in good agreement with the experimental results, with a maximum absolute relative error equal to .
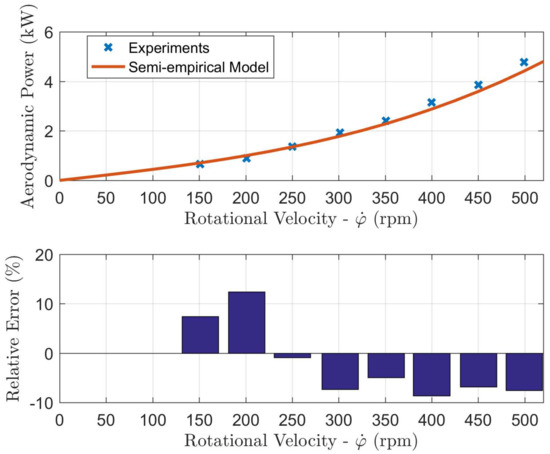
Figure 14.
Aerodynamic power: experiments vs. semi-empiric model. Free configuration.
Figure 15 and Figure 16 show a good agreement of both semi-empiric and CFD models with available experimental results, for the free and in housing configuration, respectively. However, the accuracy decreases at higher velocities. In fact, for both configurations, CFD simulations underestimate the aerodynamic torque with respect to the experimental data. Such discrepancies can be ascribed to differences between the simulated idealized geometry and the actual device: the CFD geometrical neglects the wheels spokes for the In housing configuration, while no support frame has been modelled in the Free configuration. The quantification of the impact of such simplifying assumptions will be possible by implementing a higher-fidelity CFD model (including the wheels spokes), which is a topic of future research. However, the accuracy of the model is satisfactory and acceptable for preliminary design studies and as a basis for control strategies. In fact, there is a good agreement up to 500 rpm, which is the typical upper boundary of normal operational conditions [36].
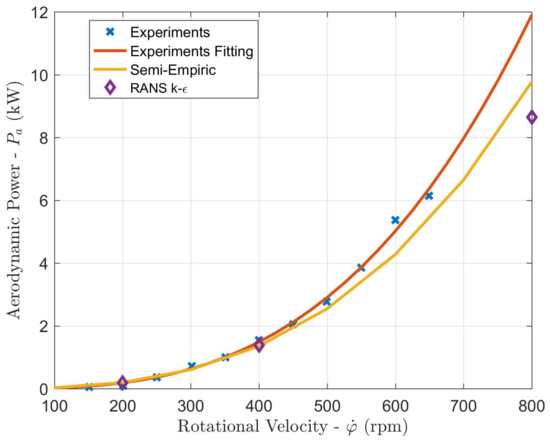
Figure 15.
Aerodynamic power: Free configuration results comparison against available experimental data.

Figure 16.
Aerodynamic power: In housing configuration results comparison against available experimental data.
8. Conclusions
As wave energy conversion technologies approach a mature stage of development, a higher level of refinement of the efficiency-maximizing strategies become mandatory in order to further reduce costs and increase the ability to deliver energy. Representative mathematical models, able to describe every relevant phenomenon involved in the power conversion chain, are essential tools for understanding sources of inefficiencies of the system and, in turn, take effective corrective actions. This paper focuses on the Inertial Sea Wave Energy Converter device, tackling the irksome problem of mathematical modelling of aerodynamic losses on the flywheel, the core of the power conversion system. A representative model of power losses is fundamental in the design stage, in order to determine appropriate geometrical properties of the system. Furthermore, mathematical models can both inspire conceptual innovations and technological leaps to reduce power losses, as well as evaluate the effectiveness of their implementation. Finally, quick models can inform the controller about sources losses and consequently facilitate fine-tuning of the control parameters of the device.
This paper focuses on modelling and validating a formulation for the aerodynamic torque on the spinning flywheel of the ISWEC, which is the largest source of power loss in the gyroscopic system. Two alternative modelling options are investigated, achieving different compromises of computational time and accuracy. The first approach is semi-empiric, pragmatically tuning some analytical solutions of the Navier–Stokes equations valid for an idealized geometry. Such an approach is appealing for its computational convenience, but its fidelity must be evaluated with more complex models and/or experimental data. On the other hand, fully-nonlinear CFD simulations have the potential to virtually obtain the highest accuracy, at the price of a high computational burden (about 3 and 6 h walltime, respectively for the free and in housing configuration, using four cores with processor Intel Xeon E5-2667). Therefore, CFD simulations are more suitable for verification and benchmarking, while semi-empiric models are best for extensive design purposes and control applications. Finally, both models are validated by comparison with experimental tests, showing a satisfactory level of agreement.
Two technological solutions are explored: while the free configuration has the flywheel rotating in an unconstrained environment at the atmospheric pressure, the in housing configuration confines the flywheel inside a bell in order to define a controlled environment and reduce the air friction. The proposed models are used to weight the advantage of enclosing the flywheel in a sealed container, allowing to reduce the pressure of the surrounding fluid, against the disadvantage of higher power consumption (due to the vacuum-pump) and loads (due to the additional weight of the housing). Furthermore, the sensitivity of the power loss to both the inner air pressure and the rotational speed of the flywheel is considered. It is found that the in housing configurations dissipate about half the power of the free configuration already at atmospheric pressure. Furthermore, the lower the pressure is reduced in the chamber, the lower the friction torque, and hence power losses. However, the entity of the reduction is very dependent on the flywheel speed as well, since a cubic dependence is shown, both in the model and in the experimental data. Such information is extremely useful to inform both design and control stages, in order to identify the most efficient working condition for a given location and sea state.
Author Contributions
Conceptualization, A.S.S., F.G., G.G., M.B., G.B. and G.M.; methodology, A.S.S. and F.G.; software, F.G.; validation, A.S. and M.B.; formal analysis, A.S.S. and F.G.; investigation, A.S.S. and F.G.; resources, F.G., G.B. and G.M.; data curation, A.S.S., F.G. and G.G.; writing—original draft preparation, A.S.S., F.G. and G.G.; writing—review and editing, G.G.; visualization, F.G. and G.G.; supervision, G.B. and G.M.; project administration, G.B. and G.M.; funding acquisition, G.B. and G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
In this work, the fluid dynamics torque experienced by the flywheel embedded into the gyroscope is computed in a frame of reference fixed with the flywheel. Such a frame is non-inertial, since the rotation axis oscillates with a frequency of the same order of magnitude of the incoming sea wave. The relevance of the consequent additional fictitious force is hereafter studied, by considering a non-dimensional scaled formulation of the Navier–Stokes equations.
In Figure A1, the absolute and the non-inertial frames of reference are indicated with Cartesian coordinates, and , respectively; the consequent vectors of velocities are ; and , respectively; the origin of both references (O) is in linear uniform motion; is the angular position of the rotation axis with respect to the local vertical direction (), and is the angular velocity.
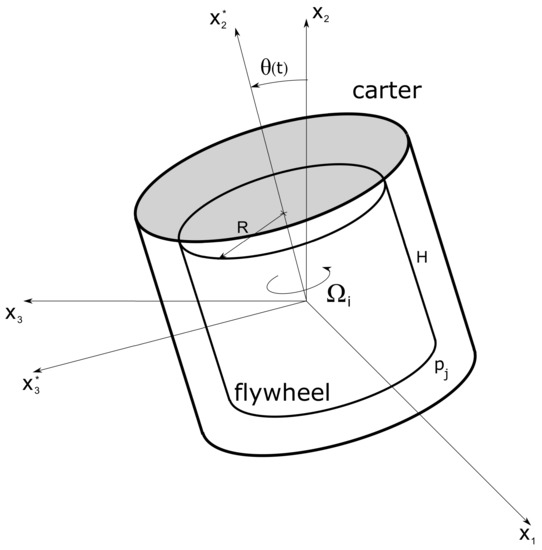
Figure A1.
Schematic representation of the absolute and non-inertial frames of reference.
The non-dimensional continuity and the NSE for a viscous and incompressible flow in a moving reference frame are the following [37]:
where , is the Reynolds number, and and are the translation vector and the rotation matrix, respectively. The mapping between the two frames of reference is defined as:
Considering only the rotation induced by the sea wave, the translation vector is null, while the rotation matrix is:
For sake of simplicity, the oscillation of the rotation axis is assumed to have a sinusoidal form , where is the amplitude of the maximum rotation of the axis and , with T the sea wave period. Therefore, the non-dimensional NSE written in the frame of reference fixed with the flywheel become:
where the components of are:
A scaling procedure is hereafter presented, which aims at weighting the relative importance of each term of the NSE in (A4), in order to asses the impact of neglecting the fictitious force components. Four different contributions can be identified in (A4), namely the convective terms (), the pressure terms (), the viscous terms (), and the fictitious terms (). Such components can be approximated as follows:
- Convective terms (C):
- Pressure terms (P):
- Viscous terms (V):
- Fictitious force terms (B):
The main goal of such a scaling procedure is to compare the order of magnitude of the fictitious force terms with respect to the other terms of the NSE. The fictitious force terms are important if the flywheel rotation velocity is low compared to the oscillation velocity. For ISWEC, the minimum working rotation velocity is rpm. Other typical parameters for ISWEC are: m, m, m, s, . A typical velocity of the flow field within the gap between the flywheel and the carter is m/s. The velocities scale as , , the lengths scale as , , and the pressure scales as .
For low Reynolds () numbers, the viscous terms are comparable with the other terms of the NSE. Given and a temperature C, the minimum value of is achieved for low pressure within the carter. For ISWEC, the minimum working pressure inside the carter is is Pa. At these conditions, the Reynolds number is finally:
Table A1 tabulates the overall contribution of different terms of equations (A6) to (A9) on the momentum equations in (A4), along the and directions. Clearly, such equations are ruled by convective and pressure terms, while fictitious terms are either small or zero. Therefore, neglecting fictitious force terms due to the non-inertial moving frame of reference is considered an acceptable assumption.

Table A1.
Terms decomposition of the momentum equation.
Table A1.
Terms decomposition of the momentum equation.
| C[%] | V[%] | P[%] | B[%] | |
|---|---|---|---|---|
| Momentum eq. - | 0 | 0 | 94 | 6 |
| Momentum eq. - | 80 | 0 | 20 | 0 |
References
- Giorgi, G.; Ringwood, J.V. A Compact 6-DoF Nonlinear Wave Energy Device Model for Power Assessment and Control Investigations. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Articulating parametric resonance for an OWC spar buoy in regular and irregular waves. J. Ocean Eng. Mar. Energy 2018, 4, 311–322. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Analytical Formulation of Nonlinear Froude-Krylov Forces for Surging-Heaving-Pitching Point Absorbers. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Todalshaug, J.H.; Asgeirsson, G.S.; Hjálmarsson, E.; Maillet, J.; Möller, P.; Pires, P.; Guérinel, M.; Lopes, M.F. Tank testing of an inherently phase-controlled wave energy converter. Int. J. Mar. Energy 2016, 15, 68–84. [Google Scholar] [CrossRef]
- Beatty, S.; Hall, M.; Buckham, B.J.; Wild, P.; Bocking, B. Experimental and numerical comparisons of self-reacting point absorber wave energy converters in regular waves. Ocean Eng. 2015, 104, 370–386. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Parametric motion detection for an oscillating water column spar buoy. In Proceedings of the 3rd International Conference on Renewable Energies Offshore RENEW, Lisbon, Portugal, 8–10 October 2018. [Google Scholar]
- Renzi, E.; Doherty, K.; Henry, A.; Dias, F. How does Oyster work? The simple interpretation of Oyster mathematics. Eur. J. Mech.-B/Fluids 2014, 47, 124–131. [Google Scholar] [CrossRef]
- Gilloteaux, J.C.; Babarit, A.; Ducrozet, G.; Durand, M.; Clément, A.H. A Non-Linear Potential Model to Predict Large-Amplitudes-Motions: Application to the SEAREV Wave Energy Converter. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 529–535. [Google Scholar] [CrossRef]
- Wello, O. Company Website. Available online: www.wello.eu (accessed on 1 January 2020).
- Bracco, G.; Cagninei, A.; Casassa, M.; Giorcelli, E.; Giorgi, G.; Mattiazzo, G.; Passione, B.; Poggi, D.; Raffero, M.; Vissio, G. Modeling and Optimization of a Wave Energy Converter Using ANSYS AQWA; ANSYS. Cobalto Casa Editrice: Bergamo, Italy, 2015; pp. 79–86. [Google Scholar]
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu, S.A.; Mattiazzo, G. PeWEC: Experimental validation of wave to PTO numerical model. Ocean Eng. 2018, 167, 114–129. [Google Scholar] [CrossRef]
- Bracco, G.; Giorcelli, E.; Mattiazzo, G. {ISWEC}: A gyroscopic mechanism for wave power exploitation. Mech. Mach. Theory 2011, 46, 1411–1424. [Google Scholar] [CrossRef]
- Read, M.G.; Smith, R.A.; Pullen, K.R. Optimisation of flywheel energy storage systems with geared transmission for hybrid vehicles. Mech. Mach. Theory 2015, 87, 191–209. [Google Scholar] [CrossRef]
- Bracco, G.; Casassa, M.; Giorcelli, E.; Giorgi, G.; Martini, M.; Mattiazzo, G.; Passione, B.; Raffero, M.; Vissio, G. Application of sub-optimal control techniques to a gyroscopic Wave Energy Converter. In Proceedings of the RENEW 2014, Renewable Energies Offshore, 1st International Conference on Renewable Energies Offshore, Lisbon, Portugal, 24–26 November 2014; pp. 265–269. [Google Scholar]
- Genuardi, L.; Bracco, G.; Sirigu, S.A.; Bonfanti, M.; Paduano, B.; Dafnakis, P.; Mattiazzo, G. An application of model predictive control logic to inertial sea wave energy converter. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2019; Volume 73, pp. 3561–3571. [Google Scholar] [CrossRef]
- Bracco, G.; Giorcelli, E.; Mattiazzo, G.; Orlando, V.; Raffero, M. Hardware-In-the-Loop test rig for the {ISWEC} wave energy system. Mechatronics 2015, 25, 11–17. [Google Scholar] [CrossRef]
- Pozzi, N.; Bonfanti, M.; Mattiazzo, G. Mathematical Modeling and Scaling of the Friction Losses of a Mechanical Gyroscope. Int. J. Appl. Mech. 2018, 10, 3. [Google Scholar] [CrossRef]
- Raffero, M.; Bracco, G.; Passione, B.; Vissio, G.; Mattiazzo, G.; Giorcelli, E. Identification of the hydrodynamic parameters of a wave energy converter. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–10 September 2015; pp. 1–10. [Google Scholar]
- Landau, L.D. Fluid Mechanics: Vol 6 (Course of Theoretical Physics); Butterworth-Heinemann Ltd.: Oxford, UK, 1987. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Pascal Chossat, G.I. Couette-Taylor Problem; Springer: New York, NY, USA, 2012. [Google Scholar]
- Andereck, C.D.; Liu, S.S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 1986, 164, 155. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of a Viscous Liquid Contained between Two Rotating Cylinders. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Stuart, J.T. On the nonlinear mechanics of hydrodynamic stability. J. Fluid Mech. 1958, 4, 1. [Google Scholar] [CrossRef]
- Bilgen, E.; Boulos, R. Functional Dependence of Torque Coefficient of Coaxial Cylinders on Gap Width and Reynolds Numbers. J. Fluids Eng. 1973, 95, 122. [Google Scholar] [CrossRef]
- Childs, P.R.N. Rotating Flow; Butterworth-Heinemann Ltd.: Oxford, UK, 2010. [Google Scholar]
- Daily, J.W.; Nece, R.E. Chamber Dimension Effects on Induced Flow and Frictional Resistance of Enclosed Rotating Disks. J. Basic Eng. 1960, 82, 217–230. [Google Scholar] [CrossRef]
- Theodorsen, T.; Regier, A. Experiments on Drag of Revolving Disks, Cylinders, and Steamline Rods at High Speeds; Technical Report NACA-TR-793; NACA: Hampton, VA, USA, 1944. Available online: https://ntrs.nasa.gov/search.jsp?R=20050241738 (accessed on 1 January 2020).
- Biage, M.; Campos, J.C.C. Visualization study and quantitative velocity measurements in turbulent taylor-couette flow by phantomm flow tagging: A description of the transition to turbulence. J. Braz. Soc. Mech. Sci. Eng. 2003, 25, 378–390. [Google Scholar] [CrossRef][Green Version]
- CD-adapco. STAR-CCM+ v11.04 User Guide. 2016. Available online: http://www.cd-adapco.com (accessed on 1 January 2020).
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; AIP: New York, NY, USA, 1997. [Google Scholar]
- Siemens. Siemens Sinamics S120/S150 List Manual. 2013. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwi-tsz0zo7nAhUyxYsBHao_AawQFjAAegQIBBAC&url=https%3A%2F%2Fsupport.industry.siemens.com%2Fcs%2Fattachments%2F68041075%2FLH10113eng.pdf&usg=AOvVaw0eCdmN2khU15NyCUQOTQ8- (accessed on 1 January 2020).
- Pantecnica. DOMSEL Tenute Radiali a Membrana per Alberi Rotanti; Pantecnica: 2020. Available online: http://www.pantecnica.it/ (accessed on 1 January 2020).
- SKF. Rolling Bearings; SKF: 2020. Available online: www.skf.com (accessed on 1 January 2020).
- Sirigu, S.A.; Bracco, G.; Bonfanti, M.; Dafnakis, P.; Mattiazzo, G. On-board sea state estimation method validation based on measured floater motion. IFAC-PapersOnLine 2018, 51, 68–73. [Google Scholar] [CrossRef]
- Takeuchi, S.; Yamazaki, T.; Kajishima, T. Study of Solid-Fluid Interaction in Body-Fixed Non-Inertial Frame of Reference. J. Fluid Sci. Technol. 2006, 1, 1–11. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).