Development of a Systematic Method for Tuning PID Control Gains in Free-Running Ship Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Approach
2.1.1. Target Ship and Propeller
2.1.2. Governing Equation
2.1.3. Numerical Schemes
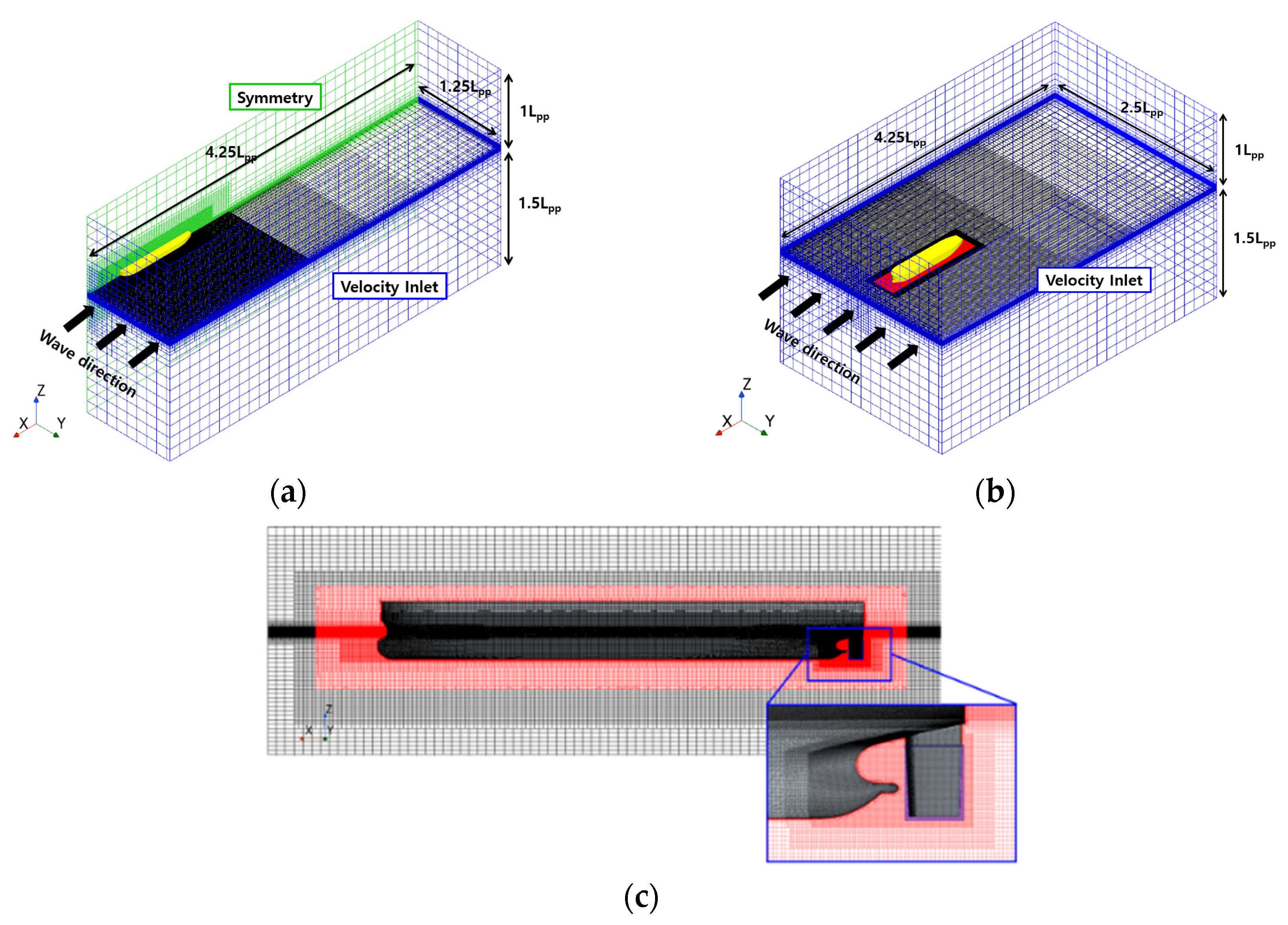
2.1.4. Computation Domain and Grid System
2.1.5. Control of Rudder Angle and Propeller Revolution
2.2. Validation
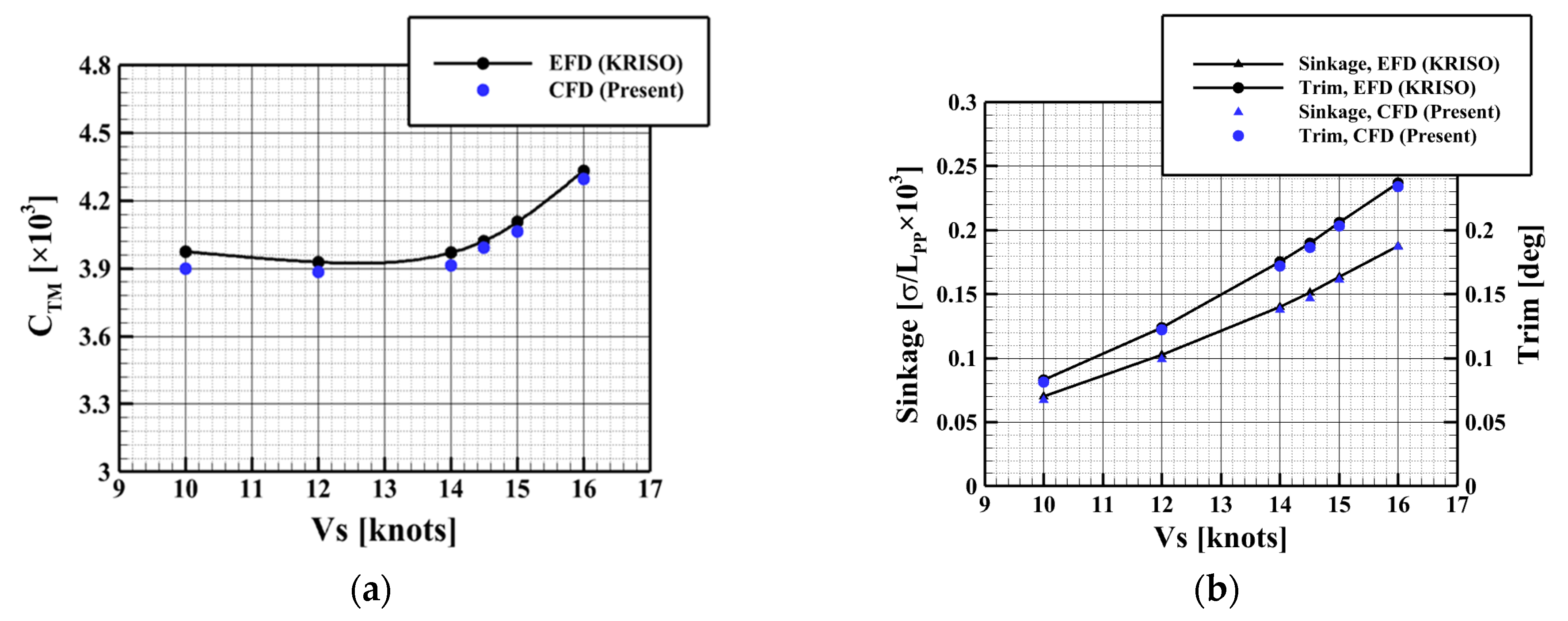
2.2.1. Validation of Resistance in Calm Water
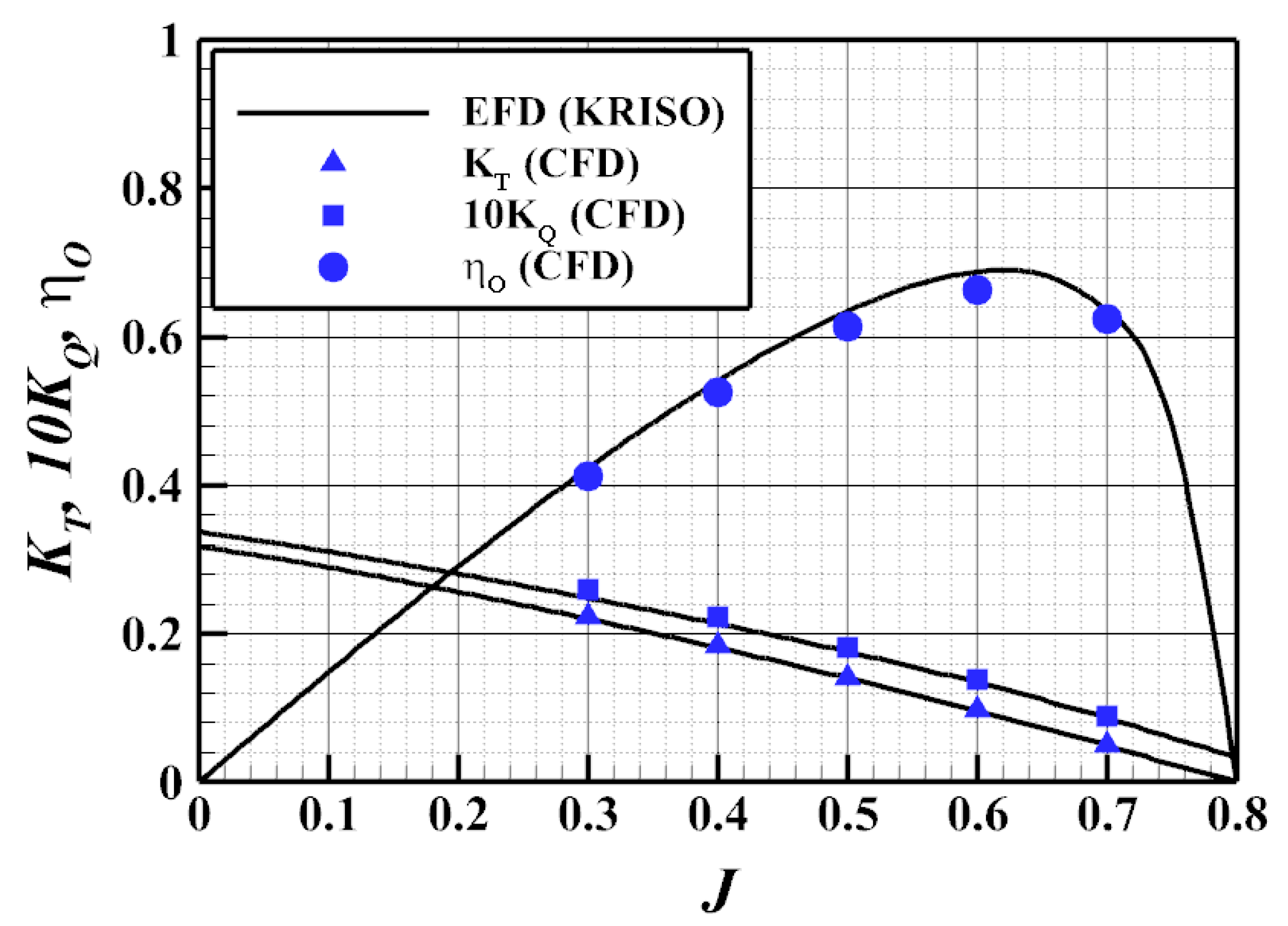
2.2.2. Validation of Propeller Open-Water Test
2.2.3. Validation of Self-Propulsion in Calm Water
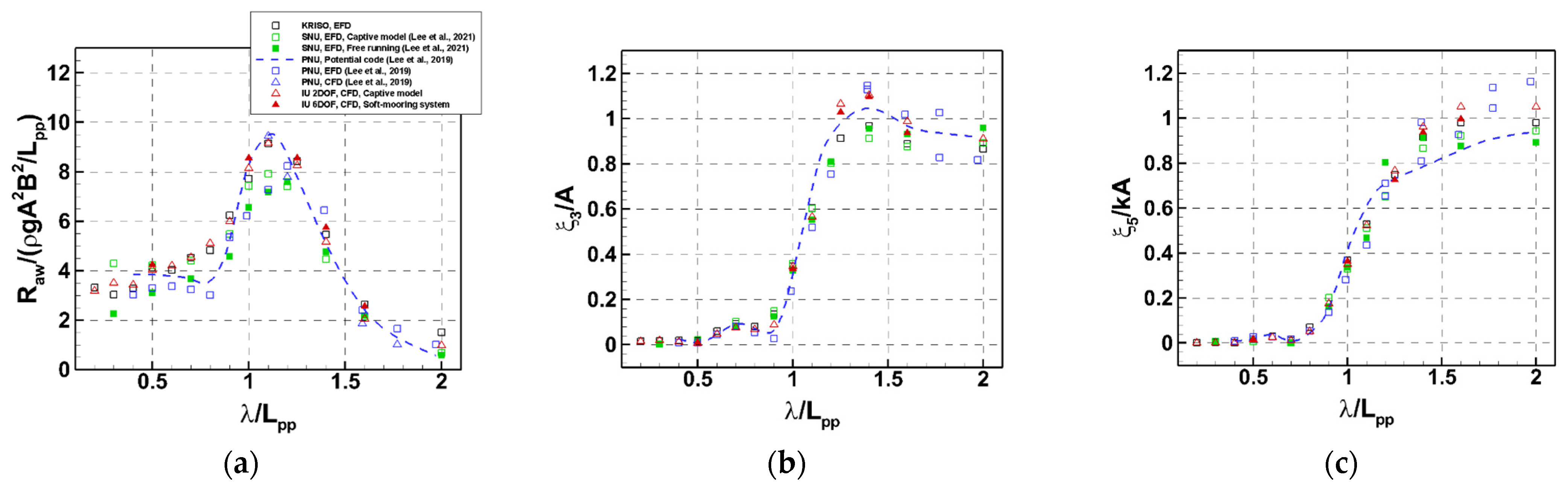
2.2.4. Validation of Added Resistance in Regular Waves
3. Results and Discussion
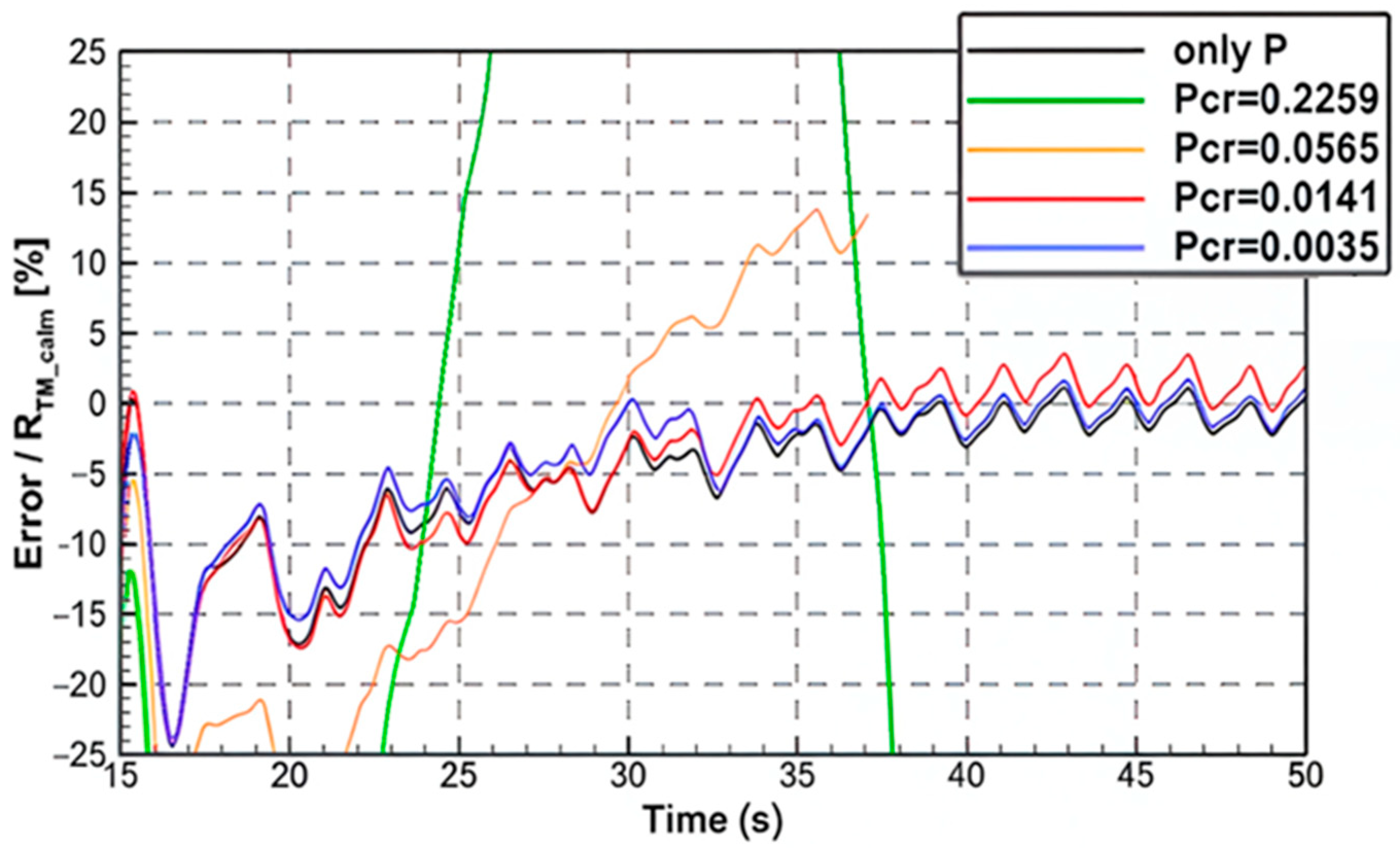
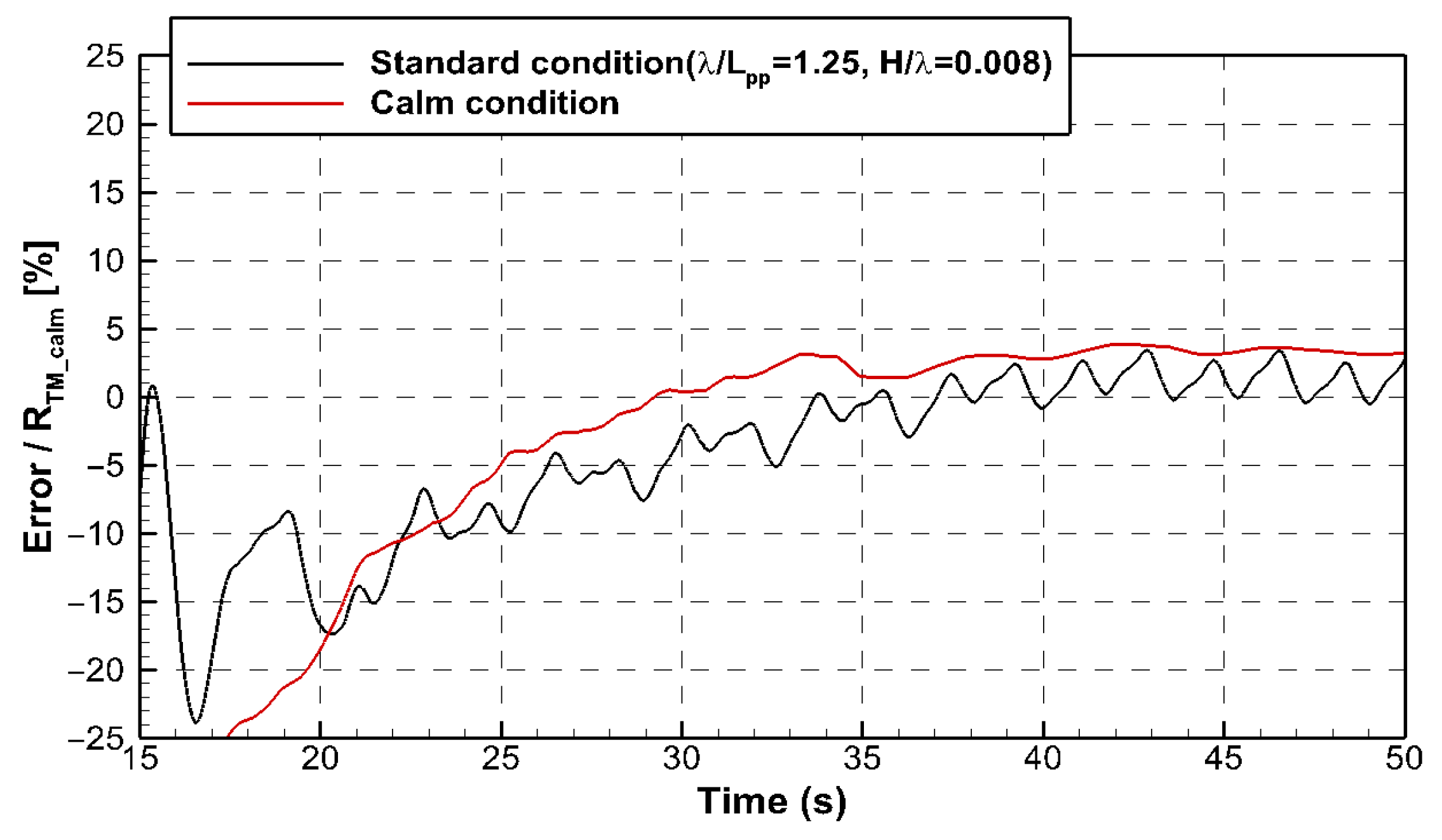
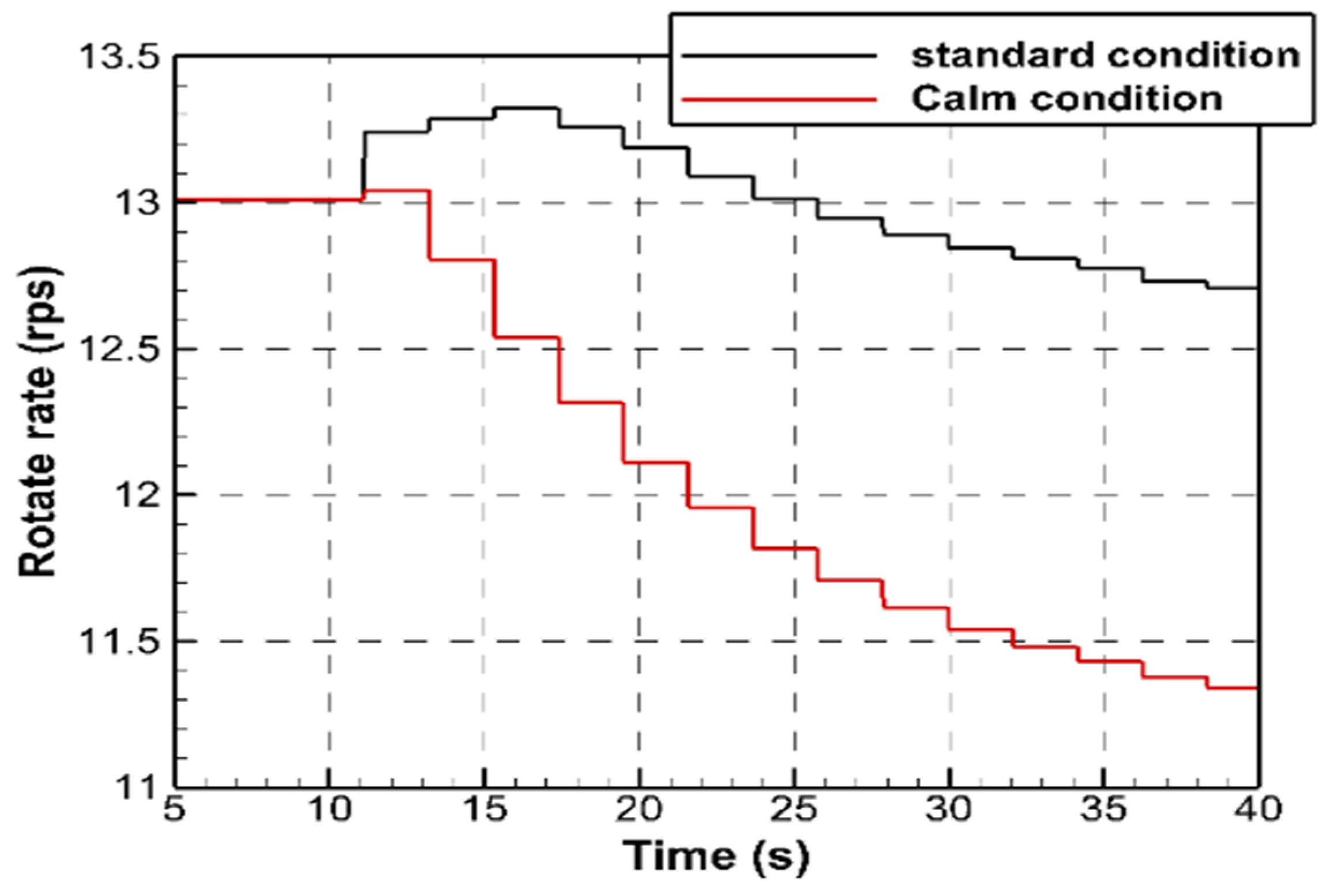
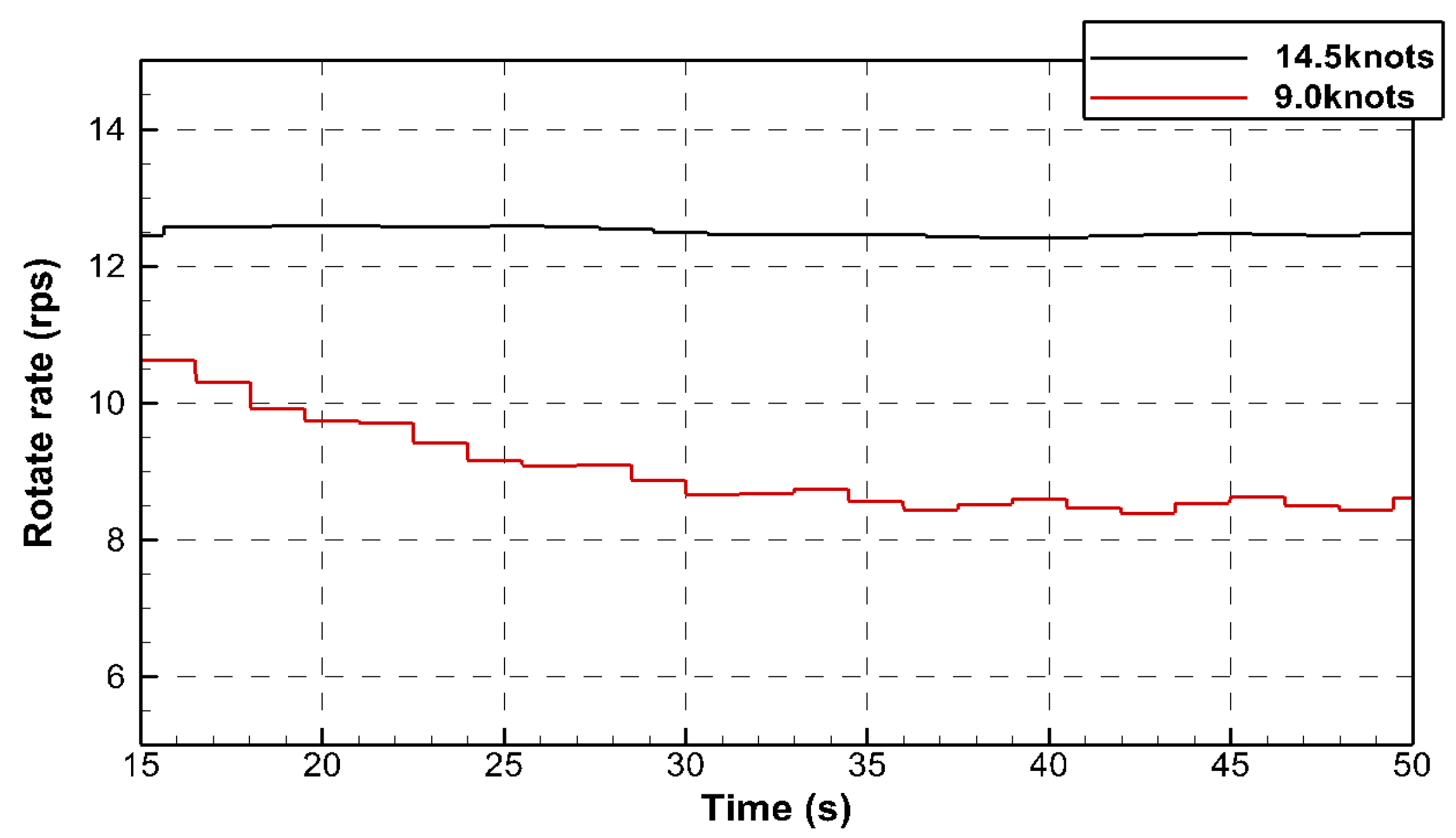
3.1. Derivation of PID Control Coefficients Under Standard Condition
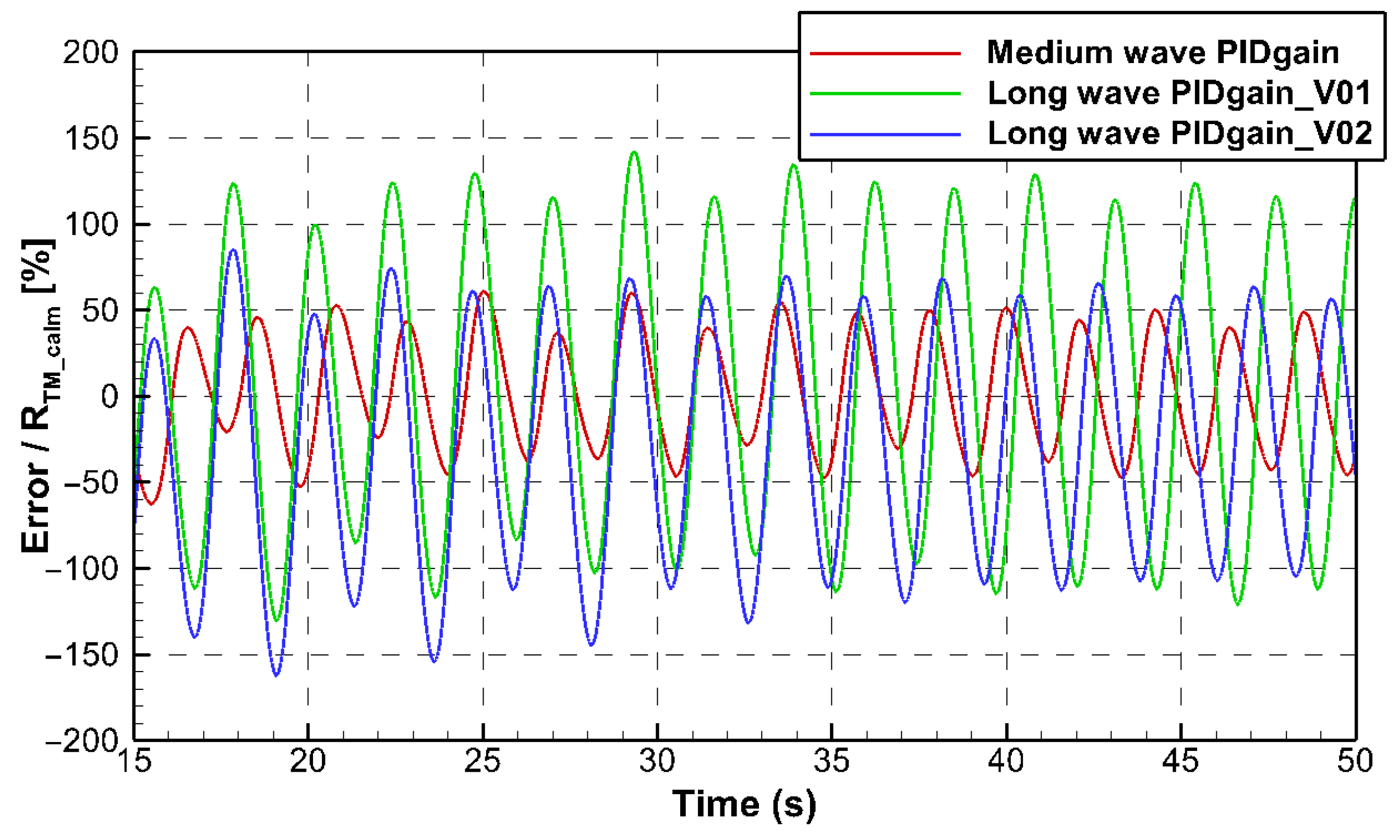
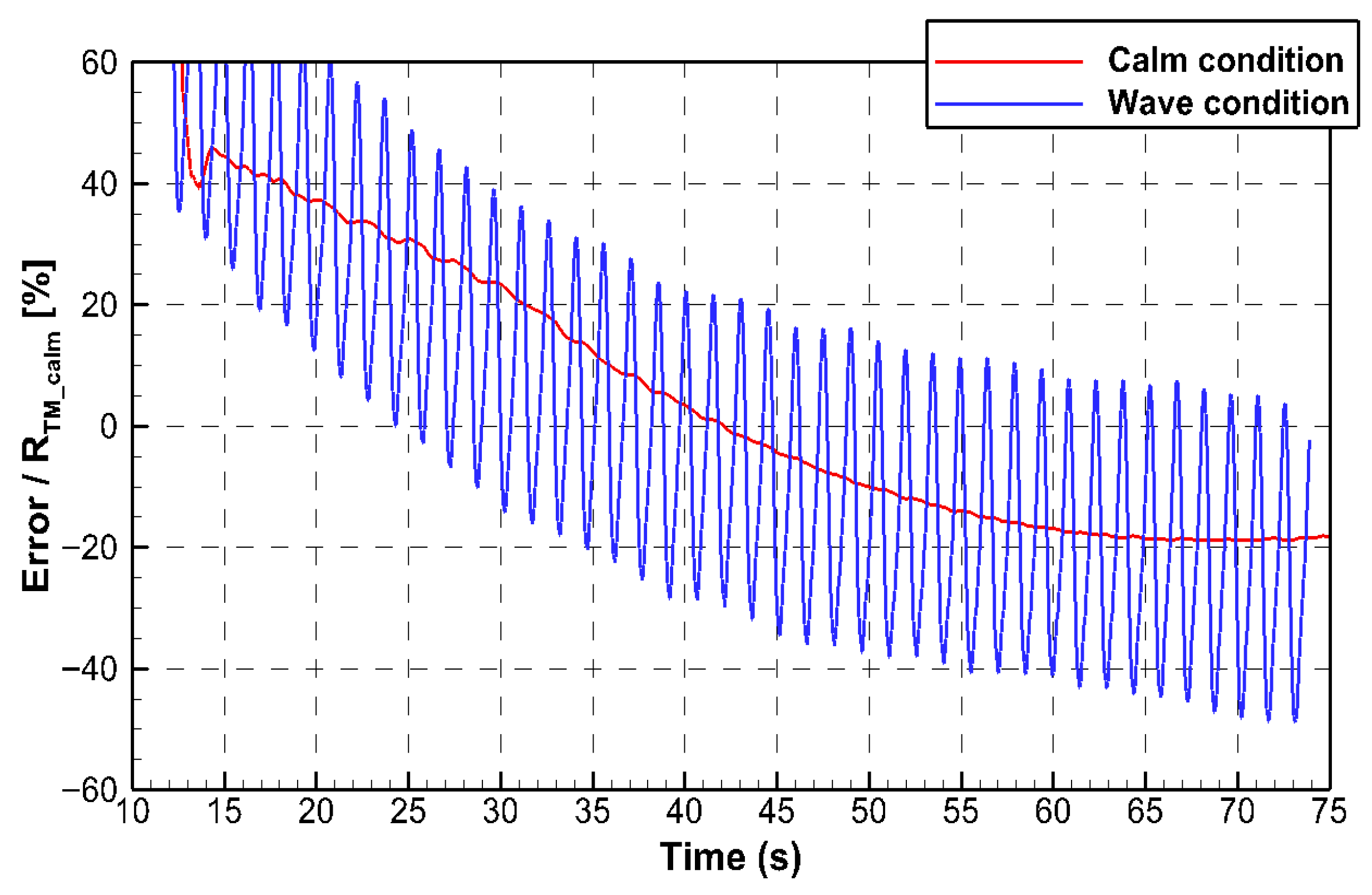
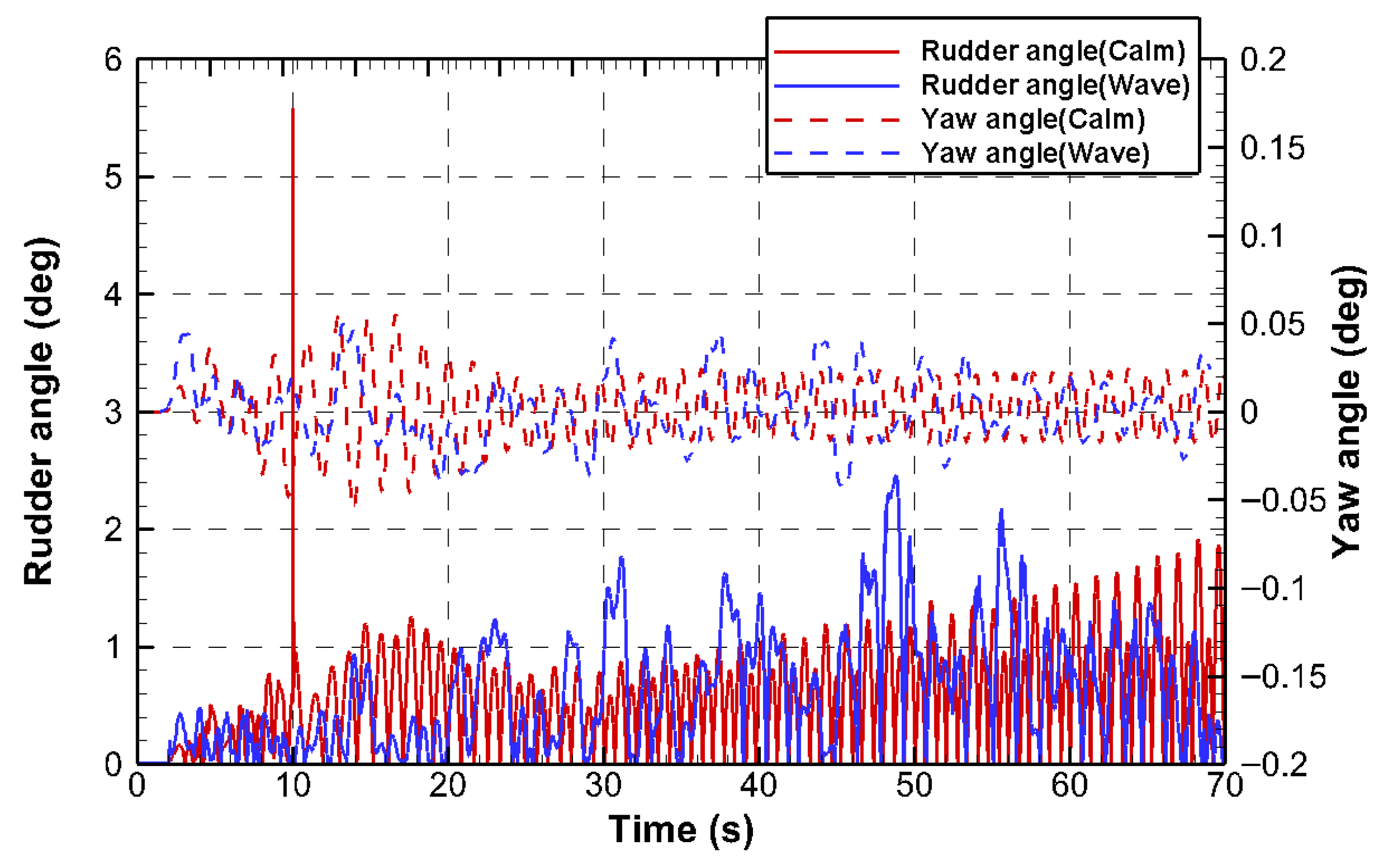
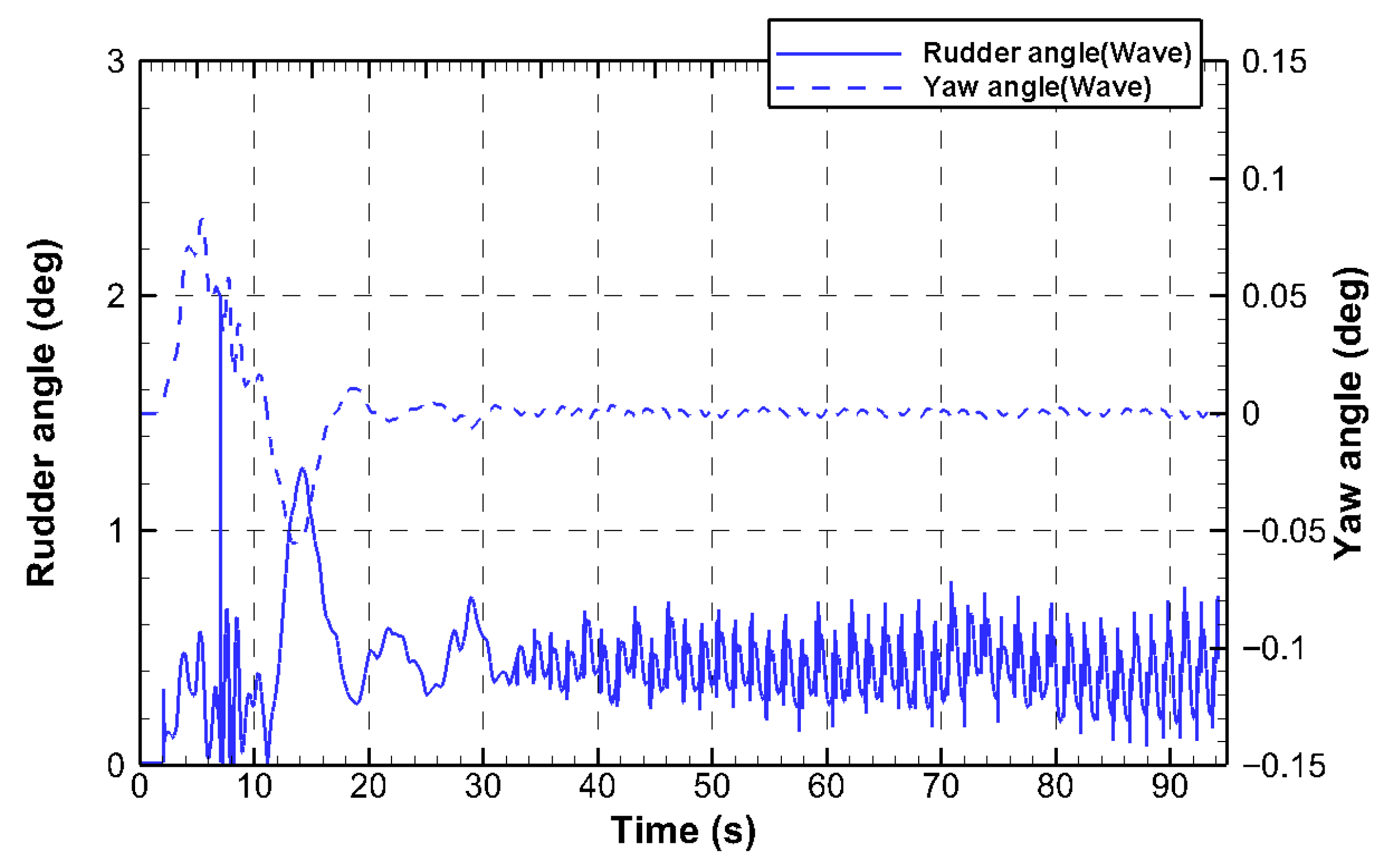
3.2. Wave Condition
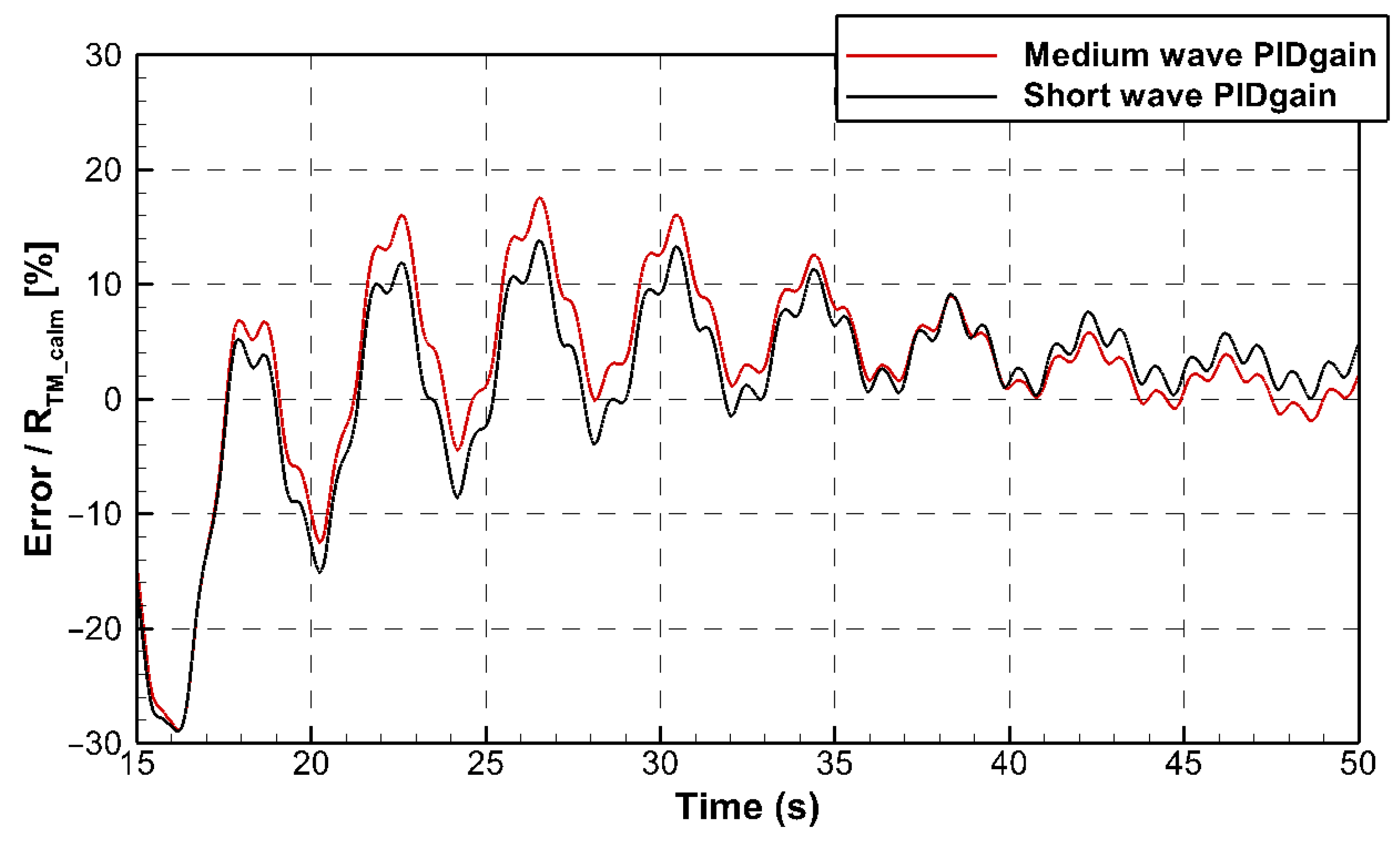
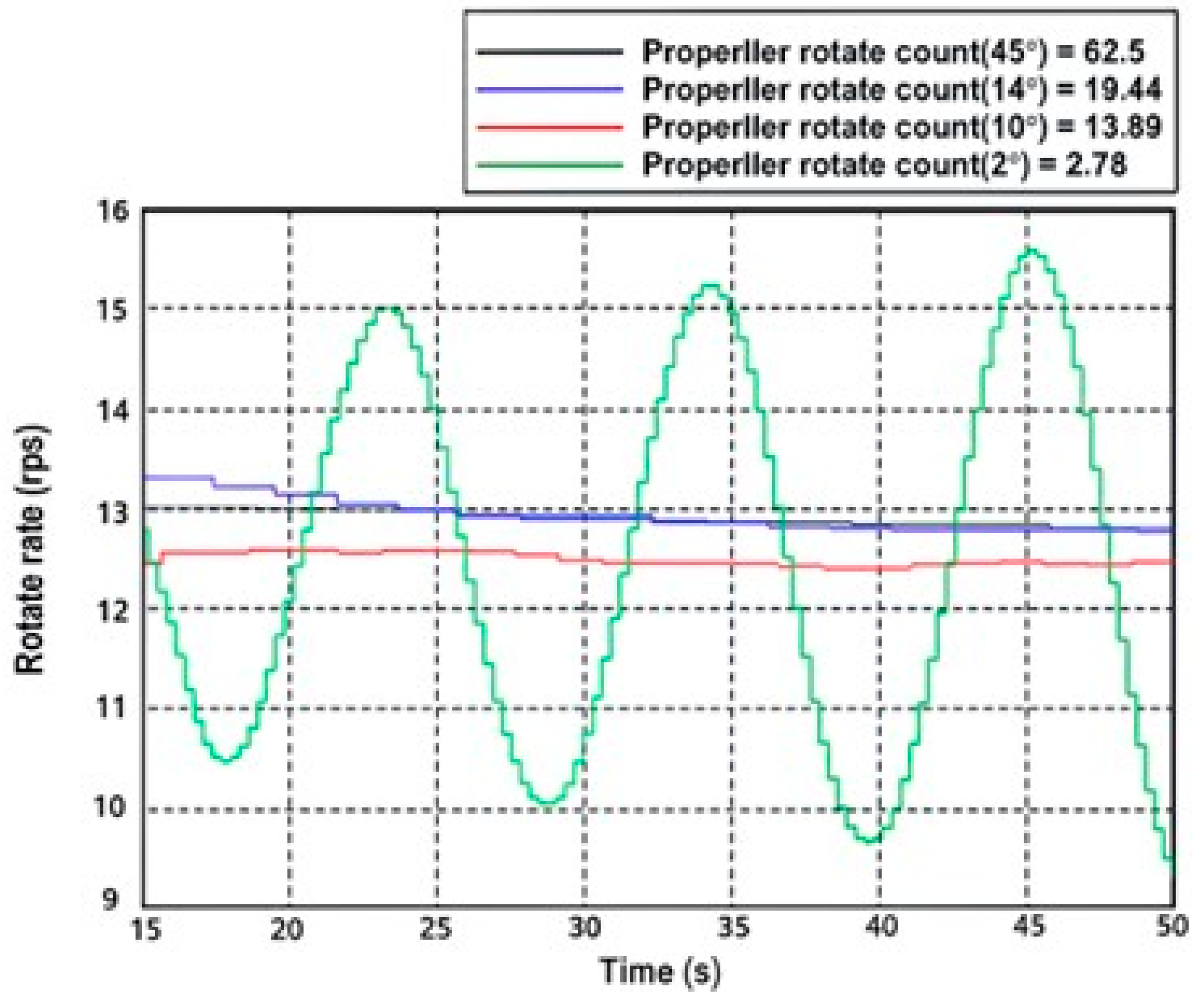
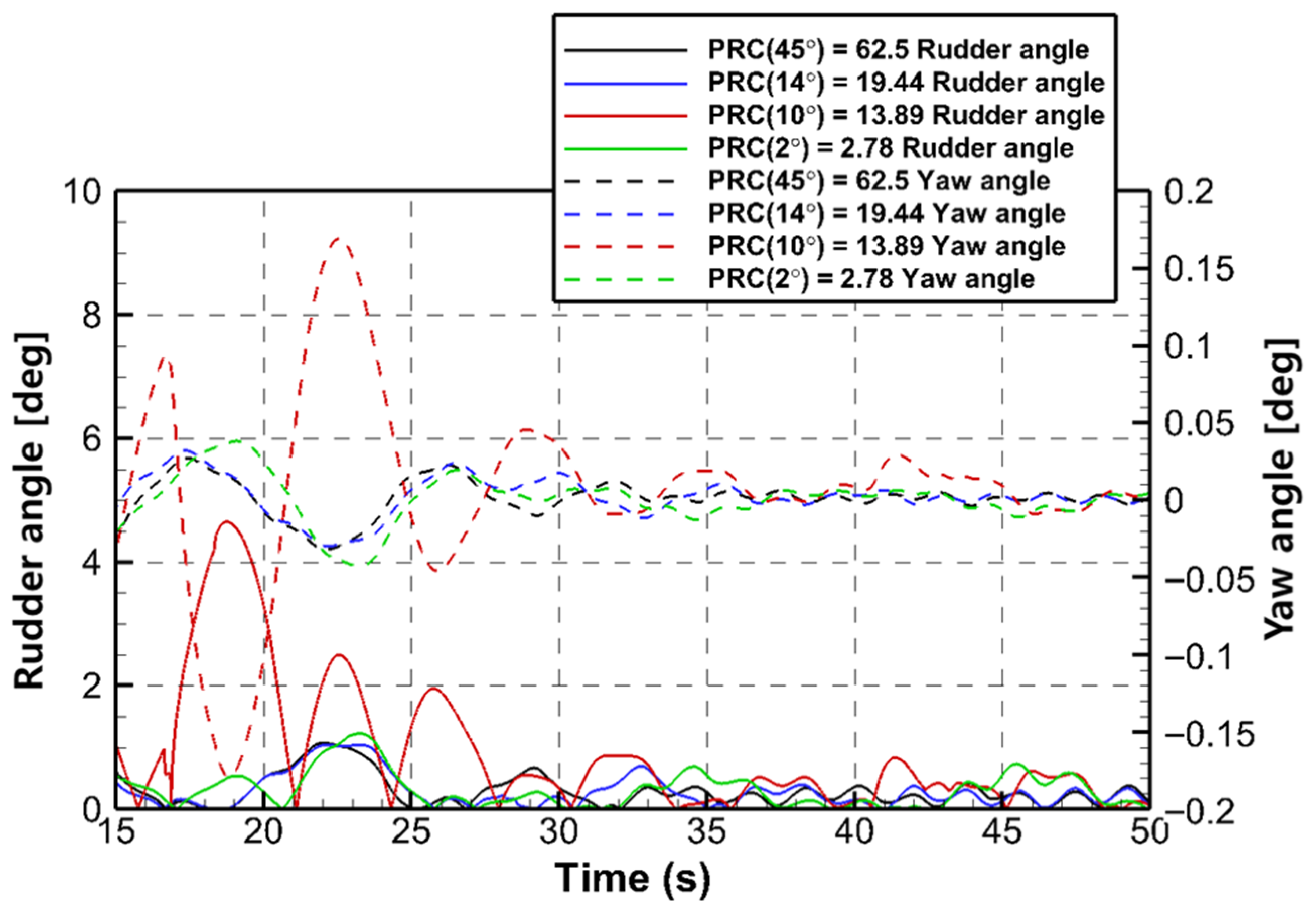
3.3. PID Period Condition
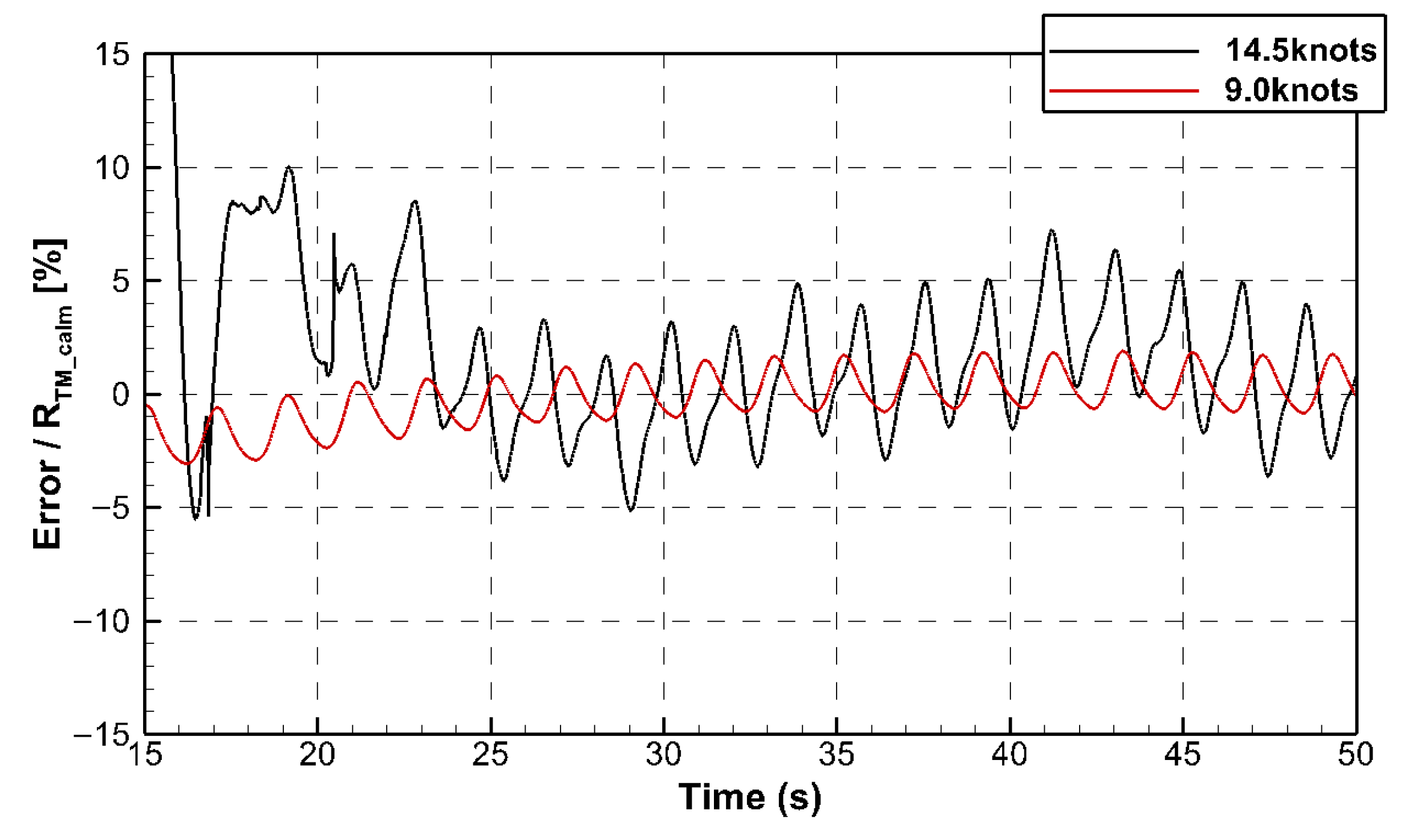
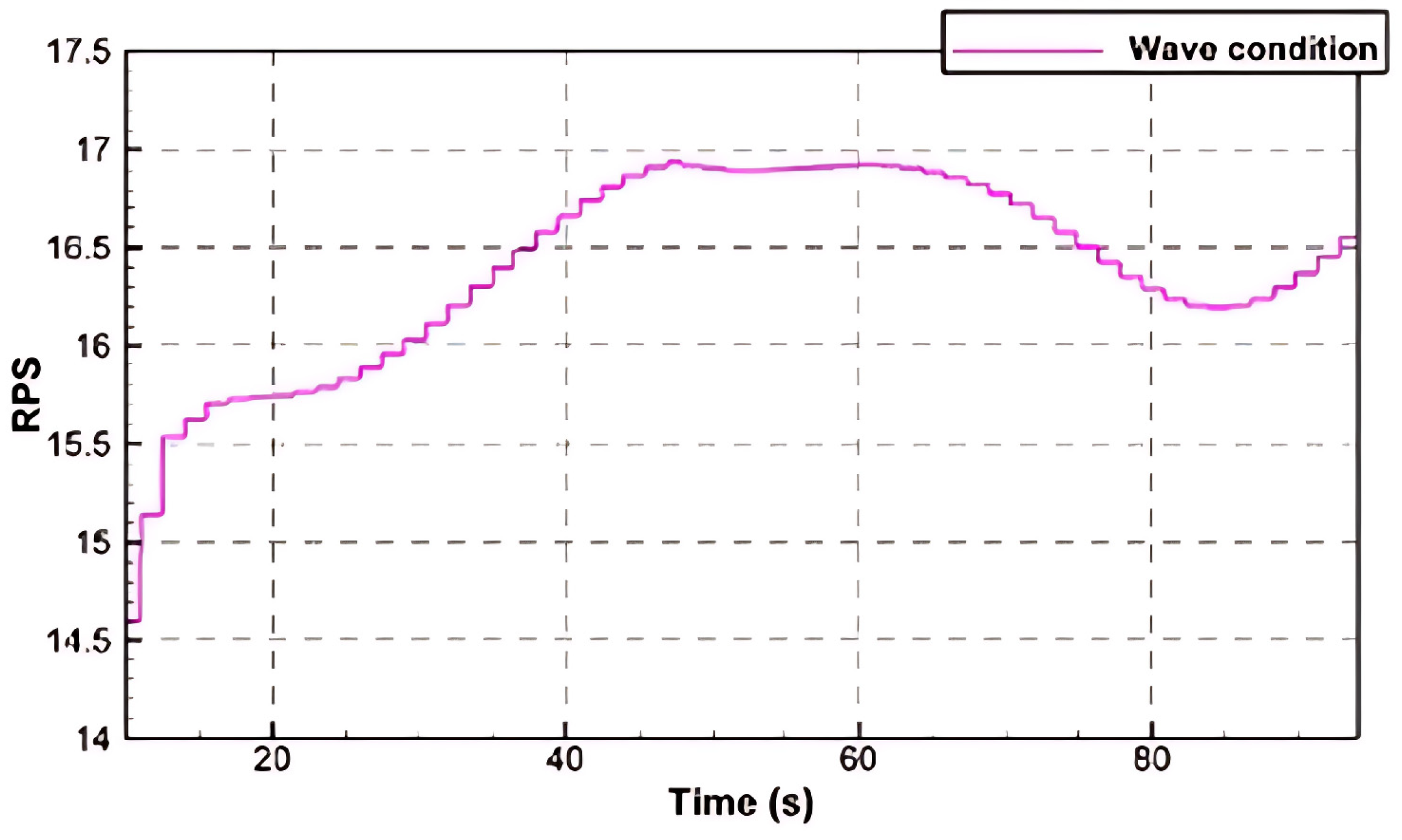
3.4. Ship Speed Condition
3.5. Scale Ratio Condition
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richter, F. The Steep Rise in Global Seaborne Trade. Statista, 16 October 2019. Available online: https://www.statista.com/chart/24527/total-volume-of-global-sea-trade/ (accessed on 7 March 2025).
- Resolution MSC.137(76); Standards for Ship Manoeuvrability. International Maritime Organization (IMO); Maritime Safety Committee: London, UK, 2002.
- SIMMAN 2020 Workshop. Available online: http://simman2020.kr (accessed on 30 March 2025).
- Okuda, R.; Qiu, W.; Yamashita, K.; Arai, M.; Kitada, K.; Ohara, K.; Kinoshita, T.; Fukasawa, T. Study of shallow-water effects on ship maneuverability without external disturbances. J. Mar. Sci. Technol. 2025, 30, 123–135. [Google Scholar] [CrossRef]
- Im, N.; Seo, J.-H. Ship manoeuvring performance experiments using a free running model ship. TransNav 2010, 4, 325–330. [Google Scholar] [CrossRef]
- Eloot, K.; Vantorre, M.; Verwilligen, J. Validation of ship manoeuvring in shallow water through free running model tests. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2015), St. John’s, NL, Canada, 31 May–5 June 2015; ASME: New York, NY, USA, 2015. [Google Scholar]
- Kim, D.; Song, S.; Tezdogan, T. Free Running CFD Simulations to Investigate Ship Manoeuvrability in Waves. Ocean Eng. 2021, 236, 109567. [Google Scholar] [CrossRef]
- Kim, I.-T.; Lee, J.; Kim, D.; Kim, J. Free-running CFD simulations to assess a ship-manoeuvring control method with motion forecast in waves. Ocean Eng. 2023, 275, 114250. [Google Scholar] [CrossRef]
- Woo, S.-C.; Hwang, J.-S. An experimental study on the manoeuvrability of a ship in heeled condition. J. Soc. Nav. Archit. Korea 2019, 56, 273–280. [Google Scholar]
- Yoon, H.-K.; Lee, G.-J.; Son, N.-S.; Yang, Y.-H. Development of free running model ship for evaluation of the performance of anti-rolling devices. J. Korean Soc. Nav. Archit. 2004, 28, 33–39. [Google Scholar]
- Yun, K.; Choi, H.; Kim, D.J. An Experimental Study on the Manoeuvrability of KCS with Different Scale Ratios by Free Running Model Test. J. Soc. Nav. Archit. Korea 2021, 58, 415–423. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, Y.; Kim, B.-S.; Gerhardt, F. Comparative study on analysis methods for added resistance of four ships in head and oblique waves. Ocean Eng. 2021, 236, 109552. [Google Scholar] [CrossRef]
- Paramesh, S.; Rajendran, S. A Unified Seakeeping and Manoeuvring Model with a PID Controller for Path Following of a KVLCC2 Tanker in Regular Waves. Appl. Ocean Res. 2021, 116, 102860. [Google Scholar] [CrossRef]
- Roberts, G.N. Trends in Marine Control Systems. Annu. Rev. Control 2008, 32, 263–269. [Google Scholar] [CrossRef]
- Kwon, Y.; Park, S.; Lee, J. PID Compensating Model for Design of Ship’s Autopilot. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Republic of Korea, 16–19 October 2016; pp. 1337–1339. [Google Scholar]
- Zhang, C.; Wan, L.; Liu, Y. Ship Heading Control Based on Fuzzy PID Control. In Proceedings of the 2019 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; pp. 607–612. [Google Scholar]
- Tomera, M. Fuzzy Self-Tuning PID Controller for a Ship Autopilot. In Proceedings of the 12th International Conference on Marine Navigation and Safety of Sea Transportation (TRANSNAV 2017), Gdynia, Poland, 21–23 June 2017; pp. 93–103. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Cañada, CA, USA, 2006. [Google Scholar]
- Patankar, S.V. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nicholls, B. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Bakica, A.; Gatin, I.; Vukčević, V.; Jasak, H.; Vladimir, N. Accurate assessment of ship-propulsion characteristics using CFD. Ocean Eng. 2019, 175, 149–162. [Google Scholar] [CrossRef]
- Simens. STAR-CCM+ User Guide, Version 16.06; Simens: Munich, Germany, 2021. [Google Scholar]
- Lee, S.H.; Paik, K.-J.; Kim, M.-M.; Hwang, S. A numerical study on estimation of ship performance under actual sea conditions considering added resistance and power of various wave conditions. Ocean. Eng. 2025, 340, 122340. [Google Scholar] [CrossRef]
- Kim, G.-H.; Hwang, S.; Lee, S.-H.; Lee, J.-H.; Hwangbo, J.; Kim, K.-S.; Paik, K.-J. A Numerical Study on the Performance of the 66k DWT Bulk Carrier in Regular and Irregular Waves. J. Mar. Sci. Eng. 2023, 11, 1913. [Google Scholar] [CrossRef]
- Lee, J.-H.; Hwang, S.; Lee, Y.-Y.; Jin, W.-S.; Kim, M.-C. Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions. J. Mar. Sci. Eng. 2025, 13, 595. [Google Scholar] [CrossRef]
- ITTC. 1978 ITTC Performance Prediction Method. ITTC Recommended Procedures and Guidelines 7.5-02-03-01.4. 2018. Available online: https://www.wartsila.com/encyclopedia/term/ittc-performance-prediction-method (accessed on 21 June 2025).
- Lee, C.-M.; Park, S.-C.; Yu, J.-W.; Choi, J.-E.; Lee, I. Effects of Diffraction in Regular Head Waves on Added Resistance and Wake Using CFD. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 736–749. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. Trans. ASME 1942, 64, 759–768. Available online: www.driedger.ca (accessed on 15 June 2025). [CrossRef]




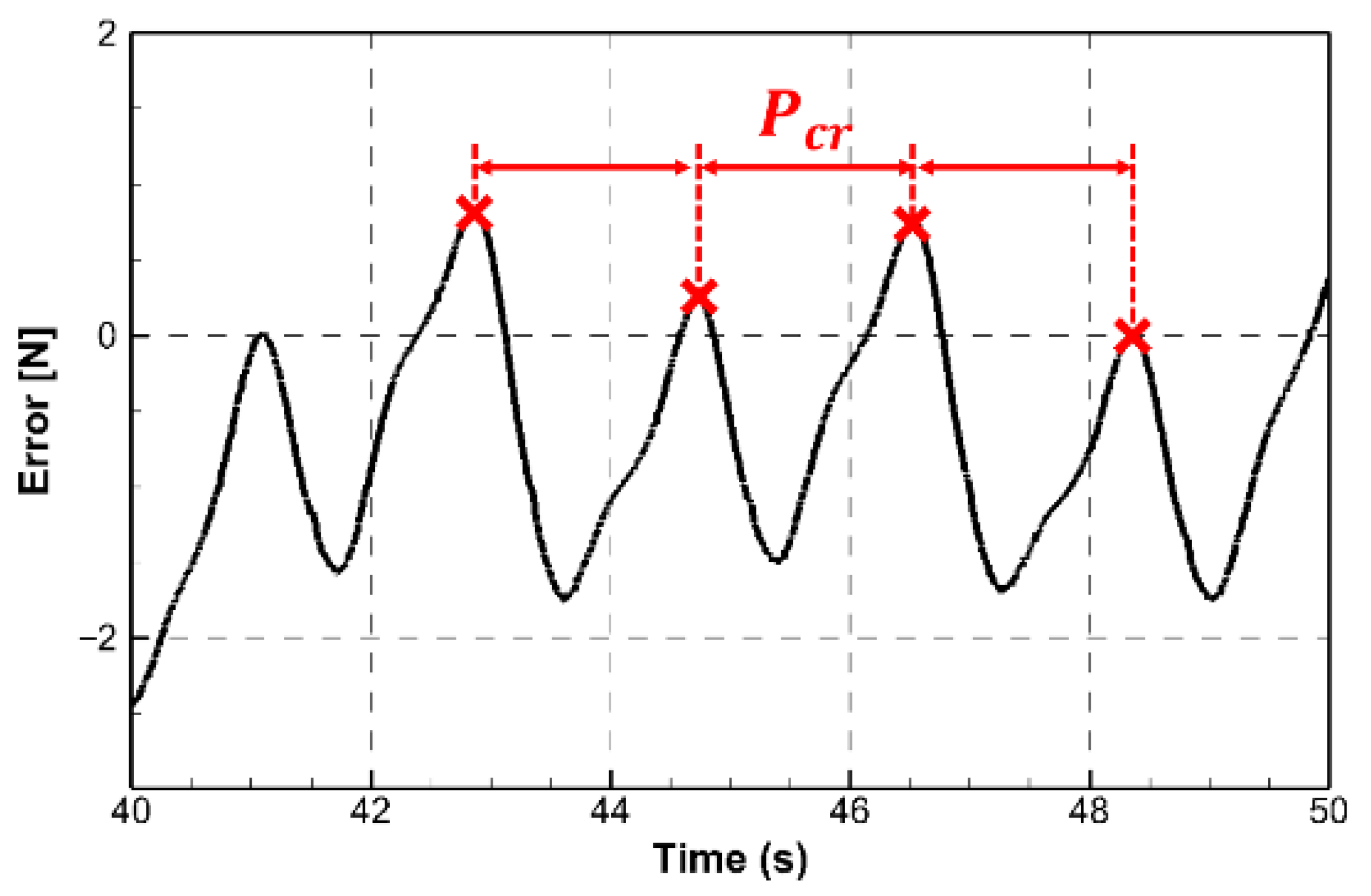
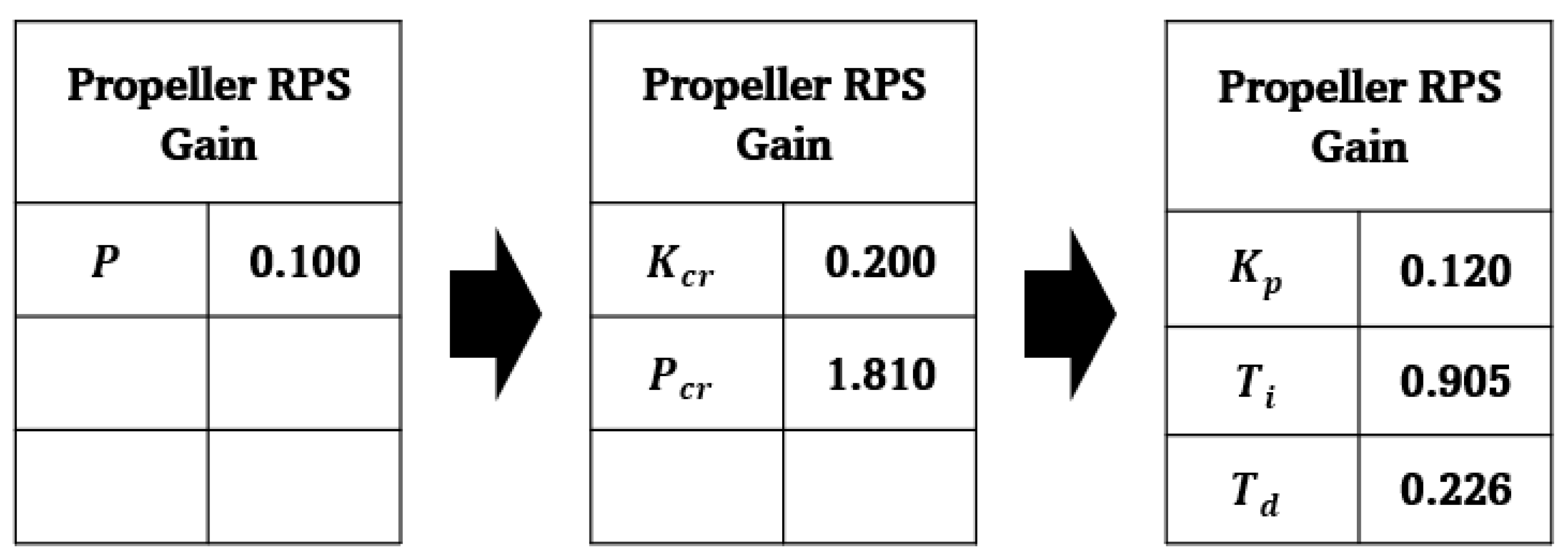
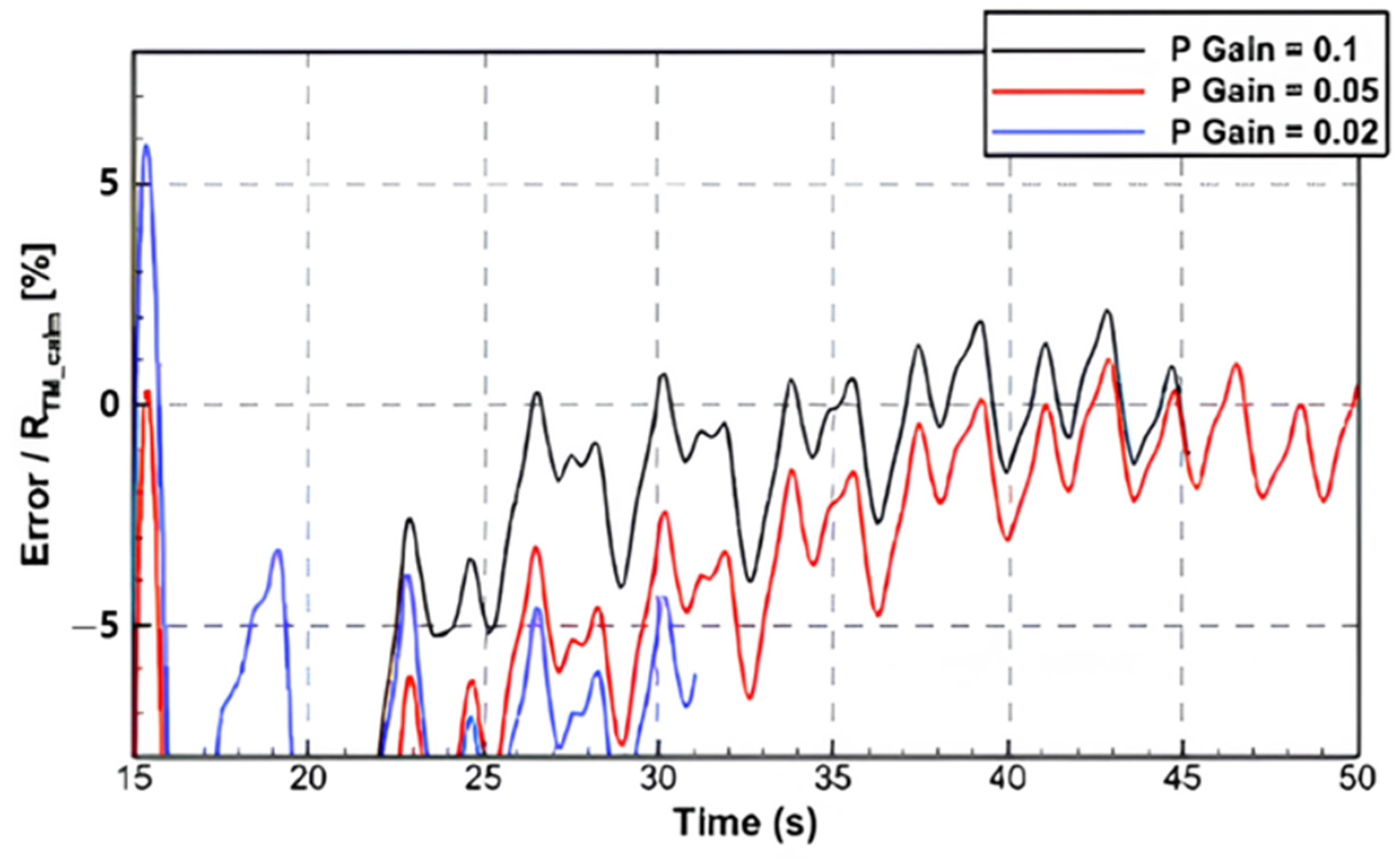
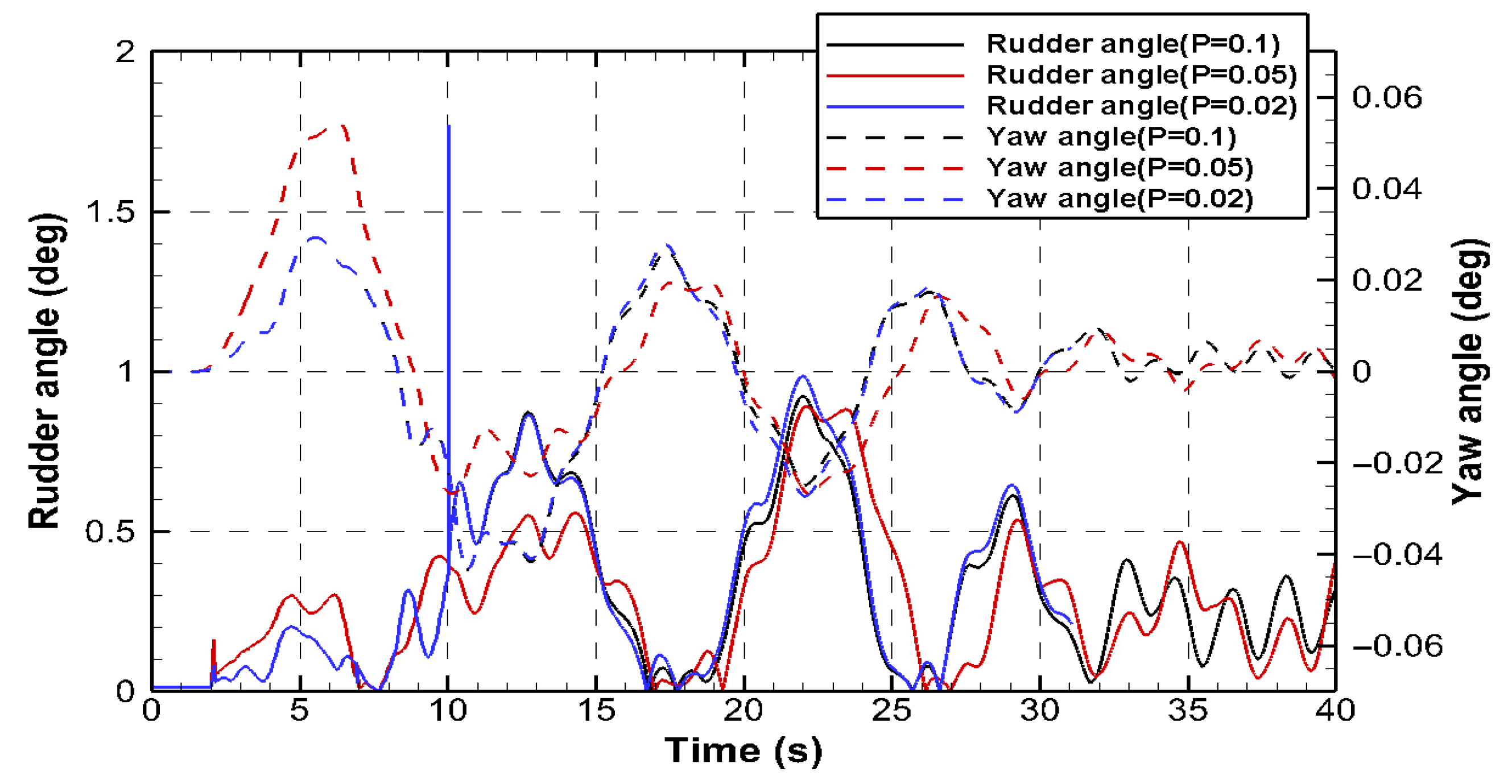







| Particulars | Unit | Full Scale | Model Scale |
|---|---|---|---|
| Scale ratio, | – | 1 | 24 |
| m | 192 | 8 | |
| Breadth, | m | 36 | 1.50 |
| Draft, | m | 11.2 | 0.47 |
| Wetted surface area (w/rudder), | m2 | 9912 | 17.0 |
| Displacement, | m3 | 65,028 | 4.704 |
| – | 0.840 | ||
| – | 14.4 | 0.6 | |
| – | 48 | 2 | |
| Design speed, | knots | 14.5 | – |
| Particulars | Unit | Full Scale | Model Scale |
|---|---|---|---|
| Number of blades, | – | 4 | |
| m | 6 | 0.25 | |
| – | 0.727 | ||
| – | 0.012 | ||
| – | 0.266 | ||
| Direction of rotation | – | Right-handed | |
| KRISO [EFD] | Present [CFD] Model Propeller | Present [CFD] Virtual Disk | |
|---|---|---|---|
| 0.437 | 0.418 (−4.3%) | 0.420 (−3.9%) | |
| 0.352 | 0.346 | ||
| 0.209 | 0.221 (5.7%) | 0.204 (−2.4%) | |
| 1.201 | 1.217 | ||
| 1.012 | 1.061 (4.8%) | 1.006 (−0.6%) | |
| 0.572 | 0.561 | ||
| 0.586 | 0.564 | ||
| 0.704 | 0.686 | ||
| 120.2 | 119.5 | ||
| 5592.38 | 5592.38 | ||
| 7948.65 | 8147.10 |
| 2 DOF | 6 DOF | |
|---|---|---|
| 0.5 | 0 | 0 | |
| 0.45 | 0 | ||
| 0.6 |
| Rudder Gain | Propeller RPS Gain (P Gain = 0.05) | ||
|---|---|---|---|
| 0.02 | 0.060 | ||
| 1.00 | 0.904 | ||
| 5.00 | 0.226 | ||
| Rudder Gain | Propeller RPS Gain (P Gain = 0.0141) | ||
|---|---|---|---|
| 0.02 | 0.0600 | ||
| 1.00 | 0.0071 | ||
| 5.00 | 0.0018 | ||
| Standard Condition ) | Short Wave Condition ) | ||
|---|---|---|---|
| 0.0143 | 0.0078 | ||
| 0.0600 | 0.0600 | ||
| 0.0071 | 0.0039 | ||
| 0.0018 | 0.0010 | ||
| Standard Condition Propeller RPS Gain ) | Long Wave Condition Propeller RPS Gain ) | ||||
|---|---|---|---|---|---|
| Version 1 | Version 2 | ||||
| 0.0143 | 0.0167 | 0.0078 | 0.0021 | ||
| 0.0600 | 0.0600 | 0.0600 | 0.0600 | ||
| 0.0071 | 0.0083 | 0.0039 | 0.0010 | ||
| 0.0018 | 0.0021 | 0.0010 | 0.0003 | ||
| Degree [deg] | Time [s] | Propeller Rotate Count | Fixed Step | PID Period [s] |
|---|---|---|---|---|
| 0.0143 | 0.0078 | 6.726 | ||
| 0.0600 | 0.0600 | 2.093 | ||
| 0.0071 | 0.0039 | 1.495 | ||
| 0.0018 | 0.0010 | 0.299 |
| Scale | ||
|---|---|---|
| INHA [CFD] | 24 ( = 8.00 m) | 3.992 (0.73%) |
| 40.42 ( = 4.75 m) | 4.057 (−0.89%) |
| Rudder Gain | Propeller RPS Gain | ||
|---|---|---|---|
| 0.02000 | 0.28662 | ||
| 1.29775 | 0.00193 | ||
| 3.85281 | 0.00029 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, J.-H.; Kim, H.-S.; Paik, K.-J. Development of a Systematic Method for Tuning PID Control Gains in Free-Running Ship Simulations. J. Mar. Sci. Eng. 2025, 13, 1813. https://doi.org/10.3390/jmse13091813
An J-H, Kim H-S, Paik K-J. Development of a Systematic Method for Tuning PID Control Gains in Free-Running Ship Simulations. Journal of Marine Science and Engineering. 2025; 13(9):1813. https://doi.org/10.3390/jmse13091813
Chicago/Turabian StyleAn, Jae-Hyeon, Hwi-Su Kim, and Kwang-Jun Paik. 2025. "Development of a Systematic Method for Tuning PID Control Gains in Free-Running Ship Simulations" Journal of Marine Science and Engineering 13, no. 9: 1813. https://doi.org/10.3390/jmse13091813
APA StyleAn, J.-H., Kim, H.-S., & Paik, K.-J. (2025). Development of a Systematic Method for Tuning PID Control Gains in Free-Running Ship Simulations. Journal of Marine Science and Engineering, 13(9), 1813. https://doi.org/10.3390/jmse13091813







