Abstract
The spatial separation of port yards and railway hubs, which relies on external truck drayage as a necessary link, hampers the seamless transshipment of sea–rail intermodal containers between ports and railway hubs. This creates challenges in synchronizing yard cranes (YCs) at the port terminal, external trucks (ETs) on the road, and rail-mounted gantry cranes (RMGs) at the railway hub. However, most existing studies focus on equipment scheduling or container transshipment organization under the port–railway integration mode, often overlooking critical time window constraints, such as train schedules and export container delivery deadlines. Therefore, this study investigates the collaborative scheduling of YCs, ETs, and RMGs for synchronized loading and unloading under the port–railway separation mode. A mixed-integer programming (MIP) model is developed to minimize the maximum makespan of all tasks and the empty-load time of ETs, considering practical time window constraints. Given the NP-hard complexity of this problem, an improved genetic algorithm (GA) integrated with a “First Accessible Machinery” rule is designed. Extensive numerical experiments are conducted to validate the correctness of the proposed model and the performance of the solution algorithm. The improved GA demonstrates a 6.08% better solution quality and a 97.94% reduction in computation time compared to Gurobi for small-scale instances. For medium to large-scale instances, it outperforms the adaptive large neighborhood search (ALNS) algorithm by 1.51% in solution quality and reduces computation time by 45.71%. Furthermore, the impacts of objective weights, equipment configuration schemes, port–railway distance, and time window width are analyzed to provide valuable managerial insights for decision-making to improve the overall efficiency of sea–rail intermodal systems.
1. Introduction
The development of economic globalization and the growth of world trade have greatly stimulated the prosperity of container transportation. However, relying solely on one mode of transportation often fails to complete the entire journey of container shipping due to the requirement for door-to-door service, and it cannot provide a cost-effective and low-carbon solution either. As a result, container intermodal transportation, which integrates various modes of transport such as sea, rail, and road, has been proposed to streamline the transportation process, reduce transportation cost, and enhance environmental sustainability []. For international containers, sea–rail intermodal transportation is the most optimal choice, combining the high capacity and low environmental impact of sea transport with the high speed of railway []. In developed countries, such as the Netherlands and the United States, the sea–rail mode typically accounts for 20% to 40% of total port container throughput []. In contrast, the adoption of the sea–rail mode in China began relatively late. According to the Annual Report on China Container Industry and Intermodal Development 2023 issued by China Container Industry Association, after years of infrastructure construction and market operations, the proportion of sea–rail intermodal containers in China has increased from just 1.2% in 2016 to 3.8% in 2023. With the vigorous promotion of multimodal transport development policies in China, the sea–rail mode is poised to experience substantial growth, driven by its untapped potential and the increasing integration of efficient logistics networks.
The significant gap between China and developed countries in container sea–rail intermodal transportation can be attributed to several factors, including the lower coverage of the railway network and the shortage of railcars. The lag in railway infrastructure development has resulted in the frequent neglect of railway access requirements during the planning of container ports, which in turn creates a spatial separation between container ports and railway hubs. Moreover, challenges such as geographical locations, space utilization, and track connection conditions further complicate efforts to achieve seamless integration between existing container ports and railway hubs. According to statistics, among the 37 container ports in China currently connected to railway hubs, only 14 have realized seamless integration between the ports and railways. Therefore, in the short term, the transportation of most sea–rail intermodal containers between ports and railway hubs will still require ET drayage to serve as an indispensable link. While optimizing the dispatching of ETs is essential for reducing drayage costs and improving drayage efficiency, it alone is insufficient to achieve overall systemic improvements. This limitation stems from the fact that the YCs in the port yard, the ETs on the road, and the RMGs in the railway yard constitute a tightly coupled tripartite system, where operational delays at any link induce cascading effects that degrade overall productivity. To address this interdependency, it is imperative to investigate the collaborative scheduling of YC, ET, and RMG under the port–railway separation mode in sea–rail intermodal systems.
Although abundant studies have concentrated on optimizing the collaborative scheduling of multiple pieces of equipment and the organization of container transshipment in seal-rail intermodal terminals, they are all limited to the port–railway integration mode [,,,]. However, the port–railway separation mode, which is the most common mode in China’s sea–rail intermodal systems, has yet to be fully explored. In this mode, the ET experiences longer transfer times than the IT due to greater road distances. The intensified temporal coupling of multiple equipment in such a spatially separated system necessitates dedicated coordination mechanisms. Furthermore, the simultaneous loading and unloading of import and export containers [] and critical time window constraints, such as train time windows [] and export container delivery deadlines [,], are often neglected in the existing literature to simplify the model. In reality, export containers can only be unloaded after the train arrives at the railway hub, and they must be unloaded before the train departs and delivered to the terminal before the vessel’s loading cutoff. Additionally, export containers must be loaded onto the train they are assigned to before its departure. Once the completion time exceeds the time window limit, it may result in the cargo missing the scheduled vessel or train, leading to delayed delivery and incurring demurrage charges. To address the research gap, this study proposes a collaborative scheduling optimization framework for RMGs, ETs, and YCs under the port–railway separation mode, integrating both train time windows and export container delivery deadlines. The key contributions are threefold:
- (1)
- The collaborative scheduling of YCs, ETs, and RMGs under the port–railway separation mode is mathematically modeled as an MIP model, considering synchronized loading and unloading scenarios, as well as practical constraints such as container task time windows and equipment operation sequence requirements. This model further advances the optimization framework for collaborative scheduling of multiple equipment systems;
- (2)
- Methodologically, this study proposes an improved GA with the First Accessible Machinery (FAM) rule to address the complexity and dependencies of the collaborative equipment scheduling problem, which integrates pickup–delivery and flexible hybrid flow shop scheduling;
- (3)
- Extensive computational experiments are conducted to evaluate both the efficacy and computational efficiency of the proposed model and algorithm. Furthermore, sensitivity analysis is performed to examine the impact of key factors and model parameters, providing managerial insights for sea–rail intermodal operators.
The remainder of this paper is organized as follows: Section 2 provides a comprehensive literature review. Section 3 formalizes the problem statement and presents the mathematical formulation. Section 4 details the improved GA framework. Section 5 discusses numerical experiments and analytical results. Section 6 concludes this study and proposes future research directions.
2. Literature Review
Over the past decade, sea–rail intermodal transportation has garnered significant attention due to its impact on container transshipment speed and overall port efficiency. For a comprehensive review, readers are referred to Abu-Aisha et al. []. The literature most relevant to our study includes works that explore the integrated scheduling of multiple equipment and the organization of container transshipment in sea–rail intermodal terminals. While the integrated scheduling of multiple equipment in automated container terminals [] and traditional container terminals [] has been studied, these works are not reviewed here due to their exclusion of railway systems.
2.1. Collaborative Scheduling of Multiple Equipment in Sea–Rail Intermodal Terminals
Most container terminals in developed countries and fewer than half of the container terminals in China have planned railway operation areas within the port or railway hubs adjacent to it. This arrangement is known as the port–railway integration mode, and the terminal is referred to as a sea–rail intermodal terminal. With this mode, the horizontal transportation of transshipment containers can be carried out by in-port vehicles (IVs), such as an internal truck (IT), an automatic guided vehicle (AGV), and an intelligent guided vehicle (IGV), within a relatively short time. The convenience of container transshipment in sea–rail intermodal terminals has significantly promoted the development of container intermodal transportation. For this reason, current research mainly focuses on the collaborative scheduling of multiple equipment in sea–rail intermodal terminals.
There are typically two types of railway layout modes for accessing a port: parallel and vertical access to the terminal. In a parallel railway layout, the tracks are parallel to the terminal shoreline, which is the most common type of layout and also the focus of most studies. Yan et al. [] formulated the integrated scheduling of RMGs, ITs, and reach stackers at the railway handling area in container terminals as an MIP model and solved it using an improved GA, with the aim of minimizing the maximum completion time and the total waiting time of all equipment. They did not consider the schedule of trains and the time window of export container deliveries. Chang et al. [] simultaneously studied the storage space allocation of the railway container yard and the job sequences of RMGs, ITs, and QCs (quay cranes) for outbound containers, aiming at minimizing the makespan of handling operations. To solve this problem, a two-stage heuristic algorithm is proposed by introducing the rolling planning horizon and a new update strategy. In their study, the unloading of outbound containers from trains as well as train schedules were not considered, and they focused on the transshipment between the railway yard and the vessel. Li et al. [] developed an MIP model with the objective of minimizing the makespan for the collaborative scheduling of RMGs and ITs by considering two operation modes, train-yard-vessel and train-vessel, and solved it using a GA. Liu et al. [] presented a multi-objective optimization model to minimize the makespan, equipment waiting time, and unnecessary IT empty travel time for coordinating the scheduling of RMGs, ITs, and YCs in a sea–rail intermodal terminal and designed an adaptive large neighborhood search (ALNS) algorithm to solve it. Unlike previous studies, Li et al. [] presented a new collaborative scheduling model of QCs, AGVs, YCs, and RMGs targeting the minimization of the makespan, the total waiting time of AGVs, and the total energy consumption of handling cranes by considering a flexible transshipment route strategy that allows containers to select the most appropriate transshipment mode during operation. To solve their problem, they designed an INSGA-II. Xia et al. [] proposed a collaborative scheduling approach for RMGs, ITs, and YCs, considering both inter-equipment interferences and the workload balance of RMGs. They formulated the problem as a binary integer programming model intended to minimize the operation time of RMGs based on a space-time-state network and developed a Lagrangian relaxation-based heuristic to efficiently solve the reformulated model.
Although many sea–rail intermodal studies have been conducted on the integrated scheduling of multiple equipment under the parallel railway layout, only two studies have focused on the traditional vertical layout, including those by Yang et al. [] and Yang et al. []. Yang et al. [] proposed a collaborative scheduling model for the RMGs and AGVs with the goal of minimizing the energy consumption of all equipment, which was solved using a two-layer scheduling rule and a self-adaptive chaotic GA. The model was applied to a scenario involving a vertical railway accessing a port under the mixed operational mode of “train-vessel” and “train-yard-vessel”. Expanding upon their previous work, Yang et al. [] studied the cooperative scheduling of RMGs, AGVs, and YCs under the loading and unloading mode. They developed an MIP model in order to minimize the maximum completion time and the operational energy consumption of the RMGs and AGVs. With the emergence of the U-shaped layout in container terminals, the collaborative scheduling for this layout from the perspective of sea–rail intermodality has also been investigated. Li et al. [] established a hybrid integer programming model to collaboratively schedule RMGs, IGVs, and YCs for container transshipment between a U-shaped automated terminal yard and a railway yard, with the objective of minimizing container transit times. They applied a solution framework based on an alternating direction method of multipliers to tackle the non-crossing constraints and safe distance constraints.
2.2. Organization of Container Transshipment in Sea–Rail Intermodal Terminals
The organization of container transshipment in the sea–rail intermodal system involves the loading/unloading of container trains, handling operations of the storage yard, and the loading and unloading of container vessels. This category of research primarily focuses on the transshipment quantity of containers between different trains, storage yards, and vessels, while it does not consider the detailed operational handling time and operational sequence of various equipment. Zhao et al. [] proposed an inbound container distribution model that considers temporal and resource constraints, with the goal of minimizing the total time import containers spend in the coordination area of the sea–rail intermodal terminal, and presented an effective two-point crossover GA to solve it. Hu et al. [] integrated the inter-terminal transportation of containers with the rail freight formulation and transportation process toward the hinterland to formulate an integer linear programming model, with the objective of minimizing the operating costs of the entire logistics system. Yan et al. [] extended Zhao et al. [] by incorporating the train schedule template decision into the inbound container transshipment operation problem. The schedules of trains were constrained to coordinate with the unloading time of vessels. The problem was formulated as an MIP model and a tailored rolling horizon approach was proposed to solve it. In contrast, Zhao et al. [] aimed to improve the transshipment efficiency of outbound intermodal containers among vessels, storage yards, and trains. They proposed an improved GA and validated the model and algorithm via simulation. To make the model more applicable to real-life scenarios, Yan et al. [] further investigated the bidirectional transshipment operations of import and export containers between vessels and trains by simultaneously determining the train schedule plan and the container transshipment plan among vessels, storage yards, and trains. An MIP model was developed to minimize the total cost by considering the service time window of trains.
In order to smooth container transshipment organization, some studies also concentrated on the space allocation of storage yards or the layout of sea–rail intermodal terminals. Chang and Zhu [] designed a two-stage model for the storage space allocation problem in the railway operation area, with the objective of balancing inbound container distribution and minimizing overlapping amounts. To solve this problem, a simulated annealing algorithm was introduced for stage 1, and a rolling-horizon-based heuristic was designed for stage 2. Abu Aisha et al. [] proposed an innovative layout for a sea–rail intermodal terminal to reduce the operation cost and accelerate container flows and established a mathematical model to validate its performance. In order to enhance the handling efficiency of double-stack trains, Zhao et al. [] proposed a new synchronous handling technology that focused on the design of an AGV with a loading/unloading function and a new articulated flatcar while also optimizing the layout of the terminal yard. Based on the concept of sharing yard, Liu et al. [] formulated a flexible YC scheduling model aimed at minimizing the mutual interference in the combined operations of railway and road containers, by considering time windows related to train schedule and uncertainty of ET arrivals.
2.3. Research Overview
To enhance the clarity of our presentation and better position our contribution within the existing body of research, Table 1 provides a comprehensive synthesis of the key characteristics identified in sea–rail intermodal studies addressing collaborative scheduling of multiple equipment.

Table 1.
Comparison of sea–rail intermodal collaborative scheduling problems.
Through a thorough review of the literature, significant progress has been made in the collaborative scheduling of various equipment and the organization of container transshipment in sea–rail intermodal terminals, providing valuable references for this study. However, the following limitations remain:
- (1)
- Existing studies on sea–rail intermodal collaborative scheduling are all limited to the port–railway integration mode, often neglecting time window constraints such as train arrival/departure schedules and the latest vessel loading deadlines for export containers. Additionally, only a few studies have incorporated both loading and unloading processes into a single mathematical model;
- (2)
- The port–railway separation mode in sea–rail intermodal systems has not yet been explored. As is well-known, the long distances in this mode lead to extended travel times for external trucks (ETs), introducing uncertainties in collaborative scheduling and complicating equipment coordination compared to the port–railway integration mode;
- (3)
- Studies on container transshipment in sea–rail intermodal systems have mainly focused on transshipment volumes between trains, storage yards, and vessels, without in-depth consideration of specific operational handling times and sequences across equipment.
To address these issues, this paper investigates the collaborative scheduling of RMGs, ETs, and YCs in the sea–rail intermodal system under the port–railway separation mode, incorporating both loading and unloading processes and practical time constraints (i.e., train schedules and export container deadlines). An MIP model is established to minimize both the maximum makespan and the total ET empty-load time, and an improved GA based on the “First Accessible Machinery” rule is designed to solve it. After verifying the correctness of the proposed MIP model and the effectiveness of the GA, this paper explores the influence of objective weights, equipment configurations, port–railway distances, and train time windows, aiming to provide managerial insights for decision-making to improve the overall efficiency of multiple equipment collaborative scheduling under the port–railway separation mode.
3. Problem Description and Formulations
In this section, we provide a detailed explanation of the problem discussed in this paper, followed by a mathematical model.
3.1. Problem Description
The collaborative scheduling problem presented in this study is defined as follows: a sea–rail intermodal system in which the port terminal is geographically separated from the railway hub (as shown in Figure 1), coupled with the lack of direct rail connectivity, necessitates container transshipment between YCs in the port yard and RMGs in the railway hub via short-distance haulage by ETs (referred to as container drayage). The temporal interdependencies among RMGs, ETs, and YCs create nonlinear propagation effects, and thus, any scheduling deviation might lead to a significant decline in overall efficiency. Therefore, this paper focuses on the collaborative scheduling problem of RMGs, ETs, and YCs for the synchronized loading and unloading operations of import containers and export containers. The objective of the problem is to determine the task assignments and operation sequences for relevant equipment, while minimizing the total operating time of all tasks and total empty-load time of dispatched trucks. The planning horizon is typically one day.
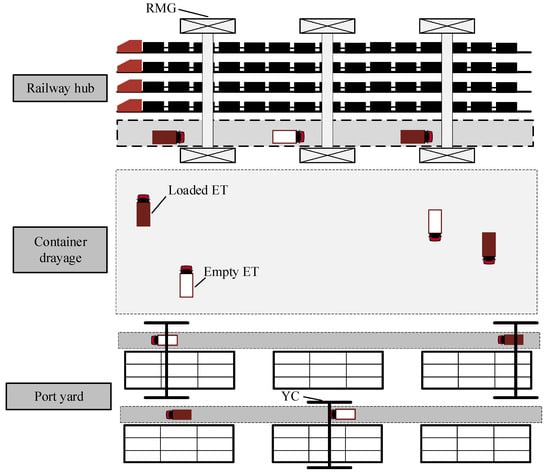
Figure 1.
The layout of railway hubs and container yards in the sea–rail intermodal system with port–railway separation.
The essence of this paper is to complete all container transshipment tasks at the earliest possible time within defined time windows using a set of RMGs, ETs, and YCs. A task may refer to the unloading of an export container from the train to the port yard or the loading of an import container onto the train from the port yard. For export containers, upon arrival at the railway operation zone via inbound trains, they need to be unloaded by RMGs before the train departs, and then transferred onto assigned ETs. Next, they will be transported to designated positions at the port yard where YCs stack them at specified slots before the latest allowable vessel loading time. The process for import containers is exactly the opposite. Due to the spatial separation between the port terminal and railway hub, the extended travel distance results in longer travel times for containers transported between them via ETs. This creates a significant challenge in efficiently dispatching ETs to minimize the waiting times of RMGs and YCs, thereby improving the continuity of operations, all while being constrained by the limited number of available ETs. While the strategic pairing of import and export container tasks can somewhat enhance ET efficiency, the coupling between ETs and the operations of RMGs and YCs necessitates the simultaneous consideration of their scheduling within the model. This complexity, along with the increased computational requirements, not only escalates the difficulty of the modeling process but also places more stringent demands on solving the problem.
3.2. Mathematical Formulation
3.2.1. Assumptions
To streamline the problem under study, we make the following assumptions, adapted from Yan et al. [] and Li et al. [], which address a similar problem:
- (1)
- Within the decision-making horizon, YCs exclusively perform container retrieval and stacking for ET loading and unloading purposes. Container relocation operations and housekeeping activities within the yard are excluded from consideration;
- (2)
- The arrival and departure times of trains are known in advance, along with the latest vessel loading deadlines for export containers. Moreover, precise wagon positions for railcar loading and yard slot locations for container stacking are known a priori;
- (3)
- All equipment operates at constant speeds, excluding acceleration or deceleration during startup or turning, as well as additional travel time due to road congestion or other factors. Each type of equipment is capable of handling a single 40 ft container per operation, with identical container sizes required for all transport tasks;
- (4)
- Containers are loaded on trains exclusively in single-layer configurations.
3.2.2. Notations and Parameters
| Set of RMGs, | |
| Set of YCs, | |
| Set of ETs, | |
| Set of import containers | |
| Set of export containers | |
| Set of all containers, | |
| Index of virtual initial tasks | |
| Index of virtual terminal tasks | |
| Index of containers, | |
| Travel time of RMG between the railside handling positions of container and container | |
| Travel time of YC moving between the yard slot positions of container and container | |
| Travel time of ET between the railside handling position (or yard slot position) of container and the yard slot position (or railside handling position) of container , if both containers and are import (or export) containers; otherwise, travel time of ET between the railside handling positions (or yard slot positions) of containers and , if container is an import (or export) container and container is an export (or import) container | |
| Handling time of RMG for container | |
| Handling time of YC for container | |
| Travel time of ET transporting container between the yard storage position and the railside handling position | |
| Arrival time of train carrying container | |
| Departure time of train carrying container | |
| The latest permitted loading time of vessel for container | |
| The minimum operational time interval between YCs operation in the same area | |
| A binary parameter which takes value 1 if container is an import container, and 0 otherwise | |
| A binary parameter which takes value 1 if containers and are loaded/unloaded within the same operational area of the yard, and 0 otherwise | |
| A binary parameter which takes value 1 if containers and are loaded/unloaded in the same wagon of the same train, and 0 otherwise | |
| The objective weight coefficient assigned to the makespan | |
| The objective weight coefficient assigned to the empty-load time of ETs | |
| A large positive integer |
3.2.3. Decision Variables
| A binary variable that equals 1 if containers and are both assigned to RMG , and 0 otherwise | |
| A binary variable that equals 1 if containers and are both assigned to YC , and 0 otherwise | |
| A binary variable that equals 1 if containers and are both assigned to ET , and 0 otherwise | |
| A binary variable that equals 1 if container is handled by RMG , and 0 otherwise | |
| A binary variable that equals 1 if container is handled by YC , and 0 otherwise | |
| A binary variable that equals 1 if container is handled by the truck , and 0 otherwise | |
| The time when the container starts to be handled | |
| The time when the handling of container finishes | |
| The time when RMG starts handling container | |
| The time when YC starts handling container | |
| The time when ET starts handling container | |
| The time when RMG finishes handling container | |
| The time when YC finishes handling container | |
| The time when ET finishes handling container | |
| The time when RMG waits for ET at the railside handling position of container | |
| The time when YC waits for ET at the yard slot position of container | |
| The time when ET arrives at the yard slot position of container , assigned to YC | |
| The time when ET arrives at the railside handling position of container , assigned to RMG |
3.2.4. Formulation
The total objective of the model is given in Function (1), which aims to minimize the maximum makespan of all tasks () and the total empty-load time of ETs (). Note that the total empty-load time of ETs consists of empty travel time between two consecutive tasks and waiting time at the next task position until operation begins. Constraints (4)–(9) ensure that each RMG, YC, and ET can have only one predecessor or successor task for the current task. Also, each container task must be performed by only one RMG, one ET, and one YC. Constraints (10) and (11) state that if containers and are adjacent predecessor and successor tasks in the operational sequence of RMG , both tasks must be exclusively handled by the same RMG . Constraints (12) and (13) specify that if containers and are adjacent predecessor and successor tasks in the operational sequence of YC , both tasks must be exclusively handled by the same YC. Constraints (14) and (15) require that if containers and are adjacent predecessor and successor tasks in the operational sequence of ET , both tasks must be exclusively handled by the same ET. Constraint (16)~(18) specifies that if containers and are predecessor–successor tasks in the operational sequence of a RMG, a YC or an ET, they can only be performed in one specific sequence. Constraints (19) and (20) specify the start time of operations for YC and RMG for container . Constraint (21) specifies the time when the truck returns to the destination. Constraints (22) and (23) state that for import containers, the start time of the container handling operation matches the start time of YC, and the finish time matches the finish time of RMG, while for export containers, the start time of the container handling operation matches the start time of RMG, and the finish time matches the finish time of YC. Constraints (24) and (25) represent the waiting time of YC and RMG at the container’s handling position until the corresponding ET arrives. Constraints (26) and (27), respectively, represent the time at which the ET arrives at the corresponding yard storage position and railside handling position when container is either an import or export container. Constraints (28)~(30), respectively, specify the completion time of container handling operation by YC , RMG , and ET . Constraints (31) and (32) governed the operation time sequence that should be followed when the RMG, YC, and ET handle the same container . Constraint (33) indicates that when the container truck handles containers and in sequence, if container is an import container, the start time of ET operations for container should be later than the start time of RMG operation for container , while if container is an export container, the start time of ET operations for container should be later than the start time of YC operation for container . Constraint (34) regulates that if container is an export container and container is an import container, and both are in the same train wagon, container must be unloaded first, followed by the loading of container . Constraint (35) states that when containers and are in the same yard area, the time gap between the start of their corresponding YC operations should meet the minimum required time interval. Constraints (36) and (37) mandate that the finish time of import containers and the start time of export containers should be within the arrival and departure time window of the train carrying them. Constraint (38) requires that the finish time of export containers must be after the train’s arrival at the railway hub and before the latest permitted loading time of the vessel.
4. Solution Algorithm
The model described in this study involves three main operations: train loading/unloading in the railway hub, container transportation on the road, and retrieval and storage of containers at the port yard. Import and export containers follow the reverse sequence in their workflow. Additionally, in the container transportation and handling operations, each task can be performed by multiple types of equipment, while the container transportation is essentially a pickup and delivery problem. Therefore, this problem shares the characteristics of both flexible hybrid flow shop scheduling (FHFS) [] and pickup and delivery problems with time windows (PDPTW) [], both of which are NP-hard, making the problem itself NP-hard. The proposed MIP model can be solved to optimality using commercial solvers, such as Gurobi, but only for small-scale instances. To overcome this challenge, we propose an improved GA to solve this problem quickly and effectively.
The GA, originally introduced by Holland [], has become widely used for solving complex optimization problems [,]. The main advantage of GA is its ability to carry out parallel searches in the solution space through population-based evaluation, selection, crossover, and mutation. To improve the algorithm’s performance and address deadlock issues in FHFS, we propose an enhanced GA that includes a First Accessible Machinery (FAM) rule, which is specifically tailored for the problem at hand. The detailed steps of the algorithm are shown in Figure 2.
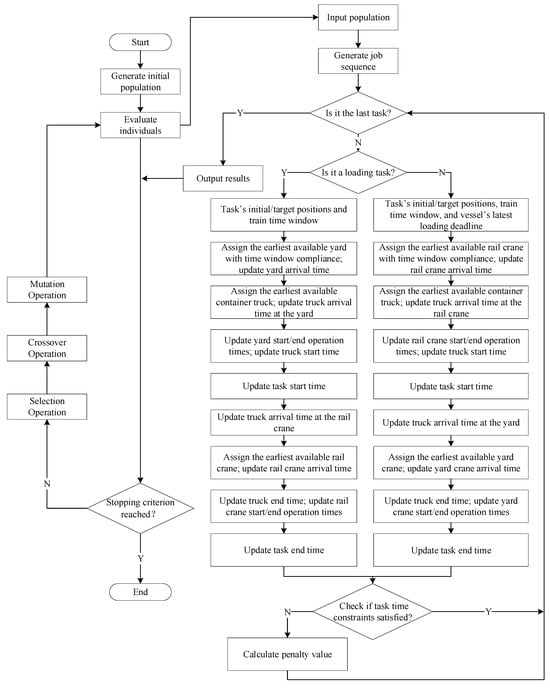
Figure 2.
Flowchart of the improved GA.
4.1. Chromosome Encoding and Decoding
Tasks are encoded using a natural number encoding scheme, where the chromosome length equals the total number of tasks, i.e., the total number of containers that need to be transshipped. For example, assuming that there are 10 tasks (5 export and 5 import containers), the chromosome consists of 10 genes. The sequence of genes represents the operational order of the containers. For export containers, the unloading operation by the RMG is denoted as “D” (Discharge), while for import containers, the loading operation is denoted as “L” (Load). An exemplary chromosome encoding is illustrated in Figure 3.

Figure 3.
Chromosome encoding.
The objective of the proposed model is to minimize the maximum makespan and truck empty-load time. To achieve this, the FAM rule is employed, which assigns RMGs, YCs, and ETs by minimizing equipment waiting times. Additionally, to meet practical operational requirements, priority is given to assignment schemes where ETs wait for RMGs and YCs. The decoding process of a task, i.e., the operational sequence of a task, is detailed using an export container as an example:
Step 0: Based on the starting position and time window information of the export container , select the RMG that completes its previous task earliest and can finish handling the export container within its time window. Calculate the time when the RMG arrives at the wagon position corresponding to the export container , denoted as , with the constraint . Initialize the start time of the export container as .
Step 1: Initialize and . Here, represents the set of ETs arriving at the wagon position of the container before or at the RMG arrival time , i.e., . records the waiting time of ETs for the RMG, defined as .
Similarly, initialize and . Here, represents the set of ETs arriving at the wagon position of container after the RMG arrival time , i.e., . records the waiting time of the RMG for ETs, defined as .
Step 2: ET time calculation.
Step 2.1: Initialize the ET set and set the ET index .
Step 2.2: Calculate the arrival time of ET at the wagon position of container after completing its previous task.
Step 2.3: If , update , ; else, update ,.
Step 2.4: Set . If , proceed to Step 3; otherwise, repeat Step 2.2.
Step 3: The FAM rule is applied for ET assignment. If , select the ET with the earliest arrival time (i.e., ). Update the start time of export container , and update the start time of the corresponding RMG. If , select the truck with the shortest RMG waiting time (i.e., ). Update the start time of export container , and update the start time of the corresponding RMG.
Step 4: YC assignment is finally determined by sequentially updating the RMG’s start/end times and the ET’s start time. Calculate the ET’s arrival time at the yard using Constraint (26), and then select the idle YC that arrives earliest at the container’s storage area. Update the YC’s start/end times, ET’s end time, and the end time of export container according to Constraints (19), (22), (24), (28), and (31).
The decoding process of import containers is reversed compared to export containers, as illustrated in Figure 2.
4.2. Selection Process
The substantial number of new individuals in the initial and newly generated populations requires an effective selection process to identify qualified parents. In this study, a tournament selection strategy is adopted as the individual selection mechanism in genetic operations. Although the original model enforces hard time windows for tasks, soft time windows are introduced during algorithm design to enhance solution feasibility and expand the explorable solution space. To avoid violations of time window constraints, a penalty term is incorporated into the fitness function, which constrains infeasible solutions and mitigates excessive deviations from time window requirements. The penalty function is formulated as follows:
Herein, denotes the penalty value of container and represents the penalty factor. Since the equipment assignment process already accounts for constraints on the task start time window, the time window penalty is calculated solely based on the task completion time. It should be noted that the two optimization objectives—minimizing the total makespan and minimizing the empty-loaded time of trucks—sometimes differ significantly in magnitude. To ensure the effectiveness of the fitness function, both metrics must undergo normalization. Therefore, the fitness function of an individual is defined as follows:
The fitness value of the current individual is denoted by , where and are the weight coefficients assigned to the makespan and empty-loaded truck time, respectively. Herein, represents the makespan (total completion time) of the current individual and corresponds to its empty-loaded truck time. () and (), respectively, denote the maximum (minimum) values of makespan and the empty-loaded truck time in the current population. The total penalty value incurred by the current individual due to violations of time window constraints is expressed as .
4.3. Crossover Operation
In order to explore more solutions in the search space, thereby enhancing the algorithm’s global search capability, this study employs the partially mapped crossover for individual crossover operations. During the procedure, two crossover points and satisfying are randomly generated on the parent chromosomes to define the crossover interval , where is the chromosome length. The gene segments within this interval are directly exchanged between parent 1 and parent 2 to construct initial offspring 1 and offspring 2. A bidirectional mapping relationship is established between the genes of the two parents within the crossover interval. Subsequently, conflicting genes outside the crossover interval are repaired through iterative replacement: if a gene exists in the mapping relationship, it is replaced by the corresponding mapped gene until no conflicts remain.
As shown in Figure 4, randomly generated crossover points are two and six, resulting in the interval [2, 6), i.e., from the third to the sixth genes. Initial offspring are generated as offspring 1: 1-3-1-7-5-4-2-8 and offspring 2: 3-2-5-6-4-7-8-6. A bidirectional mapping is established: for offspring 1, the mappings are 1-5, 7-6, 5-4, 4-7, while for offspring 2, the mappings are 5-1, 6-7, 4-5, 7-4. Both offspring initially contain duplicate genes, requiring conflict resolution. For offspring 1, genes outside the crossover interval are sequentially checked by its index. At index 0 (task 1), the mapping triggers replacements following the chain 1→5→4→7→6. The repair process of index 0 in offspring 1 terminates as task 6 is not in the mapping table, while other indices remain unchanged. The final repaired offspring 1 becomes 6-3-1-7-5-4-2-8. Similarly, for offspring 2, the conflict repair process yields the final offspring 2: 3-2-5-6-4-7-8-1.
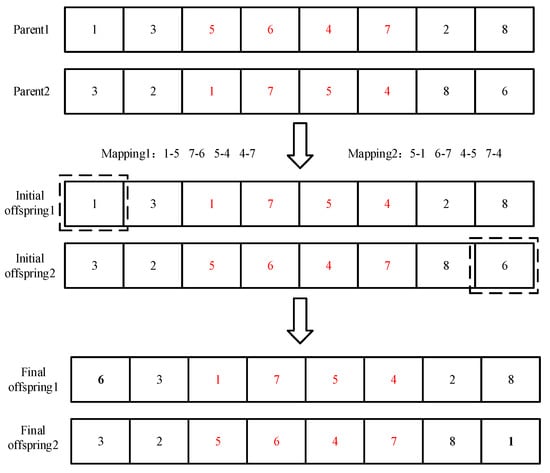
Figure 4.
Schematic diagram of partially mapped crossover.
4.4. Mutation Operation
In the design of a GA, the incorporation of mutation operators enhances local search capability and maintains population diversity, thereby mitigating premature convergence to local optima. To ensure algorithmic efficacy, this study employs two types of mutation strategies: inversion mutation and swap mutation. The inversion mutation operator randomly selects two gene positions and reverses the sequence of genes between these positions, as illustrated in Figure 5. Conversely, the swap mutation operator randomly selects multiple gene positions and exchanges their positions sequentially, as demonstrated in Figure 6.
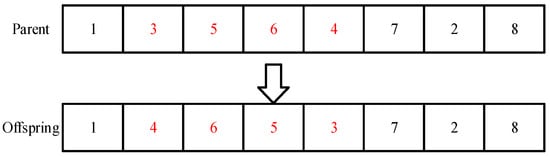
Figure 5.
Schematic diagram of an inversion mutation.
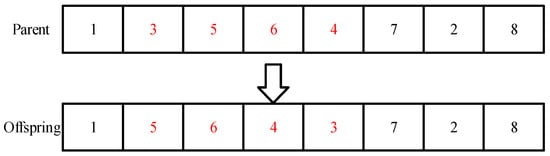
Figure 6.
Schematic diagram of a swap mutation.
4.5. Stopping Criterion
The algorithm terminates and outputs the current optimization results when the iteration count reaches the predefined maximum number of evolutionary generations. Although the proposed GA, guided by heuristic rules, does not guarantee the discovery of a globally optimal solution, it provides a near-optimal solution adhering to fundamental scheduling rules for large-scale scheduling problems within a reasonable timeframe. This solution serves as a valuable reference for practical field operations.
5. Computational Experiments
This section validates and evaluates the mathematical model and GA through numerical experiments. All experiments were conducted on a desktop computer equipped with a 12th Generation Intel Core i7-12700KF CPU @ 3.60 GHz and 32.0 GB of RAM, running a 64-bit Windows 11 operating system. The mathematical model was solved using the Gurobi 10.0.1 solver invoked via PyCharm 2021.3, while the GA was implemented in Python 3.10 within the same PyCharm 2021.3 environment.
5.1. Experiment Settings and Instances Generation
To our knowledge, no benchmark instances for the studied problem are publicly available in the literature. Therefore, the experimental instances are generated randomly. Specifically, a port terminal yard and a railway hub are generated with a benchmark distance of 10 km. There are two loading/unloading tracks in the railway hub. Container tasks are randomly generated based on the storage strategies in the port terminal yard and the train schedules in the railway hub. Time windows for the tasks are randomly assigned within [0, 1440] minutes, with each time window duration set to 120 min. Containers assigned to the same train share identical time windows. For trains parked on the same loading/unloading track, the arrival time of a subsequent train is scheduled 10 min after the departure time of the preceding one. Key parameters of the mathematical model and operational equipment are summarized in Table 2 [,]. Since the preferences of sea–rail intermodal operators are unknown, both weighting coefficients λ1 and λ2 are set to 0.5 in the result analysis section.

Table 2.
Parameters of the model and equipment.
Although the eight studies in Table 1 have already investigated problems similar to the one in this research, with the maximum task number reaching 1500, most of them do not provide solution times. Therefore, to assess the effectiveness of the proposed GA, we compare its performance against both the results obtained by directly solving the model with Gurobi and those from the ALNS algorithm in Liu et al. [], which can handle an instance scale similar to that of this study. In our experiments, the maximum runtime is limited to 7200 s per instance. Given the complex solution space and the tendency to become trapped in local optima inherent to this problem, the parameters of the GA are configured based on preliminary experiments and problem-specific characteristics to enhance global search efficiency and convergence stability. The algorithm-related parameters are configured as follows: population size , maximum iteration count , crossover probability , mutation probability , and probability of selecting inversion mutation . Based on these settings, small-scale, medium-scale, and large-scale instances are designed and solved to validate the performance of the proposed model and the improved GA. The instances are characterized by the number of export containers and import containers. For example, 4 (2, 2) denotes an instance containing 2 export containers and 2 import containers.
5.2. Results on Small-Scale Instances
Firstly, 10 small-scale instances are randomly generated to validate the correctness of the proposed MIP and the effectiveness of GA, with detailed results provided in Table 3. The performance metrics in the table are as follows: denotes the makespan of all tasks, represents the empty travel time of ETs between two consecutive tasks, indicates the waiting time of ETs at the next task position until operation begins, and Time specifies the solving time. and together constitute the total empty-load time of ETs . The decomposition of aims to thoroughly analyze the system’s bottleneck by examining the detailed composition of the total empty-load time of ETs.

Table 3.
Performance comparison between Gurobi and GA for small-scale instances.
The results of instances 1 to 10 indicate that Gurobi could solve the proposed MIP model to optima or sub-optima, demonstrating the correctness of the proposed model. However, as the size of the instances increased, the computation time of Gurobi exhibits exponential growth, which indirectly suggests that the problem belongs to the NP-hard category. Specifically, Gurobi outperforms GA in terms of computation time in instances 1 and 2, while in instances 4, 6, and 8, it achieves slightly better solution quality than GA but with significantly longer computation times. From instance 10, it can be observed that when the total number of container tasks reached 16, the solution quality of Gurobi is lower than that of GA, and the computation time has reached 7200 s, implying that Gurobi is unable to obtain an exact solution within the specified time limit. This highlights that when container quantities reach 16 or higher, the escalating problem complexity renders Gurobi inadequate in balancing solution quality and computation time, making it impractical for real-world applications. As a result, the comparison between GA and Gurobi is limited to the small-scale instances.
The performance of GA is also evaluated based on the results in Table 3. Notably, for small-scale instances, the GA could produce solutions that are either identical to or closely approximate those obtained by Gurobi, while the maximum solving time is 132.53 s, much less than the 7200 s of Gurobi. In the small-scale instances, the average values of GAP1 and GAP2 between GA and Gurobi are, respectively, −1.15% and −5.91%. The reason for the lower average objective value of GA compared to Gurobi is primarily due to Gurobi’s inability to find the optimal solution for instance 10, which results in a significantly poorer solution quality. In addition, although the GA’s solving time for instances 1 and 2 is slightly longer than that of Gurobi, its average solving time is only 89.27 s, which is far lower than that of Gurobi. The results for small-scale instances exhibits GA’s ability to find optimal or near-optimal solutions within an acceptable solving time, validating the effectiveness and efficiency of the proposed algorithm, while showcasing superior capability in handling large-scale problems.
5.3. Results on Medium- and Large-Scale Instances and Stability Tests
Given Gurobi’s inability to deliver optimal solutions for instances with more than 16 container tasks within the designated time limit, subsequent analyses focus on comparing the proposed GA and the ALNS across 10 randomly generated medium-scale instances and 10 randomly generated large-scale instances. The comparative experimental results between ALNS and GA for the medium- and large-scale instances are presented in Table 4 and Table 5, respectively. Figure 7 displays the iteration convergence curves for instances 25 and 27. The figure shows that the GA converged within a relatively short time in the two instances, denoting that the proposed GA has excellent convergence properties.

Table 4.
Performance comparison between ALNS and GA for medium-scale instances.

Table 5.
Performance comparison between ALNS and GA for large-scale instances.
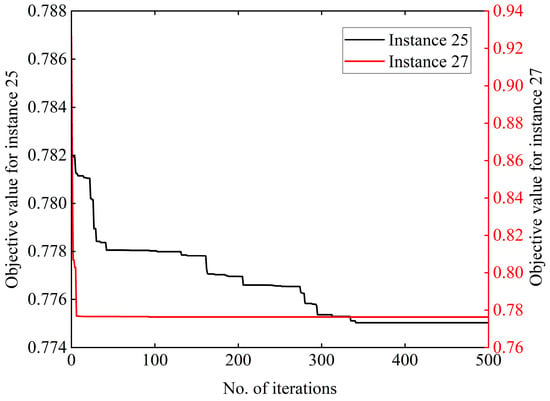
Figure 7.
Convergence curve of GA.
The results in Table 4 and Table 5 indicate that as the instance scale increases, both the objective values and the computation times of the GA and ALNS also grow accordingly, although some fluctuations are observed. For three-quarters of the 20 instances, excluding instances 16, 21, 22, 23, and 25, the maximum makespan of all tasks and the total empty-load time of ETs of GA are both superior to those of ALNS. For instances 16, 21, 22, and 25, either the maximum makespan of all tasks or the total empty-load time of ETs of GA outperforms that of ALNS. Only for instance 23 do both the objective values of GA fall short of those of ALNS. The overall average values of GAP1 and GAP2 for medium-scale instances are −0.83% and −2.69%, respectively, while for large-scale instances, they are −0.23% and −1.31%, respectively. Moreover, GA exhibits a significant advantage over ALNS in terms of computation time. When the number of container tasks reaches 270, the solving time of ALNS exceeds 7200 s, and at 300 tasks, it increases to as high as 8165.70 s. In comparison, the maximum solving time of GA is only 5044.53 s, which aligns with the algorithm’s time efficiency requirements. The average solving times of GA for medium- and large-scale instances are 844.56 s and 2887.25 s, respectively, which are significantly smaller than the corresponding times of ALNS, 1519.48 s and 5354.81 s. These results demonstrate the performance advantage of the proposed GA, particularly its significant advantage in computational time.
From the column in the tables, it can be found that the expansion of instance scale exerts a moderate influence on the makespan of all tasks, though its variation remains relatively stable compared to the more pronounced fluctuations in ET’s empty travel time and waiting time. Notably, ET waiting time exhibits a significant upward trend, reflecting intensified resource competition caused by task accumulation in large-scale scenarios, which inherently leads to increased waiting time. Additionally, the increase in the number of tasks also results in a higher number of trains in the schedule. If the tasks between two adjacent trains are not properly coordinated, it leads to ET waiting. This becomes a significant factor contributing to the increased ET waiting time.
Furthermore, the results in the columns of and for GA reveal that when the numbers of import and export containers are balanced, the empty travel time can be significantly decreased, although the waiting times increase to some extent. For instance, under the same number of tasks, due to the balanced number of import and export containers, instance 22 (26) has 571.65 (708.94) minutes less of empty travel time compared to instance 21 (25), but the waiting time only increases by 349.48 (513.61) minutes. By analyzing the detailed scheduling results, it is found that the underlying reason for this phenomenon is that task balancing can reduce the truck’s empty travel time by pairing more import and export containers. Moreover, the makespan of instance 22 (26) is also 40.43 (8.16) minutes shorter than instance 21 (25). Since the fuel consumption during the truck’s travel is much higher than that during waiting (whether idling or parking), it can be concluded that balancing the number of import and export containers during rail-sea intermodal transportation scheduling is critical to enhancing transfer efficiency and optimizing equipment utilization. In practice, the decision-makers should reasonably determine the transshipped number of import and export containers during a certain time period to reduce the empty-load time and improve the dispatching efficiency of ETs, rather than transporting them immediately as soon as a demand arises.
To examine the stability of the proposed GA, four instances are selected and repeatedly run 10 times, as shown in Table 6. For the makespan, the largest GAP value is 0.96% and the average GAP value is 0.30%, while for the empty-load time, the largest GAP value is 5.27% and the average GAP value is 2.56%. These results demonstrate the high stability of GA.

Table 6.
Statistical results of GA from 10 computational runs.
5.4. Sensitivity Analysis
Intuitively, in the spatially separated sea–rail intermodal system, factors such as equipment configuration schemes at the port yard and railway hub, the distance between port yard and railway hub, and the time window width of tasks are supposed to have an influence on the system efficiency. To investigate how these factors impact the maximum makespan of all tasks and the empty-load time of ETs, this section conducts a sensitivity analysis by comparing multiple sets of experiments.
5.4.1. Effect of Objective Weights
For the numerical experiments in Section 5.2 and Section 5.3, the weights and are set to equal values, both being 0.5. However, it can be found that the empty-load time of ETs is obviously greater than the makespan in most instances due to the long distance between the port yard and railway hub. In real-world scenarios, the decision-makers may have varying preferences regarding the makespan and empty-load time of ETs, which can significantly influence the objective value. In order to provide valuable managerial insights, this section discusses the impact of objective weights.
The objective weights ranging from 0 to 1 are investigated for instances 14, 17, and 19, with an increment of 0.1 each time. When modifying , is correspondingly adjusted as . For each instance, 10 repeated runs are conducted with identical parameter settings, and the final results for each parameter group are determined by the average value, as shown in Figure 8. As can be seen, when the weights are set to and , the three instances all achieve relatively small values for both makespan and the empty-load time of trucks, indicating that the algorithm exhibits strong optimization capability and effectiveness at this setting. Therefore, the objective function weights are set as and for the experiments in the following sensitivity analysis.
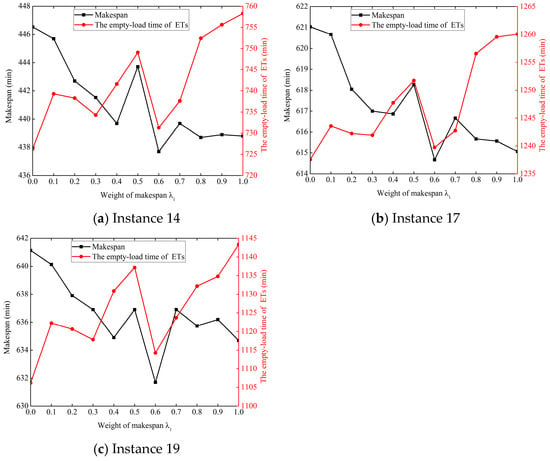
Figure 8.
Experimental results with different objective weights.
5.4.2. Effect of Equipment Configuration Schemes
The effect of equipment configuration schemes on operational efficiency is investigated by analyzing randomly selected instances: 14, 19, 24, 25, and 27. For each instance, five varying equipment configurations are deployed, with detailed results presented in Table 7. The configuration in the first line of each instance is used as the initial configuration. Due to the long distance of ETs, the increased ratio of ETs is set to be three times that of RMGs or YCs. Considering the fluctuation in GA optimization results, each configuration is independently executed 10 times to ensure stability and accuracy.

Table 7.
Effect of different equipment configuration schemes.
It can be seen from Table 7 that increasing the number of a single equipment type or all three types can reduce the makespan of all tasks to some extent, but their effects on ET’s empty travel time and waiting time display different patterns. This implies that under the initial configuration, the capability of all equipment is sufficient to complete all the container transshipment tasks. However, it does not mean that increasing the number of equipment is pointless. Compared to increasing the number of ETs, exclusively increasing the number of YCs or RMGs results in a smaller reduction in the makespan, but the reduction in ET empty travel time is more significant, and the increase in ET waiting time is also smaller. This finding reveals that the increase in handling equipment in port yards or railway hubs helps improve the dispatching flexibility of ETs. In contrast, although increasing the number of ETs can significantly shorten the makespan, this comes at the cost of sacrificing the efficiency of the ETs, that is, increasing their waiting time. The more tasks there are, the more the waiting time of ETs increases. It should be noted that the purchase cost of different equipment varies significantly. Considering the high purchase cost of RMGs and YCs, as well as the limited impact of their quantity on reducing the makespan, increasing the number of ETs may be a more cost-efficient solution in practice, especially when the availability of RMGs or YCs is constrained.
To enhance clarity, Figure 9 illustrates the trend of changes in makespan, empty travel time, and waiting time of ETs for instance 27. Although increasing the number of ETs reduces the makespan, the results of instance 27 present a significant rise in ET waiting time. For instance, when the number of ETs increases to 16, their waiting time exceeds that of the scenarios where only RMGs and yard cranes are added. The increase in waiting time primarily stems from improved operational efficiency within the same time window due to additional ETs, thereby shortening the makespan. Taking two trains on the same track as an example, the first with a time window of [0, 120] and the second with [130, 250], the initial configuration yields a maximum makespan of 120 min for the first train. With increased equipment, the makespan is shortened to 100 min. However, since the handling of tasks is required to be started once the train arrives, increased equipment extends the waiting time of ETs for the second train to 30 min, which is 20 min longer than before. To avoid prolonged waiting of ETs, decision-makers are suggested to assign an appropriate number of ETs to provide drayage operation or reasonably determine the start time of task handling.
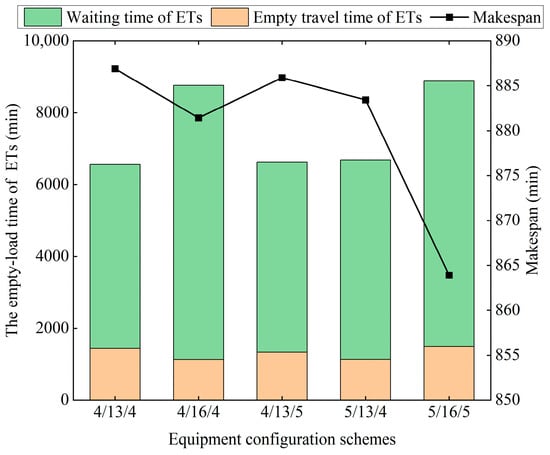
Figure 9.
Effect of equipment configuration schemes, for instance, 27.
5.4.3. Effect of Distances Between the Port Yard and Railway Hub
In practical operations, the distance between the port yard and rail hub varies significantly, and this variation critically plays a vital role in transshipment efficiency. Railway hubs located near the port typically have distinct efficiency advantages during transportation. However, for railway hubs located farther away, ETs require substantially more time to complete drayage operations, thereby complicating overall equipment scheduling. Therefore, this section evaluates the effect of increasing the port–railway distance from 5 km to 30 km on transshipment efficiency based on instance 19. The results are presented in Table 8, and the trend of normalized objective values is shown in Figure 10.

Table 8.
Effect of distances between the port yard and railway hub for instance 19.
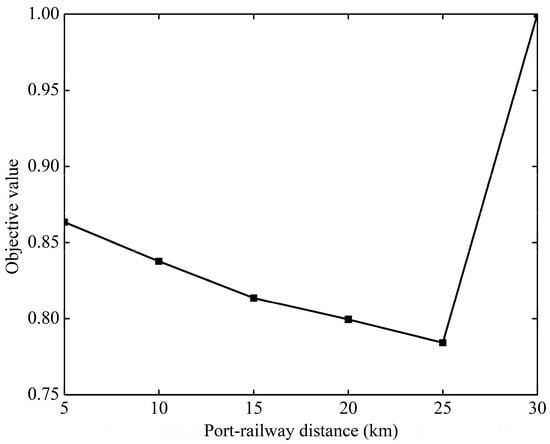
Figure 10.
Objective values under different port–railway distances for instance 19.
From Table 8, it can be observed that under the same equipment configuration and task quantity, an increase in port–railway distance directly extends the makespan of all tasks. Specifically, when the distance increases from 5 km to 30 km, the makespan is prolonged by nearly 2 h. Meanwhile, it can be seen that although the ET empty travel time and waiting time are both considerable and show opposite trends, they are inevitable due to the long distance. These findings suggest that as the distance between the port yard and the railway hub increases, a reasonable arrangement of equipment quantity is necessary to minimize the makespan. Furthermore, due to the significantly greater negative effects caused by empty travel of ETs over long distances, it is even more crucial to optimize the assignment of ETs for import and export container tasks.
It is important to note that when the port–railway distance reaches 30 km, the makespan of 670.03 min fails to meet operational demands within the predefined time windows, leading to significant penalties for some tasks, as calculated in Constraint (39). This, in turn, results in an exceptionally high objective value. To maintain consistency with the other objective values, the objective value is set to 1 for the 30 km port–railway distance in Figure 10. From this figure, it can be seen that as the distance increases, the objective values generally decrease, reaching the minimum when the distance is 25 km. However, this does not imply that longer distances from the port yard to the railway hub always result in better transshipment efficiency. Rather, it reflects that for efficient transshipment over long distances, an adequate number of initial equipment must be provided. For example, a configuration of 4/20/4, or similar, may be required. Under the 4/20/4 configuration scheme, when the distance is less than 25 km, a shorter distance results in a significant increase in ET waiting time under fixed time window widths, which far outweighs the benefits from reduced makespan and ET empty travel time, ultimately causing an increase in the overall objective value. This not only demonstrates the effect of port–railway distance but also supports the premise that the rational deployment allocation of truck quantities is crucial for specified port–railway distance.
5.4.4. Effect of Time Window Widths
Based on the analysis in Section 5.4.2, the 4/20/4 equipment configuration (4 RMGs, 20 ETs, and 4 YCs) is unable to complete all tasks for instance 19 within the predefined time window when the port–railway distance reaches 30 km, indicating that the transport capacity is insufficient under this configuration. Therefore, one may wonder whether increasing the width of the time window would allow the task to be completed successfully. To address this, the following section further examines the effect of time window width on transshipment efficiency using instance 19, under the settings of a 30 km port–railway distance and the 4/20/4 equipment configuration.
Table 9 reports the detailed results. As can be seen, the makespan of all tasks, ET empty travel time, and ET waiting time progressively increase with expanding time window width. This indicates that a wider time window enables more scheduling flexibility but sacrifices ET waiting time to reduce empty travel. Notably, the objective value indicates that a time window width of 150 min yields the optimal comprehensive result under the 4/20/4 configuration and 30 km port–railway distance. Once the time window width exceeds 150 min, sufficient equipment results in a rapid increase in ET waiting time, and thus is detrimental to the scheduling management of the overall system. Therefore, when the time window is relatively large, it is possible to reduce the dispatched equipment quantities to avoid resource waste. Figure 11 further illustrates the optimal number of ETs for instance 19 under varying time window widths at the 30 km port–railway distance. The objective value of 1 implies that the transport capacity of ETs is insufficient to complete all tasks within predefined time windows, and it is set to 1.

Table 9.
Effect of time window widths for instance 19 with a 30 km port–railway distance.
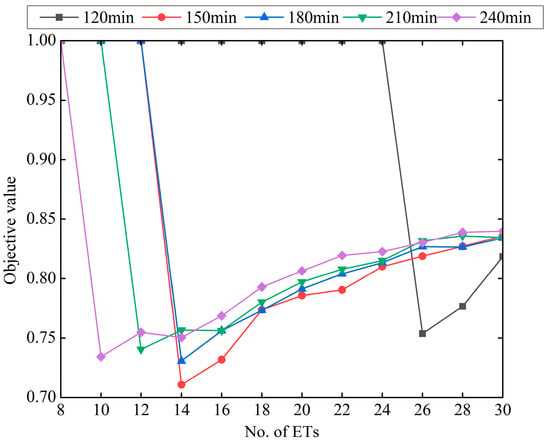
Figure 11.
Effect of time window widths under various numbers of ETs for instance 19 with a 30 km port–railway distance.
Figure 11 demonstrates that different time window widths correspond to distinct optimal truck quantities. Specifically, a 120-min time window requires 26 ETs to ensure task completion, as fewer than 26 ETs fails to meet operational deadlines. For 150-min and 180-min time windows, the optimal number of ETs decreases to 14. As the time window expands further, the optimal ET count continues to decline: 12 ETs are needed for a 210-min window, and this number drops to 10 ETs for a 240-min window. These findings suggest that larger time window widths allow a reduction in the required number of ETs. Among these configurations, the 150-min time window strikes a balance, delivering favorable makespan and truck empty-load time with fewer ETs. Thus, when port–railway distances are relatively long, adjusting time window widths and scientifically planning train schedules based on the number of tasks is essential. However, excessively large time windows may reduce the number of trains that can be processed daily, undermining transshipment efficiency and potentially disrupting the overall sea–rail intermodal workflow.
6. Conclusions
This study addresses the collaborative scheduling optimization of RMGs, ETs, and YCs for container transshipment in sea–rail intermodal transportation under port–railway separation mode. An MIP model is developed to minimize the makespan of all tasks and the empty-load time of ETs, incorporating constraints such as train arrival/departure time windows, export container delivery deadlines, and equipment operation sequences. To enhance computational efficiency, an improved GA is proposed. The results of numerical experiments at varying scales demonstrate the correctness of the model and the effectiveness of the GA. Compared to Gurobi, the GA achieves a 6.08% improvement in solution quality and a 97.94% decrease in computation time for small-scale instances. Additionally, for medium to large-scale instances, it surpasses the ALNS algorithm by 1.51% in solution quality and reduces computation time by 45.71%. Furthermore, sensitivity analysis provides valuable insights as follows: (1) The objective weights have a significant impact on makespan and ET empty-load time, and thus decision-makers should determine the appropriate weightings based on their preferences. (2) Appropriately increasing the number of ETs may be a more cost-efficient solution in practice, especially when the availability of RMGs or YCs is constrained. (3) The longer port–railway distance necessitates more ETs to ensure timely task completion within predefined time windows, which in turn makes it even more crucial to optimize the assignment of ETs for import and export container tasks. (4) Widening time windows can reduce the required number of ETs for the scenario of long port–railway distance, but excessive time window expansion may prolong makespan and compromise overall transshipment efficiency.
However, the current study has certain limitations. While it assumes pre-known information about containers requiring transportation, practical operations often encounter demand fluctuations during implementation, necessitating dynamic adjustments. For instance, port operations may experience uncertainty in container transportation demand due to factors such as vessel arrival delays, last-minute changes in container orders, or unexpected incidents. Future research should address the dynamic tasks arising from these uncertainties. Additionally, in drayage operations, ETs may encounter situations such as traffic congestion, leading to variations in speed, which can affect the timeliness of the scheduling plan. To account for this, future studies could introduce appropriate time buffers for ET travel times and further explore this cooperative scheduling problem by considering the characteristics of time-varying road networks.
Author Contributions
Conceptualization, X.Y.; methodology, X.Y. and C.H.; software, C.H.; validation, X.Y. and C.H.; formal analysis, X.Y. and C.H.; investigation, C.H.; resources, X.Y.; data curation, X.Y. and C.H.; writing—original draft preparation, C.H.; writing—review and editing, X.Y.; visualization, C.H.; supervision, X.Y.; project administration, X.Y.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 42001122.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zou, Y.; Xiao, G.; Li, Q.; Biancardo, S.A. Intelligent Maritime Shipping: A Bibliometric Analysis of Internet Technologies and Automated Port Infrastructure Applications. J. Mar. Sci. Eng. 2025, 13, 979. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Li, S. Flexible Yard Crane Scheduling for Mixed Railway and Road Container Operations in Sea-Rail Intermodal Ports with the Sharing Storage Yard. Transp. Res. E Logist. Transp. Rev. 2024, 190, 103714. [Google Scholar] [CrossRef]
- Seo, Y.J.; Chen, F.; Roh, S.Y. Multimodal Transportation: The Case of Laptop from Chongqing in China to Rotterdam in Europe. Asian J. Shipp. Logist. 2017, 33, 155–165. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, S.; He, S.; Jiang, Y.; Wang, X.; Yin, H.; Zhu, J. Research on the Multi-Equipment Cooperative Scheduling Method of Sea-Rail Automated Container Terminals under the Loading and Unloading Mode. J. Mar. Sci. Eng. 2023, 11, 1975. [Google Scholar] [CrossRef]
- Li, J.; Yan, L.; Xu, B. Research on Multi-Equipment Cluster Scheduling of U-Shaped Automated Terminal Yard and Railway Yard. J. Mar. Sci. Eng. 2023, 11, 417. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Zhang, Q.; Tan, K.C. Integrated Scheduling of Yard and Rail Container Handling Equipment and Internal Trucks in a Multimodal Port. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2987–3008. [Google Scholar] [CrossRef]
- Xia, T.; Wang, L.; Zhang, Q.; Dong, J.; Song, D.; Zhu, X. Integrated Scheduling of Gantry Cranes, Container Trucks and Yard Cranes in On-dock Railway Operation Areas at Multimodal Container Ports. IET Intell. Transp. Syst. 2025, 19, e12600. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, X.; Haghani, A. Modeling and Solution of Joint Storage Space Allocation and Handling Operation for Outbound Containers in Rail-Water Intermodal Container Terminals. IEEE Access 2019, 7, 55142–55158. [Google Scholar] [CrossRef]
- Abu-Aisha, T.; Audy, J.-F.; Ouhimmou, M. Toward an Efficient Sea-Rail Intermodal Transportation System: A Systematic Literature Review. J. Shipp. Trade 2024, 9, 23. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Hong, S. An Exact Algorithm for Multiple-Equipment Integrated Scheduling in an Automated Container Terminal Using a Double-Cycling Strategy. Transp. Res. E Logist. Transp. Rev. 2024, 186, 103565. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Chou, C.-C.; Wang, C.-N. Heuristic/Metaheuristic-Based Simulation Optimization Approaches for Integrated Scheduling of Yard Crane, Yard Truck, and Quay Crane Considering Import and Export Containers. IEEE Access 2022, 10, 64650–64670. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, X.; Wang, L.; Chang, Y. Integrated Scheduling of Rail-Mounted Gantry Cranes, Internal Trucks and Reach Stackers in Railway Operation Area of Container Terminal. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 47–58. [Google Scholar] [CrossRef]
- Li, W.; Wu, Z.; Yang, P.; Cai, L. Collaborative Scheduling Optimization of Equipment in Multimodal Transport Harbor Considering Hybrid Operation Mode of “Train-Yard-Vessel” and “Train-Vessel”. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 20–24 August 2022; IEEE: Mexico City, Mexico, 2022; pp. 86–91. [Google Scholar]
- Li, W.; Zhong, L.; He, L.; Guo, W. Integrated Scheduling in Sea–Rail Intermodal Terminals with Flexible Transshipment Routes. Swarm Evol. Comput. 2025, 93, 101852. [Google Scholar] [CrossRef]
- Yang, Y.; He, S.; Sun, S. Research on the Cooperative Scheduling of ARMGs and AGVs in a Sea–Rail Automated Container Terminal under the Rail-in-Port Model. J. Mar. Sci. Eng. 2023, 11, 557. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Liu, Y.; Wang, L.; Yan, B. A Practical Model for Inbound Container Distribution Organization in Rail-Water Transhipping Terminal. J. Control Sci. Eng. 2018, 2018, 9148405. [Google Scholar] [CrossRef]
- Hu, Q.; Corman, F.; Wiegmans, B.; Lodewijks, G. A Tabu Search Algorithm to Solve the Integrated Planning of Container on an Inter-Terminal Network Connected with a Hinterland Rail Network. Transp. Res. C Emerg. Technol. 2018, 91, 15–36. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, X.; Lee, D.-H.; Jin, J.G.; Wang, L. Transshipment Operations Optimization of Sea-Rail Intermodal Container in Seaport Rail Terminals. Comput. Ind. Eng. 2020, 141, 106296. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Wang, L. Study on Scheme of Outbound Railway Container Organization in Rail-Water Intermodal Transportation. Sustainability 2020, 12, 1519. [Google Scholar] [CrossRef]
- Yan, B.; Jin, J.G.; Zhu, X.; Lee, D.-H.; Wang, L.; Wang, H. Integrated Planning of Train Schedule Template and Container Transshipment Operation in Seaport Railway Terminals. Transp. Res. E Logist. Transp. Rev. 2020, 142, 102061. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, X. A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals. Symmetry 2019, 11, 1229. [Google Scholar] [CrossRef]
- Abu Aisha, T.; Ouhimmou, M.; Paquet, M.; Montecinos, J. Developing the Seaport Container Terminal Layout to Enhance Efficiency of the Intermodal Transportation System and Port Operations—Case of the Port of Montreal. Marit. Policy Manag. 2022, 49, 181–198. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Cheng, S.; Liu, W.; Jiang, L. A New Synchronous Handling Technology of Double Stack Container Trains in Sea-Rail Intermodal Terminals. Sustainability 2022, 14, 11254. [Google Scholar] [CrossRef]
- Teng, Y.; Li, X.; Gao, L.; Xie, J.; Li, Y. An Improved Co-Evolutionary Memetic Algorithm Based on Novel Schedule Type and Unconditional Feasibility for Hybrid Flow-Shop Scheduling Problem. Comput. Ind. Eng. 2024, 193, 110324. [Google Scholar] [CrossRef]
- Pankratz, G. A Grouping Genetic Algorithm for the Pickup and Delivery Problem with Time Windows. OR Spectr. 2005, 27, 21–41. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-27555-2. [Google Scholar]
- Chen, G.; Govindan, K.; Golias, M.M. Reducing Truck Emissions at Container Terminals in a Low Carbon Economy: Proposal of a Queueing-Based Bi-Objective Model for Optimizing Truck Arrival Pattern. Transp. Res. E Logist. Transp. Rev. 2013, 55, 3–22. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, Z.; Liu, P.; Wang, W.; Zhang, D. Container Drayage Problem Integrated with Truck Appointment System and Separation Mode. Comput. Ind. Eng. 2024, 193, 110307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).