Two-Phase Multi-Point Design Exploration of Submerged Nacelles for Marine Propulsive Pump Installation

Abstract

Outboard Dynamic-inlet Waterjets (ODW) are axisymmetric units, powered by a self-contained pump, that, by processing a uniform undisturbed streamtube, can operate more efficiently than conventional marine propulsors. This feature also provides methodological convenience, enabling accurate numerical investigations of the system alone using 2D axisymmetric models. Leveraging this property, the present study bridges the gap on the design principles required to tailor ODW geometries across multiple operating conditions. Reynolds-Averaged Navier Stokes (RANS) equations are solved, including turbulence and cavitation models, to draw the propulsor’s characteristic maps and identify two relevant operating points, set by the combination of a specified pump rotational regime with an advancing velocity. Simulations for these in- and off-design conditions are systematically performed over a database of 512 randomly sampled geometric variants. The corresponding results show that optimised shapes improving the inlet Pressure Recovery (PR) and nacelle drag at cruise conditions result in beneficial outcomes also at take-off operations, where lip cavitation may occur. Thus, analysing together the off-design PR and the cruise net force underscores their conflicting behaviour. In fact, while nacelles shortened by $12\%$ can reduce overall drag and enhance nominal net thrust by $2\%$, designs featuring a $34\%$ wider capture area improve off-design PR by over $1.5\%$, albeit at the cost of compromised propulsive efficiency under any operating range.

1. Introduction

Although conventional propellers dominate the marine propulsion market, waterjet units represent a more convenient solution for specific applications [1]. In fact, thanks to improved efficiency above 30 knots, higher manoeuvrability, and noise mitigation capabilities, they result in a proper choice for military installations [2]. Additionally, despite sharing the presence of a bladed component, required to generate a momentum unbalance, waterjets leverage diffuser inlets that delay rotor tip cavitation, enabling safer operations at high advancing speeds [3,4]. Therefore, the intake is a distinctive component, providing direct control on the pump Net Positive Suction Head (NPSH), consequently affecting the efficiency of the entire propulsion system [5]. As a result, the inlet shape characterises the specific application and is commonly classified into flush and podded types, with the flush configuration representing the standard arrangement in current applications [2]. Extensive studies have been dedicated to this component to identify its typical head losses mechanisms. Among others, up to a $20\%$ efficiency drop can be determined by: hull boundary layer ingestion and distortion, lip flow turning and evolution through bent ducts [6]. Thus, parameterising the inlet walls curves, Computational Fluid Dynamics (CFD) studies were adopted, combined with Design Of Experiments (DOE) and genetic algorithms, to mitigate detrimental effects and improve the system’s efficiency [5,7]. Optimisation of waterjet pumps is another common research theme [8,9,10].

Sharing common features with both ducted propellers and waterjets, pumpjet units are an alternative solution, usually applied to underwater vehicles. They comprise both rotating and stationary blades, shrouded by axisymmetric nacelles, and are generally installed astern, enabling an efficient exploitation of the boundary layer generated along the tailcone [11,12]. Different configurations have been devised over the years leveraging slant shafts, including scoop inlets [13] and fully-outboard devices [14]. Although providing improvements, these solutions are not capable of overcoming inherent propulsive limits, making optimisation through shape parameterisation necessary [15,16,17].

In recent years, with the introduction of Outboard Dynamic-inlet Waterjets (ODW), industrial technology has paved the way for innovation in marine propulsion [18]. In fact, the possibility of operating isolated from the ship, thanks to electric integrated engines, allows this novel propulsor to process uniform mass flow rates, aligning thrust with the advancing direction, similarly to aeronautical propulsion principles. Current related research is limited to numerical investigations, where 2D axisymmetric models [19] and 3D installed configurations [20] were adopted to measure relevant geometric parameters and characterise the system’s performance. Recent studies [21] performed detailed analyses on the intake shape to derive proper forebody design criteria for optimal pump integration. However, that investigation limited to cruise operations and no two-phase phenomenon was included.

At the present stage, substantial advancements are bounded by the lack of public experimental data to serve as a reference for validation. Therefore, the only available numerical model relies on equivalent configurations obtained from a combination of public geometries [22,23,24]. To this end, persistent efforts from the academic environment on the topic are expected to stimulate experimental research, potentially leading the way toward achievements comparable to those obtained for conventional marine propulsors. In fact, over the years, extensive testing has been conducted to accurately measure the performance of stationary [6,22,25] and rotating components [26,27,28] of waterjets and pumpjet units [29,30,31,32]. Building upon these reference measurements, reliable CFD methods could be developed, enhancing the predictive accuracy of numerical models. Particularly, this process has enabled the improvement of closure techniques applied to Reynolds-Averaged Navier Stokes (RANS) equations, making them the preferable approach for a wide range of applications. Offering robust and rapid predictions without excessive computational costs, the development of accurate turbulence and cavitation models [33,34,35,36,37] has established the role of RANS techniques as a standard within both the industrial and academic hydrodynamics communities.

In an effort to advance current knowledge on ODW, this study emphasises the need for a dedicated investigation into the design principles governing optimal nacelle shaping. The analysis aims to establish design criteria by identifying correlations between fundamental geometric features and the resulting propulsive performance. Particular focus is given to ensuring efficient operation across varying conditions while delivering a clean flow to the turbomachinery, with sufficient cavitation margin. To this end, critical points in the propulsor’s characteristic map are first identified by selecting an appropriate pump rotational speed, enabling the assessment of multi-point performance across different geometries. A database of geometric variants is then generated and modelled using two-phase RANS simulations at both cruise and take-off operations, the latter accounting for the potential onset of internal lip cavitation. From the resulting CFD solutions, relevant propulsive metrics are extracted using Thrust-Drag Bookkeeping (TDB), a technique typically adopted in aero-engine research [38,39,40] and particularly efficient for ODW characterisation [21]. The collected statistics are subsequently analysed to disclose correlations with principal geometric parameters, highlighting how local wall profiles should be shaped to enhance specific propulsive performance. In summary, the study highlights the relevant design variables for the geometric specification of ODW nacelles, setting the basis to draw design groundrules for efficient propulsive pump installed operations across mutliple operating conditions.

The paper is organised as follows: Section 2 introduces the reference model and related computational methods. In Section 3, optimisation results are presented starting from the propulsor’s characteristic maps, while in Section 4 conclusions are drawn.

2. Computational Methods

2.1. Reference Geometry

The reference ODW geometry for the present study is reported in Figure 1. Due to the limited availability of data from existing units, the outline derives from a manipulation of the waterjet ram inlet presented by Sobolewski [22], adapted to house the AxWJ-2 pump designed by Michael et al. [24]. The details regarding the integration strategy of the two components are discussed in a previous work by the authors [20], while Avanzi et al. [21] presented a systematic investigation, characterising the geometrical parameters relevant to the hydrodynamic design of the propulsor’s intake.

This study extends the focus to the full system dynamics. Thus, a generic B-spline is adopted to complete the external nacelle geometry, connecting the outer inlet skin with the nozzle inner walls while preserving tangency continuity at the two sides. This curve parameterisation is convenient for local manipulation, providing a piecewise polynomial definition that preserves $C^2$ support on the whole shape [41]. For simplicity, the exhaust section comprises only the straight duct downstream of the pump stator. The omitted section corresponds to the casing of the machine stationary blades row, whose cross-sectional area distribution is determined by the profiles of the shroud and the spike.

The machine block is considered fixed, providing operations with a known characteristic map. Consequently, the sections across the pump model inflow and outflow conditions, keeping the Pump Interface Plane (PIP) and the exhaust planes unchanged. According to the chosen model, the intake modification still plays a pivotal role in the determination of the capture streamtube, while nozzle geometry manipulation is mainly considered effective for drag behavior. Specifically, the highlight ($hl$) and throat ($th$) sizes affect the quality of the entering flow, with the former being directly connected with the concept of Inlet Velocity Ratio (IVR). This parameter provides a quantitative description of the capture streamtube shape, following its definition:

$$IVR={\displaystyle \frac{Q}{A_{hl}{v}_{\infty }}}$$

(1)

where Q is the volumetric flow rate through the ODW, $A_{hl}$ is the highlight area, which is inherently related to the highlight radius, $r_{hl}$, and $v_{\infty }$ is the free-stream velocity.

Quantifying the flow capacity of the system relative to undisturbed conditions, the IVR establishes a deterministic criterion for identifying the operating regime. Specifically, when $IVR>1$, the parameter indicates a convergent pre-entry streamtube. In this case, the flow region is bounded by a stagnation line that reaches the intake wall at a point on the outer surface, shifted downstream from the optimal position at the highlight lip. As a result, the entering flow experiences higher accelerations compared to nominal operations. Differently, when $IVR<1$, the opposite configuration arises-known as a pre-diffusion streamtube-which induces positive velocity gradients along the internal intake surface.

2.2. Numerical Setup and Boundary Conditions

A two-dimensional grid is adopted for the computational domain (Figure 2), assembling multiple structured blocks with a tessellation of quadrilateral elements. The far field boundary is separated at $100r_{hl}$ from the near-wall region (Figure 2a) and is shaped as a half circle. The cells dimension is regulated with a geometric progression, starting from a first off-the-wall normal spacing lower than ${10}^{-5}{r}_{hl}$ to ensure an estimated $y^{+}<1$. The element size increases toward the free-stream boundaries, thereby limiting the overall mesh size while maintaining adequate average cell quality. Along wall boundaries, a denser nodes distribution is chosen near rounded edges (Figure 2b), gradually enlarging over straight outlines. Across the different refinements, the maximum included angle is monitored to never exceed ${155}^{\circ }$.

Steady-state RANS equations are formulated in 2D axisymmetric coordinates and solved using the pressure/velocity coupled solver Ansys Fluent^® [42]. Continuity and momentum conservation laws are closed with the $\kappa -\omega$ Shear Stress Transport (SST) [43] and Zwart [44] models, to account, respectively, for turbulence and cavitation phenomena. A single volume fraction transport formulation is solved, coupled with the main system of governing equations, adopting a homogeneous mixture model. Second-order discretisation is adopted for momentum and turbulence terms, while volume fraction is discretised with a Quadratic Upstream Interpolation for Convective Kinematics (QUICK) approach. For pressure terms treatment, a PREssure STaggering Option (PRESTO!) scheme is chosen based on its suitability for cavitation modelling [45].

During initial iterations, mass flow rate is imposed as both inlet and outlet conditions, respectively at the PIP and the stator exit plane. Then, for two-phase simulations, the PIP boundary condition is switched to a pressure outlet to prevent the selection of the nature of the flow exiting the domain, enabling mixed-phase evolution along the connector. To mimic the “Target Mass Flow Rate” option available inside the solver only for single-phase flows, a custom approach is adopted to provide the pressure value at the boundary according to the unbalance between the current and expected mass flow rate. The implemented expression follows the definition reported in the solver’s User Guide [42] for the built-in option. Concerning the farfield boundary, the connector is split into two equal arcs: the forward edge is set as velocity inlet, enforcing free-stream conditions, while the downstream half imposes ambient pressure through pressure outlet formulation. The propulsor’s walls boundaries are treated as no-slip walls.

The solution initialisation is performed using a hybrid technique. Convergence strategies differ between single-phase and two-phase simulations. In the first case, the computations are generally smoother; therefore, a preliminary stage with first-order discretisation is sufficient to stabilise the solution. This is then followed by second-order discretisation until the convergence criteria are satisfied. These include monitoring the residuals of the governing equations, which must drop below 1 · 10⁻⁵. Additionally, the x-component of the wall forces, summed over all body boundaries, is tracked, and its variation between two successive iterations must fall below 1 · 10⁻⁶ to be considered converged.

For two-phase simulations, a dedicated strategy is employed to ensure convergence. The initial iterations are run using a first-order mixture-fluid arrangement, with phase-change phenomena temporarily deactivated. Once these computations stabilise the solution, the cavitation model is enabled, and a first-order discretisation is applied for a first set of iterations before transitioning to higher-order schemes. For both phases, solution stability is further supported by a Courant number ramp, gradually increasing the value up to its default setting. Following this procedure, a minimum of 50 iterations is performed for each incremental step of the Courant number, with a total iteration limit set to 2250. To mitigate potential numerical issues arising from non-smooth geometries, often generated during the optimisation process, an additional convergence criterion is introduced, easing the previous stop conditions. Specifically, the maximum tolerated imbalance in mass flow rate across the pump boundaries is defined as the one resulting in a relative variation in normalised thrust not exceeding 1 · 10⁻⁴.

Table 1. Summary of the numerical setup for single- and two-phase simulations.

	1-Phase	2-Phase
Turbulence model	$\kappa -\omega$ SST	$\kappa -\omega$ SST
Cavitation model	−	Zwart
Momentum discretisation	second order upwind	second order upwind
Turbulence discretisation	second order upwind	second order upwind
Pressure discretisation	second order upwind	PRESTO!
Volume fraction discretisation	second order upwind	QUICK
Free-stream inflow	velocity inlet	velocity inlet
Free-stream outflow	pressure outlet	pressure outlet
Pump inlet	mass flow outlet	target mass flow rate
Pump outlet	mass flow inlet	mass flow inlet
Solid boundaries	no-slip walls	no-slip walls
Courant number	fixed (default)	increasing ramp

compares between the relevant numerical configurations of single- and two-phase simulations.

On average, a converged simulated case took approximately 12 min on a single-node architecture, equipped with 48 Intel CascadeLake 8260 processors @$2.4$ GHz.

2.3. Thrust-Drag Bookkeeping

Providing a direct definition of the processed streamtube for axisymmetric propulsors, the aero-engine Thrust-Drag Bookkeeping (TDB) offers a convenient framework for force accounting in ODW investigations. This technique shares several similarities with the method proposed by 24th I.T.T.C. [46], traditionally employed in marine propulsion studies, yet it overcomes specific limitations, making it a more suitable approach for ODW applications, as motivated in Avanzi et al. [21].

Following typical TDB implementations [47], the adopted notation reflects a clear distinction between force components acting on walls located either inside ($\theta$) or outside ($\varphi$) the thrust domain-an axisymmetric volume bounded by the stagnation and released streamlines (Figure 3). On fluid-dynamic interfaces, gauge forces ($FG$) are applied based on momentum integration.

The corresponding expressions at a generic surface are reported below:

$$\begin{array}{cc}\hfill \varphi ,\theta & =\widehat{x}·\int \int \left[(p-p_{\infty })\widehat{n}+{\overline{\tau }}_w·\widehat{n}\right]dA\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill FG& =\widehat{x}·\int \int \left[(p-p_{\infty })\widehat{n}+\rho \overrightarrow{V}(\overrightarrow{V}·\widehat{n})\right]dA\hfill \end{array}$$

(3)

where p and $p_{\infty }$ are the field and free-stream pressures, $\widehat{n}$ is the surface unit normal, ${\overline{\tau }}_w$ is the shear stress tensor, $\rho$ is the fluid density and $\overrightarrow{V}$ is the velocity field. Then, a reference direction ($\widehat{x}$) is considered to project forces. Assuming an axisymmetric flow evolution, thrust can be considered as aligned along the advancing, axial direction, which will be adopted for projection.

Applying TDB definitions to the reference domain in Figure 3, the nacelle drag, $D_{nac}$, is computed as:

$$D_{nac}={\varphi }_{pre}+{\varphi }_{nac}+{\varphi }_{post}$$

(4)

where the pre-entry (${\varphi }_{pre}$) and post-exit (${\varphi }_{post}$) streamtube forces are required to defined a closed-volume region for the integration. Concerning the former, momentum balance can be conveniently employed to derive a straightforward expression, reading as:

$${\varphi }_{pre}=F{G}_2-F{G}_0+{\theta }_{int}+{\theta }_{sp}$$

(5)

where the free-stream gauge force computation is analytically given as $F{G}_0=\rho Q{v}_{\infty }$. Differently, the post-exit term can only be computed using Equation (2) along the released streamline.

Then, a non-dimensional drag coefficient, $c_{D_{nac}}$, can be defined upon the PIP cross-sectional area, $A_{PIP}$, as:

$$c_{D_{nac}}={\displaystyle \frac{2D_{nac}}{\rho v_{\infty }^2{A}_{PIP}}}$$

(6)

Additionally, computing the force components along all the near-field propulsor’s boundaries, the system net force, T, can be obtained as:

$$T=F{G}_7-F{G}_2-({\theta }_{int}+{\theta }_{sp}+{\varphi }_{nac}+{\theta }_{noz})$$

(7)

Finally, this parameter can be used to compute the propulsive efficiency as:

$${\eta }_{prop}={\displaystyle \frac{T{v}_{\infty }}{Q\Delta {\left(p^0\right)}_{pump}}}$$

(8)

with $\Delta {\left(p^0\right)}_{pump}$ denoting the total pressure jump across the pump boundaries.

2.4. Grid Sensitivity

While the validation of the intake model was already presented in previous works by the authors [20,21], no experimental data are currently available for comparison regarding the external nozzle wall flow distribution. However, the same numerical approach proved reliable for analysing all other components of the configuration. Therefore, this study extends the use of these techniques, assuming their applicability for predicting the fluid dynamic behaviour of the complete arrangement. Specifically, three grid refinements are adopted to assess the dependence of the computational outcomes on the spatial resolution. Coarse, medium and fine meshes account for, respectively: 82k, 184k and 441k cells.

The Grid Convergence Index (GCI) [48] is computed to quantify the discretisation error in estimating computed parameters. The index is evaluated for two relevant flow configurations at both cruise and near-take-off conditions to properly drive the resolution selection according to the tasks expected during the optimisation. A flow configuration is completely defined once three quantities are defined, respectively: the $IVR$, the highlight diameter based Reynolds number, $R{e}_{hl}$, and the cavitation number, $\sigma$. These latter are expressed as follows:

$$\begin{array}{cc}\hfill R{e}_{hl}& ={\displaystyle \frac{\rho v_{\infty }{D}_{hl}}{\mu }}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \sigma & ={\displaystyle \frac{2(p_{\infty }-p_v)}{\rho v_{\infty }^2}}\hfill \end{array}$$

(10)

where $D_{hl}$ is the highlight diameter and $\mu$ is the dynamic viscosity.

The flow field of the two operating points, obtained with the coarse grid, is reported in Figure 4 using contours of the pressure coefficient, $c_p=2(p-p_{\infty })/\left({\rho }_{\infty }{v}_{\infty }^2\right)$. Near take-off (Figure 4a), characterised by $R{e}_{hl}=2.7·{10}^6$ and $\sigma =1.64$, the streamtube at the capture section features a convergent shape, consistent with $IVR=1.11$, indicating an acceleration of the flow entering the inlet opening. Despite the shift of the stagnation point toward the external wall, the major pressure decay occurs just downstream of the highlight lip, leading to the formation of a small, localised vapour bubble before the inlet throat. However, this phenomenon does not noticeably affect the overall performance. Differently, at near-design conditions (Figure 4b), a nominal flow distribution in the proximity of the nacelle leading-edge ensures the absence of cavitation onset. In fact, at these cruise reference flow conditions ($R{e}_{hl}=3.4·{10}^6$ and $\sigma =1.02$), the capture streamtube, aligning with $IVR=0.85$, decelerates before reaching the highlight section, thus preventing local phase transitions. At the exhaust section, flow evolution is constrained by the straight duct configuration, with the throat area determined according to the assumption of a fixed pump. As a result, under both operating conditions, the pressure field within the nozzle remains mostly bounded within the range of free-stream values.

The GCI is evaluated for both the system’s drag coefficient at cruise conditions and the Pressure Recovery (PR), $PR=p_{PIP}^0/p_{\infty }^0$, at off-design conditions, with $p^0$ denoting the stagnation pressure. Following the procedure described in Celik et al. [48], these parameters are denoted by $\phi$, with subscripts indicating the specific refinement level, ranging from 3 (coarse) to 1 (fine). The results of this analysis are summarised in

Table 2. Grid convergence analysis at cruise and off-design operations. The corresponding statistics are the nacelle drag coefficient, $c_{D_{nac}}$, and the pressure recovery, $PR$.

	${\mathit{c}}_{{\mathit{D}}_{\mathit{nac}}}{|}_{\mathit{cruise}}$	${\mathit{PR}|}_{\mathit{off}-\mathit{design}}$
${\phi }_3$	$0.0588$	$0.9853$
${\phi }_2$	$0.0587$	$0.9805$
${\phi }_1$	$0.0586$	$0.9781$
${\phi }_{ext}^{32}$	$0.0581$	$0.9763$
$e_{ext}^{32}$	$0.0113$	$0.0043$
$GC{I}_{medium}^{32}$	$1.394\%$	$0.533\%$
${\phi }_{ext}^{21}$	$0.0578$	$0.9763$
$e_{ext}^{21}$	$0.0137$	$0.0019$
$GC{I}_{fine}^{21}$	$1.685\%$	$0.232\%$

.

The three mesh levels display nearly equivalent performance in predicting propulsive characteristics, with cruise drag and off-design PR GCI indexes stably below $2\%$ and $1\%$, respectively. Although the coarsest grid would offer faster computations without compromising accuracy, the medium-resolution mesh is retained for the following analyses. This conservative choice accounts for potentially non-optimal geometries generated during the optimisation process, which may be more sensitive to local spatial resolution. Retaining a finer grid ensures a more robust evaluation and allows for the inclusion of a wider range of solutions, enriching the statistical significance of the optimisation outcomes.

3. Results and Discussion

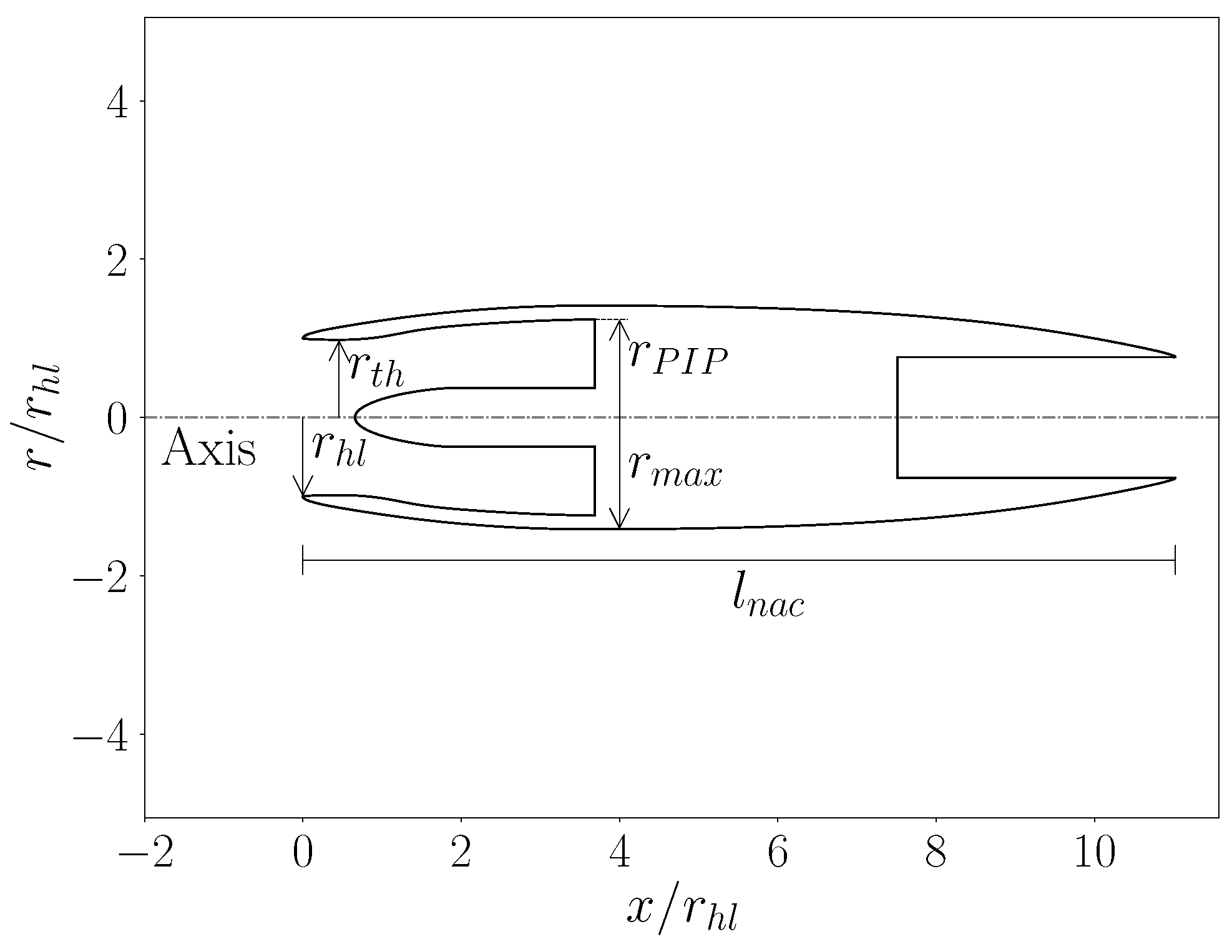
3.1. Propulsor Maps Characterisation

A comprehensive characterisation of the propulsor’s operating points is obtained through systematic analyses across a variety of conditions. The aim is to accurately identify critical scenarios to serve as drivers for the multi-point optimisation process. The investigation begins with a single-phase model to map the nominal performance of the propulsor under ambient conditions that prevent cavitation onset.

To trace the characteristic speedlines, the free-stream velocity is held constant, while the mass flow rate boundary condition across the machine is varied in each simulation. Precisely, $IVR$ is adopted as independent variable and the mass flow rate is estimated from Equation (1) according to the advance condition. This procedure is applied to four different intake geometries: the baseline and three optimised designs obtained in a previous study [21] and labelled as opt1, opt2 and opt3. These shapes are selected from opposite ends of the Pareto front resulting from a two-objective optimisation conducted in that study, which targeted forebody drag and PR under cruise conditions. All configurations are paired with the same nozzle profile to eliminate variability associated with exhaust dynamics (Figure 5).

In contrast, the variation in intake geometry is intentionally used to guide the selection of the off-design operating point, capturing the associated effects relevant to the optimisation process. Specifically, the optimised individuals feature progressively increasing highlight areas compared to the baseline. The resulting data are expressed in non-dimensional units, adopting the $IVR$ as a measure of the flow rate and a thrust coefficient computed as $2T/\left(\rho v_{ref}^2{A}_{PIP}\right)$. Here, the reference velocity, $v_{ref}$, corresponds to the cruise condition of the original design presented in Avanzi et al. [21], which is consistent with $R{e}_{hl}=3.4\times {10}^6$. Although multiple advancing conditions are analysed, the same normalisation parameter is adopted across all speedlines. While the thrust coefficient is conventionally defined with respect to the specific free-stream velocity, such a choice in this case would cause all curves to collapse into a single linear trend with respect to $IVR$, thus preventing a distinction between different speedlines. This approach also enables a clear identification of critical operating points with potential for cavitation onset, denoted with blue star labels when pressures lower than the vapour value, $p_{vap}$, are detected. Observing the behaviour of the parametric curves for any geometry, it is possible to infer that the net thrust has a monotonic smooth trend with respect to the mass flow rate variation. Data can be fitted with a quadratic law, where the second-degree term coefficient has a positive correlation with the advancing speed. In fact, as this parameter increases, the parabola concavity becomes more emphasised, inducing steeper increment of the non-dimensional thrust with augmenting $IVR$. However, the curve shape is not only dependent on the free stream conditions, but also on the geometry outline. Specifically, as the highlight area is increased from the baseline to opt3, the sensitivity to $IVR$ becomes stronger. Especially for the last individual, this dependency determines over a $60\%$ increment of the last operating point at the highest speed, compared to the same condition in opt2.

Considering that the exhaust region exhibits the same dynamics for any configuration, the propulsive performance different characters are driven by the inlet geometry. Specifically, under the same advancing conditions, an equal $IVR$ corresponds to higher mass flow rates processed by wider inlet highlight sections. Consequently, the local flow acceleration becomes stronger, inducing lower wall pressures. Since no cavitation is modelled at this stage, pressure values may reach negative values, with no lower limit restricting the evolution of the variable. The related integration results in a positive contribution to thrust, which motivates the gradual up-shift of the curves as the capture sections enlarges from the baseline to the last optimised individual. Evidently, these geometries exhibit greater susceptibility to cavitation onset. However, this behaviour is closely linked to detailed shape features, as critical pressures tend to develop in localised regions depending on the specific wall curvature. Anyhow, cavitation volumes can potentially evolve externally for low mass flow rate operations, while internal regions may be affected at high $IVR$. Specifically, the phenomenon is clearly influenced by the advancing condition, according to Equation (10). As a results, low-speed operations are in general safer across wider ranges of processed mass flow rates, while, as the free stream velocity increases, cavitation becomes more likely, with clear dependency on the local wall shape.

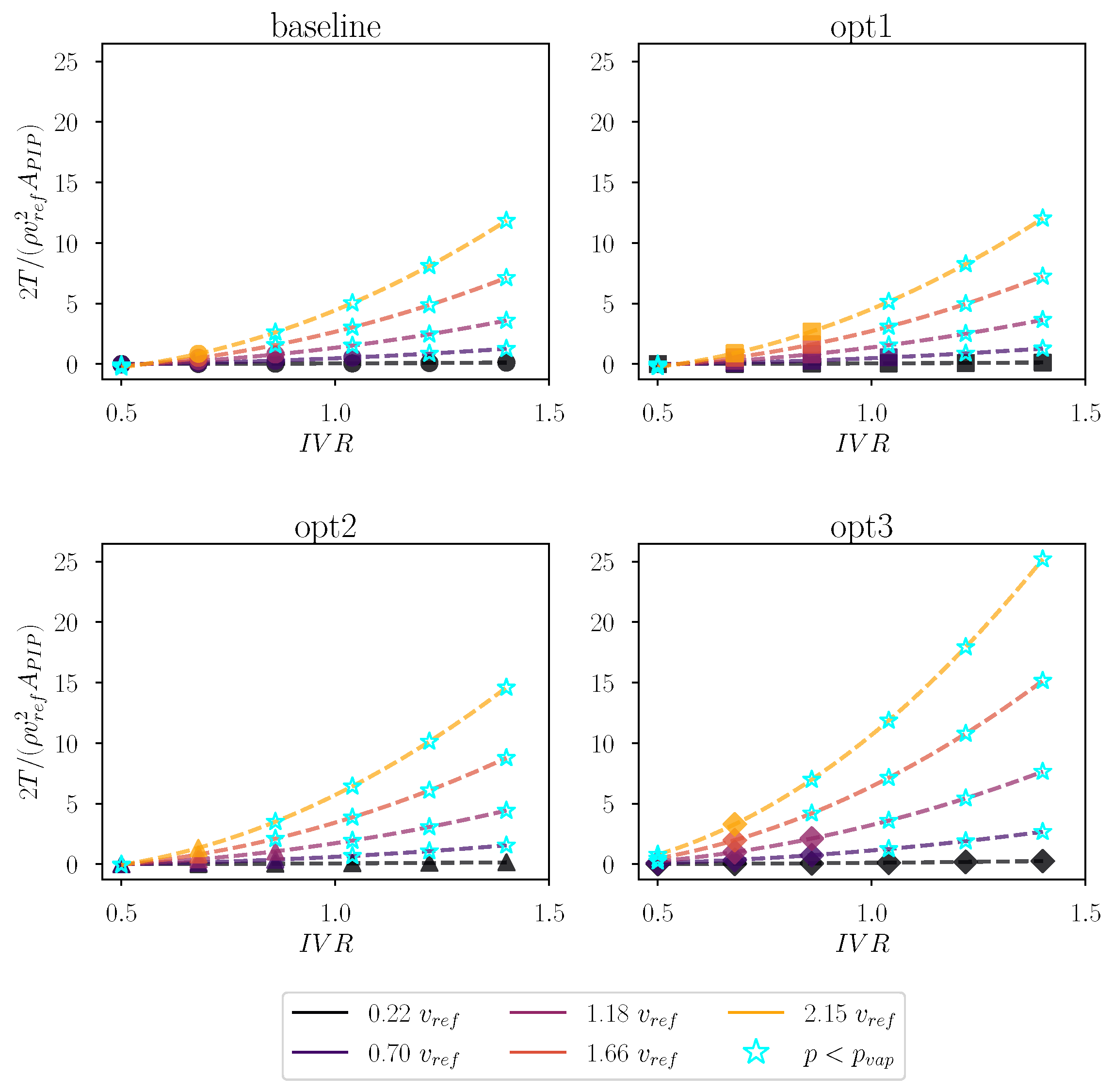
To properly investigate the propulsive behaviour of the system, the same simulations are performed with a two-phase numerical model, including Zwart cavitation formulation. Considering the increased complexity of the flow field evolution, the solution becomes more unstable. Thus, in some simulated points, either divergence or incompatibility with the mentioned convergence criteria determine the rejection of the computed solution. This generally occurs when large cavitation volumes form internally, while external bubbles can be solved with fewer computational issues.

Figure 6 reports the $PR$ as a function of the $IVR$ for the same geometries and free stream conditions analysed in the previous discussion. The results confirm a stronger tendency for cavitation onset at higher free-stream velocities. At low advancing speeds, pressure recovery shows a smooth decreasing trend with increasing $IVR$, consistent with the evolution of the captured streamtube. Specifically, when the stagnation point is located inside the intake, the diffuser operates under higher pressure levels, enhancing recovery at the PIP. As the stagnation point moves outward with increasing flow rates, the diffusion process weakens, leading to reduced $PR$ values. This trend is highly dependent on the free-stream conditions. As the far-field velocity increases, the $PR$ decay becomes more rapid, triggering local phase transitions that cause sudden performance drops. Consequently, as larger capture sections promote local accelerations, the maximum $IVR$ for which convergence is achieved tends to decrease when simulating optimised geometries. The effect of geometry, however, remains strongly localised, preventing the definition of general predictive laws. Conversely, external cavitation has negligible influence on the current performance parameter. Still, increased capture velocities are associated with greater entrance losses, leading to lower $PR$ values at equivalent $IVR$ conditions.

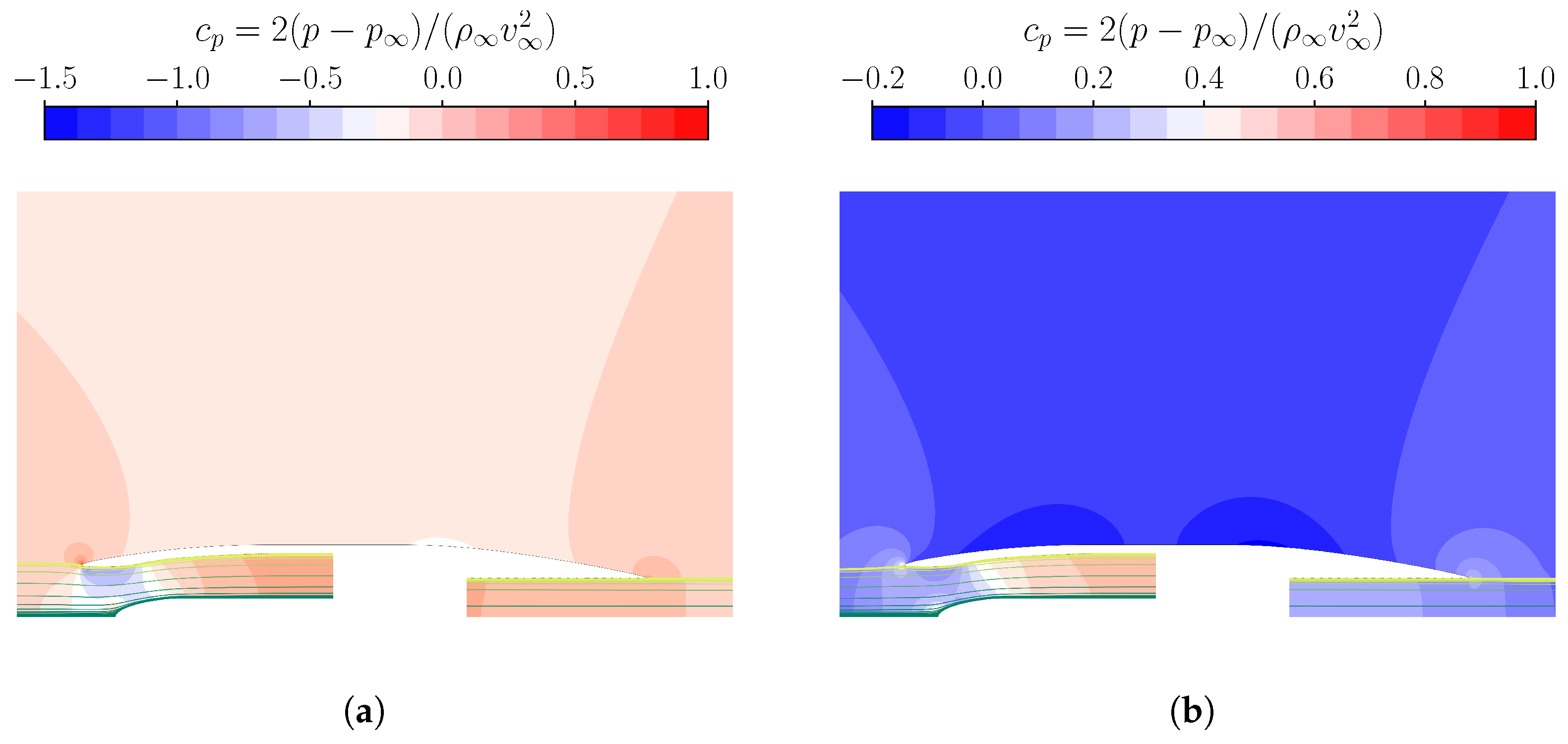
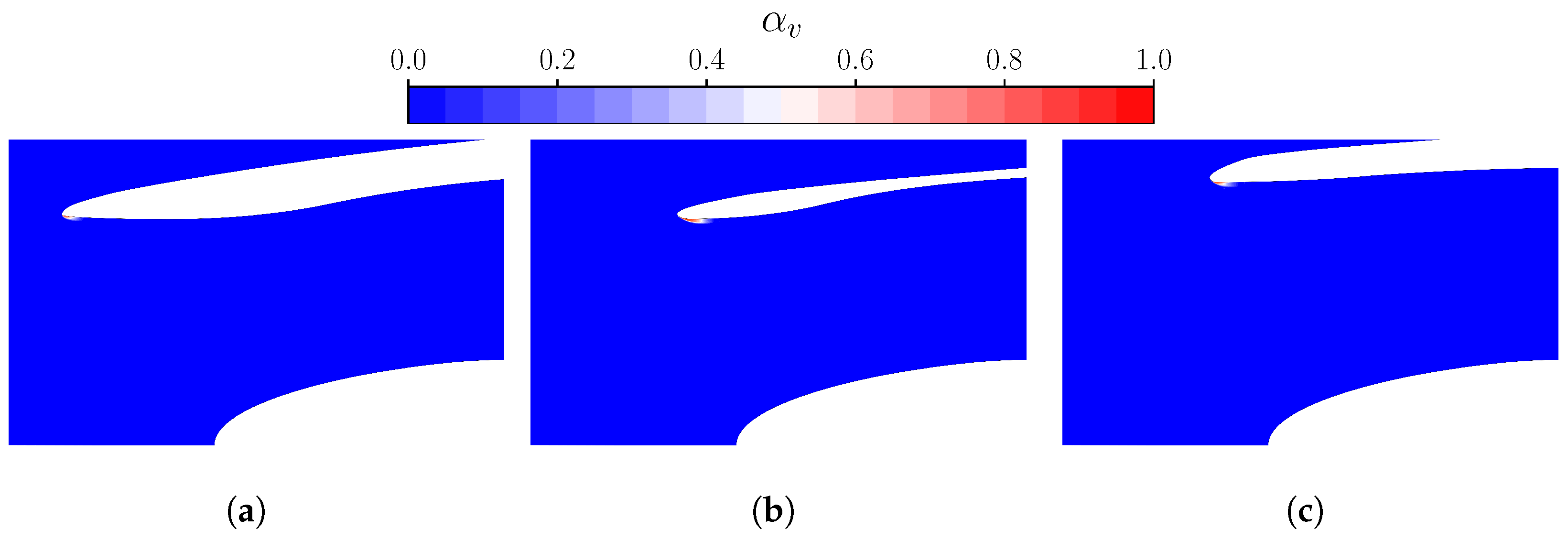
Internal lip cavitation is further examined through contours of vapour volume fractions (Figure 7). The analysis considers operating conditions at $v_{\infty }=0.70v_{ref}$ with $IVR=1.22$, comparing among three geometries: the baseline (Figure 7a), opt1 (Figure 7b) and opt3 (Figure 7c). In fact, although featuring a smaller highlight area than the last geometry, opt2 local cavitation evolution prevents the satisfaction of the continuity criterion across the machine.

For the reference geometry, vapour bubbles rapidly form near the sharp leading-edge and extend downstream over a limited distance, without reaching the inlet throat. While a rounded edge can mitigate abrupt cavitation development-as seen in the opt1 flow field-the shorter lip length in this case facilitates phase transition. This is because the minimum duct section is located closer to the stagnation point, sustaining local acceleration further downstream. As a result, thicker and longer vapour regions develop, extending beyond the throat and directly reducing pressure recovery compared to the previous configuration. In contrast, the flow field around opt3 suggests that a blunter lip slightly reduces the extent of the vapour region. This geometry partially limits the acceleration through the channel, leading to lower total pressure losses at the PIP.

As the mass flow rate increases, the vapour bubble enlarges and extends downstream into the diffuser. This structure introduces additional obstruction and distortion to the incoming flow. As a result, the reduced passage area near the throat further accelerates the flow, triggering a non-linear amplification of the phase transition that rapidly compromises solution stability. For this reason, computations tend to diverge earlier, leading to fewer valid simulations.

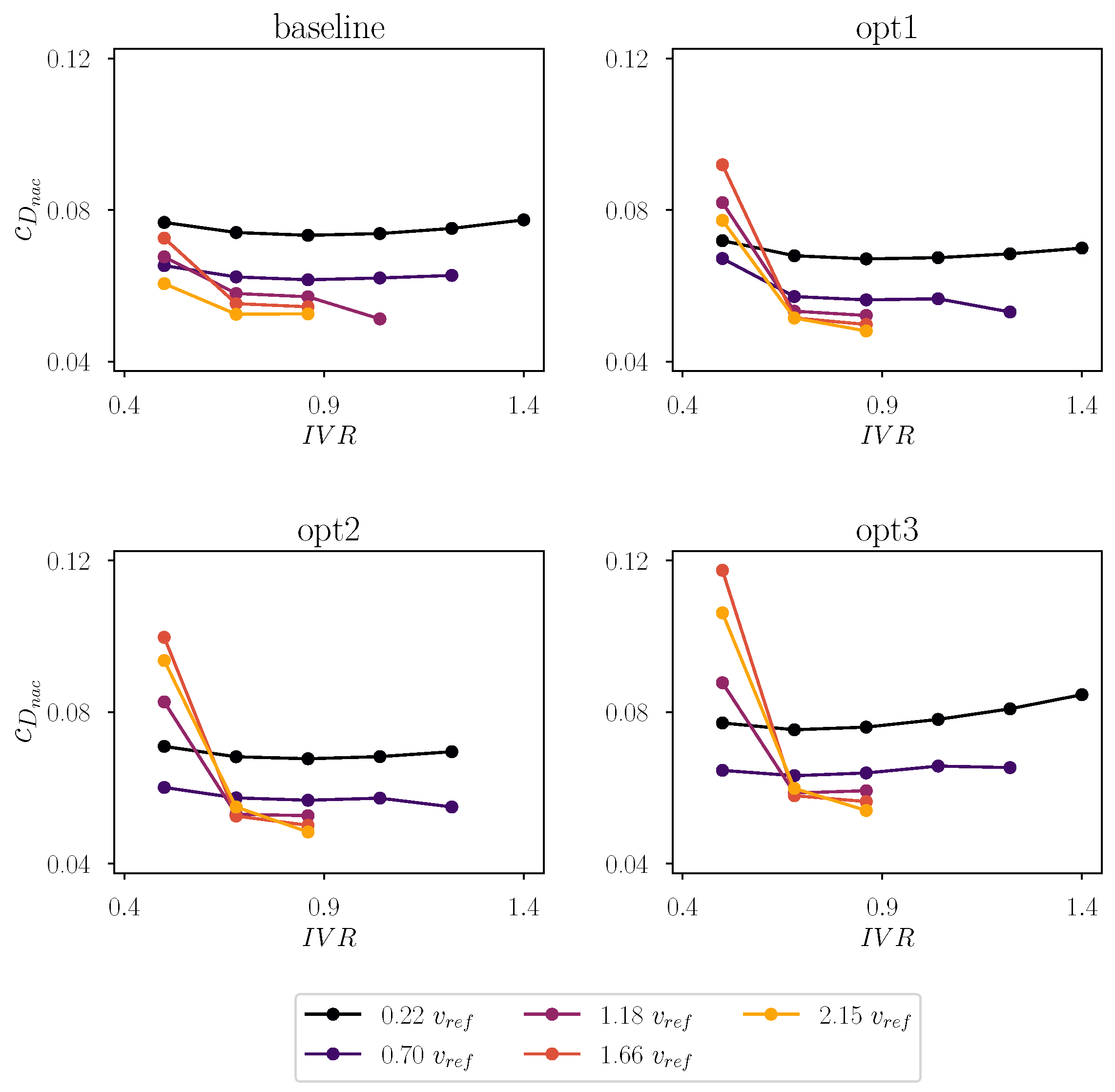
At the same free-stream conditions, the system’s resistance is evaluated by analysing the distribution of the nacelle drag coefficient as a function of the $IVR$ (Figure 8). As previously observed, lower free stream velocities mitigate cavitation evolution. Consequently, from speedlines analysis it follows that the corresponding trends are clearly non-monotonic. In fact, the curves generally agree in recognising a minimum around $IVR=1$, which would correspond to the optimal condition predicted by the potential flow theory. Again, the smooth behaviour of each speedline is corrupted as cavitation occurs, which is typical of flow rate conditions different from nominal. At the early stages of internal cavitation, when $IVR>1$, lip phase transition locally reduces the drag component, promoting the overall performance. However, this evolution is only beneficial at low velocities ($IVR=1.22$, $v=0.70v_{ref}$) where the vapour extension is limited. As cavitation covers large portions, potentially extending downstream inside the diffuser, the entering streamtube is obstructed, inducing instability and feeding distortions and local separations that compromise performance. Differently, at low $IVR$, convergence is generally reached. External cavitation significantly affects nacelle resistance, causing abrupt increases in the drag coefficient, with a stronger dependency observed as the free-stream velocity increases. This trend is further supported by the observation that external cavitation has a lesser impact on solution stability, allowing valid simulations even when vapour regions become substantially more extended compared to those formed within internal structures.

3.2. Design Space Definition and Setup

To perform a systematic analysis using a DOE approach, an automatic procedure is used. Specifically, once a database of geometrical variants is generated, the corresponding individuals need to be discretised and simulated using CFD before post-processing. To easily manipulate the geometry, reducing the number of Decision Variables (DV), the original shape is first parameterised using B-splines. Each control point is assigned a specific Degree of Freedom (DOF), which determines its allowed displacement in the x and/or y direction from its original position in the reference parameterisation (Figure 9). Bounding control points, such as the axial and radial coordinates of the highlight radius and the axial coordinate of the nozzle Trailing Edge (TE), are directly modified. Differently, internal control points are first linearly scaled to match the updated global extension. Subsequently, they are further adjusted based on locally defined ranges, specifically determined for each control point. These local bounds are illustrated in Figure 9a, either as lines or rectangles depending on whether the number of DOFs is 1 or 2, respectively. Concerning the centerbody (Figure 9b), the geometric variants only account for a rigid axial translation, exerted by applying the same x shift to all control points, while, as aforementioned, the pump sections are left unchanged. Based on this parameterisation, the resulting number of DV adopted for the optimisation is 21. An automatic grid generation process is adopted for each individual, which is characterised by a precise and unique set of DV. The mesh sizing is controlled based on the baseline medium refinement, adjusting local nodes distributions according to the specific B-spline extension. Thus, each case features its peculiar cells count, with an overall range between 166k and 210k. For the multi-point investigation, two operating conditions are considered: a near-cruise configuration with $R{e}_{hl}=3.4·{10}^6$ and $\sigma =1.02$, and an off-design scenario with $R{e}_{hl}=2.7·{10}^6$ and $\sigma =1.64$. 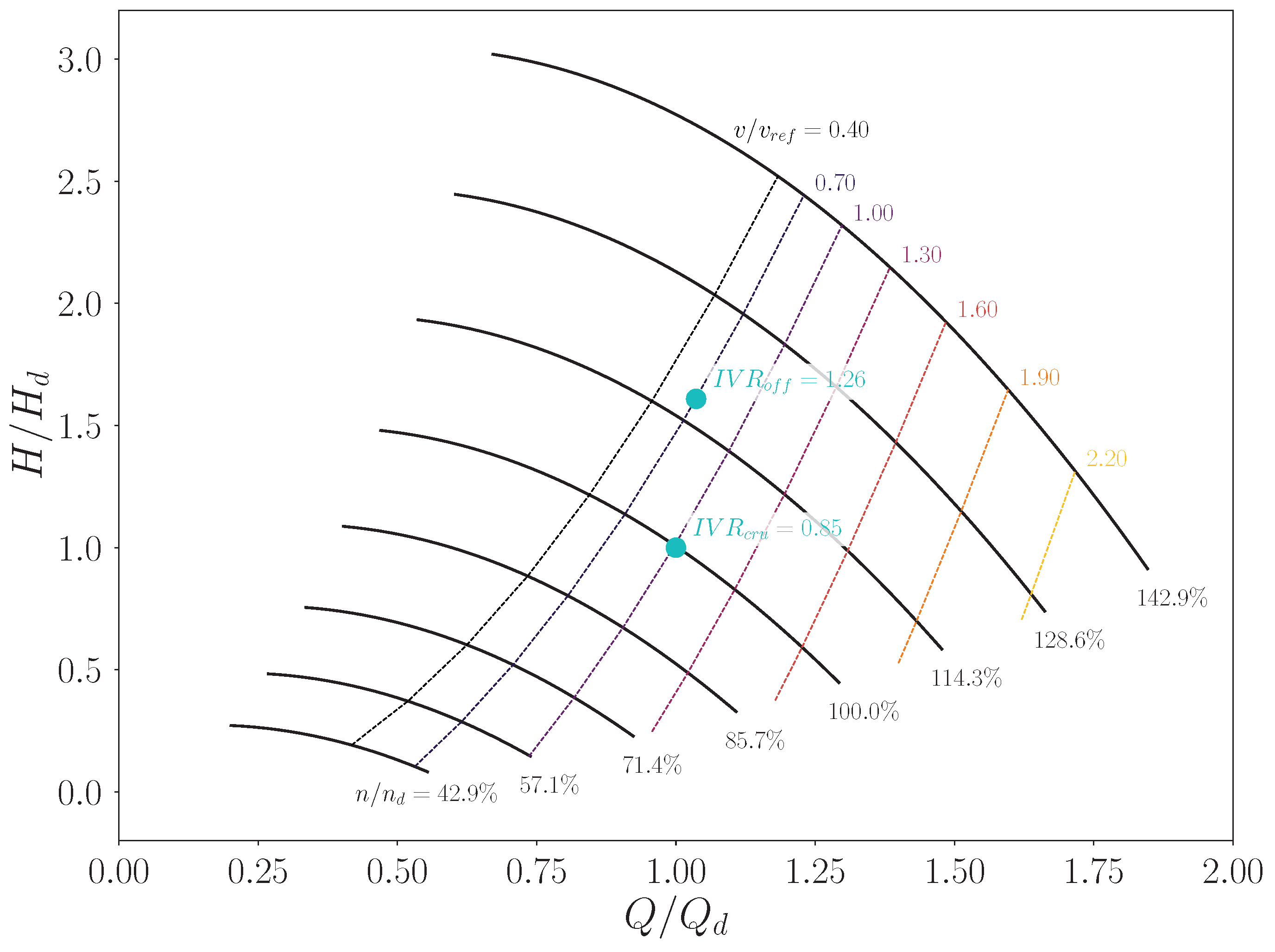Considering the baseline geometry, these points, from CFD simulations, correspond to $IVR=0.85$ and $1.11$, respectively. The same conditions are analysed, considering the potential integration between the pump and the propulsor (Figure 10). The ODW maps are estimated using a meanline approach for different advancing velocities and plotted over the pump characteristic curves, which are propagated from the non-dimensional law for different rotor velocities, n. The machine flow rate, head ($H=\Delta {\left(p^0\right)}_{pump}/\left(\rho g\right)$) and rotational regimes are normalised with the corresponding design values, $Q_d$, $H_d$ and $n_d$. The selected operating points underscore that, under the chosen off design conditions, the $IVR$ constrains the performance required from the pump, specifically indicating operations at higher flow rates and rotor speeds. Here, the discrepancy in the reported $IVR$ value depends on the different accuracy between the meanline method and CFD.

Table 3. Summary of the flow configurations of the two operating points adopted for the optimisation.

	Cruise	Off-Design
$R{e}_{hl}$	$3.4·{10}^6$	$2.7·{10}^6$
$\sigma$	$1.02$	$1.64$
$IVR$	$0.85$	$1.11$

summarises the flow configurations corresponding to the two operating points selected for the optimisation, where simulations are performed according to the solution strategy outlined in Section 2.2.

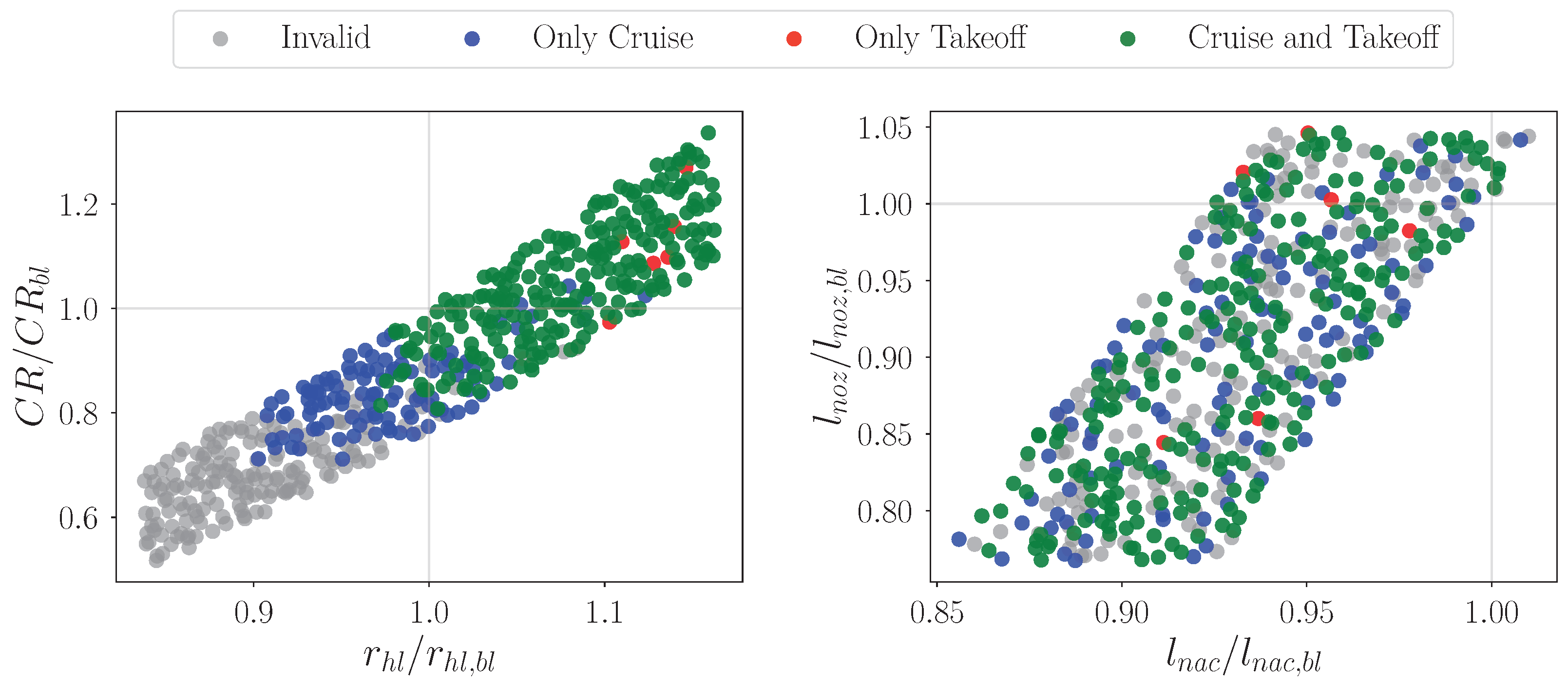
The DOE database comprises 512 individuals, generated using a Sobol sequence [49]. The design space spanned by the resulting geometric variants is illustrated in Figure 11, where the exploration bounds of key global dimensions are shown relative to their baseline values. The chart also depicts the distribution of converged individuals according to the acceptable simulation outcome. It is clear that, while a large number of valid solutions are retained, the proportion of non-converged cases remains non-negligible. A potential correlation between simulation invalidity and geometric configuration emerges when considering the intake-specific cross-sectional dimensions. Two key parameters are examined: the Contraction Ratio, $CR=A_{th}/A_{hl}$—where $A_{th}$ is the throat area—and the highlight radius. Although the overall sampling is symmetric about the baseline, the invalid cases appear predominantly clustered in the lower-left region of this subspace. This is attributed to the boundary condition setup: with a fixed mass flow rate, reducing both CR and highlight radius increases the $IVR$, potentially leading to critical lip accelerations. As a result, convergence is often not achieved at cruise conditions, and even less so under off-design scenarios. Conversely, as these two parameters increase, the number of valid individuals rises. Initially, these include cases converging only at cruise, while further enlargement allows convergence under off-design conditions as well. At the upper-right corner of the parameter space, some individuals exhibit convergence exclusively at off-design. This outcome is associated with excessively low cruise $IVR$ values, which destabilize the flow along the external wall—often due to extensive cavitation or flow separation—thus promoting off-nominal operating regimes. Regarding axial-extension parameters, such as the nacelle length ($l_{nac}$) and the nozzle length ($l_{noz}$), the design space is largely populated by compact nacelle configurations. While the database includes geometries with longer nozzles, most individuals correspond to shorter overall system lengths, with relatively few solutions representing longer configurations.

3.3. Optimal Geometries for Objectives Optimisation

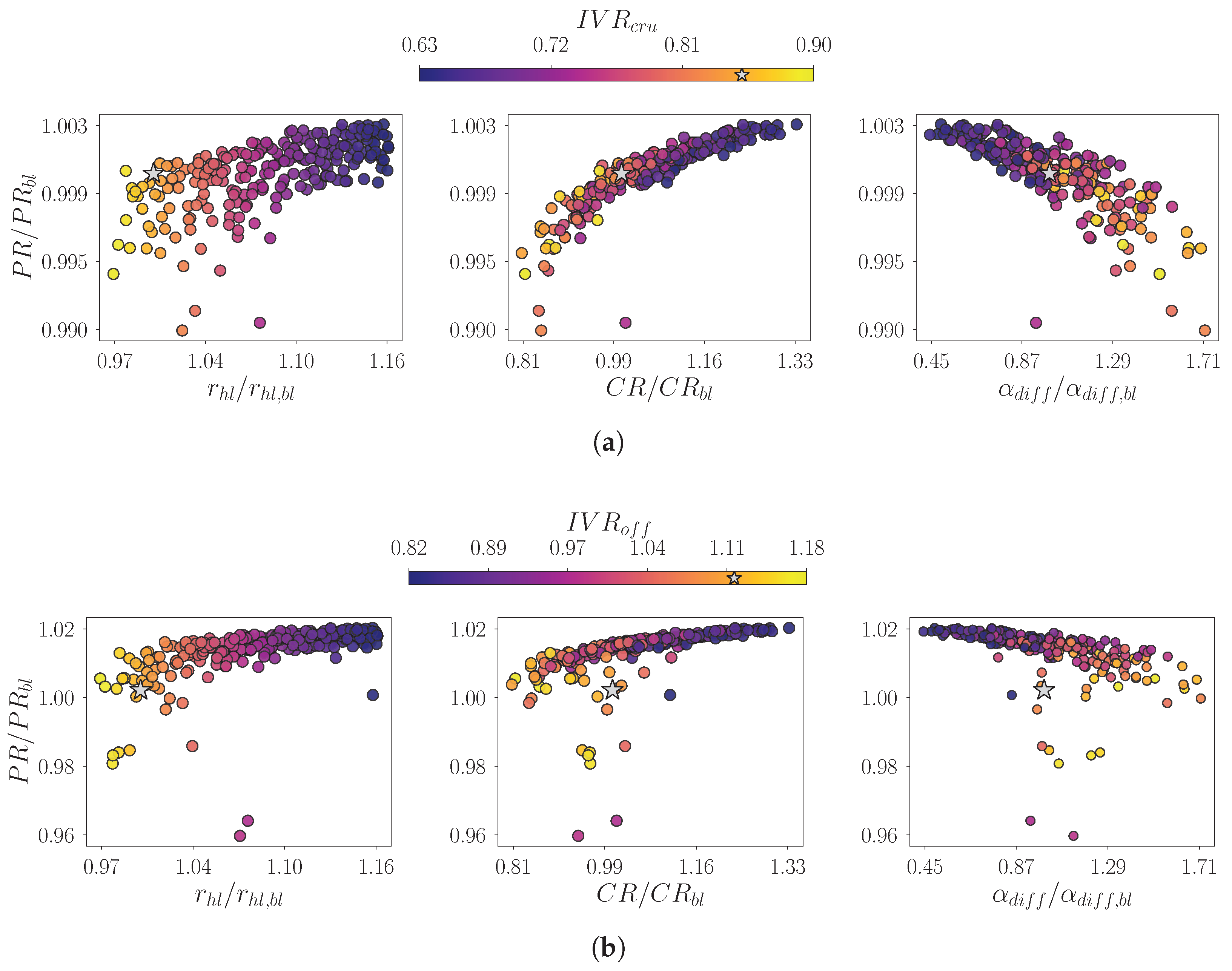
The results of the simulated geometries are analysed to detect potential correlations between propulsive statistics and relevant shape parameters at both in- and off-design operations. Specifically, the recovery sensitivity is initially investigated considering intake relevant dimensions (Figure 12). These include the highlight radius, the contraction ratio and the equivalent diffuser angle, ${\alpha }_{diff}$, computed from the axial (x) and radial (r) coordinates of the PIP and the throat sections, according to the following expression:

$${\alpha }_{diff}=2arctan{\displaystyle \frac{r_{PIP}-r_{th}}{x_{PIP}-x_{th}}}$$

(11)

At design operations (Figure 12a), the propulsive statistics exhibits an evident correlation with both $r_{hl}$ and the $IVR$. In fact, under the same flow configuration, increasing the geometric parameter results in lower streamtube capture ratios. This shape variation shows to improve the recovery capability, an evidence which is further confirmed by the reduction of the dots dispersion and the dissipation of outliers. Enhanced $PR$ can also be achieved with larger contraction ratios. However, this approach does not show a clear correlation with $IVR$, apart from a tendency for lower $IVR$ values to cluster toward the right side of the chart. Notably, the individuals distribute on a narrow band, clearly indicating a non-linear trend with reduced steepness at higher $CR$ values. Conversely, smaller diffuser angles are required to increase the recovery capability. The overall trend again displays a non-linear behaviour, with increased dispersion as the geometric parameter grows—an effect that approximately corresponds to higher capture ratios.

Performing equivalent statistics at off-design conditions, similar considerations can be drawn (Figure 12b). In fact, the $PR$ preserves the same dependencies on the geometrical parameters. However, it is interesting to notice that, in this case, all charts depict distinct correlations, made clearer by considerably narrower dispersion bands. On the other hand, a greater number of outliers arises. Even the baseline solution is evidently outside the clustering of the database individuals, especially when $CR$ and ${\alpha }_{diff}$ sensitivities are considered. This aspect highlights that most individuals’ $PR$ values lie above the reference geometry’s performance. Moreover, the trend is flatter compared to the previous analysis. This evidence suggests a wide room for optimisation at non-nominal operations, with potential to improve the parameter by at least $2\%$. This represents a clear advancement beyond the cruise design improvements reported in previous studies [21]. This combined multi-point investigation reveals that the two objectives are mutually consistent, indicating that a geometry improving cruise operations can also optimise off-design performance.

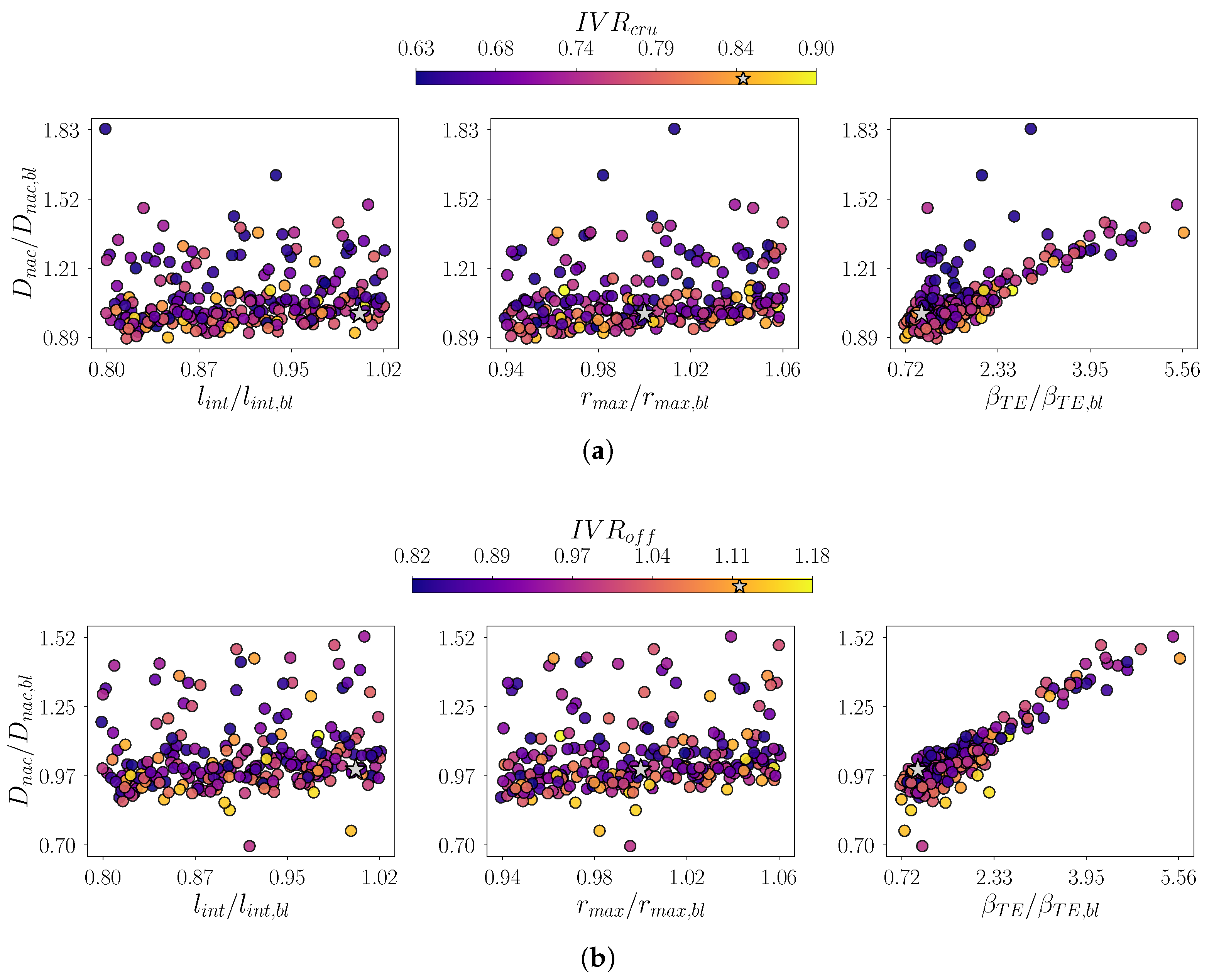
To trace the impact of the overall geometry variation, an equivalent analysis is performed on the nacelle drag, $D_{nac}$ (Figure 13). In this case, the chosen geometrical parameters are: the intake length, $l_{int}=x_{PIP}-x_{hl}$, the maximum nacelle radius, $r_{max}$, and the trailing edge cowl angle, ${\beta }_{TE}$, which can be derived directly as the slope of the segment connecting the ending control points of the external nozzle B-spline.

For in-design operations (Figure 13a), the statistic’s distribution suggests that shorter intakes generally promote drag reduction. While a significant number of outliers exceed the baseline drag, the majority of individuals cluster within a denser region. This latter exhibits a quasi-linear trend, indicating that reducing axial extension generally leads to design improvement. A comparable pattern emerges when analysing the influence of the maximum nacelle cross-sectional dimension. Although the variations are symmetrically distributed around the reference value, the results reveal a consistent reduction in nacelle drag with decreasing diameter—attributable to an overall thinner body. In contrast, the sensitivity to the boat tail angle presents a more scattered distribution. Most geometries group near the baseline, showing both improved and degraded performance. Although the geometric features of the shape variants complicate establishing a clear correlation, the wider spread across the ${\beta }_{TE}$ range reveals a discernible trend. Steeper wall gradients generally correspond to higher drag on the rear nacelle section, thereby degrading overall performance. Finally, no meaningful correlations are observed between $IVR$ and any of the three geometric parameters in the charts.

The analysis of statistics related to off-design operations (Figure 13b) confirms previous observations regarding $PR$. In fact, the sensitivities to the three parameters exhibit trends similar to those observed for cruise performance. However, most of the individuals cluster around values that have lower improvements compared to nominal conditions. Interestingly, in this case all the charts show the presence of few outliers providing significantly better performance, while the ones featuring higher drag are considerably more. Unlike pressure recovery, potential improvements at off-design operations are limited. However, the consistency with cruise design enhancements allows reducing the analysis effort by focusing on a single operating point for each performance metric.

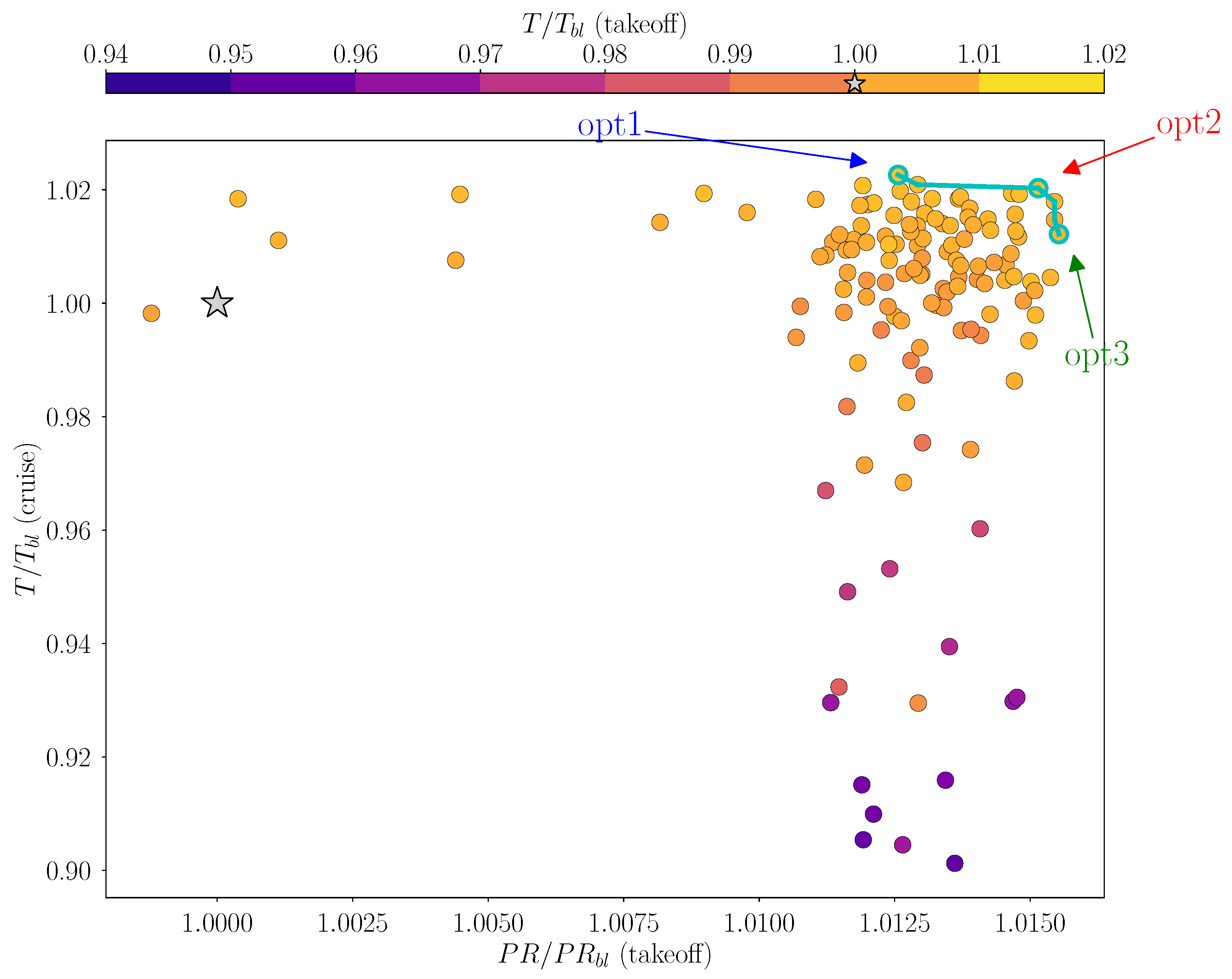
The previous analysis showed that both the $PR$ and the nacelle drag exhibit the same sensitivity to the relevant geometrical parameters at the chosen operating points. According to this consideration, the problem is further restricted and the investigation is progressed using a single objective for each advancing regime. Specifically, the $PR$ showed to be a fundamental statistic to be considered during off-design operations. Additionally, its tendency to be easily optimised under this operating regime makes it a convenient choice. On the other hand, maximising the net force during long-range operations is recommended to improve propulsive efficiency, which is also supported by the wider potential for drag minimisation at cruise conditions. Plotting the two objectives function space confirms their conflicting nature as a Pareto front emerges on the upper right region (Figure 14). To preserve the information regarding the excluded statistics, only a selected set of individuals is reported. Specifically, only the geometries featuring cruise $PR/P{R}_{bl}\ge 1$ are retained, while the off-design net force is adopted to colourise dots.

The chart indicates that almost the entire set of individuals improves off-design pressure recovery. Concerning thrust, many geometries exhibit worse performance, even though the majority groups at enhanced operations up to $+2\%$. Analysing the colour trend, its smooth distribution confirms that maximising cruise performance is also beneficial for off-design conditions, ensuring a similar range of potential improvements.

Three individuals are then selected for additional investigation, to properly characterise how geometrical properties affect the propulsive objective functions. They are chosen from different locations on the Pareto front, which enables to focus on the proper features of optimal individuals. The first and the last individuals, respectively labelled as opt1 and opt3, favour opposite objectives. Specifically, the former has the best drag performance, while the latter provides the highest $PR$ increment. A third geometry, named opt2, is chosen at mild conditions to characterise trade-off solutions. 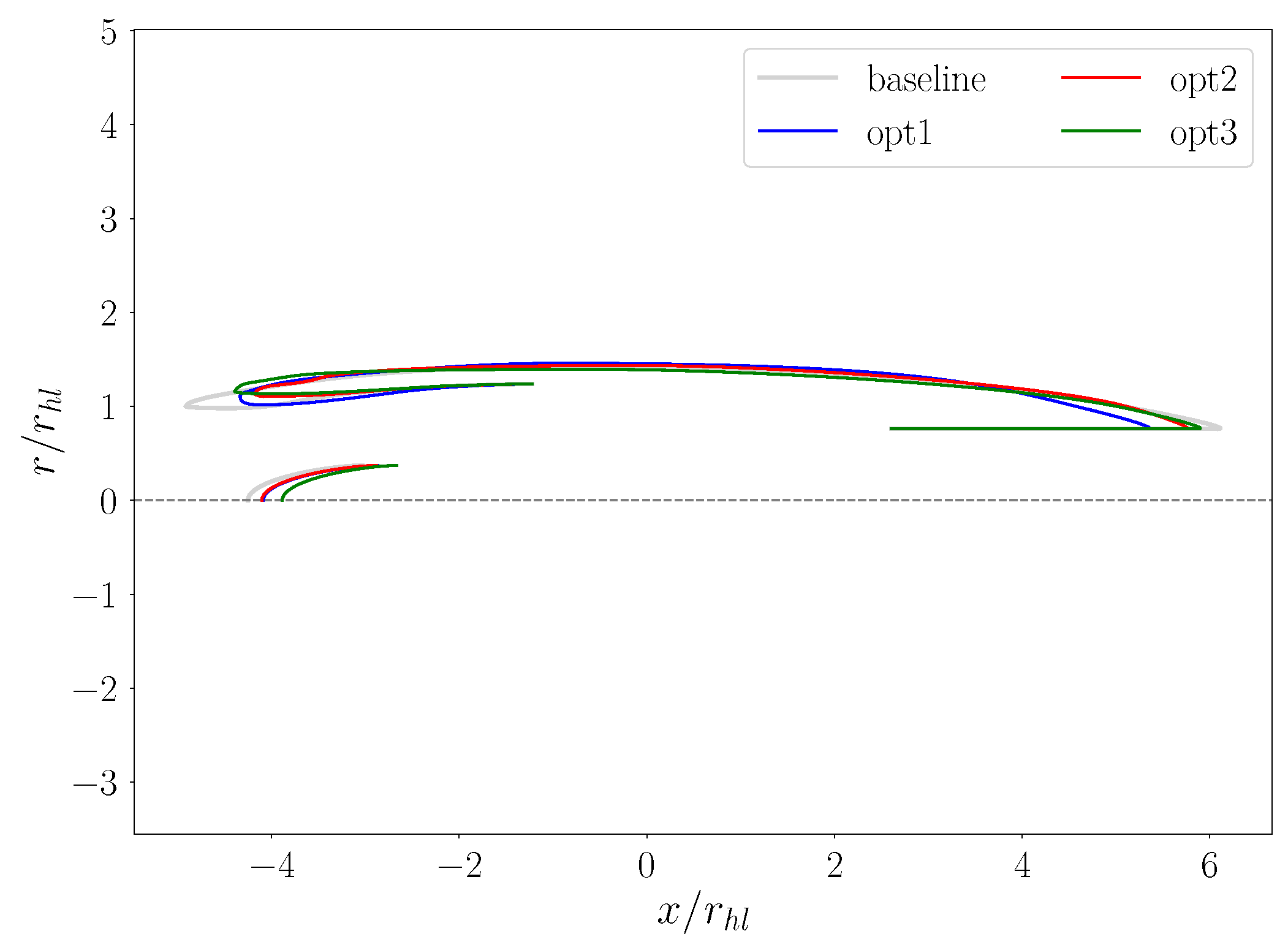The three geometries are compared with the baseline in Figure 15. Maximum net force solution is characterised by a short intake configuration ($-16\%$), where the lip extension is minimised and the spinner tip is aligned with the throat section. Compared to the baseline, the highlight section is significantly enlarged by $23\%$ with blunter leading-edge. The internal diffuser curvature results smoother, while the nozzle extension appears considerably reduced, leading to an overall length decrease by $12\%$. On the other hand, opt3 features a slightly lower intake length reduction, even though the capture section is further increased ($+34\%$). This results in a overall flat profile of the internal nacelle wall, with a considerably larger lip axial extension. In this case, the sharp profile at the leading-edge is preserved, while the spinner is significantly retracted and separated from the throat section. Concerning the trade-off geometry, opt2, its specific properties partially combines the others’ characters. In fact, while the nozzle length and capture sections feature mild sizes, the intake length is evidently the smallest among the individuals ($-20\%$). The spinner location, instead, is almost the same as opt1.

To analyse the flow field distribution locally, the wall pressure coefficient is extracted along the nacelle’s and spinner’s walls. During design operations (Figure 16), the flow acceleration on the external surface (Figure 16a) induces similar pressure coefficients values. Despite considerably exceeding the baseline negative coefficient, they do not reach vapour condition: in fact, according to Equation (10), at cavitation onset $\sigma =-c_p$. The evolution then rapidly re-aligns with baseline pressure field, depicting local overshoots, particularly pronounced in the case of opt2. It should be noted that the use of random sampling for optimisation may introduce irregular local profile curvatures, which could be avoided through more refined, direct approaches.

Major differences can be detected along the internal surface. Specifically, opt1 exhibits a generally lower curve, gradually matching the other solutions toward the PIP. Especially in the contraction region, this individual exploits higher local acceleration to reduce the resistance force pressure component. This evolution is particularly effective on the spinner walls as well (Figure 16b). In fact, the pressure distribution is generally lower along the entire profile compared to any other geometry. This enables a consistent reduction of the drag force related to the spinner, favouring the overall net force maximisation.

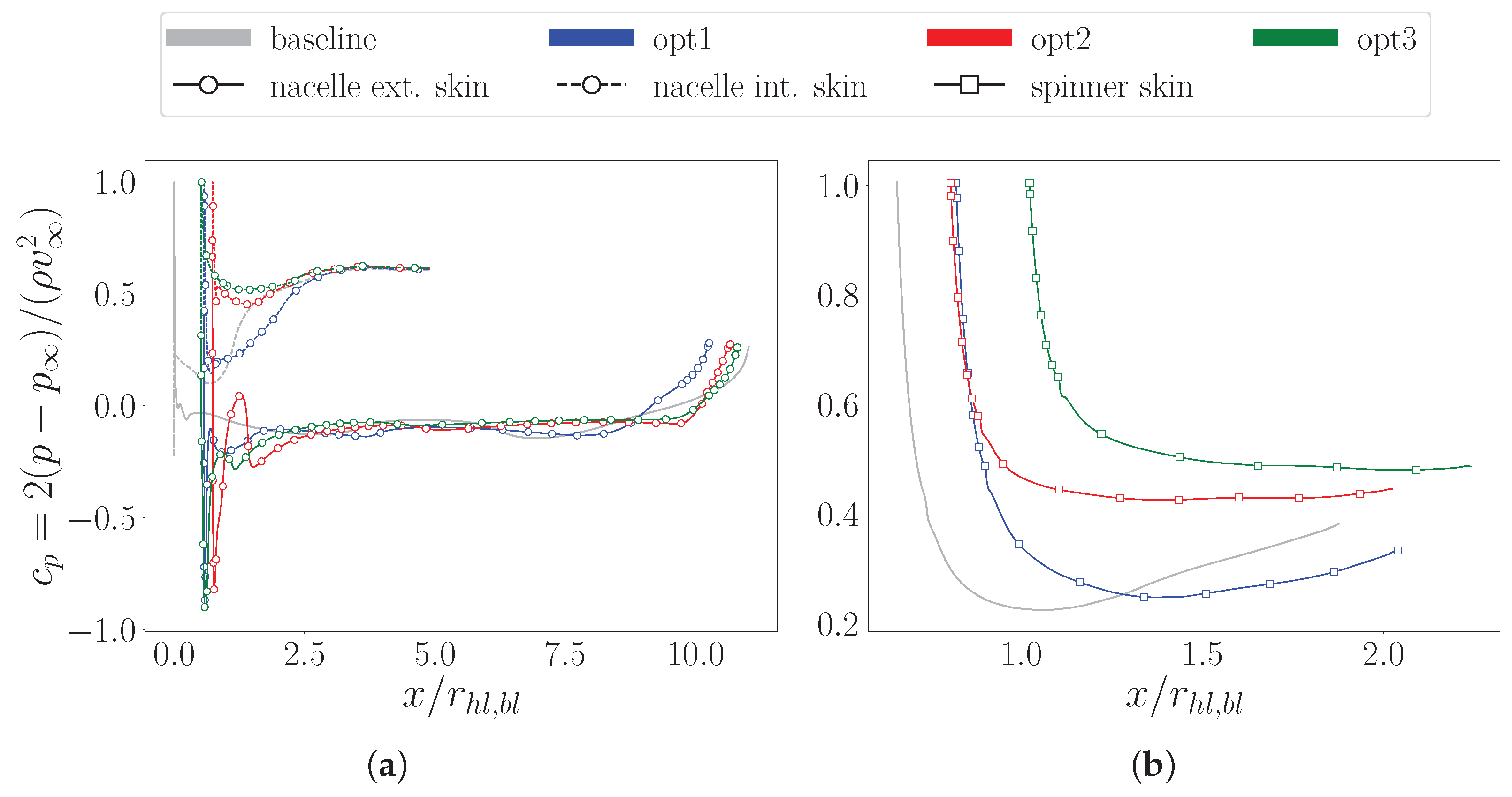
The evolution at off-design operations is considerably different (Figure 17). Specifically, as the the stagnation point shifts outward, local accelerations on the external walls result mitigated (Figure 17a). Conversely, stronger pressure drops occur on the internal surfaces. As a results, the risk of cavitation onset augments in the internal duct, critically inducing the formation of small local vapour bubbles as in the case of baseline geometry. While any other shape prevents this occurrence, the pressure variations are consistent, leading to higher depressions inside the diffuser compared to the outer shroud. The main consequence is that the inlet diffusion process is compromised by highly distorted flows which introduces additional losses, thereby affecting the pressure recovery. In this regard, the advantage of opt3 is that the internal flow is only marginally influenced compared to cruise conditions. In fact, despite exhibiting lower values, the coefficient curve depicts a similar smooth and flat behaviour. A similar consideration applies to the evolution along the spinner walls (Figure 17b). As a result, by controlling flow perturbations throughout the internal channel, this geometry ensures high recovery capability when the propulsor processes a non-optimal capture streamtube. However, this comes at the cost of compromised propulsive efficiency.

4. Conclusions

This study investigates multi-point design aspects required for optimal shaping of Outboard Dynamic-inlet Waterjets (ODW), a novel marine propulsion unit that can operate isolated from the ship. Aiming to guide the nacelle definition through insightful correlations between fundamental geometric features and key propulsive performance statistics, a systematic analysis is conducted to balance conflicting operational performance. a systematic analysis is conducted to balance conflicting operational requirements. In particular, two parameters demand focused attention for achieving efficient mission envelopes: minimisation of system drag to enhance net thrust during cruise operations, and maximisation of inlet pressure recovery to ensure sufficient cavitation margin for the pump under off-design conditions. To address these objectives, an optimisation study is performed, adopting a 2D axisymmetric, two-phase Computational Fluid Dynamics (CFD) model to simulate the flow field past the propulsor. Thus, a database of geometric variants of a baseline outline is sampled using random Design Of Experiments (DOE). The corresponding CFD solutions are analysed to extract relevant propulsive metrics using the aero-engine Thrust-Drag Bookkeeping (TDB).

Initially, the propulsor’s characteristic maps are traced through systematic simulations, varying both free stream conditions and processed mass flow rates. This starting phase underscores that operations at capture ratios higher than nominal may result critical due to the onset of internal lip cavitation, obstructing and distorting the entering streamtube. Based on this characterisation, two relevant operating points are selected-one at cruise and one at take-off-to investigate several geometries and demonstrate how optimal shapes should be designed to ensure safe operations in both scenarios. The resulting database is systematically analysed, showing that the geometrical parameters affect propulsive metrics with consistent outcomes between the two regimes. Thus, the study focuses on two different objectives: off-design Pressure Recovery (PR) and cruise nacelle drag. The corresponding distribution confirms a conflicting trend, showing the emergence of a Pareto front. To characterise the specific impact of geometric features on propulsive performance, three distinct optimised individuals are selected from this region for an in-depth analysis of the corresponding local flow field. The analysis of the intake walls’ pressure coefficient distribution indicates that the pressure field within the inlet section plays a key role, directly correlating with the location of the stagnation point. This flow evolution directly influences propulsive performance, showing that shorter nacelles and blunter lips can improve the nominal net force by $2\%$, while, compromising the propulsive efficiency, wider inlet openings can improve off-design PR over $1.5\%$.

Although the present investigation introduces novel details on the optimal geometric principles necessary to satisfy the requirements at multiple operating conditions, it is limited by the sampling approach, allowing no direct control on the walls’ curves shape. Thus, future studies aim to further advance these outcomes, approaching the optimisation with finer techniques, enabling to control splines sections with higher local accuracy, for improved high-performance geometries.