A Ship Heading Estimation Method Based on DeepLabV3+ and Contrastive Learning-Optimized Multi-Scale Similarity

Abstract

With the rapid development of global maritime trade, high-precision ship heading estimation has become crucial for maritime traffic safety and intelligent shipping. To address the challenge of heading estimation from horizontal-view optical images, this study proposes a novel framework integrating DeepLabV3+ image segmentation with contrastive-learning-optimized multi-scale similarity matching. First, a cascaded image preprocessing method is developed, incorporating linear transformation, bilateral filtering, and the Multi-Scale Retinex with Color Restoration (MSRCR) algorithm to mitigate noise and haze interference and enhance image quality with improved target edge clarity. Subsequently, the DeepLabV3+ network is employed for the precise segmentation of ship targets, generating binarized contour maps for subsequent heading analysis. Based on actual ship dimensional parameters, 3D models are constructed and multi-angle rendered to establish a heading template library. The framework introduces the Multi-Scale Structural Similarity (MS-SSIM) algorithm enhanced by a triplet contrastive learning mechanism that dynamically optimizes feature weights across scales, thereby improving robustness against image degradation and partial occlusion. Experimental results demonstrate that under noise-free, noise-interfered, and mist-occluded conditions, the proposed method achieves mean heading estimation errors of 0.41°, 0.65°, and 0.88°, respectively, significantly outperforming the single-scale SSIM and fixed-weight MS-SSIM approaches. This verification confirms the method’s effectiveness and robustness, offering a novel technical solution for ship heading estimation in maritime surveillance and intelligent navigation systems.

1. Introduction

With the rapid growth of global maritime trade, ships, as the core carriers of international logistics transportation, are experiencing increasing traffic frequency and density, particularly in congested areas such as ports and coastal waterways. The accurate estimation of ship heading has become a critical technical requirement for ensuring maritime traffic safety, improving shipping efficiency, and advancing the development of intelligent unmanned shipping systems [1]. Traditional heading estimation methods primarily rely on onboard navigation equipment (such as electronic compasses and inertial navigation systems) and external radar-based systems (such as the Automatic Identification System (AIS) and surface radars). Although these systems generally provide reliable heading information under most conditions, their accuracy can be significantly affected in complex environments. Therefore, developing heading estimation methods with higher precision and greater robustness is of considerable importance.

Against this background, image-based approaches have emerged as a research hotspot for ship heading estimation. Benefiting from the high resolution and strong adaptability of image data in information perception, image-based methods can effectively overcome some of the limitations of traditional equipment. In particular, they offer significant advantages in real-time performance and fine-grained feature extraction. By capturing images of target ships, visual features (such as shape and contour) can be extracted to infer the ship’s heading. Currently, two primary types of image data are used: optical remote sensing images acquired by optical sensors and radar images acquired by synthetic aperture radar (SAR). Each type has distinct advantages and can provide reliable support under different environmental conditions.

In the domain of optical remote sensing images acquired by optical sensors, Liu et al. [2] proposed a target scale-adaptive detection method combining Hough Transform and convolutional neural networks (CNNs), which improved the accuracy of heading detection but exhibited limited adaptability to multi-target scenarios. Dong et al. [3] utilized wake gray-level accumulation and Radon transform to extract features for estimating ship speed and heading; although the method was efficient, its robustness under weak wake conditions remained limited. Li et al. [4] proposed the point-vector net, which represented ship positions and headings as point-vector combinations through multi-scale feature extraction, achieving a high detection accuracy, but its performance deteriorated in high-density scenes. You et al. [5] introduced OPD-Net, a network based on feature enhancement and regression optimization, which significantly improved detection accuracy but incurred higher computational complexity. Gao et al. [6] developed Ship-VNet, which estimated ship speed and heading through a frequency domain analysis of Kelvin wake features, demonstrating high precision but with a strong dependency on wake quality and image resolution. In summary, although the combination of traditional methods and deep learning techniques based on optical remote sensing images shows great potential in ship heading detection, challenges related to adaptability and robustness under complex sea conditions and multi-target scenarios remain unresolved.

Regarding SAR images, Graziano et al. [7] estimated ship headings by detecting wakes and applying hydrodynamic theory, achieving a high estimation accuracy but heavily relying on the clarity of wake features. Chen et al. [8] proposed a heading estimation method based on single-baseline, large-squint-angle SAR images, combining dynamic programming and genetic algorithms; while achieving high accuracy, the approach suffers from high computational complexity. Joshi et al. [9] utilized the pixel features of SAR and ISAR images to rapidly estimate ship headings, offering high computational efficiency but remaining susceptible to interference under complex backgrounds. Li et al. [10] introduced an anchor-free convolutional framework using rotated bounding boxes to extract ship features for heading estimation, demonstrating good adaptability to multi-angle targets, although its performance declines in densely populated scenarios. Niu et al. [11] developed an efficient encoder–decoder network that achieves heading regression estimation through multi-task learning, providing high accuracy but requiring significant hardware resources due to its model complexity. In conclusion, although SAR images demonstrate excellent heading detection performance under complex environmental conditions, current methods still face challenges such as a high dependency on image resolution, limited robustness in noisy environments, and poor real-time performance.

In summary, although image-based ship heading estimation methods have achieved notable research progress, most existing techniques primarily focus on overhead-view image analysis, while studies targeting optical-sensor-based horizontal observation scenarios remain scarce. Horizontal-view optical images, due to their sea-level perspective, are more susceptible to disturbances such as wave occlusion and water mist. Additionally, monocular vision systems inherently lack depth information, making it challenging to decouple the two-dimensional image space from the ship’s three-dimensional posture. To address these challenges, this study proposes a novel heading estimation framework for horizontal-view optical images, which integrates image enhancement, ship contour segmentation and extraction, and similarity matching, aiming to improve robustness in complex maritime environments.

Considering the impact of water mist, weather conditions, and noise on ship target segmentation and extraction in practical application scenarios [12], image enhancement preprocessing is crucial. Several methods have been proposed to address issues such as image noise and blurring. For instance, Jiang et al. [13] introduced a few-shot-learning-based image denoising method (FSLID), which reduces noise through a two-stage strategy, but its computational complexity makes it challenging to meet real-time requirements. Ding et al. [14] proposed an unsupervised joint defogging and denoising network (U2D2Net), which simultaneously suppresses haze and noise, but tends to cause error propagation, resulting in poor adaptability. Sheng et al. [15] developed a frequency-domain-guided denoising algorithm (FGDNet) that suppresses noise and preserves structure by decomposing high- and low-frequency components. However, this method relies on additional static guidance images, which limits its performance in scenarios involving ship motion or occlusions. Tafti et al. [16] proposed an Adaptive Recursive Median Filter (ARMF), which improves the traditional Recursive Median Filter (RMF) by using entropy to enhance denoising performance, although it requires high computational resources. Xu et al. [17] introduced a fog removal technique combining multi-band fusion and adaptive contrast stretching (ACS) (MF-ACS), optimizing image enhancement and detail representation. However, this method requires parameter adjustments for different scenes, making it difficult for real-time processing. Tang et al. [18] proposed a self-supervised multi-scale blind spot network with adaptive feature fusion (MA-BSN), which delivers excellent performance but suffers from high computational complexity. Galdran et al. [19] proposed a fusion-based variational dehazing method (FVID), achieving dehazing through contrast and saturation optimization. This method does not rely on physical models but has poor robustness when dealing with complex images.

To address the aforementioned challenges and the specific characteristics of maritime images, this paper proposes a cascaded image enhancement method. First, a global brightness compensation is applied to the images through linear transformation. Subsequently, bilateral filtering [20] is employed to achieve a balanced optimization between noise suppression and edge preservation. Following denoising, an improved Multi-Scale Retinex algorithm (MSRCR) [21] is utilized for dehazing. Based on the traditional MSR method [22], MSRCR introduces a color restoration factor $Q$ to enhance local contrast and prevent color distortion, thereby improving both visual quality and target visibility. To clearly demonstrate the superiority of the proposed preprocessing method over existing image enhancement techniques, this paper provides a detailed comparison of the performance of each method in terms of real-time capability, resource dependency, and other factors, as shown in

Table 1. Performance comparison of image enhancement methods.

Methods	Real-Time Capability	Resource Dependency	Edge Preservation	Color Fidelity
FSLID [13]	× 1	×	√ 2	∆ 3
U2D2Net [14]	∆	∆	×	×
FGDNet [15]	×	×	√	∆
ARMF [16]	∆	×	∆	√
MF-ACS [17]	×	∆	∆	√
MA-BSN [18]	×	×	√	∆
FVID [19]	√	∆	×	∆
This Paper	√	√	√	√

¹ ×: Does not meet the requirements, ² √: Meets the requirements, ³ ∆: Partially meets the requirements.

.

To further mitigate environmental interference and accurately extract vessel contours for more precise target processing, various vessel segmentation methods have been proposed in the existing research. For example, Xue et al. [23] proposed an instance segmentation method for occluded vessels, combining residual feature fusion and contour predictors, which significantly improved segmentation accuracy in occlusion scenarios. However, this method is primarily designed for specific scenarios, and its network architecture is relatively complex, demanding higher computational resources. Zhang et al. [24] introduced MAI-SE-Net, which addresses the multi-scale and small target segmentation problem in SAR images through a multi-branch structure and attention mechanism. Although it performs well in SAR images, its applicability in optical images is limited. Yang et al. [25] proposed a probability-induced intuitionistic FCM method based on the fuzzy C-means algorithm, successfully overcoming noise and uneven grayscale issues in infrared images, which achieves good results in infrared vessel segmentation, but it is less effective in complex backgrounds. Considering that the goal of this paper is to enhance vessel target segmentation accuracy and provide reliable contour information for heading estimation, and since the DeepLabV3+ [26] network possesses strong multi-scale feature extraction capabilities and exhibits excellent robustness in complex backgrounds, it is well suited for extracting vessel contours. Therefore, this study selects the DeepLabV3+ network for vessel target segmentation, providing stable support for subsequent heading matching and estimation.

For each target ship, based on its known geometric parameters, a 3D model is constructed using 3ds Max software and rendered at multiple angles. Binary masks are generated through annotation to build a heading template library covering various orientations. Finally, a similarity matching algorithm traverses the segmented ship images and the template library; the heading angle corresponding to the template with the highest similarity is determined as the estimated heading of the target ship. Considering that the traditional Structural Similarity Index (SSIM) [27] relies on fixed weights for similarity measurement, which may be vulnerable to local noise and occlusion, leading to feature loss and judgment errors, this paper innovatively introduces a Multi-Scale Structural Similarity algorithm (MS-SSIM) [28], further optimized through contrastive learning. A triplet-based framework (anchor–positive–negative samples) is constructed between the segmented image and the heading template library, driving the network to autonomously learn optimal weighting across different scales. The overall framework is illustrated in Figure 1. Experimental results demonstrate that the proposed heading estimation framework achieves high accuracy and robust performance, offering a novel technical solution for ship heading estimation in complex maritime environments. The main contributions of this paper are described as follows:

(1)

A cascaded image enhancement framework is proposed, which integrates linear transformation, bilateral filtering, and the MSRCR algorithm to achieve brightness enhancement, denoising, and dehazing, thereby significantly improving the visibility of ship targets.

(2)

High-precision vessel contour extraction is achieved based on the DeepLabV3+ network, providing robust support for subsequent heading estimation through template matching.

(3)

A novel heading estimation method based on multi-scale similarity matching optimized via contrastive learning is proposed. By employing triplet training, the method dynamically adjusts the scale weights in the MS-SSIM algorithm, significantly enhancing robustness against image degradation and partial occlusion.

(4)

A 3D model template library of ships at multiple orientations is constructed, and the proposed method is validated in simulated scenarios, demonstrating comprehensive advantages in both robustness and accuracy.

The remainder of this paper is organized as follows: Section 2 provides a detailed description of the proposed methodology, including image preprocessing, vessel contour segmentation based on the DeepLabV3+ network, and the MS-SSIM algorithm with multi-scale weights optimized through contrastive learning. Section 3 presents the experimental results under three typical conditions: interference-free, noise-interfered, and water-mist-obstructed scenarios. Section 4 discusses the limitations of the current research. Section 5 concludes the paper and outlines directions for future work.

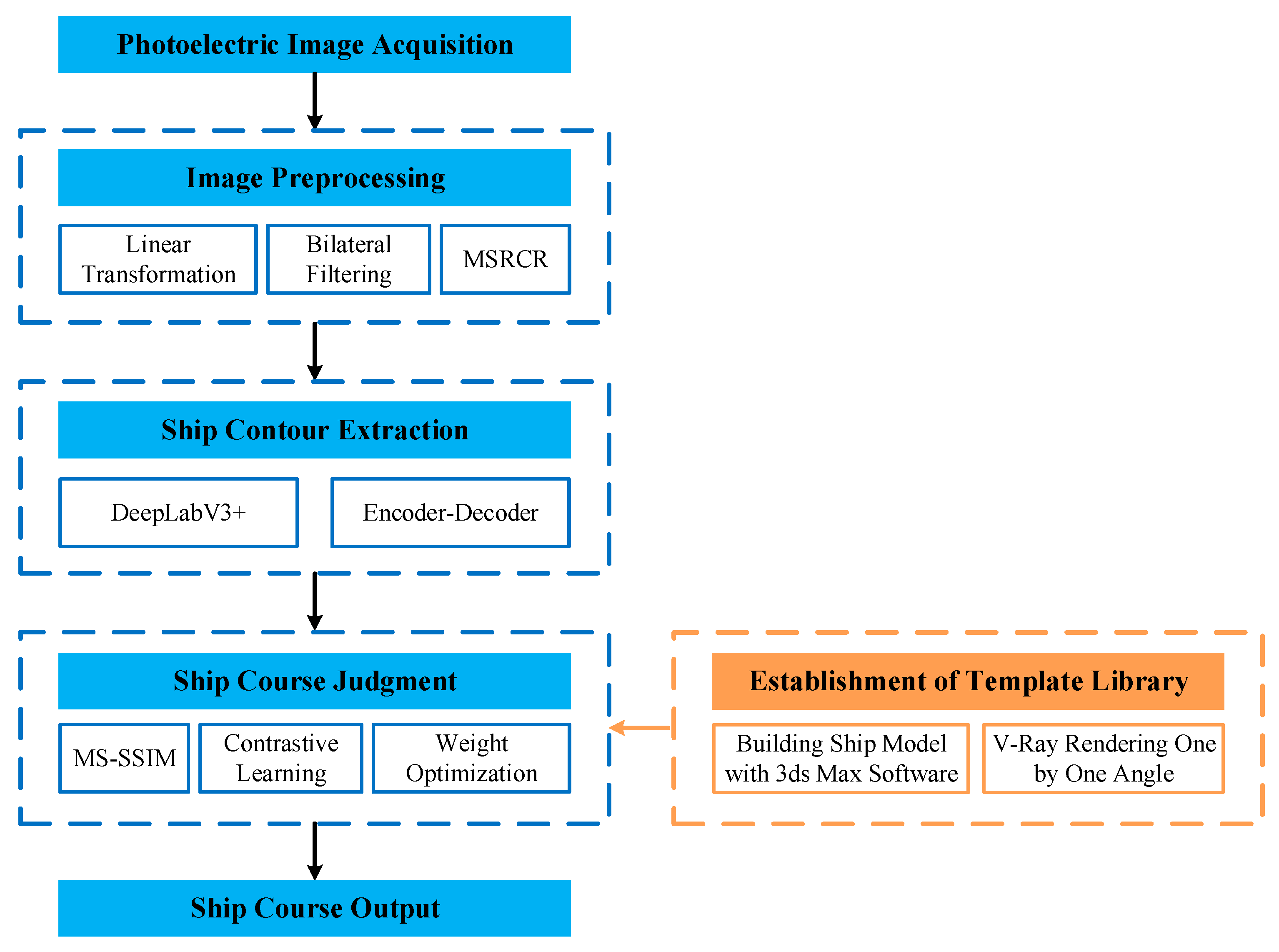
2. Methodology

2.1. Image Preprocessing

2.1.1. Brightness Enhancement

During the acquisition of maritime images, variations in natural lighting conditions—such as cloudy weather, dawn, or dusk—often result in overall insufficient image brightness. Such low-light environments hinder the discernibility of the edge details of target vessels, consequently reducing the accuracy of subsequent segmentation and matching tasks. Therefore, enhancing the brightness of images to more clearly reveal target details under low-light conditions constitutes a critical preprocessing step. Brightness enhancement not only improves the saliency of vessel targets but also provides higher-quality data input for subsequent image segmentation and template matching tasks.

In this study, a linear transformation approach is adopted to adjust image brightness. The fundamental principle involves multiplying each pixel value by a constant factor to modify the brightness, as shown in Equation (1):

$$T^{\prime }\left(x,y\right)=\omega T\left(x,y\right)+\lambda$$

(1)

where T(x, y) and T’(x, y) represent the pixel values at position (x, y) in the original and the output images, respectively; ω denotes the scaling factor; and λ represents the offset value.

2.1.2. Denoising

Maritime images acquired by optical sensors are often accompanied by various types of noise interference, such as sensor noise, sea wave textures, and noise induced by background complexity. These noises not only affect the clarity of target edges but also introduce spurious features, disrupting the accuracy of subsequent segmentation and matching tasks. Although traditional denoising methods (such as Gaussian filtering) can effectively smooth the image, they tend to result in the loss of edge information, making them unsuitable for image processing tasks that require the preservation of details. Bilateral filtering, which combines spatial distance and pixel intensity similarity for weighted averaging, can effectively remove noise while preserving target edge information and avoiding the blurring of target contours. As such, it is particularly well suited for noise reduction in maritime images.

Bilateral filtering is a nonlinear filtering method that integrates the spatial proximity of image pixels with pixel intensity similarity for comprehensive processing. During the denoising process, bilateral filtering simultaneously considers spatial information and grayscale similarity, enabling effective noise reduction without compromising edge information. The core principle involves using a kernel to perform convolution, where the output pixel l(m, n) depends on a weighted combination of neighboring pixel values, as shown in Equation (2):

$$l\left(m,n\right)={\displaystyle \frac{{\displaystyle {\sum }_{p,q}f\left(p,q\right)u\left(m,n,p,q\right)}}{{\displaystyle {\sum }_{p,q}u\left(m,n,p,q\right)}}}$$

(2)

where (m, n) represent the coordinates of the pixel being convolved, (p, q) denote the coordinates of neighboring pixels, and f(·) indicates the pixel value at a given coordinate. The weighting coefficient u(·) depends on the product of the spatial domain kernel g and the range domain kernel t, as expressed in Equation (3):

$$u\left(m,n,p,q\right)=g\left(m,n,p,q\right)\cdot t\left(m,n,p,q\right)$$

(3)

The spatial domain kernel g(·) is computed based on the pixel coordinates, as shown in Equation (4):

$$g\left(m,n,p,q\right)=\exp \left[-{\displaystyle \frac{{\left(m-p\right)}^2+{\left(n-q\right)}^2}{{\sigma }_s^2}}\right]$$

(4)

The range domain kernel t(·) is computed based on the pixel intensity values, as shown in Equation (5):

$$t\left(m,n,p,q\right)=\exp \left[-{\displaystyle \frac{{‖f\left(m,n\right)-f\left(p,q\right)‖}^2}{{\sigma }_r^2}}\right]$$

(5)

where σ_s² and σ_r² represent the variances of the Gaussian kernel functions.

2.1.3. Defogging

The haze, humidity, and atmospheric scattering effects in maritime environments often lead to reduced contrast and color distortion in optical images, especially under the conditions of long-distance observation or foggy weather, where the clarity and visual features of target vessels are severely compromised. The Multi-Scale Retinex (MSR) algorithm is a method that simulates the human visual system’s perception of images. By applying multi-scale filtering to the image’s luminance component, it effectively enhances the contrast and detail of the image. Its principle is shown in Equation (6):

$$R\left(x,y\right)={\displaystyle \sum _k^K{w}_k\log \left[\frac{I\left(x,y\right)}{F_k\left(x,y\right)\ast I\left(x,y\right)}\right]}$$

(6)

where I(x, y) and R(x, y) represent the input and output images, respectively; F_k(x, y) denotes the Gaussian convolution kernel at different scales; ∗ represents the convolution operation; K is the number of scales; and w_k is the weight coefficient. The coordinates (x, y) represent the pixel positions in the image.

However, the traditional MSR algorithm is prone to color distortion. To address this issue, the MSRCR method is adopted in this study to enhance the quality of maritime images affected by haze and other environmental factors, thereby providing high-quality input data for subsequent target segmentation and course matching tasks. Based on the MSR algorithm, the MSRCR algorithm integrates a color restoration technique by introducing a color restoration factor Q, which compensates for the color distortion caused by local contrast enhancement. This enables the algorithm to enhance contrast while simultaneously restoring the natural colors of the image, thereby significantly improving image clarity and target recognition. The principle of MSRCR is shown in Equation (7):

$$R_{\mathrm{MSRCR}}\left(x,y\right)=Q\left(x,y\right)R_{\mathrm{MSR}}\left(x,y\right)$$

(7)

The expression for the introduced color restoration factor Q is given in Equation (8):

$$Q_i\left(x,y\right)=f_r\left[{\displaystyle \frac{I_i\left(x,y\right)}{{\displaystyle \sum _{j=1}^N{I}_j\left(x,y\right)}}}\right]$$

(8)

where Q_i represents the color restoration coefficient for the i-th channel, f_r(·) denotes the color space mapping function, I_i(x, y) represents the image in the i-th channel, and N indicates the number of channels. Typically, it can be expressed in the form shown in Equation (9):

$$Q_i\left(x,y\right)=\beta \lg \left[{\displaystyle \frac{\alpha I_i\left(x,y\right)}{{\displaystyle \sum _{j=1}^N{I}_j\left(x,y\right)}}}\right]$$

(9)

where α and β are constants, β adjusts the gain intensity, and α controls the nonlinearity strength.

The preprocessing workflow and its effects are shown in Figure 2:

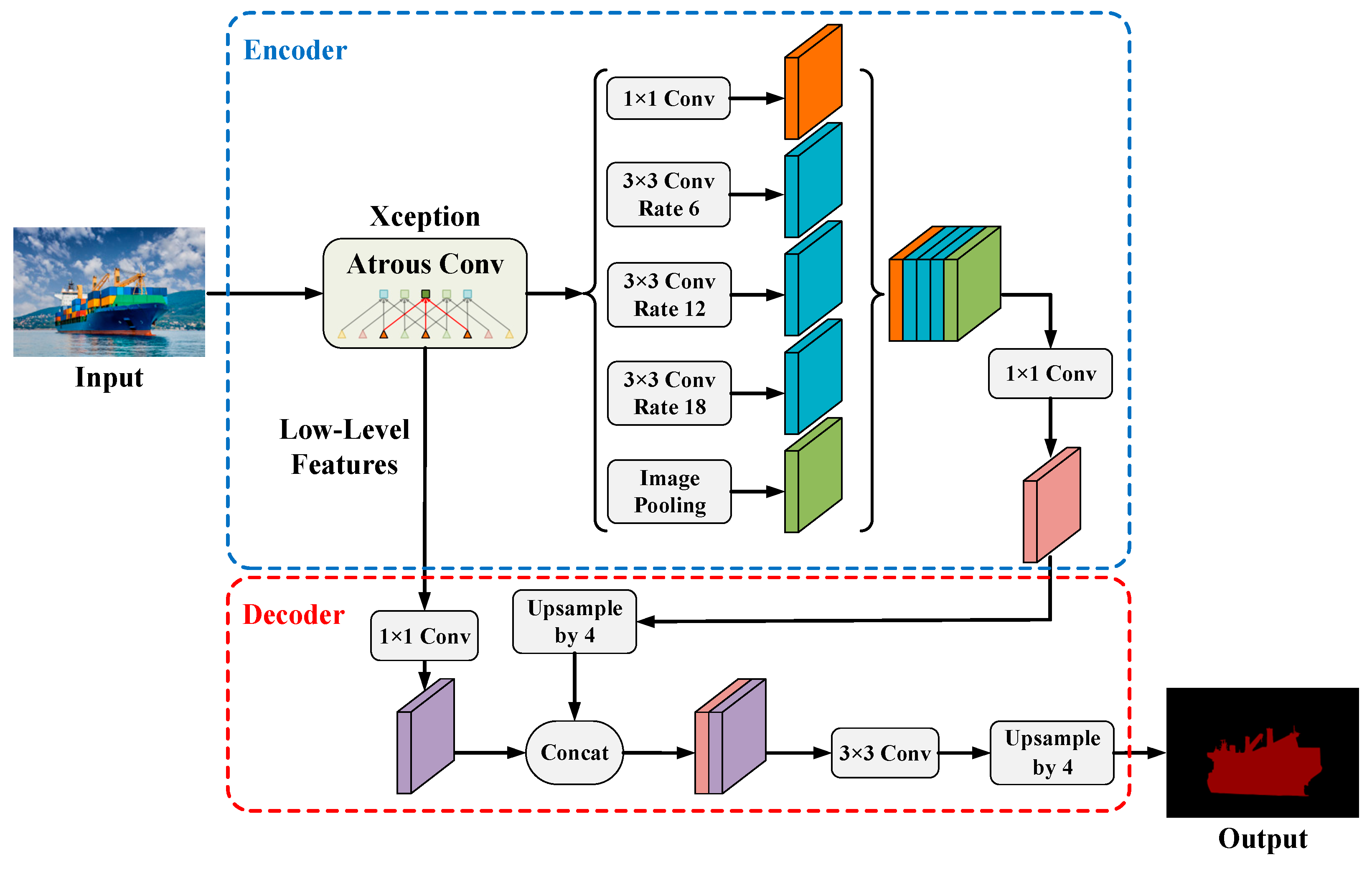
2.2. Ship Target Contour Extraction

DeepLabV3+ is a classic deep learning model for image semantic segmentation, known for its powerful feature extraction capabilities and excellent performance in segmenting target boundary regions. It is widely applied in image processing tasks under complex scenarios. Its architecture is illustrated in Figure 3.

Based on deep convolutional neural networks, DeepLabV3+ further optimizes the original DeepLabV3 [29] architecture by introducing an efficient encoder–decoder module, significantly improving the accuracy of target boundary segmentation in complex images. Additionally, the network incorporates atrous convolution (also known as dilated convolution) within both the encoder and decoder modules, enabling the model to maintain high segmentation accuracy and computational efficiency simultaneously. In this study, DeepLabV3+ is selected as the ship target segmentation model for the following reasons:

(1)

Multi-scale receptive field via atrous convolution: In the encoder part of DeepLabV3+, atrous convolution allows the model to capture the semantic features of ship targets at different scales with multi-scale receptive fields, making it particularly suitable for maritime images where targets are unevenly distributed over various distances.

(2)

Contextual fusion through the ASPP module: The Atrous Spatial Pyramid Pooling (ASPP) module effectively integrates local detail information and global contextual information, enhancing the model’s segmentation capabilities in complex environments and supporting multi-target ship segmentation tasks.

(3)

Edge feature restoration through the decoder: The decoder of DeepLabV3+ fuses high-level semantic features with low-level edge features extracted by the encoder, generating high-resolution segmentation results, which are well suited for the accurate segmentation of elongated ship structures and contours.

The DeepLabV3+ architecture consists of an encoder and a decoder. The encoder includes the Xception backbone network [30] and the ASPP module, which are responsible for extracting high-level semantic features. The decoder merges low-level features and restores the feature maps [31].

In the encoder, the input image first passes through the depthwise separable convolutions of the Xception backbone, efficiently extracting semantic information. Subsequently, features are extracted layer by layer through cascaded modules and atrous convolutions [32]. The cascaded modules employ a serial structure to progressively deepen the network, thereby enhancing feature representation capabilities. Atrous convolutions expand the receptive field to capture wide-range contextual information while reducing feature dimensionality and preserving sensitivity to broad spatial structures [33].

In the decoder, the high-level features output by the encoder are first upsampled by a factor of four to restore the resolution to one-quarter of the original image size. Simultaneously, the low-level features extracted from the backbone are processed through a 1 × 1 convolution to match the number of channels of the high-level features. The two sets of features are then fused and passed through subsequent modules of the decoder. After fusion, a 3 × 3 convolution further refines local information, and finally, a 4× upsampling restores the feature map to the original image resolution, producing the final segmentation result [34].

In the proposed method, DeepLabV3+ is employed to input preprocessed optical images into the network, accurately segment ship target regions, and eliminate background interference, thereby providing high-quality input data for subsequent template-based heading estimation.

2.3. Dynamic Multi-Scale Similarity-Based Heading Matching

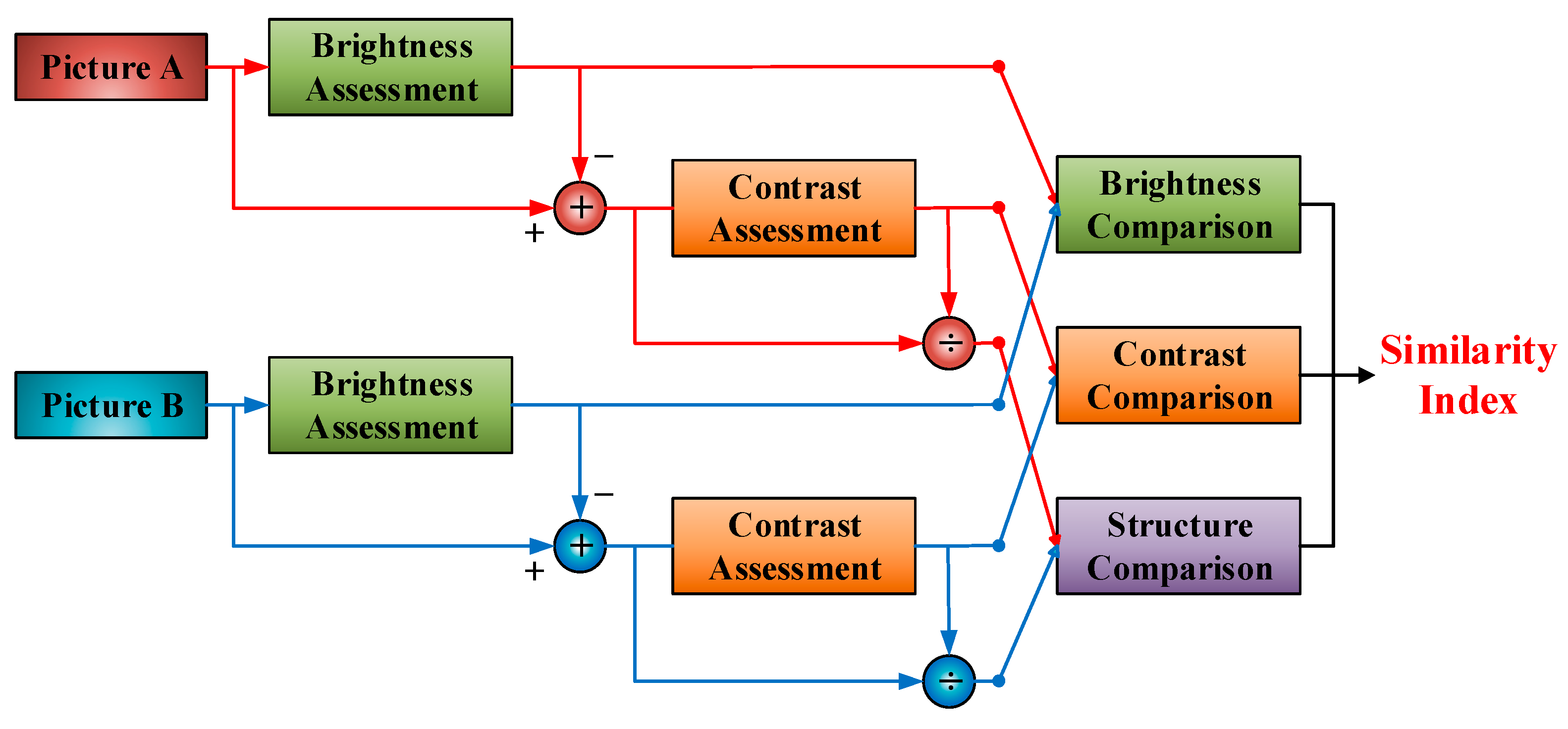
2.3.1. SSIM

The Structural Similarity Index is a widely used metric for image quality assessment, designed to evaluate the similarity between two images in terms of luminance, contrast, and structural information by simulating the perceptual mechanisms of the human visual system. Unlike traditional pixel-difference-based metrics such as Mean Squared Error (MSE) [35] and Peak Signal-to-Noise Ratio (PSNR) [36], SSIM focuses primarily on structural information within the image, allowing it to more accurately reflect the actual human visual perception of image quality. As a result, SSIM has been extensively applied in fields such as image processing, image compression, image restoration, and image segmentation, and has become an important standard for image quality evaluation.

The core concept of SSIM is to simulate the human eye’s process of perceiving image quality. When judging the quality of an image, the human eye does not rely solely on direct pixel differences but also comprehensively considers luminance, contrast, and structural features. Therefore, SSIM assesses the overall similarity between images by separately evaluating the similarities in brightness, contrast, and structure. The overall computational structure of SSIM is illustrated in Figure 4.

During the computation process, the differences in luminance, contrast, and structure between image A and image B are measured using the mean grayscale value, standard deviation, and covariance of the images, as shown in Equations (10)–(12):

$${\mu }_A={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{x}_i}$$

(10)

$${\sigma }_A=\sqrt{\left({\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{i=1}^N{\left(x_i-{\mu }_A\right)}^2}\right)}$$

(11)

$${\sigma }_{AB}={\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{i=1}^N\left(x_i-{\mu }_A\right)\left(y_i-{\mu }_B\right)}$$

(12)

where μ_A and σ_A represent the mean luminance and the standard deviation of the grayscale values of image A, respectively; σ_AB denotes the grayscale covariance between images A and B; N indicates the number of pixels in the image; and x_i represents the grayscale value of each pixel. The luminance similarity, contrast similarity, and structural similarity between images A and B are calculated as shown in Equations (13)–(16):

$$l\left(A,B\right)={\displaystyle \frac{2{\mu }_A{\mu }_B+C_1}{{\mu }_A^2+{\mu }_B^2+C_1}}$$

(13)

$$c\left(A,B\right)={\displaystyle \frac{2{\sigma }_A{\sigma }_B+C_2}{{\sigma }_A^2+{\sigma }_B^2+C_2}}$$

(14)

$$s\left(A,B\right)={\displaystyle \frac{{\sigma }_{AB}+C_3}{{\sigma }_A{\sigma }_B+C_3}}$$

(15)

$$\left\{\begin{array}{l}{C}_1={\left(H_{1}L\right)}^2\\ C_2={\left(H_{2}L\right)}^2\\ C_3=C_2/2\end{array}\right.$$

(16)

where C₁, C₂, and C₃ are constants introduced to avoid division by zero; H₁ = 0.01 and H₂ = 0.02; and L denotes the dynamic range of the image grayscale values (for an 8-bit image, L is set to 255). The formula for calculating the SSIM value is as follows:

$$SSIM\left(A,B\right)=l\left(A,B\right)\cdot c\left(A,B\right)\cdot s\left(A,B\right)$$

(17)

After simplification, the final expression is obtained:

$$SSIM\left(A,B\right)={\displaystyle \frac{\left(2{\mu }_A{\mu }_B+C_1\right)\left(2{\sigma }_{AB}+C_2\right)}{\left({\mu }_A^2+{\mu }_B^2+C_1\right)\left({\sigma }_A^2+{\sigma }_B^2+C_2\right)}}$$

(18)

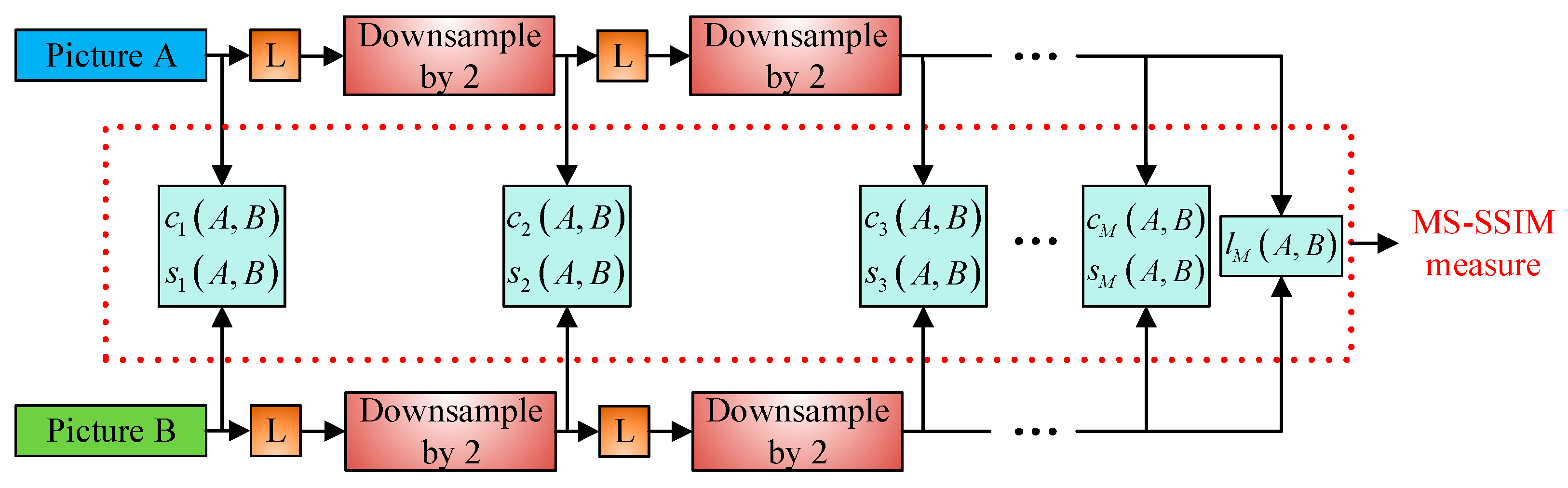
2.3.2. MS-SSIM

In the task of ship heading estimation, the traditional SSIM algorithm exhibits significant limitations. First, SSIM evaluates image similarity based solely on a single-scale analysis, whereas the representation of features such as target contours and textures in ship images varies considerably across different observational scales. This discrepancy is particularly pronounced in scenarios involving long-distance, low-resolution images or partial occlusions, where single-scale matching is prone to feature misidentification. Second, SSIM is highly sensitive to image blurring and scale variations. When target ships appear blurred due to sea wave fluctuations or sensor vibrations, the computed structural similarity may deviate significantly, thereby compromising the accuracy of heading estimation.

To address these issues, this paper proposes the use of the MS-SSIM algorithm for heading matching. MS-SSIM simulates the hierarchical perception mechanism of the human visual system through multi-scale spatial decomposition, progressively capturing the global shape and local detail features of ship contours from coarse to fine levels, as illustrated in Figure 5. Taking the candidate matching image and the template database images as inputs, a low-pass filter is iteratively applied, followed by 2× downsampling to obtain images at multiple scales. At each of the first M − 1 scales, the contrast similarity and structure similarity are calculated separately, denoted as c_j(A, B) and s_j(A, B) at the j-th scale. Luminance similarity is computed only at the final scale, i.e., the M-th scale, denoted as l_M(A, B). By combining the similarity values across different scales, the overall MS-SSIM evaluation value is obtained, as expressed in Equation (19):

$$MS-SSIM\left(A,B,\eta \right)={\left[l_M\left(A,B\right)\right]}^{ {\eta }_M}{\displaystyle \prod _{j=1}^M{\left[c_j\left(A,B\right)s_j\left(A,B\right)\right]}^{{\eta }_j}}$$

(19)

where η_j represents the weighting factor at the j-th scale. To ensure comparability across different scales and to avoid extreme weight assignments, the weighting factors are subject to a normalization constraint, as shown in Equation (20):

$${\displaystyle \sum _{j=1}^M{\eta }_j}=1$$

(20)

2.3.3. Contrastive Learning for Weight Optimization

Although the MS-SSIM algorithm enhances the robustness of heading matching by simulating the hierarchical perception mechanism of the human visual system and progressively capturing the global shape and local detail features of ship contours across multiple scales, the use of fixed-weighting design limits its adaptability to complex maritime environments. Traditional weight calibration methods, which are based on manual experience or subjective experiments, suffer from two major drawbacks:

(1)

The sensitivity of structural features at different scales to heading variations dynamically changing depending on factors such as ship size, distance, and the degree of occlusion.

(2)

Environmental noise and atmospheric disturbances at sea often degrading the feature consistency at certain scales, causing some scale-specific features to become invalid and requiring effective suppression of their weights during the dynamic process.

To address these issues, this paper proposes a dynamic weight optimization framework based on contrastive learning. By constructing triplet constraints within the feature space, the model is driven to autonomously learn the weight distribution of features at different scales, thereby achieving the adaptive adjustment of weights to better meet the feature requirements of the heading matching task.

The triplet samples are composed of an anchor image D (the segmented image of the ship to be matched), a positive sample image P (the heading template image), and a negative sample image G (the adjacent heading template). The contrastive loss function is defined as shown in Equation (21):

$$F\left(D,P,G\right)=\max \left(S\left(D,G\right)-S\left(D,P\right)+\psi ,0\right)$$

(21)

where S denotes the MS-SSIM metric value computed based on the current weighting scheme, and ψ is a predefined margin threshold used to control the minimum similarity difference between positive and negative samples. The core objective of this loss function is to maximize the similarity metric S(D, P) between the anchor image D and the positive sample image P, while minimizing the similarity metric S(D, G) between the anchor image D and the negative sample image G, thereby enhancing the model’s discriminative ability with respect to heading angles. When S(D, G) − S(D, P) + ψ ≤ 0, the loss value is set to 0, indicating that the model has satisfied the expected similarity margin; otherwise, the model needs to adjust the weight parameters through gradient descent to optimize the loss.

For the optimization of multi-scale weights, it is necessary to compute the partial derivatives of the loss function with respect to each weight. According to the chain rule, the gradient expression is given by:

$${\displaystyle \frac{\partial F}{\partial {\eta }_j}}=\left\{\begin{array}{ll}{\displaystyle \frac{\partial S\left(D,G\right)}{\partial {\eta }_j}}-{\displaystyle \frac{\partial S\left(D,P\right)}{\partial {\eta }_j}}\hfill & \mathrm{if} F>0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(22)

where ${\displaystyle \frac{\partial S\left(X,Y\right)}{\partial {\eta }_j}}$ denotes the partial derivative of the MS-SSIM value at scale j with respect to the weight η_j. Based on the definition of MS-SSIM (see Equation (19)), when 1 ≤ j < M, the partial derivative can be further expanded as follows:

$${\displaystyle \frac{\partial S\left(X,Y\right)}{\partial {\eta }_j}}=S\left(X,Y\right)\cdot \ln \left(c_j\left(X,Y\right)s_j\left(X,Y\right)\right)$$

(23)

When j = M, the partial derivative is expanded as follows:

$${\displaystyle \frac{\partial S\left(X,Y\right)}{\partial {\eta }_M}}=S\left(X,Y\right)\cdot \ln \left(l_M\left(X,Y\right)c_M\left(X,Y\right)s_M\left(X,Y\right)\right)$$

(24)

where l_M, C_M, and S_M represent the luminance, contrast, and structure similarity components at the M-th scale, respectively. This gradient calculation indicates that the direction of weight adjustment depends on the contribution of each scale component to the overall similarity. If a certain scale component significantly outperforms the negative sample in positive sample matching, its weight will be increased; otherwise, it will be suppressed. The iterative update of the weights follows the gradient descent rule:

$${\eta }_j^{\left(\delta +1\right)}={\eta }_j^{\left(\delta \right)}-\xi \cdot {\displaystyle \frac{\partial F}{\partial {\eta }_j}}$$

(25)

where ξ denotes the learning rate and δ represents the current iteration number. To ensure that the weights satisfy the non-negativity and normalization constraints, a projection operation must be performed after each update:

$${\eta }_j={\displaystyle \frac{\max \left({\eta }_j,0\right)}{{\displaystyle \sum _{j=1}^M\max \left({\eta }_j,0\right)}}}$$

(26)

This step ensures that negative weights are forced to zero and then re-normalized, thereby guaranteeing that the feature weights at each scale reflect their actual importance. This avoids interference from invalid features and enhances the model’s robustness in heading recognition, especially in cases where local regions of the ship segmentation image are missing due to target occlusion or noise.

Through multiple iterations of optimization, the weight parameters are adaptively adjusted to reflect the contribution of each scale feature. For high-frequency details that are distorted due to segmentation incompleteness, their weights will be automatically suppressed, whereas for more stable mid-to-low frequency contour features, their weights will be significantly increased.

Ultimately, during the matching process between the target segmentation image and the template image, the model will prioritize scales with higher reliability, effectively mitigating heading misjudgment caused by incomplete segmentation.

2.3.4. Algorithm Flow

To clearly illustrate the proposed ship heading determination method, the complete algorithm workflow is presented in the following pseudocode description, as shown in Algorithm 1. The algorithm takes as an input the ship segmentation images obtained after preprocessing and DeepLabV3+ network segmentation, along with a preconstructed multi-angle ship heading template library. Through contrastive learning, the multi-scale MS-SSIM weights are optimized, and the template library is traversed to search for the best match, ultimately outputting the heading angle that best matches the query image. The core stages of the method include contrastive-learning-based weight optimization and multi-scale similarity matching. The detailed workflow is as follows:

Algorithm 1 Ship heading matching algorithm based on MS-SSIM with contrastive-learning-based weight optimization
Input: Given the segmented ship image to be matched D, the set of template library images Z, positive sample images from the template library P, negative sample images G, initial weights ηinit, learning rate ξ, total number of scales for MS-SSIM computation M, margin threshold ψ, and maximum number of iterations δmax.
Output: Optimal heading estimation θopt and optimal matching similarity Smax.
	//Step 1. Contrastive Learning-Based Weight Optimization
1:	η ← ηinit//Weight Initialization
2:	for δ = 1 to δmax do
3:	∆η ← 0
4:	for each positive sample Pn ∈ P and negative sample Gn ∈ G do
5:	SDP ← MS-SSIM(D, Pn, η)//Compute the similarity of the positive sample according to Equations (10)–(16) and (19).
6:	SDG ← MS-SSIM(D, Gn, η)//Compute the similarity of the negative sample according to Equations (10)–(16) and (19).
7:	FDPG ← max(SDG − SDP + ψ, 0)//Compute the contrastive loss according to Equation (21).
8:	if FDPG > 0 then
9:	$∆{\eta }_{\mathrm{DP}} \leftarrow {\displaystyle \sum _{j=1}^M\frac{\partial S_{DP}}{\partial {\eta }_j}}$//Compute the gradient of the positive sample with respect to the weights according to Equations (23) and (24).
10:	$∆{\eta }_{\mathrm{DG}} \leftarrow {\displaystyle \sum _{j=1}^M\frac{\partial S_{DG}}{\partial {\eta }_j}}$//Compute the gradient of the negative sample with respect to the weights according to Equations (23) and (24).
11:	∆η ← ∆η + (∆ηDG − ∆ηDP)
12:	end if
13:	end for
14:	η ← η − ξ · ∆η //Update the weights according to Equation (25).
15:	$\eta \leftarrow \max (\eta , 0), \eta \leftarrow \eta / {\displaystyle \sum _{j=1}^M{\eta }_j}$//Apply weight projection and normalization constraint according to Equation (26).
16:	end for
	//Step 2. Template Library Matching
17:	for each template library sample Zn ∈ Z do
18:	Sλn ← MS-SSIM(D, Zn, η)//Parallel Computing
19:	Sλ[n − 1] ← Sλn
20:	end for
21:	θopt, Smax ← argmax(Sλ)
22:	return θopt, Smax

The notation [n − 1] refers to the corresponding index position, while argmax(·) indicates the maximization process over the elements contained in the variable.

3. Results

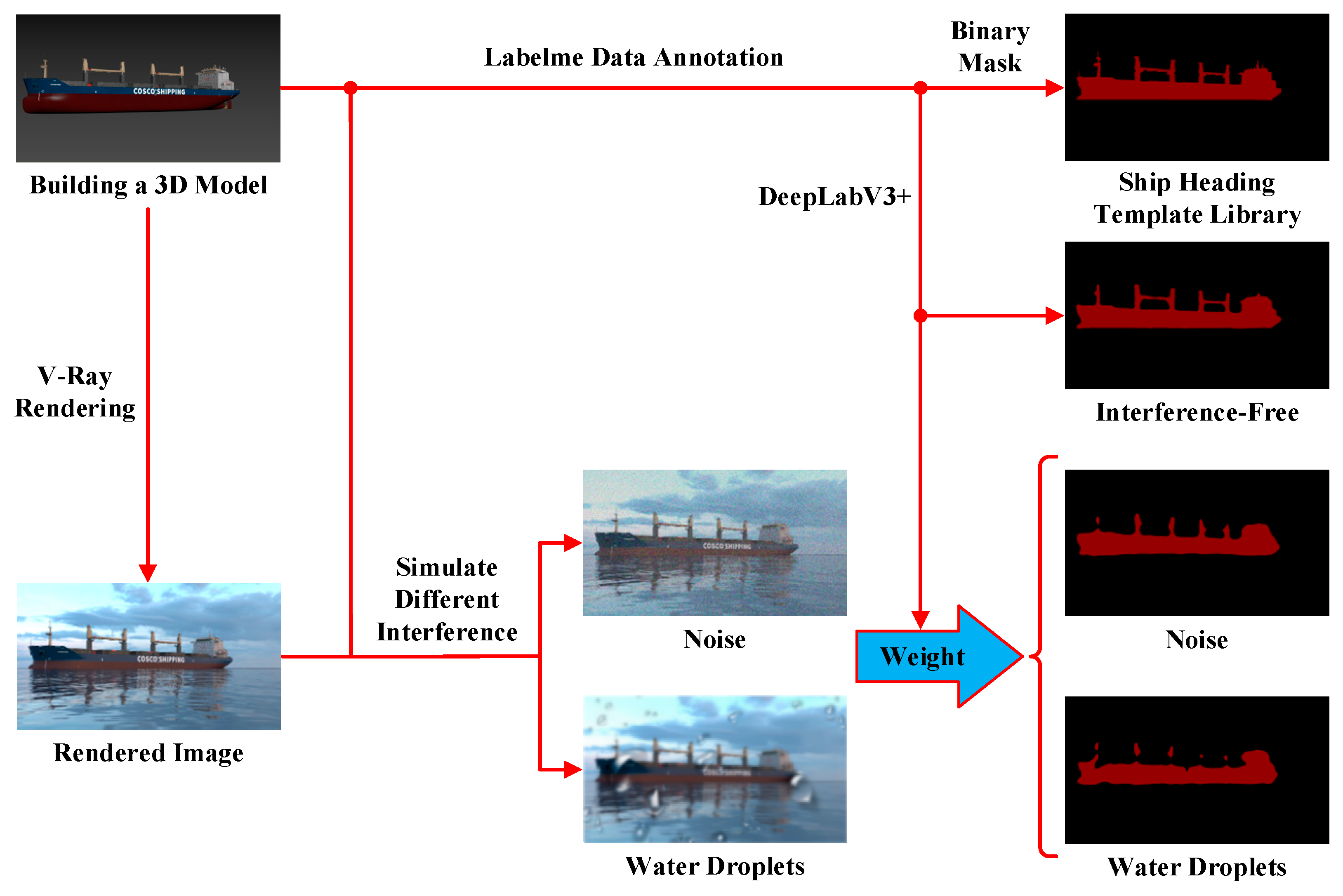
3.1. Experimental Environment and Dataset Construction

The software and hardware environment used in the experiments is detailed in

Table 2. Experimental environment.

Item	Configuration Parameters
Operating System	Windows 11 64 bit
Processor	Intel® Core™ i9–14900 KF @3.2 GHz 1
Graphics Card	NVIDIA GeForce RTX 4090 24 GB
RAM	DDR5 64 G 6400 MHz
Deep Learning Framework	Python 3.9/PyTorch 1.12.0/CUDA 12.8
Modeling and Rendering Framework	3ds Max 2023/V–Ray 6.0

¹ Manufactured by Intel Corporation, Santa Clara, CA, USA.

. The semantic segmentation network adopted the DeepLabV3+ architecture and was trained using the SGD optimizer. The total number of training epochs was set to 200, with the momentum factor of the optimizer configured to 0.9. A cosine learning rate decay strategy was employed, where the initial learning rate was set to 7 × 10⁻³, and the minimum learning rate was set to 7 × 10⁻⁵.

At present, a 3D model library of ships, covering a variety of publicly available parameters, as well as their heading models, has been constructed. To verify the feasibility and performance of the proposed method, this study selected a representative cargo ship—notable for its significant share in international trade volume—as the research object and constructed a multi-angle heading template library for it. First, a simulated virtual model of the cargo ship was constructed using 3ds Max software. The ship’s real-world dimensions are as follows: an overall length of 300 m, a beam of 50 m, and a full-load draft of 18 m. To enhance the realism of the scene, weather effects and sea surface backgrounds were added to the simulation environment. The camera was fixed at a height of 0.5 m above the sea surface and positioned 300 m away from the center of the ship, with a field of view configured to cover the entire vessel. Using the ship’s center as the rotation axis, the model was rotated incrementally by 0.1° per step. The V-Ray rendering engine was employed to generate full-angle RGB images (with a resolution of 1920 × 1080 pixels, in PNG format), resulting in 3600 images captured at different angles. To provide a clearer visualization of the vessel at different heading angles, this study presents rendered images of the ship at 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°, as shown in Figure 6. These rendered images were then annotated using the open-source tool Labelme and subsequently converted into binary images to construct the heading matching mask template library. Additionally, the template images were batch-processed using the OpenCV library to resize them to 512 × 512 pixels. Further data augmentation operations, including rotation, cropping, and flipping, were applied based on the original images, ultimately producing an enhanced dataset containing 7200 images. This augmented dataset was then used as an input for training the DeepLabV3+ network to obtain the corresponding model weights. Finally, the trained model was employed to verify the performance of the proposed method in determining ship headings under three different conditions: no interference, noise interference, and visual window splashing caused by water droplets.

Considering that real-world maritime monitoring environments often suffer from image degradation caused by equipment limitations and adverse weather conditions, which negatively impact the accurate extraction of ship targets and their heading estimation, this study systematically evaluated the adaptability and robustness of the proposed method under complex interference conditions. To this end, two data augmentation strategies were designed and implemented to simulate degraded scenarios based on the original rendered images, thereby constructing a diversified test dataset that served as a reliable basis for performance validation.

Firstly, to simulate interference factors such as maritime electromagnetic signal crosstalk and thermal noise from image sensors, Gaussian noise with a mean of 0 and a variance of 0.4 was injected into the original images. This effectively disrupted high-frequency information and produced global granular disturbances, allowing the evaluation of the method’s performance under conditions of significant texture interference and edge blurring. Secondly, to simulate local occlusions caused by sea spray or raindrops on the camera lens due to wind and wave activity, random-shaped water droplet patches were added to the images. These patches, combined with synthetic blurring, created unstructured occlusion regions resembling lens contamination. Such disturbances are common in real-world maritime scenarios, particularly during high-speed navigation or under harsh weather conditions, and can pose serious challenges to target segmentation and subsequent tasks. By introducing these localized occlusions, we further assessed the proposed method’s ability to make accurate judgments even when partial target information is missing. Multiple sets of experimental test images were generated based on the above simulation scenarios to validate the proposed heading estimation method’s adaptability and robustness. The dataset construction process is illustrated in Figure 7. Additionally, in the image preprocessing step, fixed image enhancement parameters were applied to ensure consistency in both image quality and the processing pipeline. The experimental images were captured with proper exposure, and the camera settings were optimized to avoid introducing additional errors due to variations in imaging quality. The specific preprocessing parameter settings, including key parameters used in linear transformation, bilateral filtering, and the MSRCR image enhancement method, are detailed in

Table 3. Preprocessing parameters.

Item	Parameters
Linear Transformation	ω = 1.2, λ = 0
Bilateral Filtering	σr = 40, σs = 40
MSRCR	K = 3, α = 1, β = 2

.

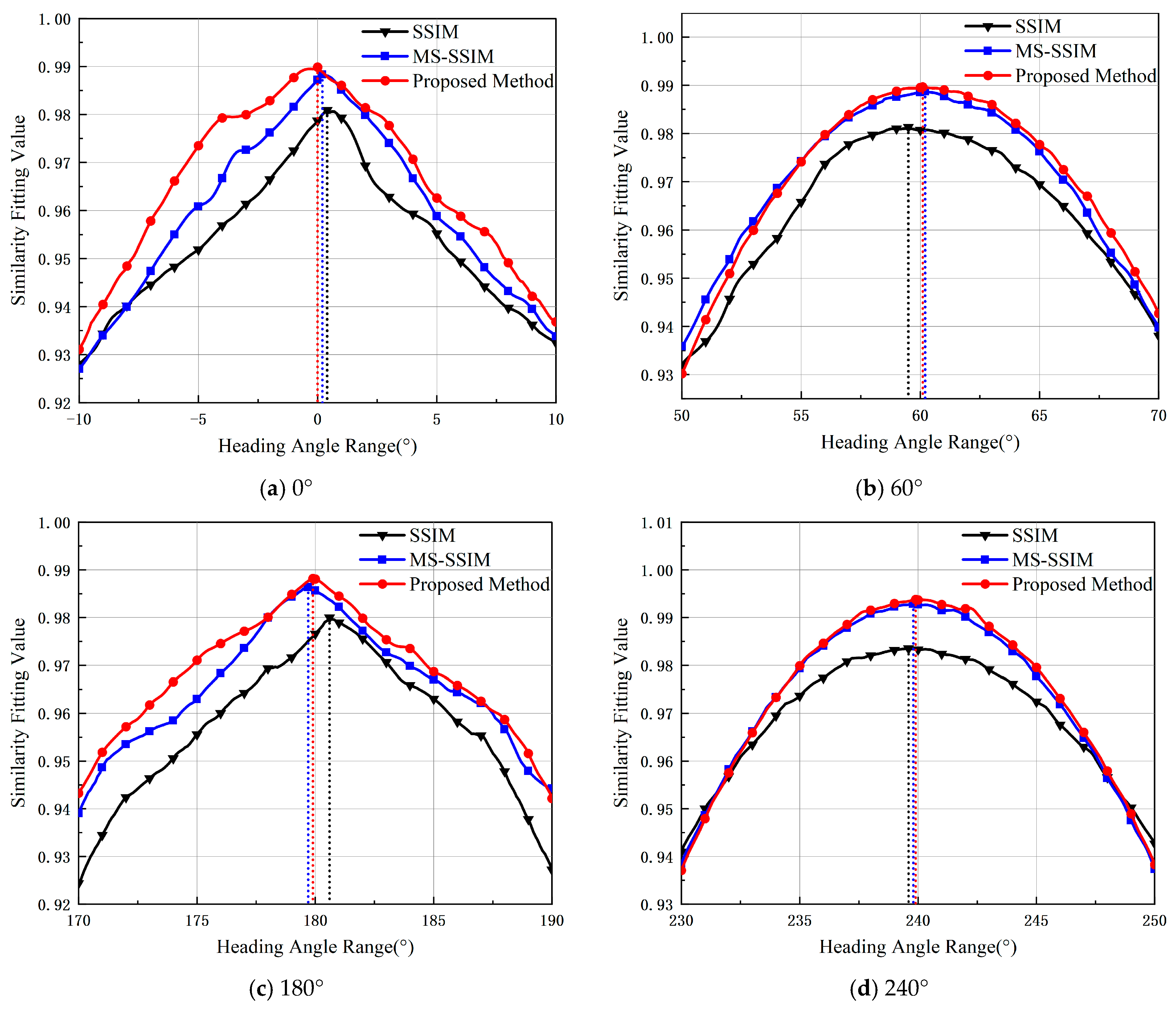
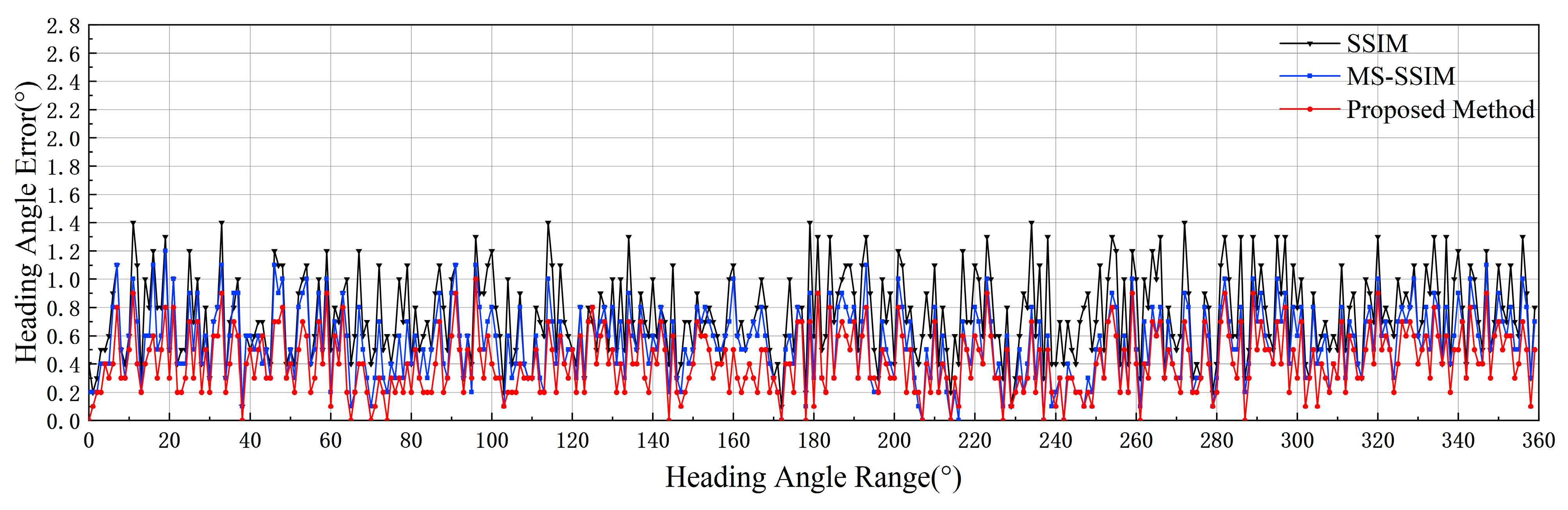
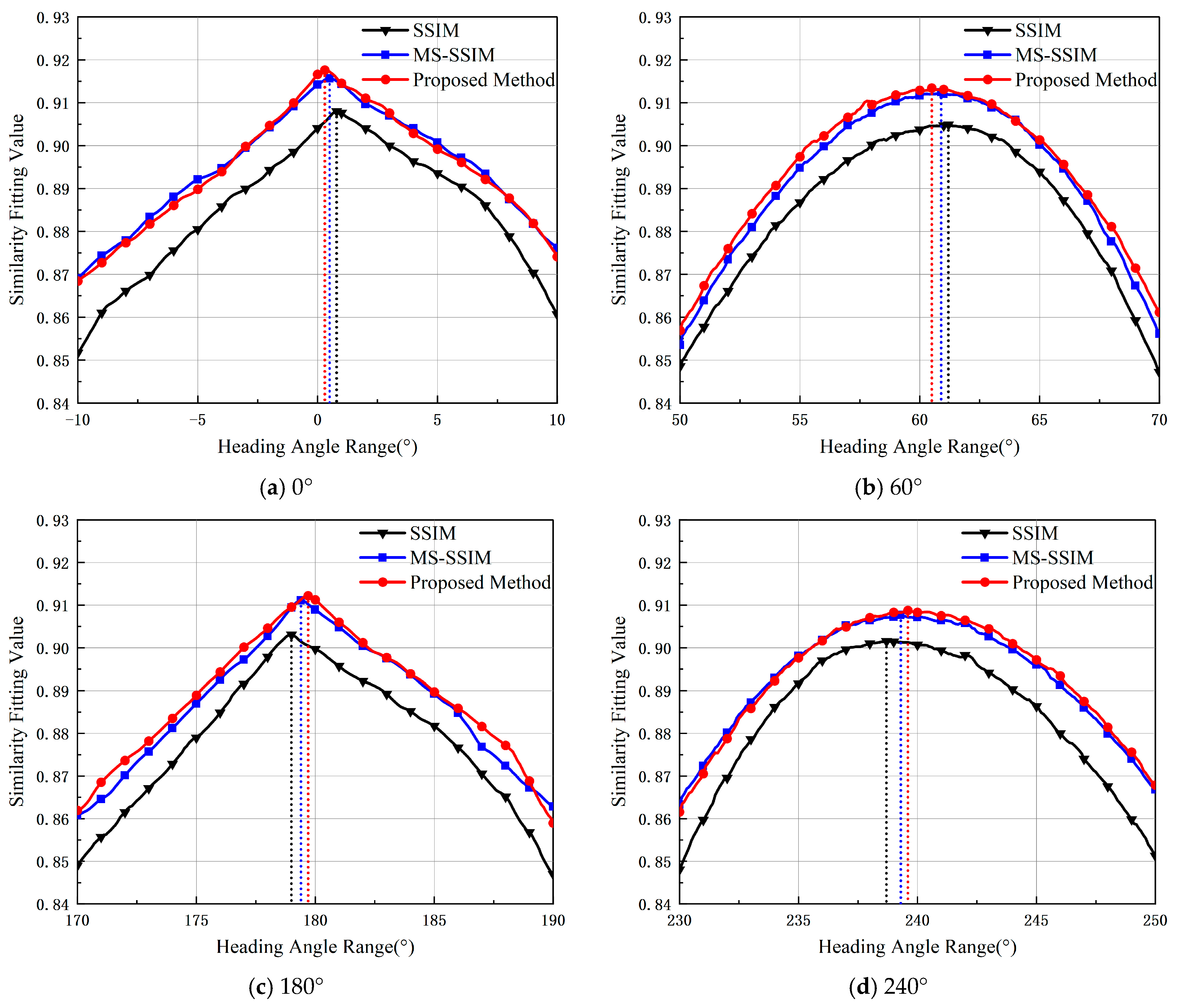
3.2. Algorithm Simulation and Validation

To validate the heading estimation performance of the proposed method under various complex scenarios, three types of simulation experiments were designed in this section, corresponding to ship heading matching tasks under conditions of no interference, noise interference, and water mist occlusion, respectively. The core evaluation metric used in the experiments is the heading angle error (unit: degrees). To comprehensively assess the performance of the algorithms, the comparative experiments involved three types of methods:

(1)

Single-scale SSIM algorithm;

(2)

Fixed-weight MS-SSIM algorithm, following the default multi-scale weight settings proposed by Wang et al. [28] (δ = [0.0448, 0.2856, 0.3001, 0.2363, 0.1333]);

(3)

The proposed contrastive-learning-based, dynamically weighted MS-SSIM algorithm (with initial weights identical to those in method (2)).

The experiments traversed images covering the full heading range from 0° to 360°, and the fitting results of the heading angles were analyzed. To illustrate the matching results at different heading angles, four specific headings (0°, 60°, 180°, and 240°) were selected for detailed result presentation and error analysis. Through these experiments, we were able to conduct an in-depth evaluation of the performance of different methods under various interference conditions, comprehensively compare their heading estimation accuracy, and verify the robustness and superiority of the proposed method in complex maritime environments.

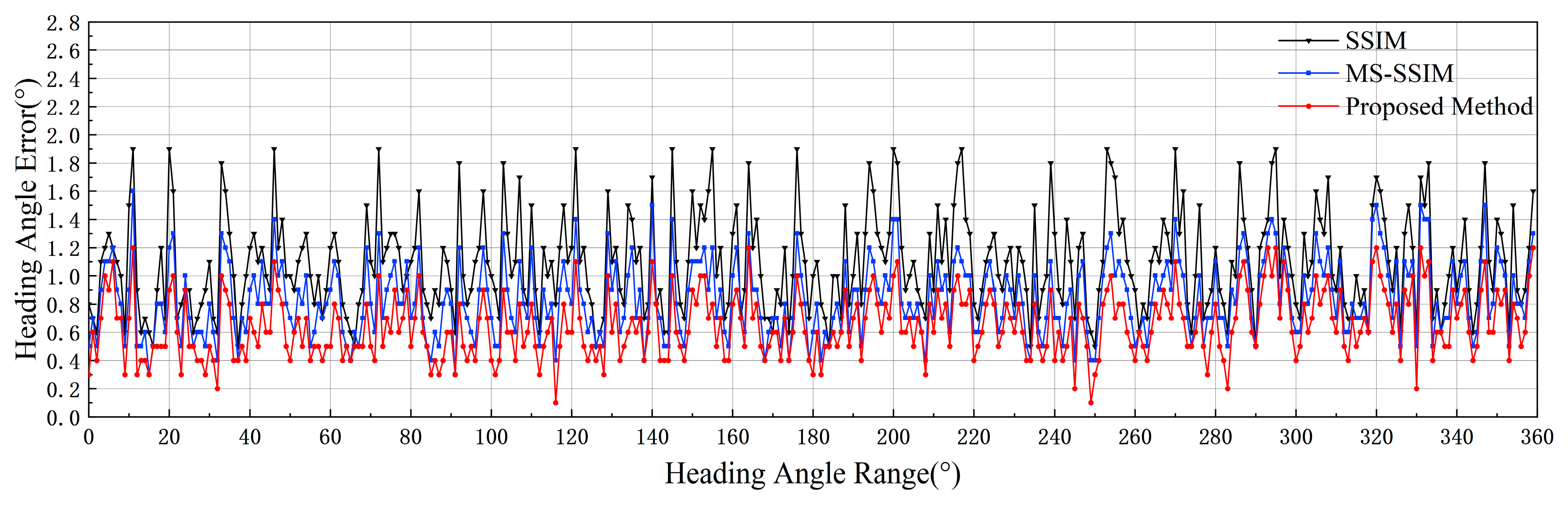
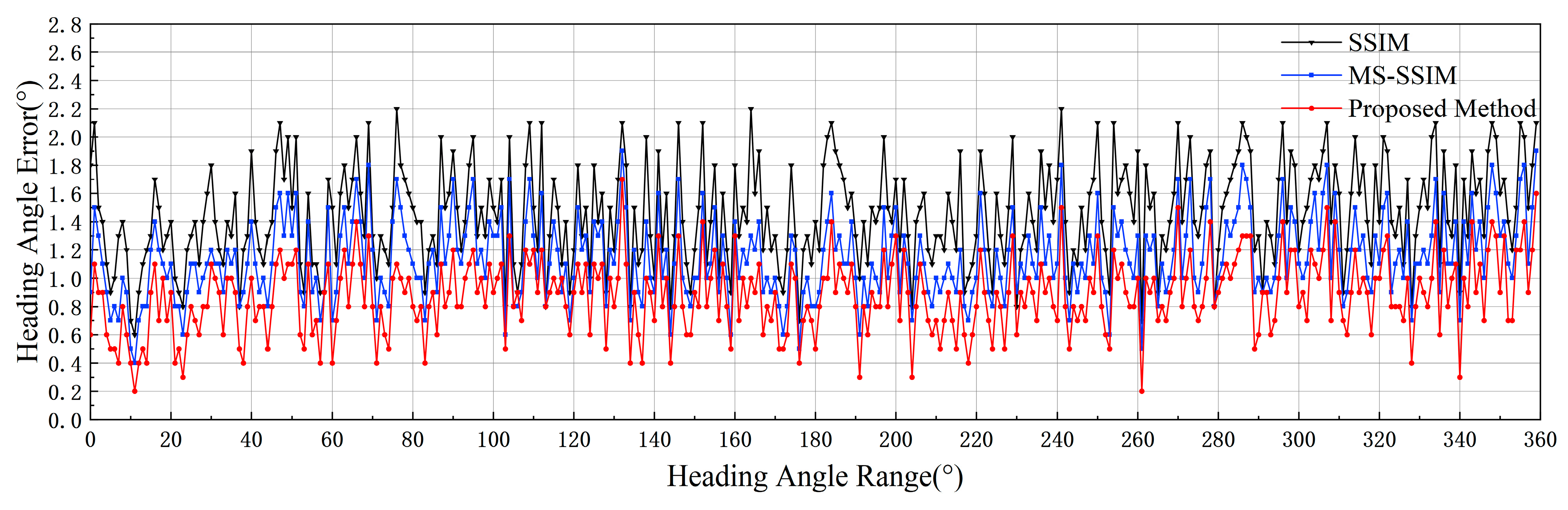
3.2.1. Interference-Free

Under the ideal condition of no interference, the original high-resolution rendered images were used as input in this experiment. The DeepLabV3+ network was employed to segment the ship target, generating a binary mask image as the input for heading matching. The binary mask image was then matched against the template images in the template library by traversing the heading values. The heading value corresponding to the template image with the highest similarity fit was taken as the heading of the ship to be matched. The results of the heading angle fitting are shown in Figure 8. Figure 8a shows the similarity fitting curves of different methods under the condition that the heading of the positive sample is 0°. Figure 8b corresponds to a heading of 60°, Figure 8c to 180°, and Figure 8d to 240°. In each subfigure, the horizontal axis represents the candidate images at various angles in the template library, while the vertical axis indicates the fitted similarity values.

The experimental results show that under no-interference conditions, when the ground truth heading is 0°, the single-scale SSIM method yields a matched heading of 0.4°, the fixed-weight MS-SSIM method results in 0.2°, and the proposed dynamically weighted method achieves zero error. When the true heading is 60°, the single-scale SSIM method outputs 59.5°, the fixed-weight MS-SSIM method gives 60.2°, and the proposed method results in 60.1°. For a true heading of 180°, the single-scale SSIM method matches 180.6°, the fixed-weight MS-SSIM method gives 179.7°, and the proposed method achieves 179.9°. When the heading is 240°, the results are 239.6° for single-scale SSIM, 239.8° for fixed-weight MS-SSIM, and 239.9° for the proposed method. These results demonstrate that the proposed method consistently yields lower matching errors compared to the unoptimized methods, indicating higher accuracy in heading estimation. As illustrated in Figure 8, for ground truth headings of 0° and 180°, the heading matching fitting curves show a steep convergence trend toward the correct heading values. In contrast, for headings of 60° and 240°, the convergence curves are more gradual and approximately follow a Gaussian distribution. This phenomenon is closely related to the morphological characteristics of the ship images: small angular deviations in bow/stern views cause significant changes in the binary mask contours, whereas side views are less sensitive to heading variations due to the relative symmetry of the contour.

To further verify the superiority of the proposed method, a heading matching experiment was conducted across the full range of 0° to 360°, with a 1° interval. For each case, the angular error between the matched heading and the ground truth was calculated. The results are presented in Figure 9.

As shown in Figure 9, the angular errors of the single-scale SSIM method are primarily concentrated within the range of [0.4°, 1.1°], with a mean error of 0.74°. The fixed-weight MS-SSIM method shows errors mostly within [0.4°, 0.9°], with a mean error of 0.55°. In comparison, the proposed method yields errors mainly in the range of [0.2°, 0.7°], with a lower mean error of 0.41°. These results indicate that the proposed method achieves lower heading estimation errors and a higher matching accuracy than the unoptimized approaches. Further analysis shows that across the full range of heading angles, the proposed method consistently yields heading estimation errors that are no worse than those of the single-scale SSIM method. At certain angles—specifically 43°, 95°, 195°, 206°, 213°, 215°, 216°, and 239°—the error of the proposed method is slightly higher than that of the fixed-weight MS-SSIM method. However, these differences are limited to a small number of angles and account for a very small proportion within the full 0–359° range, thus having a negligible impact in practical deployment. Additionally, at angles such as 40°, 125°, 152°, 153°, and 157°, the fixed-weight MS-SSIM method exhibits relatively large errors and performs worse than the single-scale SSIM method. Therefore, although the fixed-weight MS-SSIM approach shows some advantages at a few isolated angles, the proposed method demonstrates an overall higher matching accuracy and lower error under noise-free conditions.

3.2.2. Noise Interference

To simulate the impact of photonic sensor noise on heading estimation in real maritime scenarios, this experiment generated a degraded dataset by injecting Gaussian noise with a mean of 0 and a variance of 0.4 into the original rendered images. These noisy images were then used as input to the DeepLabV3+ network for ship target segmentation, resulting in binary mask images to be matched. Each binary image was matched against the template library through exhaustive heading comparison, and the heading value corresponding to the template image with the highest similarity score was taken as the estimated heading of the target ship. The numerical results of the heading angle estimation are shown in Figure 10. Figure 10a shows the similarity fitting curves of different methods under the condition that the heading of the positive sample is 0°. Figure 10b corresponds to a heading of 60°, Figure 10c to 180°, and Figure 10d to 240°. In each subfigure, the horizontal axis represents the candidate images at various angles in the template library, while the vertical axis indicates the fitted similarity values.

Experimental results indicate that under Gaussian noise interference, when the ground truth heading is 0°, the single-scale SSIM method produces a matched heading of 0.8°, the fixed-weight MS-SSIM method yields 0.5°, and the proposed dynamically weighted method achieves 0.3°. For a ground truth of 60°, the matched results are 61.2°, 60.9°, and 60.5°, respectively. At 180°, the results are 179.0° for the single-scale SSIM, 179.4° for the fixed-weight MS-SSIM, and 179.7° for the proposed method. For a heading of 240°, the methods yield 238.7°, 239.3°, and 239.6°, respectively. These findings demonstrate that the proposed method consistently achieves lower estimation errors than the unoptimized methods, exhibits higher estimation accuracy, and maintains stronger robustness against noise interference.

To further validate the superiority of the proposed method, a heading matching experiment was conducted over the full 0–360° range with 1° intervals. The angular error between each matched heading and the corresponding ground truth was calculated. The results are presented in Figure 11.

As shown in Figure 11, the angular errors of the single-scale SSIM method are primarily concentrated within the range of [0.7°, 1.6°], with a mean error of 1.09°. The fixed-weight MS-SSIM method exhibits errors mainly within the range of [0.5°, 1.3°], with a mean error of 0.84°. In comparison, the proposed method results in errors concentrated in the range of [0.4°, 1.0°], with a mean error of 0.65°. These results demonstrate that the proposed method achieves lower heading estimation errors, higher matching accuracy, and stronger robustness against noise interference compared to the unoptimized methods. Further analysis reveals that across the entire range of angles, the heading estimation error of the proposed method is consistently no worse than that of both the single-scale SSIM and the fixed-weight MS-SSIM methods. Moreover, at specific angles such as 24°, 66°, 79°, 162°, 170°, and 314°, the fixed-weight MS-SSIM method exhibits relatively large errors and performs worse than the single-scale SSIM method. Therefore, although the traditional single-scale SSIM method shows acceptable performance at a few isolated angles, the proposed method achieves lower errors and stronger noise resilience across the full angular range, demonstrating its practicality and robustness in noisy environments.

3.2.3. Water Mist Occlusion Interference

To simulate the partial occlusion interference caused by sea spray or raindrops falling on the camera lens in maritime scenarios, this study introduced randomly shaped droplet patches onto the images and applied simulated blur processing. This resulted in unstructured regions resembling lens contamination or occlusion, thereby creating a degraded dataset. The degraded images were used as an input to the DeepLabV3+ network for ship target segmentation, producing binary mask images for matching. Each binary mask was matched against the template library through exhaustive heading comparison, and the heading corresponding to the template image with the highest similarity score was taken as the estimated heading of the target ship. The numerical results of heading angle estimation are shown in Figure 12. Figure 12a shows the similarity fitting curves of different methods under the condition that the heading of the positive sample is 0°. Figure 12b corresponds to a heading of 60°, Figure 12c to 180°, and Figure 12d to 240°. In each subfigure, the horizontal axis represents the candidate images at various angles in the template library, while the vertical axis indicates the fitted similarity values.

Experimental results show that under occlusion interference caused by simulated water droplet effects, when the ground truth heading is 0°, the single-scale SSIM method yields a matched heading of −1.8°, the fixed-weight MS-SSIM method gives −0.9°, and the proposed dynamically weighted method results in −0.6°. For a ground truth heading of 60°, the respective matched results are 61.5°, 60.7°, and 60.4°. When the ground truth is 180°, the matched headings are 178.6°, 179.2°, and 179.5°, respectively. For a heading of 240°, the results are 238.3°, 238.9°, and 239.3°. These results demonstrate that the proposed method consistently achieves lower estimation errors compared to the unoptimized methods, offering higher accuracy and greater robustness to occlusion interference caused by water droplets or lens contamination.

To further validate the superiority of the proposed method, a heading matching experiment was conducted over the full 0–360° range with 1° intervals. The angular error between each matched heading and the corresponding ground truth was calculated. The results are presented in Figure 13.

As shown in Figure 13, the angular errors of the single-scale SSIM method are primarily concentrated within the range of [0.9°, 1.9°], with a mean error of 1.46°. The fixed-weight MS-SSIM method exhibits errors mainly within the range of [0.7°, 1.6°], with a mean error of 1.15°. In comparison, the proposed method results in errors concentrated in the range of [0.5°, 1.2°], with a mean error of 0.88°. These results demonstrate that the proposed method achieves lower heading estimation errors, higher matching accuracy, and stronger robustness to occlusion interference caused by water droplets or lens contamination compared to the unoptimized methods. Further analysis shows that across the entire angular range, the heading estimation error of the proposed method is consistently no worse than that of the single-scale SSIM method. At angles of 106° and 117°, the error of the proposed method is slightly higher than that of the fixed-weight MS-SSIM method. However, such discrepancies occur only at a few specific angles and represent an extremely small portion of the full 0–359° range, making them negligible in practical deployment. Additionally, at 230°, the fixed-weight MS-SSIM method yields a higher error than the single-scale SSIM method. Therefore, although the fixed-weight MS-SSIM method exhibits advantages at certain isolated angles, the proposed method demonstrates superior accuracy and stability across most angles, validating its greater practicality and robustness under foggy conditions.

3.3. Real Image Experimental Validation

To validate the adaptability of the proposed method in real maritime scenarios, this study included additional experiments using real vessel images. We selected several actual images from publicly available maritime image datasets and online resources. Gaussian noise and water fog interference were artificially added to these images, simulating complex environmental factors that reflected the image quality and interference typically encountered in real sea conditions. Initially, image preprocessing strategies were applied to enhance the original images, significantly improving the contrast and edge clarity of the target areas. Subsequently, the DeepLabV3+ network was employed for vessel segmentation, and heading estimation was performed using the proposed contrastive-learning-based multi-scale similarity matching method. The experimental results are shown in Figure 14.

The experimental results demonstrate that, even with real images, the proposed method is still able to accurately estimate the heading, showcasing a strong generalization ability. However, since these images do not provide ground truth heading data, it is not possible to calculate the specific heading estimation error metrics. As a result, the evaluation is limited to a qualitative assessment based on visual inspection and reasoning. In the future, we plan to conduct further tests on a maritime experimental platform equipped with true heading measurement capabilities. These tests will allow for quantitative validation of the algorithm’s performance using known reference heading data, and we will continue to optimize the method’s robustness and practicality in real-world scenarios.

4. Research Limitations

Although the proposed ship heading estimation method demonstrates high accuracy and robustness under experimental conditions with no interference, noise disturbance, and water fog obstruction, it still has certain limitations. The experimental environment in this study is based on idealized assumptions, and the noise model and interference factors used may be more complex and variable in real-world environments. The intensities of water fog obstruction and noise disturbance are greatly affected by specific environmental factors, which may lead to discrepancies between the simulation results and actual application scenarios. Moreover, the dataset used in this study is based on a virtual 3D model rendering of a typical cargo ship, which, while covering different heading angles and interference conditions, may not fully represent the diversity of real-world maritime conditions. The sea state, ship types, and their load variations could significantly impact the performance of the proposed method in practical applications.

Additionally, the current study faces challenges related to the training data. The image data used in this study rely on manual annotations, a process that is time-consuming and labor-intensive. During real-world deployment, the complexity and variability of marine scenes, weather conditions, and the hardware resources of different platforms will affect the model’s segmentation and heading estimation capabilities, further exacerbating the issue of scarce training data.

In conclusion, while the method proposed in this study performs well under the current experimental conditions, there remains considerable uncertainty and room for improvement when dealing with more complex and variable real-world applications.

5. Conclusions

To address the challenge of ship heading estimation from optical images under complex maritime environments and a horizontal viewing perspective, this paper proposes a heading estimation method that integrates DeepLabV3+-based segmentation with contrastive-learning-enhanced multi-scale similarity matching. A cascaded image preprocessing strategy is constructed, combining linear transformation, bilateral filtering, and an improved Multi-Scale Retinex algorithm. This approach effectively suppresses interference such as noise and haze while enhancing the visibility and edge details of ship targets, providing a stable foundation for subsequent segmentation tasks. During the ship segmentation stage, the DeepLabV3+ network leverages its multi-scale feature extraction capability to accurately delineate ship contours under complex conditions. To address the limitations of the traditional SSIM method in scale sensitivity and weight design, this study introduces the MS-SSIM approach, and further incorporates a contrastive learning mechanism to dynamically optimize the feature weights at each scale. This enhancement makes the matching process more adaptive and discriminative, thereby improving the accuracy and stability of heading estimation. Experimental results demonstrate that the proposed method achieves average heading estimation errors of 0.41°, 0.65°, and 0.88° under interference-free, Gaussian noise, and water droplet occlusion conditions, respectively. Overall, the method outperforms the traditional SSIM and fixed-weight MS-SSIM approaches, exhibiting strong robustness and wide applicability. In the future, we plan to integrate self-supervised learning with synthetic data generation techniques to construct more representative and diverse datasets, and to explore intelligent segmentation mechanisms with adaptive annotation capabilities to effectively mitigate the limitations caused by data scarcity. In addition, the research will focus on the dynamic updating mechanism of the heading template library and the lightweight design of the model architecture. We intend to introduce an online template library updating module to enable the continuous expansion and adaptive optimization of the template repository. To enhance the engineering applicability of the proposed method, we will also conduct field testing and validation in real maritime surveillance scenarios, further promoting its practical deployment in intelligent maritime monitoring and ship navigation systems.