Robust Dolphin Whistle Detection Based on Dually-Regularized Non-Negative Matrix Factorization in Passive Acoustic Monitoring

Abstract

Underwater passive acoustic monitoring (PAM) serves as a core approach pervasively applied to the long-term, non-invasive detection of biological acoustic signals. Dolphin whistles serve as a fundamental aspect of vocal communication, exhibiting intricate frequency-modulated structures. Robust detection of these whistles is essential for dolphin species diversity conservation, yet performance is frequently compromised by underwater background noise, leading to significant degradation in detection reliability. To address this issue, this paper presents an unsupervised enhancement method based on Dually-Regularized Non-Negative Matrix Factorization (DR-NMF). Beyond a standard data fidelity term, the proposed framework integrates two specialized regularizers, including Overlapping Group Shrinkage and Group Lasso. The former promotes time–frequency continuity of whistle ridges, while the latter adaptively eliminates redundant bases, achieving an improved trade-off between structural integrity and noise suppression. The optimization procedure employed a combination of majorization–minimization, iteratively reweighted least squares, and proximal gradient techniques, all of which were implemented within an alternating minimization scheme featuring nested inner–outer iterations. This architecture ensures stable convergence and computational practicality. Extensive experimental evaluations under diverse low signal-to-noise ratio (SNR) conditions reveal that the proposed method achieves a substantial improvement in recall without compromising precision, resulting in consistent enhancements in frame-level $F_1$-scores. When applied to real-world dolphin whistle recordings, our method outperforms existing baseline approaches, demonstrating remarkable robustness in detecting whistle signals when amidst challenging marine environmental noise.

1. Introduction

Passive acoustic monitoring (PAM) has become extensively applied in marine mammal ecology as a non-invasive, cost-effective, and long-term monitoring approach  [1,2]. Traditional methods rely on visual surveys or short-term captures. In contrast, PAM facilitates continuous observation of acoustic behavior at large spatial and temporal scales without disturbing the natural activities of target species [3]. This capability provides unique advantages for population monitoring and conservation. The core components of PAM research include detection, classification, and localization [4,5]. Detection serves as the prerequisite for subsequent analyses, and in odontocete studies, whistles represent the most prominent detection target. Whistles carry essential information on individual communication and group behavior [6]. Therefore, whistle detection constitutes a pivotal front-end step, responsible for separating target signals from complex acoustic backgrounds. Accurate identification of whistle events further supports population size estimation and habitat-use evaluation [7,8]. Based on differences in frequency modulation patterns among species, researchers can also perform behavioral analyses and ecological niche characterization [9]. Thus, the accuracy of whistle detection is essential not only for ensuring robust localization and classification, but also for advancing the application of PAM in revealing ecological processes and supporting conservation strategies.

However, in real marine environments, whistle signals are often affected by broadband stationary noise [10,11]. Such interference greatly masks the energy of whistles and causes severe distortion and degradation of spectral contours [6]. Under these conditions, detectors show reduced sensitivity to target signals and fail to reliably identify low-energy or partially masked ridge features. At the same time, noise-induced artifacts increase the risk of false alarms and reduce detection specificity. This combined effect substantially weakens the performance of whistle detection [12], making it difficult for researchers to accurately estimate dolphin population size, abundance, and behavioral patterns in shallow-water habitats.

Methods for whistle detection mainly include time-domain approaches [13], time-frequency domain approaches, and other transform-domain approaches [14]. Studies have shown that dolphin whistles exhibit distinct modulation characteristics in the time–frequency domain [15,16]. During individual recognition, dolphins also use the spectral contour details of continuous whistles as important cues [17]. As a result, time–frequency domain detection methods have been more widely applied in practical research. Common techniques in this category typically combine spectrogram enhancement with thresholding [18]. For example, some studies have applied various noise-cancellation techniques, such as median filtering, to spectrograms and then used thresholding to retrieve whistle candidate regions [19]. Another method combines time–frequency adaptive binary image processing with morphological operations to achieve whistle tracking and enhancement [20]. In addition, a robust unsupervised detection approach has been proposed, which integrates whistle enhancement using gammatone multichannel processing and Savitzky–Golay filtering with adaptive thresholding, enabling effective recognition of dolphin whistle events [21]. Overall, time–frequency–based enhancement methods can suppress background noise while preserving whistle structure, and when combined with adaptive thresholding, they provide a significant improvement in whistle detection performance.

Traditional time–frequency domain enhancement methods for dolphin whistles include time–frequency smoothing [22,23] and empirical mode decomposition (EMD) [24]. These techniques can improve signal intelligibility to some extent. However, under low signal-to-noise ratio (SNR) conditions, the fine-grained time–frequency structure of whistles is easily masked by noise, which limits the enhancement capacity of these approaches and prevents effective recovery of the complete target signal. As a result, the features provided to detectors become insufficient, thereby weakening their discriminative power and leading to a sharp decline in recall. In recent years, deep neural network methods, such as denoising convolutional neural networks (DNCNNs) and denoising autoencoders (DAEs) [25,26], have shown strong performance in dolphin whistle enhancement. Nevertheless, these approaches require large amounts of clean whistle data and rely heavily on manual annotation and expert supervision, which are both time consuming and costly. Therefore, there is an urgent need for an unsupervised enhancement method that does not depend on manual labeling or large-scale clean datasets, while effectively improving whistle detection performance in ocean noise environments.

In the field of speech signal processing, structured sparse modeling methods, such as Overlapping Group Shrinkage (OGS) [27,28] and Group Lasso (GL) [29], have been widely applied to speech enhancement, detection, and recognition, achieving strong performance. The main advantage of these methods lies in the introduction of structured priors into sparse modeling, which capture local continuity and global sparsity of signals and reflect their grouping and hierarchical characteristics. Similarly, dolphin whistles are produced by air sacs and controlled by laryngeal muscles [30], resulting in unique time–frequency patterns with both sparsity and group structure [31,32]. Structured sparse modeling methods, therefore, show considerable potential for dolphin whistle enhancement. However, when applied directly to whistle spectrograms without explicit reconstruction models or data fidelity constraints, these methods often fail to balance the preservation of weak whistle components, the maintenance of ridge structure integrity, and effective noise suppression, which limits their effectiveness in whistle enhancement.

In this study, we propose an unsupervised enhancement framework based on regularized Non-Negative Matrix Factorization (NMF) [33,34]. NMF decomposes the amplitude spectrum matrix into non-negative bases and activations, with a small number of narrowband bases combined with continuous activations to accurately characterize whistles and noise being dispersed to the remaining bases, thereby suppressing random disturbances and improving low SNR robustness under low rank approximation. In addition to the data fidelity term, the framework incorporates an OGS regularizer and a GL penalty. The OGS term promotes the continuity of spectral ridges through two-dimensional overlapping windows while suppressing block-like artifacts, whereas the GL term eliminates redundancy at the dictionary level by discouraging the participation of ineffective bases that would otherwise amplify residual noise. The joint effect of these two regularization strategies enables the enhanced spectrograms to preserve the structural integrity of whistle contours while markedly improving their separability from background noise, thereby providing a more robust input distribution for subsequent endpoint detection.

The remainder of this paper is organized as follows. Section 2 provides a detailed description of the proposed DR-NMF-based enhancement framework, including the formulation of the model, the associated optimization algorithm, and the design of the endpoint detection module. In addition, the experimental setup is also introduced. Section 3 reports the results of both the enhancement and detection, accompanied by a comprehensive performance analysis under varying noise conditions. Section 4 offers a critical discussion of the method, highlighting its advantages, as well as the inherent limitations that warrant further investigation. Finally, Section 5 concludes this paper.

2. Methods

2.1. STFT-Based Spectral Model of Noisy Whistles

For a PAM system with a bandwidth of $f_s$, the collected noisy whistle signal $x\left(n\right)$ can be represented as $x\left(n\right)=s\left(n\right)+p\left(n\right),n=1,\dots ,N$, where $s\left(n\right)$ denotes the clean whistle signal and $p\left(n\right)$ denotes the background noise. By applying the short-time Fourier transform (STFT), the time–frequency spectrogram $S_{k,m}$ of the signal $s\left(n\right)$ can be obtained, which can be expressed as follows:

$$S_{k,m}=\sum _{n=-\infty }^{\infty }s\left(n\right)w(n-mQ)e^{-{\displaystyle \frac{j2\pi k(n-mQ)}{M}}},$$

(1)

where $w\left(n\right)$ denotes the analysis window function, $m=1,\dots ,M$ is the frame index, $k=1,\dots ,K$ is the frequency index, and Q represents the time shift in discrete samples. Subsequently, by applying the inverse short-time Fourier transform (ISTFT), the time-domain signal $s\left(n\right)$ can be reconstructed from $S_{k,m}$, which can be expressed as follows:

$$s\left(n\right)=\sum _{m}g(n-mQ)\left[{\displaystyle \frac{1}{M}}\sum _{k=0}^{M-1}{S}_{k,m}{e}^{{\displaystyle \frac{j2\pi k(n-mQ)}{M}}}\right],$$

(2)

where $g\left(n\right)$ denotes the synthesis window function. If the analysis and synthesis windows are not identical, the condition of perfect reconstruction requires satisfying the constant overlap-add (COLA) criterion, which can be expressed as

$$\sum _{m}w(n-mQ)g(n-mQ)=C\left(n\right).$$

(3)

If the window and hop size satisfy the COLA condition and $C\left(n\right)$ is a constant, then it suffices to divide the final reconstruction result by this constant.

Since the STFT is a linear transform, the signal decomposition can be expressed as follows:

$$X_{k,m}=S_{k,m}+P_{k,m}.$$

(4)

It can be shown that the observed complex spectrogram equals the linear superposition of the signal spectrogram and the noise spectrogram. However, in practical processing, the complex spectrogram $X_{k,m}$ is usually not used directly; instead, its magnitude (amplitude spectrogram) or squared magnitude (power spectrogram) is taken as the object of analysis. Accordingly, the observation matrix is defined as follows:

$$Y_{k,m}={\left|X_{k,m}\right|}^{\beta }.$$

(5)

Commonly, $\beta =1$ (amplitude spectrogram) or $\beta =2$ (power spectrogram) is adopted. For simplicity, $X_{k,m}$, $Y_{k,m}$, $S_{k,m}$, and $P_{k,m}$ are, respectively, denoted as $\mathbf{X}$, $\mathbf{Y}$, $\mathbf{S}$, $\mathbf{P}$. Since the squared expansion of $\left|\mathbf{S}+\mathbf{P}\right|$ contains cross terms, it is strictly the case that $|\mathbf{X}{|}^{\beta }\ne |\mathbf{S}{|}^{\beta }+|\mathbf{P}{|}^{\beta }$. However, for the sake of simplified derivation and practical application in NMF, it is typically assumed that $s\left(n\right)$ and $p\left(n\right)$ are statistically independent or weakly correlated. Under this assumption, the cross terms can be neglected in expectation, yielding $\mathbb{E}\left[|\mathbf{X}{|}^2\right]\doteq \mathbb{E}\left[|\mathbf{S}{|}^2\right]+\mathbb{E}\left[|\mathbf{P}{|}^2\right]$. Therefore, it can directly assumed that

$$\mathbf{Y}\doteq \mathbf{S}+\mathbf{P},$$

(6)

where $\mathbf{Y}$, $\mathbf{S}$, and $\mathbf{P}$, respectively, denote the observed spectrogram matrix, the clean signal spectrogram matrix, and the noise spectrogram matrix. This formulation facilitates the establishment of a decomposition model in the non-negative domain, enabling the separation and reconstruction of noisy signals.

2.2. Spectrogram Enhancement Model Based on DR-NMF and Iterative Solution Method

2.2.1. Derivation of the Objective Function

In the application of PAM, the observed time–frequency spectrogram is often composed of the superposition of target signals and noise. To effectively capture the latent structure of the signal, the NMF method is employed to model the observed spectrogram, thereby obtaining spectral bases and sparse, interpretable representations of the activation coefficients. Suppose the input clean spectrogram matrix is denoted as $\mathbf{S}\in {\mathbb{R}}_{+}^{K\times M}$, where K represents the number of frequency channels and M denotes the number of time frames. By constructing the NMF model, the goal is to find a non-negative matrix pair $(\mathbf{W},\mathbf{H})$ such that

$$\widehat{\mathbf{S}}\doteq \mathbf{WH},$$

(7)

where $\widehat{\mathbf{S}}$ denotes the reconstructed T-F representation of a dolphin whistle, $\mathbf{W}\in {\mathbb{R}}_{+}^{K\times r}$ denotes the spectral basis matrix, and $\mathbf{H}\in {\mathbb{R}}_{+}^{r\times M}$ denotes the activation matrix. In practice, since the observed signal inevitably suffers from noise and modeling errors, decomposition is usually performed directly on the observed spectrogram $\mathbf{Y}$. In this case, the model can be formulated as follows:

$$\mathbf{Y}=\mathbf{WH}+\mathbf{E},$$

(8)

where $\mathbf{E}$ denotes the residual component that cannot be represented by the low-rank non-negative decomposition.

To characterize the discrepancy between the observed spectrogram $\mathbf{Y}$ and the reconstructed spectrogram $\mathbf{WH}$, an appropriate data fidelity term is introduced. In signal processing, a common assumption is that the noise follows an independent and identically distributed Gaussian distribution. Under this statistical assumption, maximum likelihood estimation can be reduced to minimizing the squared error between the observed data and the model reconstruction. Therefore, the fidelity term in the NMF model can be defined as the squared Frobenius norm:

$${\mathcal{L}}_{\mathrm{fidelity}}(\mathbf{W},\mathbf{H})={\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2.$$

(9)

Since the loss function is convex with respect to one variable when either $\mathbf{W}$ or $\mathbf{H}$ is fixed independently, the optimization strategy of alternating minimization can be adopted.

Based on the Gaussian noise assumption, the NMF fidelity term is introduced to ensure that the model can reasonably approximate the observed data under the reconstruction error criterion. However, relying solely on the fidelity term is often insufficient to handle complex broadband stationary noise environments. On the one hand, noise may introduce numerous scattered high-frequency artifacts, which, in turn, cause the temporal distribution of the activation matrix $\mathbf{H}$ to become fragmented and discontinuous; on the other hand, an excessive number of bases in $\mathbf{W}$ may participate in the decomposition indiscriminately, leading to increased redundancy of the model while weakening interpretability. Therefore, it is necessary to incorporate structural priors into the NMF framework in order to reflect the intrinsic regularity of whistle signals and to enhance robustness.

It is observed that the energy distribution of the activation matrix $\mathbf{H}$ exhibits pronounced local continuity and block-wise aggregation. If only the element-wise $l_1$ sparsity constraint is applied, the model tends to over-compress energy at isolated points, thereby disrupting the inherent trajectory continuity. Similarly, applying independent regularization along the temporal or frequency dimension alone cannot effectively capture cross-dimensional correlations, which easily leads to fragmented energy distributions. To address this issue, the OGS regularization is introduced on $\mathbf{H}$ to more appropriately characterize the local energy continuity within overlapping neighborhoods in the time–frequency domain. Specifically, let a set of overlapping local windows be denoted as $G_{p,q}$, each window centered at $(p,q)$ with a size of $K_1\times K_2$. All elements within a window are treated as one group, and the $l_2$ norm of the group is defined accordingly. The OGS regularization term can be mathematically expressed as follows:

$${\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)=\sum _{p,q}{∥{\mathbf{H}}_{G_{p,q}}∥}_F=\sum _{p,q}\sqrt{\sum _{(i,j)\in G_{p,q}}{H}_{i,j}^2},$$

(10)

where the subscripts $(i,j)$, respectively, correspond to the faulted in terms of convolution operations. Let the convolution kernel $\mathbf{G}$ be constructed as the outer product of all-ones vectors $h_1$ and $h_2$, such that the kernel size is $K_1\times K_2$. Under this definition, the squared sum within a window can be equivalently expressed as the convolution between the matrix $\mathbf{H}\odot \mathbf{H}$ and the kernel $\mathbf{G}$:

$${[\mathbf{G}\ast (\mathbf{H}\odot \mathbf{H}\left)\right]}_{p,q}=\sum _{(i,j)\in G_{p,q}}{H}_{i,j}^2.$$

(11)

Therefore, the OGS regularization term can be compactly written as follows:

$${\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)=\sum _{p,q}\sqrt{{[\mathbf{G}\ast (\mathbf{H}\odot \mathbf{H}\left)\right]}_{p,q}}.$$

(12)

In contrast to $\mathbf{H}$, the j-th column vector ${\mathbf{W}}_{:,j}\in {\mathbb{R}}_{+}^K$ of the spectral basis matrix $\mathbf{W}\in {\mathbb{R}}_{+}^{K\times r}$ represents the j-th candidate basis with dimension K, thereby spanning all frequency channels. Without additional constraints, all basis vectors may participate in the decomposition, which could result in excessive redundancy. To avoid this issue, the GL regularization ($l_{2,1}$ norm) is imposed on $\mathbf{W}$, which is expressed as follows:

$${\mathcal{R}}_{\mathrm{GL}}\left(\mathbf{W}\right)=\sum _{j=1}^r{∥{\mathbf{W}}_{:,j}∥}_2.$$

(13)

This regularization term imposes sparsity constraints at the level of entire basis columns. When a basis contributes insufficiently and fails to play a substantive role in signal reconstruction, its entire column vector will be compressed to zero, thereby achieving automatic basis selection. Compared with element-wise $l_1$ sparsity, this column-wise sparsity mechanism can more effectively eliminate redundant or ineffective bases, rather than producing sparsity only at the level of individual elements.

Therefore, by incorporating OGS and GL into the NMF fidelity term, the overall objective function is formulated as follows:

$$\begin{array}{cc}\hfill \underset{\mathbf{W}\ge 0,\mathbf{H}\ge 0}{min}\mathcal{J}(\mathbf{W},\mathbf{H})& ={\mathcal{L}}_{\mathrm{fidelity}}(\mathbf{W},\mathbf{H})+{\lambda }_{\mathrm{ogs}}{\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)+{\lambda }_{\mathrm{gl}}{\mathcal{R}}_{\mathrm{GL}}\left(\mathbf{W}\right)\hfill \\ \hfill & =\frac{1}{2}{\parallel \mathbf{Y}-\mathbf{WH}\parallel }_F^2+{\lambda }_{\mathrm{ogs}}\sum _{p,q}\sqrt{{[\mathbf{G}\ast (\mathbf{H}\odot \mathbf{H})]}_{p,q}}+{\lambda }_{\mathrm{gl}}\sum _{j=1}^r{\parallel {\mathbf{W}}_{:,j}\parallel }_2,\hfill \end{array}$$

(14)

where ${\lambda }_{ogs}$ and ${\lambda }_{gl}$ are weighting parameters that balance the fidelity term and the structural priors.

2.2.2. Optimization of the Objective Function

Since different regularization terms are imposed on W and H, distinct solution methods are employed to derive their respective update rules, thereby implementing the alternating minimization optimization strategy.

In the optimization process, the OGS regularization term exhibits strong nonlinearity due to the presence of both square-root and convolution operations, which renders direct gradient-based updates difficult to implement. To address this issue, a majorization–minimization (MM) strategy is adopted, in which the original OGS regularizer is reformulated as a sequence of progressively tightened quadratic upper bounds. This reformulation enables the problem to be solved in the form of an iteratively reweighted least squares (IRLS) scheme, thereby transforming the non-convex regularization into a tractable weighted quadratic optimization problem.

Specifically, the derivation begins by invoking the classical upper-bound inequality of the square-root function. For any non-negative scalar $z\ge 0$ and any positive constant $b>0$, the following inequality holds:

$$\sqrt{z+\epsilon }\le {\displaystyle \frac{z+\epsilon }{2b}}+{\displaystyle \frac{b}{2}},$$

(15)

where $\epsilon >0$ is introduced as a smoothing term to avoid singularity. When $b=\sqrt{z+\epsilon }$, the inequality becomes tight, and this relationship is non-convex. The square-root function, thus, provides a locally tight quadratic upper bound, which can be applied to the group energy in the OGS regularization, and it is defined as ${\mathcal{S}}_{p,q}\left(\mathbf{H}\right)={\left[\mathbf{G}\ast (\mathbf{H}\odot \mathbf{H})\right]}_{p,q}$, leading to the following:

$$\sqrt{{\mathcal{S}}_{p,q}\left(\mathbf{H}\right)+\epsilon }\le {\displaystyle \frac{{\mathcal{S}}_{p,q}\left(\mathbf{H}\right)+\epsilon }{2r_{p,q}^{\left(t\right)}}}+{\displaystyle \frac{r_{p,q}^{\left(t\right)}}{2}},$$

(16)

where $r_{p,q}^{\left(t\right)}=\sqrt{{\mathcal{S}}_{p,q}\left({\mathbf{H}}^{\left(t\right)}\right)+\epsilon }$ denotes the local energy value from the previous iteration. Consequently, an upper bound of ${\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)$ can be obtained as follows:

$${\lambda }_{ogs}{\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)\le {\displaystyle \frac{{\lambda }_{ogs}}{2}}\sum _{p,q}\left({\displaystyle \frac{{\mathcal{S}}_{p,q}\left(\mathbf{H}\right)+\epsilon }{r_{p,q}^{\left(t\right)}}}+r_{p,q}^{\left(t\right)}\right).$$

(17)

By defining the terms independent of $\mathbf{H}$ as a constant $const={\displaystyle \frac{{\lambda }_{\mathrm{ogs}}}{2}}{\displaystyle \sum _{p,q}}\left({\displaystyle \frac{\epsilon }{r_{p,q}^{\left(t\right)}}}+r_{p,q}^{\left(t\right)}\right)$, a quadratic surrogate function with respect to $\mathbf{H}$ can be constructed as $\mathcal{Q}(\mathbf{H};{\mathbf{H}}^{\left(t\right)})$:

$$\mathcal{Q}\left(\mathbf{H};{\mathbf{H}}^{\left(t\right)}\right)={\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2+{\displaystyle \frac{{\lambda }_{\mathrm{ogs}}}{2}}\sum _{p,q}{\displaystyle \frac{{\mathcal{S}}_{p,q}\left(\mathbf{H}\right)}{r_{p,q}^{\left(t\right)}}}+const.$$

(18)

For any $\mathbf{H}$, the constructed surrogate function satisfies the following:

$$\mathcal{J}\left(\mathbf{H}\right)={\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2+{\lambda }_{\mathrm{ogs}}{\mathcal{R}}_{\mathrm{OGS}}\left(\mathbf{H}\right)\le \mathcal{Q}\left(\mathbf{H};{\mathbf{H}}^{\left(t\right)}\right).$$

(19)

At $\mathbf{H}={\mathbf{H}}^{\left(t\right)}$, the two functions take identical values, i.e., $\mathcal{Q}\left({\mathbf{H}}^{\left(t\right)};{\mathbf{H}}^{\left(t\right)}\right)=\mathcal{J}\left({\mathbf{H}}^{\left(t\right)}\right)$. At the $(t+1)$-th update, the new solution is obtained by minimizing the surrogate function, namely ${\mathbf{H}}^{(t+1)}=arg{min}_{\mathbf{H}}\mathcal{Q}(\mathbf{H};{\mathbf{H}}^{\left(t\right)})$, from which the update rule can be derived:

$$\mathcal{J}\left({\mathbf{H}}^{(t+1)}\right)\le \mathcal{Q}\left({\mathbf{H}}^{(t+1)};{\mathbf{H}}^{\left(t\right)}\right)\le \mathcal{Q}\left({\mathbf{H}}^{\left(t\right)};{\mathbf{H}}^{\left(t\right)}\right)=\mathcal{J}\left({\mathbf{H}}^{\left(t\right)}\right).$$

(20)

It guarantees that the original objective function $\mathcal{J}\left(\mathbf{H}\right)$ is monotonically non-increasing.

In Equation (18), the regularization term appears in the form of local group energy; however, this formulation still involves the quadratic sum of convolution and windowing, which makes it difficult to correspond directly to the element-wise entries of matrix $\mathbf{H}$. To address this, it is necessary to interchange the order of convolution and summation. By applying the Fubini–Tonelli theorem, the double summation can be rearranged, leading to the following equivalent transformation:

$$\sum _{p,q}{\displaystyle \frac{{\mathcal{S}}_{p,q}\left(\mathbf{H}\right)}{r_{p,q}^{\left(t\right)}}}=\sum _{i,j}{w}_{i,j}^{\left(t\right)}{H}_{i,j}^2,$$

(21)

where each element of the weight matrix ${\mathbf{w}}^{\left(t\right)}$ corresponds to the aggregated result of being weighted within all local windows covering that position, and it is expressed as follows:

$${\mathbf{w}}^{\left(t\right)}=\mathbf{G}\ast \left({\displaystyle \frac{1}{{\mathbf{r}}^{\left(t\right)}}}\right),$$

(22)

where the symbol ∗ denotes the convolution operation and ${\mathbf{r}}^{\left(t\right)}$ is the matrix composed of the local quantities $r_{p,q}^{\left(t\right)}$ at all positions $(p,q)$. Through the above transformation, the OGS regularization term is converted from the complex representation of group energy into an element-wise weighted quadratic form, thereby allowing $\mathcal{Q}(\mathbf{H};{\mathbf{H}}^{\left(t\right)})$ to be simplified as follows:

$$\mathcal{Q}\left(\mathbf{H};{\mathbf{H}}^{\left(t\right)}\right)={\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2+{\displaystyle \frac{{\lambda }_{\mathrm{ogs}}}{2}}\sum _{i,j}{w}_{i,j}^{\left(t\right)}{H}_{i,j}^2+const.$$

(23)

According to Equation (23), the overall gradient can be expressed as follows:

$${\nabla }_{\mathbf{H}}\mathcal{Q}\left(\mathbf{H};{\mathbf{H}}^{\left(t\right)}\right)={\mathbf{W}}^{\top }\mathbf{WH}-{\mathbf{W}}^{\top }\mathbf{Y}+{\lambda }_{\mathrm{ogs}}\left({\mathbf{w}}^{\left(t\right)}\odot \mathbf{H}\right).$$

(24)

In theory, the update of the matrix $\mathbf{H}$ can be obtained by setting the gradient to zero, leading to a linear system involving the OGS weights. However, in the proposed method, the coefficient matrix simultaneously contains both ${\mathbf{W}}^{\top }\mathbf{W}$ and the convolution operator associated with the IRLS-based OGS weights. As a result, the system is often severely ill-conditioned, numerically unstable, and highly sensitive to noise and scaling variations. Even when iterative solvers, such as preconditioned conjugate gradient (PCG), are employed, additional preconditioners and monotonicity safeguards are required, which considerably increase the computational cost and implementation complexity. Moreover, the closed-form solution does not inherently satisfy the nonnegativity constraint, and subsequent projection steps may disrupt the monotonic descent guaranteed by the MM framework, thereby undermining the reliability of the optimization process.

By contrast, the Lee–Seung type multiplicative update rule [35], derived from the auxiliary function method, naturally guarantees nonnegativity and monotonic convergence. To construct a feasible iterative update, the gradient is decomposed as ${\nabla }^{+}={\mathbf{W}}^{\top }\mathbf{WH}+{\lambda }_{\mathrm{ogs}}{\mathbf{w}}^{\left(t\right)}\odot \mathbf{H}$ and ${\nabla }^{-}={\mathbf{W}}^{\top }\mathbf{Y}$. According to the Lee–Seung auxiliary function method, which provides the update in the form $\mathbf{H}\leftarrow \mathbf{H}\odot \frac{{\nabla }^{-}}{{\nabla }^{+}}$, the update rule for $\mathbf{H}$ can thus be obtained as follows:

$$H_{i,j}^{(t+1)}=H_{i,j}^{\left(t\right)}{\displaystyle \frac{{\left({\mathbf{W}}^{\top }\mathbf{Y}\right)}_{i,j}}{{\left({\mathbf{W}}^{\top }\mathbf{W}{\mathbf{H}}^{\left(t\right)}\right)}_{i,j}+{\lambda }_{\mathrm{ogs}}\left(w_{i,j}^{\left(t\right)}{H}_{i,j}^{\left(t\right)}\right)+\epsilon }},$$

(25)

where $\epsilon >0$ is a small positive constant introduced to prevent division by zero. The multiplicative update strictly satisfies the Karush–Kuhn–Tucker (KKT) conditions and, within the OGS-regularized framework, preserves local group coupling while ensuring nonnegativity and monotonic decrease in the objective. This provides certain effectiveness in maintaining time–frequency ridge continuity in the proposed method.

Within the modeling framework of NMF, the update of the basis matrix $\mathbf{W}$ can be formulated as the following optimization problem:

$${min}_{\mathbf{W}\ge 0}{\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2+{\lambda }_{\mathrm{gl}}\sum _{j=1}^r{∥{\mathbf{W}}_{:j}∥}_2.$$

(26)

Since the objective function contains a nonsmooth regularization term, directly applying the conventional gradient descent method cannot yield effective updates. Therefore, it is necessary to employ the proximal gradient method (PGM) to separate the optimization of the smooth and nonsmooth components.

According to the rules of matrix differentiation, the gradient of the smooth term ${\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2$ with respect to $\mathbf{W}$ is as follows:

$${\nabla }_{\mathbf{W}}f\left(\mathbf{W}\right)={\nabla }_{\mathbf{W}}{\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2=\mathbf{WH}{\mathbf{H}}^{\top }-\mathbf{Y}{\mathbf{H}}^{\top }.$$

(27)

The Lipschitz constant of the gradient is $\gamma ={\parallel {\mathbf{HH}}^{\top }\parallel }_2$, and thus the step size is chosen as $\eta \in (0,1/\gamma )$. At each iteration, the current basis matrix ${\mathbf{W}}^{\left(t\right)}$ is first updated by a single gradient descent step to obtain an intermediate point:

$$\mathbf{V}={\mathbf{W}}^{\left(t\right)}-\eta \left({\mathbf{W}}^{\left(t\right)}\left(\mathbf{H}{\mathbf{H}}^{\top }\right)-\mathbf{Y}{\mathbf{H}}^{\top }\right).$$

(28)

Then, the proximal operator is applied to the intermediate point $\mathbf{V}$, thereby simultaneously enforcing nonnegativity and group sparsity. The corresponding proximal subproblem is formulated as follows:

$${\mathbf{W}}^{(t+1)}=arg{min}_{\mathbf{W}\ge 0}{\displaystyle \frac{1}{2}}{∥\mathbf{W}-\mathbf{V}∥}_F^2+\eta {\lambda }_{\mathrm{gl}}\sum _{j=1}^r{∥{\mathbf{W}}_{:j}∥}_2.$$

(29)

Since the regularization term is decomposed column-wise, the proximal operator can be computed independently for each column. For the k-th column, the proximal subproblem can be expressed as follows:

$${\mathbf{W}}_{:j}^{(t+1)}=arg{min}_{{\mathbf{w}}_j\ge 0}{\displaystyle \frac{1}{2}}{∥{\mathbf{w}}_j-{\mathbf{v}}_j∥}_2^2+\eta {\lambda }_{\mathrm{g}1}{∥{\mathbf{w}}_j∥}_2,$$

(30)

where ${\mathbf{w}}_j$ denotes the j-th column of $\mathbf{W}$, and ${\mathbf{v}}_j$ denotes the j-th column of $\mathbf{V}$. The closed-form solution of this problem can be described as follows: if the Euclidean norm of the non-negative part of the vector, ${\left({\mathbf{v}}_j\right)}_{+}=max\left({\mathbf{v}}_j,0\right)$, is less than or equal to the threshold $\eta {\lambda }_{\mathrm{gl}}$, then the entire column is shrunk to zero; otherwise, the result is a non-negative vector scaled proportionally, which can be expressed as follows [36]:

$${\mathbf{W}}_{:j}^{(t+1)}={\left(1-{\displaystyle \frac{\eta {\lambda }_{\mathrm{gl}}}{{∥{\left({\mathbf{v}}_j\right)}_{+}∥}_2}}\right)}_{+}{\left({\mathbf{v}}_j\right)}_{+}.$$

(31)

By consolidating the column-wise derivations, the complete update rule for the entire matrix $\mathbf{W}$ is obtained:

$${\mathbf{W}}^{(t+1)}=\left[{\left(\mathbf{V}\right)}_{+}Diag{\left({\left(1-{\displaystyle \frac{\eta {\lambda }_{\mathrm{gl}}}{{∥{\left({\mathbf{V}}_{:j}\right)}_{+}∥}_2}}\right)}_{+}\right)}_{j=1}^r\right],$$

(32)

where ${\left(\mathbf{V}\right)}_{+}=max(\mathbf{V},0)$ denotes the element-wise non-negative truncation, and the term within the parentheses represents the column-wise soft-thresholding shrinkage.

Therefore, based on the alternating minimization optimization strategy, the optimal matrices $\mathbf{W}$ and $\mathbf{H}$ can be obtained after a certain number of iterations. Subsequently, the reconstructed time–frequency matrix $\widehat{\mathbf{S}}$ can be derived by $\widehat{\mathbf{S}}=\mathbf{WH}$. The whistle enhancement process based on regularized NMF is presented in Algorithm 1.

Algorithm 1 Dually-Regularized NMF Algorithm

1: Input: Collected noisy whistle signal $y\left(n\right)$;   2: Noisy whistle T-F representation $\mathbf{Y}=STFT\left(y\right(n\left)\right)$ using Equation (1);   3: Require:$\mathbf{Y},r,{\lambda }_{ogs},{\lambda }_{gl},K_1,K_2,K_{max}$;   4: $(\mathbf{W},\mathbf{H})\leftarrow \mathrm{NNDSVD}(\mathbf{Y},r)$; define kernels $h_1,h_2$;   5: $k\leftarrow 0$;   6: while $k\le K_{max}$do:   7:     H-update:   8:     $\mathbf{d}\leftarrow \mathrm{conv}2(h_1,h_2,|\mathbf{H}{|}^2)+\epsilon$;   9:     $\mathbf{D}\leftarrow {\lambda }_{ogs}\mathrm{conv}2(h_1,h_2,\mathbf{H}./\mathbf{d})$; 10:     ${\mathbf{H}}_{i,j}\leftarrow {\mathbf{H}}_{i,j}{\displaystyle \frac{{\left({\mathbf{W}}^{\top }\mathbf{Y}\right)}_{i,j}}{{\left({\mathbf{W}}^{\top }\mathbf{WH}\right)}_{i,j}+{\mathbf{D}}_{i,j}+\epsilon }}$; 11:     W-update: 12:     $\mathbf{V}\leftarrow \mathbf{W}-\eta (\mathbf{W}\left({\mathbf{HH}}^{\top }\right)-{\mathbf{YH}}^{\top })$; 13:     $\mathbf{U}\leftarrow max(\mathbf{V},0)$; 14:     for each column j do 15:         ${\mathbf{W}}_{:,j}\leftarrow {\left(1-{\displaystyle \frac{\eta {\lambda }_{gl}}{\parallel {\mathbf{U}}_{:,j}{\parallel }_2+\epsilon }}\right)}_{+}{\mathbf{U}}_{:,j}$; 16:     end for 17:     $k\leftarrow k+1$; 18: end while 19: return $\mathbf{W},\mathbf{H}$; 20: Output: Reconstructed whistle T-F representation $\widehat{\mathbf{S}}\doteq \mathbf{WH}$.

2.3. Endpoint Detector Based on Time–Frequency Spectrogram

In this paper, endpoint detection is performed on the time–frequency representations of the noisy observation matrix $\mathbf{Y}\in {\mathbb{R}}_{+}^{K\times M}$ and the reconstructed matrix $\widehat{\mathbf{S}}\in {\mathbb{R}}_{+}^{K\times M}$. Taking the matrix $\mathbf{Y}$ as an example, K denotes the number of frequency bins, M is the number of frames, $f_s$ is the sampling rate, and h is the frame shift. The frame-wise energy is defined as follows:

$$E_m=\sum _{k=1}^K{\left|Y_{k,m}\right|}^2,m=0,1,\dots ,M-1.$$

(33)

By normalizing as ${\tilde{E}}_m=E_m/max\left(E_m\right)$, the overall amplitude variation is eliminated, and the time axis is given by $t_m=mh/f_s$. To distinguish active frames from silent ones, an adaptive threshold is introduced:

$$\tau =median\left(\tilde{E}\right)+\alpha (max\left(\tilde{E}\right)-median\left(\tilde{E}\right)),$$

(34)

where $\alpha$ is set to 0.4, which biased the threshold towards the median side. It was measured that the detection performance remained good under different SNRs and dolphin whistle conditions. Therefore, there is no need to adjust the parameters separately for each signal segment. Based on this threshold, the activity indicator function is defined as $A_m=\mathbf{1}\left\{{\tilde{E}}_m>\tau \right\}$, thereby obtaining a candidate sequence of active frames.

To avoid misjudging short-term energy fluctuations as event boundaries, duration constraints are imposed. Let the total duration be $T=Mh/f_s$, then the minimum silence duration is defined as ${\mathsf{\Delta }}_{\mathrm{sil}}=max(0.1,0.01T)$ and the minimum segment duration is defined as ${\mathsf{\Delta }}_{\mathrm{dur}}=max(0.01,0.005T)$, which are converted into the corresponding frame numbers $L_{\mathrm{sil}}$ and $L_{\mathrm{dur}}$, respectively. By tracking the rising and falling edges of the detected activity indicator sequence, candidate onset–offset frame indices $\left\{s_i,e_i\right\}$ are obtained. If the gap between two adjacent segments is less than $L_{\mathrm{sil}}$ and their mean energy is below the threshold, they are merged into a single continuous segment. Finally, short segments shorter than $L_{\mathrm{dur}}$ are removed, leaving only valid event intervals. The final endpoint set is, thus, given by $\mathcal{S}={\left\{\left[t_{s_i},t_{e_i}\right]\right\}}_i$, where $t_{s_i}=s_{i}h/f_s$ and $t_{e_i}=e_{i}h/f_s$.

2.4. Experimental Setup

2.4.1. Evaluation Metrics

To evaluate the whistle-event detection performance of the proposed method, the frame-level $F_1$-score is calculated, which is defined as the harmonic mean of precision and recall. The frame-level $F_1$-score comprehensively reflects the effectiveness of the method in whistle detection. In the collected dolphin whistle signals, let there be M frames containing whistles. After enhancement and detection, $TP$ frames are correctly identified as whistle frames (true positives), while $FN$ frames remain undetected (false negatives), such that $M=TP+FN$. Meanwhile, if whistle-absent frames are mistakenly judged as containing whistles, their number is denoted as $FP$ (false positives), and those correctly judged as non-whistle frames are denoted as $TN$ (true negatives). Under this definition, precision and recall can be expressed as

$$\begin{array}{cc}\hfill \mathrm{Precision}& ={\displaystyle \frac{TP}{TP+FP}}\hfill \\ \hfill \mathrm{Recall}& ={\displaystyle \frac{TP}{TP+FN}}.\hfill \end{array}$$

(35)

The $F_1$-score, as a comprehensive indicator, is then obtained by computing the harmonic mean of precision and recall, and it is expressed as follows:

$${\displaystyle \frac{1}{F_1}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{Precision}}+{\displaystyle \frac{1}{Recall}}\right).$$

(36)

Therefore, the frame-level $F_1$-score is given by

$$F_1={\displaystyle \frac{2TP}{2TP+FP+FN}}.$$

(37)

Meanwhile, the ground-truth annotations were obtained using methods employed by audio engineers for assessing human auditory perception, as well as spectrograms commonly utilized by zoologists.

2.4.2. Baseline Methods

To validate the effectiveness and superiority of the proposed method, a systematic comparison was conducted against five representative baseline approaches. Baseline Method 1 (Blurring) employs a median filtering technique to smooth the signal, which is commonly applied to mitigate time–frequency blurring effects in dolphin whistle signals [19]. Baseline Method 2 (OGS) introduces a non-convex overlapping group sparsity regularization within a convex optimization framework [28], achieving robust and effective signal denoising by reinforcing the constraints on group-sparse structures. Baseline Method 3 (GL) imposes group-sparse constraints based on predefined group structures [37], thereby enhancing the accuracy of parameter estimation and the robustness to noise under strong group-sparsity conditions. Baseline Method 4 (NMF-OGS) involves imposing OGS regularization on the coefficient matrix $\mathbf{H}$ in standard NMF, suppressing scattered activations along the time axis and encouraging sparse patterns that are continuous in segments. Baseline Method 5 (NMF-GL) applies GL regularization to the substrate matrix $\mathbf{W}$ in the standard NMF to achieve group-level sparse selection.

To ensure objectivity and consistency in the comparison process, the performance of all methods was evaluated using the same detector. The implementation of the detector is described in detail in Section 2, and the evaluation metrics include precision, recall, and the $F_1$-score computed based on these metrics.

3. Results

3.1. Optimal Parameter Selection

To ensure that the proposed method achieves optimal performance in dolphin whistle enhancement and endpoint detection, it is necessary to systematically optimize and validate several of the input parameters involved in the model. First, regarding the number of iterations, too few iterations may result in incomplete convergence of the decomposition, whereas too many iterations would lead to excessive computational cost with limited performance gain. Based on repeated experimental validation, the number of iterations in this work is set to 200 in order to balance convergence accuracy and computational efficiency. It is noteworthy that, within each alternating update iteration, the update loop of matrix $\mathbf{H}$ is further embedded with an inner loop of 5 iterations, thereby enhancing the stability and accuracy of OGS regularization optimization. In addition, for the decomposition rank r, if it is set too small, the model will fail to adequately capture the time–frequency characteristics of whistle signals, while an excessively large r may introduce noise components and reduce the effectiveness of sparsity regularization. Considering both signal complexity and model robustness, this paper sets $r=128$ to maintain a balance between feature representation capacity and the enforcement of regularization constraints.

Within the framework of NMF, the configuration of regularization terms plays a decisive role in the final enhancement and endpoint detection performance. The proposed model involves four core hyperparameters, namely the OGS regularization coefficient ${\lambda }_{ogs}$, the GL regularization coefficient ${\lambda }_{gl}$, and the time–frequency neighborhood window sizes $(K_1,K_2)$ required by the OGS regularization. To determine the optimal combination of these hyperparameters, a grid search strategy is adopted to traverse the parameter space. The overall optimization objective function can be expressed as follows:

$${min}_{\mathbf{W},\mathbf{H}\ge 0}{\displaystyle \frac{1}{2}}{∥\mathbf{Y}-\mathbf{WH}∥}_F^2+{\lambda }_{\mathrm{ogs}}{\mathsf{\Omega }}_{\mathrm{OGS}}\left(\mathbf{H};K_1,K_2\right)+{\lambda }_{\mathrm{gl}}{\mathsf{\Omega }}_{\mathrm{GL}}\left(\mathbf{W}\right).$$

(38)

In the parameter search and optimization process, the search ranges of ${\lambda }_{ogs}$ and ${\lambda }_{gl}$ are set to [0.01, 0.1] with a step size of 0.01, while the search ranges of $K_1$ and $K_2$ are set to [3, 15] with a step size of 2. Each candidate parameter set is evaluated using the frame-level $F_1$-score obtained from endpoint detection, and the parameter combination yielding the highest score is regarded as the optimal solution, and it is denoted as $\left({\lambda }_{\mathrm{ogs}}^{\ast },{\lambda }_{\mathrm{gl}}^{\ast },K_1^{\ast },K_2^{\ast }\right)=arg{max}_{{\lambda }_{\mathrm{ogs}},{\lambda }_{\mathrm{gl}},K_1,K_2}{F}_1$.

It is noteworthy that during the alternating updates of $\mathbf{W}$ and $\mathbf{H}$, the choice of the gradient descent step size $\eta$ is also involved. In theory, the step size can be set according to the Lipschitz constant $\gamma$ as $\eta =1/\gamma$, which guarantees convergence but is often overly conservative, thereby limiting both convergence speed and performance improvement. Based on extensive experimental comparisons, the step size in this work is ultimately set to $\eta =0.5$, which balances numerical stability with practical performance without strictly relying on the Lipschitz bound.

3.2. Enhanced and Detected Results of Typical Whistle Segments

This paper selects three typical pure dolphin whistle clips emitted by two captive Southern bottlenose dolphins [16]: wav1, wav2, and wav3. These signals cover concave and upsweep morphological features and effectively characterize the modulation patterns commonly observed in acoustic monitoring of the target species. Such a selection helps prevent the evaluation from overfitting to a single type of whistle structure. According to Equation (2), the STFT was employed to convert the signals into the time–frequency domain. All STFT parameters in this article are configured as follows: a window length of 256 samples, an overlap of 128 samples, and an FFT size of 1024. The resulting clean spectrograms are presented in Figure 1a,c,e, which clearly reveal the tonal ridges characteristic of whistle contours.

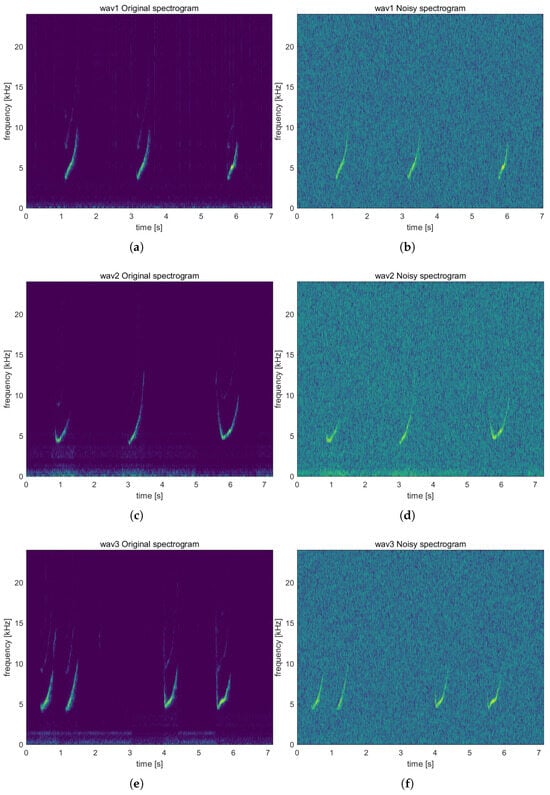
Figure 1. Comparison of the time–frequency spectrograms between the clean and noisy whistle segments under −5 dB SNR noise interference. lighter colors indicate higher energy. (a) clean wav1; (b) noisy wav1; (c) clean wav2; (d) noisy wav2; (e) clean wav3; and (f) noisy wav3.

To assess the robustness of the proposed enhancement framework under noisy conditions, Gaussian white noise was artificially added to the clean whistle signals. The input SNRs were set in the range of −10 dB to −5 dB, representing the challenging acoustic environments typically encountered in shallow-water passive acoustic monitoring. Importantly, the noise was generated using a fixed random seed, thereby eliminating stochastic variability and ensuring the reproducibility of all experiments. The spectrograms of the noisy whistle signals are illustrated in Figure 1b,d,f. As shown, under an input SNR of −5 dB, the noisy spectrograms exhibit nearly uniform background fluctuations with pronounced random granular interference. This led to a flattening of the overall energy distribution, which, in turn, significantly diminished the contrast between whistle ridges and weak-energy segments relative to the background. Such degradation highlights the necessity of effective enhancement techniques, as traditional detection algorithms may fail to reliably distinguish whistle contours from the surrounding noise under these adverse acoustic conditions.

Building upon the hyperparameter search strategy outlined in the preceding subsection, this study employed the frame-level $F_1$-score as the primary evaluation criterion. A comprehensive grid search was conducted on the validation set to explore the joint parameter space, and the globally optimal configuration was determined as $({\lambda }_{ogs},{\lambda }_{gl},K_1,K_2)=(0.02,0.03,11,3)$. This parameter set was thereafter fixed throughout the experimental stage to ensure consistency and comparability across evaluations involving the three whistle segments. As summarized in Table 1, under varying SNR conditions, the enhancement process yields marked improvements in recall across all three segments, reflecting the method’s capability to preserve weak signal components that are often masked by noise. Moreover, the frame-level $F_1$-score consistently surpassed the corresponding pre-enhancement results, underscoring the robustness of the proposed framework in low-SNR environments. Notably, the highest-performing sample achieved a maximum frame-level $F_1$-score of 0.9678, demonstrating the effectiveness of the optimized parameter combination in balancing noise suppression with signal fidelity.

Table 1. The detection precision, recall, and frame-level $F_1$-score of whistle segments under different SNRs before and after enhancement.

SNR (dB)	−10	−9	−8	−7	−6	−5
Noisy wav1
Precision	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Recall	0.4391	0.4589	0.4731	0.4986	0.5172	0.5241
$F_1$-Score	0.6102	0.6291	0.6423	0.6654	0.6779	0.6877
Enhanced wav1
Precision	0.9967	0.9970	1.0000	1.0000	1.0000	1.0000
Recall	0.6686	0.7190	0.7819	0.8499	0.8952	0.9356
$F_1$-Score	0.7999	0.8540	0.8776	0.9188	0.9267	0.9678
Noisy wav2
Precision	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Recall	0.4230	0.4360	0.4527	0.4694	0.4917	0.5083
$F_1$-Score	0.5945	0.6072	0.6232	0.6389	0.6592	0.6740
Enhanced wav2
Precision	0.9917	1.0000	1.0000	1.0000	1.0000	1.0000
Recall	0.6660	0.6827	0.7365	0.7495	0.7959	0.8590
$F_1$-Score	0.7969	0.8115	0.8483	0.8568	0.8864	0.9242
Noisy wav3
Precision	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Recall	0.4218	0.4341	0.4482	0.4499	0.4605	0.4745
$F_1$-Score	0.5933	0.6054	0.6189	0.6206	0.6306	0.6436
Enhanced wav3
Precision	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Recall	0.5677	0.6257	0.6942	0.7504	0.7645	0.7750
$F_1$-Score	0.7242	0.7697	0.8195	0.8574	0.8665	0.8733

Figure 2 presents the time–frequency spectrogram results of the wav1, wav2, and wav3 segments under −5 dB SNR noise interference after being processed by the proposed enhancement method. It can be observed that the energy distribution of the whistles becomes clearer and more continuous, with the background noise–induced random fluctuations significantly suppressed, thereby allowing the whistle ridges and weak energy components to be more prominently revealed.

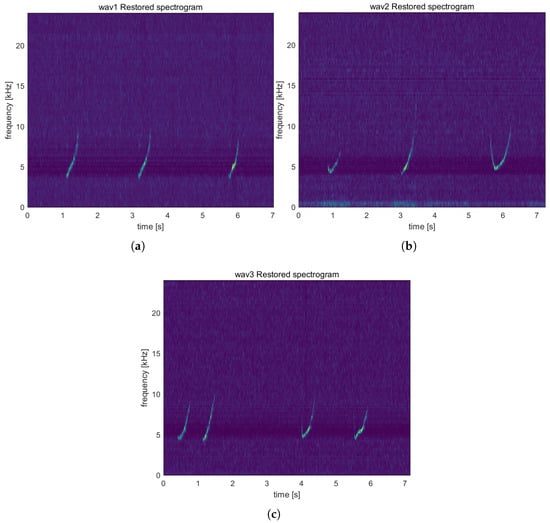
Figure 2. Time–frequency spectrograms of the whistle segments after enhancement under −5 dB SNR noise interference. lighter colors indicate higher energy. (a) wav1; (b) wav2; and (c) wav3.

Furthermore, Figure 3 compares the energy curves and the corresponding endpoint detection results of three whistle segments before and after enhancement under −5 dB noise interference. It can be observed that the enhancement processing made the peak–valley differences of the energy curves more pronounced, while the low-amplitude fluctuations caused by noise were substantially suppressed, thereby improving the robustness and accuracy of endpoint detection. Compared with the distorted and fluctuating energy curves prior to enhancement, the onset and offset boundaries of the enhanced signals are more clearly defined. This demonstrates that the proposed method not only improves the interpretability of time–frequency representations, but also significantly enhances detection performance in practical endpoint detection tasks.

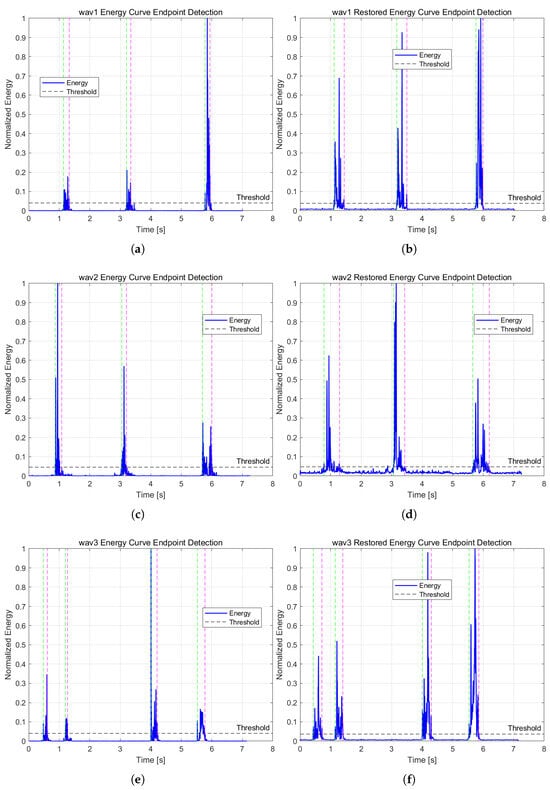
Figure 3. Comparison of the energy curves of whistle segments before and after enhancement under −5 dB SNR noise interference. The green and pink dash lines respectively represent the starting and ending points of the detected audio clips. (a) noisy wav1; (b) enhanced wav1; (c) noisy wav2; (d) enhanced wav2; (e) noisy wav3; and (f) enhanced wav3.

3.3. Comparison with Other Methods

In the cross-comparison experiments of performance, the wav1 whistle segment was selected as the test subject, and the proposed method was systematically evaluated against five baseline methods under various low-SNR conditions. Specifically, under noise interference at different SNR levels, the enhanced signals obtained by each method were analyzed using the endpoint detection algorithm introduced in Section 2, with precision, recall, and the $F_1$-score adopted as evaluation metrics to ensure consistency and fairness in the assessment process. Figure 4 illustrates the comparative results of the precision, recall, and $F_1$-score obtained after enhancement by the proposed method and the five baseline methods in environments with SNRs of −10 dB, −9 dB, −8 dB, −7 dB, −6 dB, and −5 dB.

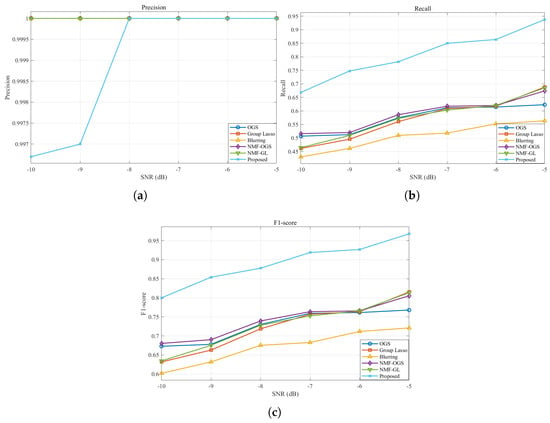
Figure 4. Comparative results of the precision, recall, and $F_1$-score obtained after enhancement by the six methods under different SNR conditions. (a) Precision; (b) recall; and (c) $F_1$-score.

It can be observed that, under different SNR conditions, the six methods exhibited distinct differences in endpoint detection performance. In terms of precision, all of the methods maintained values close to 1 across almost all noise levels, with only the proposed method showing a slight decline at −10 dB. This phenomenon indicates that all of the methods demonstrated strong stability in suppressing false detections, as the detected segments were essentially true whistle signals. It should be noted, however, that although the precision of all methods consistently remained at a high level, this does not guarantee the completeness of detection results, as some true whistle segments were still missed. Therefore, it was necessary to further examine the recall metric to evaluate the ability of each method to capture true whistles under different SNR conditions. Regarding recall, the Blurring, OGS, GL, NMF-OGS, and NMF-GL methods generally performed poorly, particularly under low-SNR conditions, where recall rates remained within the range of 0.43–0.69, suggesting limitations in enhancing and preserving weak signals. In contrast, the proposed method exhibited significant advantages across all noise levels, with recall improving from 0.6686 to 0.9377 as the SNR increased from −10 dB to −5 dB, highlighting its enhanced capability of preserving whistle signals in low-SNR environments.

From the perspective of the overall performance metric $F_1$-score, the proposed method achieved the highest values under all SNR conditions and exhibited a gradual upward trend as the SNR increased. At −5 dB, the $F_1$-score of the proposed method reached 0.9678, which was markedly superior to Blurring (0.7210), OGS (0.7679), GL (0.8154), NMF-OGS (0.8054), and NMF-GL (0.8134). This demonstrates that the proposed method effectively improves recall while maintaining a high level of precision, thereby achieving overall performance superior to the baseline methods.

3.4. Experimental Results on Real Dolphin Whistle Recordings

To further validate the effectiveness and applicability of the proposed method in real-world scenarios, two bottlenose dolphin whistle segments were selected from an open-source acoustic dataset, denoted as wav4 and wav5 (available at WHOI Dolphin Whistle Database (https://whoicf2.whoi.edu/science/B/whalesounds), accessed on 17 August 2025). The signals were processed under the same experimental framework for enhancement and endpoint detection. Since marine noise in natural environments often exhibits complex non-stationary characteristics, particularly including broadband background noise and impulsive interference, validation on such data provides a more intuitive reflection of the algorithm’s robustness and generalization capability in natural conditions.

In terms of experimental results, Figure 5 presents the original spectrograms of the wav4 and wav5 segments along with their enhanced versions. It can be observed that the original spectrograms were subject to substantial background noise interference. For the wav4 segment, the whistle energy was stronger. Most whistle tracks can still be recognized in the original state, but due to the presence of noise, some weak energy components were covered up, resulting in incomplete and inaccurate endpoint detection. After enhancement using the proposed method, the spectrogram of the wav4 segment exhibited a continuous and distinct energy distribution, with background noise significantly reduced. This highlights the whistle structure more clearly, where excellent detection performance in endpoint detection was achieved and the enhancement effect of the proposed method on common dolphin whistles is demonstrated.

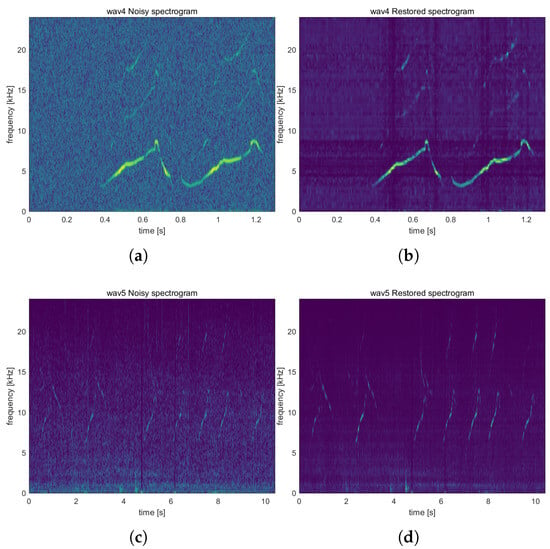
Figure 5. Comparison of spectrograms of the wav4 and wav5 whistle segments before and after enhancement. lighter colors indicate higher energy. (a) Noisy wav4; (b) enhanced wav4; (c) noisy wav5; and (d) enhanced wav5.

In contrast, the signal energy of the wav5 whistle was relatively weak. The whistle signal was almost completely submerged in the noise, and its energy trajectory was almost unrecognizable, making traditional endpoint detection methods basically ineffective in this situation. However, the enhanced spectrum processed by the proposed method effectively highlights the energy distribution of the whistle, indicating that the method still has a certain signal extraction ability for weak signals in the presence of noise. Although there was still some residual noise interference, the overall SNR had improved, allowing the whistle structure to be distinguished and, thus, restoring a certain effectiveness of endpoint detection in this segment.

Based on the comparison of the energy curves before and after enhancement, as shown in Figure 6, the effect of the enhancement method under different noise complexities can be analyzed more intuitively. For the wav4 segment, although the pre-enhancement energy curve already reflects the presence of certain whistles, its fluctuations are not sufficiently pronounced, and there exists some deviation between the threshold crossings and the ground-truth annotations. After enhancement with the proposed method, the energy curve exhibited more distinct fluctuations, thereby improving the overlap between the detected endpoints and the annotated intervals, which indicates higher detection accuracy. In contrast, for the wav5 segment, the pre-enhancement energy curve was almost entirely irregular, showing only random fluctuations close to the noise baseline, which made endpoint detection essentially ineffective. After enhancement, however, the energy curve transitioned from a disordered state to a structure with clear peaks. Although residual noise still interfered with certain intervals, the overall SNR was improved.

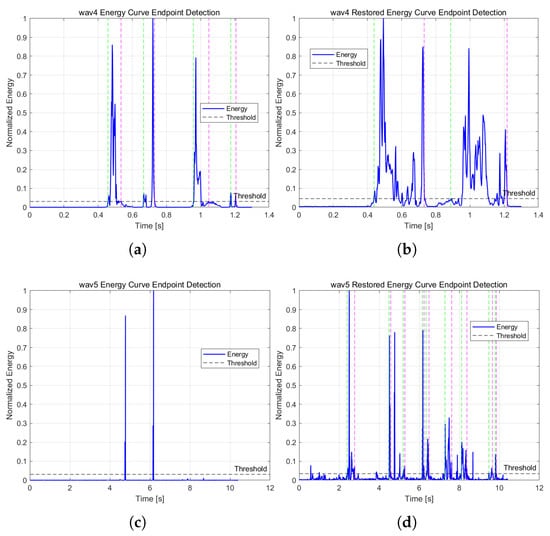
Figure 6. Comparison of the energy curves of the wav4 and wav5 whistle segments before and after enhancement. The green and pink dash lines respectively represent the starting and ending points of the detected audio clips. (a) Noisy wav4; (b) enhanced wav4; (c) noisy wav5; and (d) enhanced wav5.

Table 2 summarizes the endpoint detection results of the whistle segments wav4 and wav5 under different enhancement methods. For the wav4 segment, the noisy signal achieved a precision of 1.0000 but a low recall of 0.3137, resulting in a modest $F_1$-score of 0.4775. Traditional enhancement methods, such as Blurring, OGS, GL, NMF-OGS, and NMF-GL, slightly improved in their recall values (0.4649, 0.4594, 0.3413, 0.4668, and 0.4631), yet their $F_1$-scores remained below 0.65. In contrast, the proposed method substantially raised the recall to 0.7491 while preserving perfect precision, leading to the highest $F_1$-score of 0.8565.

Table 2. The detection precision, recall, and $F_1$-score for the different enhancement methods on the whistle segments wav4 and wav5.

	Precision	Recall	${\mathit{F}}_1$-Score
wav4 Segment
Noisy	1.0000	0.3137	0.4775
Blurring	1.0000	0.4649	0.6348
OGS	1.0000	0.4594	0.6296
GL	1.0000	0.3413	0.5089
NMF-OGS	1.0000	0.4668	0.6365
NMF-GL	1.0000	0.4631	0.6330
Proposed	1.0000	0.7491	0.8565
wav5 Segment
Noisy	0.0000	0.0000	0.0000
Blurring	0.0000	0.0000	0.0000
OGS	0.0000	0.0000	0.0000
GL	0.0000	0.0000	0.0000
NMF-OGS	0.0000	0.0000	0.0000
NMF-GL	0.0000	0.0000	0.0000
Proposed	0.9438	0.3631	0.5245

For the wav5 segment, the detection performance on the noisy input and baseline enhancement methods completely failed, with all metrics equal to 0.0000, reflecting the severe masking effect of background noise. In contrast, the proposed method demonstrated partial recovery of valid whistle segments, with a precision of 0.9438, recall of 0.3631, and an $F_1$-score of 0.5245. This demonstrates its effectiveness in extracting weak signals that were otherwise undetectable by conventional approaches.

3.5. Complexity Analysis

To evaluate the computational cost of the proposed algorithm, an approximate complexity analysis of the main sub-operations within a single outer iteration was conducted in terms of memory and arithmetic. Let the observation matrix be of size $K\times M$, the factorization rank be $r\ll min(K,M)$, and the number of outer iterations be $N_{\mathrm{it}}$. The update of $\mathbf{H}$ involves $I_h=5$ inner iterations, with a two-dimensional OGS smoothing kernel of size $K_1\times K_2$. In each inner iteration of the $\mathbf{H}$-update, the core computations are as follows: computing ${\mathbf{W}}^{\top }\mathbf{Y}$ with complexity $\mathcal{O}\left(KrM\right)$, forming ${\mathbf{W}}^{\top }\mathbf{W}$ and multiplying it by $\mathbf{H}$ with complexity $\mathcal{O}(K{r}^2+r^{2}M)$, and performing two local convolutions to construct the smoothing quantities required by the regularization with complexity $\mathcal{O}\left(rM{K}_1{K}_2\right)$. Hence, the overall complexity of the $\mathbf{H}$-update can be expressed as $\mathcal{O}\left(I_h(KrM+r^{2}M+K{r}^2+rM{K}_1{K}_2)\right)$. During the update of $\mathbf{W}$, the main computations include constructing ${\mathbf{HH}}^{\top }$ with complexity $\mathcal{O}\left(r^{2}M\right)$, computing ${\mathbf{YH}}^{\top }$ with complexity $\mathcal{O}\left(KrM\right)$, and evaluating ${\mathbf{WHH}}^{\top }$ with complexity $\mathcal{O}\left(K{r}^2\right)$. The proximal operation performed at this stage involves row-wise soft-thresholding and vector-norm shrinkage with complexity $\mathcal{O}\left(Kr\right)$. Therefore, the overall complexity of the $\mathbf{W}$-update can be expressed as $\mathcal{O}(KrM+r^{2}M+K{r}^2+Kr)$. Therefore, the total computational complexity of a single outer iteration can be approximated as $\mathcal{O}\left(I_h(KrM+K{r}^2+r^{2}M+rM{K}_1{K}_2)+(KrM+r^{2}M+K{r}^2+Kr)\right)$.

In this study, whistle signal processing was performed on an Intel Core i9-13900H processor with 9 GB RAM. The results show that the proposed method requires 8.785 s of runtime. Compared with GL (10.372 s), the proposed method reduces computation time, while providing stronger enhancement than OGS (3.146 s), Blurring (0.143 s), NMF-OGS (8.256 s), and NMF-GL (6.778 s), thereby achieving a better balance between performance and efficiency.

4. Discussion

4.1. Analysis of the Superiority of the Proposed Method

The proposed NMF enhancement framework demonstrates significant advantages in dolphin whistle detection under low SNR and complex noise conditions. Compared with conventional approaches, such as spectral subtraction and time–frequency smoothing [38,39], the proposed method not only maintains stability in achieving high precision, but it also substantially improves recall, thereby leading to overall gains in the $F_1$-score. The pivotal innovation lies in the joint incorporation of OGS and GL regularization within the NMF framework. The former enforces local time–frequency continuity to preserve whistle ridges while effectively suppressing the fragmented energy distributions caused by background noise [40]; the latter adaptively eliminates ineffective bases at the dictionary level, preventing redundant components from amplifying residual noise [41]. The synergistic effect of these two regularizers enables the enhanced spectrograms to strike a favorable balance between structural preservation and noise suppression, thereby providing more reliable inputs for subsequent endpoint detection.

In comparison with the five representative baseline methods, the proposed approach demonstrates superior performance under low-SNR conditions ranging from −10 dB to −5 dB. Although all methods maintain relatively high precision, Blurring, OGS, GL, NMF-OGS, and NMF-GL individually exhibit clear deficiencies in recall, particularly in preserving weak signals. By contrast, the proposed method consistently achieves substantial improvements in recall across different noise levels, indicating that the joint regularization possesses stronger robustness in retaining weak energy components. This finding aligns with observations in other bioacoustic studies, where a single sparsity constraint has often proven insufficient to ensure the detectability of weak target signals [42]. Notably, in experiments with real dolphin whistle recordings, the proposed method preserved high detection integrity in segments with complex background conditions and restored partial detectability under extremely low-visibility scenarios, thereby demonstrating strong practical applicability and generalization capability.

4.2. Limitations and Future Perspectives

Nevertheless, the proposed method still exhibits certain limitations. Under extremely low-SNR conditions, although the recall rate improves substantially, it remains unable to fully recover all whistle components that are severely masked by noise, indicating that the model’s separation capability requires further enhancement in the presence of strong noise interference [21]. Complexity analysis reveals that while the dual regularization and the nested iterative scheme ensure stable performance, their computational cost may cause a constraint in large-scale passive acoustic monitoring tasks [43]. Moreover, as the method is founded on sparsity and low-rank assumptions, its adaptability remains limited in environments characterized by nonstationarity or the superposition of multiple noise sources [44].

Future research will proceed along several directions. Empirical validation can be broadened by expanding datasets and evaluation scenarios, including streaming benchmarks on continuous, long-duration recordings, and multi-site deployments. Incorporating multi-noise source modeling and adaptive noise estimation is expected to improve robustness in nonstationary and complex acoustic environments [45]. In parallel, motivated by recent advances in deep learning for bioacoustic signal detection and enhancement [46,47,48], integrating the proposed regularized NMF framework with deep learning methods may enable joint optimization of enhancement and detection, thereby overcoming the limitations of conventional stage-wise processing. Finally, although extending this research to other types of acoustic signals is valuable, doing so will require new prior assumptions and tailored front-end designs.

5. Conclusions

This study presents an unsupervised enhancement framework rooted in dually-regularized NMF, specifically designed to address the challenges of dolphin whistle detection under low SNR. Beyond the conventional data fidelity term, two complementary structural priors are incorporated: an OGS regularizer, which promotes the continuity of whistle trajectories in the time–frequency domain; and a GL regularizer, which adaptively prunes redundant spectral bases. Together, these regularization strategies enhance the separability of whistle signals from noise while preserving their inherent structural integrity. To ensure efficient and reliable optimization, the activation matrix is updated using a majorization–minimization scheme with iteratively reweighted least squares (MM–IRLS), which stabilizes convergence even in the presence of non-smooth penalties. Meanwhile, the spectral basis matrix is refined via a proximal gradient method, allowing for the simultaneous enforcement of non-negativity and column-level sparsity constraints.

Comprehensive experiments conducted under a variety of low-SNR conditions demonstrate that the proposed approach achieves substantial improvements in recall while maintaining consistently high precision, resulting in robust and stable gains in the $F_1$-score. Comparative evaluations against representative baseline methods further corroborate the advantages of the framework, particularly in preserving weak whistles that are otherwise masked by background noise. Finally, the complexity analysis indicates that the algorithm achieves a favorable balance between accuracy and computational cost, confirming its practicality for deployment on modern processing platforms. This improvement in dolphin whistle detection performance enhances, to some extent, the practicality of PAM, and it also exerts a positive influence in population assessment and habitat studies.