Thermo-Mechanical Fault Diagnosis for Marine Steam Turbines: A Hybrid DLinear–Transformer Anomaly Detection Framework

Abstract

Thermodynamic fault diagnosis of marine steam turbines remains challenging due to non-stationary multivariate sensor data under stochastic loads and transient conditions. While conventional threshold-based methods lack the sophistication for such dynamics, existing data-driven Transformers struggle with inherent non-stationarity. To address this, we propose a hybrid DLinear–Transformer framework that synergistically integrates localized trend decomposition with global feature extraction. The model employs a dual-branch architecture with adaptive positional encoding and a gated fusion mechanism to enhance robustness. Extensive evaluations demonstrate the framework’s superiority: on public benchmarks (SMD, SWaT), it achieves statistically significant F1-score improvements of 2.7% and 0.3% over the state-of-the-art TranAD model under a controlled, reproducible setup. Most importantly, validation on a real-world marine steam turbine dataset confirms a leading fault detection accuracy of 94.6% under variable conditions. By providing a reliable foundation for identifying precursor anomalies, this work establishes a robust offline benchmark that paves the way for practical predictive maintenance in marine engineering.

1. Introduction

Marine steam turbine systems serve as safety-critical components in maritime operations, whose operational integrity and performance directly govern overall vessel safety, maneuverability, and navigation efficiency. These systems exhibit inherent multidisciplinary complexity due to tightly coupled thermo-fluid, mechanical, and control subsystems operating within highly dynamic and uncertain marine environments. Challenging operational conditions, such as fluctuating loads, wave-induced vibrations, and variations in seawater properties, further complicate their dynamic behavior, making accurate anomaly detection particularly difficult. Currently, the maritime industry predominantly relies on threshold-based condition monitoring methods, which use predefined limits on selected physical parameters to trigger alarms. Although straightforward to implement, these conventional methods lack the capacity to effectively process and interpret the high-dimensional, nonlinear, and temporally correlated operational data produced by modern marine steam turbine systems. As a result, they suffer from limited sensitivity to incipient faults and a high false positive rate during transient conditions, thereby falling short in supporting proactive maintenance and operational decision-making. Given the critical role of these systems and the growing availability of sensor data onboard vessels, the development and implementation of advanced data-driven anomaly detection methods specifically designed for marine steam turbines have become a research priority, offering considerable potential for enhancing safety, reliability, and efficiency in marine engineering applications.

Traditional anomaly detection techniques applied to marine steam turbine systems, such as k-means [1] clustering, support vector machines (SVMs) [2], and regression modeling [3], are primarily rule-based or grounded in conventional statistical models. While these methods perform adequately in detecting discrete anomalous data points, they exhibit considerable limitations in complex dynamic systems. In such environments, anomalies may manifest not only as isolated outliers but also as continuous anomalous subsequences, where individual time points may appear normal under predefined thresholds. Consequently, approaches focused exclusively on point-wise outlier detection are often insufficient for reliably identifying anomalies in multivariate and highly nonlinear time series [4].

In contrast, modern data-driven anomaly detection methods encompass a diverse spectrum of techniques, ranging from statistical process control models [5] to deep learning architectures such as autoencoders [6] and long short-term memory (LSTM) networks [7]. These approaches leverage automated feature extraction and sequential modeling to effectively capture non-linear temporal dependencies and dynamic system behaviors, thereby substantially improving the detection of subtle and progressive anomalies. A pivotal advancement was marked by the introduction of attention mechanisms [8] and the subsequent advent of Transformer-based models [9], which significantly enhanced the modeling of long-range dependencies in complex operational sequences. The integration of physical principles with deep learning frameworks [10] has further yielded hybrid methods that partially mitigate data fragmentation issues and improve generalization across varying vessel operating conditions. architectural evolution continued with the fusion of Transformers and generative models, as exemplified by MT-VAE [11] and MAD-GAN [12], which employ adversarial and co-evolution mechanisms to strengthen temporal pattern recognition. This innovation trajectory is further evidenced by subsequent refinements: TransAnomaly [13] leverages self-attention weights for dependency modeling, FGANomaly [14] incorporates pseudo-label filtration to enhance data integrity, AnoFormer [15] introduces adaptive masking for improved sensitivity, and TranAD [16] achieves state-of-the-art performance through deep attention fusion. These advances collectively underscoring the maturing potential of Transformer-based frameworks in tackling complex anomaly detection tasks.

Concurrently, the broader field of industrial diagnostics has made significant strides, further validating the efficacy of data-driven paradigms. Substantial performance gains have been demonstrated through enhanced convolutional architectures and advanced signal processing techniques for component-level diagnostics, as evidenced by gear and bearing fault diagnosis under variable conditions in studies by Spirto et al. [17] and Lin et al. [18]. The application scope of deep learning has expanded considerably, now encompassing strategies such as deep transfer learning and Koopman operator-based methods for turbocharger and gas turbine systems [19,20], as well as two-tier machine learning frameworks for wind turbine fault detection [21]. Notably, these paradigms are increasingly demonstrating practical efficacy in maritime energy systems. A prominent example is the work of Liu et al. [22], who successfully implemented a deep transfer learning framework for the condensate system of marine steam turbines.

This collective progress highlights the success of deep learning in applications spanning from component-level (e.g., gears, bearings) to subsystem-level (e.g., condensate systems) diagnostics. However, this predominant focus on component or subsystem-level diagnosis, often reliant on pre-processed features, reveals a critical gap in addressing system-level anomaly detection from the raw, non-stationary multivariate time series generated by an integrated marine steam turbine system under dynamic operating conditions.

When applied to this task, current models, including sophisticated Transformer-based variants, reveal fundamental limitations. Although the self-attention mechanism inherent in Transformers represents a theoretical leap in capturing long-range dependencies, its practical efficacy in highly dynamic environments remains constrained. A primary bottleneck is the inability to robustly capture explicit temporal dependencies [23] amidst pronounced non-stationarity. Compounding this issue, empirical evidence indicates that the self-attention mechanism may over-prioritize local features, inadvertently fragmenting the coherent global temporal contexts [24] and undermining the model’s inherent sequential perception [25]. These challenges are acutely magnified in marine steam turbine systems, which present unique anomaly detection challenges due to their escalating structural sophistication, highly dynamic operational regimes, and multivariate data streams stemming from intricate component interdependencies and cross-domain interactions. The resulting complex correlations within the feature data pose a formidable obstacle, significantly complicating the effective deployment of Transformer-based anomaly detection in real-world maritime settings.

To enhance information preservation in time series analysis and improve reconstruction accuracy for non-stationary sequences, we propose an enhanced framework that refines the Transformer-based collaborative reconstruction network architecture. Our methodology integrates a novel cooperative training paradigm, DLinear–Transformer, which synergizes the sequence modeling strengths of Transformer with the multi-horizon forecasting capabilities of DLinear. In this configuration, the Transformer operates as the reconstruction evaluator, while the DLinear module functions as the reconstruction module. While maintaining the original Transformer structure, this study utilizes DLinear’s direct multi-step prediction strategy, enabling it to work collaboratively with the Transformer in a cooperative setup. Furthermore, we calculate the anomaly scores at each time point and employ The Peak Over Threshold (POT) method [26] to automatically determine dynamic thresholds. The DLinear–Transformer cooperative training process effectively captures dependencies across all positions in the sequence and generates a reconstructed sequence that closely approximates the actual situation by integrating both local and global information. We have validated the effectiveness of the DLinear–Transformer algorithm on publicly available datasets, including Server Machine Dataset (SMD) [27] and the Secure Water Treatment (SWaT) benchmark [28], as well as our self-constructed marine steam turbine system dataset. The results demonstrate that this method offers a more effective solution for forecasting non-stationary time series, thereby better addressing the challenges of real-world applications.

The main contributions of this study can be summarized as follows:

• Domain-specific marine steam turbine dataset: We introduce a dataset capturing 62 dynamic parameters collected under real maritime conditions, capturing multi-regime operational states to support robust anomaly detection model development.
• Novel collaborative framework: A novel two-stage cooperative training architecture is proposed, which synergizes a DLinear-based reconstruction module and a Transformer-based reconstruction evaluator to significantly reduce reconstruction errors in non-stationary time series and enhance local-global feature representation.
• Enhanced Performance and Maritime Applicability: Our method achieves state-of-the-art results on public benchmarks, evidenced by a markedly improved F1-score. More importantly, its successful deployment in identifying marine-specific faults, such as condenser level anomalies, demonstrates substantial practical value for real-world predictive maintenance and enhanced operational safety.

The remainder of this paper is structured as follows. Section 2 elaborates on the proposed hybrid framework, detailing the architecture and synergistic mechanism of the DLinear–Transformer. Section 3 outlines the experimental design, including the configuration of the marine steam turbine dataset, benchmark datasets, and evaluation protocols. Section 4 presents the experimental results. Section 5 provides comprehensive analyses and discussion, including ablation and sensitivity studies, and concludes with an outlook on limitations and future work. Finally, Section 6 concludes the paper.

2. A Hybrid DLinear–Transformer Framework for Anomaly Detection

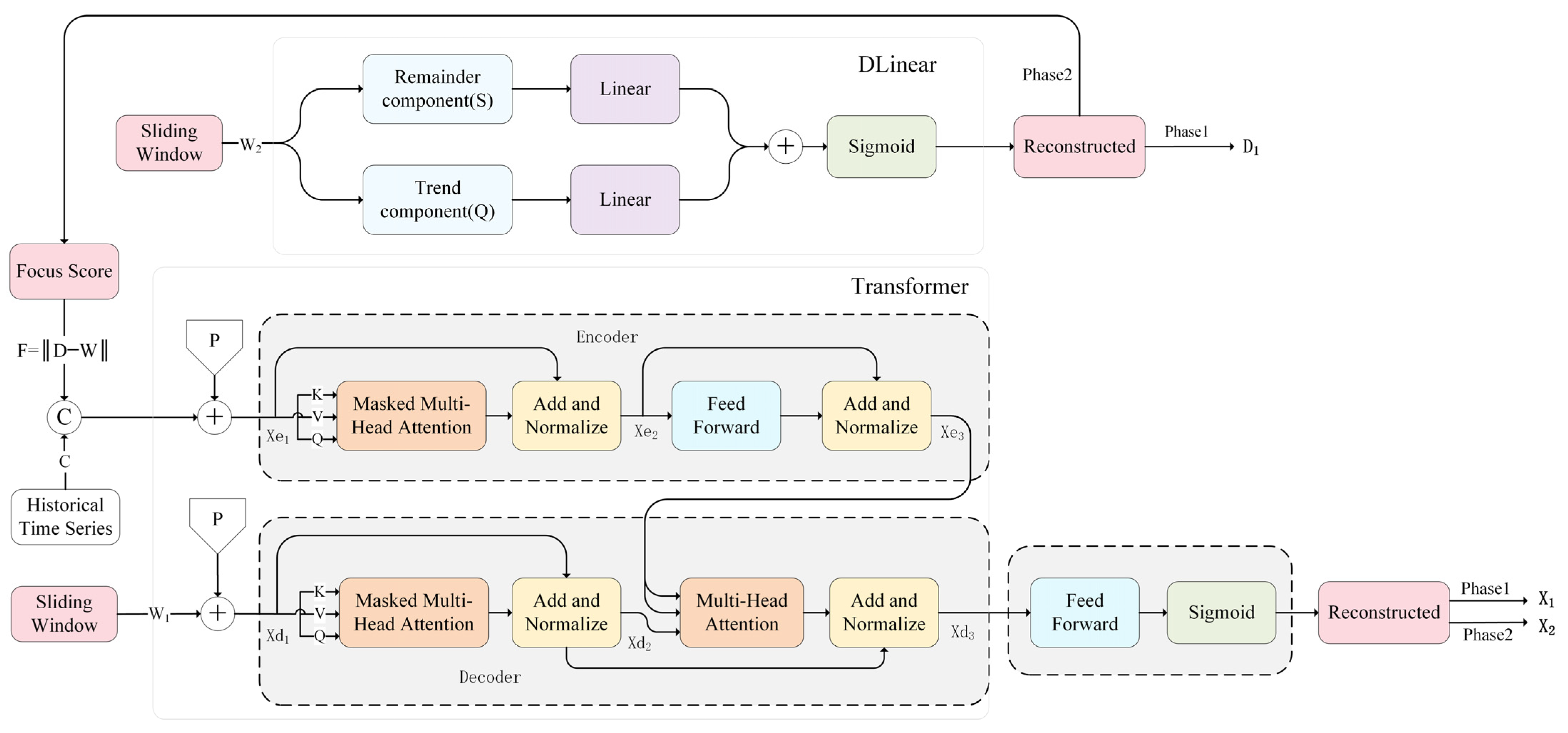
The DLinear–Transformer is a novel hybrid architecture designed to overcome the limitations of standard Transformer models in reconstructing non-smooth and non-stationary real-world time series. By integrating a DLinear-based reconstruction module with a Transformer-based module within a two-stage cooperative training framework, the model significantly enhances reconstruction accuracy and anomaly detection performance.

As illustrated in Figure 1, the proposed framework processes input data through two parallel pathways. The upper pathway is the DLinear-based reconstruction module. This component utilizes linear projections to decompose the input from a separate sliding window into seasonal and trend components, which are processed independently before being linearly aggregated. This design effectively preserves essential multi-scale temporal patterns and trend information.

Simultaneously, the lower pathway is the Transformer-based reconstruction module. It captures complex nonlinear relationships and global contextual dependencies through its encoder–decoder structure and self-attention mechanisms. The encoder processes the historical time series, while the decoder utilizes masked multi-head attention on a sliding window of the sequence, incorporating positional encodings, to reconstruct the output.

The synergy between these two components occurs within a two-stage cooperative training paradigm. The DLinear module’s output is combined and compared with the Transformer module’s reconstruction, fostering a collaborative process that iteratively refines both modules. This synergistic design allows the model to effectively combine global nonlinear representation learning with local linear temporal modeling, resulting in robust performance across diverse and dynamic operational conditions.

The proposed DLinear–Transformer architecture operates through two distinct yet interconnected processing stages. In the first stage, the Transformer encoder processes the historical time series $C$ to produce encoded representations. Concurrently, the decoder module accepts sliding window data $W_1$ incorporates positional encodings, and reconstructs temporal patterns to output the reconstructed series $X_1$. In parallel, the DLinear module processes sliding window data $W_2$, decomposing it into seasonal and residual components. These are independently reconstructed and linearly aggregated to form the final output $D_1$.

The second stage follows a similar procedure, with the critical enhancement that attention scores $F$ are integrated with the historical series $C$. This enriched input is processed identically to the first stage, yielding a refined reconstruction output $X_2$. All multivariate inputs, specifically $W_1$, $W_2$ and $C$, are represented as matrices. Among these, $W_1$ and $C$ are processed through multi-head (or masked multi-head) attention mechanisms, while $W_2$ is decomposed by DLinear into trend and residual components.

The attention and multi-head attention mechanisms are defined as follows [9]:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d}}}\right)$$

(1)

$$\begin{array}{c}{\mathrm{head}}_i=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\\ \mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_n)W^O\end{array}$$

(2)

Here, Q, K, V represent the query, key, and value matrices, respectively; $d$ denotes the dimensionality of the key vectors, and $\sqrt{d}$ serves as a scaling factor to stabilize gradients. Each head is produced via learnable projections $W_i^Q$, $W_i^K$ and $W_i^V$, and the multi-head output is obtained by concatenation and linear projection via $W^O$.

The encoder processes the input sequence through:

$$\begin{array}{c}X{e}_2=\mathrm{LayerNorm}(X{e}_1+\mathrm{MultiHeadAtt}(X{e}_1,X{e}_1,X{e}_1))\\ X{e}_3=\mathrm{LayerNorm}(X{e}_2+\mathrm{FeedForward}(X{e}_2))\end{array}$$

(3)

When $X{e}_1$ is input to the encoder, the multi-head self-attention mechanism extracts inter-feature relationships. The term $\mathrm{MultiHeadAtt}(X{e}_1,X{e}_1,X{e}_1)$ captures long-range dependencies within the historical sequence, while the residual connection $X{e}_1+\mathrm{MultiHeadAtt}(X{e}_1,X{e}_1,X{e}_1)$ preserves original sequence information. The residual connection around the attention output, followed by layer normalization ($\mathrm{LayerNorm}$) assists in stabilizing training and preserving original signal information. The subsequent feedforward network further transforms features non-linearly, enhancing representational capacity.

The decoder operates through:

$$\begin{array}{c}X{d}_2=\mathrm{LayerNorm}\left(X{d}_1+\mathrm{Mask}\left(\mathrm{MultiHeadAtt}(X{d}_1,X{d}_1,X{d}_1)\right)\right)\\ X{d}_3=\mathrm{LayerNorm}\left(X{d}_2+\mathrm{MultiHeadAtt}(X{e}_3,X{e}_3,X{d}_2)\right)\end{array}$$

(4)

Here, $X{d}_1$ represents the decoder’s input. The masked multi-head self-attention mechanism ($\mathrm{Mask}\left(\mathrm{MultiHeadAtt}\right)$) prevents the decoder from attending to future positions, ensuring autoregressive properties. The second attention mechanism performs encoder–decoder cross-attention, where the encoder output $X{e}_3$ serves as key and value, allowing the decoder to align with the encoded context.

The final reconstructed sequences are obtained through:

$${\widehat{X}}_i=\mathrm{Sigmoid}(\mathrm{Feedforward}(X{d}_4)),\hspace{1em}i=1,2$$

(5)

For the DLinear module, the reconstruction is formulated as:

$$C=T+R,\hspace{1em}\widehat{T}=\mathrm{Linear}(T),\hspace{1em}\widehat{R}=\mathrm{Linear}(R),\hspace{1em}{D}_1=\mathrm{Sigmoid}(\widehat{T}+\widehat{R})$$

(6)

The DLinear model decomposes input series $C$ into trend component $T$, representing long-term macroscopic variations, and residual component $R$, capturing short-term fluctuations. Each component undergoes separate linear transformations before being combined through linear aggregation, producing the final reconstructed output $D_1$.

This explicit decomposition establishes a crucial division of labor to handle non-stationary marine data. The DLinear module acts as a preconditioner, explicitly isolating non-stationary trends that typically overwhelm standard Transformers. This ‘clears the view’ for the Transformer to focus on modeling complex dependencies within the stabilized residuals where fault signatures reside. By creating this structured representation, the model enables more effective processing by subsequent components.

The DLinear–Transformer framework thus operates as a collaborative, dual-stage reconstruction model, where the DLinear and Transformer modules function as complementary reconstructors, each processing input through different inductive biases.

To effectively coordinate these two pathways, we introduce a dual-branch fusion mechanism. The outputs from both components are integrated via a gated aggregation layer, producing a refined, synergistic reconstruction:

$$O_1=\gamma \cdot D_1+(1-\gamma )\cdot X_1,\hspace{1em}\gamma =\sigma (\beta )$$

(7)

where $D_1$ is the reconstruction from the DLinear module, $X_1$ is the first-stage reconstruction from the Transformer module, $\sigma$ is the sigmoid function, and $\beta$ is a learnable scalar parameter initialized to zero. This design allows the model to adaptively balance the contributions from the global trend-focused and local detail-focused branches.

• The DLinear-based component aims to reconstruct input sequences with minimal error, minimizing the loss $L_D={‖D_1-W‖}_2$, where $W$ represents the true input window.
• The Transformer-based component is optimized to reconstruct sequences accurately by minimizing $L_{\mathrm{T}}={‖X_1-W‖}_2$.

The training process involves the simultaneous optimization of both components. The overall reconstruction loss function comprehensively aggregates the individual losses and the output of the fusion stage, defined as:

$$L={\displaystyle \frac{1}{n}}{‖D_1-W‖}_2+(1-{\displaystyle \frac{1}{n}}){‖X_2-W‖}_2+\lambda {‖O_1-W‖}_2$$

(8)

where n represents the number of training epochs, $X_2$ denotes the refined reconstruction from the second stage, and $\lambda$ is a weighting hyperparameter that balances the influence of the fused output $O_1$.

Anomaly scores are computed using a multi-stage reconstruction discrepancy measure:

$$s={\displaystyle \frac{1}{2}}\Vert X_1-W_{\epsilon }{\Vert }_2+{\displaystyle \frac{1}{2}}\Vert X_2-W_{\epsilon }{\Vert }_2$$

(9)

where $W_{\epsilon }$ represents the training set, and $X_1$, $X_2$ are reconstruction outputs from both stages.

The Peak Over Threshold (POT) method [26] is employed for dynamic threshold selection to classify anomalies, where time point i is flagged as anomalous when $s_i\ge \tau$, with $\tau$ determined adaptively via POT.

In summary, the DLinear–Transformer leverages the Transformer’s strength in capturing complex nonlinear dependencies and long-range contexts, while the DLinear module excels at extracting multi-scale temporal features through adaptive decomposition and linear projection. This hybrid design effectively addresses the limitations of each individual model and provides a novel framework for multivariate time series analysis.

3. Anomaly Detection Experimental Design

To comprehensively validate the effectiveness and generalizability of the proposed DLinear–Transformer framework, we designed a multi-stage experimental evaluation protocol. This chapter details the datasets, evaluation metrics, and experimental methodology employed to assess the model’s performance across three critical aspects: (1) reconstruction accuracy for non-stationary time series, (2) anomaly detection capability in marine steam turbine systems, and (3) generalization performance on public benchmarks. All core experiments were conducted under consistent training–testing splits and preprocessing procedures to ensure fair and reproducible comparisons.

3.1. Dataset and Preprocessing

To rigorously evaluate the generalization capability of the proposed DLinear–Transformer, we employ one domain-specific dataset and two public benchmarks. The key characteristics of all datasets are summarized in

Table 1. Summary of datasets used in this study.

Dataset	Domain	Features	Key Characteristics
Marine Steam Turbine	Marine Engineering	62	Real operational data from marine turbine systems under varying loads (0–80 kW); contains annotated anomalies.
SMD	Server Machine	38	Multivariate data from 28 servers over 5 weeks; includes hardware/performance metrics.
SWaT	Water Treatment	51	11-day dataset with 7 days normal operation and 4 days under cyber-attack scenarios.

.

• Marine Steam Turbine Dataset: This self-compiled dataset was acquired from a custom-designed test rig. The rig comprises industrial components from actual marine systems, including a boiler, steam turbine, condenser, and associated pumps and valves, and was engineered to emulate the operational behavior of a marine steam turbine system. High-precision sensors were employed to collect high-resolution, time-synchronized data for 62 operational parameters under diverse loads (0–80 kW). This setup provides an effective simulation of actual system operation, thereby offering a realistic and high-fidelity testbed. The principal value of this dataset lies in its inclusion of annotated real-world fault data, which provides a crucial experimental basis for evaluating fault detection methods in maritime environments.
• Public Benchmarks (SMD & SWaT): The SMD dataset provides multivariate time-series from large server clusters, ideal for validating performance on high-dimensional IT infrastructure data. The SWaT dataset, originating from a realistic water treatment testbed, contains both normal and attack sequences, making it a standard benchmark for detecting cyber-physical anomalies.

A uniform preprocessing pipeline was applied to all datasets to ensure comparability. The procedure included: (1) data cleaning using linear interpolation to handle missing values; (2) min-max normalization to scale all features to the range [0, 1]; and (3) temporal segmentation via a sliding window approach with a window length of L = 60 timesteps and 85% overlap to preserve temporal dependencies and phase continuity, which is essential for capturing dynamics in rotating machinery systems.

The model is evaluated using a hold-out strategy. To ensure a rigorous assessment of fault discrimination capability beyond the majority “normal” class, the training and test sets were carefully curated to provide a balanced representation of all fault types, avoiding the high imbalance inherent in simple temporal splits. This approach prevents performance metrics from being inflated and offers a truer measure of diagnostic utility in practice.

The integrity of the held-out test set is paramount for an unbiased assessment. For the main experiments across all datasets, a 70%/30% train-test split was employed to ensure fair and consistent comparisons. All hyperparameter optimization was performed via k-fold cross-validation within the training set to prevent information leakage. To ensure statistical reliability, all experiments were repeated over five independent runs with different random seeds. Performance metrics are reported as mean values with standard deviation, and statistical significance was assessed using two-sample t-tests. These measures account for training stochasticity and ensure robust, reproducible findings while establishing generalization performance. Unless otherwise specified, this partitioning strategy applies to all main experiments.

3.2. Evaluation Metrics

To comprehensively evaluate the performance of anomaly detection models under the severe class imbalance inherent in marine steam turbine operational data (where the normal-to-anomaly ratio exceeds 100:1), we employed two robust and widely recognized metrics: the Area Under the Receiver Operating Characteristic Curve (AUC-ROC) and the F1-score. This focused selection provides a balanced and rigorous assessment crucial for real-world applications.

• AUC-ROC:

This metric evaluates the model’s overall discriminative capacity across all possible classification thresholds. It plots the True Positive Rate against the False Positive Rate at various threshold settings. Its primary advantage is its robustness to class imbalance, making it particularly valuable for our industrial setting where anomalies are rare. A higher AUC-ROC indicates a model’s superior ability to distinguish between normal and anomalous states regardless of the chosen operating point.

• F1-score:

The F1-score is the harmonic mean of precision and recall, providing a single metric that balances these two critical concerns. It is formally defined as:

$$\mathrm{F}1\text{-}\mathrm{score}=2\times {\displaystyle \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precison}+\mathrm{Recall}}}$$

(10)

where Precision measures the model’s ability to avoid false alarms, and Recall measures its sensitivity to capture true anomalies. The F1-score is especially relevant in our context because it penalizes models that excel in one aspect (e.g., high precision) at the severe expense of the other (e.g., low recall), thus ensuring a balanced performance essential for safety-aware maritime systems.

Together, the threshold-agnostic AUC-ROC and the threshold-dependent F1-score provide a multi-faceted and reliable evaluation of model performance, effectively balancing the trade-off between missed detections and false alarms.

3.3. Experimental Design

The experimental design is structured to systematically evaluate the DLinear–Transformer framework through a comprehensive three-stage validation strategy, ensuring rigorous assessment of both its reconstruction capability and anomaly detection performance across diverse operational scenarios.

The validation strategy encompasses three critical aspects:

• Reconstruction Performance: We first assess the DLinear–Transformer model’s ability to accurately reconstruct non-stationary time series data, with particular emphasis on its handling of complex temporal patterns and transient dynamics. Comparative analysis is conducted against state-of-the-art benchmarks to establish performance baselines.
• Anomaly Detection Efficacy: The model’s performance in identifying diverse anomalous conditions within marine steam turbine operational data is evaluated through anomaly scenarios. This evaluation considers both point anomalies and contextual anomalies that manifest as subtle deviations from normal operational patterns.
• Generalization Assessment: To demonstrate cross-domain applicability, we validate the model’s adaptability and robustness on two publicly available datasets: SMD and SWaT dataset This assessment examines the model’s transfer learning capability and its performance in different industrial contexts.

The model is evaluated using the hold-out strategy detailed in Section 3.1, wherein the integrity of the held-out test set is paramount for an unbiased assessment. All hyperparameter optimization was performed via k-fold cross-validation within the training set to prevent information leakage. To ensure statistical reliability, all experiments were repeated over five independent runs with different random seeds. Performance metrics are reported as mean values with standard deviation, and statistical significance was assessed using two-sample t-tests. These measures account for training stochasticity and ensure robust, reproducible findings while establishing generalization performance.

All experiments were conducted on a standardized computing platform equipped with an NVIDIA RTX 3080 GPU and 32GB RAM, using the PyTorch (v1.12.1) and scikit-learn (v1.2.0) frameworks. This configuration ensured consistent performance measurements and reproducibility, while providing a reasonable reference for potential naval embedded system implementations.

4. Results

Building on the experimental protocol established in Section 3.3, this section systematically presents the evaluation results for the DLinear–Transformer framework. The analysis provides a robust assessment of the model’s capabilities, benchmarked against contemporary methods, by synthesizing qualitative illustrations with quantitative metrics.

4.1. Reconstruction Performance

The initial phase of our evaluation focuses on the fundamental requirement of any reconstruction-based anomaly detection model: the ability to accurately reconstruct normal operational data. This subsection assesses the performance of the DLinear–Transformer framework in replicating complex, non-stationary time series, using steam turbine inlet flow rate data as a benchmark. The evaluation is presented from two perspectives: a qualitative visual comparison and a quantitative metric-based analysis. For a comprehensive benchmark, we selected two state-of-the-art models representing distinct advanced paradigms: TranAD, recognized for its superior performance in capturing long-range dependencies in multivariate time series using deep transformer networks, and Graph Deviation Network (GDN) [29], which excels in modeling inter-sensor relationships as a graph for anomaly detection in complex systems. This selection provides a rigorous test against leading data-driven approaches.

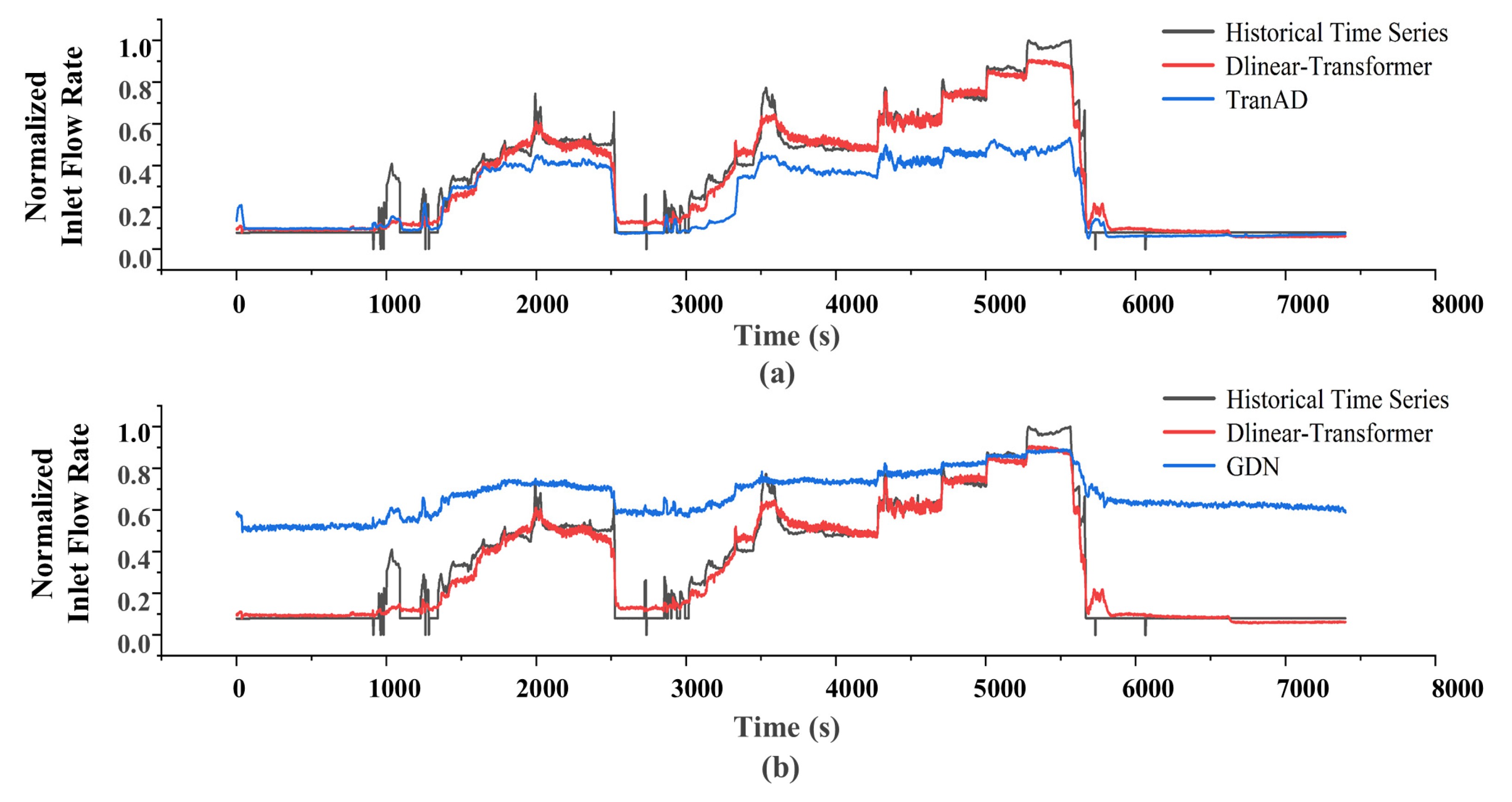
The reconstruction fidelity is first evaluated via qualitative visual analysis. As shown in Figure 2, the sequences reconstructed by DLinear–Transformer, TranAD, and GDN for the steam turbine inlet flow rate are directly juxtaposed. Evidently, the proposed framework’s output aligns more precisely with the true data trajectory, especially during transient phases. Conversely, the benchmarks display pronounced deviations and overshooting, underscoring their limitations in modeling the complex, non-stationary dynamics.

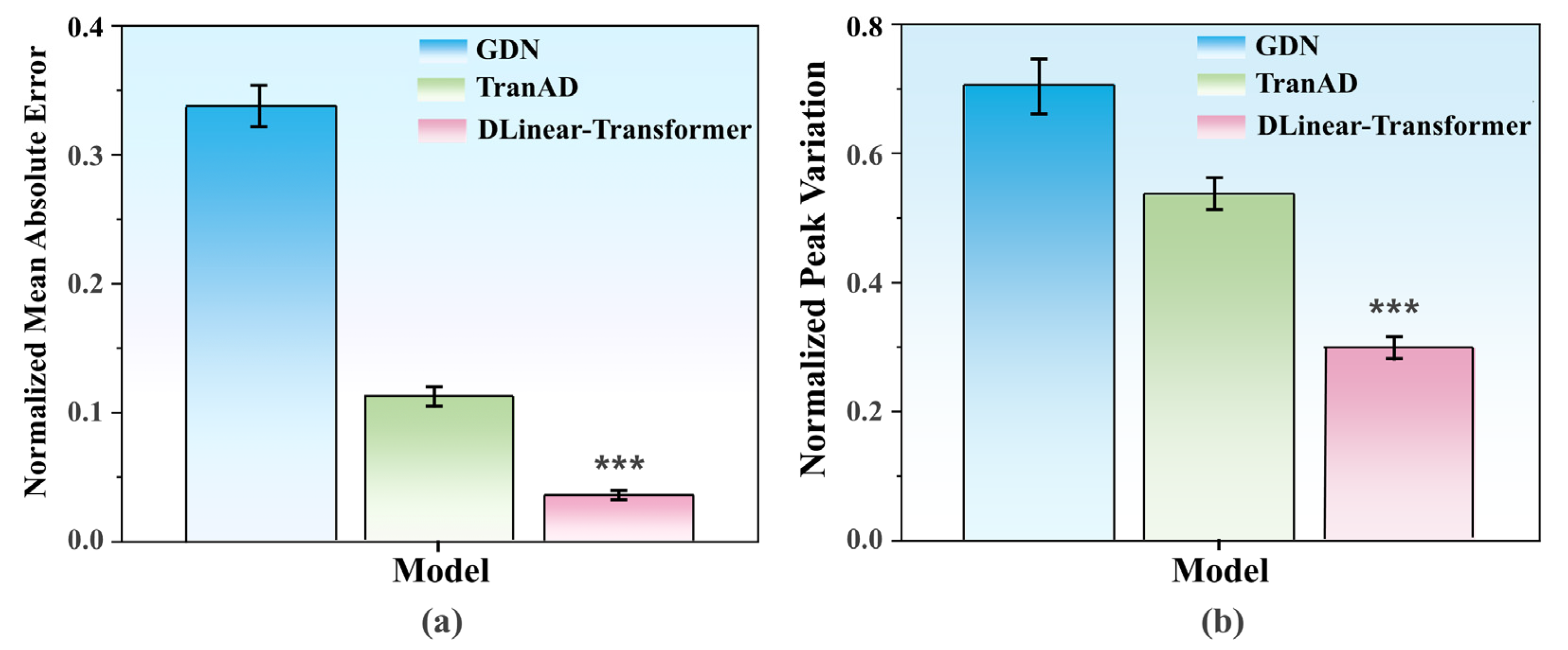
To ensure statistical reliability through five independent runs, the quantitative benchmarking substantiates the qualitative advantage of the DLinear–Transformer. As illustrated in Figure 3 and detailed in

Table 2. Comparative reconstruction performance on the Marine Steam Turbine dataset.

Model	MAE	NRMSE	PV
GDN	0.339 ± 0.015	0.398 ± 0.020	0.708 ± 0.035
TranAD	0.113 ± 0.005	0.132 ± 0.008	0.535 ± 0.025
DLinear–Transformer	0.037 ± 0.002 ***	0.042 ± 0.003 ***	0.298 ± 0.012 ***

Values are presented as mean ± standard deviation over 5 independent runs. *** indicates statistically significant improvement over all baselines (p < 0.001, two-sample t-test).

, the DLinear–Transformer achieves statistically significant superiority across all evaluation dimensions. It attains a Mean Absolute Error (MAE) of 0.037 and a Normalized Root Mean Square Error (NRMSE) of 0.042, corresponding to reductions of 67.3% and 68.2% against TranAD (p < 0.001). This statistically significant superiority extends to handling transients, with a Peak Variation (PV) of 0.298, which is 44.3% lower than that of TranAD.

This marked superiority in reconstruction is not merely quantitative but critical for downstream tasks. The low MAE and NRMSE indicate that the model establishes a high-fidelity baseline of normal system behavior. This precision ensures that subsequent spikes in reconstruction error can be attributed to genuine anomalies with higher confidence, rather than being masked by inherent model inaccuracies. Consequently, the demonstrated fidelity provides a robust foundation for the anomaly detection performance discussed in the subsequent section.

4.2. Anomaly Detection Efficacy

An empirical evaluation of the anomaly detection performance was conducted by applying the DLinear–Transformer framework to a selected 3500-s operational segment derived from a marine steam turbine system. This segment is of particular diagnostic value as it contains a well-documented critical fault event: an emergency shutdown triggered by a condenser water level regulation failure, which occurred between 2652 and 2676 s. The analysis concentrates on the detection results for six key thermodynamic and control parameters, with the outcomes visually summarized in Figure 4.

The analysis of the results clearly demonstrates the substantial anomaly detection capabilities of the DLinear–Transformer framework. The model excels not only in identifying conspicuous extreme deviations but also in capturing more subtle and complex abnormal patterns, as evidenced by its consistent performance across the multiple operational parameters examined.

First, regarding transient anomaly detection, the model proves highly effective in identifying short-duration deviations. For instance, the transient anomalies detected in the turbine inlet flow rate (Figure 4a, at 553–556 s and 579–582 s) and those in the main steam valve opening (Figure 4e, 490–507 s) exhibit clear temporal correlations with dynamic changes in the governor valve opening (Figure 4c). This capability to not only isolate anomalous events but also link them to specific control actions provides actionable insights for refining control strategies and mitigating the impact of transient operational events.

Moving beyond transient events, the framework demonstrates a critical capacity to detect nuanced fluctuation anomalies, which signify sustained operational deviations. This is exemplified by the model’s identification of persistent abnormal variations in the inlet chamber steam pressure over an extended period from 1281 to 2008 s (Figure 4b). The accurate detection of such prolonged subtle shifts indicates the model’s sensitivity to incipient faults, defined as those that develop gradually over time. This capability shifts the application’s focus from reacting to abrupt failures towards diagnosing evolving system degradation, forming the basis for condition-based monitoring.

The most significant advancement, however, lies in the framework’s proficiency for early warning. It demonstrates exceptional skill in identifying precursor anomalies that precede major system failures. During the pre-fault phase (2620–2628 s), statistically significant anomalies were detected concurrently across several interdependent parameters, including inlet steam pressure (Figure 4b), governor valve opening (Figure 4c), condenser water level (Figure 4d), and condenser vacuum (Figure 4f). The synchronous detection of these coordinated precursor signals, with a substantial lead time prior to failure, underscores the framework’s practical value beyond mere anomaly detection. Based on established maintenance practices and expert domain knowledge, such consistent early warnings are sufficient to trigger proactive interventions, such as inspection or planned component replacement, effectively enabling a shift from reactive fault handling to predictive maintenance.

The framework’s practical efficacy is further solidified by its computational efficiency, a critical factor for marine engineering applications. On a standardized testing platform, it achieved an average inference time of 15.3 ms per sample. Evaluated on a test set that was carefully constructed to ensure a balanced representation of fault types and mitigate operational data’s inherent class imbalance, the method demonstrates a favorable balance between detection capability and processing speed, achieving 94.6% overall fault detection accuracy under dynamic maritime load conditions alongside its computational performance.

In summary, the experimental results confirm the substantial practical utility of the DLinear–Transformer framework. By comprehensively identifying a spectrum of anomalies, ranging from transient events to sustained fluctuations and critical precursor signals, and doing so with high accuracy and efficiency, it effectively advances anomaly detection from post-factum identification to a proactive analytical tool. This tool is fully capable of supporting predictive maintenance decisions and operational optimization in real-world marine steam turbine systems.

4.3. Generalization Assessment

Following the experimental protocol outlined in Section 3.3, the generalization capability of the DLinear–Transformer framework was assessed on two public datasets: SMD and SWaT. This phase of validation examines the model’s adaptability and robustness across different industrial contexts. The performance, quantified by AUC-ROC and F1-score, is compared against state-of-the-art methods in

Table 3. Comparative performance evaluation on the SMD and SWaT datasets under a unified evaluation protocol.

Method	SMD		SWaT
	F1-Score	AUC-ROC	F1-Score	AUC-ROC
GDN	0.9238 ± 0.012	0.9924 ± 0.004	0.8101 ± 0.015	0.8462 ± 0.008
TranAD	0.9605 ± 0.007	0.9974 ± 0.001	0.8151 ± 0.009	0.8491 ± 0.007
DLinear–Transformer	0.9871 ± 0.004 **	0.9988 ± 0.001	0.8179 ± 0.008	0.8514 ± 0.007

Results are presented as mean ± standard deviation over 5 independent runs. All baselines were re-implemented and evaluated under our unified data preprocessing and splitting pipeline to ensure a fair comparison. ** denote statistically significant improvement over the second-best model with p < 0.01 (two-sample t-test).

, under a unified evaluation protocol.

The results clearly demonstrate the robust generalization capability of the DLinear–Transformer framework. On the SMD dataset, which captures monitoring metrics from large-scale server machines, the model achieves an AUC-ROC of 0.9988 and an F1-score of 0.9871, demonstrating a statistically significant improvement over all baselines. Notably, the F1-score exceeds that of TranAD, a strong contemporary model, by 2.7% (0.9871 vs. 0.9605), while AUC-ROC shows a 0.1% gain. This superior performance underscores the model’s exceptional accuracy in server anomaly detection.

Similarly, on the SWaT dataset, a challenging benchmark derived from an industrial water treatment system with cyber-physical attack scenarios, the proposed method also attains the highest AUC-ROC (0.8514) and F1-score (0.8179) among all compared approaches, corresponding to consistent gains of 0.2% and 0.3% over TranAD, respectively. The key insight is the model’s consistent top-tier performance across these diverse domains. Such a balanced and superior outcome suggests that the hybrid architecture effectively captures discriminative temporal patterns that generalize across domains.

The consistent superiority of DLinear–Transformer on both datasets underscores its capability to handle diverse anomaly types and operational regimes. The SMD dataset involves high-dimensional, stochastic server metrics, while SWaT embodies strong temporal constraints and physical attack signatures. That the same model excels in both contexts indicates that its design, which combines the multi-scale feature extraction of DLinear with the global dependency modeling of the Transformer, provides a generally applicable solution for multivariate time-series anomaly detection.

In summary, the compelling results on SMD and SWaT confirm the strong cross-domain generalization capacity of the DLinear–Transformer framework. These outcomes validate that the proposed hybrid architecture is not only effective in marine steam turbine applications but also possesses the versatility to address anomaly detection tasks across a wide spectrum of industrial systems, highlighting its potential as a scalable and robust solution for real-world monitoring applications.

5. Analyses and Discussion

The results confirm the performance and generalization capability of the DLinear–Transformer framework. To better understand its internal mechanisms, this section employs two analytical approaches. As a data-driven model, the framework prioritizes generalizability and pattern recognition, although it differs from physics-based models, which offer explicit mechanistic insights through embedded domain knowledge but require complete prior physical understanding. The following analyses conducted here aim to explore this data-driven paradigm: an ablation study quantifies the contributions of core components, while a sensitivity analysis evaluates robustness under varying data conditions. Finally, limitations and future potential are critically discussed to position the framework within the broader research context and suggest directions for further development.

5.1. Ablation Analysis

To quantitatively evaluate the individual contributions of the core components within the proposed DLinear–Transformer framework, a systematic ablation study was conducted. The investigation focused on two pivotal design elements: (1) the two-stage learning process, which iteratively refines reconstructions using divergence-based attention, and (2) the DLinear module, dedicated to multi-scale temporal feature extraction. The complete DLinear–Transformer model was rigorously compared against two ablated variants on the SMD and SWaT datasets, with performance quantified by the F1-score, as summarized in

Table 4. Results of the ablation study.

Method	F1-Score
	SMD	SWaT
The model without the two-stage process	0.9821	0.8151
The model without DLinear	0.9069	0.8139
The complete DLinear–Transformer model	0.9871	0.8179

.

The ablation results provide clear evidence of the distinct and complementary contributions of each component. The complete DLinear–Transformer architecture consistently achieves the highest F1-score on both datasets, affirming the synergistic effect of its integrated design.

To statistically validate these performance differences, we conducted a paired t-test based on five independent training runs. The performance improvement of the complete model over the variant without the two-stage process was statistically significant on the SMD dataset (p < 0.05). More notably, the advantage over the model without the DLinear module was highly significant on both SMD and SWaT (p < 0.01). This confirms that the observed synergies are robust and not attributable to random variation.

The exclusion of the two-stage processing framework led to a discernible performance degradation on both benchmarks. The F1-score decreased from 0.9871 to 0.9821 on SMD (ΔF1-score = −0.50%) and from 0.8179 to 0.8151 on SWaT (ΔF1-score = −0.34%). Although the absolute reduction appears modest, it is consistent and indicates that the two-stage mechanism contributes to enhanced modeling precision. This refinement process, which focuses attention on reconstruction discrepancies, is crucial for achieving state-of-the-art performance against strong baselines.

In contrast, removing the DLinear module resulted in a more substantial and dataset-dependent impact. A significant performance drop was observed on the SMD dataset, with the F1-score declining by 8.1% (from 0.9871 to 0.9069). This pronounced effect underscores the indispensable role of the DLinear component in processing the strong local trends and seasonal variations characteristic of server machine metrics. Conversely, the impact on the SWaT dataset was minimal (ΔF1-score = −0.49%), suggesting that for this cyber-physical system data, the Transformer backbone possesses a considerable capacity to model temporal dependencies even without explicit linear decomposition. Nevertheless, the full model’s superior performance on SWaT confirms that the integrated approach provides a more robust and stable solution.

Overall, the ablation study validates the necessity of both the DLinear module and the two-stage learning framework. A key finding from our scenario-specific analysis is the distinct operational preference of each component: the DLinear module proves particularly indispensable in environments with pronounced trend components, such as the SMD dataset where its removal caused a significant 8.1% performance drop, whereas the two-stage mechanism delivers consistent refinements across all scenarios but becomes critically important for achieving precise fault localization in complex, multi-sensor anomaly patterns. The DLinear component is vital for effective local feature decomposition, particularly in environments with pronounced trend components, while the two-stage mechanism delivers consistent refinements for superior accuracy. Their combination forms a complementary and versatile architecture well-suited for a broad spectrum of industrial monitoring scenarios.

5.2. Sensitivity Analysis

To comprehensively evaluate the data efficiency of the DLinear–Transformer framework, we conducted a sensitivity analysis on the proportion of training data. This analysis serves as a supplementary investigation to the fair-comparison experiments reported in Section 3 and Section 4.

We utilized four public benchmarks: the SMD and SWaT datasets from our primary evaluation, along with two additional public benchmarks, namely the Soil Moisture Active Passive (SMAP) dataset and the Mars Science Laboratory (MSL) rover dataset [30]. For this specific analysis, all four datasets were re-partitioned using a consistent temporal block-wise stratified sampling strategy. The training ratio was varied from 20% to 100% (specifically, 20%, 40%, 60%, 80%, and 100%) against a fixed test set to evaluate performance scalability with increasing data volume.

The results, summarized in Figure 5, demonstrate a clear and statistically significant positive correlation between model performance and training data volume across all four datasets, as measured by both the F1-score and the AUC-ROC.

A detailed analysis of Figure 5 reveals distinct learning phases. The framework demonstrates exceptional initial data efficiency, achieving the majority of its final performance (e.g., over 90% of the maximum F1-score for SMD and SWaT) with only 20% of the training data. Beyond this point, the learning trajectories diverge based on dataset complexity. While the SMAP dataset shows signs of performance saturation in its later stages, others like SMD and MSL continue to exhibit meaningful gains up to the full dataset, indicating that the point of diminishing returns is not universal but is instead context-dependent.

This nuanced understanding directly informs practical deployment strategies. The framework’s robustness supports two complementary approaches: (1) For rapid deployment or in cost-sensitive scenarios, a minimal viable dataset (as low as 20–40%) can bootstrap a highly competent model. (2) For maximizing performance on complex systems or for long-term asset monitoring, a strategy of continuous data collection is justified, as the model reliably converts additional data into enhanced accuracy without signs of overfitting, as evidenced by the sustained growth of curves like SMD and MSL.

Critically, the absence of performance degradation at larger data volumes across all datasets confirms the model’s stability and its capacity to beneficially utilize additional information. This provides a reliable foundation for implementing long-term predictive maintenance strategies in marine steam turbine systems.

5.3. Limitations and Future Outlook

While the proposed framework demonstrates strong performance, this study is not without its limitations, which in turn illuminate productive paths for future research.

A primary consideration lies in the practical deployment of the framework. Its computational requirements, though manageable in our experimental setup, could present challenges for implementation on extremely resource-constrained edge devices. Furthermore, the model’s current performance is contingent upon the availability of sufficient labeled fault data for training, which is often scarce in real-world naval applications. Another limitation concerns the evaluation under diverse operational conditions. Although the dataset incorporates inherent variability, a formal stratified analysis of performance across specific environmental states, such as distinct sea states or load regimes, was not conducted. This aligns with the broader challenge of Environmental and Operational Variability (EOV) in structural health monitoring, as discussed by Rezazadeh et al. [31].

To address these limitations and build upon the validated capabilities of the framework, several directions for future work are envisioned. The immediate next step involves prioritizing the transition from offline validation to online deployment. Initial implementation on a digital twin testbed has confirmed basic operational feasibility, laying the groundwork for systematic evaluation under true streaming conditions, with a focus on long-term stability, inference latency, and computational throughput.

Concurrently, technical enhancements will focus on several key areas:

• Few-Shot Anomaly Detection by developing semi-supervised or self-supervised learning strategies to mitigate the dependency on extensive labeled anomaly datasets.
• Fault Classification through the integration of a multi-class module to differentiate specific fault types (e.g., bearing wear, fouling, actuator failure), thereby advancing the system from general detection to precise diagnosis.
• Causal Analysis Extension to move beyond detection towards identifying root causes of anomalies, thereby providing more actionable insights for maintenance crews.

Finally, the framework’s data-driven nature and its proven ability to model transient dynamics and multi-sensor interactions without relying on domain-specific assumptions strongly suggest its inherent suitability for fault diagnosis in other critical rotating systems. This foundational versatility, validated by its consistent performance across several public benchmarks, indicates strong promise for immediate future implementations in systems such as gearboxes, wind turbines, and diesel engines. Consequently, a comprehensive empirical validation for these distinct assets represents a primary objective and a logical extension of this work.

6. Conclusions

This study establishes a reliable, data-driven framework for fault diagnosis in marine steam turbines through a hybrid DLinear–Transformer model. By synergistically integrating the multi-scale feature extraction of DLinear with the global dependency modeling of the Transformer, the proposed approach effectively addresses the challenge of analyzing non-stationary operational data under dynamic maritime conditions. Experimental results demonstrate the framework’s superior performance: it achieved a detection accuracy of 94.6% on real shipboard turbine data, alongside statistically significant F1-score improvements of 2.7% on the SMD dataset and 0.3% on the SWaT dataset over the advanced TranAD baseline.

Beyond performance benchmarking, comprehensive ablation studies quantitatively validated the contribution of each architectural component, while sensitivity analysis confirmed the model’s robustness. The framework’s proficiency in identifying a spectrum of anomalies, ranging from transient events to sustained deviations, underscores its practical utility for real-world condition monitoring. Looking ahead, this system-level detection framework provides a solid foundation for evolution towards automated fault diagnosis and causal analysis. These contributions collectively advance the field of intelligent marine system monitoring and ultimately represent a concrete step toward more autonomous and resilient marine propulsion systems.