Effects of Angle of Attack on Flow-Induced Vibration of a D-Section Prism

Abstract

The VIVACE device, which utilizes flow-induced vibration for harvesting ocean current energy, has been a research hotspot in the field of renewable energy. In this study, the flow-induced vibration characteristics and energy conversion efficiency of a D-section prism were investigated using the k-ω SST turbulence model and Newmark-β method. The vibration amplitude, frequency, equilibrium position offset, and energy conversion efficiency of the two-degree-of-freedom cylinder were systematically analyzed at seven angles of attack between 0 and 180 degrees. The Reynolds number ranged from 368 to 14,742, corresponding to equivalent speeds of 2 to 20. The results indicate that the angle of attack has a significant influence on the flow-induced vibration response of the D-section prism. As the angle of attack changes, the vibration amplitude of the cylinder continuously increases, and the cylinder sequentially enters the vortex-induced vibration, vortex-induced vibration-galloping, and fully galloping branches. The change in the angle of attack disrupts the symmetry of the cylinder’s vibration in the streamwise direction, leading to a shift in the equilibrium position of the cylinder’s vibration. When the angle of attack is 0°, the energy conversion efficiency of the column reaches a maximum of 11.75%. Additionally, at high Reynolds numbers, the vibration of the cylinder is not self-limiting, making it more advantageous for energy conversion devices compared to cylinders with circular cross-sections.

1. Introduction

When a fluid flows past a bluff body at a certain speed, vortices alternately shed from both sides of the body. The periodically varying forces generated by the vortex shedding induce vibrations in the bluff body. Flow-induced vibrations represent a typical fluid–structure interaction problem [1], where interactions between the fluid and the structure may lead to various complex phenomena, such as vortex-induced vibrations (VIVs) and galloping. Extensive systematic explanations of the vibration responses and underlying mechanisms of VIV have been provided by many scholars [2,3,4,5,6,7]. Galloping is an unbounded vibration with no self-limiting characteristics, manifesting as a low-frequency, high-amplitude vibrational phenomenon fundamentally driven by aerodynamic negative damping that causes fluid–structure coupling instability [8,9]. The flow-induced vibration of bluff bodies is highly sensitive to the cross-sectional shape; circular sections experience VIV, while rectangular, triangular, and D-section prisms are prone to galloping [10]. Due to geometric characteristics, blunt bodies with pointed sections have fixed separation points for vortex shedding, whereas the separation points for cylinders vary over time. For the D-section prism (Figure 1a) consisting of a flat plane, the free separation points of the upper and lower shear boundary layers are inconsistent. Moreover, the separation points switch when the angle of attack changes, altering the vortex shedding pattern and causing the prism to experience both VIV and galloping in uniform inflow. Detailed studies on the flow-induced vibrations of anisotropic sections like triangular [11,12], rectangular [13,14], and polygonal [15] prisms have been conducted. However, studies on D-section prisms are relatively scarce. Research on the flow-induced vibrations of the D-section prism has been partially conducted through wind tunnel tests [16]; however, due to significant differences in density and viscosity between air and water, there are considerable discrepancies between the flow-induced vibrations in water and those observed in wind tunnel experiments. Zhao et al. [17] investigated the flow-induced vibration responses of the D-section prism through water channel experiments, distinguishing between straight-edge and curved-edge inflow conditions. It was noted that although the wake influences the mode of vortex shedding and the vibration response of the prism, flow-induced vibrations can occur even without a wake. Song et al. [18] conducted numerical simulations of flow-induced vibrations on a D-section prism at different angles of attack and mass ratios, finding that the mass ratio alters the response branch and equilibrium position of the prism’s flow-induced vibrations, with prisms having a higher mass ratio and more likely to enter a full galloping branch. Prisms with a lower mass ratio tend to deviate more easily from their original equilibrium position during vibration.

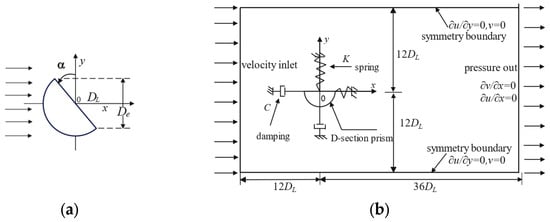
Figure 1. D-section prism: (a) schematic of D-section prism; (b) computational domain and boundary conditions.

Despite both experimental and numerical studies focusing on the flow-induced vibrations of prisms at zero-degree incidence angles, real-world engineering scenarios often encounter water currents at various angles due to differing water depths [19]. Chen et al. [20] conducted numerical simulations on an equilateral triangular prism at various flow angles, finding significant effects of inflow angles on flow-induced vibrations. Between $0^{°}$ to ${15}^{°}$, the prism remained on the VIV branch, with the vibration frequency linearly increasing with reduced velocity and no lock-in region, distinct from VIV. From ${45}^{°}$ to ${60}^{°}$, the prism entered the galloping regime. Zhang et al. [21] performed numerical simulations of flow-induced vibrations on cylinders with additional control rods at varying flow attack angles. At an inflow angle of ${30}^{°}$, the control rods significantly suppressed the cylinder’s vibration response. Between ${45}^{°}$ and ${75}^{°}$, the rods promoted vibrations, exhibiting interactions between vortex shedding and galloping. Jiang et al. [22] undertook numerical simulations of VIV on cylinders at fixed Reynolds numbers of 5000 for different incidence angles, noting that the width of the lock-in range did not vary with changes in incidence angles. At $0^{°}$ and ${75}^{°}$, a clear lock-in phenomenon was present, which disappeared as the angle increased. Additionally, the amplitude of transverse vibrations decreased with increasing incidence angle. Chen et al. [23] carried out numerical simulations of transverse flow-induced vibrations on a single-degree-of-freedom D-section prism at a Reynolds number of 100, analyzing the characteristics of different flow angles, vortex-induced vibrations, and galloping.

Previous studies have primarily focused on understanding and suppressing the flow-induced vibrations of structures to mitigate their associated risks [24,25,26]. In recent years, with the advancement of green energy, harnessing flow-induced vibrations for capturing marine current energy has also garnered scholarly interest [27,28,29,30]. In this regard, Lian et al. [31] reviewed the current state of research on flow-induced vibrations and their energy conversion capabilities in marine currents, proposing the utilization of these vibrations for novel energy development. A representative achievement in this field is the development of a low-speed marine current power generation device (VIVACE) by Bernitsas and his team. This device converts the mechanical energy of prism vibrations into electrical energy, offering potential advantages such as low initiation flow speed, simplicity in maintenance, environmental friendliness, and minimal disruption to marine traffic [32,33].

Most previous research of flow-induced vibration and energy harvesting in prisms has focused on circular cylinders of flow-induced vibration. However, due to the self-limiting characteristics of the cylinder during flow-induced vibration, the amplitude does not continuously increase. The characteristic of being prone to galloping in non-circular cross-section prisms has attracted scholars’ attention. Bai et al. [34] found that the energy harvesting efficiency of the cylinder is not directly related to the amplitude of the vibration; larger amplitudes do not necessarily result in higher energy harvesting efficiency. Li et al. [35] conducted numerical simulations of flow-induced vibration on tandem cylinders with different angles of attack and found that at smaller angles of attack, the energy conversion efficiency of the prism is higher. The optimal range is $5000\le Re\le 7000$, at an angle of $0^{\circ }\le \alpha \le {30}^{\circ }$. Sun et al. [36] used the Van der Pol model to numerically simulate flow-induced vibrations of cylinder, equilateral triangular, and D-section prisms, revealing that the power obtained during galloping is greater than that during vortex-induced vibration, and hydrodynamic coefficients have a significant impact on energy capture. Wei et al. [37], combining Gaussian process regression, conducted numerical simulations on a tandem D-section prism with angles of attack $0^{°}$ and ${180}^{°}$, revealing that the amplitude of the prism and energy utilization efficiency are not necessarily correlated, and angles and damping ratios significantly affect energy utilization efficiency. Li et al. [38] designed various combinations of cylinder and D-section prisms in series to study the effect of cross-sectional changes on vortex-induced vibration energy harvesting. The results show that when the D-section prism is sandwiched between two cylinders (ODO), the vibration of the column is suppressed, whereas the DOD arrangement of the columns can enhance vortex-induced vibration and increase the lock-in range, thereby improving the energy conversion efficiency.

In conclusion, the impact of the angle of attack on flow-induced vibrations of the D-section prism requires further investigation. Accordingly, this study conducted numerical simulations and analyses of the flow-induced vibrations of the D-section prism with two degrees of freedom, focusing on the effects of variation in the angle of attack subjected to the uniform coming flow. The first part of the paper describes the numerical model and computational methods used, while the second part analyzes the characteristics, such as amplitude of vibration, frequency response, equilibrium position offset, and energy conversion efficiency at different angles of attack. The main conclusions are presented at the end, providing reference data for engineering applications related to the exploitation of marine current energy.

2. Numerical Models and Computational Methods

2.1. Numerical Model

In the flow field, a D-section prism is placed as depicted in Figure 1a, capable of rotating around the z-axis. The angle by which the flat side of the cylinder rotates about the z-axis (transverse direction) is defined as the angle of attack $\alpha$. Considering symmetry, the variation range of the angle of attack is set from $0^{\circ }\le \alpha \le {180}^{\circ }$, with an angular increment of ${30}^{°}$. The mass ratio of the prism is $m^{\ast }=2.6$, and the mass damping ratio $\left(m^{\ast }+C_a\right)\xi =0.013$, where the added mass coefficient $C_a$ is set to 1.0. The natural frequency of the prism in still water is $f_n=0.4$ Hz, with a characteristic length $D_e=0.5\left(1+\left|\cos \alpha \right|\right)D_L$.

The computational domain setup is illustrated in Figure 1b, with the coordinate origin located at the midpoint of the straight edge of the section, the positive x-axis aligned with the flow direction, and the y-axis perpendicular to the flow. The inlet features a constant uniform flow. The outlet boundary condition is set as a pressure outlet, while the top and bottom boundaries are set as symmetric boundary conditions. The prism surface is designated as a no-slip wall. The total length of the flow computational domain (in the flow direction) is 48$D_L$, and the total width is 24$D_L$. The distance from the center of the prism’s straight side to the top and bottom boundaries, as well as the inlet boundary, is 12$D_L$ each. The blockage ratio, $D_e/\left(24D_L\right)=2.08\%$, is less than 5%, suggesting that the effect of the domain’s width on the D-section prism can be neglected [39].

2.2. Flow Dynamic Calculation Method

Two-dimensional unsteady incompressible Reynolds-Averaged Navier–Stokes (RANS) equations are employed in this numerical study, utilizing the k-ω SST turbulence model and the SIMPLEC algorithm for pressure–velocity coupling based on the ANSYS2021R1 FLUENT software. The medium is water, with a density of 995.3 kg/m³ and a dynamic viscosity of 0.000784 kg/(m·s) [40]. The turbulence intensity at the velocity inlet is 0.9% [40]. For spatial discretization in the solver, the pressure term is resolved using the PRESTO scheme, momentum terms by the QUICK method, turbulent kinetic energy by the second-order upwind scheme, and the turbulent dissipation rate by the first-order upwind scheme. Time discretization is managed using a first-order implicit method. The convergence criteria for all parameters are set to a residual of $1.0\times {10}^{-5}$, with a maximum iteration limit of 30 steps.

2.3. Prism Structure Dynamic Calculation Method

The flow-induced vibration system can be regarded as a two-degree-of-freedom spring-mass-damping model (Figure 1b), with the structural dynamics equations for the streamwise and transverse directions being:

$$m\ddot{x}(t)+c\dot{x}(t)+kx(t)=F_x(t)$$

(1)

$$m\ddot{y}(t)+c\dot{y}(t)+ky(t)=F_y(t)$$

(2)

In the equations, x and y represent the coordinates of the D-section prism in the streamwise and transverse directions, respectively, while m, c, and k denote the mass, damping, and spring stiffness of the system. The drag and lift forces in the streamwise and transverse directions are represented by F_x and F_y, respectively. The motion equations of the prism are based on Newton’s second law and are solved using the Newmark-β method to perform the numerical simulation of the fluid–structure interaction.

2.4. Energy Collection Calculation Method

In a flow field with uniform inflow, assuming that the vibrational response of the D-sectional prism approximately varies sinusoidally, without considering the phase difference, the displacements of the prism in the x and y directions (these displacements are dimensional) [41] are as follows:

$$x(t)=A_x\sin (2\omega t)$$

(3)

$$y(t)=A_y\sin (\omega t)$$

(4)

In the above equation, $A_x$ and $A_y$ are the amplitudes of the prism’s motion in the x and y directions, respectively, with their non-dimensional amplitudes denoted as $A_x^{\ast }={A_x/D}_e$ and $A_y^{\ast }={A_y/D}_e$, respectively. $\omega$ represents the circular frequency, denoted by $\omega =2\mathsf{\pi }f=2\mathsf{\pi }/T$, f is the vibration frequency of the prism, and T is the vibration period. Deriving the displacement equations of the prism with respect to time t yields the velocities of the prism in the x and y directions as ${\dot{x}}_t=2A_x\omega \cos \left(2\omega t\right)$ and ${\dot{y}}_t=A_y\omega \cos \left(2\omega t\right)$, respectively. The flow-induced vibrations of the prism are described using a spring-mass-damper model, and the equations of motion for a two-degree-of-freedom system are as follows:

$$m\ddot{x}+C_{\mathrm{system}}\dot{x}+kx=F_x(t)$$

(5)

$$m\ddot{y}+C_{\mathrm{system}}\dot{y}+ky=F_y(t)$$

(6)

In the formula m is the mass of the prism; $F_x$ and $F_y$ are the longitudinal and lateral forces exerted by the fluid on the solid; $C_{system}$ is the damping coefficient of the system; and K represents the stiffness of the system. The expression for the power $P_{\mathrm{energy}}$, representing the energy captured from the fluid through flow-induced vibrations over one vibration period T, is given in reference [42] as follows:

$$P_{\mathrm{energy}}={\displaystyle \frac{1}{T}}{\displaystyle {\int }_0^T{F}_y\dot{y}}dt+F_x\dot{x}dt$$

(7)

The displacement, velocity, and acceleration of the prism are incorporated into Equation (5) for simplification. In the integration calculations, aside from the integrals of $C_{\mathrm{system}}\dot{y}$ and $C_{\mathrm{system}}\dot{x}$, which are non-zero, the integrals of other terms similar to ${\displaystyle {\int }_0^T\sin (t)}\cos (t)dt$ result in zero. Therefore, Equation (7) can be simplified to:

$$P_{\mathrm{energy}}=0.5C_{\mathrm{system}}{\omega }^2(A_y^2+4A_x^2)$$

(8)

In a uniform flow, the power generated by the fluid can be expressed as the product of the dynamic pressure difference and the volumetric flow rate:

$$P_{\mathrm{fluid}}=P_{t}Q$$

(9)

In the context, $P_t$ represents the pressure head, given by $P_t=\rho U^2/2$; Q denotes the flow rate within the fluid action area, expressed as $Q=A_{\mathrm{flow}}U$. For a vibrating prism, the projected area in the y direction, denoted as $A_{\mathrm{flow}}$, is defined as $A_{\mathrm{flow}}=D_e$, and L is the length of the column. The power of the fluid is then given by:

$$P_{\mathrm{fluid}}=0.5\rho D_e{U}^{3}L$$

(10)

The secondary energy conversion efficiency, denoted as $\eta$, is the ratio of the energy captured during flow-induced vibrations of the prism to the intrinsic energy of the fluid. To obtain a more accurate energy conversion efficiency, it is necessary to consider the Betz limit, which represents the maximum efficiency at which the vibrating body can extract energy from water [22]. The factor for the Betz limit is 16/27, approximately 0.5926. Thus, it follows that:

$$\eta ={\displaystyle \frac{P_{\mathrm{energy}}}{P_{\mathrm{fluid}}}}={\displaystyle \frac{C_{\mathrm{system}}{\omega }^2(A_y^2+4A_x^2)}{0.5926\rho D_e{U}^{3}L}}$$

(11)

In the formula, ${\xi }_{\mathrm{system}}=C_{\mathrm{system}}/2m\omega$, where m is the total mass, $m=m_f\left(m^{\ast }+C_a\right)$; $m_f$ is the mass of the fluid displaced by the same volume. The natural frequency $f_n$ is given by $f_n=S_{t}U/D_e$. Simplifying Equation (11), the conversion efficiency $\eta$ is expressed as:

$$\eta ={\displaystyle \frac{2{\pi }^4(m^{\ast }+C_a){\xi }_{system}(A_y^{\ast 2}+4A_x^{\ast 2})S_t^2}{0.5926\cdot U_r}}$$

(12)

From the expression, it can be seen that the energy harvesting efficiency is inversely proportional to the reduced velocity and is related to various factors. The amplitude does not fully determine the overall energy conversion efficiency. According to the interval selected by the numerical simulation in previous work [18], $S_t$ is approximate to 0.18.

2.5. Mesh Generation Method and Independence Verification

For the stability of the calculations and to effectively capture the flow characteristics around and behind the D-section prism, a hybrid meshing method is employed (Figure 2) based on ANSYS2021R1 ICEM software. The fluid domain is divided into a moving zone and a deformation zone. The deformation zone uses an unstructured mesh, while the moving zone employs a structured mesh. The mesh in the moving zone synchronizes with the vibration of the prism, which helps to avoid the occurrence of negative volumes that are common in simulations with fully structured meshes. The moving zone encompasses an area of six times the diameter of the prism around it. An “O” grid method is used to refine the mesh near the wall surface, setting $y^{+}=y/\mu \sqrt{\rho {\tau }_w}<0.6$, where y is the distance from the center of the first layer of the mesh to the prism wall, ${\tau }_w$ is the wall shear stress, $\mu$ is the dynamic viscosity, and $\rho$ is the fluid density.

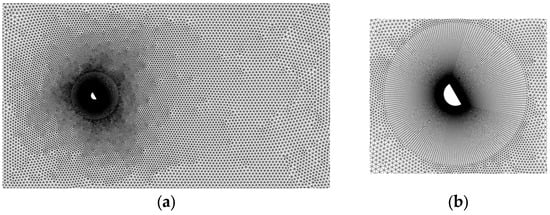
Figure 2. The computational grid (Mesh3): (a) overall grid; (b) adaptive grid.

To assess grid independence, five sets of grids with varying densities were compared, calculating the transverse response amplitude and frequency of a D-section prism at an inflow angle of 30 degrees. The reduced velocity $U_r$ = 6, $m^{\ast }$ = 2.6, $f_n=0.4$ Hz, $\xi$ = 0.003611. The primary difference between Mesh1 and Mesh5 was the height of the first layer grid, which successively decreased, enlarging the circular refinement area around the prism up to 6$D_L$, thereby increasing the number of grids in this area (as shown in Table 1). As a result, the number of grids in regions farther from the prism also slightly increased, with the total grid count rising from 31,000 to 69,000. Table 1 presents the computational results for these five grids, where $A_y/D_e$ represents the non-dimensional root mean square amplitude of the lateral flow ($A_y=y_{\mathrm{rms}}$) and $f_s/f_n$ is the ratio of the vibration frequency of the prism to its natural frequency. The data in Table 1 show that with a sufficient number of grids, the variation in the root mean square amplitude and frequency of the prism in Mesh3 was less than 1% when compared to Mesh4 and Mesh5. Considering both computational accuracy and efficiency, this study selected Mesh3 as the grid for subsequent calculations.

Table 1. Mesh independency study.

Case	Height of the First Mesh (m)	Mesh Number	${{\mathit{A}}_{\mathit{y}}/\mathit{D}}_{\mathit{e}}$	${\mathit{f}}_{\mathit{s}}/{\mathit{f}}_{\mathit{n}}$
Mesh1	0.00008	31,356	0.786	1.163
Mesh2	0.00008	37,172	0.811	1.164
Mesh3	0.00005	44,456	0.798	1.166
Mesh4	0.00005	58,586	0.801	1.166
Mesh5	0.00004	69,018	0.805	1.166

To verify the independence of the time step size, computational results with five different time steps were compared within the range $U\Delta t/D_L\le {10}^{-2}$, as shown in Table 2 (C1 to C5). From Table 2, it is evident that compared to the smallest time step C1, the amplitude deviation in C4 is 1.00%, and the frequency deviation is 0.02%, with all relative deviations being within 1%. To satisfy computational accuracy and efficiency, the time step size was set to 0.005 s in this study.

Table 2. Time step independence study.

Case	$\Delta \mathit{t}/\mathit{s}$	${{\mathit{A}}_{\mathit{y}}/\mathit{D}}_{\mathit{e}}$	${\mathit{f}}_{\mathit{s}}/{\mathit{f}}_{\mathit{n}}$
C1	0.002	0.796	1.1664
C2	0.003	0.789	1.1663
C3	0.004	0.798	1.1666
C4	0.005	0.804	1.1666
C5	0.006	0.813	1.1696

The validation of the numerical model in the simulations of the flow-induced vibrations of the D-section prism was demonstrated by previous work in Song et al. (2024) [18]. The numerical results agreed reasonably well with experimental tests [3,17]. Readers are referred to Song et al. (2024) [18] for details, which are not reiterated here.

3. Results and Discussion

3.1. Flow-Induced Vibration Modes of Cylinders at Different Reduced Velocities

Under the influence of water flow, the D-section prism undergoes time-varying displacements, and its equilibrium position of vibration often does not coincide with the initial position. Amplitude is a critical parameter for flow-induced vibration analysis. Figure 3 presents the transverse amplitude of the D-section prism as a function of the reduced velocity under the approach angle $\alpha$, where ${\overline{A}}_y$ represents the mean value of the flow-induced vibration amplitude of the prism. Figure 4 illustrates the displacement of the prism’s vibrational equilibrium position (time-averaged) relative to the initial position.

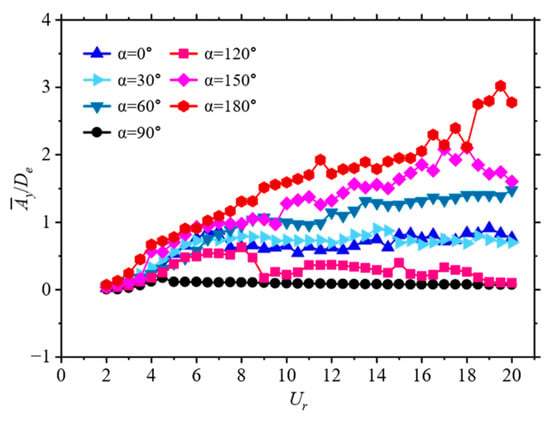
Figure 3. Variations in transverse amplitude versus reduced velocity.

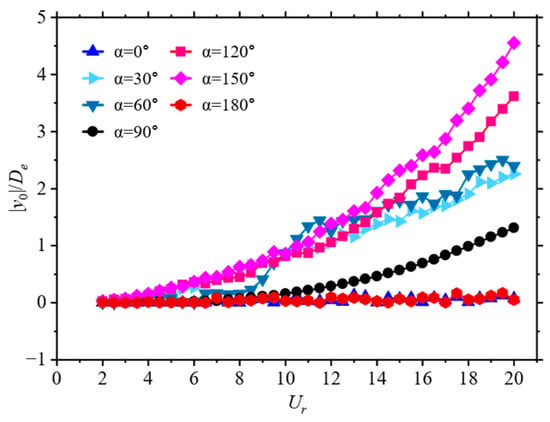
Figure 4. Variations in transverse equilibrium position offset with reduced velocity.

As seen in Figure 3, the angle of attack has a significant impact on the amplitude of the prism’s vibration. When $\alpha =0^{\circ }$, the average amplitude of the prism increases with the reduced velocity, exhibiting three typical vibration branches: the initial VIV branch, the upper VIV branch, and the full galloping branch. When $2\le U_r\le 4$, the prism is on the initial VIV branch, with its amplitude increasing as the flow speed increases. The prism then transitions from the initial branch to the upper branch, with its amplitude rapidly increasing from 0.25$D_e$ to 0.92$D_e$. At this point, the amplitude of the prism stabilizes (as can be seen from Section 3.3), with slow growth, maintaining around 0.9$D_e$, which is the characteristic of the upper VIV branch. When $7\le U_r\le 9$, the prism transitions from the upper VIV branch to galloping. After $U_r=9$, the prism enters the full galloping range, characterized by high amplitude and low frequency, resulting in irregular vibrations.

When the angle of attack $\alpha ={30}^{\circ }$, in the range of $2\le U_r\le 4$, the prism is on the initial branch of VIV with a small amplitude. As the Reynolds number increases, the prism gradually enters the upper branch. However, due to the angle of attack, the prism on the upper branch is influenced by both vortex shedding and galloping, characterized by chaotic amplitudes and a vibration frequency of about 1 to 1.2. After $U_r=18$, the prism enters the lower branch and continues to compete with VIV. When $\alpha$ is ${60}^{°}$, at lower reduced velocities, the prism’s amplitude is small. At $U_r\le 6$, the prism is on the initial branch of VIV. In the range of $6.5\le U_r\le 14$, due to the angle of attack, the prism remains in the VIV lock-in range with an amplitude of 0.8 to 1.3$D_e$. Finally, the prism transitions from the lock-in range to the galloping range, entering the region influenced by both phenomena.

When the angle of attack $\alpha$ is increased to ${90}^{°}$, the vibration of the prism is primarily VIV-dominated, and the amplitude does not change drastically with the increase in Reynolds number. The upper branch is either non-existent or very small, and the equilibrium position of the vibration continuously shifts upwards.

When the angle of attack $\alpha$ is set to ${120}^{°}$, unlike the previous angles, the equilibrium position of the prism shifts from an upward to a gradually downward vibration. At low flow speeds, the amplitude is not significant. In the range of $4\le U_r\le 8$, the prism enters the upper branch, with the maximum non-dimensional amplitude being about 0.5$D_e$. Subsequently, the prism enters the lower branch and the range influenced by galloping, with its non-dimensional amplitude reduced to 0.25$D_e$. At a reduced velocity of $U_r=19.5$, the prism transitions into the lower branch.

When the angle of attack $\alpha$ is up to ${150}^{°}$, the vibration of the prism is similar to that at ${60}^{°}$, with the overall amplitude increasing as the Reynolds number increases. At higher reduced velocities, the prism is in the range affected by both vortex-induced vibration (VIV) and galloping, with VIV being dominant. When $\alpha$ is ${180}^{°}$, the vibration of the prism is still primarily VIV, and no pure galloping phenomenon is observed. Due to the change in the angle of attack, which is symmetrical in the upstream direction, the equilibrium position of the prism’s vibration remains near zero. In the range of $3\le U_r\le 20$, the non-dimensional vibration frequency of the prism is generally maintained between 1 and 1.2, indicating that the prism is within the range influenced by both vortex shedding and galloping.

3.2. Equilibrium Position Offset of Cross Flow Displacement

This article examines the D-section prism set at seven different angles of attack. When the angle of attack of the prism is between ${30}^{°}$ and ${150}^{°}$, the prism lacks geometric symmetry along the streamwise direction, and the equilibrium position of the prism’s cross-flow vibrations no longer coincide with its original position at rest (y = 0). Merely analyzing the amplitude of the prism’s vibrations may not yield an accurate understanding of its vibrational characteristics. As shown in Figure 4, $y_0$ is defined as the equilibrium position of the prism’s lateral vibrations, and $\left|y_0\right|$ is the offset of the prism’s equilibrium position [10].

Figure 4 indicates that the offset of the prism’s equilibrium position is closely related to the angle of attack $\alpha$ and the reduced velocity $U_r$. When the angle of attack $\alpha$ is $0^{\circ }$ and ${180}^{\circ }$, the offset of the prism’s vibration equilibrium position is essentially zero, maintaining near y = 0. This is because the prism is symmetrical in the upstream direction, resulting in no significant offset within the simulated range. However, when the angle of attack becomes asymmetrical in the upstream direction, the equilibrium position of the prism’s vibration will shift significantly with changes in the reduced velocity. When the angle of attack $\alpha$ is ${90}^{\circ }$, the offset of the prism’s vibration equilibrium position is also relatively small, which may be due to the prism being asymmetrical in the upstream direction but symmetrical in the cross-flow direction, leading to a smaller displacement.

When the angle of attack $\alpha$ is fixed, the offset of the prism’s equilibrium position generally increases with the increase in reduced velocity. As the angle of attack $\alpha$ gradually increases from $0^{\circ }$ to ${90}^{\circ }$, and then from ${90}^{\circ }$ to ${180}^{\circ }$, the prism progressively loses its geometric symmetry in the upstream direction, resulting in a gradual increase in the offset of the prism’s vibration equilibrium position, which becomes significantly different from the equilibrium position when the prism is stationary. The proportion of flow encountering the curved side decreases, while the proportion encountering the flat side increases. Within the simulated range, the prism at an angle of attack $\alpha$ of ${150}^{\circ }$ exhibits the worst geometric symmetry, at which point the offset of the prism’s vibration equilibrium position reaches its maximum value. The maximum value of $\left|y_0\right|$ is approximately 4.55$D_e$. When the angle of attack $\alpha$ is ${120}^{\circ }$ and ${150}^{\circ }$, at higher reduced velocities, the time–displacement curves of the prism shift below y = 0, resulting in a negative offset of the prism’s equilibrium position. For example, as shown in Section 3.3, when $\alpha =120^{\circ }$ and $U_{\mathrm{r}}$ = 15, the entire time–displacement curve of the prism deviates below y = 0. This also illustrates from another perspective the impact of the angle of attack on the prism’s amplitude response.

The comprehensive analysis reveals that at lower Reynolds numbers, the D-section prism predominantly exhibits vortex-induced vibrations. As the reduced velocity increases, the amplitude of the prism’s vibrations continues to grow with changes in the angle of attack. This indicates that when the geometric symmetry along the streamwise direction of the prism is disrupted, the amplitude of its vibrations increases, and the presence of an angle of attack suppresses the occurrence of galloping. Additionally, since the flow-induced vibrations of the prism occur as self-excited vibrations in a stable flow, not only does the prism vibrate, but the surrounding fluid also vibrates relative to the prism. This vibration generates pulsating fluid forces on the surface of the prism. When these forces weaken the prism’s vibrations, the vibrations tend to stabilize; however, when these forces enhance the prism’s vibrations, the amplitude increases and the vibrations become unstable. If the pulsating fluid forces continuously intensify the prism’s vibrations, the vibrations enter the branch of galloping. Regarding the mechanism of galloping, Li [9] mentioned in his study that the occurrence of galloping is related to the magnitude of the slope of the lift coefficient of the prism wall with respect to the reference angle of attack. Galloping occurs when the slope is negative. The instability of the galloping phenomenon is also closely related to the turbulence intensity of the flow field

3.3. Transverse Vibration Frequency Characteristics of the Prism under Different Reduced Velocities

Figure 5 illustrates the variation of dimensionless vibration frequency ($f/f_n$) of the D-section prism at different angles of attack with respect to Reynolds number. Here, f represents the vibration frequency of the prism, which is obtained by subjecting the time history displacement curve of the prism to fast Fourier transform to extract the dominant frequency. Figure 6 presents the displacement history curves of the prism at different angles of attack, along with their corresponding dimensionless vibration spectra.

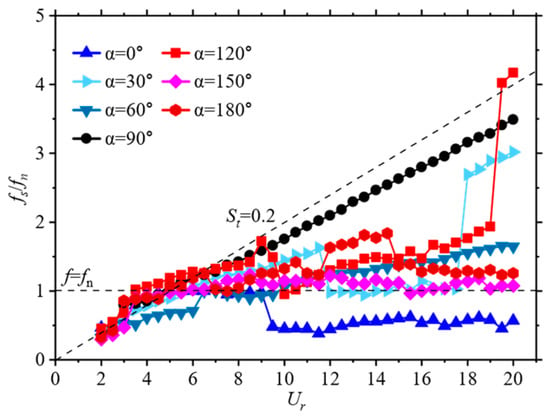
Figure 5. Variations of transverse dominant frequency with reduced velocity.

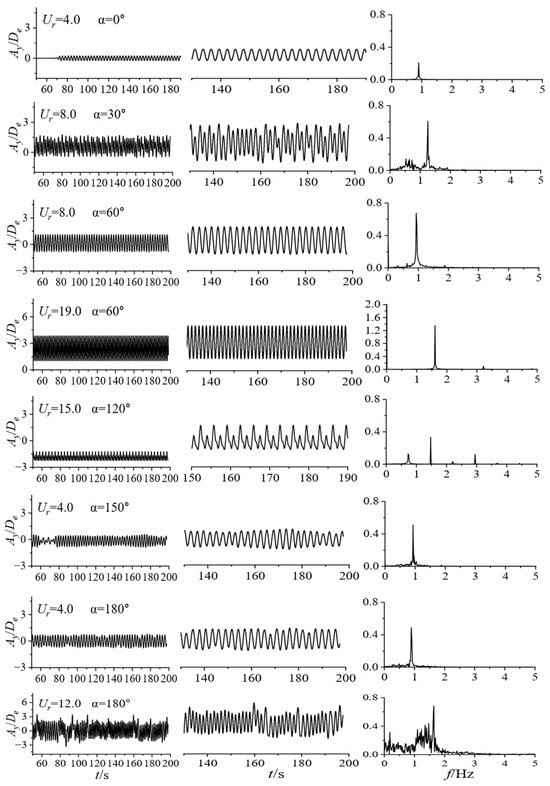
Figure 6. Transverse displacement histories and spectra of a D-section prism.

The prism has geometrical symmetry in the flow direction at $\alpha =0^{\circ }$. At lower reduced velocities ($2\le U_r\le 4$), the dimensionless vibration frequency of the prism is very small, and the prism is in the initial branch of VIV. With the increase in the Reynolds number, the prism gradually moves into the upper branch and experiences vortex-induced vibrations, with the amplitude being about 1$D_e$. The prism is “locked” by the fluid, and its dimensionless frequency is around 1. When the reduced velocity increases to $U_r=9.5$, the dimensionless vibration frequency of the prism drops to around 0.5, entering the fully galloping region with chaotic and irregular amplitudes.

At the angle of attack $\alpha ={30}^{\circ }$, the vibration frequency of the prism is similar to that of a fixed cylinder at lower reduced velocities ($2\le U_r\le 4$), while the non-dimensional vibration frequency is around 0.2, placing the prism on the initial branch of vortex-induced vibrations. In the range of $12\le U_r\le 18$, although the non-dimensional amplitude of the prism is around 1.0, the increase in amplitude is not significant, and the equilibrium position of the prism’s vibrations continuously shifts. At this time, the prism is in the overlap region of vortex-induced vibrations and galloping.

As $\alpha ={60}^{\circ }$, the vibrations of the prism are primarily dominated by VIV, and the frequency of the prism’s vibrations increases with the increase in Reynolds number. In the range of $2\le U_r\le 6$, the prism is on the initial branch of VIV. In the range of $6.5\le U_r\le 9.5$, the prism is on the upper branch of VIV, where it is in a “locked” state, with its non-dimensional vibration frequency around 1. At this time, the amplitude of the prism is approximately 1$D_e$. Subsequently, the prism enters the lower branch of vortex shedding, acting in conjunction with galloping, with vortex shedding being the dominant factor.

When $\alpha$ is set to ${90}^{\circ }$, the non-dimensional vibration frequency of the prism increases with the Reynolds number at lower reduced velocities ($2\le U_r\le 3.5$). However, the amplitude remains within a low range, indicating that the prism is on the initial branch of VIV. As the flow speed increases, the prism moves to the upper branch ($4\le U_r\le 4.5$), where its maximum non-dimensional amplitude reaches 0.1$D_e$. In the reduced velocity range of $5\le U_r\le 6$, the prism enters the lower branch. Subsequently, the prism moves into the region where both vortex shedding and galloping interact, with vortex shedding being predominant. The non-dimensional vibration frequency is near the Strouhal number.

It can be observed in Figure 6 that flow-induced vibration is dominated by VIV at $\alpha ={120}^{\circ }$,with no galloping phenomena detected, which is similar to the case at $\alpha ={60}^{\circ }$. Unlike the smaller angles, when flow-induced vibrations occur, the D-section prism shifts downward overall. The vibration frequency of the prism initially increases with the increase in Reynolds number. Then, the prism enters the lower branch and competes with galloping at $U_r=10$, ultimately moving into the unlocking region.

While $\alpha ={150}^{\circ }$, the prism maintains vortex-induced vibrations at low reduced velocities. As the Reynolds number increases, the prism remains in the interaction region of VIV and galloping across the range of $4\le U_r\le 20$. Specifically, the average amplitude changes are not significant, but the equilibrium position of the vibrations continually increases. When $\alpha ={180}^{\circ }$, the vibration of the prism results from a competition between galloping and vortex shedding, with vortex shedding still dominating. In the range of $4.5\le U_r\le 6$, the prism enters the lower branch of vortex shedding. Subsequently, the non-dimensional vibration frequency of the prism is generally maintained around 1 to 1.2, indicating that the prism’s vibrations result from the interaction between galloping and vortex shedding.

Comparing with the experimental results of smooth circular cylinders by Bearman et al. [2], it can be observed that the dominant flow-induced vibration regime for a cylinder is vortex-induced vibration, with all three response branches of VIV being clearly observed in the vibration range of the prism. However, a D-section prism exhibits differences from a cylinder. On one hand, a D-section prism not only undergoes VIV but also shows galloping phenomena. On the other hand, typical VIV branches are difficult to observe in the vibration range of the prism, and similar VIV branches are narrower compared to those of a smooth cylinder. The presence of geometric physical sharp edges on the prism causes the flow separation points to be located at these edges, leading to more complex interactions between the edges and the shear layer of flow separation, which in turn complicates the vibration and shedding structures of vortices around the prism. As the angle of attack varies, more than one peak often appears on the dimensionless vibration curve of the prism, making it difficult to identify the dominant vibration frequency of the prism.

3.4. The Secondary Energy Conversion Efficiency of the Prism

By substituting the non-dimensional amplitude of the prism into Equation (12), the energy conversion efficiency under various operating conditions can be calculated. Figure 7 presents the variation in the energy conversion efficiency of the D-section prism at different flow angles as a function of the reduced velocity.

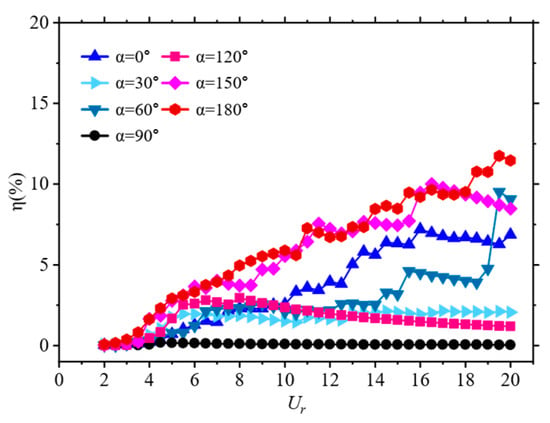
Figure 7. Comparison of the energy conversion efficiency at different angles of attack.

When the angle of attack $\alpha =0^{\circ }$, the prism is on the upper branch of VIV at low Reynolds numbers, with its energy conversion efficiency continuously increasing. At high Reynolds numbers, the prism is within the full galloping range, exhibiting irregular and chaotic amplitudes, and the overall energy conversion efficiency shows an upward trend. When the angle of attack $\alpha$ is ${30}^{\circ }$, ${60}^{\circ }$, ${120}^{\circ }$, and ${150}^{\circ }$ at low Reynolds numbers, the prism is on the initial and upper branches of VIV, with its energy conversion efficiency increasing as the Reynolds number increases. As the prism transitions from the upper branch of VIV to the galloping range, its energy conversion efficiency suddenly decreases, but then gradually increases again when it enters the branch influenced by both VIV and galloping. At this point, the prism is on the branch affected by both VIV and galloping, with galloping continuously affecting the amplitude and branches of VIV, while VIV also changes the form of galloping. This is reflected in the graphs as the prism’s amplitude increase is not significant with the increase in Reynolds number, resulting in a less noticeable increase in energy conversion efficiency. When the angle of attack $\alpha$ is ${90}^{\circ }$, the D-section prism experiences VIV throughout the entire simulated range. Although the equilibrium position of the vibration continuously increases, the amplitude increase of the prism is very small, and its conversion efficiency remains relatively stable with minor fluctuations. When the angle of attack $\alpha$ is ${180}^{\circ }$, due to the geometric characteristics of the prism itself, the range of the prism within the VIV branch is very small, and most of the range is influenced by both VIV and galloping. This causes the amplitude of the prism to be affected by galloping, showing irregular growth, while the non-dimensional vibration frequency of the prism is influenced by VIV, maintained around 1, leading to an overall upward trend in the prism’s energy conversion efficiency, but without regularity.

Overall, the energy conversion efficiency of the prism reaches the maximum at angle of attack $\alpha ={180}^{\circ }$, reaching 11.75%, and the minimum at ${90}^{\circ }$. Due to the geometric characteristics of the D-section cross-section itself, when vibrating, the prism’s vibration differs from that of the cylinder, exhibiting instability in vibration. Moreover, once entering the galloping regime, the amplitude of the prism increases continuously with the increase in Reynolds number. This indicates that the fluid kinetic energy captured by the D-section prism increases with the increase in the flow velocity. As an energy conversion device for flow-induced vibration, the D-section prism has advantages over the cylinder, especially at higher Reynolds numbers.

4. Conclusions

Numerical simulations of flow-induced vibrations of D-section prisms at seven different angles of attack, within a subcritical Reynolds number range ($368\le Re\le 14742$), were conducted in this study. The characteristics such as amplitude, frequency, lateral position offset, and energy conversion efficiency of the prism under different reduced speeds were analyzed. Within the range of computational parameters studied in this work, the following conclusions were reached:

(1)

Within the range of Reynolds numbers studied, several typical flow branches can be clearly observed: the initial branch of VIV, the upper branch of VIV, and galloping. Among the angles of attack considered, only at angle of attack $\alpha =0^{\circ }$ was a complete galloping phenomenon observed. At other angles, the prism’s vibration consistently remained in the region dominated by VIV, with interaction between galloping and VIV.

(2)

The change in the approach angle significantly affects the displacement of the equilibrium position of the prism’s vibration. Except at the symmetric approach angles in the streamwise direction, the displacement of the prism’s equilibrium position increases progressively with changes in the approach angle. When the approach angles are ${60}^{\circ }$ and ${120}^{\circ }$, the displacement of the prism’s vibrational equilibrium position reaches its maximum value.

(3)

The energy conversion efficiency of the cylinder is highest at an inflow angle of ${180}^{\circ }$ and lowest at ${90}^{\circ }$. Due to the geometric characteristics of the D-section prism, its vibrations differ from those of a cylindrical section and exhibit instability. Moreover, once the cylinder enters the galloping regime, its amplitude continuously increases with the Reynolds number. Consequently, a D-section prism holds an advantage over a cylinder in devices that convert energy from flow-induced vibrations, especially at high Reynolds numbers.

(4)

It should be noted that only one fixed set of mass and damping ratios was investigated in this work. The effects of mass damping ratio size on energy conversion efficiency, the presence of a column shielding in front, and a broader range of Reynolds numbers require further research.