A Novel Method for Estimating the Undrained Shear Strength of Marine Soil Based on CPTU Tests

Abstract

The undrained shear strength is an essential parameter in the foundation design of marine structures. Due to the complex marine environment and technical limitations, it is difficult and costly to obtain offshore samples. Piezocone penetration tests (CPTU) are relatively low-cost compared to drilling and sampling methods. Therefore, based on the soil behavior type index (I_c) derived from CPTU results, a model for estimating cone factors (N_kt, N_ke) is proposed to improve the accuracy of estimation of undrained shear strength. The result shows that the soil behavior type index (I_c) and cone factors take on a negatively correlated exponential relation. Incorporating a cone factor that varies with the soil behavior type index (I_c) significantly enhances the accuracy of undrained shear strength predictions compared to the conventional method of using a constant cone factor. This approach reduces the root mean square error (RMSE) for N_kt (N_ke) from 0.124 (0.126) MPa to 0.056 (0.06) MPa, and the mean absolute error (MAE) from 0.0154 (0.016) MPa to 0.0032 (0.0036) MPa. The method was validated at an additional location and the predictions were in high agreement with the results of the consolidated quick direct shear test. The developed method can serve as an effective tool used in the design of foundations of marine structures.

1. Introduction

The utilization of offshore wind energy resources is a crucial driver for economic development [1,2] and an essential pathway towards achieving net-zero carbon goals. In recent years, offshore wind power construction has been gradually expanded from offshore areas to deeper parts of the sea, which further causes more difficulties and costs in soil sampling of marine geotechnical surveys [3]. As a result, in situ testing techniques, such as standard penetration tests (SPT) [4], cone penetration tests (CPT) [5], and piezocone penetration tests (CPTU) [6], have been applied in marine soil investigations. Compared to the traditional SPT, CPTUs have significant advantages, such as providing continuous testing data and suitability for more complex environmental conditions; as a result, they are extensively utilized in marine geotechnical surveys. However, existing empirical formulae relating CPTU results to soil parameters are primarily based on terrestrial environments [7,8] and are unsuitable for marine conditions [9]. Therefore, it is of great importance to conduct in-depth research on the empirical formulae connecting CPTU results and marine soil parameters.

In the context of pile foundation design for marine structures, the undrained shear strength of cohesive soil emerges as a critical parameter [10]. Consequently, the accurate prediction of undrained shear strength assumes paramount importance as a central focus in exploring the correlation between CPTU data and soil parameters. The penetration mechanism of CPTU in cohesive soils can be classified into theoretical and empirical methods. The theoretical method commonly includes bearing capacity theory [11], cavity expansion theory [12], the strain path method [13], and moving point dislocation theory [14]. Due to idealized assumptions in these theoretical methods, significant deviations often occur. Hence, scholars began to explore suitable empirical methods to improve the reliability of the prediction with various empirical methods being developed, such as the “total” cone tip resistance method [15], the effective cone resistance method [12], and the excess pore water pressure method [16]. However, the cone factors are still not fixed and vary greatly. To obtain more accurate cone factors, researchers further considered soil characteristic factors to improve the estimating precision of the undrained shear strength from CPTU. When considering the plasticity index of the soil [17], the estimated undrained shear strength values obtained from CPTU are usually very close to laboratory experiment results. Nevertheless, the correlation between cone factors and the plasticity index is only valid for specific soil conditions in certain regions [18,19]. In addition, cone factors are also related to the over-consolidation ratio [20], natural moisture content [21], and fines content [22] of the soil. To obtain the plasticity index, the over-consolidation ratio of soils, etc., soil sampling is required, which unavoidably increases the engineering costs. In order to solve this problem, Bol et al. [23,24] classified soils by means of a soil behavior type index and then gave empirical coefficients for the cone coefficients corresponding to the different soil classes. Nevertheless, the quantitative relation between I_c and cone factors was not provided in Bol’s study. With the development of computer science, machine learning algorithms have been employed to estimate the undrained shear strength with high accuracy [25,26,27]. Moreover, these algorithms are gradually overcoming the limitation of not being able to provide deterministic functional relationships.

To facilitate practical engineering applications and reduce costs associated with marine geotechnical exploration, this study categorized soil into distinct intervals based on the soil behavior type index. Utilizing data obtained from indoor consolidated quick direct shear tests, it established a robust regression model to elucidate the explicit functional relationship between the soil behavior type index and the cone factor. The predictive performance of this model was rigorously assessed through comprehensive evaluation metrics, including the coefficient of determination (R²), root mean square error (RMSE), and mean absolute error (MAE). Furthermore, validation exercises were conducted in nearby marine project sites to confirm the applicability of the proposed methodology.

2. Methods for Calculating Undrained Shear Strength and Soil Behavior Type Index

The “total” cone tip resistance q_t method and the effective cone resistance q_e method are common methods for estimating undrained shear strength S_u from CPTU results. In the following part, we also discuss the undrained shear strength from a consolidated quick direct shear test and the computation of the soil behavior type index I_c.

2.1. Estimation of S_u by “Total” Cone Tip Resistance q_t

Following Lunne et al. [15], the unified formula for calculating the undrained shear strength of clayey soils can be written as:

$$S_u=\frac{q_t-{\sigma }_v}{N_{kt}}$$

(1)

where S_u is the undrained shear strength; q_t is the total cone tip resistance; σ_v is the total vertical stress of the overlying soil; N_kt is the empirical cone factor.

2.2. Estimation of S_u by Effective Cone Tip Resistance q_e

Considering the corrected total cone tip resistance q_t and the difference in pore pressure u₂, Senneset et al. [12] proposed an expression for the undrained shear strength S_u of clayey soils as listed below:

$$S_u=\frac{q_e}{N_{ke}}=\frac{q_t-u_2}{N_{ke}}$$

(2)

where N_ke is the effective cone factor.

2.3. Calculation of Undrained Shear Strength S_u

The consolidated quick direct shear test expeditiously assesses the shear strength of soil by subjecting a sample to shearing within a confined shear box under applied pressure. Despite potential limitations in accuracy, notably concerning sensitive marine soils, its widespread applicability stems from its simplicity, expediency, and cost-effectiveness. This method finds significant utility, particularly in marine geotechnical investigations, where its deployment often exceeds that of triaxial compression tests in terms of quantity. The undrained shear strength of soil at different depths can be estimated by the cohesive strength C_u, angle of internal friction φ_u, and unit weight of soil γ obtained from the consolidated quick direct shear test [28]. The average values of cohesive strength and angle of internal friction are generally used to calculate the indoor undrained shear strength. Due to the difficulties and high cost of offshore sampling [29], only a few holes are drilled for soil sampling. Hence, we adopt a combined method of indoor experiments and empirical formulae from CPTU to obtain the unit weight of the soil, which is a common practice in current practical engineering [30,31].

The consolidation stress σ₃ and the undrained shear strength S_u can be written as:

$${\sigma }_3=\frac{{\displaystyle \sum {\gamma }_i{h}_i}\left(1+2\left(1-\sin {\phi }_u\right)\right)}{3}$$

(3)

$$S_u=c_u+{\sigma }_3\tan {\phi }_u$$

(4)

where h_i and γ_i are the thickness and weight of layer i, respectively. Note that the first layer is actually seawater.

2.4. Calculation of Soil Behavior Type Index I_c

The normalized soil behavior type chart based on CPT proposed by Robertson (1990) [32] classifies soils. Jeffries and Davies [33] discovered the soil behavior type index, which defines the boundaries of soil types without the need for soil sampling. According to the generalized definition provided by Robertson [34], the soil behavior type index can be further described as follows:

$$I_c=\sqrt{{\left[3.47-{\log }_{10}Q\right]}^2+{\left[1.22+{\log }_{10}F\right]}^2}$$

(5)

$$Q=\frac{q_t-{\sigma }_v}{p_a}{(\frac{p_a}{{\sigma }_v^{\prime }})}^n$$

(6)

$$F=\frac{f_s}{q_t-{\sigma }_v}$$

(7)

where Q is the normalized tip resistance; P_a is the atmospheric pressure; F is the normalized friction ratio; f_s is the side friction resistance; ${\sigma }_v^{\prime }$ is the effective covering total stress; n is the stress index, and its value is set to 1. The revised classification of soil behavior types index [35] is listed in Table 1.

Table 1. The corrected I_c classification.

Range of Ic	Classification of the Soil in China
Ic > 3.45	Muck and mucky soil
3.00 < Ic < 3.45	Clay
2.80 < Ic < 3.00	Silty clay, clay
2.60 < Ic < 2.80	Silt, silty clay
2.40 < Ic < 2.60	Silt
2.10 < Ic < 2.40	Silty sand, silt
1.87 < Ic < 2.10	Fine sand
Ic < 1.87	Medium sand

3. CPTU Results

As depicted in Figure 1, the experimental sites A and B are located in the eastern sea area of Cangnan and the southeastern sea area of Xiangshan in Zhejiang Province, China, respectively. Figure 2 and Figure 3 illustrate the distribution of drilling holes at sites A and B. Throughout the CPTU drilling process, parameters such as “total” cone tip resistance (q_t), sleeve friction (f_s), and pore water pressure at the cone shoulder (u₂) were continuously measured with a data acquisition interval not exceeding 100 mm. At site A, there were 39 CPTU boreholes and 10 soil sampling holes, from which 202 soil samples were collected, and 68 sets of laboratory consolidated quick direct shear tests were conducted. Figure 4 displays the soil profile data of the CPTU borehole log section No. JT-1 along the depth direction at site A. The upper sediment at site A primarily consists of Quaternary (Q₄) shallow marine deposits, including mud, muddy silty clay, silt, sandy silt, and silty clay. The lower sediment comprises Late Pleistocene (Q₃²) deposits from terrestrial and coastal environments, mainly composed of silt, silty clay, and sandy silt within the depth range of the exploration. At site B, there were 19 CPTU test holes and 28 soil sampling holes, from which 484 soil samples were collected, and 68 sets of laboratory consolidated quick direct shear tests were performed. The upper sediment at site B primarily consists of Quaternary (Q₄) shallow marine deposits, including mud, muddy silty clay, sandy silt, silt, silty clay, and gravel. The lower sediment consists of Late Pleistocene (Q₃²) deposits from estuarine and coastal environments, characterized by sandy silt and silty clay within the depth range of the exploration. In summary, the geological conditions of experimental sites A and B are relatively similar. We first proposed an undrained shear strength formula based on CPTU results derived from the data of experimental site A and then verified it using the data from experimental site B. Table 2 presents the types and quantities of soil layers studied at experimental sites A and B.

Figure 1. Relative location of the experiment at sites A and B.

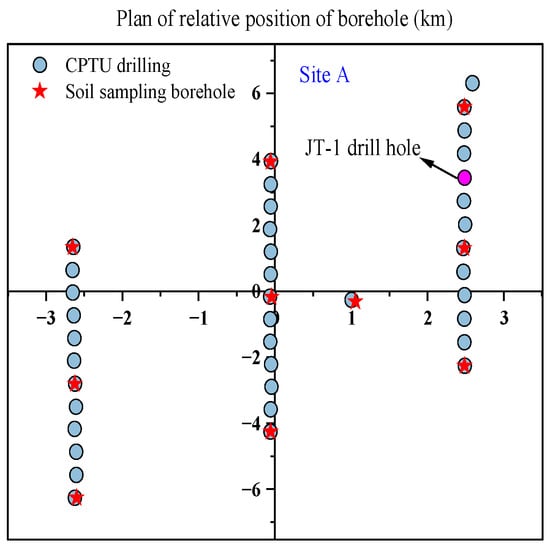
Figure 2. Distribution of boreholes at site A.

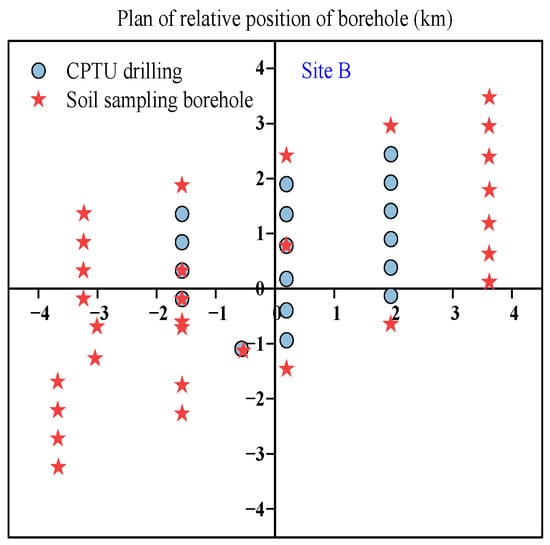
Figure 3. Distribution of boreholes at site B.

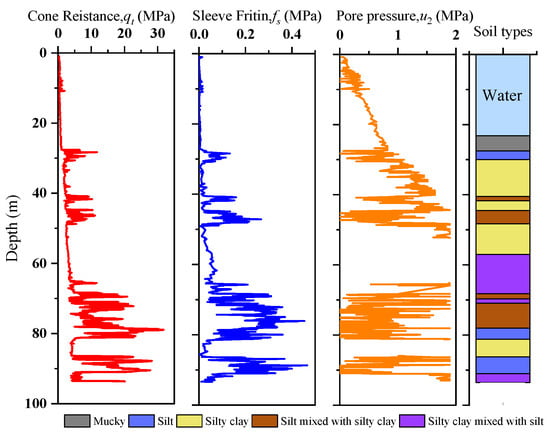
Figure 4. Soil profile data of the CPTU borehole log section No. JT-1 at site A.

Table 2. The information of soil layers.

Experiment in A		Experiment in B
Soil Layers	Statistic	Soil Layers	Statistic
Silty clay	116	Muddy silty clay	27
Silt mixed with silty clay	67	Silty clay	26
Silty clay mixed with silt	53	Muddy clay	16
Muddy silty clay	18	Silty clay mixed with silt	9
Silty clay mixed with silt	13	Clayey silt mixed with silty clay	4
Silty clay with silty sand	7
Silt mixed with silty clay	6

Data extraction was first performed on the test results from 39 CPTU boreholes at experimental site A. After eliminating data from sand layers and surface mucky layers, 344 soil layer data were obtained. The histogram in Figure 5 displays the distribution of I_c data. Figure 6 shows the results of the selection of 280 soil layer data. To minimize random errors, this study focused on the range [1.8, 2.8], which has a dense distribution of I_c data. Figure 6 shows that the data points are relatively discrete and cannot form a functional relationship.

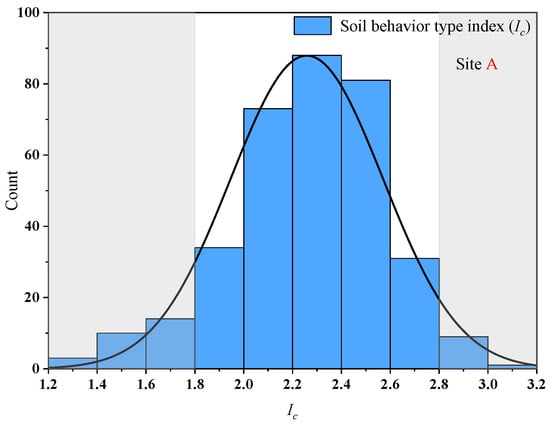
Figure 5. Histogram of I_c at site A.

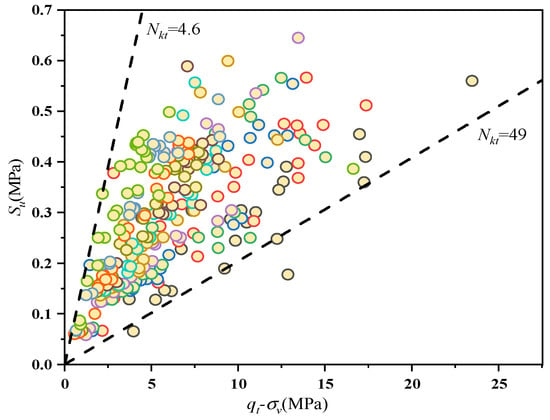
Figure 6. Empirical cone factor N_kt vs. S_u.

To investigate the functional relationship between the related variables (q_t-σ_v, S_u), 280 soil samples were divided into 12 groups based on the magnitude of I_c. Each group contained 23 soil samples, except for the last one, as shown in Figure 7. Two clear outliers were excluded based on observation. The results indicate a linear relationship between these variables, as demonstrated by the coefficient of determination R² in Table 3. All results, except for I_c ranging from 2.12 to 2.22, indicate good fitting effectiveness, with values larger than 0.95. Additionally, using the method described above, the relationship between q_t-u₂ and S_u can be determined (see Figure 8 and Table 3).

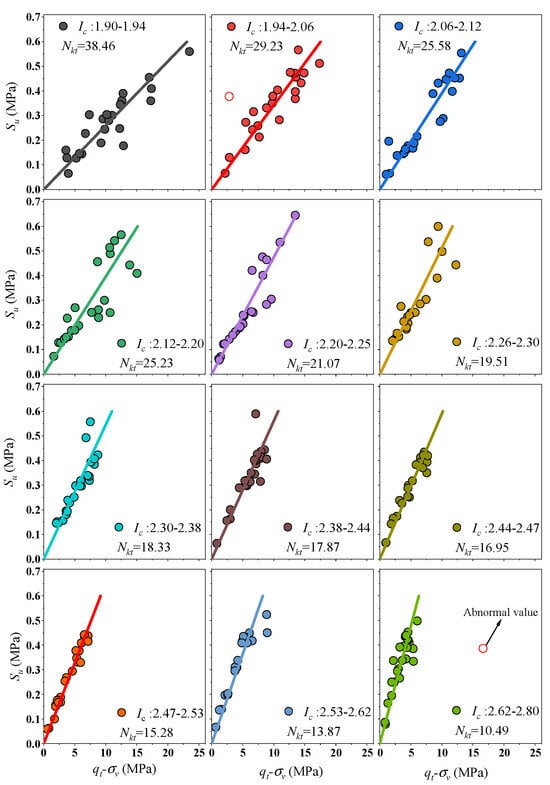
Figure 7. N_kt corresponding to different intervals of I_c at site A.

Table 3. N_kt and N_ke of I_c in different intervals at site A.

Depth Range of the Soil Layer Bottom (m)	Ic	Ic (Mean Value)	Nkt	R2	Nke	R2
[43–54]	[1.80–1.94]	1.88202	38.46	0.96	38.43	0.96
[52–65]	[1.94–2.06]	2.01657	29.23	0.97	29.36	0.97
[47–59]	[2.06–2.12]	2.09938	25.58	0.97	25.95	0.96
[46–63]	[2.12–2.20]	2.15491	25.23	0.93	25.75	0.93
[46–61]	[2.20–2.25]	2.22081	21.07	0.96	21.43	0.96
[50–65]	[2.26–2.30]	2.27726	19.51	0.95	19.69	0.94
[56–72]	[2.30–2.38]	2.34376	18.33	0.97	18.90	0.96
[67–83]	[2.38–2.44]	2.41203	17.87	0.97	18.76	0.97
[59–78]	[2.44–2.47]	2.45625	16.95	0.98	17.59	0.98
[54–74]	[2.47–2.53]	2.49873	15.28	0.99	15.86	0.98
[62–82]	[2.53–2.62]	2.57546	13.87	0.97	13.90	0.97
[67–84]	[2.62–2.80]	2.69623	10.49	0.97	10.89	0.96

Note: The water depth within this region ranges from approximately 20 m to 26 m, with the exclusion of surface mucky layers from the research scope.

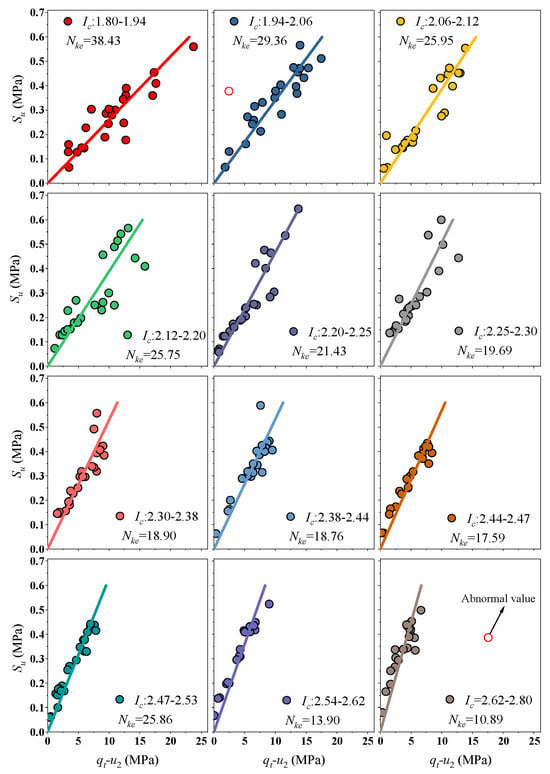
Figure 8. N_ke corresponding to different intervals of I_c at site A.

To further probe the functional relation between I_c and N_kt/N_ke, the regression analysis was performed on the average values of I_c and the empirically obtained N_kt and N_ke within each interval. It can be observed from Figure 9 that R² is greater than 0.97 and a significant nonlinear relation exists between I_c and N_kt/N_ke.

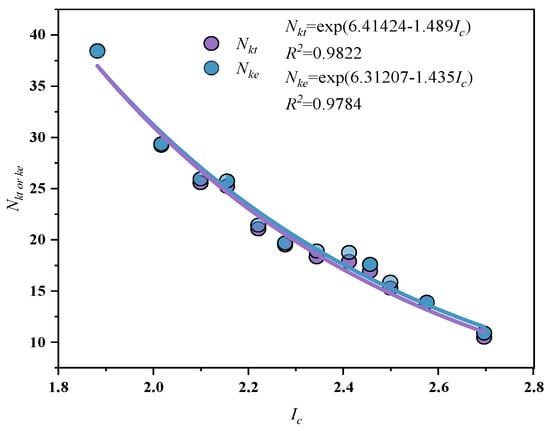
Figure 9. Relation between N_kt/N_ke and I_c at site A.

As presented in Figure 9, a new computational formula for estimating cone factors (N_kt, N_ke) can be provided as:

$$S_u=\frac{q_t-{\sigma }_v}{N_{kt}}$$

(8)

in which:

$$N_{kt}=\exp \left(6.41424-1.489I_c\right)\begin{array}{cc},& 1.8\le I_c\le 2.8\end{array}$$

(9)

$$S_u=\frac{q_t-u_2}{N_{ke}}$$

(10)

in which:

$$N_{ke}=\exp \left(6.31207-1.435I_c\right)\begin{array}{cc},& 1.8\le I_c\le 2.8\end{array}$$

(11)

According to Equation (9), the average value of N_kt in the soil behavior type index I_c range of 1.8 to 2.8 is 21.76, which is close to the statistical average value of 17.9 obtained by the consolidated quick direct shear test specified in the Technical Code for Static Penetration Test in Water Transportation Engineering of China [21]. According to Table 2, the study involved various types and numbers of soil layers. However, the lack of clay layers may result in an overestimation of the calculated value of N_kt in the formula. Furthermore, research conducted in the marine areas near Hangzhou Bay, Hangzhou City, Zhejiang Province, China, indicates that the consolidated quick direct shear tests conducted in this region yielded an overall average value of 20.25 for the cone tip factor (N_kt) in terms of undrained shear strength [36]. This further corroborates the reliability of the formula in the marine areas adjacent to Zhejiang Province, China.

Three statistical criteria (coefficient of determination R², root mean square error RMSE, and mean absolute error MAE) are utilized to evaluate the proposed predictive model. The calculation formulas are as follows:

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n(L_i-E_i)}}{{\displaystyle \sum _{i=1}^n{(L_i-\overline{E})}^2}}$$

(12)

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^{\mathrm{n}}{(L_i-E_i)}^2}}{n}}$$

(13)

$$MAE=\frac{{\displaystyle \sum _{i=1}^{\mathrm{n}}{\left(L_i-E_i\right)}^2}}{n}$$

(14)

where L_i represents the undrained shear strength obtained from consolidated quick direct shear test; E_i represents the undrained shear strength predicted from CPTU results. The closer R² is to 1, the better the model’s predictive performance. A smaller RMSE or MAE indicates better predictive performance of the model.

The cone factor values are not fixed and exhibit significant variation, making it challenging to obtain precise values for the undrained shear strength of soil. In practical engineering, traditional approaches often involve using maximum and minimum cone values of N_kt and N_ke, or directly employing empirical values specific to the region, to calculate the undrained shear strength of soil. To compare the traditional method with the new method proposed in the study, minimum errors for cone factors (N_kt = 20.97 and N_ke = 20.51) were determined using linear regression according to the “total” cone tip resistance method and effective cone resistance method, as shown in Figure 10a,b. In Figure 10c,d, cone factors N_kt and N_ke were calculated using Equations (9) and (11). By comparing Figure 10a–d, it is found that when considering the correlation between soil behavior type index and cone factors, the three predicted indicators (R², RMSE, MAE) show marked improvement. For instance, R² corresponding to N_kt (N_ke) increases from 0.09 (0.05) to 0.81 (0.78), respectively. RMSE corresponding to N_kt (N_ke) decreases from 0.124 (0.126) MPa to 0.056 (0.06) MPa, respectively. MAE corresponding to N_kt (N_ke) decreases from 0.0154 (0.016) MPa to 0.0032 (0.0036) MPa, respectively. The evaluated results show that considering the correlation between the soil behavior type index and cone factor can improve the prediction accuracy of undrained shear strength from CPTU.

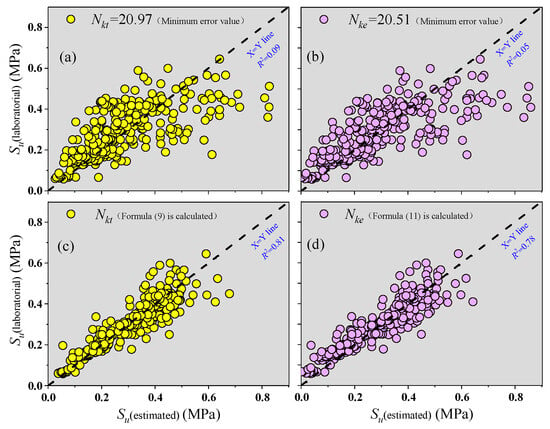
Figure 10. Predictions using traditional N_kt and N_ke methods in (a,b); predictions using the newly proposed N_kt and N_ke methods in (c,d).

An analysis of the CPTU test result plots in Figure 4 is presented to compare the difference between the traditional method and the new method, which incorporates the soil behavior type index in predicting the distribution of undrained shear strength along the depth direction. In the conventional method, the values of cone factors were kept the same as in the previous section, i.e., N_kt = 20.97 and N_ke = 20.51. Table 4 shows the soil cone factors obtained from the soil behavior type index. It is evident from Figure 11 that the undrained shear strength calculated using Equations (8) and (10) proposed in this study consistently has a smaller error than the conventional method. This indicates that the method incorporating the soil behavior type index has significant advantages in terms of prediction accuracy.

Table 4. Soil layer cone factor estimation.

Soil Number	Soil Depth (m)	Nkt	Nke
1	27.5	13.23	15.17
2	30	46.05	50.47
3	40.5	15.2	17.34
4	41.7	30.67	34.11
5	44.5	22.36	25.16
6	48.3	26.28	29.39
7	57	11.93	13.73
8	68.2	15.75	17.94
9	69.7	26.69	29.83
10	70.9	17.27	19.61
11	78	24.96	27.97
12	81.2	27.1	30.27
13	86.2	9.4	10.91
14	91	23.97	26.9
15	93.52	13.48	15.45

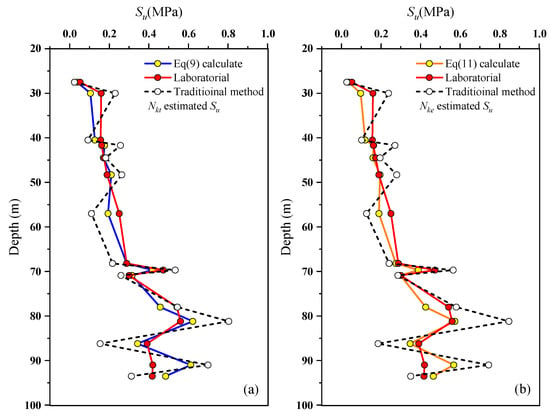
Figure 11. S_u forecasts along the depth direction ((a) with N_kt; (b) with N_ke).

To further validate the reliability of the proposed method, site B was predicted and analyzed. Soil layer data were divided into four groups with 19 data in each group. According to Equation (8), the undrained shear strength of 76 soil layers at site B within the range of the soil behavior index [2.20, 2.8] (see Figure 12) was predicted.

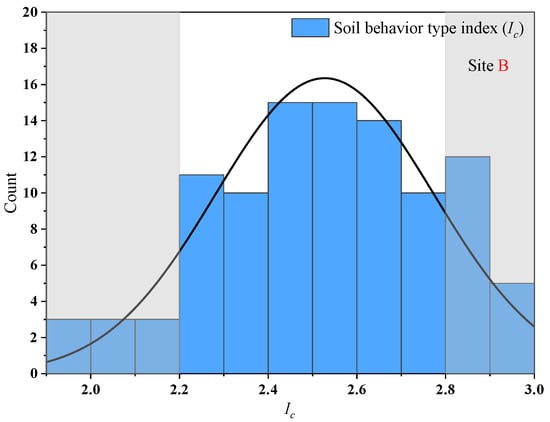
Figure 12. Histogram of I_c at site B.

Table 5 presents the evaluation results of the predicted values. It is evident that the precision of undrained shear strength prediction improves with the increase in I_c. Specifically, as I_c increases, the R² value rises while RMSE and MAE decrease accordingly. Figure 13 illustrates the predicted results for all soil layers, showing an R² value of 0.88, an RMSE of 0.0042 MPa, and an MAE of 0.0018 MPa. These results indicate that this method can effectively predict the undrained shear strength for the experimental site B. It should be noted that the data used in this study are from coastal areas near Zhejiang Province, China. Therefore, it is recommended to use Equations (8) and (10) under similar circumstances.

Table 5. Predicted accuracy of S_u corresponding to different intervals of I_c.

Ic	R2	RMSE (MPa)	MAE (MPa)
2.20–2.37	0.79	0.0595	0.0035
2.38–2.51	0.84	0.0443	0.0019
2.51–2.62	0.92	0.0342	0.0011
2.63–2.80	0.94	0.0318	0.0010
2.20–2.80	0.88	0.0042	0.0018

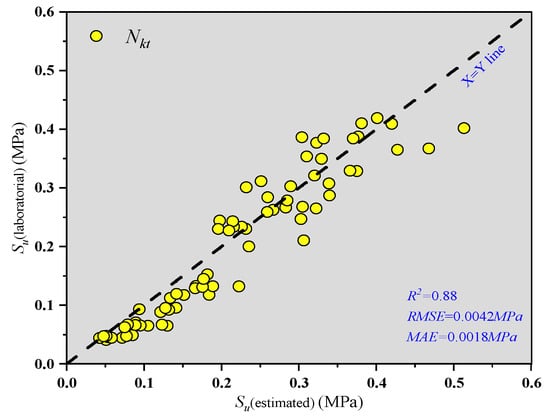
Figure 13. Analyzing the disparity between predicted and estimated values at site B.

4. Conclusions

This study aimed to improve the accuracy in predicting the undrained shear strength of fine-grained soil from CPTU. A new method for estimating the undrained shear strength of soil based on the soil behavior type index was proposed through in situ CPTU testing and an indoor consolidated quick direct shear test at one coastal area of Zhejiang Province in China. Then, a nearby site was selected to verify the accuracy and reliability of the developed method. The following conclusions were obtained:

• The soil behavior type index I_c exhibits a negatively correlated exponential relation with the cone factors N_kt, N_ke.
• Considering the correlation between cone factors N_kt, N_ke and the soil behavior type index I_c can enhance the prediction accuracy of undrained shear strength.
• As I_c increases, the predicted accuracy of undrained shear strength from CPTU can be improved.
• The functional relation between I_c and the N_kt can be applied to the adjacent regions of Zhejiang Province in China.