Risk Coupling Assessment of Vehicle Scheduling for Shipyard in a Complicated Road Environment

Abstract

Vehicle scheduling at shipyards can involve delays due to numerous risk factors encountered in the complicated shipyard road environment. This paper studies the problems of risk coupling in shipyard vehicle scheduling based on the risk matrix approach, considering the complicated road environment, assessing the degrees of coupling and disorder. Based on safety-engineering theory and comprehensive analysis of the road environment, four key criteria are identified, vehicles, the road environment, the working environment, and humans, including 12 factors and their specific contents. The degree of coupling between various combinations of risk criteria is quantitatively determined utilizing the N-K model. Additionally, the degree of disorder in the risk criteria is assessed based on information entropy theory. The model’s correction coefficients are determined through comparative analysis of experimental data. By integrating the degree of coupling and disorder, delays caused by different combinations of risk criteria in scheduling tasks are computed. The quantitative evaluation model enables accurate appraisal of risk events during shipyard vehicle scheduling. The model provides a valuable managerial tool to analyze delays caused when specific risk criteria are met and to compare these delays to the potential impact on time resulting from adjusting vehicle scheduling plans. This research has significant implications for enhancing vehicle distribution efficiency in shipyards.

1. Introduction

Large cruisers manufactured in shipyards are custom-designed and constructed, and their reliance on standardized components is significantly lower than that of automobiles built in factories. Furthermore, a substantial proportion of the hull components used in shipbuilding requires individualized processing within shipyards. Additionally, owing to the generally non-mechanical nature of ship construction, extensive labor is required, which poses significant challenges in terms of material management. The construction of large cruise ships entails a vast number of components, estimated at tens of millions [1,2]. For example, Adora Magic City, currently under construction in China, comprises 503 thin-plate structural segments and requires the assembly of approximately 25 million individual parts. Given the number and magnitude of these components, efficient and precise vehicle scheduling for shipyards (VSS) is crucial. The coordination and management of VSS, which encompasses various stages, are typically undertaken by the companies themselves. This involves the organization of fleets and establishment of distribution routes [3]. Although this approach to distribution offers benefits in terms of centralized management and increased operational efficiency, it also features drawbacks such as substantial investment requirements, diminished flexibility, and elevated risk levels.

Typically, for materials of great significance, a reliable logistics distribution service is essential. It is crucial that such goods are transported without any damage or deterioration, because such occurrences could result in the loss of the goods’ original properties, leading to the failure in meeting production-plan requirements [4]. Furthermore, timely delivery in accordance with production schedules is paramount to ensure that materials are not delivered prematurely or delayed [5,6]. When considering various logistics and distribution modes, it is important to note that the higher the number of handling, loading, and unloading processes during transit, the greater the likelihood of cargo damage. Similarly, a large number of intermediate links within the logistics mode introduces greater uncertainty regarding the timing of deliveries [7]. This uncertainty encompasses various risk events, including those related to vehicles, road conditions, working environments, and human factors, which can have a detrimental impact on vehicle scheduling [8]. Furthermore, these effects are often inadequately assessed, leading to a lack of effective managerial responses to these risk factors. To effectively assess the impact of these risk factors on vehicle scheduling, in the context of the complicated shipyard road environment, this paper studies the problems of risk coupling in the context of VSS.

Vehicles within shipyards comprise both motorized and non-motorized vehicles. Furthermore, it is important to note the presence of pedestrians on roadways. Motorized vehicles are categorized into production vehicles and non-production vehicles. There are seven types of production vehicle, including flatbed trucks, aerial trucks, forklifts, tractor trucks, car cranes, trucks, and battery forklifts [9]. Non-production vehicles are divided into commuter cars, private cars, and commercial vehicles. Owing to the substantial and intensive nature of production tasks within shipyards, both motorized vehicles and non-motorized vehicles are frequently used on shipyard roads during working days. The intersection of various vehicles on shipyards is characterized by a high level of complexity, which distinguishes such roads from environments in public areas. Moreover, shipyard roads are assigned managers who are responsible for their supervision and management. The specific nature of vehicular movement within shipyards involves a higher frequency of overtaking maneuvers, placing a greater emphasis on drivers’ situational awareness compared with that in public areas despite the fact that, overall, the speeds at which vehicles travel in these areas is lower than on regular roads. This latter factor also contributes to vehicular congestion within shipyard environments. In the shipyard, the bicycle is the predominant non-motorized vehicle and provides a high level of convenience. However, conflicts frequently occur between non-motorized and motorized vehicles, particularly in areas where roads are narrow. The large volume of bicycles occupying non-motorized vehicle lanes frequently results in traffic congestion and encroachment into motorized-vehicle lanes. This leads to lane-changing and overtaking maneuvers between bicycles and motorized vehicles that ultimately reduce the capacity of motorized-vehicle lanes. Shipyard roads also include pedestrian pathways and sidewalks, which pedestrians navigate in a random manner, often moving in multiple directions. In the presence of pedestrians on sidewalks, motorized vehicles are often required to take evasive measures to ensure a safe driving environment. However, these circumstances require adaptations in the distribution efficiency. Additionally, the distinctions between shipyard vehicles and typical road vehicles extend to specialized flatbed trucks used for transporting medium-sized ship products (Figure 1). Given the considerable dimensions of these products, flatbed trucks occupy multiple lanes during their operation. As a result, other vehicles are required to yield way, often leading to notable scheduling delays. Consequently, the shipyard road environment is often chaotic owing to the diverse array of vehicle types, compounded by the presence of pedestrians.

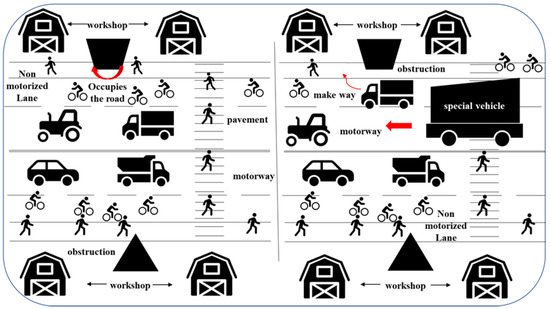
Figure 1. Road environment of shipyard.

Another contributing factor in the complexity and disorderliness of shipyard roads is the existence of workshops. These workshops, each with specific functionalities, are located on both sides of shipyard roads [10]. During their operational phases, the workshops produce various levels of noise, which has a significant impact on drivers’ and marshals’ attentiveness [11]. Furthermore, ship segments are occasionally temporarily placed on the roads, which reduces the available driving space and exacerbates disorderly road environments, with pedestrians and bicycles further restricting the flow of motorized traffic (Figure 1).

In this study, the N-K model is utilized to quantify the degree of coupling among risk factors, while information entropy theory is applied to assess the level of road congestion during scheduling. Subsequently, the two models are integrated to establish a quantitative model that calculates the degree of impact of risk factors. The contributions of this study are threefold: (1) the formation mechanism of vehicle distribution risk for shipyards is formulated based on the characteristics of shipyard roadways; (2) an innovative risk assessment model combining the N-K model and information entropy theory is developed to quantitatively evaluate the duration of delays of vehicle delivery caused by risk factors; and (3) the duration of delays is added, which is the sum of the degree of coupling and the degree of disorder.

Literature Review

Researchers investigating transportation risk predominantly utilize mathematical models and methodologies to quantitatively determine the probability and magnitude of the impact of risks. These models are applied to provide guidance to decision makers or managers regarding the implementation of necessary safety measures [12]. Since it was first proposed in 1970, the quantitative risk assessment method has been extended to the transportation industry [13,14]. However, given transportation studies in shipyards are uncommon, the research reviewed in this paper includes transportation studies in other industries. In general, quantitative risk studies focus on the following: (a) calculation of the probability of risk (CPR) [15,16,17]; (b) calculation of the risk-impact level (CRIL) [18,19]; (c) the combined model of risk probability and impact level (CMRPIL) [20,21,22]; and (d) the improvement in risk models (IRM) [23,24]. This section of this paper is devoted to a review of the literature on CMRPIL and IRM.

CMRPIL and IRM have been widely used in many areas, such as sustainable integrated logistics and the transportation industry. Yang et al. [25] propose a risk diffusion model integrating a motion mechanism to implement multiple-granularity traffic risk evaluation. Shankar et al. [26] proposed an integrated risk-assessment model based on intuitionistic fuzzy set theory and D-number theory to assess risk in freight-transportation systems. Karatzetzou et al. [27] used the multi-hazard risk-assessment model to analyze probabilities in transportation networks, while Chakrabarti and Parikh [28] evaluated risk in hazmat transportation using the HAZAN methodology. Additionally, Yang et al. [29] innovatively develop Non-Negative Matrix Factorization (NMF) to explore the quantitative risk under the coupling of multiple risk factors for traffic safety evaluation. Finally, Ambituuni et al. [30] developed a framework for regulatory improvement to assess risk in the context of transportation by road. These risk studies are based on the definition of risk as a combination of the probability of the risk factors being encountered and the consequences thereof. The process of the calculation of risk can be defined as the quantification of risk index in the arithmetic pattern other than logic implication as follows [31]: Risk = Severity × Probability. Probability and severity have different definitions depending on the object of study. The calculation of risk probabilities and severity in many studies is based on expert knowledge, leading to subjective results. Extant studies have focused more on the influence of risk in distribution processes and rarely examine the influence of the impact on tasks; furthermore, they rarely analyze risk factors based on the road environment. In the actual road environment, not all risk factors are encountered throughout; therefore, the impact of different combinations of risk factors on the distribution tasks needs to be considered.

2. Materials and Methods

The proposed integrated assessment model is implemented to quantitatively assess the risk in VSS. A flowchart of the risk coupling analysis of VSS is shown in Figure 2. Once the assessment criteria and factors are identified, the number of risk factors resulting from each criterion over a period of time can be counted. Using these data, we calculate the degree of coupling of risk criteria based on the N-K model. Based on the combination probability calculated in the N-K model, the confusability of the combined risk factors can be calculated based on information entropy theory. Next, the correction coefficient $\epsilon$ is calculated to obtain the final quantitative evaluation model. Finally, the model is used to evaluate delays in VSS.

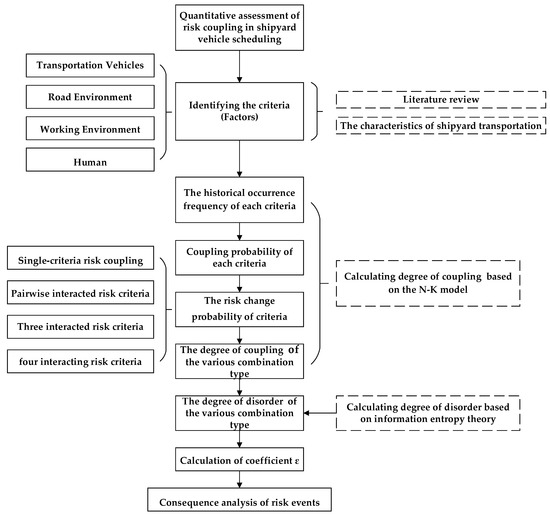
Figure 2. Flowchart of assessment of risk coupling in shipyard vehicle scheduling.

2.1. Hybrid Risk Coupling Model Based on Risk Matrix Approach

The formula for the combined risk coupling model proposed is based on the risk matrix approach [31], which is considered a combination of the severity of the consequences S and their probability P [32]. In this article, vehicle scheduling risk for shipyards is defined based on the combination of risk criteria that cause delays in scheduling tasks.

Through comprehensive analysis of shipyard road environments, distinct characteristics of VSS can be identified, leading to the formulation of the following definitions:

Definition 1.

Complexity represents the extent of the intricate interrelationships or associations observed between diverse types of criteria, denoted as the degree of coupling, C(x).

Definition 2.

Disorderliness encompasses the intricacy or complexity inherent in the operational environment of a vehicle, notably including the road and work surroundings. Disorderliness is designated as the degree of disorder, H(x).

The risk of delays arising from vehicle scheduling tasks cannot be solely attributed to the cumulative delays resulting from various risk criteria. Rather, the risk is intricately linked to the interplay between various risk criteria and road characteristics. In this paper, we add the result of risk, H, which is the sum of the degree of coupling and the degree of disorder.

Hence, we propose Equation (1) as a means of assessing the delays associated with diverse combinations of risk criteria. Equation (1) contains the form of the combination of different risk criteria and the quantitative characteristics of shipyard roads. In Equation (1), S is the total delay of the risk criteria; T_car represents the average delays resulting from inherent risk conditions specific to the vehicle; T_road denotes the average delays caused by risk conditions pertaining to the road; T_work signifies the mean delays attributed to environmental influencing vehicles; T_other represents the temporal influence exerted by additional risk criteria, including pedestrian-related criteria; T_s denotes the long-term repercussions, such as noise-related effects, of work activities that generate noise; and $\mathsf{\epsilon }$ represents the correction coefficient.

This paper increases the weight of the degree of coupling and the degree of disorder. The formula is not only a simple summation of the degree of coupling and disorder, because the calculation of the degree of disorder utilizes the probability of the degree of coupling. Finally, we modify the model as follows:

$$\mathrm{S}=\mathrm{H}\times \mathrm{I}$$

(1)

where $\mathrm{I}={\mathrm{T}}_{\mathrm{Car}}\times \mathrm{a}+{\mathrm{T}}_{\mathrm{road}}\times \mathrm{b}+{\mathrm{T}}_{\mathrm{work}}\times \mathrm{c}+{\mathrm{T}}_{\mathrm{other}}\times \mathrm{d}+{\mathrm{T}}_{\mathrm{s}}$, representing the average delay caused by the combination of risk factors. $\mathrm{H}=w_1\times \mathrm{C}\left(\mathrm{x}\right)+w_2\times \mathrm{H}\left(\mathrm{x}\right)+\epsilon$, $w_1+w_2=1$, and $\mathrm{H}\in [0,1]$, indicating the characteristics of the transportation environment that influence vehicle distribution.

This is subject to

$$0\le \mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\le 4$$

(2)

$$\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}=\left\{\begin{array}{l}1,\mathrm{if}\mathrm{combination}\\ 0,\mathrm{Otherwise}.\end{array}\right.$$

(3)

Equations (2) and (3) represent combinations of criteria, with a maximum of three and a minimum of no combinations of the various criteria occurring.

The relationship between the models is illustrated in Figure 3. The N-K model calculates the probability values of risk factors for different combinations, which can be applied to the calculation of the coupling values and to information entropy theory. Information entropy theory can be used to calculate the confusion value of the portfolio risk factors, which should be applied to the probability values. Section 2.2 and Section 2.3 introduce the N-K model and information entropy theory, respectively.

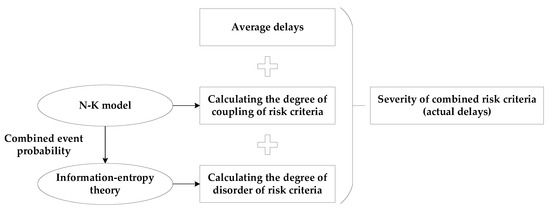
Figure 3. Relationship between models.

2.2. Calculating the Degree of Coupling of Risk Criteria Based on the N-K Model

The N-K model, which was originally proposed based on fitness-landscape theory to study the evolution of organisms, has good generalizability in solving complex problems [33]. Many studies quantify risk-causing coupling based on objective accident data [34]. The N-K model contains two important parameters, where N represents the number of subsystems that make up the system, such that when there are n kinds of states in the subsystem, the number of states in the system is n^N, while K represents the number of interdependencies in each subsystem in the system’s relationship network and determines the magnitude of the system’s adaptation. In this study, N is the number of risk criteria, and K represents the number of interacting risk criteria. n has two states, where “0” indicates the non-occurrence of a risk factor, “1” represents the occurrence of a risk factor, and “.” designates that the state is not constrained, “0” or “1”. The N-K model is calculated as follows:

$$\mathrm{C}({\mathrm{X}}_{\mathrm{n}})={\displaystyle \sum _{{\mathrm{x}}_1=1}^{{\mathrm{H}}_1}{\displaystyle \sum _{{\mathrm{x}}_2=1}^{{\mathrm{H}}_2}{\displaystyle \sum _{\cdots }^{\cdots }{\displaystyle \sum _{{\mathrm{x}}_n=1}^{{\mathrm{H}}_n}{\mathrm{P}}_{{\mathrm{x}}_1{\mathrm{x}}_2\cdots {\mathrm{x}}_{\mathrm{n}}}•{\log }_2{(\mathrm{P}}_{{\mathrm{x}}_1{\mathrm{x}}_2{\mathrm{Lx}}_{\mathrm{n}}}{/(\mathrm{P}}_{x_1\cdot \cdot \cdot }{\mathrm{P}}_{\cdot {\mathrm{x}}_2\cdot \cdot }\cdots {\mathrm{P}}_{\cdot \cdot \cdot {\mathrm{x}}_{\mathrm{n}}}))}}}}$$

(4)

where x₁ = (1, 2, …, H₁); x₂ = (1, 2, …, H₂); x_n = (1, 2, …, H_n); P_x1x2…xn represents the probability of the coupling of different criteria occurring in state x_i; (x₁, x₂, …, x_n) $\in$ x, P_x1, P_•x2, …, P_•••xn indicates the sum of the probability of the occurrence of n standard couplings when the standard is in the state x_i; and C(X_n) denotes the degree of coupling under criteria n.

2.3. Calculating the Degree of Disorder of Risk Criteria Based on Information Entropy Theory

The information measure is the information created by a specific event that has occurred, while the entropy measure refers to the amount of information that can be expected to be generated before the result is known [35]. Entropy considers all possible values of the random variable and is the amount of information that can be expected to result from all possible events. Information can be understood as the probability of occurrence of a particular kind of information (i.e., the probability of the occurrence of discrete random events). In systems with high levels of order, the information entropy tends to be lower, whereas in systems characterized by increased chaos, information entropy tends to be higher [13]. Information entropy can be considered a quantitative measure of the level of organization, or order, within a system. In this paper, information entropy is used to determine the degree of disorder in various combinations of risk criteria.

$$\mathrm{H}\left(\mathrm{x}\right)=-{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}(\mathrm{x}}_{\mathrm{i}}{\left)\log \right(\mathrm{p}(\mathrm{x}}_{\mathrm{i}}\left)\right)}$$

(5)

where p(x_i) denotes the probability of occurrence of event x_i, and H(x) is the degree of confusion in event x_i. In this paper, because p(x_i) represents the probability of the combined events, we calculate it as follows:

$${\mathrm{p}\left(\mathrm{x}\right)=\mathrm{p}(\mathrm{x}}_1{\mathrm{x}}_2\cdots {\mathrm{x}}_{\mathrm{n}})=\mathrm{p}(\stackrel{-}{{\mathrm{x}}_1{\mathrm{x}}_2\cdots {\mathrm{x}}_{\mathrm{n}}}){\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}(\mathrm{x}}_1{\left)\mathrm{p}\right(\mathrm{x}}_2)\cdots {\mathrm{p}(\mathrm{x}}_{\mathrm{n}})}$$

(6)

where p(x₁x_2…x_n) is the probability of the combined event (x₁x_2…x_n) and $\mathrm{p}(\overline{{\mathrm{x}}_1{\mathrm{x}}_2{\mathrm{Lx}}_{\mathrm{n}}})$ is the probability of the occurrence of all events. Then, H(x) is calculated as follows:

$$\mathrm{H}\left(\mathrm{x}\right)=-{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{p}(\overline{{\mathrm{x}}_1{\mathrm{x}}_2\cdots {\mathrm{x}}_{\mathrm{n}}}){\displaystyle \prod _{i=1}^{\mathrm{n}}{\mathrm{p}(\mathrm{x}}_1{\left)\mathrm{p}\right(\mathrm{x}}_2)\cdots {\mathrm{p}(\mathrm{x}}_{\mathrm{n}})}\log (\mathrm{p}(\overline{{\mathrm{x}}_1{\mathrm{x}}_2\cdots {\mathrm{x}}_{\mathrm{n}}}){\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}(\mathrm{x}}_1{\left)\mathrm{p}\right(\mathrm{x}}_2)\cdots {\mathrm{p}(\mathrm{x}}_{\mathrm{n}})})}$$

(7)

3. Analysis of the Criteria and Factors for Risk Events in VSS

In safety engineering theory, risks can be classified into the following criteria: human, machine, materials, environment, and management [36]. Since shipyard vehicle transportation processes do not involve dangerous materials or management failures, we have limited our assessment to the following criteria: machine, environment, and human. In this paper, the term “machine” pertains to the failure of a vehicle. Huang et al. [36] define environment as bad weather and the condition of the roads. However, as evidenced by the comprehensive analysis presented in Section 1, the shipyard environment exhibits a profound level of complexity. Therefore, this paper meticulously divides the environment into distinct categories, encompassing both the road environment and the working environment. The road environment is defined as the presence of risk factors on the road, including other vehicles, pedestrians [37], and obstacles. The working environment is defined as encompassing bad weather conditions [38] and risk factors emanating from other work activities, particularly noise in this paper. Drivers who perform frequent high-risk events (e.g., hard braking maneuvers) pose a significant threat to traffic [39]. The present study classifies these high-risk event attributes as human.

To investigate the factors that contribute to delays, we also conducted a survey of workstations and engaged in consultations with twelve workers, five of whom possessed a decade of experience and seven who had accrued no more than five years of expertise. Eventually, we summarize the information pertaining to these criteria as follows.

Vehicle: Vehicles play a considerable role in scheduling tasks. Because shipyard materials vary significantly in type and volume, it is difficult to transport them using manpower alone. Therefore, vehicles are the main carriers in shipyard material distribution. Table 1 shows the details of some risk events encountered during the distribution of vehicles. The Internet of Vehicles (IOV) is a system used by the shipyard to track and record incidents involving vehicles. Column 4 shows the shipyard’s documentation of factors that pose a risk to vehicle operations in the IOV. Based on the IOV, we identified six types of vehicle-related risks that cause delays in scheduling tasks: maintenance, oil leakage, tank, steering arm, tire, and network. We counted the number of vehicle-related risk events resulting from each factor and from multiple factors. According to our investigation, these factors resulted in an average delay of 30 min for scheduling tasks.

Table 1. Vehicle scheduling risk events according to Internet of Vehicles.

No.	Incidents	Maintenance Cycle	Type	Delay Time (min)
1	Equipment failure	9 h and 20 min	Maintenance	31
2	Maintenance	1 days and 40 min	Maintenance	32
3	Oil pipe bursting	23 h and 15 min	Oil leakage	30
4	Maintenance	7 h and 52 min	Maintenance	26
5	Repairing water tanks	5 days, 7 h and 45 min	Tank	30
6	High water temperature	5 days, 23 h and 10 min	Tank	35
7	Loss of steering	6 h and 45 min	Steering arm	30
8	Loss of steering	2 days, 7 h and 32 min	Steering arm	26
9	Loss of steering	7 h and 51 min	Steering arm	28
10	Maintenance of air conditioners	59 min	Maintenance	27
11	Replacement parts	18 h and 44 min	Maintenance	28
12	Flat tire	12 h and 43 min	Steering arm	29
13	Oil leakage from cylinder	3 days, 21 h and 11 min	Oil leakage	32
14	Maintenance	5 h and 54 min	Maintenance	32
15	Oil leakage from cylinder	2 days, 12 h and 2 min	Oil leakage	34
16	No signal	9 h and 59 min	Network	30

Road Environment: Shipyard roads carry vehicles and therefore feature different kinds of vehicles and obstacles to public roads. In shipyard roads, target vehicles are significantly influenced by the other vehicles present on the road during scheduling tasks. Obstacles and pedestrians can further narrow the road, which can lead to additional task delays, as shown in Table 2. Therefore, we identify other vehicles and obstacles as the factors of road environment. These two factors exert a significant influence on the extension of the duration of a task, resulting in delays of approximately 15 min.

Table 2. Road environment distribution risk events.

No.	Incidents	Type	Delay Time (min)
1	Congestion caused by other vehicles	Other vehicles	10
2	Congestion caused by pedestrians	Pedestrians	10
3	Congestion caused by obstacles	Obstructions	14
4	Congestion caused by other vehicles	Other vehicles	20
5	Congestion caused by other vehicles	Other vehicles	18
6	Congestion caused by other vehicles	Other vehicles	20
7	Congestion caused by obstacles	Obstructions	13
8	Congestion caused by obstacles	Obstructions	14
9	Congestion caused by pedestrians	Pedestrians	15
10	Congestion caused by pedestrians	Pedestrians	16

Working Environment: The factors of the working environment include noise and unfavorable weather. In Equation (1), T_s is defined as a long impact time, with a duration of persistence as long as the working day. Noise, serving as a significant risk factor, has a persistent presence throughout the working environment, encompassing sounds emanating from vehicles, workers, and other sources. This noise can potentially impact workers’ concentration levels and the dissemination of critical information. Noise is therefore classified as T_s, which affects the delay tasks by 5 min. Changes in climate can also affect transportation systems. Because shipyards are built beside the sea, unfavorable weather can occur, mainly in the form of wind or rain, which increases delays in the completion of tasks by 15 min, as shown in Table 3.

Table 3. Working environment distribution risk events.

No.	Incidents	Type	Delay Time (min)
1	Noise from the workplace	Noise	4
2	Drizzle	Bad weather	10
3	Heavy rain	Bad weather	18
4	Gale	Bad weather	20
5	Noise from the workplace	Noise	7
6	Heavy rain	Bad weather	15
7	frigid weather	Bad weather	13
8	Noise from the workplace	Noise	5
9	Hot weather	Bad weather	13
10	Gale	Bad weather	16

Human: In a shipyard road, many uncertainties in human behavior can affect driving. Human behavior is complex and variable, and therefore we do not attempt to categorize it here. Human does not belong to T_s, and this delays tasks by 15 min.

By analyzing the four types of risk factors, this paper determines the inputs and outputs of information and the average delay time of each criterion in a risk event, as shown in Table 4.

Table 4. The details of attributes of different risk criteria in VSS.

Risk Criteria	Input	Output	Average Time (min)
Vehicle (C)	Maintenance	Vehicle needs replacement parts and maintenance	30
	Oil leakage	Damage to the vehicle’s oil pipes or oil cylinders and other equipment, resulting in oil leakage from the vehicle	30
	Tank	The water temperature of the vehicle’s water tank is excessively high, or the water pump is abnormal	30
	Steering arm	The vehicle’s steering appears abnormal or its rocker arm breaks	30
	Tire	One or more of the tires on the vehicle are flat or runaway	30
	Network	There is no signal in the car network	30
Road Environment (R)	Other vehicles	Other vehicles on the road impact scheduling	15
	Obstructions	Space in the shipyard is limited and many blocks are placed on the roadside, which affects driving behavior	15
	Pedestrians	Congestion caused by pedestrians	15
Working Environment (W)	Noise	There are various workshops in the shipyard, which generate significant noise and can affect drivers and pilots	5
	Bad weather	This mainly refers to the impact of unfavorable weather, such as wind and rain, on traffic and staff	15
Human (H)	Human behavior	There are many uncertainties in human behavior that can affect driving	15

4. Analysis of Coupling of Risk Criteria in VSS

4.1. Definition of Risk Criteria Coupling in VSS

In physics, the interaction of two or more individuals or forms of motion is called “coupling”. Risk coupling is the phenomenon whereby interactions between factors within a system produce changes in the stability and risk level of the system. In a system, risk coupling is the result of nonlinear interactions between factors and can be viewed as a part of the system. Therefore, the interaction of vehicles, the road environment, the working environment, and humans in the vehicle distribution process is analyzed qualitatively from the perspective of risk criteria coupling in VSS.

We identify the historical frequency of occurrence of vehicles (C), the road environment (R), bad weather (W), and human errors (H), as well as the coupling between these risk criteria, in the quantitative assessment model mentioned above. Thereafter, we calculate the coupling probability. We use N_{c, r, w, h}, c $\in$ {0, 1}, r $\in$ {0, 1}, w $\in$ {0, 1}, and h $\in$ {0, 1} to represent the historical occurrence frequency and P_{c, r, w, h}, N_{c, r, w, h}, c $\in$ {0, 1}, r $\in$ {0, 1}, w $\in$ {0, 1}, and h $\in$ {0, 1} to denote the probability of coupling of each criterion, where C is in state c, R is in state r, W is in state w, and H is in state h.

4.2. Definition of Risk Criteria Coupling in VSS

Figure 4 illustrates the coupling mechanism of the VSS system. Based on the number of different categories of risk criteria involved in the coupling, the risk coupling of the VSS system can be divided into four categories, including single-criteria risk coupling, pairwise-interacting risk criteria, three-interacting risk criteria, and four-interacting risk criteria. The coupling values can change as the number of criteria in the combination increases.

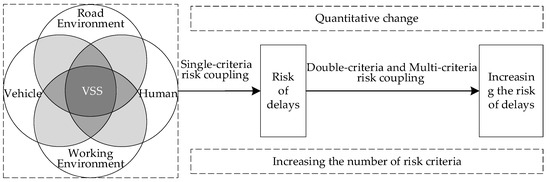
Figure 4. The coupling mechanism of the VSS system.

(1) Single-criteria risk coupling

Single-criteria risk coupling refers to the risk arising from the interaction between risk criteria within a certain category of criteria, whose coupled action risk causes an increase in the level of systemic risk. The total coupling value is expressed by P_c (Vehicle), P_r (Road Environment), P_w (Working Environment), and P_h (Human).

(2) Pairwise-interacting risk criteria

Pairwise-interacting risk criteria refer to the interaction of two categories of risk criteria that affect the safety of VSS. P_{c, r}, P_{c, w}, P_{c, h}, P_{r, h}, P_{r, w}, and P_{w, h} show the risk change value of double-criteria risk coupling in each state. For example, P_{c, r} denotes the combination of Vehicle and Road Environment.

(3) Three-interacting risk criteria

Three-interacting risk criteria refer to the interaction of three categories of risk criteria that affect the safety of VSS. The total coupling value is expressed by P_{c, r, h}, P_{c, r, w}, P_{c, w, h}, and P_{r, w, h}. For example, P_{c, r, h} denotes the combination of Vehicle, Road Environment, and Human.

(4) Four-interacting risk criteria

Four-interacting risk criteria refer to the interaction of four categories of risk criteria that affect the safety of VSS. The total coupling value is expressed by P_{c, r, w, h}, which denotes the combination of all criteria.

5. Case Application and Results

5.1. Risk Database

In this study, the selected target vehicle for the shipyard is the flatbed truck. Using this type of vehicle, we investigate 288 delays caused by risk factors of a shipyard in Shanghai in 2022, as shown in Table 5. We divide the criteria of Vehicle and Road Environment into different categories and conduct a statistical analysis of the frequency of occurrence of delay risk for each factor. Owing to the extensive diversity and complexity of the categorization of the working environment and human, we conduct a macroscopic enumeration of the incidence of delayed risks. The frequency levels of the four risk criteria are denoted as 24.66%, 24.20%, 25.11%, and 26.03%, and they exhibit a minimal degree of variance. Within the domain of vehicular criteria, maintenance and steering arm represent a significantly larger proportion of the total. Within the road environment, other vehicles and pedestrians constitute a substantial proportion of the overall total. Noise accounts for a relatively large proportion of the total because of the potential for noise generation from workshops.

Table 5. Delay distribution of risk factors.

Risk Criteria	Factors	Number	Delay Ratio (Proportion of Delays Caused by the Factor)
Vehicle (C)	Maintenance	48	7.31%	24.66%
	Oil leakage	22	3.35%
	Tank	6	0.91%
	Steering arm	43	6.54%
	Tire	32	4.87%
	Network	11	1.67%
Road Environment (R)	Other vehicles	58	8.83%	24.20%
	Obstructions	20	3.04%
	Pedestrians	81	12.33%
Working Environment (W)	Noise	101	15.37%	25.11%
	Bad weather	64	9.74%
Humans (H)	Human behavior	171	26.03%	26.03%

5.2. Analysis of Coupling Value and Disorder Value

The number and frequency of the different criteria are shown in Table 6. For example, N_{c=1,r=0,w=0,h=0} is expressed as the frequency of occurrence of Vehicle only, and ${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}$ = ${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}/{\displaystyle \sum _{\mathrm{i}=0}^1{\displaystyle \sum _{\mathrm{j}=0}^1{\displaystyle \sum _{\mathrm{g}=0}^1{\displaystyle \sum _{\mathrm{h}=0}^1{\mathrm{N}}_{\mathrm{c}=\mathrm{i},\mathrm{r}=\mathrm{j},\mathrm{w}=\mathrm{g},\mathrm{h}=\mathrm{l}}}}}}$.

Table 6. Historical occurrence frequency N_{c, r, w, h} and coupling probability of each criterion P_{c, r, w, h}.

Frequency	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}$ = 0	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}$ = 3	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=0}$ = 15
Probability	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=0}$ = 0	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}$ = 0.0208	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=0}$ = 0.0521
Frequency	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=0}$ = 18	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=1}$ = 12	—
Probability	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=0}$ = 0.0625	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=1}$ = 0.0417	—
Frequency	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=0}$ = 21	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=0}$ = 27	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=1}$ = 18
Probability	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=0}$ = 0.0729	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=0}$ = 0.0938	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=0,\mathrm{h}=1}$ = 0.0625
Frequency	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=0}$ = 9	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=1}$ = 15	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=1}$ = 24
Probability	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=0}$ = 0.0313	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=1}$ = 0.0521	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=1}$ = 0.0833
Frequency	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=0}$ = 21	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=1}$ = 36	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=1}$ = 24
Probability	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=0}$ = 0.0729	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=0,\mathrm{h}=1}$ = 0.125	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=0,\mathrm{w}=1,\mathrm{h}=1}$ = 0.0833
Frequency	${\mathrm{N}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=1}$ = 30	${\mathrm{N}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=1}$ = 12	—
Probability	${\mathrm{P}}_{\mathrm{c}=0,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=1}$ = 0.1042	${\mathrm{P}}_{\mathrm{c}=1,\mathrm{r}=1,\mathrm{w}=1,\mathrm{h}=1}$ = 0.0417	—

Using the data in Table 6, we calculate the probability of a change in risk for the different interaction-risk criteria, as shown in Table 7, Table 8, Table 9 and Table 10. For example, P_c=0 = P_{c=0,r=0,w=0,h=0} + P_{c=0,r=1,w=0,h=0} + P_{c=0,r=0,w=1,h=0} + P_{c=0,r=0,w=0,h=1} + P_{c=0,r=1,w=1,h=0} + P_{c=0,r=1,w=0,h=1} + P_{c=0,r=0,w=1,h=1} + P_{c=0,r=1,w=1,h=1} = 0 + 0.0521 + 0.0625 + 0.0417 + 0.0313 + 0.0521 + 0.0833 + 0.1042 = 0.4272. These results are applied to calculate the degree of coupling C(x) and degree of disorder H(x).

Table 7. Risk-change probabilities for each single-criteria risk coupling.

Type	Pc=0	Pc=1	Pr=0	Pr=1	Pw=0	Pw=1	Ph=0	Ph=1
Probability	0.4272	0.5729	0.4479	0.5522	0.4271	0.573	0.4063	0.5938

Table 8. Risk-change probabilities of the pairwise-interacting risk criteria (PIRC).

Type	Pc=0,r=0	Pc=0,r=1	Pc=1,r=0	Pc=1,r=1	Pr=0,w=0	Pr=1,w=0	Pr=0,w=1	Pr=1,w=1
Probability	0.1875	0.2397	0.2604	0.3125	0.125	0.3021	0.3229	0.2501
Type	Pr=0,h=0	Pr=1,h=0	Pr=0,h=1	Pr=1,h=1	Pw=0,h=0	Pw=1,h=0	Pw=0,h=1	Pw=1,h=1
Probability	0.1771	0.2292	0.2708	0.323	0.1458	0.2605	0.2813	0.3125
Type	Pc=1,h=0	Pc=1,h=1	Pc=0,h=1	Pc=0,h=0	Pc=1,w=0	Pc=1,w=1	Pc=0,w=0	Pc=0,w=1
Probability	0.2604	0.3125	0.2813	0.1459	0.2812	0.2917	0.1459	0.2813

Table 9. Risk-change probabilities of three-interacting risk criteria (TIRC).

Type	Pc=0,r=0,w=0	Pc=1,r=0,w=0	Pc=0,r=1,w=0	Pc=0,r=0,w=1	Pc=1,r=1,w=0	Pc=1,r=0,w=1	Pc=0,r=1,w=1
Probability	0.0417	0.0833	0.1042	0.1458	0.1979	0.1771	0.1355
Type	Pc=1,r=1,w=1	Pr=0,w=0,h=0	Pr=1,w=0,h=0	Pr=0,w=1,h=0	Pr=0,w=0,h=1	Pc=0,r=0,h=0	Pc=1,r=0,h=0
Probability	0.1146	0.0208	0.125	0.1563	0.1042	0.0625	0.1146
Type	Pc=0,r=1,h=0	Pc=0,r=0,h=1	Pc=1,r=1,h=0	Pc=1,r=0,h=1	Pc=0,r=1,h=1	Pc=1,r=1,h=1	Pc=0,w=0,h=0
Probability	0.0834	0.125	0.1458	0.1458	0.1563	0.1667	0.0521
Type	Pc=1,w=0,h=0	Pc=0,w=1,h=0	Pc=0,w=0,h=1	Pc=1,w=1,h=0	Pc=1,w=0,h=1	Pc=0,w=1,h=1	Pc=1,w=1,h=1
Probability	0.0937	0.0938	0.0938	0.1667	0.1875	0.1875	0.125
Type	Pr=1,w=1,h=0	Pr=1,w=0,h=1	Pr=0,w=1,h=1	Pr=1,w=1,h=1
Probability	0.1042	0.1771	0.1666	0.1459

Table 10. Risk-change probabilities of four-interacting risk criteria (FIRC).

Type	Pc=0,r=0,w=0,h=0	Pc=1,r=0,w=0,h=0	Pc=0,r=1,w=0,h=0	Pc=0,r=0,w=1,h=0	Pc=0,r=0,w=0,h=1
Probability	0	0.0208	0.0521	0.0625	0.0417
Type	Pc=1,r=1,w=0,h=0	Pc=0,r=1,w=1,h=0	Pc=0,r=1,w=0,h=1	Pc=0,r=0,w=1,h=1	Pc=1,r=1,w=1,h=0
Probability	0.0729	0.0313	0.0521	0.0833	0.0729
Type	Pc=1,r=1,w=0,h=1	Pc=1,r=0,w=1,h=1	Pc=1,r=0,w=1,h=0	Pc=1,r=0,w=0,h=1	Pc=0,r=1,w=1,h=1
Probability	0.125	0.0833	0.0938	0.0625	0.1042
Type	Pc=1,r=1,w=1,h=1
Probability	0.0417

Applying Equations (1) and (7), we calculate the degree of coupling and the degree of disorder for each combination, respectively, as shown in Table 11. In this paper, based on expert recommendations that both A and B hold equal significance, their respective weights are assigned as 0.5 each. We take the calculated coupling value as the degree of coupling of vehicle distribution. Using Equation (7) and taking the combination of A and B as an example, DC can be calculated by

H(C, R) = −P_c=1log (P_c=1) + (−P_r=1log (P_c=1)) + (−P_{c=1, r=1}log (P_{c=1, r=1})) = 0.1386 + 0.1424 + 0.1579 = 0.4389

Table 11. Values of the various combination types.

Combination Type	C(C, R)	C(C, W)	C(C, H)	C(R, W)	C(R, H)	C(W, H)
C(x)	0.003955	0.001613	0.009267	0.053291	0.000142	0.014472
H(x)	0.4389	0.4329	0.4309	0.4315	0.4353	0.4309
Sum	0.2214	0.2173	0.2201	0.2424	0.2177	0.2227
Combination Type	C(C, R, W)	C(C, R, H)	C(C, W, H)	C(R, W, H)	C(C, R, W, H)
C(x)	0.072486	0.00968	0.036161	0.083253	0.153196
H(x)	0.5274	0.5686	0.548	0.5609	0.6192
Sum	0.2999	0.2891	0.2921	0.3221	0.3862

Figure 5 shows the variation in values for different combinations. Figure 6 shows the summation of DD and DC for different interaction risk criteria. The probabilities of the combined risk criteria are displayed in Figure 7. The results in Figure 5, Figure 6 and Figure 7 indicate the following: (a) The risk level of the system increases as the number of risk criteria increases. FIRC causes the greatest risk, followed by TIRC; furthermore, the higher the number of risk criteria involved in coupling, the greater the severity of a vehicle-operation-risk event. (b) As the number of combination criteria increases, the values of DC and DD increase, indicating that the environment in which the vehicle is transported is becoming more complex and chaotic. (c) The value of DD is greater than that of DC, indicating that the vehicle is operating in a more chaotic environment. (d) In the pairwise-interacting risk criteria, C (R, W) > C (W, H) > C (C, R) > C (C, H) > C (R, H) > C (C, W); accordingly, the road environment and the working environment affect the vehicle scheduling task to an increased extent because the road environment and the working environment in both combinations reach their maximal values. (e) C(R, W, H) > C(C, R, W), indicating that the combination of road environment, working environment, and human causes a higher risk of delays. (f) C(C, R, W) > C(C, W, H) > C(C, R, H), denoting that the working environment and the road environment can contribute to a higher risk of delays in combination with vehicles. (g) The probability of a vehicle operational risk event decreases as more risk criteria are involved in coupling.

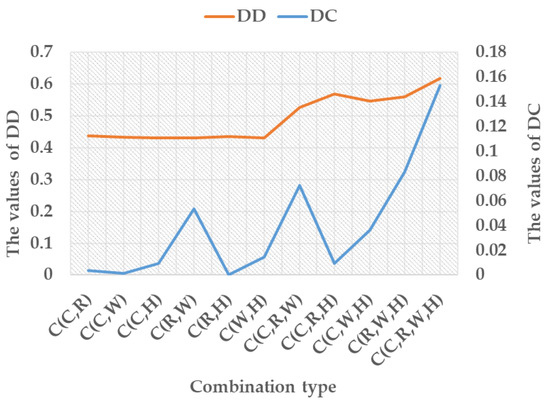
Figure 5. Values of different combinations.

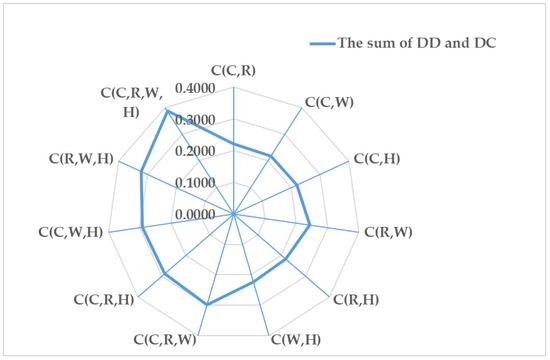
Figure 6. Summation of DD and DC for different interaction risk criteria.

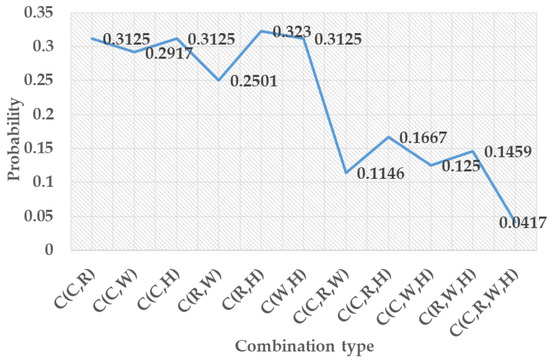
Figure 7. Probability of combining risk criteria.

5.3. Calculation of Coefficient $\epsilon$

Based on the current operational conditions, the risk-event delay times for various combinations were recorded for the period from July 2022 to October 2022, as shown in Table 12. In Equation (1), the acquisition of the optimal adjustment coefficient $\mathsf{\epsilon }$ is essential to determine the cumulative delay time. The aim of the optimization objective function in this study is to minimize the error $\mathsf{\Delta }\mathrm{T}$ between the actual measured time T_a and the theoretically calculated time T_r, from which the optimal value $\mathsf{\epsilon }$ is identified. The formula for $\mathsf{\Delta }\mathrm{T}$ is as follows:

$$\mathsf{\Delta }\mathrm{T}=\min {\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{I}}{{(\mathrm{T}}_{\mathrm{i},\mathrm{a}}{-\mathrm{T}}_{\mathrm{i},\mathrm{r}})}^2}$$

(8)

Table 12. Actual delay time for each combination of events for July 2022 to October 2022.

Combination Type	T (C, R)	T (C, W)	T (C, H)	T (R, W)	T (R, H)	T (W, H)
Delay_Time_1	45	47	55	32	36	33
Delay_Time_2	47	52	45	38	34	35
Delay_Time_3	51	53	55	32	33	32
Delay_Time_4	55	54	50	35	34	38
Delay_Time_5	52	49	50	36	33	38
Delay Time_6	50	46	50	37	35	32
Delay_Time_7	48	47	55	35	34	38
Delay_Time_8	47	55	47	32	35	36
Delay_Time_9	50	52	45	36	36	36
Delay_Time_10	55	48	50	38	37	32
Delay_Time_11	52	48	51	33	38	36
Delay_Time_12	48	49	47	36	35	34
Combination Type	T (C, R, W)	T (C, R, H)	T (C, W, H)	T (R, W, H)	T (C, R, W, H)
Delay_Time_1	60	58	69	49	103
Delay_Time_2	68	70	65	50	99
Delay_Time_3	74	56	60	52	84
Delay_Time_4	67	59	70	58	87
Delay_Time_5	58	61	75	65	103
Delay Time_6	70	59	75	73	77
Delay_Time_7	59	70	67	57	83
Delay_Time_8	64	63	66	71	79
Delay_Time_9	71	75	57	73	100
Delay_Time_10	64	70	61	57	75
Delay_Time_11	68	72	57	46	102
Delay_Time_12	57	67	58	69	88

In this study, 12 groups of data are selected, with Group Delay_Time_1 to Group Delay_Time_10 treated as the experimental groups, while Group Delay_Time_11 and Group Delay_Time_12 serve as the control group. Based on the equation $\mathsf{\Delta }\mathrm{T}$ and the statistical data, the specific optimization equation can be derived as follows:

$${\mathsf{\Delta }\mathrm{T}}_1=\min ((48-50\times ({0.2214+\mathsf{\epsilon }}_1{\left)\right)}^2+\cdots {(102-75\times ({0.3862+\mathsf{\epsilon }}_1\left)\right)}^2)$$

(9)

$${\mathsf{\Delta }\mathrm{T}}_2=\min ((52-50\times ({0.2214+\mathsf{\epsilon }}_2{\left)\right)}^2+\cdots {(75-75\times ({0.3862+\mathsf{\epsilon }}_2\left)\right)}^2)$$

(10)

Proposition 1.

When $\mathsf{\epsilon }$ takes values between 0 and 1, $\mathsf{\Delta }\mathrm{T}$ can be used to obtain the minimum value.

Proof. 

Consider any ${\mathsf{\Delta }\mathrm{T}}_{\mathrm{i}}$, where T_a, (T_{i, car}•a + T_{i, road}•b + T_{i, work}•c + T_{i, s}), and (0.5•C(x)_i + 0.5•H(x)_i) are constants. Therefore, we assume that T_a, (T_{i, car}•a + T_{i, road}•b + T_{i, work}•c + T_{i, s}), and (0.5•C(x)_i + 0.5•H(x)_i) are A, B, and E respectively. Then, ${\mathsf{\Delta }\mathrm{T}}_{\mathrm{i}}$= ${(\mathrm{A}-\mathrm{B}•(\mathrm{E}+\mathsf{\epsilon }))}^2$. When $\mathsf{\epsilon }=(\mathrm{A}-\mathrm{B}•\mathrm{E})/\mathrm{B}$, ${\mathsf{\Delta }\mathrm{T}}_{\mathrm{i}}$ obtains the minimum value. We calculate the values of ${\mathsf{\epsilon }}_{\mathrm{i}}$ for groups 1 through 10, as shown in Table 13. □

Table 13. Values of $\mathsf{\epsilon }$ for different groups.

	${\mathsf{\epsilon }}_1$	${\mathsf{\epsilon }}_2$	${\mathsf{\epsilon }}_3$	${\mathsf{\epsilon }}_4$	${\mathsf{\epsilon }}_5$	${\mathsf{\epsilon }}_6$	${\mathsf{\epsilon }}_7$	${\mathsf{\epsilon }}_8$	${\mathsf{\epsilon }}_9$	${\mathsf{\epsilon }}_{10}$
Value	0.7404	0.7657	0.7185	0.7576	0.7912	0.7489	0.7326	0.7324	0.8089	0.7156

In this paper, we take the average of ${\mathsf{\epsilon }}_{\mathrm{i}}$ as the value of $\mathsf{\epsilon }$, i.e., $\mathsf{\epsilon }$ = (0.7404 + 0.7657 + 0.7185 + 0.7576 + 0.7912 + 0.7489 + 0.7325 + 0.7324 + 0.8089 + 0.7156)/10 = 0.7511.

Finally, the optimal value of $\mathsf{\epsilon }$ is 0.7511, which is substituted into Equation (1) to derive the equation expressing the total impact on time due to each criterion being met:

$${\mathrm{T}=(\mathrm{T}}_{\mathrm{car}}•{\mathrm{a}+\mathrm{T}}_{\mathrm{road}}•{\mathrm{b}+\mathrm{T}}_{\mathrm{work}}•{\mathrm{c}+\mathrm{T}}_{\mathrm{s}})•(0.5•\mathrm{C}\left(\mathrm{x}\right)+0.5•\mathrm{H}\left(\mathrm{x}\right)+0.7511)$$

(11)

5.4. Consequence Analysis of Risk Criteria

The theoretical delays for each combination of events are calculated using Equation (9), as shown in Table 14. In this study, we use the Group Delay_Time_11 and Group_Delay_Time_12 of the data as the control group to verify the reliability of the theoretical data obtained by using R². R² is a measure of the goodness of fit of the regression model, R²$\in$(0, 1). As the value approaches 1, the model’s reliability increases correspondingly. The values of R² for Delay_Time_11, Delay_Time_12, and theoretical delay time were 0.8886 and 0.8519, which proves that the results are reliable. Figure 8 depicts a comparative analysis of the data from delays, Delay_Time_11, Delay_Time_12, and average delay time, indicating minimal discrepancy between the three outcomes. This can be attributed to the ability of the quantitative evaluation model to handle risk criteria efficiently.

Table 14. Theoretical delays for each combination of criteria.

Combination Type	T (C, R)	T (C, W)	T (C, H)	T (R, W)	T (R, H)	T (W, H)
Delays	48.63	48.42	48.56	34.78	33.91	34.09
Combination Type	T (C, R, W)	T (C, R, H)	T (C, W, H)	T (R, W, H)	T(C, R, W, H)
Delays	68.32	67.62	67.81	53.66	90.99

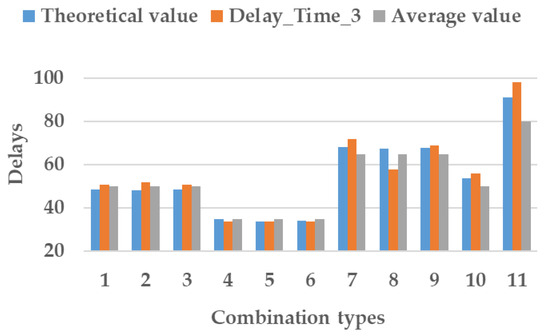
Figure 8. Comparison of theoretical delays, Delay_Time_11, Delay_Time_12, and average delays.

6. Conclusions and Future Research Directions

In this research, we present a novel quantitative framework for the assessment of risk criteria occurring in shipyard vehicle scheduling. The proposed model offers a comprehensive means of evaluating the impact of such risk events on scheduling tasks by quantifying the associated delay time. The proposed model is superior to other methods in that it incorporates more criteria and registers the real-time delays triggered by risk criteria. The availability of such information can enable managers to devise a wider range of strategies to cope with potential risks.

Based on safety engineering theory and the shipyard environment, four criteria that affect scheduling tasks are identified: vehicles, the road environment, the working environment, and human factors. These criteria, including 12 factors and their specific content, are described in detail. Furthermore, we conduct an in-depth exploration of the average duration of the delays attributed to these criteria in scheduling tasks. Based on historical occurrences of the risk events, we count the number of occurrences of each criterion, and calculate the DC of different risk-combination times using the N-K model. In addition, based on information entropy theory, we calculated the DD in the risk criteria. Our analyses reveal the following:

(1)

The risk level of the system increases as the number of risk criteria increases. Therefore, managers should avoid developing vehicle scheduling plans during times when multiple risk criteria occur.

(2)

Roadway environments and working environments have a significant and substantial impact on the execution of vehicle scheduling tasks. When developing vehicle scheduling plans, it is imperative to take into account the conditions of the roadway environment. Given the ongoing nature of vehicle scheduling, it is advisable to reconsider and potentially modify the vehicle distribution plan when risk criteria manifest in real-time.

By comparing the experimental results, we calculated the correction coefficients in the quantitative model. The R² values for the control groups and theoretical delay time are 0.8886 and 0.8519, respectively, which proves that the results are reliable. This finding has practical implications for the real-time scheduling of vehicles. Specifically, it suggests that if a risk criterion is met, the manager should analyze the delay caused by the risk and compare it to the potential delay resulting from adjusting the scheduling plan. For instance, if the delay caused by the risk exceeds the impact on timeliness resulting from changing the scheduling plan, a revised scheduling plan should be adopted. This approach can minimize the potential consequences of the risk. Overall, this quantitative model provides a reasonable and efficient approach to analyzing the delays in scheduling tasks due to risk criteria, making it an effective tool for analysis of these risk criteria.

Although this study makes several useful contributions, a limitation is that the present model is designed for shipyard scheduling; therefore, its suitability for analyzing risk in other industries requires verification. Nevertheless, the research framework established in this study can be used as a reference for other studies, which is a valuable contribution of our research. Furthermore, the findings of this study can be employed to enhance the scheduling of vehicles in shipyards. This involves developing more efficient strategies and algorithms to systematically formulate rational plans for real-time vehicle scheduling in response to fulfillment of risk criteria.