Research on Multi-Target Path Planning for UUV Based on Estimated Path Cost
Abstract
1. Introduction
- Transform the path planning problem of a mine countermeasures UUV dealing with multiple ground mines into a TSP.
- Train a neural network for estimating path costs, quickly creating a cost matrix that accurately reflects the shortest path between two target points.
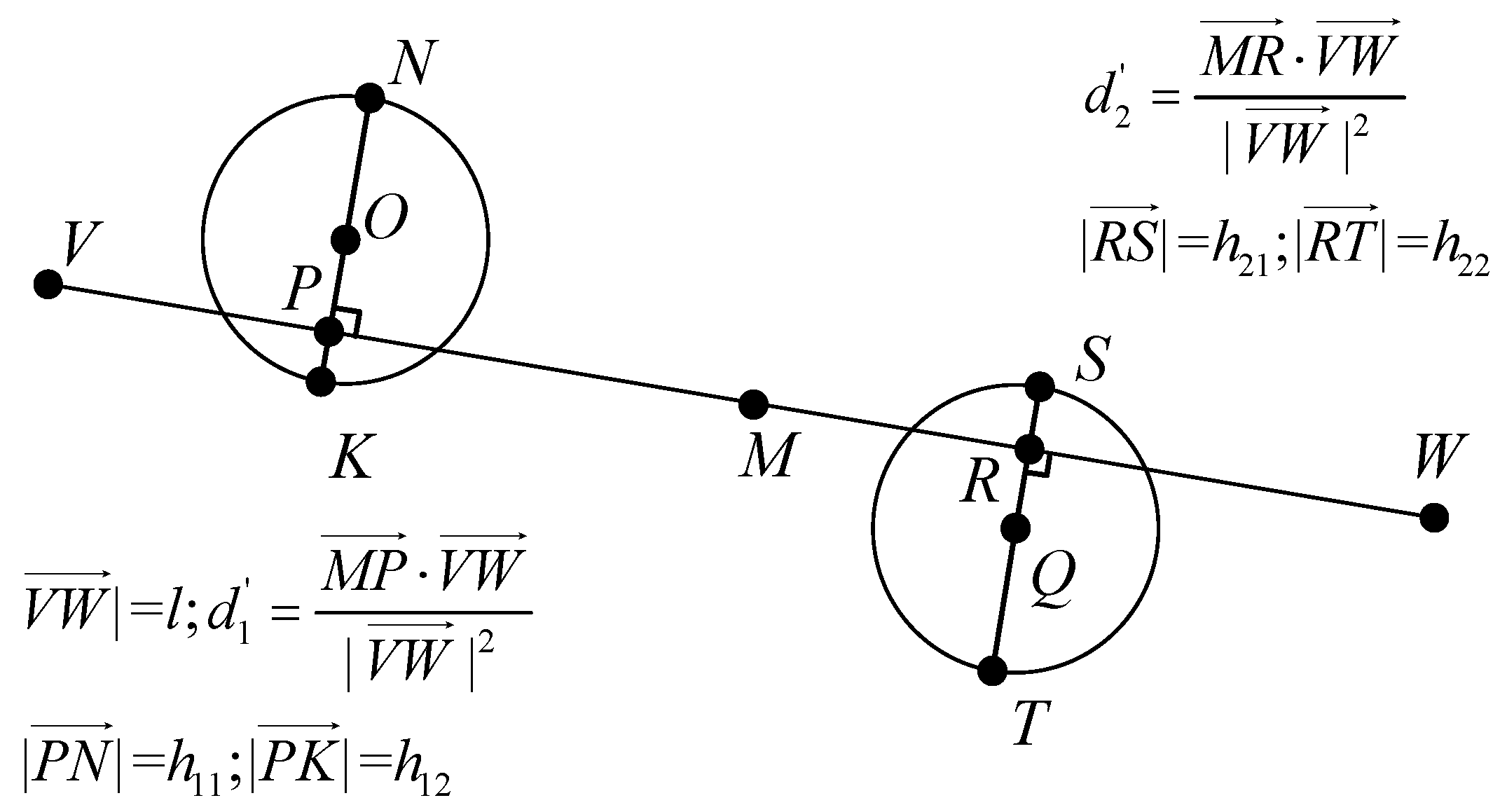
- During the global path planning process, an initial check is performed to see if the direct line segment between two points intersects any obstacles. If there is no intersection, the segment is considered as the feasible path, with its Euclidean distance serving as the path cost.
2. Examination and Analysis of the Problem
3. Estimated Path Cost-Based Multi-Target Path Planning Method
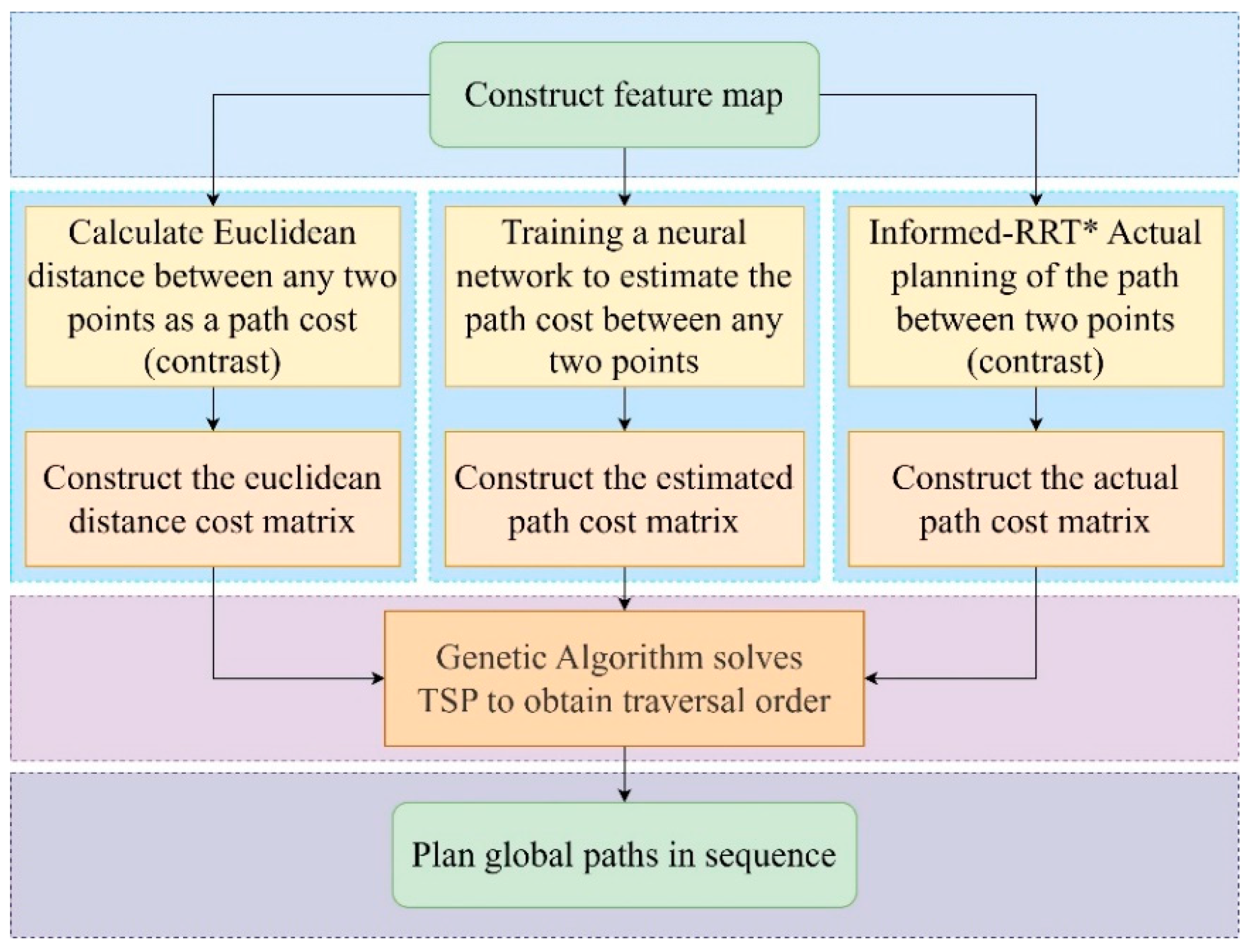
3.1. Algorithm Framework
3.2. Informed-RRT* Algorithm
3.3. Path Cost Estimation Neural Network
3.3.1. Dataset Creation
3.3.2. Neural Network Training
3.4. Construction of the Path Cost Matrix
3.4.1. Estimated Path Cost Matrix
3.4.2. Actual Path Cost Matrix
3.4.3. Euclidean Distance Cost Matrix
3.5. Genetic Algorithm for Solving the TSP
4. Simulation Experiment and Analysis
4.1. Estimation Error Analysis
4.1.1. Error Analysis in Test Sets
4.1.2. Error Analysis of Estimating Path Cost Matrix
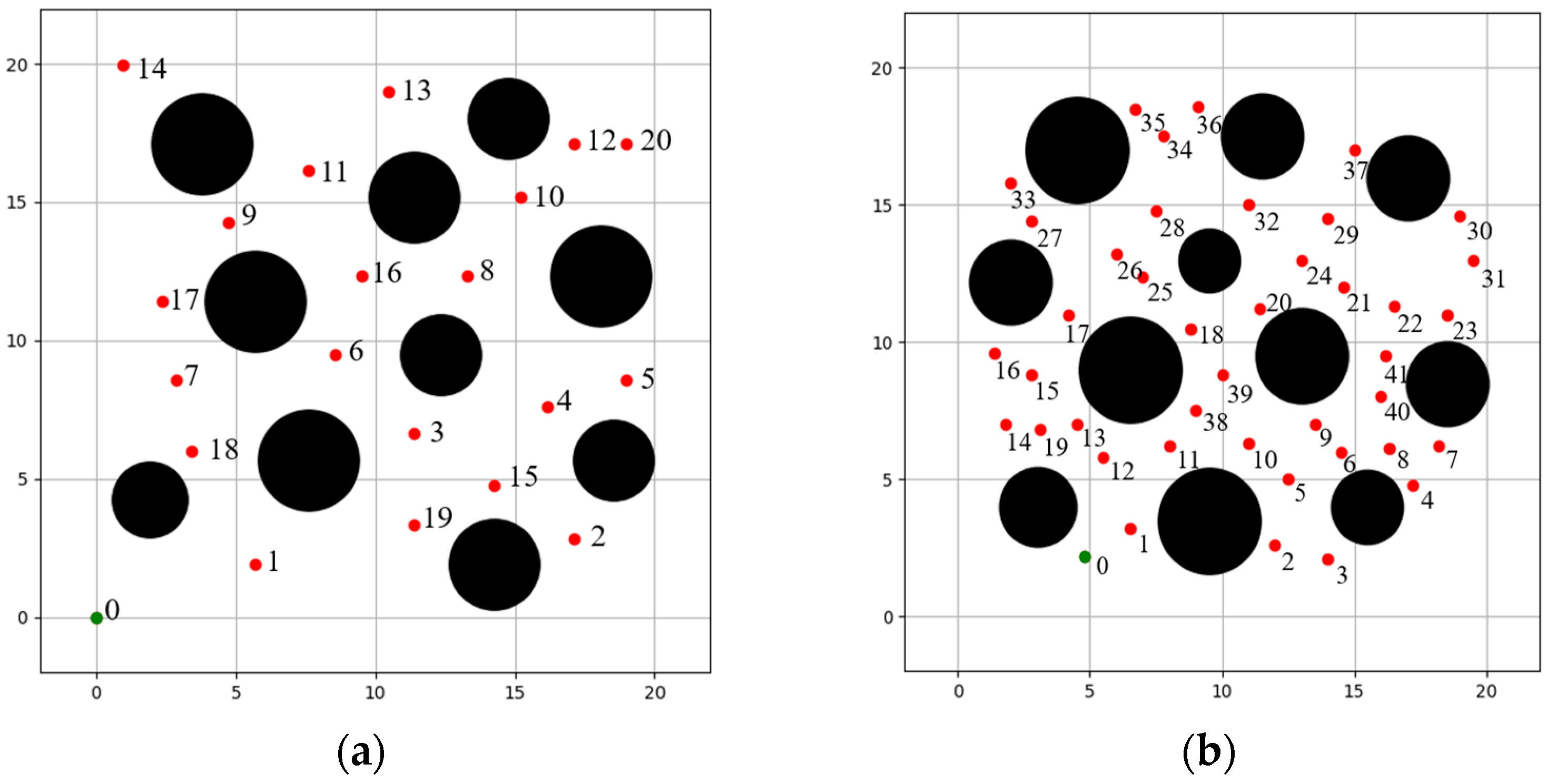
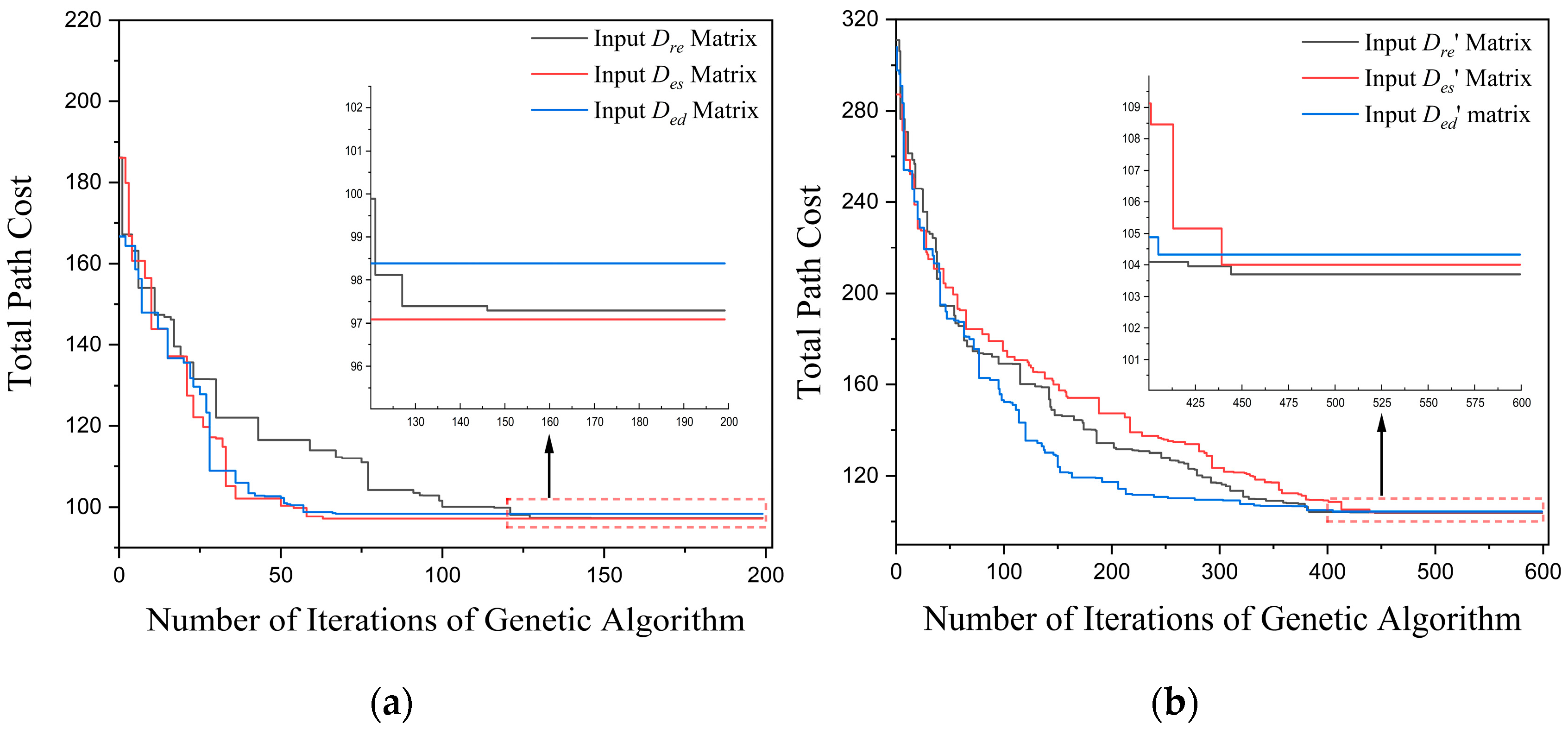
4.2. Solve the Traversal Order
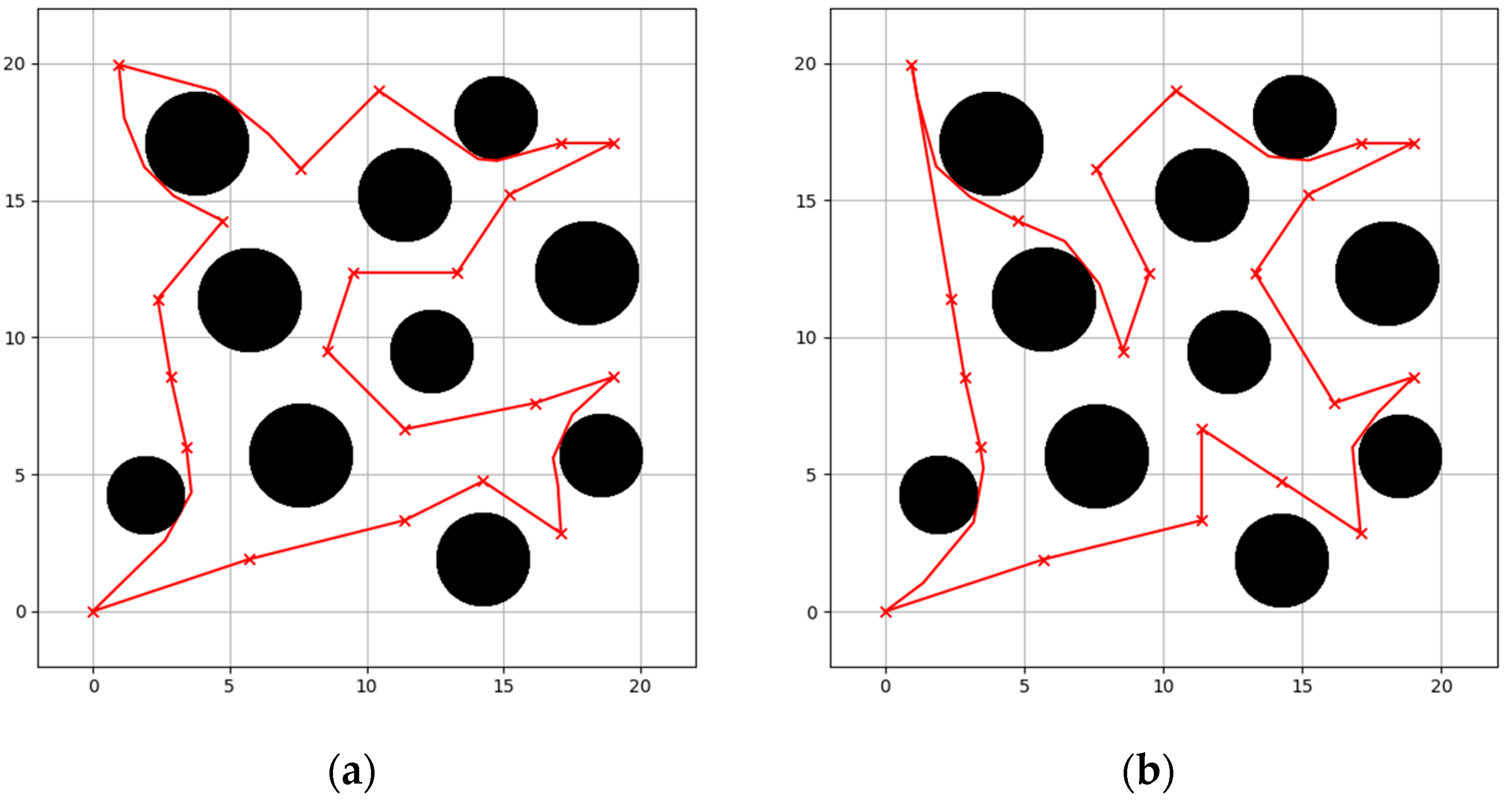
4.3. Global Path Planning
4.4. Simulation Experiment Analysis
5. Prototype Experiment Design and Analysis
6. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Galceran, E.; Palomeras, N.; Carreras, M. Profile Following for Inspection of Underwater Structures. Paladyn J. Behav. Robot. 2013, 4, 209–220. [Google Scholar] [CrossRef][Green Version]
- Manaranche, M. France Plots Route to New Unmanned MCM Capability. Warsh. Technol. 2011, 37–38. [Google Scholar]
- Daoliang, L.; Peng, W.; Ling, D. Path Planning Technologies for Autonomous Underwater Vehicles-A Review. IEEE Access 2018, 7, 9745–9768. [Google Scholar] [CrossRef]
- Lin, W.; Delgado, J.G.; Gause, D.C.; Vassiliadis, S. Hybrid Newton-raphson Genetic Algorithm for the Traveling Salesman Problem. Cybern. Syst. 1995, 26, 387–412. [Google Scholar] [CrossRef]
- Rubio-Sierra, C.; Domínguez, D.; Gonzalo, J.; Escapa, A. Path Planner for Autonomous Exploration of Underground Mines by Aerial Vehicles. Sensors 2020, 20, 4259. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, P.; Singh, A. An Artificial Bee Colony Algorithm with Variable Degree of Perturbation for the Generalized Covering Traveling Salesman Problem. Appl. Soft Comput. 2019, 78, 481–495. [Google Scholar]
- Minghao, L.; Lijun, Q.; Jianfeng, J. A Multigoal Path-Planning Approach for Explosive Ordnance Disposal Robots Based on Bidirectional Dynamic Weighted-A* and Learn Memory-Swap Sequence PSO Algorithm. Symmetry 2023, 15, 1052. [Google Scholar] [CrossRef]
- Daichuan, Y.; Chenglin, W. Multiple Targets Robot Path Planning Based on Ant Colony and Improved Probabilistic Road Map. J. Hangzhou Dianzi Univ. (Nat. Sci.) 2017, 37, 63–67. [Google Scholar] [CrossRef]
- Wenjun, Y.; Kuixiang, X.; Zhejing, B. A 3D Space Multi-Target Path Planning Method Combining RRT and Ant Colony Optimization Algorithms. Patent No. CN109211242B,2020-10-23, 23 October 2020. [Google Scholar]
- Yu, J.-b.; Chen, Z.-h.; Deng, W.; Xu, J.-p.; Zhao, Z.-y.; Wang, X.-y. A Traversal Multi-target Path Planning Algorithm for Unmanned Cruise Ship. Comput. Eng. Sci. 2023, 45, 840–848. [Google Scholar] [CrossRef]
- Xu, R.; Cao, M.; Huang, M.; Zhu, Y.H. Research on the Quasi-TSP problem based on the improved grey wolf optimization algorithm: A case study of tourism. Geogr. Geo-Inf. Sci. 2018, 34, 14–21. (In Chinese) [Google Scholar]
- Wu, X.; Gao, Z.; Yuan, S.; Hu, Q.; Dang, Z. A Dynamic Task Allocation Algorithm for Heterogeneous UUV Swarms. Sensors 2022, 22, 2122. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudzadeh, S.; Powers, D.; Atyabi, A. UUV’s Hierarchical DE-Based Motion Planning in a Semi Dynamic Underwater Wireless Sensor Network. IEEE Trans. Cybern. 2019, 49, 2992–3005. [Google Scholar] [CrossRef] [PubMed]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal Sampling-based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Idris, M.Y.I.; Anisi, M.H.; Ahmedy, I.; Ali, I. Informed RRT*-Connect: An Asymptotically Optimal Single-Query Path Planning Method. IEEE Access 2020, 8, 19842–19852. [Google Scholar] [CrossRef]
- Tao, G.; Michalewicz, Z. Evolutionary Algorithms for the TSP. In Proceedings of the 5th International Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; Springer: Berlin/Heidelberg, Germany, 2003; pp. 803–812. [Google Scholar]
- Kesheng, C.; Sidong, X.; Peng, G. Adaptive Temperature Rising Simulated Annealing Algorithm for Traveling Salesman Problem. Control. Theory Appl. 2021, 38, 245–254. [Google Scholar] [CrossRef]
- Silva, C.; Aguiar, A.; Lima, P.; Dutra, I. Mapping a logical representation of TSP to quantum annealing. Quantum Inf. Process. 2021, 20, 386. [Google Scholar] [CrossRef]
- Qing, H.; Yile, W.; Tongwei, X. Application of improved genetic simulated annealing algorithm in TSP optimization. Control. Decis. 2018, 33, 219–225. [Google Scholar] [CrossRef]
- Da, C.; Xiaoming, Y.; Sheng, L. Ant Colony Algorithm with n-α-Measure and Migration Learning. Arab. J. Sci. Eng. 2023, 48, 1873–1890. [Google Scholar] [CrossRef]
- Tuani, A.F.; Keedwell, E.; Collett, M. Heterogenous Adaptive Ant Colony Optimization with 3-opt local search for the Travelling Salesman Problem. Appl. Soft Comput. 2020, 97, 106720. [Google Scholar] [CrossRef]
- Hehua, L.; Chao, C.; Jing, C. An Improved Genetic Algorithm for Solving Travel Salesman Problem. Trans. Beijing Inst. Technol. 2013, 33, 390–393. [Google Scholar] [CrossRef]





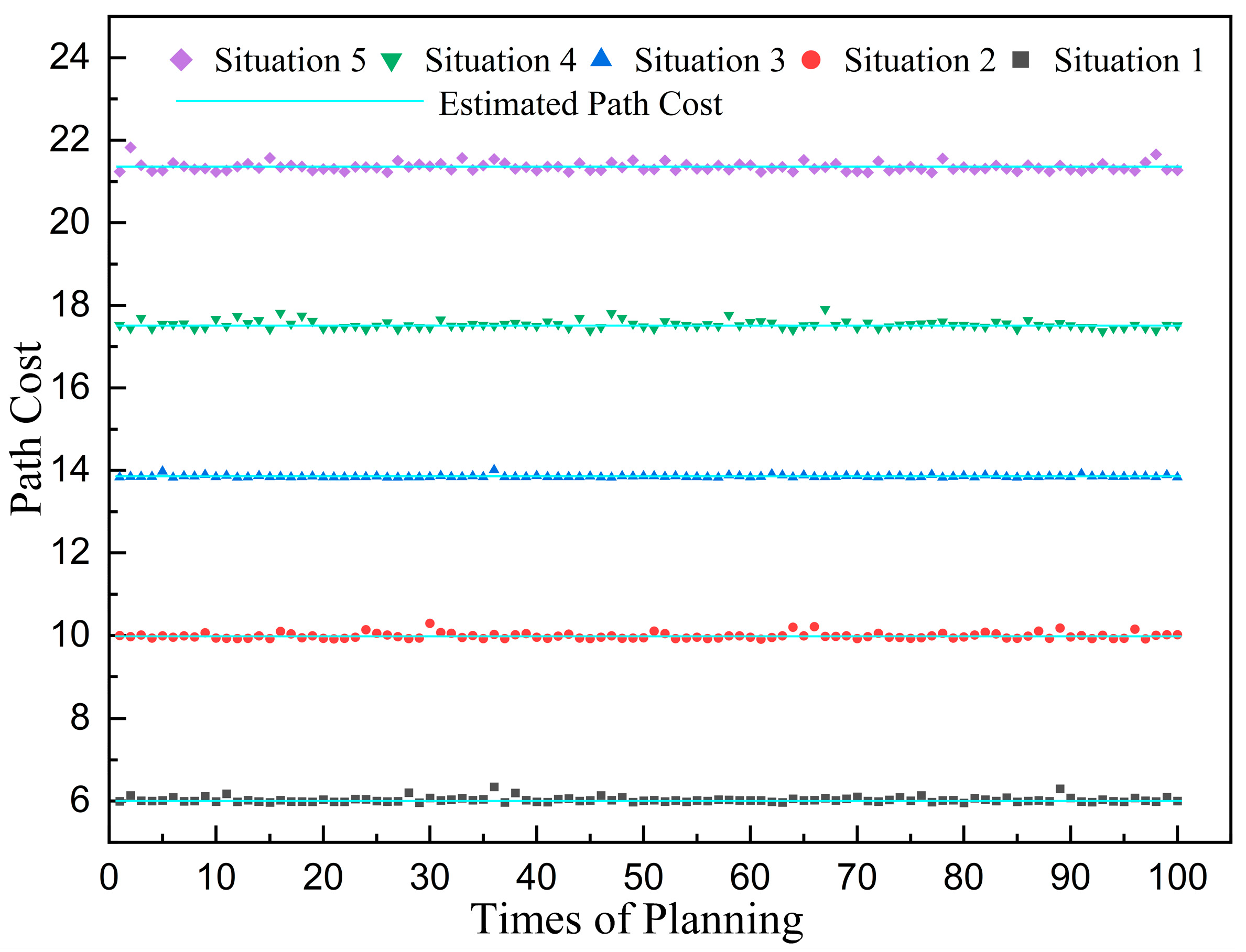



| Group | Estimated Cost Value | Mean Absolute Error | Root Mean Square Error | Up/Down Distribution |
|---|---|---|---|---|
| Situation 1 | 6.02189 | 0.04121 | 0.06505 | 41/59 |
| Situation 2 | 10.00891 | 0.05934 | 0.07397 | 39/61 |
| Situation 3 | 13.84125 | 0.01604 | 0.02854 | 55/45 |
| Situation 4 | 17.52038 | 0.06916 | 0.09788 | 50/50 |
| Situation 5 | 21.35993 | 0.07908 | 0.10278 | 36/64 |
| Parameter | Scenario A | Scenario B |
|---|---|---|
| Population Size | 80 | 100 |
| Number of Iterations | 200 | 600 |
| Mutation Probability | 0.005 | 0.008 |
| Crossover Probability | 0.8 | 0.9 |
| Number of Traversal Points | 21 | 42 |
| Task Scenarios | Input Matrix | Order Number | 10 Global Planning Average Path Cost |
|---|---|---|---|
| A | 1 | 96.6899 | |
| 2 | 100.8934 | ||
| B | 3 | 103.3183 | |
| 4 | 107.6537 |
| Task Scenarios | Input Matrix | Time Cost to Construct Cost Matrix | Time Cost to Solve TSP | Average Time Cost of 10 Plannings | Total Time Cost |
|---|---|---|---|---|---|
| A | 1296.6234 | 0.8445 | 8.4183 | 1305.8862 | |
| 0.2522 | 0.8137 | 9.4842 | |||
| 0.0000 | 0.8206 | 7.3057 | 8.1263 | ||
| B | 5326.2164 | 4.2674 | 5.2264 | 5335.7102 | |
| 0.9391 | 4.2898 | 10.4553 | |||
| 0.0000 | 4.1947 | 9.5650 | 13.7597 |
| Parameter | Specific Parameter |
|---|---|
| Size | 900 × 350 × 180 (millimeters) |
| Endurance | 1.5 (hours) |
| Maximum Speed | 3 (knots) |
| Maximum Diving Depth | 10.0 (meters) |
| Positioning Accuracy | <1.5 (meters) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Wang, Z.; Li, L.; Li, H. Research on Multi-Target Path Planning for UUV Based on Estimated Path Cost. J. Mar. Sci. Eng. 2023, 11, 1582. https://doi.org/10.3390/jmse11081582
Zhou S, Wang Z, Li L, Li H. Research on Multi-Target Path Planning for UUV Based on Estimated Path Cost. Journal of Marine Science and Engineering. 2023; 11(8):1582. https://doi.org/10.3390/jmse11081582
Chicago/Turabian StyleZhou, Shuai, Zheng Wang, Longmei Li, and Houpu Li. 2023. "Research on Multi-Target Path Planning for UUV Based on Estimated Path Cost" Journal of Marine Science and Engineering 11, no. 8: 1582. https://doi.org/10.3390/jmse11081582
APA StyleZhou, S., Wang, Z., Li, L., & Li, H. (2023). Research on Multi-Target Path Planning for UUV Based on Estimated Path Cost. Journal of Marine Science and Engineering, 11(8), 1582. https://doi.org/10.3390/jmse11081582







