Abstract
Cylindrical structures are widely used in offshore and marine engineering, but they may suffer from vortex-induced vibration under the influence of ocean or wave currents, which can lead to severe fatigue damage. In this study, we applied the open-source software Open-Source Field Operation and Manipulation (OpenFOAM) to investigate the characteristics of fluid flow around offshore cylindrical structures, taking into account the effect of helical strake parameters, such as pitch and strake number. The aim of this study is to explore the possibility of suppressing vortex shedding with different helical strake parameters. Numerical simulation results demonstrated that attaching a helical strake to the bare cylinder destroyed vortex shedding in offshore cylindrical structures. The vortex visualization showed that the helical strake destroyed the three-dimensional vortex structures. Moreover, the lift coefficient data showed that the vibration frequency of the cylinder decreased after attaching the helical strake, indicating that the vortex-induced vibrations on the wake flow tended to fade. The results suggest that the helical strake is a promising option for suppressing the wake vortex shedding of cylindrical structures in offshore engineering.
1. Introduction
Offshore cylindrical structures, such as marine risers, oil pipelines, offshore windmill foundations, and offshore platform foundations, are widely used in the structural design of marine and offshore engineering. Cylindrical structures in offshore engineering need to withstand the impact of ocean currents or waves for a long time, so the influence of vortex-induced vibration (VIV) must be taken into account during the design process. Fatigue failure may occur, especially in severe cases [1,2], regardless of the material used. To prevent fatigue, two approaches can be taken: active control (e.g., increasing safety factor and boundary condition control) and passive control (e.g., attaching spoilers or strakes). Liu et al. [3], Hong et al. [4], and Wang et al. [5] studied the passive control of VIV, including riser structure, internal velocity, top tension, structural damping, and more. In recent decades, cylindrical structures in marine engineering have been a popular research object for researchers. Mathematical theory, experimental methods, and numerical methods have been used, and there is a vast body of literature on the topic. We summarize several relevant studies below, ranging from experimental to numerical directions.
In the field of mathematical and experimental investigations, numerous studies have been conducted to improve the design of offshore cylinders. Song et al. [6] conducted an experimental study on the tuned mass damper (TMD) attached to the top tension riser (TTR). They established a relevant dynamic model and applied damping to the top of the tension riser to achieve suppression. Zhou et al. [7] conducted experiments on a scaled model of the mooring tension leg platform and determined that the cross-flow response is usually greater than the in-line flow response. Amaechi et al. [8], similar to [7], studied the characteristics of the catenary anchor leg mooring (CALM) buoy hose system and concluded that the system exhibits flow patterns while floating on the liquid. Srinil [9] mathematically analyzed the effect of linearly sheared currents on variable-tensioned risers. He developed a general low-order multi-mode interactive model for the problem and studied the influence of fluid–structure parameters. Simantiras et al. [10] investigated the effect of high incidence angles on helical strakes attached to cylinders through experimental methods. The results showed that helical strakes were effective in suppressing the 1st mode of the VIV response, even at higher inclination angles. Lubbad et al. [11] conducted a parametric study on the effect of suppressing VIV using helical strakes through experimental methods. They achieved significant results regarding the effect of different parameters. Assi et al. [12] conducted a parametric investigation on the method to suppress VIV around risers, which served as the reference for this study. Mekki et al. [13] mathematically investigated the method employed to solve the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony II (KP-BBM-II) partial differential equations. Sukarnoor et al. [14] conducted experimental investigations on the effectiveness of helical strakes and multiple cylinders in suppressing the VIV phenomenon. They concluded that both helical strakes and multiple cylinders are effective in suppressing VIV. Zhou et al. [15] conducted experimental investigations on the VIV phenomenon of cylinders with helical strakes. They concluded that after three-start helical strakes were attached to the cylinder, the vibration amplitude of the cylinder was suppressed by 98%.
Numerical methods have been widely used in the study of VIV. Wang et al. [16] numerically investigated the effect of different velocity and water depth on VIV, including the fluid–structure interaction (FSI) method. Their results indicated that the VIV response became more intense with increasing water depth and flow velocity. Wang et al. [17] conducted a numerical study on both TTR and steel catenary risers (SCRs) and found that the lift and drag coefficients of TTR were approximately twice that of SCR. They also observed that the lift–drag coefficient of TTR did not change much with water depth, and the largest lift–drag coefficient was observed in the middle section. Santillan et al. [18] conducted a numerical and experimental study on the behavior of catenary risers and validated the numerical solver with experimental results. They considered the total length, buoy attachment location, and the fixed height of the attachment point. Vasquez et al. [19] performed both experimental and numerical studies on the effect of the internal slug of flexible marine risers. The numerical results were found to be in good agreement with the experimental results, qualifying the computational tool to conduct parametric studies about the dynamic behavior of flexible marine risers with an internal slug flow. Atadan et al. [20] numerically studied the marine riser connected to a floating platform and illustrated the effect of the riser length and mass ratio. Kharazmi et al. [21] conducted a numerical study on the spar platform with strake using detached eddy simulation (DES). Their results indicated that the VIV of the spar platform was maximally suppressed by attaching a strake by up to 58%.
Several researchers have also conducted numerical studies to investigate the effect of different factors on VIV. For instance, Yang et al. [22] used a finite element method (FEM) to study the effect of internal velocity on VIV in a flexible fluid-conveying pipe. They found that the internal velocity can influence the VIV phenomenon. In another study, Wang et al. [23,24] numerically investigated the effect of metasurfaces in suppressing VIV and concluded that bluff bodies with convex tri-prism and convex hemisphere patterns can enhance VIV by enlarging the lock-in region. Joshi et al. [25] developed a novel method based on the positivity-preserving variational (PPV) method for the Spalart–Allmaras-based delayed detached eddy simulation (DDES) and investigated the effect of different Reynolds numbers. They found that the results obtained from the PPV-based DDES model were in good agreement with the experiments and with results obtained in the literature using other large eddy simulation (LES) and DES models. Chen et al. [26] conducted a numerical study to investigate the method of suppressing VIV in a flexible riser through the computational fluid dynamics/computational structural dynamics (CFD/CSD) approach. They concluded that the vibration suppression is efficient for increasing the number of starts. Ishihara et al. [27] numerically investigated the method of suppressing VIV through helical wires attached to the circular cylinder using the LES approach and validated the results through experiment. They concluded that suitable helical wires can effectively suppress VIV in the wake of the circular cylinder. Lastly, Zhu et al. [28] numerically studied the circular cylinder attached with fin-shaped strips using the direct numerical simulation (DNS) method and concluded that the amplification and alleviation of fluid forces are associated with the development of the boundary layer and the formation of vortices.
Previous research studies have been limited in scope, focusing on only one type of equipment, even though they all investigated circular cylinder structures. Additionally, many of these studies relied on the Reynolds-averaged Navier–Stokes equations (RANS) method, which has limitations for the turbulence simulation. Several sources of literature are reviewed and summarized in Table 1, which indicates that LES has been predominantly used to study the flow around a bare cylinder. The objective of this study is threefold: First is to investigate the potential for suppressing periodic vortex shedding through parameter research. The essence of the current study is to suppress the VIV phenomenon by suppressing the periodic vortex shedding of the wake. Second, according to Table 1, there are not many applications for complex shapes due to computer resource and cost. Since VIV is an unsteady phenomenon, the LES model is considered more suitable. Therefore, the LES was applied in this study. Third, we are seeking a method for marine cylindrical optimization through the parametric study. The current study is not limited to a specific structure but is more general, allowing for its applicability to offshore structures, such as risers, spar platforms, etc. The outline of this study can be summarized as follows: In the second section, we introduce the numerical analysis approach, including the problem description, numerical solver, solving scheme, and boundary conditions. The specific group results and discussions based on different parameters are presented in the third section. Finally, the conclusions of the study are summarized in the last section.

Table 1.
Literature review summary.
2. Numerical Analysis
2.1. Problem Description
The VIV phenomenon is caused by the periodic vortex shedding in the wake of a cylinder. Therefore, the focus of this study is to investigate methods to suppress the vortex shedding around the cylinder. In marine engineering, there are two main types of risers, TTR and SCR. The cylindrical structure investigated in this study can be regarded as a TTR. With these points in mind, we chose a stationary cylinder as the subject of our study. This study investigates the effect of helical strakes on the suppression of vortex shedding in the wake of a cylinder, and consists of three main parts: (1) studying cylinder with and without helical strake, (2) studying the effect of the strake start number, (3) studying the effect of the strake pitch. Figure 1 shows the schematic of the helical strake attached to the cylinder, with the strake start number (also mentioned as strake number), referring to the number of strakes attached to the cylinder. This study considers four cases—the bare cylinder, 2-, 3-, and 4-start strakes, as shown in Figure 2. The strake pitch is used to describe the ratio of the length of the helical strake, which is one complete revolution around the cylinder to the cylinder diameter. This study considers four pitch cases as shown in Figure 3. The case classifications are listed in Table 2. Previous validation and mesh independence studies related to this work were presented in our previous study [30].
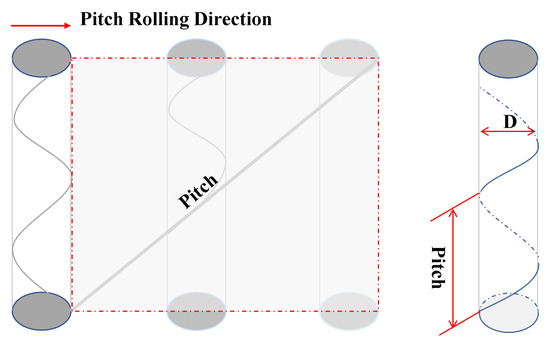
Figure 1.
The helical strake attached structure and pitch definition.
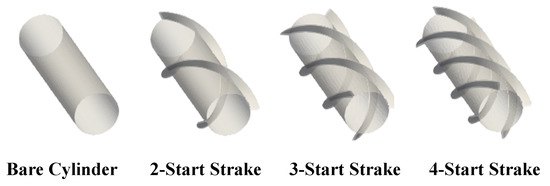
Figure 2.
Model of helical strakes.
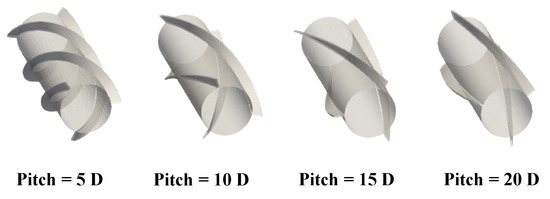
Figure 3.
Model of helical pitch.

Table 2.
Test case and relevant parameters.
2.2. Governing Equations
For the sake of solving the separating flow and turbulence flow, the LES model was chosen in this study. The governing equation can be described as the unsteady incompressible and filtered Navier–Stokes. They can be written as the following [31,32]:
where the , and are density, time, pressure, kinematic viscosity, filtered velocity, filtered pressure, and sub-grid stress. The hat means the filter operation.
Closure is obtained by modeling the residual-stress tensor, most simply by an eddy–viscosity model. In this study, the sub-grid stress is defined by
where the means the dimensional velocity, and i and j mean the dimension.
The model-filtered equations are solved numerically for U(x, t), which provides an approximation to the large-scale motions in one realization of the turbulent flow. The sub-grid stresses resulting from the filtering operation are still unknown, and they are modeled as the following:
where the and are the sub-grid scale turbulence viscosity, Kronecker delta, and the rate of the strain tensor. The rate of the strain tensor is defined as
The wall-adapting local eddy viscosity (WALE) model is used in this study. Hence, the sub-grid scale stress tensor and sub-grid scale turbulence viscosity in OpenFOAM are rewritten as
where is the model constant, which is equal to 0.325. Except this constant number, another two constants () are applied in OpenFOAM, which equal to 1.048 and 0.094. is the length scale in the model, and it can be defined by the users. is defined as
The WALE model was built to recover the expected asymptotic behavior in the near-wall region in the equilibrium turbulent boundary layers on fine grids, without any additional damping function [33,34]. Additionally, the WALE model can make the sub-grid scale turbulence viscosity return to zero for the laminar shear flow, which is a advantage point compared to the Smagorinsky model or Smagorinsky–Lilly model [35].
We simultaneously sampled and calculated the drag coefficients and lift coefficients during the simulation. We calculated the Strouhal number using the fast Fourier transform (FFT) method. The respective definitions for these terms are shown in the following equations:
where the and indicate that the drag coefficient, drag force, domain velocity, characteristic length, lift coefficient, lift force, Strouhal number and the shedding frequency, respectively.
2.3. Geometry and Mesh Generation
The computational domain used in this study is the same size for both the bare cylinder and helical strake attached cylinder. The schematic of the computational domain is presented in Figure 4. The diameter of the entire domain is 20 D, where the left semicircular surface is the inlet boundary, and the right serves as the outlet boundary. The inlet velocity flows along the X-axis from the inlet, and the far-field velocity is set to 1 m/s. The Y-axis passes through the centerline of the cylinder and the computational domain. The circular cylinder is located at the center of the domain, and the spanwise length was chosen based on previous research. According to Zdravkovich [36], the turbulent flow around a cylinder becomes three-dimensional at . Therefore, the spanwise length needs to be considered. In general, the diameter of the cylinder is D, and the spanwise length is , which has been demonstrated by other scholars [29,37] and is divided into approximately 48 layers.
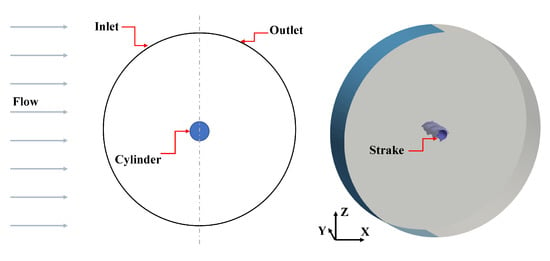
Figure 4.
The schematic of computational domain.
In this study, an unstructured tetrahedral mesh was utilized to generate the mesh and construct the complete computational domain and cylinder geometry as shown in Figure 5. The wake region around the cylinder was refined using the density box technique. Since the wall function was not employed, an initial prism layer was generated with a Y-plus target value of 1. Furthermore, 10 prism layers were used near the cylinder with a growth ratio of 1.08.

Figure 5.
Mesh generation around the cylindrical structure.
2.4. Simulation Settings
The OpenFOAM-v2012 was proceed in the current study. For temporal term integration, a second-order backward Crank–Nicolson scheme was employed. The simulation utilizes the predictor–corrector pressure implicit with splitting of operators (PISOs) algorithm to iteratively solve the coupled pressure and velocity field. The velocity matrix system solution employs the preconditioned bi-conjugate gradient (PBiCG) with a residual tolerance of , while the pressure matrix system uses a geometric agglomerated algebra multi-grid (GAMG) with a residual tolerance of . The relaxation factors for the pressure and velocity matrix solving are set at 0.3 and 0.5 initially. Additionally, the convergence criterion was not only based on the relevant variable residual tolerance but also considered the difference drag and lift coefficient recording curve.
- Only the inlet boundary has the Dirichlet boundary condition of velocity u = 1 m/s, and the corresponding turbulent intensity can be calculated using the formula , which equals 0.057;
- At the outlet boundary, the Neumann boundary condition is applied , and the pressure is the applied Dirichlet boundary condition of ;
- Both the bare cylinder and helical strake attached cylinder surfaces are set as the no-slip boundary condition. No wall function is used near circular cylinder surface.
- For the front and back surface spanwise, the boundary condition of the symmetrical plane is applied.
2.5. Validation and Sensitivity Study
The mesh independence study was conducted on the bare cylinder using the LES WALE turbulence model. The results of the mesh independence study, presented in Table 3, show that the drag coefficient and Strouhal number vary by no more than 5% and 3%, respectively (calculated using the equation ), from the medium mesh to the fine mesh. All the simulation grids used in this study are set to a higher standard than the medium mesh. In addition, the RANS SST model and LES WALE model were compared based on the previous mesh standard. The validation results and turbulence model sensitivity study are presented in Figure 6 and Table 4. The drag coefficient was found to be 0.997, the mean lift coefficient was 0, and the Strouhal number was 0.2196. The results obtained using the medium mesh and LES turbulence model are in good agreement with the experimental data reported by previous researchers [38,39]. The comparison of the streamwise velocity distributions in the figure shows that both the LES and RANS models agree well with the previous experiments. However, the LES model produces results that lie between those of different experiments in the recirculation zone, while the RANS model results are closer to the experimental findings of Lourenco et al. [40]. The computational cost of the LES model was approximately ten times compared to that of RANS model by using the same computational resource. Nonetheless, the RANS model is significantly less representative than the LES model. Based on these results, we employed a medium mesh and the LES WALE model for this study.

Table 3.
Mesh independence result.
Table 3.
Mesh independence result.
| Case | Grid Number | Drag Coefficient | Strouhal Number |
|---|---|---|---|
| Loureno [40] | - | 0.99 | 0.22 |
| Kravchenko [37] | 1.04 | 0.21 | |
| Corase | 1.13 | 0.23 | |
| Medium | 0.997 | 0.2196 | |
| Fine | 0.992 | 0.213 |
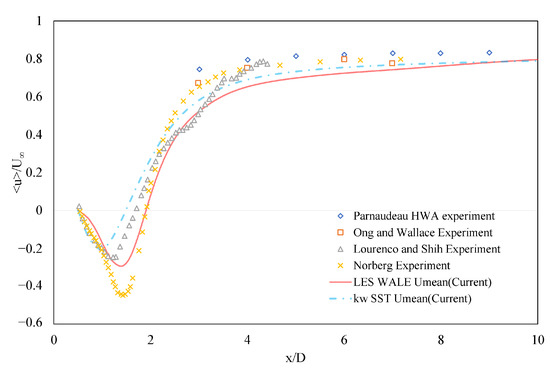
Figure 6.
Streamwise Velocity on the center line in the wake of bare cylinder [38,39,40,41].

Table 4.
Turbulence model sensitivity study.
Table 4.
Turbulence model sensitivity study.
| Case | Grid Number | Drag Coefficient | Strouhal Number |
|---|---|---|---|
| Loureno [40] | - | 0.99 | 0.22 |
| LES WALE | 0.997 | 0.2196 | |
| RANS SST | 1.005 | 0.292 |
3. Results and Discussions
In this section, we provide a brief summary of the numerical simulation results. Firstly, we compare the wake characteristics around the cylinder with and without the baseline helical strake. Then, we summarize the effects of the strake number and strake pitch. Furthermore, we present various data analyses based on the simulation results. Finally, we compare our findings with the results reported in the relevant literature.
3.1. Wake Flow with Strake Attached
Figure 7 shows the velocity distribution in the structure mid-plane. The time point selected was based on different cases. The mark time was set as the convergence time point, and the dimensionless time was calculated as . The case SP5, which can be found in Table 2, was chosen as the reference case. From the velocity contour at different time points, it is evident that the wake area of the cylinder without a helical strake experiences periodic vortex shedding. In contrast, the wake area of the structure with a helical strake shows a noticeable reduction in the periodic velocity. These results suggest that the helical strake can effectively suppress vortex shedding, consistent with the findings of previous studies. The helical strake is thus an effective device to inhibit vortex-induced vibration phenomenon. Figure 8 presents the vortex visualization from a different point of view based on the Q-criterion (Q = 0.01). The visualization allows us to observe the generation of the wake vortex in the cylinder at different times. Notably, the wake vortex of the bare cylinder generates periodic strip vortex iso-surfaces. In contrast, the wake vortex of the cylinder with helical strike presents a broken vortex structure. This observation confirms that helical strike is a feasible method to effectively suppress the generation of vortex shedding. Figure 9 shows the time-averaged wake flow and pressure distribution around the cylinder with and without helical strake. The results of our study indicate that the installation of a helical strake has a significant impact on the mean velocity and pressure distributions around the cylinder. Specifically, we observed that the presence of the helical strake effectively suppresses the periodic vortex shedding phenomenon, resulting in a change in the time-averaged state of the cylinder structure. This finding highlights the potential benefits of incorporating helical strakes into the design of offshore structures. It is desirable to suppress the generation of periodic vortex shedding in the wake without causing significant changes in the original pressure distribution. This conclusion is consistent with previous studies by other researchers [4,11]. However, the pressure distribution indicated asymmetry distribution in the wake after the strake attached onto the cylindrical structure.
Figure 10 depicts the dimensionless time history of the drag and lift coefficients from to . By comparing the results for the cylinders with and without a helical strake, it is apparent that the lift–drag curve for the bare cylinder exhibits periodic fluctuations, while that of the cylinder equipped with a helical strake shows irregular vibrations with small amplitude. Additionally, there is a significant change in the behavior of the time-average lift coefficient. It changes from zero to non-zero, leading the cylinder subject asymmetry force in the flow. This result can be attributed to the asymmetrical geometry of the cylindrical structure in the cross-flow direction after the strake is installed. The results are consistent with our previous observation that the helical strake can intersect with the periodic vortex shedding. Moreover, it can be seen that the drag coefficient curve for the helical strake case is higher than that for the case without a helical strake. Therefore, the installation of a helical strake subjects the entire offshore structure system to increased flow forces. Nevertheless, compared to the fatigue damage caused by the vortex-induced vibration phenomenon, the impact of this increased force only needs to be considered in terms of the overall structural strength.
The FFT analysis was applied in this study to analyze the lift coefficient frequency and vibration amplitude. The Strouhal number can be calculated from the FFT analysis result. Figure 11 illustrates the spectra of the lift coefficient for the cylinder with and without a helical strake. The peak of the spectra indicates the frequency of vortex shedding. The results show that the attachment of the helical strake leads to a decrease in the frequency of vortex shedding. Additionally, the amplitude of lift coefficient has a trend to decrease when the cylinder is attached to the strake. Using Equation (10), the Strouhal number, a dimensionless number, can be calculated, resulting in values of 0.2016 and 0.0058 for the cylinder with and without the helical strake, respectively. The settlement results indicate that the Strauss number and the peak of the spectra follow the same trend. To make the analysis more general, the following sections will focus on the Strouhal number. The results clearly demonstrate that the helical strake suppresses the periodic vortex shedding around cylindrical structures. The subsequent sections will provide further details about the effects of helical strake parameters.
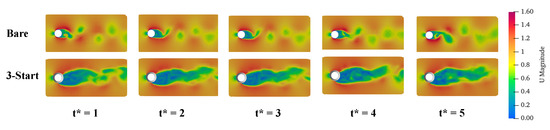
Figure 7.
Instantaneous velocity distribution of bare and strake attached cylinder.
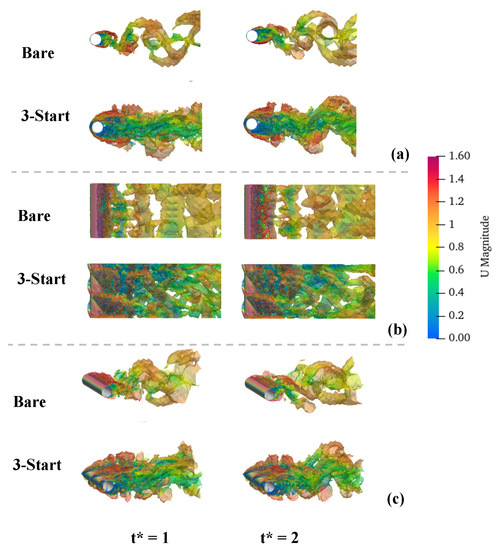
Figure 8.
Visualization of vortex (Q = 0.01). (a) Front view, (b) plan view and (c) side view.
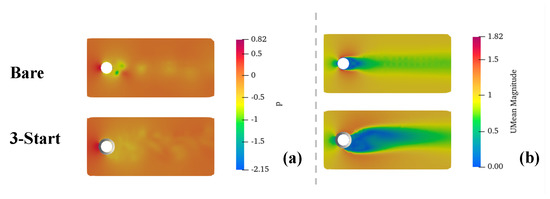
Figure 9.
Mean pressure and velocity distribution: (a) Pressure and (b) the mean velocity magnitude.
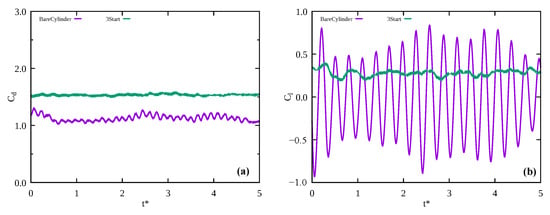
Figure 10.
Drag and lift coefficients of cylindrical structure: (a) Drag coefficient and (b) lift coefficient.
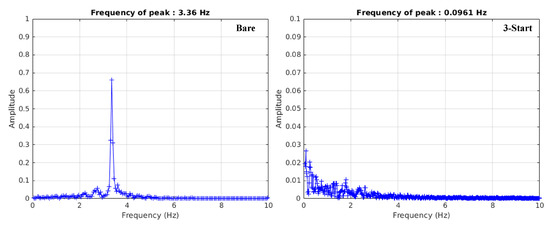
Figure 11.
Spectra of lift coefficient for the cylinder with and without helical strake.
3.2. Effect of Strake Number
In this section, the impact of the number of strakes on the wake characteristics is summarized. The analysis of the results is presented in the following three aspects. Firstly, the influence of different numbers of strakes is visually illustrated through vortex visualization. Secondly, the rendering of streamlines near the cylinder is utilized to illustrate the effect of installing the helical strake on the vicinity of the wall. Finally, the lift and drag coefficients records are analyzed to investigate the change in the lift–drag coefficient with time and implicitly explore the possibility of suppressing vortex shedding.
Figure 12 shows the vortex visualization of front view. Firstly, the results clearly demonstrate that the addition of a helical strake can effectively inhibit the formation of a Karman vortex street. Secondly, in the vortex visualization results from the top view, it is evident that the vortex velocity in the near-wall area increases as the number of strakes increases. Furthermore, the side view reveals that the wake vortex influence area becomes wider in the crosswise with an increase in the number of strakes. However, the strength of the wake vortex is not proportional to the number of strakes; instead, it is observed to be the highest when the number of strakes is equal to three, which is consistent with the findings of previous studies [11].
Figure 13 illustrates the lift and drag coefficients of the cylindrical structure for different strake numbers. It is evident that the drag coefficient increases with the strake number, and the degree of the overall increase ranges from 45% to 70% compared to the bare cylinder. Additionally, the average lift coefficient slightly increases, but the most notable change is that there is no severe periodic fluctuation compared to the bare cylinder, achieving the aim of suppressing vortex shedding through the helical strake.
In Figure 14, the spectra of lift coefficient for the cylinder with different helical strake start numbers are presented. Obviously, the impact of changing the strake number on the lift coefficient amplitude shows a downward trend as the stroke number increases. The Strouhal numbers were calculated based on Equation (10), and the results are 0.2016, 0.003, 0.0058, and 0.004 for the bare cylinder to 4-start cylinder, respectively. These results indicate that the Strouhal number decreases as the helical strake start number increases, indicating that more helical strakes can effectively suppress periodic vortex shedding. However, the addition of helical strakes cannot be increased indefinitely. This process must consider the increase of drag force during the increase in the number of strakes as well as the influence of asymmetric force on the lift force direction. Additionally, the impact of too many helical strakes on the mechanical strength of the cylinder must also be taken into account. The optimization design process should balance multiple properties. This study provides several base points regarding the effect of strake parameters.
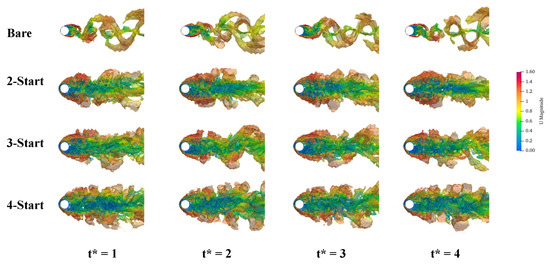
Figure 12.
Vortex visualization of front view (Q = 0.01).
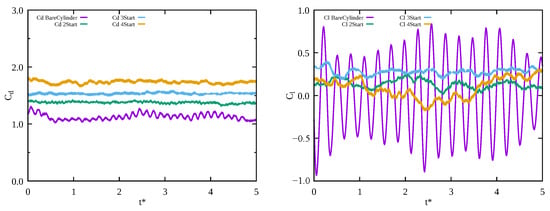
Figure 13.
Drag and lift coefficients results with different strake number.
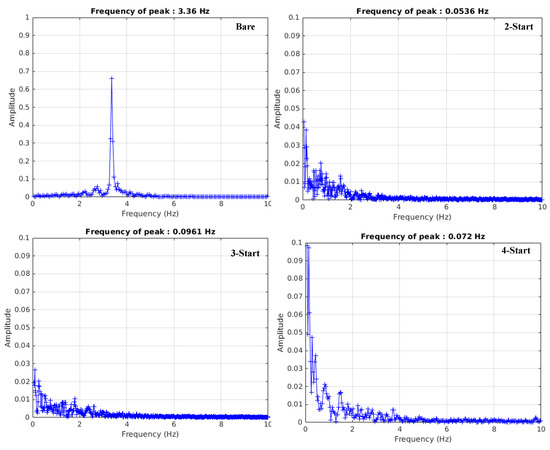
Figure 14.
Spectra of lift coefficient for the cylinder with different helical strake start number.
3.3. Effect of Strake Pitch
Figure 15 presents the vortex visualization at different times and strake pitches, using the same standard as before (Q = 0.01). From the front view, it can be observed that as the pitch increases, the Karman vortex street of the wake appears again. However, unlike the results presented in Section 3.2, when the pitch increases to 15 D, periodic vortices reappear only in the wake far field. This implies that while periodic eddies are suppressed near the wall, they can be regenerated in the far field. Nonetheless, with further increases in pitch, far field periodic eddies are suppressed again but do not disappear. The results show that both SP05 and SP10 have the effect of suppressing periodic vortex shedding, but the SP10 leads the wake vortex wider in a cross direction. By doing so, we can achieve both optimal performance and material cost savings for the installation of the helical strake. However, these results are different from those of the previous study [11], which suggest that a helical strake with a pitch equal to 15 D is more recommended. Hence, a more in-depth study is necessary to understand its underlying principles.
Figure 16 displays the variation in lift and drag coefficients of the cylindrical structure under different pitches. The drag coefficient increases with the pitch, and when the pitch is equal to 20, there is a sudden drop in the drag coefficient, which requires further research and analysis. Moreover, the lift coefficient exhibits a unique behavior. Initially, it increases with an increase in pitch, and when the pitch reaches 15 D, it demonstrates a similar periodic change. This observation may be linked to the previous vortex visualization results, where a periodic vortex was generated in the far field at 15 D. As the pitch further increases, the lift coefficient drops to approximately −0.5. This phenomenon is valuable in offshore engineering, as some offshore engineering structures need support in a specific direction.
Figure 17 depicts the lift coefficient spectra for the cylinder with a different helical strake pitch. As the strake pitch increases, the lift-coefficient amplitude shows an upward trend. The Strouhal numbers were calculated based on Equation (10), and the results are 0.0058, 0.06, 0.137, and 0.152, respectively, from SP05 to SP20 cylinders. These results indicate that the Strouhal number increases as the strake pitch increases, meaning that the larger the helical strake pitch, the weaker the effective suppression of periodic vortex shedding. This finding corresponds to the previous vortex visualization results, showing that periodic vortex shedding reoccurs in the far field after SP15. This result also implies that the increase in pitch makes the characteristics of the stroke-attached cylindrical structure more similar to those of the bare cylinder. However, even at SP20, the cylinder still has a certain degree of periodic vortex shedding inhibition compared to the bare cylinder.
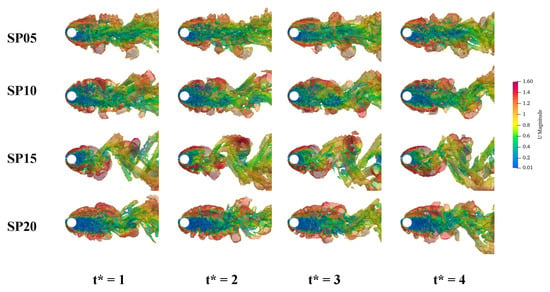
Figure 15.
Vortex visualization of front view (Q = 0.01).
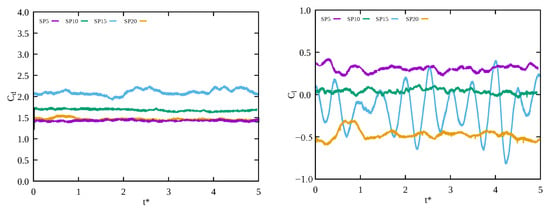
Figure 16.
Drag and lift coefficients with different strake pitch.
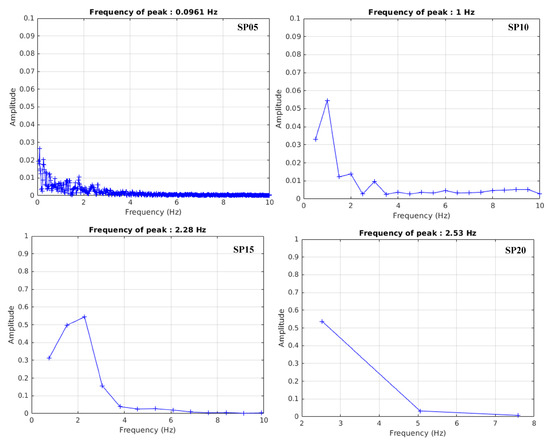
Figure 17.
Spectra of lift coefficient for the cylinder with different helical strake pitch.
3.4. Mean Drag and Lift Coefficient
In this section, we aim to analyze the influence of the strake number and pitch by processing the results obtained earlier. First, we averaged the lift–drag curves over time and drew the curves based on the results shown in Figure 18. As seen in Figure 18a, the average drag coefficient constantly rises with the increase in the strake number. However, the change in the average lift curve is not significant, and the trend is closer to the result of the fluctuations. To further analyze the influence of the average lift curve, additional cases are required. Furthermore, as shown in Figure 18b, with an increase in pitch, the overall trend of both the average lift coefficient and the average drag coefficient is downward. This implies that increasing the pitch number can suppress the periodic vortex shedding of the wake and reduce the resistance of the system to a lesser extent. However, it can be observed that there is a critical point in the average resistance curve during the process of increasing the pitch. The results namely are that the quantitative value of the strake number should be limited to a critical value based on the marine platform tolerance. The strake pitch should be less than 15 D in the case of reproducing periodic vortex shedding. Further research is needed to determine the reason for this result.
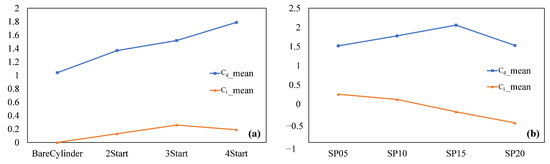
Figure 18.
Trend of mean drag and lift coefficient: (a) Different strake number. (b) Different strake pitch.
4. Conclusions
In this paper, the influence of different strake numbers and pitches on offshore cylindrical structures is studied using the LES to explore the potential of suppressing vortex shedding. The numerical simulation results indicate that helical strakes can effectively disrupt the vortex shedding phenomenon in offshore cylindrical structures. The following conclusions are drawn from this study:
- Attaching the helical strake can effectively suppress the periodic vortex shedding phenomenon in the wake, which is consistent with previous experimental results.
- The asymmetry distribution for lift will accompany the addition of the helical strake; it is mainly caused by the unbalanced pressure distribution on the up and down surfaces.
- As the strake number increases, the occurrence of the VIV phenomenon can be better suppressed. However, increasing the strike number results in drag increase.
- The strake pitch has a significant impact on the vortex shedding of the cylindrical structure. When the pitch exceeds 15D, the periodic vortex shedding phenomenon reappears. Therefore, it is necessary to prevent the occurrence of periodic vortex shedding regeneration in the far field.
- Further research is required to investigate the effects of the strake height, strake thickness, and strake shape on the vortex shedding of cylindrical structures.
Author Contributions
H.Z.: conceptualization, methodology, investigation, visualization, and writing—original draft; Y.-W.L.: conceptualization, supervision, project administration, funding acquisition, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Industrial Science and Technology Research Center of Pukyong National University (2023).
Data Availability Statement
Data available on reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Billah, K.Y.; Scanlan, R.H. Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. Am. J. Phys. 1991, 59, 118–124. [Google Scholar] [CrossRef]
- Guyer, J.P.; Pe, R. Ethical Issues from the Tacoma Narrows Bridge Collapse; Continuing Education and Development, Inc.: Woodcliff Lake, NJ, USA, 1999. [Google Scholar]
- Liu, G.; Li, H.; Qiu, Z.; Leng, D.; Li, Z.; Li, W. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 106704. [Google Scholar] [CrossRef]
- Hong, K.S.; Shah, U.H. Vortex-induced vibrations and control of marine risers: A review. Ocean Eng. 2018, 152, 300–315. [Google Scholar] [CrossRef]
- Wang, J.s.; Fan, D.; Lin, K. A review on flow-induced vibration of offshore circular cylinders. J. Hydrodyn. 2020, 32, 415–440. [Google Scholar] [CrossRef]
- Song, J.; Wang, T.; Chen, W.; Guo, S.; Yan, D. Vibration control of marine top tensioned riser with a single tuned mass damper. J. Mar. Sci. Eng. 2020, 8, 785. [Google Scholar] [CrossRef]
- Zhou, W.; Duan, M.; Chen, R.; Qiu, H.; Li, H.; Wang, S.; Wang, Y. Experimental Study on Vortex-Induced Vibration of Tension Leg and Riser for Full Depth Mooring Tension Leg Platform. J. Mar. Sci. Eng. 2023, 11, 180. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Ye, J. Experimental study on motion characterisation of CALM buoy hose system under water waves. J. Mar. Sci. Eng. 2022, 10, 204. [Google Scholar] [CrossRef]
- Srinil, N. Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents. Appl. Ocean Res. 2011, 33, 41–53. [Google Scholar] [CrossRef]
- Simantiras, P.; Willis, N. Investigation on vortex induced oscillations and helical strakes effectiveness at very high incidence angles. In Proceedings of the International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]
- Lubbad, R.K.; Løset, S.; Moe, G. Experimental investigations of the efficiency of round-sectioned helical strakes in suppressing vortex induced vibrations. J. Offshore Mech. Arct. Eng. 2011, 133, 041102. [Google Scholar] [CrossRef]
- Assi, G.R.; Crespi, T.; Gharib, M. Novel geometries of serrated helical strakes to suppress vortex-induced vibrations and reduce drag. Appl. Ocean Res. 2022, 120, 103034. [Google Scholar] [CrossRef]
- Mekki, A.; Ali, M.M. Numerical simulation of Kadomtsev–Petviashvili–Benjamin–Bona–Mahony equations using finite difference method. Appl. Math. Comput. 2013, 219, 11214–11222. [Google Scholar] [CrossRef]
- Sukarnoor, N.I.M.; Lee, K.Q.; Abu, A.; Kuwano, N.; Hooi-Siang, K.; Mat Desa, S. The effectiveness of helical strakes in suppressing vortex-induced vibration of tandem circular cylinders. Ain Shams Eng. J. 2022, 13, 101502. [Google Scholar] [CrossRef]
- Zhou, T.; Razali, S.M.; Hao, Z.; Cheng, L. On the study of vortex-induced vibration of a cylinder with helical strakes. J. Fluids Struct. 2011, 27, 903–917. [Google Scholar] [CrossRef]
- Wang, C.; Ge, S.; Jaworski, J.W.; Liu, L.; Jia, Z. Effects of Different Design Parameters on the Vortex Induced Vibration of FRP Composite Risers Using Grey Relational Analysis. J. Mar. Sci. Eng. 2019, 7, 231. [Google Scholar] [CrossRef]
- Wang, J.; He, Z.; Li, D.; Wu, W. Numerical Simulation of Vortex-Induced Vibration of TTR and SCR. J. Mar. Sci. Eng. 2022, 10, 708. [Google Scholar] [CrossRef]
- Santillan, S.T.; Virgin, L.N. Numerical and experimental analysis of the static behavior of highly deformed risers. Ocean Eng. 2011, 38, 1397–1402. [Google Scholar] [CrossRef]
- Vásquez, J.A.M.; Julca Avila, J.P. A parametric analysis of the influence of the internal slug flow on the dynamic response of flexible marine risers. Ocean Eng. 2019, 174, 169–185. [Google Scholar] [CrossRef]
- Atadan, M.; Das, B.; Gopalakrishnan, S. Analytical and numerical analysis of the dynamics of a marine riser connected to a floating platform. J. Sound Vib. 1997, 208, 579–603. [Google Scholar] [CrossRef]
- Kharazmi, R.; Ketabdari, M.J. Numerical modeling to develop strake design of Spar platform for Vortex-Induced motions suppression. Ocean Eng. 2022, 250, 111060. [Google Scholar] [CrossRef]
- Yang, W.; Ai, Z.; Zhang, X.; Chang, X.; Gou, R. Nonlinear dynamics of three-dimensional vortex-induced vibration prediction model for a flexible fluid-conveying pipe. Int. J. Mech. Sci. 2018, 138, 99–109. [Google Scholar] [CrossRef]
- Yao, J.; Zhen, X.; Huang, Y.; Wang, W. Numerical Investigation on Hydrodynamic Characteristics of Immersed Buoyant Platform. J. Mar. Sci. Eng. 2021, 9, 168. [Google Scholar] [CrossRef]
- Wang, J.; Sun, S.; Tang, L.; Hu, G.; Liang, J. On the use of metasurface for Vortex-Induced vibration suppression or energy harvesting. Energy Convers. Manag. 2021, 235, 113991. [Google Scholar] [CrossRef]
- Joshi, V.; Jaiman, R.K. A variationally bounded scheme for delayed detached eddy simulation: Application to vortex-induced vibration of offshore riser. Comput. Fluids 2017, 157, 84–111. [Google Scholar] [CrossRef]
- Chen, D.Y.; Abbas, L.K.; Wang, G.P.; Rui, X.T.; Lu, W.J. Suppression of vortex-induced vibration features of a flexible riser by adding helical strakes. J. Hydrodyn. 2018, 31, 622–631. [Google Scholar] [CrossRef]
- Ishihara, T.; Li, T. Numerical study on suppression of vortex-induced vibration of circular cylinder by helical wires. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104081. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, W.; Zhou, T. Direct numerical simulation of the wake adjustment and hydrodynamic characteristics of a circular cylinder symmetrically attached with fin-shaped strips. Ocean Eng. 2020, 195, 106756. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Flow Turbul. Combust. 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Zhao, H.; Chakma, P.; Jeon, J.; Lee, Y. Numerical Study on the Effect of the Rotating Ratio of Circular Cylinder on Wake Vortex Suppression using OpenFOAM. In Proceedings of the Korean Society of Mechanical Engineers KSME Annual Meeting, Jeju, Republic of Korea, 22–24 June 2022; p. 867. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- OPENCFD. OpenFOAM v2012 Userguide. 2020. Available online: https://www.openfoam.com/documentation/guides/v2112/doc/ (accessed on 1 February 2021).
- Ducros, F.; Nicoud, F.; Poinsot, T. Wall-adapting local eddy-viscosity models for simulations in complex geometries. Numer. Methods Fluid Dyn. VI 1998, 293–299. Available online: https://www.researchgate.net/publication/248366844_Wall-Adapting_Local_Eddy-Viscosity_Models_for_Simulations_in_Complex_Geometries (accessed on 29 September 2020).
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Zdravkovich, M.M.; Bearman, P.W. Flow around Circular Cylinders—Volume 1: Fundamentals; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at Re D = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Lourenço, L.M.; Shih, C. Characteristics of the Plane Turbulent Near Wake of a Circular Cylinder. 1993, Quoted in Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at Re D = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar]
- Norberg, C. An experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J. Fluid Mech. 1994, 258, 287–316. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).