Study of Mechanical Properties of Three-Dimensional Framed Plate Protective Structures with Negative Poisson’s Ratio

Abstract

In this paper, the negative Poisson’s ratio and rigidity of a protective structure are improved to allow the structure to exert a negative Poisson’s ratio effect in multiple directions and to enhance the structural load-carrying capacity. Therefore, a 3D framed plate honeycomb is designed on the basis of a traditional 2D negative Poisson’s ratio honeycomb. The Poisson’s ratio and modulus of elasticity are derived, and the equivalent mechanics model (EMM) of a 3D framed plate protective structure is established by combining bending deformation, shear deformation, and compression deformation. To verify the validity of the equivalent mechanics model (EMM), a compression test and numerical simulation study are carried out by combining 3D printing technology and numerical simulation methods. In addition, the effects of structural parameters on the modulus of elasticity, negative Poisson’s ratio, and other mechanical properties are discussed. The results show that, under vertical loading, the equivalent Poisson’s ratio and the modulus of elasticity of the cell elements decrease with the increase in the ratios of the lengths of the cell element walls in the upper and lower planes to the length of the diagonal cell element in the concave direction. In addition, it is shown that the elastic modulus increases with increasing concave angle and thickness. Moreover, under lateral loading, the equivalent Poisson’s ratio of the cell elements increases with the ratios of the lengths of the upper and lower planar cell element walls to the length of the diagonal cell element walls, with the angle of concavity and with the thickness of the plate frame, while the modulus of elasticity of the cell elements exhibits the opposite trend and decreases with the thickness of the framed plate structure.

1. Introduction

Advanced protective structures are crucial for providing explosion and impact protection for ships. Strategies for improving the anti-explosive and anti-impact properties of ships have evolved, leading to the development of lightweight and efficient protection systems from traditional metal framed plate structures. Negative Poisson’s ratio structures, classified as a unique type of mechanical metamaterial, offer distinctive advantages in terms of bending resistance [1], impact resistance [2,3,4], energy absorption [5,6], vibration isolation [7], load carrying [8], shear modulus [9], fracture toughness [10], and fatigue resistance. Consequently, these structures have been rapidly developed in aerospace, automotive manufacturing, construction engineering, and biomedicine [11,12,13]. The new design of an advanced negative Poisson’s ratio structure is significant for enhancing the anti-explosive and anti-impact properties of ships.

Negative Poisson’s ratio structures can exhibit different mechanical properties through structural design. Typical inner concave [14], rotating polygona [15], chiral [16], and other negative Poisson’s ratio structures can be manufactured to show different mechanical properties through structural design. Fu [17] generated a new honeycomb structure with a negative Poisson’s ratio, incorporating a rhombic design into a concave honeycomb and increasing flexural strength and in-plane stiffness. Larsen [18] designed optimized 2D concave triangular structures using topological optimization methods, which can exhibit negative Poisson’s ratio properties after adjusting the length of the bars and the angle between adjacent bars. Rafsanjani [19] proposed a concave negative Poisson’s ratio metamaterial with structural biostability that maintained its shape after unloading. Grima [20] proposed a semirigid rotating square, which is a particular type of negative Poisson’s ratio structure. Lu [21] proposed a 3D crossed chiral structure with the same chiral negative Poisson’s ratio structure in the three principal stress directions by connecting neighboring layers of a chiral material to diagonal rods. Some research has been carried out by scholars on two-dimensional negative Poisson’s ratio structures. Ingrole et al. [22] obtained a 2D negative Poisson’s ratio hybrid structure with controlled failure modes by improving the conventional inner-concave negative Poisson’s ratio structure and combining it with a positive hexagon. Qiao et al. [23] combined functional gradient materials to design honeycomb structural forms with different thickness gradients and angles. Relative to traditional two-dimensional honeycombs with a uniform distribution, the reasonable allocation of the relative density of the honeycomb could effectively improve the structural impact resistance. Tang et al. [24] designed a 2D hybrid graded negative Poisson’s ratio honeycomb structure with excellent compressibility and ductility. Ajdar et al. [25] explored the effects of initial defects in 2D honeycombs on the overall performance by removing some cell elements in a uniform structure.

To further exploit the bidirectional properties of a negative Poisson’s ratio and improve the structural energy absorption, scholars have focused on 3D negative Poisson’s ratio structures. Choi [26] developed an analytical formula for the mechanical properties of three-dimensional concave hexagonal honeycomb structures, and analytical equations were derived for the equivalent modulus of elasticity and Poisson’s ratio of the system. Yang et al. [27] theoretically studied 3D concave structures. The scholars showed that the mechanical properties of this form of honeycomb structure were mainly determined by the ratio of the length of the members to the angle of the concavity. Wang et al. [28] optimized the design of triangular cells, making it a three-dimensional spatial configuration, and a cylindrical negative Poisson’s ratio honeycomb structure was obtained using this cell element arrayed in all directions. A cylindrical negative Poisson’s ratio honeycomb structure was obtained using this cell element dressed in all orders. A flexible negative Poisson’s ratio structure with flexural crystals serving as cell elements was proposed in a paper by Babaee et al. [29]. Wei et al. [30,31,32] introduced triangles into the traditional star-shaped honeycomb structure, proposed a novel star-triangle honeycomb structure, and investigated its deformation behaviors at different velocities. The negative Poisson’s ratio effect of the star-triangle honeycomb under pressure in two directions was analyzed via numerical simulation, and a theoretical model was developed to accurately predict its Young’s modulus and Poisson’s ratio. The star-triangle honeycomb structure was extended to three dimensions, and a combination of experimental and simulation methods was used to study its deformation mode and analyze the effects of gradient design on the deformation and energy absorption of the structure. The above studies showed that the honeycomb structure maintained the negative Poisson’s ratio effect even under large strains. Bodaghi M et al. [33] fabricated a new type of ship fender plate using a 4D printing technique using a fusible filament of shape memory polylactic acid polymer, and its thermomechanical behavior was analyzed experimentally and simultaneously. The results showed that the proposed fender structure had a good energy absorption capacity, and the plastic deformation could be fully recovered by simple heating. Hamzehei R et al. [34] fabricated a novel 3D zero Poisson’s ratio metamaterial by 4D printing and achieved piecemeal energy absorption (PEA) by introducing horizontal bars in the cells. Existing 3D negative Poisson’s ratio structures primarily enhance energy absorption through the gaps between cell elements. It is essential to note that, for advanced naval explosion-proof impact and vibration isolation protection measures, such as equipment impact bases and vibration isolation bases, a negative Poisson’s ratio structure should not only provide high energy absorption and vibration isolation performance but also have a certain degree of stiffness performance. Therefore, the protective structure required not only a smooth platform stress but also a high equivalent modulus of elasticity to meet the load-carrying requirements.

Based on the background of a ship’s protective structure, the meaning of the present scenario is obvious, which is to bring some high energy absorption structures with a certain degree of stiffness. In order to fulfill this, the 3D framed plate protection structure was proposed, the derivation of Poisson’s ratio and elastic modulus, and an EMM of the 3D framed plate protection structure by combining bending deformation, shear deformation, and compression deformation were constructed, which is the novelty of the present work. The specimens were manufactured via 3D printing technology and a numerical simulation was conducted, and the proposed EMM was verified through a combination of tests and simulation. The main contents are as follows: In Section 2, cell element forms for 3D framed plate protective structures are constructed from a negative Poisson’s ratio honeycomb structure. In Section 3, the equivalent parameters of 3D negative Poisson’s ratio structures in cell element form are derived using theoretical methods, and an EMM is established by combining bending deformation, shear deformation, and compression deformation characteristics. The Young’s modulus and equivalent Poisson’s ratio of framed plate protective structures in different directions are deduced. In Section 4, compression tests are carried out to obtain the mechanical properties of 3D negative Poisson’s ratio structures, and the theoretical model is verified by comparing the experimental and simulation results. The conclusions are shown in Section 5.

2. Structural Design

The framed plate protective structure proposed in this paper is a dimension extension of the 2D negative Poisson ratio structure. Stretch the 2D cell outward toward the face by a distance b to form spatial configurations. Then, a 2D cell is rotated 90 degrees around the Y-axis and orthogonally combined with another cell to form a 3D cell. The top and bottom portions of the 3D cell are shown as crossed plates, and the middle portion has concave plates in both directions. After obtaining 3D cell elements, single cell elements are arrayed along the lateral (X), vertical (Y), and axial (Z) directions to form a 3D honeycomb structure. The single-cell element parameters and 3D negative Poisson’s ratio honeycomb are shown in Figure 1.

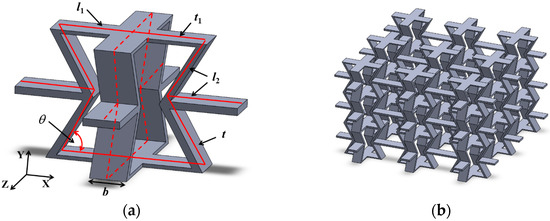
Figure 1. (a) 3D framed plate cell element and (b) 3D negative Poisson’s ratio honeycomb structures.

3. Theoretical Analysis of Mechanical Properties

3.1. Relative Density

The specific derivation of the relative density of a 3D framed plate protective structure with a negative Poisson’s ratio $\rho$ is shown below [35]:

$$\rho =\frac{\mathrm{Actual}\mathrm{volume}\mathrm{of}\mathrm{all}\mathrm{rods}\mathrm{of}\mathrm{a}\mathrm{single}\mathrm{cell}\mathrm{element}\text{\_}{V}_a}{\mathrm{Volume}\mathrm{occupied}\mathrm{by}\mathrm{the}\mathrm{corresponding}\mathrm{size}\mathrm{of}\mathrm{the}\mathrm{outer}\mathrm{edge}\mathrm{of}\mathrm{the}\mathrm{cytosol}\_V_0}$$

(1)

The actual volume of all rods within a single cell element $V_a$ is calculated as follows:

$$V_a=2(2l_1{t}_1+4l_{2}t+2l_{2}t)b-2t_1{b}^2=b(4l_{1}t+12l_{2}t-tb)$$

(2)

The equations for the macroscopic dimensions, such as the length and width $W$, and height $H$ of a single typical cell element, are as follows:

$$H=2l_2\sin \theta$$

(3)

$$W=l_1+2l_2-2l_2\cos \theta$$

(4)

Therefore, the expression for the volume of the equivalent space occupied by the outermost edge of the cell element $V_0$ is as follows:

$$V_0=H\times W^2=2l_2(l_1+2l_2-2l_2\cos \theta )\sin \theta$$

(5)

Due to the thicknesses of the framed plate protective structures, there is an overlapping effect of the cell element at positions A and B, and the exact overlap is illustrated in Figure 2. The overlapping effect is shown in Figure 3.

Figure 2. Overlapping effects of cell elements.

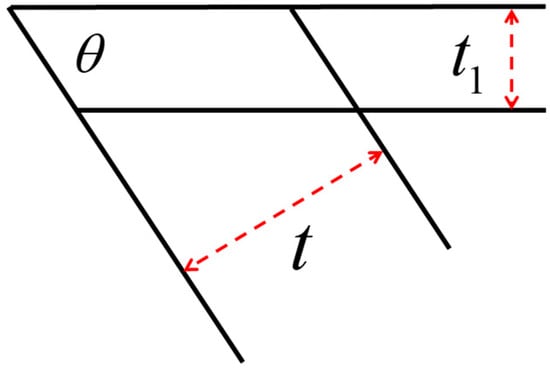
Figure 3. Overlapping effects of cell elements.

The volume is $V_1=\frac{16t_{1}tb}{\sin \theta }$, and the actual volume after correction to account for overlap effects is as follows:

$$V_a=b(4l_{1}t+12l_{2}t-tb-\frac{16t_{1}t}{\sin \theta })$$

(6)

Therefore, the relative density can be expressed as follows:

$$\rho =\frac{V_a=b(4l_{1}t+12l_{2}t-tb-\frac{16t_{1}t}{\sin \theta })}{2l_2(l_1+2l_2-2l_2\cos \theta )\sin \theta }$$

(7)

3.2. Compression in Vertical Direction (Y Direction)

When subjected to pressure, the deformation form of the negative Poisson’s ratio honeycomb is different from that of other ordinary structures [36], as shown in Figure 4. For the negative Poisson’s ratio, under the compressed load, the material shrinks in the lateral direction. When the 3D structure is subjected to uniaxial compression in the vertical (Y)-direction, its mechanical responses in X and Z directions are consistent due to structural symmetry. Assuming that the cell element is subjected to a stress of ${\sigma }_Y$, the pressure on the tilted wall of the cell element is $F_Y$, and the bending displacement of the tilted wall of the cell element under loading is ${\delta }_{YR}$. In addition, ${\delta }_{YS}$ is the shear displacement of the tilted wall of a cell element under loading, and ${\delta }_{YT}$ is the compressive displacement of the tilted wall under loading. The force situation with the simplified force model is shown in Figure 5. For ease of analysis, the deformed portion of the structure is simplified to a cantilever beam model. To improve the accuracy of the calculation results, Timoshenko beam theory was used for the analysis.

Figure 4. Differences between positive and negative Poisson’s ratios.

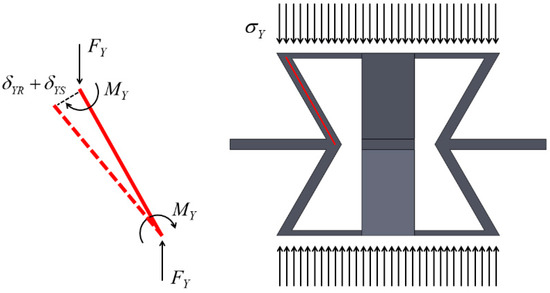
Figure 5. Vertical (Y) direction force and simplified model.

The pressure $F_Y$ on the cell element can be expressed as follows:

$$F_Y=\frac{{\sigma }_Y(2l_1-b)b}{4}$$

(8)

From the static equilibrium condition, the relationship between the bending moment $M_Y$ and the pressure $F_Y$ can be obtained and expressed in the following equation:

$$M_Y=\frac{1}{2}{F}_Y{l}_1\cos \theta$$

(9)

Then, the bending deformation ${\delta }_{YR}$ of the inclined wall of the cell element under the action of the bending moment is as follows:

$${\delta }_{YR}=\frac{F_Y{l}_2{}^3\cos \theta }{3EI}-\frac{M_Y{l}_2{}^2}{2EI}=\frac{F_Y{l}_2{}^3\cos \theta }{12EI}$$

(10)

where $I$ is the moment of inertia of the inclined wall section, which can be expressed as $I=\frac{b{t}^3}{12}$, and $E$ is Young’s modulus of the base material.

When the ratio of the length of the inclined wall to the thickness of the section is small, the effect of shear on the deformation needs to be considered, and the displacement of the inclined wall of the cell element due to shear ${\delta }_{YS}$ can be expressed as follows:

$${\delta }_{YS}=\frac{\partial U_{YS}}{\partial Q_Y}$$

(11)

where $Q_Y$ is the shear stress and $U_{YS}$ is the shear energy of the inclined wall. To obtain the total shear energy of the inclined wall, the shear stresses distributed on the inclined wall are integrated, and the expressions for $Q_Y$ and $U_{YS}$ are as follows:

$$Q_Y=F_Y\cos {\theta }_0$$

(12)

$$U_{YS}={\displaystyle \underset{0}{\overset{l_2}{\int }}\frac{Q_Y{}^2}{2G{A}_S}}dx=Y\frac{3Q_Y{}^2{l}_2}{5GA}$$

(13)

The displacement ${\delta }_{YS}$ of the inclined wall due to shear is as follows:

$${\delta }_{YS}=\frac{U_{YS}}{Q_Y}=\frac{3Q_Y{l}_2}{5GA}$$

(14)

where $A$ represents the cross-sectional area of the inclined wall, $B$ represents the inclined wall shear modulus, and $G=E/\left(2\left(1+v\right)\right)$, where $v$ represents the Poisson’s ratio of the substrate.

The partial force $T_Y$ generated by pressure $F_Y$ in the direction of the inclined wall causes the compressive deformation of the inclined wall.

$${\delta }_{YT}=\frac{F_Y{l}_2\sin \theta }{Ebt}$$

(15)

The displacements ${\delta }_X$ and ${\delta }_Y$ of the cell element in Y and X axes upwards are shown below:

$${\delta }_X=2\left({\delta }_{YR}+{\delta }_{YS}\right)\sin \theta -2{\delta }_{YT}\cos \theta$$

(16)

$${\delta }_Y=2\left({\delta }_{YR}+{\delta }_{YS}\right)\cos \theta +2{\delta }_{YT}\sin \theta$$

(17)

In the elastic deformation stage of the material, the stress should become proportional with Hooke’s law, and its proportional coefficient is called the elastic modulus. Then, the equivalent modulus of elasticity $E_Y$ of the cell element in the Y direction is as follows:

$$E_Y=\frac{{\sigma }_Y}{{\epsilon }_Y}=\frac{{\sigma }_Y}{\frac{2\left({\delta }_{YR}+{\delta }_{YS}\right)\cos \theta +2{\delta }_{YT}\sin \theta }{2l_2\sin \theta }}$$

(18)

The equivalent Poisson’s ratio $v_Y$ of the cell element can be expressed as follows:

$$v_Y=-\frac{{\epsilon }_X}{{\epsilon }_Y}=-\frac{\left({\delta }_{YR}+{\delta }_{YS}\right)\sin \theta -{\delta }_{YT}\cos \theta }{\left({\delta }_{YR}+{\delta }_{YS}\right)\cos \theta +{\delta }_{YT}\sin \theta }\left(\frac{2l_2\sin \theta }{l_1+2l_2\pm 2l_2\cos \theta }\right)$$

(19)

3.3. Compression in Lateral Direction (X Direction)

Assuming the cell element is subjected to a stress of ${\sigma }_X$, the pressure on the inclined wall of the cell element is $F_X$ and ${\delta }_{XR}$ is the bending displacement of the tilted wall of the cell element under loading. Moreover, ${\delta }_{XS}$ is the shear displacement of the tilted wall of a cell element under loading, and ${\delta }_{XT}$ is the compressive displacement of the tilted wall of the cell element under loading. The force on the cell element in the lateral direction (X direction) with the simplified force model is shown in Figure 6.

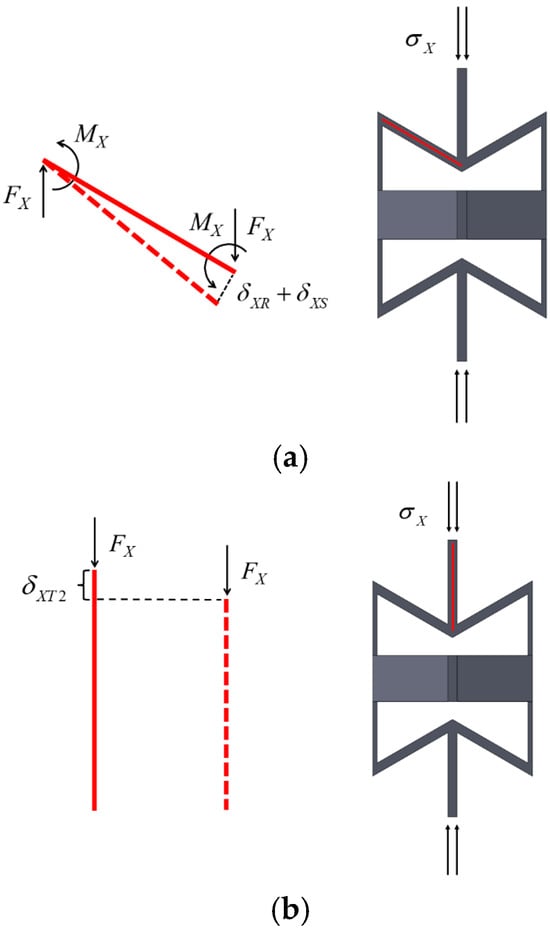
Figure 6. (a) Bending and shear deformation; (b) compressive deformation lateral (X) direction force case and simplified model.

The pressure $F_X$ on the inclined wall of the cell element is as follows:

$$F_X={\sigma }_{X}bt$$

(20)

From the static equilibrium condition, the relationship between the bending moment $M_x$ and the pressure $F_x$ can be obtained as follows:

$$M_X=\frac{1}{2}{F}_X{l}_2\sin \theta$$

(21)

Then, the overall deformation of the tilted wall of the cell element is divided into three parts: bending deformation, shear deformation, and compression deformation. The expressions are as follows:

Bending deformation:

$${\delta }_{XR}=\frac{F_X{l}_2{}^3\sin \theta }{3EI}-\frac{M_X{l}_2{}^2}{2EI}=\frac{F_X{l}_2{}^3\sin \theta }{12EI}$$

(22)

Shear deformation:

$$Q_X=F_X\sin \theta$$

(23)

$$U_{XS}={\displaystyle \underset{0}{\overset{l_2}{\int }}\frac{Q{x}^2}{2G{A}_S}}dx=\frac{3Q_X{}^2{l}_2}{5GA}$$

(24)

$${\delta }_{XS}=\frac{U_{XS}}{Q_X}=\frac{3Q_X{l}_2}{5GA}$$

(25)

Compression deformation:

$${\delta }_{XT1}=\frac{F_X{l}_2\cos \theta }{Ebt}$$

(26)

$${\delta }_{XT2}=2\frac{{\sigma }_x{l}_1}{E}=2\frac{F_X{l}_1}{Ebt}$$

(27)

In summary, the displacements when the cell element is loaded in the X-axis direction can be expressed as follows:

$${\delta }_X=2\left({\delta }_{XR}+{\delta }_{XS}\right)\sin \theta +2{\delta }_{XT1}\cos \theta +{\delta }_{XT2}$$

(28)

$${\delta }_Z=2\left({\delta }_{XR}+{\delta }_{XS}\right)\cos \theta +2{\delta }_{XT1}\sin \theta$$

(29)

Therefore, the equivalent modulus of elasticity of the cell element in the X-axis upward $E_X$ is as follows:

$$E_X=\frac{{\sigma }_X}{{\epsilon }_X}=\frac{{\sigma }_X}{\frac{2\left({\delta }_{XR}+{\delta }_{XS}\right)\sin \theta +2{\delta }_{X{T}_1}\cos \theta +{\delta }_{X{T}_2}}{2(l_2-l_2\cos \theta )+2l_2}}$$

(30)

The expression for the equivalent Poisson’s ratio $v_X$ of the cell element is as follows:

$$v_X=-\frac{{\epsilon }_Y}{{\epsilon }_X}=-\frac{2\left({\delta }_{XR}+{\delta }_{XS}\right)\cos \theta +2{\delta }_{X{T}_1}\sin \theta }{2\left({\delta }_{XR}+{\delta }_{XS}\right)\sin \theta +2{\delta }_{XT1}\cos \theta +{\delta }_{X{T}_2}}\left(\frac{l_1+2l_2\pm 2l_2\cos \theta }{2l_2\sin \theta }\right)$$

(31)

4. Verification and Discussion

4.1. Experimental Test

A 3D framed plate protective structure with a negative Poisson’s ratio is fabricated using rapid prototyping 3D printing technology with C-UV9400R material. The material properties are shown in Table 1. Compression tests of 3D framed plate protective structures with negative Poisson’s ratios are carried out. The parameters of the cell elements of the designed specimen are shown in Table 2. Six specimens are processed and prepared. The experimental specimens are designed based on GB1453-2022 [37] with five cell elements (more than four) in both the horizontal and vertical directions. The compression load is applied to the specimens using an electronic universal testing machine (WDW-100) at a constant speed of 1 mm/min, and the compression test setup is shown in Figure 7. [36,38].

Table 1. Material properties of C-UV 9400R.

Densities g/cm3	Poisson’s Ratio ν	Modulus of Elasticity E (MPa)
1.11	0.4	2600

Table 2. Parameters of cell elements 1–3.

$\mathit{\theta }$	$\mathit{b}$ (mm)	$\mathit{t}$ (mm)	${\mathit{l}}_1$ (mm)	${\mathit{l}}_2$ (mm)
50°	10	2	40	20
60°	10	2	40	20
70°	10	2	40	20

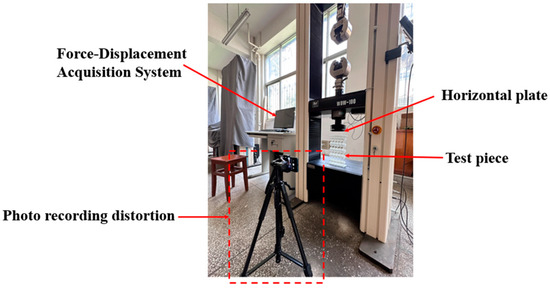
Figure 7. Compression test setup.

Four nodes on the cell elements in the region are selected as calibration points, as shown in Figure 8. The cells are labeled according to their rows as $A_{1~2}$ or $B_{1~2}$. By assuming that the deformed calibration points are denoted as $A_{1~2}{}^{\prime }$ or $B_{1~2}{}^{\prime }$, the displacement in the vertical and lateral directions before and after the deformation can be expressed as follows:

$$\Delta X=\frac{\left(A_1{B}_1+A_2{B}_2-A_1^{\prime }{B}_1^{\prime }-A_2^{\prime }{B}_2^{\prime }\right)}{2}$$

(32)

$$\Delta Y=\frac{\left(A_1{A}_2+B_1{B}_2-A_1^{\prime }{A}_2^{\prime }-B_1^{\prime }{B}_2^{\prime }\right)}{2}$$

(33)

Figure 8. Measuring points of specimen.

The equivalent Poisson’s ratio of the specimen can be expressed as follows:

$$v_Y=-\frac{\Delta X/X_0}{\Delta Y/Y_0}$$

(34)

$$v_X=-\frac{\Delta Y/Y_0}{\Delta X/X_0}$$

(35)

where $X_0$ and $Y_0$ are the initial lengths of the specimen measurement area in the X and Y directions, respectively.

When the specimen is loaded in the X direction, the oblique cell wall is convex along the Y direction, and the curvature decreases as the concave angle increases. When the specimen is loaded in the Y direction, the central cell wall is concave along the X direction, and the curvature increases with the concave angle. The specimen compression is shown in Table 3 (the first row corresponds to the concave angle, and the first column corresponds to the loading direction). The equivalent Poisson’s ratio and equivalent elasticity modulus values of the specimens are obtained, as shown in Table 4.

Table 3. Compression deformation of specimens.

	$50°$	$60°$	$70°$
X
Y

Table 4. Equivalent mechanical properties of specimens.

$\mathit{\theta }$$(°$)	Loading Direction	Equivalent Poisson’s Ratio	Equivalent Modulus of Elasticity (EX/E&EY/E)
50	X	−1.382	0.0480
50	Y	−0.646	0.00231
60	X	−0.904	0.0311
60	Y	−0.955	0.00362
70	X	−0.547	0.0269
70	Y	−1.426	0.00769

4.2. Numerical Simulation

Structural stress analysis of cell elements is performed using ABAQUS (2022) finite element software, adopting an ideal elastic-plastic model with material parameters consistent with the test parameters. The FE (finite element) model is shown in Figure 9. A finite element model is developed using eight-node solid cells, reduced integral equations, and an hourglass control method. Considering model complexity, simulation accuracy, and efficiency, a mesh of 1 mm is selected, which has been verified as an appropriate mesh element in relevant studies [39]. To investigate the mechanical response of the structure in the corresponding directions, a forced displacement of 1 mm/min is applied to the upper and side (left) surfaces of the unit element in X and Y directions, respectively, and a fixed constraint is applied on the opposite side.

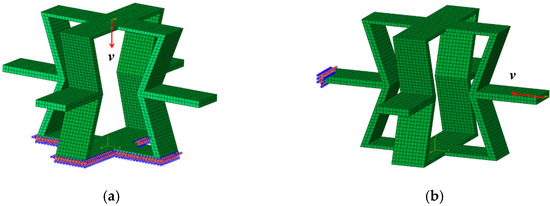
Figure 9. Cell element of 3D framed plate structures in finite element models in (a) X direction; (b) Y direction.

The compression response process of the specimen is shown in Figure 10. When the specimen is loaded in the X direction, with the compression process, the diagonal rod is initially compressed and bent, and the upper and lower cell walls are bent outwardly, exhibiting a negative Poisson’s ratio phenomenon. When the specimen is loaded in the Y direction, with the compression process, the diagonal rod first undergoes compression and bending. Moreover, the wall of the diagonal cell element is concave to the central axis, showing a negative Poisson’s ratio phenomenon. The bidirectional negative Poisson’s ratio effect is noticeable. As the concave angle increases, the stress increases, and the degree of rod bending becomes more significant.

Figure 10. Compression process response of (a) $\theta ={50}^{°}$ in the X direction; (b) $\theta ={50}^{°}$ in the Y direction; (c) $\theta ={60}^{°}$ in the X direction; (d) $\theta ={60}^{°}$ in the Y direction; (e) $\theta ={70}^{°}$ in the X direction; and (f) $\theta ={70}^{°}$ in the Y direction.

Figure 11 illustrates the variations in the Poisson’s ratio and the equivalent modulus of elasticity values with concave angle $\theta$ of the framed plate honeycomb structure when compressed in the Y direction. As shown in the figure, the results are consistent with the finite element simulation results and test results. The figure shows the variations in the Poisson’s ratio and the equivalent modulus of elasticity values with concave angle $\theta$ when the framed plate honeycomb structure is compressed in the X direction. The variation curve of the Poisson’s ratio with concave angle $\theta$ in the experimental and simulation results is consistent with that of the theoretical EMM.

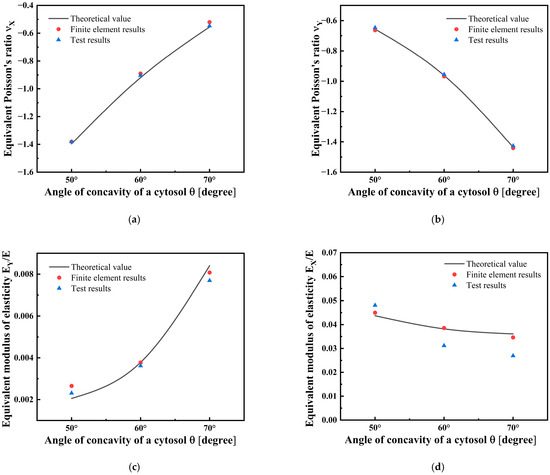
Figure 11. Poisson’s ratio of the 3D framed plate structure in the (a) X direction and (b) Y direction and the modulus of elasticity in the (c) X direction and (d) Y direction.

4.3. Validation of Results and Discussion

The variations in the mechanical properties with cell element design parameters are analyzed. Based on the theoretical derivation of the equivalent modulus of elasticity and the equivalent Poisson’s ratio, the cell element parameters are substituted into the equations to analyze the effects of $\theta$, $t$, and $l_1/l_2$ on the mechanical properties of the framed plate structure. The thickness of the framed plate $t$ is set to three values: 1.5 mm, 2 mm, and 2.5 mm. Moreover, $l_1/l_2$ is set to five ratios: 2, 2.5, 3, 3.5, and 4. In addition, $\theta$ is set to a range of values ${40}^{°}~{65}^{°}$, and $b$ is set to a fixed value of 5 mm.

The variation patterns of the equivalent Poisson’s ratio and modulus of elasticity in the Y direction with $\theta$, $t$, and $l_1/l_2$ are shown in Figure 12. When the framed plate cell element form is loaded in the Y direction, the absolute magnitude of the cell element equivalent Poisson’s ratio decreases as $l_1/l_2$ increases. With a constant $l_2$ value, an increase in $l_1$ implies a decrease in transverse strain, and the negative Poisson’s ratio effect weakens. As $\theta$ increases, the structural negative Poisson’s ratio effect becomes more pronounced. With increasing Poisson’s ratio, the effect is increasingly sensitive to the values of $l_1/l_2$ and $\theta$. A cross-sectional comparison of the trends of the equivalent Poisson’s ratios of cell elements with three different plate frame thicknesses shows that $t$ has little effect on the absolute value of the Poisson’s ratio of the structure. The modulus of elasticity ratio $E_Y/E$ increases as $l_1/l_2$ decreases and both $\theta$ and $t$ increase. A decrease in $l_1/l_2$ leads to a decrease in strain in the Y direction, which causes an increase in $E_Y/E$. An increase in $t$ implies a thickening of the bars. In addition, the stiffness of the structure is improved, and the value of $E_Y/E$ is increased. As $\theta$ increases, the size of the cell element along the Y direction increases; thus, the strain decreases, and the equivalent elastic modulus increases. Additionally, $l_1/l_2$ has a greater effect on the structural equivalent modulus of elasticity than both $\theta$ and $t$.

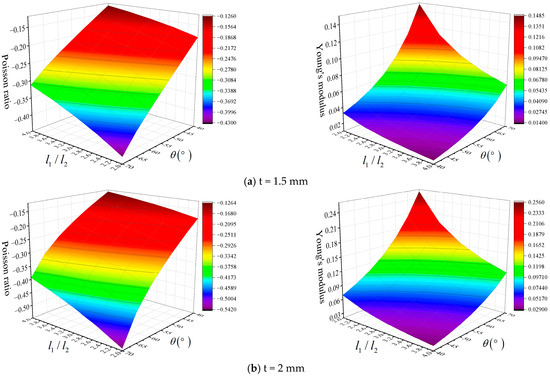
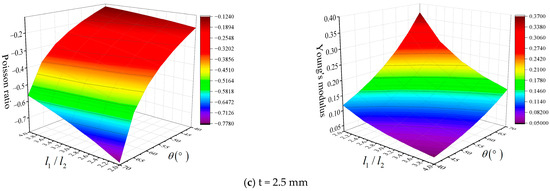
Figure 12. Variations in the equivalent Poisson and elastic modulus ratios of cell elements in the Y direction with $l_1/l_2$ and $\theta$.

The variations in the equivalent Poisson’s ratio and modulus of elasticity in the X direction with $\theta$, $t$, and $l_1/l_2$ are shown in Figure 13. When framed plate structures with negative Poisson’s ratios are subjected to X-direction loading, the Poisson’s ratio decreases with increasing $\theta$, $t$, and $l_1/l_2$. Similar to the Y-direction pressure, the cell element along the Y-direction size increases with $\theta$. Moreover, the decrease in the Y-direction strain leads to a decrease in the Poisson’s ratio. Furthermore, $l_1/l_2$ and $t$ have little effect on the Poisson’s ratio, but the absolute value of Poisson’s ratio is relatively sensitive to $\theta$. As $l_1/l_2$ increases and $t$ decreases, the parameter $E_X/E$ decreases. An increase in $t$ indicates a greater stiffness and an increase in $E_X/E$. In addition, $l_1/l_2$ has a large effect on $E_X/E$, and both $\theta$ and $t$ have little effect.

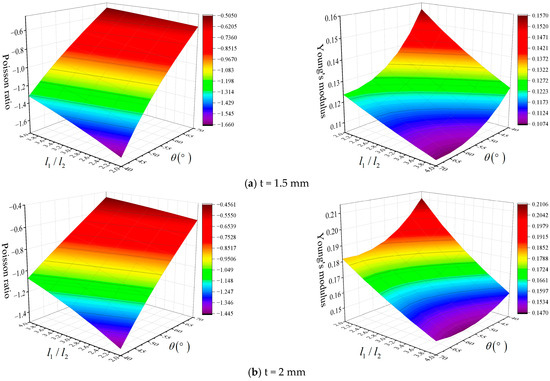
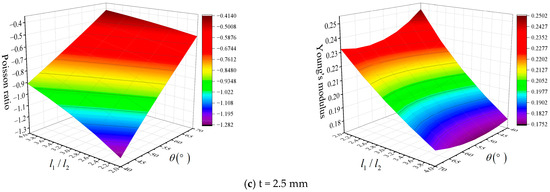
Figure 13. Variations in the equivalent Poisson and elastic modulus ratios of cell elements in the X direction with $l_1/l_2$ and $\theta$.

5. Conclusions

To adapt to the development trend of ship structure protection, today’s protection structure should take into account a certain degree of stiffness while playing the role of energy absorption and impact resistance. Based on the tendencies of a ship’s protective structure, the meaning of the present scenario is obvious, which is to bring some high energy absorption structures with a certain degree of stiffness. To fulfill this, the 3D framed plate protection structure, the derivation of Poisson’s ratio and elastic modulus, and the EMM of the 3D framed plate protection structure was proposed by combining the bending deformation, shear deformation, and compression deformation were constructed. The main conclusions drawn from this investigation are as follows:

(1) In this paper, based on the traditional 2D negative Poisson’s ratio honeycomb, a 3D plate-and-shelf honeycomb is proposed, which can exert the negative Poisson’s ratio effect in multiple directions, and simultaneously has a certain degree of load carrying capacity. An EMM of the cell in the vertical and lateral directions is established by combining bending deformation, shear deformation, and compression deformation.

(2) Compression tests of 3D framed plate protective structures with a negative Poisson’s ratio are carried out. The Poisson’s ratio and modulus of elasticity values of the specimen with different concave angles in distinct loading directions are obtained. The evolution trends of the elements are obtained based on numerical simulations. The validity of the theoretical EMM is verified through a combination of the experimental and numerical results.

(3) The effects of structural parameters on the mechanical properties, such as the modulus of elasticity and Poisson’s ratio, are investigated. In the Y direction, the equivalent Poisson’s ratio of the element decreases with increasing $l_1/l_2$. When the Poisson’s ratio is large, the material is more sensitive to the values of $l_1/l_2$ and $\theta$. In addition, as $l_1/l_2$ decreases, $\theta$, $t$, and $E_Y/E$ increase. In the X direction, the Poisson’s ratio decreases with increasing $\theta$, $t$, and $l_1/l_2$. However, $l_1/l_2$ and $t$ have little effect on the Poisson’s ratio. Moreover, the Poisson’s ratio is more sensitive to $\theta$. The parameters $t$ and $E_X/E$ decrease when $l_1/l_2$ and $\theta$ increase.