Abstract
The article deals with some issues of geometric modeling of ship hull structures in specialized CAD system. Stiffened shells and platings should be idealized as a set of elementary plate panels for the purpose of structural design using local strength and buckling requirements. In the process of geometric modeling and creating the database for calculation, a special searching algorithm for closed loops of every panel should be used. This algorithm is to have good performance and versatility. In this paper, the authors suggest an original algorithm used in CADS-Hull software developed in SMTU. It is based on a regular field of points generation within the large contour of the considered structure. A series of rays is built from every point to find intersections. It is shown that this algorithm is quite good for structures (expansions, decks, bulkheads, etc.) with non-orthogonal boundaries. Some tasks for logical operations with found panels are also discussed. One of them is the clipping of a panel or plate polygon by boundaries of a considered structure (expansion contour, hull lines). The authors developed a generic method of polygons clipping. It is based on a rotation of clipping convex polygons together with the clipped polygons. All faces of the latter that are in the negative half-plane are removed. Some problems of collecting data for every found panel are discussed. An original algorithm of smaller and larger size definition for irregular and triangular panels is also given in this paper.
1. Introduction
The requirements of the Rules of Classification Societies for platings’ local strength and buckling are formulated within the scope of a plate model. In terms of real structure, the plates correspond to panels of platings and framing beams. The supporting structure of the panels is formed using stiffening elements—primary supporting members, stiffeners, brackets or adjoining adjacent structures (decks, bulkheads, etc.). The Rules of Register of Shipping, Part II [1], uses the term “plate element” for such panels. The Rules of other Classification Societies and CSR documents use the term “elementary plate panel”, or EPP (see, for example, ref. [2]). The literal definition in [2] states that it is “an unsupported part of the plate located between the ordinary and/or primary supporting member”.
Each plate can include a few score of panels. Notably, in recent decades, one of the development trends of the Rules has been the transition to more physical methods for determining calculated load, which involves determining loads for each panel for dozens of different scenarios. This, in particular, predetermines the need to use specialized software to verify the compliance of the structure sizes with the Rules requirements.
If we talk about the CAD system for ship structures, then the determining of the required thickness of platings just begins with the design level of the elementary plate panel according to the requirements for local strength, minimum thicknesses, and buckling [3]. At the same time, each panel’s data are further used at various stages up to data transfer for the FEM verification calculation. In addition, each panel must have a unique identifier in the CAD system, which makes it possible to uniquely determine whether the panel belongs to the plate and indicates the beam elements located along the panel borders.
Considering the above, at the stage of geometric and structural modeling in the specialized CAD system, in addition to the obvious problems of describing the ship hull and internal structures shape, setting the position of welds and framing beams, the problem of identifying the panel loops arises. Their number for the entire ship hull usually reaches dozens of thousands. As well as the massive scale problem, there is another thing that complicates the named problem. Panels in real structures usually have a shape that significantly differs from the ideal rectangular shape (quadrangular) described in the Rules. In ship structures, most especially located outside the parallel middle body area and on bulkheads, there are often found panels in the shape of a parallelogram, an arbitrary convex polygon or a triangle (see Figure 1). Consequently, the main requirements for algorithms for panels loops searching in specialized CAD system are speed, reliability and flexibility.
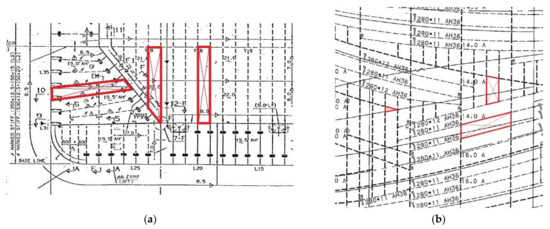
Figure 1.
Variants of the loop shape of real EPPs on the transverse bulkhead (a) and ship outer shell plating (b).
The order of subtasks for automated data preparation for plate panels as applicable for ship structural design is shown on Figure 2. At first, a considered part of a structure should be selected (Figure 2A). Usually, it is a part of a hull (side, deck, inner bottom, etc.) bounded by adjacent structures. Then, the contour of structure boundaries and their strengthening topology should be considered (B). The user of a CAD-system needs to enter data about the position of welding joints, stiffeners and primary supporting members forming the arrangement of a structure. After that, coordinates and other data for every plate (C) and EPP (D) must be found.
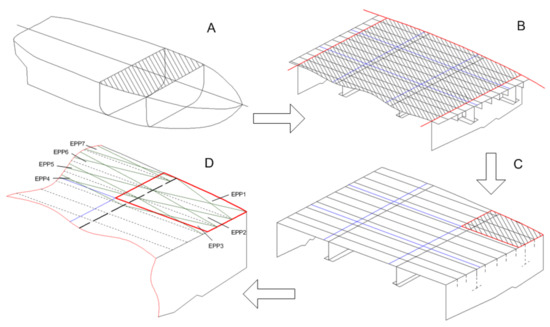
Figure 2.
Sequence of steps for preparing data as applicable for elementary plate panel strength calculations. (A) selection of part of the structure; (B) consideration of the contour of structure boundaries and their strengthening topology; (C) determination of coordinates and calculation data for the of each plate; (D) determination of coordinates and calculation data for each EPP. Plate borders are shown in blue, in red—the borders of the selected plate or structure.
Then, there is a problem of a smaller and larger panel size calculation. Section 1 of this article is devoted to this issue. Some difficulties and solutions for the problem of identifying plate contours are described in Section 4 of this article. Section 2 and Section 3 are devoted to the issues of identifying contours of plate panels for structures with orthogonal and non-orthogonal boundaries.
In addition to the text of the IACS CSR, some aspects of EPP idealization are described in [4,5]. These articles deal with the creation of finite element models, mainly, and do not contain any detailed algorithms for panel loops searching.
At this point a rather small number of publications devoted to solving the problems of automated panel borders identification have been found, but the software package “CADS-Hull”, intended to solve such problems, has been successfully developed and is constantly being improved at SPbSMTU by specialists from the departments of Structure and operation of the ships and ship design [6]. Further, all algorithms and examples of visualization are given on the basis of this package execution.
Additionally, each panel corresponds to a set of parameters which have to be determined. The authors also considered it appropriate to briefly discuss in this article the issue of reducing non-rectangular panels to the calculated rectangular ones and determining their sizes. Moreover, there is the related problem of clipping a polygon by another convex polygon. The corresponding original algorithm is also described in this work.
2. The Main Issues of Panels Idealization in Rules—The Set of Parameters for Each Panel
The main geometric parameters, determined for the calculation according to the Rules, are its larger size a 1 and its smaller size b, as well as the coordinates of points at which it is appointed to calculate the load (load calculation point—LCP), Figure 3.
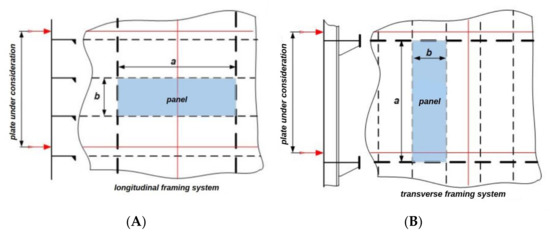
Figure 3.
Calculation panels for longitudinal (A) and transverse (B) framing systems.
Prescriptive requirements 2 of the Rules for local strength and buckling are formulated for rectangular plates. Additionally, if correction factors for curvilinear plates are introduced [2], then there are no instructions on how to perform prescriptive calculations for non-rectangular plates. Meanwhile, in section Ch.8, Sec.4, 2.3 [2] (requirements for the panel idealization for the purposes of buckling verifying with consideration to FEM), the algorithm for reducing the panel to the equivalent is included and will be described below.
In that case, it seems that the strength and buckling verifying of such panels should be carried out only according to the FEM. However, the authors are of the opinion that analytical–empirical calculations are quite appropriate for elongate plates, the shape of which can be reduced to a rectangular one, although the question of such reduction method justification requires separate studies.
Currently, the CADS-Hull software package implements the following reduction algorithm (for smaller and larger panel sizes searching for the purposes of calculations according to prescriptive requirements), developed by the authors of present article:
- The content and the center of gravity of the figure that makes up the panel is determined;
- Straight lines are drawn through the center of gravity with a certain step (it is convenient to choose 1°), on which figure boundaries form sections;
- A section with minimum length is detected. The smaller size of the reduced rectangular plate b is considered equal to this length;
- The larger plate size a is determined by dividing the panel content by the smaller size.
The shape of the EPP is a convex polygon with the number of vertices equal to k. Its centroid position can be easily found: x = Σxi/k; y = Σyi/k;
Then, a number of segments are drawn from the centroid to each vertex. The contour of the considered EPP becomes divided into k − 1 triangles. For each triangle, the area can be determined according to the Heron formula:
where m, n, k—triangle sides lengths,
p—semi-perimeter of a triangle:
The total area of all triangles is an area of EPP:
The larger size of EPP b can be found as
The basic principles of analytical geometry used in the system (calculation of the position of the point of intersection of segments, calculation of the length of a segment, etc.) are programmed based on the methods proposed in well-known works, for example [7]. The calculation of the intersection points of a segment and a polygon bounding a panel is well described in many publications, for example in [8], so there is no need to give its mathematical foundations in detail.
The algorithm for smaller and larger panel sizes searching proposed in Ch.8, Sec.4, 2.3 [2] for non-triangular plates:
- The panel content is calculated;
- The figure angles constituting the panel that are closest to right, as well as the sides corresponding to these angles, are found;
- The pairs of opposite sides with smallest length sum are found;
- The middle line is drawn as a section drawn through the midpoints of the side lengths found in the previous paragraph. The length of the middle line is equal to the larger size of the reduced panel b;
- The smaller size a is determined by dividing the panel content by the larger size b.
There is also an algorithm for triangular panels, which can be found in Ch.8, Sec.4, 2.3.3 [2].
Let us compare the described algorithms on the example of two panels—quadrangular and triangular (Figure 4, Table 1).
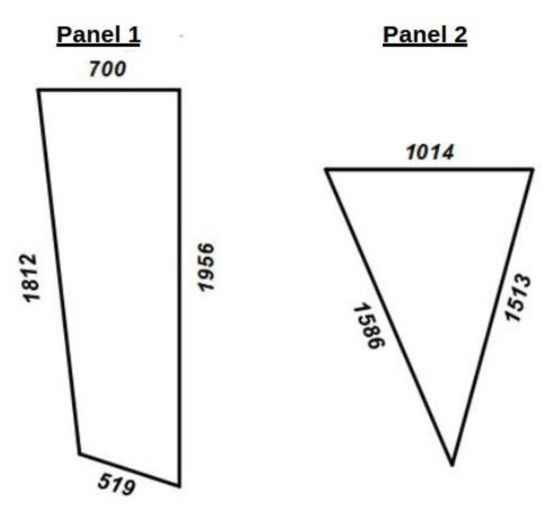
Figure 4.
Panels for comparing reduction methods (numbers show the lengths of each side in mm).

Table 1.
Comparison of the reduced plate sizes.
It can be seen that these two methods and their corresponding algorithms give close results. The thickness required in terms of the criterion of local strength is proportional 3 to the panel’s smaller side, which does not depend on its larger size for elongated plates. Critical stresses non-linearly depend on the plate sizes and their ratio, but in different ways depending on the framing system, so it is quite difficult to give such a simple estimate. However, it can be expected that the difference in required thicknesses when using these two different methods will not be significant. In any case, the issue of reducing non-rectangular panels is also the issue of improving the Rules.
As was said in the Introduction, the Rules require a calculation for each panel. However, this or other required site thickness must finally be assigned to each specific plate. For real ships, it is possible for one panel to belong to four plates at once (Figure 5).
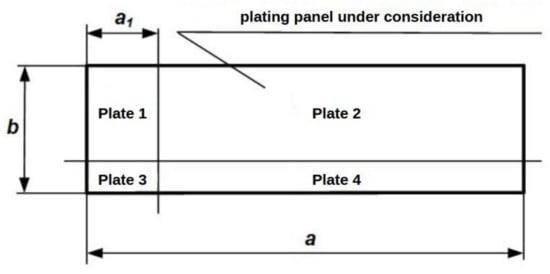
Figure 5.
An example of the panel with two intersecting welds.
For such cases, a criterion is needed that allows one to judge whether a given panel should be taken into account when determining plate thickness. The requirements [2] are presented in Table 2.

Table 2.
The requirements [2] on the need to take into account the panel as a part of the plate (see Figure 5).
Regularly strengthened structures in the way of intersections with the sloped adjacent structure (for example, transverse bulkheads in the area of intersection of the hopper tank top or sloped upper deck, see Figure 1a) consist of EPPs, the large sides of which are parallel to each other. It should be noticed that using the proposed algorithm, the smaller panel size will be equal to regular spacing in contrast to the algorithm from the IACS CSR.
In addition to the geometric parameters listed above, the following data for each plate calculation are required:
- framing system (longitudinal or transverse);
- coordinates of load calculation point (LCP)—according to the Rules requirements, there are used different methods for longitudinal and transverse framing systems;
- slope angles of the panel relative to the vertical and horizontal axes;
- flow permeability sign of the ship;
- panel curvature (for example, for bilge or rounded shear streak).
Additional parameters (required for load calculation):
- characteristics of compartments on both sides of the considered panel (compartment type, environment/cargo in the compartment, compartment space, presence of heating, water escape valve, etc.);
- material of the plate to which it is “assigned” by the panel;
- category of ice strengthenings;
- minimum thickness and corrosion addition in accordance with the requirements of the Rules.
Therefore, determining the position of calculated points and other geometric parameters is one of the main problems of plate structural modeling and is the basis for all further calculations of their required thickness.
3. Panel Identifying in Design Mode with Orthogonal Supporting Structure
The expansion of shell plating or the framing scheme with an orthogonal supporting structure is, in the first instance, typical for structures in the area of the ship’s parallel middle body. Additionally, it can apply to decks and house walls, as well as some other structures at the ship’s ends.
Panel borders recognition in the rectangular expansion is carried out using a matrix, including tags of the intersection presence at all possible points where longitudinal and transverse frames can intersect. Thus, firstly, an array ArrX is formed of coordinates of all frames along the longitudinal axis (for example, the transverse members) with a saving of abscissas ArrX.X and values of the length of the stiffener along the direction of expansion ArrX[i].Y1 и ArrX[i].Y2, then an array ArrY is formed of coordinates along the transverse axis (longitudinal members, junction lines of adjacent structures). Further, a matrix is formed of all points of possible intersections between vertical and horizontal frames. If for a transverse member with abscissa X no intersection with longitudinal structures is found (Y is not in the range from Y1 to Y2), then the value “0” is written into the matrix. If there is an intersection at the point (Xi, Yi), “1” is written.
The expansion shown in Figure 6 can be expressed using a 6 × 6 matrix, which will include the following values:
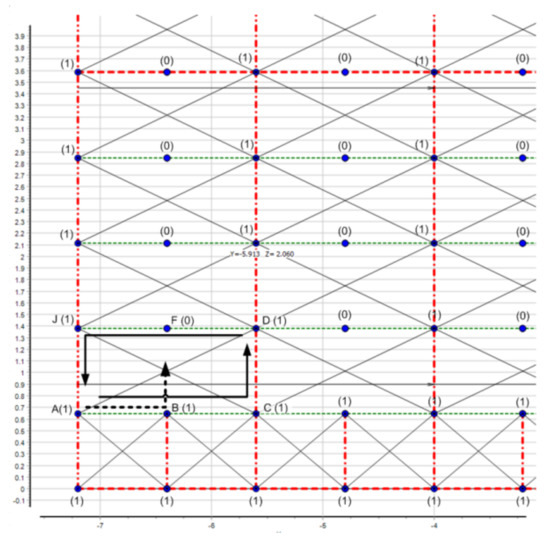
Figure 6.
Searching for the panel borders (A-C-D-J points) on the expansion of shell plating in the area of a ship’s parallel middle body. The primary supporting members and adjacent structures are shown in red, the stiffeners are shown in green.
Further, each value of the matrix is analyzed (i.e., each node of frame intersection)—moving along the matrix values from each non-zero value to the right, a search is made for the first node that has a non-zero node value above. This “non-zero node” from above will be the second diagonal point of the panel, i.e., the search for one panel will be completed.
| Algorithms 1. The algorithm can be presented as an Object Pascal code |
| for i: = 0 to HIGH(ArrX) do {enumeration of transverse supporting members} |
| for j: = 0 to HIGH(ArrY) do {enumeration of longitudinal supporting members} |
if InDiapazon(ArrX[i].Y1, ArrX[i].Y2, AY[j]) then Pts[i,j]: = 1 {there is an intersection} |
else Pts[i,j]: = 0; {there is no intersections} |
for i: = 0 to HIGH(Pts)-1 do {moving along X axis} |
for j: = 0 to HIGH(Pts[i])-1 do {moving along Y axis} |
begin |
if ((Pts[i,j] = 1) AND (Pts[i,j + 1] = 1)) then {if there is an intersection searching for the next point starts} |
begin |
k: = 1; |
{move along X until the point = 1 is found, i.e. there is an intersection} |
while ((Pts[I + k,j + 1] = −1) OR (pts[i+k,j] = −1)) AND (k < High(Pts) − i) do k: = k + 1; |
{Found a non-zero point along the diagonal} |
ii: = I + k; |
jj: = j + 1; |
iX1: = ArrX[i]; |
iX2: = ArrX[ii]; |
EPP.Points [1,0]: = IX1; EPP.Points [1,1]: = AY[j]; {first point of EPP loop} |
EPP.Points [2,0]: =IX1; EPP.Points [2,1]: =AY[jj]; {second point of EPP loop} |
EPP.Points [3,0]: =IX2; EPP.Points [3,1]: = AY[jj]; {third point of EPP loop} |
EPP.Points[4,0]: =IX2; EPP.Points [4,1]: = AY[j]; {fourth point of EPP loop} |
end; |
end; |
Such a method is quite easy to automate and it has an acceptable speed. Measurements have shown that the search for panel borders and the calculation of all the characteristics of more than two hundred panels for one grillage (for example, side) are performed on a modern personal computer in less than 0.01 s.
The result of searching for panels using the forgoing method for the bottom structures in the limit of one cargo hold in midship is shown below in Figure 7.
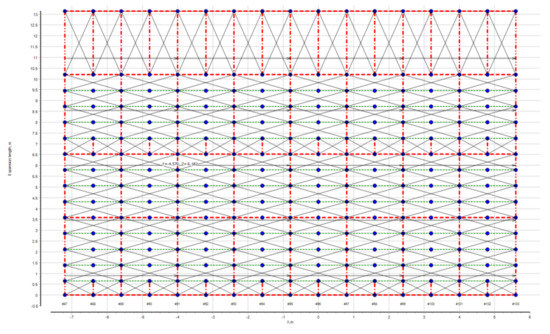
Figure 7.
The result of the searching for panels for the bottom structures of the tanker. The primary supporting members and adjacent structures are shown in red, the stiffeners are shown in green. Blue dots are nodes from the matrix shown in Figure 6.
4. Identifying Panels for Bulkheads and Structures with Non-Orthogonal Boundaries
As was shown earlier (Figure 1), the main problem of automated identification of the structure panels that are outside the middle hull area or on the transverse bulkheads is the “arbitrary” outline shaping when it can have the shape of a trapezoid, a triangle or another that differs from the ideal (rectangular). In such configurations, it is not possible to draw a panel using an intersection matrix.
This case needs a highly reliable method to detect all present panels in complex grillage.
To solve this problem, it is necessary to apply a multi-stage search method. Its algorithm is shown in Figure 8.
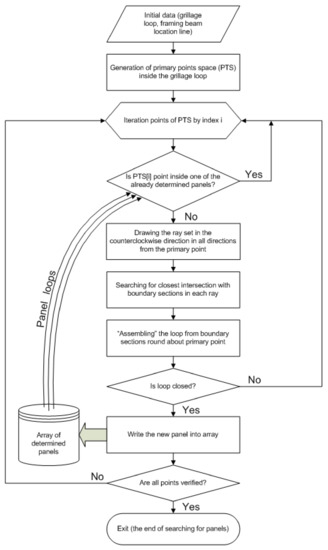
Figure 8.
An algorithm for panels searching for a structure (shell expansion) with a supporting structure of arbitrary shape.
Initially, a set of segments limiting future EPPs (corresponding to stiffeners and primary supporting members) should be constructed. The ends of the members that do not have support are cut off (see Figure 9). Each segment corresponding to the stiffener route is written into the data array with a unique number as the following data set: coordinates of two end points—Pt1(x1,y1), Pt2(x2,y2) and a reference index pointing to a stiffener in the array.
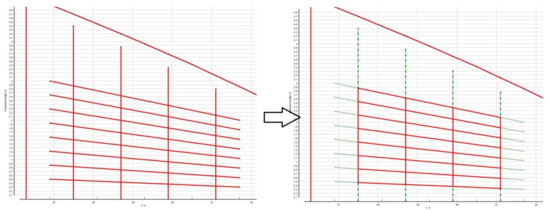
Figure 9.
Result of deleting borders for EPPs that are not anchored at both ends.
The operation of the considered method is cyclic and begins with the generation of regular points space applied to the grillage scheme (see Figure 10).
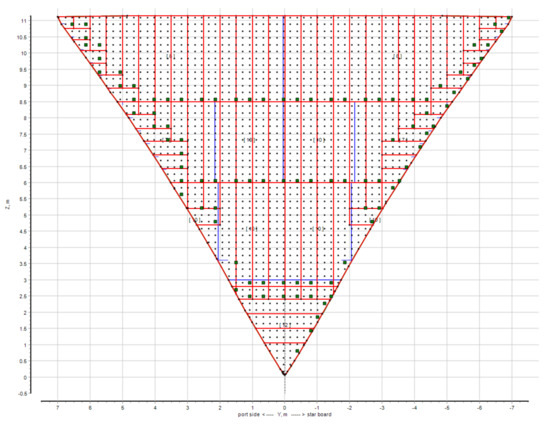
Figure 10.
Primary points space for panels searching. Green color boxes shows the points, the creation of which led to the panel detection, gray color shows passes along the already detected loops and these are not taken into account, the red lines are the borders of the EPP, the blue lines are the borders of the plates.
The distance between points is taken as a quarter spacing of the grillage ordinary members. Each point is verified for hitting the outlines of previously detected panels, and in the case of the absence of this, from a point (there and then—“primary point”), a set of sections is generated located on the rays, created with a step of one degree and having a length of three to four spacing (such values are enough for all known frames, which was established empirically). When the angle step decreases, the performance increases, but the reliability of the panel searching reduces.
The location of a point inside the contour of the already found EPP is determined by the well-known procedure for finding the number of intersections of a polygon with a ray starting at a point. If the point lies inside the polygon, then an odd number of intersections will be detected. Such an algorithm, taking into account the coincidence of intersection points with the faces and vertices of the polygon, is described in [9].
Let us assume that the “primary point” has coordinates Pt_base(x0,y0).
For each ray, a search is made for all found intersections with trace lines of beams of the set (see Figure 11) and the result is written to temporary arrays of intersection points and indices of beams with which the intersection was found—Pts[x,y]i and Indexes[], after which the distances from the Pt_base point to the Ptsi points are calculated, and the intersections located at the minimum distance from the base point are written to the intermediate results data array. In Figure 11, white dots denote the intersections of the search sections with the boundary lines first registered and defining the panel boundary; blue points denote the points that are most distant from the primary point, i.e., are not taken into account; yellow points denote the intersections of the section with the boundary line that are closest to the primary point, but that are repeated once with the already registered section in the loop and, therefore, they are not taken in account. For each intersection written to the array, the identifier of the line with which it has an intersection is stored. After verifying all the sections and storing all intersection identifiers into a single array, the loop is assembled for the panel, for which the intersection points of all lines bounding the panel are sequentially calculated. The intersection point set is the desired loop. The results of the panel searching are shown in Figure 12, Figure 13 and Figure 14.
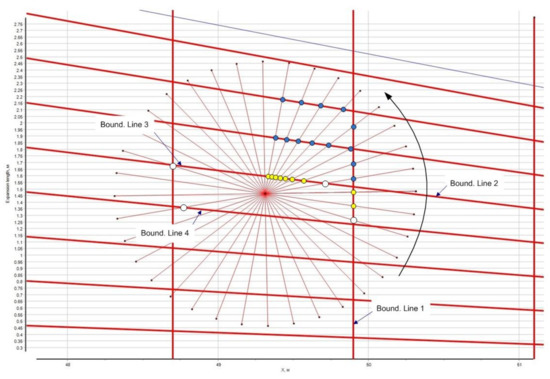
Figure 11.
Primary point (in the middle), ray sections and panel borders.
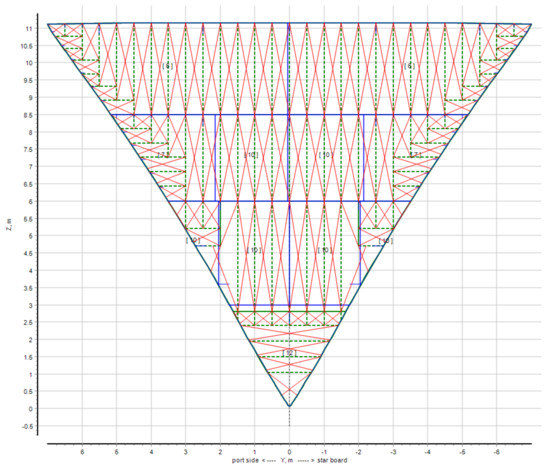
Figure 12.
The result of panel searching on a flat transverse bulkhead at the fore end of the hull (CPU Intel Core i7 11th gen, 8 Gb RAM, 95 EPPs, 0.45 s required). In this Figure the blue lines are the borders of the plates, the stiffeners are shown in green, red crosshairs—detected EPP.
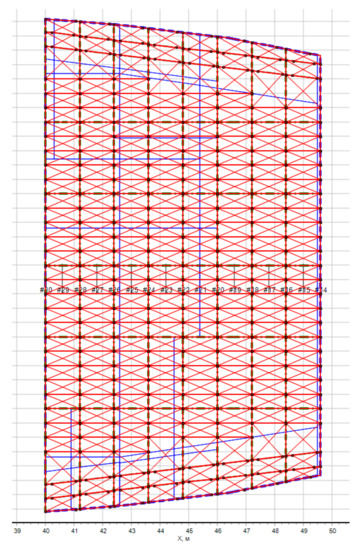
Figure 13.
The result of EPPs identification for the upper deck in the fore part of a ship (242 EPPs, 1.15 s required). In this Figure the blue lines are the borders of the plates, red crosshairs—detected EPP.
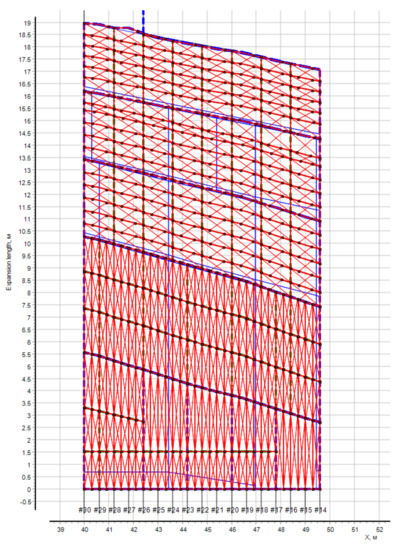
Figure 14.
The result of EPPs identification for side structures (307 EPPs, 3.8 s required). In this Figure the blue lines are the borders of the plates, red crosshairs—detected EPP.
5. Solving Geometric Problems Related to the Determining and Formation of Panels and Plates Loops
When developing software intended to solve the problems of the automated formation of ship 3D-models and databases of additional data, it is necessary to ensure the maximum possible stability of the basic procedures of geometric transformations (drawing lines, sections, searching for intersection points, etc.). One such procedure is drawing the loops of plates and panels that are part of them onto real extension and ship deck plate schemes.
It is necessary to avoid situations when the operator of the automated system has to manually correct the position of plate edges, elementary plate panels, beam location lines, etc., due to the use of unstable mathematical and geometric methods. A project database can operate several thousands of plates and dozens of thousands of panels, and the labor intensity of correcting erroneously generated loops can invalidate all the time-saving from using an automated system.
To solve this problem, it is necessary to solve a variety of basic geometric problems when developing the system code:
- the problem of detecting a sign of a point being inside a convex/non-convex polygon;
- the problem of section ends clipping that are outside the polygon loop;
- the problem of a convex/non-convex polygon clipping by another convex polygon.
The solution of the first two problems is not difficult in most cases. There is a wide range of scientific efforts addressing to their solution, using software implementation of analytical geometry methods; see [10,11] and others. It should be added that many of the proposed algorithms work stably only when the line does not coincide with one of the sides or points of the contour. If they are applied to solving problems of real ship structures, it is necessary to introduce a set of conditions that check such coincidences of faces and lines.
In the terms of the implementation of the reliable operation of the software package, it emerged that the last problem from the foregoing list is the rather difficult problem in forming the plates and panels database, in a part of the formation/generation of the plate loops. In open sources, one can find a wide range of methods that offer various candidate solutions for solving this problem. For example, the algorithm of Sutherland and Hodgman described in [12] works well for polygon clipping, including non-convex, by the so-called rectangular window. It is used for drawing plate loops if plate parameters are specified in rectangle. However, the ship grillage outlines do not always have a rectangular shape.
In the case of “clipping polygon”, Rogers [13] suggests using the methods of Liang and Barsky [10], and Weiler–Atherton [14], but the author remarks that these methods can work incorrectly in the case of edges conjunction and the appearance of so-called “hanging” edges (see Figure 15). Much the same situation arises when specifying deck plates and outer shell plating (see Figure 16 and Figure 17).
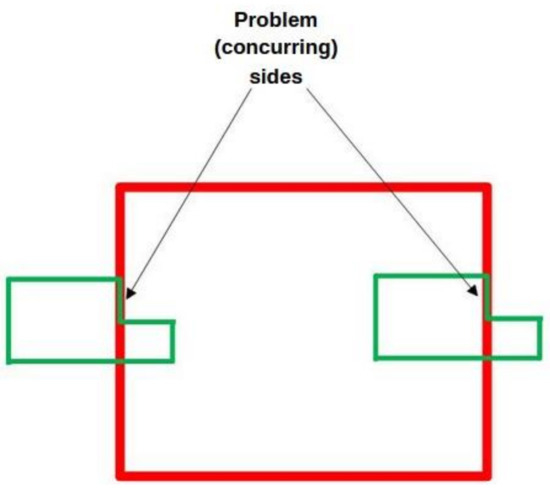
Figure 15.
An example of sides (“hanging edges”) that cause problems when forming clipped loops (the red color shows a polygon that clips, the green color shows one that is clipped).
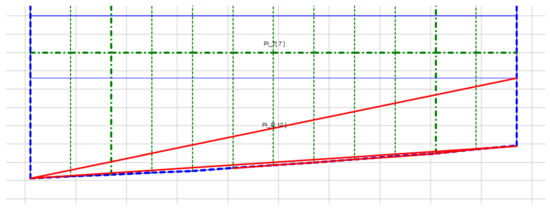
Figure 16.
Incorrect formation of plate outlines due to the partial conjunction of two sides of clipping polygon (deck grillage outlines) and two sides of clipped polygon (deck plating outlines). In this Figure green thick dashed line—primary supporting members, thin dashed line—stiffeners, blue dotted line—deck grillage borders, solid blue—plate borders. The red thick line shows the invalid plate border.
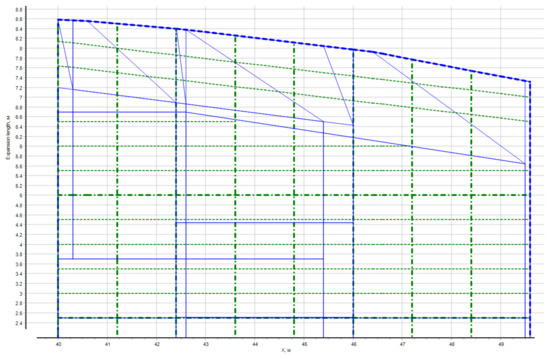
Figure 17.
Incorrect generation of plate contours due to the partial coincidence of one or two faces of the cutting polygon (contour of the deck floor) and the faces of the cut polygon (contours of deck plates). The blue lines show a large number of incorrectly generated plate contours.
From here, the foregoing methods give a stable result only under certain conditions. For example, it is mentioned, in their description, that the sides and/or point of clipped or clipping polygon should not conjunct or partially overlap/touch each other.
Experience has proved that the problem of drawing a plate loop within the scope of extensions or ship plating schemes can be narrowed down to solving the problem of the clipping of a non-convex non-intersecting polygon (loop of the expansion of outer shell plating, bulkhead, deck, etc.) by a convex polygon (plate loop that is defined by user).
This problem, according to the experience of operating leading automated systems (AutoCad [15], ASCON [16] and others), has been successfully solved, but, unfortunately, current developers of programs for computer graphics implementation do not disclose the algorithms they use. One of the solutions is given in [17,18].
For the contours of the plate panels of ship structures, such a solution seems to be difficult. Therefore, for a reliable solution to this problem when developing the CADS-Hull system, a simplified modifying method was proposed that is based on a combination of foregoing approaches. The closest to this is the “clipping window” method described, for example, in [19].
The proposed method is that the clipping convex polygon is regularly rotated together with the clipped polygon, and all sides of the last one that are in the negative half-plane are removed. At the same time, the side sequence and the loop total integrality are not lost.
For a direct description of the method operation, let us consider two polygons—clipping (red) and clipped (green). The red polygon here acts as a non-rectangular “clipping window”, and its vertices are numbered from one to seven. The initial appearance and position of the polygons are shown in Figure 18.
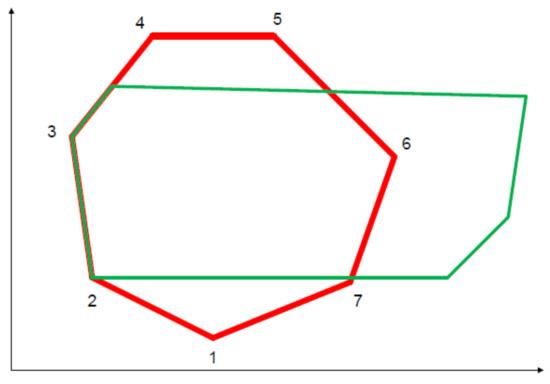
Figure 18.
Initial position of processed polygons—clipping (red) and clipped (green) The numbers on the picture are the vertex identifiers of the red polygon.
The clipping of elements protruding over the red polygon is carried out cyclically. The first action is joint transposition of polygons in the coordinate system in such a way that the side 1–7 lies on the horizontal coordinate axis. After that, a search is made for points of horizontal axis intersection with the side of “green” polygon (A and B points, Figure 19a). A gray color shows elements that are caught in the area below the horizontal axis. These elements are removed, and corresponding sides are reduced to A and B points.
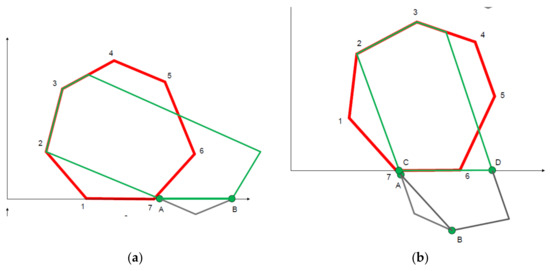
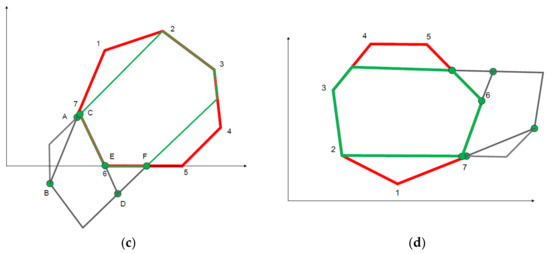
Figure 19.
The search for points of horizontal axis intersection with the clipped polygon: (a) first rotation, (b) second rotation, (c) third rotation, (d) returning the polygons to their initial positions. A, B, C, D, E, F—temporary points of intersection of the polygon and the horizontal axis at different angles of rotation.
Further, the same actions are performed, only just with respect to 7–6 sides (Figure 19b), 6–5 sides (Figure 19c) and so on, until the polygon is rotated to the last side (1–2). After these actions are completed, the polygons are transposed to their initial positions in the coordinate system, but the “green” polygon is already in a transformed form (Figure 19d). An example of the operation of the described algorithm can be seen in Figure 20 (and can be compared with Figure 16).
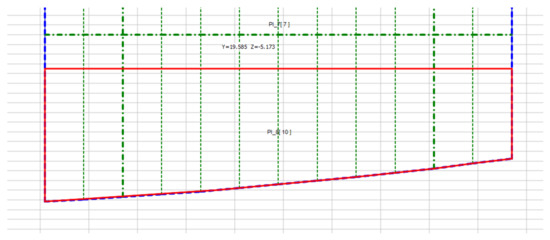
Figure 20.
An example of the correct formation of the plate loop in the case of the conjunction of a clipping polygon side (deck grillage outlines) and a clipped polygon side (deck plating loop). In this Figure green thick dashed line—primary supporting members, thin dashed line—stiffeners, blue dotted line—deck grillage borders. The red thick line shows the correct plate border.
The example of the correct identification of the contour of the plate on complex structural elements is also shown in Figure 21 (joining the bulkhead plate to the margin plate and bilge strake).
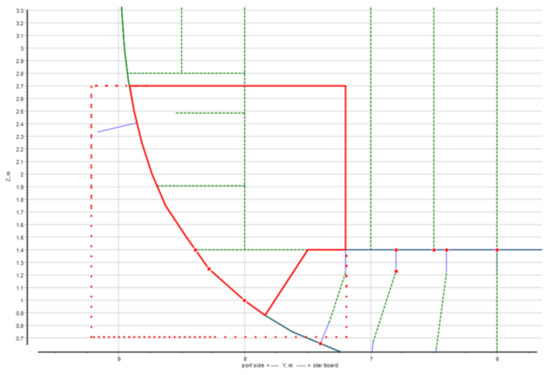
Figure 21.
An example of forming the contour of a transverse bulkhead plate in the area of adjacency of the double-bottom plate; while the first polygon is the contour of the transverse bulkhead, the second is the quadrangle of the plate borders. In this Figure: green lines—stiffeners, primary supporting members and adjoining structures, blue lines—beams shown in section, red dotted line—user-specified plate boundaries, red thick line—the result of generating the plate contour.
It should be noted that the contour of most plates is successfully generated by the previously proposed methods, and only about 1–2% of the plate contours have errors associated with the imposition of polygon faces. In this regard, it is required to test the effectiveness of the proposed algorithm. For this, one deck plate was considered (deck stringer plate). The time that is necessary for 100,000 operations of cutting the contour of this plate with the contour of the deck was measured. The calculation time for the modified Weiler–Atherton method (with a recalculation of incoming–outgoing faces, etc.) was 7.39 s on the test computer, and 4.2 s for the proposed method. The modified Weiler–Atherton method (described, for example, in [18]) is more advanced and suitable for working with two non-convex polygons with holes. For typical polygons corresponding to the ship hull, the number of vertices very rarely exceed four for plate contours and twenty for the border of the structure. We suppose the proposed algorithm to be more suitable for structural modelling when considering the ship CAD system.
The proposed algorithm can be considered as an intermediate stage between complex algorithms for crossing two arbitrary polygons, using the tactics of recalculating intersections and the “clipping window” algorithm.
The proposed method makes it possible to form loops of not only panels and plate boundaries, as considered in this article, but also a wide range of ship elements—grillages, stiffening elements, etc.—and can also be used to automate the development of line drawing and general ship allocations.
6. Conclusions
This article considers the main issues of working with plates’ (panels’) geometric models in a computer-aided design system for ship structures.
On first reading, these problems may seem trivial. However, the development of methods invariant to the considering structure for determining closed loops and logical operations with them led the authors to the idea of original algorithms development. Now, they are implemented in the CADS-Hull software package that is being developed at SPbSMTU. Currently, their work is being testing in designing hull structures of modern cargo ships.
As noted earlier in the “Introduction” section of this article, working with elementary sheet panels consists of several stages, the main ones of which are the following: forming of the structure contour, setting the sheet contour, identification of the panel contour and the calculation of its parameters. The search for the contours of elementary plate panels should be carried out using different methods for structures with orthogonal and non-orthogonal boundaries. The algorithms of the methods used at all the stages are given in this paper, and their application can significantly reduce the complexity of preparing information for calculating the strength of ship structures and structural design.
Author Contributions
Conceptualization, methodology, V.T.; project administration, S.R.; system structure, software, analysis, S.R. and K.P.; writing a draft article, S.R.; editing the article, V.T. and K.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out as a part of the strategic academic leadership program “Prioritet-2030” for the period 2021–2022 and beyond until 2030, funded by the Ministry of Education and Science of the Russian Federation and as part of the World-class Research Center program: Advanced Digital Technologies (contract No. 075-15-2020-903 dated 16 November 2020).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Notes
| 1 | The article section is written on the basis of the requirements for the panel geometry idealization in [2]. Firstly, they overlap the relevant requirements of the Rules of Register of Shipping, and secondly, they are similar to such requirements in the Rules of most classification societies. |
| 2 | Requirements of analytical–empirical nature, in contrast the requirements for ‘direct’ calculations according to FEM. |
| 3 | The relationship will not be absolutely linear due to the fact that LCP will slightly change its position when reducing the plate. |
References
- Rules for the Classification and Construction of Sea-going Ships. Russian Maritime Register of Shipping. 2022. Available online: https://lk.rs-class.org/regbook/rules (accessed on 30 November 2022).
- Common Structural Rules for Bulk Carriers and Oil Tankers, IACS. 1 January 2022. Available online: https://iacs.org.uk/publications/common-structural-rules/csr-for-bulk-carriers-and-oil-tankers/ (accessed on 30 November 2022).
- Tryaskin, V.N. Metodologiya parametricheskogo proektirovaniya konstruktsiy korpusa sudna [Methodology of parametric design of ship’s hull structures]. Trans. Krylov State Res. Cent. 2018, 2, 9–14. (In Russian) [Google Scholar] [CrossRef]
- Roh, M.-I.; Lee, K.-Y. Development of a 3D CAD system for modeling hull structure at the initial ship design stage. Ships Offshore Struct. 2006, 1, 135–151. [Google Scholar] [CrossRef]
- Wilken, M.; Eisen, H.; Krömer, M.; Cabos, C. Mapping Hull Condition and Finite Element Models for Hull Structure Assessment of Ships in Operation. Ship Technol. Res. 2011, 58, 168–181. [Google Scholar] [CrossRef]
- Tryaskin, V.N.; Ryumin, S.N. Implementation of methods and algorithms for geometric and structural modelling in the problems of parametric design of a ship’s hull structure. Mar. Intellect. Technol. 2021, 4 Pt 2, 159–170. [Google Scholar] [CrossRef]
- Simmons, G.F. Calculus with Analytic Geometry, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Matthes, D.; Drakopoulos, V. Line Clipping in 2D: Overview, Techniques and Algorithms. J. Imaging 2022, 8, 286. [Google Scholar] [CrossRef] [PubMed]
- Hormann, K.; Agathos, A. The point in Polygon Problem for Arbitrary Polygons. Comput. Geom. 2001, 20, 131–144. [Google Scholar] [CrossRef]
- Liang, Y.-D.; Barsky, B. A new concept and method for line clipping. ACM Trans. Graph. 1984, 3, 1–22. [Google Scholar] [CrossRef]
- Scala, V. A new approach to line and line segment clipping in homogeneous coordinates. Vis. Comput. 2005, 21, 905–914. [Google Scholar] [CrossRef]
- Sutherland, I.; Hodgman, G. Reentrant Polygon Clipping. Commun. ACM 1974, 17, 32–42. [Google Scholar] [CrossRef]
- Rogers, D. Procedural Elements for Computer Graphics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Weiler, K.; Atherton, P. Hidden Surface Removal Using Polygon Area Sorting. Comput. Graph. 1977, 11, 214–222. [Google Scholar] [CrossRef]
- Autodesk Official Site. Available online: https://www.autodesk.com/ (accessed on 30 November 2022).
- Ascon Official Site. Available online: https://ascon.ru/ (accessed on 30 November 2022).
- Liu, Y.K.; Wang, X.Q.; Bao, S.Z.; Gomboši, M.; Žalik, B. An algorithm for polygon clipping, and for determining polygon intersections and unions. Comput. Geosci. 2007, 33, 589–598. [Google Scholar] [CrossRef]
- Foster, E.L.; Hormann, K.; Popa, R.T. Clipping simple polygons with degenerate intersections. Comput. Graph. X 2019, 2, 100007. [Google Scholar] [CrossRef]
- Andreev, R. Algorithm for Clipping Arbitrary Polygons. Comput. Graph. Forum 1989, 8, 183–191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).