Abstract
A novel modular floating structure (MFS) system moored by tension legs was proposed, which is composed of hexagonal floating modules, floating artificial reefs and wave energy converters (WECs). The integration of floating artificial reefs and WECs into the MFS can improve the marine environment and produce considerable electricity. The effects of both wave characteristics and the module quantity on the hydrodynamic responses of the MFS system were studied in depth, based on a time-domain numerical model. Both the modules’ hydrodynamic interaction effect and the connectors’ mechanical coupling effect were considered. The results indicate that floating artificial reefs combined with WECs can effectively reduce wave loads and convert wave energy into electricity for the MFS system. More modules involved in the MFS system could significantly reduce motion response and produced more wave energy output, which indicates that the MFS system is suitable for large-scale expansion. The effect of different power take-off (PTO) damping coefficients on the WECs’ performance was further investigated, and the optimal damping coefficient was recommended for the MFS system. Finally, the main extreme responses of the MFS system were further investigated, and its safety was checked thoroughly. One survival strategy was proposed, which could efficiently reduce extreme connector loads by more than 50%.
1. Introduction
A modular floating structure (MFS) provides a feasible way to create useable land on the sea to solve the challenges brought from the increasing population and land scarcity of coastal cities, because about 70% of the earth is covered by the sea [1,2,3,4]. Compared with the traditional very large floating structures (VLFS), the production, transportation, installation and maintenance of the MFS are more convenient [5,6,7]. More importantly, it can greatly reduce the hydroelastic response of the structure [8]. Based on this background, a number of studies on the MFS have been developed [9,10]. Among these, Jiang et al. [11] investigated the effect of module arrangement on the hydrodynamic sensitivity of the MFS. Results revealed that the hydrodynamic responses were similar in chain-type and parallel-type, and the motion responses of the first up-wave module were the largest. Michailides et al. [12] developed a numerical analysis framework for evaluating the internal loads of MFS connectors. The correlation between connector parameters and hydroelastic responses were investigated. Jiang et al. [13] compared the hydroelastic responses of MFS composed of hexagonal and square modules; the results showed that the geometry had little effect.
Habitability and comfort are important factors to be considered in the study of the MFS, so the site is usually located in sheltered waters [14,15]. The breakwater is one of the most effective ways to reduce the transmitted wave energy. Wang et al. [16] carried out a hydrodynamic analysis for the MFS, which was simulated in open and sheltered waters, respectively. The results indicated that the motion responses of each module are less affected by short-wave periods, and the floating breakwater can effectively improve the stability of the MFS in open waters. In addition, the integration of wave energy converters (WECs) into floating structures can also absorb wave energy and produce electricity, as well as reduce the survival risk of the WECs [17,18,19,20]. Ren et al. [21] coupled WECs with outermost modules, and the outermost connector type were further optimized. Nguyen et al. [22] used raft WEC-type modules to convert wave energy and reduce hydroelastic responses for a VLFS. Cheng et al. [23] integrated modular floating breakwaters (array WECs) into a VLFS. The synergy between energy extraction of WEC modules and hydroelastic response reduction of the VLFS were well clarified.
For the MFS, the mooring system is of great importance [24,25]. Due to the large number of modules, relative movement inevitably occurs between adjacent modules under waves. From the research of both Shi et al. [26] and Ding et al. [27], it was found that there tend to be considerable relative heave responses between adjacent modules with mooring lines. However, compared with the mooring line system, the tension-leg system has significant advantages for the MFS. The relative heave, pitch and roll between adjacent modules of the MFS with tension legs were all very small, which can be found in the research by Ren et al. [28].
In the process of exploring and exploiting marine resources, it is inevitable that the ocean environment will be affected to a certain extent [29,30]. An artificial reef, as a kind of artificial facility simulating a natural reef, can gather fish and other aquatic creatures, and then provide a habitat [31,32]. The combination of floating artificial reefs with the MFS can also serve as breakwaters, as well as improving the marine ecological environment. In addition, Wang et al. [33] proved the feasibility of expanding coastal cities with MFSs from the two aspects of civil engineering and naval architecture, which showed that the construction of offshore floating cities with MFSs is promising. Since the future floating city designed by architects is mainly composed of hexagonal modules, it is necessary to study the hexagonal floating structure [34].
So far, there are very limited studies on the integration of hexagonal floating structures, floating artificial reefs and WECs for the MFS system. Therefore, the present work proposes a novel MFS system moored by tension legs, which is composed of hexagonal floating modules, floating artificial reefs and WECs. The proposed novel MFS system is initially designed for a representative sea zone with the well-shielded effect of the natural surrounding islands in the South China Sea. Compared with the current general MFS [11,13], the integration of floating artificial reefs can provide habitats for marine species, thereby improving the marine ecological environment around the MFS system. The outermost floating artificial reef modules coupled with WECs can attenuate the wave loads, as well as producing considerable wave energy. In addition, the hexagonal floating structure has the advantage of multi-directional expansion, which is beneficial for future scale expansion. Considering both the hydrodynamic interaction effect and the mechanical coupling effect, the main hydrodynamic responses of the proposed MFS system have been analyzed under typical sea conditions. Effects of the module quantity and the power take-off (PTO) damping on the dynamic responses of the MFS have been further investigated. In addition, the safety of the MFS system has been checked thoroughly under extreme sea conditions.
This paper is structured as follows. Both the conceptual design and numerical model of the proposed MFS system are described in Section 2; the numerical results of the MFS system under typical sea conditions are shown and discussed in Section 3. The main conclusions are summarized in Section 4. Finally, future work is shown in Section 5.
2. Numerical Methods
2.1. Conceptual Design of the MFS System
The proposed MFS system is composed of five inner hexagonal floating structures, two outermost floating artificial reefs coupled with WECs. Each hexagonal floating structure is symmetrically moored to the seabed by four tension legs in “chain-type”. The hexagonal floating structure has good multi-directional expansion characteristics. Two floating artificial reefs coupled with WECs are combined to both sides of the MFS, which aim to attenuate wave loads, as well as producing considerable wave energy using the relative motion between the outermost reef module and adjacent inner hexagonal module. Floating artificial reefs also provide a habitat for marine species, with the aim of improving the marine ecological environment around the MFS system to a certain extent. In addition, fenders are installed at the bottom edge of adjacent connected modules to monitor possible collisions. The simplified sketch is given in Figure 1. The main parameters of the MFS system are given in Table 1, which refer to the References [12,21]. Each module and each connector are marked as Mi (i = 1~7) and Ci (i = 1~6), respectively, as shown in Figure 1. The WEC between the M1 and the M2 is defined as WEC1, while the WEC between the M6 and the M7 is defined as WEC2.
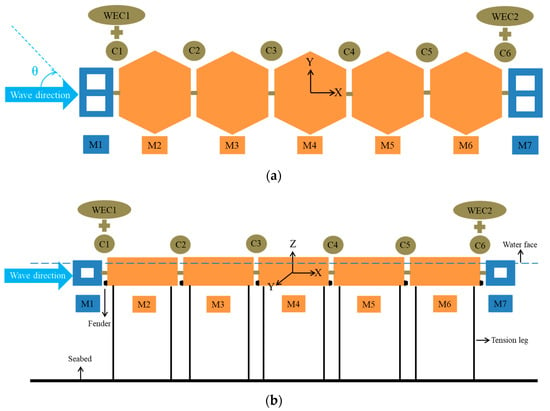
Figure 1.
The simplified sketch of the MFS system: (a) top view; (b) side view.

Table 1.
Main design parameters of the MFS system.
Referring to the previous research of Ren et al. [21,28], they indicate that the fixed connector can completely limit the relative motion among adjacent modules, which is beneficial for improving the stability of the modules. However, the fixed connector loads significantly increase as the quantity of the continuously fixed modules increases. Therefore, three connector types have been considered for the proposed MFS system to further optimize the hydrodynamic response, as shown in Figure 2.

Figure 2.
The sketch of three connector types: (a) fixed connector; (b) hinge connector; (c) hinge connector with a pitch damper.
- (a)
- The fixed connector (marked as f) is applied to the C3 and the C4: there is no relative movement in any direction between two adjacent modules.
- (b)
- The hinge connector (marked as h) is applied to the C2 and the C5: there is only relative pitch between two adjacent modules.
- (c)
- The hinge connector with an additional linear rotational damper (marked as H, worked as a WEC’s PTO) is applied to the C1 and the C6: There is only relative pitch between two adjacent modules, and the pitch velocity can be adjusted by the damper.
2.2. Hydrodynamic Model
The hydrodynamic model of the proposed MFS system has been established by the AQWA code, which can effectively simulate both the hydrodynamic and mechanical coupling effects among modules [35]. The hydrodynamic model is shown in Figure 3, and each module is regarded as a rigid body. For the flow field with floating rigid bodies in a harmonic wave, the velocity potential can be divided into three parts:
where ϕI is the incident potential of the wave without disturbance by the floating body. ϕD is the diffraction potential generated after the wave passes through the floating body. i (i = 1~7) denotes the number of the i-th module. j (j = 1~6) denotes the j-th modal of six degrees of freedom (6-DOF). denotes the complex amplitude of the i-th module in the j-th modal. denotes the complex amplitude of the i-th module in the j-th modal (6-DOF). denotes the potential induced by a unit amplitude motion of the i-th module only, meanwhile other modules are regarded as fixed.
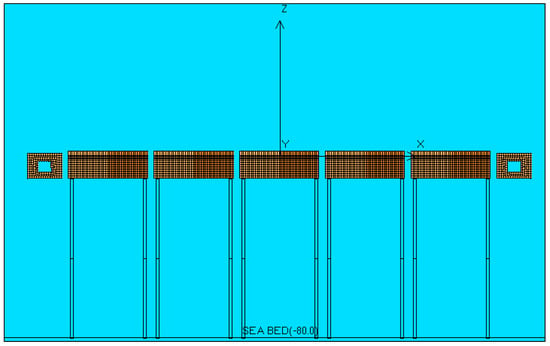
Figure 3.
Hydrodynamic model of the MFS system.
The wave force consists of the wave exciting force and the radiation force, which can be derived by integrating the wave velocity potential along the wet surface of the i-th module.
where Fi,Wave is the wave exciting force induced by scattering potential (ϕI and ϕD), and the radiation force is induced by the interaction radiation potential of multi-body. Aij and Bij denote added mass and radiation damping, respectively.
2.3. Theoretical Basis
The governing equation of the MFS system can be written as:
where Mi, Ci and Ki are the mass matrix, radiation damping (with certain artificial damping commonly used to compensate for viscous fluid effects), and the hydrostatic restoring matrix, respectively. Xi (6-DOF) denotes the generalized displacement vector of the i-th module. Fi,Wave, Fi,Con, Fi,Tlp and Fi,Fender denote the matrix of the generalized wave force, the connector force, the tension matrix of tension legs and the impact force matrix of the fender, respectively.
The connector force between adjacent modules can be written as:
where φij denotes a topology matrix. The value of φij is 1 when the i-th module is connected to the j-th module, otherwise the value of φij is 0. Kcij and δ(Xi, Xj) denote the connection stiffness matrix and the relative motion matrix between the i-th module and the j-th module, respectively.
The total tension-leg force of the i-th module can be written as:
where Ei denotes the elastic modulus. Ai denotes the sectional area of the tension leg of the i-th module. εij denotes the strain of the j-th tension leg of the i-th module.
The possible bottom fender impact force Fi,Fender can be written as:
where Kfij (1.0 × 107 N/m) is the bottom fender linear stiffness coefficient between the i-th module and the adjacent j-th module. δx(Xi, Xj) is the relative bottom surge motion between the i-th module and the adjacent j-th module. If the negative relative bottom surge motion δx(Xi, Xj) is smaller than the module’s gap (3 m), the two adjacent modules will impact on the bottom. Then, the contact force of the bottom fender will be monitored.
2.4. Estimation of the Wave Energy Output
The PTO system of the WEC can be regarded as an equivalent linear pitch damper. Under the action of waves, the relative pitch motion between the floating artificial reef and its adjacent hexagonal floating structure is used to drive the WEC to generate electric. The output power of the WEC can be estimated as:
where denotes the corresponding relative pitch velocity between the floating artificial reef module and its adjacent hexagonal floating structure module. MBpto and Kp denote the bending moment and the linear pitch damping, respectively.
3. Numerical Results
Hydrodynamic responses and the WECs’ performance of the MFS system under typical sea conditions have been investigated as follows:
3.1. Damping Effect on Wave Power Generation Performance
The wave power generation characteristics of the WEC for the MFS system were investigated with different PTO damping coefficients (Kp). Numerical simulations were carried out under typical regular sea conditions (θ = 0°, H = 2 m, T = 6 s) [36], and the main results are shown in Figure 4. It can be seen that, due to the shielding effect, the pitch bending moment, the pitch amplitude and the WEC performance of the head-wave outermost artificial reef module (M1) were all significantly greater than those of the back-wave outermost artificial reef module (M7). By comparing Figure 4a,b, it was found that the increase in Kp caused the connector to suffer larger pitch bending moment, while the pitch of the outermost reef module was effectively limited. In Figure 4c, the average output power of the head-wave WEC1 increased steadily until the Kp reached 3 × 108 Nms/rad, after that, it began to gradually decrease. However, the average output power of the back-wave WEC2 was much smaller (only about 5 kW) and almost unchanged. Therefore, the optimal damping for WECs is suggested as 3 × 108 Nms/rad from the view of the largest wave energy power production, and this damping coefficient was applied for the following research.
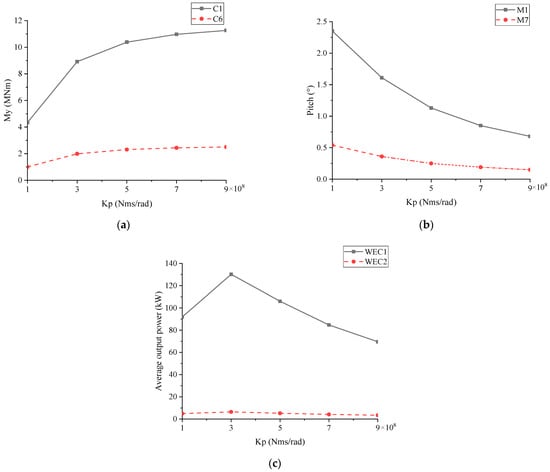
Figure 4.
Effect of the Kp on WECs’ performance: (a) pitch bending moment; (b) pitch; (c) average output power.
3.2. Effect of the Incident Wave Angle
Since the incident wave angle is random for real sea conditions, hydrodynamic responses of the MFS system have been studied under different wave directions. Typical regular sea conditions (H = 2 m, T = 6 s) [36] were selected for the simulation, and three representative incident wave angles (θ) of 0°, 30°, and 60° were considered. The main motion responses of each hexagonal module under different incident wave angles are compared in Figure 5.
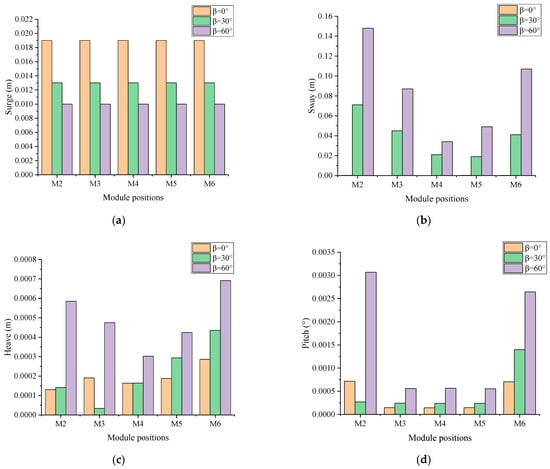
Figure 5.
Comparison of main motion responses of each module under different incident wave angles: (a) surge; (b) sway; (c) heave; (d) pitch.
In Figure 5a,b, it is reasonable that the surge of each module decreases with the increase in the incident wave angle, while the corresponding sway increases. The surge of each module was almost the same for the same incident wave angle, which reflects the consistency of the surge response. Compared with the surge, the sway was more significant with greater wave angles, which were due to less module shielding effect. In Figure 5b, for the action of oblique waves, the sway responses of three inner fixed modules (M3, M4 and M5) were more stable than two outer modules (M2 and M6). In Figure 5c,d, both the heave and the pitch of each module tended to increase with the increase in the incident wave angle. The connection of the floating artificial reef module tends to lead to both greater heave and pitch responses for the adjacent modules M2 and M6, especially for greater wave angles. In addition, due to the good performance of the tension-leg system, both the heave and the pitch responses of all hexagonal modules were negligibly small (only about 0.0007 m and 0.003°, respectively).
The main connector loads of each connector under different incident wave angles are compared in Figure 6. It can be seen that the peaks of the main connector loads (Fx, Fy and My) for almost all connectors occurred at the incident wave angle of 60°, indicating that a larger incident wave angle tends to induce larger connector loads due to a less significant shielding effect among the modules. The main connector loads of the inner connectors (C2, C3, C4 and C5) were much larger than those of the two outermost connectors (C1 and C6), due to the significant mass difference between the floating artificial reef module and the hexagonal floating structure module. In Figure 6c, the Fz responses of all connectors were much lower than both the Fx and the Fy responses, which can be attributed to the good performance of the tension-leg system. In Figure 6d, the My responses of both the C2 and the C5 were all zero, due to their hinge-connector type.
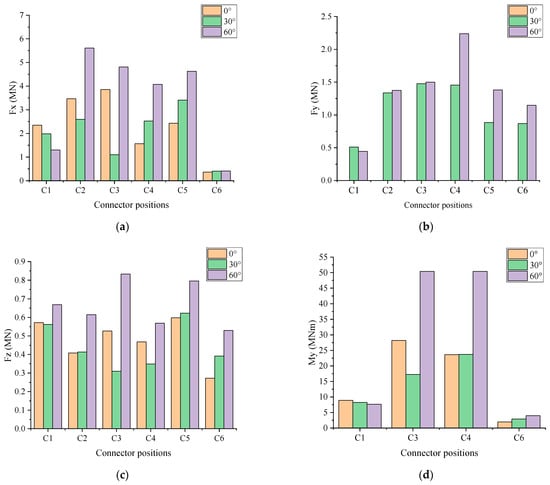
Figure 6.
Comparison of main connector forces of each connector under different incident wave angles: (a) horizontal force; (b) vertical force; (c) shear force; (d) pitch bending moment.
The effect of incident wave angle on WECs’ performance was further analyzed, and the results are presented in Figure 7. It can be seen that both the pitch of the M1 and the average output power of the WEC1 tended to gradually decrease with the increase in the incident wave angle, while the corresponding responses of the M7 and the WEC2 showed an opposite trend. The WEC2’s performance improved with the increase in the incident wave angle, which was due to more significant pitch responses of the M7 with less shielding effect. The maximum total output wave energy (all WECs) appeared at the incident wave angle of 0°. Therefore, perpendicular waves (θ = 0°) are the most favorable for wave energy conversion.
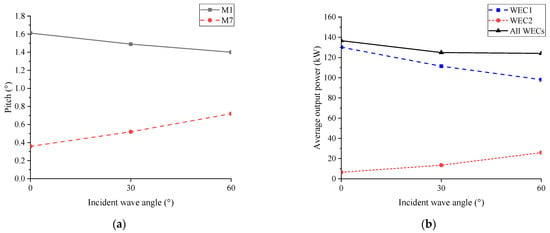
Figure 7.
Effects of incident wave directions on WECs’ performance: (a) pitch; (b) average output power.
3.3. Effect of the Wave Period
To investigate the effect of the wave period, the hydrodynamic characteristics of the MFS system have been further analyzed with different wave periods (H = 2 m and θ = 0°). Considering that the inner hexagonal modules’ surge and pitch are very similar, the corresponding results were simplified (with the representative module). The main motion responses of each hexagonal module under different wave periods are presented in Figure 8. In Figure 8a,b, both the surge and the heave increased with the increase in the wave period. They gradually rose for the wave period less than 12 s, while they sharply rose for the wave period larger than 12 s. It indicates that both the surge and the heave of the MFS system are more sensitive to long-wave periods. In Figure 8c, the pitch responses of all hexagonal modules rose first and then gradually fell, reaching the peak for the wave period of about 12 s. The pitch peak phenomenon of each module was attributed to the module’s certain natural period. In addition, the pitch of the head-wave M2 was much larger than other hexagonal modules, due to less shielding effect.
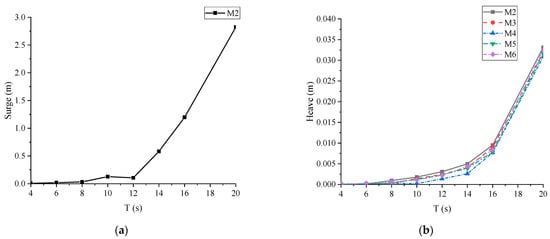
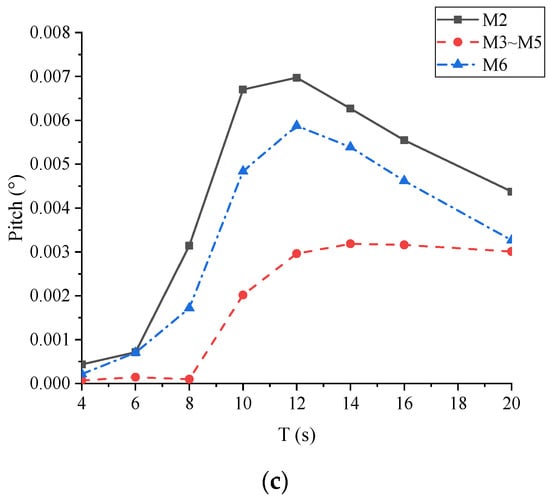
Figure 8.
Main motion responses of each hexagonal module versus wave periods: (a) surge; (b) heave; (c) pitch.
The main connector loads of each connector versus wave periods are presented in Figure 9. Main connector loads (the Fx, the Fz and the My) of the two outermost connectors (C1 and C6) were significantly less sensitive to the wave period than those of the other connectors, especially for the wave period larger than 8 s. It may be beneficial for the ultimate design of the outermost connectors. The Fx, the Fz and the My of the inner connectors almost presented the same trend, which first increased rapidly and then decreased steadily with the increase in the wave period. The peaks of the main connector loads for different connectors occurred in the wave period range from 6 s and 12 s, due to the coupling effect between different degrees of freedom. In addition, it should be noted that both the Fx and the Fz of the head-wave C2 were the largest among the connectors, corresponding to wave peak periods of 8 s and 10 s, respectively. The My of both the two fixed connectors (C3 and C4) were much larger than those of the others, corresponding to the wave peak period of 10 s.
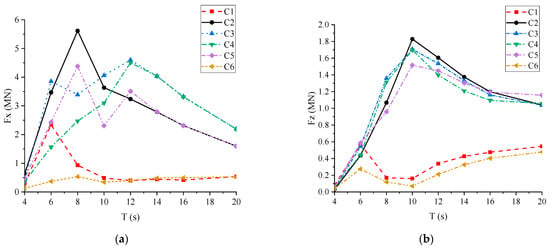
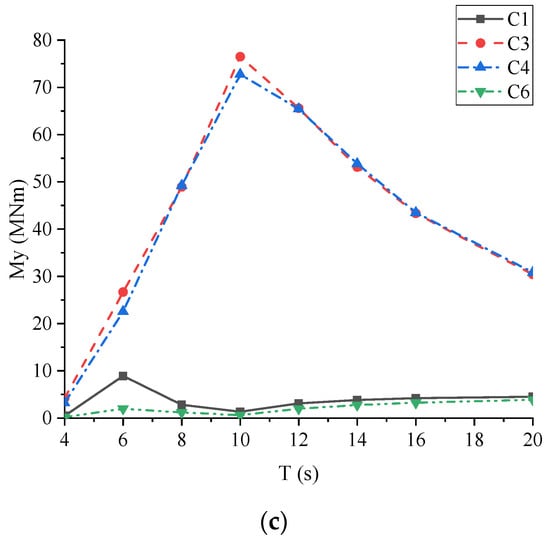
Figure 9.
Main connector forces of each connector versus wave periods: (a) horizontal force; (b) shear force; (c) pitch bending moment.
The WECs’ performance versus wave periods is presented in Figure 10. It can be seen that the pitch and the average output power show the same trend. They increased when the wave period was less than 6 s, and gradually fell until 10 s. After that, they steadily rose again for the wave period larger than 10 s. It is mainly due to the correlation between the wave length and the module dimension. In addition, it can be concluded that an ideal wave period for WECs is about 6 s, for which there is usually a high probability in natural waves.
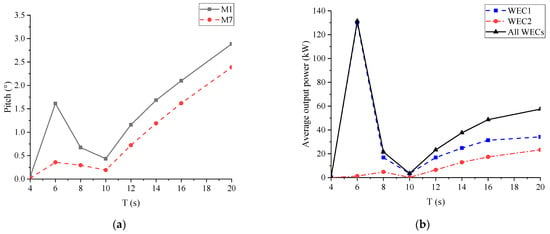
Figure 10.
The WECs’ performance versus wave periods: (a) pitch; (b) average output power.
3.4. Effect of the Module Quantity
To investigate the effect of module quantity, four structural layouts with different module quantities were designed, as shown in Table 2. Except for the module quantity, the corresponding design parameters and input parameters were identical, as given in Section 2. The main hydrodynamic responses of four different MFS systems were analyzed under typical sea conditions (θ = 0°, H = 2 m, T = 4~20 s) [36].

Table 2.
Four structural layouts of the MFS system with different module numbers.
According to the research in Section 3.3, the motion responses of the first head-wave hexagonal module are the most significant among all hexagonal modules. So, the main motion responses of the first head-wave hexagonal module under different layouts have been analyzed, and the results are shown in Figure 11.
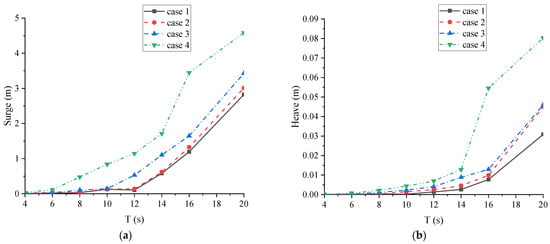
Figure 11.
Main motion responses of the first head-wave hexagonal module under different layouts: (a) surge; (b) heave.
In Figure 11a,b, the increase in module quantity can reduce the surge and the heave, especially for the long wave period. By comparing Case 1 with Case 2, it was found that the floating artificial reef could effectively reduce both the surge and the heave of the hexagonal module under wave periods less than 12 s, acting as a wave-breaker. For the representative wave period of 6 s, the surge amplitude and heave amplitude could be reduced by about 57 and 46%, respectively.
Since the first head-wave connector between adjacent hexagonal modules is the most loaded, the main connector forces of the first head-wave connector under different layouts were investigated, as shown in Figure 12. It can be seen that the main connector forces between Case 1 and Case 2 almost overlapped for the wave period less than 10 s, and gradually separated to a certain degree for the wave period longer than 10 s. This means that the head-wave floating artificial reef module does not significantly affect the inner connector forces. Among the first three Cases (the Case 1~3), Case 3 had the lowest connector forces, especially for the shear force. It indicates that more modules tend to result in larger connector forces to a certain extent, and the connector shear force seems sensitive to the module quantity.
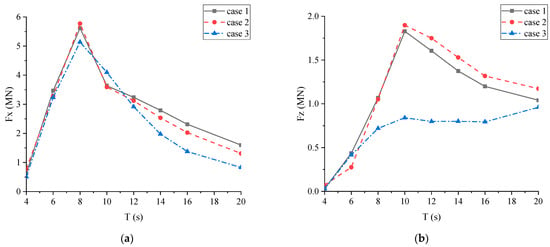
Figure 12.
Main loads of the first connector between adjacent hexagonal modules in head sea under different layouts: (a) horizontal force; (b) shear force.
The effect of the module quantity on WECs’ performance was further studied, and the corresponding results concerning the head-wave WEC1 are shown in Figure 13. It was observed that more modules could result in a larger pitch bending moment and more wave energy production. However, when the quantity of hexagonal modules increased to three, both the pitching bending moment and the average output power seemed almost not to change with more modules. Therefore, it can be concluded that the performance of the WEC tends to steady with a certain number of modules.
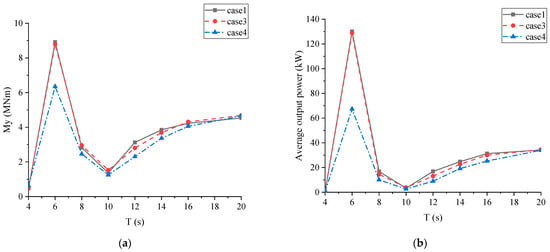
Figure 13.
WEC performance in head sea under different layouts: (a) pitch bending moment of C1; (b) average output power of WEC1.
3.5. Extreme Sea Conditions
Given the complexity of real ocean conditions, the JONSWAP spectrum was applied to check the safety of the MFS system under representative extreme sea conditions (λ = 3.3, Hs = 4 m, Tp = 10 s) [36]. To limit the potential excessive bending moment loads caused by inner fixed connectors, one new survival strategy for the MFS system with seven modules was proposed, replacing the inner fixed connectors with hinge connectors. The main extreme responses of the two representative MFS systems are compared in Table 3.

Table 3.
Main extreme responses of the two representative MFS systems.
In Table 3, it can be seen that main motion responses (surge, heave and pitch) of the representative MFS systems were very similar, and both the heave and the pitch responses were limited well, due to the good performance of the tension legs. Both the tension-leg force and the WEC performance seemed not to be sensitive to the inner connector type. The maximum output power of the head-wave WEC1 can reach 600 kW, and the maximum tension-leg force can reach 14 MN (still within the safe range). The connector Fx of the two representative MFS systems were very similar, while both the connector Fz and My of the two representative MFS systems were quite different. The new survival strategy (H-h-h-h-h-H) can significantly reduce the extreme responses of the connector Fz and My by about 50 and 95%, respectively. This indicates that the survival strategy with inner hinge connectors is much better for the ultimate design of the inner connector. In addition, there was no impact force monitored by the bottom fenders during the time-domain analysis. Therefore, the safety of the MFS system was validated under extreme sea conditions.
4. Conclusions
The present work proposed a novel modular floating structure (MFS) system integrated with floating artificial reefs and wave energy convertors (WECs). Both the multi-body hydrodynamic interaction effect and the connector mechanical coupling effect were considered. The effects of the PTO damping, incident wave angle, wave period and module quantity on the hydrodynamic responses of the MFS system were investigated. The main conclusions are summarized as follows:
- (1)
- The outermost floating artificial reefs with WECs showed good capacity of wave attenuation and energy conversion. The main hydrodynamic responses of the MFS system were sensitive to both the incident wave angle and the wave period. Larger incident wave angles tended to lead to the increase in both motion responses and connector forces, due to less shielding effect from the outermost artificial reef. The motion responses of the MFS system were more sensitive to long wave periods than short wave periods. In addition, the optimal PTO damping and the corresponding optimal wave period of the WEC for the MFS system were about 3 × 108 Nms/rad and 6 s, respectively. That was mainly due to the relationship between the structure dimension and the wavelength.
- (2)
- More modules can provide a better shielding effect for the central module, so that the MFS system can be of better stability with expansion. The extreme connector loads did not seem significantly sensitive to the increase in the module quantity, which provided feasibility for the expansion of the MFS system with more modules. In addition, more inner modules were beneficial for improving the performance of the WECs to some degree.
- (3)
- A survival strategy of the MFS system with inner hinge connectors was proposed for reducing extreme connector loads, especially for the bending moment (My) and the shear force (Fz). The extreme connector Fz and My could be efficiently reduced by about 50 and 95%, respectively. Both the heave and the pitch responses of the MFS system were limited well, due to the good performance of the tension legs. The security of the MFS system under typical extreme sea conditions was verified.
5. Future Work
Much work still needs to be carried out for the MFS system, including the optimization design of each module, the validation of the scale model test, and the attractive effect of the floating artificial reef. In addition, the effects of the seabed and the current [37] on the dynamic responses of the proposed MFS system should also be further investigated based on more detailed sea information. These challenging works should be investigated in future.
Author Contributions
Conceptualization and supervision: N.R. and J.O.; investigation, methodology and writing: Y.L. and X.L.; funding acquisition: X.L. and N.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Natural Science Foundation of Hainan Province (Grant NO. 520RC552, 520RC543, ZDYF2021GXJS034), the National Natural Science Foundation of China (Grant No. 52161041), Foundation of State Key Laboratory of Coastal and Offshore Engineering (Grant NO. LP2119). The financial supports are greatly acknowledged.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DOF | Degree of freedom |
| Fx | Horizontal force of connector |
| Fz | Shear force of connector |
| H | Wave height |
| JONSWAP | Joint North Sea Wave Project |
| Kp | Damping coefficient |
| MFS | Modular floating structure |
| My | Pitch bending moment of connector |
| PTO | Power take-off |
| T | Wave period |
| TLP | Tension-leg platform |
| WEC | Wave energy converter |
| VLFS | Very large floating structure |
| θ | Incident wave angle |
References
- Strain, E.M.A.; Alexander, K.A.; Kienker, S.; Morris, R.; Jarvis, R.; Coleman, R.; Bollard, B.; Firth, L.B.; Knights, A.M.; Grabowski, J.H.; et al. Urban blue: A global analysis of the factors shaping people’s perceptions of the marine environment and ecological engineering in harbours. Sci. Total Environ. 2019, 658, 1293–1305. [Google Scholar] [CrossRef]
- Wang, C.M.; Watanabe, E.; Utsunomiya, T. Very Large Floating Structures; Taylor and Francis: Abingdon, UK, 2014. [Google Scholar]
- Flikkema, M.; Waals, O. Space@ Sea the floating solution. Front. Mar. Sci. 2019, 6, 553. [Google Scholar] [CrossRef]
- Koekoek, M. Connecting Modular Floating Structures; Gemeente: Rotterdam, The Netherlands, 2010. [Google Scholar]
- Drummen, I.; Olbert, G. Conceptual design of a modular floating multi-purpose island. Front. Mar. Sci. 2021, 8, 615222. [Google Scholar] [CrossRef]
- Souravlias, D.; Dafnomilis, I.; Ley, J.; Assbrock, G.; Duinkerken, M.B.; Negenborn, R.R.; Schott, D.L. Design framework for a modular floating container terminal. Front. Mar. Sci. 2020, 7, 545637. [Google Scholar] [CrossRef]
- Dai, J.; Zhang, C.; Lim, H.V.; Ang, K.K.; Qian, X.; Wong, J.L.H.; Tan, S.T.; Wang, C.L. Design and construction of floating modular photovoltaic system for water reservoirs. Energy 2020, 191, 116549. [Google Scholar] [CrossRef]
- Tseranidis, S.; Theodoridis, L.; Loukogeorgaki, E.; Angelides, D. Investigation of the condition and the behavior of a modular floating structure by harnessing monitoring data. Mar. Struct. 2016, 50, 224–242. [Google Scholar] [CrossRef]
- Ren, N.; Wu, H.; Ma, Z.; Ou, J. Hydrodynamic analysis of a novel modular floating structure system with central tension-leg platforms. Ships Offshore Struc. 2020, 15, 1011–1022. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Lentsiou, E.N.; Aksel, M.; Yagci, O. Experimental investigation of the hydroelastic and the structural response of a moored pontoon-type modular floating breakwater with flexible connectors. Coast. Eng. 2017, 121, 240–254. [Google Scholar] [CrossRef]
- Jiang, C.; El Moctar, O.; Schellin, T.E. Hydrodynamic Sensitivity of Moored and Articulated Multibody Offshore Structures in Waves. J. Mar. Sci. Eng. 2021, 9, 1028. [Google Scholar] [CrossRef]
- Michailides, C.; Loukogeorgaki, E.; Angelides, D.C. Response analysis and optimum configuration of a modular floating structure with flexible connectors. Appl. Ocean Res. 2013, 43, 112–130. [Google Scholar] [CrossRef]
- Jiang, D.; Tan, K.H.; Dai, J.; Ang, K.K.; Nguyen, H.P. Behavior of concrete modular multi-purpose floating structures. Ocean Eng. 2021, 229, 108971. [Google Scholar] [CrossRef]
- Liang, N.-K.; Huang, J.-S.; Li, C.-F. A study of spar buoy floating breakwater. Ocean Eng. 2004, 31, 43–60. [Google Scholar] [CrossRef]
- Ng, A.; Ölçer, A. A new human comfort model onboard a vessel based on Sugeno type fuzzy inference system. Ocean Eng. 2012, 55, 116–124. [Google Scholar] [CrossRef]
- Wang, G.; Drimer, N.; Goldfeld, Y. Modular floating structures (MFS) for offshore dwelling a hydrodynamic analysis in the frequency domain. Ocean Eng. 2020, 216, 107996. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, C.; Tay, Z.; Luong, V. Wave energy converter and large floating platform integration: A review. Ocean Eng. 2020, 213, 107768. [Google Scholar] [CrossRef]
- Li, L.; Ruzzo, C.; Collu, M.; Gao, Y.; Failla, G.; Arena, F. Analysis of the coupled dynamic response of an offshore floating multi-purpose platform for the Blue Economy. Ocean Eng. 2020, 217, 107943. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Cocard, M.; Yuan, Z.; Incecik, A. Performance characteristics and parametric analysis of a novel multi-purpose platform combining a moonpool-type floating breakwater and an array of wave energy converters. Appl. Energy 2021, 292, 116888. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, W.; Michailides, C.; Wan, L.; Kim, H.; Li, X. WEC shape effect on the motion response and power performance of a combined wind-wave energy converter. Ocean Eng. 2022, 250, 111038. [Google Scholar] [CrossRef]
- Ren, N.; Zhang, C.; Magee, A.R.; Hellan, Ø.; Dai, J.; Ang, K.K. Hydrodynamic analysis of a modular multi-purpose floating structure system with different outermost connector types. Ocean Eng. 2019, 176, 158–168. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, C.; Flocard, F.; Pedroso, D. Extracting energy while reducing hydroelastic responses of VLFS using a modular raft wec-type attachment. Appl. Ocean Res. 2019, 84, 302–316. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Collu, M.; Li, M.; Yuan, Z.; Incecik, A. Wave energy extraction and hydroelastic response reduction of modular floating breakwaters as array wave energy converters integrated into a very large floating structure. Appl. Energy 2022, 306, 117953. [Google Scholar] [CrossRef]
- Liang, M.; Xu, S.; Wang, X.; Ding, A. Experimental evaluation of a mooring system simplification methodology for reducing mooring lines in a VLFS model testing at a moderate water depth. Ocean Eng. 2021, 219, 107912. [Google Scholar] [CrossRef]
- Ren, Y.; Venugopal, V.; Shi, W. Dynamic analysis of a multi-column TLP floating offshore wind turbine with tendon failure scenarios. Ocean Eng. 2022, 245, 110472. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, H.; Xu, D.; Qi, E.; Tian, C.; Ding, J.; Wu, Y.; Lu, Y.; Li, Z. Experimental validation of network modeling method on a three-modular floating platform model. Coast. Eng. 2018, 137, 92–102. [Google Scholar] [CrossRef]
- Ding, J.; Geng, Y.; Xu, S.; Yang, W.; Xie, Z. Experimental study on responses of an 8-module VLFS considering different encounter wave conditions. Mar. Struct. 2021, 78, 102959. [Google Scholar] [CrossRef]
- Ren, N.; Wu, H.; Liu, K.; Zhou, D.; Ou, J. Hydrodynamic Analysis of a Modular Floating Structure with Tension-Leg Platforms and Wave Energy Converters. J. Mar. Sci. Eng. 2021, 9, 424. [Google Scholar] [CrossRef]
- Ohkura, Y. The roles and limitations of newspapers in environmental reporting. Case study: Isahaya Bay land reclamation project issue. Mar. Pollut. Bull. 2003, 47, 237–245. [Google Scholar] [CrossRef]
- Peduzzi, P. Sand, rarer than one thinks. Environ. Dev. 2014, 11, 208–218. [Google Scholar]
- Lima, J.S.; Zalmon, I.R.; Love, M. Overview and trends of ecological and socioeconomic research on artificial reefs. Mar. Environ. Res. 2019, 145, 81–96. [Google Scholar] [CrossRef]
- Wang, G.; Wan, R.; Wang, X.; Zhao, F.; Lan, X.; Cheng, H.; Tang, W.; Guan, Q. Study on the influence of cut-opening ratio, cut-opening shape, and cut-opening number on the flow field of a cubic artificial reef. Ocean Eng. 2018, 162, 341–352. [Google Scholar] [CrossRef]
- Wang, G.; Goldfeld, Y.; Drimer, N. Expanding coastal cities–Proof of feasibility for modular floating structures (MFS). J. Clean Prod. 2019, 222, 520–538. [Google Scholar] [CrossRef]
- Abrams, M. Building cities on the sea. Mech. Eng. 2020, 142, 42–47. [Google Scholar] [CrossRef]
- ANSYS, Inc. Aqwa User’s Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Wang, Z.; Zhou, L.; Dong, S.; Wu, L.; Li, Z.; Mou, L.; Wang, A. Wind wave characteristics and engineering environment of the South China Sea. J. Ocean Univ. China 2014, 13, 893–900. [Google Scholar] [CrossRef]
- Faraci, C.; Musumeci, R.E.; Marino, M.; Ruggeri, A.; Carlo, L.; Jensen, B.; Foti, E.; Barbaro, G.; Elsaßer, B. Wave- and current-dominated combined orthogonal flows over fixed rough beds. Cont. Shelf Res. 2021, 220, 104403. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).