Abstract
In this study, a hydraulic system generator power converter was modeled to verify the performance of a hydraulic-based power take-off (PTO) system. Moreover, the characteristics and output performance of the PTO system were analyzed with various load control algorithms applied for maximum power control. The simulation performance was verified through a comparison with actual sea test results. Unlike previous studies on hydraulic-based PTO system control for input power performance, the performance of a hydraulic-based PTO system was analyzed through electrical load control in this study. The electrical load control was analyzed by applying a speed control algorithm based on the perturb and observe algorithm and an optimal torque control algorithm. A load control algorithm suitable for maximum power control of the PTO system was proposed by analyzing the characteristics and power generation performance of the system according to the control variables of each algorithm. The proposed optimal torque control algorithm proved to be suitable for maximum power control of the considered PTO system.
1. Introduction
Wave Energy Converters (WECs) are an emerging technology. Therefore, technological growth for device development and testing is continuously required [1,2]. Several models have already been implemented at sea for the commercialization of wave power plants [3,4]. However, in order to enter the commercialization stage, it is necessary to study a control strategy that can extract maximum power by adjusting the power take-off in response to irregular marine environment conditions. Therefore, PTO studies for various WEC devices have recently been conducted.
The floating wave energy converter (FWEC) concept is based on extracting wave energy using floating bodies in the sea [5,6]. In an FWEC, the floating body moves by wave energy and a power take-off (PTO) system generates power using this movement. Because the wave period in an actual sea is generally long, FWEC motion tends to be slow. For instance, Wavestar, a representative FWEC, requires a bidirectional load torque of 1 MNm to extract an average of 27 kW of power [7,8]. Therefore, the average and peak wave energy converter (WEC) power levels may differ by a factor of 10 or more [9]. However, it cannot be simply discarded because the peak power significantly contributes to the overall production. Consequently, energy storage is required to store the energy peak and maintain the wave energy variability. Regarding PTO system implementation for FWEC, a study was conducted on a linear generator directly driven using the movement of a floating body. However, owing to the slow motion of the floating body, the existing permanent-magnet linear generator was very large [8]. Wavestar requires a load of 400 kN, but the general linear generator void shear stress level is 20–25 kN/m2 [10]. In other words, even if the necessary support structure is ignored, the weight becomes excessive, making it impossible to implement a linear generator [11]. Direct drive linear generators have been proposed many times because of their advantages due to their ability to directly convert linear input motion into electrical energy. In this way, the energy conversion chain is greatly simplified using a limited number of components [9]. Instead, we used another system that was more prevalent in real-world applications. Other systems first store sea wave energy, pressurize the fluid through a piston pump, and then convert this energy into electricity using an alternator driven by a hydraulic turbine or volumetric expander [12]. In other words, linear generators are currently the subject of ongoing research [13,14], as direct drive solutions have sufficient advantages.
A method of using mechanical transmission (gearbox, belts, etc.) was also studied, but the size was large owing to the high gearing ratio and bidirectional movement characteristics, making it difficult to implement.
Hydraulic systems are suitable for PTO systems for FWECs. A hydraulic system can control high forces at low speeds and can easily control movement in both directions with a small actuator.
Figure 1a shows the initial hydraulic system of a PTO system for an FWEC. The cylinders act as a pump to create bidirectional flow that drives the hydraulic motor. The generator rotates in one direction through the hydraulic motor drive. In [15], a PTO system was optimized from wave energy to grid power using this model in the case of Wavestar. At the optimum point, the overall PTO power conversion efficiency was 65%, but in small waves, it quickly dropped to 45%. However, the system shown in Figure 1a does not allow energy storage or smoothing. Therefore, as shown in Figure 1b, a PTO system with a cylinder operated by a pump at a constant pressure was used in [16,17], where energy smoothing could be performed using an accumulator. This approach enables hydraulic motors and generators to operate at fairly constant loads, resulting in a PTO efficiency of up to 80%. However, the cylinder is limited to providing a Coulomb damping force, which reduces the amount of energy absorbed [18]. Therefore, in [19], a hydraulic transformer capable of controlling the force of the cylinder was proposed to overcome the force load. However, the load efficiency of a hydraulic transformer was poor because there were two variable displacement pumps or motors in series. In [20], discrete control of hydraulic cylinders was applied. A mobile hydraulic system was investigated, showing a promising increase in energy efficiency compared to a conventional load system. Meanwhile, [21] discussed a PTO system using two asymmetric cylinders. The efficiency of cylinder force control by pressure movement was between 88% and 94%, excluding the friction of the cylinder. In addition, [22] described a hydraulic transmission with an accumulator for energy smoothing that operated at 70% efficiency, and [23] proposed a system similar to that in [17]. Furthermore, [24] presented a scaled version capable of applying a 16 kNm torque to the system of [23]. The overall efficiency was estimated to be 69–80%.
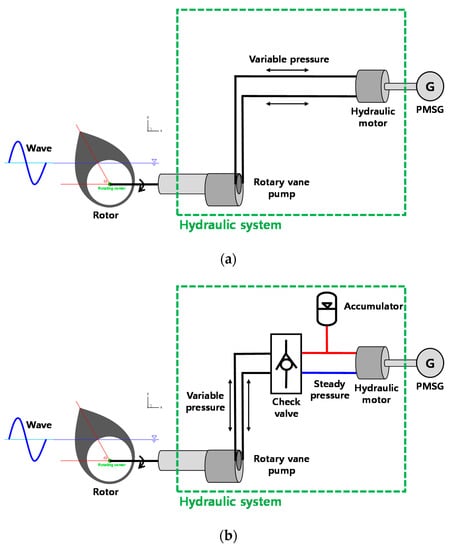
Figure 1.
Basic hydraulic transmission system model: (a) direct hydraulic motor system and (b) rectifying valve accumulator motor.
In this study, the hydraulic transmission system shown in [16,17] was used. The maximum output control was analyzed through electrical load control of the power converter, rather than mechanical control using the discrete displacement cylinder system shown in [18,25]. The load control method described in [16,17] is difficult to directly apply to an actual system because it provides theoretical load control. Therefore, in this study, the force of the PTO system and amount of power generated were calculated by analyzing the PTO system characteristics based on the hydraulic system according to the load control of the power converter. There is a lack of research on hydraulic-based PTO system analysis with the application of a maximum power control algorithm using the existing power conversion method. Various maximum power control algorithms exist in wind power systems that have already been studied [26,27,28,29,30]. Among them, the most frequently applied algorithms can be classified into two categories. The perturb and observe (P&O) algorithm shown in [29] does not rely on knowledge of the characteristic curves of wind turbines. This method observes turbine speed fluctuations and checks for changes in the output power accordingly. That is, this approach can simply control the maximum output. However, it reduces the convergence rate at the maximum power point (MPP) depending on the turbine inertia and control period, and the MPP may not be reached.
Recently, a study was conducted to ensure that the generated power reaches the maximum power based on the parameters of the hydraulic PTO because it is difficult to adapt to various sea conditions when the parameters of the hydraulic PTO are fixed [30]. However, it is difficult to follow the electrical maximum power point tracking(MPPT) control response. The MPPT control strategy is a well-known adaptive control strategy with great success in other renewable energy industries (mainly solar and wind). In order to apply this in wave power generation, there have been some studies on linear generators for MPPT. However, there are few studies using MPPT technology for hydraulic PTO so far, and it is mainly used for research on linear generators [31,32,33,34,35].
Therefore, this method is mainly used for solar power generation with little change or small-capacity wind power generation, requiring a simple controller configuration. The power signal feedback algorithm shown in [29] can converge to the MPP and produce a fast convergence speed. This method is controlled based on the turbine curve for maximum power, depending on the turbine speed. However, to converge to the MPP, a characteristic curve for a wind turbine must be obtained, which must be done experimentally. This method was applied to improve the efficiency and convergence of large wind power generation. Maximum FWEC power control can be derived based on the algorithm that is most often applied to wind power generation systems. Therefore, a load control algorithm suitable for a hydraulic-based PTO system was developed in this study by comparing various load algorithms and control variables for maximum power control. The characteristic analysis of the PTO system was conducted using a simulation that included a hydraulic system, generator, and power converter. The developed simulator was verified using the power generation data obtained from an actual sea test, and it was proven that the proposed algorithm can be directly applied to actual sea tests.
2. PTO System Configuration and Modeling
2.1. FWEC Power Conversion Chain
An FWEC converts wave energy into relative linear or rotational motion. The power conversion chain converts mechanical power into electrical power. Figure 2 illustrates the power conversion chain used in this study. According to the Office of Energy Efficiency and Renewable Energy WEC database, there are 34 power conversion chain structures with technology readiness levels (TRL) of 5 or higher. Among them, the most commonly used PTO system is a hydraulic system [26,27].
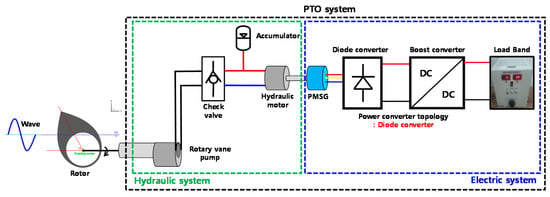
Figure 2.
FWEC power conversion chain.
The input energy variability of an FWEC is large, so the development of an efficient and reliable PTO system for power conversion is important. In other words, using a hydraulic system as the PTO system of an FWEC can provide stable power generation. Therefore, a hydraulic system was used as the PTO system in this study. The floating body used Salter’s duck [36] to transform blue energy into pitch motion. The pitch motion of the floating body was converted into bidirectional rotational motion using a rotary vane pump. The bidirectional flow generated by the rotary vane pump was converted into unidirectional flow through a check valve. The flow of the check valve was directed towards the accumulator and hydraulic motor, and the flow rate to the hydraulic motor was determined by the electrical torque. The number of revolutions per minute (rpm) of the generator was determined by the flow rate of the hydraulic motor, and the power converter current was controlled to perform appropriate load control according to the rpm. In other words, the amount of power generated by the FWEC could be adjusted through appropriate load current control according to the input energy. The next section describes the load control algorithm in detail.
2.2. Hydraulic System Modeling
A hydraulic system was used as a suitable PTO system for FWEC because it can provide low speed and high torque. In particular, it can generate stable power using an accumulator even with irregular wave energy [4]. The flow rate generated by the rotary vane pump using the pitch angle of the floating body can be expressed as follows:
The pitch angle of the floating body moves according to the input energy but is also affected by the PTO force generated by the hydraulic system, which is given by
The flow generated by the rotary vane pump is bidirectional and can be converted into unidirectional flow through a check valve, as follows:
The flow rate of the check valve is the sum of the flow rates of the accumulator and hydraulic motor:
The hydraulic system circuit pressure can be calculated based on the accumulator flow rate. The accumulator volume changes according to the accumulator flow rate, and the pressure increases accordingly. Because the accumulator pressure is the same as the hydraulic motor input, the pressure is the same. The change in pressure according to the accumulator flow rate can be calculated as follows:
In this study, several accumulators were used to reduce the rate of change in pressure. To check the pressure change with multiple accumulators, the pressure change with two accumulators can be expressed as follows:
Because accumulators 1 and 2 are the same node, the pressure is the same, and the accumulator pressure is the same as the pressure in the circuit. Using this information, the mechanical torque of the hydraulic motor can be calculated as follows:
The dynamic state of the hydraulic motor assumes that there is no loss due to friction, and modeling is performed as follows, using the difference between the mechanical and electrical torques of the generator:
The rpm of the hydraulic motor is changed by the electrical torque, and the hydraulic motor flow rate can be calculated as follows:
That is, the rpm and flow rate of the hydraulic motor change according to the electrical load, and the flow rate of the accumulator changes according to Equation (5), so the pressure in the circuit changes. The pressure in the circuit affects the motion of the floating body according to Equation (3), which affects the overall power generation.
2.3. Permanent Magnet Synchronous Generator (PMSG) Modeling
Because the PMSG is directly coupled to the hydraulic motor, the mechanical dynamic state of the PMSG can be expressed using Equation (14). The PMSG-based model can be expressed by applying the Kirchhoff voltage law. The generator model based on PMSG is displayed using the dq-axis coordinate system, which is a rotating coordinate system synchronized with the speed of the generator’s rotor:
represent the stator dq-axis inductances, is the stator resistance, is the electrical angular frequency, is the flux linkage of the permanent magnet, and and are the stator dq-axis terminal voltages.
The instantaneous power generation, Pe of PMSG, can be expressed as follows
In other words, if the loss due to resistance is very small, it can be expressed in terms of Pe using Equations (11) and (12) as follows:
In the PMSG considered in this study, and are the same because the rotor uses a motorized structure. Thus, Equation (14) can be written as follows:
Electrical torque Te can be calculated as follows, using the relationship between the instantaneous power generation and the angular velocity of the turbine:
The ratio of the electrical angular frequency to the angular velocity of the turbine is equal to the number of dipoles of the rotor. From Equation (16), it can be seen that the electrical torque changes according to the q-axis current of the generator. Figure 3 shows the configuration diagram of the applied hydraulic-based PTO system in this paper.
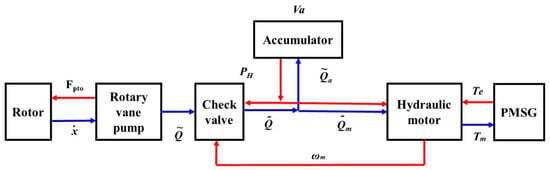
Figure 3.
Hydraulic-based PTO system.
2.4. Power Converter Configuration and Modeling
The FWEC power converter supplies output power of variable voltage and variable frequency to the grid in the form of constant voltage and frequency. In general, a back-to-back converter is used to perform this function, and the back-to-back converter consists of an AC/DC converter and a DC/AC inverter. The AC/DC converter mainly applies electrical torque control for generator speed control, and the DC/AC inverter controls the system output power factor for grid connection. In this study, the generator-side converter was analyzed because the power generation performance and the maximum power control algorithm were compared through the generator-side load control. The structure of the generator-side converter of the wave power generator uses a diode DC/DC converter structure. This structure is used in small-capacity renewable energy systems. Because the structure and control are simple and the price is low, this structure is mainly used for small capacity systems with little power generation, even if the efficiency is rather low. The variable voltage and variable frequency power of the generator is converted into constant DC power using a diode rectifier, and the DC/DC converter boosts the DC output. Because this structure uses a diode rectifier, the input power factor is low because it does not directly control the AC output, but rather passively converts it into a DC output. This approach can reduce the power generation; however, because the PTO system used in this study employs a hydraulic transmission system, the variability of the generator rpm was not as large as that of the input energy. Therefore, even if the structure of a diode DC/DC converter is used, the electrical torque control performance is not significantly reduced. As shown in Figure 4, the power converter calculates the reference voltage using the reference and inductor currents, and the reference voltage creates a duty ratio through comparison with the carrier.
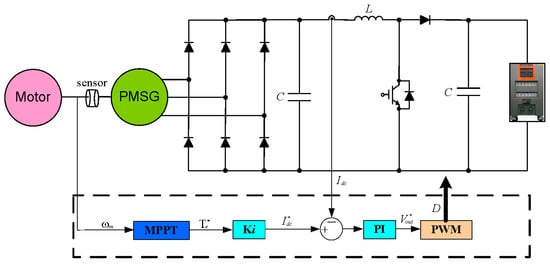
Figure 4.
DC/DC boost converter control block diagram.
The output for converter operation can be expressed using the duty ratio as follows:
3. Load Control Algorithm for Maximum Power Control of FWEC
Owing to the FWEC power generation characteristics, a large amount of input energy must be absorbed to increase the amount of power generation. The power absorbed by the FWEC can be calculated using the floating body movement and PTO force. The floating body movement changes according to the PTO force, and part of it becomes the MPP. The PTO force of the hydraulic transmission system is proportional to the pressure in the circuit, and the PTO force can be calculated using Equation (3).
This section presents the circuit pressure and PTO force of the hydraulic system according to various load control algorithms for maximum power control. The load control algorithm for maximum FWEC power control was applied to the P&O algorithm-based speed control algorithm and the optimal torque control algorithm, and performance analysis of each algorithm was conducted to develop a maximum FWEC power control algorithm.
3.1. Speed Control Algorithm-Based P&O Algorithm
Through electrical load control, the speed of the hydraulic motor and generator of the PTO system can be controlled. The pressure in the circuit of the hydraulic transmission system fluctuates according to the changes in generator speed. That is, as the generator speed increases with the same input energy, the pressure and PTO force decrease. Through speed control, it is possible to change the circuit pressure of the hydraulic transmission system; thus, the PTO force can be adjusted. Similar to existing renewable energy systems such as solar and wind power generation systems, FWEC can yield the maximum power by using the power generation characteristic curve according to the PTO force, as shown in Figure 5.
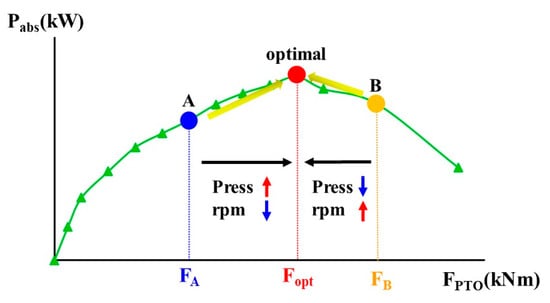
Figure 5.
P&O algorithm-based power versus PTO force.
The specific point of the PTO force can be changed according to the period and wave height of the input wave, but the controller can be designed by applying the P&O algorithm using the characteristic curve shown in Figure 5. As the speed increases or decreases, the pressure in the circuit of the hydraulic system changes, and the PTO force that affects the movement of the floating body changes. In other words, the reference speed increases or decreases according to the increase or decrease in the amount of power generated, and accordingly, the PTO force that can yield the maximum power is sought. Owing to the large wave energy variability, there may be limitations in applying the P&O algorithm, but because the PTO system used in this study is a hydraulic transmission system, the speed variability can be significantly reduced. Figure 6 shows a flow chart of the P&O algorithm used in this study.
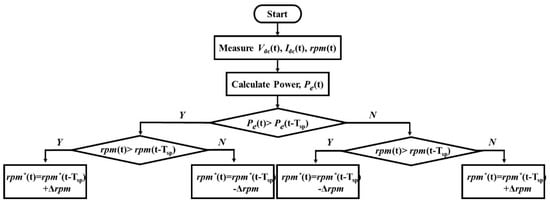
Figure 6.
Flow chart of speed control algorithm based on the P&O algorithm for FWEC.
3.2. Optimal Torque Control Algorithm
Optimal torque control can yield the maximum power by using the PTO force to satisfy the FWEC resonance condition [28,29,30,31]. To obtain the maximum power, the wave must have the resonance frequency, in which case the wave frequency can be expressed as:
When the wave frequency satisfies Equation (24), the power absorbed by the floating body can be summarized as:
For the absorbed power to be the maximum power, the following equation must be satisfied:
Using Equations (26) and (27), the PTO damping factor for following the maximum power can be summarized as:
The optimal PTO damping coefficient in the resonance period can be expressed as Equation (28), but the PTO damping coefficient changes every period. Figure 7a shows the optimal PTO damping coefficient for each period. Figure 7b presents the output power generation performance obtained using the optimal PTO damping coefficient for each period and the PTO damping coefficient of the resonance period. When the optimal PTO damping coefficient for each period is applied, the generation power performance is high, but it is almost identical to that obtained using the other method near the resonance period. In particular, because the input wave conditions are irregular, it is difficult to change the PTO damping coefficient according to the period. Therefore, the optimal torque control adjusts the load by using the optimal PTO damping coefficient in the resonance period.
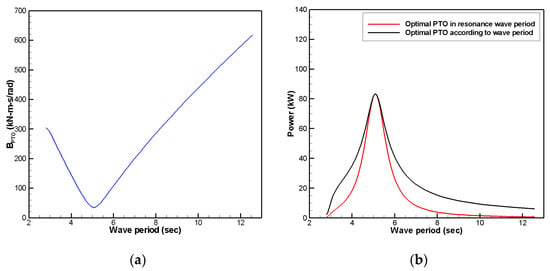
Figure 7.
(a) Optimal PTO damping coefficient for each period. (b) Output power generation performance according to the optimal PTO damping coefficient for each period and resonance period PTO damping coefficient.
To obtain the maximum power by using the optimal PTO damping coefficient, it is necessary to control the electrical torque of the generator accordingly. If the loss of the PTO system is not considered, the mechanical power can be expressed as the movement of the floating body and the PTO force:
The PTO force can be written as follows if expressed as a simplified model using the PTO damping coefficient:
As shown in Equation (28), if the mechanical power is expressed using the optimal PTO damping coefficient calculated to obtain the maximum power, it can be written as:
If the above equation is expressed using the rotary vane pump volume, hydraulic motor volume, and rpm of the hydraulic motor, it can be written as:
Using the relationship between torque and power, the optimum mechanical torque can be calculated as:
The electrical torque reference value for obtaining the maximum output can be calculated as:
However, under irregular wave input conditions, the optimal PTO damping coefficient may include components of various periods rather than the resonance period. Therefore, in this study, the output performance was compared and verified according to the PTO damping coefficient by utilizing various parameters.
4. Results
Through hydraulic-based PTO system modeling, the performance of the maximum power control algorithm with speed control based on the P&O algorithm and optimal torque control was verified. The floating body movement changed by reflecting the PTO system characteristics according to the MPP tracking (MPPT) algorithm under the same wave conditions and the overall power generation performance changed accordingly. Through computational fluid dynamics (CFD) analysis, the motion of the sub-fluid under electrical load control was applied, as shown in Figure 8a. CFD analysis was performed through a commercial program called STAR CCM+, and the simulation was performed considering the fluid viscosity of the floating body. The model was verified by performing model tests using the Froude scale [37].
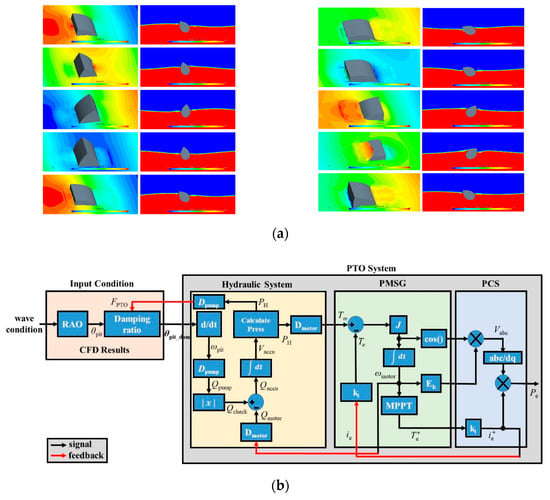
Figure 8.
(a) CFD analysis plot for input conditions [37]. (b) Simulation block diagram for comparison of load control algorithm performance.
The simulation was conducted under regular and irregular wave conditions, and the power generation performance according to the variable change of the MPPT algorithm was compared under each set of wave conditions. Figure 8b provides a block diagram of this simulation. To ensure the accuracy of the simulation, the model was verified through lab tests.
4.1. Simulation Results Obtained under Regular Wave Conditions
The input conditions in the regular wave simulation were a resonance period of 0.75 m wave height and 4.75 s wave period. Under the input conditions, the pitch angle of the floating body according to the load and the absorbed power were calculated using CFD, and Figure 9 presents the results.
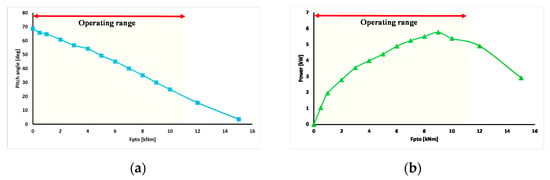
Figure 9.
(a) Heave motion and (b) absorbed power versus PTO force under regular wave conditions.
Figure 9 shows the floating body movement and absorbed power generation according to the PTO force acting on the floating body. As the PTO force increases, the floating body movement decreases. In addition, there is a load that yields an optimal amount of power generation as the PTO force increases and floating body movement decreases. Because the PTO force can be calculated according to the pressure of the hydraulic system, the operating range is determined by the maximum pressure in the circuit, as shown in Figure 9. The power generation performance was compared by applying the P&O algorithm-based speed control algorithm and optimal torque control algorithm for maximum power control under the following input conditions, and a maximum power control algorithm was developed that is suitable for hydraulic-based PTO systems.
Figure 10 shows the motion characteristics and PTO force of the floating body according to the initial reference rpm of the speed control algorithm based on the P&O algorithm under regular wave conditions. The load control and pressure in the circuit change according to the initial reference rpm, and the PTO force changes accordingly. As shown in Figure 10a,b, the pressures all differ according to the initial reference rpm, and as the PTO force increases, the floating body movement decreases. As shown in Figure 10b, the PTO force was operated in a one-way manner to increase the floating body movement. In other words, the part where the pitch angle of the floating body is affected is where the PTO force operates. As shown in Figure 10c, the floating body velocity changes according to its movement, which affects the flow rate generated in the circuit, as shown in Figure 10d. In other words, when the floating body movement decreases, the velocity and generated flow rate also decrease.
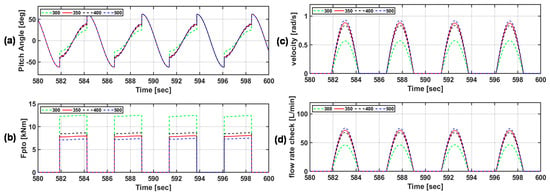
Figure 10.
(a) Floating body motion, (b) PTO force, (c) floating body speed, and (d) generated flow rate according to the initial reference rpm of the speed control algorithm under regular wave conditions (legend indicates initial rpm).
Figure 11 shows the characteristics of the hydraulic and electrical systems according to the initial reference rpm of the P&O algorithm-based speed control algorithm under regular wave conditions. The pressure in the circuit and rpm of the hydraulic motor change according to the input energy and load. Because the speed control algorithm based on the P&O algorithm changes the reference rpm according to the amount of power generation, the rpm continuously changes, as shown in Figure 11b. However, as shown in Figure 11c,d, the lower the initial reference rpm, the higher the load at the same input energy; thus, the pressure increases. As the pressure increases, the PTO force increases, and as shown in Figure 11b, the generation amount can be increased until a constant PTO force is reached. In other words, the pressure in the circuit can be adjusted by applying a speed control algorithm based on the P&O algorithm, and the maximum power generation can be obtained by adjusting the PTO force.
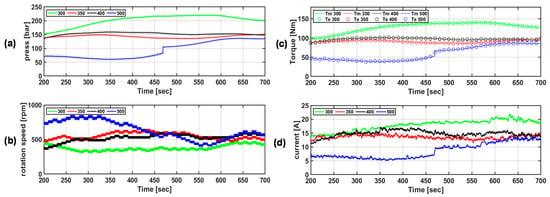
Figure 11.
(a) Pressure in the circuit, (b) hydraulic motor rpm, (c) mechanical and electrical torques, and (d) load current according to the initial reference rpm of the speed control algorithm under regular wave conditions (legend indicates initial rpm).
In conclusion, the speed control algorithm based on the P&O algorithm can perform maximum power control only by adjusting the initial reference rpm setting and rpm change rate according to the system and environmental characteristics.
Figure 12 shows the input power generation and mechanical and electrical power generation according to the initial reference rpm of the speed control algorithm based on the P&O algorithm under regular wave conditions. The input power generated can be obtained according to the pitch angular velocity and PTO force of the floating body, the mechanical power generated can be obtained from the flow rate and pressure of the hydraulic motor, and the electrical power generated can be calculated from the output power of the power converter. The power generation can be increased by controlling the PTO force, which can absorb as much energy as possible through load control. As shown in Figure 12, the pressure changes according to the initial reference rpm, and the closer to the PTO force that can absorb the maximum power, the more power that can be obtained. As shown in Figure 9, in the case of an initial reference of 400 rpm, the PTO force was 9 kNm (160 bar), which yielded the greatest power absorption, and the highest power generation of 5.35 kWh was obtained. Table 1 lists the input power, output power, and efficiency of the PTO system for each case.
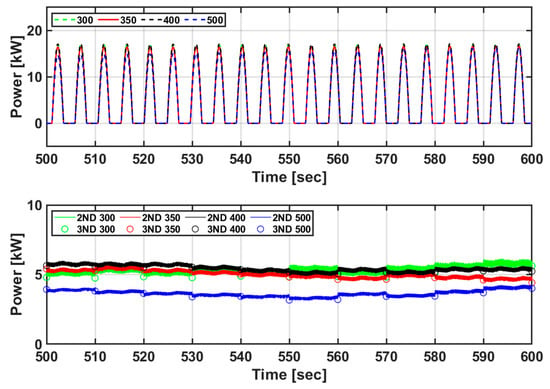
Figure 12.
Comparison of power generation results according to the initial reference rpm of the speed control algorithm under regular wave conditions (legend indicates initial rpm).

Table 1.
Input and output power of the PTO system and efficiency of the PTO system according to the initial reference rpm of the speed control algorithm based on the P&O algorithm.
Figure 13 shows the motion characteristics and PTO force of the floating body according to the torque coefficient of the optimal torque control algorithm under regular wave conditions. The load and pressure in the circuit change according to the torque coefficient, and the PTO force changes accordingly. As shown in Figure 13a,b, the pressures are all different according to the torque coefficient, and the movement of the floating body decreases as the PTO force increases. As shown in Figure 13b, the PTO force operates one way using the same method as the speed control algorithm. As shown in Figure 13c,d, the movement of the floating body affects the float velocity and the flow rate generated in the circuit. In other words, the optimal torque control algorithm can produce the maximum amount of power generation by changing the torque coefficient.
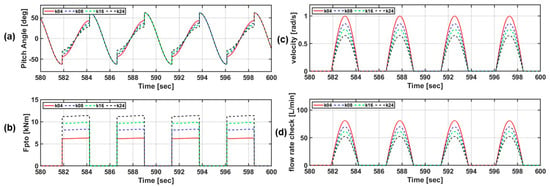
Figure 13.
(a) Float pitch angle, (b) Fpto, (c) float velocity, and (d) generated flow rate according to the torque coefficient of the optimal torque control algorithm under regular wave conditions (legends indicate torque coefficients).
Figure 14 shows the characteristics of the hydraulic and electrical systems according to the torque coefficient of the optimal torque control algorithm under regular wave conditions. The pressure in the circuit and rpm of the hydraulic motor change according to the input energy and load control. Because the load control changes according to the torque coefficient, the pressure and speed are different under the same input conditions. As shown in Figure 14c,d, as the torque coefficient increases, the pressure increases. As the pressure increases, the PTO force increases, and as shown in Figure 9, it is possible to control the load that can absorb the maximum power generation. In other words, the pressure in the circuit can be adjusted according to the torque coefficient of the optimal torque control, and the maximum power generation can be obtained by adjusting the PTO force.
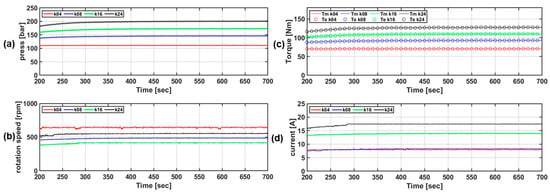
Figure 14.
(a) Circuit pressure, (b) hydraulic motor rpm, (c) mechanical and electrical torques, and (d) load current according to the torque coefficient of the optimal torque control algorithm under regular wave conditions (legends indicate torque coefficients).
In conclusion, the maximum power generation can be obtained by adjusting the torque coefficient according to the system and environmental characteristics of the optimal torque control algorithm.
Figure 15 shows the input, mechanical, and electrical power generation according to the torque coefficient of the optimal torque control algorithm under regular wave conditions. The overall efficiency of the PTO system is quite high, so absorbing as much energy as possible through load control can increase the amount of power generated. As shown in Figure 14, as in the speed control algorithm, the pressure changes according to the torque coefficient, and the maximum power can be obtained as the PTO force approaches the force that can absorb the most power. As shown in Figure 9, the torque coefficient k close to 9 kNm (160 bar), which is the PTO force capable of absorbing the most power, was 1.6, and the greatest power generation was obtained at 5.53 kWh. Table 2 shows the input power, output power, and efficiency of the PTO system for each case.
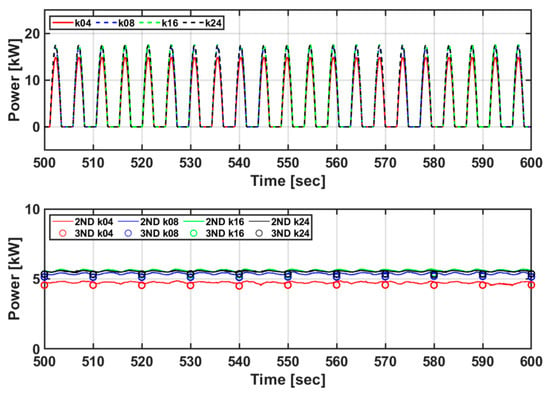
Figure 15.
Power generation comparison according to torque coefficient of optimal torque control algorithm under regular wave conditions (legends indicate torque coefficients).

Table 2.
Input and output power according to the torque coefficient of the optimal torque control algorithm and the efficiency of the PTO system.
4.2. Simulation Results Obtained under Irregular Wave Conditions
The input conditions for the irregular wave simulation were Hs = 0.75 m and Tp = 4.75 s. The pitch RAO for each period of the floating body and damping ratio of the floating body motion according to the PTO force in the irregular wave input conditions were calculated using CFD and are shown in Figure 16.
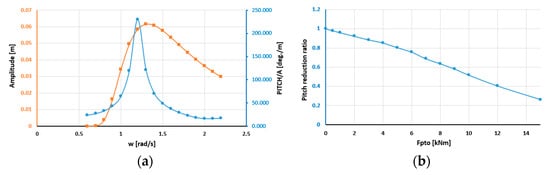
Figure 16.
(a) Wave spectrum and pitch RAO and (b) floating body pitch motion damping ratio according to the PTO force under irregular wave input conditions (Hs = 0.75 m, Tp = 4.75 s).
Figure 16a presents the input wave spectrum and pitch RAO of the float obtained under the irregular wave input conditions (Hs = 0.75 m, Tp = 4.75 s). Figure 16b shows the damping ratio of the pitch motion of the floating body according to the load. According to the irregular wave input conditions, the pitch angle of the floating body can be calculated as the product of the wave spectrum and pitch PAO of the floating body. The damping of the pitch angle of the floating body due to the increase in Fpto as the pressure of the hydraulic system increases can be calculated using the damping ratio shown in Figure 16b. In the simulation for the maximum power control algorithm under irregular wave conditions, the speed control algorithm based on the P&O algorithm and the optimal torque control algorithm were applied. The power generation performance and characteristics of the PTO system according to each algorithm were analyzed under irregular input conditions, and a suitable load control algorithm for a PTO system applying a hydraulic system was developed. Because actual sea wave energy is an irregular input condition, the performance of the proposed maximum power control algorithm for a hydraulic-based PTO system can be verified by analyzing the control algorithm under irregular wave input conditions.
Figure 17 shows the motion characteristics and PTO force of the floating body according to the initial reference rpm of the speed control algorithm based on the P&O algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s). Unlike the regular wave conditions, because the input energy changes rapidly, a large difference occurs in the load control value and the pressure change according to the initial reference rpm; accordingly, a large difference occurs in the PTO force. As shown in Figure 17c,d, because the pitch angle of the floating body decreases with increasing PTO force, the velocity of the floating body and the flow rate generated in the circuit also decrease. As the PTO force increases and the floating body motion decreases, there is a PTO force that can yield the maximum power, similar to the regular wave simulation. That is, because the actual input wave cannot be predicted, the speed control algorithm based on the P&O algorithm can control the maximum output power by appropriately adjusting the initial reference rpm and the rpm change rate according to the input wave energy.
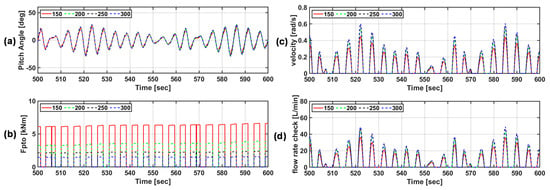
Figure 17.
(a) Float pitch angle, (b) Fpto, (c) float velocity, and (d) generated flow rate according to the initial rpm of the speed control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legend indicates initial rpm).
Figure 18 shows the characteristics of the hydraulic and electrical systems according to the initial reference rpm of the speed control algorithm based on the P&O algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s). If the initial reference rpm is high, the pressure cannot increase because a significant flow rate is used to drive the hydraulic motor. Therefore, owing to the low pressure, the PTO force required to absorb a large amount of input power cannot be achieved. However, when the initial reference rpm is low, the pressure in the circuit increases, and accordingly, the necessary PTO force can be obtained, which can further increase the absorbed power. As the pressure in the circuit increases, the electrical load can be increased, as shown in Figure 18c,d, and, accordingly, the output power can be increased.
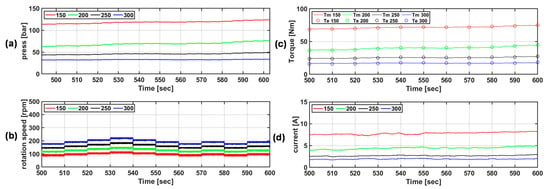
Figure 18.
(a) Pressure in the circuit, (b) hydraulic motor rpm, (c) mechanical and electrical torque, and (d) load current according to the initial rpm of the speed control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legend indicates initial rpm).
In conclusion, the speed control algorithm based on the P&O algorithm can achieve the maximum power generation by selecting the appropriate initial rpm according to the input energy and environmental characteristics.
Figure 19 shows the input, mechanical, and electrical power generation according to the initial reference rpm of the P&O algorithm-based speed control algorithm under irregular wave conditions. By controlling the pressure and PTO force to absorb as much energy as possible through load control, the output power can be increased. Under the input conditions of Hs = 0.75 m, Tp = 4.75 s, using 150 rpm initially corresponded to 0.602 kWh, which yielded the highest power generation. At ≤150 rpm initially, the pressure in the circuit increased further, and more power could be obtained. However, at ≤80 rpm, the power supply of the power converter did not operate; therefore, it was not considered as a control reference value.
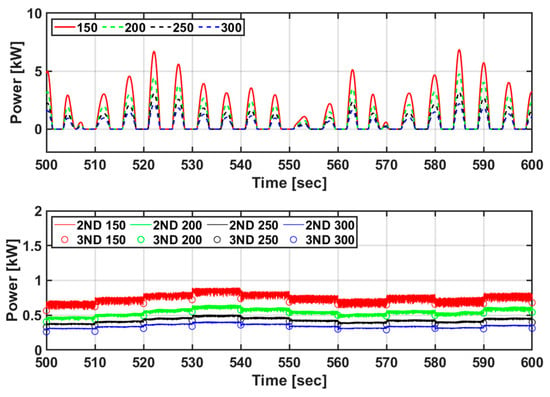
Figure 19.
Comparison of the amount of power generated according to the initial rpm of the speed control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legend indicates initial rpm).
Figure 20 shows the motion characteristics and PTO forces of the floating body according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s). Similar to the speed control algorithm based on the P&O algorithm, because the input energy changes rapidly, there are large differences in the load control value and pressure variability with the torque coefficient; accordingly, the PTO force also varies considerably. As shown in Figure 20c,d, because the movement of the floating body decreases according to the PTO force, the speed of the floating body and the flow rate generated in the circuit also decrease. These tendencies are the same as those observed using the speed control algorithm. The higher the torque coefficient, the more the load is applied at the same rpm; thus, the pressure increases further.
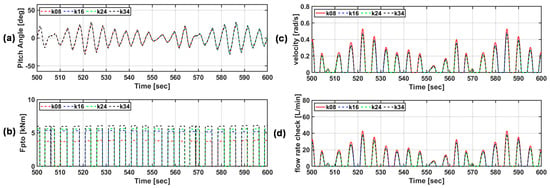
Figure 20.
(a) Floating body pitch angle, (b) PTO force, (c) floating body velocity, and (d) occurrence flow rate according to torque coefficient of optimal torque control algorithm flux under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legends indicate torque coefficients).
In other words, as in the speed control algorithm, adjusting the torque coefficient appropriately according to the input wave energy is a way to obtain the maximum power.
Figure 21 shows the characteristics of the hydraulic and electrical system according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s). If the torque coefficient is low, the initial rpm is high, and accordingly, the flow rate for driving the hydraulic motor is high. That is, the pressure in the circuit is low, making the PTO force far from the optimal value for absorbing the input energy. However, as the torque coefficient increases, the pressure in the circuit increases, and accordingly, the PTO force that can further increase the absorbed power can be obtained. As the pressure in the circuit increases, the electrical load can be increased, as shown in Figure 21c,d, and accordingly, the amount of output power can be increased. However, as shown in Figure 21, when the torque coefficient increases to a certain value (k = 0.34), the output power generation decreases because the rpm decreases as the load increases. That is, as the torque coefficient increases and the pressure in the circuit increases, the movement of the floating body decreases. Therefore, the maximum power generation can only be obtained by selecting an appropriate torque coefficient according to the input energy and environmental characteristics.
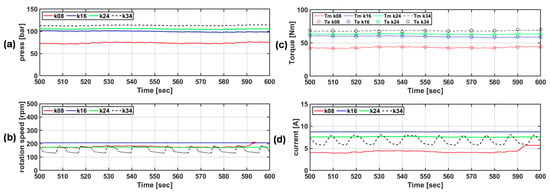
Figure 21.
(a) Pressure in the circuit, (b) hydraulic motor rpm, (c) mechanical and electrical torque, and (d) electrical load current according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legends indicate torque coefficients).
Figure 22 shows the input power generation and mechanical and electrical power generation according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions. Similar to the speed control algorithm, the amount of power generated can be increased by controlling the pressure and the PTO force to absorb as much energy as possible through load control. However, if the torque coefficient increases above a certain value, the PTO force increases and the input power increases, but the rpm decreases owing to an increase in pressure, and the output power generated may decrease. In conclusion, under input conditions of Hs = 0.75 m, Tp = 4.75 s, the torque coefficient for obtaining the maximum power generation of the optimal torque control algorithm was 0.24, and 0.911 kWh of power could be generated.
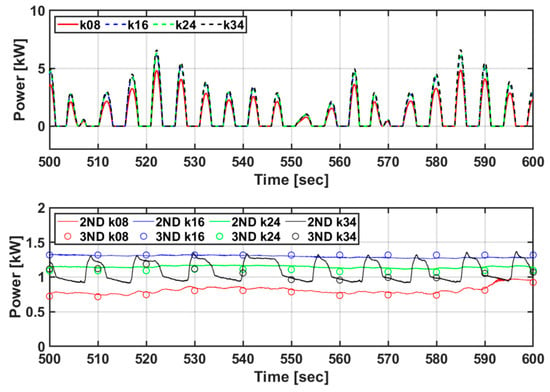
Figure 22.
The result of comparing the generation amounts according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions (Hs = 0.75 m, Tp = 4.75 s) (legends indicate torque coefficients).
Figure 23 shows the power generation performance according to the torque coefficient of the optimal torque control algorithm under irregular wave conditions. In case A (k = 0.08) with the lowest torque coefficient, the pressure was also low because the load was low, so the input power was low; thus, the output power generation was low. In case B (k = 0.16) with an increased torque coefficient, the pressure was increased compared to that in case A because the load value was increased, and both the input generation amount and the output generation amount were increased. That is, when the torque coefficient increases, the pressure in the circuit increases, which increases the input power, and the load value increases, thereby increasing the output power generation.
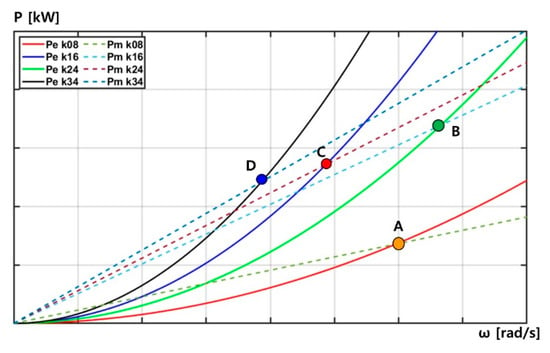
Figure 23.
Comparison of output power generation performance according to torque coefficient of optimal torque control algorithm (legends indicate torque coefficients).
In addition, in cases C and D (k = 0.24 and k = 0.34, respectively), the torque coefficient was increased, but the output power generation was decreased compared to that in case B. As the torque coefficient increases, the pressure increases, but the rpm decreases, and the output power generation decreases. However, as the circuit pressure increases, the amount of input power generated can increase according to the optimal PTO force of the rotor. As shown in Figure 23, under irregular wave conditions, the maximum output can be obtained using the torque coefficient.
Figure 24 shows the power generation performance and efficiency for each algorithm under the same irregular wave input conditions. In the speed control algorithm based on the P&O algorithm, the pressure changes according to the initial reference rpm, and the input absorbed power appears to differ accordingly. The lower the initial reference rpm, the higher the pressure that can be obtained, and the higher the input absorbed power. However, the speed control algorithm based on the P&O algorithm has a lower output power than the optimal torque control algorithm because it is difficult to change the reference speed appropriately according to the input energy, and load control is performed to maintain the reference speed for a certain period of time. The optimal torque control algorithm yielded greater power generation through appropriate load control according to the input energy than the speed control algorithm based on the P&O algorithm. In addition, high efficiency and output energy are increased through appropriate circuit pressure control according to the input energy. However, as the torque coefficient increases with the input energy, the circuit pressure increases; thus, the input energy may increase, but the efficiency and power generation of the PTO system are reduced.
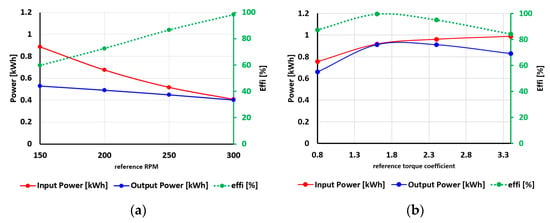
Figure 24.
Input and output power generation and PTO system efficiency according to (a) speed control algorithm and (b) optimal torque control algorithm under the same irregular wave input conditions (Hs = 0.75 m, Tp = 4.75 s).
Figure 25 compares the power generation of the algorithms under various input energy conditions to verify the performance of each algorithm. Input energy was performed under irregular wave conditions, and results were derived based on 30 min data. It was confirmed that the optimal torque control algorithm obtained high power generation under all input conditions.
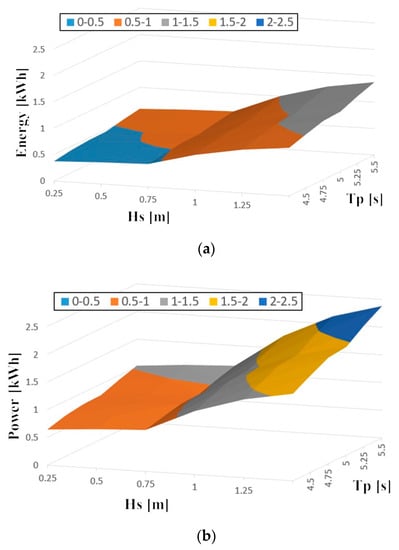
Figure 25.
Performance of (a) P&O algorithm-based speed control algorithm and (b) optimal torque control algorithm according to input condition change.
In conclusion, under the irregular wave conditions, the optimum torque control could produce high power generation, which enabled the appropriate load change according to the change in input energy. In addition, it is possible to increase the input absorbed power by increasing the circuit pressure and increasing the load; however, if a large amount of energy is used to increase the pressure, the efficiency and power generation of the PTO system may be reduced.
5. Comparison of Real Sea Test and Simulation
The simulator developed in this study was verified based on the output data of an actual FWEC sea test conducted in the western sea of Jeju Island, Korea. The PTO system of the simulator was modeled based on the specifications used in the actual sea test.
Figure 26 shows the FWEC rotor, PTO systems, and measurement and control systems used in the actual sea test. The data used for the simulator verification were verified using approximately 400 s of actual sea test power generation data. Data measurement was performed at 20 Hz and measurement was performed using NI DAQ equipment. For the verification method, the characteristics of the simulator PTO system were compared under the same floating body pitch motion input conditions as in the actual sea test. In addition, the validity of applying the load control algorithm was verified by comparing the results of the simulator and applying the load control algorithm for maximum power control with actual sea data. Because an actual sea test is limited in terms of the variety of data that can be obtained, a simulation with various input conditions could be conducted and used as basic data for the actual sea test later.

Figure 26.
Actual FWEC sea test photos: (a) rotors, (b) PTO system (including the hydraulic system, generator, and PCS), (c) actual sea experiment, and (d) measurement and control system.
5.1. Comparison of P&O Algorithm-Based Speed Control Algorithm
As shown in Figure 27, the simulator used the same input conditions as the actual sea test to analyze the characteristics of the PTO system. To verify the simulator performance based on actual sea data, the load control algorithm was analyzed by applying the speed control algorithm based on the P&O algorithm and optimal torque control algorithm described in the previous section. Firstly, the speed control algorithm based on the P&O algorithm selects an initial reference speed based on the speed data of the actual sea test and manages control while changing the reference speed according to the P&O algorithm. The hydraulic system, electrical load, and power generation characteristics were compared between the P&O algorithm-based speed control algorithm results and those of a PTO system with actual sea data.
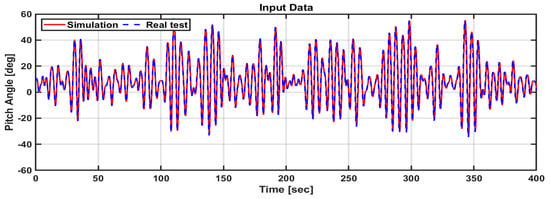
Figure 27.
Simulator input data results obtained using pitch angle data of a floating body in an actual sea test.
Figure 28 shows the actual sea test data and the results of the speed control algorithm based on the simulator P&O algorithm. By applying the speed control algorithm, it was possible to obtain results similar to the pressure data of the actual sea test. It was possible to verify the PTO system results of the simulator through load control under the same input conditions based on the data obtained in the actual sea test. In addition, as shown in Figure 28b–d, the mechanical pressure (Figure 28b) and flow rate (Figure 28c) characteristics of the PTO system according to the speed control and electrical load current (Figure 28d) were also compared with the actual sea test results. Some numerical differences may exist due to physical losses and the limited ability to simulate the load control in the same way as in the actual test, but the trends of the data are similar.
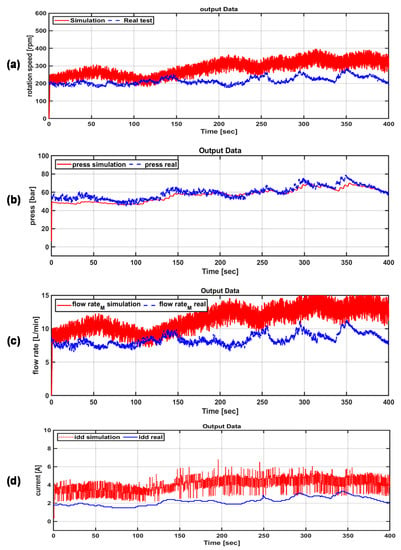
Figure 28.
Comparison of PTO system characteristics according to real sea test results and P&O algorithm-based speed control algorithm of the simulator. (a) rotation speed; (b) mechanical pressure; (c) flow rate; (d) electrical load current.
Figure 29 shows the power generation results of the actual sea test and the P&O algorithm-based speed control algorithm. The amount of power generated was compared to the amounts of input power (first generation amount, P1), mechanical power (second generation amount, P2), and electrical power (third generation amount, P3) generation. The actual sea area test and the average input power generated in the simulation were 1.3021 kW and 1.3177 kW, respectively; hence, similar results were obtained. The same floating body motion was applied, and because the pressure of the hydraulic system was almost identical in the two cases, the PTO force was almost identical, and there was little difference in the input power generation. P2 and P3 appear similar to one another. Because the simulator cannot consider the loss that occurs physically, the amount of power generated appeared slightly larger. The average output in the actual sea test and simulation were 0.766 kW and 1.067 kW, and the PTO system efficiencies were 42% and 81%, respectively. In addition, the amount of input power generated rapidly changes with time in the PTO system using the hydraulic system, but the variability of the mechanical and electrical outputs is reduced.
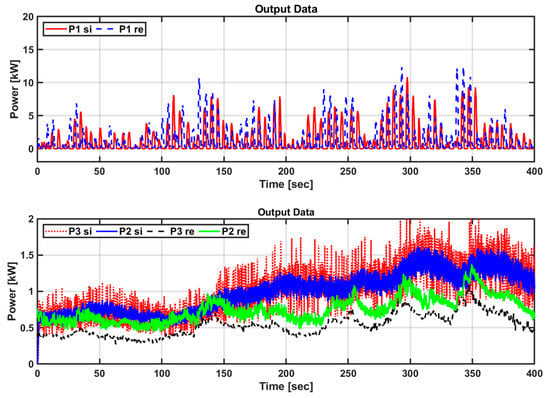
Figure 29.
Comparison of the amounts of power generated in the actual sea test and with the speed control algorithm based on the P&O algorithm of the simulator.
5.2. Comparison of Torque Control Algorithm
Similar to the verification of the speed control algorithm based on the P&O algorithm, the input data shown in Figure 27 were used as the input data to verify the optimal torque control algorithm. Unlike the P&O algorithm, which monitors the output power amount, the optimal torque control algorithm adjusts the electrical torque based on the rpm change, according to the input energy required to obtain the maximum amount of power generation.
Figure 30 shows the results of the actual sea test and the characteristics of the PTO system according to the optimal torque control simulation. The pressures obtained using the simulated PTO system to which the optimal torque control algorithm was applied appear to be almost identical to the actual sea data. In addition, the changes in the rpm and the trend of the load change according to the input energy change are similar between the actual test and the simulation. Under the same input conditions as the P&O algorithm-based speed control algorithm, the PTO system and electrical load characteristics are similar. These findings were also verified by comparing the results of the optimal torque control algorithm with actual sea test data.
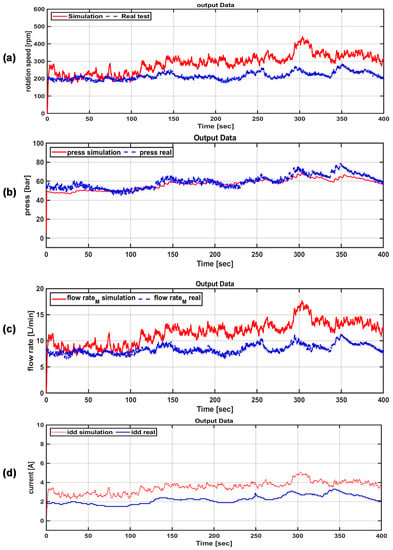
Figure 30.
Comparison of the PTO system characteristics according to the actual sea test and optimal torque control simulation. (a) rotation speed; (b) mechanical pressure; (c) flow rate; (d) electrical load current.
Figure 31 shows the amounts of power generated in the actual sea test according to the optimal torque control algorithm. Specifically, the input power generation and mechanical and electrical power generation were compared. The amounts of input power generated in the actual sea test and simulation were 1.3021 kW and 1.3107 kW, respectively. Because the simulator does not consider loss, the amount of power generation appears slightly larger, but the trend of the generation data is similar. The actual sea test result and average output of the simulator were 0.7661 kW and 1.061 kW, respectively, and the efficiency of the PTO system was 42% and 81%, respectively. In addition, it can be confirmed that the output power generation amount is constant, even though the input energy changes rapidly.
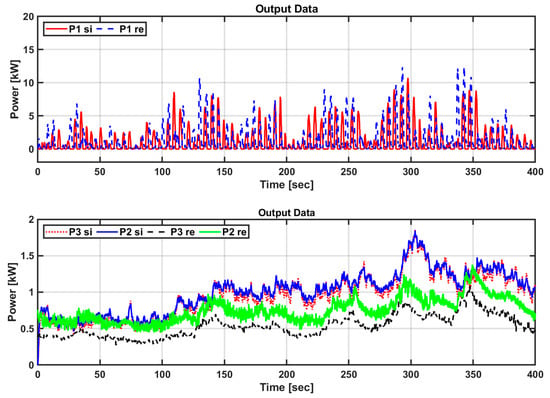
Figure 31.
Comparison of power generation in actual sea test and simulation results.
In conclusion, by applying the speed and torque control algorithms, output performance similar to that in the actual sea test could be confirmed under the same input energy conditions. That is, it was confirmed that the maximum power control algorithms proposed in this paper can be applied to a hydraulic-based PTO system. However, it was not possible to compare the performances of the algorithms under various conditions, as in the previous simulation. As a future study, we will analyze the power generation performance considering changes in each algorithm and control variables.
6. Conclusions
Among the PTO systems for FWEC, the hydraulic system type has already been widely used because it facilitates the achievement of low speed and high torque. Therefore, in this study, modeling was conducted using a hydraulic system generator power converter to analyze the performance of a PTO system using a hydraulic system. Using this approach, the characteristics and power generation performance of the PTO system to which a load control algorithm for maximum power control was applied were analyzed. Unlike previous studies on input power generation using a hydraulic-based PTO system, the characteristics of a hydraulic-based PTO system were analyzed through electrical load control in this study. Based on this, the input power, output power, and PTO system efficiency were analyzed. The maximum power control algorithm was analyzed by applying the P&O algorithm-based speed control algorithm and optimal torque control algorithm. By analyzing the characteristics and power generation performance of the PTO system according to the control variables of each algorithm, a maximum power control algorithm suitable for load control of a hydraulic-based PTO system was proposed. Although the power generation performance and PTO system efficiency characteristics differed depending on the algorithm and control variable, input power control was possible by controlling the pressure of the hydraulic circuit through electrical load control.
In conclusion, the optimal torque control algorithm proposed in this paper proved to be suitable for load control of a PTO system based on a hydraulic system. This simulator was verified based on actual sea test results. In addition, the simulation results can be used as basic data for load control in actual sea tests of the PTO system based on a hydraulic system for wave power generation in the future.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Pitch angular velocity of floating body | |
| Pitch angle of the floating body | |
| Rotary vane pump flow | |
| Rotary vane pump displacement | |
| FTO force on floating body | |
| Force of the FTO to obtain the maximum power generation | |
| High pressure in hydraulic piping | |
| Low pressure in hydraulic piping | |
| Flow of check valve | |
| Accumulator flow | |
| Hydraulic motor flow | |
| Accumulator volume | |
| Initial high pressure of hydraulic pipe | |
| Accumulator initial volume | |
| Accumulator specific weight | |
| Hydraulic motor displacement | |
| Mechanical torque | |
| Electrical torque | |
| Hydraulic motor angular speed | |
| D-Q axis inductance of generator | |
| Electrical angular frequency | |
| D-Q axis generator current | |
| D-Q axis generator voltage | |
| Generator flux linkage | |
| Generator armature resistance | |
| Electrical power | |
| Number of generator poles | |
| DC/DC Converter duty ratio | |
| DC/DC Converter controlled sampling | |
| Period of input wave energy | |
| Resonance period of input wave energy | |
| Power take-off damping factor | |
| Input absorption power | |
| Mechanical power | |
| Torque damping factor |
References
- Noble, D.R.; O’Shea, M.; Judge, F.; Robles, E.; Martinez, R.; Khalid, F.; Thies, P.R.; Johanning, L.; Corlay, Y.; Gabl, R.; et al. Standardising Marine Renewable Energy Testing: Gap Analysis and Recommendations for Development of Standards. J. Mar. Sci. Eng. 2021, 9, 971. [Google Scholar] [CrossRef]
- Davey, T.; Sarmiento, J.; Ohana, J.; Thiebaut, F.; Haquin, S.; Weber, M.; Gueydon, S.; Judge, F.; Lyden, E.; O’Shea, M.; et al. Round Robin Testing: Exploring Experimental Uncertainties through a Multifacility Comparison of a Hinged Raft Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 946. [Google Scholar] [CrossRef]
- Xu, R.; Wang, H.; Xi, Z.; Wang, W.; Xu, M. Recent Progress on Wave Energy Marine Buoys. J. Mar. Sci. Eng. 2022, 10, 566. [Google Scholar] [CrossRef]
- Martins, J.C.; Fragassa, C.; Goulart, M.M.; dos Santos, E.D.; Isoldi, L.A.; Gomes, M.D.N.; Rocha, L.A.O. Constructal Design of an Overtopping Wave Energy Converter Incorporated in a Breakwater. J. Mar. Sci. Eng. 2022, 10, 471. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Cruz, J. Ocean Wave Energy—Current Status and Future Perspectives; Springer: Berlin, Germany, 2008; p. 434. [Google Scholar]
- Salter, S.H.; Taylor, J.R.M.; Caldwell, N.J. Power conversion mechanisms for wave energy. Proc. Inst. Mech. Eng. M 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Rico, H.H.; Morten, M.K.; Enrique, V. Discrete displacement hydraulic power take-off system for the Wavestar wave energy converter. Energies 2013, 6, 4001–4044. [Google Scholar]
- Markel, P.; John, V.R. A review of wave-to-wire models for wave energy converters. Energies 2016, 9, 506. [Google Scholar]
- Mueller, M.; Baker, N. Direct Drive Wave Energy Converters. Available online: http://www.cder.dz/download/upec-1.pdf (accessed on 23 July 2013).
- Polinder, H.; Mueller, M.; Scuotto, M.; Prado, M. Linear generator systems for wave energy conversion. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–14 September 2007. [Google Scholar]
- Li, B.; Macpherson, D.E.; Shek, J.K.H. Direct drive wave energy converter control in irregular waves. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011) IET, Edinburgh, UK, 6–8 September 2011; p. 64. [Google Scholar]
- Poullikkas, A. Technology Prospects of Wave Power Systems. Electron. J. Energy Environ. 2014, 2, 47–69. [Google Scholar]
- Arof, H.; Nor, W.; Nor, K.M. Linear generator: Design and simulation. In Proceedings of the National Power Engineering Conference IEEE, Bangi, Malaysia, 15–16 December 2003; pp. 306–311. [Google Scholar]
- Hansen, R.; Andersen, T.; Pedersen, H. Model based design of efficient power take-off systems for wave energy converters. In Proceedings of the 12th Scandinavian International Conference on Fluid Power (SICFP 2011), Tampere, Finland, 18–20 May 2011; Volume 2, pp. 35–49. [Google Scholar]
- António, F.D.O. Modeling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator. Ocean Eng. 2007, 34, 2021–2032. [Google Scholar]
- Babarit, A.; Guglielmi, M.; Clément, A.H. Declutching control of a wave energy converter. Ocean Eng. 2009, 36, 1015–1024. [Google Scholar] [CrossRef] [Green Version]
- Hansen, R.; Andersen, T.; Pedersen, H. Comparison of reactive and non-reactive control strategies for wave energy converters with non-ideal power take-off systems. Renew. Energy 2013. submitted for publication. [Google Scholar]
- Skinner, N. Wave Energy Converter Device. European Patent EP2284386A2, 16 February 2011. [Google Scholar]
- Linjama, M.; Vihtanen, H.P.; Sipola, A.; Vilenius, M. Secondary controlled multi-chamber hydraulic cylinder. In Proceedings of the 11th Scandinavian International Conference on Fluid Power (SICFP09), Linkoeping, Sweden, 2–4 June 2009. [Google Scholar]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Phil. Trans. R Soc. A 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joseba, L.A.; Carlos, A.U.J.; Jose, E.A.F. Power Take-Off Device for Wave Energy Transformation. European Patent EP2466118A1, 20 June 2012. [Google Scholar]
- Lasa, J.; Antolin, J.C.; Angulo, C.; Estensoro, P.; Santos, M.; Ricci, P. Design, construction and testing of a hydraulic power take-off for wave energy converters. Energies 2012, 5, 2030–2052. [Google Scholar] [CrossRef] [Green Version]
- Hansen, R.; Andersen, T.; Pedersen, H. Determining required valve performance for discrete control of PTO cylinders for wave energy. In Proceedings of the ASME Symposium on Fluid Power and Motion Control (FPMC 2012), Bath, UK, 12–14 September 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 565–578. [Google Scholar]
- Ratanak, S.; Sean, C.; Sam, K.; Asher, S.; Ted, K.A. PTO-Sim: Development of a power take off modeling tool for ocean wave energy conversion. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting (IEEE-PES 2015), Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Ratanaks, S.; Asher, S.; Ted, B.; Kelley, R.; Carlos, M. Development of PTO-SIM: A power performance module for the open-source wave energy converter code WEC-SIM. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2015), St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Abdelsalam, K.; Massoud, A.M.; Ahmed, S.; Enjeti, P.N. High-performance adaptive perturb and observe MPPT technique for photovoltaic based microgrids. IEEE Trans. Power Electron. 2011, 26, 1010–1021. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Xu, J.; Yang, Y.; Hu, Y.; Xu, T.; Zhan, Y. MPPT Control of Hydraulic Power Take-Off for Wave Energy Converter on Artificial Breakwater. J. Mar. Sci. Eng. 2020, 8, 304. [Google Scholar] [CrossRef]
- Amon, E.A.; Brekken, T.K.A.; Schacher, A.A. Maximum Power Point Tracking for Ocean Wave Energy Conversion. IEEE Trans. Ind. Appl. 2012, 48, 1079–1086. [Google Scholar] [CrossRef]
- Hardy, P.; Cazzolato, B.S.; Ding, B.; Prime, Z. A maximum capture width tracking controller for ocean wave energy converters in irregular waves. Ocean Eng. 2016, 121, 516–529. [Google Scholar] [CrossRef]
- Mendes, R.; Calado, M.D.R.; Mariano, S.J.P.S. Maximum Power Point Tracking for a Point Absorber Device with a Tubular Linear Switched Reluctance Generator. Energies 2018, 11, 2192. [Google Scholar] [CrossRef] [Green Version]
- Ding, B.; Cazzolato, B.S.; Arjomandi, M.; Hardy, P.; Mills, B. Sea-state based maximum power point tracking damping control of a fully submerged oscillating buoy. Ocean Eng. 2016, 126, 299–312. [Google Scholar] [CrossRef]
- Li, W.; Chau, K.T.; Hua, F.; Ching, T.W. Maximum power point tracking control of a linear magnetic-geared generator for direct-drive wave energy conversion. In Proceedings of the 10th International Conference on Advances in Power System Control, Operation & Management (APSCOM 2015), Hong Kong, China, 8–12 November 2015; pp. 1–6. [Google Scholar]
- Salter, S.H.; Jeffrey, D.C.; Taylor, J.R.M. The Architecture of Nodding Duck Wave Power Generators. 1976. Available online: https://hdl.handle.net/1842/37407 (accessed on 21 March 2022).
- Ha, Y.J.; Park, J.Y.; Shin, S.H. Numerical Study of Non-Linear Dynamic Behavior of an Asymmetric Rotor for Wave Energy Converter in Regular Waves. Processes 2021, 9, 1477. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).