Fire Risk Assessment of a Ship’s Power System under the Conditions of an Engine Room Fire

Abstract

This paper presents a risk assessment method for a ship’s power system under the conditions of an engine room fire based on the expert comprehensive evaluation (ECE) method combined with the fuzzy fault tree analysis (FFTA) method. The composition of the main engine system in the engine room and the failure logic of each subsystem were analyzed, and the fuzzy fault tree of a ship engine room fire was constructed. The probability of system failure and the importance of basic events were calculated. The fire safety risk assessment model was established using the safety risk matrix. The risk assessment of a ship engine room fire was implemented. The results demonstrated that the fire frequency of the ship engine room was 5.232 × 10⁻⁶ h⁻¹. The fire risk of the main engine fuel system was the highest. Fuel leakages from diesel supply tanks and heavy fuel oil tanks are the main cause of accidents. The proposed method eliminated the influence of incomplete statistics in the risk assessment process and improved the accuracy and credibility of the reassessment results.

1. Introduction

Fire accidents seriously threaten the safety of ship navigation. Fires in engine rooms account for up to two-thirds of ship fire accidents, which are particularly difficult to tackle and directly destroy the operation of power systems. In recent years, ship fire accidents have occurred frequently. In 2017 alone, there were dozens of accidents caused by ship engine room fires. According to the IMO, among the 1400 incidents reported from 2000 to 2017, 270 were related to fires and explosions, which accounted for 19.2 percent of reported incidents. Engine room fires account for more than 75 percent of all ship fires [1]. The engine room of a ship is narrow and the pipelines are crisscrossed. It has a large fire load, hidden ignition point, and the potential for a rapid spread of fire that is difficult to extinguish [2]. The engine room is the power center of the ship. It is highly likely that a ship will lose power and be damaged once a fire occurs, which can seriously threaten the navigation safety of the ship. Therefore, it is significant to assess the fire risk to a ship’s power system under the conditions of a ship engine room fire.

Previous research on ship engine room fires has mainly focused on addressing the characteristics of various aspects, including oxygen concentration, pressure, mass loss rate, temperature distribution, heat transfer, etc. [3]. Wang et al. [4] investigated the vertical distribution of maximum smoke temperatures by conducting a series of experiments on a sealed ship cabin fire. Chen et al. [5] demonstrated that the increased oxygen concentration would lead to positive feedback on the conductive, convective, and radiant heat fluxes. Overall, the current studies on the risk of engine room fire in ships are very limited.

In the process of risk assessment, the incompleteness of the calculation data is a key factor affecting the accuracy and credibility of the assessment results [6]. In studies of fire accident risks, severe damage resulting from fires can great difficulties in the investigation of the causes of the accidents. Fires destroy vast amounts of evidence. Experts can only make inferences about the causes of fires based on clues. This is the main reason for incomplete computational data and incomplete cognition. The expert comprehensive evaluation method is based on the fuzzy set theory, which converts an expert’s fuzzy language judgments of events into fuzzy numbers for quantitative calculation [7] and the failure probability of a system can be obtained. The method considers all the evaluation factors and the levels of the experts so it can obtain comprehensive and objective evaluation results [8]. Kaptan [9] adopted the bow-tie method based on the fuzzy set theory to convert the linguistic variables of experts into quantitative calculation data suitable for the fuzzy logic method. The risk of the loss of anchors in anchorage operations was analyzed. Sakar et al. [10], in a study of an accident risk assessment of confined spaces onboard ships, also used the fuzzy set theory to solve the problem of a lack of data. Therefore, the expert comprehensive evaluation method based on the fuzzy set theory is an effective solution to incomplete computational data.

In terms of fire risk assessment methods for ship engine rooms, Zong et al. [11] developed a Bayesian network model for ship engine room fires using a Bayesian network method to evaluate the risk of fires. However, Bayesian network methods rely on a solid database and it is difficult to obtain accurate quantitative results. Quantitative evaluation methods commonly used in the field of marine engineering include the analytic hierarchy process (AHP) [12,13], fault tree analysis (FTA) method [14,15], and numerical simulation method [16]. Lavasani et al. [17] proposed that the usual lack of data for calculating component failure rates was a challenge for system risk assessment. The fault tree model of oil and gas leakage accidents in the drilling industry was developed by the fuzzy fault tree analysis method. The fuzzy probability of an event at the bottom of the system was obtained by the expert comprehensive evaluation method. This method provides a theoretical basis for system risk assessment in the absence of data. Sarıalioğlu et al. [18] employed the human factors analysis and classification system (HFACS) method to classify the contributing factors of engine room fires into a hierarchical structure. The possible accident scenarios and probabilities were calculated using the fuzzy fault tree analysis (FFTA) method. The causes of the accident were studied, and proposals were presented to prevent fire accidents. Tuncel et al. [19] analyzed the fuzzy logic of fire and explosion accidents on bulk carriers. The fuzzy fault tree model of bulk carrier fire and explosion accidents was developed and the cut-set importance was calculated. The accident formation process was revealed. Among them, the fuzzy fault tree analysis method is based on the fault tree theory in the reliability analysis. It is based on probability theory and Boolean algebra using logic block diagrams to express the relationships between the system components. It is an effective tool for the quantitative assessment of a system’s fire risk [20]. On the one hand, the ambiguity of the evaluation language and the cognitive uncertainty in the fire risk assessment of a ship’s power system can be solved. On the other hand, it overcomes the problem of the lack of a statistical data foundation in the fuzzy fault tree operation. Compared with FTA, ETA, BBN, AHP, Delphi [21], and other methods, it is a good method for reliability assessment. However, it is limited by factors such as incomplete data when applied to the evaluation of actual engineering projects [22]. This is the advantage of the method proposed in this paper, which is a method worth studying for the fire risk assessment of ship power systems. Considering the shortcomings of the above studies, this paper established a ship engine room fire risk assessment model integrating the expert comprehensive evaluation method and the fuzzy fault tree analysis method. The model aims to quantify the fire risk of a ship’s power system under the influence of cognitive uncertainty. It provides a series of measures to reduce a ship engine room’s fire risk under the consideration of uncertainty. Firstly, an affiliation function for expert evaluation is established. The function takes into account the fuzzy characteristics of the experts’ language. In addition, the fuzzy language of the experts is normalized. The normalization results are used for the fuzzy fault tree basic event probability input. Thus, a fuzzy model of a ship engine room’s fire fault tree is constructed based on the ship engine room’s failure logic under fire conditions. The calculation results clarify the areas with high fire risk in the ship’s engine room. Finally, the system failure rate, basic event importance, and fire safety risk index are used as indicators to describe the fire risk of a ship’s power system. The objective of the research work is to complete the risk assessment of a ship’s power system under the conditions of an engine room fire. The novelty of this work is to eliminate the problem of incomplete data and cognitive uncertainty in the fire risk assessment process. It provides a promising solution for the risk assessment of complex systems. In summary, the contributions of this paper are as follows:

(1)

A ship power system fire risk assessment model based on the expert comprehensive evaluation (ECE) method and fuzzy fault tree analysis method is established. The ship engine room fire risk is evaluated.

(2)

The influence of cognitive uncertainty on the assessment of the ship power system fire risk is quantified. The engine room fire risk is identified.

(3)

The system failure rate, basic event importance, and fire safety risk index are used as indicators to characterize the ship engine room fire risk. A series of measures to reduce the fire risk is provided.

The rest of the paper is organized as follows: The methodology is presented in Section 2. In Section 3, a fuzzy fault tree model for ship engine room fires is established and calculations are performed for analysis. In Section 4, the calculation results and conclusions are given.

2. Methods

In this paper, a fire risk assessment method for ship power systems is proposed based on the ECE-FFTA method. The method invites experts to use fuzzy language to determine the basic event and safety risk severity grades of the ship’s power system. The aggregated fuzzy numbers normalized by the opinion are input into the fault tree. The aggregated fuzzy number of the upper system is solved. After defuzzification, the fuzzy probabilities of the upper-level events and subsystems can be obtained. Finally, the annual fire frequency, basic event importance, and fire safety risk index are used as indicators to comprehensively assess and analyze the fire risk of ship power systems. This method can be implemented to deal with the uncertainty and ambiguity of the research object and solve the problem of lacking the probability of the underlying events in the fault tree analysis method. The specific flow chart is shown in Figure 1.

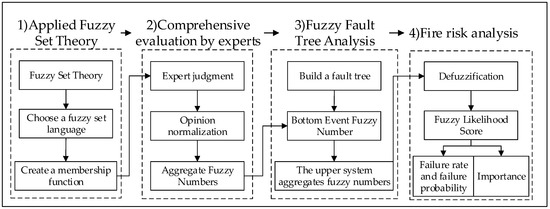
Figure 1. Calculation flow chart based on FFTA-ECE evaluation method.

2.1. Fuzzy Set Theory

The fuzzy judgment language is introduced from the fuzzy set theory as the research object. The appropriate membership function is established. After the operation and transformation, the research object is quantitatively calculated. A fuzzy set is defined as

$$\tilde{A}=\left\{\left(x, {\mu }_{\tilde{A}}\left(x\right)\right)|x\in U,{\mu }_{\tilde{A}}\in \left[0,1\right]\right\},$$

(1)

where $\tilde{A}$ is the fuzzy set belonging to $U$; ${\mu }_{\tilde{A}}$ is the membership function of the fuzzy set $\tilde{A}$; ${\mu }_{\tilde{A}}\left(x\right)$ represents the membership degree of any element $x$ in the fuzzy set.

(1)

Establish a membership function

The reasonable selection of the membership function determines the accuracy of the evaluation results. The use of triangular and trapezoidal fuzzy numbers to establish the membership functions can better express the possibility and degree of certainty of the event. These two classes of fuzzy numbers can more effectively map fuzzy languages to fuzzy membership functions (Figure 2). Its expression is as follows:

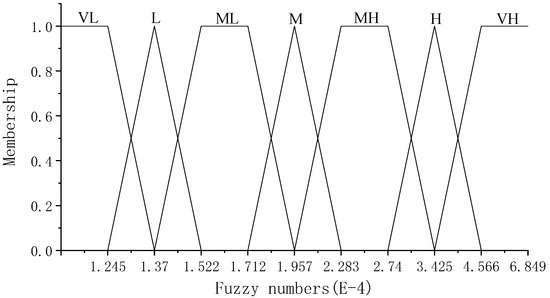
Figure 2. Membership function.

Membership function for very-low-risk states:

$$f_{VL}=\{\begin{array}{ccc}1& ,& 1.142 \times {10}^{-4}\le x\le 1.245 \times {10}^{-4}\\ \frac{-x+1.370 \times {10}^{-4}}{0.125 \times {10}^{-4}}& ,& 1.245 \times {10}^{-4}<x\le 1.370 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(2)

Membership function for low-risk states:

$$f_L=\{\begin{array}{ccc}\frac{x-1.245 \times {10}^{-4}}{0.125 \times {10}^{-4}}& ,& 1.245 \times {10}^{-4}\le x\le 1.370 \times {10}^{-4}\\ \frac{-x+1.522 \times {10}^{-4}}{0.152 \times {10}^{-4}}& ,& 1.370 \times {10}^{-4}<x\le 1.522 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(3)

Membership function for middle low-risk states:

$$f_{ML}=\{\begin{array}{ccc}\frac{x-1.370 \times {10}^{-4}}{0.152 \times {10}^{-4}}& ,& 1.370 \times {10}^{-4}\le x\le 1.522 \times {10}^{-4}\\ 1& ,& 1.522 \times {10}^{-4}<x\le 1.712 \times {10}^{-4}\\ \frac{-x+1.957 \times {10}^{-4}}{0.245 \times {10}^{-4}}& ,& 1.712 \times {10}^{-4}<x\le 1.957 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(4)

Membership function for medium-risk states:

$$f_M=\{\begin{array}{ccc}\frac{x-1.712 \times {10}^{-4}}{0.245 \times {10}^{-4}}& ,& 1.712 \times {10}^{-4}\le x\le 1.957 \times {10}^{-4}\\ \frac{-x+2.283 \times {10}^{-4}}{0.326 \times {10}^{-4}}& ,& 1.957 \times {10}^{-4}<x\le 2.283 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(5)

Membership function for middle high-risk states:

$$f_{MH}=\{\begin{array}{ccc}\frac{x-1.957 \times {10}^{-4}}{0.326 \times {10}^{-4}}& ,& 1.957 \times {10}^{-4}\le x\le 2.283 \times {10}^{-4}\\ 1& ,& 2.283 \times {10}^{-4}<x\le 2.740 \times {10}^{-4}\\ \frac{-x+3.425 \times {10}^{-4}}{0.685 \times {10}^{-4}}& ,& 2.740 \times {10}^{-4}<x\le 3.425 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(6)

Membership function for high-risk states:

$$f_H=\{\begin{array}{ccc}\frac{x-2.740 \times {10}^{-4}}{0.685 \times {10}^{-4}}& ,& 2.740 \times {10}^{-4}\le x\le 3.425 \times {10}^{-4}\\ \frac{-x+4.566 \times {10}^{-4}}{1.141 \times {10}^{-4}}& ,& 3.425 \times {10}^{-4}<x\le 4.566 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(7)

Membership function for very-high-risk states:

$$f_{VH}=\{\begin{array}{ccc}\frac{x-3.425 \times {10}^{-4}}{1.141 \times {10}^{-4}}& ,& 3.425 \times {10}^{-4}\le x\le 4.566 \times {10}^{-4}\\ 1& ,& 4.566 \times {10}^{-4}<x\le 6.849 \times {10}^{-4}\\ 0& ,& otherwise\end{array},$$

(8)

2.2. Expert Comprehensive Evaluation Method

The expert comprehensive evaluation method invites relevant experts to use fuzzy language to judge basic events and convert the fuzzy language into triangular fuzzy numbers or trapezoidal fuzzy numbers for quantitative calculation [23]. In order to accurately obtain the fuzzy probability of the event and reduce the subjective influence of the expert opinions, the weight factor of each expert’s opinion is determined by the professional status, work experience, and education level of the expert. The expert opinions can then be normalized. Table 1 shows the scoring rules for the importance of the experts. The importance scores of the experts are the product of the three scores of the expert’s title, work experience, and education level.

Table 1. Expert importance scoring rules.

Project	Classification	Score
Job title	Positive height	5
	Deputy high	4
	Intermediate	3
Work experience	>20 years	5
	15–20 years	4
	10–15 years	3
	5–10 years	2
	<5 years	1
Education level	PhD	5
	Master	4
	Bachelor	3

Table 2 shows the fuzzy numbers corresponding to the linguistic variables. The commonly used fuzzy linguistic variables are very low (VL), low (L), middle low (ML), medium (M), middle high (MH), high (H), and very high (VH) [24].

Table 2. Fuzzy numbers corresponding to language variables.

Linguistic Variables	Fuzzy Numbers
VL (Very low)	(1.14 × 10−4, 1.14 × 10−4, 1.25 × 10−4, 1.37 × 10−4)
L (Low)	(1.25 × 10−4, 1.37 × 10−4, 1.37 × 10−4, 1.52 × 10−4)
ML (Middle low)	(1.37 × 10−4, 1.52 × 10−4, 1.71 × 10−4, 1.96 × 10−4)
M (Medium)	(1.71 × 10−4, 1.96 × 10−4, 1.96 × 10−4, 2.28 × 10−4)
MH (Middle high)	(1.96 × 10−4, 2.28 × 10−4, 2.74 × 10−4, 3.42 × 10−4)
H (High)	(2.74 × 10−4, 3.42 × 10−4, 3.42 × 10−4, 4.57 × 10−4)
VH (Very high)	(3.42 × 10−4, 4.57 × 10−4, 6.85 × 10−4, 6.85 × 10−4)

The specific process of the consensus aggregation method of the expert opinions is as follows:

(1) When the fuzzy failure probability of the system is calculated by the expert comprehensive evaluation method, the approval degree of the opinions between any two experts is expressed as

$$S_{ij}=S\left({\tilde{A}}_i,{\tilde{A}}_j\right)=1-\frac{1}{4}{\displaystyle \sum _{k=1}^4{\displaystyle |}{a}_{ik}-a_{jk}{\displaystyle |}},$$

(9)

where ${\tilde{A}}_i$ is the opinion of the expert $E_i$, ${\tilde{A}}_i=\left(a_{i1},a_{i2},a_{i3},a_{i4}\right)$; ${\tilde{A}}_j$ is the opinion of the expert $E_j$, ${\tilde{A}}_j=\left(a_{j1},a_{j2},a_{j3},a_{j4}\right)$.

(2) A consensus matrix can be constructed from the approval degrees of the opinions between two experts as follows:

$$M=\left[\begin{array}{cccc}{s}_{11}& s_{12}& \cdots & s_{1n}\\ s_{21}& s_{22}& \cdots & s_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ s_{n1}& s_{n2}& \cdots & s_{nn}\end{array}\right],$$

(10)

where when $i=j$, $S_{ij}=1$.

(3) The average recognition of each expert is

$$A\left(E_i\right)=\frac{1}{n-1}{\displaystyle \sum _{j=1,j\ne i}^n{S}_{ij}},$$

(11)

(4) The relative recognition of each expert is

$$R\left(E_i\right)=A\left(E_i\right)/{\displaystyle \sum _{i=1}^{n}A\left(E_i\right)},$$

(12)

(5) The importance of each expert is

$$IM\left(E_i\right)=\frac{score\left(i\right)}{{\displaystyle \sum _{i=1}^{n}score\left(i\right)}},$$

(13)

where $score\left(i\right)$ is the importance score of the expert $E_i$.

(6) The weight coefficient of the expert is

$$w\left(E_i\right)=\alpha IM\left(E_i\right)+\left(1-\alpha \right)R\left(E_i\right),$$

(14)

where $\alpha$ is the relaxation factor representing the importance of the expert’s personal experience and opinion. Usually, $\alpha$ is taken as 0.5.

(7) The normalized result of the expert opinion is

$${\tilde{\lambda }}_j={\displaystyle \sum _{i=1}^n{w}_i}\cdot {\tilde{\lambda }}_{ij}, j=1,2,\dots m,$$

(15)

where ${\tilde{\lambda }}_j$ is the aggregated fuzzy number of basic events j; ${\tilde{\lambda }}_{ij}$ is the fuzzy number corresponding to the opinion of expert $E_i$; $m$ is the number of basic events.

2.3. Fuzzy Fault Tree Analysis

The aggregated fuzzy number of the bottom event after normalization is input into the fuzzy fault tree. The aggregated fuzzy number of the top event and the upper system can be obtained by Equations (15) and (16).

(1) “AND” gate:

$$P\left(E_{upper}\right)={\displaystyle \prod _{i=1}^{n}p\left(B{E}_i\right)},$$

(16)

(2) “OR” gate:

$$P\left(E_{upper}\right)=1-{\displaystyle \prod _{i=1}^n\left(1-p\left(B{E}_i\right)\right)},$$

(17)

where $P\left(E_{upper}\right)$ denotes the probability of occurrence of upper-level events; $p\left(B{E}_i\right)$ denotes the probability of occurrence of basic events i.

For trapezoidal fuzzy numbers $q_1=\left(a_1,b_1,c_1,d_1\right)$ and $q_2=\left(a_2,b_2,c_2,d_2\right)$, the operation rules are

$$\begin{array}{l}{q}_1\oplus q_2=\left(a_1+a_2,b_1+b_2,c_1+c_2,d_1+d_2\right)\\ q_1\Theta q_2=\left(a_1-d_2,b_1-c_2,c_1-b_2,d_1-a_2\right)\\ q_1\otimes q_2=\left(a_1{a}_2,b_1{b}_2,c_1{c}_2,d_1{d}_2\right)\end{array},$$

(18)

According to the trapezoidal fuzzy number, the probability of the upper event in the fuzzy fault tree is calculated. The algorithm is as follows:

(1) “AND” gate:

$$q_{AND}={\displaystyle \prod _{i=1}^n{q}_i=\left({\displaystyle \prod _{i=1}^n{a}_i,{\displaystyle \prod _{i=1}^n{b}_i},{\displaystyle \prod _{i=1}^n{c}_i},{\displaystyle \prod _{i=1}^n{d}_i}}\right)},$$

(19)

(2) “OR” gate:

$$q_{OR}=1\Theta {\displaystyle \prod _{i=1}^n\left(1\Theta q_i\right)=\left[1-{\displaystyle \prod _{i=1}^n\left(1-a_i\right),1-{\displaystyle \prod _{i=1}^n\left(1-b_i\right)},1-{\displaystyle \prod _{i=1}^n\left(1-c_i\right)},1-{\displaystyle \prod _{i=1}^n\left(1-d_i\right)}}\right]},$$

(20)

2.4. Fire Risk Analysis

(1)

Defuzzification

To represent the probability of occurrence of the top event, the aggregated fuzzy number of the top event in the fuzzy fault tree should be converted into a clear value. This process is called defuzzification and uses the center of gravity method (COG) to convert the fuzzy number into a fuzzy probability score (FPS) [25], which is expressed as

$$X^{*}=\frac{{\displaystyle \int x{\mu }_{\tilde{A}}\left(x\right)dx}}{{\displaystyle \int {\mu }_{\tilde{A}}\left(x\right)dx}},$$

(21)

For trapezoidal fuzzy numbers, the above formula can be expressed as

$$X^{*}=\frac{1}{3}\frac{{\left(d+c\right)}^2-dc-{\left(a+b\right)}^2+ab}{d+c-b-a},$$

(22)

(2)

Importance analysis

Importance is an essential indicator of the contribution of basic events to the probability of occurrence of top events. By analyzing the importance of each fundamental event, the importance of each component of the system is determined. The weak points in the system can be identified and the system can be protected with more targeted equipment, which is expressed as [20]

$$I_{FV}^i=\frac{1-{\displaystyle \prod _{j=1}^N\left(1-P_j^i\right)}}{p_t},$$

where $P_j^i$ represents the probability of occurrence of the ith basic event in the jth smallest cut set; $p_t$ represents the probability of occurrence of the top event.

(3)

Safety Risk Index

The risk matrix method was proposed by the acquisition team at the U.S. Air Force Electronic Systems Center in 1995 and has been used extensively in many large programs. The core of the risk matrix method is risk classification by calculating a safety risk index (R). The equation is as follows:

$$R=P\times C,$$

where P is the security risk severity and C is the security risk level.

The safety risk severity grades, P, are generally divided into four grades at the domestic and international levels. The divisions of the safety risk severity grades are shown in Table 3.

Table 3. The divisions of the safety risk severity grades.

Grade	Severity	Accident Consequence
4	Disastrous	Total destruction or scrapping of equipment, severe irreversible environmental damage
3	Serious	Severe damage to equipment, more serious but reversible environmental damage
2	Mild	Mild damage to equipment or environment
1	Slight	Minor damage to equipment or environment

According to the frequency of accidents, the possibility of safety risks is divided into four grades. The safety risk possibilities are shown in Table 4.

Table 4. The divisions of the safety risk possibilities grades.

Grade	Description	Probability Range
4	Frequently	$C\ge 0.3$
3	Possible	$0.3>C\ge 0.03$
2	Occasional	$0.03>C\ge 0.003$
1	Rare	$0.003>C$

The fuzzy probability score is the failure rate of the basic event. The failure rate needs to be converted to a failure probability. The equation is

$$P\left(t\right)=1-e^{-\lambda t},$$

where P(t) denotes the failure probability of the event at time t; λ denotes the failure rate of the event.

The risk grading is based on the safety risk index (R). The safety risk is divided into four grades: general risk, greater risk, major risk, and mega risk. The divisions of the safety risk grades are shown in Table 5.

Table 5. The divisions of the safety risk grades.

Grade	Evaluation Value	Description
4	$16\le R\le 25$	The system suffers from mega-safety risk factors that could lead to mega-accidents and result in huge losses.
3	$9<R<16$	The system has major safety factors that could lead to a major accident and result in major losses.
2	$4\le R\le 9$	The system has high safety risk factors that may lead to serious accidents and result in serious losses.
1	$1\le R\le 4$	The system has minor safety risk factors that may lead to smaller incidents and result in smaller losses.

3. Risk Assessment of Ship Power System under Engine Room Fire

Taking the Panamax container ship as an example, the fire risk of a ship’s power system under the conditions of an engine room fire is carried out based on the ECE-FFTA method.

3.1. Construction of Fuzzy Fault Tree for Ship Power System

A ship’s power system is mainly composed of three subsystems: the main engine fuel system, the propulsion motor room, and the gas turbine room. The main engine fuel system provides fuel oil for the main engine of the ship. The propulsion motor room is the space for the power plant of the ship. The gas turbine room is the space for the mechanical device where the fuel energy is converted into useful energy. A fire in any of the subsystems can result in the loss of functionality of the entire power system. The fault tree model of each subsystem is established, respectively. The fault tree information is shown in Table 6. The fault tree is shown in Figure 3. The “or” gate means that the failure of any basic event under the gate will cause that upper-level event to fail. The “and” gate means that all basic events under this gate fail to cause the upper-level event to fail.

Table 6. Failure information of an engine room fire.

Codes	Description
M1	Main engine fuel system fire
M2	Propulsion motor room fire
M3	Gas turbine cabin fire

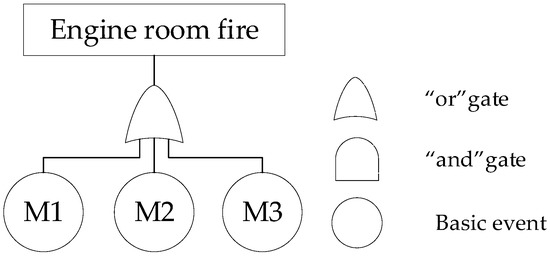
Figure 3. Fault tree of an engine room fire.

3.1.1. Main Engine Fuel System Fire

The function of the main engine fuel system (M1) is to supply quantitative and constant pressure fuel to the main engine injectors, which is the power source for the main engine operation. In this system, fuel supply tank overflows, valve or flange leaks, and filter leakage resulting in the exposure of fuel to environments with high-temperature hot walls and bright contacts are the main factors leading to main engine fuel system fires. The fire logic gate and event information of a main engine fuel system fire are listed in Table 7. The fault tree diagram is shown in Figure 4.

Table 7. Logic gates and principal events of a main engine fuel system fire.

Codes	Description	Codes	Description
G1	Fire and explosion caused by diesel fuel supply tank generates combustible material	E9	Electrical failure causes the electrical appliance to overheat
G2	Fire and explosion caused by fuel overflow from diesel supply tank	G6	Fire and explosion caused by heavy fuel oil tanks produce combustible materials
E1	Diesel supply tank oil overflow	G7	Fire and explosion caused by oil spill from heavy fuel oil tank
G3	Ignition source	E10	Heavy fuel oil tank fuel overflow
E2	Insulation failure on the surface of the exhaust pipe of the host	G8	Fire and explosion caused by volatilization of heavy fuel oil tanks
E3	Welding slag left over during repair welding	E11	Heavy fuel oil tank volatilization
E4	Insulation failure on the surface of boiler exhaust pipe	G9	Oil leakage from valve or flange causes fire and explosion
G4	Fire and explosion caused by volatilization of oil and gas in diesel supply tank	E12	Valve or flange leakage
E5	Diesel supply tank volatilization of oil and gas	E13	Insulation failure on the surface of the exhaust pipe of the auxiliary machine
E6	Illegal smoking	G10	Fire and explosion caused by circulating pump produce combustible material
E7	Static electricity produces an open flame	E14	Circulating pump leaks
G5	Fire and explosion caused by supply pump produce combustible materials	G11	Fire and explosion caused by oil filters produce combustible materials
E8	Oil supply pump leaks	E15	Oil filter leaks

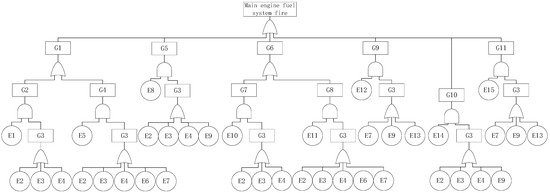
Figure 4. Fault tree of a main engine fuel system fire.

3.1.2. Propulsion Motor Room Fire

The propulsion motor room (M2) has rotating motors that provide propulsion power for the ship, including propulsion generators and propulsion motors. High-temperature hot surfaces caused by the long-term operation of the mechanical equipment in the engine room, the combustible material in the engine room, and electrical equipment failures are the typical causes of fire failures in the propulsion engine room. The propulsion engine room fire logic gate and time information are shown in Table 8. The fault tree diagram is shown in Figure 5.

Table 8. Logic gates and principal events of a propulsion motor room fire.

Codes	Description	Codes	Description
G12	Electrical equipment causes fire	E21	Electrical aging
G3	Ignition source	G15	Combustible
E16	High-temperature live conductor caused by circuit failure	E22	Cable insulation layer, protective layer
G13	High-temperature hot wall	E23	Surrounding combustibles
E17	Cooling failure in the motor room	G16	Hot work in the propulsion motor room caused fire
E18	Excessive temperature in special parts	E24	Combustible gas accumulates in the engine room
G14	Electric spark	G17	Open flame
E19	Electrical leakage	E25	Welding during maintenance in the engine room
E20	Electrical short circuit	E26	Cutting during maintenance in the engine room

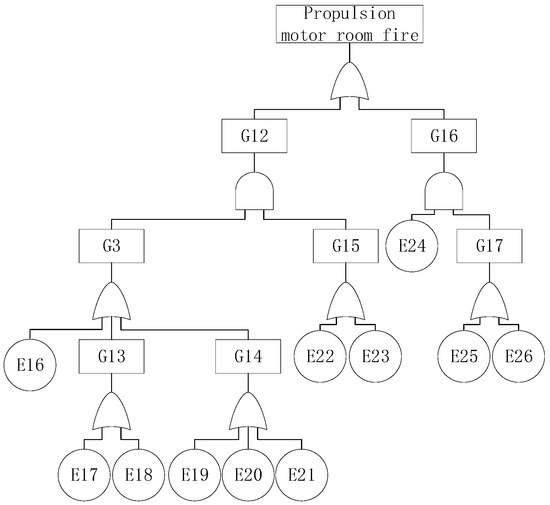
Figure 5. Fault tree of a propulsion motor room fire.

3.1.3. Gas Turbine Room Fire

The gas turbine room is an internal combustion power machine that converts the energy from fuel into useful energy. The high-temperature operation of the machinery and equipment in the gas turbine room and the aging of the electrical equipment components are the main causes of fire. The fire logic gate and time information of a gas turbine room fire are listed in Table 9. The fault tree diagram is shown in Figure 6.

Table 9. Logic gates and principal events of a gas turbine room fire.

Codes	Description
G18	Fire caused by machinery and equipment
G19	Oil leak
E27	Leakage of oil filter
E28	Leakage of oil heater
E29	Leakage of oil supply pipes and joints
E30	Fuel tank drip
E31	Lubricant leak
G13	High-temperature hot wall
E18	Excessive temperature in special parts
E32	Failure of the coolant in the gas tank
G20	Fire caused by electrical equipment
E33	Cable or surrounding combustibles
G21	Getting hot or sparking
E20	Electrical short circuit
E34	The components of the electric control box are aging
E35	Aging of cable insulation material
G21	Hot work in the gas turbine cabin caused fire
E24	Combustible gas accumulates in the engine room
G17	Open flame
E25	Welding during maintenance in the engine room
E26	Cutting during maintenance in the engine room

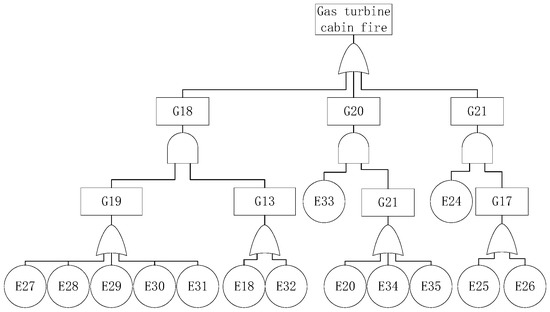
Figure 6. Fault tree of a gas turbine room fire.

3.2. Comprehensive Assessment of Ship Power System by Fire Experts

In order to obtain information on fires of ship power system equipment, five experts were invited to judge the basic events of the system. The five experts were chief engineers, senior engineers, and engineers from relevant research institutes who have been engaged in the design, operation, and maintenance of naval systems for a long time, as well as university teachers who are engaged in the study of naval vitality.

According to the importance score rules, the importance scores of each expert were calculated and are shown in Table 10. Their importance coefficients were 0.328, 0.246, 0.197, 0.131, and 0.098, respectively. The above experts were invited to use fuzzy language to judge the failures of the basic events of a ship’s power system. The judgments of the relevant basic events were normalized. The fuzzy numbers of the basic events after the experts’ evaluations and the normalization are shown in Table 11.

Table 10. The scores of expert importance.

Expert	Job Title	Score	Work Experience	Score	Education Level	Score	Total Score
1	Chief engineer	5	18	4	PhD	5	100
2	Professor	5	13	3	PhD	5	75
3	Senior engineer	4	12	3	PhD	5	60
4	Associate Professor	4	9	2	PhD	5	40
5	Engineer	3	5	2	PhD	5	30

Table 11. Failure judgments of experts of basic events.

Numbering	E1	E2	E3	E4	E5	Aggregate Fuzzy Numbers
E1	VH	H	H	H	VH	(3.021 × 10−4, 3.895 × 10−4, 4.837 × 10−4, 5.512 × 10−4)
E2	H	VH	VH	VH	H	(3.139 × 10−4, 4.095 × 10−4, 5.433 × 10−4, 5.908 × 10−4)
E3	H	H	M	H	MH	(2.419 × 10−4, 2.960 × 10−4, 3.029 × 10−4, 3.944 × 10−4)
E4	MH	H	MH	H	M	(2.226 × 10−4, 2.675 × 10−4, 2.888 × 10−4, 3.697 × 10−4)
E5	ML	M	ML	M	L	(1.484 × 10−4, 1.669 × 10−4, 1.756 × 10−4, 2.019 × 10−4)
E6	M	M	ML	L	L	(1.498 × 10−4, 1.687 × 10−4, 1.725 × 10−4, 1.977 × 10−4)
E7	H	M	M	M	ML	(1.931 × 10−4, 2.280 × 10−4, 2.308 × 10−4, 2.837 × 10−4)
E8	H	ML	M	L	H	(1.984 × 10−4, 2.367 × 10−4, 2.410 × 10−4, 3.029 × 10−4)
E9	VH	H	H	MH	VH	(2.892 × 10−4, 3.706 × 10−4, 4.724 × 10−4, 5.321 × 10−4)
E10	H	ML	MH	VH	H	(2.392 × 10−4, 2.961 × 10−4, 3.472 × 10−4, 4.137 × 10−4)
E11	ML	H	L	ML	L	(1.634 × 10−4, 1.891 × 10−4, 1.973 × 10−4, 2.389 × 10−4)
E12	MH	M	M	MH	MH	(1.855 × 10−4, 2.145 × 10−4, 2.411 × 10−4, 2.940 × 10−4)
E13	H	MH	M	M	MH	(2.075 × 10−4, 2.464 × 10−4, 2.636 × 10−4, 3.309 × 10−4)
E14	L	ML	H	ML	L	(1.592 × 10−4, 1.835 × 10−4, 1.909 × 10−4, 2.296 × 10−4)
E15	M	ML	VH	M	H	(2.127 × 10−4, 2.597 × 10−4, 3.092 × 10−4, 3.457 × 10−4)
E16	VH	H	L	L	VH	(2.479 × 10−4, 3.149 × 10−4, 4.091 × 10−4, 4.402 × 10−4)
E17	M	MH	L	L	MH	(1.636 × 10−4, 1.864 × 10−4, 2.036 × 10−4, 2.428 × 10−4)
E18	H	VH	L	MH	H	(2.467 × 10−4, 3.081 × 10−4, 3.665 × 10−4, 4.283 × 10−4)
E19	L	MH	H	H	L	(1.951 × 10−4, 2.319 × 10−4, 2.422 × 10−4, 3.054 × 10−4)
E20	H	MH	MH	VH	H	(2.524 × 10−4, 3.130 × 10−4, 3.701 × 10−4, 4.463 × 10−4)
E21	M	H	H	VH	MH	(2.464 × 10−4, 3.055 × 10−4, 3.501 × 10−4, 4.172 × 10−4)
E22	VH	H	H	MH	MH	(2.674 × 10−4, 3.365 × 10−4, 4.111 × 10−4, 4.810 × 10−4)
E23	H	MH	VH	MH	H	(2.572 × 10−4, 3.205 × 10−4, 3.836 × 10−4, 4.575 × 10−4)
E24	H	L	L	MH	VH	(2.085 × 10−4, 2.539 × 10−4, 2.955 × 10−4, 3.435 × 10−4)
E25	H	H	H	MH	H	(2.611 × 10−4, 3.231 × 10−4, 3.307 × 10−4, 4.380 × 10−4)
E26	M	H	H	L	MH	(2.105 × 10−4, 2.525 × 10−4, 2.594 × 10−4, 3.289 × 10−4)
E27	MH	ML	VH	L	ML	(1.912 × 10−4, 2.301 × 10−4, 2.945 × 10−4, 3.242 × 10−4)
E28	MH	ML	H	L	L	(1.760 × 10−4, 2.050 × 10−4, 2.214 × 10−4, 2.725 × 10−4)
E29	MH	MH	H	L	L	(1.891 × 10−4, 2.220 × 10−4, 2.444 × 10−4, 3.050 × 10−4)
E30	M	M	MH	L	H	(1.837 × 10−4, 2.144 × 10−4, 2.235 × 10−4, 2.722 × 10−4)
E31	M	M	VH	L	L	(1.904 × 10−4, 2.292 × 10−4, 2.744 × 10−4, 2.947 × 10−4)
E32	M	MH	L	L	ML	(1.548 × 10−4, 1.751 × 10−4, 1.882 × 10−4, 2.210 × 10−4)
E33	VH	H	MH	MH	M	(2.482 × 10−4, 3.091 × 10−4, 3.860 × 10−4, 4.412 × 10−4)
E34	M	L	MH	M	MH	(1.694 × 10−4, 1.940 × 10−4, 2.100 × 10−4, 2.507 × 10−4)
E35	MH	MH	H	MH	H	(2.231 × 10−4, 2.676 × 10−4, 2.976 × 10−4, 3.820 × 10−4)

3.3. Fire risk Analysis of Ship Power System

3.3.1. The Annual Fire Frequency Analysis of Ship Power Systems

According to the quantitative calculation of the fuzzy fault tree, the annual fire frequency of a ship’s power system is 5.232 × 10⁻⁶ h⁻¹. The ship engine room is under major fire risk. The calculation results of the annual fire frequencies and safety risk indexes of the subsystems are shown in Table 12.

Table 12. The annual fire frequencies and safety risk indexes of the subsystems.

System	Annual Fire Frequencies (h−1)	Fire Probability	P	C	R
Engine room fire	5.232 × 10−6	4.48 × 10−2	3	4	12
Main engine fuel system fire	2.557 × 10−6	2.22 × 10−2	2	3	6
Propulsion motor room fire	1.553 × 10−6	1.35 × 10−2	2	1	2
Gas turbine room fire	1.123 × 10−6	9.79 × 10−3	2	2	4

The calculation results show that the annual fire frequency of the main engine fuel system is 2.557 × 10⁻⁶ h⁻¹. It is exposed to a high fire risk. Compared with the other two subsystems, the main engine fuel system has the highest fire frequency. Its annual fire frequency is twice that of the other subsystems because the main engine fuel system is an important system for supplying fuel to the main engine of the ship. It is one of the most critical systems in a ship’s power system and is the basis for the normal navigation of the ship. There are many piping systems in the area. Fuel leakage can easily cause a huge fire [26]. The annual fire frequency of the propulsion motor room is 1.553 × 10⁻⁶ h⁻¹ and that of the gas turbine room is 1.123 × 10⁻⁶ h⁻¹. The fire risk is rated as Grade 1. The fire risk is minor. The annual fire frequency of the propulsion motor room is slightly higher than that of the gas turbine room. Compared with the gas turbine room, the annual fire frequency of the propulsion motor room is slightly higher because the propulsion motor room contains mostly electrical equipment. As an important system in the ship’s power system, the propulsion motor room is responsible for the propulsion of the ship. The electrical equipment in the engine room continues to operate under high load, resulting in a local temperature rise of some equipment in the engine room. It is easy to cause a fire after contact with the surrounding combustibles such as aging components. The risk of fire caused by mechanical equipment in the gas turbine room should not be underestimated. The results for the annual fire frequencies of the specific subsystems are shown in Figure 7.

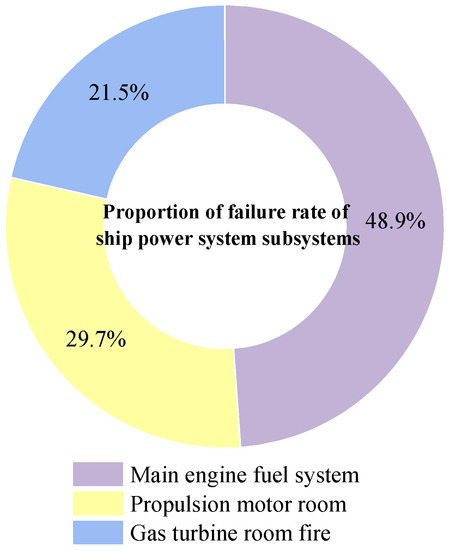
Figure 7. Proportion of annual fire frequencies of a ship power system’s subsystems.

The annual fire frequencies of the typical failure modes of ship power systems are shown in Table 13. The ranking of the typical failure modes of a ship power system’s subsystems is shown in Figure 8, in which fire caused by electrical equipment is the main failure mode, with the highest annual fire frequency. There are two main reasons for this. One is that the equipment comes into contact with combustibles such as cable insulation and protective layers after high temperatures, causing fires. The other is that the electrical equipment is aging and faulty, causing engine room fires. The surface temperature of the equipment in the engine room should be monitored. The inspection of the electrical equipment in the engine room should be strengthened. Equipment failures should be found and eliminated in time, and the aging components should be replaced. Fires and explosions caused by diesel supply tanks and heavy fuel oil tanks are also important failure modes with high annual fire frequencies. High-temperature surfaces such as pipes must be isolated and protected. Internal inspections should be strengthened to prevent fuel leakage accidents, thus preventing fires. The failure mode of fires caused by mechanical equipment is high [27]. Damaged oil filters and heaters should be replaced in a timely manner. Fuel supply pipes and joints should be checked to prevent fuel leakage. The mailbox coolant should be replaced in a timely manner to avoid the overheating of components [28], thereby reducing the risk of fire.

Table 13. The annual fire frequencies of typical failure modes.

Failure Mode	Annual Fire Frequency	Failure Mode	Annual Fire Frequency
G1	7.41 × 10−7	G12	1.38 × 10−7
G5	3.77 × 10−7	G16	1.73 × 10−7
G6	6.60 × 10−7	G18	6.44 × 10−7
G9	2.22 × 10−7	G20	3.06 × 10−7
G10	2.92 × 10−7	G21	1.73 × 10−7
G11	2.66 × 10−7

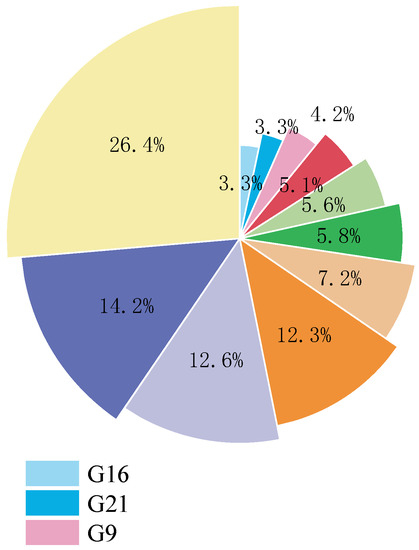
Figure 8. Ranking of typical failure modes of each subsystem.

3.3.2. Basic Event Importance Analysis

To identify the susceptibility of a ship’s power system to fire in the ship engine room, the weak points in the system were detected and the basic events were classified according to their importance. The higher the importance, the more critical the basic events, so it is necessary to pay attention to them. The calculation results of the basic event importance are shown in Table 14. Figure 9 shows the variations in the basic event importance levels.

Table 14. Importance and ranking of basic events.

Rank	Importance	Numbering	Rank	Importance	Numbering
1	23.922	E22	19	4.904 × 10−2	E16
2	22.716	E23	20	4.873 × 10−2	E5
3	22.079	E33	21	4.100 × 10−2	E12
4	1.383 × 10−1	E2	22	3.991 × 10−2	E7
5	1.238 × 10−1	E18	23	3.771 × 10−2	E25
6	9.311 × 10−2	E3	24	3.420 × 10−2	E19
6	8.738 × 10−2	E1	25	2.923 × 10−2	E26
8	8.645 × 10−2	E4	26	2.786 × 10−2	E17
9	7.570 × 10−2	E9	27	2.702 × 10−2	E27
10	6.954 × 10−2	E8	28	2.603 × 10−2	E13
11	6.581 × 10−2	E10	29	2.565 × 10−2	E31
12	6.556 × 10−2	E24	30	2.514 × 10−2	E29
13	5.562 × 10−2	E11	31	2.337 × 10−2	E30
14	5.409 × 10−2	E14	32	2.289 × 10−2	E28
15	5.406 × 10−2	E20	33	2.060 × 10−2	E35
16	5.299 × 10−2	E32	34	1.446 × 10−2	E34
17	5.136 × 10−2	E21	35	1.227 × 10−2	E6
18	4.911 × 10−2	E15

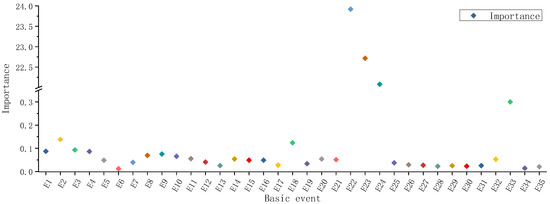
Figure 9. Changes in the importance levels of basic fire events in ship power system fires.

The results of the importance of the basic events in ship power system fires can be seen in Table 14 and Figure 9. It can be seen that the cable insulation layer, protective layer, and surrounding combustibles are the key factors leading to ship power system fires. High-temperature surfaces and open flames are prone to fire accidents. The obtained results were consistent with similar studies conducted in the past. Puisa et al. [29] studied fire incidents in the engine room of Le Boreal passenger ships. Routine maintenance procedures and inadequate insulation were the main causes of fires. Baalisampang et al. [30] indicated that human error in the maintenance process leads to more frequent fire and explosion accidents, especially during “fire operations”. Therefore, the primary way to prevent the risk of fire is to develop safety awareness among the crew. Compliance with safety management regulations is an important factor in the safe operation of ships. The inspection of cable insulation and protection layers should be strengthened and aging and damaged cables should be replaced in a timely manner. Combustible materials in the machine room should be regularly cleaned up to avoid accumulation. This way, the contents of the machine room are prevented from being ignited and the risk of fire can be reduced.

4. Conclusions and Future Scope

In this paper, a fire risk assessment method for ship power systems based on an ECE-FFTA method was established together with the annual fire frequency of the system, the importance of basic events, and the fire safety risk index as the risk assessment indicators. The fire risk assessment of a ship’s power system was carried out under the conditions of a ship engine room fire and the following conclusions were obtained.

The annual fire frequency and fire risk of the main engine fuel system are the highest. The main failure mode is a fire in the main engine fuel system caused by fuel leakages from the diesel supply tanks and the heavy fuel oil tanks. As an important system to ensure the normal navigation of the ship, the inspection of the parts prone to fuel leakage should be strengthened. Fire-induced explosions should be prevented to reduce the risk of ship fires.

The annual fire frequencies of the propulsion motor room and the gas turbine room are relatively high. The risk of fire is relatively minor. Electrical equipment and mechanical equipment are the main causes of fires in these two subsystems. With the accumulation of combustibles, however, the risk of fire is increased. Inspections in the area should be strengthened to prevent fires.

The analysis of the results shows that there is a high risk of fire and explosion due to crews’ incorrect operations. This means that regular training for crew members is crucial, including general safety knowledge, safety work regulations, and fire emergency drills.

The ship fire risk assessment method established in this paper has reference significance for the fire protection design of ship power systems and the fire risk assessment of other important systems.

In the future, the proposed method can be applied to the fire risk assessment of other important compartments of ships. Meanwhile, the method can be applied to the risk assessments of complex systems in other fields. It can solve the problems of a lack of data and cognitive uncertainty. Moreover, a complete database of ship fire incidents should be established in the future to improve the accuracy of risk assessment results.