An Efficient Ship Automatic Collision Avoidance Method Based on Modified Artificial Potential Field

Abstract

A novel collision avoidance (CA) algorithm was proposed based on the modified artificial potential field (APF) method, to construct a practical ship automatic CA system. Considering the constraints of both the International Regulations for Preventing Collisions at Sea (COLREGS) and the motion characteristics of the ship, the multi-ship CA algorithm was realized by modifying the repulsive force model in the APF method. Furthermore, the distance from the closest point of approach-time to the closest point of approach (DCPA-TCPA) criterion was selected as the unique adjustable parameter from the perspective of navigation practice. Collaborative CA experiments were designed and conducted to validate the proposed algorithm. The results of the experiments revealed that the actual DCPA and TCPA agree well with the parameter setup that keeps the ship at a safe distance from other ships in complex encountering situations. Consequently, the algorithm proposed in this study can achieve efficient automatic CA with minimal parameter settings. Moreover, the navigators can easily accept and comprehend the adjustable parameters, enabling the algorithm to satisfy the demand of the engineering applications.

1. Introduction

The automatic collision avoidance (CA) of maritime autonomous surface ships (MASS) is highly complex and uncertain. When considering the motion of the ship, the International Regulations for Preventing Collisions at Sea (COLREGS), and the restricted water areas, the automatic CA and path planning of ship are important challenges [1,2].

In recent years, a series of artificial potential field (APF)-based CA approaches for MASS have been proposed [3]. The APF-based approach established a virtual potential field near the navigating area of MASS. The attraction between MASS and the goal, repulsions between MASS and obstacles, and repulsions between MASS and other ships were comprehensively studied. The sum of these potential fields determines the resultant virtual force to guide the motion of the MASS [2]. Because the APF controller is easy to construct, intuitive, effective for handling static and dynamic constraints [4], and can obtain an ideal effect on the CA and obstacle avoidance of MASS, the APF-based approach has been widely applied to the intelligent ship CA system in open and restricted waters.

Despite its extensive applications in robot path planning and unmanned aerial vehicle CA, the APF-based approach is faced with major technological problems, owing to the complicated CA conditions of MASS [2,3]. Presently, the research priorities of the APF-based CA approach are optimization of the traditional APF method, solving local minima problems [4,5,6] and the goals non-reachable with obstacles nearby (GNRON), cooperative CA, and obstacle avoidance, through modeling of the environment potential field [7,8,9,10,11,12], and solving the CA problems based on COLREGS [6,12,13,14].

Li [15] and Cheng-Bo [16] proposed a path planning method with CA function, based on deep reinforcement learning and APF, in which the APF method was utilized to improve the action space and reward function of the deep Q-learning network algorithm. Fan [17] presented an improved APF method to solve the inherent shortcomings of local minima, the inaccessibility of the target, and the GNRON problem. Sang [18] proposed a hybrid path planning algorithm based on improved A* and APF for unmanned surface vehicle formations.

Lyu systematically studied the intelligent multi-ship CA algorithm using an improved APF method, and considered the rules of COLREGS, maneuverability of the ship, and uncoordinated CA actions for the target ships (TS). Lyu overcame numerous drawbacks of the traditional APF methods (such as local minima and the GNRON problems), and performed a series of tests in open and restricted waters, including dynamic TSs and complex static obstacles [13,14].

To trigger the autonomous system, the CA parameters are introduced to determine whether and when to take evasive action [19]. Many risk indicators are introduced into the CA system, such as relative distance [20], relative bearing [21], ratio of speed [22], and ship domain [23]. Some researchers are aware that the risk measurement needs to consider different scenarios [24], such as the nature environment conditions, wave conditions, visibility, day/night, navigation areas, etc., and different encounter types. Because DCPA–TCPA is the most popular method to measure the risk of collision in practice, some researchers utilize DCPA–TCPA as a risk indicator.

Lyu introduced a series of CA parameters into the repulsive force calculation, such as the prohibited zone (using a small adjustable parameter, τ, to express a circular area), radius of the ship domain (d_m = R_os + d_safe + R_ts, where Ros and R_ts denote the expanded radius to the domain radius of one’s own ship (OS) and TS, and d_safe is the shortest allowable safe distance), and the influence range of TS (ρ_o). These parameters should be defined by the navigators, according to the navigation area (open or restricted water), dimension and motion of OS, dimension and motion of TS, and visibility. Some CA parameters have no real meaning, and dynamic adjustment of the parameters is extremely difficult. In the applications of the ship, as the CA results have no direct relationship to the CA parameters, the work of Lyu is incomprehensible and unacceptable for navigators.

In various CA algorithms and navigation practices, DCPA–TCPA is the basic criterion for the “risk of collision” and is also the most important CA parameter [2,25]. The ship usually takes CA action when there is an existing “risk of collision” with other ships. In the MAXCMAS (machine executable collision regulations for marine autonomous system) of the Rolls Royce project, the desired DCPA was maintained with all the vessels in the vicinity, and the DCPA–TCPA criterion was set as 2.0 nm and 12.0 min, respectively [26]. This study investigates the multi-ship CA algorithm under the constraint of COLREGS and the motion of the ship by modifying the repulsive force model in the APF method and considering the DCPA–TCPA criterion as the unique adjustable parameter from the perspective of navigation practices. Thereafter, a series of tests were performed to verify the effectiveness and reliability of the proposed approach, as well as the consistency between the CA parameters and the results.

2. Collision Avoidance Based on Modified Artificial Potential Field

The CA for MASS is a complex system that is constrained by COLREGS, and should cope with the static and dynamic environment in real time. According to the work of Lyu [12,14], we employed the path-guided hybrid artificial potential field method to realize the CA algorithm of a MASS and establish a 6-DOF mathematical model to describe its motion in CA.

2.1. Modeling of Motions of MASS

When planning collision avoidance, the ships maneuverability and hydrometeorological conditions must be taken into account [27]. To describe the motion of MASS in CA, earth- and body-fixed coordinate systems were constructed, as shown in Figure 1. The vector $\mathit{\eta }={\left[x,y,z,\varphi ,\theta ,\psi \right]}^{\mathrm{T}}$ represents the position and attitude of a MASS in the earth-fixed system, whereas vector $\mathit{\nu }={\left[u,v,w,p,q,r\right]}^{\mathrm{T}}$ denotes the speed and rotation speed in the body-fixed system. The 6-DOF mathematical model of a MASS [28,29] can be expressed as follows:

$$\{\begin{array}{l}\left(m+m_x\right)\dot{u}-\left(m+m_y\right)vr+\left(m+m_z\right)wq=X_H+X_G+X_P+X_R+X_{\mathrm{Env}}\\ \left(m+m_y\right)\dot{v}+\left(m+m_x\right)ur-\left(m+m_z\right)wp=Y_H+Y_G+Y_P+Y_R+Y_{\mathrm{Env}}\\ \left(m+m_z\right)\dot{w}-\left(m+m_x\right)uq+\left(m+m_y\right)vp=Z_H+Z_G+Z_P+Z_R+Z_{\mathrm{Env}}\\ \left(I_{xx}+J_{xx}\right)\dot{p}+(I_{zz}+J_{zz}-I_{yy}-J_{yy})qr+\left(m_z-m_y\right)vw=K_H+K_G+K_P+K_R+K_{\mathrm{Env}}\\ \left(I_{yy}+J_{yy}\right)\dot{q}+(I_{xx}+J_{xx}-I_{zz}-J_{zz})pr+\left(m_x-m_z\right)uw=M_H+M_G+M_P+M_R+M_{\mathrm{Env}}\\ \left(I_{zz}+J_{zz}\right)\dot{r}+(I_{yy}+J_{yy}-I_{xx}-J_{xx})pq+\left(m_y-m_x\right)uv=N_H+N_G+N_P+N_R+N_{\mathrm{Env}}\end{array}$$

(1)

where $m={\rho }_s\nabla$ represents the mass of the ship; ${\rho }_s$ is the seawater density; $\nabla$ is the displacement; $m_x$, $m_y$ and $m_z$ denote the added masses to the ship; $I_{xx}$, $I_{yy}$, $I_{zz}$, $J_{xx}$, $J_{yy}$, and $J_{zz}$ denote the moment and added moment of inertia; the subscripts “H” and “G” denote the viscous hydrodynamics and hydrostatic force exerted on the naked hull ship; the subscripts “P” and “R” denote the forces and moments generated by the propeller and ruder; the subscript “Env” denotes the external disturbance force induced by the wind, waves, and current.

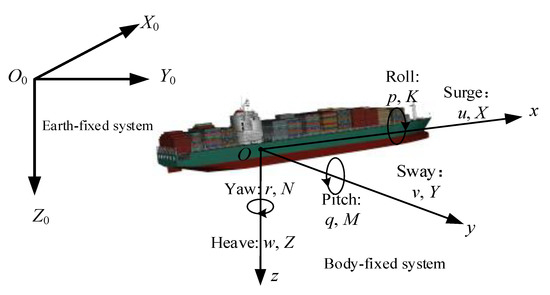
Figure 1. Coordinate systems of ship motions.

2.2. Modified APF Model

The attractive $F_{\mathrm{att}}$ and repulsive force $F_{\mathrm{rep}}$ were established by referring to the work of Lyu [12,14]. As the DCPA–TCPA is the essential criterion rule for the “risk of collision” in navigation, we modify the negotiation CA repulsive force $F_{\mathrm{rd}}$ and emergency CA repulsive force $F_{\mathrm{re}}$ as follows:

$$F_{\mathrm{att}}=\epsilon d_{\mathrm{og}}{\mathit{n}}_{\mathrm{og}}$$

(2)

$$F_{\mathrm{rep}}(p,v)=\{\begin{array}{l}{F}_{\mathrm{rd}1}+F_{\mathrm{rd}2}+F_{\mathrm{rd}3}, d_{\mathrm{emg}}<d\le d_{\mathrm{neg}}, \theta <{\theta }_{\mathrm{TOL}},0\le d_{\mathrm{CPA}}\le d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}},0\le t_{\mathrm{CPA}}\le t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}\\ F_{\mathrm{re}1}+F_{\mathrm{re}2}+F_{\mathrm{re}3}, d\le d_{\mathrm{emg}},0\le {\mathrm{d}}_{\mathrm{CPA}}\le d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}},0\le t_{\mathrm{CPA}}\le t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}\\ \mathrm{otherwise}\end{array}$$

(3)

$$\begin{array}{l}{F}_{\mathrm{rd}1}=-{\eta }_d{d}_g{}^2\\ \left[\left(\frac{1}{d-d_{\mathrm{emg}}}-\frac{1}{d_{neg}-d_{\mathrm{emg}}}\right)e^{{\theta }_m-\theta }\left(\frac{d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}}{d\sqrt{d^2-d_{\mathrm{emg}}{}^2}}+\frac{\sin \theta }{\Vert {\mathit{v}}_{ot}\Vert }\right)+\frac{e^{{\theta }_{\mathrm{TOL}}-\theta }-1}{{(d-d_{\mathrm{emg}})}^2}-\left(\frac{1}{d-d_{\mathrm{emg}}}-\frac{1}{d_{neg}-d_{\mathrm{emg}}}\right)\left(\frac{d_{\mathrm{emg}}}{d\sqrt{d^2-d_{\mathrm{emg}}{}^2}}+\frac{\sin {\theta }_{\mathrm{TOL}}}{\Vert {\mathit{v}}_{ot}\Vert }\right)\right]{\mathit{n}}_{ot}\end{array}$$

(4)

$$\begin{array}{l}{F}_{\mathrm{rd}2}=\pm {\eta }_d{d}_g{}^2\\ \left[\left(\frac{1}{d-d_{\mathrm{emg}}}-\frac{1}{d_{neg}-d_{\mathrm{emg}}}\right)e^{{\theta }_{\mathrm{TOL}}-\theta }\left(\frac{1}{\Vert {\mathit{p}}_{ot}\Vert }+\frac{\cos \theta }{\Vert {\mathit{v}}_{ot}\Vert }\right)+\frac{\Vert {\mathit{v}}_{ot\perp }\Vert (e^{{\theta }_{\mathrm{TOL}}-\theta }-1)}{d{(d-d_{\mathrm{emg}})}^2}-\left(\frac{1}{d-d_{\mathrm{emg}}}-\frac{1}{d_{neg}-d_{\mathrm{emg}}}\right)\left(\frac{1}{\Vert {\mathit{p}}_{ot}\Vert }+\frac{\cos {\theta }_{\mathrm{TOL}}}{\Vert {\mathit{v}}_{ot}\Vert }\right)\right]{\mathit{n}}_{ot\perp }\end{array}$$

(5)

$$F_{\mathrm{rd}3}={\eta }_d{d}_g\left(\frac{1}{d-d_{\mathrm{emg}}}-\frac{1}{d_{neg}-d_{\mathrm{emg}}}\right)(e^{{\theta }_{\mathrm{TOL}}-\theta }-1){\mathit{n}}_{og}$$

(6)

$$F_{\mathrm{re}1}=-2{\eta }_{\mathrm{e}}{d}_g{}^2\left[(\frac{1}{d\text{-}d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}}-\frac{1}{d_{\mathrm{emg}}})\times \frac{1}{{\left(d\text{-}d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}\right)}^2}+\Vert {\mathit{v}}_{ot}\Vert \cos \theta \right]{\mathit{n}}_{ot}$$

(7)

$$F_{\mathrm{re}2}=2{\eta }_{\mathrm{e}}\frac{d_g{}^2}{d}({\Vert {\mathit{v}}_{ot}\Vert }^2\cos \theta \sin \theta ){\mathit{n}}_{ot\perp }$$

(8)

$$F_{\mathrm{re}3}=2{\eta }_{\mathrm{e}}{d}_g\left[{\left(\frac{1}{d\text{-}d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}}-\frac{1}{d_{emg}}\right)}^2+{\Vert {\mathit{v}}_{ot}\Vert }^2{\cos }^2\theta \right]{\mathit{n}}_{og}$$

(9)

where the direction and significance of each force are listed in Table 1 and illustrated in Figure 2. ${\eta }_{\mathrm{d}}$ and ${\eta }_{\mathrm{e}}$ are the scaling factors for negotiation and emergency CA, respectively, and $\epsilon$ is the scaling factor for the attractive force. The OS is driven by the resultant force, moving to the goal and simultaneously keeping a safe distance with the TSs. The term ${\mathit{n}}_{\mathit{o}\mathit{g}}$ denotes a unit vector pointing to the goal from the OS. The term ${\mathit{n}}_{ot}$ denotes a unit vector pointing to TSs, or obstacles from the OS; $d_g$ is the distance between the OS and the goal; $d$ is the distance between the OS and TS; ${\theta }_{\mathrm{TOL}}$ is the angle between any tangent line (T₁p_os or T₂p_os) and the relative position vector $p_{\mathit{o}\mathit{s}}{p}_{ts}$; $\theta$ is the angle between the relative position vector $p_{ot}$($p_{ot}=p_{ts}-p_{os}$) and the relative speed vector $v_{ot}$($v_{ot}=v_{os}-v_{ts}$). The risk of collision occurs when the extension line of $v_{os}$ crosses the circle of radius $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$($\theta <{\theta }_{\mathrm{TOL}}$); otherwise, the OS can pass through the TS with a safe distance.

Table 1. Direction and action of the repulsive force potential field.

CA Module	Repulsive Force	Direction	Action
Negotiation CA	Frd1	Point from TS to OS	Make OS move away from TS
	Frd2	Perpendicular to Frd1 and to right side	Make OS alter course to starboard when $d_{\mathrm{emg}}<d\le d_{\mathrm{neg}}$ based on the practice of seafarers, as the appropriate passing side for each encounter is determined by COLREGS
	Frd3	Point from OS to goal	Make OS head for goal
Emergency CA	Fre1	Point from TS to OS	Make OS move away from TS
	Fre2	Perpendicular to Fre1	Make OS alter course to starboard or port side depending on which side of $p_{ot}$ the vector is located
	Fre3	Point from OS to goal	Make OS head for the goal

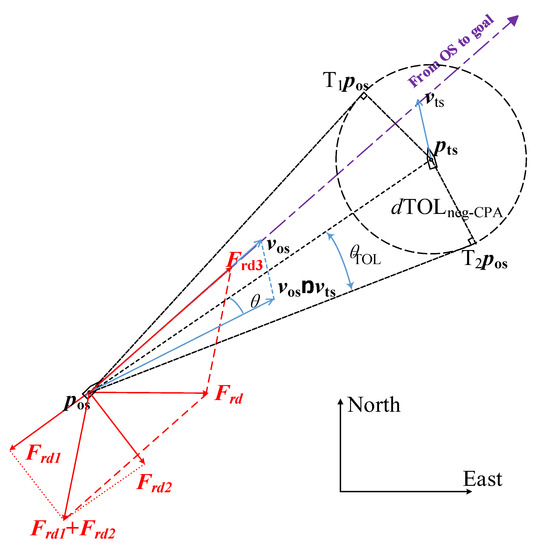
Figure 2. Modified repulsive forces for a dynamic TS.

The terms $d_{\mathrm{emg}}$ and $d_{\mathrm{neg}}$ represent the range criterion of emergency CA and negotiation CA, $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ and $t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ denote the distance and time criteria of negotiation CA, and $d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ and $t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ represent the distance and time criteria of emergency CA, respectively. Because all the CA parameters have actual meanings in navigation, as the CA results correspond to the CA parameters, the modification made to the repulsion force model can be comprehended and accepted by navigators.

A flow chart of the modified APF model is given in Figure 3. If there are N TSs, the total repulsive force can be obtained by adding the repulsive forces generated by each TS. The ship will take corresponding CA action under the resultant $F_{sum}$, in varying conditions, and will reach the goal. Based on the calculation of attractive and repulsive forces, the total virtual force exerted on the ship can be obtained as follows:

$$F_{sum}=F_{att}+F_{rep}$$

(10)

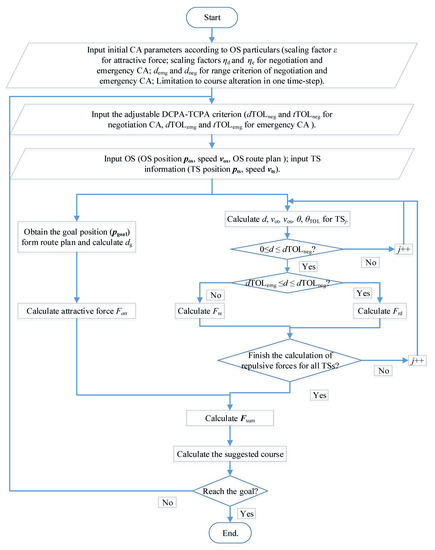
Figure 3. Flow chart of the modified APF method.

3. Tests and Results

3.1. Range Criterion and Results

In this section, we use a container ship, “KangHe” (OS), as a smart ship and two target container ships, named “YinHe” (TS1) and “AnGuangJiang” (TS2), to complete the experiment of collaborative CA. The initial conditions and specifications of the ships are summarized in Table 2. As listed in Table 3, we set the range criterion as $d_{\mathrm{emg}}$ = 1.0 nm and $d_{\mathrm{neg}}$ = 3.0 nm in test 1, and $d_{\mathrm{emg}}$ = 3.0 nm and $d_{\mathrm{neg}}$ = 6.0 nm in test 2.

Table 2. Particulars of ships and initial conditions.

	Name	Length (m)	Breadth (m)	Draft (m)	Disp. (m3)	Speed (kn)	Course (°)	Initial Position	Position of Goal
OS	“KangHe”	259.0	32.0	9.5	43,067.0	16.0	358.6	39°00.1482′ 122°47.6834′	39°05.8285′ 122°47.6834′
TS1	“YinHe”	168.0	28.0	9.5	28,849.0	12.0	113.1	39°03.6780′ 122°43.3710′	39°01.1824′ 122°50.6475′
TS2	AnGuangJiang	147.0	22.0	9.0	19,708.0	11.0	226.7	39°05.4892′ 122°51.1232′	39°01.4012′ 122°45.3875′

Table 3. Parameters for CA tests.

	Parameters	Value	Parameters	Value
Test 1	Emergency CA range criterion	$d_{\mathrm{emg}}$ = 1.0 nm	Negotiation CA range criterion	$d_{\mathrm{neg}}$ = 3.0 nm
Test 2	Emergency CA range criterion	$d_{\mathrm{emg}}$ = 3.0 nm	Negotiation CA range criterion	$d_{\mathrm{neg}}$ = 6.0 nm
	Emergency CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ = 6.0 min $d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$= 1.0 nm	Negotiation CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 12.0 min $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$= 2.0 nm

As shown in Figure 4 and Figure 5, the DCPA–TCPA criterion was fulfilled at the beginning of test 1, but the range criterion was not fulfilled. The action time of “KangHe” was later and the CA amplitude was smaller than that in test 2. To fulfill the DCPA–TCPA criterion, “KangHe” needs to take a larger course alteration to the TSs, but the final CA results are unsatisfactory in test 1.

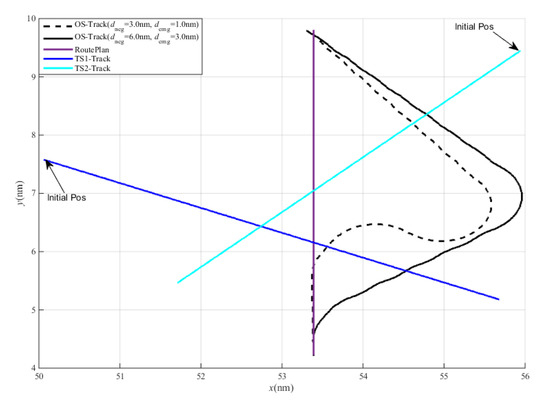
Figure 4. OS tracks under different CA range criteria.

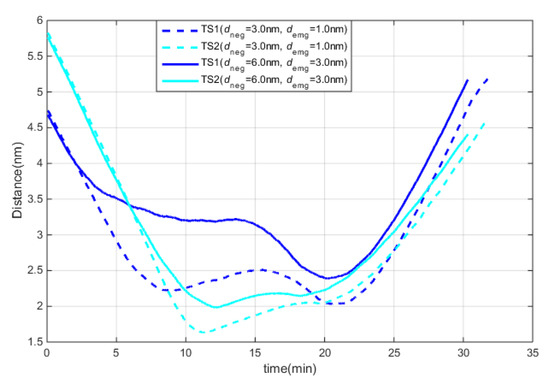
Figure 5. Distances under different CA range criteria.

Figure 6 and Figure 7 show the OS speed and course, and Figure 8 and Figure 9 show the DCPAs and TCPAs during the CA processes. In test 1, “KangHe” navigated according to the route plan during the first 5 min, as the CA criteria were not fulfilled. At 5 min, the CA criteria were satisfied and “KangHe” turned to starboard; at 12 min, “KangHe” passed and cleared both TSs, and started to turn left to return to its route plan; at 17 min, “KangHe” started to head for the destination. In test 2, “KangHe” turned to starboard at the beginning, as the range and DCPA–TCPA criteria were all satisfied. At 13 min, “KangHe” passed and cleared both TSs and started to turn left to return to its route plan, and at 15 min, “KangHe” started to head for the destination. In both tests, the speed of the ship decreased because of frequent operation of the rudder. As listed in Table 4, the maximum course alteration was 125° in test 1 and 65° in test 2.

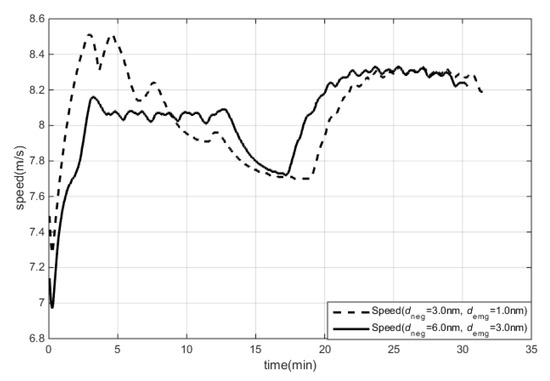
Figure 6. OS speed under different CA range criteria.

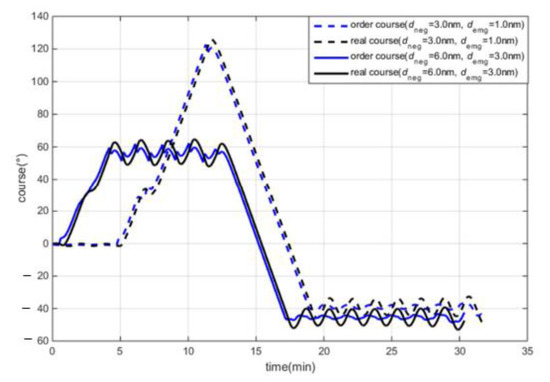
Figure 7. OS course under different CA range criteria.

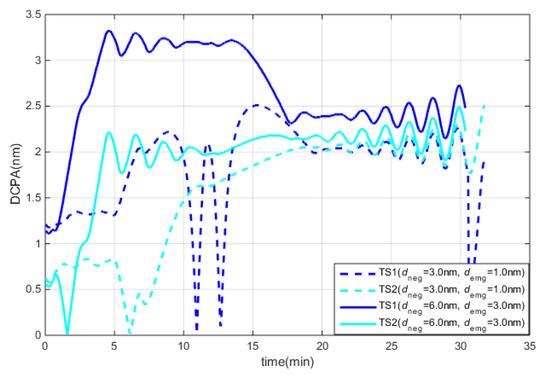
Figure 8. DCPAs under different CA range criteria.

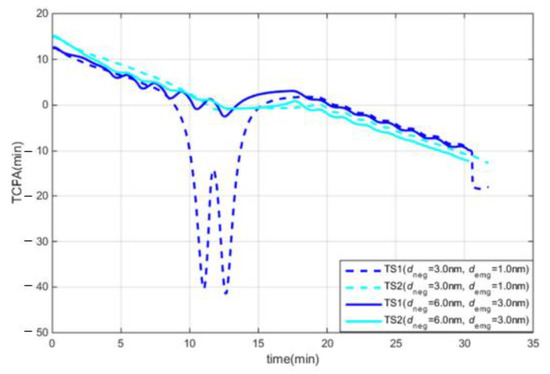
Figure 9. TCPAs under different CA range criteria.

Table 4. CA results by “KangHe”.

Item	Test 1	Test 2
Course alteration	125°	65°
Pass and clear distance with TS1	2.0 nm	2.4 nm
Pass and clear distance with TS2	1.63 nm	2.0 nm
Head for destination course	315°	320°

According to the criteria in Table 3, “KangHe” should maintain a distance of 2.0 nm from other ships. In test 1, because the action time was later than that in test 2, even though the largest CA actions were applied, “KangHe” passed and cleared TS2 at a distance of 1.63 nm (as listed in Table 4). In test 2, as the range and DCPA–TCPA criterion were appropriate, “KangHe” passed and cleared TS1 and TS2 at distances of 2.4 and 2.0 nm, respectively. Because of the existence of the DCPA–TCPA criterion, the range criterion is an extra filter for the involved ships, but has no substantial effect on the CA actions and CA results. Therefore, this study considers the DCPA–TCPA criterion as a unique adjustable parameter in the CA algorithm.

3.2. DCPA–TCPA Criterion and Results

The emergency CA range criterion was set as $d_{\mathrm{emg}}$= 3.0 nm, the negotiation CA range criterion was set as $d_{\mathrm{neg}}$= 6.0 nm, and the DCPA–TCPA criterion was set as the unique adjustable parameter (as listed in Table 5), and the CA tests were performed. The tracks of the ship are shown in Figure 10, the speed and course are shown in Figure 11, the DCPAs and TCPAs between OS and TSs are shown in Figure 12 and Figure 13, and the distances between “KangHe” and TSs are shown in Figure 14; some CA results are listed in Table 6.

Table 5. Parameters for CA test.

	Parameters	Value	Parameters	Value
	Emergency CA range criterion	$d_{\mathrm{emg}}$= 3.0 nm	Negotiation CA range criterion	$d_{\mathrm{neg}}$= 6.0 nm
Test 1	Emergency CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ = 6.0 min $d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$= 1.0 nm	Negotiation CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 12.0 min $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$= 2.0 nm
Test 2	Emergency CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ = 5.0 min $d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$= 0.75 nm	Negotiation CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 10.0 min $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$= 1.5 nm
Test 3	Emergency CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$ = 4.5 min $d{\mathrm{TOL}}_{\mathrm{emg}\text{-}\mathrm{CPA}}$= 0.5 nm	Negotiation CA DCPA–TCPA criterion	$t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 9.0 min $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$= 1.0 nm

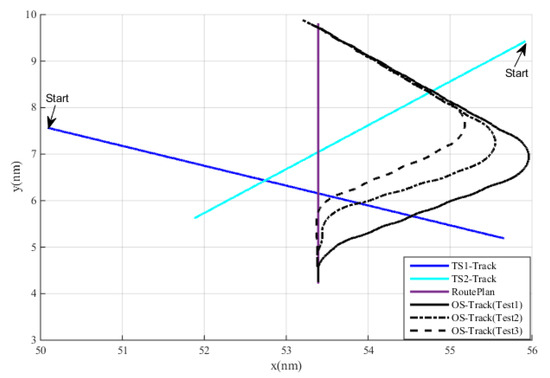
Figure 10. OS tracks under different DCPA–TCPA criteria.

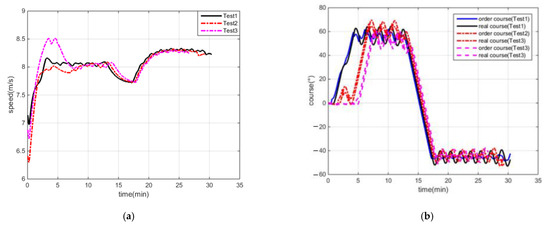
Figure 11. OS speed and course under different DCPA–TCPA criteria: (a) speed, (b) course.

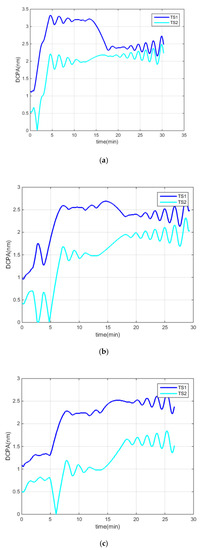
Figure 12. DCPAs under different DCPA–TCPA criteria: (a) test 1, (b) test 2, (c) test 3.

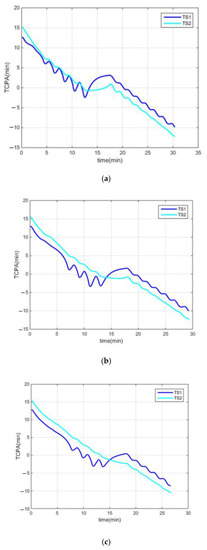
Figure 13. TCPAs under different DCPA–TCPA criteria: (a) test 1, (b) test 2, (c) test 3.

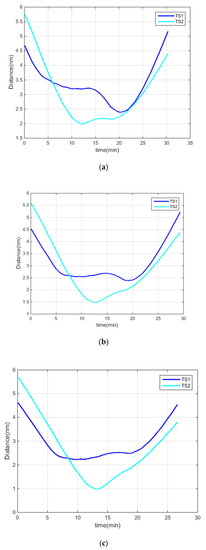
Figure 14. Distances under different DCPA–TCPA criteria: (a) test 1, (b) test 2, (c) test 3.

Table 6. CA results by “KangHe”.

Item	Test 1	Test 2	Test 3
Course alteration	55°	60°	53°
Pass and clear distance with TS1	2.5 nm	2.4 nm	2.2 nm
Pass and clear distance with TS2	2.0 nm	1.5 nm	1.0 nm
Head for destination course	312°	314°	314°

In test 1, “KangHe” altered the course to starboard at the beginning, as the CA criteria with TS1 were all fulfilled. At 2 min, the CA criteria with TS2 were fulfilled, while TS1 was avoided; at 13 min, “KangHe” passed and cleared TS2, and started to turn left to return to its route plan; at 17 min, it started to head for the destination. The course alteration of “KangHe” was 55°, and it passed and cleared TS1 and TS2 at distances of 2.5 nm and 2.0 nm (in accordance with $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 2.0 nm), respectively; it headed for the destination at an angle of 312° after finishing the CA procedure.

In test 2, “KangHe” navigated in accordance with its route plan, as the CA criteria were not fulfilled at the beginning of the test. At 1.6 min, “KangHe” altered its course to starboard, as the CA criteria with TS1 were all fulfilled; at 2.8 min, the ship passed and cleared TS1, and returned to its route plan; at 4 min, she started the CA action on TS2, as the CA criteria were fulfilled; at 13.0 min, “KangHe” passed and cleared TS2, and started to turn left to return to its route plan; at 17 min, it started to head for the destination. The course alteration of “KangHe” was 15° in the CA procedure with TS1 and 60° in the CA procedure with TS2. Finally, it passed and cleared TS1 and TS2 at distances of 2.4 nm and 1.5 nm (in accordance with $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 1.5 nm), respectively, and headed for the destination at an angle of 314° after finishing the CA procedure.

In test 3, “KangHe” navigated in accordance with its route plan, as the DCPA–TCPA criteria were not fulfilled at the beginning. At 4.5 min, “KangHe” altered its course to starboard, as the CA criteria with TS2 were all fulfilled; at 13.5 min, the ship passed and cleared TS2, and returned to its route plan; at 18 min, it started to head for the destination. The course alteration of “KangHe” was 53°, and it passed and cleared TS1 and TS2 at distances of 2.2 nm and 1.0 nm (in accordance with $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 1.0 nm), respectively, and, thereafter, headed for the destination at an angle of 314° after finishing the CA procedure.

Through the three aforementioned tests, we observe that, for the same CA scene, the different DCPA–TCPA CA parameters have an immediate effect on the involved ships and the CA results. A smaller DCPA–TCPA parameter leads to a later action time and a smaller action amplitude. The ship can take effective action at the right time according to the set DCPA–TCPA criterion, and finally pass the TSs at a desired safe distance, defined by $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$. The CA results are also in accordance with the DCPA–TCPA criterion.

3.3. Onboard Tests

We provided an auxiliary collision avoidance terminal (as illustrated in Figure 15) for a real ship. As shown in Figure 16, the essential input data (OS static and dynamics information, TS static and dynamics information, route plan, and electronic navigation chart (ENC) data) were collected based on the existing sensors (such as the automatic identification system (AIS), global positioning system (GPS), etc.) and electronic chart display information system (ECDIS) of a ship. The auxiliary CA terminal receives the input data and calculates all the virtual forces exerted on the ship, according to the modified APF model in Section 2.2, and finally generates the CA suggestions (advised path, course and/or speed) for the navigators. As shown in Figure 15, the auxiliary CA terminal provides an integrated information display interface for OS, TS, route plan, and ENC data, as well as CA suggestions. At the present stage, whether the CA suggestions are accepted and sent to the actuator of the ship is decided by the duty officer.

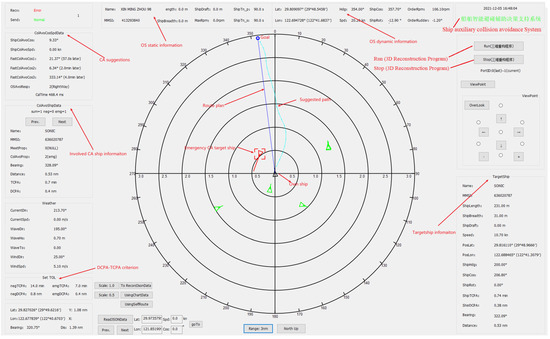
Figure 15. The auxiliary collision avoidance terminal.

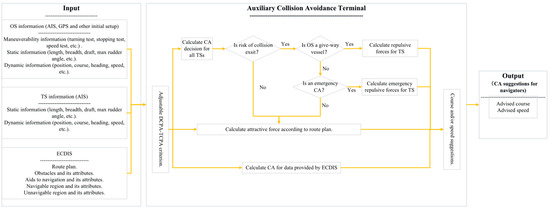
Figure 16. Frame diagram of the auxiliary collision avoidance terminal.

We conducted the onboard test on a 1868TEU container ship from 2 November to 3 November 2021. Figure 17 shows that the algorithm could give a larger course alteration when a larger DCPA–TCPA criterion was set. Figure 18 shows the suggestions in different situations. The algorithm could give a right turn suggestion in most situations, while in an emergency CA situation, the suggestion might be a left turn. Due to the small range criterion in the tests, $d_{\mathrm{neg}}$ = 1.5 nm, even though the largest CA actions were applied, the ship could not pass and clear the TSs at the desired distance of 1.6 nm. Figure 19 shows the CA suggestions for an approaching ship. Even though the largest CA actions were applied, the action scope of the ship decreased as the other ship approaches. In Figure 17, Figure 18 and Figure 19, the green marked TS indicates that there is no risk of collision with OS, and the yellow and red marked ship represents that the ship was fulfilled with the negotiation CA DCPA–TCPA criterion and emergency CA DCPA–TCPA criterion, respectively.

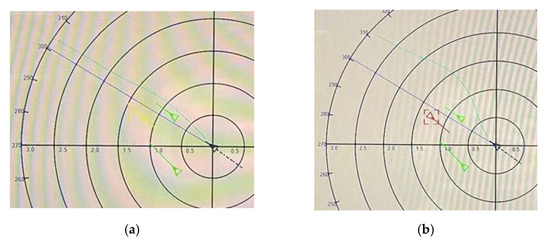
Figure 17. CA suggestions under different DCPA–TCPA criteria: (a) $t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 4.0 min, $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 0.4 nm, (b) $t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 8.0 min, $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 0.9 nm.

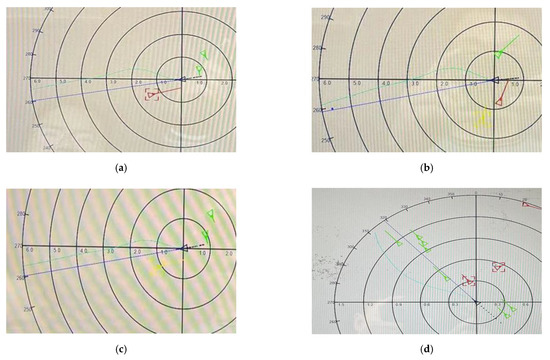
Figure 18. CA suggestions for different situations ($t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 14.0 min, $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 1.6 nm): (a) emergency CA suggestion for port side ship; (b) negotiation and emergency CA suggestion for port side ships; (c) negotiation CA suggestion for port side ship; (d) emergency CA suggestion for starboard side ship.

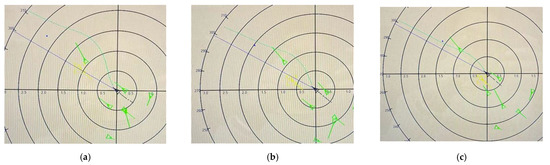
Figure 19. CA suggestions for an approaching ship ($t{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 4.0 min, $d{\mathrm{TOL}}_{\mathrm{neg}\text{-}\mathrm{CPA}}$ = 0.4 nm): (a) 0.5 nm < $d$ < 1.0 nm; (b) 0.5 nm $d$ ≤ 1.0 nm; (c) $d$ < 0.5 nm.

4. Discussion

Constrained by COLREGS and the motion characteristics of the ship, this study established a multi-ship CA algorithm by modifying the repulsive force model and applying the DCPA–TCPA criterion as the unique adjustable parameter from the perspective of navigation practice. Collaborative CA experiments were designed and conducted in both simulated and real-ship environments. The actual DCPA and TCPA agree well with the DCPA–TCPA criterion in a simulated environment, and the CA suggestions and advised path were presented in a real-ship environment.

This study innovatively introduced the DCPA–TCPA criterion as the unique CA parameter into the improved APF method, and solved the problems associated with the use of numerous, undefined CA parameters that are difficult for navigators to comprehend and accept. This study also integrated the MASS motion model and improved APF-based CA approach in a simulated environment; the consistency between the CA results and parameters for a large merchantman ship was proved. The improved APF-based CA approach was first applied to a real merchantman ship as an auxiliary system; this system received the same acceptance from the navigators as the personifying intelligent decision making for vessel collision avoidance (PIDVCA) [30] method.

However, there are still some shortcomings in this study. For instance, because the CA suggestions were not sent to the real-ship actuator, the actual CA results for a real MASS were not well presented. This algorithm needs more tests and improvements because of the extremely complicated navigation environment in a real ship, such as the small fishing vessels and their unpredictable motions, the anchorage and anchored vessels, the fact that the ship does not proceed in the channel and does not navigate on the route plan of OS, etc. In addition, the speed suggestion, which is extremely important in restricted waters or channels, was not given in this algorithm, which is also extremely difficult to realize when combining with course suggestions. The input data were collected based on the existing sensors (AIS and GPS) and ECDIS, which is not sufficient and reliable enough for real-ship automatic CA. Although some rules from COLREGS have been considered in the algorithm, more efforts are needed to apply all the COLREGS rules and good seamanship.

5. Conclusions

This study investigated the CA method of MASS from the perspective of engineering applications. By modifying the repulsive force model in the APF method, and taking the DCPA–TCPA criterion as the unique adjustable parameter, a multi-ship CA algorithm, constrained by COLREGS and the motion characteristics of the ship, is presented in this paper. The proposed method solved the problems associated with the use of numerous, undefined CA parameters that are difficult for navigators to comprehend and accept, due to the inconsistency between the CA results and parameters. As the proposed method is accurate and reliable, and satisfies the demands of engineering applications, this paper has important significance in the study of APF-based CA approaches.