Abstract
This paper studied the resonant behaviors of a bottom-hinged oscillating wave surge converter (OWSC) as well as the relationship of resonance with the response and capture width ratio (CWR). The time-domain dynamic equation of an OWSC in shallow water based on the boundary element method (BEM) was solved by a Python code, considering the corrected wave surface and the nonlinearities of restoring moment, drag, and friction. The unknown factors, such as wave surface corrected factor and drag coefficient, were effectively calibrated with computational fluid dynamics (CFD) method. An intermediate initial angle in free decay is appropriate for use to determine the natural period. Under regular waves, the resonance occurs near the natural period for the uniform wave amplitude, rather than the uniform wave torque amplitude, and can disappear due to the amplification of Power Take-Off (PTO) friction. Under unit-amplitude regular waves, the period of maximum CWR is relatively close to the period of maximum velocity, but far from the resonant period. Under irregular waves, no stable resonance is observed because the maximum equivalent pitch angle appears at different peak periods of wave spectra with the variation in PTO damping. When the period of a regular wave or the peak period of an irregular wave is close to the natural period, a phase hysteresis of velocity relative to wave torque always occurs.
1. Introduction
The bottom-hinged oscillating wave surge converter (OWSC), a nearshore wave energy converter, captures wave energy by oscillating under waves. It is installed in shallow water and benefits from the advantage of the amplification of horizontal water particle velocity due to shoaling effects [1]. Budal’s upper bound [2] explained that the maximum value of theoretical capture width ratio (CWR) of the flap-type absorber was double that of the axisymmetric point absorber. It was reported in [3] that the bottom-hinged OWSC captures greater mean annual power than most types of wave energy converters (WECs).
Oyster 1, a full-scale prototype of OWSC with a rated power of 315 kW, was developed by Aquamarine Power, collaborating with Queen’s University Belfast, installed at the European Marine Energy Center (EMEC) in Orkney, Scotland, in 2009, and decommissioned after its 2-year design life. The second-generation Oyster 800, with a rated power of 800 kW, was tested at EMEC in 2011, and successfully exported electricity to the national grid [4].
The hydrodynamic research of OWSCs has received attention in recent decades. Some experimental investigations on the motions and power capture of OWSCs in two-dimensional (2D) wave tank [5,6,7] and three-dimensional (3D) wave basin [8,9] were conducted by researchers. With the development of cheap and powerful computer hardware, numerical simulation is becoming more popular and there is a rapidly growing number of modelling WECs. Boundary element method (BEM) numerical simulation, based on potential flow theory, was employed in the analysis of OWSCs under waves, and validated via experiments [10]. Some hydrodynamic studies of OWSCs based on BEM can be found in [11,12,13]. BEM has the merit of efficient computation, but the nonlinearities, e.g., wave breaking [14], flow separation [15], vortex shedding [16], slamming [17], and wave overtopping, cannot be perfectly considered. A numerical wave tank (NWT), based on computational fluid dynamics (CFD) via the solving of Navier–Stokes equations, has been widely applied in the high-fidelity modeling of the interaction between waves and the motion of OWSCs [18,19,20,21,22] and other types of WECs [23]. The smoothed particle hydrodynamics (SPH) method, a purely Lagrangian meshless interpolation method [24], was used to accurately simulate the wave intertion with the rectangular OWSCs [25,26] and a cylindrical OWSC [27]. The details of these approaches (BEM, CFD, and SPH) were comparatively summarized in [28,29]. However, in the simulation of CFD and SPH, long-term motion modeling is not feasible for engineering tasks due to the high computational cost. Therefore, to ensure the accuracy, and simultaneously shorten the elapsed time, of computation, the BEM results calibrated with CFD simulations contribute to a better overall application of the hydrodynamic analysis of OWSCs.
Resonance study is one of the subsystems of hydrodynamic research. Some studies demonstrated the structural dynamic amplifications near resonance in calculating the reaction forces for offshore platforms [30], coastal bridges [31], and piles [32] subjected to the wave impacts. Taking inspiration from the above phenomenon, resonance could be prosepctive in the promotion of wave energy absorption by amplifying the dynamic response of WECs. For example, tuning a point absorber to resonance, when its undamped natural period is close to the period of a regular wave [33] or the dominant period of an irregular wave [34], can be recognized as an effective approach to derive more energy. However, a flap-type WEC, usually of relatively large size, has a different resonant mechanism to the traditional point absorber, due to its diffracting of the wave’s propagation. The resonant behaviors of an OWSC in a channel were investigated using a semi-analytical method and concluded that the resonant sloshing modes lead to increase the maximum CWR [35]. The research of an OWSC in front of a vertical wall also proved that the much higher levels of CWR were achieved when the OWSC was located at a specific distance from the vertical wall, in which the larger wave torque was produced due to an appropriate phase difference between the reflected wave and the exciting wave [36]. However, less attention has been paid to the study of resonant wave interactions with OWSCs in the open sea.
In this work, the dynamic equation of a 3D OWSC in shallow water under regular and irregular waves is formulated in Section 2, based on time-domain BEM, and the nonlinear restoring stiffness, drag, and friction are taken into account. To calibrate the BEM results in relation to two unknown factors ((1) the wave surface corrected factor altering the restoring moment and drag moment, and (2) the drag coefficient), the numerical methodology of CFD is introduced in Section 3. The study model and mesh are described in Section 4. The free decay analysis, and the relationship of resonance to the responses and CWRs under regular and irregular waves, are discussed in Section 5, Section 6 and Section 7. Finally, the conclusions are summarized in Section 8.
2. Numerical Model Based on BEM
A 3D bottom-hinged OWSC, often called a flap, of width , thickness and height , captures wave power by oscillating about a horizontal hinge , fixed to a base constructed on the seabed at water depth , as shown in Figure 1. The distance between the axis and the still water surface is , called the axis depth. If , the flap is a surface-piercing flap, the height of which above still water is , refered to as freeboard. As the water level increases to , the flap will become fully submerged, but the top of the flap may emerge out of the water when a wave trough approaches. Points and are, respectively, buoyant center and gravity center. is the rotational angle. and are angular velocity and acceleration, respectively.

Figure 1.
An illustration of a 3D bottom-hinged oscillating wave surge converter.
The wave propagation direction is assumed to be unidirectional, and perpendicular to the flap (x-axis of a Cartesian coordinate system), which is an ideal scenario. Some studies on different types of coastal structures, such as low-crested structures [37], dikes [38], and bridge decks [39] demonstrated a significant reduction in wave overtopping and the wave-induced forces in relative non-normal angles between the structures and the waves (e.g., oblique waves or skewed structures). Although the effects of oblique waves is not negligible, the research of OWSCs under perpendicular waves in this work is still meaningful as the foundation for future studies, comparing the influence of oblique waves with perpendicular waves.
The incident waves are not allowed very high, based on the assumption of a linear relationship between wave amplitude and wave exciting moment amplitude. In addition, some nonlinearities, such as wave breaking, wave overtopping, flow separation, vortex shedding, and slamming, cannot be taken into account in BEM-based methodology. However, viscous drag will be simply considered (see Section 2.1.5).
2.1. Environmental Load in the Sea
2.1.1. Incident Wave Elevation and Corrected Wave Surface
Incident wave elevation at an arbitrary position, in the absence of flap, can be expressed by a sine function for regular waves, or the summarization of multi-components of sinusoidal waves for irregular waves:
where is the incident wave amplitude of a regular wave and is the wave amplitude of the -th wave component of an irregular wave; is the wave number for a finite depth and functionally related to the dispersion relation ; is the wave number of the -th wave component; is the gravity acceleration; and are the angular frequencies; is the time; is the number of wave components; is the random phase.
For irregular waves, is determined by the wave spectrum,
where is the modified wave spectrum for a finite water depth, introduced in Section 7.1; is the wave frequency interval of wave components.
However, the actual wave surface, with the existence of a flap, is different from the incident wave. In this study, the wave surface is corrected, as shown in Figure 2, to adjust the restoring stiffness and drag moment for more accurate results. is the instantaneous distance between the hinge point and its projection on the corrected wave surface along the mid-surface of the flap, and this can be given by
where is the wave surface corrected factor; is the instantaneous distance between point and its projection on the incident wave surface, obtained via geometric measurement according to the incident wave elevation and the flap angle .

Figure 2.
A schematic diagram of a corrected wave surface.
2.1.2. Wave Exciting Moment
The wave exciting moment , including the Froude–Krylov moment and the diffraction moment for a 3D model, can be described as
where is the wave exciting moment amplitude for unit wave amplitude, and is the phase difference between the incident wave and the wave exciting moment.
2.1.3. Radiation Damping Moment
Based on the Cummins equation [40] and the convolution integral [41], the time domain radiation damping moment , incorporating the effects of wave-making memory, is given by
where is the added inertia torque at infinite frequency; is the impulse response function,
where is the radiation damping coefficient.
2.1.4. Restoring Moment
Considering the variations of the buoyant center and buoyant force due to the time-varying corrected wave surface, the nonlinear hydrostatic restoring moment can be described as
where is the buoyant force; is the force arm of buoyancy; is the mass. Both and are dependent on the wet surface (below the corrected wave surface),
where is the instantaneous height of the wet surface above the hinge.
2.1.5. Drag Moment
As evolved from the Morison equation [42], the nonlinear drag moment acting on the wet surface (below the corrected wave surface) can be expressed as
where is the drag coefficient; is the radial coordinate of the flap based on the hinge; is the normal velocity of the water particles (in the absence of the flap) on the mid-surface of the flap, and is given by
where and are, respectively, the horizontal and vertical components of the water particle velocities in the absence of the flap at a finite depth [43],
2.1.6. Power Take-Off (PTO) Moment
Ignoring the inertia and stiffness, the PTO system can be simplified as constant damping and friction, and the PTO moment can be expressed as
where is the damping of the PTO system for wave energy harvesting; is the frictional moment against the motion of the flap,
where is a constant value of friction.
2.2. Time Domain Dynamic Equation
In the time domain analysis, the dynamic equation of the pitch motion can be written as
where is the inertia torque around the hinge.
The workflow of solving the dynamic equation is illustrated in Figure 3. For a certain geometry of study model, the hydrodynamic coefficients , , , and are obtained for one time from NEMOH, an open source frequency domain BEM program. According to the inputted wave parameters (e.g., in still water, under regular waves or under irregular waves) and initial conditions of the flap (e.g., at an inclined angle for free decay or at the vertical position under waves), a Python code was developed by the authors to implement a time marching computation. In each time step, the process is as follows:

Figure 3.
A workflow of solving the dynamic equation in Nemoh and Python.
- Using the solutions of angle and angular velocity at the previous time , the environmental loads can be calculated by Equations (4), (5), (7), (10) and (14);
- Substitute the values of environmental loads into Equation (16) to assemble a dynamic differential equation;
- By 4th-order Runge–Kutta integration, the hydrodynamic responses of the flap at the current time () can be computed, where is the time step of integration.
2.3. Perormance Assessment
In the PTO system, the time–averaged capturing power is given by
where and are, respectively, the beginning and end time for recording angular velocity in a duration.
The incident wave power of the resource per unit width of regular and irregular waves at a finite depth is given by
where is the wave group velocity,
The CWR under regular or irregular waves can be expressed as
2.4. Response of Motion
Although the actual time–history response under a regular wave is not perfectly harmonic, an equivalent sinusoidal response, based on energy conservation for a duration, can be introduced as
where is the equivalent amplitude of pitch; is the phase of the pitch. According to the kinetic energy conservation of equivalent sinusoidal motion with the actual response during the recording time, can be calculated by
Then, the equivalent amplitude of angular velocity can be written as
The phase angle of angular velocity relative to the wave exciting moment under regular waves can be estimated by measuring the averaged time difference between peak angular velocity and peak wave exciting moment in the time–history curves,
where is the number of peak values after the beginning time ; and are, respectively, the time of peak moment and peak angular velocity. Similarly, the phase angle relative to the wave exciting moment can also be extracted with the same method, and expressed as . Because the phase of the wave exciting moment is , derived from Equation (4), the phase of pitch can be calculated by
For a one-degree-of-freedom structure with constant inertia, stiffness, and damping, perfect resonance occurs when the period of harmonic excitation is close to its natural period. Simultaneously, the motion amplitude is maximal, and the velocity is in phase with the excitation, i.e., . However, due to the strong nonlinearities of the flap under waves, the phase results are different from perfect resonance, discussed in Section 6.
Equations (21)–(25) are only available for regular waves. Table 1 presents the phase angles of various items for clear comparison.

Table 1.
The phase angles of various items for regular waves.
To examine the response under irregular waves, according to kinetic energy conservation, the irregular response is also equivalent to the harmonic motion, the period of which is equal to the peak period, and the equivalent pitch amplitude is defined as
where is the peak frequency of an irregular wave.
3. Numerical Model Based on CFD
3.1. Governing Equations
Based on the assumption of fluid incompressibility, the mass conservation equation for the NWT based on the Volume of Fluid (VOF) method [44] is given by
where is the fluid velocity vector; is the equivalent fluid density, calculated by air density , water density , and the volume fraction of water . The equivalent dynamic viscosity is also determined by , where and are the dynamic viscosity of air and water, respectively. The volume fraction can be calculated by the mass conservation equation.
The Reynolds-averaged Navier–Stokes (RANS) equation is given by
where is the pressure; is the stress tensor, including viscous stress and turbulent stress; is the body force per unit mass (such as gravity). For incompressible Newtonian fluids and a turbulent model of eddy viscosity, is defined as
where is the turbulent viscosity.
The dynamic equation of the flap pitch is written by
where is the total fluid moment acting on the flap surface, and is obtained by integrating the pressure and shear stress over the fluid–structure interface,
where is the fluid–structure interface; is the position vector of the point on the flap surface; is the position vector of the hinge; and is the unit outer-pointing normal vector of the surface elements of the flap.
The motion of the flap and fluid are fully coupled by velocity and pressure on the fluid–structure interface. The velocity on the fluid–structure interface is related to the motion of the flap based on the position of the hinge point,
3.2. Set-Up in OpenFOAM
The interaction of the flap with waves is simulated by the finite volume method solver overInterDyMFoam in the package OpenFOAM, an open source CFD toolbox.
In order to calibrate the BEM results, some settings in CFD should be same or similar with BEM. Therefore, the Stokes I wave model (corresponding to the linear waves in BEM) is applied for regular waves, and 100 wave components with different wave periods, wave heights, and random phases are utilized for irregular waves. Shallow water wave absorption works on both inlet and outlet.
For simulating the motion of a flap with a potential large amplitude, the overset mesh approach [21] is used. The domain is separated into two zones—a stationary main zone and a moving overset zone. The flap rotation is simulated by the motion of the whole overset zone and the cell volume weight interpolation of velocity, pressure, and volume fraction between the overlapping volume of these two zones. The flap surface is restricted by a hinged axel with a torsional spring-damper (i.e., a joint constraint releasing only Ry degree of freedom and a restraint of linear axial angular spring inputting rotational stiffness and damping) to simulate the PTO system.
A turbulence model of eddy viscosity of type standard - (SKE), where and are, respectively, turbulent kinetic energy and dissipation rate, is applied to calculate the turbulent viscosity , which will be introduced into Equation (29) for the calculation of stress tensor . Although the SST - model is widely applied for the simulation of wave–structure interaction [45,46], Wei et al. [18] compared the variable types of turbulence model and found that the torque on the flap due to the wave force is not sensitive to the turbulence model. Hence, the SKE model is employed in the present study, due to the relatively low computational cost [18].
In iterative processing, the pressure field is coupled to the velocity field via the PISO-SIMPLE (PIMPLE) method, a merged algorithm of the Pressure Implicit Splitting Operator (PISO) [47] and the Semi-Implicit Method for Pressure-linked Equations (SIMPLE) [48].
All other numerical solver settings were chosen based on the tutorial case of floating body in [49].
4. Model and Mesh
4.1. Study Model
The research model is a 3D surface-piercing flap, of which the , , , and are referred to the Oyster 800-like model in [50]. , , and are given in [51]. Some parameters, and , are estimated by the authors. is calculated by the given restoring stiffness at a small rotational angle in [51].
In BEM, 40 wave cycles for the end time of simulation, and for the time–averaged response and CWR, and for the measurement of phases are imposed for regular waves. We used 100 peak periods as the simulation time, and , ( is the peak period of wave spectrum) and for wave components from 0.1 to 4.6 rad/s in irregular waves. To eliminate the effects of random phase, the solutions of equivalent pitch amplitude and CWR for five arrays of random phases have been averaged.
To reduce the computational cost in CFD, one half of the wave basin is built as the computational domain of NWT, as shown in Figure 4a, since the geometry, restriction of the flap, and boundary conditions are symmetric. The lengths of the upstream and downstream in the main zone are set as 5 times the flap width, and the width of the main zone (one half of the full model) is 3 times the flap width. The height of the initial air zone is 11 m. The distance between external cubic surface of the overset zone and the flap surface, as shown in Figure 4b, should contain multi-layer grids. We define the number of grid layer as . A small value of could result in the divergence of computation due to inaccurate interpolation in the overlapping region. However, for more layers (i.e., a large value of ), the implement of dynamic overset grid algorithm [52] in each iteration is time consuming. The influence of the value of will be discussed in Section 4.2.2.

Figure 4.
CFD computational domain: (a) an overall diagram of NWT with a symmetry xz plane bisecting the tank; (b) the overset zone with grid layers between the external cubic surface and the flap surface (in blue).
Due to the expensive computational cost of long-duration modeling, the duration of simulation under regular waves is 5–13 times the legth of the wave period, according to the stability of the response. Usually, more cycles in a short wave are necessary. The method of extracting pitch amplitude results in CFD is similar to that in the time domain BEM when the response is steady. The recording period for the computation of pitch amplitude is the last 1–3 periods in regular waves.
4.2. Mesh
4.2.1. BEM Grids
Only the grids on the wet surface should be generated in BEM. The quadrilateral grids are applied, and the element sizes are almost uniform. Three different element sizes (coarse, medium, and fine meshes), as shown in Table 2, are tested for mesh independence by comparing the results of the hydrodynamic coefficients, which are calculated by Nemoh program on a desktop of 3.4 GHz CPU with 16 processors and 32GB RAM. Unfortunately, Nemoh does not provide the parallel computation with multi-processors. The normalized root mean square error (NRMSE) is utilized to estimate the agreement of the results of a certain mesh configuration (coarse mesh or medium mesh) with the results of fine mesh. In Figure 5, each hydrodynamic coefficient seems to be insensitive to the mesh size. Finally, the medium grids, as shown in Figure 6, are selected for the case studies. The calculated value of added inertia torque at infinite frequency .

Table 2.
The mesh statistics and computational cost (on 1 processor) for three configurations of grids in BEM.
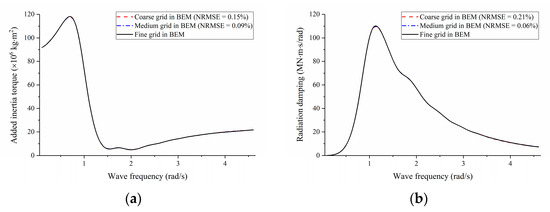

Figure 5.
The comparison of the hydrodynamic coefficients under unit-amplitude regular waves for different element sizes in BEM: (a) the added inertia torque ; (b) the radiation damping ; (c) the wave exciting moment ; (d) the phase difference between the incident wave and the wave exciting moment .

Figure 6.
The selected mesh model (medium size) of mean wet surface input into NEMOH for computation of hydrodynamic coefficients.
4.2.2. CFD Grids
The mixed grids consisting of cut-cell elements [53] for the main zone and hexahedral elements for the overset zone are employed in CFD, as shown in Figure 7. To understand the generation of cut-cell grids, the meshes in the main zone are created as follows:

Figure 7.
The cut-cell elements in transition region (4–6 grid layers in z-direction) and refined region (12 grid layers in z-direction near the water surface).
- The overall Cartesian meshes with almost uniform size are constructed;
- The transition region and refined region (near the water surface and overset zone) are cut off once, and their grid size bisects;
- Cut off the meshes in the refined region again, so the grid size of refined region is a quarter of outermost Cartesian region.
Thus, the grids near the overset zone and the water surface are fine for the accurate simulation of flap motion and wave propagation. The length of refined region in x-direction is set to more than to guarantee a larger coverage area than the range of flap motion. The cell size in the overset zone should be approximately same as the grid size in refined region of the main zone, as this will diminish the interpolation error between these two zones [23].
In the overset zone, the boundary layer (very fine mesh near the structure surface), which affects the calculation of tangential fluid shear stress on the structure surface, is neglected in this work, because the shear stress is not essential relatively to the normal stress for the prototype OWSC [18]. The simulations in [54] indicate that the shear forces on the fixed flap calculated are less than 1% of the total surge force.
Three different element sizes (the number of grid layer between external cubic surface of overset zone and the flap surface is uniformly set to ), as shown in Table 3, are tested for mesh independence by comparing the wave elevation at 20 m in front of the flap and the time–history total fluid moment (for 55 s simulation time) on a fixed flap under a regular wave ( and ) in CFD. The mean cell sizes of the refined regions for coarse, medium and fine mesh configurations are 0.56 m, 0.41 m and 0.30 m, respectively. Because of the limitation in BEM, the wave height is not allowed very high (see Section 2). With the purpose of calibrating for BEM, the unit-amplitude wave is choosen. The selected wave period is a representative period close to the resonant period of the flap (see Section 5) with greatest interests in this study.

Table 3.
The mesh statistics and computation cost (on 16 processors) for three configurations of grids in CFD.
The NRMSE is applied to estimate the agreement of the results of current mesh with the results of fine mesh. A more than 5% NRMSE related to the results are found in Figure 8 from a comparison between coarse and fine grids. However, the result for the medium grid is very close to that of the fine grid, in which the total number of elements is almost double of the medium grid. In addition, the computation for medium mesh is much faster than fine mesh (see Table 3). Accordingly, the medium grids with acceptable accuracy and efficient computation is selected for the case studies.

Figure 8.
The comparison of the results for different element sizes in CFD: (a) time–history wave elevation at 20 m in front of the flap; (b) time–history total fluid moment on a fixed flap under a representative regular wave ( and ).
To assess the influence of the grid layers between the external cubic surface of overset zone and flap surface, four different numbers of grid layer (, , and , as shown in Figure 9) are tested to assess the effects of overset zone dimension. The solver with the current settings cannot produce the converged result of flap motion in the case of 5 layers (), possibly caused by the amplified interpolation error (mentioned in Section 4.1).

Figure 9.
Four different numbers of grid layer (, , and ) in overset zone.
The comparison of time–history responses of a flap without a PTO system ( and ) under a regular wave ( and ) for 10 layers, 15 layers and 20 layers exhibits a negligible difference, as shown in Figure 10. Similarly, a slight influence of overset zone size can also be found in [21].

Figure 10.
The comparison of time–history responses of a flap without a PTO system ( and ) under a regular wave ( and ) among different overset zone sizes (, and ).
The computational costs of three different on a desktop (see Section 4.2.1) using 16 processors are approximately 90 h (), 95 h () and 105 h (), respectively, for a 55 s simulation time. Because of a shorter time consumption of computation in the smaller number of grid layer and insignificant influence on the motion of flap, are adopted. Figure 11 illustrates the selected mesh model in CFD for the case studies.

Figure 11.
The selected mesh model (medium size) of the NWT in CFD, including a main zone and a overset zone, in which the flap (in blue) is restricted by a hinge.
5. Free Decay Analysis
In the free decay analysis of a flap with an initial inclination under still water, , , , , and a nonzero are set.
The response of free decay in still water is studied with different initial angles. According to the time–history curve of response extracted from OpenFOAM, as shown in Figure 12, the natural period can be estimated by measuring the time distance between the first and second valley values of the response. Without friction (), the averaged periods of response in cases with different initial angles and either an undamped flap () or a damped flap () are, respectively, 17.57 s or 19.15 s. The measured period of response lengthens when configuring PTO damping. In actuality, the natural period without additional declaration usually defaults as the natural period of an undamped flap without friction for the judgment of resonance, i.e., 17.57 s.

Figure 12.
The time–history free decay response based on CFD for three distinct initial angles of a no-friction flap () with different PTO damping: (a) ; (b) .
In BEM, the actual water surface, affected by the moving flap’s radiating wave, is difficult to determine. We assume that the water surface is always horizontal in free decay analysis, i.e., in Equation (3). The free decay responses for different drag coefficients in BEM are calibrated with CFD, as shown in Figure 13. It is noticed by observation from the periods of these signals that the case of a 30 deg. intial angle matches relatively well with OpenFOAM, as shown in Figure 13b. However, a longer period with a small initial angle (15 deg.) and a shorter period with a large initial angle (45 deg.) are observed in Figure 13a,c, respectively. The authors believe that these inaccurate results in BEM are caused by the assumption of a horizontal water surface.

Figure 13.
The comparison of free decay between BEM and CFD for a flap without a PTO system ( and ) and with different initial angles: (a) 15 deg.; (b) 30 deg.; (c) 45 deg.
To understand the distinctions between BEM and CFD in free decay analysis, Figure 14 shows some typical frames in the CFD of a flap without a PTO system at three different initial angles. The water surface near the flap is elevated in several frames, and the elevation seems quantitatively unpredictable. Theoretically, the values of the radiation damping moment, the restoring moment, and the drag moment are disturbed by the change in the realistic wet surface, but cannot be accurately considered in BEM.

Figure 14.
Screenshots of free decay analysis of a flap without a PTO system ( and ) and with different initial angles in CFD: (a) 15 deg.; (b) 30 deg.; (c) 45 deg.
We scan the values of from 2 to 6 to find a proper drag coefficient with a minimum NRMSE of BEM against CFD in the case of a 30 deg. intial angle. As shown in Figure 15a, leads to the lowest NRMSE. The comparison of time–history free decay response between BEM () and CFD is illustrated in Figure 15b. For engineering applications of the free decay analysis based on BEM, an intermediate initial angle (e.g., 30 deg.) with a selection of for the current model is more appropriate.

Figure 15.
The results in the case of a 30 deg. intial angle: (a) NRMSE of BEM against CFD vs. ; (b) comparison of time–history free decay response between BEM () and CFD.
For a 40 s simulation time of a 30 deg. initial angle free decay response, the computational cost on the same desktop (see Section 4.2.1) is about 30 s for the Python code based on BEM (on 1 processor), except the elapsed time of extracting hydrodynamic coefficients for one time from Nemoh. However, it takes about 40 h for the CFD simulation with 16 processors in OpenFOAM.
6. Under Regular Waves
In this section, the responses of the flap under regular waves are studied. The range of wave period is from 5 s to 23 s. The unit-amplitude waves and the varying wave heights corresponding to the uniform wave exciting moment are considered, respectively. The range of PTO damping is from 0 to 64 , and the range of PTO friction is from 0 to 3 . However, the expanded range of PTO parameters can be included in some study cases with additional illustrations.
6.1. Calibration of BEM with CFD
There are two undecided factors in the computation of the response under waves in BEM: wave surface corrected factor and drag coefficient . We calculate the NRMSE of the pitch amplitude in BEM with respect to the CFD solutions (the results of equivalent pitch amplitude in CFD are extracted according to Equation (22)) of both the undamped () and damped () flaps, without friction and under unit-amplitude regular wave conditions ( with interval 2.5 s).
Figure 16 indicates that and are well calibrated for the time domain BEM results in the study’s model. It should be noted that the corrected wave surface is not a realistic water surface, and it only numerically influences the computations of restoring moment and drag moment for the sake of better accuracy.

Figure 16.
NRMSE of BEM against CFD for different values of and .
With the calibrated factors, a good agreement of BEM with CFD in the whole range of wave periods from 5 s to 23 s is shown in Figure 17. However, BEM slightly overestimated the response in short periods due to the constant drag coefficient, which was Keulegan–Carpenter () and Reynolds () number-dependent [55]. Using a larger value of the non-constant drag coefficient would seem to be necessary for a high number under short waves in future work. Given its acceptable accuracy and efficient computation, the calibrated BEM will be adopted in the next subsections.

Figure 17.
The comparison of pitch amplitude under regular waves of unit-amplitude between BEM and CFD of a no-friction flap () with different PTO damping: (a) ; (b) .
Taking an example of a simulation under a unit-amplitude regular wave, the computational cost to run the Python code based on BEM (on 1 processor) on the same desktop (see Section 4.2.1) is about 4 min for 40 wave cycles. However, it takes about 190 h for 6 wave cycles in OpenFOAM with 16 processors.
6.2. When Does the Maximum Pitch Occur?
The responses of the flap under regular waves of uniform amplitude () and uniform wave exciting moment (e.g., ), assessed by varying the wave amplitude for each period, are studied to determine the maximum pitch amplitude.
Figure 18a shows the wave amplitudes for different wave periods with respect to . When the wave period is longer than 15 s, the wave amplitude is greater than 1 m (the freeboard height ). Based on the assumption of a linear relationship between wave amplitude and wave exciting moment amplitude, the wave torque of a high wave in BEM may be imprecise, due to wave overtopping. Figure 18b shows a comparison of the pitch amplitude of a flap without a PTO system ( and ) between BEM and CFD, confirming the reasonable precision of BEM related to the slight influence of wave overtopping under such intermediate waves (the wave amplitude slightly exceeds the freeboard height).

Figure 18.
The parameters and results for regular waves of uniform wave exciting moment amplitude : (a) the incident wave amplitude vs. period; (b) comparison between BEM and CFD of a flap without a PTO system ( and ).
Figure 19 shows the pitch amplitude results of a no-friction flap with various values of PTO damping under regular waves of uniform amplitude and exciting moment amplitude. The maximum pitch amplitudes (solid point on each curve, between 16 s and 19 s in Figure 19a) with different values occur within a small range of wave periods from 17.6 s to 18.3 s, close to the natural period (17.57 s is obtained from the free decay analysis in CFD). This means that the flap resonates near the natural period. However, there are no obvious maximum values of pitch amplitude near the natural period with uniform wave exciting moment amplitude, as shown in Figure 19b. Therefore, the resonant conditions of regular waves, in which an incident wave near the natural period produces the maximum response over wave periods, should be restricted by employing the same amplitude of incident wave elevation, rather than the same amplitude of wave torque.

Figure 19.
The pitch amplitude results of a no-friction flap () for various values of PTO damping under regular waves of: (a) uniform wave amplitude; (b) uniform wave exciting moment amplitude.
Figure 20a shows the effects of friction (with an expanded range) on the period of maximum pitch amplitude of a damped flap (). The increasing value of friction breaks the resonance rule (the maximum response occurs near the natural period) by moving the period of maximum pitch amplitude towards the period of peak wave exciting moment, which is near 7 s for the current model, as shown in Figure 20b.

Figure 20.
(a) The pitch amplitude results for a damped flap () with various values of PTO friction under unit-amplitude regular waves; (b) wave exciting moment for unit wave amplitude.
6.3. Phase Characteristics Near and Far from Resonance
We have studied the phase angle of angular velocity relative to the wave exciting moment ( in Equation (24)) of a flap with different PTO damping and friction values under unit-amplitude regular waves. A negative value of means that the angular velocity lags behind the wave exciting moment, and a positive value denotes the advance of angular velocity. As mentioned in Section 2.4, the velocity is in phase with the wave torque, i.e., represents the occurrence of resonance in a one-degree-of-freedom structure with constant inertia, stiffness, and damping. It is evident from Figure 21 that the values of are not zero near the natural period (orange circle). Therefore, the standard of for the assessment of resonance in the hydrodynamics of a flap is unreliable, due to the strong nonlinearities of the restoring and drag moments.

Figure 21.
The phases of angular velocity relative to wave exciting moment under unit-amplitude regular waves: (a) various values of and ; (b) various values of and .
A higher value of or generally produces a trend of diminishing hysterical angles of angular velocity (absolute value of a negative ) within a shorter period than the natural period, and it causes increases in hysteretic angle or reductions in advanced angle (value of a positive ) over a longer period. However, the intersections of these phase vs. period curves always occur near the natural period.
To understand the phase characteristics near to or far from resonance, Figure 22 shows the time–history curves of the ratios of the wave exciting moment and angular velocities for a no-friction flap with various PTO damping during one wave cycle, over periods of 12 s, 17.5 s (near the natural period), and 23 s. The ratios are defined as below with a steady response,
where and are, respectively, the ratio of the wave exciting moment and the ratio of the angular velocity.

Figure 22.
Time–history of the ratios of wave exciting moment and angular velocities of a no-friction flap () for various values of PTO damping under unit-amplitude regular waves: (a) ; (b) , near the natural period (resonance); (c) .
With various values of PTO damping, there are obviously different phases of angular velocity relative to the wave exciting moment in a wave period of 12 s, but the distinctions are slight over a wave period of 17.5 s, close to the natural period. Under a long wave of period 23 s, the angular velocity of an undamped flap () precedes the wave exciting moment slightly, shown as the red dotted line in Figure 22c, but the angular velocities are almost in phase with the wave torque for various values of PTO damping from 16 to 64 .
6.4. Relationship of Maximum CWR with Resonance
To understand the relationship between the maximum CWR and the resonance, Figure 23a shows the CWRs of a no-friction flap with various degrees of PTO damping under unit-amplitude regular waves. The period of maximum CWR is apparently shorter than the natural period 17.57 s, and the difference increases almostly with the increase in PTO damping. Figure 23b,c exhibits the curves of time–averaged capturing power vs. period and angular velocity amplitude vs. period, respectively. For each value of PTO damping, the period of maximum capturing power is identical with the period of maximum angular velocity amplitude. However, the period of maximum CWR is closer to the period of maximum angular velocity amplitude than to the period of maximum angle amplitude (near the natural period), as listed in Table 4. This implies that the highest CWR does not occur simultaneously with resonance.

Figure 23.
The results of a no-friction flap () with various values of PTO damping under unit-amplitude regular waves: (a) CWR; (b) time–averaged capturing power; (c) angular velocity amplitude.

Table 4.
The periods of peak values of various items under unit-amplitude regular waves.
7. Under Irregular Waves
7.1. Wave Spectrum and Modification
Goda [56] introduced the JONSWAP spectrum , formulated from the significant wave height and the peak period,
where is the significant wave height and is the peak period, and
where is the peak enhancement factor, the range of which is 1–7, with a mean value of 3.3 [57].
When a severe wave in an offshore region propagates into the nearshore area, the energy will be attenuated by wave-breaking and seabed friction. In shallow water, the original spectral values should be modified to describe the reduction in wave energy according to water depth. The modified wave spectrum [58] is given by
where is the wave number at infinite depth.
Figure 24a shows a comparison between the original and modified JONSWAP spectra for an irregular wave ( and ) in 12.5 m-deep water, and Figure 24b shows the time–history elevation (generated by Equation (1)) of a modified irregular wave with the specific array of random phase used for the validation of BEM. Due to the assumption of linear relationship between wave exciting moment and wave amplitude in BEM, the significant wave height is also not allowed very high. After correcting the spectral values, the highest wave elevation is a little more than 1 m (the freeboard heigh of the flap). It implicates that a higher significant wave height might cause the overestimated results because of ignoring the wave overtopping in BEM.

Figure 24.
Irregular wave parameters: (a) comparison between original JONSWAP spectral values for and and its modified spectral values in 12.5 m-deep water; (b) time–history wave elevation of the modified irregular wave for a specific array of random phases of wave components.
7.2. Validation of BEM against CFD
The wave surface corrected factor and drag coefficient described in Section 6.1 are continuously applied in irregular waves. Figure 25 shows that the time–history response in BEM matches well with that in CFD, using the same wave components and the identical array of random phases within the time–history wave elevation of Figure 24b. Due to the relatively small wave elevation in the modified wave spectrum, the linear assumption of wave exciting moment vs. wave amplitude is still applicable for such an intermediate irregular wave. Considering the linear assumption of wave exciting moment vs. wave amplitude in BEM, a relatively small significant wave height with lower nonlinerities will be applied in the next case studies.

Figure 25.
Comparison of the time–history responses of a flap without a PTO system ( and ) between BEM and CFD under a modified irregular wave ( and ) in 12.5 m-deep water.
For the 120 s simulation time under an irregular wave, running the Python code based on BEM (on one processor) spends about 4 min on the same desktop (see Section 4.2.1), and the elapsed time for CFD with 16 processors is about 192 h.
7.3. When Does the Maximum Equivalent Pitch Occur?
Under modified irregular waves with the same significant wave height , the equivalent pitch amplitudes of each peak period for various values of PTO damping are calculated. The maximum equivalent pitch amplitude of a flap without a PTO system ( and ) appears in a peak period longer than the natural period, shown via the black dotted lines in Figure 26a, but the period of maximum decreases significantly with the increase in . This reveals that the maximum equivalent pitch amplitude cannot consistently occur near the natural period, which differs from the results under regular waves. This can be explained via the response under an irregular wave, achieved from the linear combination of the results derived using multi-components of regular waves.

Figure 26.
The equivalent pitch amplitude results under modified irregular waves of in 12.5 m-deep water: (a) various values of PTO damping and ; (b) various values of friction and .
In a specifc JONSWAP spectrum, the proportion of longer waves relative to the peak period is less than that of the shorter waves due to the asymmetry of spectral values, and the transfer function (i.e., the response for unit-amplitude regular waves in Figure 19a) under shorter waves thus dominates the synthetic solution. Figure 19a shows that the difference between the transfer function in a short period and its maximum value near the natural period reduces with the increase in . In other words, the short-period transfer function for a large contributes relatively more to the equivalent pitch amplitude than a small . That is why the maximum equivalent pitch amplitude for a larger appears within a shorter peak period.
As shown in Figure 26b, the impact of the friction on the peak period of maximum equivalent pitch amplitude is similar to that under regular waves, as discussed in Section 6.2.
7.4. Phase Characteristics near the Natural Period
Figure 27 shows the time–history wave exciting moment and angular velocities for different values of PTO damping and friction when the peak period is close to the natural period, . It is found that the angular velocity lags behind the wave exciting moment (orange arrows), and the phase difference reduces with the increase in either PTO damping or friction , as opposed to the near-constant phase difference (hardly affected by and ) near the natural period under regular waves, shown in Figure 21.

Figure 27.
Time–history wave exciting moment and angular velocities under a modified irregular wave ( and in 12.5 m-deep water) during five repetitions of the peak period: (a) various values of PTO damping and ; (b) various values of friction and .
7.5. CWR vs. Peak Period
Figure 28 shows the curves of CWR vs. peak period for various values of PTO damping. Similar to the results under regular waves, the maximum CWR here appears in a peak period lower than the peak period of the maximum equivalent pitch amplitude, as quantitatively compared with Figure 26a, and it declines with the increase in PTO damping.

Figure 28.
The CWRs of a no-friction flap () for various values of PTO damping under modified irregular waves of in 12.5 m-deep water.
8. Conclusions
Based on BEM, the time domain dynamic equation of a 3D bottom-hinged OWSC in shallow water, considering the nonlinear restoring moment, drag moment, and friction, is solved by a Python code importing the hydrodynamic coefficients obtained from NEMOH. The wave surface corrected factor and drag coefficient are calibrated with the CFD results in OpenFOAM. For an Oyster 800-like flap, the factors and are applicable for free-decay analysis in still water, and and are suitable in regular and irregular waves.
In the analysis of free decay, an intermediate angle—30 deg. in this study— is recommended as the initial inclination in BEM for the estimation of the natural period, because a small initial angle overestimates the natural period and a large initial angle underestimates it.
Under regular waves, one criterion when judging resonance is the period of maximum pitch amplitude with uniform wave amplitude, rather than the uniform amplitude of the wave exciting moment. A large value of friction destroys the resonant condition and drives the period of maximum pitch closer to the period of peak wave torque. Perfect resonance cannot be achieved, because a hysteresis of angular velocity relative to the wave exciting moment near the natural period is always present, and is almost independent of PTO damping and friction. Maximum CWR does not coexist with resonance but relatively near the largest angular velocity, the period of which is lower than that of maximum pitch (resonance).
Under irregular waves of the same significant height, the peak period of maximum equivalent pitch amplitude reduces with the increase in PTO damping. This implies that resonance cannot exist stably at a peak period near the natural period. The angular velocity also lags behind the wave torque within the current regime of PTO damping and friction when the peak period is close to the natural period. Here, one discrepancy from the results under regular waves is that the hysterical angle of angular velocity relative to wave torque relies on either PTO damping or friction. In addition, the curves of CWR vs. peak period for different PTO damping exhibit a similar trend to the results under regular waves.
Author Contributions
Conceptualization, Y.L., N.M. and Y.-H.C.; methodology, Y.L. and N.M.; software, Y.L. and T.N.; validation, Y.L. and Y.-H.C.; investigation, Y.L.; writing—original draft preparation, Y.L. and N.M.; writing—review and editing, Y.-H.C. and T.N.; supervision, N.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Nagoya University Ph. D. grant and JDC Foundation Research Grant in Japan.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Folley, M.; Whittaker, T.J.T.; Henry, A. The Effect of Water Depth on the Performance of a Small Surging Wave Energy Converter. Ocean Eng. 2007, 34, 1265–1274. [Google Scholar] [CrossRef]
- Budal, K.; Falnes, J. Wave Power Conversion by Point Absorbers: A Norwegian Project. Int. J. Ambient. Energy 1982, 3, 59–67. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical Benchmarking Study of a Selection of Wave Energy Converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- O’Boyle, L.; Doherty, K.; van’t Hoff, J.; Skelton, J. The Value of Full Scale Prototype Data-Testing Oyster 800 at Emec, Orkney. In Proceedings of the 11th European wave and tidal energy conference (EWTEC), Nantes, France, 6–11 September 2015; pp. 6–11. [Google Scholar]
- Brito, M.; Ferreira, R.M.L.; Teixeira, L.; Neves, M.G.; Canelas, R.B. Experimental Investigation on the Power Capture of an Oscillating Wave Surge Converter in Unidirectional Waves. Renew. Energy 2020, 151, 975–992. [Google Scholar] [CrossRef]
- Cho, Y.-H.; Nakamura, T.; Mizutani, N.; Lee, K.-H. An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics. Appl. Sci. 2020, 10, 6734. [Google Scholar] [CrossRef]
- Brito, M.; Ferreira, R.M.L.; Teixeira, L.; Neves, M.G.; Gil, L. Experimental Investigation of the Flow Field in the Vicinity of an Oscillating Wave Surge Converter. J. Mar. Sci. Eng. 2020, 8, 976. [Google Scholar] [CrossRef]
- Ning, D.; Liu, C.; Zhang, C.; Göteman, M.; Zhao, H.; Teng, B. Hydrodynamic Performance of an Oscillating Wave Surge Converter in Regular and Irregular Waves: An Experimental Study. J. Mar. Sci. Technol. 2017, 25, 4. [Google Scholar]
- Choiniere, M.A.; Tom, N.M.; Thiagarajan, K.P. Load Shedding Characteristics of an Oscillating Surge Wave Energy Converter with Variable Geometry. Ocean Eng. 2019, 186, 105982. [Google Scholar] [CrossRef]
- Schmitt, P.; Windt, C.; Nicholson, J.; Elsässer, B. Development and Validation of a Procedure for Numerical Vibration Analysis of an Oscillating Wave Surge Converter. Eur. J. Mech.-B/Fluids 2016, 58, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Cummins, C.; Dias, F. A New Model of Viscous Dissipation for an Oscillating Wave Surge Converter. J. Eng. Math. 2017, 103, 195–216. [Google Scholar] [CrossRef] [Green Version]
- Magkouris, A.; Bonovas, M.; Belibassakis, K. Hydrodynamic Analysis of Surge-Type Wave Energy Devices in Variable Bathymetry by Means of BEM. Fluids 2020, 5, 99. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, G.; Ji, C.; Fan, T.; Zhai, G. Fully Nonlinear Investigations on Performance of an OWSC (Oscillating Wave Surge Converter) in 3D (Three-Dimensional) Open Water. Energy 2020, 210, 118526. [Google Scholar] [CrossRef]
- Galvin, C. Wave Breaking in Shallow Water. In Waves on Beaches and Resulting Sediment Transport; Elsevier: Amsterdam, The Netherlands, 1972; pp. 413–456. [Google Scholar]
- Maskell, E. Flow Separation in Three Dimensions. In RAE Report No. Aero 2565; Royal Aircraft Establishment: Farnborough, UK, 1955. [Google Scholar]
- King, R. A Review of Vortex Shedding Research and Its Application. Ocean Eng. 1977, 4, 141–171. [Google Scholar] [CrossRef]
- Wei, Y.; Abadie, T.; Henry, A.; Dias, F. Wave Interaction with an Oscillating Wave Surge Converter. Part II: Slamming. Ocean Eng. 2016, 113, 319–334. [Google Scholar] [CrossRef]
- Wei, Y.; Rafiee, A.; Henry, A.; Dias, F. Wave Interaction with an Oscillating Wave Surge Converter, Part I: Viscous Effects. Ocean Eng. 2015, 104, 185–203. [Google Scholar] [CrossRef]
- Schmitt, P.; Elsaesser, B. On the Use of OpenFOAM to Model Oscillating Wave Surge Converters. Ocean Eng. 2015, 108, 98–104. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, P.; Asmuth, H.; Elsäßer, B. Optimising Power Take-off of an Oscillating Wave Surge Converter Using High Fidelity Numerical Simulations. Int. J. Mar. Energy 2016, 16, 196–208. [Google Scholar] [CrossRef] [Green Version]
- Windt, C.; Davidson, J.; Akram, B.; Ringwood, J.V. Performance Assessment of the Overset Grid Method for Numerical Wave Tank Experiments in the OpenFOAM Environment. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51319, p. V010T09A006. [Google Scholar]
- Benites-Munoz, D.; Huang, L.; Anderlini, E.; Marín-Lopez, J.R.; Thomas, G. Hydrodynamic Modelling of An Oscillating Wave Surge Converter Including Power Take-Off. J. Mar. Sci. Eng. 2020, 8, 771. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-Fidelity Numerical Modelling of Ocean Wave Energy Systems: A Review of Computational Fluid Dynamics-Based Numerical Wave Tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Zhang, D.H.; Shi, Y.X.; Huang, C.; Si, Y.L.; Huang, B.; Li, W. SPH Method with Applications of Oscillating Wave Surge Converter. Ocean Eng. 2018, 152, 273–285. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.B.; García-Feal, O.; Domínguez, J.M.; Crespo, A.J.C.; Ferreira, R.M.L.; Neves, M.G.; Teixeira, L. A Numerical Tool for Modelling Oscillating Wave Surge Converter with Nonlinear Mechanical Constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Hua, X. Numerical Studies and Proposal of Design Equations on Cylindrical Oscillating Wave Surge Converters under Regular Waves Using SPH. Energy Convers. Manag. 2020, 203, 112242. [Google Scholar] [CrossRef]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical Modelling of Wave Energy Converters: A Review of Nonlinear Approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Dias, F.; Renzi, E.; Gallagher, S.; Sarkar, D.; Wei, Y.; Abadie, T.; Cummins, C.; Rafiee, A. Analytical and Computational Modelling for Wave Energy Systems: The Example of Oscillating Wave Surge Converters. Acta Mech. Sin. 2017, 33, 647–662. [Google Scholar] [CrossRef] [Green Version]
- Anagnostopoulos, S.A. Dynamic Response of Offshore Platforms to Extreme Waves Including Fluid-Structure Interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G. Effect of Fluid-Structure Interaction on Connection Forces in Bridges Due to Tsunami Loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–24 October 2014. [Google Scholar]
- Choi, S.-J.; Lee, K.-H.; Gudmestad, O.T. The Effect of Dynamic Amplification Due to a Structure’s Vibration on Breaking Wave Impact. Ocean Eng. 2015, 96, 8–20. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O. Wave Energy Utilization: A Review of the Technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Korde, U.A. Efficient Primary Energy Conversion in Irregular Waves. Ocean Eng. 1999, 26, 625–651. [Google Scholar] [CrossRef]
- Renzi, E.; Dias, F. Resonant Behaviour of an Oscillating Wave Energy Converter in a Channel. J. Fluid Mech. 2012, 701, 482–510. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, D.; Renzi, E.; Dias, F. Effect of a Straight Coast on the Hydrodynamics and Performance of the Oscillating Wave Surge Converter. Ocean Eng. 2015, 105, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave Transmission and Reflection at Low-Crested Structures: Design Formulae, Oblique Wave Attack and Spectral Change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Van der Werf, I.; van Gent, M. Wave Overtopping over Coastal Structures with Oblique Wind and Swell Waves. J. Mar. Sci. Eng. 2018, 6, 149. [Google Scholar] [CrossRef] [Green Version]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges—Part 2: Numerical Investigation and Design Recommendations; No. FHWA-OR-RD-21-13; Department of Transportation. Research Section: Salem, OR, USA, 2021.
- Cummins, W.E. The Impulse Response Function and Ship Motions; AD0288277; DTIC: Washington, DC, USA, 1962; pp. 101–109.
- Jefferys, E.R. Simulation of Wave Power Devices. Appl. Ocean Res. 1984, 6, 31–39. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The Force Exerted by Surface Waves on Piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Newman, J. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1977; pp. 253–256. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Finnegan, W.; Goggins, J. Numerical Simulation of Linear Water Waves and Wave–Structure Interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Dolguntseva, I.; Savin, A.; Zhang, Y.; Li, W.; Svensson, O.; Leijon, M. Numerical Modelling of a Point-Absorbing Wave Energy Converter in Irregular and Extreme Waves. Appl. Ocean Res. 2017, 63, 90–105. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3, pp. 196–200. [Google Scholar]
- ESI OpenCFD Releases OpenFOAM v1912. Available online: https://www.openfoam.com/news/main-news/openfoam-v1912 (accessed on 13 December 2021).
- Renzi, E.; Dias, F. Mathematical Modelling of a Flap-Type Wave Energy Converter. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 9–4 July 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55430, p. V009T12A005. [Google Scholar]
- Tay, Z.Y.; Venugopal, V. Hydrodynamic Interactions of Oscillating Wave Surge Converters in an Array under Random Sea State. Ocean Eng. 2017, 145, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Tisovska, P. Description of the overset mesh approach in ESI version of OpenFOAM. In Proceedings of the CFD with OpenSource Software; Nilsson, H., Ed.; Chalmers University of Technology: Gothenburg, Sweden, 2019. [Google Scholar]
- Causon, D.M.; Ingram, D.M.; Mingham, C.G.; Yang, G.; Pearson, R.V. Calculation of Shallow Water Flows Using a Cartesian Cut Cell Approach. Adv. Water Resour. 2000, 23, 545–562. [Google Scholar] [CrossRef]
- Schmitt, P.; Bourdier, S.; Whittaker, T.; Sarkar, D.; Renzi, E.; Dias, F.; Doherty, K.; van’t Hoff, J. Hydrodynamic Loading on a Bottom Hinged Oscillating Wave Surge Converter. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; International Society of Offshore and Polar Engineers: Cupertino, CA, USA, 2012. [Google Scholar]
- Sarpkaya, T. Vortex Shedding and Resistance in Harmonic Flow about Smooth and Rough Circular Cylinders at High Reynolds Numbers; Technical Report; Naval Postgraduate School: Monterey, CA, USA, 1976. [Google Scholar]
- Goda, Y. Statistical Variability of Sea State Parameters as a Function of Wave Spectrum. Coast. Eng. Jpn. 1988, 31, 39–52. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutsches Hydrographisches Institut: Berlin/Hamburg, Germany, 1973. [Google Scholar]
- Kitaigordskii, S.A.; Krasitskii, V.P.; Zaslavskii, M.M. On Phillips’ Theory of Equilibrium Range in the Spectra of Wind-Generated Gravity Waves. J. Phys. Oceanogr. 1975, 5, 410–420. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).