DEM-Based Parameter Calibration of Soils with Varying Moisture Contents in Southern Xinjiang Peanut Cultivation Zones

Abstract

To address the insufficient adaptability of imported peanut harvesting equipment’s soil-engaging components to the specific soil conditions in Xinjiang, this study conducted Discrete Element Method (DEM)-based calibration of soil mechanical parameters using field soil samples with 1–20% moisture content from typical peanut cultivation areas in southern Xinjiang. Through the EDEM simulation platform, a comprehensive approach integrating the Hertz–Mindlin with the JKR adhesion model and Hertz–Mindlin with the Bonding model was employed to systematically calibrate nine key parameters: coefficient of restitution, static friction coefficient, rolling friction coefficient, JKR surface energy, normal/tangential stiffness per unit area, critical normal/tangential force, and soil bonding disk radius. Adopting static angle of repose (SAOR) and unconfined compressive force (UCF) as dual-response indicators, a hybrid experimental design strategy combining Central Composite Design (CCD), Plackett–Burman (PB) screening, and Box–Behnken Design (BBD) optimization was implemented. Regression models for SAOR and UCS were established, yielding six sets of soil parameters optimized for different moisture conditions through parameter optimization. Field validation demonstrated the following: ≤3.27% error in SAOR, ≤1.46% error in UCF, and ≤5.05% error in drawbar resistance validation for field digging shanks. Experimental results confirm that the model demonstrates strong prediction accuracy for soils in typical peanut harvesting regions of southern Xinjiang, thereby providing key parameter references for the future self-developed, highly adaptive soil-engaging components with drag reduction optimization in peanut harvesters for the Xinjiang region.

1. Introduction

In response to China’s Western Relocation of Grain and Oil Production Strategy, Xinjiang is projected to witness exponential expansion of peanut cultivation acreage in the coming period. As a geocarpic crop, peanut yield quality exhibits pronounced sensitivity to soil physicochemical characteristics. The region’s distinctive pedological properties, shaped by unique climatic conditions, demonstrate significant divergence from conventional peanut-growing regions. Consequently, targeted determinations of soil parameters under varying moisture gradients in representative Xinjiang peanut cultivation zones become imperative, establishing fundamental data for subsequent elucidation of interaction mechanisms between soil-contacting components and edaphic matrices [1,2].

DEM serves as the predominant approach for soil parameter calibration, where appropriate selection of contact models ensures alignment between the simulated and experimental mechanical characteristics of granular materials. Zhong et al. [3] employed the Edinburgh Elasto-Plastic Adhesion (EEPA) contact model to calibrate soil parameters through confined uniaxial compression tests and UCF trials, demonstrating a strong correlation with soil plastic deformation behavior. Cheng et al. [4] implemented the Hertz–Mindlin model to quantify multiphase interaction parameters between South China’s lateritic soil and tool interfaces, systematically investigating cohesive forces in soil–soil and soil–tool systems. This foundational dataset advances bionic drag reduction design optimization for agricultural implements under region-specific tillage conditions. Gong et al. [5] innovatively substituted interparticle cohesion with bonding elements in their modified Hertz–Mindlin with Bonding model, successfully simulating soil aggregate responses across varying compaction energy inputs through discrete bond breakage mechanisms.

Based on the aforementioned research, to address the calibration challenges of soil parameters under Xinjiang’s unique natural conditions, this study specifically accounts for the influence of van der Waals forces between soil particles prior to air-drying. The Hertz–Mindlin with JKR (Johnson–Kendall–Roberts) contact model was employed as the foundational framework to characterize pre-desiccation soil behavior, while the Hertz–Mindlin with Bonding model was integrated to simulate interparticle cohesive interactions, thereby reproducing soil clod fragmentation mechanisms. Six distinct soil models with varying moisture contents (ranging from 1% to 20%) were developed for Xinjiang’s typical peanut cultivation areas. Comprehensive calibration of critical model parameters was conducted. This systematic parameterization framework provides essential reference values for DEM simulations of agricultural soils in arid regions, particularly facilitating accurate modeling of soil–tool interaction dynamics and tillage energy optimization in mechanized peanut farming systems. At the same time, it is conducive to the optimal design of subsoil components.

The Hertz–Mindlin with JKR contact model is a framework designed to describe the contact behavior of particles. It combines the Hertz contact theory and the Mindlin–Deresiewicz tangential force model, incorporating the JKR surface energy parameters to simulate the adhesion forces between particles. The Bonding model is used to simulate particle adhesion and fracture. It employs a finite-sized “adhesive” to bind particles, which can withstand both tangential and normal displacements until the maximum normal and tangential shear stresses—i.e., the bonding failure point—are reached. After this point, the particles interact as hard spheres with no adhesive properties. During the peanut planting and growth stages, the soil retains a certain moisture content. Over time, the combined effects of gravitational settling, mechanical compaction, prolonged drought, and soil salinity lead to the formation of numerous clods. Throughout the peanut production cycle, the soil undergoes a series of physical changes, including plastic deformation and fracture. Therefore, the model can be simplified as the combined effect of the Hertz–Mindlin with JKR model and the Bonding model. This study integrates the Bonding model into the Hertz–Mindlin with JKR contact model to replicate the changes in soil characteristics during peanut harvesting operations. The surface tension properties of the Hertz–Mindlin with JKR contact model and the bonding fracture characteristics of the Bonding model are illustrated in Figure 1 [6,7,8,9,10].

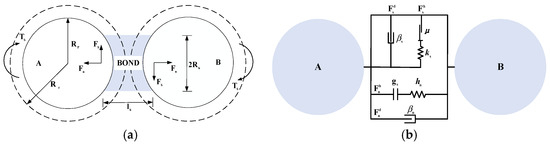
Figure 1. Schematic diagram of the relevant parameters of the contact model: (a) The Bonding contact mechanics model; (b) the JKR contact mechanics model.

In Figure 1a, F_n and F_s represent the normal and tangential forces between particles A and B, respectively; T_s denotes the torque between the particles; R_p is the particle radius; R_b is the bonding radius; R_c is the contact radius; and l_b is the bond length. The Bonding model primarily provides adhesive force between particles, which is represented by the normal and tangential forces between them. When the normal and tangential forces between particles exceed their respective limit values, the bond breaks, and the adhesive properties are lost. Subsequently, the contact forces between the particles can be modeled using the Hertz–Mindlin with JKR model (Figure 1b). $F_n^d$, $F_n^h$, $F_s^d$, and $F_s^h$ represent the normal/tangential damping forces and Hertzian forces (in the contact coordinate system); β_n and β_s are the normal/tangential damping coefficients; hn and ks are the normal and tangential elastic coefficients of the soil particles; and μ is the coefficient of friction [11].

2. Materials and Methods

2.1. Soil Parameter Determination Methods

The soil samples were collected from the Peanut Experimental Field of the Chinese Academy of Agricultural Sciences, located in Tumxuk City, Xinjiang (39.5243° N, 79.0845° W). This area represents the typical geological conditions of southern Xinjiang. Soil sampling was performed at a depth of 0~200 mm using a 100 cm³ soil core sampler (Figure 2). A five-point sampling method was employed, with samples taken from five different plots within the site. For soil moisture determination, the drying method was applied, where the samples were dried at 105 °C for 8 h continuously. Soil bulk density was measured using the air displacement method. The equipment used for weighing was the TD50002 (Tian Ma Technologies, China) electronic balance (precision error ± 0.01 g) (Figure 3). The drying oven was a Supper 101 model (Shang Dao Instrument, Shang Hai, China) (temperature error ± 1 °C). The liquid volume was measured using a 100 mL graduated cylinder (Bo Mei Technologies, China) (precision error ± 1 mL), and mechanical properties were determined with the Riegel-4002 (Reger Instrument, Guang Zhou, China) universal testing machine. Length measurements were taken using a vernier caliper (precision error ± 0.02 mm).

Figure 2. Schematic diagram of soil sampling depth.

Figure 3. Determination of soil particle density by volume displacement method.

2.2. Soil Density and Particle Size Distribution

Soil bulk density was determined for Tumxuk regions by weighing five soil samples collected from distinct areas within each test plot using soil core sampler (height 5 cm, diameter 5 cm), followed by calculation through density formula. Analysis of soil bulk density distribution at 0~200 mm depth in Tumxuk region (Table 1) demonstrated progressively increasing density with depth. Considering peanut pods predominantly distribute at 100~150 mm depth, excavation tools should ideally operate within 150~200 mm depth during harvesting. This study therefore focused on parameter determination for 150~200 mm depth soils with varying moisture contents. Measurements revealed average bulk densities of 1.45 g/cm³ and 1.49 g/cm³ for 150~200 mm depth soils in Tumxuk region. An air displacement methodology was employed where controlled soil samples were placed in fixed-volume containers. Gradual addition of 100 mL water into these containers facilitated observation of volumetric and gravimetric variations. Particle density calculation via Equation (1) yielded an average value of 2500 kg/m³.

Table 1. Bulk density distribution of soil at a depth of 0–200 mm in Tumshuk area.

Sampling Depth/(mm)	Bulk Density/(g·cm−3)
	Sampling Point 1	Sampling Point 2	Sampling Point 3	Sampling Point 4	Sampling Point 5
0~50	1.4285	1.4500	1.3670	1.3393	1.4592
50~100	1.4284	1.4643	1.3930	1.3522	1.4550
100~150	1.4293	1.4939	1.4022	1.3814	1.4717
150~200	1.4702	1.5109	1.4032	1.3978	1.4857

$${\rho }_{\mathrm{soil}}={\displaystyle \frac{{\mathrm{m}}_1-{\mathrm{m}}_2}{{\mathrm{V}}_1-{\mathrm{V}}_2}}$$

(1)

In Equation (1), soil denotes soil particle density, kg/m³; m₁ represents the combined mass of soil and specimen container, kg; m₂ indicates the mass of empty specimen container, kg; V₁ corresponds to the internal volume of specimen container, m³; V₂ signifies the injected water volume, m³.

Following standardized air-drying protocols and meticulous sieve-gravimetric analysis, particle size distribution data presented in Table 2 demonstrate average mass values per gradational fraction of soil samples. In accordance with the geotechnical soil classification standard (GB/T 17296-2009) [12], the analyzed Tumxuk soil specimens were classified texturally as sandy soils (sand particle fraction > 85% by mass). The detailed experimental procedure is illustrated in Figure 4.

Table 2. Soil particle distribution.

Particle Size/(mm)	Average Mass/(g)	Percentage/(%)
>0.4	9.86	10.90
0.315~0.4	7.24	8.00
0.2~0.315	15.16	16.76
0.154~0.2	10.32	11.41
0.1~0.154	15.17	16.77
0.056–0.1	26.03	28.77
<0.056	6.69	7.39

Figure 4. The specific experimental procedures and methodologies.

2.3. Determination and Preparation of Soils with Varied Moisture Contents

Moisture content determination was conducted through thermogravimetric methodology whereby standardized soil masses were oven-dried in specimen containers following soil quality guidelines (HJ 613-2011) [13]. Technical parameters were precisely controlled with desiccation temperature maintained at 105 °C for 8 h duration. Quantitative assessment of hydroscopic characteristics involved meticulous gravimetric analysis pre- and post-desiccation, with moisture content computation achieved through Equation (2).

$${\omega }_1=\left(1-{\displaystyle \frac{{\mathrm{m}}_3}{{\mathrm{m}}_4}}\right)\times 100\%$$

(2)

In Equation (2), ω₁ denotes soil moisture content, %; m₃ denotes desiccated soil mass, g; m₄ denotes initial soil mass prior to desiccation, g.

To prepare soil specimens with varying moisture content parameters, standardized hydrometric conditioning procedures were implemented. This involved precise measurement of baseline soil moisture content and mass, followed by calculation of requisite water additions through Equation (3) to achieve designated moisture gradients. The conditioning protocol comprised thorough homogenization of base soil with calculated water volumes within sealed polyethylene bags until reaching hydraulic equilibrium.

$$m_6={\displaystyle \frac{{\mathrm{m}}_5\cdot {\omega }_1\cdot \left({\omega }_2-{\omega }_1\right)}{1+{\omega }_1}}$$

(3)

In Equation (3): m₆—required water mass to be added, g; m₅—base soil mass, g; ω₁-initial moisture content of base soil, %; ω₂—target moisture content, %.

2.4. Determination of SAOR for Soils with Varied Moisture Contents

The soil moisture content significantly influences peanut harvesting efficiency. To investigate the physical properties of soils with different moisture levels, six specifically conditioned moisture gradients were subjected to SAOR testing. The cylinder lift method was employed, utilizing a steel cylinder (42 mm internal diameter × 150 mm height) vertically elevated at 0.01 m/s. Post-elevation, three-dimensional stabilization was achieved through 5~10 s static settlement, followed by orthogonal photography of frontal and lateral soil deposits. Image contour coordinates were extracted using ImageJ Win 64 software as depicted in Figure 5a. The contour profiles were reconstructed, and curve fitting was conducted via Origin to derive the contour line equations. The tangent value of the SAOR was calculated to determine the SAOR. Figure 5b illustrates the analytical workflow, where each measurement represents the mean value of bilateral SAOR (left and right summation), with three replicated trials performed. Statistical results of SAOR under varying conditions are detailed in Table 2. Digital image analysis via Image J software (Figure 5a–f) facilitated coordinate extraction of deposit profiles. Contour mapping and nonlinear curve fitting through Origin yielded profile equations whose slope derivatives provided tangent values of natural SAOR. Triplicate measurements of bilateral angles were averaged per moisture condition. Data presented in Table 2 demonstrate that the SAOR for Tumxuk soils exhibited a monotonic decrease from 39.71° to 28.684° as moisture content increased within the range of 1 ± 1% to 20 ± 1% water content.

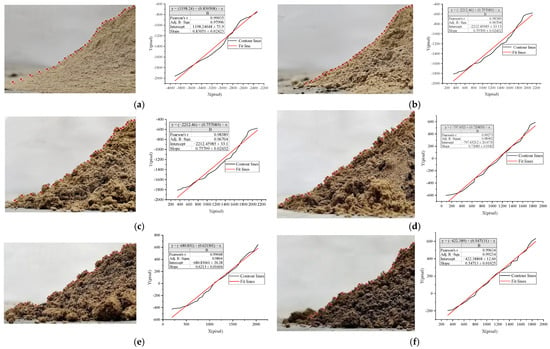
Figure 5. SAOR with different moisture contents: (a) Moisture content 1 ± 1%, SAOR 39.71°; (b) Moisture content 4 ± 1%, SAOR 37.129°; (c) Moisture content 8 ± 1%, SAOR 35.995°; (d) Moisture content 12 ± 1%, SAOR 35.786°; (e) Moisture content 16 ± 1%, SAOR 31.853°; (f) Moisture content 20 ± 1%, SAOR 28.684°.

3. Results and Discussion

3.1. Parameter Calibration for Soil JKR Simulation Model

To replicate the physical characteristics of soil under loose conditions, fundamental parameters were determined according to the requirements of the DEM utilizing the Hertz–Mindlin with JKR contact model. Intrinsic parameters include Poisson’s ratio, particle density, and shear modulus, while contact parameters comprise the coefficient of restitution, static friction coefficient, and rolling friction coefficient. The JKR model surface energy between soil particles constitutes the key contact model parameter. Soil baseline parameters were established based on the previously determined physical characteristics, with other parameters derived from literature sources. The complete set of calibrated DEM parameters for soil modeling is presented in Table 3.

Table 3. Determination of soil simulation parameters under the JKR model.

Parameter Type	Parameters	Value	Source
Intrinsic parameters	Soil Poisson’s Ratio	0.5	[14]
	Soil Particle Density	2500 kg·m−3	Determination
	Soil Shear Modulus	1 × 106 Pa/1 × 108 Pa	[11,15]
	Steel Poisson’s Ratio	0.3	[16]
	Steel Particle Density	7850 kg·m−3	Determination
	Steel Shear Modulus	7.9 × 1010 Pa	[17]
Contact parameters	Soil-Steel Coefficient of Restitution	0.3	[18,19,20,21]
	Soil-Steel Coefficient of Static Friction	0.5	[18,19,20,21]
	Soil-Steel Coefficient of Rolling Friction	0.05	Bibliographic

Soil parameters including coefficient of restitution, static friction coefficient, rolling friction coefficient, and surface energy were determined through comprehensive benchmarking of the EDEM 2022 software’s GEMM (Generic EDEM Material Model) database. The parametric configuration integrated preliminary DEM simulation trials with empirical values extracted from granular mechanics literature, with operational ranges detailed in Table 4. Simulation setup maintained geometric fidelity through identical cylinder dimensions (42 mm diameter × 150 mm height) and vertical lifting velocity (0.01 m/s) to experimental conditions, while employing spherical soil particles with 2 mm radius for computational optimization.

Table 4. Parameters to be calibrated for the JKR model.

Factors Type	Factors	Range	Source
Contact parameters	Soil-Soil Coefficient of Restitution/X1	0.15–0.75	Pending calibration
	Soil-Soil Coefficient of Static Friction/X2	0.2–1.16	Pending calibration
	Soil-Soil Coefficient of Rolling Friction/X3	0.005–0.105	Pending calibration
Model parameters	Surface Energy/X4	0.5–2.5 J·m−2	Pending calibration

Leveraging the analytical advantages of Central Composite Design (CCD), this experimental framework employed five-level factorial processing of variables to mitigate localized parameter fluctuations. The experimental matrix for SAOR simulations incorporated systematically configured factor levels as detailed in Table 5.

Table 5. Determination of the level of factors in the stacking angle test.

Levels	Factors
	X1	X2	X3	X4/J·m−2
−2	0.15	0.2	0.005	0.5
−1	0.3	0.44	0.03	1
0	0.45	0.68	0.055	1.5
1	0.6	0.92	0.08	2
2	0.75	1.16	0.105	2.5

Within the EDEM 2022 software suite, orthogonal projections along the X and Y axes of the conical deposit were analyzed. SAOR measurements were conducted using the standardized protocol delineated in Section 2.4. (as illustrated in Figure 6), where four angular measurements were acquired per simulation framework. These measurements underwent arithmetic mean calculation, with resultant simulation data statistically summarized in Table 6.

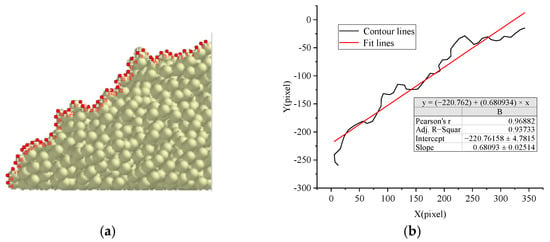
Figure 6. Extraction and fitting of soil SAOR contour line in simulated environment: (a) simulated soil SAOR profile extraction; (b) SAOR contour fitting.

Table 6. Soil SAOR Central Composite test scheme and results.

Test No.	Factors				SAOR/(°)	Relative Error/(%)
	X1	X2	X3	X4
1	−1	−1	−1	−1	14.776	62.7902
2	1	−1	−1	−1	9.917	75.0264
3	−1	1	−1	−1	14.439	63.6389
4	1	1	−1	−1	12.335	68.9373
5	−1	−1	1	−1	23.887	39.8464
6	1	−1	1	−1	14.92	62.4276
7	−1	1	1	−1	29.729	25.1347
8	1	1	1	−1	13.789	65.2757
9	−1	−1	−1	1	21.752	45.2229
10	1	−1	−1	1	16.059	59.5593
11	−1	1	−1	1	29.542	25.6056
12	1	1	−1	1	21.869	44.9282
13	−1	−1	1	1	51.78	−30.3954
14	1	−1	1	1	25.057	36.9000
15	−1	1	1	1	48.183	−21.3372
16	1	1	1	1	40.957	−3.1403
17	−2	0	0	0	6.631	83.3014
18	2	0	0	0	15.462	61.0627
19	0	−2	0	0	18.538	53.3165
20	0	2	0	0	22.133	44.2634
21	0	0	−2	0	10.666	73.1403
22	0	0	2	0	37.202	6.3158
23	0	0	0	−2	13.2	66.7590
24	0	0	0	2	51.76	−30.3450
25	0	0	0	0	19.708	50.3702
26	0	0	0	0	23.761	40.1637
27	0	0	0	0	18.466	53.4979
28	0	0	0	0	21.542	45.7517
29	0	0	0	0	24.98	37.0939
30	0	0	0	0	23.354	41.1886

3.2. Parameter Calibration via SAOR Analysis in Simulated Environments

Statistical analysis of the five-level Central Composite Design (CCD) results in Table 6 revealed significant parametric convergence towards the target SAOR within Groups 16 and 22. Since it was the first parameter screening test, the parameter value range was large, and some relative errors exceeded 80%, and then the parameters gradually converged after squeezing screening. This critical spatial clustering guided the implementation of a Plackett–Burman screening design within these refined parameter ranges to eliminate factors with non-significant effects on the response metric. The experimental factor matrix with optimized levels is presented in Table 7, with corresponding numerical outputs systematically documented in Table 8.

Table 7. Factors and horizontal design of the Plackett–Burman test.

Levels	Factors
	X1	X2	X3	X4/(J·m−2)
−1	0.45	0.68	0.08	1.5
1	0.6	0.92	0.105	2

Table 8. Statistical results of SAOR in the Plackett–Burman test.

Test No.	Factors				SAOR/(°)	Relative Error/(%)
	X1	X2	X3	X4
1	1	1	−1	1	34.6155	12.829
2	−1	1	1	−1	31.292	21.199
3	1	−1	1	1	54.0405	−36.088
4	−1	1	−1	1	39.188	1.315
5	−1	−1	1	−1	37.9275	4.489
6	−1	−1	−1	1	42.4835	−6.984
7	1	−1	−1	−1	28.3945	28.495
8	1	1	−1	−1	27.602	30.491
9	1	1	1	−1	36.004	9.333
10	−1	1	1	1	47.543	−19.726
11	1	−1	1	1	52.4755	−32.147
12	−1	−1	−1	−1	30.9735	22.001

Statistical significance analysis of factorial effects was conducted through Design-Expert 13^® software, yielding comprehensive diagnostic outputs (Table 9). ANOVA results demonstrated significant global effects (p < 0.05) on SAOR, with standardized effect ordering: X₄ > X₃ > X₂ > X₁. Parametric influence validation confirmed X₄, X₃, and X₂ as critical factors (p < 0.05), whereas X₁ exhibited non-significant association (p = 0.6629 > 0.05) with the response metric.

Table 9. ANOVA of soil SAOR regression model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	846.96	4	211.45	37.92	<0.0001 **
X1	1.16	1	1.16	0.2070	0.6629
X2	75.25	1	75.25	13.48	0.0080 **
X3	261.57	1	261.57	46.84	0.0002 **
X4	508.98	1	508.98	91.15	>0.0001 **
Residual	39.09	7	5.58
Cor Total	886.05	11
R2				0.9674

** Indicates a highly significant effect (p < 0.01).

As illustrated in Figure 7, variables X₄ and X₃ exhibit positive effect values on the target parameter, while X₂ demonstrates a negative contribution. This phenomenon arises from the intensified static friction force, which enhances interparticulate interactions under combined surface energy effects. Such heightened friction restricts particle sliding and rearrangement, thereby modulating the SAOR. Notably, simulations reveal that increasing the static friction coefficient paradoxically destabilizes structural configurations during accumulation, leading to angle reduction. A pronounced nonlinear interaction exists between static friction coefficients and other parameters influencing the SAOR, as will be rigorously analyzed in subsequent Box–Behnken studies.

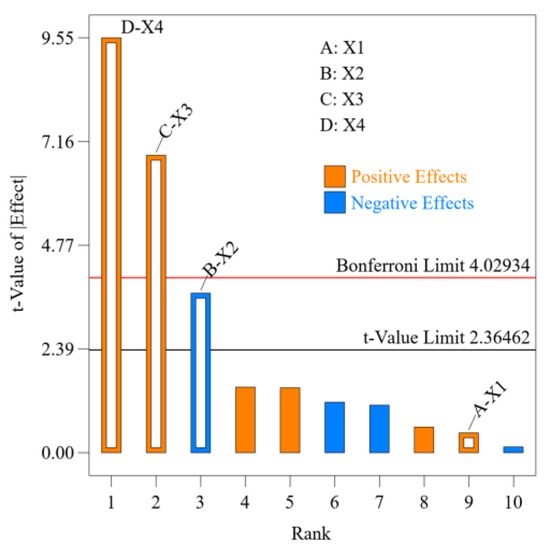
Figure 7. Pareto diagram of the significance of factors influencing the SAOR.

The Plackett–Burman experimental design identified static friction coefficient (X₂), rolling friction coefficient (X₃), and JKR surface energy (X₄) as statistically significant factors. Upon eliminating the non-significant restitution coefficient (X₁), parametric configurations derived from Table 8 demonstrated proximate alignment with target SAOR (Relative error = 1.315%). Consequently, the conventional steepest ascent optimization phase was bypassed, and direct progression to Box–Behnken response surface methodology was implemented. This approach leveraged parameter levels from Table 7 to investigate optimal parameter combinations and interaction effects on response metrics. Detailed factor level specifications and experimental matrices for the Box–Behnken design are provided in Table 10 and Table 11, supplemented by ANOVA validation results in Table 12.

Table 10. Factor-level design of the SAOR Box–Behnken test.

Levels	Factors
	X2	X3	X4/J·m−2
−1	0.68	0.08	1.5
0	0.80	0.0925	1.8
1	0.92	0.105	2

Table 11. Box–Behnken protocol and results.

Test No.	Factors			SAOR/(°)	Relative Error/(%)
	X2	X3	X4
1	−1	−1	0	41.6625	−4.92
2	1	−1	0	37.586	5.35
3	−1	1	0	42.6035	−7.29
4	1	1	0	45.0225	−13.38
5	−1	0	−1	39.6105	0.25
6	1	0	−1	34.431	13.29
7	−1	0	1	43.005	−8.30
8	1	0	1	52.0275	−31.02
9	0	−1	−1	33.0695	16.72
10	0	1	−1	34.8475	12.25
11	0	−1	1	40.7365	−2.58
12	0	1	1	44.1315	−11.13
13	0	0	0	44.737	−12.66
14	0	0	0	38.1165	4.01
15	0	0	0	40.787	−2.71
16	0	0	0	42.981	−8.24
17	0	0	0	43.476	−9.48

Table 12. Analysis of variance of the SAOR Box–Behnken test.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	305.59	9	33.95	6.13	0.0130 **
X2	0.0296	1	0.0296	0.0053	0.9438
X3	21.27	1	21.27	3.84	0.0909
X4	179.95	1	179.95	32.49	0.0007 **
X2X3	10.55	1	10.55	1.90	0.2100
X2X4	45.68	1	45.68	8.25	0.0239 *
X3X4	0.9200	1	0.9200	0.1661	0.6958
${\mathrm{X}}_2^2$	14.97	1	14.97	2.70	0.1441
${\mathrm{X}}_3^2$	20.13	1	20.13	3.63	0.0983
${\mathrm{X}}_4^2$	1.95	1	1.95	0.3526	0.5713
X2X3X4	0.0000	0
Residual	38.77	7	5.54
Lack of Fit	11.58	3	3.86	0.5682	0.6649
Pure Error	27.18	4	6.80
Cor Total	344.36	16
R2				0.8874

* Indicates a highly significant effect (p < 0.05). ** Indicates a highly significant effect (p < 0.01).

Statistical analysis of the model reveals significant validation (p = 0.0130 < 0.05), confirming robust alignment between experimental outcomes and theoretical predictions. The coefficient of determination (R² = 0.874) and adjusted R² (${\mathrm{R}}_{\mathrm{Adj}}^2$ = 0.7427) fell below the 0.2 threshold recommended for multivariate regression models. This demonstrates strong correlation consistency and adequate explanatory power of regression terms. Consequently, the Box–Behnken experimental framework proves statistically valid, enabling precise calibration of soil constitutive parameters and reliable prediction of angle of repose variations under differing parameter configurations.

Analysis demonstrates that the main effects of X₃ and X₄ moderately influenced the SAOR response variable, with X₄ exhibiting exceptional significance (p = 0.0007 < 0.01). Among interaction terms, only X₂X₄ reached statistical significance, whereas all quadratic terms (${\mathrm{X}}_2^2$, ${\mathrm{X}}_3^2$, ${\mathrm{X}}_4^2$) and other cross-terms showed negligible impacts. Although the primary effect of X₂ was non-significant (p > 0.05), its synergistic interactions and secondary effects warranted retention in the final model based on hierarchical inclusion criteria during backward elimination. Notably, the dominant role of X₄ aligns with interparticle mechanics governed by static friction thresholds. The observed X₂X₄ interaction (Figure 8) likely reflects moisture-dependent tribological modulation, as detailed in subsequent Box–Behnken confirmation trials.

$$Repose\begin{array}{c}\end{array}angle=41.1-0.0614{\mathrm{X}}_2+1.65{\mathrm{X}}_3+4.74{\mathrm{X}}_4+1.62{\mathrm{X}}_2{\mathrm{X}}_3+3.35{\mathrm{X}}_2{\mathrm{X}}_4+0.4749{\mathrm{X}}_3{\mathrm{X}}_4+1.89{\mathrm{X}}_2^2-2.19{\mathrm{X}}_3^2-0.7168{\mathrm{X}}_4^2$$

(4)

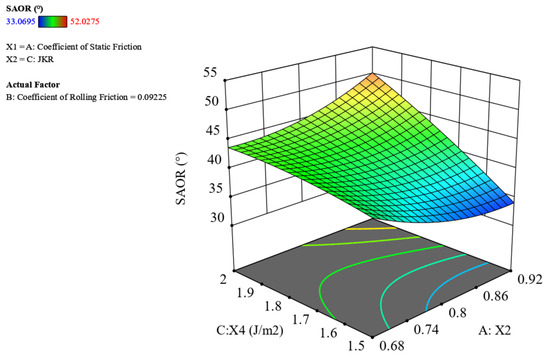
Figure 8. Surface diagram of the response of the interaction term X₂X₃ to the SAOR.

Replicate experiments were conducted across five distinct moisture content gradients (4% ± 1 to 20% ± 1) to determine SAOR parameters for Tumxuk region soils. Parameter optimization based on derived numerical solutions yielded calibrated constitutive properties, with comprehensive results systematically tabulated in Table 13.

Table 13. SAOR size under soil simulation conditions with different moisture contents.

Moisture Content/(%)	Factors				SAOR/(°)				Relative Error/(%)
	X1	X2	X3	X4	Measured	Simulation	Measured Values	Simulated Values
1 ± 1	0.450	0.800	0.097	1.734			39.710	39.1615	−1.38
4 ± 1	0.569	0.819	0.093	1.649			37.129	36.7315	−1.07
8 ± 1	0.600	0.920	0.105	1.500			35.995	36.004	0.02
12 ± 1	0.474	0.851	0.08	1.576			35.786	34.616	3.27
16 ± 1	0.450	0.920	0.105	1.500			31.853	31.292	1.76
20 ± 1	0.557	0.832	0.087	1.535			28.684	28.395	1.00

3.3. Parameter Calibration for Soil Bonding Simulation Model

To calibrate the physical properties of soil with varying moisture content in peanut harvesting fields, the Bonding model in EDEM 2022 software was utilized to simulate soil compaction and the fracture behavior under contact forces. The specific experimental method involved placing soil with a moisture content of 20 ± 1% into a cylindrical container made from two equally divided acrylic plates cut along the axis. The container was secured using a clamp. The inner walls of the cylinder were coated with a lubricant to facilitate sample removal. A universal testing machine was used to perform uniaxial compression on the soil, applying a force of 660 N (a value close to the compaction force experienced by field soils, under which the soil consolidates effectively). Once the pressure reached 660 N, the universal testing machine immediately retracted to completely release the pressure. The compacted soil cores (5 cm in diameter, 5 cm in height) were placed in a laboratory setting at a constant temperature of 26 °C under shaded conditions and air-dried to the target mass, as per Equation (4), during which a certain amount of water was sprayed to prevent uneven drying (outer dry and inner wet), which could affect parameter measurement. This process resulted in soil columns with different moisture contents. Subsequently, these soil columns were crushed using the universal testing machine (Compression rate: 0.5 mm/s) to observe the fracture behavior and changes in UCF. This was repeated twice, with the mean recorded. The pressure at the instant of soil column collapse was recorded.

$$m_7={\displaystyle \frac{{\mathrm{m}}_5\left(1+{\omega }_2\right)}{1+{\omega }_1}}$$

(5)

In Equation (4), m₇ denotes target soil mass in grams, g; m₅ denotes base soil mass in grams, g; ω₁ denotes moisture content of the base soil in percentage,%; and ω₂ denotes target soil moisture content in percentage,%.

UCF testing of soil columns revealed significant moisture-dependent mechanical behavior, exhibiting non-monotonic progression with initial strength enhancement followed by degradation beyond critical moisture thresholds. As demonstrated in Figure 9 through standardized axial loading protocols.

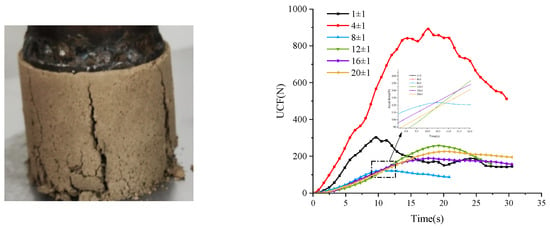
Figure 9. Unconfined pressure resistance of soil with different moisture contents.

Soil mechanics under differential moisture regimes exhibit distinct force mediation pathways. At low hydration states, intergranular interactions are primarily governed by van der Waals forces and electrostatic interactions, with limited capillary water contribution. Weak aqueous adhesion leads to diminished interparticulate bonding forces, resulting in structurally unconsolidated aggregates prone to particulate dispersion. Moderate moisture saturation initiates capillary water meniscus formation at grain contact points, amplifying cohesive stresses through Laplace pressure dynamics. This hydrous phase facilitates stable water film development, optimizing shear parameters to achieve peak bearing capacity and structural stability. Hyperhydric conditions induce saturated pore networks with liquid bridging effects governed by viscous shear resistance. Excessive interfacial water layers disrupt direct solid-phase contacts, triggering cohesive strength degradation through particle decoupling. Corresponding rheological transitions manifest as reduced yield stress and enhanced thixotropic behavior under cyclic loading. Schematic representations of particulate kinematics across hydration gradients are provided in Figure 10, illustrating critical phase boundaries in moisture-dependent soil fabric evolution. In the picture, A and B are soil particles A and soil particles B.

Figure 10. Variation trend of interparticle forces in soil with varying moisture contents: (a) dry soil (moisture content 1~4%); (b) soil with intermediate moisture content (moisture content 4~12%); (c) soil with elevated moisture content (moisture content 12~20%).

In EDEM software, the Bonding model incorporates five principal parameters whose empirically validated value ranges, derived from literature review, are systematically compiled in Table 14 [21,22,23,24].

Table 14. Values of each parameter of the bonding model.

Type	Parameters	Range	Source
Model Parameters	Normal Stiffness per unit area Z1	3.5 × 108–2.55 × 109 N·m−3	Pending calibration
	Shear Stiffness per unit area Z2	1 × 108–9 × 108 N·m−3	Pending calibration
	Critical Normal Stress Z3	1 × 105–9 × 105 Pa	Pending calibration
	Critical Shear Stress Surface Energy Z4	1 × 105–9 × 105 Pa	Pending calibration
	Bonded Disk Radius Z5	2–4 mm	Pending calibration [24,25,26,27,28,29,30,31,32,33]

The experimental design employed a Central Composite framework incorporating multi-factor and multi-level variations based on the parameter ranges specified in Table 14 for the Bonding model. Primary factors were discretized into five distinct levels to enhance design resolution, thereby minimizing the influence of minor factor fluctuations.

3.4. Parameter Calibration via UCF Analysis in Simulated Environments

Level configurations for Values of each simulation parameters are systematically detailed in Table 15. Subsequent unconfined compression testing of soil columns was performed using a universal testing machine, with synchronized acquisition and documentation of mechanical response data (Table 16).

Table 15. Levels of factors in bonding model experiments.

Levels	Factors
	Z1/(N·m−3)	Z2/(N·m−3)	Z3/(Pa)	Z4/(Pa)	Z5/(mm)
−2.378	3.5 × 108	1 × 108	1 × 105	1 × 105	2
−1	9 × 108	3 × 108	3 × 105	3 × 105	2.5
0	1.45 × 109	5 × 108	5 × 105	5 × 105	3
1	2 × 109	7 × 108	7 × 105	7 × 105	3.5
2.378	2.55 × 109	9 × 108	9 × 105	9 × 105	4

Table 16. Simulation test scheme and results of Central Composite without confined compression.

Test No.	Factors					UCF/(N)	Relative Error/(%)
	Z1	Z2	Z3	Z4	Z5
1	−1	−1	−1	−1	1	766	152.81
2	1	−1	−1	−1	−1	314.3	3.73
3	−1	1	−1	−1	−1	336.8	11.16
4	1	1	−1	−1	1	658.5	117.33
5	−1	−1	1	−1	−1	555	83.17
6	1	−1	1	−1	1	990.2	226.80
7	−1	1	1	−1	1	734	142.24
8	1	1	1	−1	−1	420.4	38.75
9	−1	−1	−1	1	−1	472.4	55.91
10	1	−1	−1	1	1	548.6	81.06
11	−1	1	−1	1	1	818.3	170.07
12	1	1	−1	1	−1	387.2	27.79
13	−1	−1	1	1	1	1598.6	427.59
14	1	−1	1	1	−1	788.2	160.13
15	−1	1	1	1	−1	737	143.23
16	1	1	1	1	1	1335.9	340.89
17	−2.378	0	0	0	0	606	100.00
18	2.378	0	0	0	0	895.2	195.45
19	0	−2.378	0	0	0	672.9	122.08
20	0	2.378	0	0	0	815.6	169.17
21	0	0	−2.378	0	0	65.5	−78.38
22	0	0	2.378	0	0	947.4	212.67
23	0	0	0	−2.378	0	255.8	−15.58
24	0	0	0	2.378	0	840.6	177.43
25	0	0	0	0	−2.378	478.2	57.82
26	0	0	0	0	2.378	1276.7	321.35
27	0	0	0	0	0	866.1	185.84
28	0	0	0	0	0	866.1	185.84
29	0	0	0	0	0	866.1	185.84
30	0	0	0	0	0	866.1	185.84
31	0	0	0	0	0	866.1	185.84
32	0	0	0	0	0	866.7	186.04

Guided by the results from the 5-level Central Composite Design (CCD) experiments documented in Table 16, parametric ranges approximating the reference UCF were delineated through discernible convergence patterns in Runs 2 and 23. Since it was the first parameter screening test, the parameter value range was large, and some relative errors exceeded 80%, and then the parameters gradually converged after squeezing screening. Building upon these constraints, a Box–Behnken design (BBD) was implemented with experimental factors and levels rigorously structured as per Table 17. The resultant mechanical responses were tabulated in Table 18, the relative error of No. 28 and No. 39 data in Table 18 is greater than 80% due to excessive interval selection, but the experimental results will gradually converge. ANOVA (Analysis of Variance) outcomes in Table 19.

Table 17. Factor-level design of the UCF Box–Behnken test.

Levels	Factors
	Z1/(N·m−3)	Z2/(N·m−3)	Z3/(Pa)	Z4/(Pa)	Z5/(mm)
−1	1.45 × 109	3 × 108	300,000	100,000	2.5
0	1.73 × 109	4 × 108	400,000	200,000	2.75
1	2.00 × 109	5 × 108	500,000	300,000	3

Table 18. Results of Box–Behnken test.

Test No.	Factors					UCF/(N)	Relative Error/(%)
	Z1	Z2	Z3	Z4	Z5
1	−1	−1	0	0	0	429.2	41.65
2	1	−1	0	0	0	431.6	42.44
3	−1	1	0	0	0	380.9	25.71
4	1	1	0	0	0	374.5	23.60
5	0	0	−1	−1	0	271	−10.56
6	0	0	1	−1	0	338.4	11.68
7	0	0	−1	1	0	376.3	24.19
8	0	0	1	1	0	523.3	72.71
9	0	−1	0	0	−1	378	24.75
10	0	1	0	0	−1	389.5	28.55
11	0	−1	0	0	1	473.8	56.37
12	0	1	0	0	1	457.2	50.89
13	−1	0	−1	0	0	394.6	30.23
14	1	0	−1	0	0	331.7	9.47
15	−1	0	1	0	0	428.6	41.45
16	1	0	1	0	0	440	45.21
17	0	0	0	−1	−1	223.6	−26.20
18	0	0	0	1	−1	420.6	38.81
19	0	0	0	−1	1	301.8	−0.40
20	0	0	0	1	1	544.9	79.83
21	0	−1	−1	0	0	350.9	15.81
22	0	1	−1	0	0	341.1	12.57
23	0	−1	1	0	0	460.3	51.91
24	0	1	1	0	0	410	35.31
25	−1	0	0	−1	0	262.2	−13.47
26	1	0	0	−1	0	289.6	−4.42
27	−1	0	0	1	0	500.7	65.25
28	1	0	0	1	0	554.5	83.00
29	0	0	−1	0	−1	305.4	0.79
30	0	0	1	0	−1	374.7	23.66
31	0	0	−1	0	1	390	28.71
32	0	0	1	0	1	477.9	57.72
33	−1	0	0	0	−1	345.4	13.99
34	1	0	0	0	−1	349.1	15.21
35	−1	0	0	0	1	457.9	51.12
36	1	0	0	0	1	464.3	53.23
37	0	−1	0	−1	0	342.9	13.17
38	0	1	0	−1	0	227.9	−24.79
39	0	−1	0	1	0	570.5	88.28
40	0	1	0	1	0	481.6	58.94
41	0	0	0	0	0	394	30.03
42	0	0	0	0	0	411.9	35.94
43	0	0	0	0	0	393.9	30.00
44	0	0	0	0	0	404.1	33.37
45	0	0	0	0	0	412	35.97
46	0	0	0	0	0	409.7	35.21

Table 19. Analysis of variance of the UCF Box–Behnken test.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	185.69	19	9.77	63.07	<0.0001 **
Z1	0.0025	1	0.0025	0.0161	0.8999
Z2	0.3045	1	0.3045	1.97	0.1728
Z3	19.16	1	19.16	123.64	<0.0001 **
Z4	110.76	1	110.76	714.77	<0.0001 **
Z5	24.20	1	24.20	156.19	<0.0001 **
Z1Z2	0.0124	1	0.0124	0.0799	0.7797
Z1Z3	0.9268	1	0.9268	5.98	0.0215 *
Z1Z4	0.0300	1	0.0300	0.1937	0.6635
Z2Z4	0.5487	1	0.5487	3.54	0.0711
Z3Z4	0.5958	1	0.5958	3.84	0.0607
${\mathrm{Z}}_1^2$	0.1030	1	0.1030	0.6647	0.4223
${\mathrm{Z}}_2^2$	0.5223	1	0.5223	3.37	0.0778
${\mathrm{Z}}_3^2$	1.04	1	1.04	6.69	0.0157 *
${\mathrm{Z}}_4^2$	2.62	1	2.62	16.90	0.0003 **
${\mathrm{Z}}_1^2$Z2	0.5662	1	0.5662	3.65	0.0670
Z1${\mathrm{Z}}_3^2$	0.3500	1	0.3500	2.26	0.1449
Z1${\mathrm{Z}}_4^2$	0.6181	1	0.6181	3.99	0.0564
Z2${\mathrm{Z}}_4^2$	3.50	1	3.50	22.57	<0.0001 **
${\mathrm{Z}}_3^2$Z4	4.21	1	4.21	27.14	<0.0001 **
Residual	4.03	26	0.1550
Lack of Fit	3.80	21	0.1812
Pure Error	0.2238	5	0.0448	4.05	0.0634
Cor Total	189.72	45
R2				0.9788
${\mathrm{R}}_{\mathrm{Adj}}^2$				0.9632
${\mathrm{R}}_{\mathrm{Pre}}^2$				0.9009

* Indicates a highly significant effect (p < 0.05). ** Indicates a highly significant effect (p < 0.01).

The statistical analysis presented in Table 19 demonstrates that the developed model achieved exceptional significance (p < 0.0001). This outcome indicates that the model exhibits a good fit with experimental observations and can effectively characterize the quantitative relationships between various input parameters and experimental outcomes. The model’s coefficient of determination (R² = 0.9009) exhibited a difference less than 0.2 when compared to the adjusted R² value (0.9632), suggesting strong consistency between the regression equation and actual empirical correlations. These validation metrics confirm that the Box–Behnken experimental design methodology was appropriately applied for calibrating key parameters in the soil bonding model. The established model demonstrates sufficient reliability for both parameter quantification and predictive analysis of UCF under varying parametric conditions.

The model’s primary terms Z₃, Z₄, and Z₅ demonstrated extraordinary significance (all p-values < 0.01) in influencing the UCF magnitude of the response variable. Among interaction terms, Z₁Z₃ showed significant effects (Figure 11) while others proved non-significant. Quadratic term ${\mathrm{Z}}_4^2$ exhibited extreme significance (p < 0.001), with ${\mathrm{Z}}_3^2$ displaying moderate significance (0.01 < p < 0.05), whereas other squared terms showed negligible impacts on the model’s predictive capability.

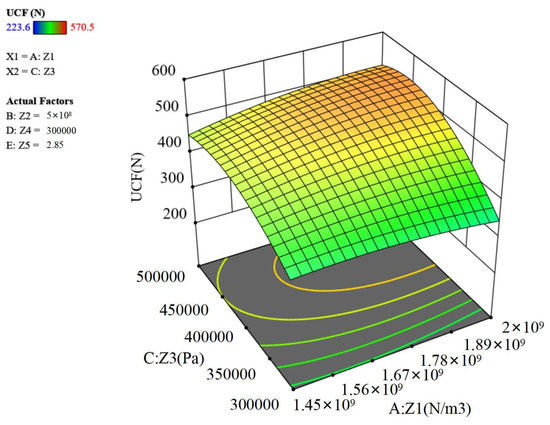
Figure 11. Interaction of Z₁Z₃ on axial force.

These predictive models were examined for adequacy and fitness, and the best model was selected for each response variable. The summary fit table of Z₁~Z₄ are presented in Table 20. A comparative analysis was conducted between simulation and experimental results of UCF under six distinct moisture content conditions. As shown in Table 21, when the moisture content ranged from 1 ± 1% to 20 ± 1%, the relative error between simulated and measured UCF varied between 0.06% and 1.69%. Figure 12 demonstrates congruent temporal evolution patterns of UCF in both simulation and physical testing environments. These findings confirm that the UCF simulation effectively replicates experimental outcomes, providing validated characterization of stress distributions under unconfined loading conditions.

Table 20. Summary of model response value suitability.

Soil Type	Source	Sequential p-Value	Lack of Fit p-Value	Adjusted R2	Predicted R2
4 ± 1	Linear	0.0241	0.1415	0.4304	0.1391	Suggested
	2FI	0.3066	0.1365	0.4402	−0.1314
	Quadratic	0.0923	0.2419	0.6356	−0.0547
	Cubit	0.1129	0.6041	0.7868	0.4552	Aliased
8 ± 1	Linear	0.0015	0.0023	0.6724	0.5494
	2FI	0.5182	0.0019	0.6535	0.4821
	Quadratic	<0.0001	0.1998	0.9734	0.9196	Suggested
	Cubit	0.3611	0.1296	0.9752	0.6768	Aliased
12 ± 1	Linear	<0.0001	0.0420	0.8677	0.8425	Suggested
	2FI	0.9850	0.0252	0.8378	0.7237
	Quadratic	0.1108	0.0339	0.8613	0.7004
	Cubit	0.1170	0.0621	0.9169	0.0286	Aliased
16 ± 1	Linear	<0.0001	0.0011	0.8207	0.6954
	2FI	0.0374	0.0022	0.8801	0.8169
	Quadratic	0.0005	0.0664	0.9823	0.9376	Suggested
	Cubit	0.3623	0.0359	0.9834	0.6846	Aliased
20 ± 1	Linear	0.0015	0.0023	0.6724	0.5494
	2FI	0.5182	0.0019	0.6535	0.4821
	Quadratic	<0.0001	0.1998	0.9734	0.9196	Suggested
	Cubit	0.3611	0.1296	0.9752	0.6768	Aliased

Table 21. Comparison of simulated and measured pressure resistance of soils with different moisture contents.

Moisture Content /(%)	Factors					UCF/(N)		Relative Error/(%)
	Z1/(N·m−3)	Z2/(N·m−3)	Z3/(Pa)	Z4/(Pa)	Z5/(mm)	Measured Values	Simulation Values
1 ± 1	1.8 × 109	4.89 × 108	315,298	157,644	2.751	303	303.2	0.06
4 ± 1	1.72 × 109	5 × 108	541,703	500,000	3	892	893	0.11
8 ± 1	1.45 × 109	5 × 108	140,800	151,000	3	123.5	125.3	1.46
12 ± 1	1.69 × 109	4.01 × 108	339,308	104,379	2.724	258	260.7	1.04
16 ± 1	1.45 × 109	5 × 108	161,048	172,073	3	189	192	1.69
20 ± 1	1.45 × 109	5 × 108	179,380	176,998	3	226	226.6	0.265

Figure 12. UCF Testing in simulation frameworks: (a) Cylindrical soil specimen modeling in simulation frameworks; (b) Schematic illustration of unconfined compression numerical simulation; (c) UCF curves of soils with varied moisture content.

3.5. Numerical Simulation Tests

To further validate the calibrated soil parameters, field-restoration simulations were implemented using the acquired parametric dataset. Operational configurations mirrored actual peanut-harvester shovel working conditions. In EDEM 2022 software, a virtual soil mass (1000 mm × 1000 mm × 400 mm) (Figure 13a) was established as a particle factory containing 460,000 spherical particles (radius = 5 mm) to ensure simulation adequacy.

Figure 13. Interparticle bond contact states in discrete element soil simulation frameworks: (a) construction of soil particulate bed; (b) post-operational soil particulate bed configuration after shovel interaction; (c) bonding state of soil particles in simulated environments.

JKR model parameters and Bonding model parameters were configured according to 8% moisture-adjusted values, with contact radii and bonding disk dimensions proportionally scaled from experimental data. The shovel’s placement angles replicated field conditions, with Bond activation programmed at 1 s post-initiation. Maintained at a constant velocity of 0.2 m/s during the 6 s operation period. After the shovel machine’s operation, the soil particles are in a consolidated earth block form (Figure 13b,c).

3.6. Field Experimental Validation

Field verification of soil parameters was conducted using the critical digging shovel component of a peanut combine harvester (4HD-2A) (Dongtai Machinery Co., Ltd., Linyi, China). The experiment was performed in a peanut cultivation test field in Tumxuk City, Xinjiang Uygur Autonomous Region (39.5243° N, L79.0845° E). Field soil moisture content was determined to be 9.56%. Force dynamics on the digging shovel were recorded utilizing a strain gauge data acquisition system (RKCMCU6 data acquisition module, Figure 14). Field validation experiments as Figure 15 data processing through Origin 2022 yielded horizontal draft force ranging between 1000 and 2500 N, with a mean horizontal draft force of 2397.62 N (Figure 16).

Figure 14. Sensor placement positions.

Figure 15. Field validation experiments.

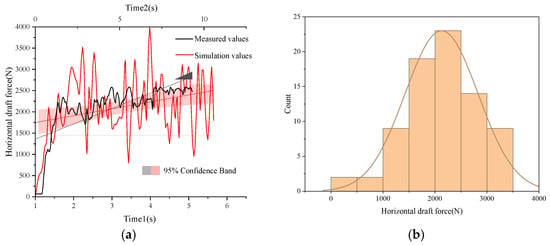
Figure 16. Diagram of change of test parameters: (a) comparison of simulation and field experiment data; (b) normal distribution of simulation parameters.

Simulation analysis using EDEM post-processing modules revealed that the horizontal draft force of excavation tools within soil media maintained a range between 1000 N and 3500 N (Figure 16). After eliminating outlying data points, the mean stabilized resistance was calculated as 2276.58 N, demonstrating a relative percentage error of 5.05% compared to field-measured values (2397.62 N). The 95% confidence band exhibited significant overlap between simulated and experimental parameters, indicating that the earthmoving simulation effectively replicates actual soil behavior under operational conditions and accurately characterizes mechanical interactions between excavation components and soil matrices.

4. Conclusions

This translation was conducted using systematic optimization methodology. The parameter screening phase implemented Central Composite Design (CCD) to narrow experimental ranges. Subsequent statistical analysis applied Plackett–Burman design for significance screening, followed by Box–Behnken response surface methodology to identify statistically significant factors and optimize their values. This multi-stage experimental strategy culminated in developing a comprehensive soil constitutive model framework for numerical simulation environments.

Calibration trials showed strong model significance for SAOR and UCF. Rolling friction coefficient and JKR surface energy models achieved exceptional significance for SAOR. Tangential stiffness, critical normal/tangential forces, and bonding disk radii significantly affected UCF. Regression solutions provided contact parameters matching measurements, achieving validation errors ≤ 3.27% for SAOR and ≤1.46% for UCF across different moisture levels.

Field verification tests of calibration results demonstrated a 5.05% relative error between simulated soil channel resistance and measured values under actual field conditions. This discrepancy primarily stems from moisture content variations between simulated and natural soils, as calibration procedures established point-to-point correlations for specific moisture levels and UCF values without comprehensively investigating their interactive mechanisms. The current research scope excluded soil sampling from diverse peanut cultivation regions across Xinjiang. Subsequent research will implement extensive sampling from characteristic peanut-growing areas throughout the province to establish a soil physical property database accounting for Xinjiang’s diverse climatic impacts.