Loading Model and Mechanical Properties of Mature Broccoli (Brassica oleracea L. Var. Italica Plenck) Stems at Harvest

Abstract

Stem cutting is the main process of broccoli harvesting, and the structure and mechanical properties of the stem significantly affect the cutting efficiency. In the current research, the structural characteristics and component contents of the broccoli stem are analyzed. Through different processing methods of stretching, compressing and bending, the aim is to obtain the parameters for mechanical properties of broccoli stem, and to provide basic data and reference for establishing visual models of broccoli stem. The test results show: The content of rind is highest in the middle of the stem, the content of xylem is highest in the bottom of the stem, and the content of pith is highest in the top of the stem. The densities of rind, xylem and pith of broccoli stem were 1056.1, 938.9 and 1009.9 kg·m⁻³, respectively. The elastic modulus of the rind of broccoli stem was 27.2~47.5 MPa, the elastic modulus of the xylem was 19.2~110.7 MPa, and the elastic modulus of the pith was 6.5~7.5 MPa. The compressive elastic modulus of the stem was 1.3~2 MPa. The bending strength of the broccoli stem was 6.9 MPa, and the bending modulus was 3.1 MPa. The mechanical model of broccoli stem established in this study provides a theoretical basis for cutting and other processes.

1. Introduction

Broccoli is an important economic vegetable grown all over the world and belongs to the cruciferous family [1]. According to the statistics of the Food and Agriculture Organization of the United Nations in 2018, the planting area of broccoli is about 1.4 trillion hectares in the world, and China has the largest cauliflower production (10 million tons) [2]. According to the statistics of China’s ministry of agriculture, China’s cauliflower cultivation area exceeded 70,000 hectares in 2017 [3,4]. Broccoli is rich in nutrition and low in calories, and has anti-cancer properties, and the effects of promoting weight loss and preventing cardiovascular and cerebrovascular diseases [5,6,7]. Broccoli is a food of very high food value, and broccoli cultivation is rapidly increasing due to the recognition of the presence of high-value health-protecting compounds in it [8]. Both broccoli stems and curds (broccoli florets) have high moisture content (90.6% and 86.1%, respectively) [9]. Currently, broccoli leaves and stems are discarded because only the florets (heads) and adjacent stems are utilized [10]. However, other parts of cauliflower such as leaves and stems, as well as broccoli that are discarded as too small, could also be used. More than 75% of broccoli plant parts are left in the field, most of which are edible [11].

Two approaches have been presented regarding the management and use of broccoli stems: the traditional method is for feeding animals, making fertilizers and incineration; the new method is to provide active compounds for developing food products and health products [12]. Currently, broccoli stems are used as feed for cattle in the form of flour [13]. Broccoli stems can be used as materials for the food industry due to their rich nutritional content. Adding crop residues to animal feed can reduce waste in the food industry and conserve natural resources for animal feed production [14]. As the global green economy continues to develop, more agricultural wastes will be generated in the future, and they will be continuously exploited to meet future energy demands [15].

Broccoli stem is a composite material, and the main chemical components are cellulose, hemicellulose, and lignin [16]. The “hollow stem” of broccoli refers to the existence of a cavity in the stem of broccoli, and the shape of the cavity inside the stem is related to the release of mechanical strain [17]. The main reason for the fracture of straw rope is the shear fracture and tensile fracture of the stem fiber, and the shear strength and tensile strength are the main factors affecting the fracture of rice straw [18]. After threshing, the microstructure of rice straw was destroyed, and the main connections between rice leaves were destroyed [19]. The fracture of rice stalks during threshing includes bending and tensile fracture of the internodes of the stalks, fracture of the stem core under compression and tension, and damage to the stalk nodes due to bending or compression [20]. Du et al. [21] counted the differences in physical properties and chemical components in different tea stem nodes. Previous studies have shown that sturdy stems can significantly reduce crop lodging [22,23]. Therefore, studying stem strength may provide new insights into stem lodging resistance. Zhou et al. [24] used simulations to calculate the anisotropic elastic properties of rice stalks. The mechanical properties of stems are related to diameter, internode distance, density and water content [25,26,27]. The maturity stage and moisture content of plant tissues strongly influence their elastic properties [28,29]. Du et al. [30] analyzed and evaluated the influence of physical parameters (stem diameter, internode distance, fresh weight, dry weight, volume, fresh density, dry density) and chemical components (cellulose, hemicellulose, lignin) on the mechanical properties of oil peony stems. Thiru et al. [31] investigated the static and dynamic mechanical properties of composites of palmyra palm leaf stalk fibers (PPLSF) using scanning electron microscopy. Due to the difference in the form and direction of the load, the structural deformation and mechanical properties of the stem vary accordingly [32]. Al-Zube et al. [33] obtained the elastic modulus of maize husks through multiple loading modes. In order to develop and optimize reed production equipment, Tian et al. [34] completed the reed stalks compression, tension, and bending tests using a testing machine. Baley et al. [35] studied the influence mechanism of flax physical parameters on the mechanical properties of fibers and their composites through mechanical property experiments.

The simulation calculation method based on the real parameters of the research object has the advantages of being accurate, efficient, reliable and repeatable [36,37]. Zhang et al. [38] studied the displacement, stress and shear stress of cassava stems during compressive fracture through finite element analysis (FEA) software ANSYS. Wang et al. [39] measured the mechanical parameters of citrus stalks, and established a discrete element model of citrus stalks using the discrete element method (DEM) to simulate the bending and shearing processes of citrus stalks. Stubbs et al. [40] investigated the Young’s modulus of maize husk and pith tissue through a finite element model and determined the effectiveness of the method. Zhang et al. [41] studied the effects of moisture content and internode location on the tensile strength and Young’s modulus of corn pith, and established a discrete element model (DEM) to simulate the tensile test process. Sadrmanesh et al. [42] simulated the stretching process of plant fibers through PFC 3D software and determined the key parameters of the model through physical experiments. Guo et al. [43] established a discrete element model of banana stalks and corrected the key parameters of the model according to the experimental results. The bending process leads to highly nonlinear and plastic deformation behavior, and linear elastic DEM models can realistically describe the reversible bending of stems at small deformations, but they cannot adequately describe the bending behaviors of stems at large deformations [44]. The type and parameters of the stem model significantly affect the accuracy of the simulation results.

With the rapid development of modern computer technology, the method used in research on biomechanical characteristics of plant stems has gradually changed from the traditional experimental method to the simulation method. Combining physical test and computer simulation technology, the micro-mechanical properties and failure mechanism of plant stems can be deeply analyzed and studied, and then the macro-mechanical properties of plant stems can be discussed. Related research on broccoli stem as biomass energy source has been reported, but there is a lack of research on the mechanical properties of broccoli stem. In this paper, the biomechanical properties of broccoli stem were analyzed and studied by combining simulation and physical experiments, the parameters and symbols in the modeling and physical experiments are shown in Table 1. A mechanical model of broccoli stem was established to characterize the structural characteristics, mechanical properties and failure morphology of the stem. At the same time, the differences in the structure and mechanical properties of different positions of the stem were analyzed. The mechanical property parameters and models of stems are of great significance for mechanized harvesting and stem processing of broccoli.

Table 1. The parameters and symbols in the modeling and physical experiments.

Symbol	Parameter	Symbol	Parameter
L	Sample length, mm	σc	Maximum shear stress, MPa
W	Sample width, mm	Mmax	Maximum bending moment, N·m
T	Sample thickness, mm	σmax	Bending strength (MPa)
ρ	Density, kg·m−3	d	Diameter of the broccoli, mm
E	Elastic modulus, Pa	d1	Thickness of rind, mm
μ	Poisson’s ratio	d2	Thickness of xylem, mm
K	Bulk modulus, Pa	d3	Diameter of the pith, mm
G	Shear modulus, Pa	Δl	Maximum stretch deformation, m
Rm	Maximum tensile stress, Pa	ymax	Maximum bending deformation, m

2. Materials and Methods

2.1. Material Content of Broccoli Stems

The broccoli variety in this study was Yanxiu, which was planted in Yancheng City, Jiangsu Province, China. In order to avoid sample differences affecting the experimental results, broccoli plants with the same morphology and maturity were selected for the experiment. The growth state and plant composition of broccoli in the field were shown in Figure 1. The broccoli plant grows upright, and the floret grows on the top of the stem. The floret and leaves are blue-green, and the stems are light green.

Figure 1. Structure and characteristics of broccoli plants: (a) broccoli florets; (b) leaves; (c) lateral branch; (d) broccoli plant; and (e) stem.

As shown in Figure 2, the leaves, lateral branches and roots of the whole broccoli were removed, and 10 measuring points (or measuring positions) were selected at equal intervals on the stem. The diameter of each measuring point was measured 3 times by MNT-150T electronic vernier caliper (MNT, Germany), and the average value was taken as the diameter d of each measuring point. The cross section of each measuring point of the broccoli stem was cut as shown in Figure 3. The thickness of rind and xylem of each measuring point were measured three times through the electronic vernier caliper, and the average value was taken as the thickness of rind d₁ and thickness of xylem d₂. The diameter of the pith d₃ is calculated by Equation (1):

$$d_3=d-2d_1-2d_2$$

(1)

where d₃ is the diameter of the pith, mm; d is the diameter of the stem, mm; d₁ is the thickness of rind, mm; and d₂ is the thickness of xylem, mm.

Figure 2. Measuring position of stem composition: (a) measuring position 1; (b) measuring position 2; and (j) measuring position 10.

Figure 3. Transverse cross-section of a broccoli stem: (a) rind; (b) xylem; and (c) pith.

Based on the measured values, the area of the cross-section of the rind, xylem and pith at each measuring point was calculated. The ratio between the area of the material and the cross section indicates the content of the material.

2.2. Density of Material of Broccoli Stems

Broccoli stems were separated into rind, xylem and pith as shown in Figure 4. The test equipment includes a measuring cylinder and an electronic scale (RADWAG, Poland), as shown in Figure 5.

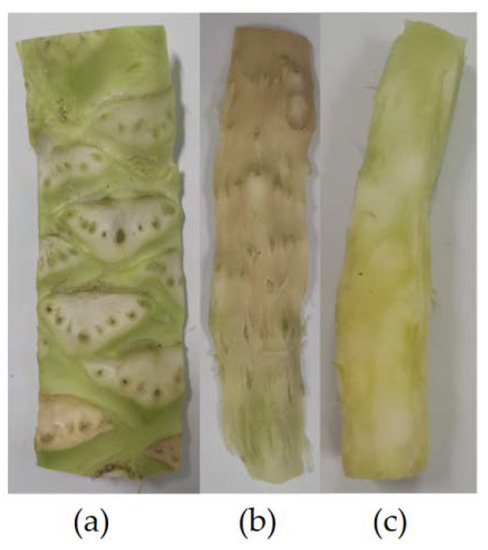
Figure 4. Stem samples for density measurement: (a) rind; (b) xylem; and (c) pith.

Figure 5. The experiment of measuring the density of broccoli stems: (a) measuring cylinder; and (b) electronic scale.

The mass m_i (i = 1, 2, 3…) of each rind, xylem and pith sample was measured sequentially using an electronic scale. The liquid level in the graduated cylinder is v_1i, the sample is completely immersed in water, and the liquid level is recorded as v_2i. The experiment was repeated 15 times, the volume and mass of rind, xylem, and pith were recorded, and the density ρ of each sample was calculated by Equation (2):

$$\rho =\frac{m_i}{v_{2i}-v_{1i}}$$

(2)

where m_i is the mass of the sample, g; v_1i is volume of water in measuring cylinder, cm³; v_2i is volume of water and sample in graduated cylinder, cm³.

2.3. Modeling of Virtual Samples of Broccoli Stem

2.3.1. Axial Tensile Modeling of Stem

In the SolidWorks software, the three-dimensional model of the tensile test sample was established, as shown in Figure 6. The model was imported into the static structure of the workbench. Material properties were assigned, and then the model was meshed with a mesh element size of 1 mm, and the result is shown in Figure 7.

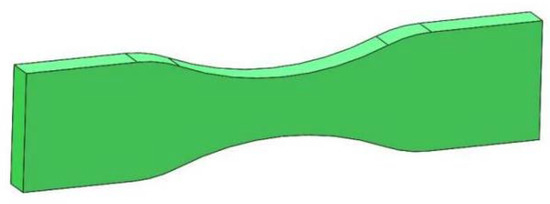
Figure 6. Geometric model of broccoli stem for tensile experiment.

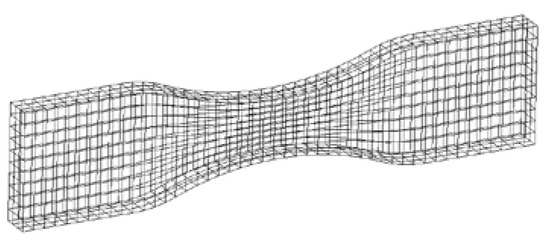
Figure 7. Model meshing results in workbench software.

Constraints and loads were applied to the model according to the procedures of physical experiments. The left plane of the model is fixed, the right plane is applied with horizontal displacement, and the model can move freely in other directions. The simulation process of broccoli stem stretching is basically consistent with the physical experiment. The main parameters of the axial tensile model are shown in Table 2.

Table 2. Parameters of broccoli stem model for virtual tensile experiment.

Parameter	Symbol	Value
		Rind	Xylem	Pith
Sample length (mm)	L	90	90	90
Sample width (mm)	W	7	7	7
Sample thickness (mm)	T	3.57	2.17	7
Density (kg/m3)	ρ	1056.1	938.9	1009.9
Elastic modulus (Pa)	E	2.68 × 107	1.288 × 108	7.5 × 106
Poisson’s ratio	μ	0.3	0.43	0.3
Bulk modulus (Pa)	K	2.231 × 107	1.0733 × 108	6.2703 × 106
Shear modulus (Pa)	G	1.0297 × 107	4.9539 × 107	2.894 × 106
Maximum tensile stress (Pa)	Rm	1.8314 × 106	1.911 × 106	3.23 × 105
Maximum shear stress (Pa)	σc	7.141 × 105	2.2581 × 106	2.8086 × 105

In Table 1, bulk modulus and shear modulus are automatically solved by the workbench software. Previous studies showed that the effect of Poisson’s ratio was negligible. Therefore, Poisson’s ratio was set to 0.3 [37,38]. Other parameters were generated based on a large number of experiments.

2.3.2. Modeling of Radial Compression of Stem

In order to simplify the model, the broccoli stem was simplified as a cylinder with smooth surface. Before the radial compression simulation, the main parameters of the radial compression model were determined through a large number of experiments, calculations and calibrations, as shown in Table 3.

Table 3. Parameters of broccoli stem model for compression experiment.

Parameter	Symbol	Value
Sample length (mm)	L	25
Sample diameter (mm)	W	40
Density (kg/m3)	ρ	1022.4
Elastic modulus (Pa)	E	1.6 × 106
Poisson’s ratio	μ	0.3
Bulk modulus (Pa)	K	1.3672 × 106
Shear modulus (Pa)	G	6.31 × 105
Maximum tensile stress (Pa)	Rm	4.075 × 105
Maximum shear stress (Pa)	σc	2.8086 × 105

The radial compression model of the broccoli stem is shown in Figure 8. The material properties of the broccoli stem material library are given to the stem model, and the material of the fixed platform and the upper indenter is structural steel. The contact type is geometric interaction, and the model mesh element size is 1 mm. The fixed platform is fixedly constrained, and the upper indenter is displaced downward.

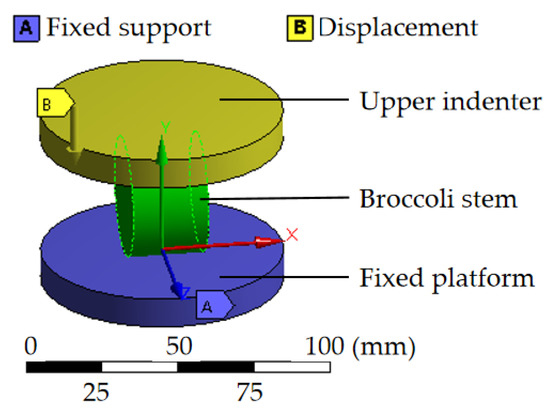
Figure 8. Schematic diagram of radial compression model of broccoli stem.

2.3.3. Modeling of Stem Bending

The three-point bending model of the broccoli stem is shown in Figure 9. The stem was placed between the indenter and the two support points. Each part was assigned the corresponding material properties, and the contact type was set to geometry interaction. The mesh size of the model was adjusted to 2 mm. The fixed platform is fixedly constrained, and the upper indenter is displaced downward. Through a large number of experiments and calculations, the main parameters of the stem model in the three-point bending simulation were determined as shown in Table 4.

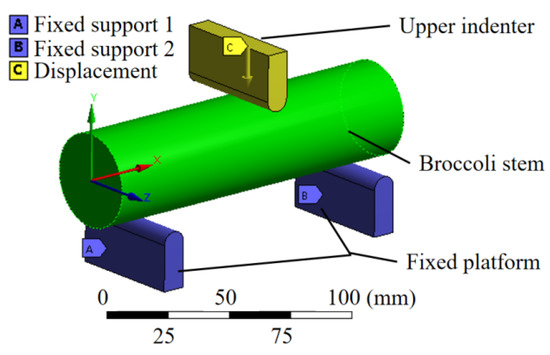
Figure 9. Schematic diagram of bending of broccoli stem.

Table 4. Parameters of broccoli stem model for bending experiment.

Parameter	Symbol	Value
Sample length (mm)	L	150
Sample diameter (mm)	W	40
Density (kg/m3)	ρ	1022.4
Elastic modulus (Pa)	E	3.6 × 106
Poisson’s ratio	μ	0.3
Bulk modulus (Pa)	K	2.9682 × 106
Shear modulus (Pa)	G	1.3699 × 106
Maximum tensile stress (Pa)	Rm	4.075 × 105
Maximum shear stress (Pa)	σc	7.055 × 105

2.4. Sample Preparation and Experiment of Broccoli Stem

2.4.1. Axial Tensile Experiment of Broccoli Stem

Samples for tensile experiments of rind, xylem and pith were prepared using the middle stem of broccoli, as shown in Figure 10. The length of the sample is 90 mm, the length of the stretch zone is 50 mm, and the width of the middle section is 7 mm. There are differences in the thickness of the prepared samples, and the thickness of the samples is measured and recorded during the experiment.

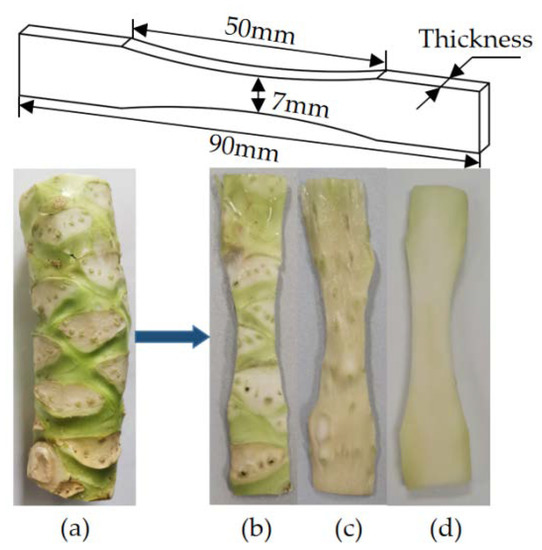
Figure 10. Tensile samples of broccoli stem: (a) stem; (b) rind; (c) xylem; and (d) pith.

As shown in Figure 11, the tensile test of broccoli stems was carried out on a texture tester TA-XTplus (Stable Mycro System, United Kingdom). The bottom of the sample was fixed through the clamp and the top of the sample was mounted on the cantilever of the texture tester. The load and displacement data points (with sampling time interval of 0.005 s) were collected by the test system in real time. The experiment was terminated when the sample broke and the load dropped rapidly.

Figure 11. Tensile test of broccoli stem.

The tensile strength σ of broccoli stem samples was calculated by Equation (3):

$$\sigma =\frac{F}{A}$$

(3)

where F is the maximum tensile force, N; and A is the cross sectional area of broccoli stem at tensile plane, m².

The normal strain ε of the test sample was calculated by Equation (4):

$$\epsilon =\frac{∆l}{l}$$

(4)

where l is the length of the tensile area of the sample, with l equal to 0.05 m in this test; and Δl is the deformation of the sample in the elastic deformation state, m.

The tensile elastic modulus E of the stem sample was calculated by Equation (5).

$$E=\frac{\sigma }{\epsilon }$$

(5)

2.4.2. Radial Compression Experiments on Broccoli Stem

The stem was divided into 6 segments at equal intervals, and each segment was a measuring point. The length of the compression test sample was 25 mm. Three stems of similar shape and size were used in repeated compression experiments for a total of 18 experiments. The compression experiment of broccoli stems is shown in Figure 12.

Figure 12. Radial compression experiment of broccoli stem: (a) upper indenter; (b) broccoli stem; and (c) fixed platform.

The compressive strength σ_max of broccoli stems are calculated by Equation (6) [41]:

$${\sigma }_{max}=\frac{F_{max}}{lD}$$

(6)

where F_max is the maximum compressive force, N; l is the length of the sample, m; and D is the diameter of the sample, m.

2.4.3. Bending Experiments of Broccoli Stem

Four samples with a length of 15 ± 1 cm, all of which were straight and without mechanical damage, were selected for bending experiments. The bending experiment of the broccoli stem is shown in Figure 13. The distance between the two fixed supports was 10.2 cm, and the pressure of the upper indenter acted on the middle of the stem. The bending strength σ_max and elastic modulus E of the broccoli stem were calculated by Equations (7) and (8), respectively:

$${\sigma }_{max}=\frac{M_{max}}{W_z}$$

(7)

$$E=\frac{F{l}^3}{48I_z{y}_{max}}$$

(8)

with

$$W_z=\frac{\pi d^3}{32}$$

(9)

$$I_z=\frac{\pi d^4}{64}$$

(10)

where M_max is the maximum bending moment, N·m; W_z is the bending section factor, m³; F is the bending force at failure, N; l is the distance between the fixed supports, m; I_z is the moment of inertia, m⁴; y_max is the maximum deflection, m; and d is the diameter of the stem, m.

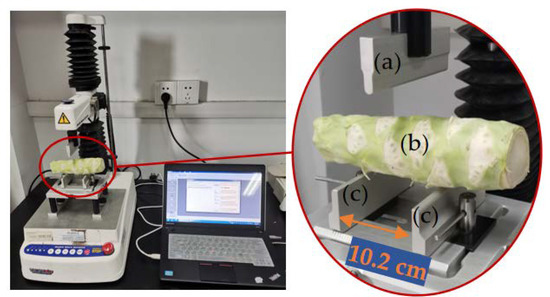
Figure 13. Three-point bending experiment of broccoli stem: (a) upper indenter; (b) broccoli stem; and (c) fixed support.

3. Results and Discussion

3.1. Structure and Content of Broccoli Stem

The radial dimensions and contents of broccoli stems are shown in Table 5, and the contents of epidermis, xylem and pith at different measurement points were calculated through the radial dimensions. The content of rind is most in the middle of the stem by rind thickness was greater in the middle of the stem. The content of xylem is most in the bottom of the stem by xylem thickness was greater in the bottom of the stem. The content of pith is most in the top of the stem by pith thickness was greater in the top of the stem.

Table 5. Axial distribution of the content of broccoli stems.

Measuring Position	Diameter of Stem d (mm)	Rind		Xylem		Pith
		Thickness d1 (mm)	Ratio Area (%)	Thickness d2 (mm)	Ratio Area (%)	Diameter d3 (mm)	Ratio Area (%)
1	30.78	2.09	25.32	3.32	32.63	19.96	42.05
2	34.03	2.45	26.62	2.64	24.17	23.87	49.20
3	37.33	2.30	23.13	2.31	20.17	28.11	56.70
4	39.11	2.96	28.03	2.07	16.84	29.04	55.13
5	41.01	4.03	35.41	2.40	17.44	28.16	47.15
6	42.07	3.70	32.12	2.04	15.04	30.58	52.84
7	41.98	3.59	31.24	2.15	15.94	30.51	52.82
8	40.82	2.98	27.11	2.10	16.51	30.65	56.38
9	36.99	2.39	24.22	1.54	13.80	29.12	61.97
10	35.96	2.49	25.73	1.54	14.03	27.91	60.24

The distribution of broccoli component content is shown in Figure 14. From the bottom to the top of the broccoli stem, the diameter of the stem, the thickness of the rind and the diameter of the pith first increased and then decreased, and the thickness of the xylem continued to decrease. The maximum diameter of the stem is 42.07 mm at measuring point 6, the maximum thickness of the rind is 4.03 mm at measuring point 5, the maximum thickness of the xylem is 3.32 mm at measuring point 1, and the maximum diameter of the pith is 30.65 mm at measuring point 8.

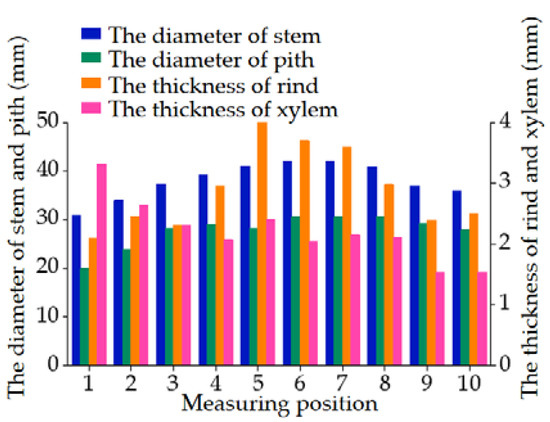
Figure 14. The distribution characteristics of broccoli stem size.

According to the measurement results of stem size and material content, the relationship between measuring points and the contents of rind, xylem and pith is shown in Figure 15. The polynomial equations for the content of rind, xylem and pith obtained by further fitting are Equations (11)–(13):

$$y_1=-93.762+263.345x-211.006x^2+82.053x^3-17.19x^4+1.991x^5-0.12x^6+0.003x^7$$

(11)

$$y_2=45.735-16.156x+3.291x^2-0.293x^3+0.009x^4$$

(12)

$$y_3=167.496-293.659x+249.036x^2-99.882x^3+21.488x^4-2.555x^5+0.158x^6-0.004x^7$$

(13)

where y₁ is the content of rind; y₂ is the content of xylem; y₃ is the content of pith; and x is the measuring point.

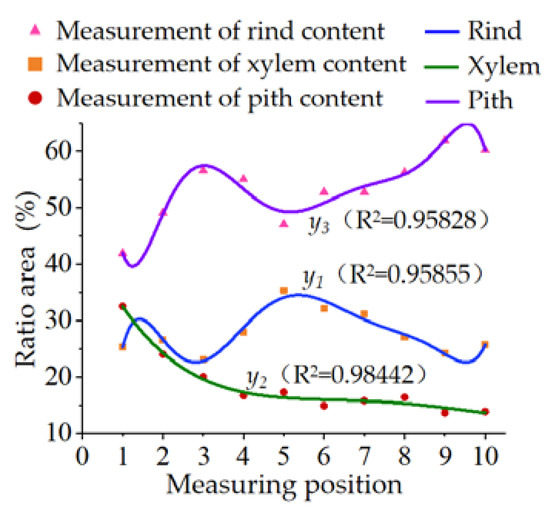
Figure 15. Relationship between the content—of epidermis, xylem and pith—and radial position.

3.2. Experimental Results of Density of Broccoli Stems

The volume, mass and density of the rind, xylem and pith samples of broccoli stems are shown in Table 6. The density of rind is 1056.1 kg·m⁻³, the density of xylem is 938.9 kg·m⁻³, and the density of pith is 1009.9 kg·m⁻³.

Table 6. Density of rind, xylem and pith of broccoli stem.

Material	Sample	Volume (cm3)	Quality (g)	Density (g·cm−3)	The Average Density (kg·m−3)
Rind	1	8	7.85	0.9813	1056.1
	2	6	6.88	1.1467
	3	5	5.65	1.1300
	4	7	7.26	1.0371
	5	7.5	7.39	0.9853
Xylem	1	11	9.98	0.9073	938.9
	2	12.5	10.72	0.8576
	3	10	10.18	1.0180
	4	9.5	8.95	0.9421
	5	11.5	11.15	0.9696
Pith	1	17.5	18.19	1.0394	1009.9
	2	14	14.44	1.0314
	3	24	23	0.9583
	4	18.5	18.93	1.0232
	5	20	19.94	0.9970

3.3. Results of Virtual Experiment with Broccoli Stem

3.3.1. Virtual Experiments for Axial Tension

The results of the simulation of stem tissue stretching are shown in Figure 16, and the equivalent stress is concentrated in the middle of the sample during stretching. At the time of tensile fracture of broccoli stem samples, the maximum equivalent stress of the rind is 1.4 MPa, the maximum equivalent stress of the xylem is 1.9 MPa, and the maximum equivalent stress of the pith is 0.3 MPa. The morphology of tensile fracture of rind, xylem and pith is shown in Figure 17. The fractured areas are all in the middle of the stem tissue samples, and the fractured cross-sections are irregular.

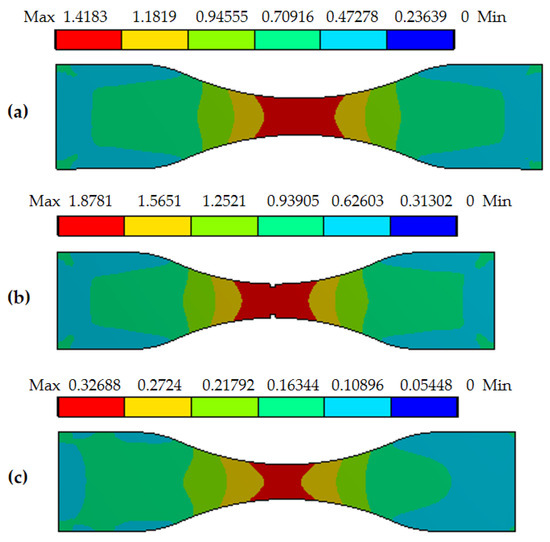
Figure 16. The stem model and its equivalent stress after tensile failure: (a) rind; (b) xylem; and (c) pith.

Figure 17. Characteristics of different materials after tensile fracture: (a) rind; (b) xylem; and (c) pith.

The tensile strength–displacement characteristic curve of the sample model in the tensile simulation is shown in Figure 18. The results show that the virtual stretching process can be divided into elastic stage and fracture failure stage, indicating that the broccoli stem model has the tensile properties of elastoplastic materials in the simulation process. The tensile displacements at fracture of the rind, xylem and pith models are 2.5 mm, 0.7 mm and 2.2 mm. It can be seen from the figure that the maximum tensile strengths of rind, xylem and pith are 1.4 MPa, 1.7 MPa and 0.3 MPa, respectively.

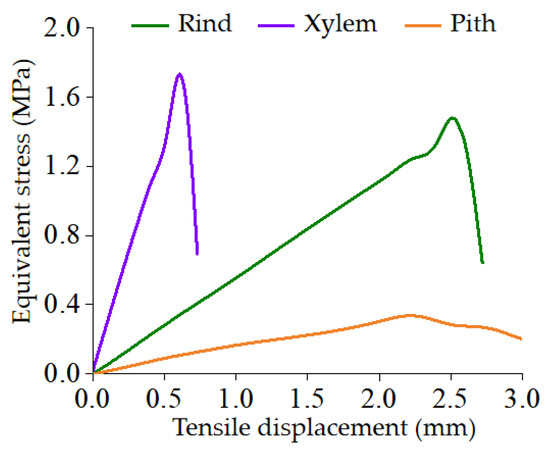
Figure 18. The tensile strength–displacement characteristic curve of model in tensile experiment.

3.3.2. Virtual Experiments for Radial Compression

The simulation process of radial compression of broccoli stem is shown in Figure 19. The morphology and equivalent stress of the stem model were recorded when the radial compression displacement was 6.5 mm, 13 mm and 19.5 mm. The total deformation of the stem increases with the compression displacement, and the damage to the stem structure becomes gradually more serious. The area of the stem in contact with the indenter and the fixed support becomes severely damaged.

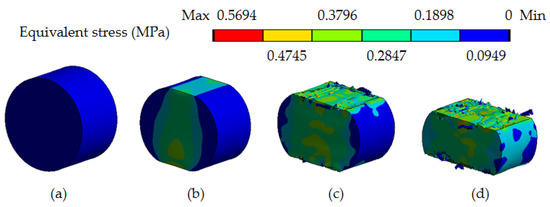
Figure 19. Equivalent stress of stem model in compression, with compression displacement of: (a) 0 mm; (b) 6.5 mm; (c) 13 mm; and (d) 19.5 mm.

The equivalent stress and compressive strength of broccoli stems are shown in Figure 20. The equivalent stress and compressive strength increased linearly at the initial stage, which indicates that the stem is elastically deformed. When part of the stem tissue is damaged, the equivalent stress no longer increases and fluctuates slightly. The maximum equivalent stress of radial compression of broccoli stem is 0.56 MPa, and the maximum compressive strength is 0.59 MPa.

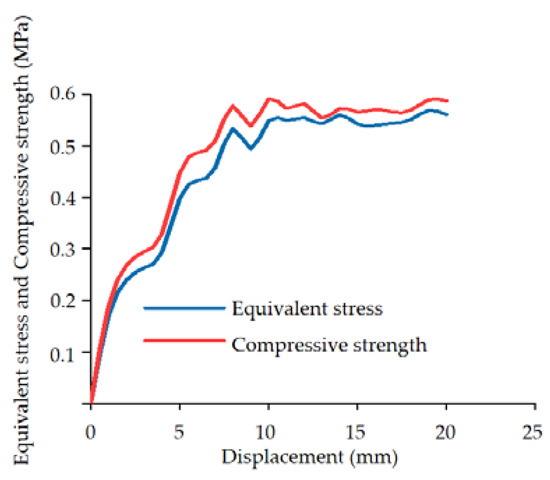
Figure 20. Equivalent stress and compressive strength characteristic curves of radial compression simulation process of broccoli stem.

3.3.3. Virtual Experiments for Bending

The equivalent stress and bending strength of the three-point bending of the broccoli stem model are shown in Figure 21. At the time of stem fracture, the maximum equivalent stress is 1.3 MPa, and the maximum bending strength is 1.4 MPa. The stem appears damaged in the area of contact with the indenter and the fixed support, and the fractured section is almost flat.

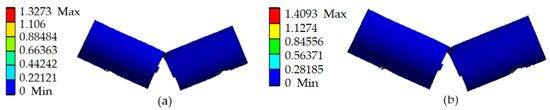
Figure 21. The broccoli stem model after bending failure: (a) equivalent stress of bending; and (b) bending strength.

The equivalent stress and bending strength curves are shown in Figure 22, and the trends of equivalent stress and flexural strength are consistent. The process of stem bending can be divided into three stages. In the initial stage of bending, the stem is elastically deformed, and the equivalent stress and bending strength increase linearly. With the increase of the displacement of the indenter, the deformation of the broccoli stem gradually increased. The fluctuation of equivalent stress and bending strength was due to yield failure of some stem tissues. When the displacement is about 22 mm, the broccoli stem bending displays fracture failure, and the equivalent stress and bending strength drop sharply. The maximum bending equivalent stress is 1.27 MPa, and the bending strength is 1.3 MPa.

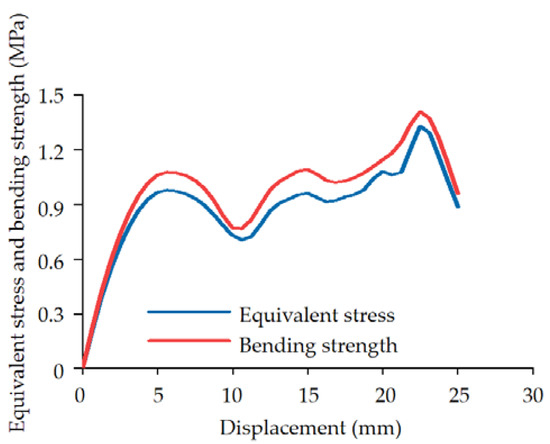
Figure 22. Equivalent stress and bending strength characteristic curves of bending simulation process of broccoli stem.

3.4. Results of Physical Experiment on Broccoli Stem

3.4.1. Physical Experiment of Axial Tension

Fracture-failed rind, xylem and pith samples are shown in Figure 23. The fractured area is in the middle of the sample, the cross section of the rind is flat, and the cross section of the xylem and pith samples are irregular.

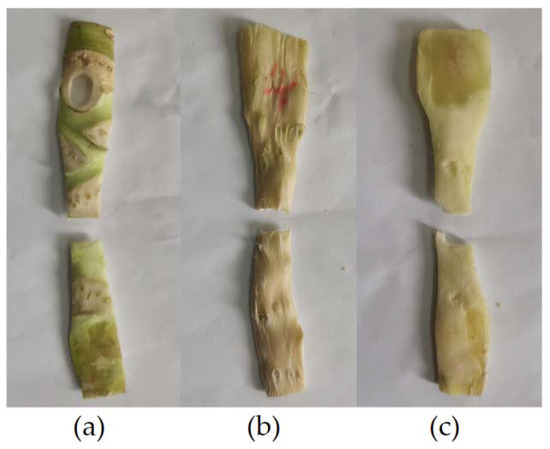
Figure 23. The broccoli stem with stretching failure: (a) rind; (b) xylem; and (c) pith.

The tensile force–displacement curve of the rind sample is shown in Figure 24, and the trend of all curves is to increase to a peak and then decline sharply. At the initial stage of the tensile test, the tensile force increases linearly with the displacement, which indicates that the rind is elastically deformed by the tensile force. When the tensile force exceeds its limit value, the rind sample is broken. The peak value of the tension force of the middle rind is the smallest, and the peak of the tension force of the top rind is the largest.

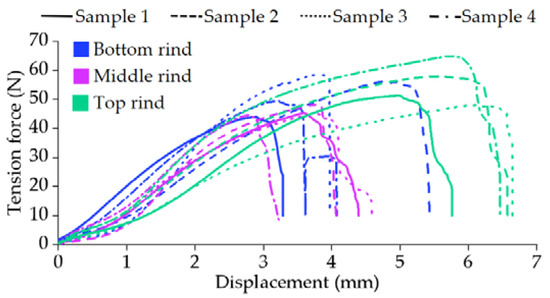
Figure 24. The force–displacement characteristic curves of rind in tensile physical experiment.

The tensile force–displacement curves of the xylem samples are shown in Figure 25. The xylem stretching process is divided into elastic stage, yield stage and fracture failure stage according to the characteristics of the curve. The tensile force increases linearly with the displacement in the initial stage, which indicates that the xylem elastically deforms through the action of the tensile force. The tensile force fluctuates slightly with the increasing displacement. During the yield stage, the slight fluctuation in tensile force was due to the fracture of part of the vascular bundle inside the xylem, which was caused by the increase in sample deformation. The peak value of the tensile force of the top xylem is significantly smaller than that of the bottom and middle xylem.

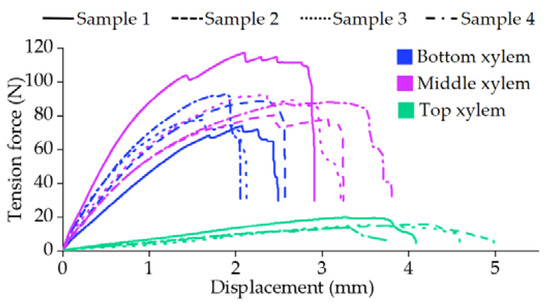
Figure 25. The force–displacement characteristic curves of xylem in tensile physical experiment.

The tension–displacement curve of the pith is shown in Figure 26. The stretching process of the pith is divided into elastic stage, linear elastic stage and fracture failure stage. The tensile force increased significantly at the initial stage of the experiment, indicating that the pith was elastically deformed. As the displacement continuously increased, the increasing trend of the tension force became slower. When the tensile force exceeds the ultimate tension force, the sample is broken. There is no significant difference in the peak tension force of the bottom, middle and top pith.

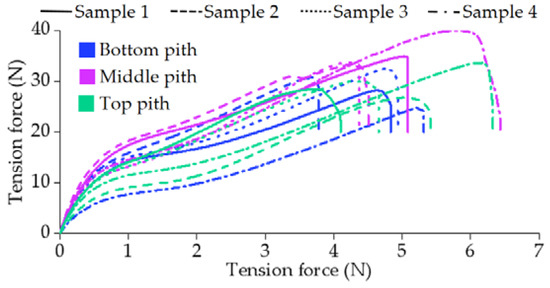
Figure 26. The force–displacement characteristic curves of pith in tensile physical experiment.

The results of the broccoli stem tissue tensile experiments are shown in Table 7. According to the tensile force–displacement curve, the maximum tensile force and deformation of each sample were obtained, and the tensile strength and elastic modulus were calculated. The tensile strengths of the bottom, middle and top rind are 3.3, 1.8 and 3 MPa, respectively, and the elastic moduli are 45.5, 26.8 and 27.2 MPa, respectively. The tensile strengths of the bottom, middle and top xylem are 4.3, 6.2 and 1.4 MPa, respectively, and the elastic moduli are 110.7, 128.8 and 19.2 MPa, respectively. The tensile strengths of the bottom, middle and top of the pith are 0.6, 0.7 and 0.6 MPa, respectively, and the elastic moduli are 6.7, 7.5 and 6.5 MPa, respectively.

Table 7. Tensile test results of broccoli stem.

Material	Position	Sample	Maximum Tension force F (N)	Deformation Δl (×10−3m)	Tensile Strength σ (MPa)		Elastic Modulus E (MPa)
					Value	Mean	Value	Mean
Rind	Bottom	1	49.51	3.195	3.1	3.3	48.5	45.5
		2	44.04	2.883	2.8		47.9
		3	56.14	4.730	3.5		37.2
		4	58.47	3.772	3.7		48.6
	Middle	1	45.30	3.588	1.8	1.8	25.3	26.8
		2	48.07	3.768	1.9		25.5
		3	45.09	3.741	1.8		24.1
		4	44.61	2.773	1.8		32.2
	Top	1	51.32	4.966	2.8	3.0	28.2	27.2
		2	57.94	5.594	3.2		28.2
		3	48.07	6.123	2.6		21.4
		4	65.05	5.744	3.5		30.9
Xylem	Bottom	1	73.97	2.074	3.8	4.3	92.4	110.7
		2	88.50	2.314	4.6		99.1
		3	77.82	1.642	4.0		122.8
		4	92.77	1.867	4.8		128.7
	Middle	1	117.18	2.095	7.7	6.2	184.5	128.8
		2	80.65	2.466	5.3		107.9
		3	92.73	2.364	6.1		129.4
		4	87.96	3.103	5.8		93.5
	Top	1	20.04	3.262	1.7	1.4	25.4	19.2
		2	16.12	4.222	1.3		15.8
		3	15.62	3.522	1.3		18.3
		4	13.77	3.264	1.1		17.4
Pith	Bottom	1	28.23	4.623	0.6	0.6	6.2	6.7
		2	30.79	3.657	0.6		8.6
		3	32.56	4.786	0.7		6.9
		4	24.99	5.265	0.5		4.8
	Middle	1	34.90	5.034	0.7	0.7	7.1	7.5
		2	33.40	4.330	0.7		7.9
		3	33.75	4.231	0.7		8.1
		4	39.96	5.815	0.8		7.0
	Top	1	28.43	3.669	0.6	0.6	7.9	6.5
		2	26.81	5.041	0.5		5.4
		3	30.04	4.311	0.6		7.1
		4	33.69	6.112	0.7		5.6

3.4.2. Physical Experiment of Radial Compression

The shape of broccoli stem compression failure is shown in Figure 27. As the displacement of the indenter increased, the stem surface in contact with the upper indenter and the fixed platform was destroyed. Cracks appeared in the pith tissue, which were caused by the lateral expansion of the stem tissue due to vertical pressure. When the pressure peaked again, the damage to the stem tissue was more severe, and the shape of the damaged area was irregular. Structural damage caused by compression was primarily in the pith. Other parts of the stem were damaged to varying degrees, especially in the areas where the pith was in contact with the xylem.

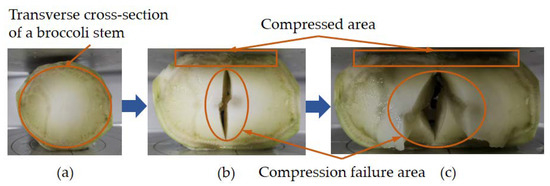
Figure 27. The broccoli stem with compression failure: (a) before compression; (b) as the crack appears; and (c) when severely damaged.

The results of the broccoli stem compression experiment are shown in Figure 28. Overall, the pressure of the sample gradually decreased from measuring point 1 to measuring point 6, indicating that the stem at the bottom resisted greater radial pressure. The pressure range of stem cracking is 243.372~553.522 N, and the pressure range of severe fracture is 370.385~552.728 N. The compression force increased approximately linearly before the first peak, when the stem was elastically deformed. The reason for the sharp drop in the pressure curve is that the pressure exceeds the bond strength between the stem tissues, causing the stem to crack. When the stem tissue is damaged again, the pressure curve reaches a second peak and drops off sharply. The compression force of cracks and serious damage in the stem at measuring point 6 is lower than that at the other measuring points. Therefore, the top stem is easily broken under radial compression. The displacement when the stem is split is 7.388 mm at measuring point 6, and the displacement of the top stem when it is split is the smallest at radial compression. The displacement of stem cracking is the largest at measuring point 2, while the displacement interval between stem cracking and severe damage is the smallest at measuring point 2. The displacement interval of the stem when cracked and severely damaged at measuring point 3 is larger than that at the other measuring points.

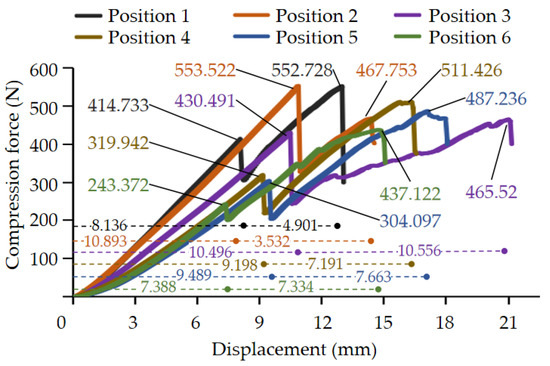
Figure 28. Compression force and displacement characteristic curves of radial compression experiment process on broccoli stem.

The maximum compressive force, deformation, and sample size of the stem were recorded in the compression experiments, and the compressive strength and elastic modulus of the broccoli stem were solved. The results of the compression experiment are shown in Table 8. The compressive force when the stem breaks is 243.372~553.522 N, and the strain is 0.21~0.28. The compressive strength at measuring point 2 is the largest, and the compressive strength at measuring point 6 is the smallest. The maximum and minimum elastic moduli are 2.0 MPa and 1.3 MPa, respectively.

Table 8. Experimental results of radial compression of broccoli stem.

Measuring Position	Maximum Compression Force (N)	Deformation (mm)	Diameter (mm)	Strain	Compressive Strength (MPa)	Elastic Modulus of Compression (MPa)
1	414.733	8.136	30.78	0.26	0.5	2.0
2	553.522	10.893	38.99	0.28	0.6	2.0
3	430.491	10.496	42.26	0.25	0.4	1.6
4	319.942	9.198	42.57	0.22	0.3	1.4
5	304.097	9.489	38.67	0.25	0.3	1.3
6	243.372	7.388	35.92	0.21	0.3	1.3

There were differences in compressive strength and elastic modulus at different positions of the stem, which were due to differences in stem size and component content. In order to explore the difference in compressive strength and elastic modulus at different measuring points, the polynomial equations for compressive strength and elastic modulus were further fitted. As shown in Figure 29, the R² of the quartic polynomial of elastic modulus is 0.9998, and the R² of the quartic polynomial of compressive strength is 0.9981, indicating that both fits are significant. The compressive elastic modulus and compressive strength decrease gradually from the bottom to the top of the stem.

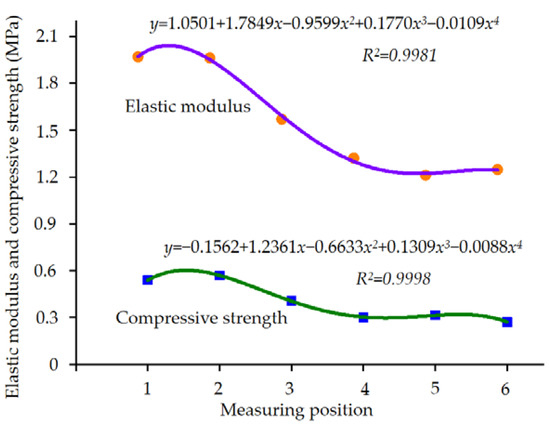
Figure 29. Elastic modulus and compressive strength characteristic curves of radial compression experiment process of broccoli stem.

3.4.3. Physical Experiment of Bending

In the process of stem bending, the upper half of the stem was compressed longitudinally, while the lower half of the stem was stretched laterally, so the cross-section of the stem changed from a circle to an ellipse. Both compression and tension have components directed towards the center of the stem, so the stem is able to resist bending moments [45]. The characteristics of broccoli stem bending fracture failure are shown in Figure 30. The area where the stem broke was located below the action of the indenter, and the shape of the fracture surface was irregular. Damaged areas of the rind were in contact with the fixed support and the upper indenter.

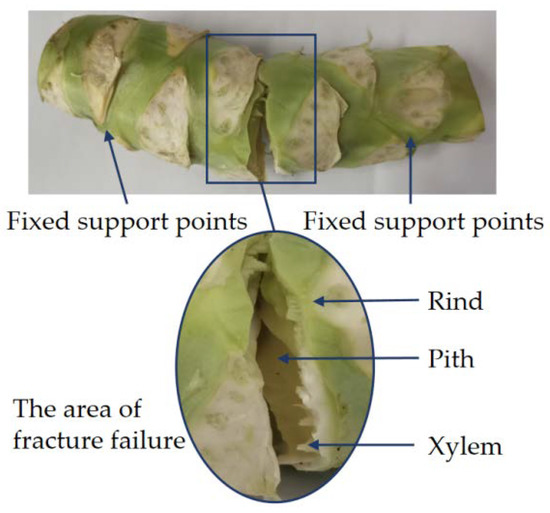
Figure 30. The broccoli stem with bending failure.

The force–displacement characteristic curve of the broccoli stem bending experiment is shown in Figure 31. The bending process is divided into elastic stage and yield fracture stage. In the stage of elastic deformation of the stem, the value of the pressure increases linearly with the increase in displacement. A sharp drop in pressure results in the broccoli stems breaking. This means that the pressure exceeds the adhesive strength of the vascular bundles of the stem tissue. The pressure peaks for the four samples were 500.22 N, 449.588 N, 401.441 N and 549.894 N. Differences in the diameter and structure of the stem samples resulted in differences in load peaks. The rind and xylem are not broken in the area in contact with the indenter, so the pressure is not zero and remains constant at the end of the curve.

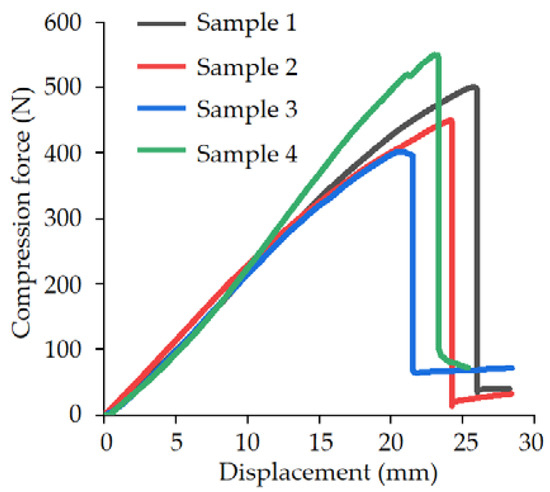
Figure 31. The compression force–displacement characteristic curves of broccoli stem in bending experiment.

In order to obtain the bending characteristics of broccoli stems, the bending strength and bending elastic modulus were calculated according to the compression force–displacement characteristic curve, and the results are shown in Table 9.

Table 9. Experimental results of bending of broccoli stem.

	Maximum Bending Force F (N)	Maximum Deflection ymax (m)	Maximum Bending Moment Mmax (N·m)	Bending Strength σmax (MPa)	Elastic Modulus of Bending E (MPa)
Sample 1	500.220	25.8	51.0	6.8	2.7
Sample 2	449.588	24.2	45.9	6.1	2.6
Sample 3	401.441	20.6	40.9	6.7	3.6
Sample 4	549.894	23.1	56.1	7.9	3.6
Mean	475.3	23.4	48.5	6.9	3.1
Standard deviation	60.0	2.2	6.5	0.7	0.5

According to the bending experiment of broccoli stem, the average value of the maximum bending force is 475.3 N, and the standard deviation of the maximum bending force is 60.0 N. The average diameter of the stem fracture area is 41.5 mm and the average maximum deflection is 23.4 mm. The average value of the maximum bending moment is 48.5 N·m, and the standard deviation of the maximum bending moment is 6.5 N·m. The average bending strength is 6.9 MPa. The average bending modulus is 3.1 MPa.

3.5. Proofreading Model

The study of stem models is inevitably affected by the accuracy of parameters and the performance of computer operations. Therefore, the improvement of model parameters will improve the accuracy of simulation results. In order to verify whether the model parameters can accurately reflect the mechanical properties of broccoli stalks, the results of virtual experiments and physical experiments were compared. The parameters of the model are consistent with the parameters of the middle of the stem, so the simulation results are compared with the mechanical properties of the middle of the stem. The results are shown in Table 10. According to the standard deviation of stem strength and displacement, the results of the virtual experiment and the physical experiment were similar. However, the virtual experiments of xylem stretching and stem bending are quite different from physical experiments. The displacement of the stalk failure in the virtual experiment is close to the physical experiment.

Table 10. Comparison of broccoli stalk strength between virtual and physical experiments.

Load	Parameter	Virtual Experiments		Physical Experiment	Standard Deviation
Axial tension	Tensile strength (MPa)	Rind	1.4	1.8	0.28
		Xylem	1.7	6.2	3.18
		Pith	1.3	0.7	0.42
	Displacement (mm)	Rind	2.5	3.5	0.71
		Xylem	0.7	2.5	1.27
		Pith	2.2	4.8	1.84
Radial compression	Compressive strength (MPa)		0.59	0.4	0.13
	Displacement (mm)		7.8	10.5	1.91
Bending	Bending strength (MPa)		1.3	6.9	3.96
	Displacement (mm)		22.5	23.4	0.64

4. Conclusions

The diameter of the middle of the stem is larger than of the bottom and top of the stem. The content of rind is highest in the middle of the stem and rind thickness is greater in the middle of the stem. The content of xylem is highest in the bottom of the stem and xylem thickness was greater in the bottom of the stem. The content of pith is highest in the top of the stem and pith thickness is greater in the top of the stem. The rind content of the bottom, middle and top are 25.32%, 35.41% and 24.22%, respectively. The xylem content of broccoli stem decreases from 32.63% to 13.80% from bottom to top of the stem. The pith content of the stem increases from 42.05% to 61.97% from the bottom to the top. The densities of rind, xylem and pith of broccoli stem are 1056.1, 938.9 and 1009.9 kg·m⁻³, respectively.

The mechanical properties of broccoli stems were tested and the differences in mechanical properties of different positions of broccoli stems were investigated. The elastic modulus of the rind of the bottom stem is the largest, at 45.5 MPa, and the tensile strength of the rind of the middle stem is the smallest. The elastic modulus of the xylem of the middle stem is the largest, at 128.8 MPa, and the tensile strength of the top xylem of the stem is the smallest. The elastic modulus of the pith of the middle stem is the largest, at 7.5 MPa, and the tensile strength of the pith of the bottom stem is the smallest. The compressive strength of the bottom stem is the greatest, and the compressive strength of the top stem is the least. The maximum pressure of stem compression failure is 553.5 N, and the range of stem compression elastic modulus is 1.3~2 MPa. The bending strength of the broccoli stem is 6.9 MPa, and the bending modulus is 3.1 MPa.

In this study, the damage and failure process of broccoli stem was demonstrated and analyzed, and the application of finite element simulation technology in stem mechanics research was verified. The established mechanical model of broccoli stalk can fully characterize the failure state of broccoli, and this result is consistent with physical experiments. The characteristics of deformation and failure of broccoli stem were discussed by combining finite element simulation technology and physical experiments. These results provide the basis for mechanized harvesting, post-harvest dicing and stem crushing of broccoli.