Convective and Microwave Assisted Drying of Wet Porous Materials with Prolate Spheroidal Shape: A Finite-Volume Approach
Abstract
1. Introduction
2. Methodology
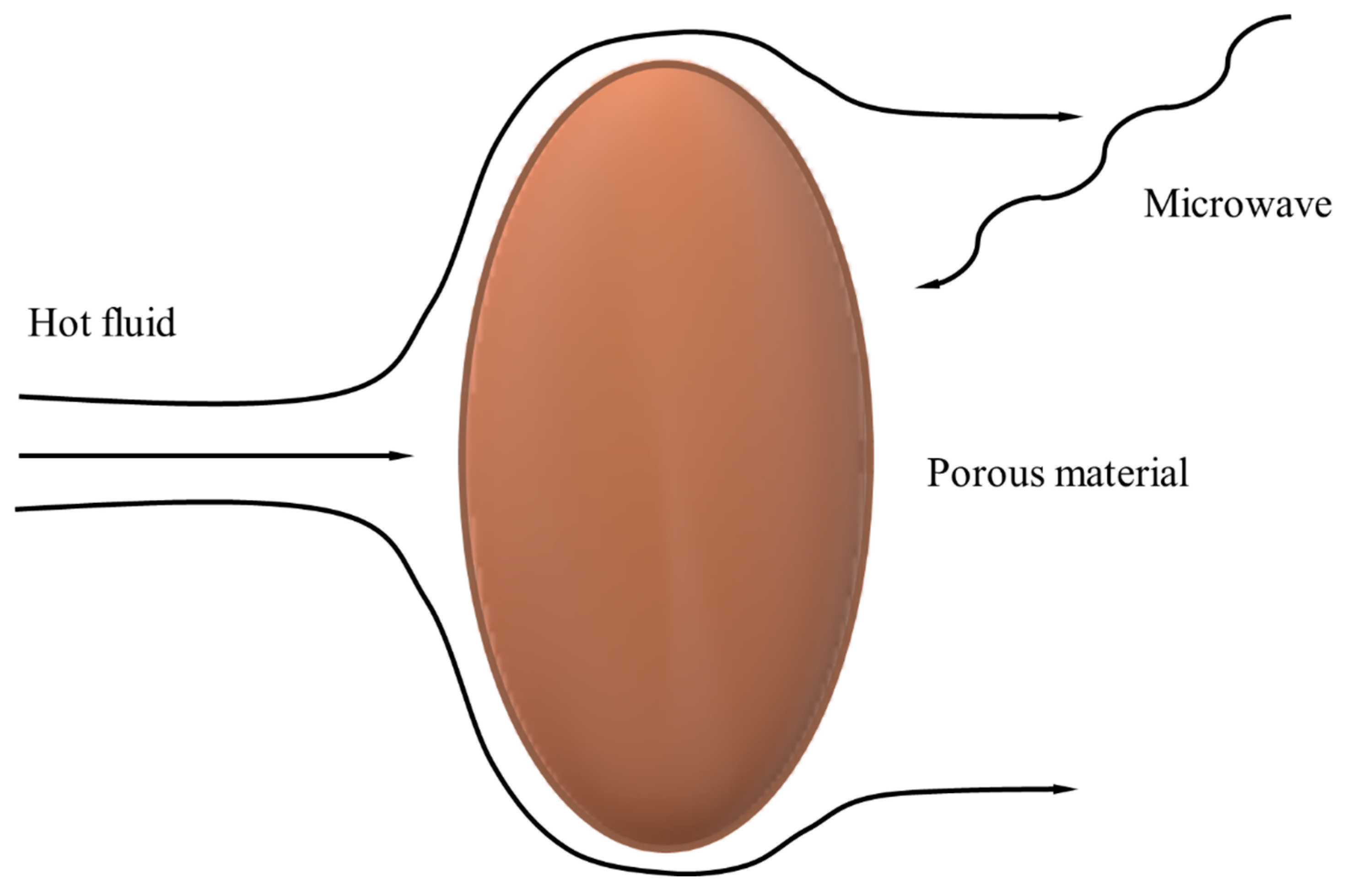
2.1. The Geometry and Physical Problem
2.2. Mathematical Modeling
- (a)
- The porous body is assumed to be isotropic;
- (b)
- The mass transport occurred only by diffusion inside the body and convection at the surface;
- (c)
- The heat transfer occurred only by conduction and volumetric heating inside the solid, and convection at the surface;
- (d)
- Thermo-physical properties are considered to be constant;
- (e)
- Dimension variations were neglected.
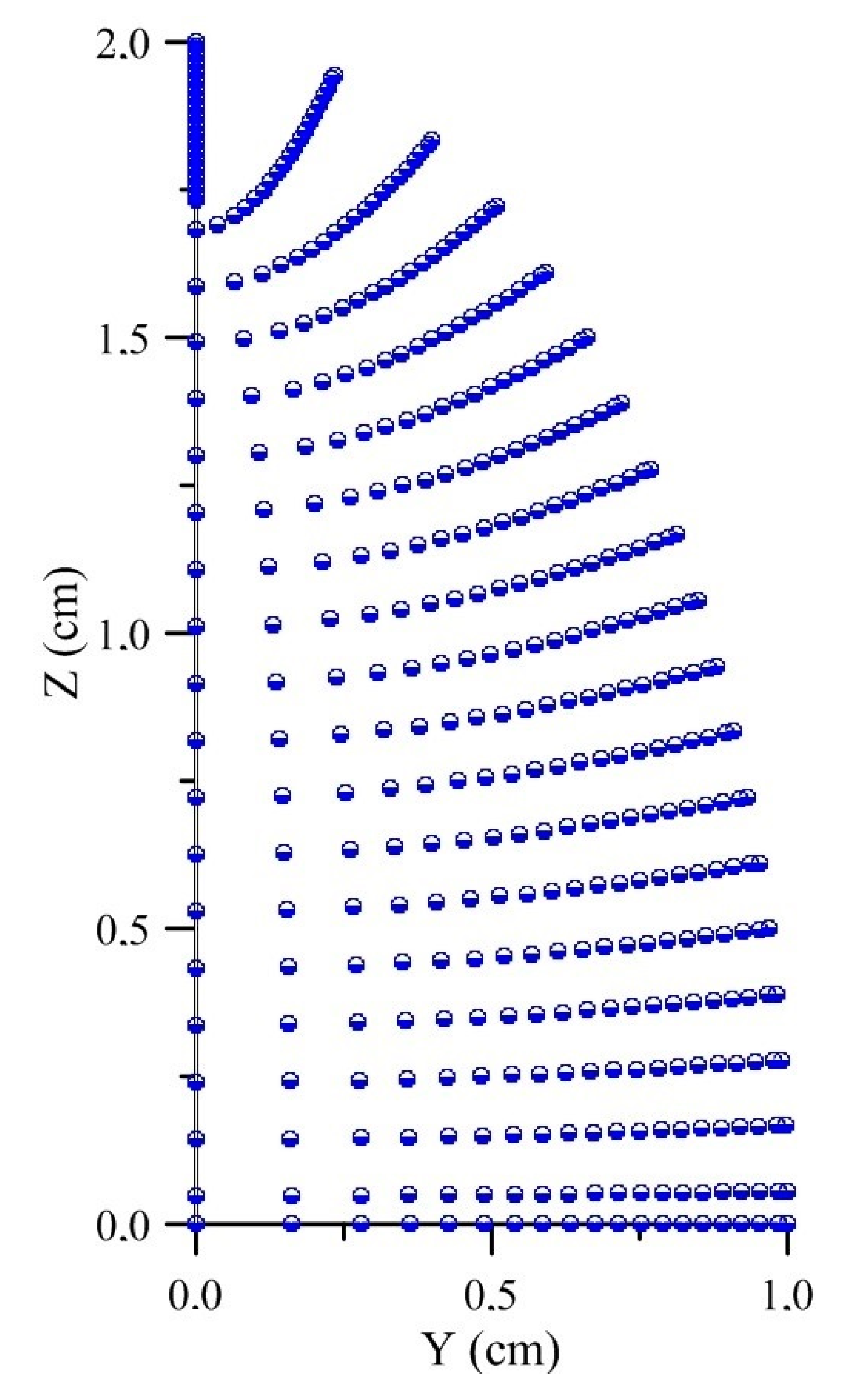
2.3. Numerical Solution
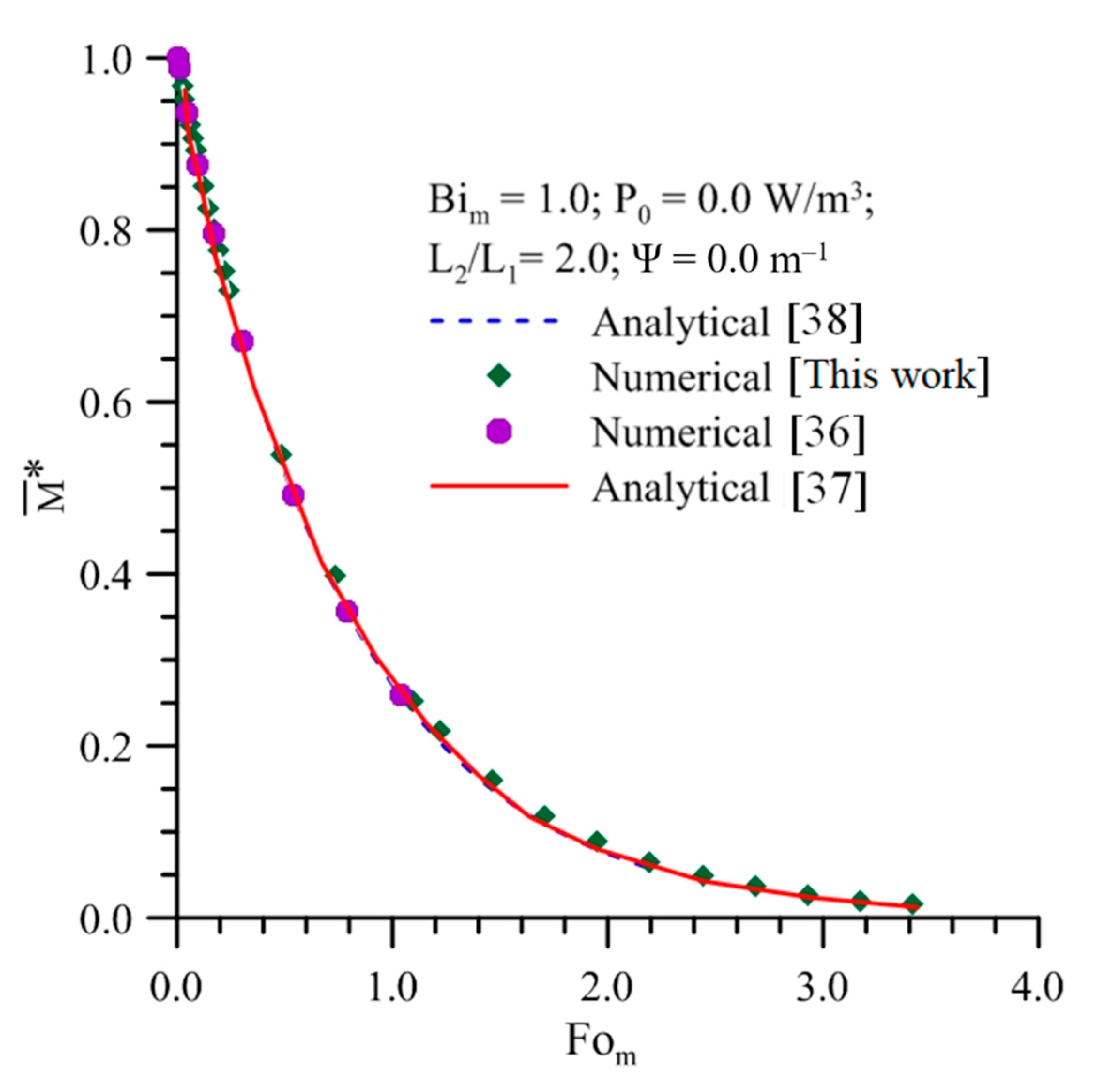
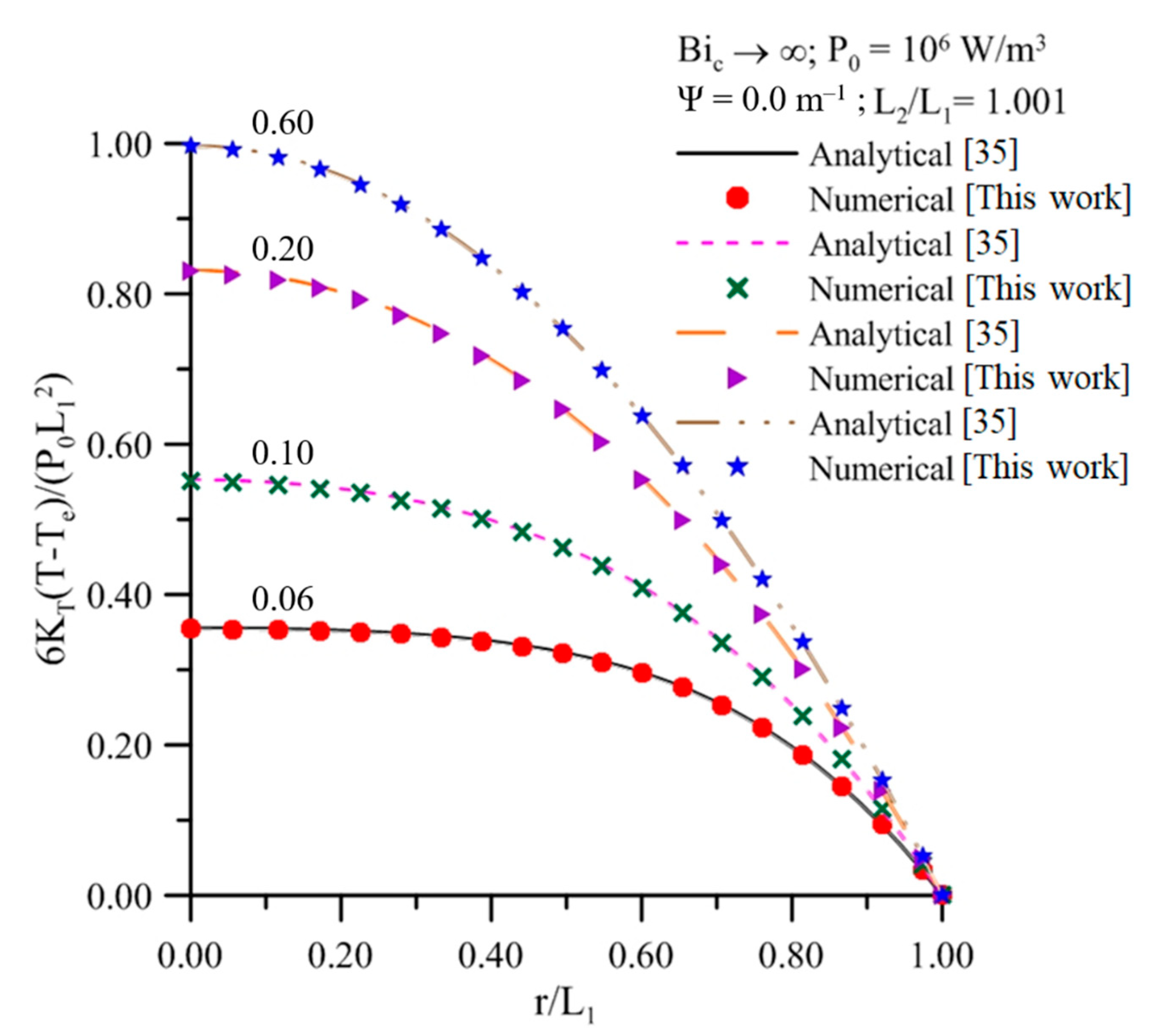
2.4. Validation
- (a)
- Mass transfer process in a prolate spheroidal body , without heat transfer and convective condition at the surface.
- (b)
- Heating process of a spherical body with a constant volumetric heat source, without mass transfer and equilibrium condition at the surface.
2.5. Simulated Cases
3. Results
4. Conclusions
- (a)
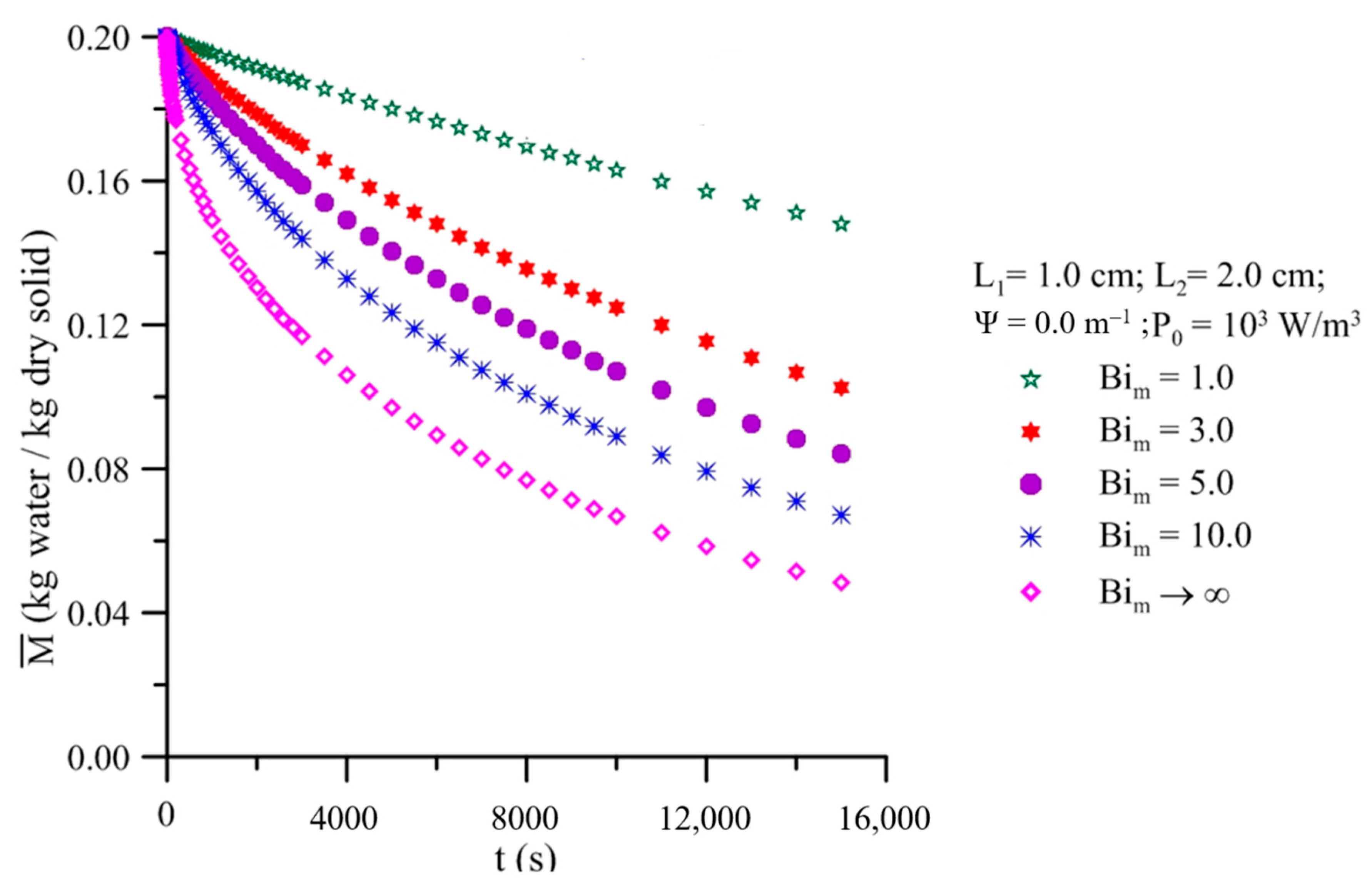
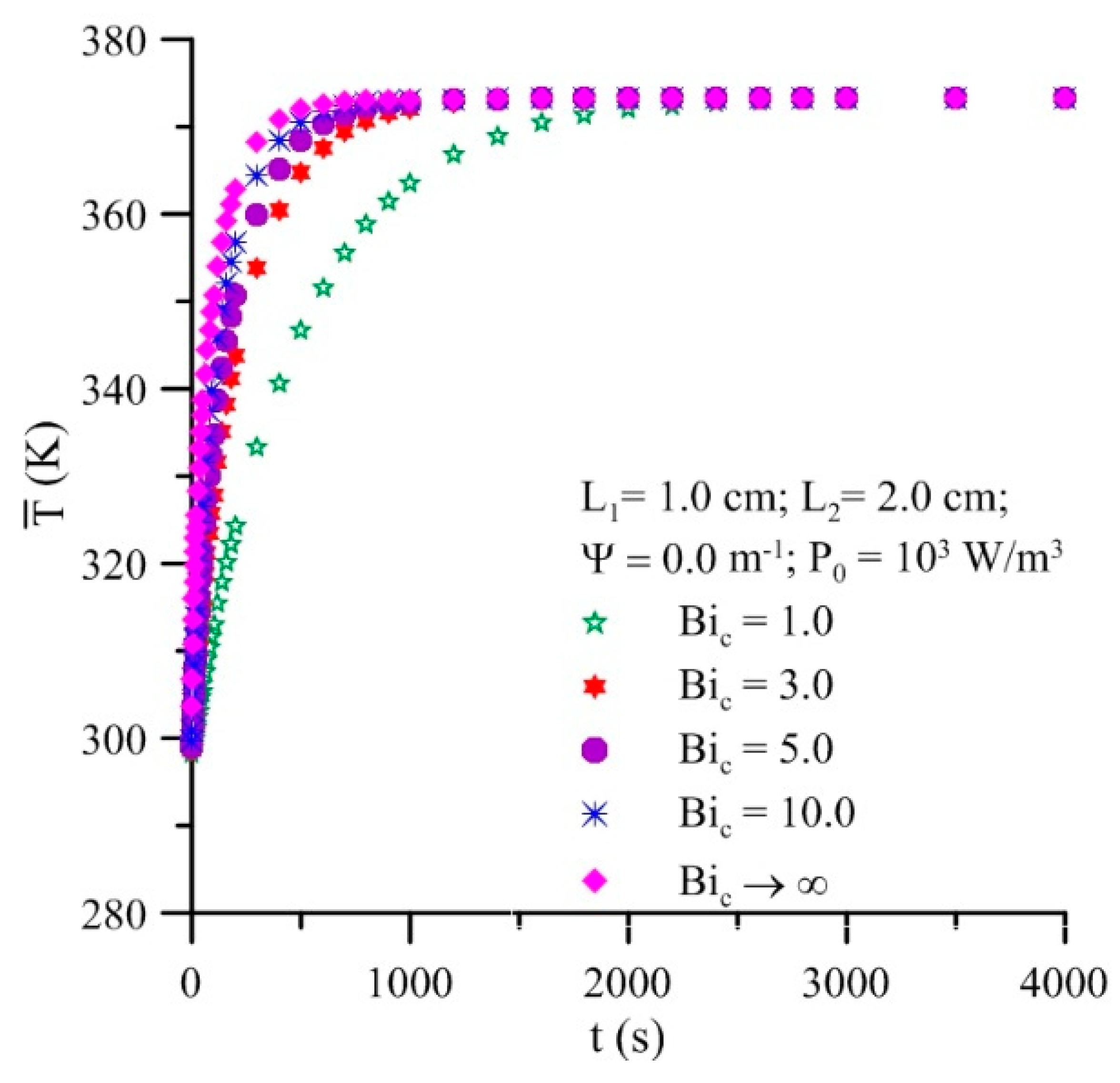
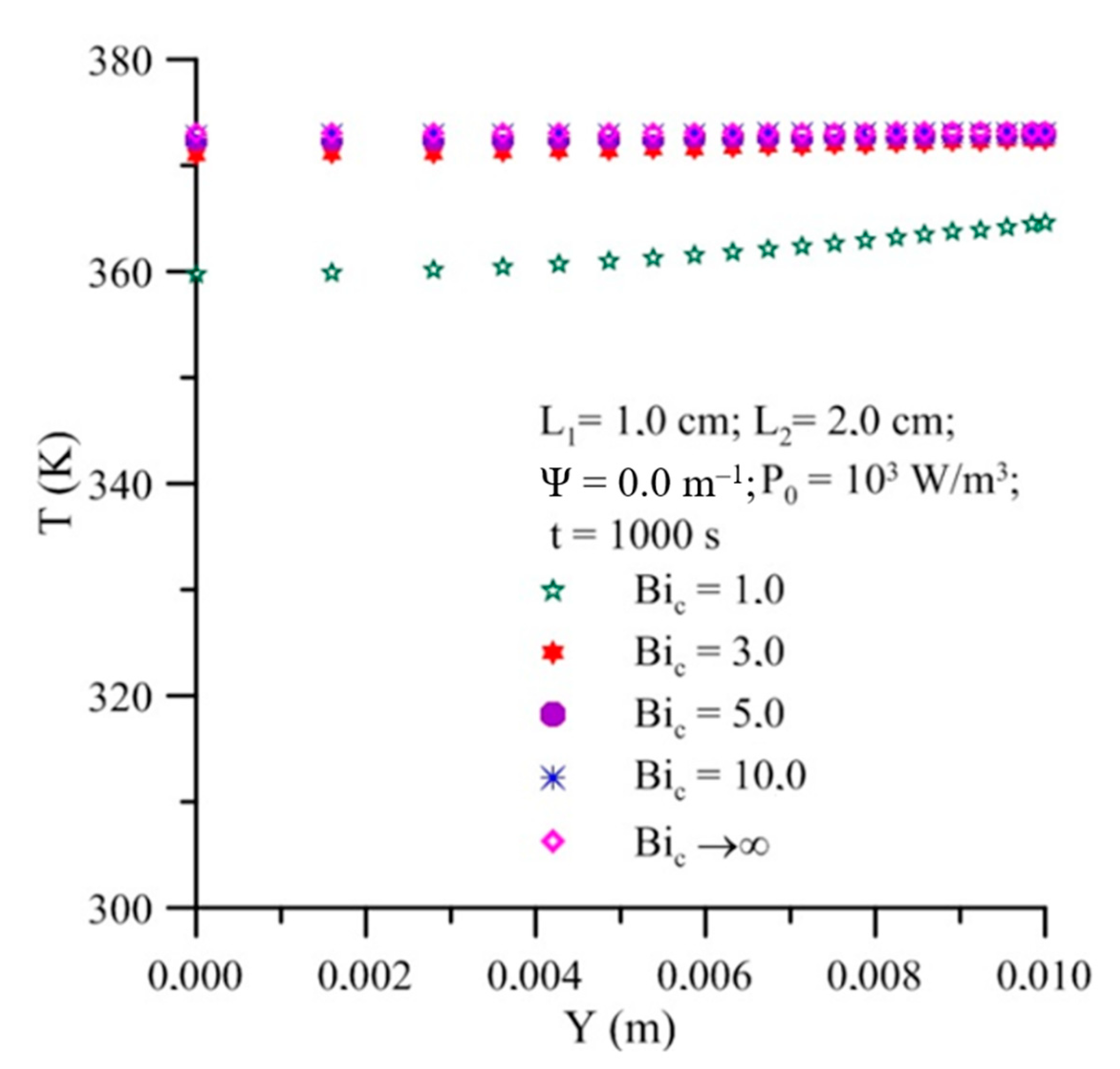
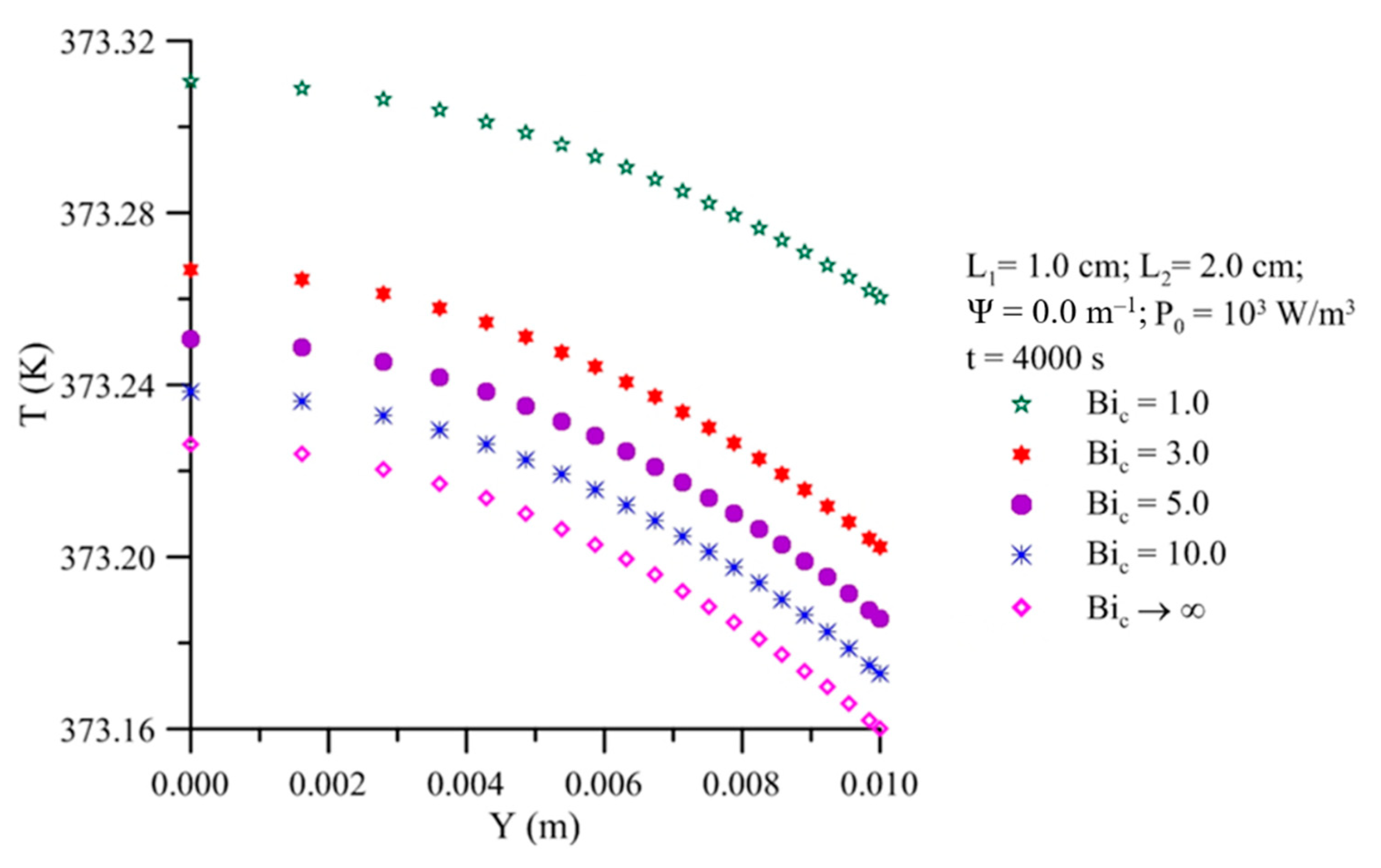
- For a fixed microwave power density, a drying process with a higher Biot number for heat and mass transfer will result in the solid drying and heating up faster. The effect is more evident in moisture ratio than in average temperature;
- (b)
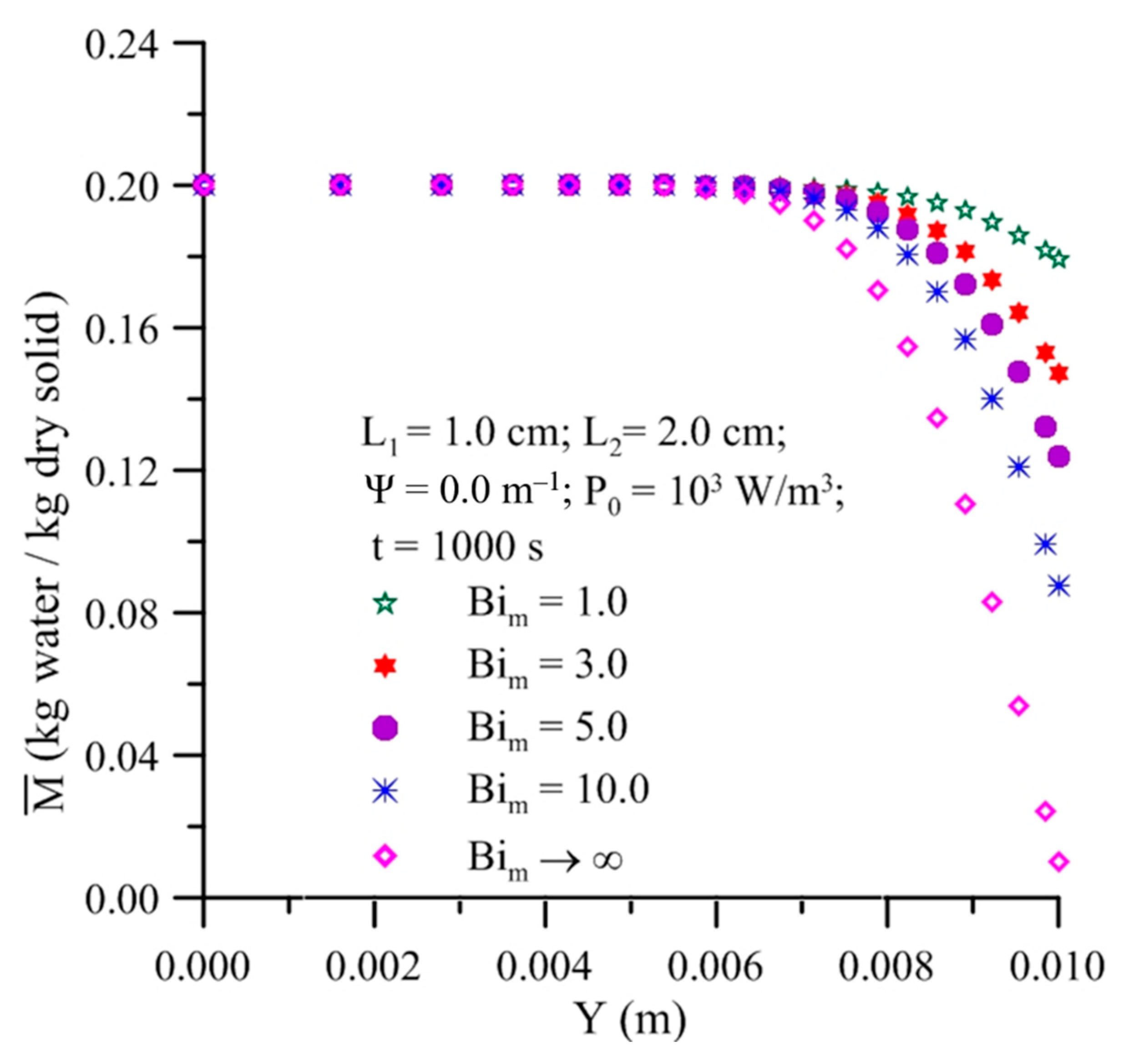
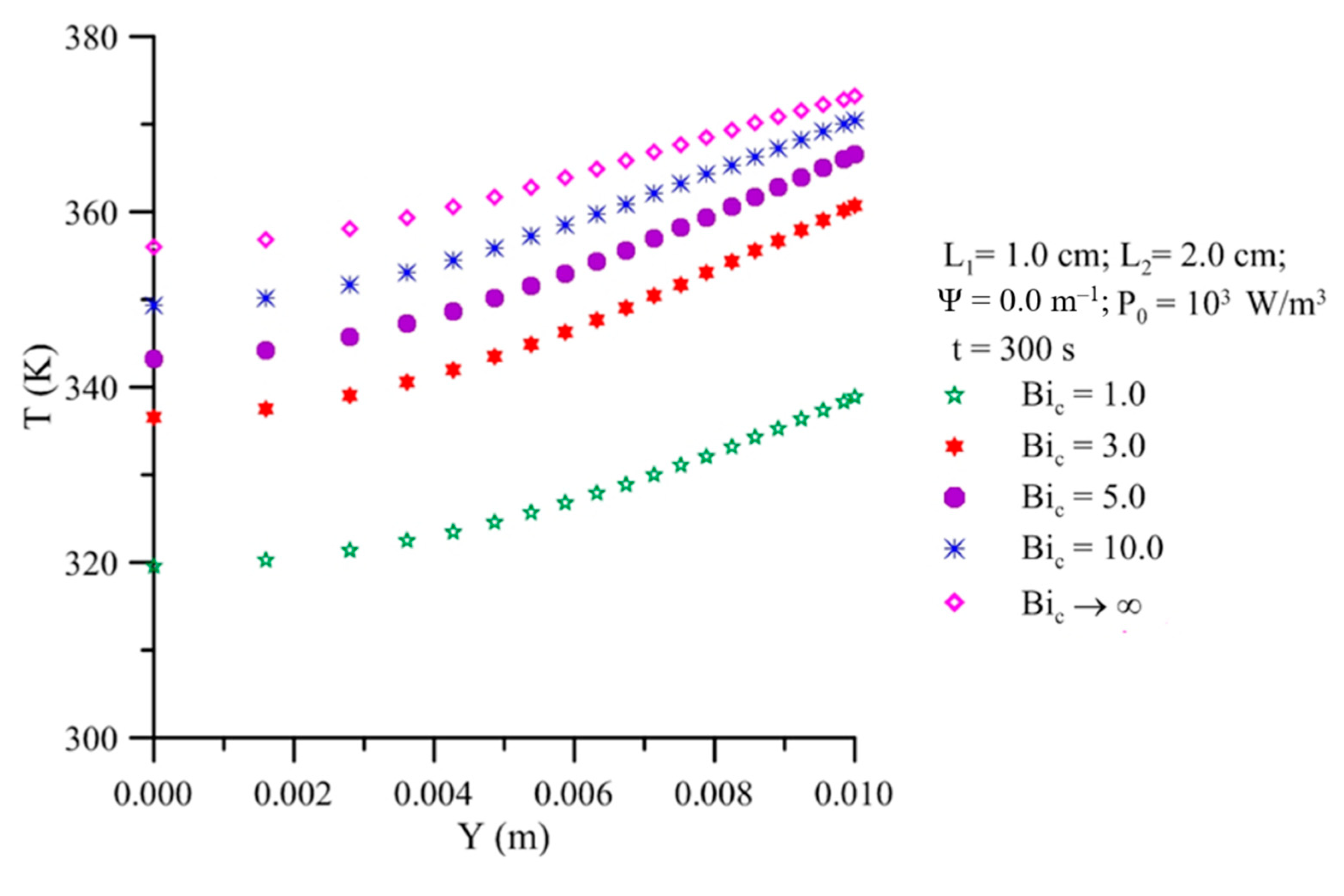
- In hybrid processes, for a shorter drying time, moisture migration occurs from the center to the surface and heat flux occurs in the opposite direction, generating high thermal and hydric gradients inside the solid;
- (c)
- In hybrid processes, for a longer dying time, moisture migration and heat flux occurs in the same direction, from the center to the surface, generating low hydric gradients and high thermal gradients inside the solid;
- (d)
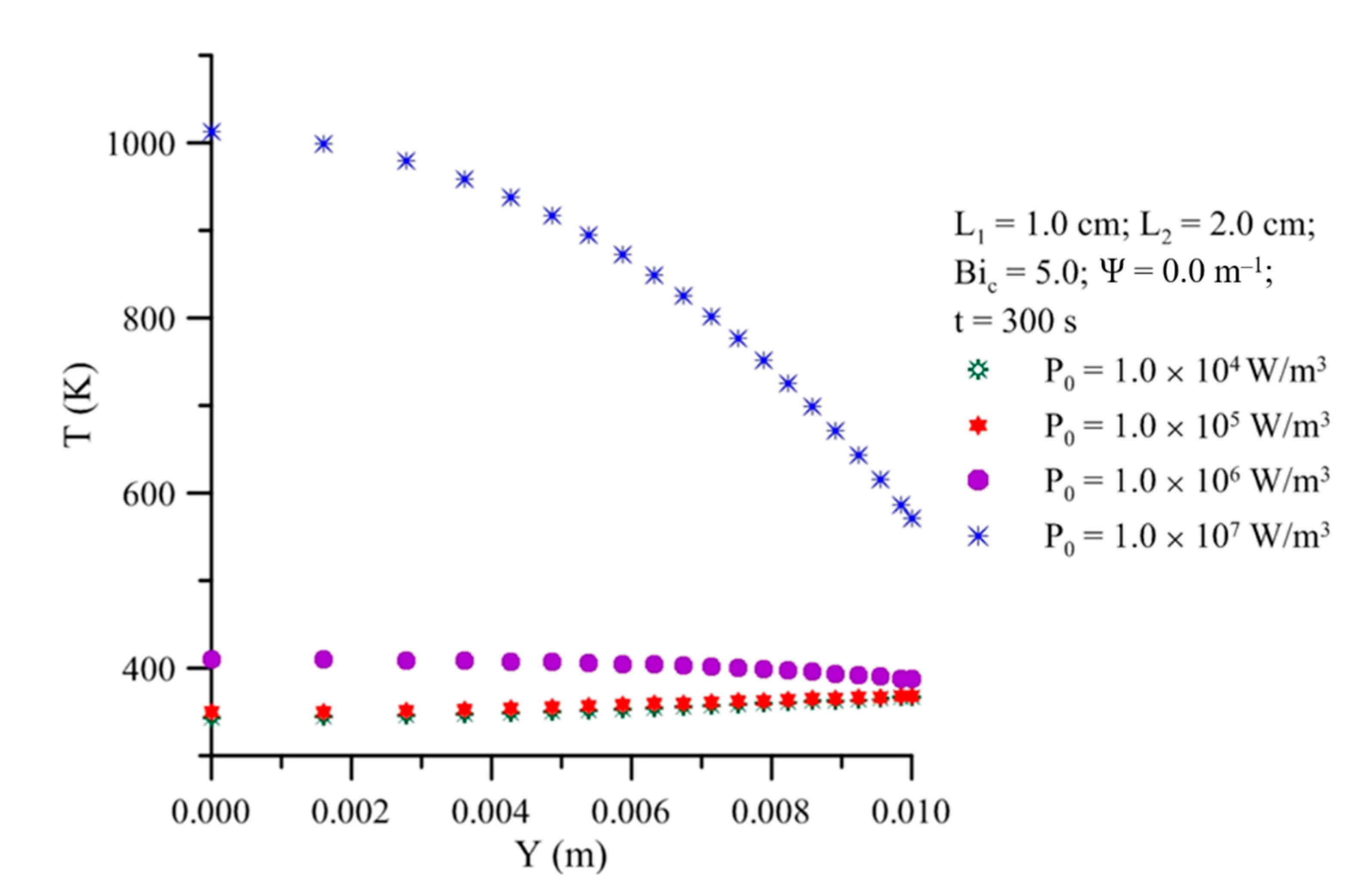
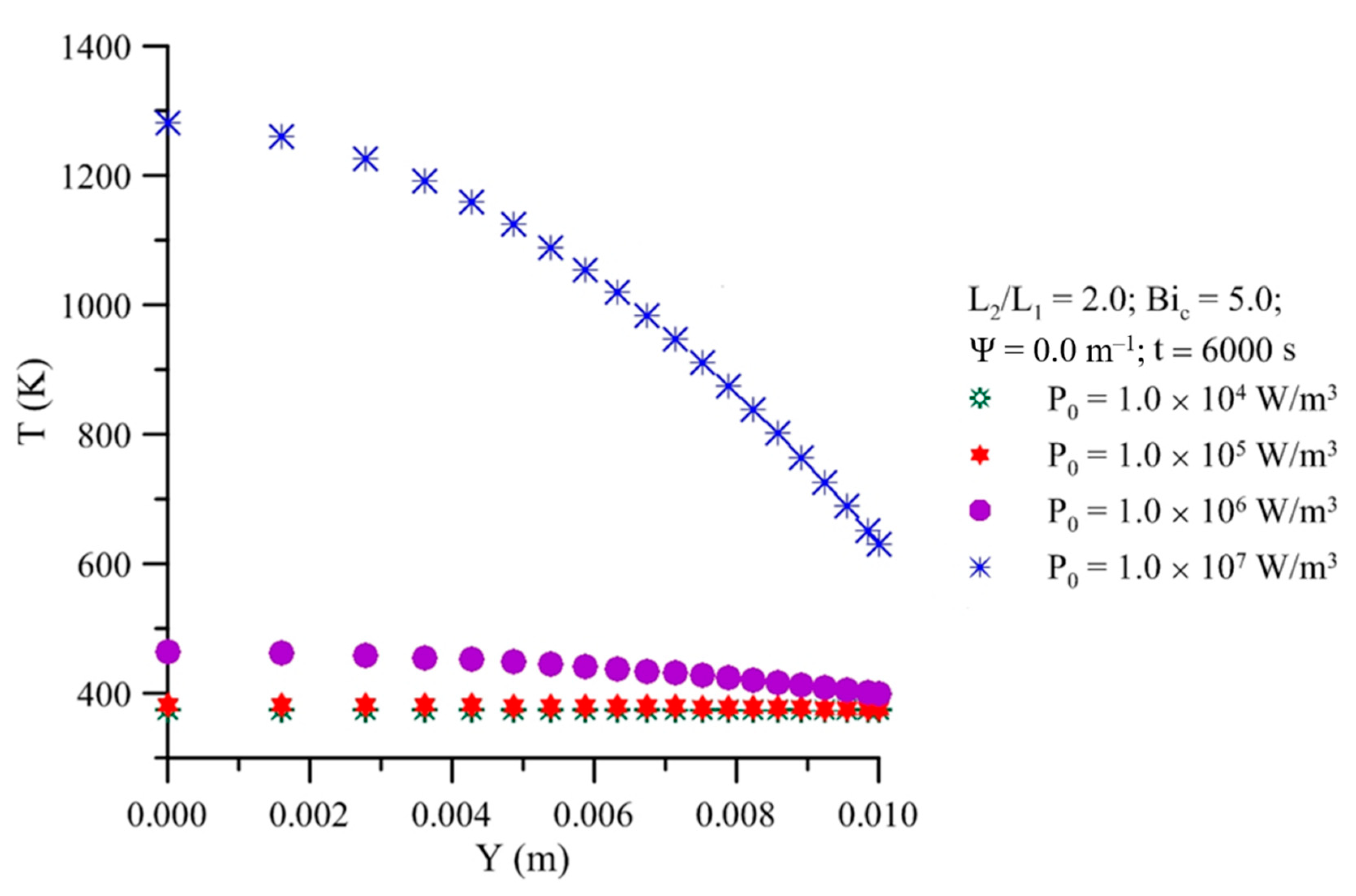
- The higher the microwave power density, the greater the amount of heat generated, and the higher the temperature inside the solid. For the drying of prolate spheroidal solids, a microwave power density less than 106 W/m3 provoked temperatures less than 450 K inside the solid.
- (e)
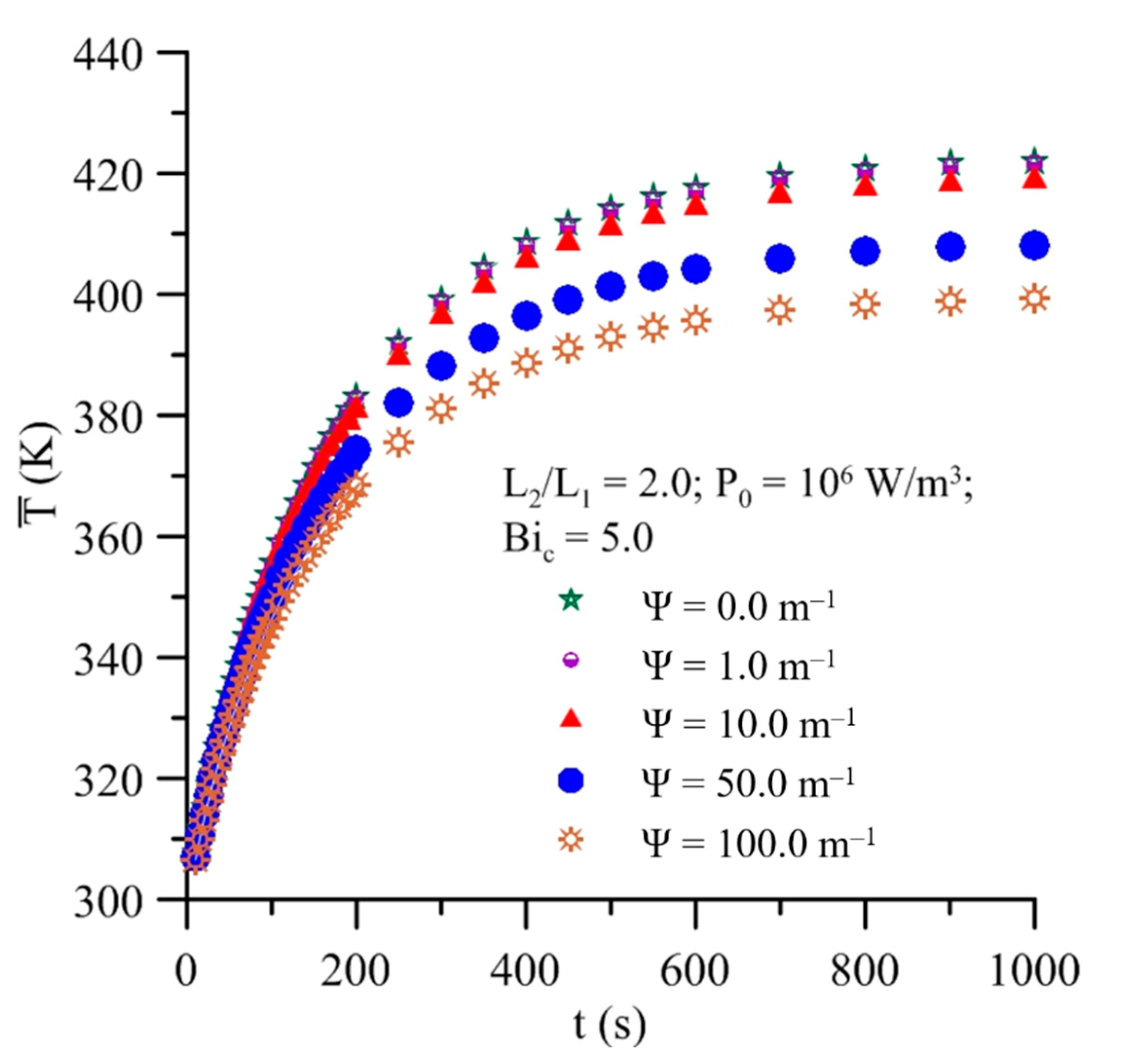
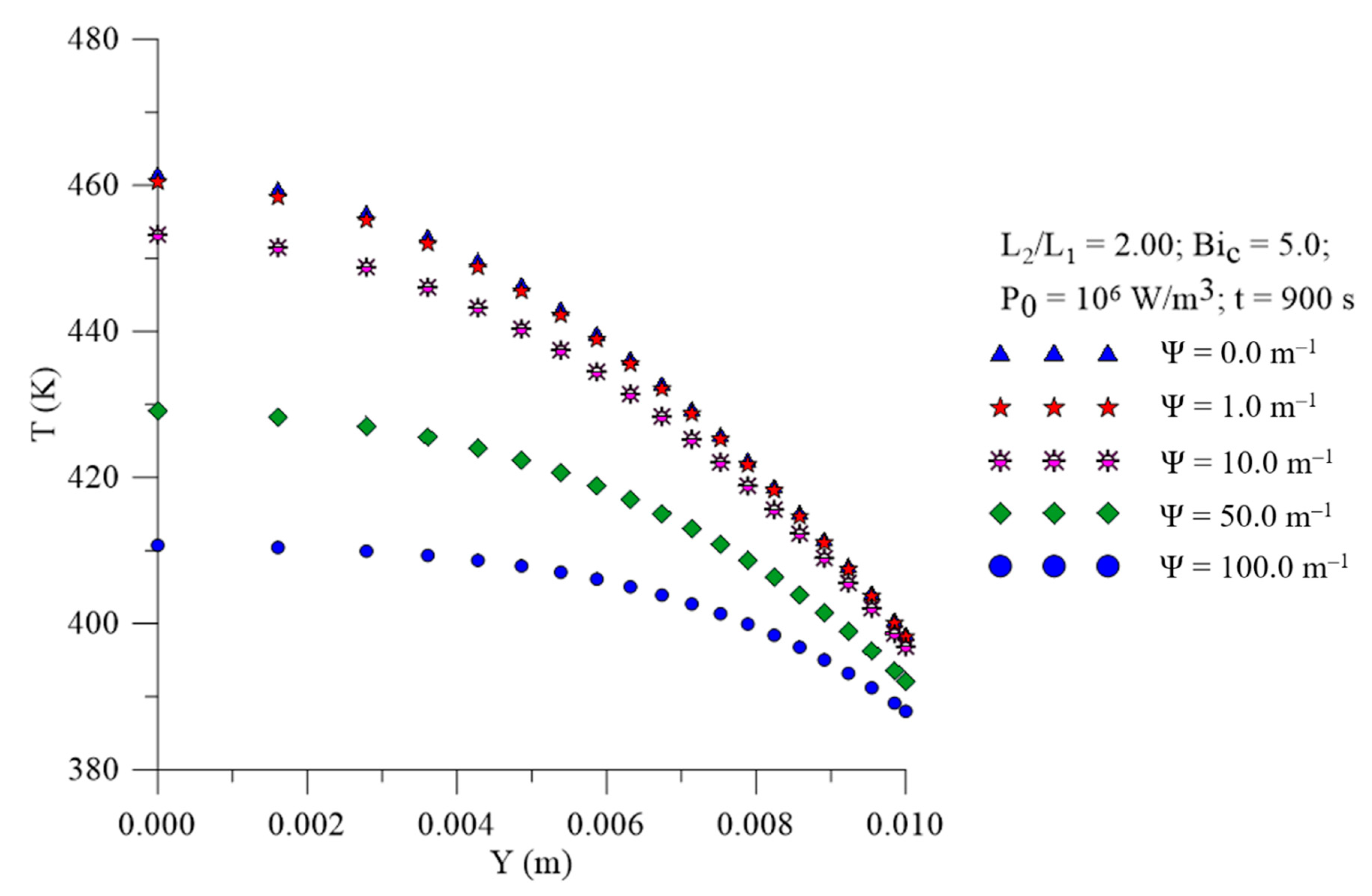
- The lower the attenuation factor (higher penetration depth), the higher the temperature inside the solid. For the drying of prolate spheroidal solids, an attenuation factor less than 50 m−1 provoked an average temperature greater than 410 K inside the solid.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haghi, A.K.; Amanifard, N. Analysis of heat and mass transfer during microwave drying of food products. Braz. J. Chem. Eng. 2008, 25, 491–501. [Google Scholar] [CrossRef]
- Dunaeva, T.; Manturov, A. The phenomenological model microwave drying kinetics of food products. In Proceedings of the International Kharkov Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW), Kharkov, Ukraine, 21–26 June 2004; pp. 1–3. [Google Scholar] [CrossRef]
- Metaxas, A.C.; Meredith, R.J. Industrial Microwave Heating; Peter Peregrinus Ltd.: London, UK, 1983. [Google Scholar]
- Lima, A.G.B.; Delgado, J.M.P.Q.; Silva, E.G.; Farias Neto, S.R.; Santos, J.P.S.; Lima, W.M.P.B. Drying process in electromagnetic fields. In Drying and Energy Technologies; Delgado, J.M.P.Q., Lima, A.G.B., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 89–110. [Google Scholar]
- Bingo, L.G.; Pan, Z.; Roberts, J.S.; Devres, Y.O.; Balaban, M.O. Mathematical modeling of microwave-assisted convective heating and drying of grapes. Int. J. Agric. Biol. Eng. 2008, 1, 46–54. [Google Scholar] [CrossRef]
- Maskan, M. Microwave/air and microwave finish drying of banana. J. Food Eng. 2000, 44, 71–78. [Google Scholar] [CrossRef]
- Torringa, E.; Esveled, E.; Scheewe, I.; Bartels, P.; Berg, R. Osmotic dehydration as a pre-treatment before combined microwave-hot-air drying of mushrooms. J. Food Eng. 2001, 49, 185–191. [Google Scholar] [CrossRef]
- Fumagalli, F. Pear Drying in Microwave Drier. Master’s Thesis, Federal University of São Carlos, São Carlos, Brazil, 2003. (In Portuguese). [Google Scholar]
- Srikiatden, J.; Roberts, J.S. Measuring moisture diffusivity of potato and carrot (core and cortex) during convective hot air and isothermal drying. J. Food Eng. 2006, 74, 143–152. [Google Scholar] [CrossRef]
- Ribeiro, R.C. Semi-Dehydrated Tomatoes Obtained by Drying Convective Microwaves Preceded by Osmotic Dehydration. Master’s Thesis, Federal University of Lavras, Lavras, Brazil, 2013. (In Portuguese). [Google Scholar]
- Silva, E.G. Combined (Convective and Microwave) Drying of Prolate Spheroidal Solids: Modeling, Simulation and Experimentation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2016. (In Portuguese). [Google Scholar]
- Lima, A.G.B.; Queiroz, M.R.; Nebra, S.A. Simultaneous moisture transport and shrinkage during drying of solids with ellipsoidal configuration. Chem. Eng. J. 2002, 86, 85–93. [Google Scholar] [CrossRef]
- Lima, A.G.B.; Queiroz, M.R.; Nebra, S.A. Heat and mass transfer model including shrinkage applied to ellipsoidal products: Case study for drying of bananas. Dev. Chem. Eng. Miner. Process. 2002, 10, 281–304. [Google Scholar] [CrossRef]
- Lima, A.G.B.; Farias Neto, S.R.; Silva, W.P. Heat and mass Transfer in Porous Materials with Complex Geometry: Fundamentals and Applications. In Heat and Mass Transfer in Porous Media, 1st ed.; Series: Advanced Structured Materials; Springer: Heidelberg, Germany, 2011; Volume 13, pp. 161–185. [Google Scholar] [CrossRef]
- Lima, A.G.B.; Farias, R.P.; Silva, W.P.; Farias Neto, S.R.; Farias, F.P.M.; Lima, W.M.P.B. Convective Drying of Food: Foundation, Modeling and Applications In Advanced Structured Materials, 1st ed.; Springer International Publishing: Heidelberg, Germany, 2014; Volume 48, pp. 95–115. [Google Scholar] [CrossRef]
- Oliveira, V.A.B.; Lima, A.G.B. Drying of wheat based on the non-equilibrium thermodynamics: A numerical study. Dry. Tech. 2009, 27, 306–313. [Google Scholar] [CrossRef]
- Oliveira, V.A.B.; Lima, W.C.P.B.; Farias Neto, S.R.; Lima, A.G.B. Heat and mass diffusion and shrinkage in prolate spheroidal bodies based on non-equilibrium thermodynamics: A numerical investigation. J. Porous Media 2011, 14, 593–605. [Google Scholar] [CrossRef]
- Lima, A.G.B.; Delgado, J.M.P.Q.; Oliveira, V.A.B.; Melo, J.C.S.; Joaquina e Silva, C. Porous Materials Drying Model Based on the Thermodynamics of Irreversible Processes: Background and Application. In Advanced Structured Materials, 1st ed.; Springer International Publishing: Heidelberg, Germany, 2014; Volume 48, pp. 1–23. [Google Scholar] [CrossRef]
- Lima, A.G.B.; Delgado, J.M.P.Q.; Santos, I.B.; Silva Santos, J.P.; Barbosa, E.S.; Joaquina e Silva, C. GBI Method: A Powerful Technique to Study Drying of Complex Shape Solids. In Advanced Structured Materials, 1st ed.; Springer International Publishing: Heidelberg, Germany, 2014; Volume 48, pp. 25–43. [Google Scholar] [CrossRef]
- Santos, J.P.S.; Santos, I.B.; Pereira, E.M.A.; Silva, J.V.; Lima, A.G.B. Wheat Convective Drying: An Analytical Investigation via Galerkin-Based Integral Method. Def. Diffus. Forum 2015, 365, 82–87. [Google Scholar] [CrossRef]
- Hacihafizoğlu, O.; Cihan, A.; Kahveci, K.; Lima, A.G.B. A liquid diffusion model for thin-layer drying of rough rice. Eur. Food Res. Technol. 2008, 226, 787–793. [Google Scholar] [CrossRef]
- Cihan, A.; Kahveci, K.; Hacihafizoğlu, O.; Lima, A.G.B. A diffusion based model for intermittent drying of rough rice. Heat Mass Transf. 2008, 44, 905–911. [Google Scholar] [CrossRef]
- Silva, J.V.; Silva, F.N.; Andrade, T.H.F.; Lima, A.G.B. Drying of Rough Rice: A Numerical Investigation. Defect Diffus. Forum 2013, 334–335, 131–136. [Google Scholar] [CrossRef]
- Franco, C.M.R.; Lima, A.G.B.; Silva, J.V.; Nunes, A.G. Applying Liquid Diffusion Model for Continuous Drying of Rough Rice in Fixed Bed. Defect Diffus. Forum 2016, 369, 152–156. [Google Scholar] [CrossRef]
- Franco, C.M.R.; de Lima, A.G.B.; Farias, V.S.O.; Silva, W.P. Modeling and experimentation of continuous and intermittent drying of rough rice grains. Heat Mass Transf. 2020, 56, 1003–1014. [Google Scholar] [CrossRef]
- Franco, C.M.R.; Lima, A.G.B.; Farias, V.S.O.; Machado, E.A. Intermittent Drying of Rice Grains with Husk: Modelling and Experimentation. Diffus. Found. 2020, 25, 9–36. [Google Scholar] [CrossRef]
- Carmo, J.E.F.; Lima, A.G.B. Drying of Lentil Including Shrinkage: A Numerical Simulation. Drying Technol. 2005, 23, 1977–1992. [Google Scholar] [CrossRef]
- Carmo, J.E.F.; de Lima, A.G.B.; Silva, C.J. Continuous and Intermittent Drying (Tempering) of Oblate Spheroidal Bodies: Modeling and Simulation. Int. J. Food Eng. 2012, 8. [Google Scholar] [CrossRef]
- Melo, J.C.S.; Lima, A.G.B.; Silva, W.P.; Lima, W.M.P.B. Heat and Mass Transfer during Drying of Lentil Based on the Non-Equilibrium Thermodynamics: A Numerical Study. Defect Diffus. Forum 2015, 365, 285–290. [Google Scholar] [CrossRef]
- Melo, J.C.S.; Gomez, R.S.; Silva Júnior, J.B.; Queiroga, A.X.M.; Dantas, R.L.; Lima, A.G.B.; Silva, W.P. Drying of Oblate Spheroidal Solids via Model Based on the Non-Equilibrium Thermodynamics. Diffus. Found. 2020, 25, 83–98. [Google Scholar] [CrossRef]
- Whitaker, S. Heat and mass transfer in granular porous media. In Advances in Drying; Mujumdar, A.S., Ed.; Hemisphere Publishing Company: London, UK, 1980; Volume 1, pp. 23–61. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, the Finite Volume Method, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007; ISBN 978-0-13-127498-3. [Google Scholar]
- Maliska, C.R. Computational Heat Transfer and Fluid Mechanics, 2nd ed.; LTC: Rio de Janeiro, Brazil, 2004. (In Portuguese) [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: New York, NY, USA, 1959; 510p. [Google Scholar]
- Lima, A.G.B. Diffusion Phenomenon in Prolate Spheroidal Solids. A Case Study: Banana Drying. Ph.D. Thesis, State University of Campinas, Campinas, Brazil, 1999. (In Portuguese). Available online: http://repositorio.unicamp.br/jspui/handle/REPOSIP/265133 (accessed on 24 October 2020).
- Oliveira, V.A.B. Heat and Mass Transfer in the Interior of Solid with Prolate Spheroidal Shape Via Thermodynamic of Irreversible Processes. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2006. (In Portuguese). Available online: http://dspace.sti.ufcg.edu.br:8080/jspui/handle/riufcg/6853 (accessed on 24 October 2020).
- Franco, C.M.R. Modeling, Simulation and Experimentation of the Continuous and Intermittent Drying of Elipsoidal Solids: Case Sudies: Rough Rice Grain Drying. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2016. (In Portuguese). Available online: http://dspace.sti.ufcg.edu.br:8080/jspui/handle/riufcg/950 (accessed on 24 October 2020).


| Case | (-) | hm (m/s) | hc (W/m2K) | P0 (W/m3) | Bi (-) | (m−1) |
|---|---|---|---|---|---|---|
| 1 | 2.000 | 1.22 × 10−7 | 33.95 | 1.0 × 103 | 1.0 | 0.0 |
| 2 | 2.000 | 3.66 × 10−7 | 101.85 | 1.0 × 103 | 3.0 | 0.0 |
| 3 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 103 | 5.0 | 0.0 |
| 4 | 2.000 | 12.20 × 10−7 | 339.50 | 1.0 × 103 | 10.0 | 0.0 |
| 5 | 2.000 | 1.00 × 1030 | 1.00 × 1030 | 1.0 × 103 | ∞ | 0.0 |
| 6 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 107 | 5.0 | 0.0 |
| 7 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 0.0 |
| 8 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 105 | 5.0 | 0.0 |
| 9 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 104 | 5.0 | 0.0 |
| 10 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 0.0 |
| 11 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 1.0 |
| 12 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 10.0 |
| 13 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 50.0 |
| 14 | 2.000 | 6.10 × 10−7 | 169.75 | 1.0 × 106 | 5.0 | 100.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, E.G.; Gomez, R.S.; Gomes, J.P.; Figueirêdo, R.M.F.; Queiroz, A.J.M.; Silva, W.P.; Santiago, Â.M.; Macedo, A.D.B.; Ferreira, J.P.L.; Gomes, Í.A.; et al. Convective and Microwave Assisted Drying of Wet Porous Materials with Prolate Spheroidal Shape: A Finite-Volume Approach. Agriculture 2020, 10, 507. https://doi.org/10.3390/agriculture10110507
Silva EG, Gomez RS, Gomes JP, Figueirêdo RMF, Queiroz AJM, Silva WP, Santiago ÂM, Macedo ADB, Ferreira JPL, Gomes ÍA, et al. Convective and Microwave Assisted Drying of Wet Porous Materials with Prolate Spheroidal Shape: A Finite-Volume Approach. Agriculture. 2020; 10(11):507. https://doi.org/10.3390/agriculture10110507
Chicago/Turabian StyleSilva, Edna G., Ricardo S. Gomez, Josivanda P. Gomes, Rossana M. F. Figueirêdo, Alexandre J. M. Queiroz, Wilton P. Silva, Ângela M. Santiago, Antonio D. B. Macedo, João P. L. Ferreira, Ítalo A. Gomes, and et al. 2020. "Convective and Microwave Assisted Drying of Wet Porous Materials with Prolate Spheroidal Shape: A Finite-Volume Approach" Agriculture 10, no. 11: 507. https://doi.org/10.3390/agriculture10110507
APA StyleSilva, E. G., Gomez, R. S., Gomes, J. P., Figueirêdo, R. M. F., Queiroz, A. J. M., Silva, W. P., Santiago, Â. M., Macedo, A. D. B., Ferreira, J. P. L., Gomes, Í. A., & Lima, A. G. B. (2020). Convective and Microwave Assisted Drying of Wet Porous Materials with Prolate Spheroidal Shape: A Finite-Volume Approach. Agriculture, 10(11), 507. https://doi.org/10.3390/agriculture10110507







