Optimization of Replaced Grinding Wheel Diameter for Minimum Grinding Cost in Internal Grinding

Abstract

This paper shows an optimization study on calculating the optimum replaced wheel diameter in internal grinding of stainless steel. In this work, the effects of the input factors, including the initial diameter, the grinding wheel width, the ratio between the length and the diameter of the work-pieces, the dressing depth of cut, the wheel life and the radial grinding wheel wear per dress on the optimum replaced grinding wheel diameter were considered. Also, the effects of cost components, including the cost of the grinding machine and the wheel cost were examined. Moreover, to estimate the influences of these parameters on the optimum replaced diameter, a simulation experiment was given and conducted by programming. From the results of the study, a regression equation was proposed to calculate the optimum replaced diameter.

1. Introduction

Nowadays, grinding is broadly used in industries. It is reported that about 20–25% of the total mechanical parts are made with the use of grinding machining [1]. Accordingly, studies on optimization of the grinding process have caught much interest from numerous researchers.

Up to now, a number of studies have been done on the optimization of different grinding types. The researches have been carried out on external cylindrical grinding [2,3,4,5], surface grinding [6,7,8] and belt grinding [9]. The studies in this area have been implemented not only on the CNC (Computer Numerical Control) grinding machine [10] but also on the CNC milling machine [11].

Regarding internal grinding process, scientists have paid substantial attention to monitoring and optimizing the grinding process [12], investigating the impact of the wheel dressing on the surface finish [13], online-optimizing the grinding process and the dressing parameters for the reduction of the grinding time [14], and applying adaptive control to increase the efficiency of the grinding process [15]. In addition, to decrease the grinding cost, a cost optimization study on internal grinding process was presented [16]. It was reported that there is an optimum replaced grinding wheel diameter at which the grinding cost is minimum. Moreover, grinding with this optimum replaced diameter can significantly reduce both the time and the cost of the grinding process.

This article presents research on cost optimization of the internal grinding process. The aim of the study is to find the optimum replaced wheel diameter in internal grinding stainless steel. In the study, the effects of the cutting and the cost factors on the optimum replaced diameter were explored. Also, a simulation experiment was created and accomplished by programming for evaluation of the influences of these factors on the optimum replaced diameter. The influences of the cutting factors and the cost elements on the optimum replaced diameter were scientifically weighed. Furthermore, to determine the optimum replaced diameter, a regression equation was proposed.

2. Cost Analysis

The internal grinding cost per part $C_{ig}$ is determined by [16]:

$$C_{ig}=C_{m,h}·t_s+C_{gw,p},$$

(1)

where, C_m,h is the cost of the grinding machine (USD/h), including the wages, the overhead cost, the labor cost etc.; t_s is the grinding time which is discussed later in this section; C_gw,p is the wheel cost per part (USD/p) which is calculated by:

$$C_{gw,p}=C_{gw}/n_{p,w}.$$

(2)

In which, C_gw is the cost of a piece of wheel (USD/p); n_p,w is the entire parts ground per wheel; n_p,w can be determined as follows [17]:

$$n_{p,w}=\left(D_0-D_e\right)·n_{p,d}/\left[2\left({\mathrm{W}}_{pd}+a_{ed}\right)\right],$$

(3)

where, D₀ is the initial diameter of wheel (mm); D_e is the replaced diameter of the wheel (mm); ${\mathrm{W}}_{pd}$ is the radial grinding wheel wear per dress (mm/dress); a_ed is the dressing depth of cut (mm); n_p,d is the number of parts per dress which is found by:

$$n_{p,d}=T_w/t_c,$$

(4)

wherein, T_w is the wheel life (h); t_c is the grinding time (h) which is calculated as follows:

$$t_c=l_w·a_{e,tot}/\left(v_{fa}·f_r\right),$$

(5)

$$f_r=f_{r,tab}·c_1·c_2·c_3·c_4.$$

(6)

In Equations (5) and (6), v_fa and f_r,tab can be determined by the following Equations [18]:

$$v_{fa}=22.88·W_{gw}^{0.9865}·d_w^{0.0821}·S_{rg}^{-2.9833}·n_w^{1.2471},$$

(7)

and

$$f_{r,tab}=30.2944·a_{e,tot}^{0.567}·v_{fa}^{-0.9693}·d_w^{-0.1269}.$$

(8)

In the above equations, l_w is the length of part (mm); a_e,tot is the total depth of cut (mm); v_fa is the axial feed speed (mm/min); f_r,tab is the tabled radial wheel feed (mm/stroke); f_r is the radial wheel feed (mm/ stroke); c₁, c₂, c₃ and c₄ are the coefficients for determining the radial wheel feed (Table 1); W_gw is the grinding wheel width; $d_w$ is the work-piece diameter; S_rg is the surface roughness grade; $n_w$ is the work-piece speed; As it is grinding stainless steel, $n_w$ can be determined by [18]:

$$n_w=1255.8·d_w^{-0.3491}.$$

(9)

t_s is the grinding time, including auxiliary time (h), which is determined by:

$$t_s=t_c+t_{sp}+t_{d,p}+t_{wr,p}+t_{lu}.$$

(10)

Table 1. Coefficients for determining the radial wheel feed.

Coefficient depends on	Code	Value	Reference
Work-piece material and tolerance grade	c1	$c_1=0.0288·t{g}^{1.4153}$	[18]
Grinding wheel diameter	c2	$c_2=0.5657·d_s^{0.153}$	[18]
Measurement type	c3	1 (using micrometer)	[19]
Ratio of length to diameter of work-piece	c4	$c_4=1.0642·R_{ld}^{-0.5079}$	[18]

In which, t_c is the grinding time (h); t_sp is the spark-out time (h); t_d,p is the dressing time per piece (h); t_cw is the wheel replacing time (h) and t_lu is the loading and unloading work-piece time (h). These time components can be determined by the equations presented in Table 2 in which t_d is the dressing time (h).

Table 2. Time components.

Name	Code	Equation
Grinding time	tc	$t_c=l_w·a_{e,tot}/(v_{fa}·v_{fr})$
Dressing time	td,p	$t_{d,p}=t_d/n_{p,d}$
Wheel replacing time per work-piece	twr,p	$t_{wr,p}=t_{wr}/n_{p,w}$

To investigate the influence of input factors on the grinding cost, a program was conducted based on the above cost analysis. From the results of the program, the effects of several input factors on the grinding cost are exhibited in Figure 1. Moreover, the relation between the grinding cost and the replaced wheel diameter is described in Figure 2. This relation was calculated by Equation (1), in which D₀ = 20 (mm); W_gw = 25 (mm); a_ed = 0.12 (mm); C_mh = 5 (USD/h); C_gw = 3 (USD); T_w = 20 (min.); W_pd = 0.02 (mm/dress); S_rg = 7; t_g = 7; R_ld = 2. As it was reported in [16], the grinding cost is powerfully affected by the replaced grinding wheel diameter. In addition, this cost is minimum when the replaced wheel diameter reaches an optimum value (in this case D_e,op = 17.2 (mm)). Besides, the optimum diameter is considerably bigger than the conventional replaced grinding wheel diameter (about 13 to 14 mm [20]). It is observed from the figures that the grinding cost depends on various factors, such as the initial diameter, the grinding wheel width, the ratio between the length and the diameter of the workpieces, the total depth of dressing cut, the wheel life, the radial grinding wheel wear per dress, the replaced wheel diameter and so on. In addition, among these parameters, the replaced wheel diameter is the unique factor holding an optimum value at which the grinding cost is minimum. Hence, the optimum replaced wheel diameter has been selected to be the objective of the cost optimization problem.

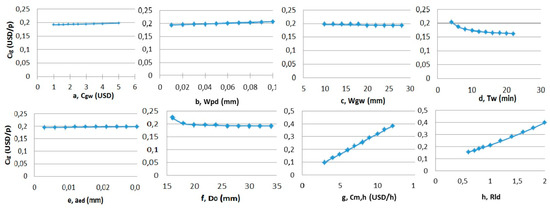
Figure 1. Grinding cost versus input factors.

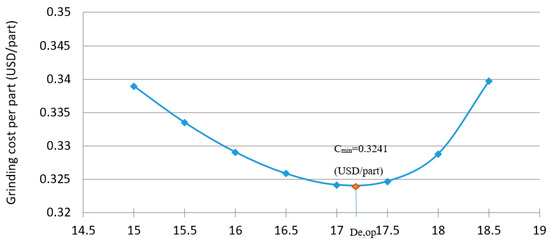
Figure 2. Grinding cost versus replaced wheel diameter.

From the above analyses, the cost optimization problem to determine the optimum replaced wheel diameter D_e,op is expressed by:

$$\min C_{ig}=\min f(D_e)$$

(11)

With the following constraint:

$$D_{e,\min }\le D_e\le D_{e,\max }$$

(12)

Additionally, as reported above, the optimum replaced wheel diameter is affected by a number of parameters. In this study, seven main input factors, including the initial wheel diameter D₀, the width of wheel W_gw, the ratio of work-piece length per work-piece diameter R_ld, the dressing depth of cut a_ed, the wheel life T_w, the radial grinding wheel wear per dress W_pd, the cost of the grinding machine C_m,h and the wheel cost C_gw were carefully selected to evaluate their effects on the optimum replaced diameter. Hence, the optimum replaced wheel diameter can be described as follows:

$$D_{e,op}=f(D_0,W_{gw},R_{ld},a_{ed},T_{\mathrm{w}},{\mathrm{W}}_{pd},C_{m,h},C_{gw})$$

(13)

3. Experimental Work

To learn the influences of input parameters on the optimum replaced diameter, a simulation experiment was planned. For the investigation, 8 input parameters, including the initial wheel diameter $D_0$, the width of wheel, the ratio of length to diameter of the work-piece, the dressing depth of cut $a_{ed}$, the life of wheel $T_{\mathrm{w}}$, the radial grinding wheel wear per dress ${\mathrm{W}}_{pd}$, the cost of the grinding machine $C_{m,h}$ and the wheel cost per piece were selected (Table 3). In practice, the cost components (the cost of the grinding machine and the wheel cost per piece) depend on the policies and the location of the company which owns the grinding machine. In addition, they vary from time to time. For example, the grinding machine cost per hour in the USD can be 7 to 10 USD/h while it is only about 4 to 5 USD/h in Vietnam. Therefore, the low and high levels of the cost components were selected based on the above mentioned factors (Table 3).

Table 3. Experimental input factors.

Factor	Code	Unit	Low	High
Initial grinding wheel diameter	D0	mm	10	40
Grinding wheel width	Wgw	mm	8	40
L/d ratio	Rld	-	1.2	4
Total depth of dressing cut	aed	mm	0.05	0.15
Life of wheel	Tw	min	10	30
Radial grinding wheel wear per dress	Wpd	mm	0.01	0.03
Cost of the grinding machine	Cm,h	USD/h	4	10
Wheel cost per piece	Cgw	USD/p.	0.3	5

Since this is a simulation experiment, there is no need to reduce the number of experiments. Therefore, the factorial design of experiments was chosen instead of Taguchi’s method. Furthermore, the experimental design with which a 2-level factorial design with ½ fraction was setup with eight mentioned parameters. Therefore, the number of experiments was calculated as $2^{\left(8-1\right)}=128$ (Figure 3). To perform the experiments, based on the cost analysis (see Section 2) a computer program was created. The input factors and the output response (the optimum replaced diameter $D_{e,op}$) are shown in Table 4.

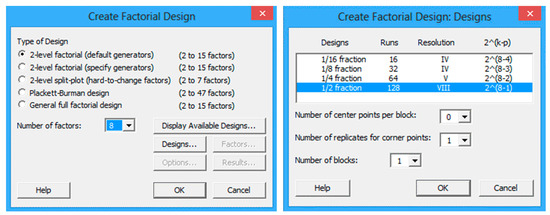
Figure 3. Creation of factorial design.

Table 4. Experimental plans and output response.

StdOrder	RunOrder	CenterPt	Blocks	D0	Wgw	Rld	aed	Tw	Wpd	Cm,h	Cgw	De,op
97	1	1	1	10	8	1.2	0.05	10	0.03	10	0.3	7.84
82	2	1	1	40	8	1.2	0.05	30	0.01	10	5	32.2
51	3	1	1	10	40	1.2	0.05	30	0.03	4	5	5.33
89	4	1	1	10	8	1.2	0.15	30	0.01	10	5	5.86
108	5	1	1	40	40	1.2	0.15	10	0.03	10	5	25.69
104	6	1	1	40	40	4	0.05	10	0.03	10	5	28.24
…
54	127	1	1	40	8	4	0.05	30	0.03	4	0.3	36.23
9	128	1	1	10	8	1.2	0.15	10	0.01	4	5	3.23

4. Results and Discussion

The influences of input parameters on the optimal replaced diameter are illustrated in Figure 4. From this figure, the optimal replaced diameter $D_{e,op}$ is powerfully contingent on the original wheel diameter. Also, it depends on the dressing depth of cut $a_{ed}$, the life of wheel $T_w$, the cost of the grinding machine $C_{m,h}$ and the grinding wheel cost $C_{g\mathrm{w}}$. In addition, ${\mathrm{D}}_{e,op}$ is not affected by the width of wheel W_gw, the ratio of the length to the diameter of work-piece R_ld and the radial grinding wheel wear per dress W_pd.

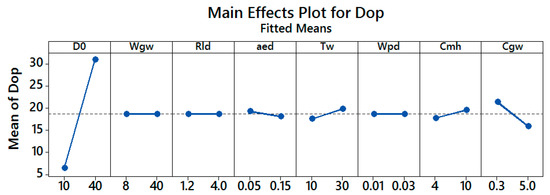
Figure 4. Main effects plot for optimum replaced grinding wheel diameter.

The Normal Plot of the standardized effects is described in Figure 5. From this graph it is known that the initial diameter of grinding wheel (factor A), the life of wheel (factor C), the cost of the grinding machine (factor G) and the interactions AE, GH, AG and EH have positive standardized effects. That means if their values increase, the optimal replaced diameter raises. Also, the cost of the wheel (factor H), the dressing depth of cut (factor D) and the interactions AH, AD, DH and EG have negative standardized effects. If their values grow, the optimum replaced diameter drops.

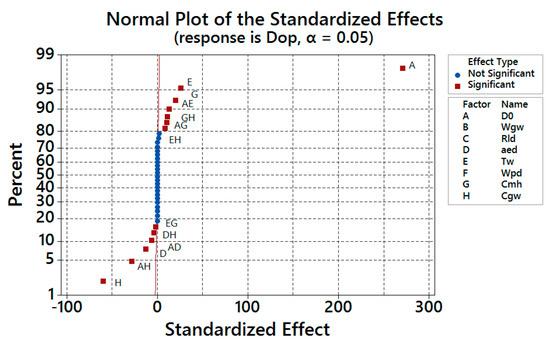
Figure 5. Normal Plot for D_e,op.

Figure 6 presents the Pareto chart for the optimal replaced diameter. It can be seen from the figure that the reference line crosses characterized factors A (the initial diameter of wheel), H (the cost of the wheel), E (the life of wheel), G (the cost of the grinding machine), D (the dressing depth of cut) and the interactions AH, AE, EF, AE, GH, AG, EH, AD, DH and EG. Therefore, these parameters are significant with the optimum diameter.

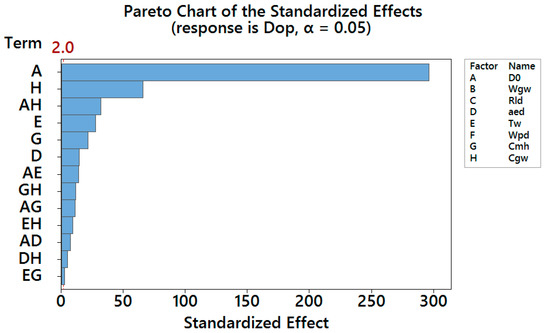
Figure 6. Pareto chart for D_op.

To find the significant effects on the optimum replaced diameter, the insignificant effects which have the P-values higher than 0.05 were ignored. Consequently, it can be found from the figure that the initial diameter of wheel $D_0$, the dressing depth of cut $a_{ed}$, the life of wheel $T_w$, the cost of the grinding machine $C_{m,h}$, the cost of the wheel $C_{gw}$ and the interactions between $D_0$ and $a_{ed}$, $T_w$, $C_{m,h}$ and $C_{g\mathrm{w}}$; $a_{ed}$ and $C_{gw}$; $T_w$ and $C_{m,h}$ and $C_{gw}$ and between $C_{m,h}$ and $C_{gw}$ have significant effects on the response (Figure 6). In addition, the following equation was proposed to calculate the optimum replaced wheel diameter:

$$\begin{array}{l}{D}_{op}=-0.58+0.814·D_0+2.44·a_{ed}-0.0004·T_{\mathrm{w}}-0.0692·C_{mh}-0.8698·C_{gw}-0.4021·D_0·a_{ed}+\\ +0.003865·D_0·T_w+0.01034·D_0·C_{mh}-0.03742·D_0·C_{gw}-1.678·a_{ed}·C_{gw}-0.00339·T_w·C_{mh}+\\ +0.0164·T_w·C_{gw}+0.06769·C_{mh}·C_{gw}\end{array}$$

(14)

The regression model (14) fits the experimental data very well because all of the values of adj-R2 and pred-R2 are greater than 99.85% (Figure 7). This model is used to determine the optimum replaced wheel diameter when grinding stainless steel.

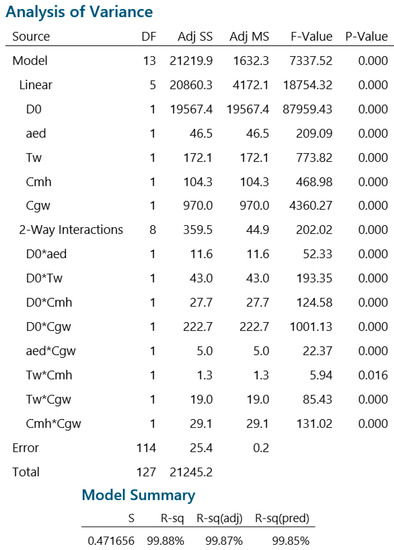
Figure 7. Estimated effects and coefficients for D_e,op.

5. Conclusions

A cost optimization study on the calculation of the optimal replaced wheel diameter when internal grinding stainless steel was carried out. For doing this, the internal grinding cost was analyzed. Moreover, the influence of many input factors, as well as the cost elements on the optimum replaced diameter were inspected by designing and conducting a simulation experiment computationally. More considerably, an equation for determination of the optimum replaced diameter was presented. As the proposed equation is explicit, the optimum replaced diameter in internal grinding of stainless steel is predicted precisely and effortlessly.