A Hybrid Crow Search Algorithm for Solving Permutation Flow Shop Scheduling Problems

Abstract

The permutation flow shop scheduling problem (PFSP) is a renowned problem in the scheduling research community. It is an NP-hard combinatorial optimization problem that has useful real-world applications. In this problem, finding a useful algorithm to handle the massive amounts of jobs required to retrieve an actionable permutation order in a reasonable amount of time is important. The recently developed crow search algorithm (CSA) is a novel swarm-based metaheuristic algorithm originally proposed to solve mathematical optimization problems. In this paper, a hybrid CSA (HCSA) is proposed to minimize the makespans of PFSPs. First, to make the CSA suitable for solving the PFSP, the smallest position value rule is applied to convert continuous numbers into job sequences. Then, the HCSA uses a Nawaz–Enscore–Ham (NEH) technique to create a population with the required levels of quality and diversity. We apply a local search to enhance the quality of the solutions and avoid premature convergence; simulated annealing enhances the local search of a method based on a variable neighborhood search. Computational tests are used to evaluate the algorithm using PFSP benchmarks with job sizes between 20 and 500. The tests indicate that the performance of the proposed HCSA is significantly superior to that of other algorithms.

1. Introduction

Several optimization methods have been proposed in artificial intelligence to find interesting patterns or optimization results for larger NP-hard optimization problems within a reasonable amount of time. To date, several real-world problems have been investigated to address this issue, such as data mining [1,2,3,4], DNA fragment assembly [5,6], DNA compression [7], Internet of Things [8,9], knapsack problem [10], networks of evolutionary processors [11], scheduling [12], and traveling salesman [13].

Among these, the permutation flow shop scheduling problem (PFSP) has attracted significant attention and has important roles in scheduling research. The PFSP was first proposed by Johnson [14] in 1953, and has attracted extensive attention since then. Several theoretical, algorithmic, and computational research studies have addressed this problem. The basic concept of the PFSP is that n jobs need to be processed on a sequence of m machines, such that each job needs to be processed on all machines in the same order. Johnson addressed it as a two-machine problem. Kan proved that the makespan minimization of the PFSP is an NP-hard problem [15]. For large problem instances, both the traditional dynamic programming approach and the heuristic approach require excessive computational time. To date, the Nawaz–Enscore–Ham (NEH) heuristic [16] is considered to be one of the most effective heuristic approaches for solving the PFSP; numerous variants of the NEH algorithm have been proposed, such as those in References [17,18,19,20,21,22]. Metaheuristic approaches are often applied to solve NP-hard combinatorial optimization problems. Various metaheuristic algorithms [23] continue to attract increasing interest in optimization research. This type of research is typically inspired by natural behavior, and has yielded algorithms such as the artificial bee colony (ABC) [24], ant colony optimization (ACO) [25], cuckoo search (CS) [26], differential evolution (DE) [27], firefly algorithm (FA) [28], gravitational search algorithm (GSA) [29], particle swarm optimization (PSO) [30], and whale optimization (WA) [31]. Recently, the combinatorial optimization community has attempted to solve the PFSP by using metaheuristic approaches, such as those in References [32,33,34,35,36,37]. One of the recently proposed swarm-based intelligence algorithms is the crow search algorithm (CSA) [38]. The CSA is based on the intelligent behavior of crows, who tend to store excess food in hiding places and retrieve it when required. Crows may try to follow other crows to steal their hidden food. The CSA simulates crow strategies with awareness probability and flight length parameters. The CSA provides an efficient search strategy for solving optimization problems. Furthermore, it is considered to be quicker than and superior to the PSO algorithm.

The performance of a simple CSA is controlled by two parameters: the flight length $fL$ and the awareness probability $AP$. Although the CSA is better than PSO, similar issues occur; namely, it is necessary to avoid premature convergence and enhance diverse abilities [39,40]. In addition, the original CSA is more suitable for continuous optimization problems, whereas little research has been done on transferring the approach to combinatorial optimization problems. It is a challenge to map the CSA to PFSP problems. Thus, in this paper, we propose a hybrid CSA (HCSA) approach to minimize makespan in PFSP problems. First, to make the CSA suitable for solving the PFSP, the smallest position value rule is applied to convert continuous numbers into job sequences. Our HCSA applies an NEH technique to create a population with excellent quality and diversity. Finally, to enhance the quality of the solutions and avoid premature convergence, simulated annealing (SA) [41] is combined with the variable neighborhood search (VNS) [23] to produce SA-VNS, which provides a local search to enhance the exploitation and exploration of HCSA. Performance evaluations proved that our HCSA outperformed existing algorithms. In summary, HCSA applies the evolutionary searching of CSA to generate the population, individual update, and competition, and effectively find better solutions by utilizing and initializing adaptive local searches to create diversity.

The remainder of this paper is organized as follows. Background and related work are described in Section 2. The problem definition is stated in Section 3. Section 4 presents the proposed HCSA. The performance evaluation is outlined in Section 5. Finally, conclusions and suggestions for future research are provided in Section 6.

2. Background Knowledge and Related Works

This section reviews relevant background and related studies. The following topics are discussed in detail:

• Nawaz–Enscore–Ham heuristic (NEH);
• Crow search algorithm (CSA);
• Simulated annealing (SA);
• Variable neighborhood search (VNS).

2.1. NEH Heuristic

The NEH [16] algorithm is the best constructive heuristic for solving the PFSP, as has previously been discussed in References [17,18,19,20,21,22,42]. Two main concepts underpin the NEH algorithm: 1. the order of the jobs; and 2. that jobs are prioritized based on priority rules and tie-breaking strategies, such as NEHD [17], NEHKK1 [18], NEHKK2 [19], CL [20], and NEHLJP1 [22]. The procedure employed by the NEH algorithm is presented in Algorithm 1.

Algorithm 1 Standard Nawaz–Enscore–Ham (NEH) algorithm.
	Input:	n jobs, s machines, and the processing time of each job on each machine
	Output:	A solution with a minimized makespan
	Step:	Description:
	1.	Obtain a permutation $\pi$ of n jobs such that each job is in a descending order of its processing time on the machines.
	2.	Choose the first two jobs from job sequence $\pi$, and obtain the superior order according to the makespan values
	3.	Generate a new job permutation by inserting the q-th job (q = 3, …, n) in job sequence $\pi$ in every possible slot of job sequence $\pi$, and choose the order with the minimum makespan.
	4.	Finally, output the current best solution—the one with the minimum makespan value.

2.2. Crow Search Algorithm (CSA)

Crows are among the most intelligent types of birds; the behavior of crows indicates substantial cognitive ability. Although crows are less intelligent than humans, crows make tools and recognize themselves in mirrors [43]. In a typical community of crows, each crow has its own cache of food, and each crow hides its cache from potential burglars. Askazadeh published the CSA [38]—a stochastic swarm-based optimization method. The main points of the CSA are as follows:

• Crows live in flocks;
• Crows recall where their caches are;
• Crows pursue each other and opportunistically burglarize food caches;
• Crows protect their hiding spaces from attackers with a probability in the interval [0, 1].

The CSA represents crows as software entities. Each crow has some flight length $fL$ and an awareness probability $AP$. If the value of $fL$ is small, then the CSA conducts a local search; if the value of $fL$ is large, then the CSA conducts a global search. The values of $AP$ control crow intensity and diversity. The CSA generates crow positions randomly. For N crows in a solution space with dimension d, at iteration t, Equation (1) calculates each crow’s position in the solution space:

$$X_i^t=\{x_{i,1}^t,x_{i,2}^t,x_{i,j}^t,\cdots ,x_{i,d}^t\}\mathrm{for}i=1,2,3\cdots ,N,$$

(1)

where $x_{i,j}^t$ is the j-th potential position of crow i.

Our model considers that crow c may be followed by crow i, and crow c may or may not be aware of this pursuer. Equation (2) calculates the updated position of crow i at time $t+1$:

$$x_{i,j}^{t+1}=\left\{\begin{array}{cc}{x}_{i,j}^t+ran{d}_i\times fl\times (m_{c,j}^i-x_{i,j}^i)\hfill & \mathrm{if}ran{d}_i\ge AP,\hfill \\ \mathrm{random}\mathrm{position}\hfill & \mathrm{if}ran{d}_i<AP,\hfill \end{array}\right.$$

(2)

where $x_{i,j}^t$ is the location of crow i in dimension j at iteration t, $m_{i,j}^t$ is the location of the hiding place of crow i at iteration t. $fL$ is the flight length of crow i at iteration t, $AP$ is the awareness probability of crow c at iteration t, and $ran{d}_i$ is a random variable in the range [0, 1].

The CSA algorithm is outlined in Algorithm 2.

Algorithm 2 Standard crow search algorithm (CSA).
	Input:	Number of crows N, flight length $fL$, awareness probability $AP$
	Output:	The best solution
	Step:	Description:
	1.	Randomly initialize the position of all crows.
	2.	Initialize the memory of all crows.
	3.	Obtain the fitness value of all crows.
	4.	Obtain the memory of all crows.
	5.	Update the position of all crows according to Equation (2).
	6.	Repeat Steps 3 to 5 until the termination criterion is reached.
	7.	Output the best solution.

2.3. Simulated Annealing (SA)

The SA algorithm is a metaheuristic method proposed by Kirkpatrick et al. [41]. The concept underlying the SA algorithm is derived from the annealing of solids. SA is extensively applied to solve complex combinatorial problems, as it employs a perturbation search strategy. Some studies have applied SA to solve the PFSP [21,44,45,46,47]. The detailed procedure employed by the SA algorithm is shown in Algorithm 3.

Algorithm 3 A standard simulated annealing (SA) algorithm.
	Input:	Initial temperature T, cooling rate $\beta$, and frozen temperature $T_{end}$
	Output:	The best solution
	Step:	Description:
	1.	Initialize with a random solution.
	2.	Generate a new solution by using the perturbation method and computing a fitness function.
	3.	Calculate the energy change $\Delta E=f^{new}-f^{old}$.
	4.	If $\Delta E<0$, the new solution will be accepted and adopted as the best solution.
	5.	If $\Delta E>0$, calculate the probability of accepting the solution according to $r_p<(e^{-\Delta E/T})$.
	6.	Adjust temperature T using $T=T\ast \beta$.
	7.	Repeat Steps 2 to 6 until temperature T reaches the freezing point, $T_{end}$.
	8.	Finally, the best solution is found.
		In the above, $f^{new}$ is the new solution object value, $f^{old}$ is the current best solution value, and $r_p$ is a uniform random variable in the interval [0, 1].

2.4. Variable Neighborhood Search

VNS [23] is a local search strategy used to improve metaheuristic methods. VNS can be used to maintain the diversity of solutions throughout the metaheuristic process. Four common neighborhood perturbation operators are adopted in VNS: pair-swap, inversion, insertion, and displacement. These are described as follows::

• Pair-swap: Randomly select two different positions from the permutation sequence and swap these positions;
• Inversion: Invert the subsequence between two random positions from the permutation sequence;
• Insertion: Randomly select two different positions from the permutation sequence and insert the front position before the back position;
• Displacement: Randomly choose a position and a subsequence; then, insert the subsequence before the chosen position.

Figure 1 shows a simple example of each of these VNS local search operations. The VNS algorithm continues to run until a stopping condition is reached; this is the maximum number of iterations.

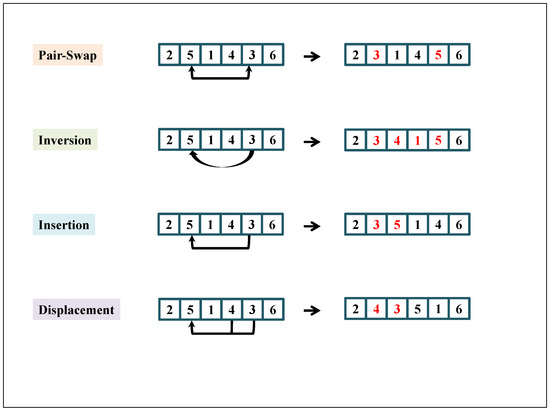
Figure 1. Examples of the different operations in the variable neighborhood search (VNS) local search algorithm.

3. Problem Definition

The PFSP requires running n jobs on a sequence of m machines, such that every job must be processed on all machines in the same order; the goal is to minimize the makespan. The detailed description is as follows: Given n jobs $\{1,2,\cdots ,n\}$, each job is processed on a series of s machines $\{1,2,\cdots ,s\}$ in a sequence defined by the job permutation. The job permutation $\pi =\{{\pi }_1,{\pi }_2,\cdots ,{\pi }_n\}$ is calculated by ordering the operations into a permutation. The processing time of job i on machine j is denoted by $p_{{\pi }_i,j}$, where each job is permitted to be processed on no more than one machine at a time and each machine can process only one job at a time. The completion time of job i on the machine is denoted by $C({\pi }_i,k)$. The objective function for PFSP is expressed in Equation (3).

$$\begin{array}{cc}C({\pi }_1,1)\hfill & =p_{{\pi }_{1,1}},\hfill \\ C({\pi }_i,1)\hfill & =C({\pi }_{i-1},1)+p_{{\pi }_i,1},i=2,3,\cdots ,n,\hfill \\ C(1,{\pi }_k)\hfill & =C({\pi }_1,k-1)+p_{{\pi }_1,k},k=2,3,\cdots ,s,\hfill \\ C({\pi }_j,k)\hfill & =\max \{C({\pi }_i,k-1),C({\pi }_{i-1},k)\}+p_{{\pi }_i,k},\hfill \\ & \mathrm{for}i=2,3,\cdots ,n;k=2,3,\cdots ,s.\hfill \end{array}$$

(3)

The optimal permutation ${\pi }^{\ast }$ from the set of all different permutations $F_m$ (i.e., the permutation with the minimum makespan) can be found by the optimization in Equation (4):

$$\begin{array}{cc}{\pi }^{\ast }=\underset{}{arg\; min}{C}^{\ast }(\pi ),\hfill & \forall \pi \in F_m,\hfill \\ C_{max}(\pi )=C({\pi }_n,s).\hfill \end{array}$$

(4)

4. Proposed Algorithm

4.1. Solution Representation

The CSA uses continuous number encoding for a swarm-based metaheuristic representation. Whereas typical metaheuristics generate permutations to solve NP-hard problems, the CSA does not directly generate permutations. In this study, we use a smallest position value (SPV) rule inspired by the random keys approach [48] to convert continuous numbers into a job sequence [49]. With the SPV rule, the position values of all crows are first sorted in ascending order, and then the job permutation is determined based on the results. Table 1 presents an example of the SPV transformation of continuous values into permutations of a job sequence. Assuming we have six jobs and six dimensions, the position values of the crows are presented in the second column as (1.35, −2,46, −1.52, 2.31, 0.52, and −1.68). Based on the SPV values, the smallest position value is −2.46; therefore, the first job order is two. The second smallest position value is −1.68; therefore, the second job order is six. Similarly, the ranking order values produce the job values and the output permutation is [2, 6, 3, 5, 1, 4].

Table 1. Example of the smallest position value (SPV) approach.

Dimension d	Position Value	Job Permutation
1	1.35	2
2	−2.46	6
3	−1.52	3
4	2.31	5
5	0.52	1
6	−1.68	4

4.2. Initial Population

The NEH algorithm is an efficient heuristic method for solving the PFSP. Thus, to guarantee that the initial population can receive a quality solution with high diversity, one of the crows uses an NEH-based algorithm to generate the job permutation, which is then mapped to the position values according to the SPV rule. Table 2 shows how the SPV is applied to transform the permutations of the job sequence into a continuous value. To limit the search space, Equation (5) is applied to the first crow population:

$$\begin{array}{ccc}\hfill x_{i,d}& =x_{min}+(x_{max}-x_{min})\ast r_i.\hfill & \hfill d=1,2,\dots ,n,\end{array}$$

(5)

where d is the quantity of jobs at the agent position and $x_{i,d}$ refers to the dth position value of crow i. Further, $r_i$ is a random variable uniformly distributed in the interval [0, 1]. $x_{min}=-5.0$ and $x_{max}=5.0$ are respectively the lower and upper bounds of the position or velocity values.

Table 2. Mapping a job permutation to position values.

Dimension d	Job Permutation from NEH Heuristic	Initial Value	Remapped Values
1	2	−1.02	1.31
2	6	0.45	−1.02
3	3	1.31	0.45
4	5	−0.76	2.87
5	1	2.87	0.56
6	4	0.56	−0.76

4.3. SA-VNS Local Search

The VNS procedure can be combined with other heuristic algorithms to ameliorate the solution quality [23]. Thus, in this study, the SA algorithm was combined with VNS for a local search after the CSA procedure. This improved the local search ability and avoided premature convergence. Incorporating the SA algorithm into the VNS process enables an appropriate balance between exploration and exploitation to be maintained at different temperatures.

4.4. The Proposed HCSA Algorithm

Figure 2 presents a flowchart of the hybrid crow search algorithm (HCSA). Initially, NEH-based algorithms are used to obtain a solution for one crow; the values for the remaining crows are generated randomly. The SPV rules and the evolutionary CSA are used to generate numerous possible solutions. The SPV rules and the evolutionary CSA are then used to randomly generate numerous possible solutions, and the system delivers the global best solution (out of all known possibilities) before the stopping criterion is met. The SA-VNS local search improves the quality of the global best solution obtained from the CSA. Finally, the approximate best permutation is obtained.

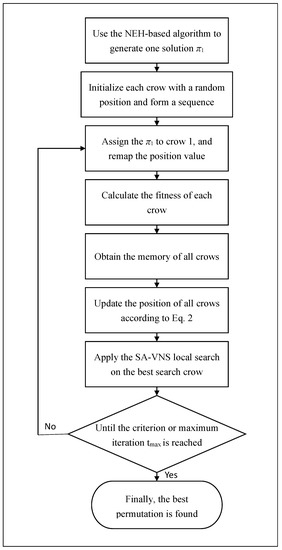
Figure 2. Proposed hybrid CSA (HCSA) for solving the permutation flow shop scheduling problem (PFSP).

5. Experimental Results

In this section, the performance of the proposed HCSA is presented.

5.1. Environment Setting

The proposed HCSA’s performance was evaluated by solving the PFSP benchmarks generated by Taillard [50], which comprise 12 instances ranging from 20 jobs with five machines (Ta01) to 500 jobs with 20 machines (Ta111), as shown in Table 3. All programs were implemented in Java and executed on a Windows 10 operating system running on a computer with an AMD Ryzen 3 1200 Quad-Core 3.10 GHz CPU, and 8 GB RAM.

Table 3. Taillard [50] benchmarks for the permutation flow shop scheduling problem (PFSP).

Problem	Jobs	Machines
ta01	20	5
ta11	20	10
ta21	20	20
ta31	50	5
ta41	50	10
ta51	50	20
ta61	100	5
ta71	100	10
ta81	100	20
ta91	200	10
ta101	200	20
ta111	500	20

5.2. Parameter Setting

Table 4 lists the parameter settings for all experiments. The performance of the CSA was assessed based on Equations (6) and (7):

$$\mathrm{ARPD}=\frac{{\sum }_{i=1}^R((\frac{S_i-UB}{UB})\times 100\%)}{\mathrm{R}},$$

(6)

$$\mathrm{BRPD}=\frac{{\sum }_{i=1}^R((\frac{S_{bst}-UB}{UB})\times 100\%)}{\mathrm{R}},$$

(7)

where ARPD is the average percentage relative deviation, BRPD is the best percentage relative deviation, $S_i$ is the average values of the makespan found by the algorithm, $S_{bst}$ is the best makespan found by the algorithm, $UB$ indicates the upper bound of the benchmark, and R is the number of independent runs.

Table 4. Parameter settings of the proposed algorithm.

Algorithm	Parameter	Value
CSA
	Number of crows	20
	Number of iterations $t_{max}$	1000
	Number of independent runs R	20
	Flight length $fL$	10
	Awareness probability $AP$	0.25
SA
	Initial temperature T	100
	cooling coefficient $\mathsf{\beta }$	0.99

5.3. Comparison of CSA Algorithms Incorporated with Variants of the NEH

To validate the effectiveness of each initialization approach, the CSA was combined with several variants of the NEH-based algorithm and their respective performance levels were compared. A new priority rule and a new tie-breaking rule based on the NEH [16] algorithm were used; elements included NEHD [17], NEHKK1 [18], NEHKK2 [19], CL [20], and NEHLJP1 [22]. The BRPD and ARPD values for the simulation of the CSA coupled with six initialization NEH algorithms are summarized in Table 5 and the values in bold font represent the algorithms that achieve superior performance.

Table 5. Comparison of different variants of initialization algorithms. ARPD: average percentage relative deviation; BRPD: best percentage relative deviation.

		NEH	NEHD	NEHKK1	NEHKK2	CL	NEHLJP1
Problem
ta01	BRPD	0.70	1.49	0.47	1.48	0.70	1.48
	ARPD	0.73	1.55	1.36	1.48	0.71	1.48
ta11	BRPD	2.52	2.84	2.14	2.46	2.72	2.66
	ARPD	3.28	3.66	4.79	3.73	4.08	3.12
ta21	BRPD	3.22	2.82	2.39	1.92	2.05	2.66
	ARPD	4.22	2.82	3.93	2.42	2.73	3.37
ta31	BRPD	0.18	0.00	1.02	0.18	0.18	0.18
	ARPD	0.18	0.39	1.98	0.21	0.25	0.18
ta41	BRPD	4.74	3.81	3.51	4.54	4.54	3.51
	ARPD	5.05	5.62	4.33	4.54	5.48	4.57
ta51	BRPD	3.45	5.61	4.52	4.55	4.50	4.16
	ARPD	3.65	7.20	5.21	4.96	4.71	4.38
ta61	BRPD	0.38	0.38	1.36	0.43	0.04	0.09
	ARPD	0.38	0.43	1.37	0.43	0.04	0.45
ta71	BRPD	1.06	1.87	0.88	0.92	0.74	0.88
	ARPD	1.19	2.10	1.06	0.94	1.14	0.98
ta81	BRPD	2.85	3.14	3.64	2.77	3.19	3.17
	ARPD	3.21	4.14	3.93	3.31	3.56	3.31
ta91	BRPD	0.74	0.20	0.72	0.52	0.68	0.75
	ARPD	0.75	0.49	0.72	0.61	0.68	0.75
ta101	BRPD	2.46	1.57	2.13	2.76	2.28	1.89
	ARPD	2.66	1.69	2.24	2.88	2.59	2.24
ta111	BRPD	1.47	1.59	1.54	1.22	1.52	1.15
	ARPD	1.79	1.69	1.70	1.43	1.77	1.38
Average	BRPD	1.98	2.11	2.03	1.98	1.93	1.88
	ARPD	2.26	2.65	2.72	2.25	2.31	2.18

The best BRPD and ARPD values of the tested NEH-based algorithms were 1.88 and 2.18, respectively. From the aforementioned simulation results, it can be concluded that the CSA combined with the NEHLJP1 heuristic is more effective than other NEH-based heuristic algorithms. In addition, the original NEH algorithm had better ARPD values than the NEHD and NEHKK1 variants. Therefore, we incorporated NEHLJP1 into the CSA algorithm as the initialization strategy. To present the previous experimental results more clearly, the data from Table 5 are depicted visually in Figure 3. The x-axis shows the different sizes of the benchmarks, and the y-axis shows the ARPD and BRPD values for each test function.

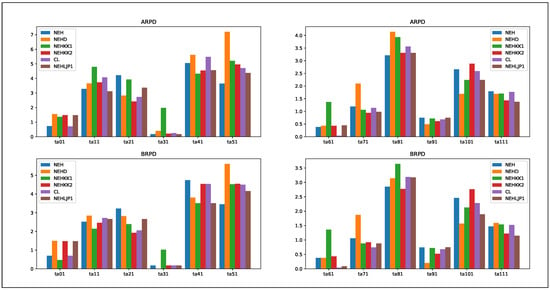
Figure 3. Comparison of the results for all different NEH-based algorithms.

5.4. Comparison of CSA Algorithms Incorporated with the SA-Based Local Search

NEHLJP1 combined with the CSA algorithm provided the best BRPD and ARPD values. In this section, we validate the effectiveness of the algorithm on the number of iterations in the SA local search. We compared two different iterations of the local search, 1000 and $jobs\times (jobs-1)$ [49], using the BRPD and ARPD values and the average computation time $t_{a}vg$, where $jobs$ indicates the number of jobs of the benchmark and the values in bold font represent the algorithms that achieve superior performance.

The computed BRPD and ARPD results are listed in Table 6 and Table 7. The $jobs\times (jobs-1)$ strategy achieved better BRPD and ARPD values for small jobs (0.54 and 0.69, respectively). However, the BRPD and ARPD values were almost the same for large jobs. Additionally, the computation times were almost identical for two different numbers of iterations. In summary, the $jobs\times (jobs-1)$ strategy achieved the most desirable BRPD and ARPD values for all benchmarks, specifically 0.61 and 0.81, respectively.

Table 6. Comparison of different iterations of the local search for small job sizes.

		1000	$\mathit{jobs}\times (\mathit{jobs}-1)$
Problem
ta01	BRPD	0.00	0.00
	ARPD	0.00	0.00
	$t_{avg}$	1.43	1.43
ta11	BRPD	0.00	0.00
	ARPD	0.06	0.00
	$t_{avg}$	1.67	1.65
ta21	BRPD	0.00	0.00
	ARPD	0.27	0.18
	$t_{avg}$	2.26	2.23
ta31	BRPD	0.00	0.00
	ARPD	0.00	0.00
	$t_{avg}$	3.08	3.21
ta41	BRPD	1.47	1.24
	ARPD	2.29	1.70
	$t_{avg}$	3.75	3.82
ta51	BRPD	2.18	1.95
	ARPD	2.42	2.25
	$t_{avg}$	5.22	5.31
Average	BRPD	0.61	0.54
	ARPD	0.84	0.69
	$t_{avg}$	2.90	2.94

Table 7. Comparison of different iterations of the local search for large job sizes.

		1000	$\mathit{jobs}\times (\mathit{jobs}-1)$
Problem
ta61	BRPD	0.00	0.00
	ARPD	0.02	0.02
	$t_{avg}$	6.02	6.22
ta71	BRPD	0.26	0.23
	ARPD	0.51	0.50
	$t_{avg}$	7.32	7.56
ta81	BRPD	1.72	1.59
	ARPD	2.11	2.10
	$t_{avg}$	10.28	10.32
ta91	BRPD	0.16	0.16
	ARPD	0.48	0.56
	$t_{avg}$	14.70	15.32
ta101	BRPD	1.08	1.26
	ARPD	1.41	1.39
	$t_{avg}$	19.88	20.79
ta111	BRPD	1.47	0.89
	ARPD	1.79	1.06
	$t_{avg}$	54.14	55.92
Average	BRPD	0.69	0.69
	ARPD	0.94	0.94
	$t_{avg}$	18.72	19.36

5.5. Comparison of Meta-Heuristic Algorithms

We compared the performance level of the HCSA with those of one GSA-based and two PSO-based algorithms, namely, MGELS [37], PSOVNS [49], and PSOMA [51], for 1000 iterations of the 12 Taillard benchmarks. The settings employed for HCSA are detailed in Table 4. MGELS is a GSA-based algorithm with an emulated local search algorithm. PSOVNS is an SPV-rule-based algorithm that combines PSO and VNS. PSOMA is an SPV-rule-based algorithm that combines PSO and NEH, and also adopts an SA-based local search.

As shown in Table 8 and the values in bold font represent the algorithms that achieve superior performance. In terms of the BRPD values, the HCSA was superior to the MGELS, PSOVNS, and PSOMA algorithms, except for ta081 (100*20). In terms of the ARPD values, the HCSA was better than the MGELS, PSOVNS, and PSOMA algorithms, except for ta081 (100*20) and ta091 (200*10). The average ARPD value from HCSA was 0.61%, in comparison to the values of 6.00%, 2.05%, and 0.90% obtained by MGELS, PSOVNS, and PSOMA, respectively. In addition, because MGELS does not apply any initialization algorithm or local search, its performance had significant differences from other algorithms for large benchmarks. For the local search, using an SA-based search with the metaheuristic algorithm achieved better results than not using SA. In summary, from the aforementioned simulation results, it can be concluded that HCSA is more effective than the MGELS, PSOVNS, and PSOMA metaheuristic algorithms. To present the previous experimental results more clearly, the data from Table 8 are depicted visually in Figure 4. The x-axis shows the different sizes of the benchmarks, and the y-axis shows the ARPD and BRPD values for each test function.

Table 8. Comparison tests of various meta-heuristic algorithms.

		HCSA	MGELS	PSOVNS	PSOMA
Problem
ta01	BRPD	0.00	1.48	0.23	0.00
	ARPD	0.00	2.45	1.63	0.00
ta11	BRPD	0.00	2.84	0.26	0.00
	ARPD	0.00	4.95	2.28	0.10
ta21	BRPD	0.00	2.84	0.74	0.00
	ARPD	0.18	4.14	1.77	0.20
ta31	BRPD	0.00	0.77	0.00	0.00
	ARPD	0.00	1.65	0.51	0.04
ta41	BRPD	1.24	8.42	1.61	1.61
	ARPD	1.70	8.82	1.75	2.43
ta51	BRPD	1.98	7.74	2.91	2.15
	ARPD	2.25	10.26	4.31	2.54
ta61	BRPD	0.00	0.52	0.00	0.00
	ARPD	0.02	1.10	0.02	0.11
ta71	BRPD	0.23	4.92	1.19	0.26
	ARPD	0.50	5.70	1.98	0.50
ta81	BRPD	1.59	9.38	2.33	1.29
	ARPD	2.10	10.51	3.82	1.62
ta91	BRPD	0.16	2.17	1.12	0.16
	ARPD	0.56	4.17	1.17	0.21
ta101	BRPD	1.26	8.50	1.96	1.45
	ARPD	1.39	9.47	3.03	1.53
ta111	BRPD	0.80	7.40	1.64	1.35
	ARPD	1.06	8.82	2.37	1.48
Average	BRPD	0.61	4.75	1.15	0.69
	ARPD	0.81	6.00	2.05	0.90

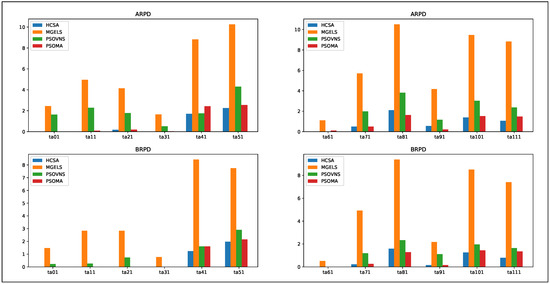
Figure 4. Comparison of the results for various metaheuristic algorithms.

6. Conclusions

This paper proposed an HCSA approach to solve the PFSP. The proposed HCSA adopts an SPV rule to convert the continuous position values to job permutations and incorporates an NEH-based heuristic algorithm for population initialization. It also adopts the SA-based VNS local search method to balance exploitation and exploration, and ultimately enhance the quality of the solution. Simulation results demonstrate that the proposed HCSA, which incorporates NEHLJP1 and an SA-based VNS local search, produced a better makespan for all benchmark datasets than other algorithms. In our future research, we hope to analyze the following four aspects of the HCSA: (1) applying the HCSA to large real-world problems, such as nurse scheduling, basketball tournament scheduling, automotive manufacturing, and the vehicle routing scheduling problem; (2) adapting the Lévy searching strategy to improve the local search; (3) using graph structures and neighborhood structures to speed up the local search; and (4) implementing a new NEH-based heuristic algorithm and solving the larger benchmarks.